Đề cương học kỳ 1 Toán 12 năm 2021 – 2022 trường THPT Nguyễn Du – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HỒ CHÍ MINH

TRƯỜNG THPT NGUYỄN DU

ĐỀ CƯƠNG HỌC KỲ I

TOÁN 12TOÁN 12

NĂM HỌC:

2021 -2022-2022

Lớp:. . . . . . . . .

Họ và tên:. . . . . . . . . . . . . . . . . . . . . . . . . . .

Lưu hành nội bộ

S

A

B

O

H

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 1

§1. GIỚI THIỆU BỘ MÔN

--------------------------------------------------------------------------------------------------------------------------------

Chương

1

ỨNG DỤNG ĐẠO HÀM ĐỂ

KHẢO SÁT VÀ VẼ ĐỒ THỊ

CỦA HÀM SỐ

1. GIỚI THIỆU BỘ MÔN

2. SỰ ĐỒNG BIẾN - NGHỊCH BIẾN

CỦA HÀM SỐ

3. CỰC TRỊ CỦA HÀM SỐ

4. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ

NHỎ NHẤT CỦA HÀM SỐ

5. ĐƯỜNG TIỆM CẬN

6. KHẢO SÁT SỰ BIẾN THIÊN VÀ

VẼ ĐỒ THỊ CỦA HÀM SỐ

7. MỘT SỐ CHUYÊN ĐỀ

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 2

§2. SỰ ĐỒNG BIẾN – NGHỊCH BIẾN CỦA HÀM SỐ

A. TÓM TẮT LÝ THUYẾT

1. Định nghĩa tính đơn điệu:

Cho hàm số

( )y f x

xác định trên tập

.K

 Hàm số

( )y f x

đồng biến (tăng) trên

K

nếu

1 2

, ,x x K

 

1 2 1 2

( ) ( )x x f x f x

   .

 Hàm số

( )y f x

nghịch biến (giảm) trên

K

nếu

1 2

, ,x x K

 

1 2 1 2

( ) ( )x x f x f x

   .

 Hàm số đồng biến hoặc nghịch biến trên

K

thì được gọi là đơn điệu trên

K

.

 Nhận xét: Trong chương trình lớp 10, để xét sự đồng biến, nghịch biến của hàm

( )f x

, ta hay

dùng tỉ số :

1 2

( ) ( )

,

f x f x

T x x

x x



  



và

1 2

,

x x K

. Cụ thể là:

 Nếu

0

T



thì hàm

( )f x

đồng biến trên

.K

(Tức là

1 2

( ) ( )f x f x

 cùng dấu với

1 2

x x

).

 Nếu

0

T



thì hàm

( )f x

nghịch biến trên

.K

(Tức là

1 2

( ) ( )f x f x

 trái dấu với

1 2

x x

).

2. Định lí (tính đơn điệu và dấu của đạo hàm):

Cho hàm số

( )y f x

có đạo hàm trên

.K

 Nếu

( ) 0

f x





với mọi

x K

thì hàm

( )f x

đồng biến trên

K

.

 Nếu

( ) 0

f x





với mọi

x K

thì hàm

( )f x

nghịch biến trên

K

.

 Chú ý:

 Định lí trên được mở rộng với

( ) 0

f x





(hay

( ) 0

f x





) trong trường hợp

( ) 0

f x





tại một

số hữu hạn điểm; khi đó kết luận hàm số đồng biến (hay nghịch biến) vẫn đúng.

 Nếu hàm số

( )y f x

liên tục trên

 

;a b

và có đạo hàm

( ) 0, ( ; )f x x a b



  

thì hàm số

đồng biến trên

 

;a b

. (Tương tự cho trường hợp hàm số nghịch biến trên

 

;a b

).

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 3

B. CÁC DẠNG TOÁN THƯỜNG GẶP

— Bài toán. Tìm các khoảng đơn điệu ( khảo sát chiều biến thiên) của hàm số

 

y f x

.

— Phương pháp:

 Bước 1. Tìm tập xác định

D

của hàm số. Tính đạo hàm

 

' '

y f x

.

 Bước 2. Tìm các điểm tại đó

 

 

' '

0

y f x hoặc

 

'

f x

không xác định.

 Bước 3. Sắp xếp các điểm theo thứ tự tăng dần và lập bảng biến thiên ( xét dấu

'

y

).

 Bước 4. Từ bảng biến thiên, kết luận:

'

0y  

đồng biến và

'

0y  

nghịch biến.

CÁC VÍ DỤ

Ví dụ 1: Xét sự đồng biến , nghịch biến của các hàm số sau:

a)

3 2

2 – 3 1

y x x

 

b)

4 2

– 2 – 5

y x x

c)

2 3

2

x

y

x





 

d)

2

y x x 

--------------------------------------------------------------------------------------------------------------------------------

Dạng 1:

Tìm các khoảng đơn điệu của hàm số

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 4

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Cho hàm số

3 2

3 4

y x x

   

.Mệnh đề nào dưới đây đúng?

Ⓐ Hàm số đồng biến trên khoảng

 

0;



. Ⓑ Hàm số nghịch biến trên khoảng

 

2;0



.

 

2;0



. Ⓓ Hàm số đồng biến trên khoảng

 

; 2 

.

Câu 2. Xét tính đơn điệu của hàm số

2 1

1

x

y

x







.Ta có:

Ví dụ 2. Hàm số

3 2

3 9y x x x   

nghịch biến trên khoảng nào dưới đây ?

Ⓐ

 

1;3

 . Ⓑ

 

3;



.

Ⓒ

 

2;4

. Ⓓ

 

;1

.

Lời giải :....................................................................

......................................................................................

Ví dụ 3. Các khoảng nghịch biến của hàm số

4 2

2 4

y x x

   

là

Ⓐ

( 1;0)

và

(1; ).

Ⓑ

( ;1)

và

(1; ).

Ⓒ

( 1;0)

và

(0;1).

Ⓓ

( ; 1) 

và

(0;1).

Lời giải:.....................................................................

......................................................................................

Ví dụ 4. Chọn mệnh đề đúng về hàm số

2 1

2

x

y

x







.

Ⓐ Hàm số nghịch biến trên từng khoảng xác

định của nó.

Ⓑ Hàm số đồng biến trên tập xác định của nó.

của nó.

Ⓓ Hàm số nghịch biến trên tập xác định của

nó.

Lời giải:.....................................................................

......................................................................................

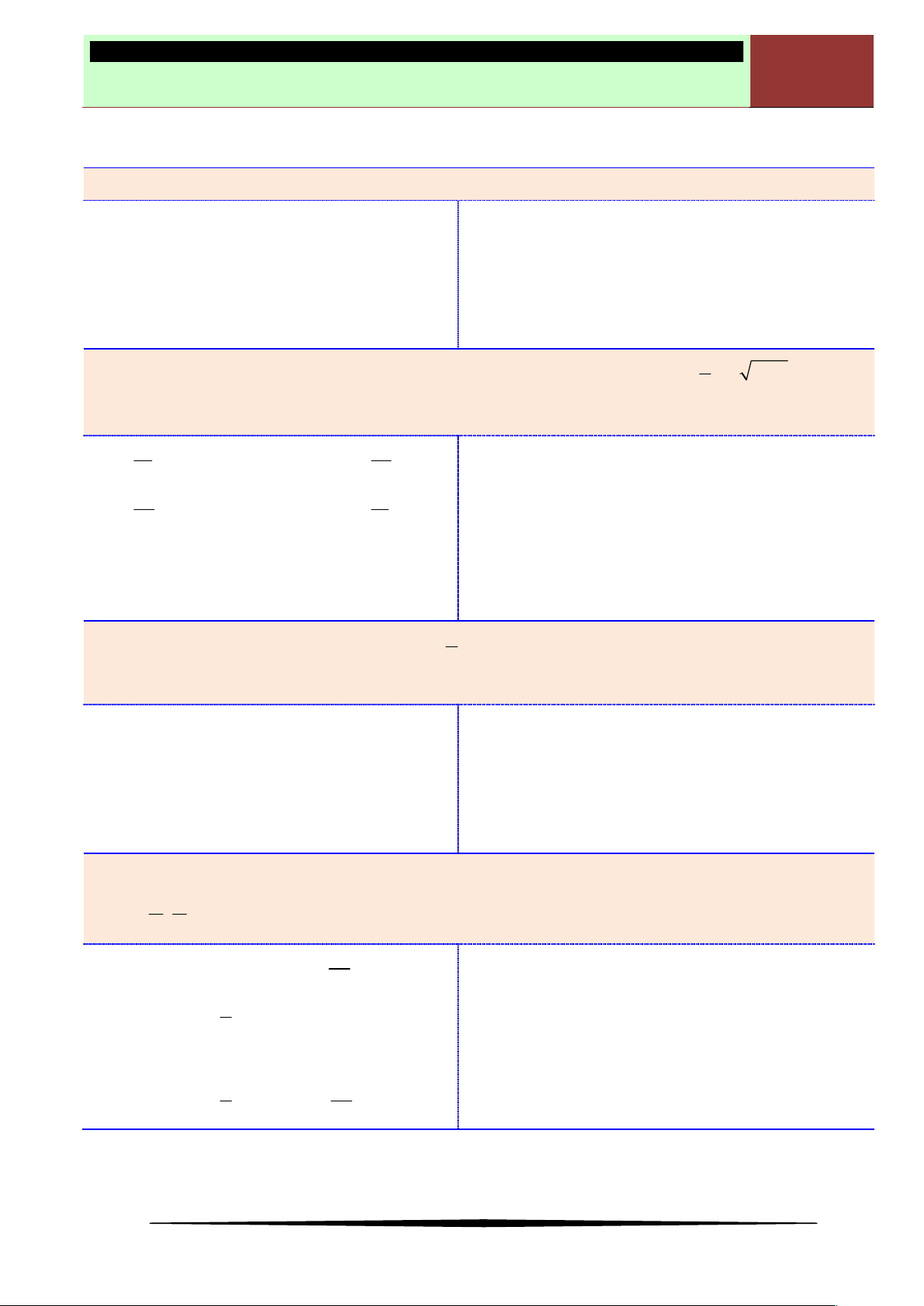
Ví dụ 5. Cho hàm số

2

3

y x x 

.Hàm số đồng biến trên khoảng nào?

Ⓐ

3

0;

2

 

 

 

. Ⓑ

 

0;3

.

Ⓒ

3

;3

2

 

 

 

. Ⓓ

3

;

2

 



 

 

.

Lời giải:.....................................................................

......................................................................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 5

Ⓐ Hàm số nghịch biến trên tập xác định

 

\ 1

D 



.

Ⓑ Hàm số đồng biến trên các khoảng

   

;1 1;

  

.

 

;

 

.

Ⓓ Hàm số nghịch biến trên các khoảng

 

;1

và

 

1;



.

Câu 3. Cho hàm số

2

3

x

y

x







.Mệnh đề nào sau đây đúng?

Ⓐ Hàm số nghịch biến trên khoảng

 

;

 

.

Ⓑ Hàm số nghịch biến trên từng khoảng xác định.

Ⓓ Hàm số đồng biến trên khoảng

 

;

 

.

Câu 4. Hàm số

3 2

3 5

y x x

  

đồng biến trên khoảng

Ⓐ

 

0;2 .

Ⓑ

 

0;



. Ⓒ

 

;2



. Ⓓ

 

;0



và

 

2;



.

Câu 5. Hàm số

3

3 2y x x   

nghịch biến trên khoảng

Ⓐ

   

; 1 1; .   

Ⓑ

 

1;



. Ⓒ

 

1; . 

. Ⓓ

 

1;1 .



Câu 6. Cho hàm số

3 2

2 6 6 1y x x x   

.Mệnh đề nào dưới đây sai ?

Ⓐ Hàm số đã cho đồng biến trên khoảng

 

; . 

Ⓑ Hàm số đã cho nghịch biến trên khoảng

 

; . 

 

; 2 

hàm số đã cho đồng biến.

Ⓓ Trên khoảng

 

2;



hàm số đã cho đồng biến.

Câu 7. Hàm số nào sau đây nghịch biến trên khoảng

 

; . 

Ⓐ

3 2

3y x x

  . Ⓑ

3 2

3 3 2

y x x x

    

.

Ⓒ

3

3 1.

y x x

   

Ⓓ

3

2018.

y x 

Câu 8. Cho hàm số

4 2

2y x x

  .Mệnh đề nào dưới đây đúng?

Ⓐ Hàm số đã cho đồng biến trên khoảng

 

1;1



.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 6

Ⓑ Hàm số đã cho nghịch biến trên khoảng

 

; 2 

.

 

; 2 

.

Ⓓ Hàm số đã cho nghịch biến trên khoảng

 

1;1



.

Câu 9. Hỏi hàm số

4 2

2 2

y x x

   

nghịch biến trong khoảng nào trong các khoảng sau.

Ⓐ

 

3; 2 

. Ⓑ

 

2; 1 

. Ⓒ

 

0;1

Ⓓ

 

1;2

Câu 10. Cho hàm số

4 2

4 3

y x x

  

.Mệnh đề nào sau đây là đúng?

Ⓐ Hàm số đã cho nghịch biến trên khoảng

 

;

 

.

Ⓑ Hàm số đã cho đồng biến trên khoảng

 

0;



.

 

;0



và đồng biến trên khoảng

 

0;



.

Ⓓ Hàm số đã cho đồng biến trên khoảng

 

;0



và nghịch biến trên khoảng

 

0;



.

Câu 11. Cho hàm số

2 1

1

x

y

x







.Mệnh đề nào dưới đây đúng?

Ⓐ Hàm số đồng biến trên các khoảng

 

; 1 

và

 

1;

 

.

Ⓑ Hàm số nghịch biến trên các khoảng

 

; 1 

và

 

1;

 

.

 

;

 

.

Ⓓ Hàm số đã cho đồng biến trên các khoảng

 

; 1 

và

 

1;



,nghịch biến trên khoảng

 

1;1



.

Câu 12. Cho hàm số

5

2

x

y

x







.Mệnh đề nào đúng?

Ⓐ Hàm số nghịch biến trên mỗi khoảng

 

; 2 

và

 

2;

 

.

Ⓑ Hàm số đồng biến trên mỗi khoảng

 

; 2 

và

 

2;

 

.

 

;5



.

Ⓓ Hàm số nghịch biến trên

 

\ 2

.

Câu 13. Hàm số

2

1

mx m

y

x

 





với

m

là tham số.Mệnh đề nào đúng?

Ⓐ Hàm số đã cho đồng biến trên

 

\ 1

.

Ⓑ Hàm số đã cho nghịch biến trên khoảng

 

;

 

.

Ⓓ Hàm số đã cho đồng biến trên các khoảng mà nó xác định.

Câu 14. Hàm số nào đưới đây đồng biến trên

 

;

 

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 7

Ⓐ

3

3 3 2

y x x

  

. Ⓑ

3

2 5 1y x x  

. Ⓒ

4 2

3y x x

  . Ⓓ

2

1

x

y

x







.

Câu 15. Hàm số nào đưới đây nghịch biến trên

 

;

 

.

Ⓐ

1

y

x



. Ⓑ

2

1

x

y

x







.

Ⓒ

3

3 1y x x   

. Ⓓ

3 2

4 1y x x x    

.

Câu 16. Cho hàm số

2

y x

x

  

.Khẳng định nào sau đây Đúng ?

Ⓐ Hàm số đã cho đồng biến trên khoảng

 

;0



.

Ⓑ Hàm số đã cho nghịch biến trên khoảng

 

;

 

.

 

0;



.

Ⓓ Hàm số đã cho nghịch biến trên các khoảng

 

;0



và

 

0;



.

Câu 17. Hàm số

2

1

y

x





nghịch biến trên khoảng nào dưới đây ?

Ⓐ

 

1;1



. Ⓑ

 

;

 

. Ⓒ

 

0;



. Ⓓ

 

;0



.

Câu 18. Tìm tất cả các khoảng nghịch biến của hàm số

2

2 2

1

x x

y

x

 





?

Ⓐ

 

; 1 

và

 

1;

 

. Ⓑ

 

2;0



.

Ⓒ

 

2; 1 

và

 

1;0



. Ⓓ

 

; 2 

và

 

0;



.

Câu 19. Tìm tất cả các khoảng đồng biến của hàm số

2

1

x

y

x





?

Ⓐ

 

1;1



. Ⓑ

 

0;



.

Ⓒ

 

; 1 

và

 

1;



. Ⓓ

 

;

 

.

Câu 20. Hàm số

2

24

y x 

nghịch biến trên khoảng nào trong các khoảng sau đây?

Ⓐ

 

5;0 .



Ⓑ

 

0;5 .

Ⓒ

 

;0 .



Ⓓ

 

0; . 

Câu 21. Cho hàm số

2

6 5.

y x x

  

Mệnh đề nào sau đây là đúng?

Ⓐ Hàm số đã cho đồng biến trên khoảng

 

5; . 

Ⓑ Hàm số đã cho đồng biến trên khoảng

 

3; . 

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 8

 

;1 .



Ⓓ Hàm số đã cho nghịch biến trên khoảng

 

;3 .



Câu 22. Hàm số

2

y x x 

nghịch biến trên khoảng nào dưới đây?

Ⓐ

 

;1 .



Ⓑ

 

1;2 .

Ⓒ

 

1; . 

Ⓓ

 

0;1 .

Câu 23. Cho hàm số

2

1.

y x

 

Mệnh đề nào dưới đây đúng?

Ⓐ Hàm số đã cho đồng biến trên khoảng

 

0; . 

Ⓑ Hàm số đã cho đồng biến trên khoảng

 

; .  

 

1; . 

Ⓓ Hàm số đã cho nghịch biến trên khoảng

 

;0 .



Câu 24. Tìm tất cả các khoảng đồng biến của hàm số

2 2020?

y x x  

Ⓐ

 

0;1 .

Ⓑ

1

0; .

4

 

 

 

Ⓒ

1

; .

4

 

 

 

 

Ⓓ

 

1; . 

Câu 25. Cho hàm số

2

2 .y x x x  

Hỏi hàm số nghịch biến trên khoảng nào sau đây?

Ⓐ

 

0;1 .

Ⓑ

 

;1 .



Ⓒ

 

1; . 

Ⓓ

 

1;2 .

CÁC VÍ DỤ

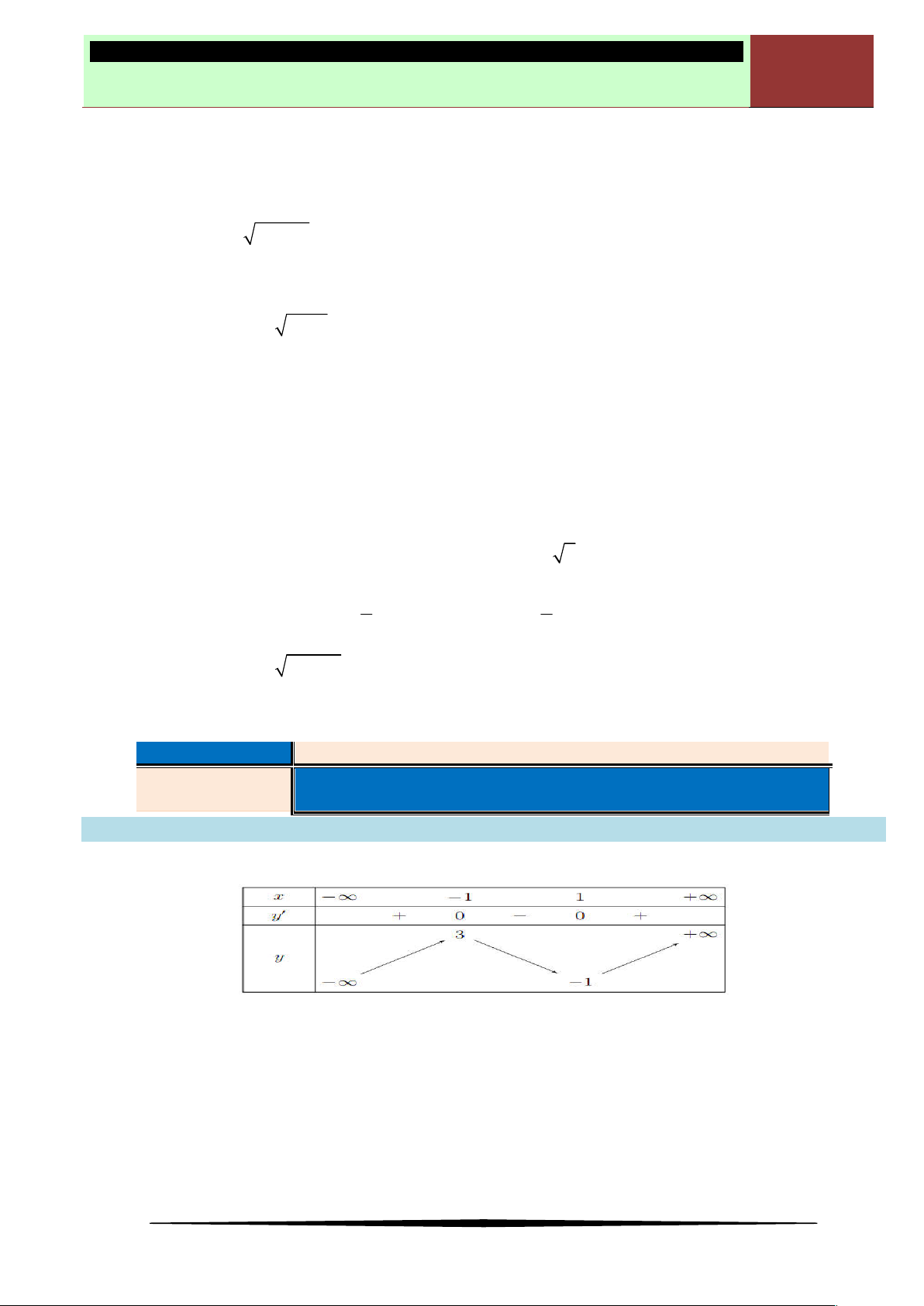
Ví dụ 1. Cho hàm số

 

y f x



có bảng biến thiên như sau:

Mệnh đề nào dưới đây đúng?

Ⓐ Hàm số nghịch biến trên khoảng

 

1; 3



. Ⓑ Hàm số đồng biến trên khoảng

 

;1

.

 

1;1



. Ⓓ Hàm số đồng biến trên khoảng

 

1;

  

.

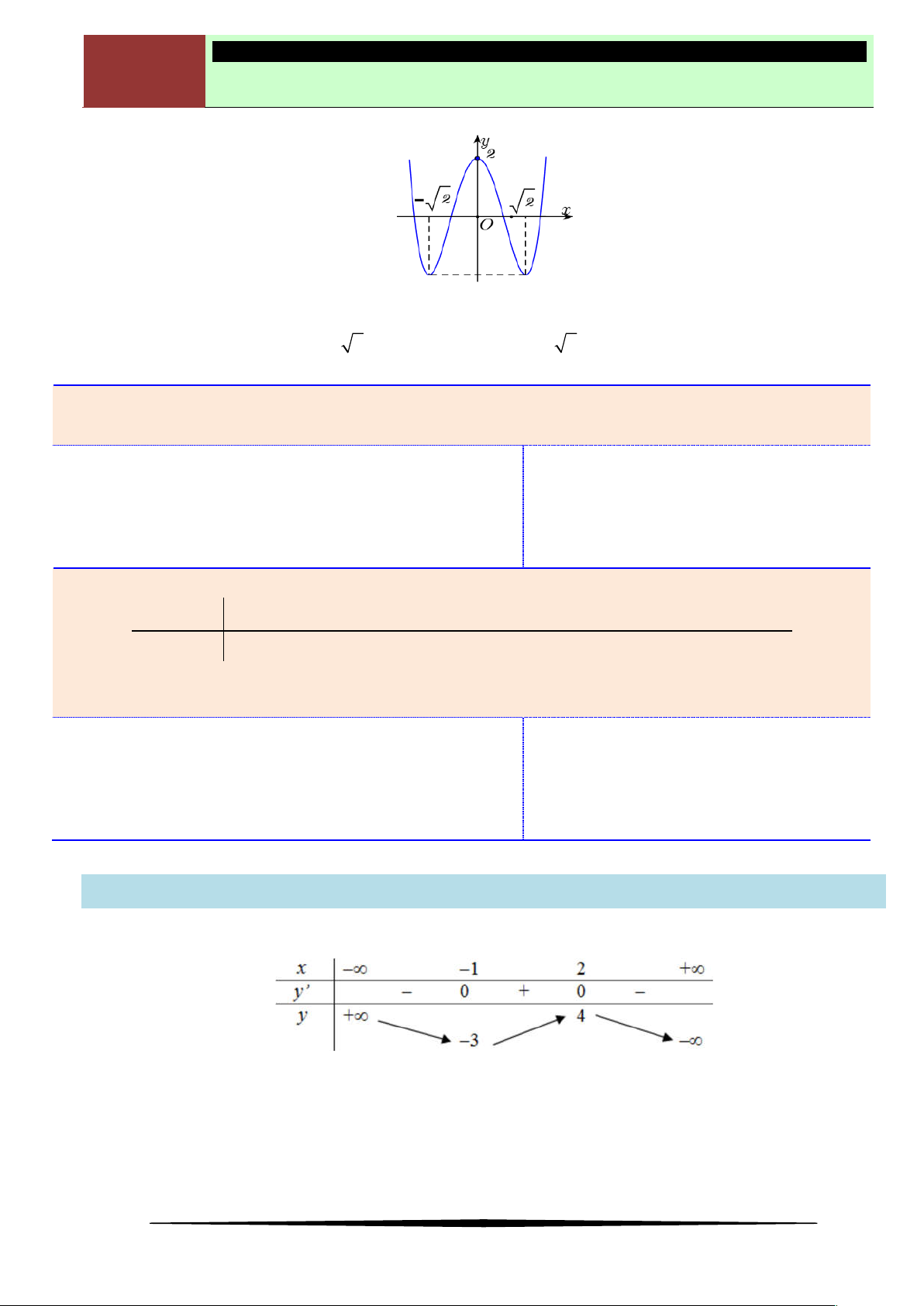
Ví dụ 2. Cho hàm số

 

y f x



có đồ thị như hình vẽ.

Dạng 2:

Dựa vào bảng biến thiên hoặc đồ thị để kết luận sự biến thiên của

hàm số

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 9

Hàm số nghịch biến trên khoảng nào dưới đây?

Ⓐ

 

2;2

. Ⓑ

 

2; . Ⓒ

 

0; 2 . Ⓓ

 

;0

.

Ví dụ 3. Cho hàm số

 

f x

có đạo hàm trên



là

   

2

1f x x x



 

.Hàm số đã cho đồng biến trên

khoảng:

Ⓐ

 

1;

. Ⓑ

 

; 

. Ⓒ

 

0;1

. Ⓓ

 

;1

.

Lời giải :....................................................................

......................................................................................

Ví dụ 4. Cho hàm số

 

xf

.Hàm số

 

xfy





có bảng xét dấu như sau:

x



2

1

3



( )f x





0



0



0



Hàm số

 

xxfy 2

2

 nghịch biến trên khoảng nào dưới đây?

Ⓐ

 

0;1

. Ⓑ

 

2; 1 

.

Ⓒ

 

2;1

. Ⓓ

 

4; 3 

.

Lời giải :....................................................................

......................................................................................

BÀI TẬP VỀ NHÀ

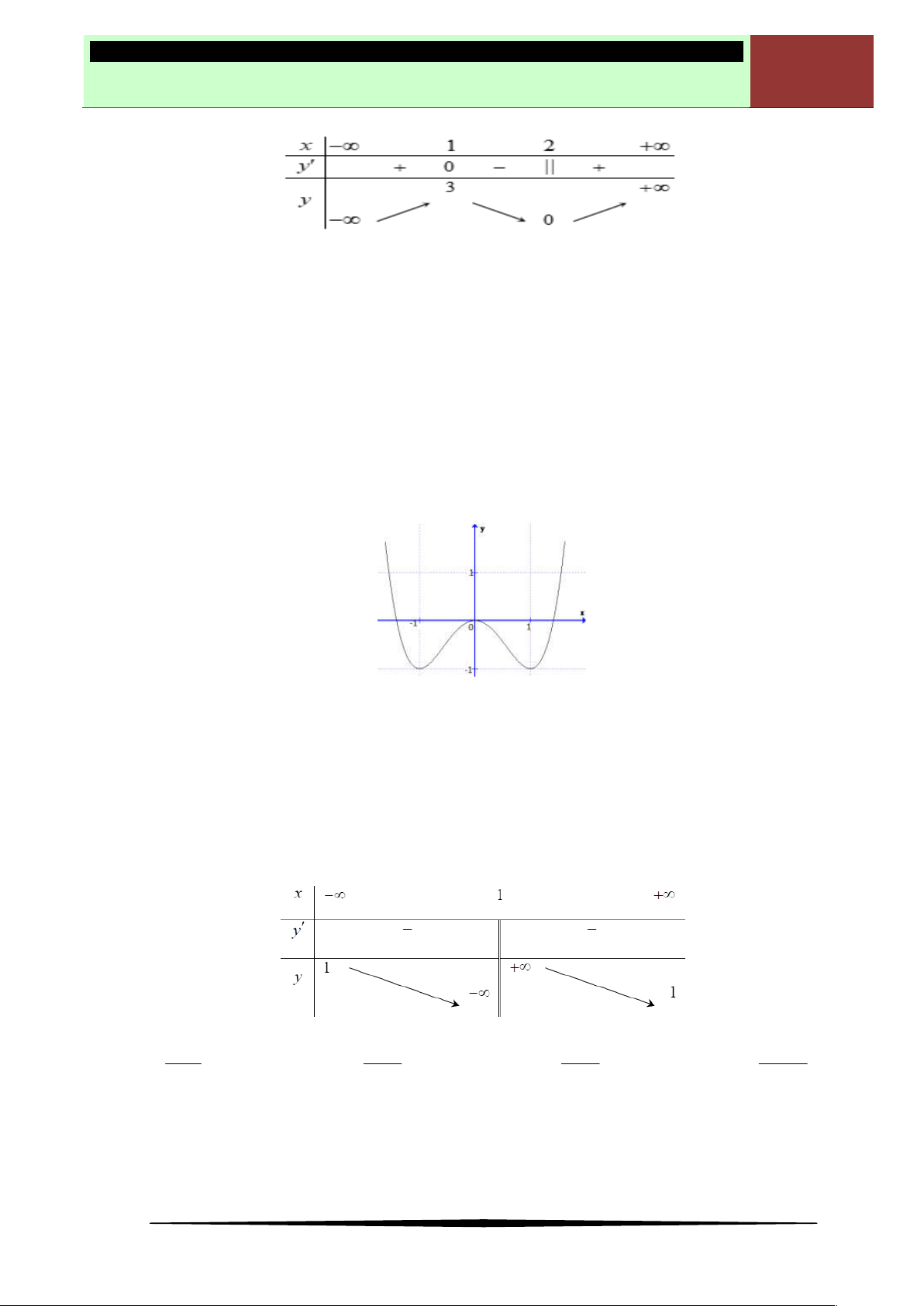
Câu 1. Cho hàm số

 

y f x

có bảng biến thiên như sau:

Hàm số

 

y f x

đồng biến trên khoảng nào dưới đây?

Ⓐ

 

1;2

. Ⓑ

 

; 1 

. Ⓒ

 

2; 

. Ⓓ

 

3;4

.

Câu 2. Cho hàm số

 

y f x

có bảng biến thiên như hình vẽ bên.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 10

Mệnh đề nào sau đây là sai?

Ⓐ Hàm số đã cho đồng biến trên khoảng

 

;1

.

Ⓑ Hàm số đã cho đồng biến trên khoảng

 

2;

 

.

 

3;

 

.

Ⓓ Hàm số đã cho nghịch biến trên khoảng

 

0;3

.

Câu 3. Cho đồ thị hàm số như hình vẽ.

Mệnh đề nào dưới đây đúng ?

Ⓐ Hàm số đồng biến trên

 

1;

 

. Ⓑ Hàm số nghịch biến trên

 

; 1 

.

 

1;



. Ⓓ Hàm số luôn đồng biến trên



.

Câu 4. Cho bảng biến thiên như hình vẽ bên.Hỏi đây là bảng biến thiên của hàm số nào trong các hàm số

sau?

Ⓐ

3

1

x

y

x







. Ⓑ

2

1

x

y

x







. Ⓒ

2

1

x

y

x







. Ⓓ

2

1

x

y

x

 





.

Câu 5. Cho hàm số

 

y f x



có đạo hàm

   

2 ,y f x x x x



    

.Hàm số

 

y f x



nghịch biến

trên khoảng nào dưới đây?

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 11

Ⓐ

 

0;2

Ⓑ

 

2;



Ⓒ

 

0;



Ⓓ

 

;0



Câu 6. Cho hàm số

 

y f x



liên tục trên



và có đạo hàm

      

2018 2019

2 1 2 .

f x x x x



   

Khẳng

định nào sau đây đúng?

Ⓐ Hàm số đạt cực đại tại điểm

1x 

và đạt cực tiểu tại các điểm

2

x

 

.

Ⓑ Hàm số đồng biến trên mỗi khoảng

 

1;2

và

 

2;

 

.

Ⓓ Hàm số nghịch biến trên khoảng

 

2;2



.

Câu 7. Cho

 

y f x



có đạo hàm

 

2

' 5 6,f x x x x

     

.Hàm số

 

5

y f x

 

nghịch biến trên

khoảng nào?

Ⓐ

 

;2



và

 

3;



. Ⓑ

 

3;



.

Ⓒ

 

2;



. Ⓓ

 

2;3

.

Câu 8. Cho

K

là một khoảng hoặc nữa khoảng hoặc một đoạn.Hàm số

 

y f

x

liên tục và xác định trên

K

.Mệnh đề nào không đúng?

Ⓐ Nếu hàm số

 

y f

x

đồng biến trên

K

thì

 

0,



  f x K

x

.

Ⓑ Nếu

 

0,



  f x K

x

thì hàm số

 

y f

x

đồng biến trên

K

.

 

0,



  f x K

x

thì hàm số

 

y f

x

không đổi trên

K

.

Ⓓ Nếu hàm số

 

y f

x

là hàm số hằng trên

K

thì

 

0,



  f x K

x

.

Câu 9. Cho hàm số

 

f x

đồng biến trên tập số thực



,mệnh đề nào sau đây là đúng?

Ⓐ Với mọi

   

1 2 1 2

,

x x f x f x

  



. Ⓑ Với mọi

   

1 2 1 2

x x f x f x

   



.

   

1 2 1 2

,

x x f x f x

  



. Ⓓ Với mọi

   

1 2 1 2

x x f x f x

   



.

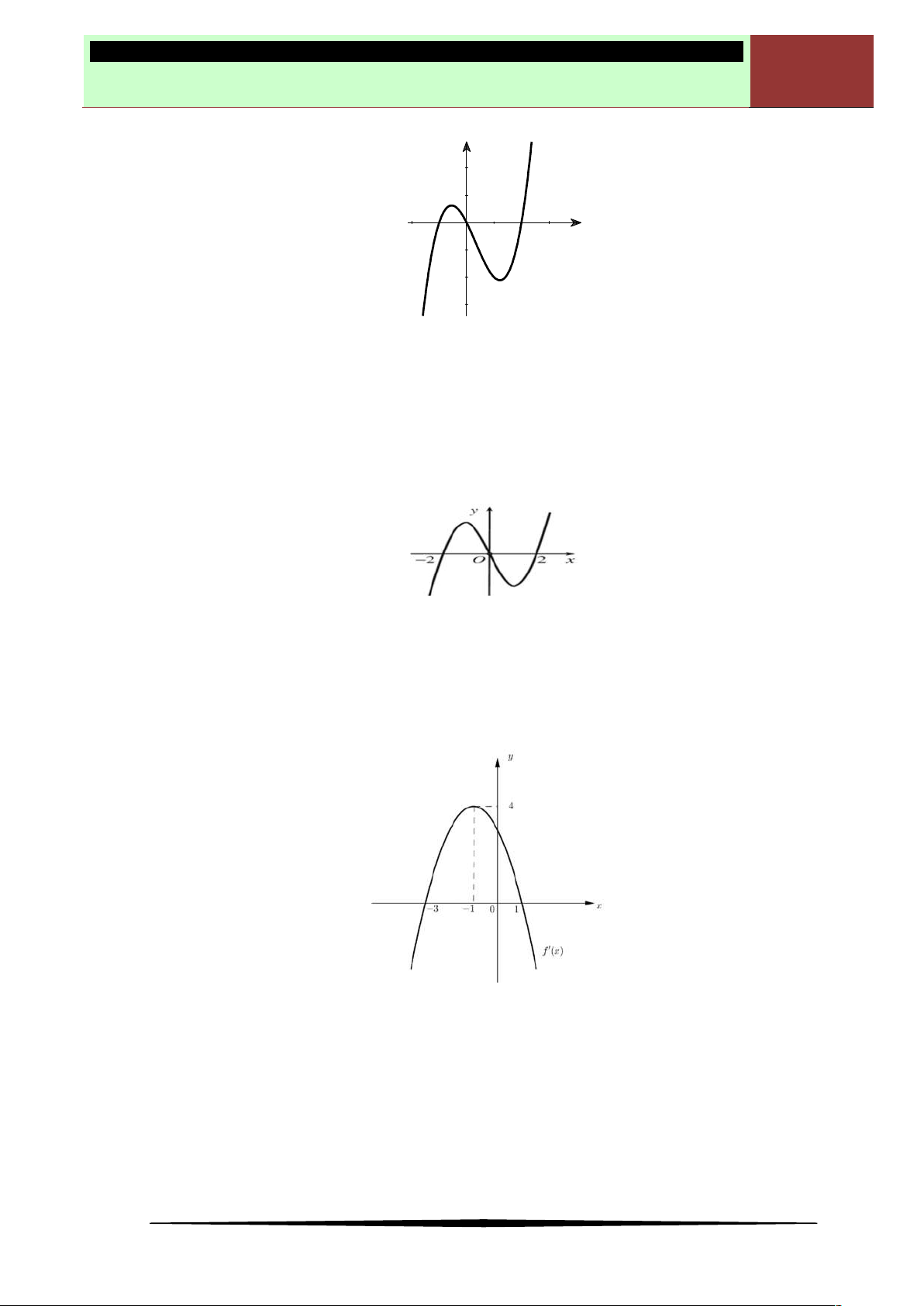
Câu 10. Cho hàm số

 

y f x



có đồ thị hàm số

 

'y f x



như hình vẽ bên.Khẳng định nào sau đây đúng

về hàm số

 

y f x



?

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 12

Ⓐ Hàm số đồng biến trên khoảng

 

1; 

. Ⓑ Hàm số đồng biến trên khoảng

 

1 0;

.

 

1 2;

. Ⓓ Hàm số nghịch biến trên khoảng

 

0;

.

Câu 11. Cho hàm số

( )f x

xác định trên



và có đồ thị hàm số

 

y f x





là đường cong trong hình

bên.Mệnh đề nào dưới đây đúng?

Ⓐ Hàm số

( )y f x

đồng biến trên

 

1;2

. Ⓑ Hàm số

( )y f x

đồng biến trên

 

2;1

.

( )y f x

nghịch biến trên

 

1;1

. Ⓓ Hàm số

( )y f x

nghịch biến trên

 

0;2

.

Câu 12. Cho hàm số

 

y f x

có đồ thị

 

f x



là đường cong như hình vẽ bên.Tìm khẳng định đúng.

Ⓐ

 

f x

đồng biến trên

 

2;0

. Ⓑ

 

f x

nghịch biến trên

 

0; 

.

Ⓒ

 

f x

đồng biến trên

 

;3

. Ⓓ

 

f x

nghịch biến trên

 

3; 2 

.

Câu 13. Cho hàm số

 

y f x xác định,liên tục trên

R

và có đạo hàm

 

f x



.Biết rằng

 

f x



có đồ thị

như hình vẽ bên.Mệnh đề nào sau đây đúng?

y

=

f'x

x

y

-1

2

O

1

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 13

Ⓐ Hàm số

 

y f x



đồng biến trên khoảng

 

2;0



.

Ⓑ Hàm số

 

y f x



nghịch biến trên khoảng

 

0;



.

 

y f x



đồng biến trên khoảng

 

;3



.

Ⓓ Hàm số

 

y f x



nghịch biến trên khoảng

 

3; 2 

.

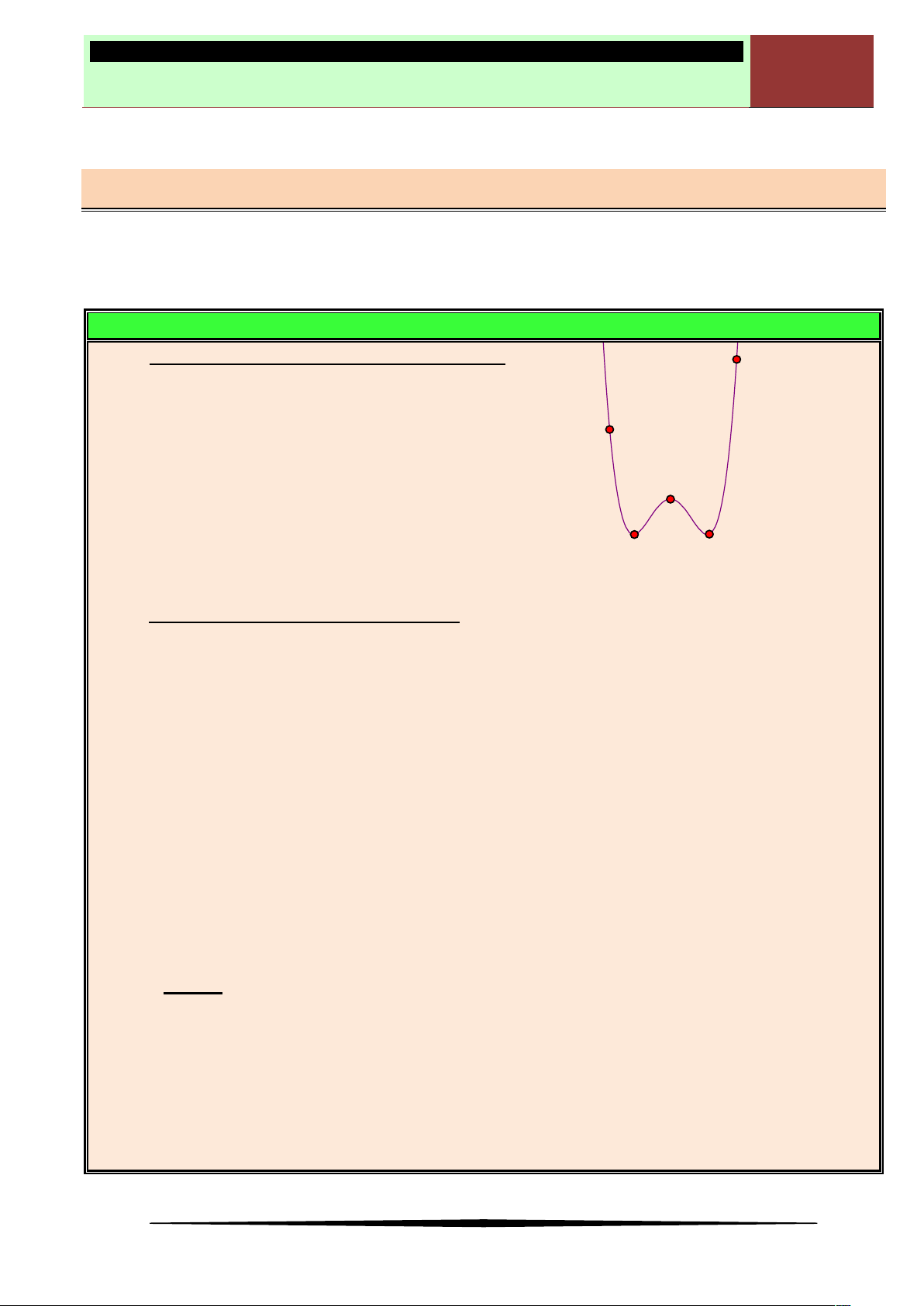
Câu 14. Hàm số

 

y f x



có đồ thị như hình vẽ bên dưới

Hàm số

 

y f x

  đồng biến trên khoảng

Ⓐ

 

2;

 

. Ⓑ

 

;1

. Ⓒ

 

;0



. Ⓓ

 

1;

 

.

Câu 15. Cho hàm số

 

y f x



xác định trên



và có đạo hàm

 

'y f x



thỏa mãn

      

' 1 2 2021

f x x x g x   

trong đó

 

0, .

g x x

  

Hàm số

 

1 2021 2020

y f x x   

nghịch biến trên khoảng nào?

Ⓐ

 

0;3

. Ⓑ

 

;3



. Ⓒ

 

1;



. Ⓓ

 

3;



.

Câu 16. Cho hàm số

 

y f x



có đạo hàm liên tục trên



và

     

2 1 . 1

f x x x g x



  

trong đó

 

0,g x x

  

.Hàm số

 

2

y f x x  

đồng biến trên khoảng nào trong các khoảng sau?

Ⓐ

5

2;

2

 

 

 

. Ⓑ

 

; 1



. Ⓒ

3

1;

2

 

 

 

. Ⓓ

 

0; 1

.

O

x

y

2

3

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 14

§3. CỰC TRỊ CỦA HÀM SỐ

A. TÓM TẮT LÝ THUYẾT

1. Những khái niệm cơ bản về cực trị:

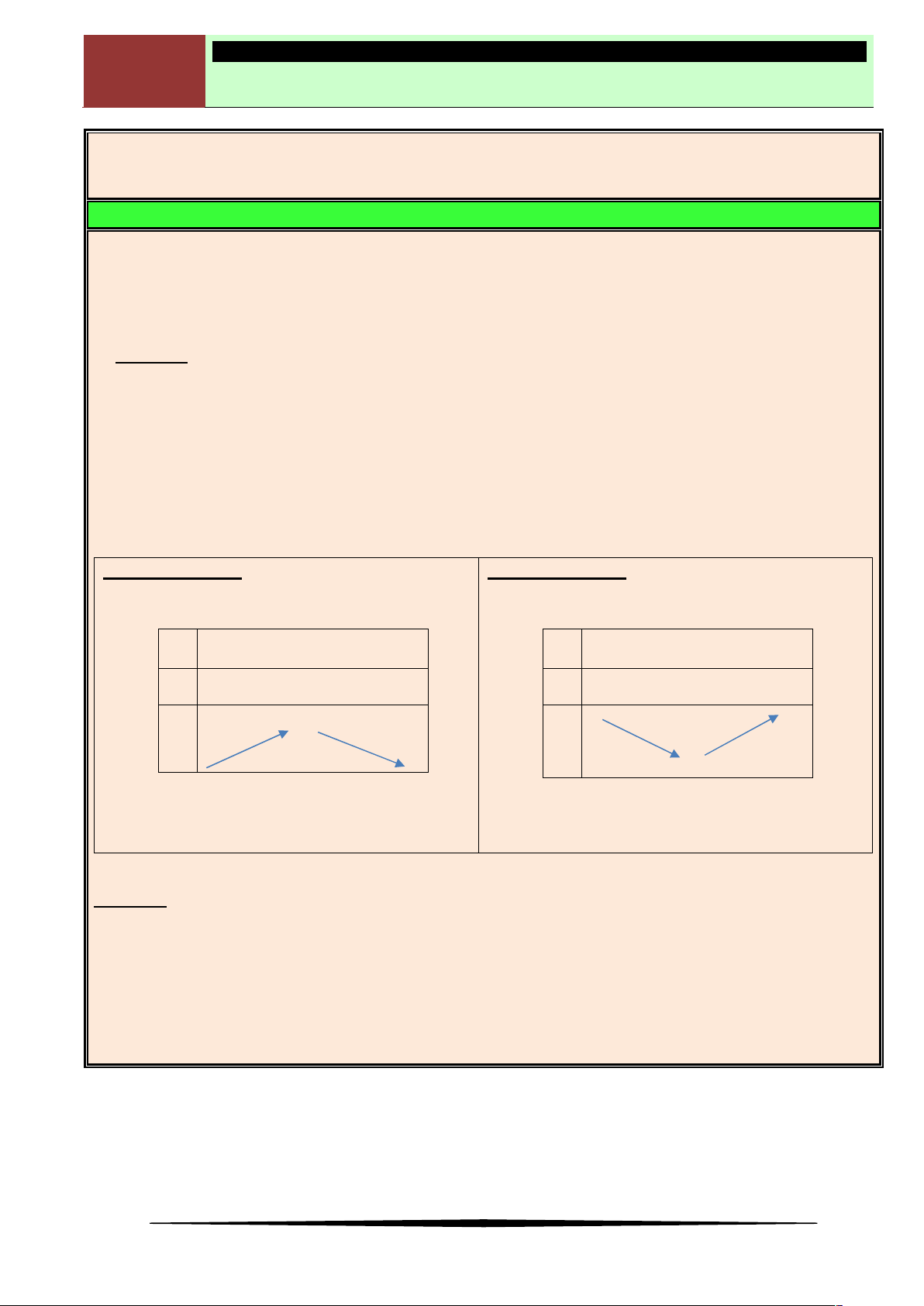
 Điểm cực đại, điểm cực tiểu của đồ thị hàm số:

Xét đồ thị hàm số như hình vẽ bên, ta có: điểm A

gọi là điểm cực đại của đồ thị, điểm B và điểm

C gọi là điểm cực tiểu của đồ thị. Điểm cực đại,

cực tiểu của đồ thị hàm số gọi chung là điểm

cực trị của đồ thị hàm số đó.

 Khái niệm điểm cực đại, điểm cực tiểu:

Cho hàm số

( )y f x

xác định trên

D

.

• Ta nói

0

x

là một điểm cực đại của hàm số

( )y f x

nếu tồn tại khoảng

( ; )

a b D

và

0

( ; )x a b

 sao cho

0 0

( ) ( ), ( ; ) \{ }f x f x x a b x

   .

Khi đó

0

( )f x

được gọi là giá trị cực đại của hàm số

( )y f x

và điểm

0 0

( ; ( ))M x f x

được gọi

là điểm cực đại của đồ thị hàm số

( )y f x

.

• Ta nói

0

x

là một điểm cực tiểu của hàm số

( )y f x

nếu tồn tại khoảng

( ; )

a b D

và

0

( ; )x a b

 sao cho

0 0

( ) ( ), ( ; ) \{ }f x f x x a b x

   .

Khi đó

0

( )f x

được gọi là giá trị cực tiểu của hàm số

( )y f x

và điểm

0 0

( ; ( ))M x f x

được gọi

là điểm cực tiểu của đồ thị hàm số

( )y f x

.

 Chú ý:

 Điểm cực đại hay điểm cực tiểu gọi chung là điểm cực trị, giá trị cực đại hay giá trị cực tiểu

được gọi chung là cực trị.

 Giá trị cực đại (cực tiểu) không phải là giá trị lớn nhất (nhỏ nhất) của hàm số

( )y f x

trên tập

D

.

A

điểm

cực

đại

B

điểm

cực

tiểu C

điểm

cực

tiểu

D

E

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 15

2. Điều kiện có cực trị của hàm số:

a. Điều kiện cần: Nếu hàm số

( )y f x

có đạo hàm trên

( ; )a b

và đạt cực trị tại

0

( ; )x a b

 thì

0

'( ) 0

f x



.

b. Điều kiện đủ:

Định lý 1: Cho hàm số

( )y f x

liên tục trên khoảng

( ; )a b

chứa

0

x

đồng thời có đạo hàm trên

khoảng

( ; )a b

hoặc

0

( ; ) \{ }a b x

. Khi đó:

 Nếu

0

'( ) 0, ( ; )

f x x a x

f x x x b

  





  



thì hàm số

( )y f x

đạt cực đại tại điểm

0

x x

.

 Nếu

0

'( ) 0, ( ; )

f x x a x

f x x x b

  





  



thì hàm số

( )y f x

đạt cực tiểu tại điểm

0

x x

.

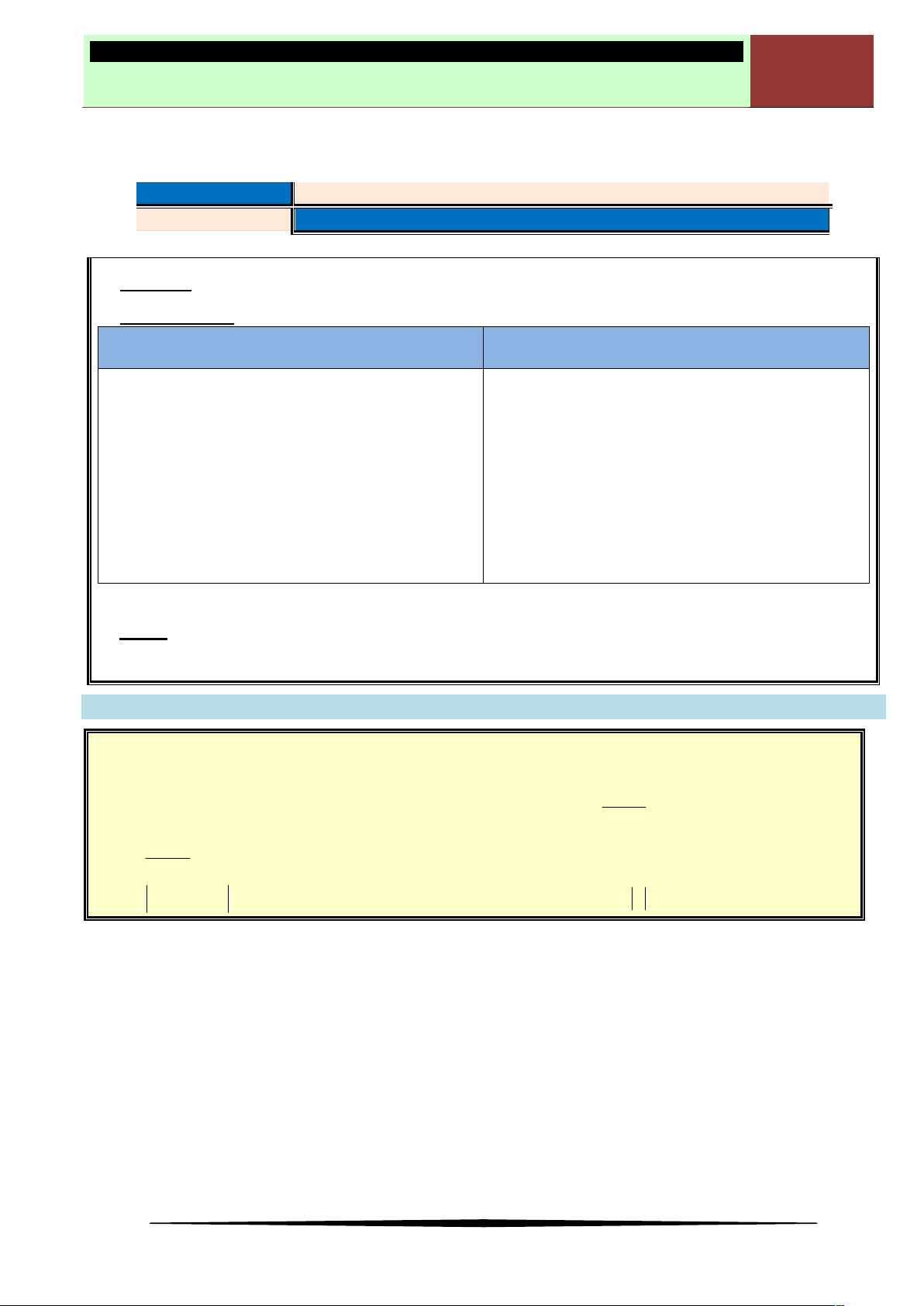
Bảng biến thiên 1: Hàm số đạt cực đại tại

0

x x

x

a

0

x

b

'y

+ 0 -

y

CD

y

Nhận thấy:

'( )f x

đổi dấu từ dương sang âm khi

x

đi qua

0

x

Bảng biến thiên 2: Hàm số đạt cực tiểu tại

0

x x

.

x

a

0

x

b

'y

- 0 +

y

CT

y

Nhận thấy:

'( )f x

đổi dấu từ âm sang dương khi

x

đi qua

0

x

Định lý 2: Cho hàm số

( )y f x

có đạo hàm cấp 2 trên khoảng

( ; )a b

chứa

0

x

. Khi đó:

 Nếu

0

'( ) 0

''( ) 0

f x











thì hàm số

( )y f x

đạt cực đại tại điểm

0

x x

.

 Nếu

0

'( ) 0

''( ) 0

f x











thì hàm số

( )y f x

đạt cực tiểu tại điểm

0

x x

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 16

B. CÁC DẠNG TOÁN THƯỜNG GẶP

— Bài toán. Tìm cực trị của hàm số

 

y f x

.

— Phương pháp:

Quy tắc 1 Quy tắc 2

 Bước 1: Tìm tập xác định.

 Bước 2: Tính đạo hàm

'( )f x

, cho

'( ) 0f x 

tìm nghiệm hoặc tìm

x

khi

'( )f x

không xác định.

 Bước 3: Lập bảng biến thiên.

 Bước 4: Dựa vào bảng biến thiên suy ra

điểm cực đại, điểm cực tiểu của hàm số.

 Bước 1: Tìm Tập xác định

 Bước 2: Tính đạo hàm

'( )f x

, cho

'( ) 0f x 

tìm nghiệm

1 2

, ,...x x

nếu có.

 Bước 3: Tính

''( )f x

và

1 2

''( ), ''( ),...f x f x

 Bước 4: Dựa vào dấu của

1 2

''( ), ''( ),...f x f x

để suy ra điểm cực đại,

điểm cực tiểu của hàm số.

 Chú ý: Quy tắc 2 không dùng được trong trường hợp

'( ) 0f x 

vô nghiệm hoặc

0

'( ) 0

''( ) 0

f x











.

CÁC VÍ DỤ

Ví dụ 1: Tìm cực trị của các hàm số sau:

a)

3 2

– 3 1

y x x

 

b)

4 2

2

1

y x x 



c)

3 2

3 3 1y x x x   

d)

2 1

2

x

y

x







e)

2

3

1

x

y

x







f)

2sin

y x x 

g)

2

– 2 3

y x x

 

h)

2

y x x 

--------------------------------------------------------------------------------------------------------------------------------

Dạng 1:

Xét dấu của đạo hàm để tìm cực trị của hàm số

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 17

--------------------------------------------------------------------------------------------------------------------------------

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 18

Ví dụ 2. Giá trị cực đại của hàm số

3

3 2y x x  

là

Ⓐ

 1

CÑ

y

. Ⓑ

 4

CÑ

y

.

Ⓒ

1

CÑ

y

. Ⓓ

 0

CÑ

y

.

Lời giải :....................................................................

......................................................................................

Ví dụ 3. Hàm số

4 2

2 4

y x x

   

đạt cực tiểu tại

Ⓐ

0

x



Ⓑ

1x 

Ⓒ

1

x

 

Ⓓ

4

x

 

Lời giải:.....................................................................

......................................................................................

Ví dụ 4. Chọn mệnh đề đúng về hàm số

3

1

y x

 

.

Ⓐ Hàm số đạt cực tiểu tại

0

x



.

Ⓑ Hàm số có cực đại không có cực tiểu.

1

y

 

.

Ⓓ Hàm số không có cực trị.

Lời giải:.....................................................................

......................................................................................

Ví dụ 5. Cho hàm số

2

y x x 

. Hàm số đạt cực đại tại

Ⓐ

0

x



. Ⓑ

1x 

.

Ⓒ

2

x



. Ⓓ

1y 

.

Lời giải:.....................................................................

......................................................................................

Ví dụ 6. Cho hàm số

( )y f x

có đạo hàm

2 3 4

'( ) 2 (1 ) ( 3) ( 2) ,f x x x x x x

      

. Hàm số đạt cực

tiểu tại

Ⓐ

0

x



. Ⓑ

1x 

.

Ⓒ

2

x



. Ⓓ

3

x



.

Lời giải:.....................................................................

......................................................................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 19

BÀI TẬP VỀ NHÀ

Câu 1. Cho hàm số

 



y f x

xác định, có đạo hàm cấp một và cấp hai trên khoảng

 

;a b

và

 

0

;



x a b

.

Khẳng định nào sau đây sai?

Ⓐ Hàm số đạt cực đại tại

0

x

thì

 

0

' 0

y x

.

Ⓑ

 

0

' 0

y x

và

 

0

'' 0

y x

thì

0

x

là điểm cực tiểu của hàm số.

Ⓒ

 

0

' 0

y x

và

 

0

'' 0

y x

thì

0

x

không là điểm cực trị của hàm số.

Ⓓ

 

0

' 0

y x

và

 

0

'' 0

y x

thì

0

x

là điểm cực trị của hàm số

Câu 2. Phát biểu nào sau đây là sai?

Ⓐ Nếu

 

0

f x





và

 

0

f x





thì hàm số đạt cực tiểu tại

0

x

.

Ⓑ Nếu

 

0

f x





và

 

0

f x





thì hàm số đạt cực đại tại

0

x

.

 

f x



đổi dấu khi

x

qua điểm

0

x

và

 

f x

liên tục tại

0

x

thì hàm số

 

y f x



đạt cực trị tại

điểm

0

x

.

Ⓓ Hàm số

 

y f x



đạt cực trị tại

0

x

khi và chỉ khi

0

x

là nghiệm của đạo hàm.

Câu 3. Khẳng định nào sau đây là khẳng định đúng?

Ⓐ Nếu

 

f x

đạt cực tiểu tại

0

x x

thì

 

0

f x





.

Ⓑ Nếu

 

0

f x





thì

 

f x

đạt cực trị tại

0

x x

.

 

0

f x





và

 

0

f x





thì

 

f x

đạt cực đại tại

0

x x

.

Ⓓ Nếu

 

f x

có đạo hàm tại

0

x

và đạt cực đại tại

0

x

thì

 

0

f x





.

Ví dụ 7. Cho hàm số

 

y f x



có

 

2

( 2)( 1)( 3)

f x x x x x



   

, x

 

. Hàm số

2

( ) ( )g x f x

 có

bao nhiêu cực trị?

Ⓐ

4.

Ⓑ

3

.

Ⓒ

5

. Ⓓ

2

.

Lời giải:.....................................................................

......................................................................................

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 20

Câu 4. Cho hàm số

2 3

1

x

y

x







có bao nhiêu điểm cực trị?

Ⓐ

1

. Ⓑ

3

. Ⓒ

0

. Ⓓ

2

.

Câu 5. Cho hàm số

2

3

1

x

y

x







. Mệnh đề nào dưới đây đúng?

Ⓐ Cực tiểu của hàm số bằng

3

.

Ⓑ Cực tiểu của hàm số bằng

1

.

6

.

Ⓓ Cực tiểu của hàm số bằng

2

.

Câu 6. Đồ thị hàm số

3

3y x x  

có điểm cực tiểu là

Ⓐ

 

1; 2 

. Ⓑ .

 

1;0

Ⓒ

 

1; 2

Ⓓ

 

1;0



Câu 7. Điểm cực đại của đồ thị hàm số

3 2

6 9y x x x  

có tổng hoành độ và tung độ là

Ⓐ

5.

Ⓑ

1

. Ⓒ

3

. Ⓓ

1

.

Câu 8. Hàm số

3

3 4y x x   

có giá trị cực tiểu là

Ⓐ

6.

CT

y

 

Ⓑ

1

CT

y

 

. Ⓒ

2.

. Ⓓ

1.

Câu 9. Cho hàm số

4 2

2 1

y x x

   

có giá trị cực đại và giá trị cực tiểu lần lượt là

1

y

và

2

y

. Khi đó, khẳng

định nào sau đây đúng?

Ⓐ

1 2

3 1

y y

  

. Ⓑ

1 2

3 5

y y

 

. Ⓒ

1 2

3 1

y y

 

. Ⓓ

1 2

3 5

y y

  

.

Câu 10. Đồ thị hàm số

4 2

1

y x x

  

có bao nhiêu điểm cực trị có tung độ là số dương?

Ⓐ

3.

Ⓑ

1.

Ⓒ

2.

Ⓓ

0.

Câu 11. Hàm số nào sau đây không có cực trị?

Ⓐ

2

1

x

y

x



 . Ⓑ

2 2

1

x

y

x







.

Ⓒ

2

2 1.

y x x

  

Ⓓ

3

1.

y x x

   

Câu 12. Hàm số nào sau đây không có điểm cực trị?

Ⓐ

3

3 1y x x  

. Ⓑ

2

2y x x 

. Ⓒ

4 2

4 1

y x x

  

. Ⓓ

3

3 1y x x  

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 21

Câu 13. Điểm cực đại của đồ thị hàm số

3

3 1y x x   

là

Ⓐ

 

1; 1

M

 

. Ⓑ

 

0;1

N . Ⓒ

 

2; 1

P



. Ⓓ

 

1;3

Q .

Câu 14. Tìm số điểm cực trị của hàm số

4 2

2y x x

  ?

Ⓐ

2

. Ⓑ

4

. Ⓒ

3

. Ⓓ

1

.

Câu 15. Số cực trị của hàm số

4 2

2 3

y x x

  

là

Ⓐ

0

. Ⓑ

2

. Ⓒ

3

. Ⓓ

1

.

Câu 16. Cho hàm số

4 2

1

y x x

  

. Mệnh đề nào dưới đây đúng?

Ⓐ Hàm số có

1

điểm cực đại và

2

điểm cực tiểu.

Ⓑ Hàm số có

2

điểm cực đại và

1

điểm cực tiểu.

1

điểm cực trị.

Ⓓ Hàm số có

2

điểm cực trị.

Câu 17. Trong các hàm số sau, hàm số nào có hai điểm cực đại và một điểm cực tiểu?

Ⓐ

4 2

3

y x x

   

. Ⓑ

4 2

3

y x x

  

. Ⓒ

4 2

3

y x x

   

. Ⓓ

4 2

3

y x x

  

.

Câu 18. Hàm số nào sau đây có ba điểm cực trị?

Ⓐ

3 2

1

3 7 2.

3

y x x x

   

Ⓒ

4 2

2 1.

y x x

   

Ⓑ

4 2

2 .y x x

   Ⓓ

2 1

.

1

x

y

x







Câu 19. Hàm số

3 2

1

3 1

3

y x x x   

đạt cực tiểu tại

Ⓐ

1

x

 

. Ⓑ

1x 

. Ⓒ

3

x

 

. Ⓓ

3

x



.

Câu 20. Biết hàm số

3

3 1y x x  

có hai điểm cực trị

A

và

B

. Phương trình đường thẳng

AB

là

Ⓐ

2 1y x  

. Ⓑ

2 1y x 

Ⓒ

2y x 

. Ⓓ

2y x  

.

Câu 21. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

2

2 3

2 1

x x

y

x

 





.

Ⓐ

2 2

y x

 

. Ⓑ

1y x 

Ⓒ

2 1y x 

. Ⓓ

1y x 

.

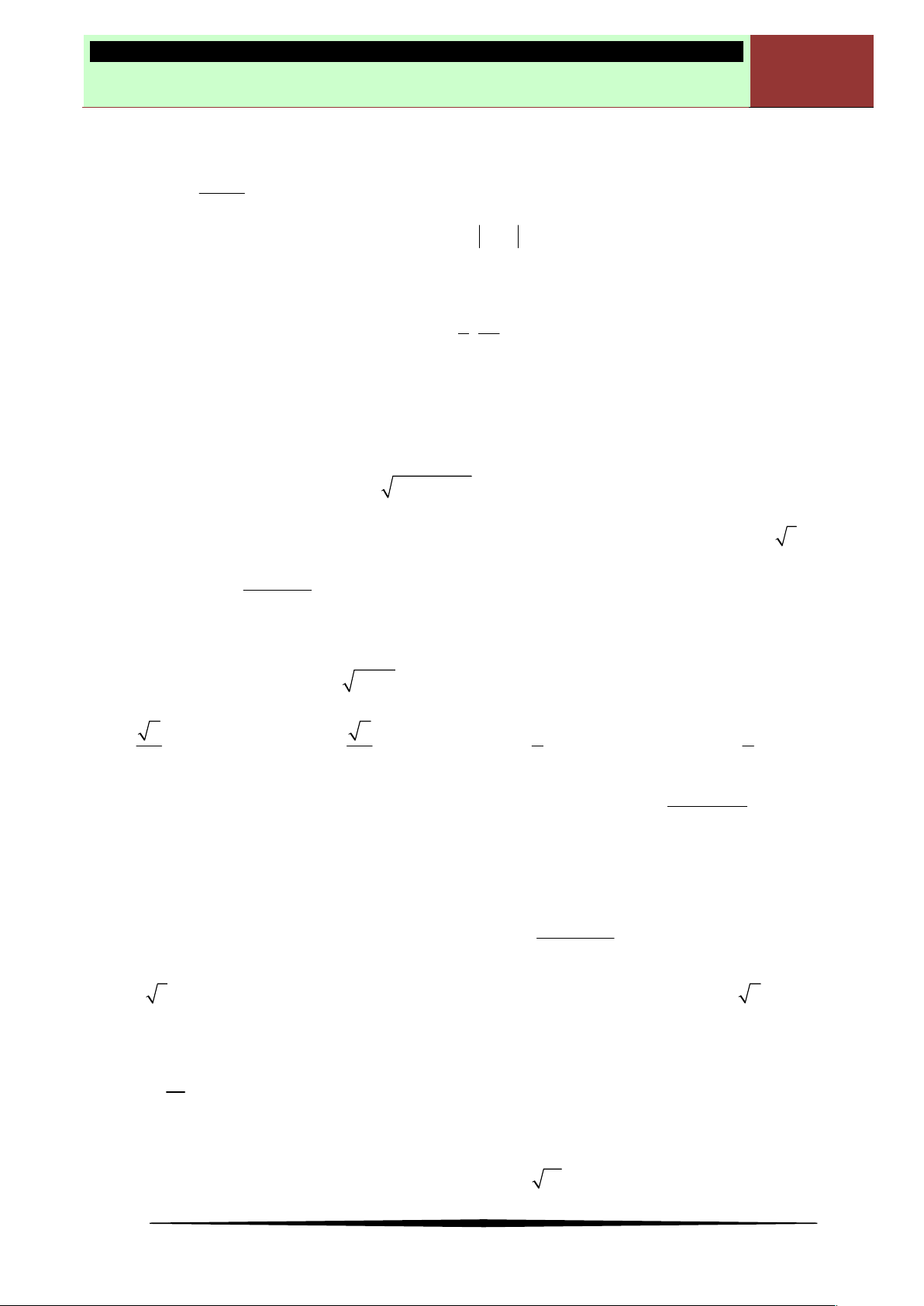
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 22

Câu 22. Hàm số nào sau đây không có cực trị?

Ⓐ

2 3

2

x

y

x







. Ⓒ

3

y x x  

.

Ⓑ

4

y x

. Ⓓ

2

y x

 

.

Câu 23. Điểm cực tiểu của đồ thị hàm số

3 2

5 5y x x x    

là

Ⓐ

 

1; 8 

. Ⓒ

5 40

;

3 27

 

 

 

.

Ⓑ

 

0; 5

. Ⓓ

(1;0)

.

Câu 24. Số cực trị của hàm số

3

3 3y x x  

là

Ⓐ

3

. Ⓑ

2

. Ⓒ

0

. Ⓓ

1

.

Câu 25. Giá trị cực đại của hàm số

2

3 2

y x x  

là

Ⓐ

 0

CÑ

y

. Ⓑ

2

CĐ

y



. Ⓒ

3

CĐ

y



. Ⓓ

3

CĐ

y 

.

Câu 26. Hàm số

2

1

x x

y

x

 





đạt cực đại tại

Ⓐ

1

x

 

. Ⓑ

2

x

 

. Ⓒ

0

x



. Ⓓ

2

x



.

Câu 27. Cực đại của hàm số

2

1

y x x 

là

Ⓐ

2

. Ⓑ

2



. Ⓒ

1

2

. Ⓓ

1

2



.

Câu 28. Gọi

,M n

lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số

2

3 3

2

x x

y

x

 





. Giá trị

2

2M n

bằng

Ⓐ

6

. Ⓑ

7

. Ⓒ

8

. Ⓓ

9

.

Câu 29. Khoảng cách giữa hai cực trị của đồ thị hàm số

2

2 1

1

x x

y

x

 





bằng

Ⓐ

4 5

. Ⓑ

4

. Ⓒ

8

. Ⓓ

5 2

.

Câu 30. Đồ thị của hàm số

3 2

3 5

y x x

   

có hai điểm cực trị

A

và

B

. Tính diện tích

S

của tam giác

OAB

với

O

là gốc tọa độ.

Ⓐ

10

3

S 

. Ⓑ

9

S



. Ⓒ

10

S



. Ⓓ

5

S



.

Câu 31. Gọi

, ,A B C

là ba điểm cực trị của đồ thị hàm số

4 2

2 2

y x x

  

. Diện tích của tam giác

ABC

bằng

Ⓐ

4

. Ⓑ

2

. Ⓒ

10

. Ⓓ

1

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 23

Câu 32. Gọi A, B là hai điểm cực trị của đồ thị hàm số

3

1 2

3 3

y x x

   

, toạ độ trung điểm của AB là

Ⓐ

2

0;

3

 



 

 

. Ⓑ

1 2

;

3 3

 



 

 

.

Ⓒ

 

0;1

. Ⓓ

 

1;0

.

Câu 33. Đồ thị hàm số

3 2

y x ax bx c   

đi qua

(1;0)

A

và có điểm cực trị

( 2;0)

M



. Giá trị

2 2 2

a b c 

bằng

Ⓐ

25

. Ⓑ

1

. Ⓒ

7

. Ⓓ

14

.

Câu 34. Cho hàm số

( )y f x

có đạo hàm

3

'( ) ( 1)( 3) ,f x x x x x

     

. Số điểm cực trị của hàm số đã

cho là

Ⓐ

1.

Ⓑ

3.

Ⓒ

2.

Ⓓ

5.

Câu 35. Cho hàm số

( )y f x

có đạo hàm

2 2

'( ) ( 4)( 3 2),f x x x x x

     

. Số điểm cực trị của hàm

số đã cho là

Ⓐ

5.

Ⓑ

4.

Ⓒ

3.

Ⓓ

2.

Câu 36. Cho hàm số

3 2

( ) 3y f x x x

   . Đồ thị hàm số

3 2

( ) ( ) 3g x f x x x

  

có bao nhiêu điểm cực trị?

Ⓐ

2.

Ⓑ

3.

Ⓒ

4.

Ⓓ

5.

Câu 37. Cho hàm số

( )y f x

có đạo hàm

2 3

'( ) ( 1)( 2) ,f x x x x x

    

. Hàm số đạt cực tiểu tại

Ⓐ

2

x

 

Ⓑ

0.

x



Ⓒ

1.

x



Ⓓ

3.

x

 

Câu 38. Cho hàm số

 

y f x



có đạo hàm

 

   

2 3

2 2

1 4

f x x x x



   . Số điểm cực tiểu của hàm số là

Ⓐ

3

. Ⓑ

2

. Ⓒ

1

. Ⓓ

5

.

Câu 39. Cho hàm số

( )y f x

có đạo hàm

3 2

'( ) ( 2) ( 9),f x x x x x

     

. Hàm số đạt cực đại tại

Ⓐ

0.

x



Ⓑ

2.

x



Ⓒ

9.

x



Ⓓ

1.

x



Câu 40. Cho hàm số

( )y f x

có đạo hàm

2

'( ) ( 1)( 2),f x x x x

     

. Số điểm cực trị của hàm số

2

( ) ( 1)

g x f x

 

là

Ⓐ

5.

Ⓑ

6.

Ⓒ

7.

Ⓓ

8.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 24

CÁC VÍ DỤ

Ví dụ 1. Cho hàm số

 

y f x



có bảng biến thiên như sau:

Hàm số đã cho có giá trị cực tiểu bằng

Ⓐ

4

y



. Ⓑ

2

y

 

. Ⓒ

0

y



. Ⓓ

3

x



.

Ví dụ 2. Cho hàm số

 

f x

xác định trên



và có xét dấu của

 

f x



như sau:

Hàm số đã cho có mấy điểm cực đại?

Ⓐ

3

. Ⓑ

4

. Ⓒ

2

. Ⓓ

1

.

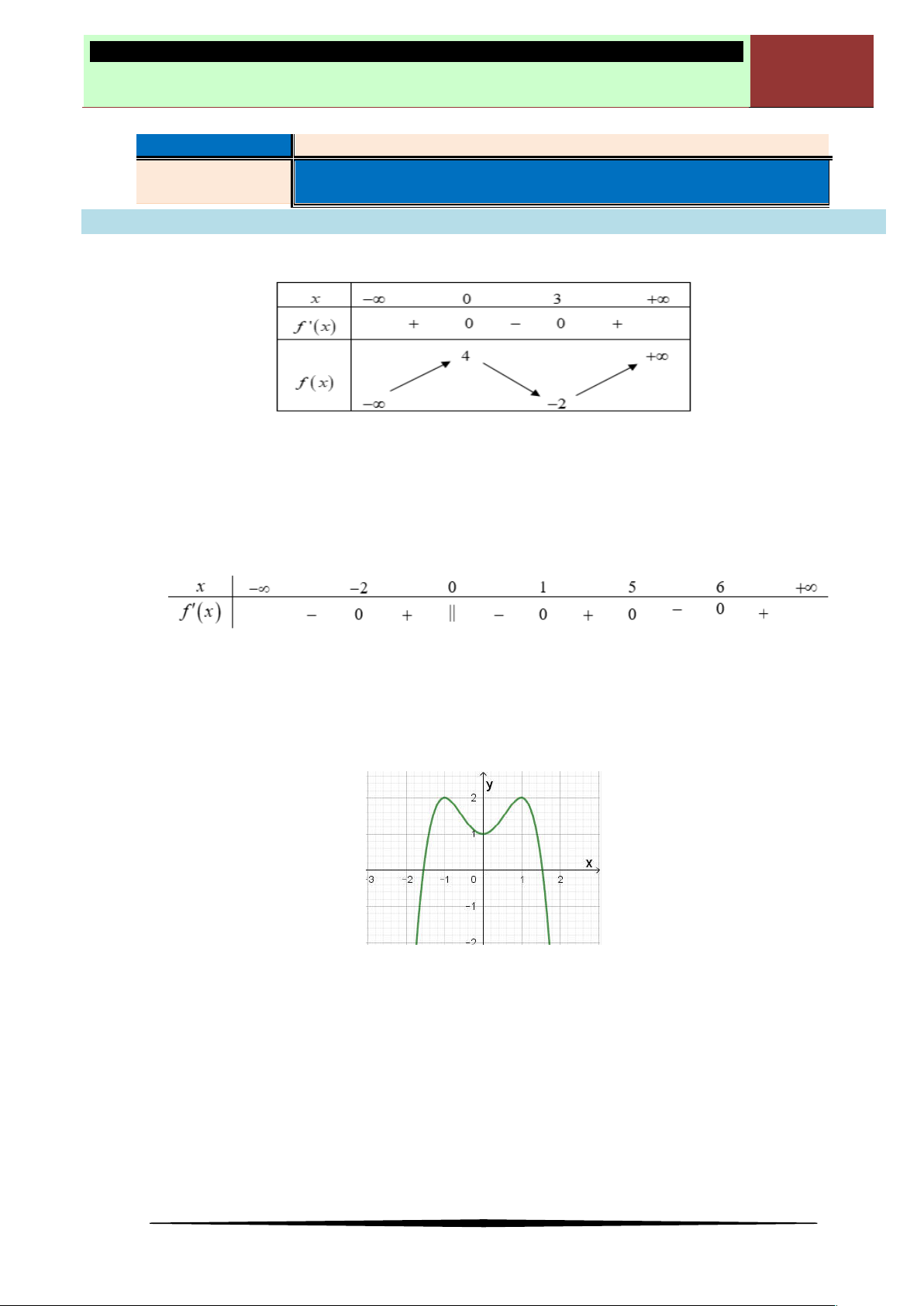
Ví dụ 3. Cho hàm số

 

y f x



có đồ thị như hình vẽ.

Đồ thị hàm số trên có điểm cực đại là

Ⓐ

 

0;1

. Ⓑ

 

1;2

. Ⓒ

 

1; 2 

. Ⓓ

 

2;1

.

Dạng 2:

Dựa vào bảng biến thiên hoặc đồ thị để kết luận cực trị của hàm

số

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 25

Ví dụ 4. Cho hàm số

( )y f x

có đồ thị

( )f x



như hình vẽ:

Số điểm cực trị của hàm số đã cho là

Ⓐ

1

. Ⓑ

2

. Ⓒ

3

. Ⓓ

4

.

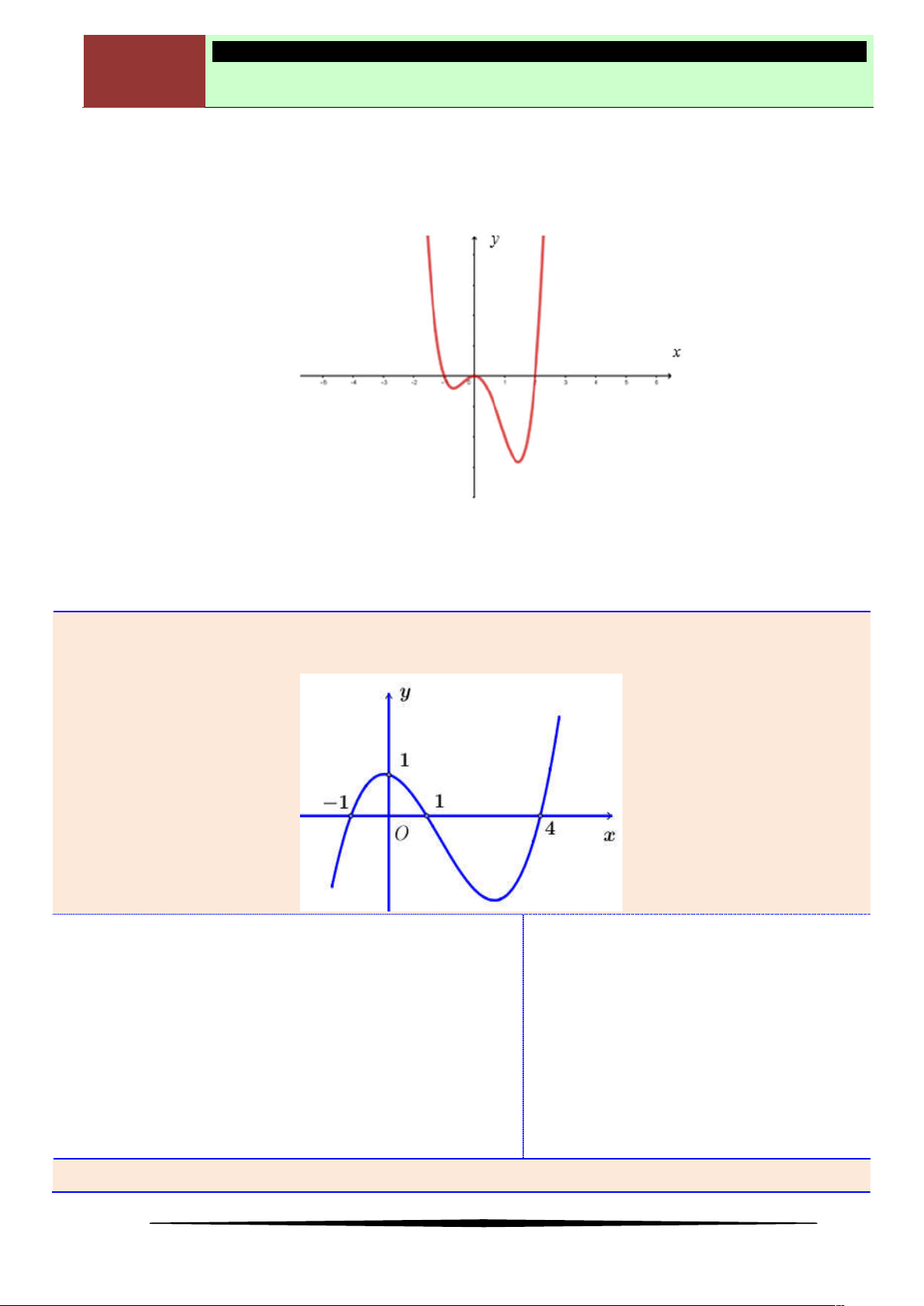
Ví dụ 5. Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình vẽ dưới. Hàm số

 

2

1y f x 

có

bao nhiêu điểm cực trị?

Ⓐ

5

. Ⓑ

7

.

Ⓒ

4

. Ⓓ

3

.

Lời giải :....................................................................

......................................................................................

........ .............................................................................

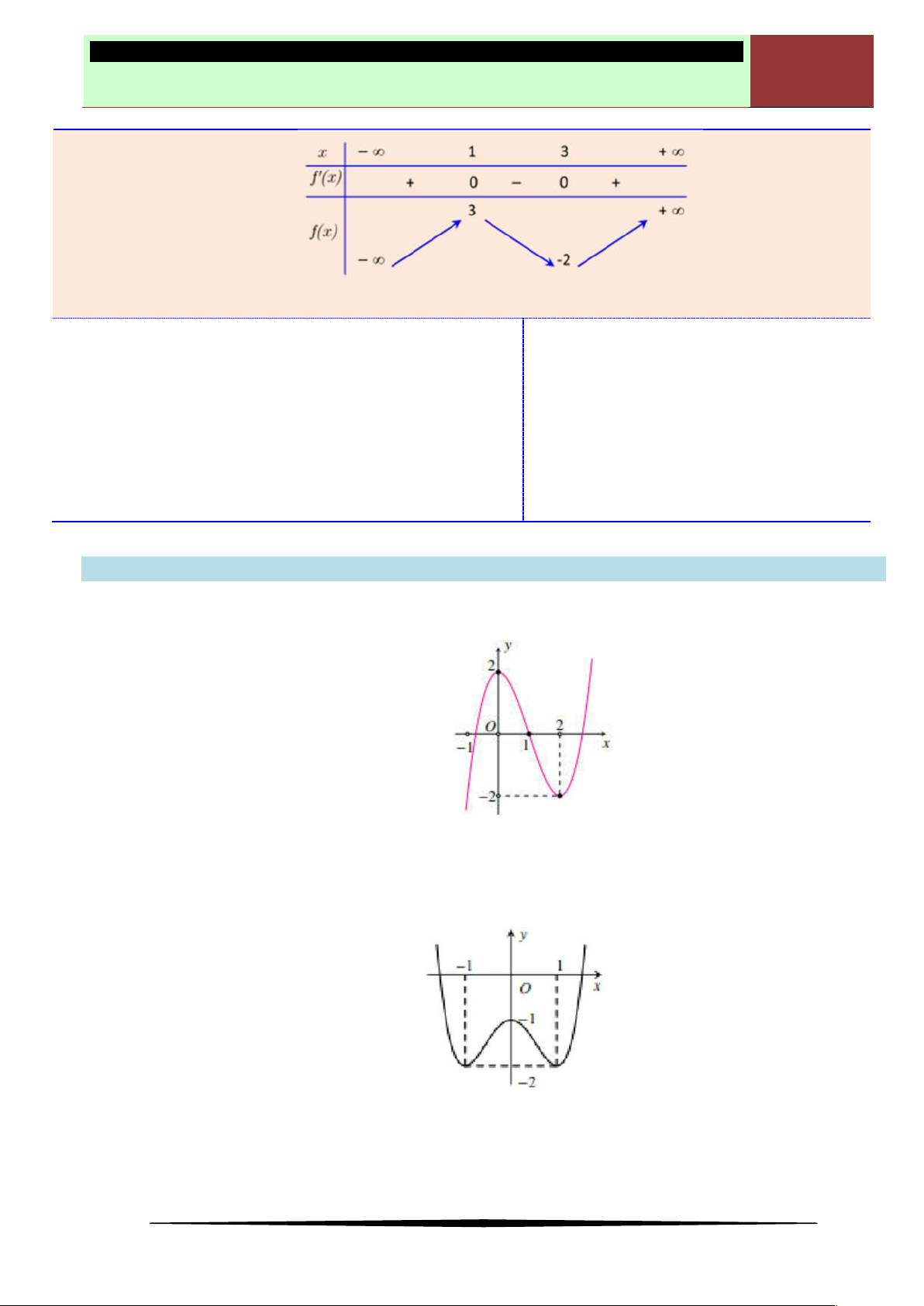
Ví dụ 6. Cho hàm số

 

y f x

có bảng biến thiên như sau

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 26

Số điểm cực đại của hàm số

 

2

3y f x 

là

Ⓐ

1

. Ⓑ

3

.

Ⓒ

0

. Ⓓ

2

.

Lời giải :....................................................................

......................................................................................

BÀI TẬP VỀ NHÀ

Câu 1. Tìm điểm cực tiểu của hàm số

 

y f x

, biết hàm số

 

y f x

có đồ thị như hình vẽ.

Ⓐ

2x 

. Ⓑ

2x  

. Ⓒ

1x 

. Ⓓ

0x 

.

Câu 2. Cho hàm số

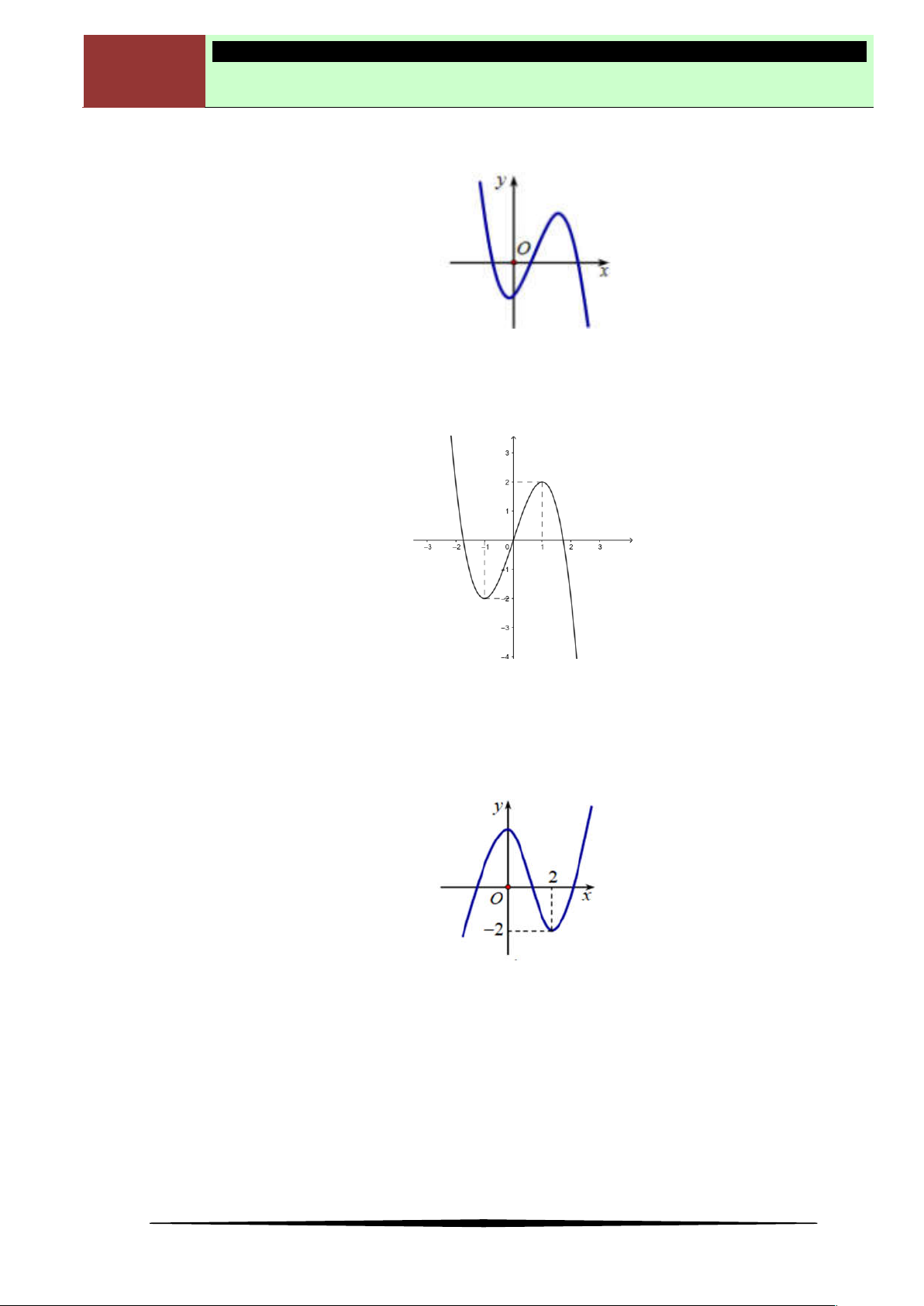
( )y f x

có đồ thị như hình vẽ dưới đây.

Giá trị cực đại của hàm số bằng

Ⓐ

2.

Ⓑ

0.

Ⓒ

1.

Ⓓ

1.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 27

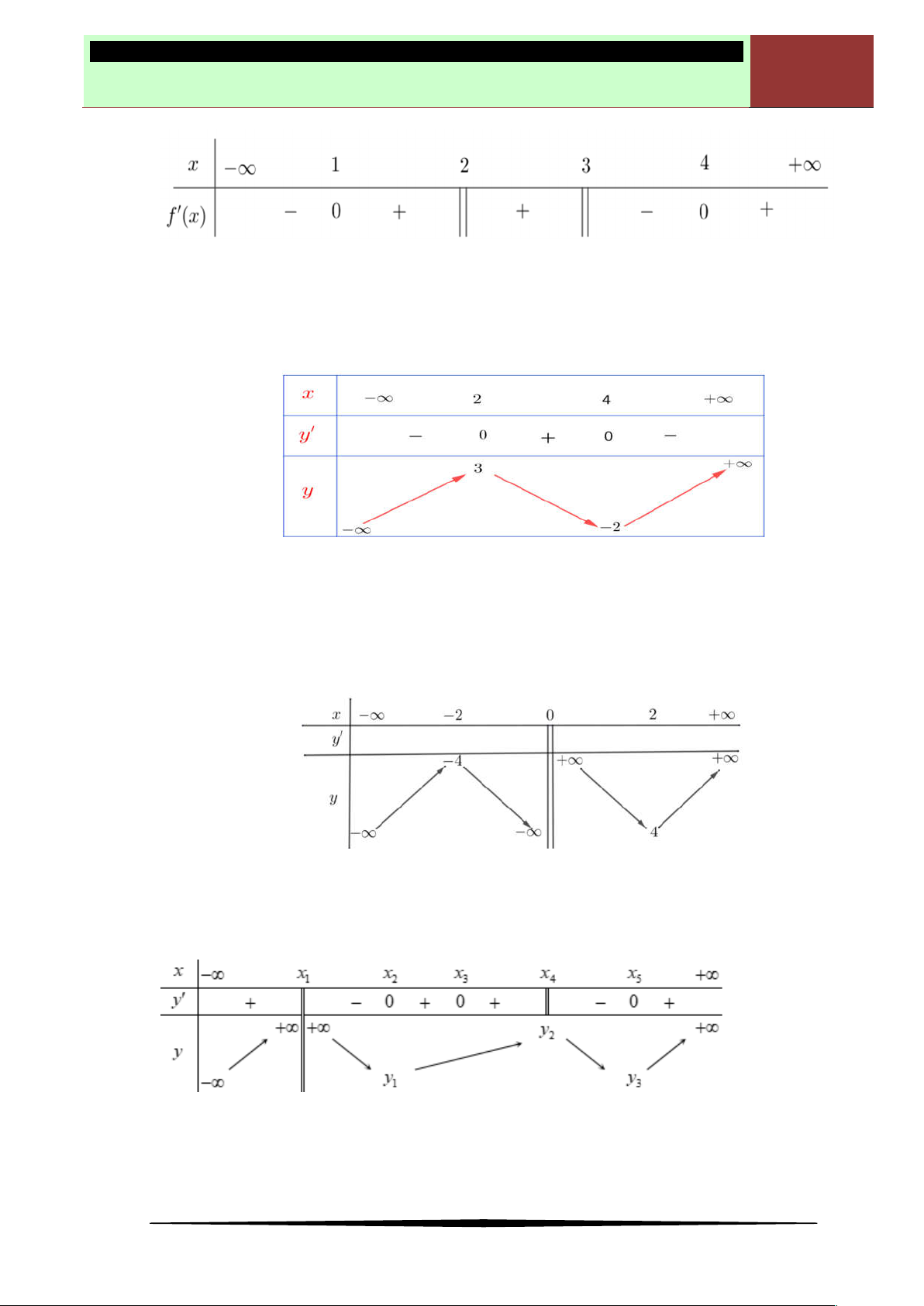
Câu 3. Cho hàm số

( )y f x

có đồ thị như hình vẽ dưới đây. Hàm số đã cho có mấy điểm cực trị?

Ⓐ

0

. Ⓑ

4

. Ⓒ

2

. Ⓓ

1

.

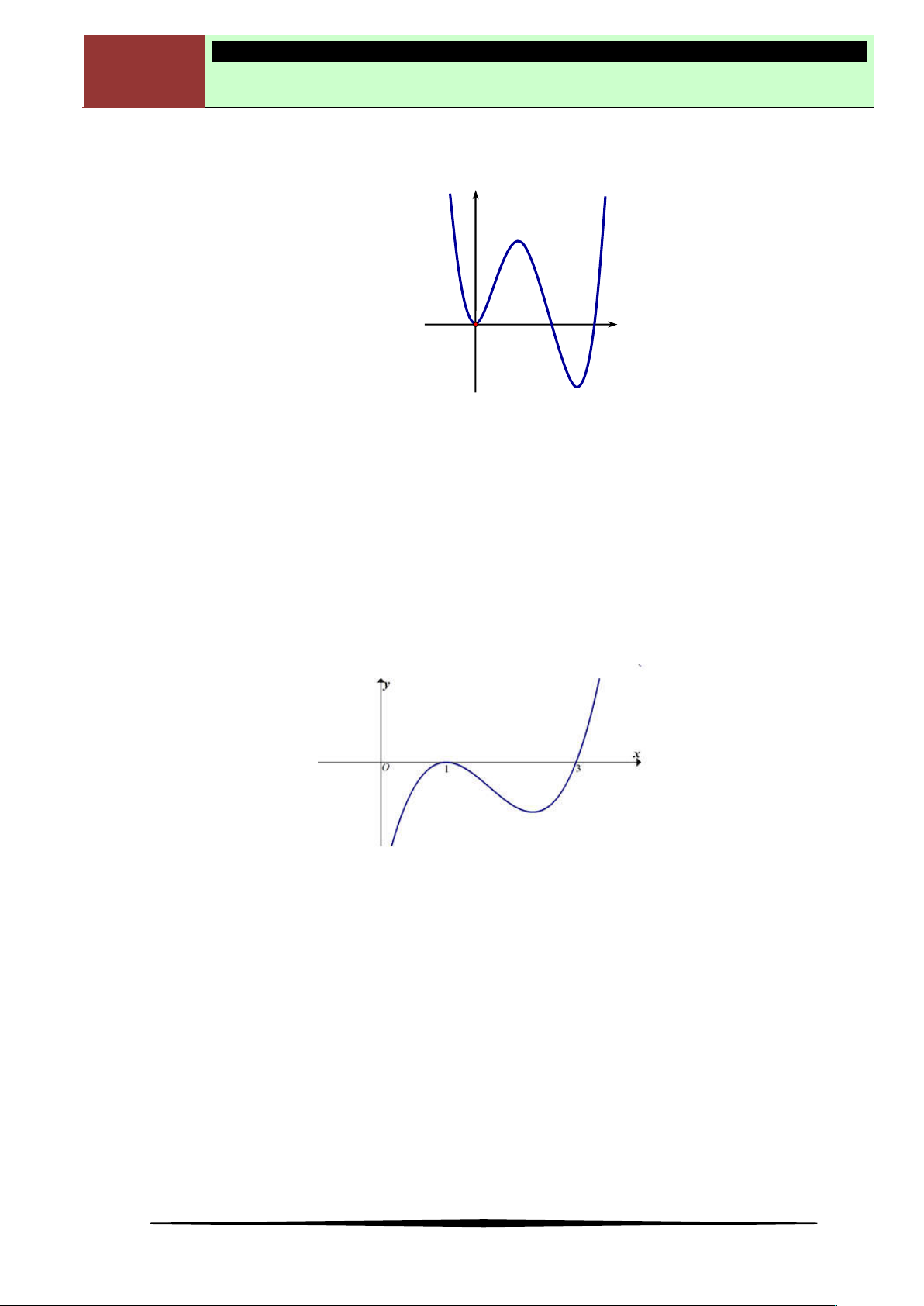
Câu 4. Cho hàm số

 

f x

có đồ thị như hình vẽ bên.

Điểm cực tiểu của đồ thị hàm số đã cho là

Ⓐ

1

. Ⓑ

 

1; 2 

. Ⓒ

 

1; 2

. Ⓓ

1

.

Câu 5. Cho hàm số

 

y f x

có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

Ⓐ Hàm số có giá trị cực tiểu bằng 2 .

Ⓑ Hàm số đạt cực đại tại

0x

và đạt cực tiểu tại

2x

.

2

và giá trị nhỏ nhất bằng

2

.

Ⓓ Hàm số có ba điểm cực trị.

Câu 6. Cho hàm số

 

y f x

liên tục trên



và có bảng xét dấu của

 

f x



như sau:

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 28

Kết luận nào sau đây đúng?

Ⓐ Hàm số có 2 điểm cực đại. Ⓑ Hàm số có 4 điểm cực trị.

Ⓒ

Hàm số có 2 điểm cực trị. Ⓓ Hàm số có 2 điểm cực tiểu.

Câu 7. Cho hàm số

( )y f x

có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây đúng?

Ⓐ Hàm số đạt cực tiểu tại

2.x  

ⒷHàm số đạt cực đại tại

2.x 

4.x 

Ⓓ Hàm số đạt cực tiểu tại

3.x 

Câu 8. Cho hàm số

( )y f x

có bảng biến thiên như hình. Giá trị cực tiểu của hàm số bằng

Ⓐ

2

. Ⓑ

2

. Ⓒ

4

. Ⓓ

4

.

Câu 9. Cho hàm số

 

y f x

có bảng biến thiên như hình vẽ. Hàm số có bao nhiêu điểm cực trị?

Ⓐ

4

. Ⓑ

2

. Ⓒ

3

. Ⓓ

5

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 29

Câu 10. Cho hàm số

 

y f x

có đạo hàm trên



và đồ thị hàm số

 

y f x





trên



như hình vẽ. Mệnh

đề nào đúng?

Ⓐ Hàm số

 

y f x

có 1 điểm cực đại và 1 điểm cực tiểu.

Ⓑ Hàm số

 

y f x

có 2 điểm cực đại và 2 điểm cực tiểu.

 

y f x

có 1 điểm cực đại và 2 điểm cực tiểu.

Ⓓ Hàm số

 

y f x

có 2 điểm cực đại và 1 điểm cực tiểu.

Câu 11. Cho hàm số

 



y f x

. Hàm số

 





y f x

có đồ thị như hình vẽ:

Chọn mệnh đề đúng trong các mệnh đề sau?

Ⓐ Hàm số

 



y f x

đồng biến trên

 

;1

.

Ⓑ Hàm số

 



y f x

đạt cực đại tại

1x

.

 



y f x

có một điểm cực tiểu.

Ⓓ Đồ thị hàm số

 



y f x

có hai điểm cực trị.

O

x

y

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 30

Câu 12. Cho hàm số

 

y f x

có đạo hàm liên tục trên



. Đồ thị hàm số

 

y f x





như hình vẽ sau:

Số điểm cực trị của hàm số

 

5y f x x  là:

Ⓐ

2

. Ⓑ

3

. Ⓒ

4

. Ⓓ

1

.

Câu 13. Cho hàm số

 

y f x

có đạo hàm trên



và có đồ thị

 

f x



như hình vẽ

Hàm số

 

2

2g x f x x 

có bao nhiêu điểm cực đại?

Ⓐ

1

. Ⓑ

2

Ⓒ

3

. Ⓓ

4

.

Câu 14. Biết rằng hàm số

 

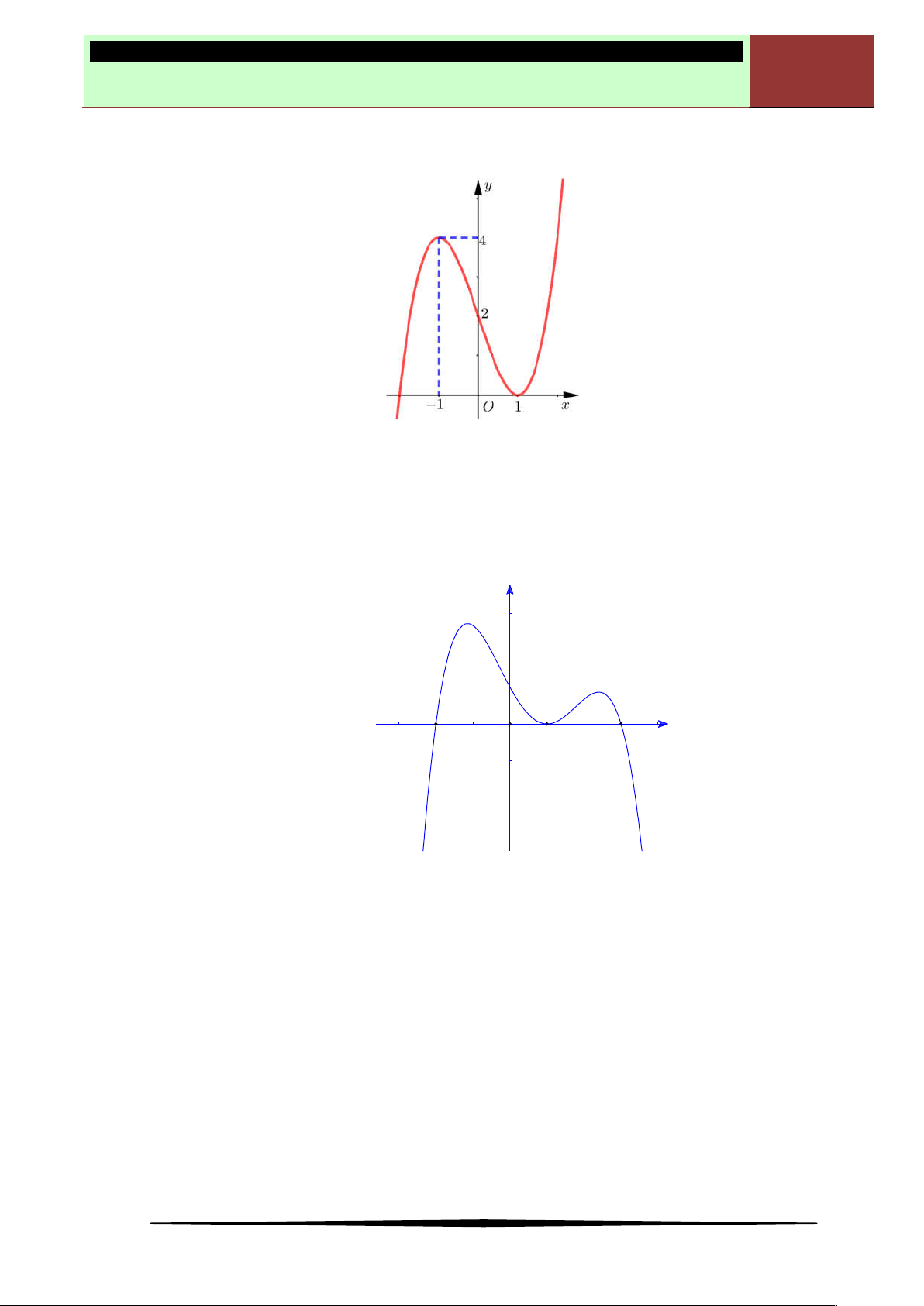
f x

xác định, liên tục trên



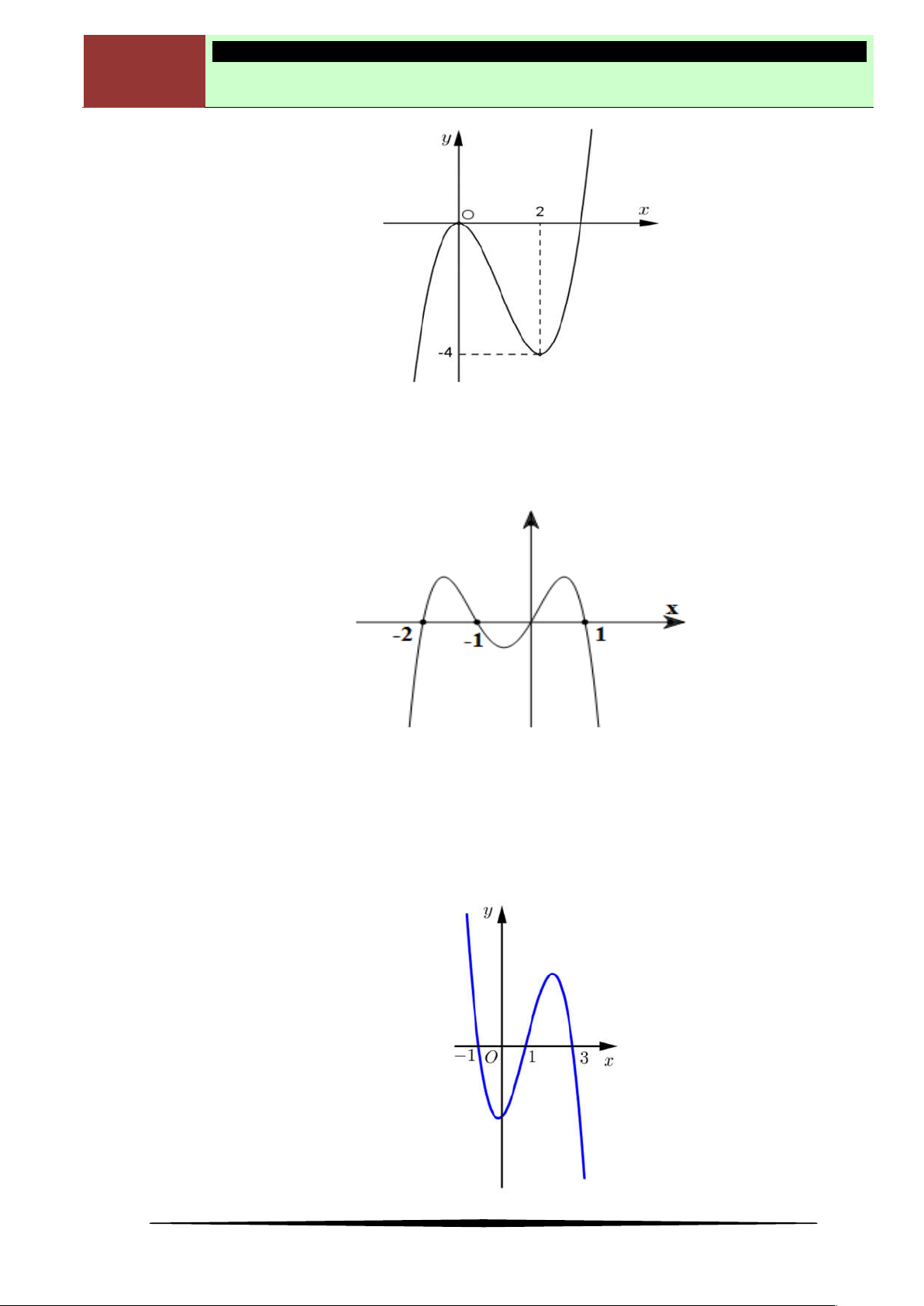
có đồ thị được cho như hình vẽ bên. Tìm số điểm

cực đại của hàm số

 

2020y f f x  

 

.

x

y

-2

3

O

1

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 31

Ⓐ

1

. Ⓑ

3

. Ⓒ

2

. Ⓓ

4

.

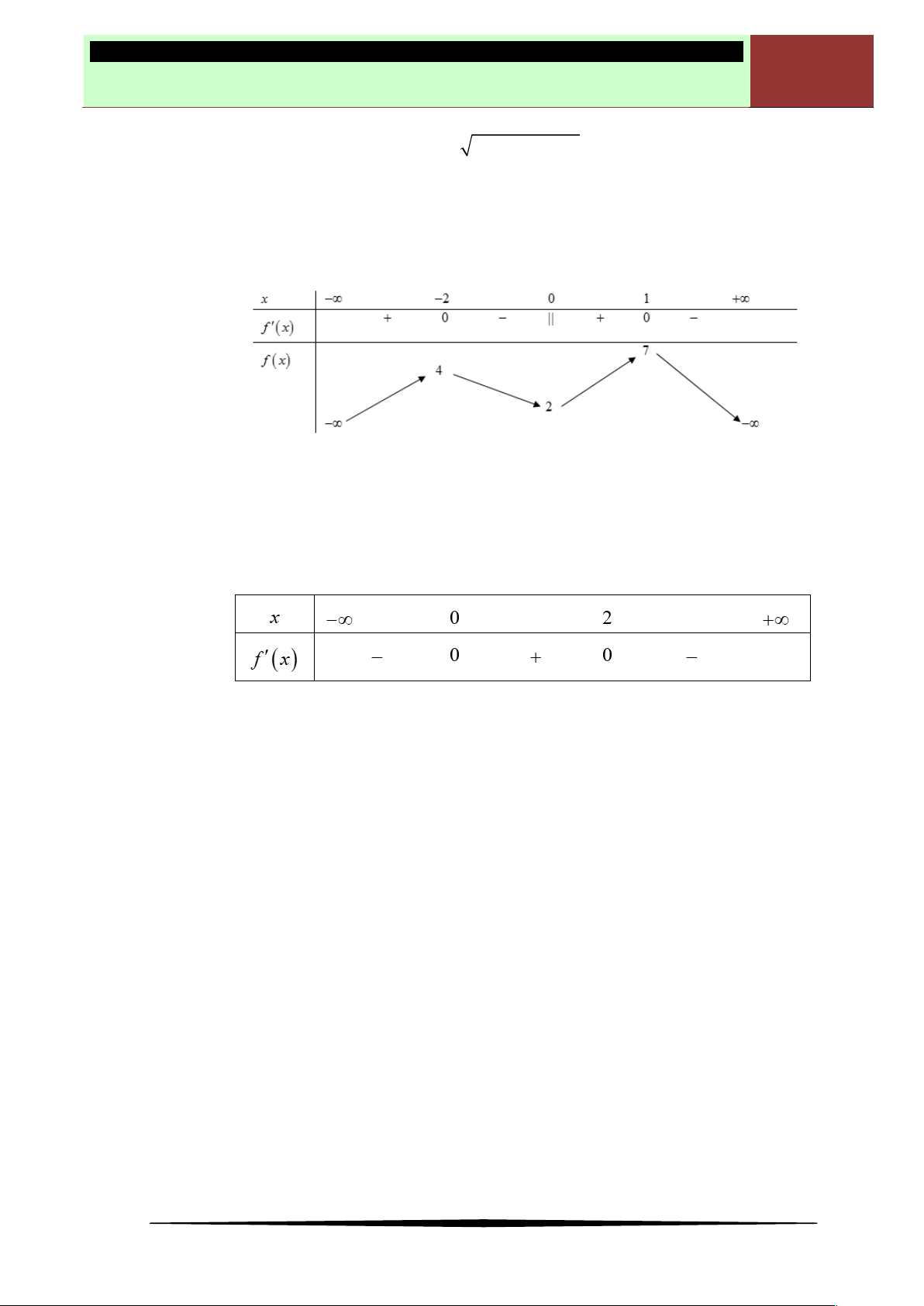
Câu 15. Cho hàm số bậc bốn

 

y f x

có đồ thị như hình dưới.

Số điểm cực trị của hàm số

 

3 2

( ) 3 2g x f x x   

là

Ⓐ 5. Ⓑ 7. Ⓒ 9. Ⓓ 11.

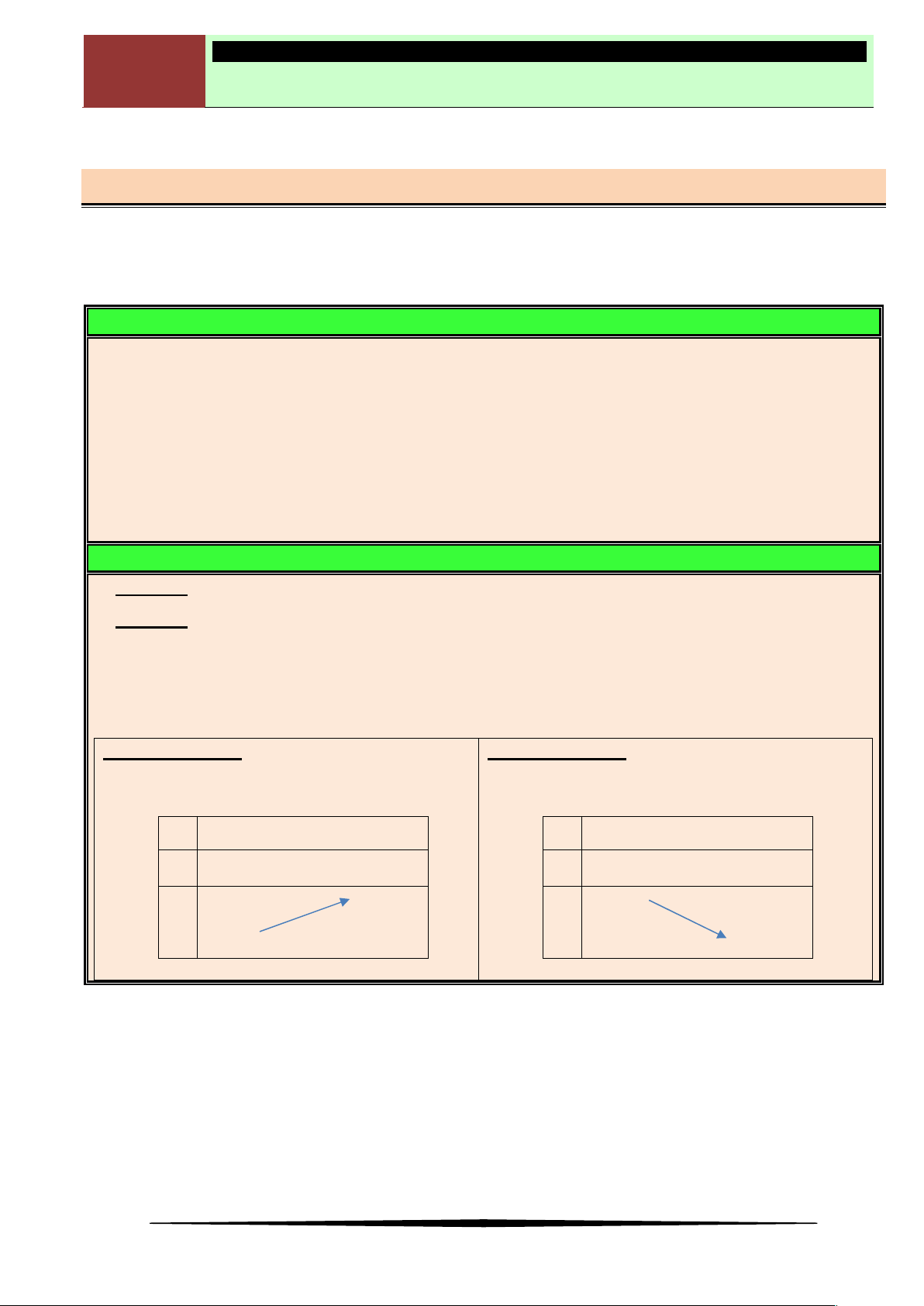
Câu 16. Cho hàm số

 

y f x

là hàm số bậc bốn. Hàm số

 

y f x





có đồ thị như hình vẽ.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 32

Số điểm cực tiểu của hàm số

 

2

2 2020

g x f x x  

là

Ⓐ

3

. Ⓑ

2

. Ⓒ

1

. Ⓓ

0

.

Câu 17. Cho hàm số

 

y f x



có bảng biến thiên

Hỏi hàm số

   

2

2 2020

y g x f x

 

   

 

có bao nhiêu điểm cực đại?

Ⓐ

1

. Ⓑ

3

. Ⓒ

2

. Ⓓ

4

.

Câu 18. Cho hàm số

 

y f x



có đạo hàm liên tục trên



và có bảng xét dấu đạo hàm như sau.

Tổng giá trị tất cả các điểm cực trị của hàm số

 

2019 2020

y f x  

là

Ⓐ

4040

. Ⓑ

6080

. Ⓒ

2

. Ⓓ

2021

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 33

§4. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ

A. TÓM TẮT LÝ THUYẾT

1. Khái niệm cơ bản:

Cho hàm số

( )y f x

xác định trên tập

 K

. Khi đó:

a. Nếu tồn tại

0

x K

sao cho

0

( ) ( ),

  f x f x x K

thì số

0

( )



M f x

được gọi là giá trị lớn nhất

của hàm số

( )y f x

trên

K

. Kí hiệu

max ( )





x K

M f x

.

b. Nếu tồn tại

0

x K

sao cho

0

( ) ( ),

  f x f x x K

thì số

0

( )



M f x

được gọi là giá trị nhỏ nhất

của hàm số

( )y f x

trên

K

. Kí hiệu

min ( )





x K

m f x

.

2. Định lí:

Định lý 1: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn đó.

Định lý 2:

• Nếu hàm số

( )y f x

đồng biến trên đoạn

 

;a b

thì

 

;

max ( ) ( )





x a b

f x f b

và

 

;

min ( ) ( )





x a b

f x f a

.

• Nếu hàm số

( )y f x

nghịch biến trên đoạn

 

;a b

thì

 

;

max ( ) ( )





x a b

f x f a

và

 

;

min ( ) ( )





x a b

f x f b

.

Bảng biến thiên 1: Hàm số

( )y f x

đồng biến

trên đoạn

 

;a b

x

a

b

'y

+

y

( )f b

( )f a

Bảng biến thiên 2: Hàm số

( )y f x

nghịch biến

trên đoạn

 

;a b

x

a

b

'y

-

y

( )f a

( )f b

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 34

B. CÁC DẠNG TOÁN THƯỜNG GẶP

Bài toán 1: Tìm GTLN, GTNN của hàm số

trên đoạn

 

;a b

.

Bài toán 2: Tìm GTLN, GTNN của hàm số trên

khoảng

 

;a b

 Bước 1: Hàm số đã cho xác định và liên tục

trên

 

;a b

. Tính

'( ) 0

f x

tìm nghiệm

 

; .



i

x a b

 Bước 2: Tính

( ), ( ), ( )

i

f a f b f x

.

 Bước 3: Kết luận

 

 

;

max ( ) max ( ), ( ), ( )





i

x a b

f x f a f b f x

 

 

;

min ( ) min ( ), ( ), ( )





i

x a b

f x f a f b f x

 Bước 1: Tìm Tập xác định. Tính

'( )f x

cho

'( ) 0f x 

tìm nghiệm.

 Bước 2: Lập bảng biến thiên (tính các giới hạn

nếu có)

 Bước 3: Dựa vào bảng biến thiên kết luận GTLN,

GTNN của hàm số.

Bài toán 3: Tìm GTLN, GTNN của hàm số bằng cách đặt ẩn phụ.

• Bước 1: đặt biến

t

theo

x

, đặt điều kiện

t

dựa vào điều kiện của

x

, ta được

( ) ( )f x g t

.

• Bước 2:

+ Nếu

 

;



t a b

ta tìm GTLN, GTNN của

( )g t

theo phương pháp bài toán 1

+ Nếu

 

;



t a b

ta tìm GTLN, GTNN của

( )g t

theo phương pháp bài toán 2

CÁC VÍ DỤ

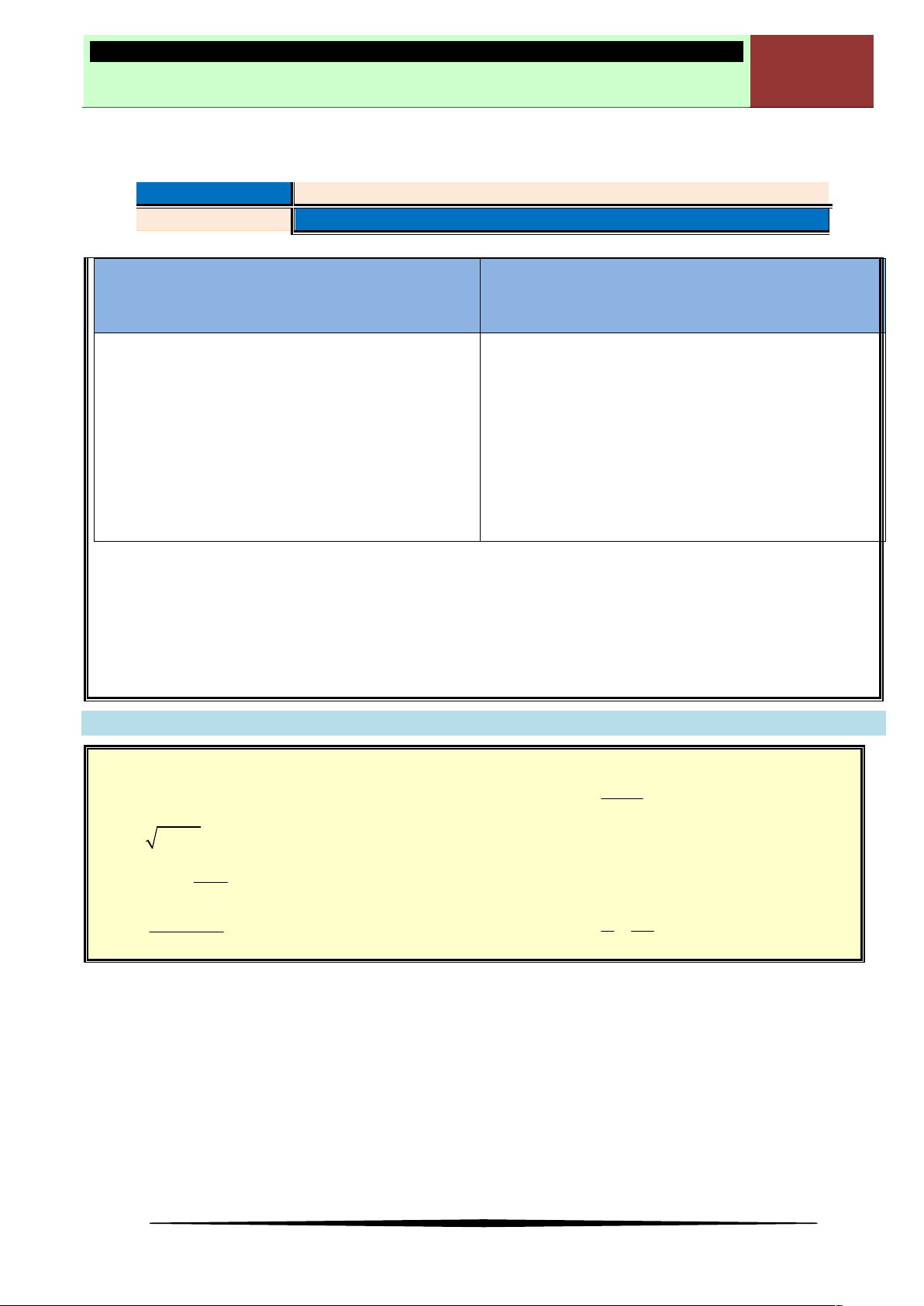
Ví dụ 1: Tính GTLN, GTNN của các hàm số sau:

a)

3

3 4y x x  

,

 

0;2

x

b)

2

1



x

y

x

,

 

1;3

x

c)

2

5

y x x  

d)

3

3 1y x x   

,

 

0;

 

x

e)

4

1

y x

x

  



,

 

1;

 

x

. f)

3 2

cos 2sin cosy x x x

  

g)

sin 1

3 2sin

x

y

x







h)

4x y

S

y x

 

,

 

, 1;3

x y

.

--------------------------------------------------------------------------------------------------------------------------------

Dạng 1:

Tìm GTLN, GTNN của hàm số trên đoạn, khoảng cho trước.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 35

--------------------------------------------------------------------------------------------------------------------------------

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 36

Ví dụ 2. Giá trị lớn nhất của hàm số

 

4 2

8 16

f x x x

  

trên đoạn

 

1;3



bằng

Ⓐ

19

. Ⓑ

9

.

Ⓒ

25

. Ⓓ

0

.

Lời giải :....................................................................

......................................................................................

Ví dụ 3. Gọi lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn

. Tính tổng .

Ⓐ

13

2

Ⓑ

63

2

Ⓒ

25

2

Ⓓ

11

2

Lời giải:.....................................................................

......................................................................................

Ví dụ 4. Biết rằng hàm số

 

1

2018f x x

x

  

đạt giá trị lớn nhất trên khoảng

 

0;4

tại

0

x

. Tính

0

2020

P x  .

Ⓐ 4034 Ⓑ 2020

Lời giải:.....................................................................

......................................................................................

Ví dụ 5. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

 

3

2cos cos2f x x x

 

trên đoạn

;

3 3

D

 

 

 

 

 

.

Ⓐ

   

19

max 1;min

27

x D

f x f x



 

.

Ⓑ

   

3

max ;min 3

4

x D

f x f x



  

.

Ⓒ

   

max 1;min 3

x D

f x f x



  

.

Ⓓ

   

3 19

max ;min

4 27

x D

f x f x



 

.

Lời giải:.....................................................................

......................................................................................

;m M

1

2

y x x

  

 

1;34



3

S m M 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 37

BÀI TẬP VỀ NHÀ

Câu 1. Tìm giá trị lớn nhất của hàm số

3

3 5y x x  

trên đoạn

 

0;2

.

Ⓐ

 

0;2

max 0.

y



Ⓑ

 

0;2

max 3.

y



Ⓒ

 

0;2

max 7.

y



Ⓓ

 

0;2

max 5.

y



Câu 2. Tìm giá trị lớn nhất của hàm số

3 1

3

x

y

x







trên đoạn

 

0;2

.

Ⓐ

1

3



. Ⓐ

5

. Ⓒ

5

. Ⓓ

1

3

Câu 3. Tìm giá trị nhỏ nhất

m

của hàm số

4 2

13

y x x

  

trên đoạn

 

2;3



.

Ⓐ

51

4



m

Ⓑ

49

4

m 

. Ⓒ

13

m



. Ⓓ

51

2

m



Câu 4. Giá trị nhỏ nhất của hàm số

1

x

y

x







trên đoạn

 

0;3

là

Ⓐ

 

0; 3

1

min

2

y



. Ⓑ

 

0; 3

min 3

y

 

. Ⓒ

 

0; 3

min 1y 

. Ⓓ

 

0; 3

min 1

y

 

.

Câu 5. Gọi

M

,

m

lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số

 

3 2

3f x x x

 

trên đoạn

 

1;1



.

Tính

M m

.

Ⓐ

4

. Ⓑ 4. Ⓒ

2

. Ⓓ 2.

Câu 6. Cho hàm số

4 2

2 3

y x x

  

. Giá trị lớn nhất, nhỏ nhất của hàm số trên

 

2;2



là

Ⓐ

 

2;2

min 2

y





, không có giá trị lớn nhất. Ⓑ

 

2;2

max 11

y





,

 

2;2

min 2

y





.

Ví dụ 6. Giá trị lớn nhất của hàm số

3 2

3 7

y x x

  

trên đoạn

 

0;4

là

Ⓐ

0

. Ⓑ

11

.

Ⓒ

9

. Ⓓ

7

.

Lời giải:.....................................................................

......................................................................................

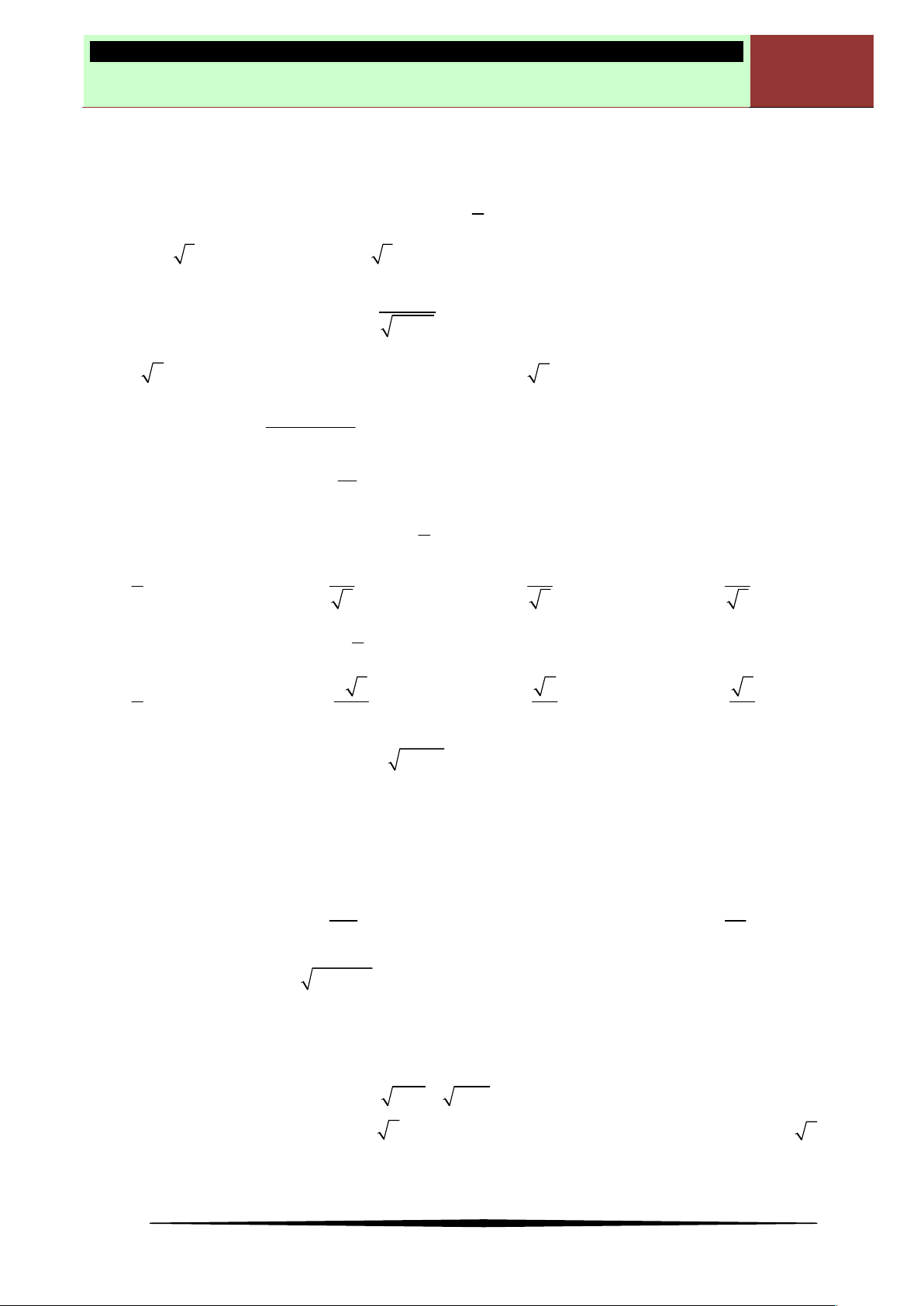
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 38

Ⓒ

 

2;2

max 3

y





,

 

2;2

min 2

y



 

. Ⓓ

 

2;2

max 3

y





,

 

2;2

min 2

y





.

Câu 7. Tìm giá trị nhỏ nhất

m

của hàm số

3

y x

x

 

trên

 

0;



.

Ⓐ

4

4 3

m  . Ⓑ

2 3

m  . Ⓒ

4

m



Ⓓ

2

m



Câu 8. Giá trị lớn nhất của hàm số

2

1







x

y

x

trên khoảng

 

;

 

bằng

Ⓐ

2 2

. Ⓑ

1

. Ⓒ

2

. Ⓓ

2

.

Câu 9. Cho hàm số

2

3 2 3

1

x x

y

x

 





, tập giá trị của hàm số là

Ⓐ

 

2;4

. Ⓑ

15

;5

2

 

 

 

. Ⓒ

 

2;3

. Ⓓ

 

3;4

.

Câu 10. Trên khoảng

 

0;1

hàm số

3

1

y x

x

 

đạt giá trị nhỏ nhất tại

0

x

bằng

Ⓐ

1

2

. Ⓑ

4

1

3

. Ⓒ

3

1

3

. Ⓓ

1

3

.

Câu 11. Cho

 

2

:

P y x

và

1

2;

2

A

 



 

 

. Gọi

M

là một điểm bất kì thuộc

 

P

. Khoảng cách

MA

bé nhất là

Ⓐ

5

4

. Ⓑ

2 3

3

. Ⓒ

2

. Ⓓ

5

2

.

Câu 12. Giá trị lớn nhất của hàm số

2

4

y x 

là

Ⓐ 2. Ⓑ 0. Ⓒ 4. Ⓓ 1.

Câu 13. Gọi

M

và

m

là giá trị lớn nhất và nhỏ nhất của hàm số

 

3 2

2 1f x x x x   

trên đoạn

 

0;2

.

Giá trị của

M m

bằng

Ⓐ

3

. Ⓑ

112

27

. Ⓒ

4

. Ⓓ

58

27

.

Câu 14. Cho hàm số

2

12 3y x x

   . Giá trị lớn nhất của hàm số bằng

Ⓐ

2

. Ⓑ

4

. Ⓒ

3

. Ⓓ

1

.

Câu 15. Tìm tập giá trị của hàm số

1 9

y x x   

Ⓐ

 

1; 9

T 

. Ⓑ

2 2; 4

 



 

T . Ⓒ

 

1; 9

T 

. Ⓓ

0; 2 2

T

 



 

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 39

Câu 16. Gọi

M

,

m

tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2cos 1

cos 2

x

y

x







. Khẳng định

nào sau đây đúng?

Ⓐ

9 0

M m

 

. Ⓑ

9 0

M m

 

. Ⓒ

9 0

M m

 

. Ⓓ

0

M m

 

.

Câu 17. Giá trị lớn nhất của hàm số

2

y x x  

là

Ⓐ

5

4



. Ⓑ

2

. Ⓒ

9

4

. Ⓓ

3 1

.

Câu 18. Giá trị nhỏ nhất của biểu thức

2

3 8 6

2 1

x x

A

x x

 



 

là

Ⓐ

2

. Ⓑ

1

. Ⓒ

1

. Ⓓ

2

.

Câu 19. Gọi

M

,

m

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2 cosy x x

 

trên đoạn

0;

2



 

 

 

. Tính

M m

.

Ⓐ

1 2

4



 

. Ⓑ

2





. Ⓒ

1

4





. Ⓓ

1 2

4



 

.

Câu 20. Giá trị nhỏ nhất của hàm số

2

1

x

y

x







trên miền

0

x



là

Ⓐ

2

. Ⓑ

1

2

. Ⓒ

1

. Ⓓ

2 1

.

Câu 21. Giá trị nhỏ nhất của hàm số

3

sin cos2 sinx 2

y x x

   

bằng

Ⓐ

5

. Ⓑ

1

27

. Ⓒ

1

. Ⓓ

23

27

Câu 22. Giá trị lớn nhất của hàm số

3

4

2cos cos

3

y x x

 

trên

 

0;



.

Ⓐ

 

0;

2

max

3

y





. Ⓑ

 

0;

10

max

3

y





. Ⓒ

 

0;

2 2

max

3

y





. Ⓓ

 

0;

max 0

y





.

Câu 23. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số

3 2

cos 9cos 6sin 1y x x x   

là

Ⓐ

2

. Ⓑ

1

. Ⓒ

1

. Ⓓ

2

.

Câu 24. Gọi

M

,

m

lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số

 

cos 1 2cos2y x x

 

. Tìm

M m

.

Ⓐ

3

. Ⓑ

0

. Ⓒ

1

. Ⓓ

2

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 40

Câu 25. Gọi

M

và

m

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

3 2

4 2

2 4

8 16

x x x

y

x x

 



 

. Tính

M m

.

Ⓐ

2

. Ⓑ

1

. Ⓒ

1

2

. Ⓓ

1

4

.

Câu 26. Cho hàm số

2

sin 1

sin sin 1

x

y

x x





 

. Gọi

M

là giá trị lớn nhất và

m

là giá trị nhỏ nhất của hàm số đã

cho. Chọn mệnh đề đúng.

Ⓐ

3

2

M m

 

. Ⓑ

3

2

M m



. Ⓒ

1

M m

 

. Ⓓ

2

3

M m

 

.

Câu 27. Gọi

,M m

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2

4 5

y x x

  

trên đoạn

 

3;0



. Khi đó tổng

M m

là

Ⓐ

5

. Ⓑ

9

. Ⓒ

14

. Ⓓ

8

.

Câu 28. Cho hàm số

4 2

16 7

y x x

  

, gọi

,M m

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

trên đoạn

 

0;4

. Tính giá trị biểu thức

2M m

.

Ⓐ

14

. Ⓑ

57

. Ⓒ

64

. Ⓓ

60

.

Câu 29. Gọi

M

,

m

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

 

2 1

2

x

f x

x







trên đoạn

 

1;1



. Giá trị của biểu thức

2 3M m

là

Ⓐ

1

. Ⓑ

1

3

. Ⓒ

0

. Ⓓ

6

.

Câu 30. Gọi

M

,

m

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2 2

1 3

y x x

   

. Khi đó

4

a

M m b c

  

, với

a

,

b

,

c

nguyên. Tính

T a bc 

.

Ⓐ

7

. Ⓑ

9

. Ⓒ

12

. Ⓓ

8

.

CÁC VÍ DỤ

Ví dụ 1. Tìm giá trị nhỏ nhất của hàm số

 

y f x



trên

 

1; 1



, biết đồ thị hàm số

 

y f x



như hình vẽ.

Dạng 2:

Dựa vào bảng biến thiên hoặc đồ thị để kết luận GTLN, GTNN

của hàm số

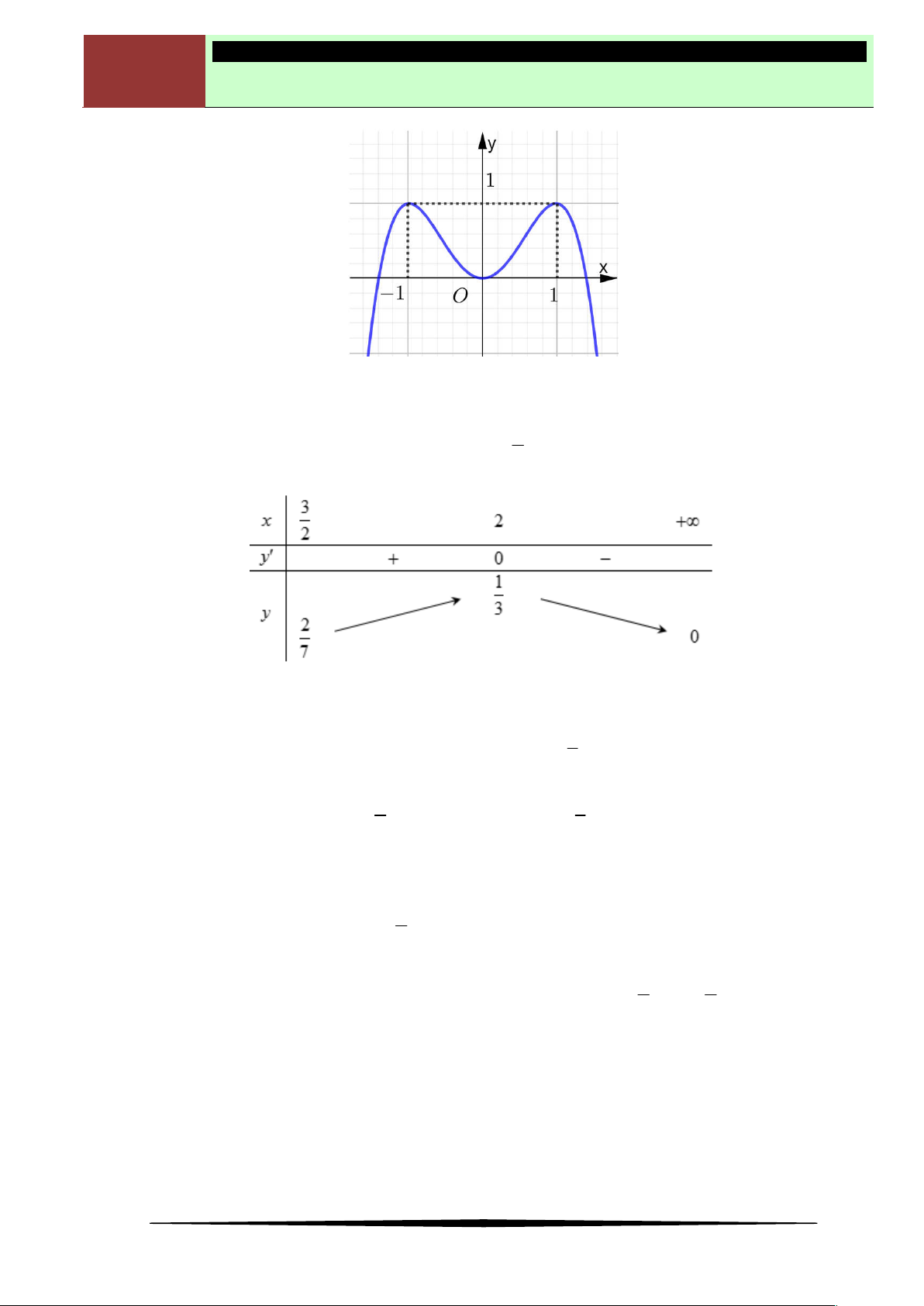
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 41

Ⓐ

0

. Ⓑ

1

. Ⓒ

1

. Ⓓ

2

.

Ví dụ 2. Cho hàm số

 

y f x



xác định trên nửa khoảng

3

;

2

 







 

và có bảng biến thiên dưới đây:

Khẳng định nào sau đây đúng?

Ⓐ Hàm số có giá trị nhỏ nhất bằng

0

và giá trị lớn nhất bằng

1

3

.

Ⓑ Hàm số có giá trị nhỏ nhất bằng

2

7

và giá trị lớn nhất bằng

1

3

.

Ⓓ Hàm số đạt giá trị nhỏ nhất khi

3

2

x



.

Ví dụ 3. Cho hàm số

 

y f x



xác định và liên tục trên khoảng

1

;

2

 



 

 

và

1

;

2

 



 

 

. Đồ thị hàm số

 

y f x



là đường cong trong hình vẽ bên.

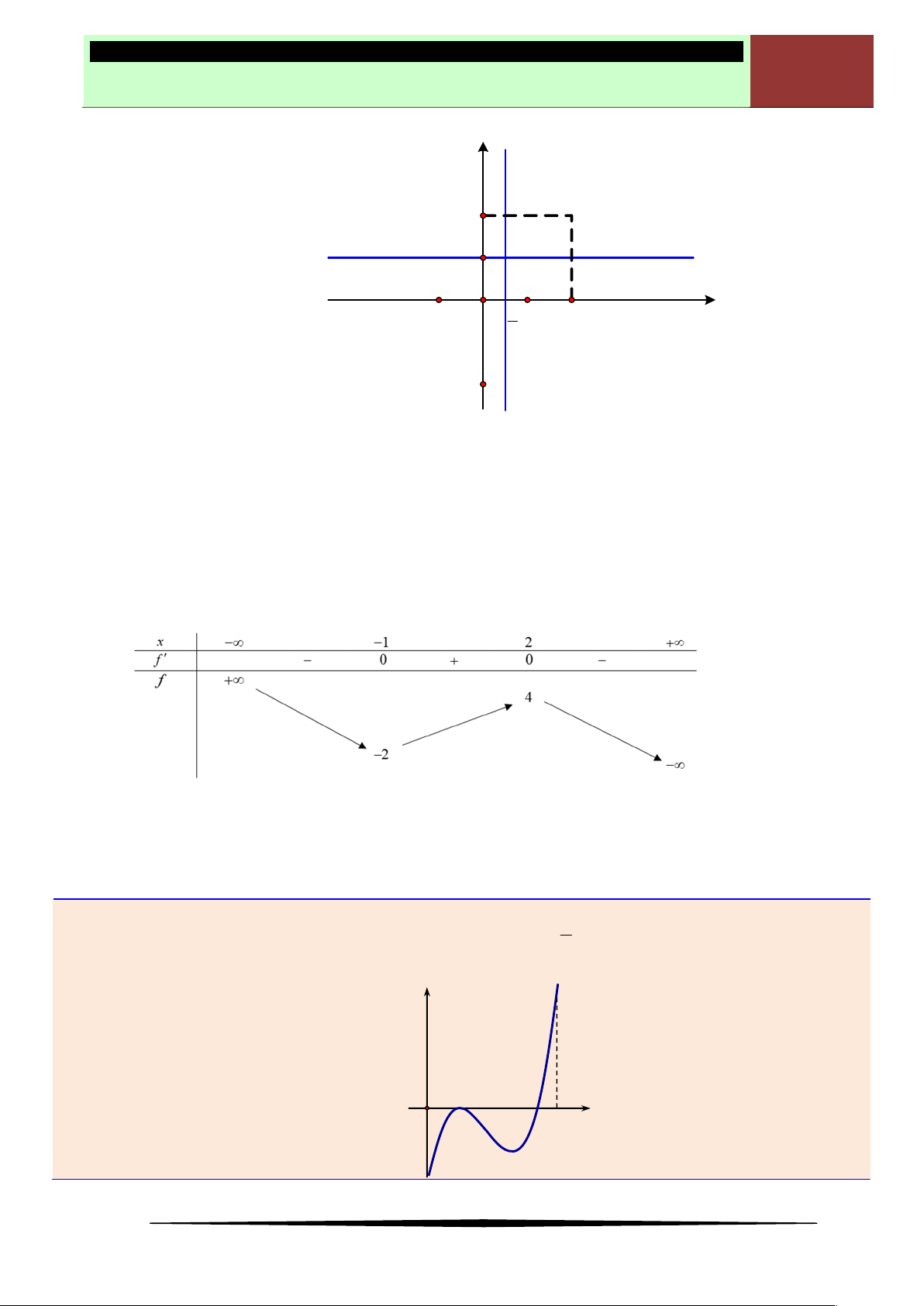
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 42

O

x

y

1

2

1

2

1

2

1

2

Tìm mệnh đề đúng trong các mệnh đề sau.

Ⓐ

 

 

1;2

max 2f x 

. Ⓑ

 

 

2;1

max 0f x





.

Ⓒ

 

   

3;0

max 3f x f



 

. Ⓓ

 

   

3;4

max 4f x f

Ví dụ 4. Cho hàm số

 

y f x

liên tục trên R và có bảng biến thiên như sau:

Gọi M là giá trị lớn nhất của hàm số

   

3y g x f x  

trên

 

0;3

. Mệnh đề nào sau đây đúng?

Ⓐ

 

0M f

. Ⓑ

 

3M f

. Ⓒ

 

1M f

. Ⓓ

 

2M f

.

Ví dụ 5. Cho hàm số

 

y f x

xác định và liên tục trên đoạn

7

0;

2

 

 

 

có đồ thị hàm số

 

y f x





như hình

vẽ.

O

x

1

3

3,5

y

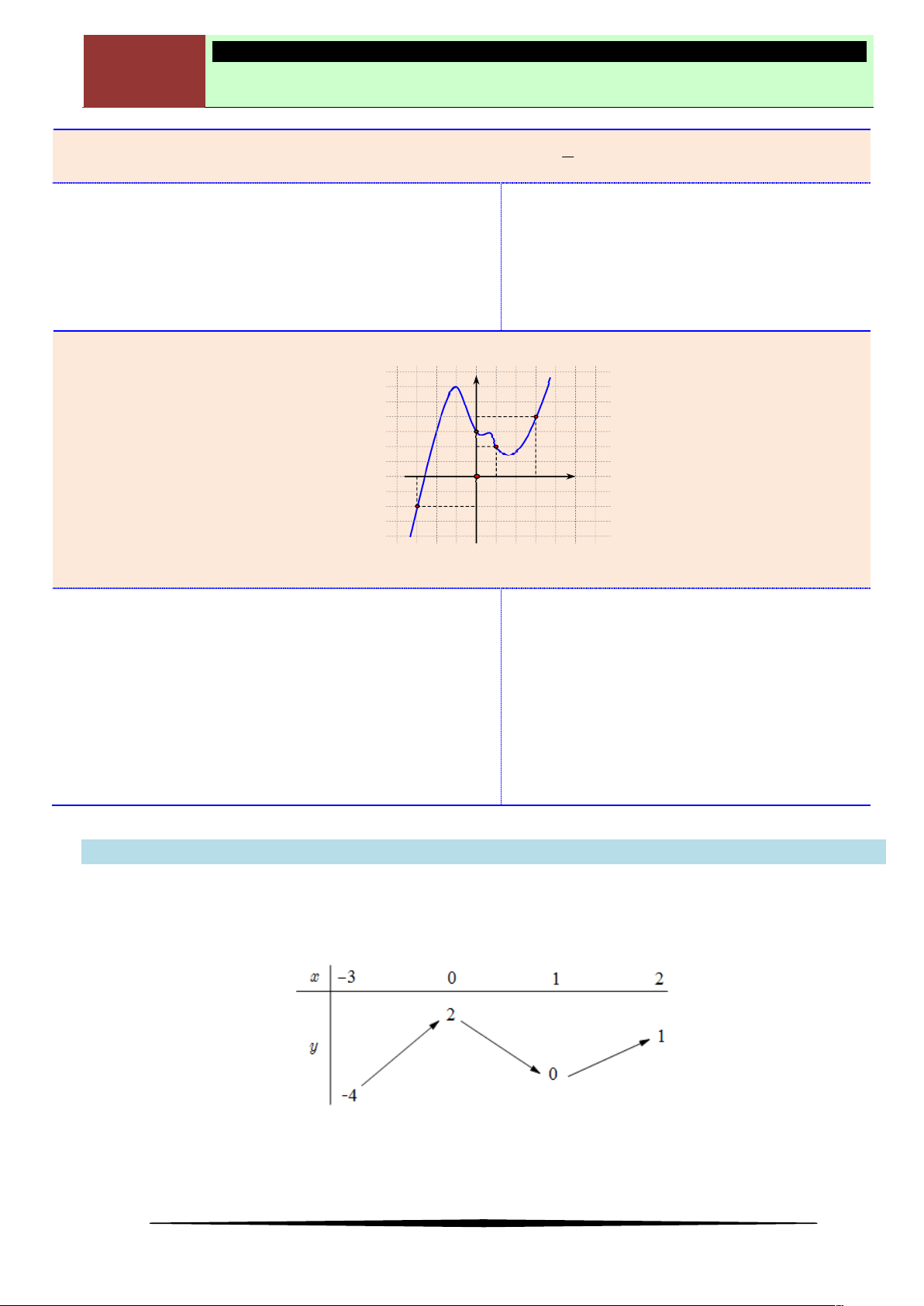
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 43

Hỏi hàm số

 

y f x

đạt giá trị nhỏ nhất trên đoạn

7

0;

2

 

 

 

tại điểm

0

x nào dưới đây?

Ⓐ

0

2x  . Ⓑ

0

1x  .

Ⓒ

0

0x  . Ⓓ

0

3x .

Lời giải

..................................................................................

Ví dụ 6. Cho hàm số

 

y f x

liên tục trên

R

. Đồ thị của hàm số

 

y f x





như hình bên.

Đặt

     

2

2 1g x f x x  

. Mệnh đề nào dưới đây đúng.

Ⓐ

 

3;3

( ) (1).Min g x g





Ⓑ

 

3;3

( ) (1).Max g x g





Ⓒ

 

3;3

( ) (3).Max g x g



 .

Ⓓ Không tồn tại giá trị nhỏ nhất của

( )g x

trên

 

3;3 .



Lời giải

............................................................................................

...................

BÀI TẬP VỀ NHÀ

Câu 1. Cho hàm số

 

y f x

liên tục trên

 

3;2

và có bảng biến thiên như hình dưới. Gọi

M

,

m

lần

luợt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

 

y f x

trên

 

3;2

. Tính

M m

.

Ⓐ

5

. Ⓑ

7

. Ⓒ

6

Ⓓ

4

.

Câu 2. Cho hàm số

 

y f x

xác định, liên tục trên

R

và có bảng biến thiên:

O

1

3

x

2

4

2

3

y

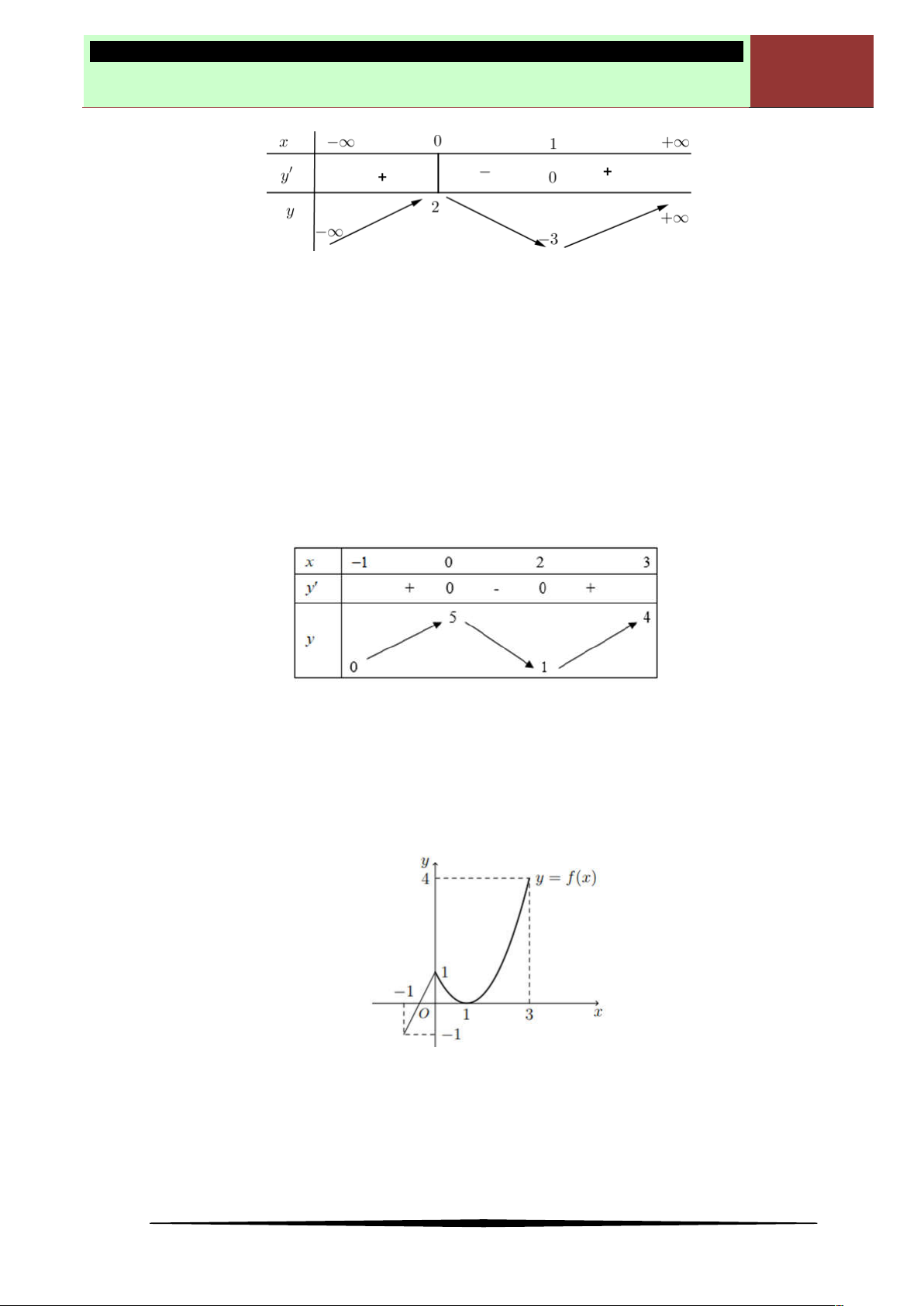
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 44

Khẳng định nào sau đây là khẳng định đúng:

Ⓐ Hàm số có giá trị lớn nhất bằng

2

và giá trị nhỏ nhất bằng

3.

Ⓑ Hàm số có đúng một cực trị.

0x 

và đạt cực tiểu tại

1.x 

Ⓓ Hàm số có giá trị cực tiểu bằng

2.

Câu 3. Hàm số

( )y f x

liên tục và có bảng biến thiên trong đoạn

[ 1; 3]

cho trong hình bên. Gọi

M

là

giá trị lớn nhất của hàm số

 

y f x



trên đoạn

 

1;3



. Tìm mệnh đề đúng?

Ⓐ

( 1)M f 

. Ⓑ

 

3M f

. Ⓒ

(2)M f

. Ⓓ

(0)M f

.

Câu 4. Cho hàm số

 

f x

liên tục trên

 

1;3

và có đồ thị như hình vẽ bên.

Gọi

,M m

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

 

y f x

trên

 

1;3

. Tính

M m

.

Ⓐ

3

. Ⓑ

4

. Ⓒ

5

. Ⓓ

1

.

Câu 5. Cho hàm số

 

y f x

liên tục trên



và có đồ thị như hình vẽ bên.

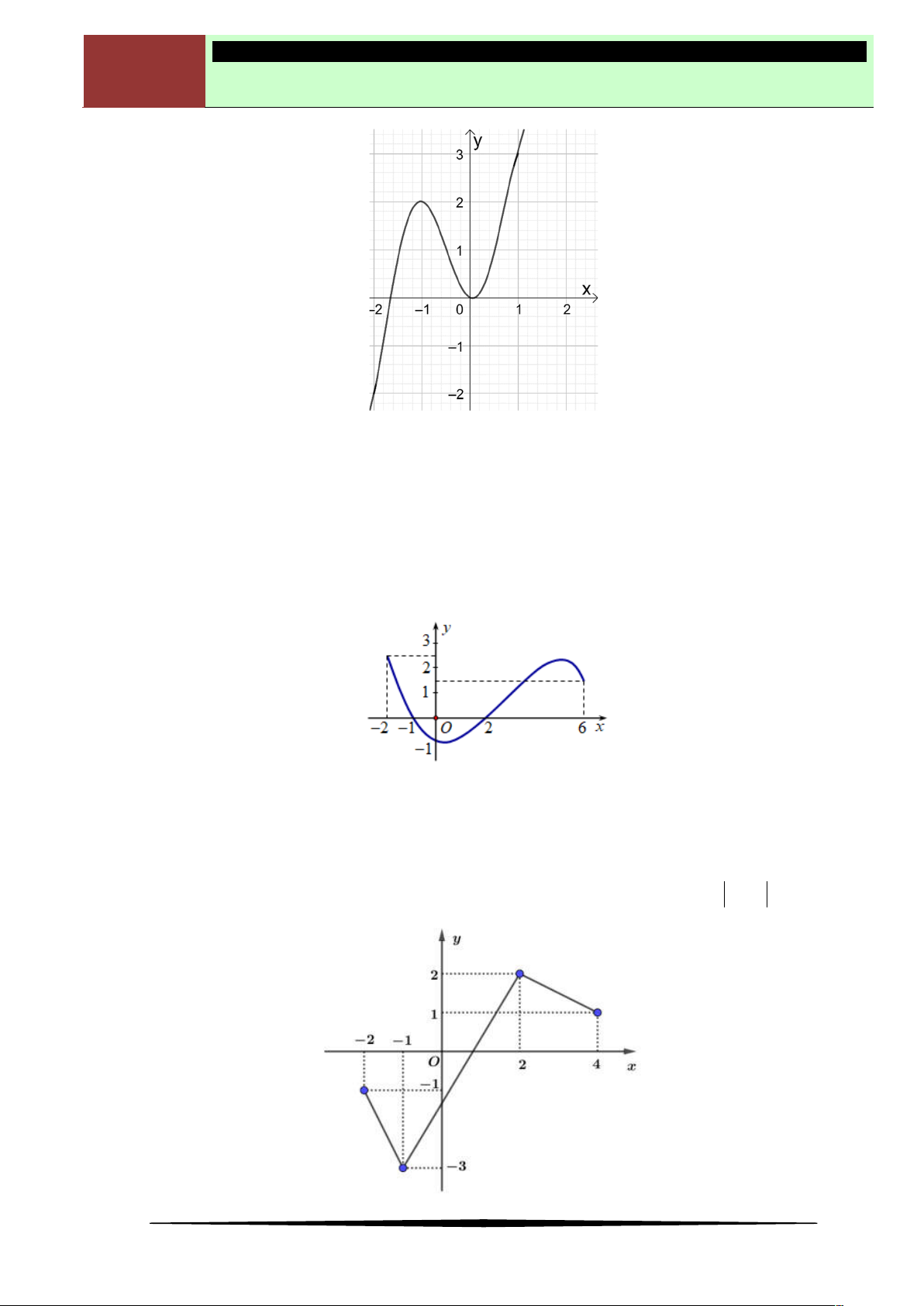
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 45

Gọi

a

,

A

lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số

 

1f x 

trên đoạn

 

1;0

. Giá trị

a A

bằng

Ⓐ

1

. Ⓑ

2

. Ⓒ

0

. Ⓓ

3

.

Câu 6. Cho hàm số

 

y f x

có đạo hàm

 

y f x





liên tục trên



và đồ thị của hàm số

 

f x



trên đoạn

 

2;6



như hình vẽ bên.

Tìm khẳng định đúng trong các khẳng định sau.

Ⓐ

   

[ 2;6]

max 2 .f x f



  Ⓑ

   

[ 2;6]

max 6 .f x f





Ⓒ

     

 

[ 2;6]

max max 1 , 6 .f x f f



  Ⓓ

   

[ 2;6]

max 1 .f x f



 

Câu 7. Cho hàm số

 

y f x

có đồ thị trên đoạn

 

2; 4

như hình vẽ bên. Tìm

 

 

2; 4

max f x



.

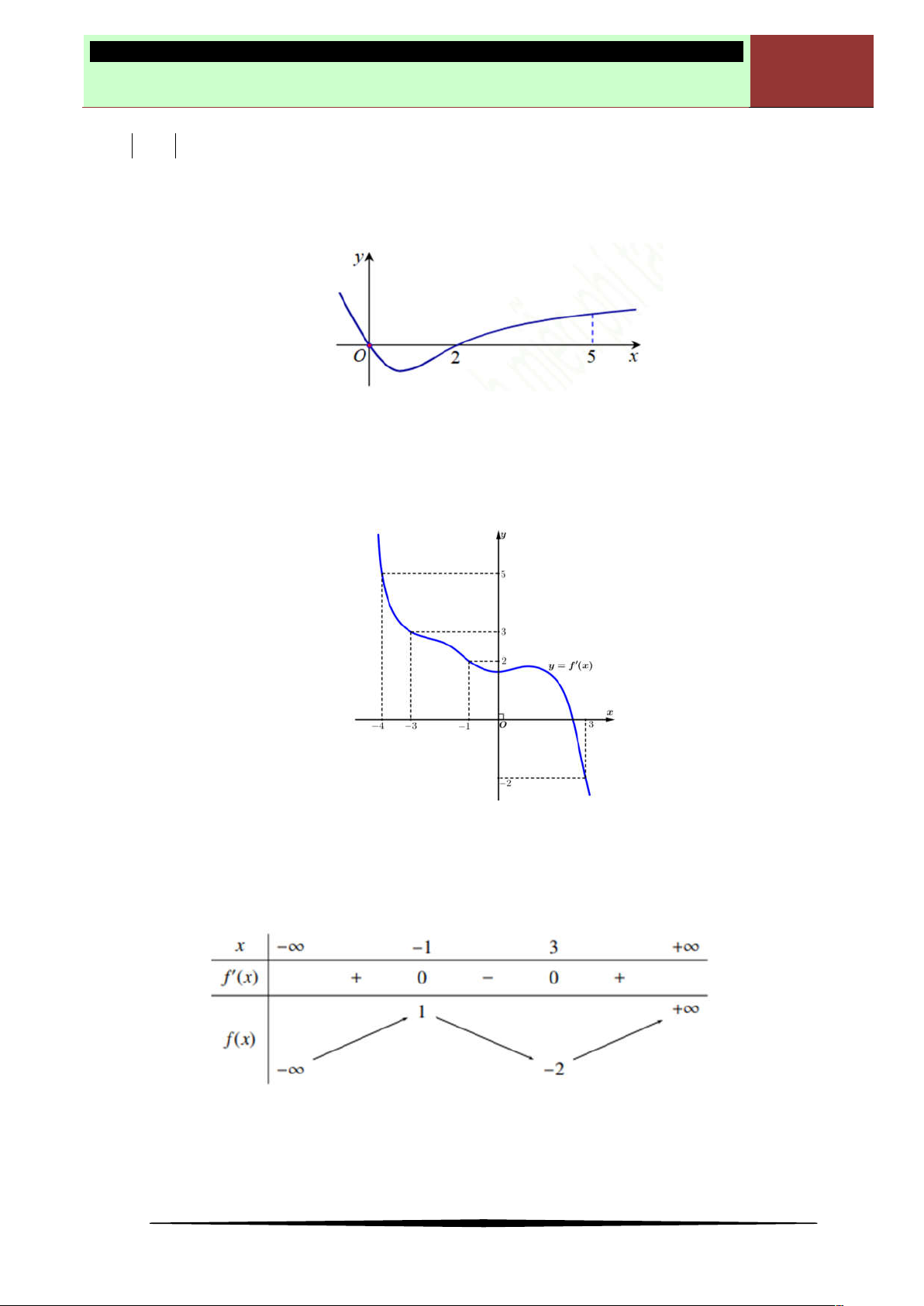
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 46

Ⓐ

 

0f

. Ⓑ

2

.

Ⓒ

3

. Ⓓ

1

.

Câu 8. Cho hàm số

 

f x

có đạo hàm trên



và có đồ thị của hàm

 



y f x

như hình vẽ. Biết rằng

       

0 3 2 5  f f f f

. Giá trị nhỏ nhất và giá trị lớn nhất của

 

f x

trên đoạn

 

0;5

lần lượt là:

Ⓐ

 

0f

,

 

5f

. Ⓑ

 

2f

,

 

0f

.

Ⓒ

 

1f

,

 

3f

. Ⓓ

 

2f

,

 

5f

.

Câu 9. Cho hàm số

 

f x

. Biết hàm số

 

f x



có đồ thị như hình dưới đây. Trên đoạn

 

4;3

, hàm số

     

2

2 1g x f x x  

đạt giá trị nhỏ nhất tại điểm

Ⓐ

3x  

. Ⓑ

4x  

. Ⓒ

3x 

. Ⓓ

1x  

.

Câu 10. Cho hàm số

 

y f x

có bảng biến thiên như sau:

Gọi

, M m

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

 

2cos 1 y f x

. Tính

M m

.

Ⓐ

1

. Ⓑ

2

. Ⓒ

1

. Ⓓ

0

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 47

CÁC VÍ DỤ

Dạng 3:

Một số bài toán vận dụng

Ví dụ 1. Một vật chuyển động theo quy luật

3 2

1

9

3

s t t t  

với

t

(giây) là khoảng thời gian tính từ

lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong

khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao

nhiêu ?

Ⓐ

 

89 /m s

. Ⓑ

 

109 /m s

Ⓒ

 

71 /m s

. Ⓓ

 

25

/

3

m s

Lời giải:.....................................................................

......................................................................................

Ví dụ 2. Một bác nông dân cần xây dựng một hố ga không có nắp dạng hình hộp chữ nhật có dung tíchlà

3

3200cm

, tỉ số giữa chiều cao của hố và chiều rộng của đáy bằng

2

. Hãy xác định diện tích của đáy hố

ga để khi xây tiết kiệm nguyên vật liệu nhất?

Ⓐ

2

1200cm

. Ⓑ

2

120cm

.

Ⓒ

2

160cm

. Ⓓ

2

1600cm

.

Lời giải:.....................................................................

......................................................................................

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 48

BÀI TẬP VỀ NHÀ

Câu 1. Một vật chuyển động theo quy luật

3 2

1

6

2

s t t

  

với

t

(giây)là khoảng thời gian từ khi vật bắt đầu

chuyển động và

s

(mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian

6

giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng bao nhiêu?

Ⓐ

 

24 m/s

. Ⓑ

 

108 m/s

. Ⓒ

 

64 m/s

. Ⓓ

 

18 m/s

.

Câu 2. Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu

 

m

h

của mực nước trong

kênh tính theo thời gian

 

ht

được cho bởi công thức

3cos 12

6 3

t

h

 

 

  

 

 

.

Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?

Ⓐ

 

22 h

t 

. Ⓑ

 

15 h

t 

. Ⓒ

 

14 h

t 

. Ⓓ

 

10 h

t 

.

Câu 3. Trong các tam giác vuông có tổng của một cạnh góc vuông và cạnh huyền là

 

0

a a



, tam giác có

diện tích lớn nhất là

Ⓐ

2

5 6

a

. Ⓑ

2

3 6

a

. Ⓒ

2

6 5

a

.

Ⓓ

2

6 3

a

.

Câu 4. Một cơ sở sản xuất khăn mặt đang bán mỗ chiếc khăn với giá

30.000

đồng một chiếc và mỗi tháng

cơ sở bán được trung bình

3000

chiếc khăn. Cơ sở đang có kế hoạch tăng giá bán để có lợ nhuận tốt hơn.

Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá

30.000

đồng mà cứ tăng giá thêm

1.000

đồng thì mỗi tháng sẽ bán ít hơn

100

chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là

18.000

đồng. Hỏi cơ sở sản xuất phải bán là mức giá bao nhiêu để đạt lợi nhuận lớn nhất.

Ví dụ 3. Từ một tấm tôn có hình dạng elip với độ dài trục lớn bằng

6

độ dài trục bé bằng

4

. Người thợ

cần cắt một tấm tôn có dạng hình chữ nhật nội tiếp elíp, sau đó gò tấm tôn hình chữ nhật này thành một

hình trụ không có đáy (như hình bên).Tính thể tích lớn nhất có thể thu được của khối trụ đó?

Ⓐ

4 3

V





. Ⓑ

3 2

V





.

Ⓒ

5 2

V





. Ⓓ

8 3

V





.

Lời giải:.....................................................................

......................................................................................

x

B

A

H

C

B

2x

A

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 49

Ⓐ

43.000

đồng. Ⓑ

36.000

đồng. Ⓒ

39.000

đồng. Ⓓ

42.000

đồng.

Câu 5. Từ một tấm tôn hình chữ nhật có kích thước

40

cm và

60

cm người ta cắt bỏ bốn hình vuông ở bốn

góc để gập lại được một cái hộp không nắp.

Để thể tích của hộp đó lớn nhất thì cạnh hình vuông cắt bỏ có giá trị gần với giá trị nào sau đây?

Ⓐ

7,85

cm. Ⓑ

15

cm. Ⓒ

3,92

cm. Ⓓ

18

cm.

Câu 6. Ông

A

dự định sử dụng hết

2

5m

kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không

nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có thể tích lớn nhất

bằng bao nhiêu (kết quả làm tròn đến hang phần trăm)?

Ⓐ

3

1,01m

. Ⓑ

3

1,51m

. Ⓒ

3

1,33m

. Ⓓ

3

0,96 m

.

Câu 7. Một cửa hàng bán lẻ bán 2500 cái tivi mỗi năm. Chi phí gửi trong kho là 10USD một cái một năm.

Để đặt hàng nhà sản xuất thì mỗi lần chi phí cố định là 20USD, cộng thêm 9USD mỗi chiếc. Biết rằng số

lượng tivi trung bình gửi trong kho bằng một nửa số tivi của mỗi lần đặt hàng. Như vậy cửa hàng nên đặt

hàng nhà sản xuất bao nhiêu lần mỗi năm và mỗi lần đặt bao nhiêu cái để chi phí hàng tồn kho là thấp nhất?

Ⓐ 20 lần mỗi năm và 90 cái mỗi lần. Ⓑ 25 lần mỗi năm và 110 cái mỗi lần.

Câu 8. Một công ty bất động sản có

50

căn hộ cho thuê. Biết rằng nếu cho thuê

mỗi căn hộ với giá

2.000.000

đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần

tăng giá cho thuê, mỗi căn hộ thêm

50.000

đồng một tháng thì có thêm một căn hộ bị bỏ

trống. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công

ty có thể đạt được trong một tháng là bao nhiêu?

Ⓐ

115.250.000

. Ⓑ

101.250.000

. Ⓒ

100.000.000

. Ⓓ

100.250.000

.

60cm

40cm

x

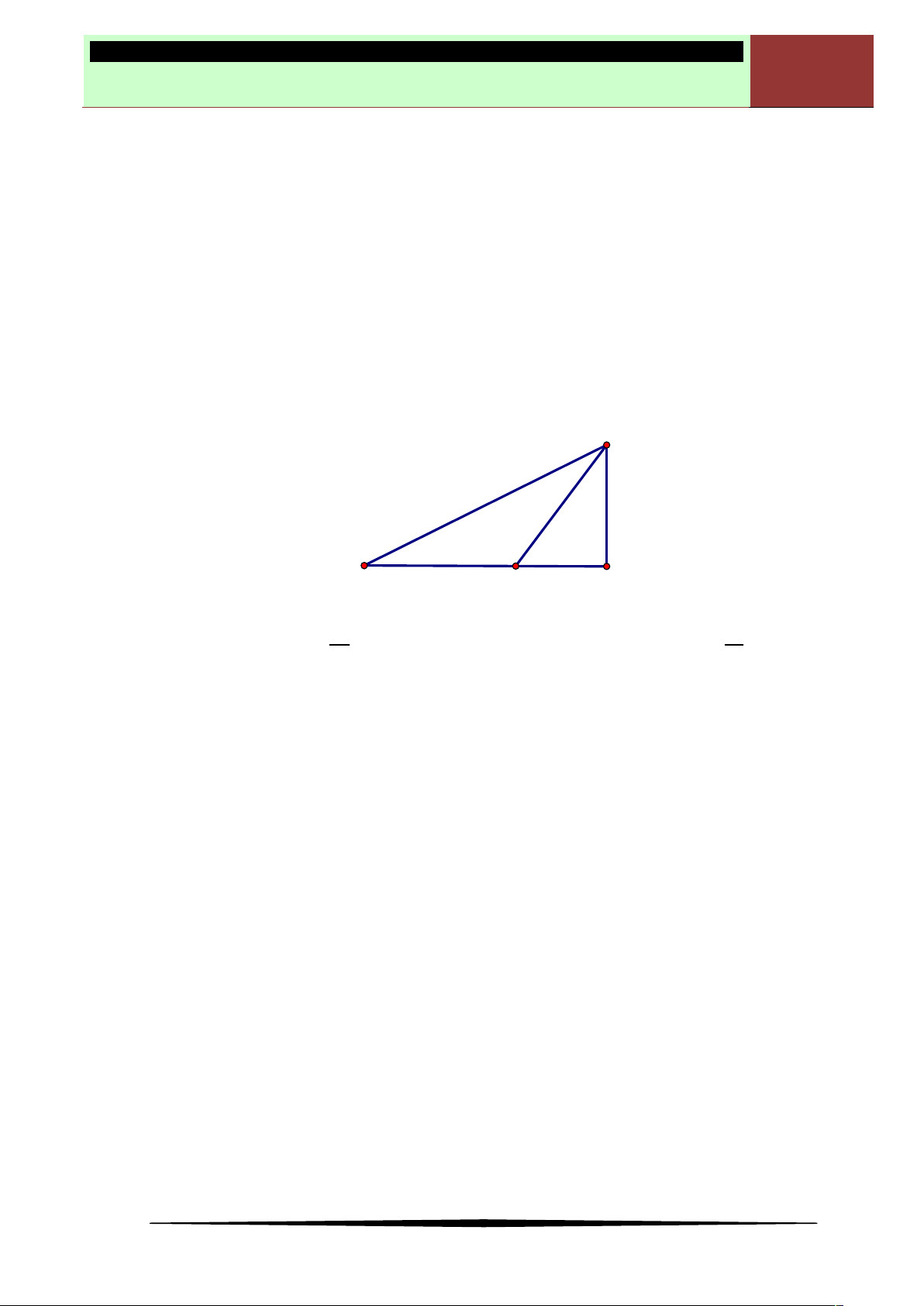
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 50

Câu 9. Công ty xe khách Thiên Ân dự định tăng giá vé trên mỗi hành khách. Hiện tại giá vé là

50.000

VNĐ

một khách và có

10.000

khách trong một tháng. Nhưng nếu tăng giá vé thêm

1.000

VNĐ một hành khách

thì số khách sẽ giảm đi

50

người mỗi tháng. Hỏi công ty sẽ tăng giá vé là bao nhiêu đối với một khách để

có lợi nhuận lớn nhất?

Ⓐ

50.000

VNĐ. Ⓑ

15.000

VNĐ. Ⓒ

35.000

VNĐ. Ⓓ

75.000

VNĐ.

Câu 10. Một người cần đi từ khách sạn

A

bên bờ biển đến hòn đảo

C

. Biết rằng khoảng cách từ đảo

C

đến

bờ biển là

10km

, khoảng cách từ khách sạn

A

đến điểm

B

trên bờ gần đảo

C

nhất là

40km

. Người đó có

thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy (như hình vẽ bên). Biết kinh phí đi đường thủy là

5 USD/km

, đi đường bộ là

3 USD/km

. Hỏi người đó phải đi đường bộ một khoảng bao nhiêu để kinh phí

nhỏ nhất? (

40km

AB



,

10km

BC



)

Ⓐ

10km

. Ⓑ

65

km

2

. Ⓒ

40km

. Ⓓ

15

km

2

.

Câu 11. Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng

3

200 m

. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là

300

nghìn đồng/

2

m

(chi phí được tính theo diện tích xây dựng, bao gồm diện tích đáy và diện tích xung quanh, không tính chiều

dày của đáy và diện tích xung quanh, không tính chiều dày của đáy và thành bể). Hãy xác định chi phí thấp

nhất để xây bể(làm tròn đến đơn vị triệu đồng)

Ⓐ

75

triệu đồng. Ⓑ

51

triệu đồng. Ⓒ

36

triệu đồng. Ⓓ

46

triệu đồng.

Câu 12. Một người bán buôn Thanh Long Đỏ ở Lập Thạch – Vĩnh Phúc nhận thấy rằng: Nếu bán với giá

20000

nghìn

/kg

thì mỗi tuần có

90

khách đến mua và mỗi khách mua trung bình

60

kg

. Cứ tăng giá

2000

nghìn

/kg

thì khách mua hàng tuần giảm đi

1

và khi đó khách lại mua ít hơn mức trung bình

5

kg

, và như

vậy cứ giảm giá

2000

nghìn

/kg

thì số khách mua hàng tuần tăng thêm

1

và khi đó khách lại mua nhiều

hơnmức trung bình

5

kg

. Hỏi người đó phải bán với giá mỗi

kg

là bao nhiêu để lợi nhuận thu được hàng

tuần là lớn nhất, biết rằng người đó phải nộp tổng các loại thuế là

2200

nghìn

/kg

. (Kết quả làm tròn đến

hàng nghìn)

Ⓐ

16000

nghìn

/kg

. Ⓑ

24000

nghìn

/kg

. Ⓒ

22000

nghìn

/kg

. Ⓓ

12000

nghìn

/kg

.

A

B

C

D

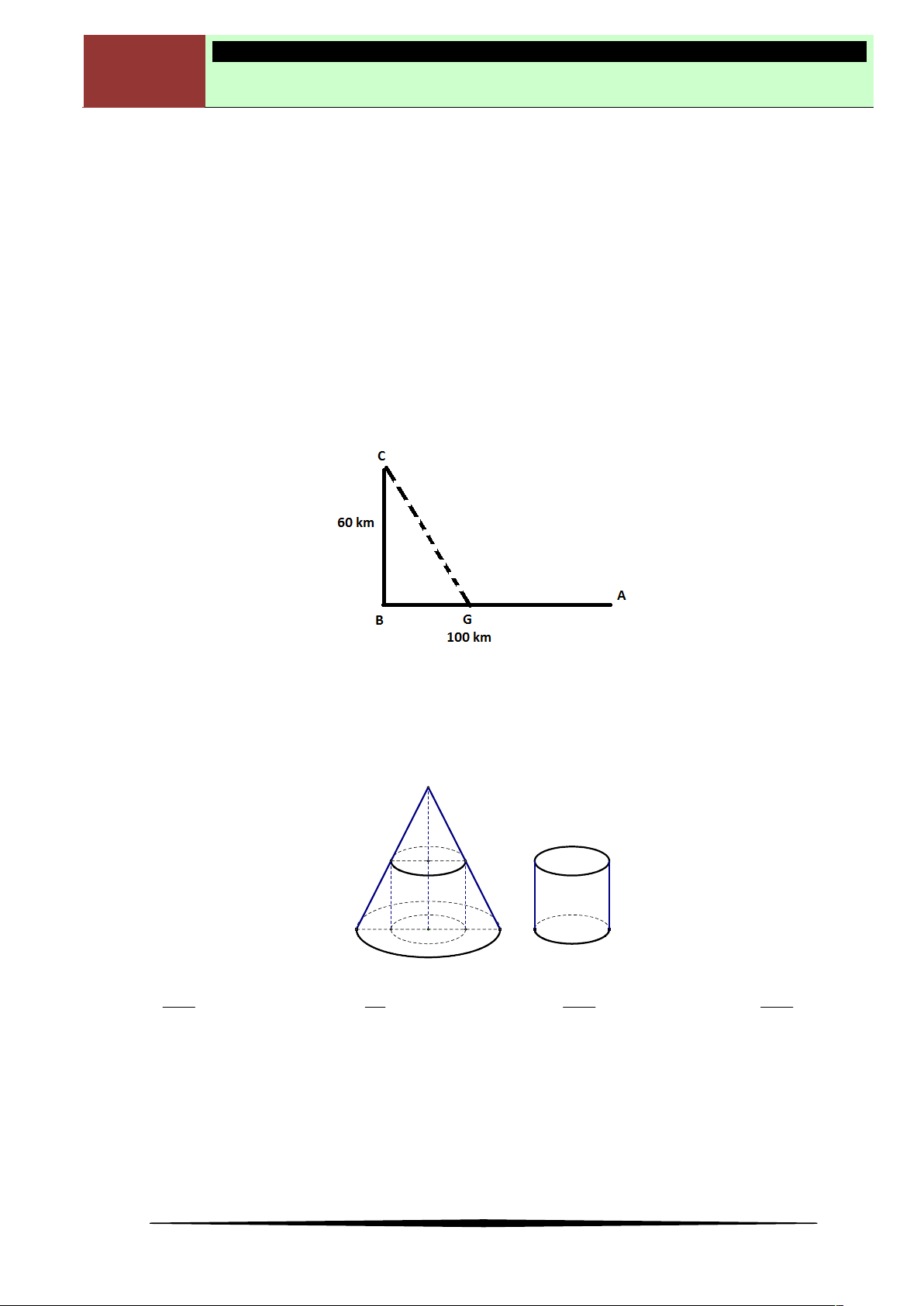
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 51

Câu 13. Ông A muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích

bằng

3

2304m

. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là

600000

đồng/

2

m

. Nếu ông A biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp

nhất. Hỏi ông A trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu (biết độ dày thành bể và đáy bể không

đáng kể)?

Ⓐ

584.1

triệu đồng. Ⓑ

548.1

triệu đồng. Ⓒ

581.4

triệu đồng. Ⓓ

518.4

triệu đồng.

Câu 14. Đường dây điện 110 KV kéo từ trạm phát ( điểm A) trong đất liền ra Côn Đảo ( điểmC). Biết khoảng

cách ngắn nhất từ điểm C đến điểm B trên đất liền là 60km, khoảng cách từ A đến B là 100km, góc ABC

bằng

0

90

. Mỗi km dây điện dưới nước chi phí là 5000 USD, chi phí cho mỗi km dây điện trên bờ là 3000

USD. Hỏi điểm G cách A bao nhiêu để mắc dây điện từ A đến G rồi từ G đến C chi phí ít nhất.

Ⓐ 55 km. Ⓑ 40 km. Ⓒ 60 km. Ⓓ 45 km.

Câu 15. Một khúc gỗ có dạng hình khối nón có bán kính đáy bằng

2mr 

, chiều cao

6m

h



. Bác thợ

mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi

V

là thể tích lớn

nhất của khúc gỗ hình trụ sau khi chế tác. Tính

V

?

Ⓐ

 

2

32

m

9

V





. Ⓑ

 

2

32

m

9

V 

. Ⓒ

 

2

32

m

3

V





. Ⓓ

 

2

32

m

9

V





.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 52

Câu 16. Một người muốn làm cho con gái 1 chiếc lều từ vải và các ống nhựa PVC có dạng hình chóp tứ

giác đều như hình vẽ.

Biết rằng nếu em bé đi dọc theo 1 cạnh của chiếc lều với vận tốc

0,3m/s

thì phải mất

6s

, và góc giữa mỗi

ống nhựa với mặt sàn nhà là

60

. Hỏi người đó cần dùng hết ít nhất bao nhiêu mét vuông vải để may chiếc

lều trên? (Chỉ dùng vải để may các mặt bên của chiếc lều)

Ⓐ

2

9 m

. Ⓑ

2

8,5 m . Ⓒ

2

8,6m . Ⓓ

2

9,2 m

.

Câu 17. Bác Nam muốn xây dựng một hố ga không nắp hình trụ với dung tích

3

3m

. Hãy tính chi phí ít

nhất mà bác Nam phải bỏ ra xây dựng hố ga, biết tiền công và vật liệu cho

2

1m

thành bê tông của hố ga

(thành bê tông đáy và thành bê tông xung quang) là

685000

đồng. Trong các đáp án sau thì đáp án nào gần

nhất với số tiền bác Nam phải bỏ ra?

Ⓐ

6890000

đồng. Ⓑ

6260000

đồng. Ⓒ

7120000

đồng. Ⓓ

5960000

đồng.

Câu 18. Một sân chơi cho trẻ em hình chữ nhật có chiều dài

100

m và chiều rộng là

60

m người ta làm

một con đường nằm trong sân (tham khảo hình bên). Biết rằng viền ngoài và viền trong của con đường là

hai đường elip, elip của đường viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh hình chữ

nhật và chiều rộng của mặt đường là

2

m. Kinh phí cho mỗi m

2

làm đường

600.000

đồng. Tính tổng số

tiền (làm tròn đến hàng nghìn) làm con đường đó.

Ⓐ

294.053.000

đồng. Ⓑ

283.904.000

đồng. Ⓒ

293.804.000

đồng. Ⓓ

283.604.000

đồng.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 53

§5. ĐƯỜNG TIỆM CẬN

A. TÓM TẮT LÝ THUYẾT

1. Tiệm cận ngang:

• Cho hàm số

()y f x

xác định trên một khoảng vô hạn ( là khoảng dạng

( ; )a

,

( ; ) b

hoặc

( ; ) 

.

• Đường thẳng



y

được gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số

()y f x

nếu ít nhất một trong các điều kiện sau được thoả mãn

lim ( )







x

fx

,

lim ( )







x

fx

.

 Chú ý:

 Để tìm tiệm cận ngang của đồ thị hàm số ta cần tính giới hạn của hàm số tại vô cực.

 Tìm giới hạn ở vô cực của hàm số

()



Px

y

Qx

, trong đó

( ), ( )P x Q x

là các đa thức

+ Nếu bậc

()Px

bậc

()Qx

thì

lim 0





x

y

suy ra tiệm cận ngang là trục

:0Ox y

.

+ Nếu bậc

()Px

bậc

()Qx

thì

()

lim

()

x

HesobaccaonhatP x

y

HesobaccaonhatQ x







Suy ra tiệm cận

ngang



y

.

+ Nếu bậc

()Px

bậc

()Qx

thì

lim



 

x

y

suy ra đồ thị hàm số không có tiệm cận

ngang.

2. Tiệm cận đứng:

Đường thẳng

0

xx

được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số

()y f x

nếu ít nhất một trong các điều kiện sau được thoả mãn:

0 0 0 0

lim , lim , lim , lim

   

   

       

x x x x x x x x

y y y y

 Chú ý:

• Để tìm tiệm cạn đứng của đồ thị hàm số ta cần tính các giới hạn một bên của

0

x

, với

0

x

thường là

điều kiện biên của hàm số ( hay tại

0

x

hàm số không xác định)

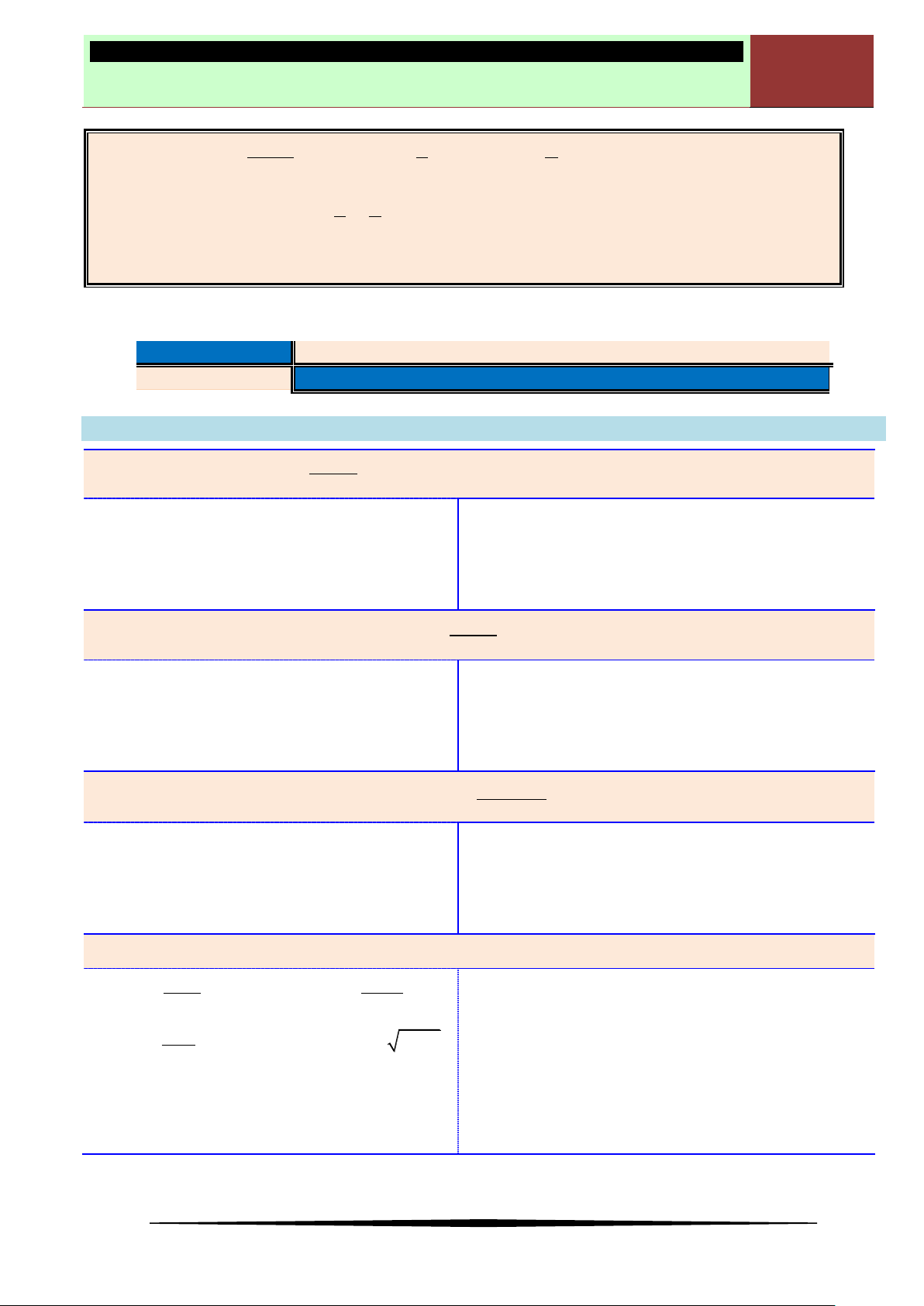
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 54

• Đồ thị hàm số







ax b

y

cx d

có TCN là



a

y

c

, TCĐ là



d

x

c

, đồ thị hàm số có tâm đối xứng là

giao điểm hai đường tiện cận

( ; )

ad

I

cc

.

B. CÁC DẠNG TOÁN THƯỜNG GẶP

CÁC VÍ DỤ

Dạng 1:

Tìm các đường tiệm cận của đồ thị các hàm số cơ bản

Ví dụ 1. Đồ thị hàm số

23

1

x

y

x

-

=

+

có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:

Ⓐ

2; 1xy==

.

Ⓑ

3; 1xy= - = -

.

Ⓒ

1; 1xy= - = -

.

Ⓓ

1; 2xy= - =

.

Lời giải :....................................................................

......................................................................................

Ví dụ 3. Tiệm cận đứng của đồ thị hàm số

2

22

1

x

y

x







là

Ⓐ

1y 

Ⓑ

1x 

Ⓒ

1x 

Ⓓ

1x 

và

1x 

.

Lời giải:.....................................................................

......................................................................................

Ví dụ 4. Số đường tiệm cận của đồ thị hàm số

2

1

2

xx

y

xx







là

Ⓐ

4

.

Ⓑ

1

.

Ⓒ

3

.

Ⓓ

2

.

Lời giải:.....................................................................

......................................................................................

Ví dụ 5. Đồ thị hàm số nào sau đây không có tiệm cận ngang?

Ⓐ

2

1

x

y

x







. Ⓑ

2

1

x

y

x







.

Ⓒ

2

1

x

y

x





. Ⓓ

2

1y x x  

.

Lời giải:.....................................................................

......................................................................................

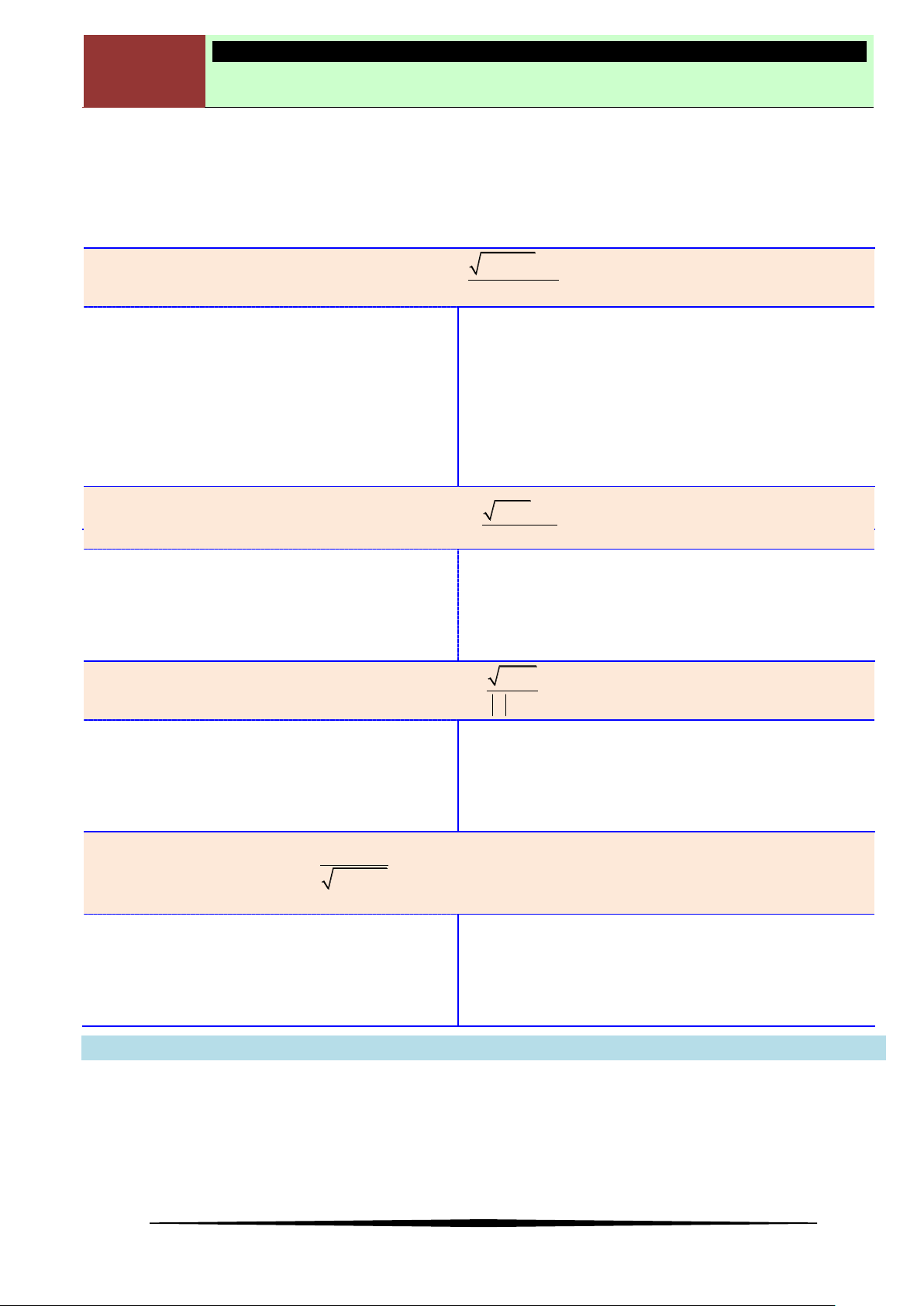
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 55

BÀI TẬP VỀ NHÀ

Câu 1. Cho hàm số

 

y f x

có

 

lim 4

x

fx





và

 

lim 4

x

fx





. Phát biểu nào sau đây là đúng?

ⒶĐồ thị hàm số có 1 tiệm cận ngang và 1 tiệm cận đứng.

Ⓑ Đồ thị hàm số có 2 tiệm cận ngang là các đường thẳng

4y 

và

4y 

.

Ví dụ 6 Số đường tiệm cận của đồ thị hàm số

2

21

1

xx

y

x







?

Ⓐ

2

. Ⓑ

1

.

Ⓒ

0

. Ⓓ

3

.

Lời giải:.....................................................................

......................................................................................

Ví dụ 7. Số đường tiệm cận của đồ thị hàm số

2

32

1

x

y

x







là

Ⓐ

0.

Ⓑ

3

.

Ⓒ

1

. Ⓓ

2

.

Lời giải:.....................................................................

......................................................................................

Ví dụ 8. Số đường tiệm cận của đồ thị hàm số

2

x

y

x







là

Ⓐ

1.

Ⓑ

0

.

Ⓒ

2

. Ⓓ

3

.

Lời giải:.....................................................................

......................................................................................

Ví dụ 9. Đồ thị hàm số

2

58

3

x

y

xx







có bao nhiêu đường tiệm cận?

Ⓐ

2.

Ⓑ

4

.

Ⓒ

1

. Ⓓ

3

.

Lời giải:.....................................................................

......................................................................................

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 56

Ⓓ Đồ thị hàm số có 2 tiệm cận đứng là các đường thẳng

4x 

và

4x 

.

Câu 2. Cho hàm số

 

y f x

có đồ thị là đường cong

 

C

và các giới hạn

 

2

lim 1

x

fx







;

 

2

lim 1

x

fx







;

 

lim 2

x

fx





;

 

lim 2

x

fx





. Hỏi mệnh đề nào sau đây đúng?

ⒶĐường thẳng

2y 

là tiệm cận ngang của

 

C

.

Ⓑ Đường thẳng

1y 

là tiệm cận ngang của

 

C

.

2x 

là tiệm cận ngang của

 

C

.

Ⓓ Đường thẳng

2x 

là tiệm cận đứng của

 

C

.

Câu 3. Cho hàm số

()y f x

có

3

lim ( )

x

fx





 

và

3

lim ( ) 2

x

fx







. Mệnh đề nào sau đây đúng?

ⒶĐường thẳng

3x 

là tiệm cận đứng của đồ thị hàm số

()y f x

.

Ⓑ Đường thẳng

3x 

không phải là tiệm cận của đồ thị hàm số

()y f x

.

2y 

là tiệm cận ngang của đồ thị hàm số

()y f x

.

Ⓓ Đồ thị hàm số

()y f x

không có tiệm cận đứng.

Câu 4. Tiệm cận ngang của đồ thị hàm số

21

23

x

y

x







là

Ⓐ.

1y 

. Ⓑ

2

3

y 

. Ⓒ

3

2

x 

. Ⓓ

1

2

y 

.

Câu 5. Tiệm cận ngang của đồ thị hàm số

5

1

y

x





là đường thẳng có phương trình

Ⓐ

1x 

. Ⓑ

5y 

. Ⓒ

0x 

. Ⓓ

0y 

.

Câu 6. Các đường tiệm cận của đồ thị hàm số

1

2

x

y

x

-

=

+

có phương trình là

Ⓐ

1; 2xy= = -

. Ⓑ

2; 1xy= - =

Ⓒ

2; 1xy==

. Ⓓ

1; 1xy==

.

Câu 7. Tiệm cận đứng của đồ thị hàm số

2

3

x

y

x







là

Ⓐ

3x 

. Ⓑ

1y 

. Ⓒ

1x 

. Ⓓ

3y 

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 57

Câu 8. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số

14

21

x

y

x







.

Ⓐ

2y 

. Ⓑ

4y 

. Ⓒ

1

2

y 

. Ⓓ

2y 

.

Câu 9. Đồ thị hàm số

2

32

1

xx

y

x







có tất cả bao nhiêu đường tiệm cận đứng?

Ⓐ

3

. Ⓑ

1

. Ⓒ

0

. Ⓓ

2

Câu 10. Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng?

Ⓐ

2

1

.

1





y

x

Ⓑ

2

.y

x

Ⓒ

2

1

.

2





y

xx

Ⓓ

4

3

.

1





y

x

Câu 11. Đồ thị của hàm số nào sau đây có đúng ba đường tiệm cận ?

Ⓐ

2

9

x

y

xx





. Ⓑ

12

1

x

y

x







. Ⓒ

2

1

4

y

x





. Ⓓ

3

51

x

y

x







.

Câu 12. Đồ thị của hàm số nào sau đây có tiệm cận ngang?

Ⓐ

2

12x

y

x





. Ⓑ

12x

y

x





. Ⓒ

2

12x

y

x





. Ⓓ

2

1 x

y

x





.

Câu 13. Đồ thị hàm số

2

9

x

y

x

-

=

-

có bao nhiêu tiệm cận?

Ⓐ

4

. Ⓑ

2

. Ⓒ

1

. Ⓓ

3

.

Câu 14. Đường thẳng

1x 

là tiệm cận đứng của đồ thị hàm số nào sau đây?

Ⓐ

2

1

x

y

x







. Ⓑ

2

1yx

. Ⓒ

2

1

x

y

x







. Ⓓ

2

1

y

x





.

Câu 15. Đồ thị của hàm số nào sau đây không có tiệm cận?

Ⓐ

12

1

x

y

x







. Ⓑ

2

1

xx

y

x







. Ⓒ

42

3 2020  y x x

Ⓓ

3

1

x

y

x





.

Câu 16. Số đường tiệm cận của đồ thị hàm số

2

32

4

xx

y

x







là

Ⓐ

4

. Ⓑ

1

. Ⓒ

2

. Ⓓ

3

.

Câu 17. Đồ thị hàm số nào dưới đây không có tiệm cận ngang?

Ⓐ

2

9

x

y

x







. Ⓑ

2

1

3 2 5

xx

y

xx







. Ⓒ

2

32

1

xx

y

x







. Ⓓ

1

x

y

x







.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 58

Câu 18. Đồ thị của hàm số nào dưới đây có hai tiệm cận đứng?

Ⓐ

2

1

3 10 3







x

y

xx

. Ⓑ

2

5 3 2

43







xx

y

xx

. Ⓒ

2

1







x

y

x

. Ⓓ

2

21

3 3 2







x

y

xx

.

Câu 19. Tổng số các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

4

1

x

y

x







là

Ⓐ

0

. Ⓑ

1

. Ⓒ

2

. Ⓓ

3

.

Câu 20 Số đường tiệm cận đứng của đồ thị hàm số

53

4

x

y

x







là

Ⓐ

2T 

. Ⓑ

1T 

. Ⓒ

0T

. Ⓓ

3T 

.

Câu 21. Đồ thị hàm số

2

9

x

y

x







có bao nhiêu đường tiệm cận?

Ⓐ

2.

Ⓑ

3.

Ⓒ

0.

Ⓓ 1.

Câu 22. Đồ thị hàm số

2

1xx

y

x





có bao nhiêu tiệm cận?

Ⓐ

0

. Ⓑ

3

. Ⓒ

1

. Ⓓ

2

.

Câu 23. Đồ thị hàm số

2

1

x

y

x





có số đường tiệm cận là

Ⓐ

2

. Ⓑ

1

. Ⓒ

3

. Ⓓ

4

.

Câu 24. Số đường tiệm cận của đồ thị hàm số

2

4

1

x

y

x







là

Ⓐ

3

. Ⓑ

2

. Ⓒ

4

. Ⓓ

1

.

Câu 25. Đồ thị hàm số

2

5 1 1

2

xx

y

xx

  





có tất cả bao nhiêu đường tiệm cận?

Ⓐ

3

. Ⓑ

0

. Ⓒ

1

. Ⓓ

2

Câu 26. Cho hàm số

21

2

x

y

x







có đồ thị

 

C

. Tìm tọa độ giao điểm

I

của hai đường tiệm cận của đồ thị

 

C

.

Ⓐ

 

2;2I

Ⓑ

 

2;2I

. Ⓒ

 

2; 2I 

. Ⓓ

 

2; 2I 

.

Câu 27. Cho hàm số

1ax

y

bx c







 

,,abc

có bảng biến thiên như sau:

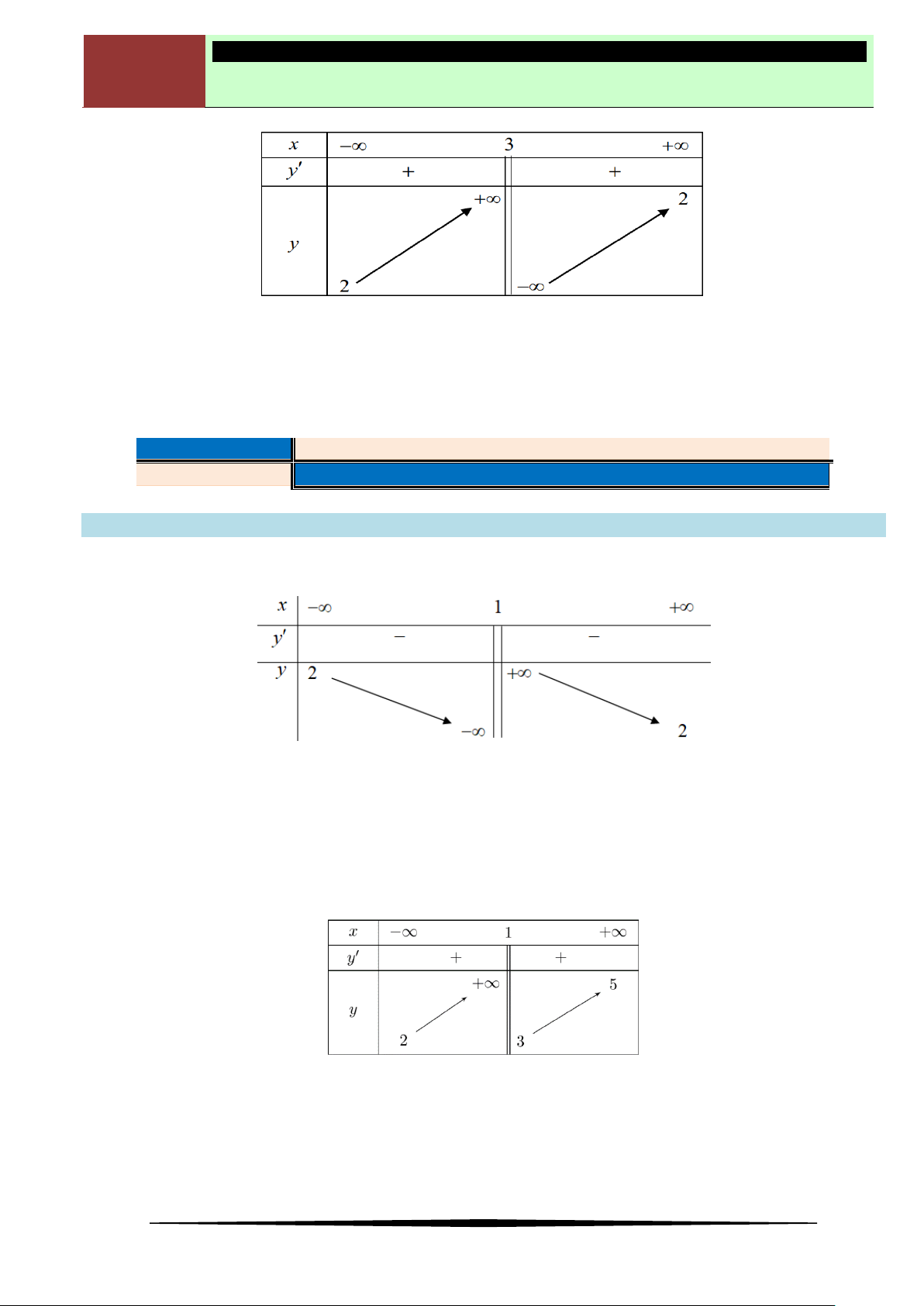
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 59

Trong các số

,,abc

có bao nhiêu số dương?

Ⓐ

1

. Ⓑ

0

. Ⓒ

2

. Ⓓ

3

.

CÁC VÍ DỤ

Ví dụ 1. Cho hàm số

 

y f x

có bảng biến thiên như sau

Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình

Ⓐ

2x 

. Ⓑ

2y 

. Ⓒ

1x

Ⓓ

1y 

.

Ví dụ 2. Cho hàm số

 

y f x

có bảng biến thiên như hình dưới. Số đường tiệm cận ngang của đồ thị hàm

số đã cho là

Ⓐ

2

Ⓑ

3

. Ⓒ

1

. Ⓓ

4

.

Ví dụ 3. Cho hàm số

 

y f x

có bảng biến thiên như sau:

Dạng 2:

Dựa vào bảng biến thiên hoặc đồ thị để kết luận tiệm cận

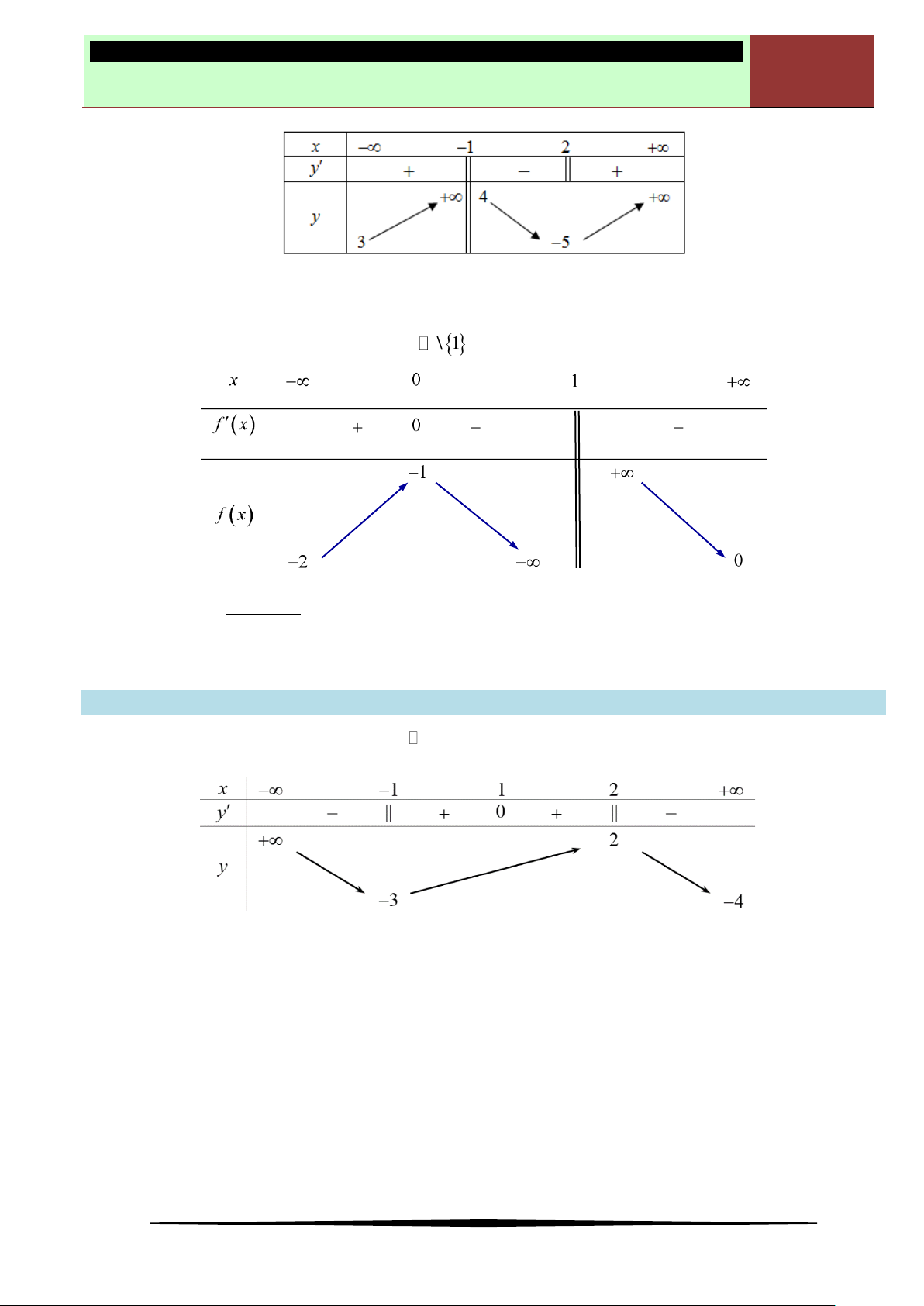
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 60

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số bằng

Ⓐ

4

. Ⓑ

1

. Ⓒ

2

. Ⓓ

3

.

Ví dụ 4. Cho hàm số

 

y f x

liên tục trên

 

\1

và có bảng biến thiên như sau:

Đồ thị hàm số

 

1

23

y

fx





có bao nhiêu đường tiệm cận đứng?

Ⓐ

1

. Ⓑ

2

. Ⓒ

0

. Ⓓ

2

.

BÀI TẬP VỀ NHÀ

Câu 1. Cho hàm số

 

y f x

liên tục trên và có bảng biến thiên như sau:

Trong các mệnh đề sau, mệnh đề nào sai?

ⒶHàm số có hai điểm cực trị.

Ⓑ Hàm số đạt giá trị lớn nhất bằng

2

và giá trị nhỏ nhất bằng

3

.

Ⓓ Hàm số nghịch biến trên các khoảng

 

;1 

,

 

2;

.

Câu 2. Cho hàm số

 

y f x

có bảng biến thiên như sau:

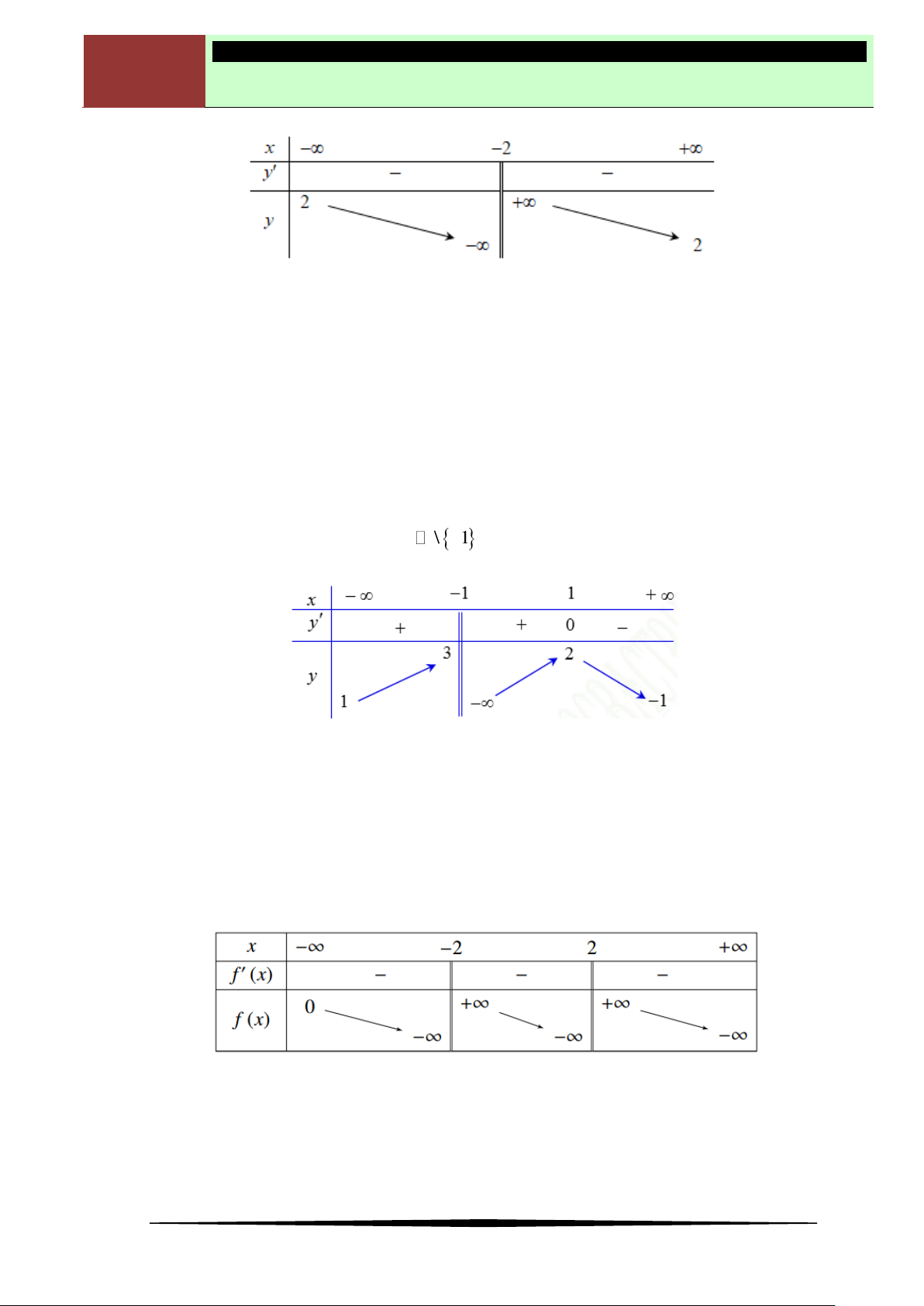
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 61

Mệnh đề nào dưới đây đúng?

ⒶĐồ thị hàm số có tiệm cận đứng là đường thẳng

1x 

và tiệm cận ngang là đường thẳng

2y 

.

Ⓑ Đồ thị hàm số không có đường tiệm cận.

Ⓓ Đồ thị hàm số có tiệm cận ngang là đường thẳng

1x 

và tiệm cận đứng là đường thẳng

2y 

.

Câu 3. Cho hàm số

 

y f x

xác định trên

 

\1

, liên tục trên mỗi khoảng xác định và có bảng biến

thiên

Hỏi khẳng định nào dưới đây là khẳng định sai?

ⒶĐồ thị hàm số có hai tiệm cận ngang là các đường thẳng

1y 

và

1y 

.

Ⓑ Hàm số đã cho đạt cực đại tại điểm

1x 

.

Ⓓ Hàm số đã cho không có đạo hàm tại điểm

1x 

.

Câu 4. Cho hàm số

 

y f x

có bảng biến thiên như sau

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

Ⓐ

1

. Ⓑ

2

. Ⓒ

3

. Ⓓ

0

.

Câu 5. Cho hàm số

()y f x

có bảng biến thiên như hình vẽ

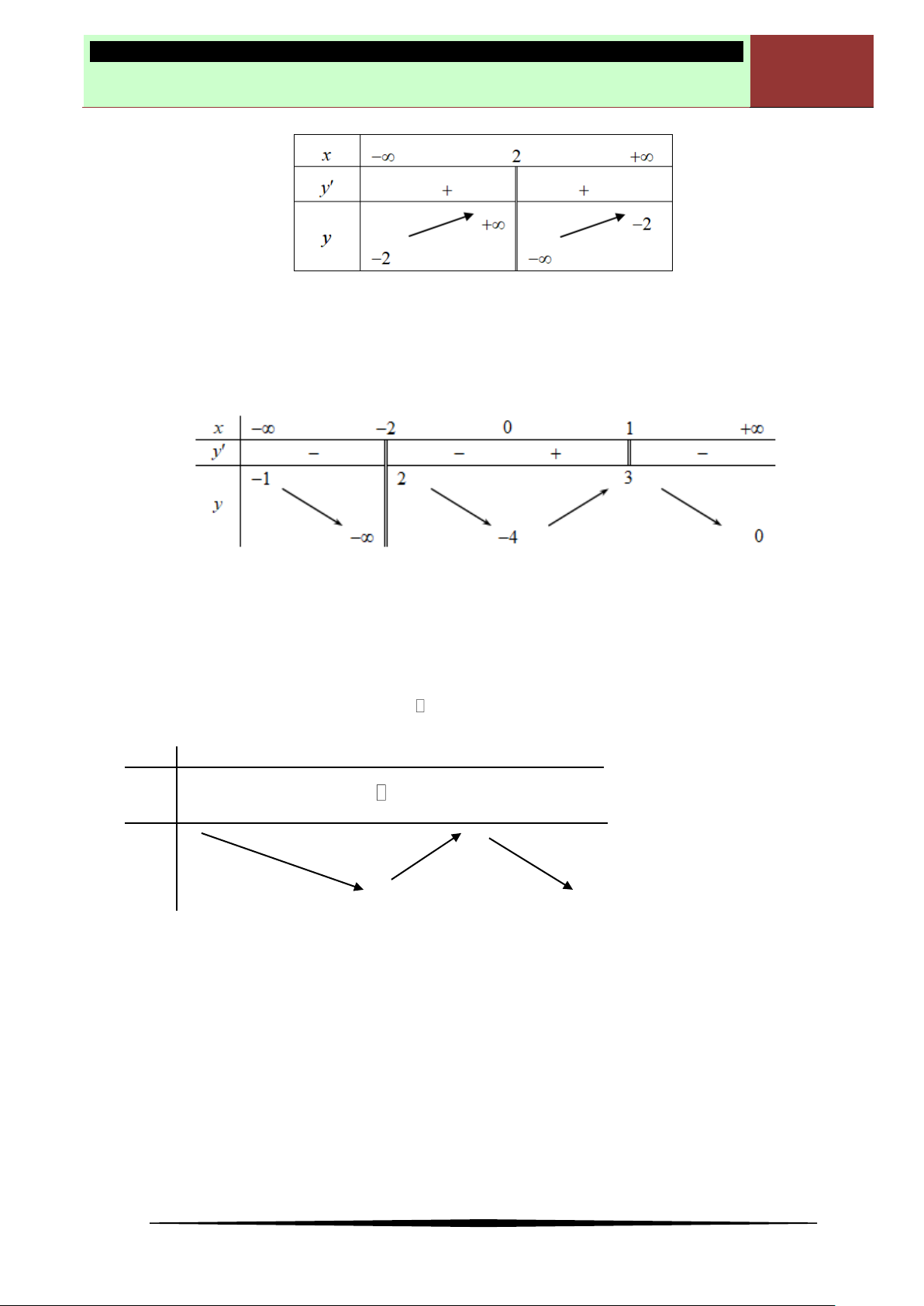
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 62

Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

Ⓐ

2, 2xy  

. Ⓑ

2, 2xy  

. Ⓒ

2, 2xy   

. Ⓓ

2, 2xy

.

Câu 6. Hàm số

 

y f x

có bảng biến thiên dưới đây.

Số tiệm cận của đồ thị hàm số

 

y f x

là:

Ⓐ

2

. Ⓑ

3

.

Ⓒ

1

. Ⓓ

4

.

Câu 7. Cho hàm số

 

y f x

xác định trên và có bảng biến thiên sau:

Hỏi mệnh đề nào sau đây là mệnh đề sai?

ⒶHàm số nghịch biến trên khoảng

 

;0

.

Ⓑ Hàm số có ba điểm cực trị.

Ⓒ

Đồ thị hàm số

 

y f x

không có tiệm cận ngang.

Ⓓ Điểm cực tiểu của đồ thị hàm số là

0x 

.

x

 

fx





 

fx

1

0

1



0









1

3



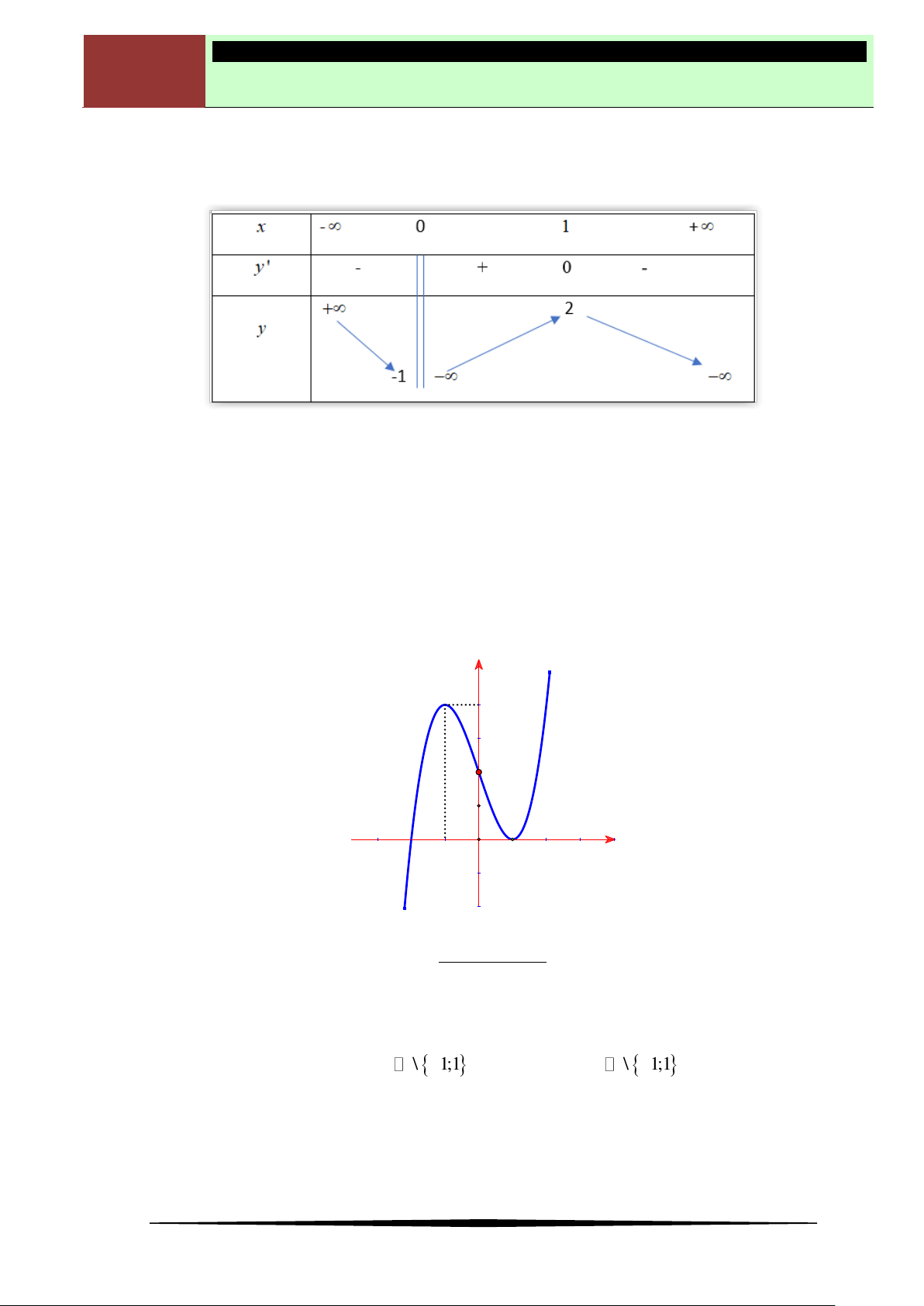
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 63

Câu 8. Cho hàm số

 

y f x

liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau. Chọn

khẳng định đúng?

ⒶĐồ thị hàm số có đúng một tiệm cận ngang.

Ⓑ Đồ thị hàm số có hai tiệm cận ngang.

Ⓓ Đồ thị hàm số không có tiệm cận đứng và tiệm cận ngang.

Câu 9. Cho hàm số

 

y f x

có đạo hàm liên tục trên

¡

. Đồ thị hàm số

 

y f x

như hình vẽ.

Số đường tiện cận đứng của đồ thị hàm số

2

1

( ) 4 ( )







x

y

f x f x

là

Ⓐ

4

. Ⓑ 1. Ⓒ 2. Ⓓ

3

.

Câu 10. Hàm số

 

y f x

xác định trên

 

\ 1;1

, có đạo hàm trên

 

\ 1;1

và có bảng biến thiên như

sau:

x

-2

y

4

-1

O

1

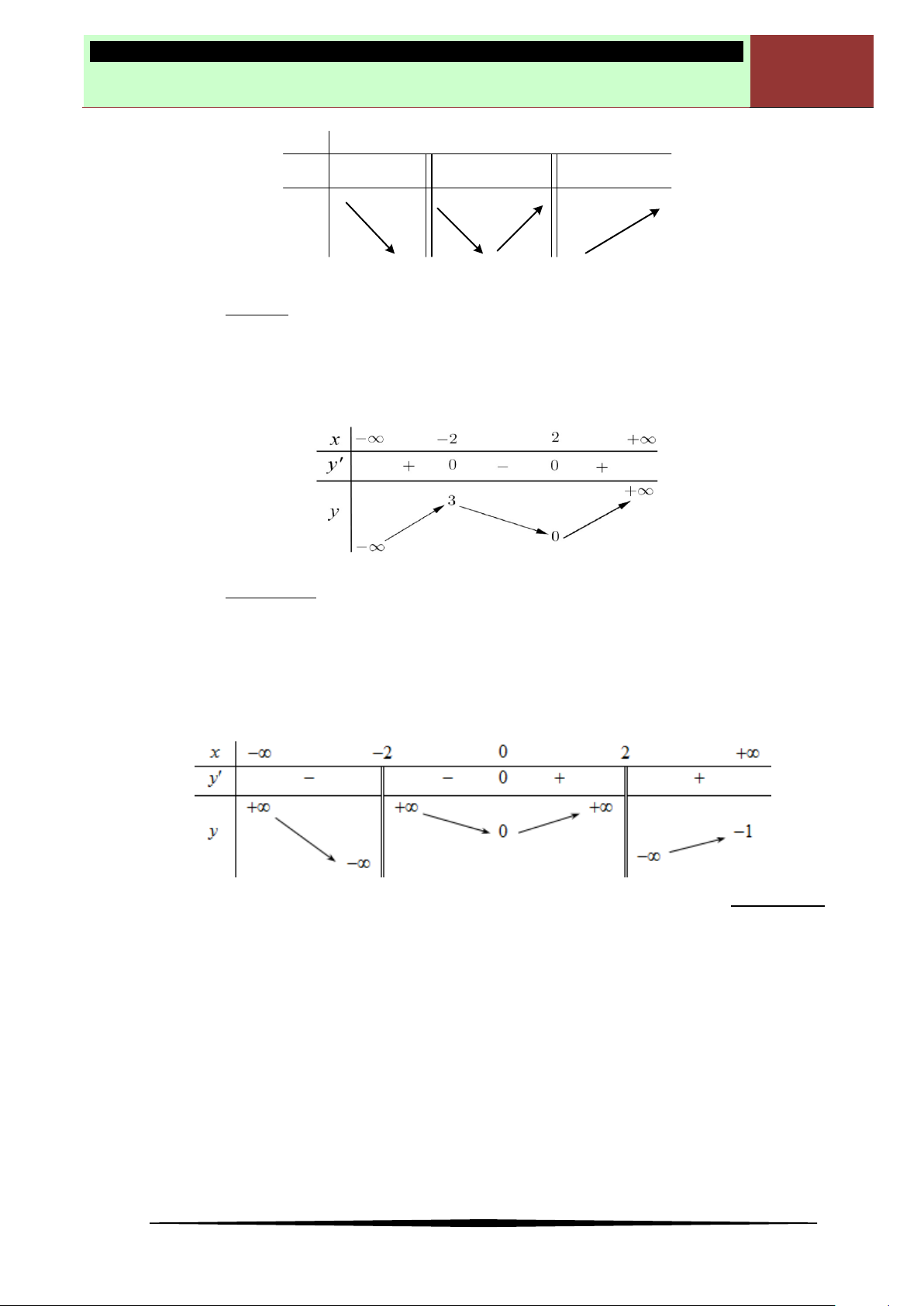
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 64

x

y



y





1

1

0









0

1

Đồ thị hàm số

 

1

y

fx





có bao nhiêu tiệm cận (tiệm cận đứng và tiệm cận ngang)?

Ⓐ

2

. Ⓑ

3

. Ⓒ

4

. Ⓓ

5

.

Câu 11. Cho hàm số

 

y f x

có bảng biến thiên như sau

Đồ thị hàm số

 

1

32

y

fx





có bao nhiêu tiệm cận đứng?

Ⓐ

2.

Ⓑ

3.

Ⓒ

1.

Ⓓ

0.

Câu 12. Hàm số

 

y f x

có đạo hàm trên

 

\ 2;2R

, có bảng biến thiên như sau:

Gọi

k

,

l

lần lượt là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

 

1

2018

y

fx





. Tính

kl

.

Ⓐ

2kl

. Ⓑ

3kl

. Ⓒ

4kl

. Ⓓ

5kl

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 65

§6. KHẢO SÁT HÀM SỐ VÀ VẼ ĐỒ THỊ

A. TÓM TẮT LÝ THUYẾT



1. Sơ đồ khảo sát hàm số

g

Bước 1. Tìm tập xác định

D

của hàm số.

g

Bước 2. Xét chiều biến thiên của hàm số:

― Tính giới hạn (nếu có) để suy ra các đường tiệm cận của hàm số.

― Tính đạo hàm

,y

¢

cho đạo hàm

0y

¢

=

tìm nghiệm.

― Lập bảng biến thiên, suy ra các khoảng đơn điệu, cực trị của hàm số (nếu có).

g

Bước 3. Vẽ đồ thị hàm số:

― Vẽ các đường tiệm cận (nếu có).

― Lập bảng giá trị để xác định vài điểm đặc biệt.

― Nhận xét đồ thị: chỉ ra trục đối xứng, tâm đối xứng, điểm uốn (nếu có).

2. Hình dáng đồ thị của một số hàm thường gặp

a) Hàm số bậc ba

32

, ( 0).y ax bx cx d a= + + + ¹

0a >

0a <

Phương trình

0y

¢

=

có

2

nghiệm phân

biệt

Phương trình

0y

¢

=

có

nghiệm kép

Phương trình

0y

¢

=

vô

nghiệm

b) Hàm số bậc bốn trùng phương

42

, ( 0).y ax bx c a= + + ¹

0a >

0a <

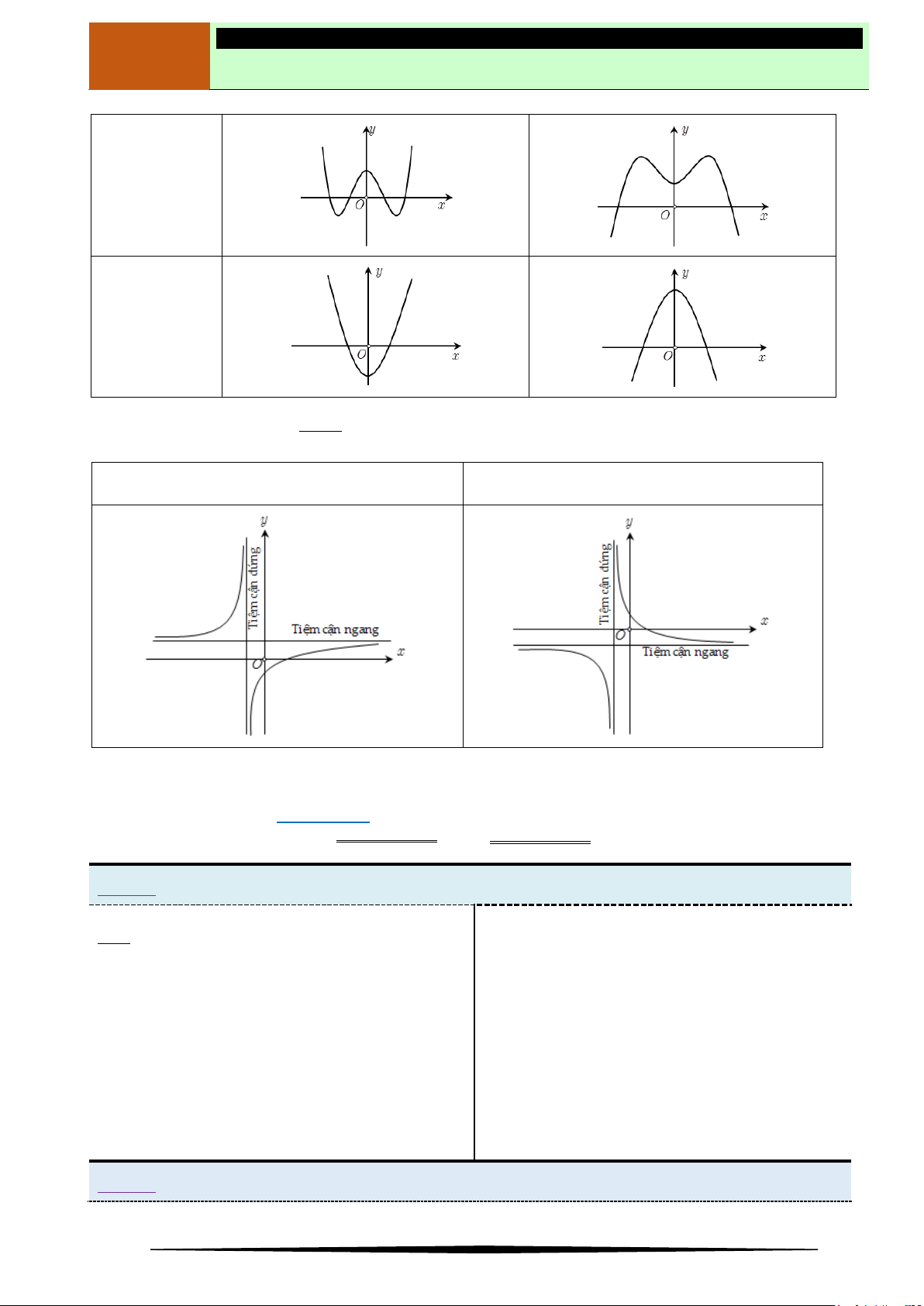
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 66

Phương trình

0y

¢

=

có

3

nghiệm phân

biệt

Phương trình

0y

¢

=

có

1

nghiệm

c) Hàm số nhất biến

( 0, 0).

ax b

y c ad bc

cx d

+

= ¹ - ¹

+

0,D ad bc= - >

hàm số đồng biến

0,D ad bc= - <

hàm số nghịch biến

B. CÁC DẠNG TOÁN THƯỜNG GẶP

Daïng toaùn 1: Khaûo saùt söï bieán thieân vaø veõ ñoà thò haøm soá



Ví dụ 1. Khảo sát sự biến thiên và vẽ đồ thị hàm số

32

3 4.y x x= + -

Giải. ..........................................................................................................................................................

................................................................................................................................................................................

.

...............................................................................................................................................................................

Ví dụ 2. Khảo sát sự biến thiên và vẽ đồ thị hàm số

32

3 4 2.y x x x= - + - +

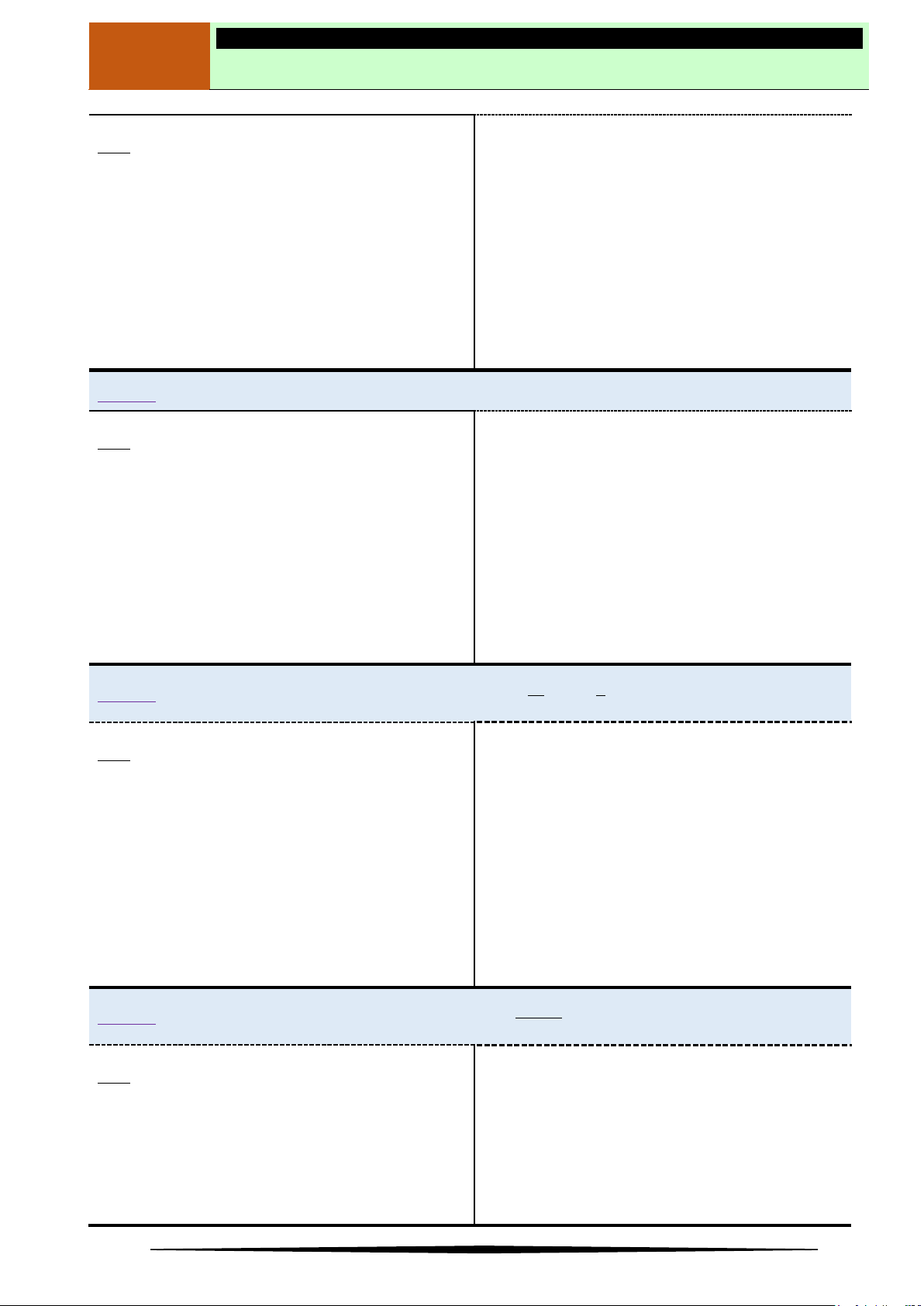
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 67

Giải. ..........................................................................................................................................................

................................................................................................................................................................................

.

...............................................................................................................................................................................

Ví dụ 3. Khảo sát sự biến thiên và vẽ đồ thị hàm số

42

2 3.y x x= - -

Giải. ..........................................................................................................................................................

................................................................................................................................................................................

.

...............................................................................................................................................................................

Ví dụ 4. Khảo sát sự biến thiên và vẽ đồ thị hàm số

4

2

3

22

x

yx= - - + ×

Giải. ..........................................................................................................................................................

................................................................................................................................................................................

.

...............................................................................................................................................................................

.

...............................................................................................................................................................................

Ví dụ 5. Khảo sát sự biến thiên và vẽ đồ thị hàm số

2

1

x

y

x

-+

=×

+

Giải. ..........................................................................................................................................................

................................................................................................................................................................................

.

...............................................................................................................................................................................

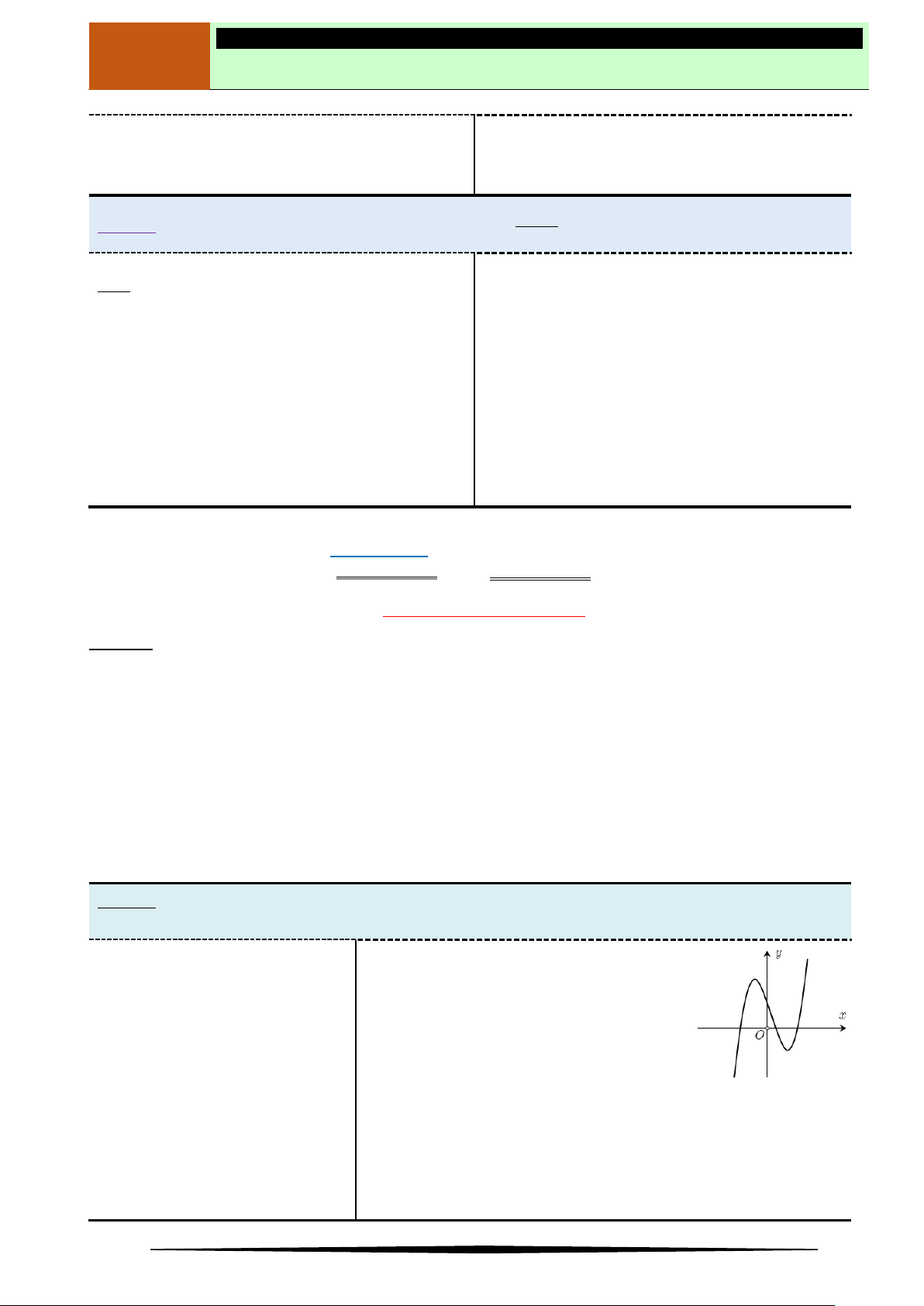
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 68

................................................................................................................................................................................

...............................................................................................................................................................................

Ví dụ 6. Khảo sát sự biến thiên và vẽ đồ thị hàm số

2

21

x

y

x

-

=×

+

Giải. ..........................................................................................................................................................

................................................................................................................................................................................

.

...............................................................................................................................................................................

Daïng toaùn 2: Nhaän daïng ñoà thò haøm soá



ĐỒ THỊ HÀM SỐ BẬC BA

Cần nhớ: .........................................................................................................................................................................................................................................................................................................................................

............................................................................................................................................................................................................................................................................................................................................................................

Ví dụ 1. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở

bốn phương án

A, B, C, D

dưới đây. Hỏi hàm số đó là hàm số nào ?

Ⓐ

2

1.y x x= - + -

Ⓑ

3

3 1.y x x= - + +

Ⓒ

42

1.y x x= - +

Ⓓ

3

3 1.y x x= - +

.........................................................................................................................................................................................................................................

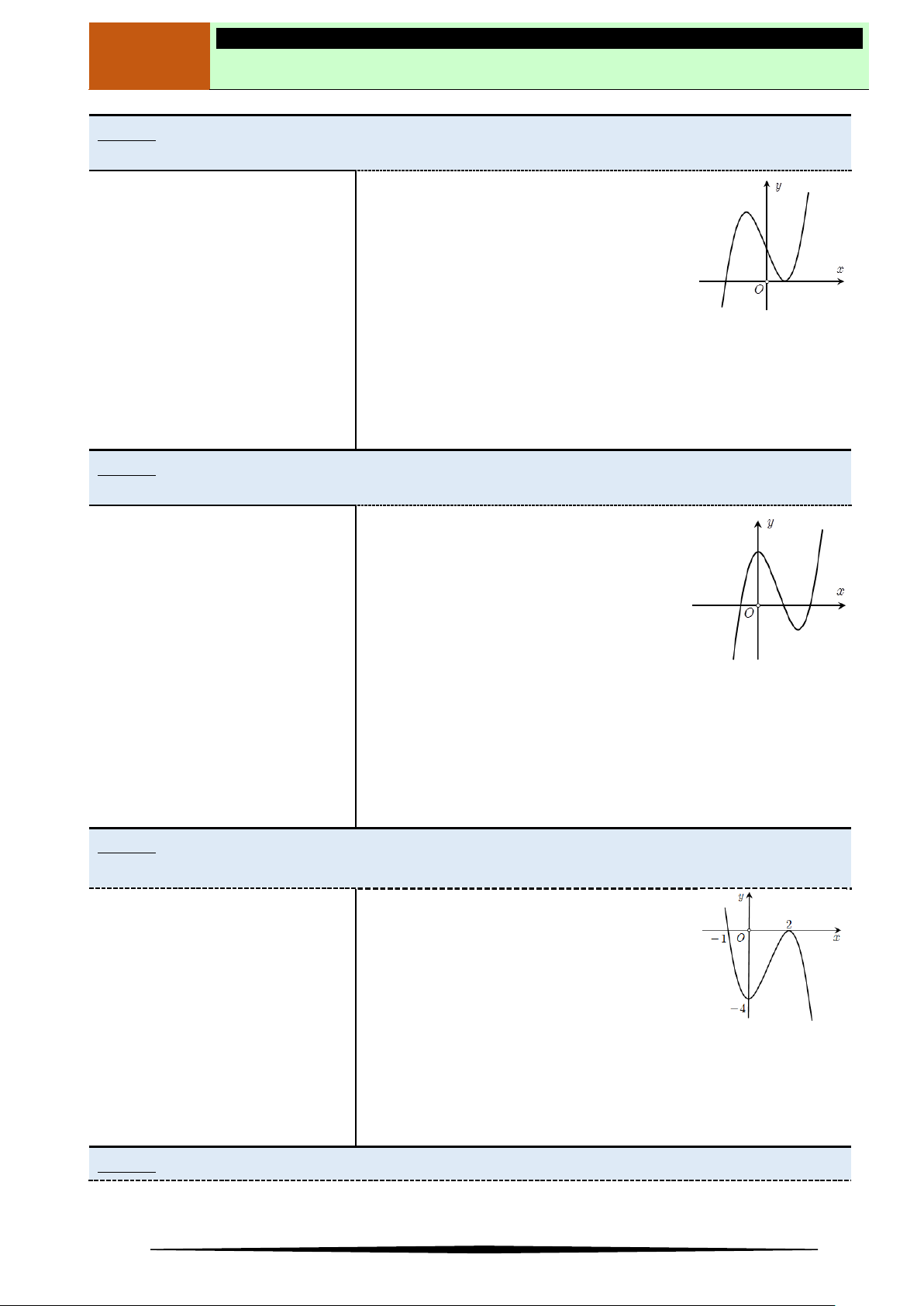
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 69

Ví dụ 2. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào

?

Ⓐ

3

3 2.y x x= - +

Ⓑ

42

1.y x x= - +

Ⓒ

42

1.y x x= + +

Ⓓ

3

3 2.y x x= - + +

.........................................................................................................................................................................................................................................

Ví dụ 3. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào

?

Ⓐ

42

2 1.y x x= - +

Ⓑ

42

2 1.y x x= - + +

Ⓒ

32

3 1.y x x= - + +

Ⓓ

32

3 3.y x x= - +

.........................................................................................................................................................................................................................................

Ví dụ 4. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở

bốn phương án

A, B, C, D

dưới đây. Hỏi hàm số đó là hàm số nào ?

Ⓐ

3

4.yx= - -

Ⓑ

32

3 4.y x x= - -

Ⓒ

32

3 4.y x x= - + -

Ⓓ

32

3 2.y x x= - + -

.........................................................................................................................................................................................................................................

Ví dụ 5. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

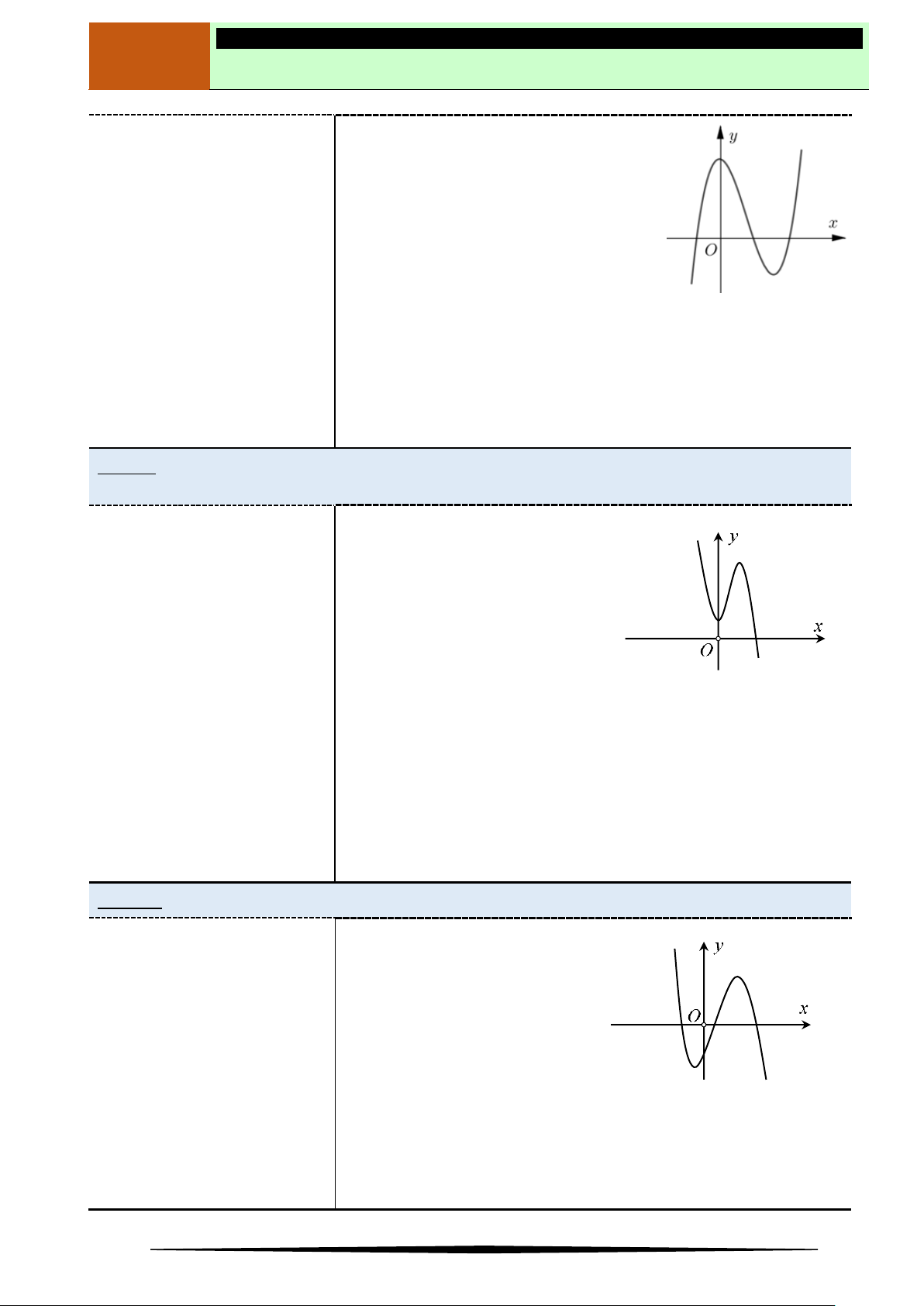
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 70

Ⓐ

32

33y x x= - +

Ⓑ

32

33y x x= - + +

Ⓒ

42

23y x x= - +

Ⓓ

42

23y x x= - + +

...................................................................................................................................................................................................................................................

Ví dụ 6. Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình vẽ bên. Hỏi mệnh đề nào dưới đây

đúng?

Ⓐ

0, 0, 0, 0.a b c d< > > >

Ⓑ

0, 0, 0, 0.a b c d< < = >

Ⓒ

0, 0, 0, 0.a b c d> < > >

Ⓓ

0, 0, 0, 0.a b c d< > = >

...................................................................................................................................................................................................................................................

Ví dụ 7. Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng ?

Ⓐ

0, 0, 0, 0.a b c d< > > <

Ⓑ

0, 0, 0, 0.a b c d< < > <

Ⓒ

0, 0, 0, 0.a b c d> < < >

Ⓓ

0, 0, 0, 0.a b c d< > < <

...................................................................................................................................................................................................................................................

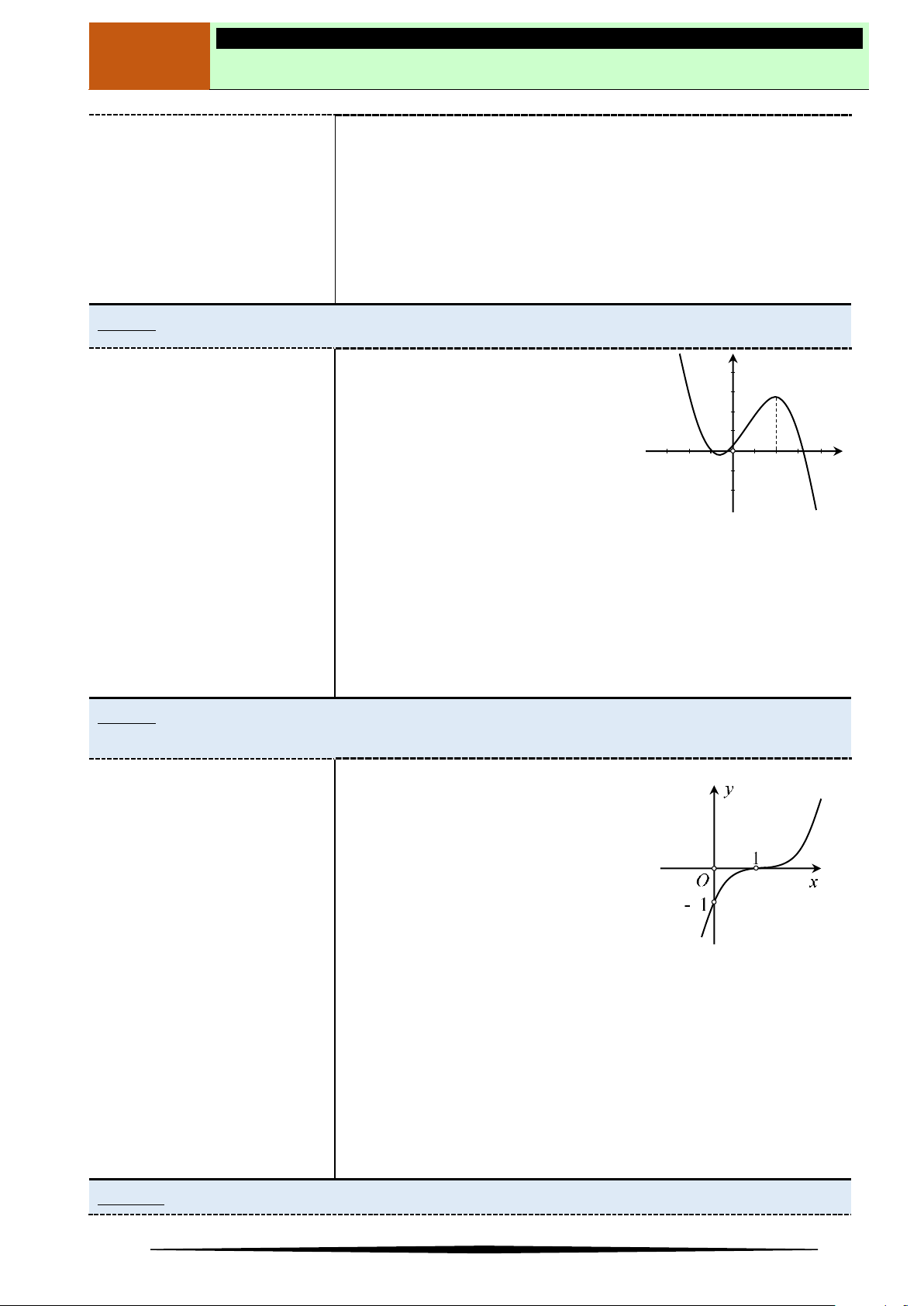
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 71

...................................................................................................................................................................................................................................................

Ví dụ 8. Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng ?

Ⓐ

0, 0, 0, 0.a b c d< > < >

Ⓑ

0, 0, 0, 0.a b c d< < > >

Ⓒ

0, 0, 0, 0.a b c d< > > >

Ⓓ

0, 0, 0, 0.a b c d< < < >

...................................................................................................................................................................................................................................................

Ví dụ 9. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở

bốn phương án

A, B, C, D

dưới đây. Hỏi hàm số đó là hàm số nào ?

Ⓐ

3

( 1) .yx=-

Ⓑ

3

1.yx=+

Ⓒ

3

1.yx=-

Ⓓ

3

( 1) .yx=+

...................................................................................................................................................................................................................................................

Ví dụ 10. Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng ?

O

x

y

2

1-

3

1

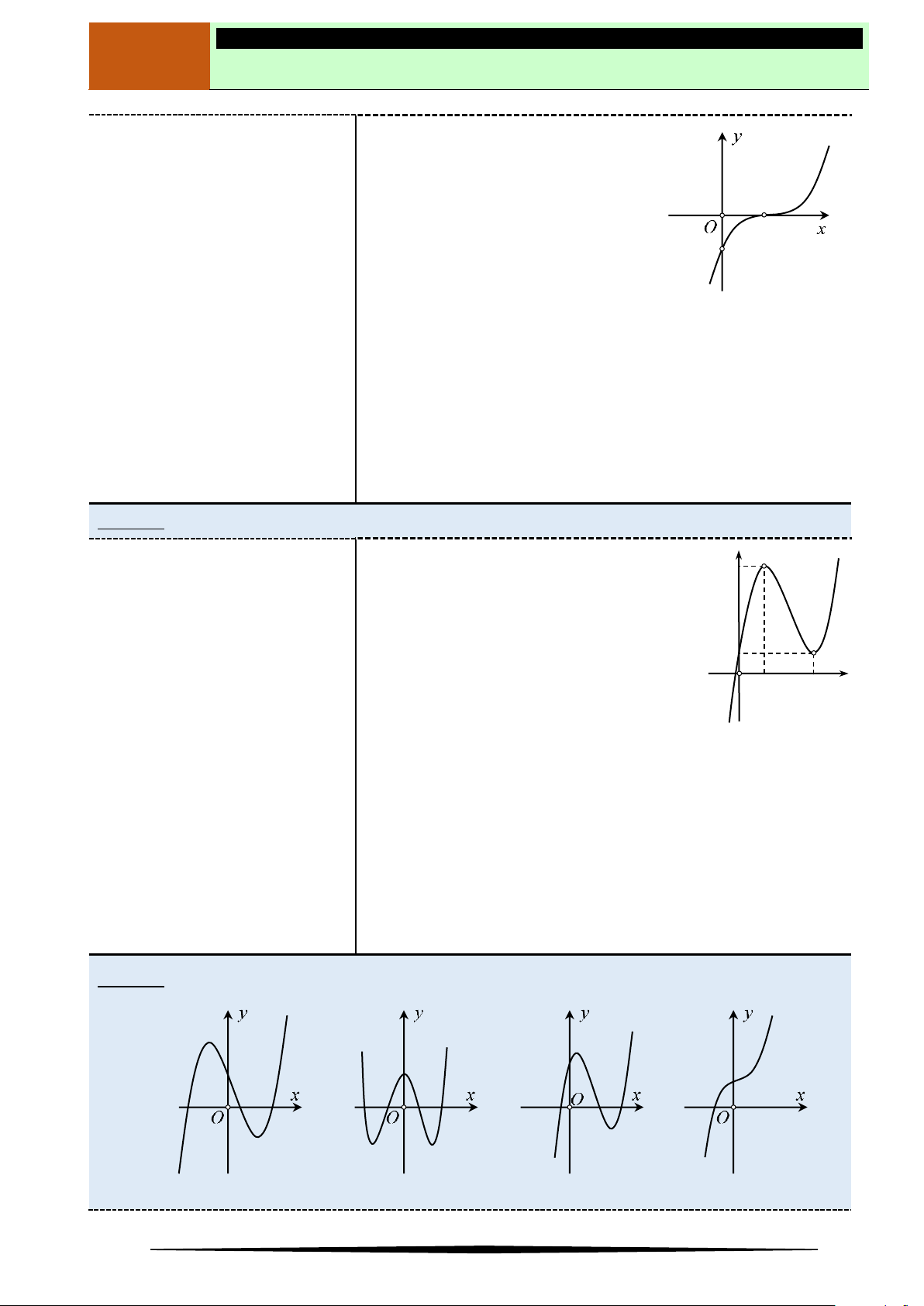
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 72

Ⓐ

0, 0, 0, 0.a b c d< > > <

Ⓑ

0, 0, 0, 0.a b c d> > > <

Ⓒ

0, 0, 0, 0.a b c d> < < >

Ⓓ

0, 0, 0, 0.a b c d> < > <

.........................................................................................................................................................................................................................................

Ví dụ 11. Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình vẽ ở bên. Mệnh đề nào sau đây đúng ?

Ⓐ

0, 0, 0, 0.a b c d> > < <

Ⓑ

0, 0, 0, 0.a b c d< > < >

Ⓒ

0, 0, 0, 0.a b c d> < > >

Ⓓ

0, 0, 0, 0.a b c d< < > <

.........................................................................................................................................................................................................................................

Ví dụ 12. Cho hàm số

32

,y x bx cx d= + + +

với

0,c <

có đồ thị

()C

là một trong bốn hình dưới đây:

Hình 1 Hình 2 Hình 3 Hình 4

O

x

y

5

1

3

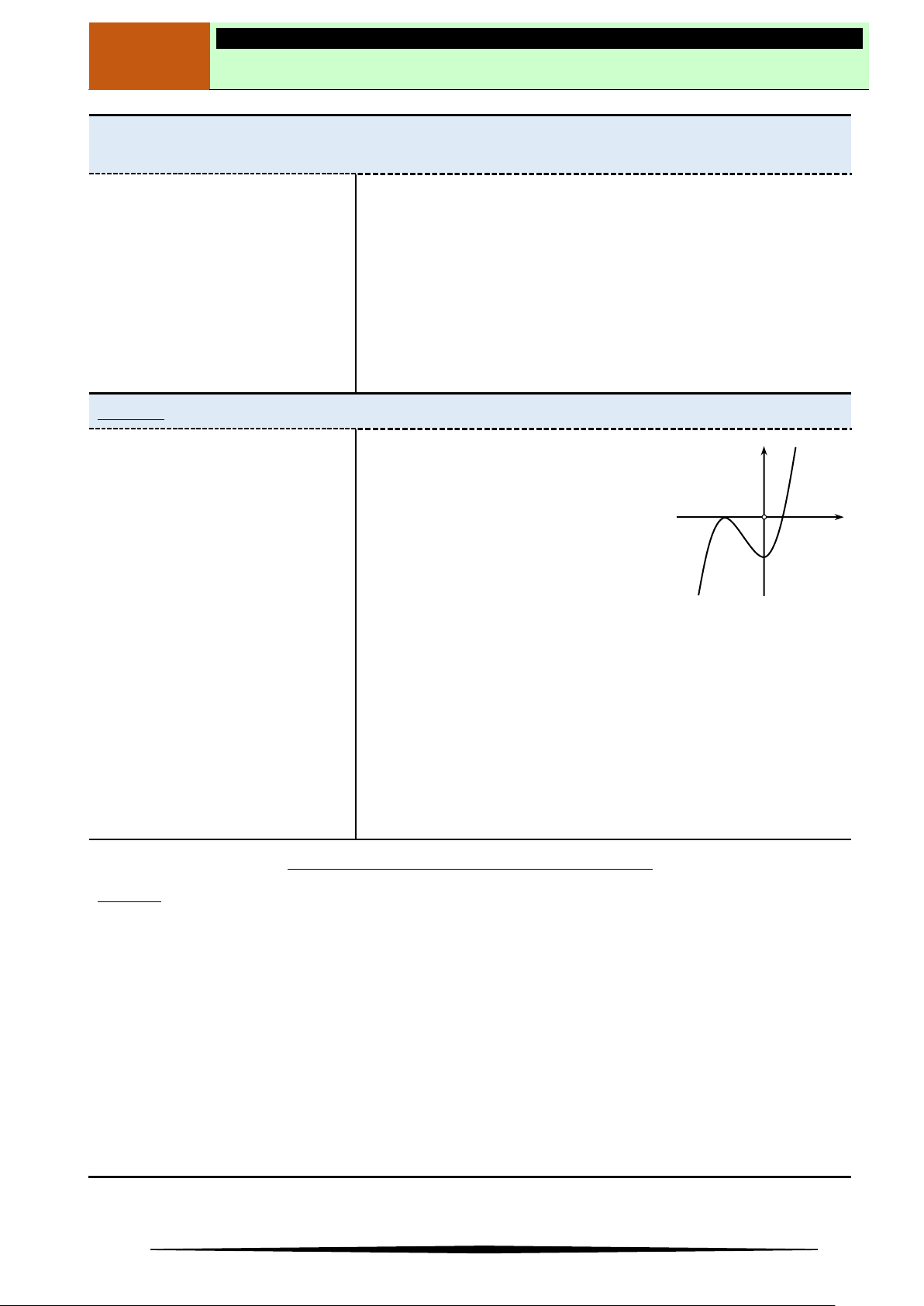
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 73

Hỏi đồ thị

()C

là hình nào ?

Ⓐ Hình 1. Ⓑ Hình 2 Ⓒ Hình 3. Ⓓ Hình 4.

.........................................................................................................................

.........................................................................................................................................................................................................................................

Ví dụ 13. Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng ?

Ⓐ

0, 0, 0, 0.a b c d> > = <

Ⓑ

0, 0, 0, 0.a b c d> > = >

Ⓒ

0, 0, 0, 0.a b c d> > > >

Ⓓ

0, 0, 0, 0.a b c d> < = <

.........................................................................................................................................................................................................................................

ĐỒ THỊ HÀM SỐ BẬC BỐN TRÙNG PHƯƠNG

Cần nhớ:

...........................................................................................................................................................................................................................................................................................................................................................................

O

x

y

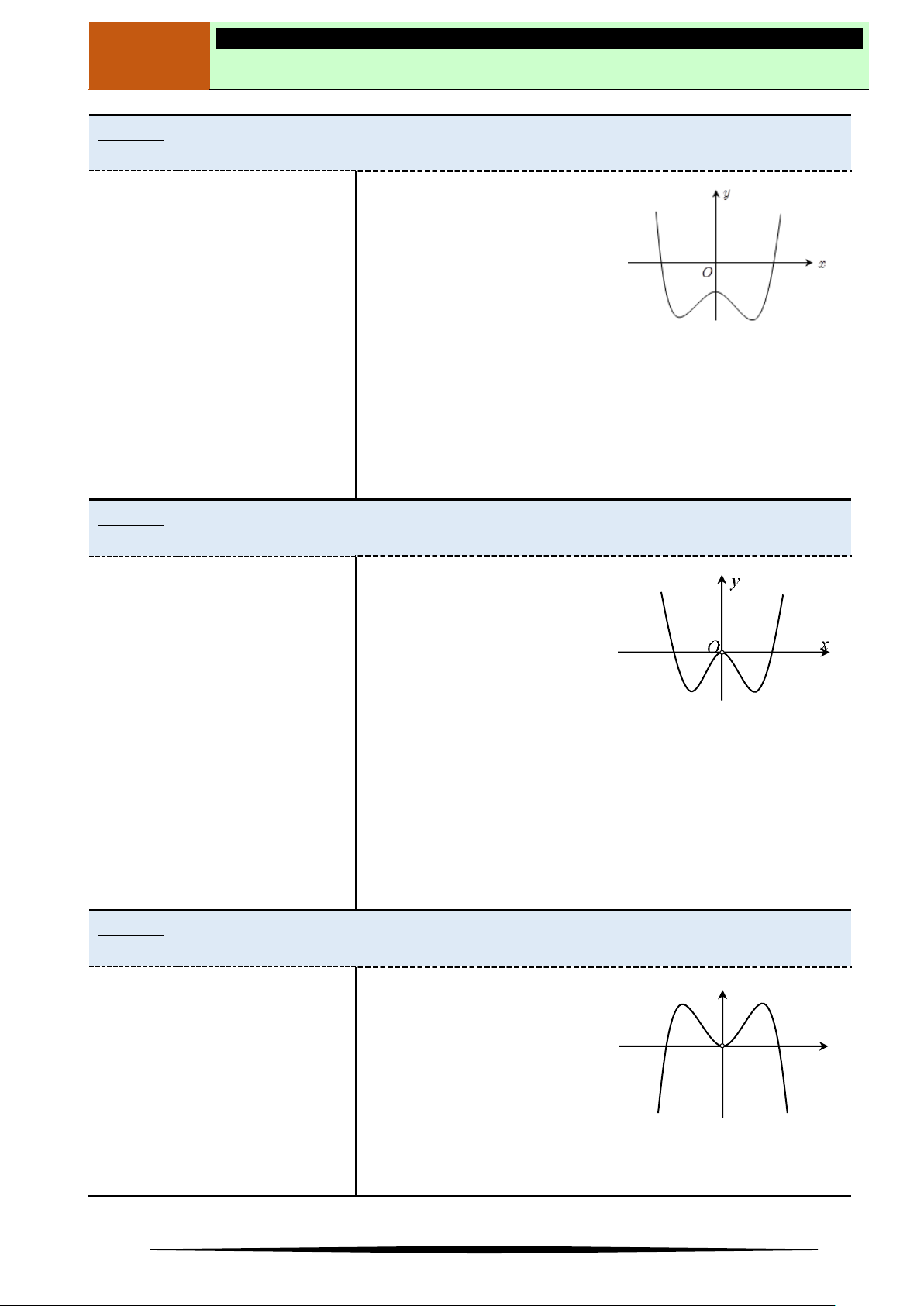
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 74

Ví dụ 14. Đường cong ở hình bên là đồ thị của một trong bốn hàm số đưới đây. Hàm số đó là hàm số

nào ?

Ⓐ

32

1.y x x= - + -

Ⓑ

42

1.y x x= - -

Ⓒ

32

1.y x x= - -

Ⓓ

42

1.y x x= - + -

.........................................................................................................................................................................................................................................

Ví dụ 15. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn

phương án

A, B, C, D

dưới đây. Hỏi hàm số đó là hàm số nào ?

Ⓐ

42

2.y x x= - +

Ⓑ

42

2 1.y x x= - +

Ⓒ

42

2.y x x= - -

Ⓓ

42

2.y x x=-

.........................................................................................................................................................................................................................................

Ví dụ 16. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn

phương án

A, B, C, D

dưới đây. Hỏi hàm số đó là hàm số nào ?

Ⓐ

42

( ) 2 .f x x x=-

Ⓑ

42

( ) 2 .f x x x=+

Ⓒ

42

( ) 2 1.f x x x= - + -

Ⓓ

42

( ) 2 .f x x x= - +

.........................................................................................................................................................................................................................................

O

x

y

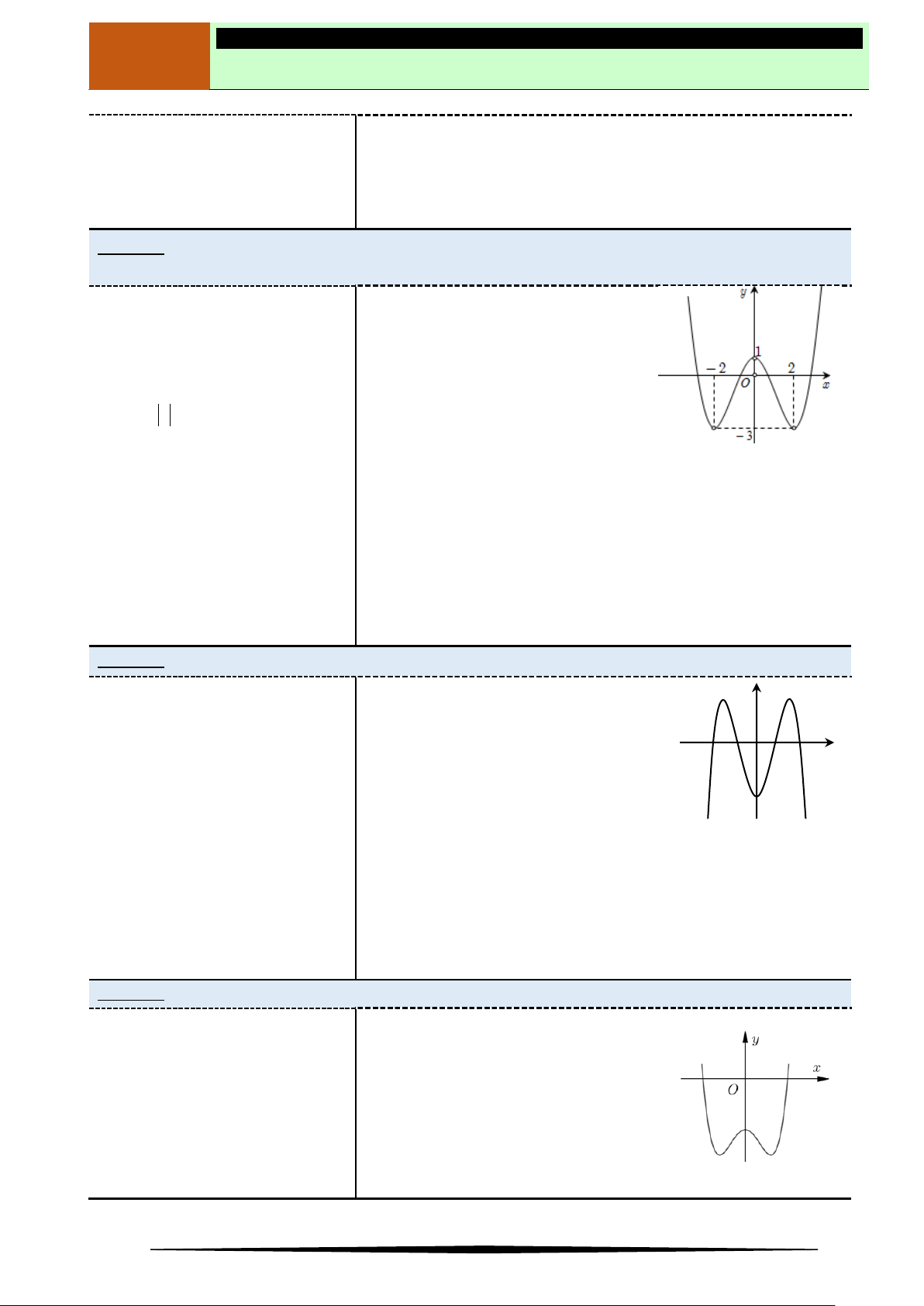
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 75

.........................................................................................................................................................................................................................................

Ví dụ 17. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn

phương án

A, B, C, D

dưới đây. Hỏi hàm số đó là hàm số nào ?

Ⓐ

42

8 1.y x x= - + +

Ⓑ

42

8 1.y x x= - +

Ⓒ

32

3 1.y x x= - + +

Ⓓ

3

2

3 1.y x x= - +

.........................................................................................................................................................................................................................................

Ví dụ 18. Cho hàm số

42

y ax bx c= + +

có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?

Ⓐ

0, 0, 0.a b c> < <

Ⓑ

0, 0, 0.a b c< > <

Ⓒ

0, 0, 0.a b c> < >

Ⓓ

0, 0, 0.a b c<<<

.........................................................................................................................................................................................................................................

Ví dụ 19. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

Ⓐ

42

22y x x= - -

Ⓑ

42

22y x x= - + -

Ⓒ

32

32y x x= - + -

Ⓓ

32

32y x x= - -

.........................................................................................................................................................................................................................................

O

x

y

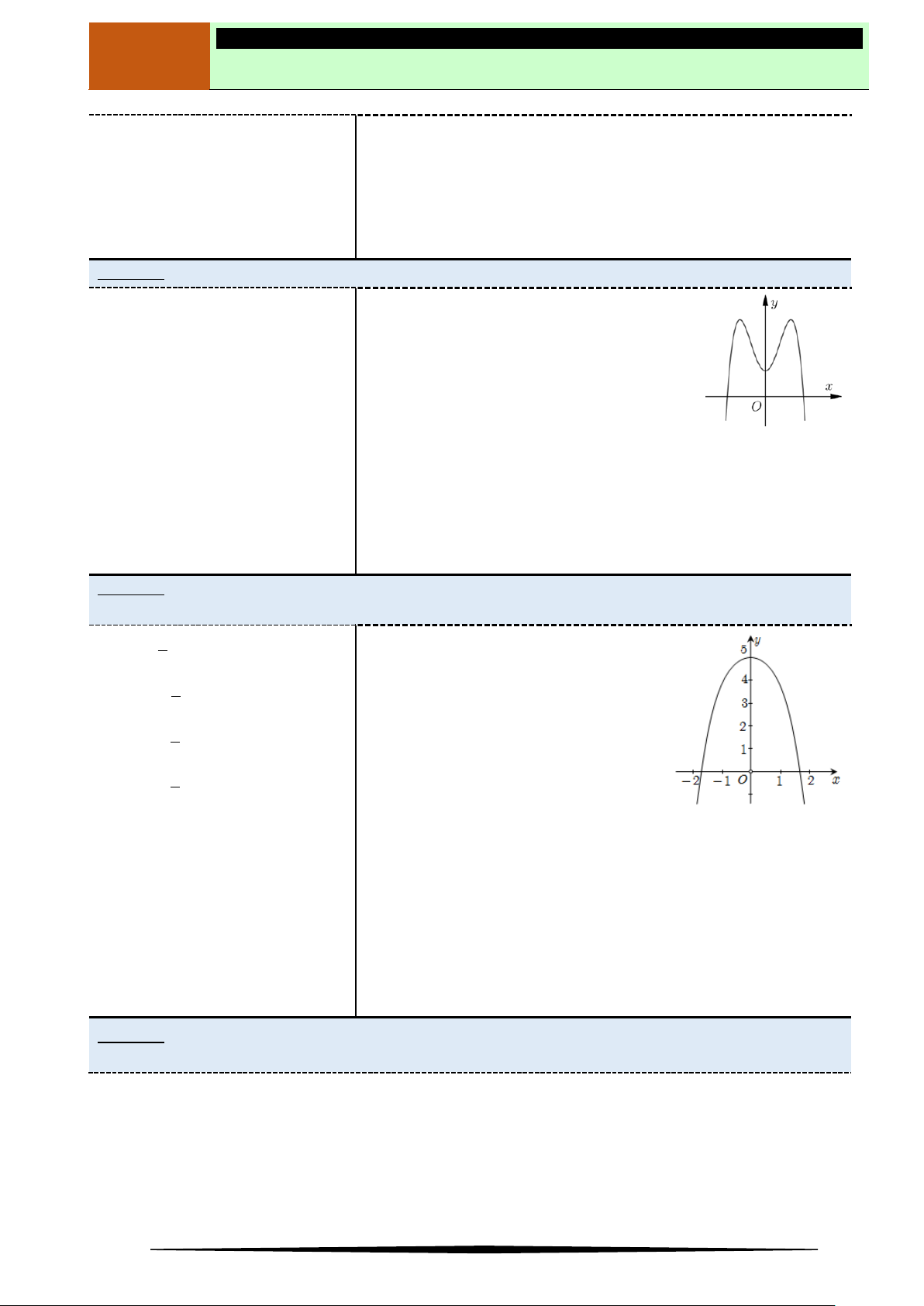
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 76

.........................................................................................................................................................................................................................................

Ví dụ 20. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

Ⓐ

3

2 3 1y x x= - +

Ⓑ

32

2 4 1y x x= - + +

Ⓒ

42

2 4 1y x x= - +

Ⓓ

3

2 3 1y x x= - + +

.........................................................................................................................................................................................................................................

Ví dụ 21. Đồ thị hình bên là đồ thị của một trong 4 đồ thị của các hàm số ở các phương án A, B, C, D

dưới đây. Chọn phương án đúng ?

Ⓐ

42

1

5.

4

y x x= + +

Ⓑ

42

1

5.

4

y x x= - - +

Ⓒ

4

1

5.

4

yx= - +

Ⓓ

42

1

2 5.

4

y x x= - + +

.........................................................................................................................................................................................................................................

Ví dụ 22. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn

phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

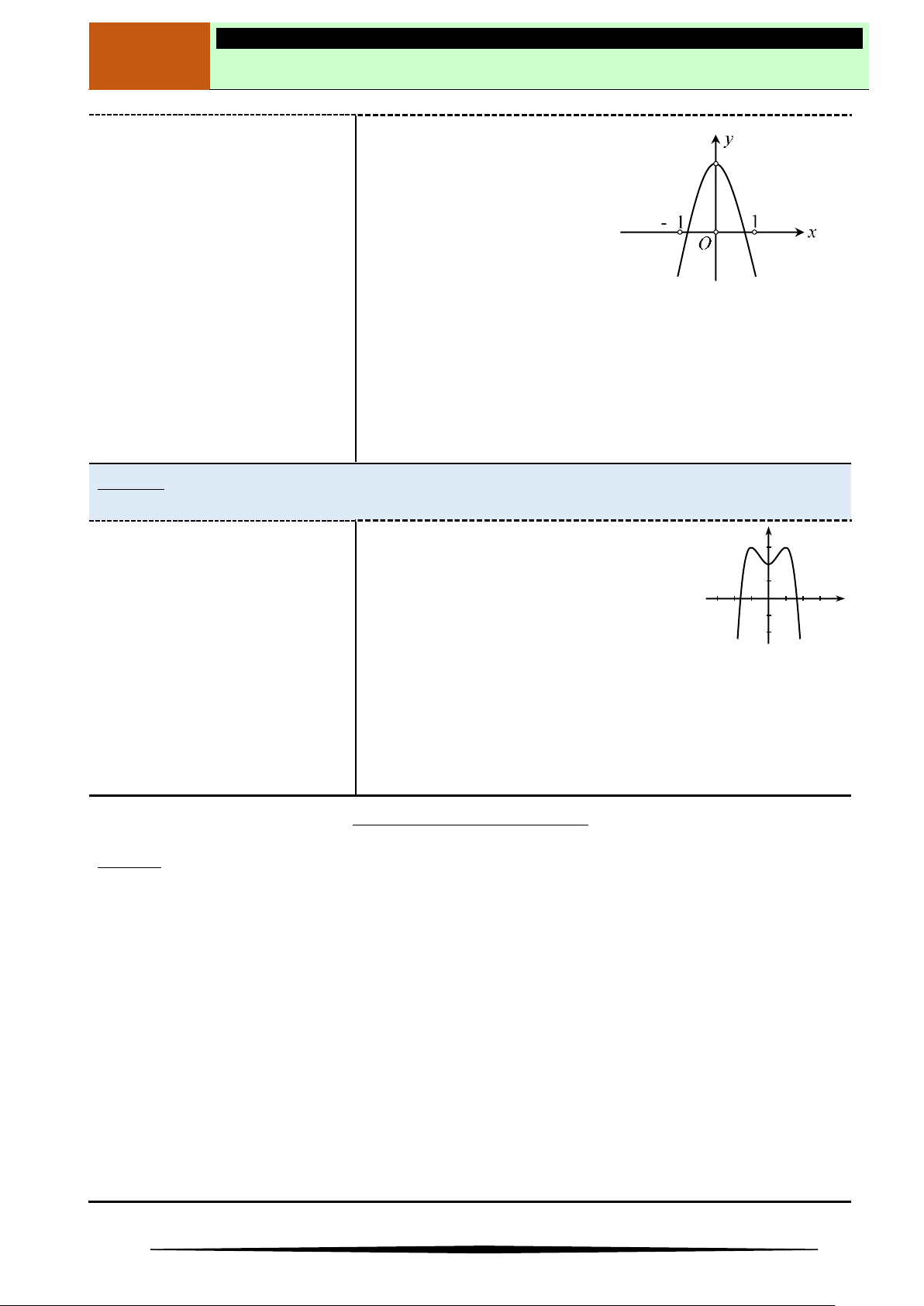
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 77

Ⓐ

32

3 2.y x x= - + +

Ⓑ

2

3 2.yx=+

Ⓒ

4

2.yx= - +

Ⓓ

42

2 2.y x x= - - +

.........................................................................................................................................................................................................................................

Ví dụ 23. Cho hàm số

42

y ax bx c= + +

có đồ thị như hình vẽ dưới đây. Trong các mệnh đề sau, mệnh

đề nào đúng ?

Ⓐ

0, 0, 0.a b c< < >

Ⓑ

0, 0, 0.a b c>>>

Ⓒ

0, 0, 0.a b c> < >

Ⓓ

0, 0, 0.a b c< > >

.........................................................................................................................................................................................................................................

ĐỒ THỊ HÀM SỐ NHẤT BIẾN

Cần nhớ:

...........................................................................................................................................................................................................................................................................................................................................................................

O

x

y

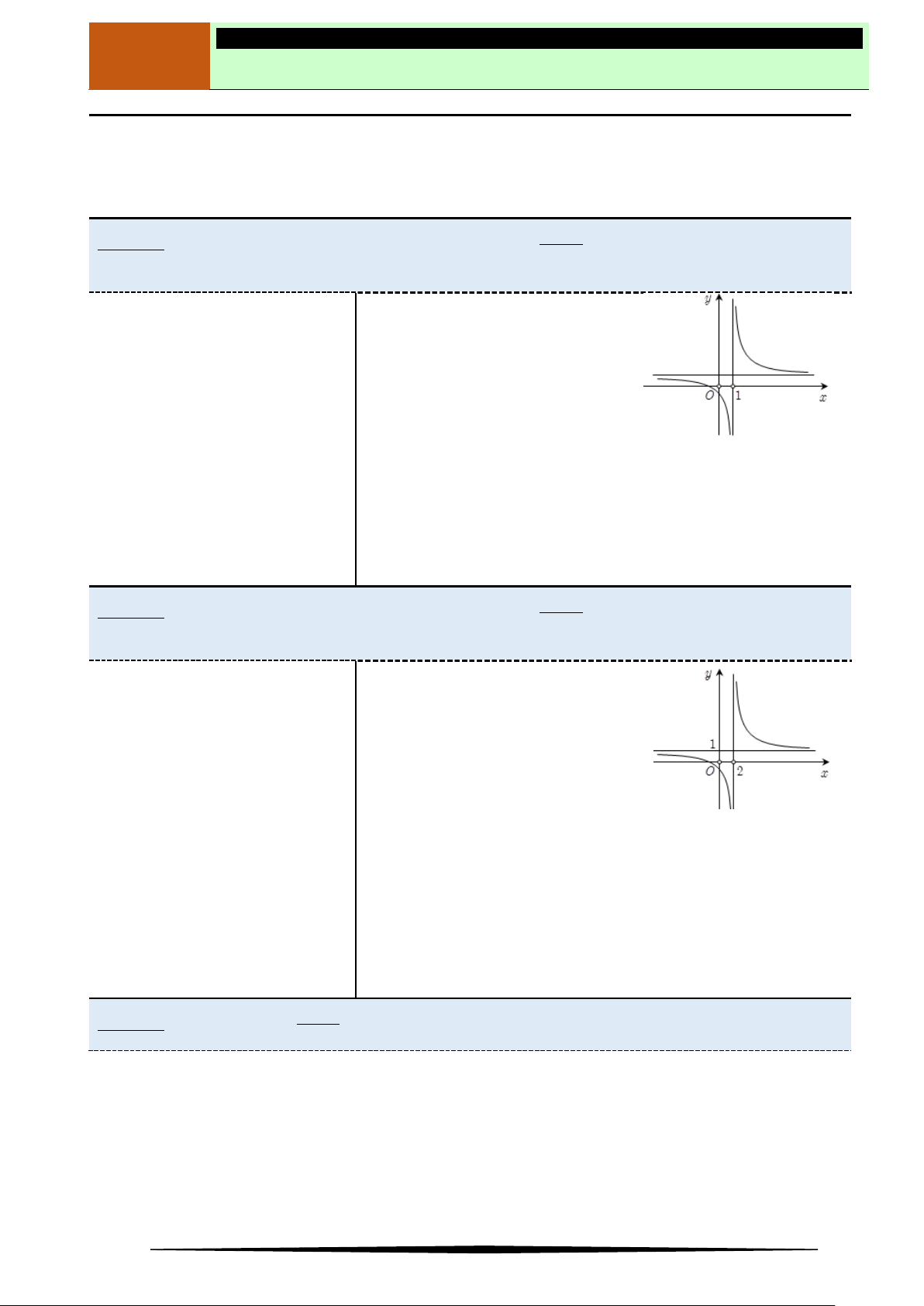
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 78

...........................................................................................................................................................................................................................................................................................................................................................................

Ví dụ 24. Đường cong của hình bên là đồ thị của hàm số

ax b

y

cx d

+

=

+

với

, , , a b c d

là các số thựⒸ Mệnh

đề nào đúng ?

Ⓐ

0, .yx

¢

> " Î ¡

Ⓑ

0, .yx

¢

< " Î ¡

Ⓒ

0, 1.yx

¢

> " ¹

Ⓓ

0, 1.yx

¢

< " ¹

.........................................................................................................................................................................................................................................

Ví dụ 25. Đường cong của hình bên là đồ thị của hàm số

ax b

y

cx d

+

=

+

với

, , , a b c d

là các số thựⒸ Mệnh

đề nào đúng ?

Ⓐ

0, 2.yx

¢

< " ¹

Ⓑ

0, 1.yx

¢

< " ¹

Ⓒ

0, 2.yx

¢

> " ¹

Ⓓ

0, 1.yx

¢

> " ¹

.........................................................................................................................................................................................................................................

Ví dụ 26. Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị là hình vẽ bên. Hỏi mệnh đề nào sau đây đúng ?

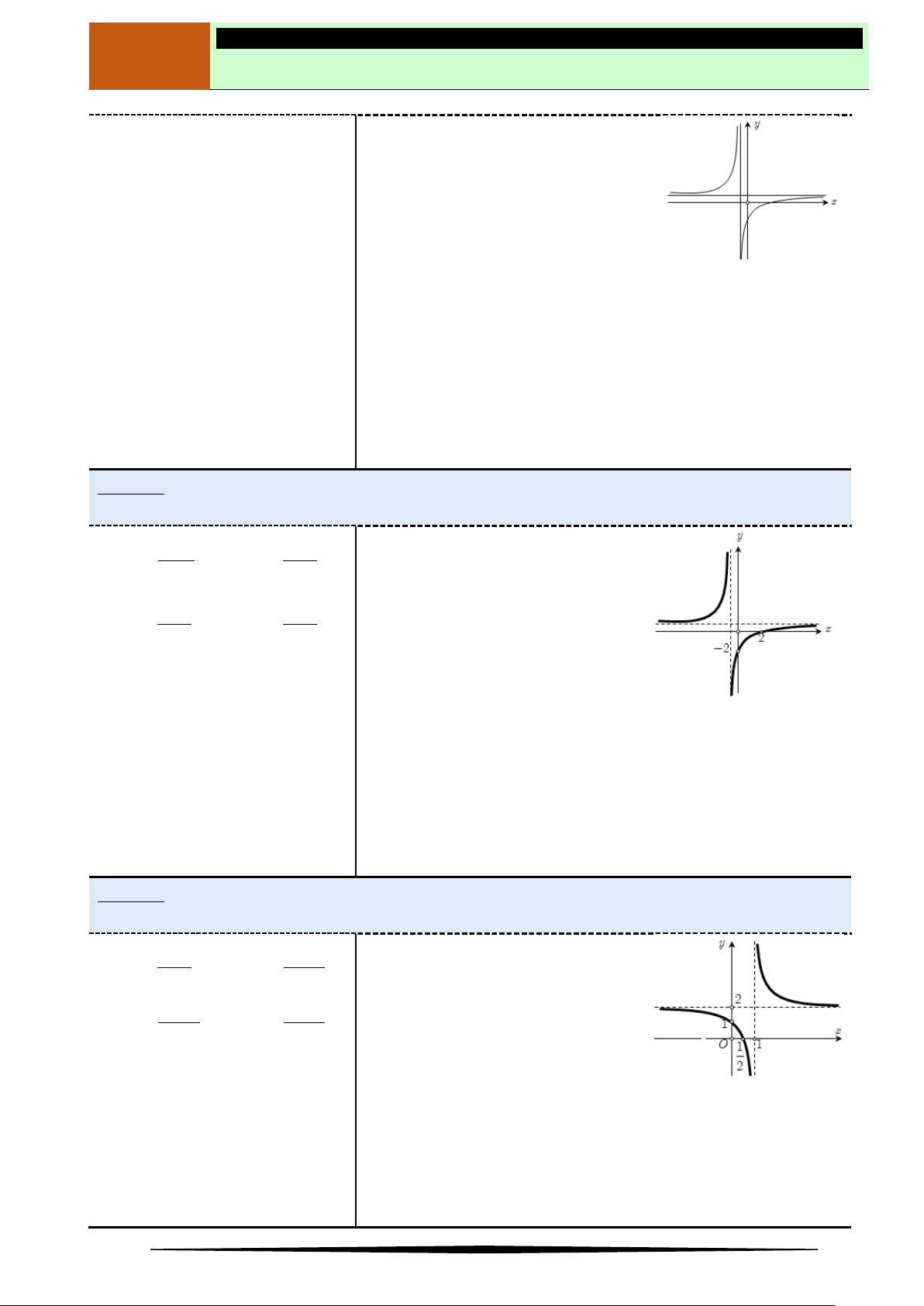
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 79

Ⓐ

0ad >

và

0.bd >

Ⓑ

0ad >

và

0.ab <

Ⓒ

0bd <

và

0.ab >

Ⓓ

0ad <

và

0.ab <

.........................................................................................................................................................................................................................................

Ví dụ 27. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở

bốn phương án

A, B, C, D

dưới đây. Hỏi hàm số đó là hàm số nào ?

Ⓐ

2

1

x

y

x

+

=×

-

Ⓑ

2

1

x

y

x

-

=×

+

Ⓒ

2

1

x

y

x

-

=×

+

Ⓓ

2

1

x

y

x

-

=×

-

.........................................................................................................................................................................................................................................

Ví dụ 28. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở

bốn phương án

A, B, C, D

dưới đây. Hỏi hàm số đó là hàm số nào ?

Ⓐ

1

2

x

y

x

-

=×

-

Ⓑ

21

1

x

y

x

-

=×

-

Ⓒ

21

1

x

y

x

+

=×

-

Ⓓ

21

1

x

y

x

-

=×

+

.........................................................................................................................................................................................................................................

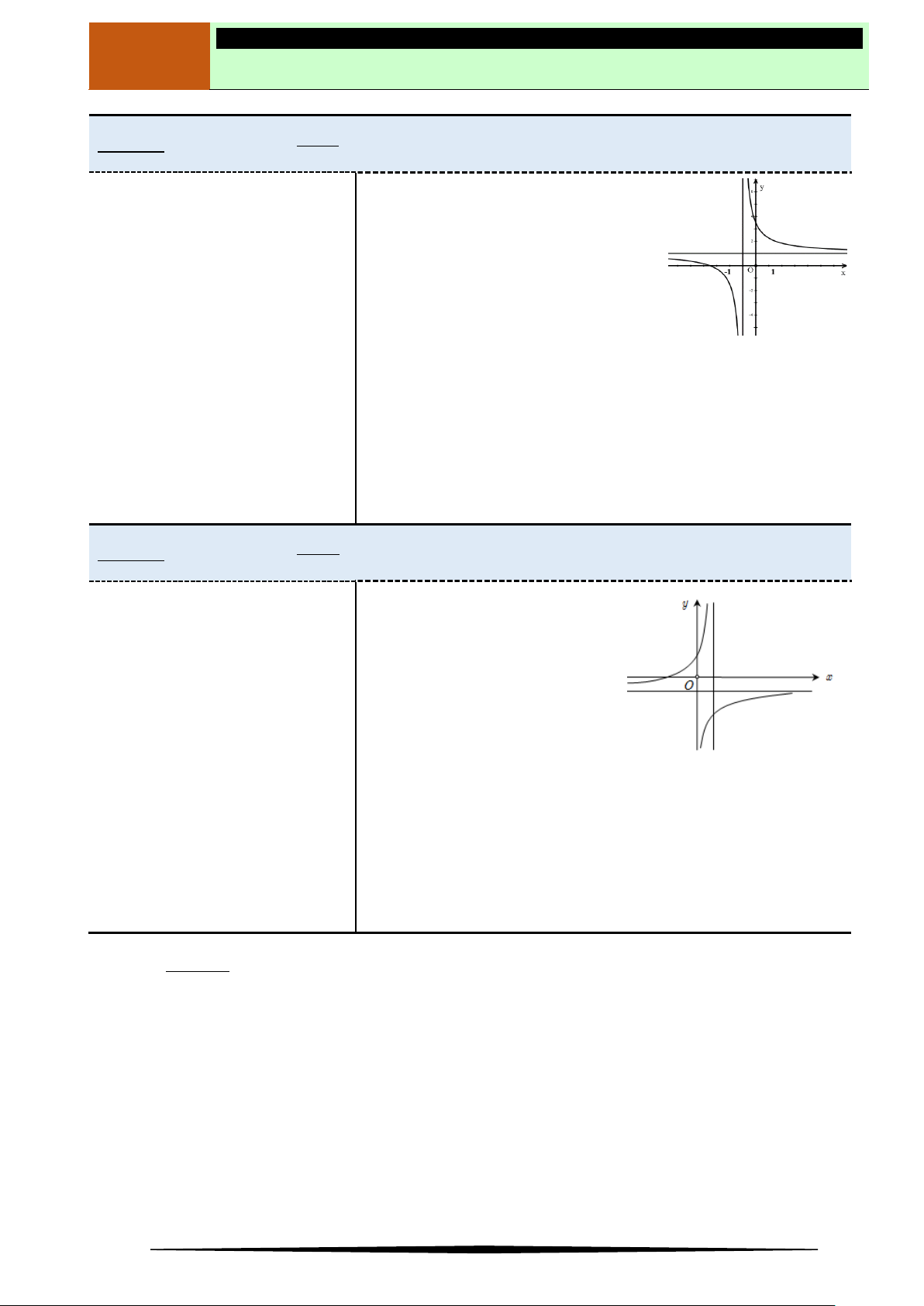
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 80

Ví dụ 29. Cho hàm số

1

ax b

y

x

+

=

+

có đồ thị như hình vẽ bên dưới. Tìm khẳng định đúng ?

Ⓐ

0.ab<<

Ⓑ

0.ba<<

Ⓒ

0.ba<<

Ⓓ

0.ab<<

.........................................................................................................................................................................................................................................

Ví dụ 30. Cho hàm số

ax b

y

cx d

+

=

+

có đồ thị như hình vẽ dưới. Mệnh đề nào dưới đây đúng ?

Ⓐ

0, 0, 0, 0.a b c d< > < >

Ⓑ

0, 0, 0, 0.a b c d> < < >

Ⓒ

0, 0, 0, 0.a b c d< < < >

Ⓓ

0, 0, 0, 0.a b c d< < > <

.........................................................................................................................................................................................................................................

Tổng kết:

..............................................................................................................................................................................................................................................................................................................................................................

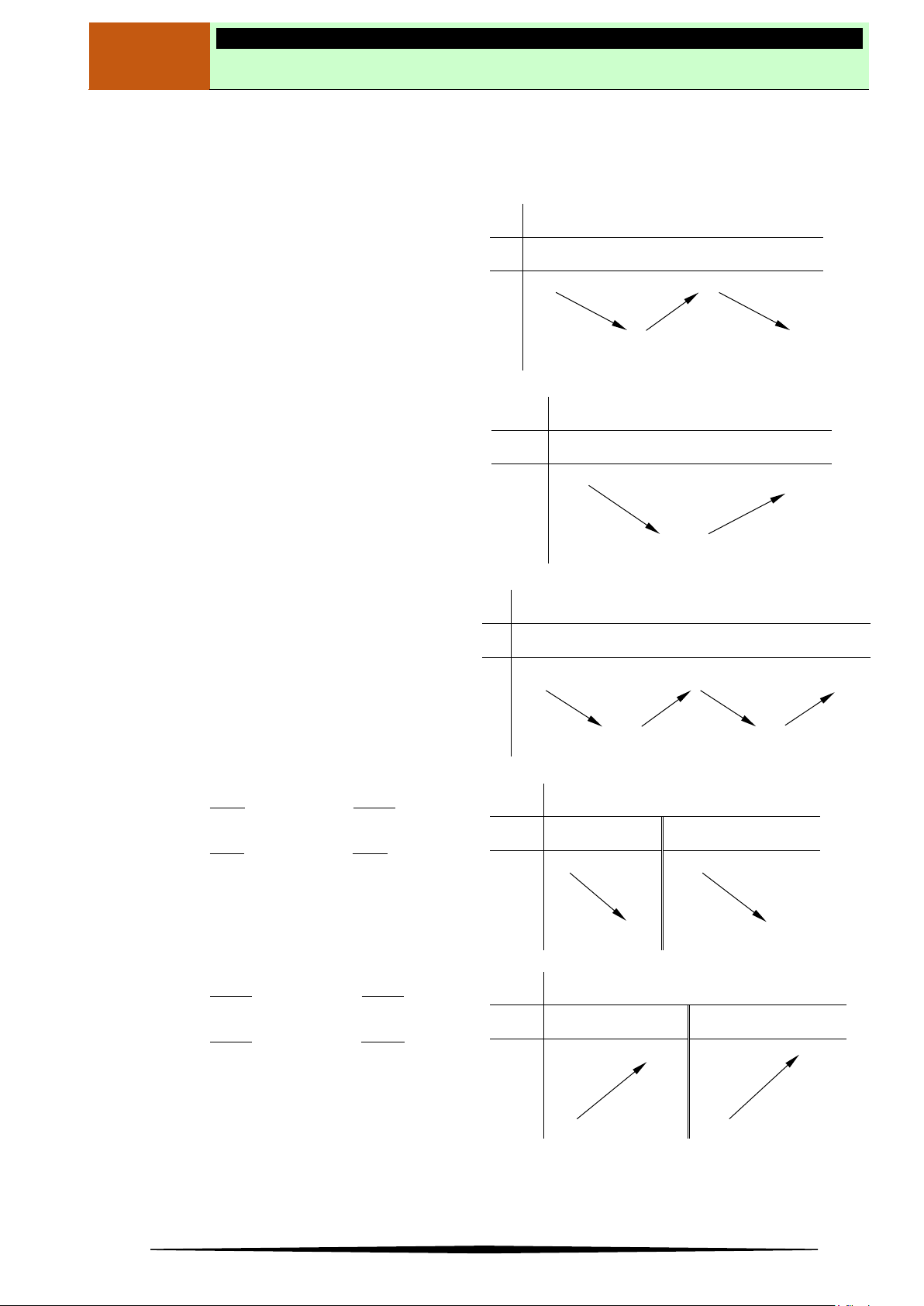
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 81

..............................................................................................................................................................................................................................................................................................................................................................

C. BÀI TẬP TỰ LUYỆN

Câu 1: Bảng biến thiên sau là của hàm số nào?

Ⓐ

32

31y x x= - -

Ⓑ

32

31y x x= - + -

Ⓒ

32

31y x x= + -

Ⓓ

32

31y x x= - - -

x

-¥

0

2

+¥

y’

-

+

-

y

3

-1

Câu 2: Bảng biến thiên sau là của hàm số nào?

Ⓐ

42

31y x x= - -

Ⓑ

42

31y x x= - + -

Ⓒ

42

31y x x= + -

Ⓓ

42

31y x x= - - +

x

0

y’

y

1

Câu 3: Bảng biến thiên sau là của hàm số nào?

Ⓐ

42

23y x x= - + -

Ⓑ

42

23y x x= - -

Ⓒ

42

23y x x= - +

Ⓓ

42

23y x x= - + +

x

-¥

1-

0

3

+¥

y’

-

0

+

0

-

0

+

y

+¥

3-

+¥

4-

Câu 4: Bảng biến thiên sau là của hàm số nào?

Ⓐ

3

2

x

y

x

-

=

-

Ⓑ

1

21

x

y

x

-

=

+

Ⓒ

1

2

x

y

x

+

=

-

Ⓓ

3

2

x

y

x

+

=

+

x

-¥

2

+¥

y’

-

y

1

+¥

-¥

1

Câu 5: Bảng biến thiên sau là của hàm số nào?

Ⓐ

21

1

x

y

x

+

=

+

Ⓑ

1

21

x

y

x

-

=

+

Ⓒ

21

1

x

y

x

+

=

-

Ⓓ

23

1

x

y

x

+

=

+

x

-¥

-1

+¥

y’

-

y

+¥

2

-¥

Câu 6: Một trong những dạng của đồ thị hàm số

42

y ax bx c= + +

.















GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 82

Ⓐ

Ⓑ

Ⓒ

Ⓓ

Câu 7: Đường cong trong hình bên dướ i là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn

phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

Ⓐ

3

3y x x=-

Ⓑ

3

31y x x= - + -

Ⓒ

42

1y x x= - +

Ⓓ

3

3y x x= - +

Câu 8: Đường cong trong hình bên dướ i là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn

phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

Ⓐ

3

31y x x= - +

Ⓑ

42

1y x x= - +

Ⓒ

2

1y x x= - + -

Ⓓ

32

3 3 1y x x x= - + -

Câu 9: Đồ thị hàm số

32

32y x x= - - +

có dạng:

Ⓐ

Ⓑ

Ⓒ

Ⓓ

Câu 10: Đồ thị hàm số

42

21y x x= - + -

có dạng:

Ⓐ

Ⓑ

Ⓒ

Ⓓ

Câu 11: Đồ thị của hàm số

42

21y x x= - -

là đồ thị nào trong các đồ thị sau đây?

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 83

Ⓐ

Ⓑ

Ⓒ

Ⓓ

Câu 12: Đồ thị của hàm số

42

3 6 1y x x= - - +

là đồ thị nào trong các đồ thị sau đây?

Ⓐ

Ⓑ

Ⓒ

Ⓓ

Câu 13: Đường cong trong hình bên là đồ thị một hàm số trong bốn hàm số được liệt kê ở bốn phương án A,

B, C, D dưới đây. Hỏi đó là đồ thị hàm số nào?

Ⓐ

42

42y x x= - +

Ⓑ

42

42y x x= - -

Ⓒ

42

42y x x= + +

Ⓓ

42

42y x x= - + +

Câu 14: Đường cong trong hình bên là đồ thị một hàm số trong bốn hàm số được liệt kê ở bốn phương án A,

B, C, D dưới đây. Hỏi đó là đồ thị hàm số nào?

Ⓐ

2

1yx=-

Ⓑ

2

1yx= - -

Ⓒ

42

1y x x= - -

Ⓓ

42

1y x x= + -

Câu 15: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương

án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

Ⓐ

42

31y x x= - +

Ⓑ

42

21y x x= - +

Ⓒ

42

21y x x= - + +

Ⓓ

42

21y x x= - - +

Câu 16: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án

A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 84

Ⓐ

42

21y x x= - +

Ⓑ

42

21y x x= - +

Ⓒ

42

31y x x= - +

Ⓓ

42

21y x x= - - +

Câu 17: Hàm số

22

2

x

y

x

+

=

+

có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.

Ⓐ

Ⓑ

Ⓒ

Ⓓ

Câu 18: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án

A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

Ⓐ

32

31y x x= + +

Ⓑ

25

1

x

y

x

+

=

+

Ⓒ

42

1y x x= - +

Ⓓ

21

1

x

y

x

+

=

-

Câu 19: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án

A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

Ⓐ

21

1

x

y

x

-

=

+

Ⓑ

21

1

x

y

x

+

=

-

Ⓒ

21

1

x

y

x

+

=

+

Ⓓ

12

1

x

y

x

-

=

-

Câu 20: Đồ thị trong hình bên là của hàm số nào sau đây?

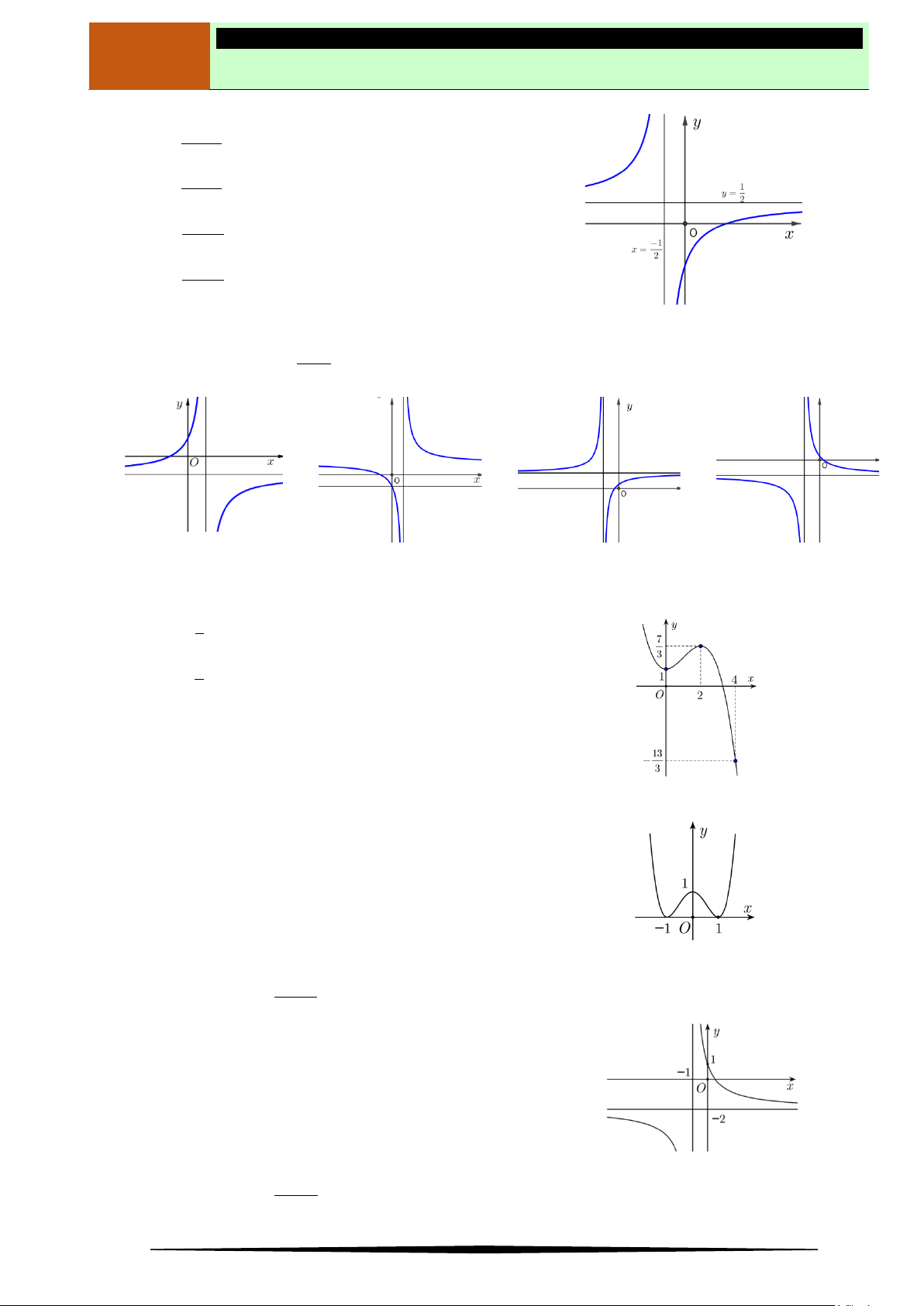
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 85

Ⓐ

1

.

12

x

y

x

-

=

-

Ⓑ

1

.

21

x

y

x

-

=

-

Ⓒ

1

.

21

x

y

x

+

=

+

Ⓓ

1

.

21

x

y

x

-

=

+

Câu 21: Đồ thị hàm số

1

x

y

x

+

=

-

có dạng:

Ⓐ

Ⓑ

Ⓒ

Ⓓ

Câu 22: Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình vẽ bên. Xác định

, , , .a b c d

Ⓐ

1

, 1, 0, 1.

3

a b c d= - = = =

Ⓑ

1

, 1, 2, 1.

3

a b c d= - = = =

Ⓒ

1, 1, 0, 1.a b c d= - = = =

Ⓓ

1, 11, 0, 1.a b c d= - = = =

Câu 23: Cho hàm số

42

y ax bx c= + +

có đồ thị như hình vẽ bên. Xác định

, , .a b c

Ⓐ

1, 2, 1.a b c= = - =

Ⓑ

1, 2, 1.a b c= = - = -

Ⓒ

1, 2, 1.a b c= - = =

Ⓓ

2, 2, 1.a b c= = - =

Câu 24: Cho hàm số

1

ax b

y

x

+

=

+

có đồ thị như hình vẽ bên. Xác định

,.ab

Ⓐ

1, 2.ab= - = -

Ⓑ

1, 2.ab= = -

Ⓒ

2, 1.ab= - =

Ⓓ

2, 1.ab==

Câu 25: Cho hàm số

2ax

y

cx b

+

=

+

có đồ thị như hình vẽ bên. Xác định

, , .a b c

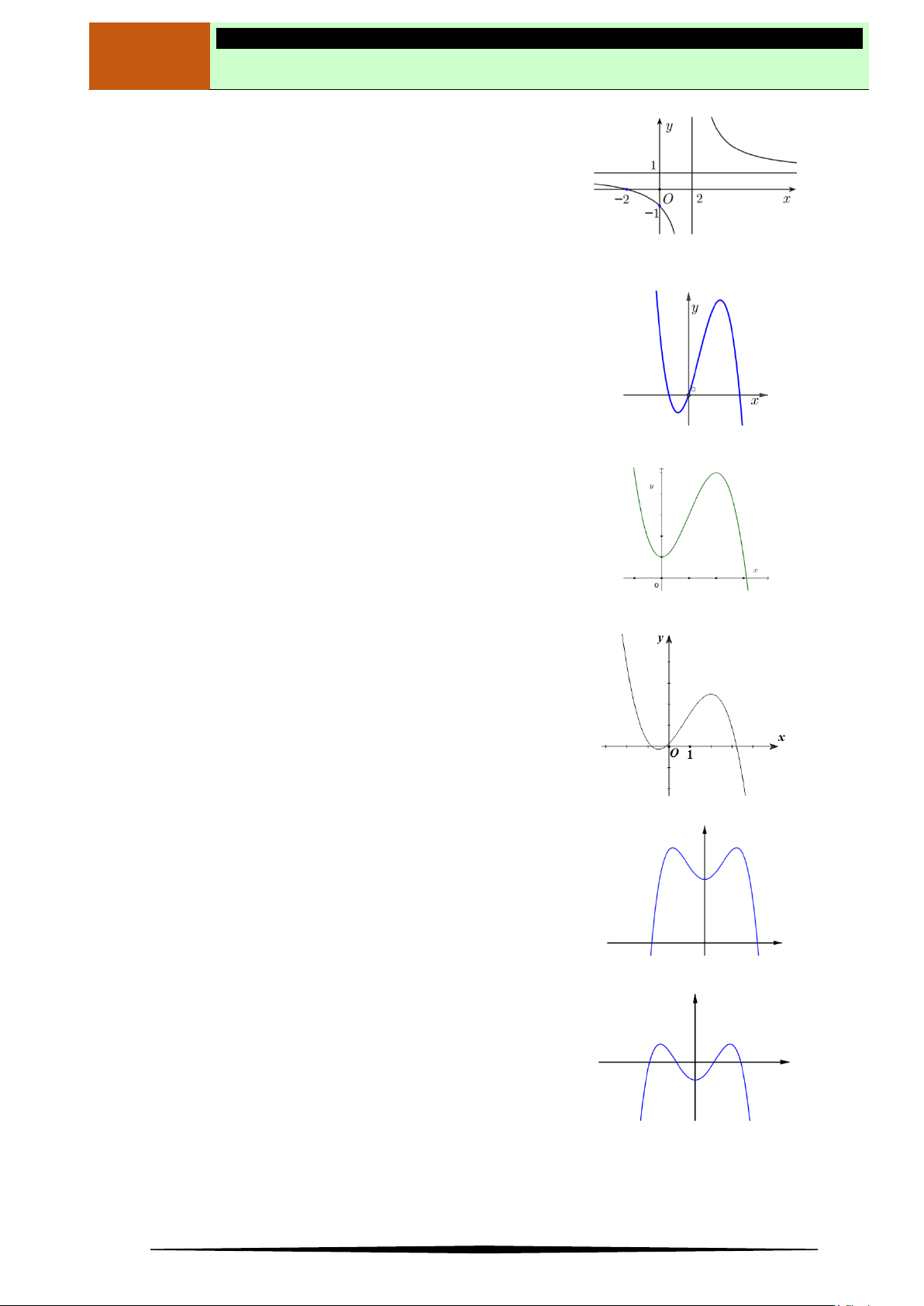
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 86

Ⓐ

2, 2, 1.a b c= = = -

Ⓑ

1, 1, 1.a b c= = = -

Ⓒ

1, 2, 1.a b c= = =

Ⓓ

1, 2, 1.a b c= = - =

Câu 26: Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

Ⓐ

0, 0, 0, 0.a b c d< > > <

Ⓑ

0, 0, 0, 0.a b c d< < > <

Ⓒ

0, 0, 0, 0.a b c d> < < >

Ⓓ

0, 0, 0, 0.a b c d< > < <

Câu 27: Cho hàm số

( )

32

0y ax bx cx d a= + + + ¹

có đồ thị như hình bên dưới. Mệnh đề nào sau đây đúng?

Ⓐ

0, 0, 0, 0.a b c d< > = >

Ⓑ

0, 0, 0, 0.a b c d> < > >

Ⓒ

0, 0, 0, 0.a b c d< > > >

Ⓓ

0, 0, 0, 0.a b c d< < = >

Câu 28: Cho hàm số có đồ thị như hình bên dưới. Mệnh đề nào sau đây đúng?

Ⓐ

  0; 0; 0; 0.a b c d< > > >

Ⓑ

  0; 0; 0; 0.a b c d< < < >

Ⓒ

0; 0; 0; 0.a b c d< < > >

Ⓓ

  0; 0; 0; 0.a b c d< > < >

Câu 29: Cho hàm số

42

y ax bx c= - +

có đồ thị như hình vẽ bên dưới. Mệnh đề nào dưới đây đúng?

Ⓐ

0; 0; 0a b c< > >

Ⓑ

0; 0; 0.a b c<<>

Ⓒ

0; 0; 0.a b c> < >

Ⓓ

0; 0; 0.a b c< > >

Câu 30: Cho hàm số

42

y ax bx c= + +

có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

Ⓐ

0; 0; 0a b c< > >

Ⓑ

0; 0; 0.a b c<<>

Ⓒ

0; 0; 0.a b c> < >

Ⓓ

0; 0; 0.a b c< > <

Câu 31: Cho hàm số

42

y ax bx c= + +

có đồ thị như hình bên. Xác định dấu của a, b, Ⓒ

 

32

0    y ax bx cx d a

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 87

Ⓐ

0, 0, 0.a b c><<

Ⓑ

0, 0, 0.a b c> < >

Ⓒ

0, 0, 0.a b c< < <

Ⓓ

0, 0, 0.a b c> > <

Câu 32: Biết rằng hàm số

42

()y f x ax bx c= = + +

có đồ thị là đường cong trong hình vẽ bên. Tính giá trị

( ).f a b c++

Ⓐ

( ) 1.f a b c+ + = -

Ⓑ

( ) 2.f a b c+ + =

Ⓒ

( ) 2.f a b c+ + = -

Ⓓ

( ) 1.f a b c+ + =

Câu 33: Xác định các hệ số a, b, c để đồ thị hàm số :

42

y ax bx c= + +

có đồ thị như hình vẽ.

Ⓐ

1

; 3; 3

4

a b c= - = = -

Ⓑ

1; 2; 3a b c= = - = -

Ⓒ

1; 3; 3a b c= = - =

Ⓓ

1; 3; 3a b c= = = -

Câu 34: Cho hàm số

( )

42

0y ax bx c a= + + ¹

có đồ thị như hình dưới. Kết luận nào sau đây đúng?

Ⓐ

0; 0; 0a b c> ³ <

Ⓑ

0; 0; 0a b c><£

Ⓒ

0; 0; 0a b c> > >

Ⓓ

0; 0; 0a b c< < <

Câu 35: Hình vẽ bên là đồ thị của hàm số

ax b

y

cx d

+

=

+

. Mệnh đề nào sau đây là đúng?

Ⓐ

0, 0bd ab<>

Ⓑ

0, 0ad ab><

Ⓒ

0, 0.bd ad>>

Ⓓ

0, d 0.ab a<<

Câu 36: Hình vẽ bên là đồ thị của hàm số

ax b

y

cx d

+

=

+

. Mệnh đề nào sau đây là đúng?

Ⓐ

0ad bc<<

Ⓑ

0ad bc>>

Ⓒ

0ad bc<<

Ⓓ

0 ad bc<<

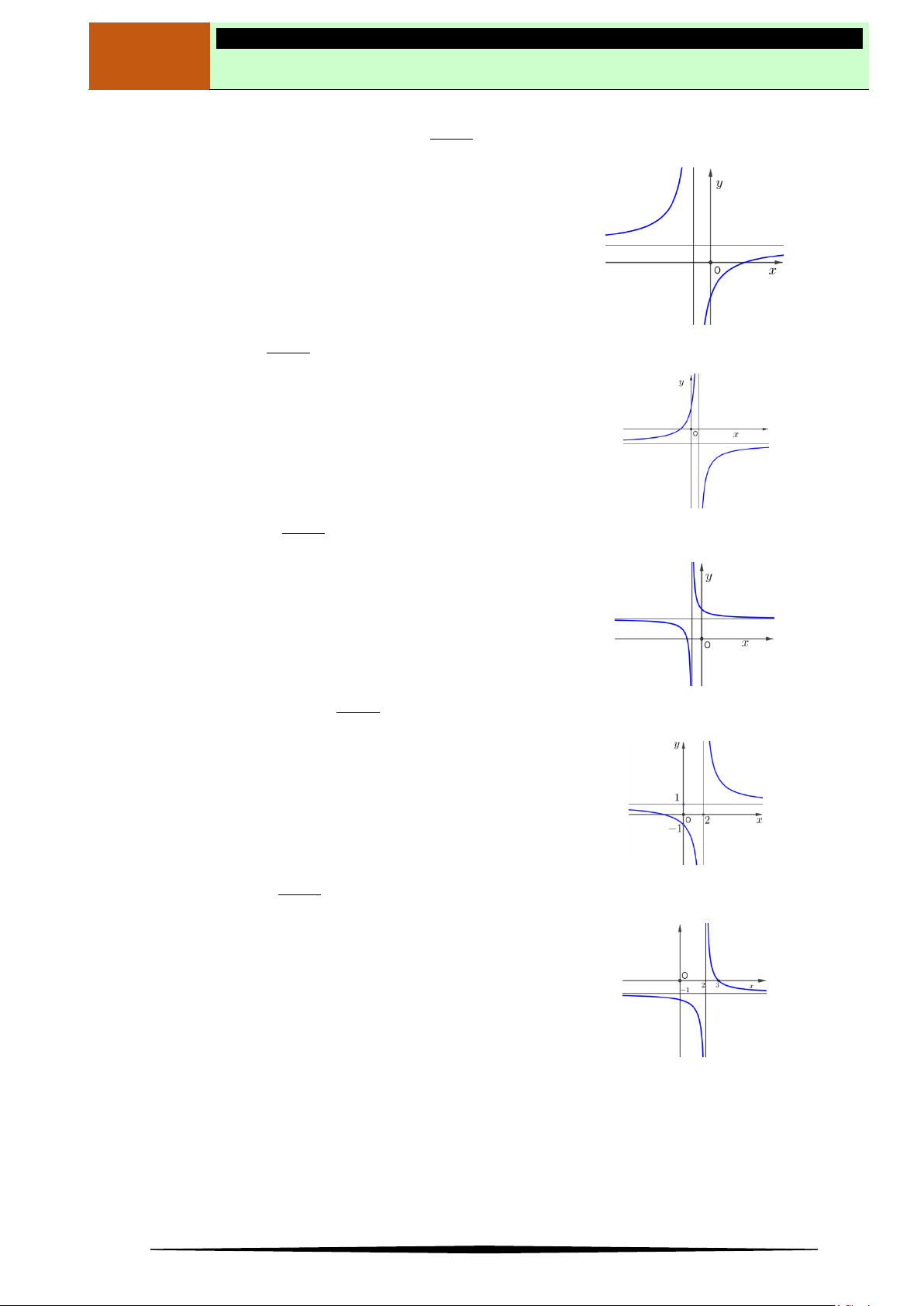
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 88

Câu 37: Hình vẽ bên là đồ thị của hàm số

ax b

y

cx d

+

=

+

. Mệnh đề nào sau đây là đúng?

Ⓐ

0

ad

bc

ì

ï

<

ï

í

ï

<

ï

î

Ⓑ

0

ad

bc

ì

ï

>

ï

í

ï

>

ï

î

Ⓒ

0

ad

bc

ì

ï

>

ï

í

ï

<

ï

î

Ⓓ

0

ad

bc

ì

ï

<

ï

í

ï

>

ï

î

Câu 38: Cho hàm số

( 0)

ax b

ya

cx d

+

=<

+

có đồ thị như hình vẽ dưới. Mệnh đề nào dưới đây đúng?

Ⓐ

0, 0, 0, 0.a b c d< > < >

Ⓑ

0, 0, 0, 0.a b c d> < < >

Ⓒ

0, 0, 0, 0.a b c d< < < >

Ⓓ

0, 0, 0, 0.a b c d< < > <

Câu 39: Cho hàm số

1

ax b

y

x

+

=

+

có đồ thị như hình vẽ bên. Tìm khẳng định đúng?

Ⓐ

0ab<<

Ⓑ

0ba<<

Ⓒ

0 ba<<

Ⓓ

0 ab<<

Câu 40: Tìm

,,a b c

để hàm số

2ax

y

cx b

+

=

+

có đồ thị như hình vẽ:

Ⓐ

2, 2; 1a b c= = = -

Ⓑ

1; 1; 1a b c= = = -

Ⓒ

1, 2; 1a b c= = =

Ⓓ

1, 2; 1a b c= = - =

Câu 41: Cho hàm số

ax b

y

xc

+

=

+

có đồ thị như hình vẽ bên. Tính giá trị của

2.a b c++

Ⓐ

1.-

Ⓑ

2.-

Ⓒ

0.

Ⓓ

3.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 89

§7. MỘT SỐ CHUYÊN ĐỀ

CĐ7.1: SỰ TƯƠNG GIAO

A. TÓM TẮT LÝ THUYẾT



Cho hai đồ thị hàm số

( ) : ( )C y f x

và

( ) : ( ).C y g x





Tọa độ giao điểm (nếu có) của

( )C

và

( )C



là

nghiệm của hệ phương trình:

( )

( ) ( )

( )

y f x

f x g x

y g x









 











( )

― Phương trình

( )

được gọi là phương trình hoành độ điểm chung của

( )C

và

( ).C



― Số nghiệm của

( )

chính là số điểm chung của hai đồ thị.

― Nếu

( )

vô nghiệm thì hai đồ thị không có điểm chung.

B. CÁC DẠNG TOÁN THƯỜNG GẶP

Daïng toaùn 1. Töông giao cuûa haøm soá nhaát bieán vaø ñöôøng thaúng



 Bài toán tổng quát: Tìm các giá trị của tham số

m

để để đường thẳng

:d y Ax B 

cắt đồ thị

hàm số

( ) :

Cx D

C y

Ex F







tại hai điểm phân biệt thỏa mãn điều kiện K ?

 Phương pháp giải:

Bước 1. Lập phương trình hoành độ giao điểm của

d

và

( )C

là:

Cx D

Ax B

Ex F



 



Biến đổi về dạng phương trình bậc hai

2

( ) 0.g x ax bx c   

Bước 2. Để

d

cắt

( )C

tại 2 điểm phân biệt



phương trình

( ) 0g x 

có 2 nghiệm phân biệt và

khác

2

( ) ( )

0, 4 0

0

g x g x

a b ac

F

g

E





    



 

  











 















 





Giải hệ

1

.

m

  D

Bước 3. Gọi

1 1 2 2

( ; ), ( ; )A x Ax B B x Ax B 

là hai tọa độ giao điểm của

d

và

( ),C

trong đó

1 2

, x x

là

2

nghiệm của

( ) 0.g x 

Theo Viét:

1 2

b

S x x

a

   

và

1 2

c

P x x

a

 

(1)

Bước 4. Biến đổi điều kiện

K

về dạng tổng và tích của

1 2

, x x

(2)

Thế (1) vào (2) sẽ thu được phương trình hoặc bất phương trình với biến là

.m

Giải chúng

sẽ tìm được giá trị

2

.

m

 D

Kết luận giá trị

1 2

.

m

 D D

Lưu ý:

Nếu đề bài chỉ yêu cầu tìm tham số

m

để hai đồ thị cắt nhau tại

n

điểm, ta chỉ cần tìm điều kiện

để phương trình hoành độ giao điểm có

n

nghiệm phân biệt.

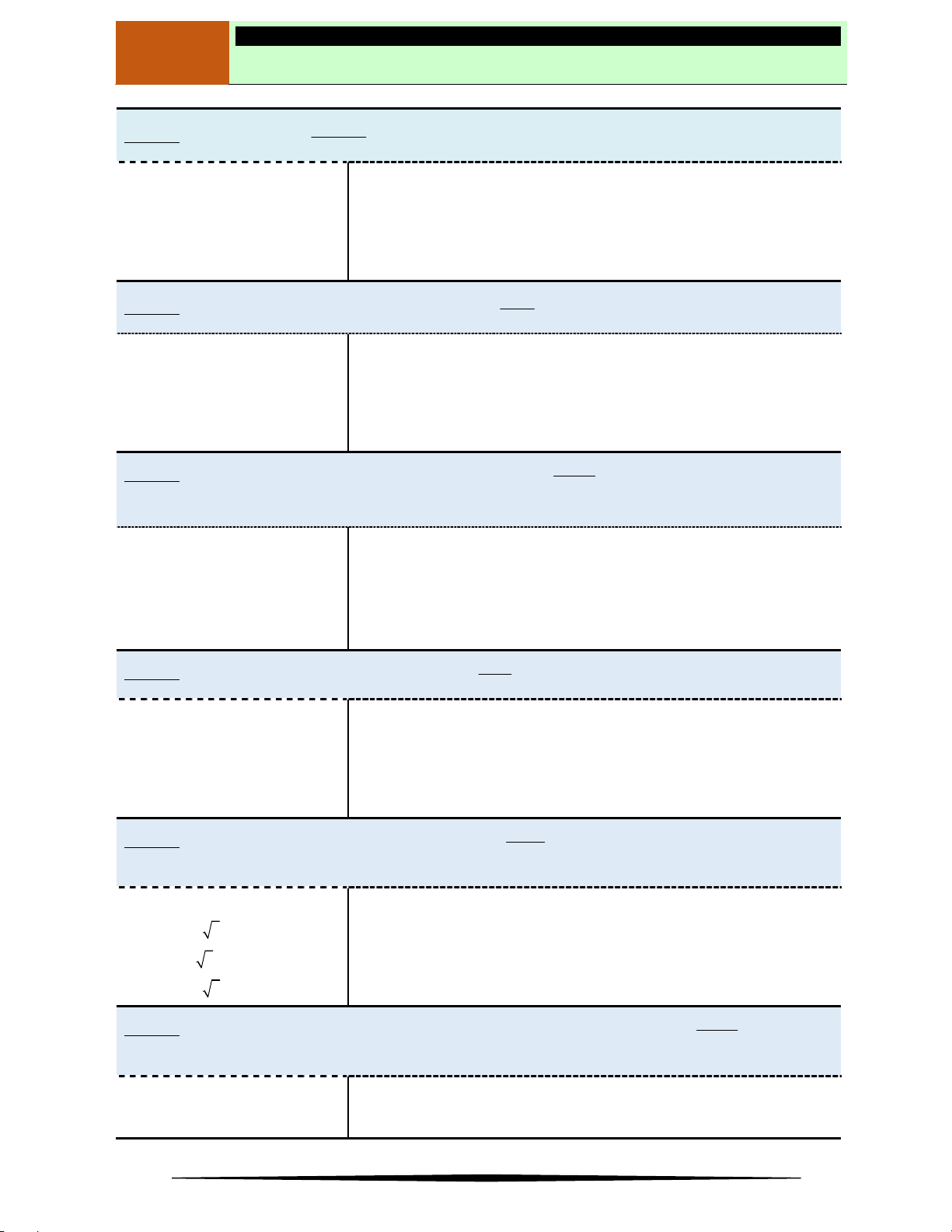
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 90

Ví dụ 1. Cho hàm số

2019

1

x

y

x







có đồ thị

( ).C

Tìm tọa độ giao điểm của

( )C

với trục tung ?

Ⓐ

( 2019; 0).M 

Ⓑ

(0; 2019).M 

Ⓒ

(0;2019).M

Ⓓ

(2019; 0).M

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2. Tìm tọa độ giao điểm của đồ thị hàm số

4

2

x

y

x







với các trục tọa độ ?

Ⓐ

(0; 4)A

và

( 2; 0).B 

Ⓑ

(4; 0)A

và

(0; 2).B 

Ⓒ

(4;0)A

và

(–2;0).B

Ⓓ

(4; 0)A

và

(0;2).B

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3. Biết đường thẳng

3 4y x 

cắt đồ thị hàm số

4 2

1

x

y

x







tại hai điểm phân biệt có tung độ

lần lượt là

1

y

và

2

.y

Tính

1 2

.y y

Ⓐ

1 2

10.

y y

 

Ⓑ

1 2

11.

y y

 

Ⓒ

1 2

9.

y y

 

Ⓓ

1 2

1.

y y

 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4. Tìm tọa độ giao điểm của đồ thị

4

( ) :

1

x

C y

x





và đường thẳng

: 1.y x  

Ⓐ

1

(0;1).

M

Ⓑ

2

(2;3).

M

Ⓒ

3

(1;2).

M

Ⓓ

4

(1;3).

M

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 5. Gọi

, A B

là giao điểm của đồ thị hàm số

2 1

1

x

y

x







và đường thẳng

: 1.d y x 

Tính độ dài

đoạn thẳng

.AB

Ⓐ

2.AB 

Ⓑ

2 2.AB 

Ⓒ

2.AB 

Ⓓ

2 3.AB 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 6. Gọi

, M N

là giao điểm của đường thẳng

1y x 

và đường cong

2 4

1

x

y

x



 



Khi đó, hãy

tìm tọa độ trung điểm

I

của đoạn thẳng

.MN

Ⓐ

(1;2).I

Ⓑ

( 2; 3).I  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

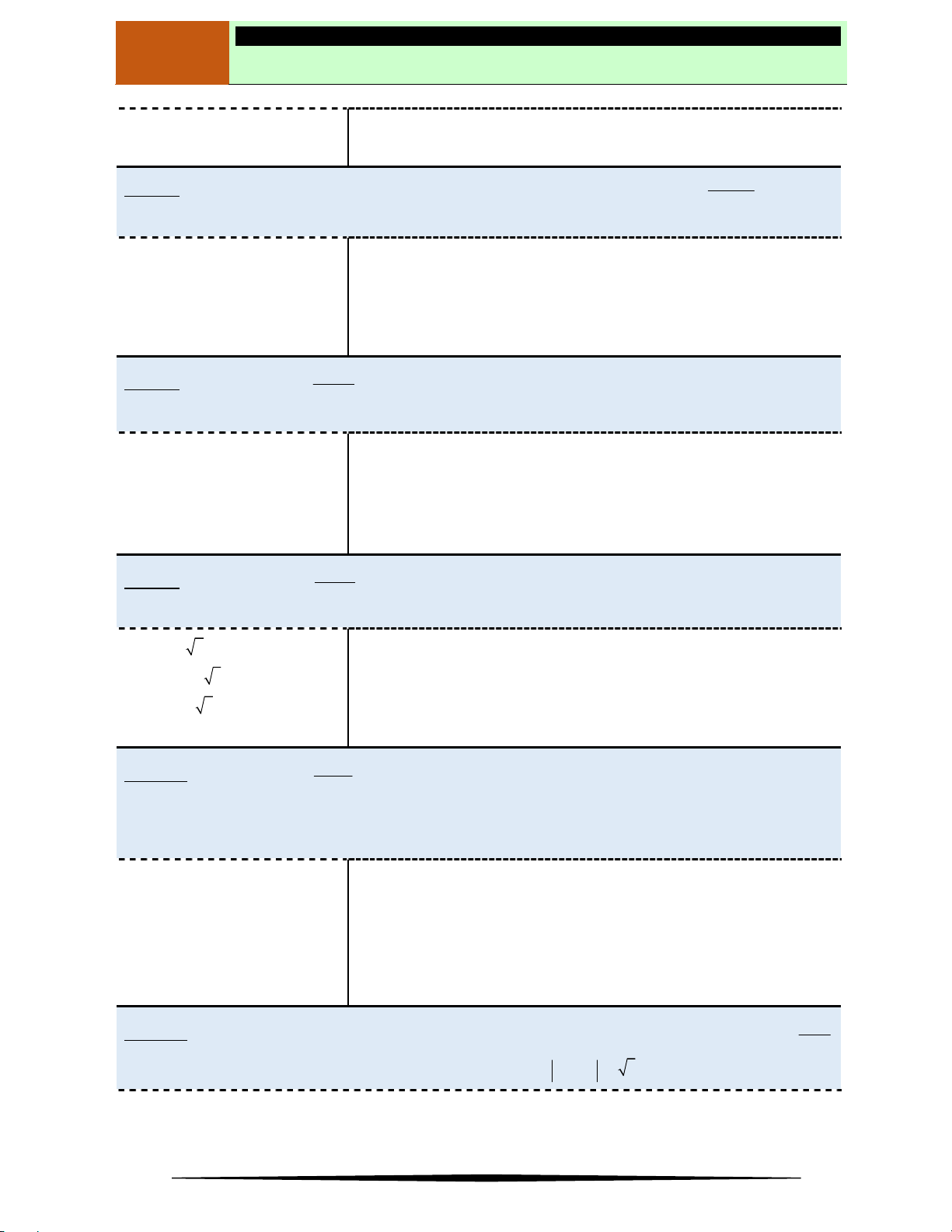
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 91

Ⓒ

(1; 3).I

Ⓓ

(2;3).I

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 7. Tìm tập hợp tất cả các giá trị thực của tham số

m

để đồ thị hàm số

2

1

x m

y

x







cắt đường

thẳng

1y x 

tại hai điểm phân biệt.

Ⓐ

( ;2].

Ⓑ

( ;2).

Ⓒ

( ; 2). 

Ⓓ

(2; ).

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 8. Cho hàm số

2 3

2

x

y

x







có đồ thị

( )C

và đường thẳng

: .d y x m 

Tìm tất cả các giá trị của

tham số

m

để đường thẳng

d

cắt đồ thị

( )C

tại

2

điểm phân biệt ?

Ⓐ

2.m 

Ⓑ

6.m 

Ⓒ

2.m 

Ⓓ

2m 

hoặc

6.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 9. Cho hàm số

2 3

1

x

y

x



 



Tìm tham số

m

để đồ thị hàm số đã cho tiếp xúc với đường thẳng

2 .y x m 

Ⓐ

8.m 

Ⓑ

2 2.m  

Ⓒ

8.m  

Ⓓ

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 10. Cho hàm số

2 1

1

x

y

x







có đồ thị

( ).C

Hỏi tham số thực

m

thuộc tập nào sau đây để đường

thẳng

: 2d y m x 

cắt

( )C

tại hai điểm phân biệt có hoành độ

1 2

, x x

thỏa mãn

1 2 1 2

2 8( ) 7.

x x x x

  

Ⓐ

( ; 8). 

Ⓑ

( 8; 1). 

Ⓒ

(0;7).

Ⓓ

(8; ).

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 11. Tìm các giá trị thực của tham số

m

để đường thẳng

y x m  

cắt đồ thị hàm số

1

x

y

x





tại hai điểm phân biệt có hoành độ

1 2

, x x

thỏa mãn

1 2

5.

x x 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 92

Ⓐ

3

1

m



 













Ⓑ

1

2

m



 







 





Ⓒ

0

2

m

















Ⓓ

3.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 12. Cho hàm số

2

2 1

x

y

x



 



Xác định tất cả các giá trị của tham số

m

để đường thẳng

1y mx m  

luôn cắt đồ thị hàm số tại hai điểm thuộc về hai nhánh của đồ thị.

Ⓐ

0.m 

Ⓑ

0.m 

Ⓒ

0.m 

Ⓓ

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 13. Cho hàm số

2 1

1

x

y

x







có đồ thị

( )C

và đường thẳng

( ) : 3 .d y x m  

Tìm tất cả các giá trị

của tham số

m

để

( )d

cắt

( )C

tại hai điểm phân biệt thuộc nhánh phải của

( ).C

Ⓐ

11.m 

Ⓑ

1.m  

Ⓒ

1m  

hoặc

11.m 

Ⓓ

5.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 14. Cho hàm số:

2

2 1

x

y

x







. Xác định tất cả các giá trị của tham số

m

để đường thẳng

1y mx m  

luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc cùng một nhánh của đồ

thị.

Ⓐ

3

0

m





 















Ⓑ

0.m 

Ⓒ

0.m 

Ⓓ

3

.

1

m





 













................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 15. Tìm tập hợp tất cả các giá trị của tham số

m

để đường thẳng

: 1d y x 

cắt đồ thị hàm số

2

1

x m

y

x







tại hai điểm phân biệt có hoành độ dương.

Ⓐ

( ; 1). 

Ⓑ

( ;1).

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 93

Ⓒ

( 2; 1). 

Ⓓ

( 2;1).

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 16. Tìm tất cả các giá trị thực của tham số

m

để đường thẳng

: –d y x m 

cắt đồ thị

2 1

1

x

y

x

 





tại hai điểm

, A B

sao cho độ dài đoạn thẳng

2 2.AB 

Ⓐ

1m 

hoặc

7.m  

Ⓑ

1m 

hoặc

2.m 

Ⓒ

7m  

hoặc

5.m 

Ⓓ

1m 

hoặc

1.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Daïng toaùn 2. Töông giao cuûa haøm soá baäc ba vaø ñöôøng thaúng



 Bài toán tổng quát: Tìm các giá trị của

m

để để đường thẳng

:d y px q 

cắt đồ thị hàm số

3 2

( ) :C y ax bx cx d   

tại 3 điểm phân biệt thỏa điều kiện

K

?

 Phương pháp giải:

Bước 1. Phương trình hoành độ giao điểm

3 2

ax bx cx d px q    



d q

thì

2

0

PT ( ) 0

( ) 0

x x

x ax bx c p

g x ax bx c p



 



      



    









,d q

ta đưa về phương trình bậc ba và nhẩm nghiệm đặc biệt

x x



và chia

Hoócner thì phương trình tương đương:

2

( )( ) 0

( ) 0

x x

x x ax b x c

g x ax b x c







 

     



 

   







Bước 2. Để

d

cắt

( )C

tại ba điểm phân biệt



phương trình

( ) 0g x 

có

2

nghiệm phân biệt

khác

( )

0

( ) 0

g x

x

g x





 



 













Giải hệ này, tìm được giá trị

1

.

m

 D

Bước 3. Gọi

1 1 2 2

( ; ), ( ; ), ( ; )

o o

A x px q B x px q C x px q  

với

1 2

, x x

là hai nghiệm của phương

trình

( ) 0.g x 

Theo Viét, ta có:

1 2

b

x x

a



  

và

1 2

c

x x

a





(1)

Bước 4. Biến đổi điều kiện

K

về dạng tổng và tích của

1 2

, x x

(2)

Thế (1) vào (2) sẽ thu được phương trình hoặc bất phương trình với biến là

.m

Giải

chúng sẽ tìm được giá trị

2

.

m

 D

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 94

Kết luận:

1 2

.

m

 D D

Nguyên tắc nhẩm nghiệm: Nếu phương trình chứa tham số, ta sẽ chọn nghiệm

x

sao cho triệt

tiêu đi tham số

m

và thử lại tính đúng sai. Hoặc có thể sử dụng casio.

Ví dụ 1. Cho hàm số

2

( 2)( 1)y x x  

có đồ thị

( ).C

Mệnh đề nào dưới đây đúng ?

Ⓐ

( )C

cắt trục hoành tại hai điểm.

Ⓑ

( )C

cắt trục hoành tại một điểm.

Ⓒ

( )C

không cắt trục hoành.

Ⓓ

( )C

cắt trục hoành tại ba điểm.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2. Cho hàm số

3

3y x x 

có đồ thị hàm số là

( ).C

Tìm số giao điểm của

( )C

và trục hoành.

Ⓐ

2.

Ⓑ

3.

Ⓒ

1.

Ⓓ

0.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3. Số giao điểm của đồ thị hàm số

3 2

2 4 1y x x x   

và đường thẳng

1 2y x 

là bao

nhiêu ?

Ⓐ

1.

Ⓑ

3.

Ⓒ

0.

Ⓓ

2.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4. Cho hai hàm số

3

2y x x 

và

2

1.y x x 

Biết rằng đồ thị của hai hàm số trên cắt nhau

tại

A

và tiếp xúc nhau tại

.B

Xác định tọa độ điểm

.A

Ⓐ

(1;1).A

Ⓑ

(1; 1).A 

Ⓒ

( 1; 1).A  

Ⓓ

( 1;1).A 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 5. Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị của hàm số

3

2 (2 )y x m x m   

cắt trục hoành tại

3

điểm phân biệt ?

Ⓐ

1

2

m

 

Ⓑ

1

2

m

 

và

4.m 

Ⓒ

1

2

m

  

Ⓓ

1

2

m

 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 6. Tìm tập hợp tất cả các giá trị thực của tham số

m

sao cho đường thẳng

1y mx 

cắt đồ thị

hàm số

3

3 1y x x  

tại ba điểm phân biệt.

Ⓐ

3.m  

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 95

Ⓑ

3.m 

Ⓒ

3.m  

Ⓓ

3.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 7. Cho hàm số

3

3 2y x x  

có đồ thị

( ).C

Gọi

d

là đường thẳng đi qua

(3;20)A

và có hệ số

góc

.m

Tìm tập hợp các giá trị của tham số thực

m

để đường thẳng

d

cắt

( )C

tại ba điểm

phân biệt.

Ⓐ

15

;

4

 







 











Ⓑ

 

15

; \ 24

4

 







 











 

Ⓒ

 

15

; \ 24

4

 







 











Ⓓ

15

;

4

 







 











 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 8. Tìm tập hợp các giá trị của tham số thực

m

để đồ thị hàm số

3 2 2

3 2 2y x x m m   

cắt

trục hoành tại ba điểm phân biệt.

Ⓐ

( 2; 2) ( 1;1).   

Ⓑ

(1; ).

Ⓒ

( 2; 0).

Ⓓ

( 1;0) (1;2). 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 9. Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị của hai hàm số

3 2

2 2y x x mx   

và

2

y x m 

cắt nhau tại một điểm duy nhất.

Ⓐ

3.m  

Ⓑ

3.m  

Ⓒ

3.m 

Ⓓ

3.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 10. Cho hàm số

3 2

2 (1 ) ,y x x m x m    

với

m

là tham số. Tìm tập hợp các giá trị của

m

để

đồ thị hàm số đã cho cắt trục hoành

Ox

tại ba điểm phân biệt có hoành độ

1 2 3

, , x x x

thỏa

mãn

2 2 2

1 2 3

4.

x x x

  

Ⓐ

1

;1 \{0}.

4

 



















 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 96

Ⓑ

( ;1).

Ⓒ

( ;1]\{ 1}. 

Ⓓ

( 1;1)\{0}.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 11. Tìm tất cả các giá trị thực của tham số

m

để đường thẳng

y mx 

cắt đồ thị hàm số

3 2

3 2y x x m   

tại

3

điểm phân biệt

, , A B C

sao cho

.AB BC

Ⓐ

( ; 3).m  

Ⓑ

( ; 1).m   

Ⓒ

( ; ).m   

Ⓓ

(1; ).m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 12. Tìm tất cả các giá trị thực của tham số

m

để đường thẳng

1y mx m  

cắt đồ thị hàm số

3 2

3 2y x x x   

tại ba điểm

, , A B C

phân biệt sao cho

.AB BC

Ⓐ

( ;0] (4; ).m    

Ⓑ

5

;

4

m

 







   











 

Ⓒ

( 2; ).m   

Ⓓ

.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 13. Biết rằng đồ thị

( )C

của hàm số

3 2

3 4y x x  

và đường thẳng

:d y mx m 

cắt nhau tại

ba điểm phân biệt

( 1;0), , A B C

sao cho tam giác

OBC

có diện tích bằng

8,

với

O

là gốc

tọa độ. Hỏi kết luận nào sau đây về tham số thực

m

là đúng ?

Ⓐ

m

là một số chẵn.

Ⓑ

m

là một số nguyên tố.

Ⓒ

m

là một số vô tỉ.

Ⓓ

m

là một số chia hết cho

3.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 97

................................................................................................................................................................................................................................

................................

Ví dụ 14. Tìm tập hợp tất cả các giá trị của tham số

m

để đồ thị hàm số

3 2

2 3( 1) 6 1y x m x mx m     

cắt trục hoành tại ba điểm phân biệt có hoành độ dương.

Ⓐ

(4 2; ). 

Ⓑ

(1 2; ). 

Ⓒ

( 1; 0) (1 2; ).   

Ⓓ

(4 3; ). 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 15. Gọi

S

là tập hợp các giá trị của tham số

m

để đồ thị hàm số

3 2

y x mx x m   

cắt trục

hoành tại ba điểm phân biệt với các hoành độ lập thành cấp số cộng. Hỏi

S

có bao nhiêu

phần tử ?

Ⓐ

5.

Ⓑ

1.

Ⓒ

3.

Ⓓ Vô số.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 98

Daïng toaùn 3. Töông giao cuûa haøm soá baäc boán vaø ñöôøng thaúng



 Bài toán tổng quát: Tìm m để đường thẳng

:d y 

cắt đồ thị

4 2

( ) :C y ax bx c  

tại n

điểm phân biệt thỏa mãn điều kiện K cho trước ?



Phương pháp giải:

Bước 1. Phương trình hoành độ giao điểm của

d

và

( )C

:

4 2

0ax bx c    

(1)

Đặt

2

0t x 

thì

2

(1) 0at bt c     

(2)

Tùy vào số giao điểm

n

mà ta biện luận để tìm giá trị

1

.

m

 D

Cụ thể:



Để

( ) 4d C n  

điểm phân biệt

(1)

có 4 nghiệm phân biệt

(2)

có

2

nghiệm

1 2

, t t

dương

1 2 1

0

0 0 .

0

t t S m

P





 



     





 





D



Để

( ) 3d C n  

điểm phân biệt

(1)

có

3

nghiệm phân biệt

(2)

có nghiệm

1 2

, t t

thỏa:

1 2 1

0

0 .

0

c

t t m

b

a







 



    











D



Để

( ) 2d C n  

điểm phân biệt

(1)

có 2 nghiệm phân biệt

(2)

có

2n



trái dấu hoặc có nghiệm kép dương

1

0

.

0

ac

m

S











 

  





















D



Để

( ) 1d C n  

điểm

(1)

có đúng 1 nghiệm

(2)

có nghiệm kép

0

hoặc

1

2

0

0 0

.

0 0

0

c

t

m

b

t c

a







 

 



 

  



 

  

   

  

  

  



  

 

 





D

Bước 2. Biến đổi điều kiện

K

về dạng có chứa tổng và tích của

1 2

, t t

(3)

Thế biểu thức tổng, tích vào

(3)

sẽ thu được phương trình hoặc bất phương trình với

biến số là

.m

Giải chúng ta sẽ tìm được

2

.

m

 D

Kết luận:

1 2

.

m  

D D

Ví dụ 1. Đồ thị hàm số

4 2

2 3y x x   

và trục hoành có bao nhiêu điểm chung ?

Ⓐ

2.

Ⓑ

1.

Ⓒ

3.

Ⓓ

4.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2. Đồ thị hàm số

4 2

1 1

3

4 2

y x x

  

cắt trục tung tại mấy điểm ?

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 99

Ⓐ

2

điểm. Ⓑ

3

điểm.

Ⓒ

4

điểm. Ⓓ

1

điểm.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3. Đồ thị của hàm số

4 2

2 2y x x  

và đồ thị của hàm số

2

4y x  

có tất cả bao nhiêu

điểm chung ?

Ⓐ

0.

Ⓑ

4.

Ⓒ

1.

Ⓓ

2.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 4. Đồ thị của hàm số

4 2

7 6y x x  

và đồ thị hàm số

3

13y x x 

có bao nhiêu điểm chung ?

Ⓐ

1.

Ⓑ

2.

Ⓒ

3.

Ⓓ

4.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 5. Biết đồ thị hàm số

4 2

3 5y x x  

và đường thẳng

9y 

cắt nhau tại hai điểm phân biệt

1 1 2 2

( ; ), ( ; ).A x y B x y

Tính

1 2

.x x

Ⓐ

1 2

3.

x x

 

Ⓑ

1 2

0.

x x

 

Ⓒ

1 2

18.

x x

 

Ⓓ

1 2

5.

x x

 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 6. Gọi

A

là giao điểm của các đồ thị hàm số

4 2

7 6y x x  

và

3

13y x x 

có hoành độ nhỏ

nhất. Tìm tung độ

A

y

của điểm

.A

Ⓐ

18.

A

y  

Ⓑ

12.

A

y



Ⓒ

12.

A

y

 

Ⓓ

18.

A

y



................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 7. Tìm số giao điểm của đồ thị hàm số

4 2 2

2 1y x x m   

với trục hoành (với

m

là tham số

thực).

Ⓐ

1.

Ⓑ

2.

Ⓒ

3.

Ⓓ

4.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 8. Cho hàm số

4 2

8 7y x x  

có đồ thị

( ).C

Tìm tham số

m

để đường thẳng

: 60d y x m 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 100

tiếp xúc với

( ).C

Ⓐ

164.m  

Ⓑ

0.m 

Ⓒ

60.m  

Ⓓ Không có

.m

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 9. Tìm các giá trị của tham số

m

để đồ thị hàm số

4 2 2

1y x m x m   

tiếp xúc với đường

thẳng

: 2 2d y x 

tại điểm có hoành độ

1.x 

Ⓐ

1m  

hoặc

1.m 

Ⓑ

1.m  

Ⓒ

0.m 

Ⓓ

1m  

hoặc

0.m 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 10. Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

4 2

8 3y x x  

cắt đường thẳng

: 2 7d y m 

tại bốn điểm phân biệt ?

Ⓐ

3 5.m  

Ⓑ

6 10.m  

Ⓒ

5.m 

Ⓓ

3.m  

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 11. Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

4 2

2 2y x mx m   

cắt trục

Ox

tại

4

điểm phân biệt ?

Ⓐ

(2; ).m  

Ⓑ

( ;1).m  

Ⓒ

( ; 1) (2; ).m     

Ⓓ

(0; ).m  

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 12. Tìm tất cả các giá trị của tham số

m

để đường thẳng

1y  

cắt đồ thị hàm số

4 2

(3 2) 3y x m x m   

tại bốn điểm phân biệt ?

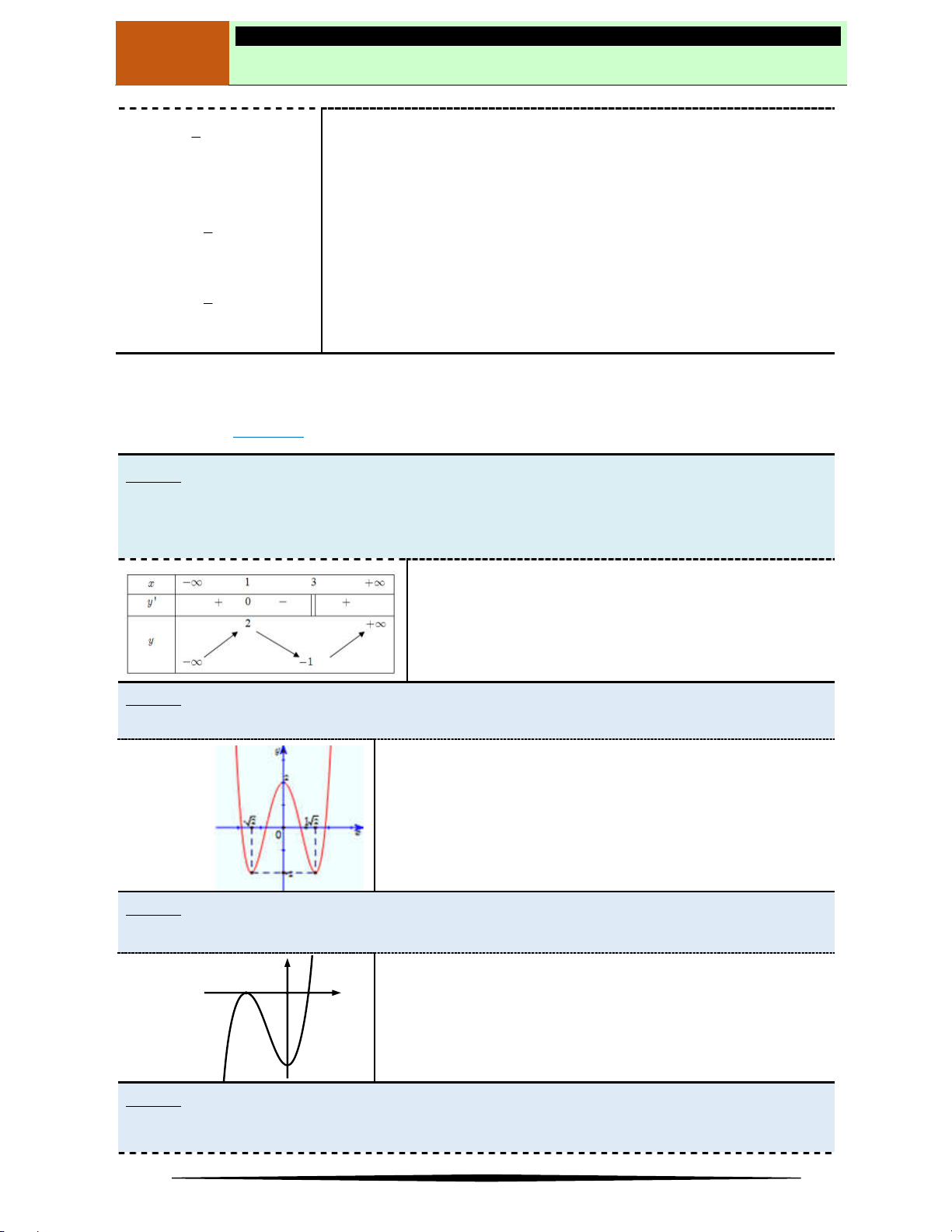
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 101

Ⓐ

1

3

1

m





















Ⓑ

1 0.m  

Ⓒ

1

3

0

m





 















Ⓓ

1

3

0

m





 















................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Daïng toaùn 4. Töông giao cuûa haøm soá vaø ñöôøng thaúng chöùa döïa vaøo ñoà thò, baûng bieán thieân

Ví dụ 1. Cho hàm số

( )y f x

xác định, liên tục trên



và có bảng biến thiên như sau:

Số nghiệm của phương trình

 

1 0f x  

.

Ⓐ

3

. Ⓑ

0

. Ⓒ

1

. Ⓓ

2

.

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

Ví dụ 2. Cho hàm số

( )y f x

có đồ thị như hình bên dưới. Số nghiệm của phương trình

2 ( ) 3 0f x  

là:

Ⓐ

4

.

Ⓑ

2

.

Ⓒ

0

.

Ⓓ

3

.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3. Cho hàm số

( )y f x

có đồ thị như hình vẽ sau:

Tìm số nghiệm thực phân biệt của phương trình

( ) 1f x 

.

Ⓐ

2.

Ⓑ

1.

Ⓒ

0.

Ⓓ

3.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4. Cho hàm số

( )y f x

có bảng biến thiên như sau:

Tập tất cả các giá trị của tham số

m

để phương trình

( ) 0f x m 

có ba nghiệm phân biệt là:

O

x

y

2

1

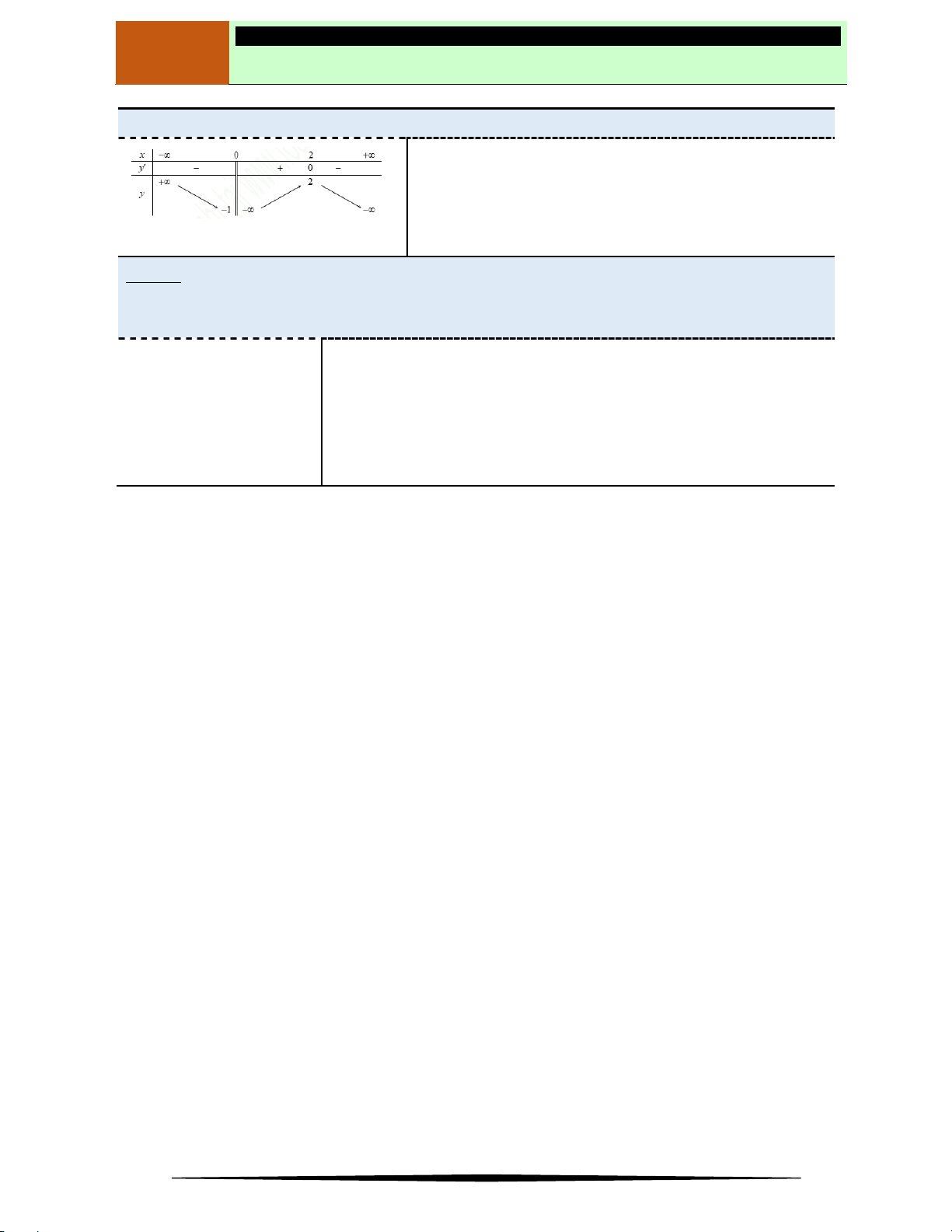
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 102

Ⓐ

( 2;1).

Ⓑ

[ 1;2).

Ⓒ

( 1;2).

Ⓓ

( 2;1].

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

Ví dụ 5. Tìm tất cả các giá trị của

m

để đồ thị hàm số

3

3 2y x x  

cắt đường thẳng

1y m 

tại

ba điểm phân biệt.

Ⓐ

0 4m 

. Ⓑ

1 5m 

. Ⓒ

1 5m 

. Ⓓ

1 5m 

.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 103

CĐ7.2: BÀI TOÁN TIẾP TUYẾN, SỰ TIẾP XÚC



Bài toán tổng quát: Viết phương trình tiếp tuyến của đồ thị hàm số

( ) : ( )C y f x

tại

( ; ).

o o

M x y

 Phương pháp giải:

Bước 1. Tính đạo hàm

( ).y f x

 



Suy ra hệ số góc tiếp tuyến

( ) ( ).

o o

k y x f x

 

 

Bước 2. Phương trình tiếp tuyến của đồ thị tại điểm

( ; )

o o

M x y

có dạng

: .( ) .

o o

d y k x x y

  

 Lưu ý:

 Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại điểm có hoành độ

,

o

x

thì khi đó ta tìm

o

y

bằng

cách thế vào hàm số ban đầu, tức

( ).

o o

y f x

Tương tự cho trường hợp đề cho

.

o

y

 Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị

( ) : ( )C y f x

và đường

thẳng

: .d y ax b 

Khi đó các hoành độ tiếp điểm là nghiệm của phương trình hoành độ giao điểm

giữa

d

và

( ).C

Đặc biệt: trục hoành

: 0,Ox y 

trục tung

: 0.Oy x 

Daïng toaùn 1: Vieát phöông trình tieáp tuyeán taïi ñieåm

0 0

( ; ).M x y

Ví dụ 1. Cho hàm số

3

2 1y x x  

có đồ thị

( )C

. Hệ số góc của tiếp tuyến với

( )C

tại điểm

( 1;2)M 

bằng:

Ⓐ

3.

Ⓑ

5.

Ⓒ

25.

Ⓓ

1.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2. Tiếp tuyến của đồ thị hàm số

3 2

1 1

( ) 4 6

3 2

f x x x x

   

tại điểm có hoành độ là nghiệm của

phương trình

( ) 0f x





có hệ số góc bằng

Ⓐ

4.

Ⓑ

47

.

12

Ⓒ

13

.

4



Ⓓ

17

.

4



................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số

3 2

1

2 3 5.

3

y x x x

   

Ⓐ Có hệ số góc dương.

Ⓑ Song song với trục hoành.

1

.

Ⓓ Song song với đường

thẳng

1x 

.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4. Phương trình tiếp tuyến của đồ thị hàm số

1

2

x

y

x







tại điểm có hoành độ bằng 3 là

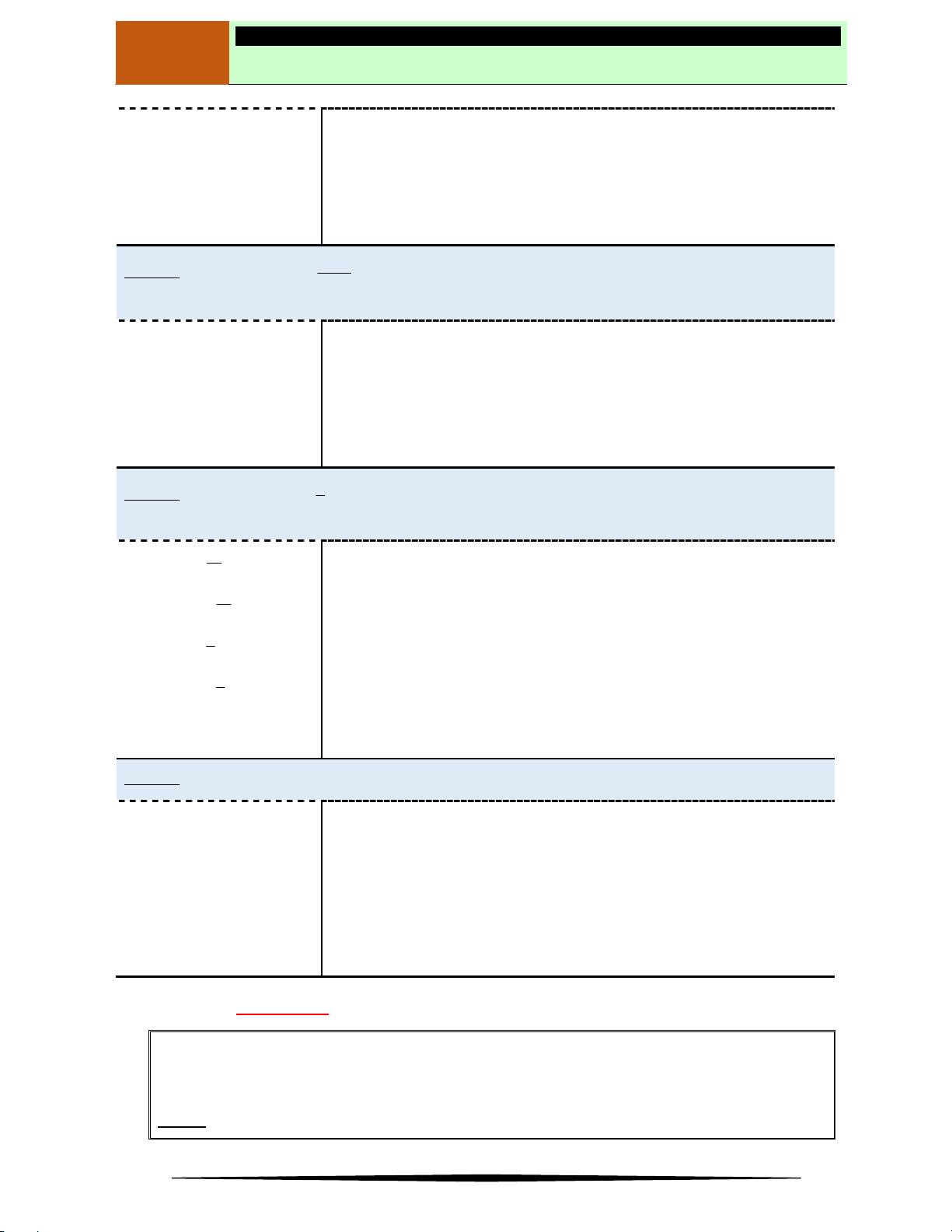
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 104

Ⓐ

3 13.y x 

Ⓑ

3 5.y x 

Ⓒ

3 5.y x  

Ⓓ

3 13.y x  

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 5. Cho hàm số

2

1

x

y

x







có đồ thị

( )C

. Phương trình tiếp tuyến với đồ thị hàm số tại giao

điểm của đồ thị

( )C

với trục tung là

Ⓐ

2.y x  

Ⓑ

1.y x  

Ⓒ

2.y x 

Ⓓ

2.y x  

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 6. Cho hàm số

y 

3 2

1

2 3 1

3

x x x

  

. Tiếp tuyến tại điểm uốn của đồ thị hàm số có phương

trình là:

Ⓐ

11

.

3

y x 

Ⓑ

11

.

3

y x  

Ⓒ

1

.

3

y x 

Ⓓ

1

.

3

y x  

Điểm uốn có hoành độ là

nghiệm của

( ) 0.f x





................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 7. Phương trình tiếp tuyến của đồ thị hàm số

3 2

3 1y x x  

tại điểm

( 3;1)A

là:

Ⓐ

9 26.y x  

Ⓑ

9 26.y x 

Ⓒ

9 3.y x  

Ⓓ

9 2.y x 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Daïng toaùn 2: Vieát phöông trình tieáp tuyeán khi bieát heä soá goùc k cho tröôùⒸ

 Bài toán tổng quát: Viết phương trình tiếp tuyến của đồ thị hàm số

( ) : ( )C y f x

biết hệ số góc

tiếp tuyến là

k

cho trướⒸ

 Phương pháp giải:

Bước 1. Gọi

( ; )

o o

M x y

là tiếp điểm và tính

( ).y f x

 



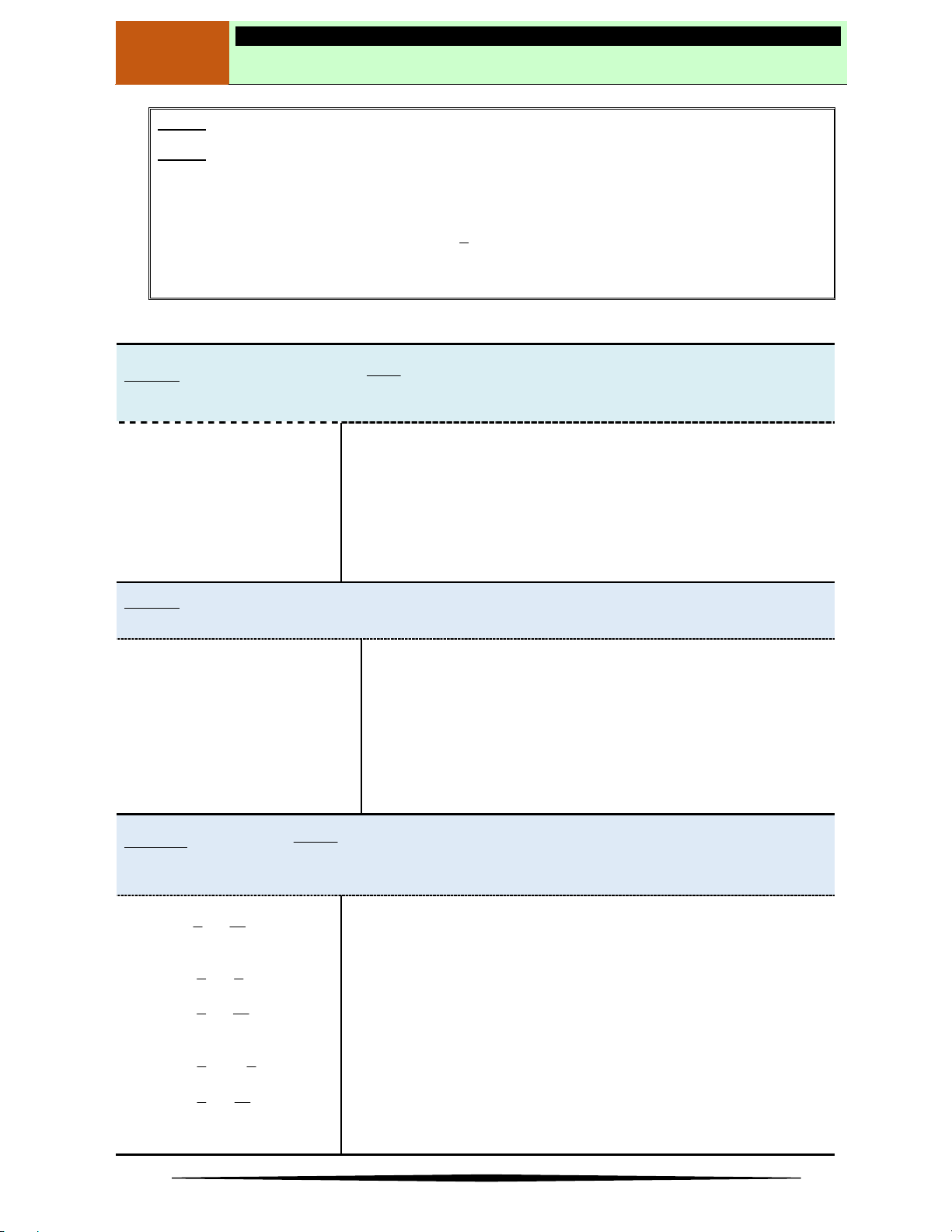
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 105

Bước 2. Ta có hệ số tiếp tuyến

( )

o

k f x





và giải phương trình này tìm được

,

o

x

suy ra

.

o

y

Bước 3. Ứng với mỗi tiếp điểm, tìm được các tiếp tuyến

: .( ) .

o o

d y k x x y  

 Lưu ý. Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:

 Nếu tiếp tuyến

// : .d y ax b k a    

 Nếu tiếp tuyến

1

:d y ax b k

a

       

 Nếu tiếp tuyến tạo với trục hoành

Ox

một góc



thì

tan .k  

Ví dụ 8. Biết trên đồ thị

( )C

:

1

2

x

y

x







có hai điểm mà tiếp tuyến tại các điểm đó đều song song với

đường thẳng

d

:

3 15 0x y  

. Tìm tổng

S

các tung độ tiếp điểm.

Ⓐ

3.S 

Ⓑ

6.S 

Ⓒ

4.S  

Ⓓ

2.S 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 9. Cho hàm số

3 2

3 2y x x   

có đồ thị

( )C

. Phương trình tiếp tuyến của

( )C

mà có hệ số

góc lớn nhất là:

Ⓐ

3 1.y x 

Ⓑ

3 1.y x  

Ⓒ

3 1.y x  

Ⓓ

3 1.y x 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 10. Cho hàm

5

2

x

y

x







( )C

. Viết phương trình tiếp tuyến của đồ thị

( )C

sao cho tiếp tuyến đó

song song với đường thẳng

: 7 5 0.d x y  

Ⓐ

1 23

.

7 7

y x  

Ⓑ

1 5

7 7

.

1 23

7 7

y x





  



  





Ⓒ

1 5

7 7

.

1 23

7 7

y x





   



  





................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 106

Ⓓ

1 23

.

7 7

y x  

Ví dụ 11. Tiếp tuyến của đồ thị hàm số

3

3 2y x x  

vuông góc với đường thẳng

1

9

y x

 

là

Ⓐ

1

18

9

y x  

,

1

5.

9

y x

  

Ⓑ

1

18

9

y x 

;

1

14.

9

y x 

Ⓒ

9 18y x 

;

9 14.y x 

Ⓓ

9 18y x 

;

9 5.y x 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Daïng toaùn 3: Tìm m ñeå ñoà thò

( )y f x

tieáp xuùc vôùi ñöôøng thaúng

.y ax b 

Để tiếp xúc thì hệ

 

'

f x ax b

f x a





 













có nghiệm.

Ví dụ 12. Đường thẳng

y m

tiếp xúc với đồ thị

 

C

:

4 2

2 4 1y x x   

tại hai điểm phân biệt. Tìm

tung độ tiếp điểm.

Ⓐ

1.

Ⓑ

1.

Ⓒ

0.

Ⓓ

3.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 13. Tập hợp tất cả các giá trị của tham số

m

để đường thẳng

2y x m  

tiếp xúc với độ thị

hàm số

1

x

y

x







là

Ⓐ

{6; 1}.m  

Ⓑ

1.m  

Ⓒ

6.m 

Ⓓ

{7; 1}.m  

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 14. Đường thẳng

2x y m 

là tiếp tuyến của đường cong

3

2 4y x x   

khi

m

bằng

Ⓐ

3

hoặc

1

.

Ⓑ

1

hoặc

3

.

Ⓒ

1

hoặc

3

.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 107

Ⓓ

3

hoặc

1

.

................................................................................................................................................................................................................................................................

......................

Ví dụ 15. Giá trị của

m

để đồ thị hàm số

 

3 2

2 3 3 18 8

y x m x mx

    

tiếp xúc với trục hoành?

Ⓐ

5m 

.

Ⓑ

7m 

.

Ⓒ

1m 

.

Ⓓ

6m 

.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 16. Với giá trị nào của

m

thì đường thẳng

2y x m 

tiếp xúc với đồ thị hàm số

2 3

1

x

y

x







.

Ⓐ

2 2m 

.

Ⓑ

2

1

2

m

  

.

Ⓒ

2m  

.

Ⓓ

2 2m  

.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 108

CĐ7.3: ĐIỂM ĐẶC BIỆT

 Bài toán tổng quát: Cho hàm số

( )y f x

có đồ thị (C). Tìm tọa độ điểm

( )M C

thỏa mãn

điều kiện K cho trước ?

 Phương pháp giải:

Bước 1. Gọi điểm

 

; ( ) ( ).

o o

M x f x C

Bước 2. Từ điều kiện K cho trước, biến đổi dẫn đến phương trình (hoặc bất phương trình)

theo

,

o

x

giải tìm

 

( ) ; ( ) .

o o o o o

x y f x M x f x  

 Một số kiến thức cần nhớ:



Khoảng cách giữa hai điểm A và B là:

2 2

( ) ( ) .

B A B A

AB x x y y   



Khoảng cách

( ; )

o o

M x y

đến

: 0ax by c   

là

2 2

( ; )

o o

ax by c

d M

a b

 

  





Nếu

: ( ; ) .

o

x a d M x a

     



Nếu

: ( ; ) .

o

y b d M y b

     



Tổng khoảng cách từ điểm

( ; )

o o

M x y

đến hai trục tọa độ là:

o o

x y



.



Để hai điểm A, B đối xứng nhau qua điểm

I I

là trung điểm AB

2

A B I

x x x

y y y





 









 





.



Để hai điểm A, B đối xứng nhau qua đường thẳng

AB

I





 



 





 





(với I là trung điểm AB).



Để hai điểm A, B đối xứng nhau qua trục hoành

A B

x x

Ox

y y















 





.



Để hai điểm A, B đối xứng nhau qua trục tung

A B

x x

Oy

y y





 















.



Khoảng cách giữa đường thẳng



với đường cong (C) bằng khoảng cách nhỏ nhất giữa

một điểm

M  

và một điểm N  (C).



Điểm

( ; )M x y

được gọi là có toạ độ nguyên nếu x và y đều là số nguyên.

Ví dụ 1. Tâm đối xứng của đồ thị hàm số nào sau đây cách gốc tọa độ một khoảng lớn nhất ?

Ⓐ

2 1

3

x

y

x







. Ⓑ

1

x

y

x







.

Ⓒ

3 2

2 3 2y x x  

.

Ⓓ

3

3 2y x x   

.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2. Đồ thị hàm số nào dưới đây có tâm đối xứng là điểm

(1; 2)I 

?

Ta đã biết đối với hàm phân thức bậc

nhất trên bậc nhất thì giao điểm hai

tiệm cận là tâm đối xứng của đồ thị,

đối với hàm bậc ba thì điềm uốn chính

là tâm đối xứng của đồ thị.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 109

Ⓐ

2 3

2 4

x

y

x







.

Ⓑ

3 2

2 6 1y x x x   

.

Ⓒ

3 2

2 6 1y x x x    

.

Ⓓ

2 2

1

x

y

x







.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 3. Trên đồ thị hàm số

2 1

3 4

x

y

x







có bao nhiêu điểm có tọa độ nguyên?

Ⓐ

1.

Ⓑ

2.

Ⓒ

0.

Ⓓ

4.

................................................................................................

................................

................................................................................................

................................

................................................................................................

................................

................................................................................................

................................

................................................................................................

................................

................................................................................................

................................

Ví dụ 4. Trên đồ thị hàm số

2 5

3 1

x

y

x







có bao nhiêu điểm có tọa độ là các số nguyên?

Ⓐ

4

.

Ⓑ Vô số.

Ⓒ

2

.

Ⓓ

0

.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 5. Trên đồ thị

 

C

của hàm số

10

1

x

y

x







có bao nhiêu điểm có tọa độ nguyên?

Ⓐ

4

.

Ⓑ

2

.

Ⓒ

10

.

Ⓓ

6

.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 6. Số điểm có tọa độ nguyên thuộc đồ thị hàm số

2

2 3 10

2

x x

y

x

 





là:

Ⓐ

16

.

Ⓑ

12

.

Ⓒ

10

.

Ⓓ

8

.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Bước 1.

( )

( ) ( )

f x

a

y h x

g x g x

  

Bước 2. Để

M

là có tọa độ nguyên thì x nguyên và y cũng

nguyên. Có nghĩa là

 

a g x



. Suy ra

 

g x

là ước của

.a

Vì a là hằng số. Nên chúng ta dễ dàng tìm được các ước

của nó. Thông qua đó ta sẽ tìm được

x

.

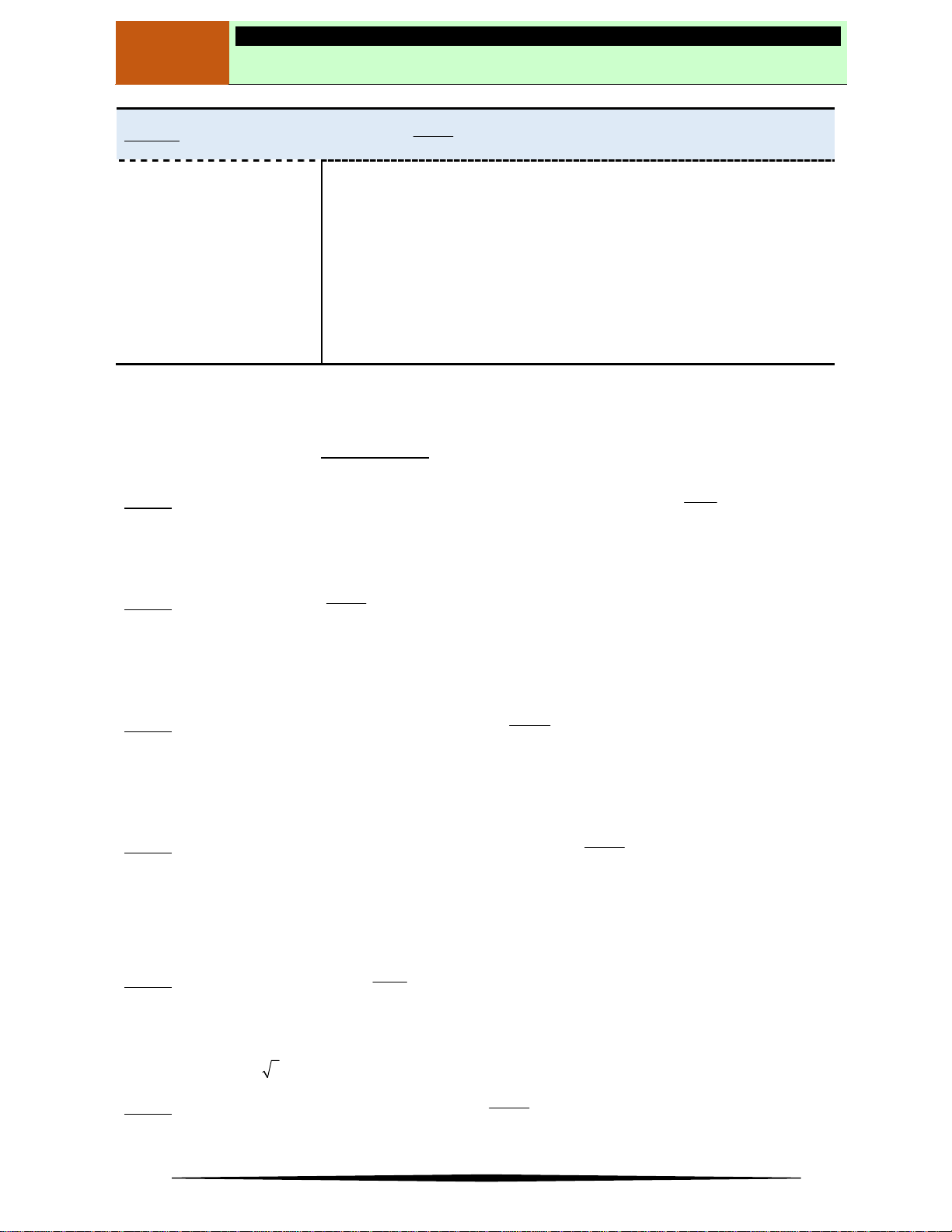
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 110

Ví dụ 7. Số điểm trên đồ thị hàm số

2 1

1

x

y

x







có tọa độ nguyên là:

Ⓐ

5

.

Ⓑ

3

.

Ⓒ

4

.

Ⓓ

2

.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

C. BÀI TẬP TỰ LUYỆN

MỨC ĐỘ 1 & 2: NHẬN BIẾT & THÔNG HIỂU

Câu 1.

Tìm tọa độ giao điểm của đường thẳng

1y x 

với đồ thị hàm số

1

2

x

y

x



 



Ⓐ

(4;3), (0; 1).A B 

Ⓑ

( 1;3).C 

Ⓒ

(3; 1).D 

Ⓓ

( 1;0), (3; 4).I J

Câu 2.

Đồ thị hàm số

4 1

4

x

y

x







cắt đường thẳng

4y x  

tại hai điểm phân biệt

, .A B

Tìm điểm

C

là trung điểm của

.AB

Ⓐ

( 2;6).C 

Ⓑ

(2; 6).C 

Ⓒ

(0;4).C

Ⓓ

(4; 0).C

Câu 3.

Đường thẳng

1y x 

cắt đồ thị hàm số

2 2

1

x

y

x







tại hai điểm phân biệt

1 1

( ; )A x y

và

2 2

( ; ).B x y

Tính

1 2

.S y y 

Ⓐ

1.S 

Ⓑ

4.S 

Ⓒ

3.S 

Ⓓ

0.S 

Câu 4.

Biết rằng đường thẳng

2y x 

cắt đồ thị hàm số

2 1

1

x

y

x







tại hai điểm phân biệt

, A B

có

hoành độ lần lượt

, .

A B

x x

Tính

.

A B

x x

Ⓐ

2.

A B

x x

 

Ⓑ

1.

A B

x x

 

Ⓒ

5.

A B

x x

 

Ⓓ

3.

A B

x x

 

Câu 5.

Biết đồ thị hàm số

3

1

x

y

x







và đường thẳng

2y x 

cắt nhau tại hai điểm phân biệt

( ; )

A A

A x y

và

( ; ).

B B

B x y

Tính

.

A B

S x x 

Ⓐ

4.S 

Ⓑ

4.S  

Ⓒ

2 5.S 

Ⓓ

2.S 

Câu 6.

Tìm tung độ giao điểm của đồ thị

2 3

( ) :

3

x

C y

x







và đường thẳng

: – 1.d y x

Ⓐ

3.

Ⓑ

1.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 111

Ⓒ

1.

Ⓓ

3.

Câu 7.

Đồ thị của hàm số

3 1

1

x

y

x







và đồ thị của hàm số

4 5y x  

có tất cả bao nhiêu điểm chung ?

Ⓐ

2.

Ⓑ

3.

Ⓒ

1.

Ⓓ

0.

Câu 8.

Gọi

( ; )x y

 

là tọa độ giao điểm của hai đồ thị hàm số

1y x 

và

2 2

.

1

x

y

x







Tính

.y



Ⓐ

4.

y





Ⓑ

2.

y





Ⓒ

1.

y

 



Ⓓ

0.

y





Câu 9.

Số giao điểm của đồ thị hàm số

2

4

x

y

x





với trục hoành là bao nhiêu ?

Ⓐ

1.

Ⓑ

3.

Ⓒ

2.

Ⓓ

4.

Câu 10.

Đồ thị hàm số

2 1

5

x

y

x







và đường thẳng

1y x 

cắt nhau tại hai điểm phân biệt

, .A B

Tìm

hoành độ trung điểm

I

của đoạn thẳng

.AB

Ⓐ

1.

I

x



Ⓑ

2.

I

x

 

Ⓒ

2.

I

x



Ⓓ

1.

I

x

 

Câu 11.

Gọi

, M N

là giao điểm của đường thẳng

1y x 

và đường cong

2 4

1

x

y

x



 



Tìm tọa độ

trung điểm

I

của đoạn thẳng

.MN

Ⓐ

(1;2).I

Ⓑ

( 2; 3).I  

Ⓒ

(1; 3).I

Ⓓ

(2; 3).I

Câu 12.

Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm ?

Ⓐ

4 1

2

x

y

x



 



Ⓑ

3 4

1

x

y

x



 



Ⓒ

2 3

1

x

y

x

 

 



Ⓓ

2 3

3 1

x

y

x



 



Câu 13.

Cho hàm số

2 1

1

x

y

x







có đồ thị

( ).C

Lập phương trình đường thẳng

d

đi qua điểm

(0; 2)M 

và cắt

( )C

tại hai điểm phân biệt

, A B

sao cho

M

là trung điểm của

.AB

Ⓐ

: 2.d y x  

Ⓑ

: 2 2.d y x  

Ⓒ

: 3 2.d y x  

Ⓓ

: 4 2.d y x  

Câu 14.

Biết đường thẳng

2y x 

cắt đường cong

2 1

x

y

x







tại hai điểm

,A

.B

Tính độ dài đoạn

.AB

Ⓐ

5 2

4

AB

 

Ⓑ

5 2.AB 

Ⓒ

5 2

2

AB

 

Ⓓ

9 2

2

AB

 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 112

Câu 15.

Đồ thị hàm số

2 1

1

x

y

x







cắt các trục tọa độ tại hai điểm

, .A B

Tính độ dài đoạn

.AB

Ⓐ

5

2

AB

 

Ⓑ

1

2

AB

 

Ⓒ

2

AB

 

Ⓓ

5

4

AB

 

Câu 16.

Đồ thị hàm số

2

y x x 

và đồ thị hàm số

3

5y

x

 

cắt nhau tại hai điểm

A

và

.B

Tính độ dài

đoạn

.AB

Ⓐ

8 5.AB 

Ⓑ

25.AB 

Ⓒ

4 2.AB 

Ⓓ

10 2.AB 

Câu 17.

Biết đường thẳng

2 2y x  

cắt đồ thị hàm số

3

2y x x  

tại một điểm duy nhất, kí hiệu

( ; ).x y

 

Tìm

.y



Ⓐ

4.

y





Ⓑ

0.

y





Ⓒ

2.

y





Ⓓ

1.

y

 



Câu 18.

Đồ thị hàm số

3 2

16 13 2y x x x   

cắt trục tung tại điểm nào sau đây ?

Ⓐ

(1; 0).

Ⓑ

( 1;0).

Ⓒ

(0;2).

Ⓓ

(0; 0).

Câu 19.

Tìm to

a đ

ộ giao điểm của đồ thị hàm số

3

3 2y x x  

và đường thẳng

2.y x 

Ⓐ

(0; 3).

Ⓑ

(0; 2).

Ⓒ

(2; 0).

Ⓓ

(0;2).

Câu 20.

Biết rằng đồ thị các hàm số

3

5

2

4

y x x

  

và

2

2y x x  

tiếp xúc nhau tại điểm

( ; ).M x y

 

Tìm

.x



Ⓐ

3

2

x

 



Ⓑ

1

2

x

 



Ⓒ

5

2

x

  



Ⓓ

3

4

x

 



Câu 21.

Hỏi hai đồ thị

3

( ) : 2 2C y x x  

và

2

( ) : 3 1C y x x



  

có bao nhiêu giao điểm ?

Ⓐ

0.

Ⓑ

1.

Ⓒ

2.

Ⓓ

3.

Câu 22.

Tìm số giao điểm của đồ thị hàm số

3

3 1y x x  

với đường thẳng

1 2 .y x 

Ⓐ

3.

Ⓑ

2.

Ⓒ

1.

Ⓓ

0.

Câu 23.

Hỏi đồ thị của hàm số

3 2

2 1y x x x   

và đồ thị của hàm số

2

3y x x  

có tất cả bao

nhiêu điểm chung phân biệt?

Ⓐ Có

2

điểm chung.

Ⓑ Không có điểm chung.

3

điểm chung.

Ⓓ Có 1 điểm chung.

Câu 24.

Số điểm chung của hai đồ thị hàm số

3 2

3 5 1y x x x   

và

1y x 

là bao nhiêu ?

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 113

Ⓐ

2

điểm chung. Ⓑ

3

điểm chung.

Ⓒ

1

điểm chung. Ⓓ

4

điểm chung.

Câu 25.

Biết đường thẳng

2 4y x 

cắt đồ thị hàm số

3 2

4y x x  

tại điểm duy nhất

( ; ).x y

 

Tìm

.x y



 

Ⓐ

6.

x y

 

 

Ⓑ

2.

x y

 

 

Ⓒ

10.

x y

 

 

Ⓓ

8.

x y

 

 

Câu 26.

Parabol

2

2y x x 

cắt đường cong

3 2

3 2 1y x x x    

tại bao nhiêu điểm ?

Ⓐ

1.

Ⓑ

2.

Ⓒ

3.

Ⓓ

0.

Câu 27.

Tìm số giao điểm của đồ thị hàm số

3 2

2 2 1y x x x   

với đường thẳng

1y x 

.

Ⓐ

1.

Ⓑ

0.

Ⓒ

2.

Ⓓ

3.

Câu 28.

Đồ thị hàm số

3

1y x 

và đồ thị hàm số

2

y x x 

có tất cả bao nhiêu điểm chung ?

Ⓐ

0.

Ⓑ

1.

Ⓒ

2.

Ⓓ

3.

Câu 29.

Số điểm chung của đồ thị hàm số

3 2

3 2y x x  

và đồ thị hàm số

1y x 

là bao nhiêu ?

Ⓐ

0.

Ⓑ

2.

Ⓒ

1.

Ⓓ

3.

Câu 30.

Hỏi hai đồ thị

3

( ) : 2 2

C y x x

  

và

2

( ) : 3 1

C y x x



  

có bao nhiêu giao điểm ?

Ⓐ

0.

Ⓑ

1.

Ⓒ

2.

Ⓓ

3.

Câu 31.

Tìm tập hợp các hoành độ giao điểm của đồ thị hàm số

2y x 

và đồ thị hàm số

3 2

6 6 2.y x x x   

Ⓐ

{1; 3;5}.

Ⓑ

{0;1;5}.

Ⓒ

{0;3; 5}.

Ⓓ

{1;2;5}.

Câu 32.

Số giao điểm của đồ thị hàm số

3

3 2y x x  

và trục hoành là bao nhiêu ?

Ⓐ

3

điểm. Ⓑ

2

điểm.

Ⓒ

1

điểm. Ⓓ

0

điểm.

Câu 33.

Số giao điểm của đường thẳng

2y x 

và đường cong

3

2y x 

là bao nhiêu ?

Ⓐ

0.

Ⓑ

1.

Ⓒ

2.

Ⓓ

3.

Câu 34.

Đồ thị của hàm số

23

3 2 1x xy x   

và đồ thị của hàm số

2

2 13x xy  

có tất cả bao

nhiêu điểm chung ?

Ⓐ

1.

Ⓑ

3.

Ⓒ

2.

Ⓓ

0.

Câu 35.

Tìm hoành độ giao điểm của hai đồ thị hàm số

3 2

4 6y x x  

và

4 9y x  

là bao nhiêu ?

Ⓐ

3.x 

Ⓑ

3.y 

Ⓒ

8.x  

Ⓓ

1.x 

Câu 36.

Tung độ giao điểm của đồ thị hai hàm số

3 4y x  

và

3

2 4y x x  

là bao nhiêu ?

Ⓐ

3.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 114

Ⓑ

4.

Ⓒ

0.

Ⓓ Không có giao điểm.

Câu 37.

Đường thẳng

3 1y x  

cắt đồ thị hàm số

3 2

2 1y x x 

tại điểm có tọa độ

( ; ).x y

 

Tìm

.y



Ⓐ

1.

y





Ⓑ

2.

y





Ⓒ

2.

y

 



Ⓓ

1.

y

 



Câu 38.

Gọi

( ; )M x y

 

là điểm chung của hai đồ thị hàm số

2

5y x x   

và

3 2

2.y x x x   

Tìm

.y



Ⓐ

4.

y





Ⓑ

1.

y

 



Ⓒ

3.

y





Ⓓ

0.

y





Câu 39.

Biết đồ thị hàm số

4 2

3 5y x x  

và đường thẳng

9y 

cắt nhau tại hai điểm phân biệt

1 1 2 2

( ; ), ( ; ).A x y B x y

Tính

1 2

.x x



Ⓐ

1 2

3.

x x

 

Ⓑ

1 2

0.

x x

 

Ⓒ

1 2

18.

x x 

Ⓓ

1 2

5.

x x

 

Câu 40.

Hỏi đồ thị hàm số

4 2

y x x 

và đồ thị hàm số

2

1y x  

có bao nhiêu điểm chung ?

Ⓐ

0.

Ⓑ

1.

Ⓒ

2.

Ⓓ

4.

Câu 41.

Đồ thị hàm số

4 2

2 7 4y x x  

cắt trục hoành tại bao nhiêu điểm ?

Ⓐ

2.

Ⓑ

3.

Ⓒ

4.

Ⓓ

1.

Câu 42.

Cho hàm số

( )y f x

xác định, liên tục trên



và có bảng biến thiên như hình bên. Đồ thị hàm

số

 

y f x



cắt đường thẳng

2018y  

tại bao nhiêu điểm?

Ⓐ

0.

Ⓑ

1.

Ⓒ

4.

Ⓓ

2.

Câu 43.

Cho hàm số

3 2

( )

y f x ax bx cx d    

có đồ thị như hình vẽ:

Số nghiệm của phương trình

( ) 1 0f x  

là:

Ⓐ

1.

Ⓑ

0.

Ⓒ

3.

Ⓓ

2.

Câu 44.

Cho hàm số

( )y f x

có bảng biến thiên sau

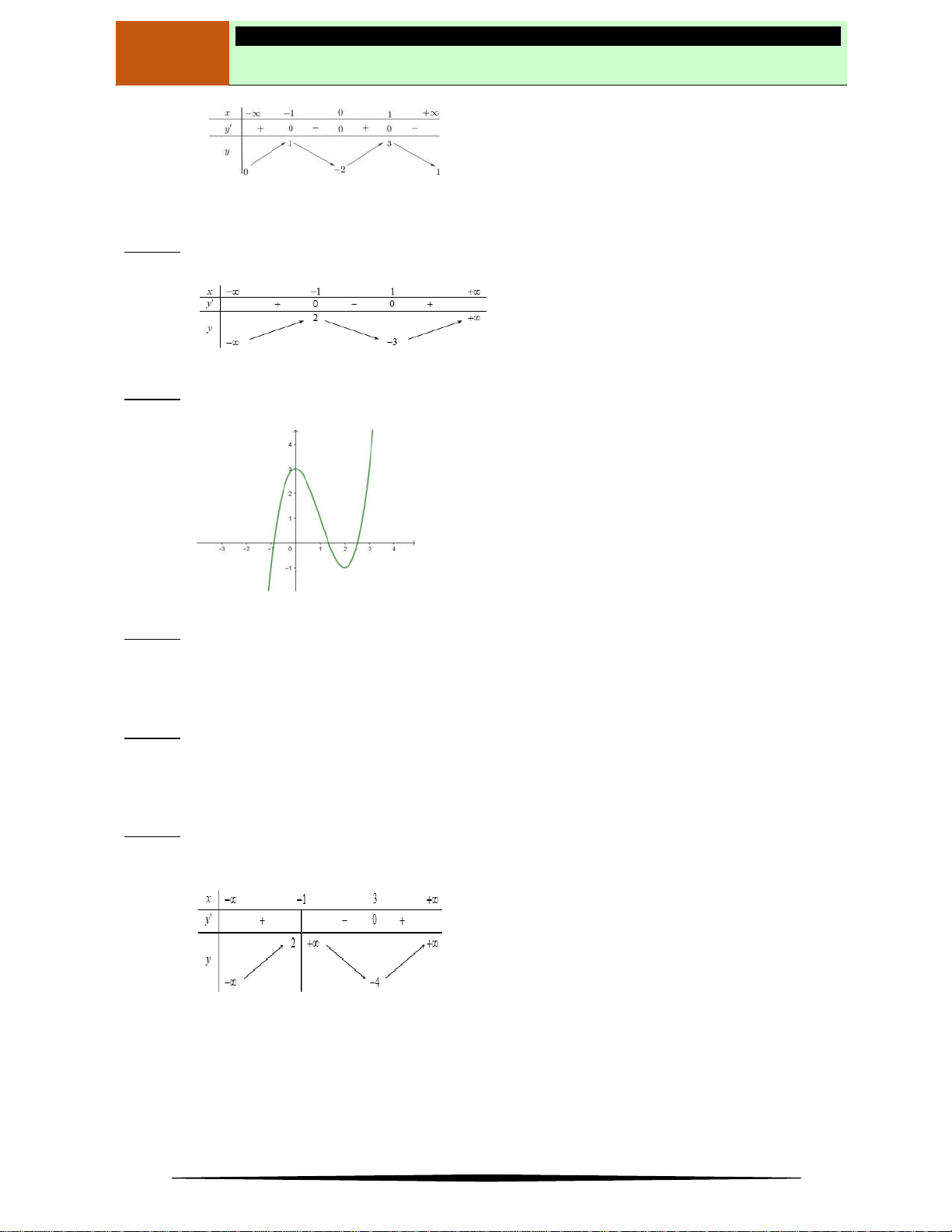
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 115

Số nghiệm của phương trình

( ) 1 0f x  

là

Ⓐ

3.

Ⓑ

0.

Ⓒ

4.

Ⓓ

2.

Câu 45.

Cho hàm số

( )y f x

có bảng biến thiên như hình bên. Số nghiệm của phương trình

( ) 3 0f x  

là:

Ⓐ

3.

Ⓑ

2.

Ⓒ

0.

Ⓓ

1.

Câu 46.

Cho hàm số

3 2

3 3y x x  

có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

3 2

3 3x x m  

có hai nghiệm thựⒸ

Ⓐ

1.

Ⓑ

3.

Ⓒ

2.

Ⓓ

5.

Câu 47.

Tìm tất cả các giá trị thực của tham số

m

để đường thẳng

y m

cắt đồ thị hàm số

4 2

2 3y x x  

tại

4

điểm phân biệt.

Ⓐ

1 1m  

Ⓑ

4m  

Ⓒ

4 3m   

Ⓓ

1m  

Câu 48.

Đồ thị hàm số

3 2

3 1y x x  

cắt đường thẳng

y m

tại ba điểm phân biệt thì tất cả các giá trị

tham số

m

thỏa mãn là

Ⓐ

1 .m 

Ⓑ

3 1 .m  

Ⓒ

3 1 .m  

Ⓓ

3.m  

Câu 49.

Cho hàm số

( )y f x

xác định trên

\ { 1}

, liên tục trên mỗi khoảng xác định và có bảng biến

thiên như hình sau. Tìm tập hợp tất cả các giá trị của tham số thực

m

sao cho phương trình

( )f x m

có đúng ba nghiệm thực phân biệt

Ⓐ

( 4;2).

Ⓑ

[ 4;2).

Ⓒ

( 4;2].

Ⓓ

( ;2].

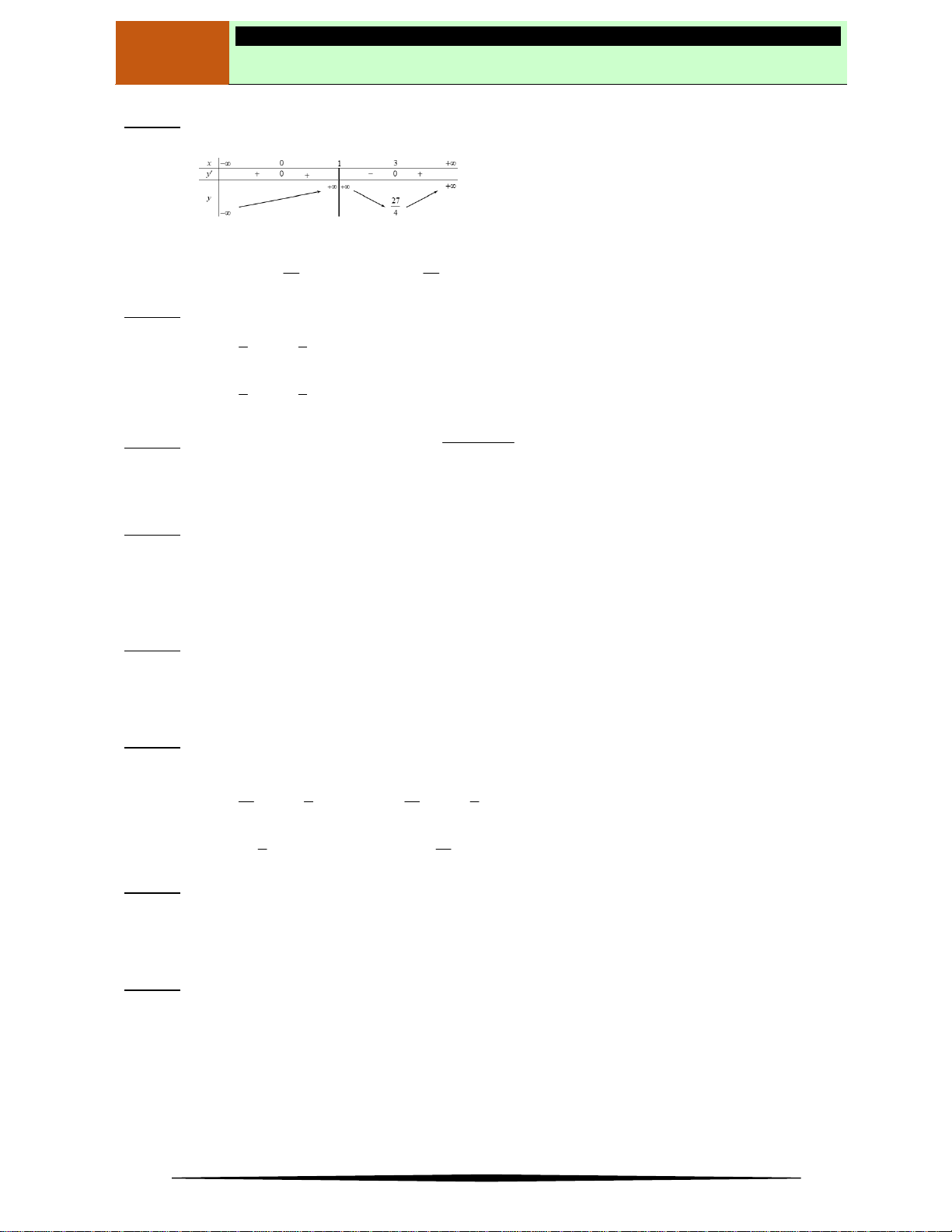
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 116

Câu 50.

Cho hàm số

( )y f x

xác định, liên tục trên

\ {1}

và có bảng biến thiên như sau. Tìm điều

kiện của

m

để phương trình

( )f x m

có 3 nghiệm phân biệt.

Ⓐ

0.m 

Ⓑ

0.m 

Ⓒ

27

0 .

4

m 

Ⓓ

27

.

4

m 

Câu 51.

Giá trị của tham số

m

để phương trình

3

3 2 1x x m  

có ba nghiệm phân biệt là:

Ⓐ

3 1

.

2 2

m  

Ⓑ

2 2.m  

Ⓒ

3 1

.

2 2

m  

Ⓓ

2 2.m  

Câu 52.

Số giao điểm của đồ thị hàm số

2

2 3

1

x x

y

x

 





với đường thẳng

3 6y x 

là bao nhiêu ?

Ⓐ

3.

Ⓑ

0.

Ⓒ

1.

Ⓓ

2.

Câu 53.

Biết đồ thị hàm số

4 2

3 5y x x  

và đường thẳng

9y 

cắt nhau tại hai điểm phân biệt

1 1 2 2

( ; ), ( ; ).A x y B x y

Tính

1 2

.x x



Ⓐ

1 2

3.

x x

 

Ⓑ

1 2

0.

x x

 

Ⓒ

1 2

18.

x x 

Ⓓ

1 2

5.

x x

 

Câu 54.

Đồ thị của hàm số

4 2

2 2y x x  

và đồ thị của hàm số

2

4y x  

có tất cả bao nhiêu điểm

chung ?

Ⓐ

0.

Ⓑ

4.

Ⓒ

1.

Ⓓ

2.

Câu 55.

Tìm tất cả các giá trị thực của tham số

m

để đường thẳng

4y m

cắt đồ thị hàm số

4 2

8 3y x x  

tại bốn điểm phân biệt ?

Ⓐ

13 3

.

4 4

m  

Ⓑ

13 3

.

4 4

m  

Ⓒ

3

.

4

m 

Ⓓ

13

.

4

m  

Câu 56.

Tìm số giao điểm của đồ thị hàm số

4 2 2

2 1y x x m   

với trục hoành (với

m

là tham số

thực).

Ⓐ

1.

Ⓑ

2.

Ⓒ

3.

Ⓓ

4.

Câu 57.

Có tất cả bao nhiêu giá trị nguyên của

m

để phương trình

3 2

6 0x x m  

có 3 nghiệm phân

biệt.

Ⓐ

31.

Ⓑ

32.

Ⓒ

21.

Ⓓ

34.

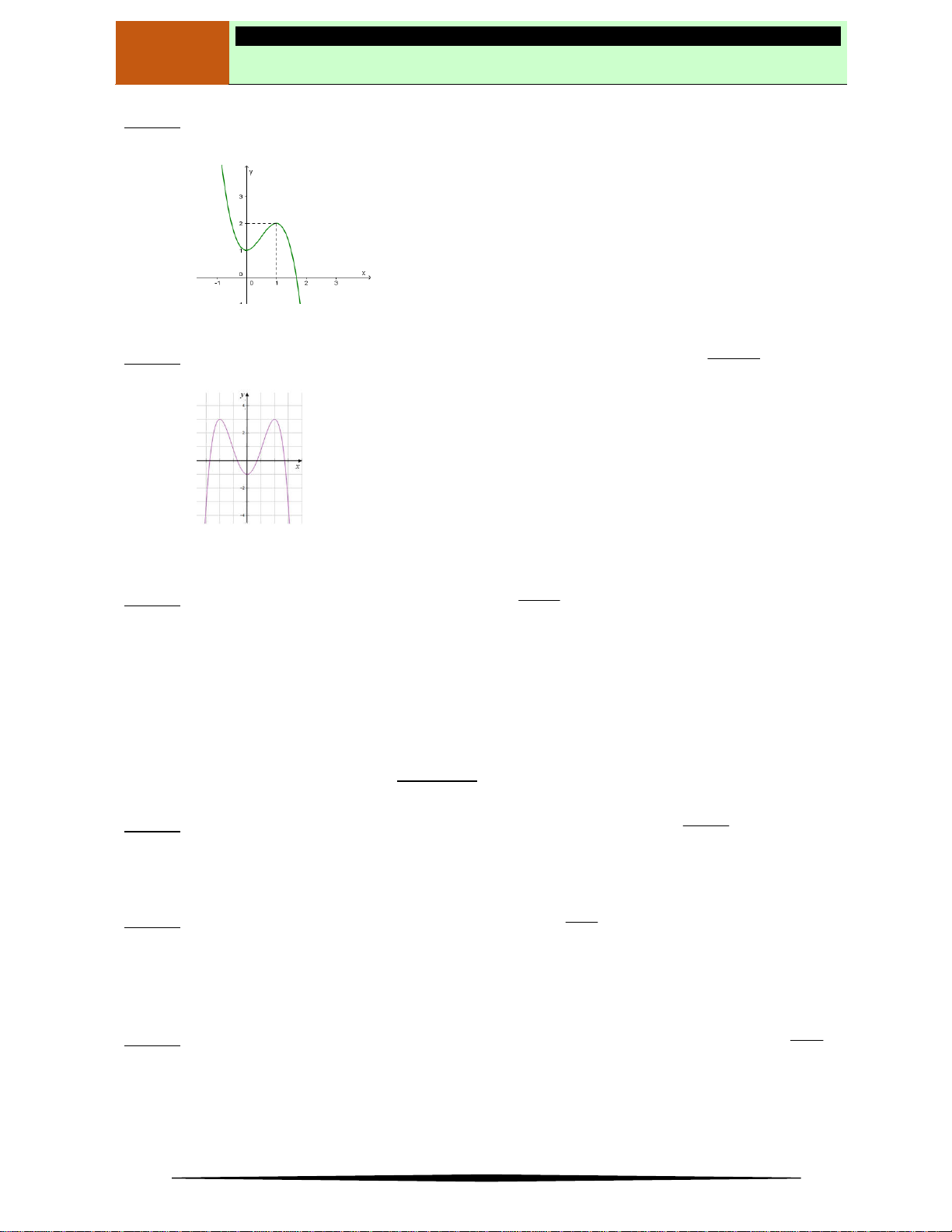
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 117

Câu 58.

Cho hàm số

3 2

( )f x ax

bx cx d  

( , , , )a b c d  

. Đồ thị của hàm số

( )y f x

như hình vẽ bên.

Số nghiệm thực của phương trình

3 ( ) 4 0f x  

là

Ⓐ

3.

Ⓑ

0.

Ⓒ

1.

Ⓓ

2.

Câu 59.

Cho hàm số

 

y f x

có đồ thị như hình sau: Số nghiệm của phương trình

 

1

2

1

f x







là:

Ⓐ

3.

Ⓑ

1.

Ⓒ

2.

Ⓓ

4.

Câu 60.

Đường thẳng

3 4y x 

cắt đồ thị hàm số

4 2

1

x

y

x







tại hai điểm phân biệt có tung độ là

1

y

và

2

.y

Tính

1 2

.y y



Ⓐ

1 2

10.

y y 

Ⓑ

1 2

11.

y y 

Ⓒ

1 2

9.

y y

 

Ⓓ

1 2

1.

y y

 

MỨC ĐỘ 3: VẬN DỤNG

Câu 61.

Tìm tập hợp tất cả các giá trị thực của tham số

m

để đồ thị hàm số

2

1

x m

y

x







cắt đường thẳng

1y x 

tại hai điểm phân biệt ?

Ⓐ

( ;2].

Ⓑ

( ;2).

Ⓒ

( ; 2). 

Ⓓ

(2; ).

Câu 62.

Tìm tất cả các giá trị tham số

m

để đồ thị hàm số

1

x

y

x





cắt đường thẳng

y x m  

tại hai

điểm phân biệt.

Ⓐ

1 4.m 

Ⓑ

0m 

hoặc

2.m 

Ⓒ

0m 

hoặc

4.m 

Ⓓ

1m 

hoặc

4.m 

Câu 63.

Tìm tất cả các giá trị của tham số

m

để đường thẳng

y x m 

cắt đồ thị hàm số

1

x

y

x





tại

hai điểm phân biệt.

Ⓐ

0m 

hoặc

4.m 

Ⓑ

.m  

Ⓒ

0 4.m 

Ⓓ

4 0.m  

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 118

Câu 64.

Cho hàm số

2 3

2

x

y

x







có đồ thị

( )C

và đường thẳng

: .d y x m 

Tìm tất cả các giá trị thực

của tham số

m

để

d

cắt

( )C

tại hai điểm phân biệt ?

Ⓐ

2.m 

Ⓑ

6.m 

Ⓒ

2.m 

Ⓓ

2m 

hoặc

6.m 

Câu 65.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

2 1

1

x

y

x







cắt đường thẳng

3y x m  

tại hai điểm phân biệt.

Ⓐ

0 10.m 

Ⓑ

0.m 

Ⓒ

10.m 

Ⓓ

1.m  

Câu 66.

Gọi

( )C

là đồ thị hàm số

2 1

1

x

y

x







và đường thẳng

4.y 

Tìm tất cả các giá trị thực của tham

số

m

để đường thẳng

d

cắt đồ thị

( )C

tại hai điểm phân biệt ?

Ⓐ

5 1.m   

Ⓑ

5m  

hoặc

1.m  

Ⓒ

1.m  

Ⓓ

5.m  

Câu 67.

Gọi

d

là đường thẳng đi qua điểm

(2;1)A

và có hệ số góc

.k

Tìm tất cả các giá trị của

k

để

d

cắt đồ thị hàm số

8

4

x

y

x







tại hai điểm phân biệt ?

Ⓐ

0.k 

Ⓑ

1k 

hoặc

3.k 

Ⓒ

1 1.k  

Ⓓ

0k 

hoặc

4.k 

Câu 68.

Tìm tất cả các giá trị thực của tham số

m

để đường thẳng

2y x m 

tiếp xúc với đồ thị hàm số

2 3

1

x

y

x



 



Ⓐ

2 8.m 

Ⓑ

1.m 

Ⓒ

.m  

Ⓓ

2 2.m  

Câu 69.

Tìm tất cả các giá trị của tham số

m

để đường thẳng

2 1y x 

cắt đồ thị hàm số

1

x m

y

x



 



Ⓐ

3

1.

2

m

   

Ⓑ

3

2

m

  

Ⓒ

3

1.

2

m

   

Ⓓ

3

2

m

  

Câu 70.

Tìm tất cả các giá trị của tham số

m

để đường thẳng

2 0x y m  

cắt đồ thị hàm số

3

1

x

y

x







tại hai điểm phân biệt.

Ⓐ

3 4 2 3 4 2

2 2

m

 

  

Ⓑ

3 4 2 3 4 2.m   

Ⓒ

3 4 2

2

m





hoặc

3 4 2

2

m



 

Ⓓ

3 4 2m  

hoặc

3 4 2.m  

Câu 71.

Tìm tất cả các giá trị của tham số

m

để đồ thị của hàm số

3

2 (2 )y x mx m   

cắt trục hoành

tại ba điểm phân biệt.

Ⓐ

1

2

m

 

Ⓑ

1

; 4.

2

m m

  

Ⓒ

1

2

m

  

Ⓓ

1

2

m

 

Câu 72.

Tìm tập hợp tất cả các giá trị thực của tham số

m

để đường thẳng

1y mx 

cắt đồ thị hàm số

3

3 1y x x  

tại ba điểm phân biệt.

Ⓐ

3.m  

Ⓑ

3.m 

Ⓒ

3.m  

Ⓓ

3.m 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 119

Câu 73.

Tìm tập hợp các giá trị của tham số thực

m

để đồ thị hàm số

2

( )(2 3 )y x m x x m   

cắt trục

hoành tại ba điểm phân biệt.

Ⓐ

\ {0;1}.

Ⓑ

1

; \ {0;1}.

24

 



















 

Ⓒ

1

; \ {0;1}.

24

 







 











 

Ⓓ

1

;

24

 







  











 

Câu 74.

Tìm tập hợp tất cả các giá trị của tham số

m

để đồ thị hàm số

2

( 1)(2 1)y x x mx   

cắt trục

hoành tại ba điểm phân biệt.

Ⓐ

( ; 2 2) (2 2; ).m     

Ⓑ

( ; 2 2) (2 2; )\{ 3}.m      

Ⓒ

( 2 2;2 2).m  

Ⓓ

( ; 2 2] [2 2; )\{ 3}.m      

Câu 75.

Tìm tất cả các giá trị của tham số

m

sao cho đồ thị của hai hàm số

3 2

2 2y x x mx   

và

2

y x m 

cắt nhau tại một điểm duy nhất.

Ⓐ

3.m  

Ⓑ

3.m  

Ⓒ

3.m 

Ⓓ

3.m  

Câu 76.

Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị của hai hàm số

3 2

3 2y x x mx m    

cắt trục hoành tại ba điểm phân biệt ?

Ⓐ

2.m 

Ⓑ

3.m 

Ⓒ

3.m 

Ⓓ

3.m 

Câu 77.

Cho hàm số

3

3 2y x x  

có đồ thị

( ).C

Gọi

d

là đường thẳng đi qua

(3;20)A

và có hệ số góc

.m

Tìm tập hợp các giá trị của tham số thực

m

để đường thẳng

d

cắt

( )C

tại ba điểm phân biệt.

Ⓐ

15

;

4

 







 











Ⓑ

 

15

; \ 24

4

 







 











 

Ⓒ

 

15

; \ 24

4

 







 











Ⓓ

15

;

4

 







 











 

Câu 78.

Tìm tập hợp các giá trị của tham số thực

m

để đồ thị hàm số

3 2 2

3 2 2y x x m m   

cắt trục

hoành tại ba điểm phân biệt.

Ⓐ

( 2; 2) ( 1;1).   

Ⓑ

(1; ).

Ⓒ

( 2; 0).

Ⓓ

( 1; 0) (1;2). 

Câu 79.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

3 2

3 1y x x  

cắt đường thẳng

2 3y m 

tại ba điểm phân biệt ?

Ⓐ

0 4.m 

Ⓑ

0 2.m 

Ⓒ

3 1.m  

Ⓓ

0 2.m 

Câu 80.

Tìm tất cả các giá trị của

m

để đồ thị hàm số

3

3 2y x x  

cắt đường thẳng

1y m 

tại ba

điểm phân biệt.

Ⓐ

1 5.m 

Ⓑ

1 5.m 

Ⓒ

1 5.m 

Ⓓ

0 4.m 

Câu 81.

Tìm tất cả các giá trị của tham số

m

để đồ thị của hàm số

3 2

3 2 1y x x m   

cắt trục hoành

tại ba điểm phân biệt.

Ⓐ

1 3

2 2

m

   

Ⓑ

5 1

2 2

m

    

Ⓒ

0 4.m 

Ⓓ

4 0.m  

Câu 82.

Tìm tất cả các giá trị của tham số

m

để đường thẳng

3 1y x 

và đồ thị

3

3 3y x mx  

có

duy nhất một điểm chung.

Ⓐ

.m  

Ⓑ

0.m 

Ⓒ

0.m 

Ⓓ

3.m 

Câu 83.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

3

3 1y x mx m   

tiếp xúc với trục

hoành.

Ⓐ

1.m  

Ⓑ

1.m 

Ⓒ

1.m 

Ⓓ

1.m  

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 120

Câu 84.

Đường thẳng

y ax b 

tiếp xúc với đồ thị hàm số

3 2

2 2y x x x   

tại điểm

(1; 0).M

Tính

tích số

.ab

Ⓐ

36.ab  

Ⓑ

6.ab  

Ⓒ

36.ab 

Ⓓ

5.ab  

Câu 85.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

2

( 1)[ (2 1) ]y x x m x m    

cắt trục

hoành tại ba điểm phân biệt.

Ⓐ

.m  

Ⓑ

1

0.

2

m

  

Ⓒ

0 2.m 

Ⓓ

0.m 

Câu 86.

Với giá trị nào của

m

thì đồ thị hàm số

3

( 1) 5y x m x   

cắt trục hoành tại điểm có hoành

độ bằng

2 ?

Ⓐ

1

2

m

 

Ⓑ

1

2

m

  

Ⓒ

15

2

m

 

Ⓓ

15

2

m

  

Câu 87.

Với giá trị nào của tham số thực

m

thì đồ thị hàm số

3 2

– 6 9 1y x x x  

tiếp xúc với parabol

2 2

3

4 .

4

y x m

   

Ⓐ

1.m 

Ⓑ

0.m 

Ⓒ

1.m  

Ⓓ

2.m 

Câu 88.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

3 2

3 ( 2)y x x m x m    

cắt đường

thẳng

2 2y x 

có ba điểm chung phân biệt ?

Ⓐ

2.m 

Ⓑ

2.m 

Ⓒ

3.m 

Ⓓ

3.m 

Câu 89.

Cho hàm số

2 3

1

x

y

x







. Đồ thị hàm số tiếp xúc với đường thẳng

2y x m 

khi và chỉ khi giá

trị

m

bằng bao nhiêu ?

Ⓐ

8.m 

Ⓑ

2 2 .m  

Ⓒ

8.m  

Ⓓ

1.m 

Câu 90.

Cho hàm số

3 2

2 1y x x  

có đồ thị

( ).C

Tìm tất cả các giá trị của tham số

m

để đường thẳng

d:

y mx m 

cắt đồ thị

( )C

tại ba điểm phân biệt ?

Ⓐ

5

4

1

m





 









 





Ⓑ

5

4

1

m















 





Ⓒ

5

4

1

m















 





Ⓓ

5

4

1

m





 









 





Câu 91.

Đồ thị của hàm số

3 2

( )

f x x ax bx c   

tiếp xúc với trục hoành tại gốc tọa độ và cắt đường

thẳng

1x 

tại điểm có tung độ bằng

3.

Tính

.S a b c  

Ⓐ

4.S 

Ⓑ

5.S 

Ⓒ

3.S 

Ⓓ

2.S 

Câu 92.

Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

3 2

2 ( 2)y x mx m x   

cắt trục

hoành tại 3 điểm phân biệt.

Ⓐ

2

1

m











 





Ⓑ

1 2.m  

Ⓒ

2

1

m











 





Ⓓ

2

1

2

m



















 











 





Câu 93.

Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị hàm số

3 2

( ) : 6 9 6C y x x x  

cắt

đường thẳng

: – 2 – 4d y m x m

tại ba điểm phân biệt ?

Ⓐ

3.m  

Ⓑ

1.m 

Ⓒ

3.m  

Ⓓ

1.m 

Câu 94.

Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

4 2 2

( ) : 1C y x m x m   

tiếp xúc

với đường thẳng

: 2 2d y x 

tại điểm có hoành độ

1.x 

Ⓐ

1m  

hoặc

1.m 

Ⓑ

1.m  

Ⓒ

0.m 

Ⓓ

1m  

hoặc

0.m 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 121

Câu 95.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

4 2

2 2y x mx m   

cắt trục

Ox

tại

4

điểm phân biệt.

Ⓐ

(2; ).m  

Ⓑ

( ;1).m  

Ⓒ

( ; 1) (2; ).m     

Ⓓ

(0; ).m  

Câu 96.

Tìm tất cả các giá trị của tham số

m

để dường thẳng

1y  

cắt đồ thị hàm số

4 2

(3 2) 3y x m x m   

tại bốn điểm phân biệt.

Ⓐ

1

3

1

m





















Ⓑ

1 0.m  

Ⓒ

1

3

0

m





 















Ⓓ

1

3

0

m





 















MỨC ĐỘ 4: VẬN DỤNG CAO

Câu 97.

Tìm tập hợp tất cả các giá trị của tham số

m

để đường thẳng

: 1d y x 

cắt đồ thị hàm số

2

1

x m

y

x







tại hai điểm phân biệt có hoành độ dương.

Ⓐ

( ; 1). 

Ⓑ

( ;1).

Ⓒ

( 2; 1). 

Ⓓ

( 2;1).

Câu 98.

Cho hàm số

2 1

1

x

y

x







có đồ thị

( )C

và đường thẳng

: .

m

d y x m 

Tìm giá trị của tham số

thực

m

để

( )C

cắt

m

d

tại hai điểm phân biệt

, A B

sao cho

OAB

vuông tại

.O

Ⓐ

1

3

m

 

Ⓑ

4

3

m

 

Ⓒ

2

3

m

 

Ⓓ

1

3

m

  

Câu 99.

Cho hàm số

1

y

x





có đồ thị

( )C

và đường thẳng

.: y md x  

Hỏi giá trị thực của tham

số

m

thuộc tập nào sau đây để đường thẳng

d

cắt đồ thị

( )C

tại hai điểm phân biệt

, A B

sao

cho tam giác

OAB

có bán kính đường tròn ngoại tiếp bằng

2 2,

với

O

là gốc tọa độ.

Ⓐ

( ; 2). 

Ⓑ

( 2; 0).

Ⓒ

(0; 3).

Ⓓ

(3; ).

Câu 100.

Cho hàm số

2 1

1

x

y

x







có đồ thị

( ).C

Tìm tất cả giá trị thực của tham số

m

để đường thẳng

: 1d y x m  

cắt

( )C

tại hai điểm phân biệt

, A B

sao cho

2 3.AB 

Ⓐ

4 3.m  

Ⓑ

4 10.m  

Ⓒ

2 3.m  

Ⓓ

2 10.m  

Câu 101.

Với giá trị nào của tham số thực

m

thì đường thẳng

2 1y x 

cắt đồ thị

1

2

mx

y

x







tại hai

điểm phân biệt

, A B

sao cho độ dài đoạn thẳng

10.AB 

Ⓐ

1

2

m

  

Ⓑ

1

2

m

  

Ⓒ

3.m 

Ⓓ

3.m 

Câu 102.

Cho hàm số

2

1

x

y

x







có đồ thị

( )C

và đường thẳng

: 2 .

m

d y x m  

Tìm tham số

m

để

( )C

cắt

m

d

tại hai điểm phân biệt

, A B

sao cho

30.AB 

Ⓐ

2.m 

Ⓑ

1.m  

Ⓒ

0.m 

Ⓓ

1.m 

Câu 103.

Cho hàm số

2

2 1

x

y

x



 



Tìm tập hợp các giá trị thực của tham số

m

để đường thẳng

1y m x m  

luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc cùng một nhánh của đồ thị.

Ⓐ

( ;0)\{ 3}. 

Ⓑ

{0}.

Ⓒ

(0; ).

Ⓓ

( ;1)\{ 3}. 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 122

Câu 104.

Cho hàm số

1

x

y

x







và đường thẳng

2 .y x m  

Hỏi giá trị của tham số

m

thuộc tập nào

sau đây thì đồ thị hai hàm số đã cho cắt nhau tại hai điểm

A

và

B

phân biệt, đồng thời điểm

trung điểm của đoạn thẳng

AB

có hoành độ bằng

5

2



Ⓐ

( 2; 3).

Ⓑ

( ; 3). 

Ⓒ

(7; ).

Ⓓ

(3;7).

Câu 105.

Cho hàm số

2 1

1

x

y

x







có đồ thị

( )C

và đường thẳng

: 3 .d y x m  

Biết rằng

d

cắt

( )C

tại hai

điểm phân biệt

, A B

sao cho trọng tâm tam giác

OAB

thuộc đồ thị

( ),C

với

O

là gốc tọa độ.

Hỏi giá trị của tham số

m

thuộc tập hợp nào sau đây ?

Ⓐ

( ; 3]. 

Ⓑ

(3; ).

Ⓒ

( 1;3].

Ⓓ

( 5; 2]. 

Câu 106.

Tìm giá trị thực của tham số

m

để đồ thị hàm số

3 2

4 3y x x mx m    

cắt trục hoành tại ba

điểm phân biệt

, , A B C

với

A B C

x x x 

thỏa mãn

5.AC 

Ⓐ

0.m 

Ⓑ

1.m 

Ⓒ

2.m  

Ⓓ

1.m  

Câu 107.

Tìm tập hợp tất cả các giá trị của tham số

m

để đồ thị hàm số

3 2

2 3( 1) 6 1y x m x mx m     

cắt trục hoành tại ba điểm phân biệt có hoành độ dương.

Ⓐ

(4 2; ). 

Ⓑ

(1 2; ). 

Ⓒ

( 1;0) (1 2; ).   

Ⓓ

(4 3; ). 

Câu 108.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

3 2 2 2

3 3( 1) 1y x m x m x m     

cắt

trục hoành tại ba điểm phân biệt có hoành độ dương ?

Ⓐ

1.

m



Ⓑ

3 1 2.m  

Ⓒ

1 1.m  

Ⓓ

3 1.m   

Câu 109.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

3 2

4y x mx  

cắt trục hoành tại ba

điểm phân biệt có hoành độ

1 2 3

, , x x x

thoả mãn

1 2 3

1 .x x x

  

Ⓐ

5.m 

Ⓑ

3 5.m 

Ⓒ

3.m 

Ⓓ

3.m 

Câu 110.

Cho hàm số

3 2

3 9 5y x x x   

có đồ thị

( ).C

Gọi

, A B

là giao điểm của

( )C

và trục hoành.

Số điểm

( )M C

sao cho



90AMB  

là bao nhiêu ?

Ⓐ

1.

Ⓑ

2.

Ⓒ

0.

Ⓓ

3.

Câu 111.

Tìm các giá trị của tham số thực

m

để đường thẳng

: 4d y x 

cắt đồ thị

3 2

( ) : 2 ( 3) 4

C y x m x m x

    

tại ba điểm phân biệt

(0;4), A B

và

C

sao cho diện tích

MBC

bằng

4,

với

(1;3).M

Ⓐ

2m 

hoặc

3.m 

Ⓑ

2m  

hoặc

3.m 

Ⓒ

3.m 

Ⓓ

2m  

hoặc

3.m  

Câu 112.

Cho hàm số

3 2

6 9 ,y x x x m   

(m

là tham số thực) có đồ thị

( ).C

Giả sử

( )C

cắt trục hoành tại

ba điểm phân biệt có hoành độ

1 2 3 1 2 3

, , , ( ).x x x x x x 

Hỏi khẳng định nào sau đây đúng ?

Ⓐ

1 2 3

0 1 3 4.

x x x

     

Ⓑ

1 2 3

1 3 4.

x x x

    

Ⓒ

1 2 3

1 3 4 .x x x    

Ⓓ

1 2 3

0 1 3 4.

x x x

     

Câu 113.

Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị hàm số

4 2 2

2(2 1) 4y x m x m   

cắt

trục hoành tại bốn điểm phân biệt

1 2 3 4

, , , x x x x

thỏa mãn

2 2 2 2

1 2 3 4

6.

x x x x

   

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 123

Ⓐ

1

4

m

 

Ⓑ

1

2

m

  

Ⓒ

1

4

m

  

Ⓓ

1

4

m

  

Câu 114.

Cho các số thực

, , a b c

thỏa mãn điều kiện

8 4 2 0

a b c





    









   





Hỏi đồ thị hàm số

3 2

y x ax bx c   

cắt trục hoành tại bao nhiêu điểm ?

Ⓐ

0.

Ⓑ

1.

Ⓒ

2.

Ⓓ

3.

Câu 115.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

2 2

( 4 1) 7y x m x    

có điểm chung

với trục hoành.

Ⓐ

7

1

3

m

   

Ⓑ

0 3.m 

Ⓒ

7

2

3

m

  

Ⓓ

2 3.m 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 124

CĐ7.4: CÁC BÀI TOÁN TÌM THAM SỐ

VÀ HÀM ẨN

Daïng toaùn 1.1. Tìm tham soá m ñeå haøm soá ñôn ñieäu treân mieàn xaùc ñònh cuûa noù



 Tìm tham số m để hàm số bậc ba

3 2

y ax bx cx d   

đơn điệu trên tập xác định

Phương pháp:

—

Bước 1. Tập xác định:

. D

Tính đạo hàm

2

3 2 .y ax bx c



  

—

Bước 2. Ghi điều kiện để hàm đơn điệu, chẳng hạn:

Để

( )f x

đồng biến trên

0

0, ?

0

y

a

y x m













     





 





 

Đề

( )f x

nghịch biến trên

0

0, ?

0

y

a

y x m













     





 





 

 Lưu ý: Dấu của tam thức bậc hai

2

( ) .f x ax bx c  



0

( ) 0,

0

a

f x x









    





 









0

( ) 0,

0

a

f x x









    





 







 Tìm tham số m để hàm số nhất biến

ax b

y

cx d







đơn điệu trên tập xác định của nó.

Phương pháp:

—

Bước 1. Tập xác định:

\

d

c

 

 

  

 

 

 

D

Tính đạo hàm

2

. .

( )

a d b c

y

cx d





 



—

Bước 2. Ghi điều kiện để hàm đơn điệu. Chẳng hạn:

Để

( )f x

đồng biến trên

0, . . 0 ?y x D a d b c m



       D

Để

( )f x

nghịch biến trên

0, 0 ?y x ad bc m



       D D

 Lưu ý: Nếu hàm số

3 2

y ax bx cx d   

có

a

chứa tham số hoặc hàm số

ax b

y

cx d







có

a

hay

c

chứa tham số thì khi giải toán, cần chia ra hai trường hợp. Đó là trường hợp

0a 

để xét tính đúng sai (nhận loại

)m

và trường hợp

0.a 

Ví dụ 1.

Có bao nhiêu giá trị nguyên của

m

để hàm số

3 2

(4 9) 5

y x m x m x

     

nghịch biến

trên

( ; ). 

Ⓐ

7.

Ⓑ

4.

Ⓒ

6.

Ⓓ

5.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2.

Tập hợp các tham số

m

để hàm số

3 2

( 1) 3 1y x m x x    

đồng biến trên

( ; ) 

là

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 125

một đoạn có dạng

[ ; ],a b

với

, a b

là các số nguyên. Tính tổng

.a b

Ⓐ

6.a b 

Ⓑ

2.a b  

Ⓒ

7.a b 

Ⓓ

6.a b  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3.

Hỏi có bao nhiêu số nguyên

m

để hàm số

2 3 2

( 1) ( 1) 4y m x m x x     

nghịch biến trên

khoảng

( ; ). 

Ⓐ

2.

Ⓑ

1.

Ⓒ

0.

Ⓓ

3.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4.

Tìm tất cả các giá trị thực của tham số

m

sao cho hàm số

2

1

x m

y

x







đồng biến trên từng

khoảng xác định của nó.

Ⓐ

1.m 

Ⓑ

1 1.m  

Ⓒ

3 3.m  

Ⓓ

1 1.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 5.

Cho hàm số

4mx m

y

x m







với

m

là tham số. Gọi

S

là tập hợp tất cả các giá trị nguyên của

m

để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của

.S

Ⓐ

5.

Ⓑ

4.

Ⓓ

3.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 6.

Cho hàm số

2 3

mx m

y

x m

 





với

m

là tham số. Gọi

S

là tập hợp tất cả các giá trị nguyên

của

m

để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của

.S

Ⓐ

5.

Ⓑ

4.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 126

Ⓓ

3.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 7.

Tìm tập hợp các giá trị của tham số

m

để hàm số

sin 7 5 3y m x x m   

đồng biến trên

.

Ⓐ

[ 7;7].

Ⓑ

( ; 1]. 

Ⓒ

( ; 7]. 

Ⓓ

[7; ).

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 127

Daïng toaùn 1.2. Tìm tham soá m ñeå haøm soá ñôn ñieäu treân mieàn cho tröôùc



 Tìm tham số

m

để hàm số nhất biến

ax b

y

cx d







đồng biến trên

( ; ). 

Phương pháp:

—

Bước 1. Tìm tập xác định:

\

d

c

 

 

 

 

 

 

D

và tính

2

( )

ad cb

y

cx d





 



—

Bước 2. Hàm số tăng trên

 

0

; .

( ; )

ad cb

y

ad cb

d

x m

d

c

d

c

x

c



 







 



 











 









  

 

     

  



  

  

  









 

 



 















 Lưu ý: Lý luận tương tự cho trường hợp nghịch biến hoặc trên

( ; ), [ ; ),...  

 Tìm tham số

m

để hàm số bậc ba, bậc bốn đơn điệu trên miền

D

cho trướⒸ

Phương pháp 1. Dùng phương pháp xét dấu của

y



và biện luận để suy ra các giá trị

.m

Phương pháp 2. Dùng phương pháp miền giá trị (sau khi học bài 3: GTLN, GTNN)

—

Bước 1. Ghi điều kiện để

( ; )y f x m

đơn điệu trên

.D

Chẳng hạn:

Đề yêu cầu

( ; )y f x m

đồng biến trên

( ; ) 0.y f x m

 

  D

Đề yêu cầu

( ; )y f x m

nghịch biến trên

( ; ) 0.y f x m

 

  D

—

Bước 2. Độc lập

m

ra khỏi biến số và đặt vế còn lại là

( )g x

được:

( )

m g x

















—

Bước 3. Khảo sát tính đơn điệu của hàm số

( )g x

trên

.D

—

Bước 4. Dựa vào bảng biến thiên kết luận:

Khi ( ) max ( )

Khi ( ) min ( )

m g x m g x



  







  





D

Hai bài toán thường gặp khi tìm giá trị lớn nhất và giá trị nhỏ nhất:

Bài toán 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

( )y f x

trên đoạn

[ ; ].a b

—

Bước 1. Tính

( )f x



và cho

( ) 0f x





tìm nghiệm

, ( 1, )

i

x i n



trên đoạn

[ ; ].a b

—

Bước 2. Tính

( ), f( ), ( )

i

f a b f x

và kết luận:

[ ; ]

max ( ) max{ ( ); ( ); ( )}

i

a b

f x f a f b f x



và

[ ; ]

min ( ) min{ ( ); ( ); ( )}.

i

a b

f x f a f b f x

Bài toán 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất hàm số

( )y f x

trên khoảng

( ; ).a b

—

Bước 1. Tính

( ).f x



Cho

( ) 0f x





tìm nghiệm.

—

Bước 2. Xét dấu biểu thức

( )y f x

 



và lập bảng biến thiên, rồi kết luận.

Lưu ý. Hàm số chỉ tồn tại giá trị lớn nhất và nhỏ nhất khi chúng liên tục trên

.K



Nếu

( )y f x

đồng biến trên

[ ; ]a b

thì

[ ; ]

min ( ) ( )

a b

f x f a



và

[ ; ]

max ( ) ( ).

a b

f x f b





Nếu

( )y f x

nghịch biến trên

[ ; ]a b

thì

[ ; ]

min ( ) ( )

a b

f x f b



và

[ ; ]

max ( ) ( ).

a b

f x f a



GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 128

Ví dụ 1.

Tìm tập hợp tất cả các giá trị của tham số

m

để hàm số

2 1

x

y

x m







nghịch biến trên

(2; ).

Ⓐ

1

2;

2

 







 











Ⓑ

1

2;

2

 







 











 

Ⓒ

1

;

2

 





 











Ⓓ

1

;

2

 







 











 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2.

Tìm tất cả các giá trị thực của tham số

m

để hàm số

x

y

x m





nghịch biến trên

[1; ).

Ⓐ

0 1.m 

Ⓑ

0 1.m 

Ⓒ

0 1.m 

Ⓓ

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3.

Tìm tập hợp

S

các giá trị của tham số thực

m

để hàm số

4

mx

y

x m







đồng biến trên nửa

khoảng

( ; 3). 

Ⓐ

( , 2) (2; 3].S    

Ⓑ

( , 2) (2, ).S     

Ⓒ

( , 2] (2, 3].S    

Ⓓ

( , 2] (2, ).S     

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4.

Tìm tất cả các giá trị thực của tham số

m

để hàm số

9

mx

y

x m







đồng biến trên khoảng

(2; ).

Ⓐ

3 2.m  

Ⓑ

3 2.m  

Ⓒ

2.m 

Ⓓ

2 3.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 5.

Tìm tất cả các giá trị thực của tham số

m

sao cho hàm số

tan 2

tan

x

y

x m







đồng biến trên

khoảng

0;

4



 



















 

Ⓐ

0m 

hoặc

1 2.m 

Ⓑ

0.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 129

Ⓒ

1 2.x  

Ⓓ

2.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 6.

Tìm tất cả các giá trị thực của tham số

m

để hàm số

cot 1

x

y

m x







đồng biến trên khoảng

;

4 2

 

 



















 

Ⓐ

( ; 0] (1; ).m    

Ⓑ

( ; 0].m  

Ⓒ

(1; ).m  

Ⓓ

( ;1) \ {0}.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 7.

Tìm tất cả các giá trị thực của tham số

m

sao cho hàm số

2cos 1

cos

x

y

x m







đồng biến trên

khoảng

(0; ).

Ⓐ

1.m  

Ⓑ

1

2

m

  

Ⓒ

1.m 

Ⓓ

1

2

m

  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 8.

Cho hàm số

( 1)sin 2

sin

m x

y

x m

 

 



Tìm tất cả các giá trị của tham số

m

để hàm số nghịch biến

trên khoảng

0;

2



 



















 

Ⓐ

1 2m  

Ⓑ

1

2

m



 













Ⓒ

1

2

m



 













Ⓓ

0

1

m

















................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 9.

Tìm tất cả các giá trị thực của tham số

m

sao cho hàm số

1 4 2

1 4

x

y

x m

 



 

nghịch biến trên

khoảng

1

0;

4

 



















 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 130

Ⓐ

0m 

hoặc

1 2.m 

Ⓑ

0.m 

Ⓒ

1 2.m 

Ⓓ

2.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 10.

Tìm tập hợp các giá trị của tham số thực

m

để hàm số

3 2

3y x mx m  

nghịch biến trên

khoảng

(0;1).

Ⓐ

1

2

m

 

Ⓑ

1

2

m

 

Ⓒ

0.m 

Ⓓ

0.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 11.

Tìm tất cả các giá trị của tham số thực

m

để hàm số

3 2

1 2

( 1) (2 3)

3 3

y x m x m x

     

đồng biến trên

(1; ).

Ⓐ

2.m 

Ⓑ

2.m 

Ⓒ

1.m 

Ⓓ

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 12.

Tìm tất cả các giá trị thực của tham số

m

để hàm số

3 2

( 1) 2 3

y x m x x

     

đồng biến

trên đoạn

[0;2] ?

Ⓐ

3

2

m

 

Ⓑ

3

2

m

 

Ⓒ

3

2

m

 

Ⓓ

3

2

m

 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 13.

Hỏi có bao nhiêu giá trị nguyên của tham số

m

để hàm số

3 2

3( 1) 3 ( 2)y x m x m m x    

nghịch biến trên đoạn

[0;1] ?

Ⓐ

2.

Ⓑ

4.

Ⓒ

7.

Ⓓ Vô số.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 131

................................................................................................................................................................................................................................

................................

Ví dụ 14.

Gọi

S

là tập các giá trị của tham số

m

để hàm số

3 2 2 2 2

3( 3 3) 3( 1) 2y x m m x m x m       

đồng biến trên

[1; ).

Hỏi

S

là tập hợp con

của tập hợp nào sau đây ?

Ⓐ

( ;0).

Ⓑ

( ; 2). 

Ⓒ

( 1; ). 

Ⓓ

( 3;2).

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 15.

Cho hàm số

4 2

(2 3) .y x m x m    

Nếu hàm số luôn nghịch biến trên khoảng

(1;2)

thì sẽ

tồn tại các giá trị của tham số

; ;

p

m

q

 





 











trong đó phân số

p

q

tối giản và

0.q 

Hỏi tổng

p q

bằng bao nhiêu ?

Ⓐ

3.p q 

Ⓑ

5.p q 

Ⓒ

7.p q 

Ⓓ

9.p q 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 16.

Tìm tất cả các giá trị của tham số

m

để hàm số

2 4 2

1)( 2

y m x mx 

đồng biến trên

(1; ).

Ⓐ

1m  

hoặc

1 5

2

m



 

Ⓑ

1m  

hoặc

1 5

2

m



 

Ⓒ

1m  

hoặc

1.m 

Ⓓ

1.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 17.

Tìm tập hợp tất cả các giá trị của tham số

m

để hàm số

2

1 1y x mx   

đồng biến trên

khoảng

( ; ). 

Ⓐ

( ; 1]. 

Ⓑ

( ;1).

Ⓒ

[ 1;1].

Ⓓ

[1; ).

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 18.

Cho hàm số

3 2

1

( 1) ( 3) 4

3

y x m x m x

      

. Tìm tất cả các giá trị thực của tham số

m

để hàm số đã cho đồng biến trên khoảng

(0; 3).

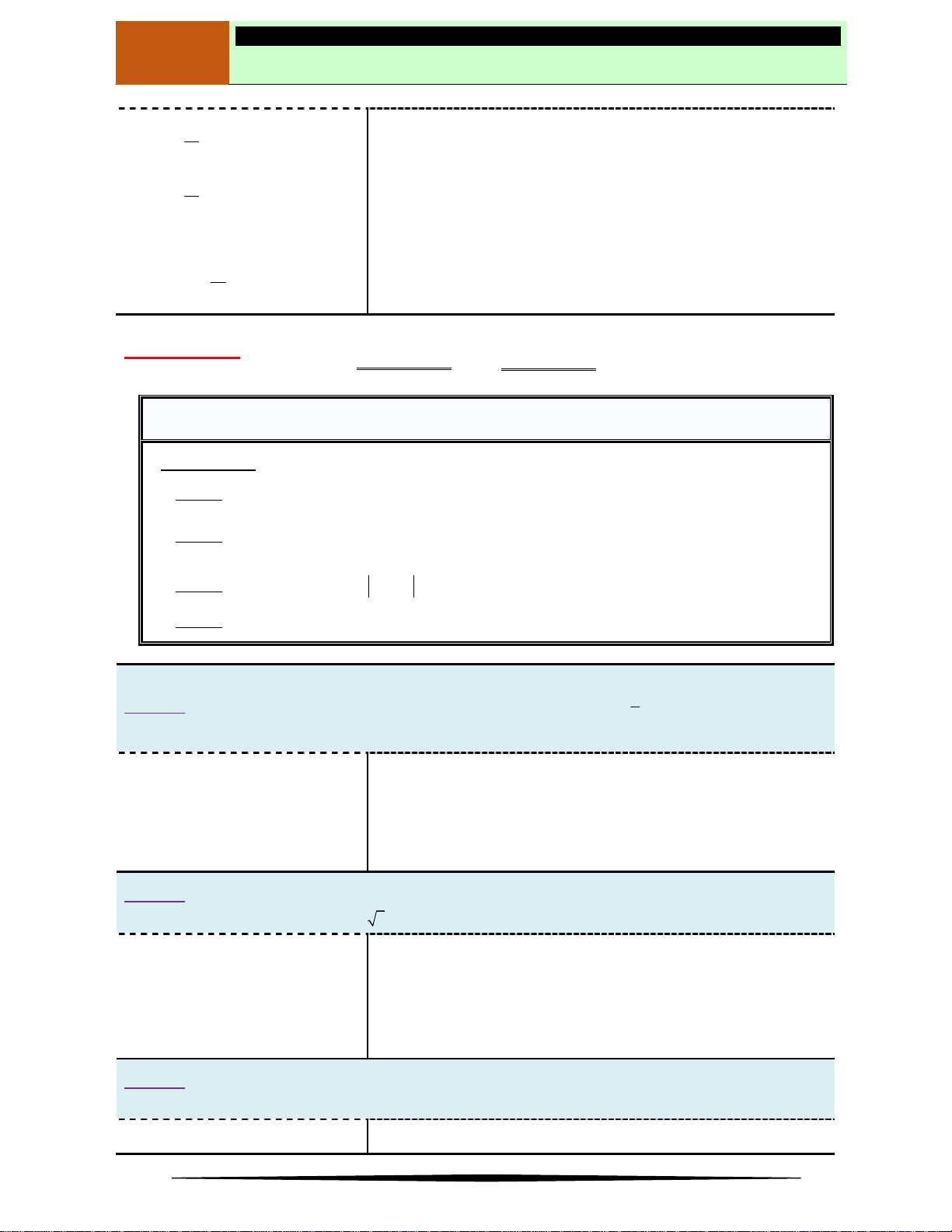
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 132

Ⓐ



12

.

7

m

Ⓑ



12

.

7

m

Ⓒ

 1.m

Ⓓ

 

12

1 .

7

m

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Daïng toaùn 1.3. Tìm tham soá m ñeå haøm soá baäc 3 ñôn ñieäu khoaûng coù ñoä daøi l



Tìm

m

để hàm số

3 2

y ax bx cx d   

đơn điệu trên khoảng có độ dài đúng bằng l

Phương pháp:

—

Bước 1. Tính

2

3 2 .y ax bx c



  

—

Bước 2. Hàm số đơn điệu trên

1 2

( ; ) 0

x x y



 

có

2

nghiệm phân biệt

0

a















 





( )i

—

Bước 3. Yêu cầu bài toán

1 2

x x l  

2 2

1 2 1 2

( ) 4 .

x x x x l   

( )ii

—

Bước 4. Giải

( )ii

và giao với

( )i

để suy ra giá trị

m

cần tìm.

Ví dụ 1.

Tìm tất cả các giá trị thực của tham số

m

sao cho hàm số

3 2

1

( 1) 3

3

y x mx m x m

      

đồng biến trên đoạn có độ dài đúng bằng

2.

Ⓐ

1m  

hoặc

2.m 

Ⓑ

1.m  

.m

Ⓓ

2.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2.

Tìm các giá trị của tham số

m

sao cho hàm số

3 2

( 1) 4 7y x m x x    

có độ dài khoảng

nghịch biến đúng bằng

2 5.

Ⓐ

2m  

hoặc

4.m 

Ⓑ

1m 

hoặc

3.m 

Ⓒ

0m 

hoặc

1.m  

Ⓓ

2m 

hoặc

4.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3.

Tìm tất cả các giá trị thực

m

để hàm số

3 2

( ) 3 ( 1) 2 3f x x x m x m      

đồng biến trên

một khoảng có độ dài lớn hơn

1.

Ⓐ

0.m 

................................................................................................................................................................................................................................

................................

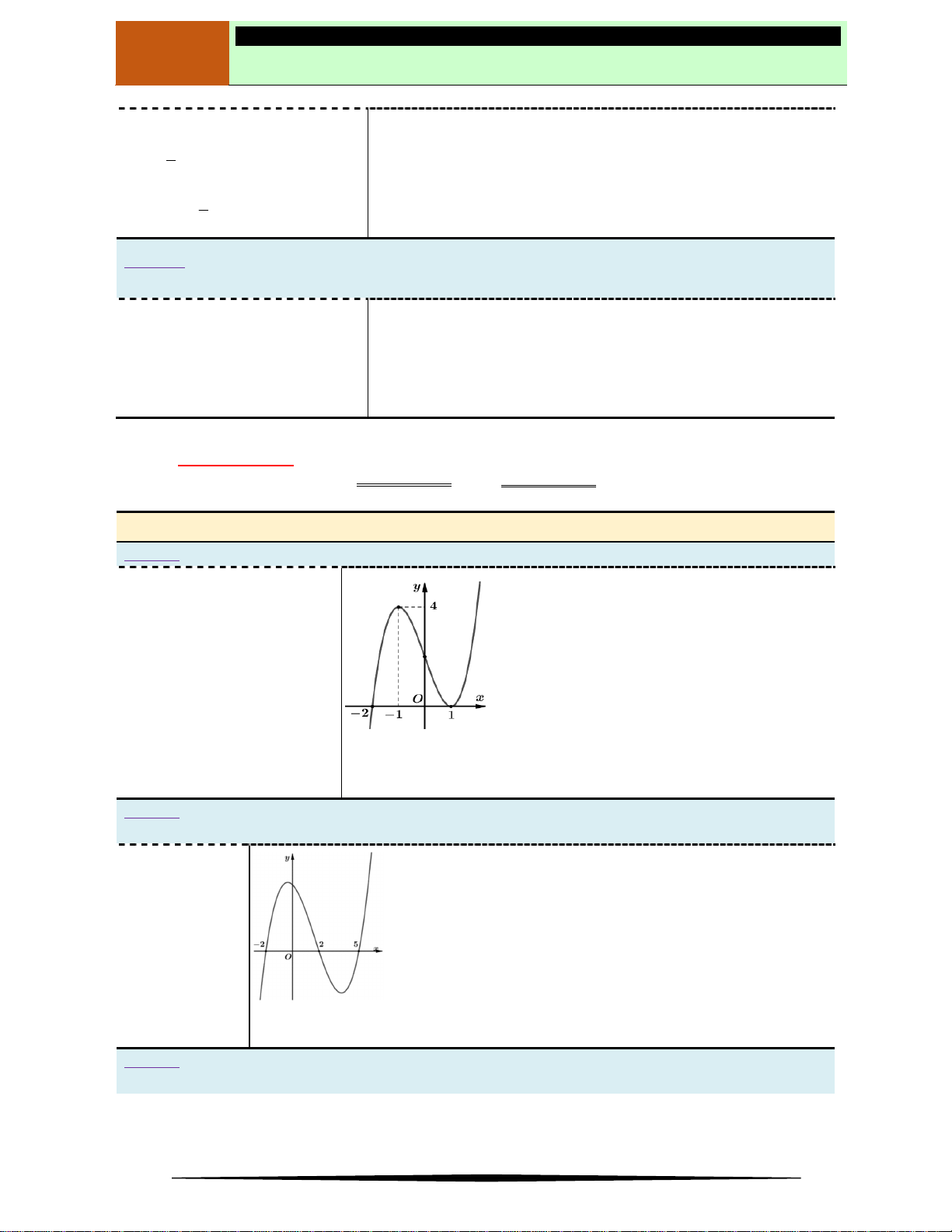
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 133

Ⓑ

0.m 

Ⓒ

5

0.

4

m  

Ⓓ

5

4

m   

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4.

Hỏi có bao nhiêu giá trị nguyên dương của

m

để hàm số

3 2

3 3( 1)y x m x m x   

nghịch

biến trên đoạn có độ dài lớn hơn

4.

Ⓐ

3.

Ⓑ

5.

Ⓒ

9.

Ⓓ Vô số.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Daïng toaùn 1.4: Nh÷ng vÊn ®Ò liªn quan ®Õn sö dông tÝnh ®¬n ®iÖu ®Ó gi¶i to¸n hµm Èn.



a) Cho ñoà thò

( ).f x



Hoûi khoaûng ñôn ñieäu cuûa haøm soá

( ) .f u x

 

 

 

Ví dụ 1.

Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên. Khẳng định nào sau đây sai?

Ⓐ Hàm số

( )f x

đồng biến

trên

( 2;1).

Ⓑ Hàm số

( )f x

đồng biến

trên

(1; ).

( )f x

nghịch biến

trên đoạn có độ dài bằng

2

.

Ⓓ Hàm số

( )f x

nghịch biến

trên

( ; 2). 

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2.

Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên dưới. Hàm số

( ) (3 2 )g x f x 

nghịch biến trên khoảng nào trong các khoảng sau?

Ⓐ

(0;2).

Ⓑ

(1;3).

Ⓒ

( ; 1). 

Ⓓ

( 1; ). 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................................................................................

........................

Ví dụ 3.

Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên dưới. Hàm số

( ) (1 2 )g x f x 

đồng biến trên khoảng nào trong các khoảng sau ?

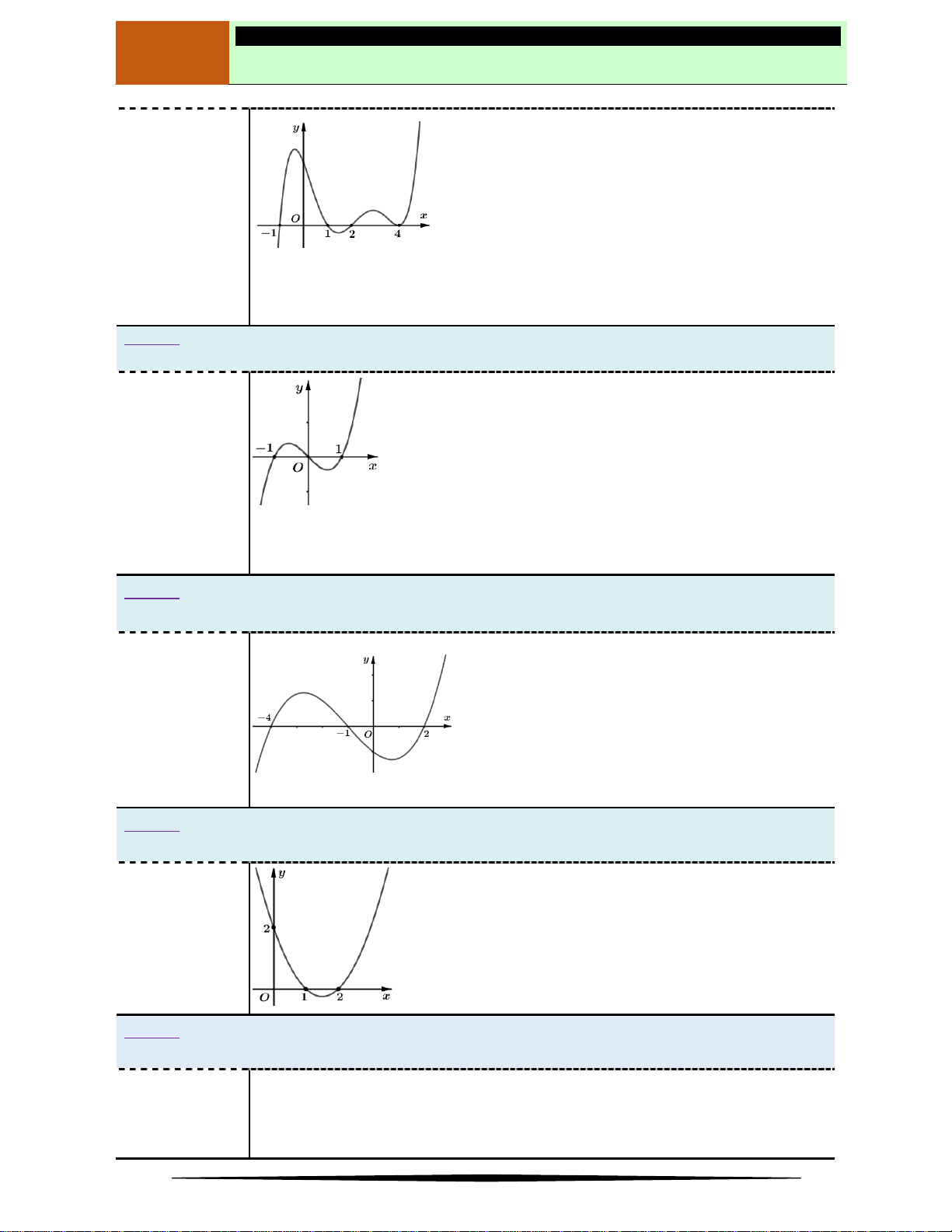
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 134

Ⓐ

 

1; 0 .

Ⓑ

 

;0 .



Ⓒ

 

0;1 .

Ⓓ

 

1; .

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

..........................................................................................................................................................................................................................................................................................................

Ví dụ 4. Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên. Hỏi hàm số

2

( ) ( )g x f x

đồng

biến trên khoảng nào trong các khoảng sau?

Ⓐ

( ; 1). 

B

( 1; ). 

Ⓒ

( 1; 0).

Ⓓ

(0;1).

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

..........................................................................................................................................................................................................................................................................................................

Ví dụ 5. Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên dưới. Hỏi hàm số

2

( ) ( 5)

g x f x

 

có bao nhiêu khoảng nghịch biến?

Ⓐ

2.

Ⓑ

3.

Ⓒ

4.

Ⓓ

5.

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

..........................................................................................................................................................................................................................................................................................................

Ví dụ 6. Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên. Hỏi hàm số

2

( ) (1 )g x f x 

nghịch biến trên khoảng nào trong các khoảng sau?

Ⓐ

(1;2).

Ⓑ

 

0; .

Ⓒ

( 2; 1). 

Ⓓ

( 1;1).

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

Ví dụ 7. Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên. Hỏi hàm số

2

( ) (3 )g x f x 

đồng biến trên khoảng nào trong các khoảng sau?

Ⓐ

(2;3).

Ⓑ

( 2; 1). 

......................................................................................................................................................................................................................................................................................

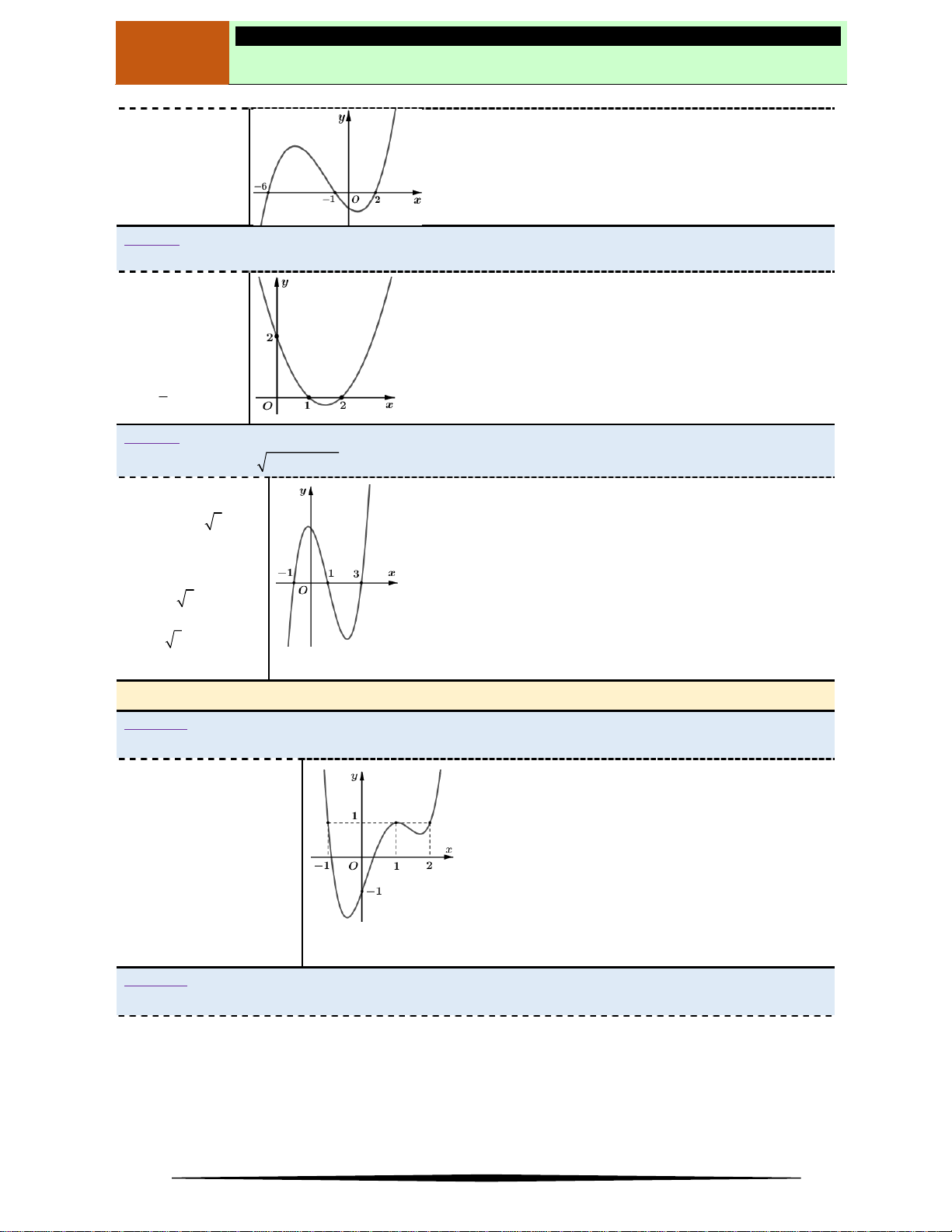
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 135

Ⓒ

(0;1).

Ⓓ

( 1; 0).

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

Ví dụ 8.

Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên. Hỏi hàm số

2

( ) ( )g x f x x 

nghịch biến trên khoảng nào trong các khoảng sau?

Ⓐ

(1;2).

Ⓑ

( ; 0).

Ⓒ

( ;2).

Ⓓ

1

; .

2

 



















 

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

Ví dụ 9.

Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên dưới. Hàm số

2

( ) ( 2 2)g x f x x  

nghịch biến trên khoảng nào trong các khoảng sau?

Ⓐ

( ; 1 2 2).  

Ⓑ

( ;1).

Ⓒ

(1;2 2 1).

Ⓓ

(2 2 1; ). 

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

......................................................................................................................................................................................................................................................................................

b) Cho ñoà thò

( ).f x



Hoûi khoaûng ñôn ñieäu cuûa haøm soá

( ) ( ).f u x g x

 



 

 

Ví dụ 10.

Cho hàm số

( )y f x

có đạo hàm liên tục trên

.

Đồ thị hàm số

( )y f x





như hình bên dưới.

Đặt

( ) ( ) ,g x f x x 

khẳng định nào sau đây là đúng?

Ⓐ

(2) ( 1) (1).g g g  

Ⓑ

( 1) (1) (2).g g g  

Ⓒ

( 1) (1) (2).g g g  

Ⓓ

(1) ( 1) (2).g g g  

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................................................................................................................

......................

Ví dụ 11.

Cho hàm số

( )y f x

có đạo hàm liên tục trên

.

Đồ thị hàm số

( )y f x





như hình bên dưới.

Hàm số

2

( ) 2 ( )g x f x x 

đồng biến trên khoảng nào trong các khoảng sau đây?

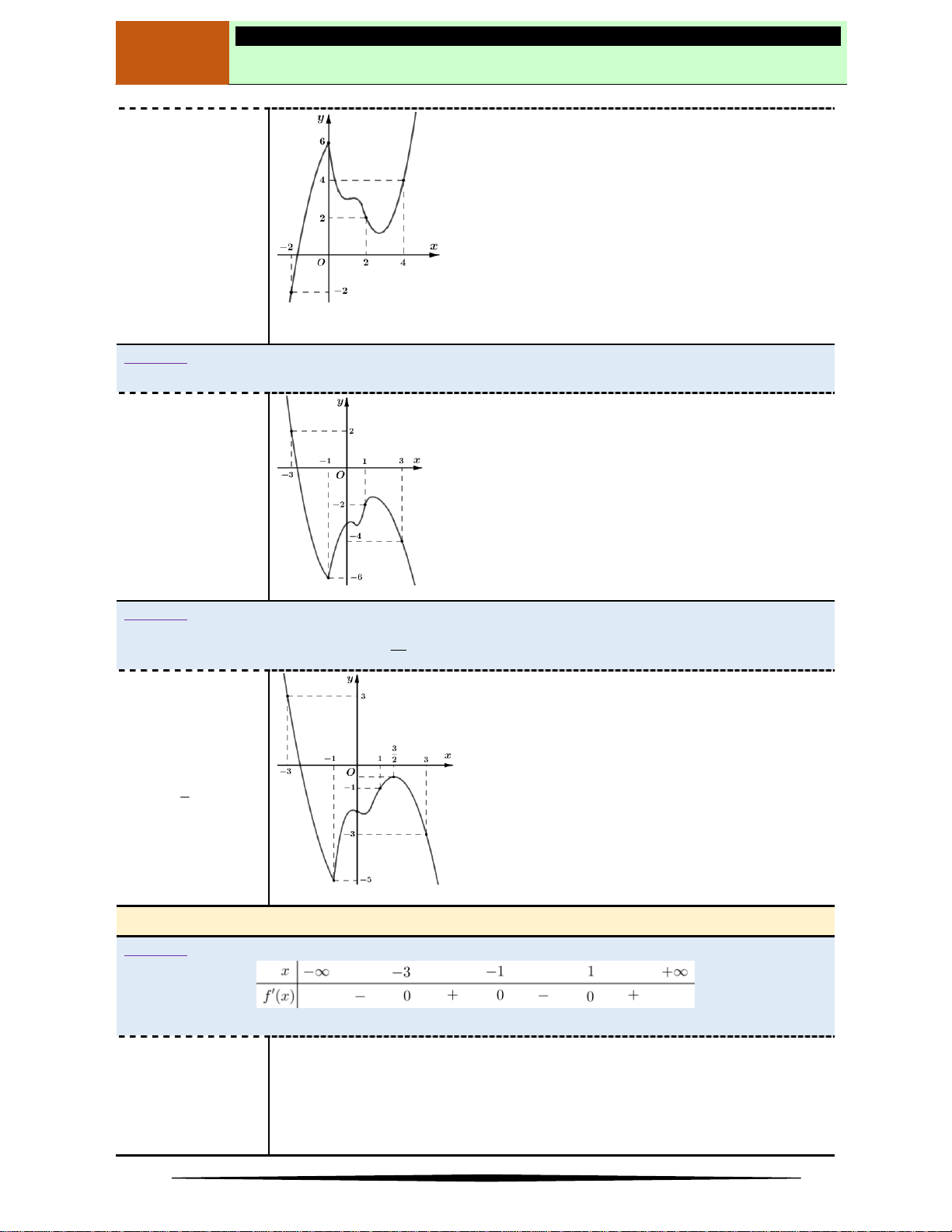
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 136

Ⓐ

( ; 2). 

Ⓑ

( 2;2).

Ⓒ

(2;4).

Ⓓ

(2; ).

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................................................................................

Ví dụ 12.

Cho hàm số

( )y f x

có đạo hàm liên tục trên

.

Đồ thị hàm số

( )y f x





như hình bên dưới.

Hỏi hàm số

2

( ) 2 ( ) ( 1)

g x f x x

  

đồng biến trên khoảng nào trong các khoảng sau?

Ⓐ

( 3;1).

Ⓑ

(1;3).

Ⓒ

( ; 3).

Ⓓ

(3; ).

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

Ví dụ 13.

Cho hàm số

( )y f x

có đạo hàm liên tục trên

.

Đồ thị hàm số

( )y f x





như hình bên dưới.

Hỏi hàm số

2

( ) (1 )

2

x

g x f x x   

nghịch biến trên khoảng nào trong các khoảng sau?

Ⓐ

( 3;1).

Ⓑ

( 2; 0).

Ⓒ

3

1; .

2

 



















 

Ⓓ

(1;3).

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

................................................................................................................................................................

................................

c) Cho baûng bieán thieân. Hoûi khoaûng ñôn ñieäu cuûa haøm soá

( ) .f u x

 

 

 

Ví dụ 14. Cho hàm số

( )f x

, bảng xét dấu của

( )f x



như sau:

Hàm số

(3 2 )y f x 

nghịch biến trên khoảng nào dưới đây?

Ⓐ

(4; ).

Ⓑ

( 2;1).

Ⓒ

(2;4).

................................................................................................................................................................................................................................................................................................

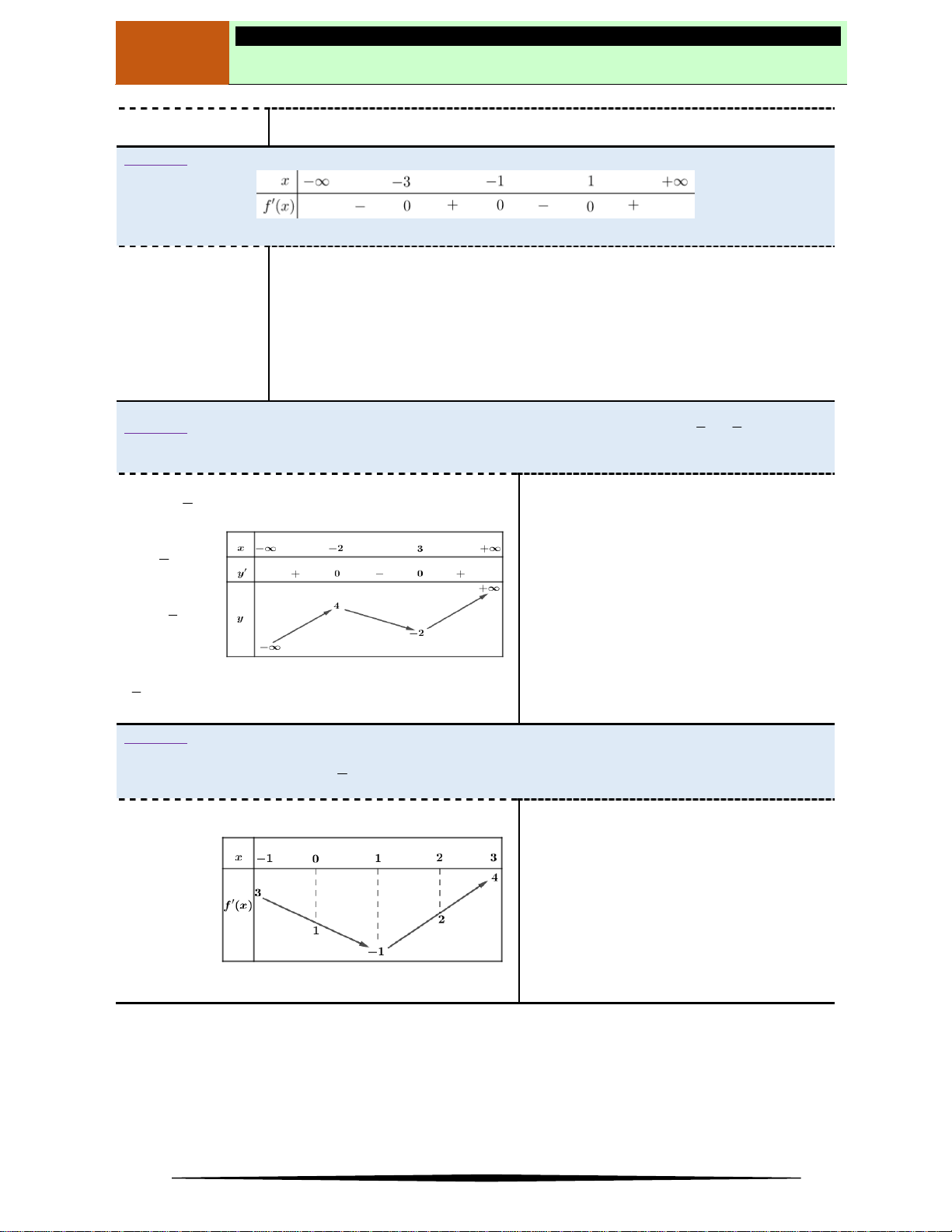
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 137

Ⓓ

(1;2).

................................................................................................................................................................................................................................................................................................

Ví dụ 15.

Cho hàm số

( )f x

, bảng xét dấu của

( )f x



như sau:

Hàm số

(5 2 )y f x 

đồng biến trên khoảng nào dưới đây?

Ⓐ

( ; 3). 

Ⓑ

(4;5).

Ⓒ

(3; 4).

Ⓓ

(1; 3).

................................................................................................................................................................................................................................................................................................

Ví dụ 16. Cho hàm số

( )f x

có bảng biên thiên như hình vẽ. Hàm số

 

2

5 3

2

2 2

g x f x x

 







  











 

ng

ịch biến

trên khoảng nào trong các khoảng sau?

Ⓐ

1

1; .

4

 



















 

Ⓑ

1

;1 .

4

 

















 

Ⓒ

5

1; .

4

 

















 

Ⓓ

9

; .

4

 



















 

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

Ví dụ 17.

Cho hàm số

( )f x

có đạo hàm liên tục trên

.

Bảng biến thiên của hàm số

( )f x



như hình vẽ.

Hàm số

( ) 1

2

x

g x f x

 







  











 

nghịch biến trên khoảng nào trong các khoảng sau?

Ⓐ

( 4; 2). 

Ⓑ

( 2;0).

Ⓒ

(0;2).

Ⓓ

(2;4).

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

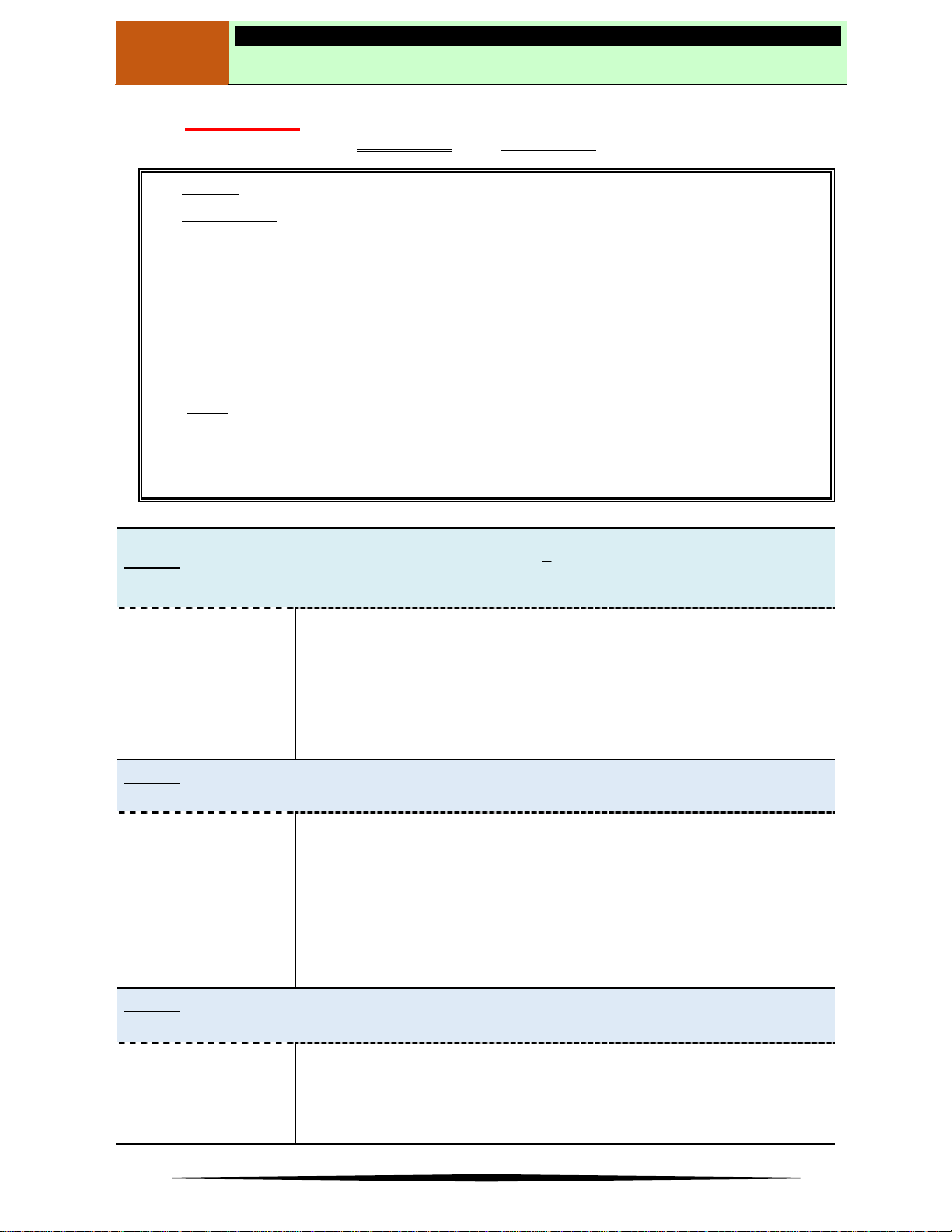
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 138

Daïng toaùn 2.1. Tìm tham soá m ñeå haøm soá ñaït cöïc trò taïi ñieåm x = x

o

cho tröôùc



 Bài toán. Tìm tham số để hàm số

( )y f x

đạt cực trị tại điểm

?

x x





 Phương pháp:



Bước 1. Tìm tập xác định

D .

Tính đạo hàm

y



và

.y





Bước 3. Dựa vào nội dung định lí 3:

Giả sử

( )y f x

có đạo hàm cấp

2

trong khoảng

( ; ),x h x h

 

 

với

0.h 

Nếu

( ) 0, ( ) 0

y x y x

 

 

 

thì

x



là điểm cực tiểu.

Nếu

( ) 0, ( ) 0

o o

y x y x

 

 

thì

x



là điểm cực đại.



Bước 4. Với

m

vừa tìm, thế vào hàm số và thử lại.

 Lưu ý. Nếu đề bài yêu cầu tìm giá trị cực trị tương ứng, ta sẽ thế

, ?

x x m

 



vào

( ).y f x

Còn nếu đề bài yêu cầu xác định tại đó là điểm cực đại hay cực tiểu, ta thế

, ?

x x m

 



vào

,y



nếu giá trị

( ) 0

y x x x



  

 

là điểm cực tiểu và nếu

( ) 0

y x x x



  

 

là điểm cực đại.

Ví dụ 1. Tìm giá trị thực của tham số

m

để hàm số

3 2 2

1

( 4) 3

3

y x mx m x

    

đạt cực đại tại

3.x 

Ⓐ

1.m 

Ⓑ

1.m  

Ⓒ

5.m 

Ⓓ

7.m  

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 2. Tìm tất cả các giá trị của tham số

m

để hàm số

3 2 2

2 2y x mx m x   

đạt cực tiểu tại

1.x 

Ⓐ

1.m 

Ⓑ

3.m 

Ⓒ

1m 

hoặc

3.m 

Ⓓ

1.m  

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 3. Tìm tập hợp giá trị của tham số

m

để hàm số

3 2 2

( 2 3) 1y x mx m m x      

đạt cực đại

tại

0.x 

Ⓐ

{1}.

Ⓑ

{ 3;1}.

Ⓒ

{ 1}.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

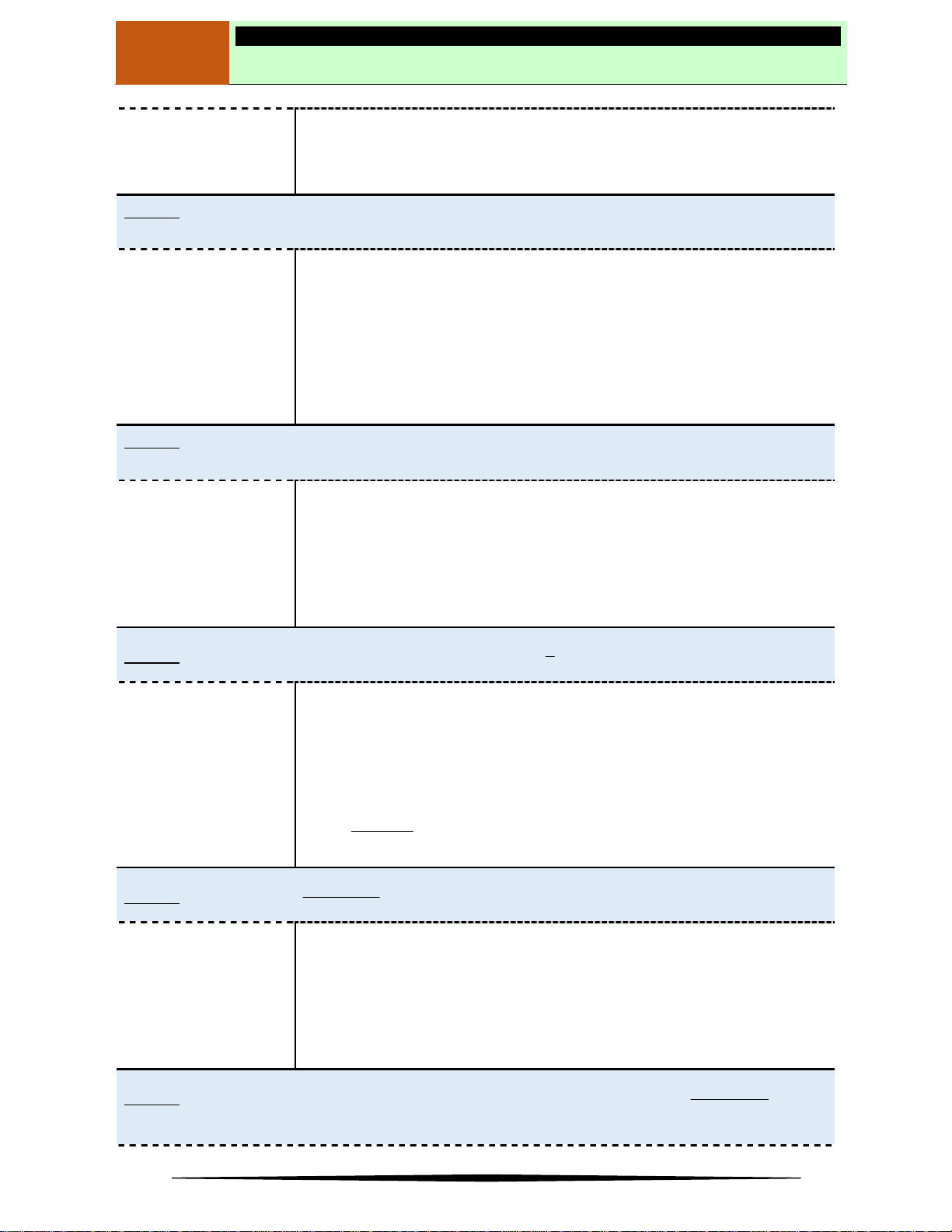
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 139

Ⓓ

{ 3}.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 4. Tìm tất cả các giá trị của tham số

m

để hàm số

3 2 2

3 (6 3)y x mx m x   

đạt cực trị tại

1.x 

Ⓐ Không có

.m

Ⓑ

0.m 

Ⓒ

1.m 

Ⓓ

0m 

hoặc

1.m 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 5. Tìm tất cả các giá trị của tham số

m

để hàm số

4 2 4

2 2 5y x mx m m    

đạt cực tiểu tại

1.x  

Ⓐ

1.m  

Ⓑ

1.m 

Ⓒ

1.m 

Ⓓ

1.m  

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 6. Tìm tất cả các giá trị của tham số

m

để hàm số

4

1

( 1)

4

y m x

 

đạt cực đại tại

0.x 

Ⓐ

1.m 

Ⓑ

1.m 

.m

Ⓓ

1.m 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................



Nhận xét:

................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................................................

......................

Ví dụ 7. Để hàm số

2

1

x mx

y

x m

 





đạt cực đại tại

2x 

thì tham số

m

thuộc khoảng nào sau đây ?

Ⓐ

(0;2).

Ⓑ

( 4; 2). 

Ⓒ

( 2; 0).

Ⓓ

(2;4).

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 8. Tìm tập hợp tất cả các giá trị của tham số thực

m

sao cho hàm số

2 2

1

x x m

y

x

 





đạt cực

đại tại

1.x 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 140

Ⓐ

{ 2}.

Ⓑ

{2}.

Ⓒ

{ 2;2}.

Ⓓ

.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 141

Daïng toaùn 2.2. Tìm tham soá m ñeå haøm soá coù n cöïc trò



 Bài toán. Tìm tham số

m

để hàm số

( )y f x

có

n

cực trị?

 Phương pháp: Hàm số có

n

cực trị khi

0y





có

n

nghiệm phân biệt.

 Xét hàm số bậc ba

3 2

.y ax bx cx d

   

Ta có

2

3 2y ax bx c



  

và lập biệt số

2

3 .b ac



  



Hàm số không có cực trị khi

0y





có nghiệm kép hoặc vô nghiệm

2

3 0.b ac  



Hàm số có

2

cực trị khi

0y





có

2

nghiệm phân biệt

2

0

3 0

a

b ac









 







   





Khi đó gọi

1 2

, x x

1 2

( )x x



là

2

nghiệm của

0.y







Nếu

0 :a 

C

Đ

(x

bên trái

CT

).

x



Nếu

0 :a 

CT

(x

bên trái

CĐ

).

x

 

1

x

2

x



x

 

1

x

2

x



y





0



0



y





0



0



y

C

Đ

y

CT

y

C

Đ

y

CT

y

 Xét hàm số bậc bốn trùng phương

4 2

, ( 0).

y ax bx c a   

Ta có:

3 2

4 2 2 (2 ) 0 0

y ax bx x ax b x



      

hoặc

2

b

x

a

  



Khi phương trình

2

b

x

a

 

có nghiệm

0

hoặc vô nghiệm thì

y

có

1

cực trị.



Nếu

0

ab

a



















(có

CT

,x

không

CĐ

).

x



Nếu

0

ab

a



















(có

C

Đ

,x

không

CT

).

x

 

0



x

 

0



y





0



y





0



y

CT

y

C

Đ

y



Khi

2

0 0 0

2 2

b b

x ab

a a

      

thì

0y





có

3

nghiệm phân biệt.



Nếu

0 :a 

(có

1

CĐ,

2

CT)



Nếu

0 :a 

(có 2CĐ,

1

CT)

x

 

1

x

0

2

x



x

 

1

x

0

2

x



y





0



0



0



y





0



0



0



y

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 142

Ví dụ 1. Cho hàm số

3 2 2

1

( 1) (3 4 1) .

3

y x m x m m x m

      

Biết rằng nếu hàm số có cực đại cực,

cực tiểu thì giá trị của tham số thực

( ; ).m a b

Tính tổng

.S a b 

Ⓐ

1.S 

Ⓑ

2.S 

Ⓒ

3.S  

Ⓓ

5.S 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2. Cho hàm số

3 2

( 2) 3 5.y m x x mx    

Có bao nhiêu giá trị nguyên của tham số

m

để đồ

thị hàm số đã cho có điểm cực đại nằm bên trái điểm cực tiểu.

Ⓐ

3.

Ⓑ Vô số.

Ⓒ

2.

Ⓓ

4.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3. Cho hàm số

3 2

1

( 1) 7.

3

y mx m x mx

    

Biết rằng nếu đồ thị hàm số có điểm cực tiểu

nằm bên trái điểm cực đại thì

( ; ).m a b

Tính

.P b a 

Ⓐ

1

2

P

 

Ⓑ

2.P 

Ⓒ

3

2

P

 

Ⓓ

2

3

P

 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4. Có bao nhiêu giá trị nguyên của

m

để hàm số

3 2

2 ( 2) (6 3 )y x m x m x    

không có cực

trị ?

Ⓐ Vô số.

Ⓑ

4.

Ⓒ

18.

Ⓓ

19.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 5. Tìm tập hợp tất cả các giá trị thực của tham số

m

để hàm số

4 2

( 1) 4y x m x   

có ba

điểm cực trị ?

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 143

Ⓐ

1.m 

Ⓑ

1.m 

Ⓒ

1.m  

Ⓓ

1.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 6. Tìm tất cả các tham số thực

m

để hàm số

4 2

2( 1) 2y mx m x   

có

2

điểm cực tiểu và

1

điểm cực đại ?

Ⓐ

0.m 

Ⓑ

0 1.m 

Ⓒ

2.m 

Ⓓ

1 2.m 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 7. Tìm tập hợp của tham số

m

để hàm số

4 2 2

( 9) 1

y m x m x

   

có

2

điểm cực đại và

1

điểm cực tiểu ?

Ⓐ

( 3; 0).

Ⓑ

(0; 3).

Ⓒ

( ; 3). 

Ⓓ

(3; ).

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 8. Tìm tập hợp các giá trị của tham số

m

để đồ thị hàm số

4 2

(2 1) 2y mx m x m    

chỉ

có một cực đại và không có điểm cực tiểu ?

Ⓐ

1

( ;0] ;

2

m

 







    











Ⓑ

( ;0].m  

Ⓒ

1

( ; 0] ;

2

m

 







    











 

Ⓓ

1

;

2

m

 





  











................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 9. Tìm tập hợp các giá trị của tham số

m

để hàm số

4 2

1

( 2) ( 1) 5

6

y m x m x

    

có đúng

một cực tiểu ?

Ⓐ

[ 2;1).

Ⓑ

( ; 2]. 

Ⓒ

( ;1].

Ⓓ

( ; 2). 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 144

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................



Nhận xét:

................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................................................

......................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 145

Daïng toaùn 2.3. Phöông trình ñöôøng thaúng noái hai ñieåm cöïc trò



 Phương trình đường thẳng nối hai điểm cực trị hàm số

3 2

.y ax bx cx d   

Để viết phương trình đường thẳng nối

2

điểm cực trị của hàm số bậc ba, thường dùng phương

pháp tách đạo hàm (phần dư bậc nhất trong phép chia

y

cho

),y



nghĩa là:



Phân tích (bằng cách chia đa thức

y

cho

)y



:

1 1

2 2

( )

. ( ) ( )

( )

y h x

y y q x h x

y h x











   













Đường thẳng qua 2 điểm cực trị là

: ( ).d y h x

 Phương trình đường thẳng nối hai điểm cực trị hàm số

2

ax bx c

y

dx e

 

 



Đường thẳng nối hai điểm cực trị có dạng

2

( )

2

:

( )

ax bx c

a b

d y x

dx e d d



 

   





 Lưu ý: Cho hai đường thẳng

1 1 1

:

d y a x b 

và

2 2 2

: .d y a x b 

1 2

a a

d d

b b









 











 

1 2 1 2

1.

d d a a

   



Ví dụ 1. Biết rằng đồ thị của hàm số

3 2

3 9 1y x x x   

có hai điểm cực trị

A

và

.B

Hỏi điểm nào

dưới đây thuộc đường thẳng

?AB

Ⓐ

(1; 0).P

Ⓑ

(0; 1).M 

Ⓒ

(1; 10).N 

Ⓓ

( 1;10).Q 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 2. Tìm

m

để đường thẳng nối điểm cực đại với điểm cực tiểu của đồ thị hàm số

3

y x x m  

đi qua điểm

(3; 1).M 

Ⓐ

1.m 

Ⓑ

1.m  

Ⓒ

0.m 

Ⓓ Một giá trị kháⒸ

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 3. Tìm giá trị thực của tham số

m

để đường thẳng

: (2 1) 3d y m x m   

vuông góc với

đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

3 2

3 1.y x x  

Ⓐ

3

2

m

 

Ⓑ

3

4

m

 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 146

Ⓒ

1

2

m

  

Ⓓ

1

4

m

 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 4. Tìm giá trị thực của tham số

m

sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm

số

3 2

3 2y x x mx   

song song với đường thẳng

: 4 3 0.d x y  

Ⓐ

1.m 

Ⓑ

2.m 

Ⓒ

3.m 

Ⓓ

4.m 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 5. Có bao nhiêu giá trị của tham số

m

để khoảng cách từ điểm

(0; 3)M

đến đường thẳng đi qua

hai điểm cực trị của đồ thị hàm số

3

3 1y x mx  

bằng

2 5

?

5

Ⓐ

1.

Ⓑ

0.

Ⓒ

2.

Ⓓ Vô số.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Cần nhớ: Công thức tính ghoảng cách từ

( ; )M x y

 

đến đường

thẳng

: 0d ax by c  

:

.................................

;

....................

d M d

 

 

 

 

Ví dụ 6. Đồ thị hàm số

2

3 5

2

x x

y

x

 





có hai điểm cực trị

, A B

nằm trên đường thẳng

d

có phương

trình

: .d y ax b 

Tính

.a b

Ⓐ

1.a b  

Ⓑ

1.a b 

Ⓒ

3.a b 

Ⓓ

5.a b 

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 7. Cho hàm số

2

2 1

mx x m

y

x

  

 



Tìm tham số

m

để đường thẳng nối hai điểm cực trị của

đồ thị hàm số này vuông góc với đường phân giác của góc phần tư thứ nhất trong mặt

phẳng tọa độ.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 147

Ⓐ

0.m 

Ⓑ

1.m 

Ⓒ

1.m  

Ⓓ

1

2 .m





................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Cần nhớ: Phương trình góc phần tư thứ (I), (III):

.........................................

, góc phần tư

(II), (IV)

..........................................

Daïng toaùn 2.4. Bieän luaän hoaønh ñoä cöïc trò



 Bài toán 1: Cho hàm số

3 2

( ; ) .y f x m ax bx cx d    

Tìm tham số

m

để đồ thị hàm số có

2

điểm cực trị

1 2

, x x

thỏa mãn điều kiện

K

cho trước ?

 Phương pháp:

— Bước 1. Tập xác định

. D

Tính đạo hàm:

2

3 2 .y ax bx c



  

— Bước 2. Để hàm số có

2

cực trị

0y



 

có

2

nghiệm phân biệt

2

0

3 0

a

b ac

















   





và giải hệ này sẽ tìm được

1

.

m

 D

— Bước 3. Gọi

1 2

, x x

là

2

nghiệm của phương trình

0.y





Theo Viét, ta có:

1 2

b

S x x

a

   

và

1 2

c

P x x

a

  

— Bước 4. Biến đổi điều kiện

K

về dạng

S

và

.P

Từ đó giải ra tìm được

2

.

m 

D

— Bước 5. Kết luận các giá trị

m

thỏa mãn:

1 2

.

m  

D D

 Bài toán 2: Khảo sát hàm số bậc bốn trùng phương

4 2

( ; ) .y f x m ax bx c   

— Bước 1. Ta có:

3 2

4 2 2 (2 ).y ax bx x ax b



   

Cho

2

0

( ) 2 0

x y c

y

g x ax b



  





  



  





— Bước 2. Hàm số có

3

điểm cực trị

( ) 0g x 

có hai nghiệm phân biệt

0

1

0

.

. 0

b

m

a b









  











D

— Bước 3. Giải

1,2 1 2

( ) 0

2 2

b b

g x x y y f

a a

 









         













 

Do đó tọa độ ba điểm cực trị sẽ là:

1 1 2 2

(0; ), ( ; ), ( ; )A c B x y C x y

và do tính đối xứng

nên tam giác

ABC

luôn cân tại

.A

— Bước 4. Dựa vào điều kiện đề bài cho để tìm

2 1 2

.

m m

   D D D

Ví dụ 1. Tìm tất cả các giá trị của tham số

m

sao cho hàm số

3 2

1

3

y x mx x m

    

có hai điểm

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 148

cực trị

1

x

và

2

x

thỏa mãn điều kiện

2 2

1 2

2.

x x

 

Ⓐ

0.m 

Ⓑ

1.m  

Ⓒ

3.m  

Ⓓ

2.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2. Cho hàm số

3 2

1

( 1) ( 2) ( 3) 1.

3

y m x m x m x

      

Hỏi tham số

m

nằm trong khoảng nào

sau đây thì hàm số có

2

điểm cực trị

1 2

, x x

thỏa

1 2

(4 1)(4 1) 18.

x x  

Ⓐ

( 1;1).m  

Ⓑ

(5; ).m  

Ⓒ

(6;10).m 

Ⓓ

(7; ).m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3. Tìm tất cả các giá trị của tham số

m

sao cho hàm số

3 2

1 1

( 5)

3 2

y x m x mx

   

có cực đại,

cực tiểu và

CĐ CT

5.

x x

 

Ⓐ

0.m 

Ⓑ

0m 

hoặc

6.m 

Ⓒ

6m  

hoặc

0.m 

Ⓓ

6.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4. Tìm tất cả các giá trị thực của tham số

m

sao cho hàm số

3 2

4 3y x mx x  

có hai điểm cực

trị

1 2

, x x

thỏa mãn

1 2

4 .x x 

Ⓐ

9

2

m



hoặc

3

2

m

  

Ⓑ

9

2

m

 

hoặc

9

2

m

 

Ⓒ

3

2

m

 

hoặc

3

2

m

 

Ⓓ

9

2

m

 

hoặc

3

2

m

 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 5. Tìm tập hợp các giá trị của tham số

m

để hàm số

3 2 2

1

( 3) 4( 3)

3

y x m x m x m m

      

có các điểm cực trị tại

1 2

, x x

thỏa mãn điều kiện

1 2

1 .x x  

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 149

Ⓐ

( ; 2). 

Ⓑ

7

; 2

2

 







  











 

Ⓒ

7

; 3

2

 







  











 

Ⓓ

( ; 3) (1; ).   

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 6. Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

3 2 2

4 (1 ) 1y x x m x    

có hai

điểm cực trị nằm về hai phía khác nhau đối với trục tung ?

Ⓐ

1 1

3 3

m

   

Ⓑ

1m 

hoặc

1.m  

Ⓒ

1 1.m  

Ⓓ

1 1.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 7. Cho hàm số

3

3 1 .y x x m   

Tìm tất cả tham số

m

để hàm số có giá trị cực đại và giá trị

cực tiểu trái dấu.

Ⓐ

1m  

hoặc

3.m 

Ⓑ

1m  

hoặc

3.m 

Ⓒ

1 3.m  

Ⓓ

1 3.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 8. Tìm các giá trị của tham số thực

m

để đồ thị hàm số

3 2

1

( 1) 2

3

y x x m x

    

có hai điểm

cực trị đều nằm bên trái trục tung.

Ⓐ

1 2.m 

Ⓑ

1.m 

Ⓒ

2.m 

Ⓓ

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 9. Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị hàm số

3 2

1

(6 9) 12

3

y x mx m x    

có các điểm cực đại và cực tiểu nằm cùng một phía đối với

trục tung.

Ⓐ

2.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 150

Ⓑ

3

2

m

    

Ⓒ

3

; 3.

2

m m

   

Ⓓ

3

2

m

  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 10. Với giá trị nào của

m

thì hai điểm cực đại và cực tiểu của đồ thị hàm số

3 2

3 2y x x mx m    

nằm về hai phía so với

.Ox

Ⓐ

3.m 

Ⓑ

1 2.m  

Ⓒ

3.m 

Ⓓ

2 3.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 11. Gọi

S

là tập hợp tất cả các giá trị thực của tham số

m

để đồ thị của hàm số

3 2 2

1

( 1)

3

y x mx m x

   

có hai điểm cực trị là

A

và

B

sao cho

, A B

nằm khác phía và

cách đều đường thẳng

: 5 9.d y x 

Tính tổng tất cả các phần tử của

.S

Ⓐ

0.

Ⓑ

6.

Ⓒ

9.

Ⓓ

3.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 12. Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị hàm số

3 2 3

2 3( 1) 6y x m x mx m    

có hai điểm cực trị

A

và

,B

đồng thời độ dài đoạn thẳng

2.AB 

Ⓐ

2m  

hoặc

2.m 

Ⓑ

1m 

hoặc

2.m 

Ⓒ

0m 

hoặc

2.m 

Ⓓ

0m 

hoặc

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 13. Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

3

3 1y x mx  

có hai điểm cực

trị

B

và

,C

đồng thời tam giác

ABC

cân tại

(2; 3).A

Ⓐ

1

2

m

  

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 151

Ⓑ

3

2

m

  

Ⓒ

1

2

m

 

Ⓓ

3

2

m

 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 14. Tìm tất cả các giá trị thực của tham số

m

để đồ thị của hàm số

3 2 3

3 4y x mx m  

có hai

điểm cực trị

A

và

B

sao cho tam giác

OAB

có diện tích bằng

4,

với

O

là gốc tọa độ.

Ⓐ

4

1

2

m  

hoặc

4

1

2

m

 

Ⓑ

1m  

hoặc

1.m 

Ⓒ

1.m 

Ⓓ

0.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 15. Tìm các giá trị của tham số thực

m

để đồ thị hàm số

3 2

3 1y x mx  

có hai điểm cực trị

A

và

B

sao cho tam giác

OAB

có diện tích bằng

1, (O

là gốc tọa độ).

Ⓐ

3.m  

Ⓑ

1.m  

Ⓒ

5.m  

Ⓓ

2.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 16. Tìm các giá trị thực của

m

sao cho hàm số

3 2 2

3 2y x x m m   

có giá trị cực tiểu bằng

4.

Ⓐ

2.m 

Ⓑ

0m 

hoặc

2.m  

Ⓒ

1m 

hoặc

2.m 

Ⓓ

2m 

hoặc

3.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 17. Tìm tất cả các giá trị thực của tham số

m

sao cho hàm số

4 2 2

2 2 1y x mx m   

có giá trị

cực tiểu bằng

2.

Ⓐ

1

2

m 

hoặc

1.m 

Ⓑ

1m  

hoặc

0.m 

Ⓒ

1

2

m 

hoặc

1.m  

Ⓓ

1m  

hoặc

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 18. Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

3 2

2( 1) (4 1)y x m x m x    

có

hai điểm cực trị cách đều trục tung.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 152

Ⓐ

1.m  

Ⓑ

1.m 

Ⓒ

1.m  

Ⓓ

0.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 19. Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị của hàm số

4 2

2 1y x mx  

có ba

điểm cực trị tạo thành một tam giác vuông cân.

Ⓐ

3

1

9

m

  

Ⓑ

1.m  

Ⓒ

3

1

9

m

 

Ⓓ

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 20. Với

m

là một tham số thực sao cho đồ thị hàm số

4 2

2 1y x mx  

có ba điểm cực trị tạo

thành một tam giác vuông. Mệnh đề nào dưới đây đúng ?

Ⓐ

2.m 

Ⓑ

2 0.m  

Ⓒ

2.m  

Ⓓ

0 2.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 21. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số

4 2

4( 1) 2 1

y x m x m

    

có ba

điểm cực trị là ba đỉnh của một tam giác có số đo một góc bằng

120 .

Ⓐ

3

1

24

m

  

Ⓑ

3

1

16

m

  

Ⓒ

3

1

48

m

  

Ⓓ

3

1

2

m

  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 22. Tìm tham số thực

m

để đồ thị hàm số

4 2

2( 1) 2 5

y x m x m

    

có ba điểm cực trị lập thành

tam giác đều ?

Ⓐ

1.m 

Ⓑ

3

1 3.m  

Ⓒ

3

1 3.m  

Ⓓ

1 3.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 153

Ví dụ 23.

Tìm tập hợp tất cả các giá trị thực của tham số

m

sao cho tất cả các điểm cực trị (nếu có) của

đồ thị hàm số

4 2

( ) ( 1) 1

f x m x m x m

    

nằm trên các trục tọa độ.

Ⓐ

1

0; { 1}

3

 

 

  

 

 

Ⓑ

1

1;

3

 

 

 

 

 

Ⓒ

1

0; 1;

3

 

 

 

 

 

 

Ⓓ

1

1;0

3

 

 

 

  

 

 

 

 

 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 24. Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

4 2

2 4y x mx  

có

3

điểm cực

trị nằm trên các trục tọa độ.

Ⓐ

2.m 

Ⓑ

2m  

hoặc

2.m 

m

nào.

Ⓓ

2.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 25. Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

4 2 4

2 2y x mx m m   

có ba cực

trị, đồng thời ba tọa độ ba điểm cực trị này tạo thành một tam giác có diện tích bằng

2.

Ⓐ

5

4.m 

Ⓑ

16.m 

Ⓒ

5

16.m 

Ⓓ

3

16.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 26. Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

4 2

2y x mx 

có ba điểm cực trị

tạo thành một tam giác có diện tích nhỏ hơn

1.

Ⓐ

0.m 

Ⓑ

1.m 

Ⓒ

3

0 4.m 

Ⓓ

0 1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 27. Tìm tất cả các giá trị thực của tham số

m

để đồ thị của hàm số

4 2

2 1y x mx  

có ba điểm

cực trị là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng

1.

Ⓐ

1m 

hoặc

1 5

2

m

 

 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

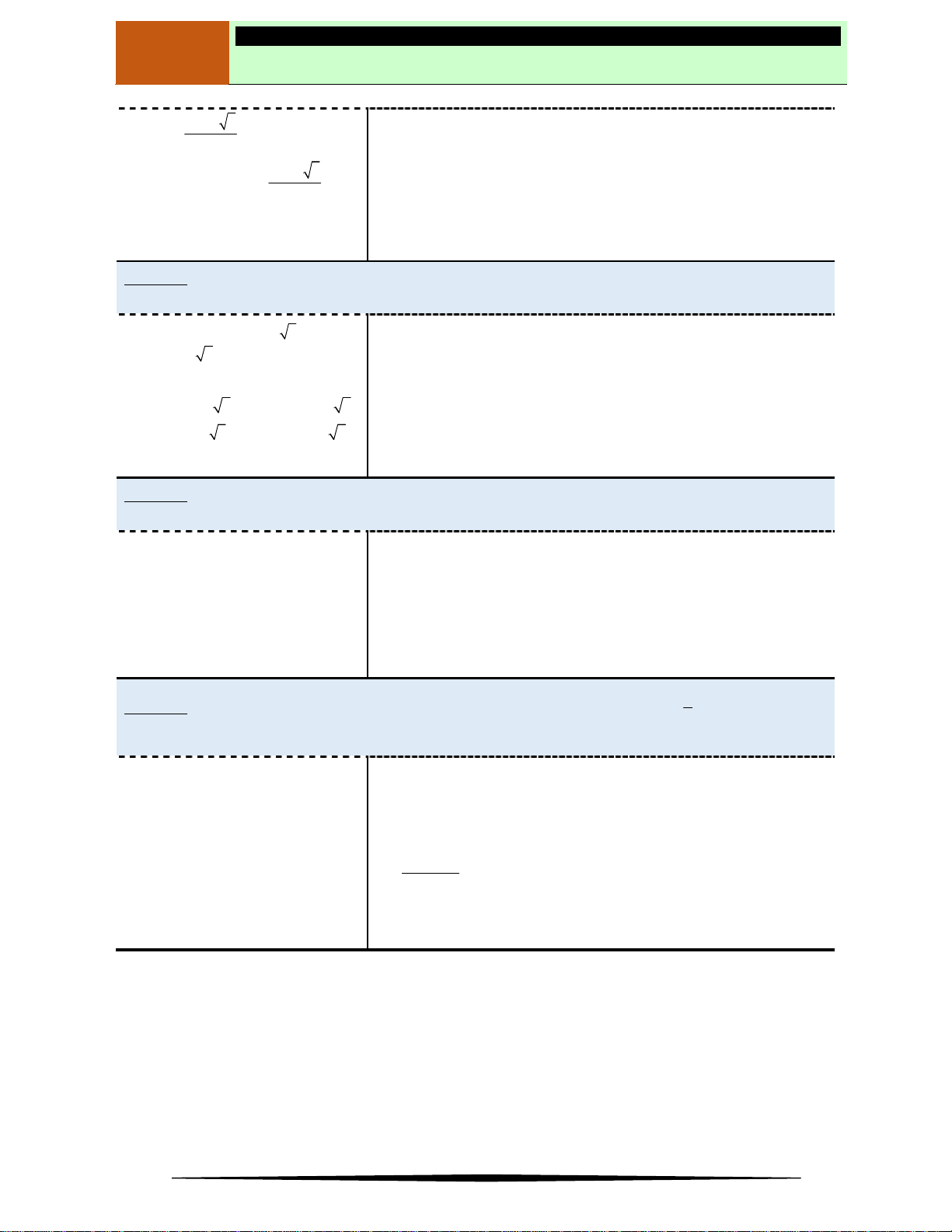
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 154

Ⓑ

1 5

2

m

 

 

Ⓒ

1m 

hoặc

1 5

2

m

 

 

Ⓓ

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 28. Tìm tất cả các giá trị thực của tham số

m

để đồ thị của hàm số

4 2

2 1y x mx m   

có ba

điểm cực trị cùng với gốc tọa độ tạo thành bốn đỉnh của một hình thoi.

Ⓐ

1 2m  

hoặc

1 2.m   

Ⓑ Không có giá trị

.m

Ⓒ

4 2m  

hoặc

4 2.m  

Ⓓ

2 2m  

hoặc

2 2.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 29. Cho hàm số

4 2

2 1 .y x mx m   

Tìm tất cả các giá trị thực của

m

để đồ thị hàm số có ba

điểm cực trị tạo thành một tam giác nhận gốc tọa độ

O

làm trực tâm.

Ⓐ

1.m 

Ⓑ

2.m 

Ⓒ

0.m 

Ⓓ

1.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 30. Gọi

( )P

là đường parabol qua ba điểm cực trị của đồ thị hàm số

4 2 2

1

.

4

y x mx m

  

Hãy

tìm

m

để

( )P

đi qua điểm

(2;24).A

Ⓐ

4.m  

Ⓑ

4.m 

Ⓒ

3.m 

Ⓓ

6.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Cần nhớ:

................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

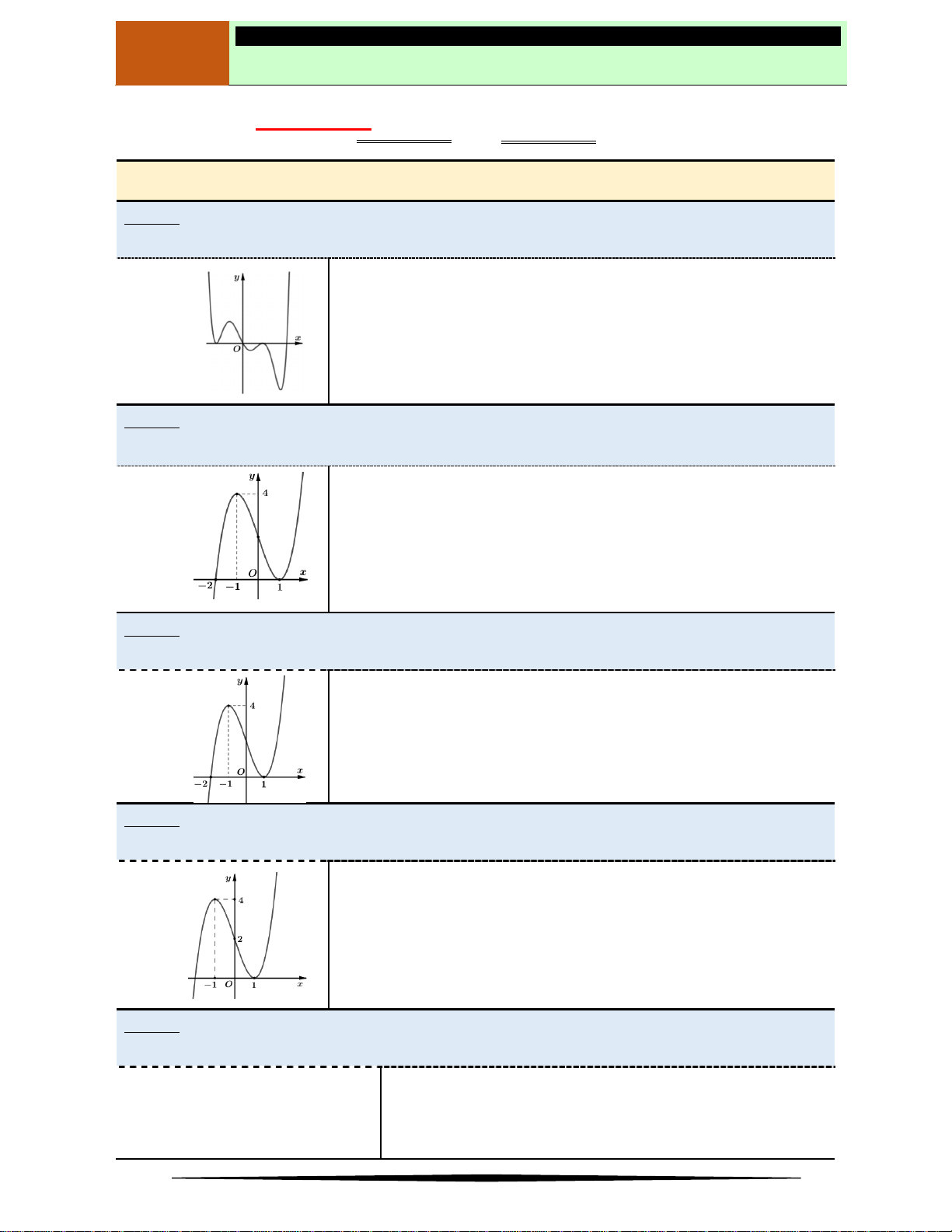
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 155

Daïng toaùn 2.5. Moät soá vaán ñeà lieân quan ñeán cöïc trò haøm aån



Vaán ñeà 1: Cho ñoà thò

( ).f x



Hoûi soá ñieåm cöïc trò cuûa haøm soá

( ) .f u x

 

 

 

Ví dụ 1. Đường cong trong hình vẽ bên dưới là đồ thị hàm số

( ).y f x





Số điểm cực trị của hàm số

( )y f x

là

Ⓐ

2.

Ⓑ

3.

Ⓒ

4.

Ⓓ

5.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 2. Cho hàm số

( ).y f x

Đồ thị hàm số

( )y f x





như hình bên. Tìm số điểm cực trị của hàm số

2

( ) ( 3).g x f x 

Ⓐ

2.

Ⓑ

3.

Ⓒ

4.

Ⓓ

5.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 3. Cho hàm số

( )y f x

có đạo hàm liên tục trên



và

(0) 0,f 

đồng thời đồ thị hàm số

( )y f x





như hình vẽ bên dưới. Số điểm cực trị của hàm số

2

( ) ( )g x f x

là

Ⓐ

1.

Ⓑ

2.

Ⓒ

3.

Ⓓ

4.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

Ví dụ 4. Cho hàm số

( )y f x

có đạo hàm trên

.

Đồ thị hàm số

( )y f x





như hình vẽ bên dưới. Số

điểm cực trị của hàm số

( ) ( 2017) 2018 2019g x f x x   

là

Ⓐ

1.

Ⓑ

2.

Ⓒ

3.

Ⓓ

4.

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

......................

................................................................................................................................................................................................................................................................

................................

Ví dụ 5. Cho hàm số

( )y f x

có đạo hàm trên

.

Đồ thị hàm số

( )y f x





như hình vẽ bên dưới. Hỏi

hàm số

( ) ( )g x f x x 

đạt cực tiểu tại điểm nào dưới đây?

Ⓐ

 0.x

Ⓑ

 1.x

Ⓒ

 2.x

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

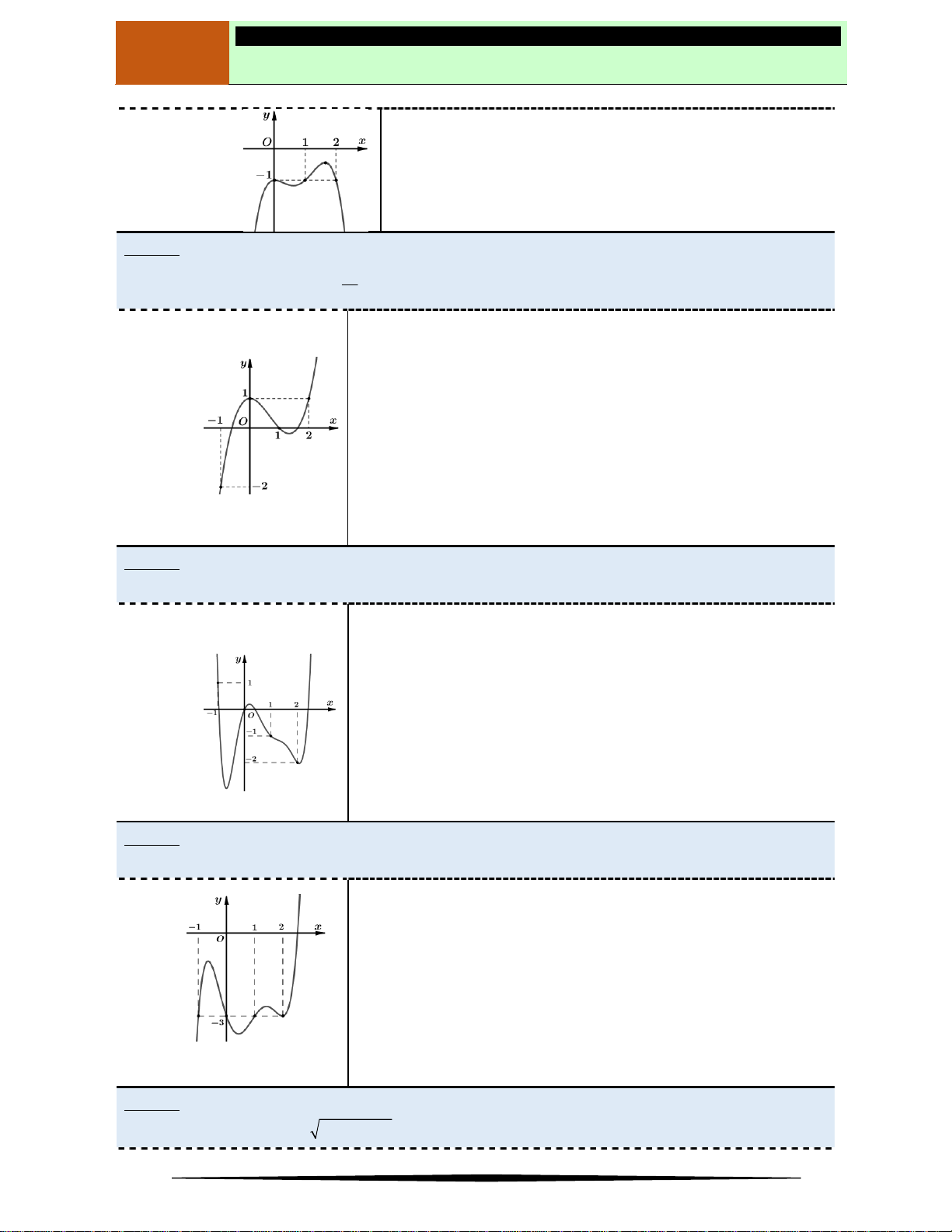
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 156

Ⓓ Không có

điểm cực tiểu.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 6. Cho hàm số

( )y f x

có đạo hàm trên

.

Đồ thị hàm số

( )y f x





như hình vẽ bên dưới.

Hàm số

3

2

( ) ( ) 2

3

x

g x f x x x

    

đạt cực đại tại

Ⓐ

1.x  

Ⓑ

0.x 

Ⓒ

1.x 

Ⓓ

2.x 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 7. Cho hàm số

( )y f x

có đạo hàm trên

.

Đồ thị hàm số

( )y f x





như hình vẽ bên dưới.

Hàm số

2

( ) 2 ( )g x f x x 

đạt cực tiểu tại điểm

Ⓐ

1.x  

Ⓑ

0.x 

Ⓒ

1.x 

Ⓓ

2.x 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 8. Cho hàm số

( )y f x

có đạo hàm trên

.

Đồ thị hàm số

( )y f x





như hình vẽ bên dưới. Hỏi

đồ thị hàm số

( ) ( ) 3g x f x x 

có bao nhiểu điểm cực trị ?

Ⓐ

2.

Ⓑ

3.

Ⓒ

4.

Ⓓ

7.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 9. Cho hàm số bậc bốn

( ).y f x

Đồ thị hàm số

( )y f x





như hình vẽ bên. Số điểm cực đại của

hàm số

2

( ) ( 2 2)g x f x x  

là

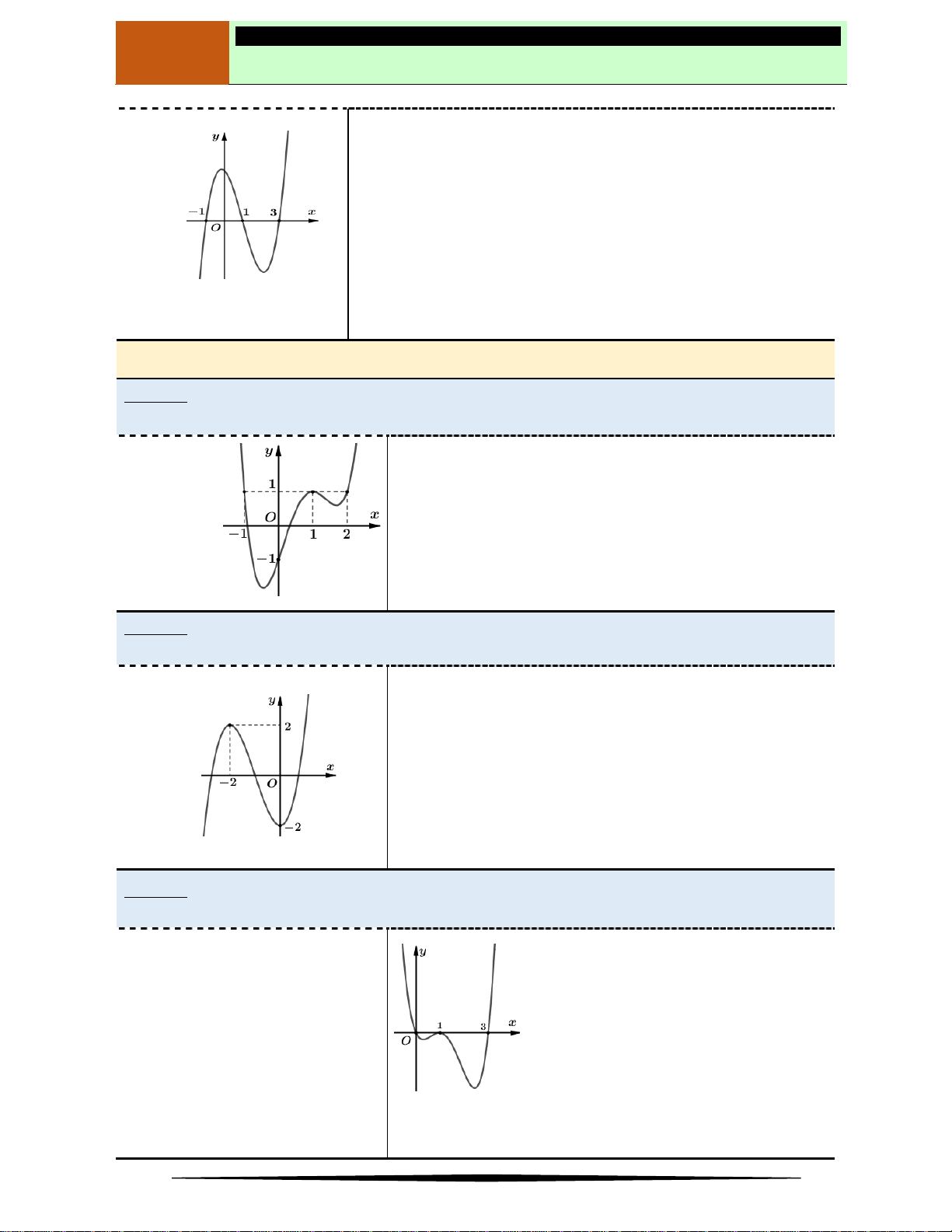
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 157

Ⓐ

1.

Ⓑ

2.

Ⓒ

3.

Ⓓ

4.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Vaán ñeà 2: Cho ñoà thò

( ).f x

Hoûi soá ñieåm cöïc trò cuûa haøm soá

( ) .f u x

 

 

 

Ví dụ 10. Cho hàm số

( )f x

xác định trên



và có đồ thị

( )f x

như hình vẽ bên dưới. Hàm số

(( ))g f x xx  

đạt cực đại tại

Ⓐ

 1.x

Ⓑ

 0.x

Ⓒ

 1.x

Ⓓ

 2.x

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 11. Cho hàm số

( )y f x

có đồ thị hàm số như hình bên. Hàm số

2

( ) ( 3 )g x f x x  

có bao nhiêu

điểm cực đại?

Ⓐ

3.

Ⓑ

4.

Ⓒ

5.

Ⓓ

6.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 12. Cho hàm số

( )y f x

có đồ thị như hình bên. Đồ thị của hàm số

2

( ) [ ( )]g x f x

có bao nhiêu

điểm cực đại, bao nhiêu điểm cực tiểu?

Ⓐ

1

điểm cực đại,

3

điểm cực tiểu.

Ⓑ

2

điểm cực đại,

2

điểm cực tiểu.

Ⓒ

2

điểm cực đại,

3

điểm cực tiểu.

Ⓓ

3

điểm cực đại,

2

điểm cực tiểu.

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

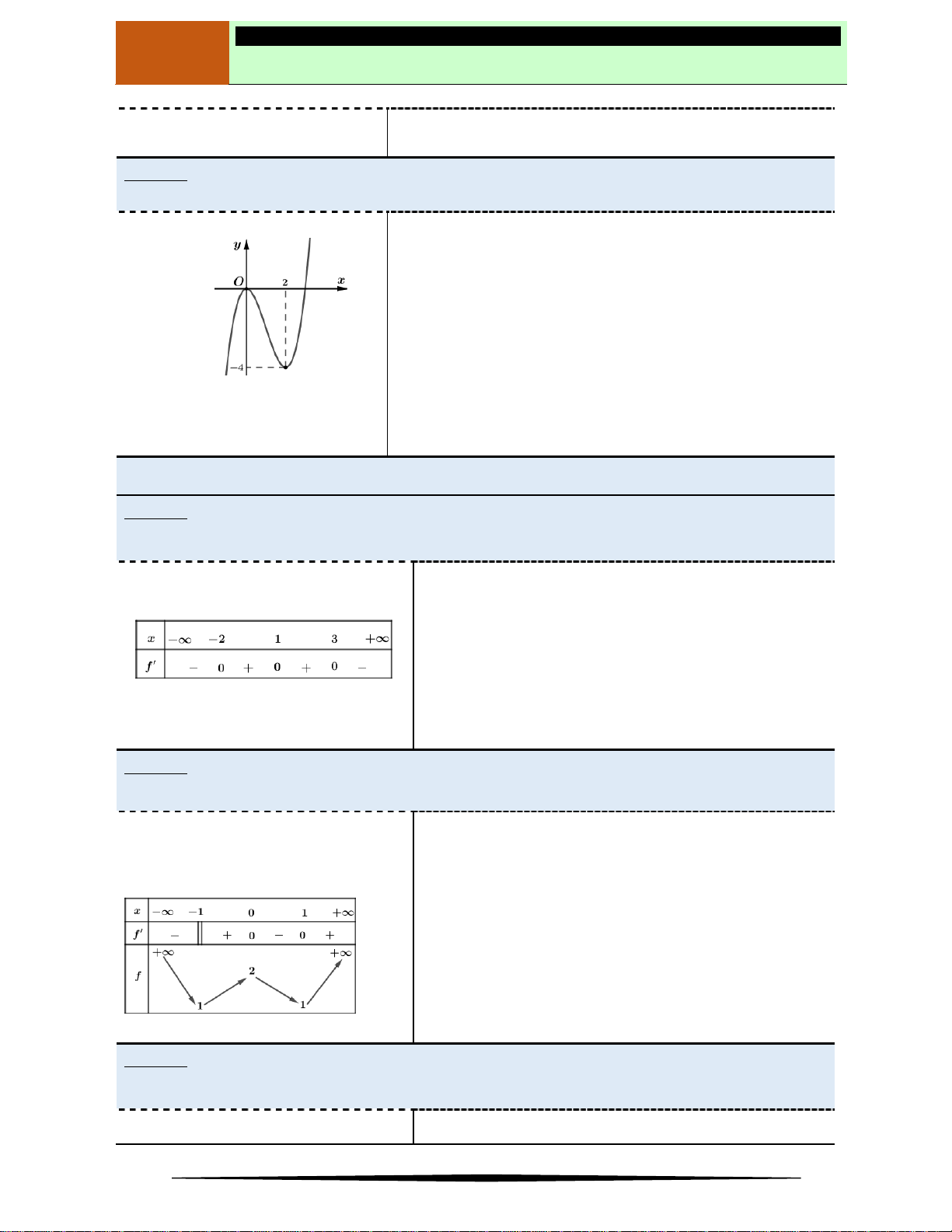
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 158

Ví dụ 13. Cho hàm số

( )y f x

có đồ thị như hình vẽ bên. Hàm số

( ) [ ( )]g x f f x

có bao nhiêu điểm cực

trị?

Ⓐ

3.

Ⓑ

4.

Ⓒ

5.

Ⓓ

6.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Vaán ñeà 3: Cho baûng bieán thieân cuûa haøm

( ).f x

Hoûi soá ñieåm cöïc trò cuûa haøm soá

( ) .f u x

 

 

 

Ví dụ 14. Cho hàm số

( )y f x

có đạo hàm trên



và có bảng xét dấu của

( )y f x





như sau

Hỏi hàm số

2

( ) ( 2 )g x f x x 

có bao nhiêu điểm cực tiểu?

Ⓐ

1.

Ⓑ

2.

Ⓒ

3.

Ⓓ

4.

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

Ví dụ 15. Cho hàm số

( )y f x

xác định, liên tục trên



và có bảng biến thiên như sau

Hàm số

( ) 3 ( ) 1g x f x 

đạt cực tiểu tại điểm nào sau đây?

Ⓐ

1.x  

Ⓑ

1.x 

Ⓒ

1.x  

Ⓓ

0.x 

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

Ví dụ 16. Cho hàm số

( )y f x

có bảng biến thiên như hình vẽ bên dưới

Hỏi hàm số

2

( ) ( 1)g x f x 

có bao nhiêu điểm cực trị?

Ⓐ

0.

Ⓑ

1.

................................................................................................................................................................................................

................................

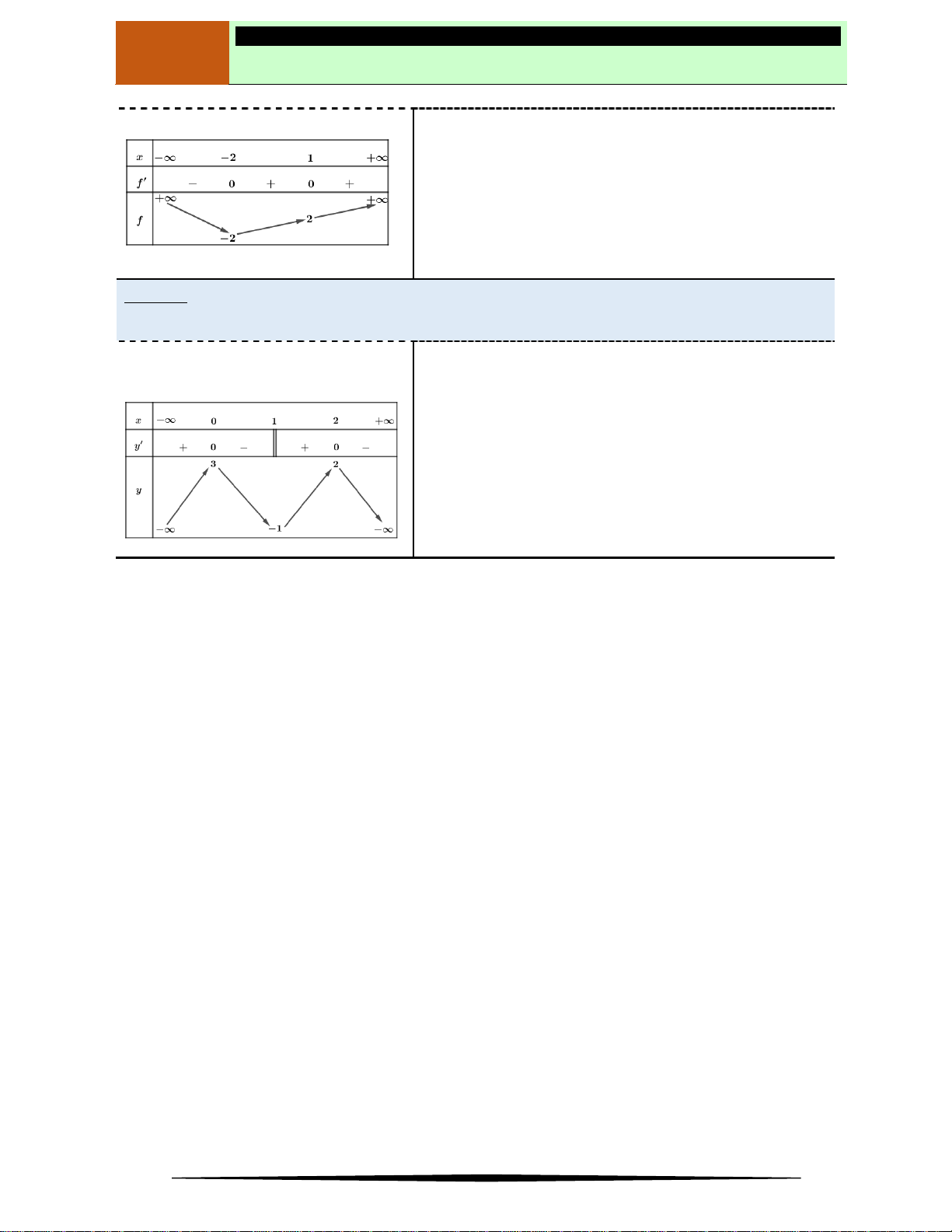
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 159

Ⓒ

2.

Ⓓ

3.

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

Ví dụ 17. Cho hàm số

( )y f x

có bảng biến thiên như sau

Tìm số điểm cực trị của hàm số

( ) (3 ).g x f x 

Ⓐ

2.

Ⓑ

3.

Ⓒ

5.

Ⓓ

6.

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

................................................................................................................................................................................................

................................

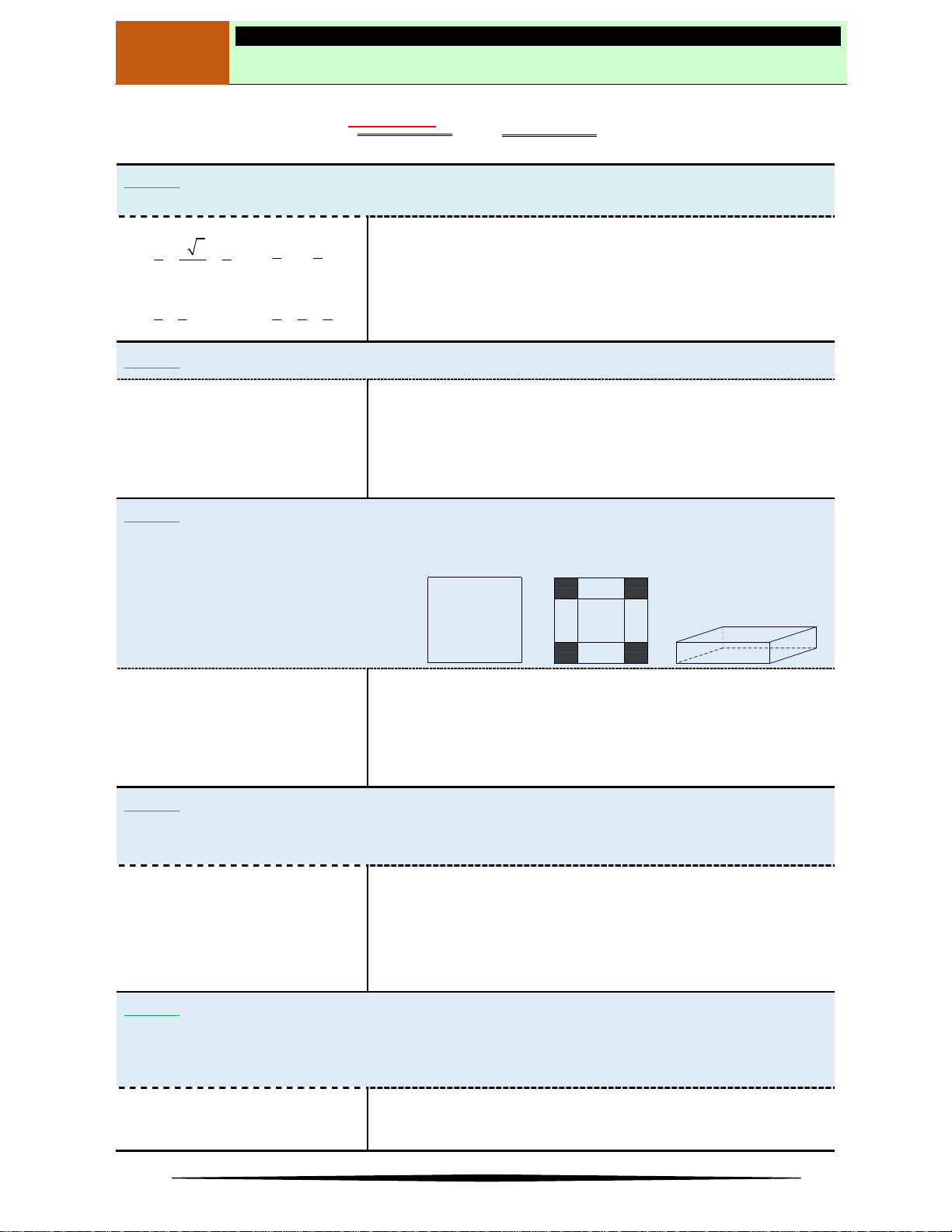
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 160

Daïng toaùn 3: ÖÙng duïng cuûa max – min



Ví dụ 1. Cho tam giác vuông có tổng một cạnh góc vuông và cạnh huyền bằng

2.

Tìm độ dài ba cạnh

của tam giác sao cho diện tích của tam giác lớn nhất.

Ⓐ

2 2 3 4

; ;

3 3 3



Ⓑ

2 4

; 1;

3 3



Ⓒ

3 4

; ; 1.

5 5

Ⓓ

2 2 4

; ;

3 3 3



................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2. Hình chữ nhật có chu vi không đổi là

8m.

Tìm diện tích lớn nhất

max

S

của hình chữ nhật đó.

Ⓐ

2

max

.4m

S 

Ⓑ

2

max

.8m

S 

Ⓒ

2

max

1

.6m

S



Ⓓ

2

max

.2m

S



................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3. Cho một tấm nhôm hình vuông cạnh

12 .cm

Người ta cắt ở bốn góc của

tấm

nhôm đó

bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng

( ),x cm

rồi gập

tấm

nhôm lại

như hình vẽ dưới đây để được một cái hộp không nắp. Tìm

x

để hộp

nhận

được có

thể tích lớn

nhất.

Ⓐ

4.x 

Ⓑ

6.x 

Ⓒ

3.x 

Ⓓ

2.x 

................................................................................................

................................

................................................................................................

................................

................................................................................................

................................

................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4. Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức

2

( ) 0, 024 (30 ),G x x x 

trong đó

x

là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp

(x

được tính bằng

mg).

Tìm lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.

Ⓐ

20 m g.

Ⓑ

0, 5 m g.

Ⓒ

2, 8 m g.

Ⓓ

15 mg.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 5. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng Nếu trên mỗi đơn vị diện

tích của mặt hồ có

n

con cá thì trung bình mỗi con cá sau một vụ cân nặng

( ) 480 20P n n 

(gam). Tính số con cá phải thả trên một đơn vị diện tích của mặt hồ để sau

một vụ thu hoạch được nhiều cá nhất.

Ⓐ

14

con.

Ⓑ

12

con.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

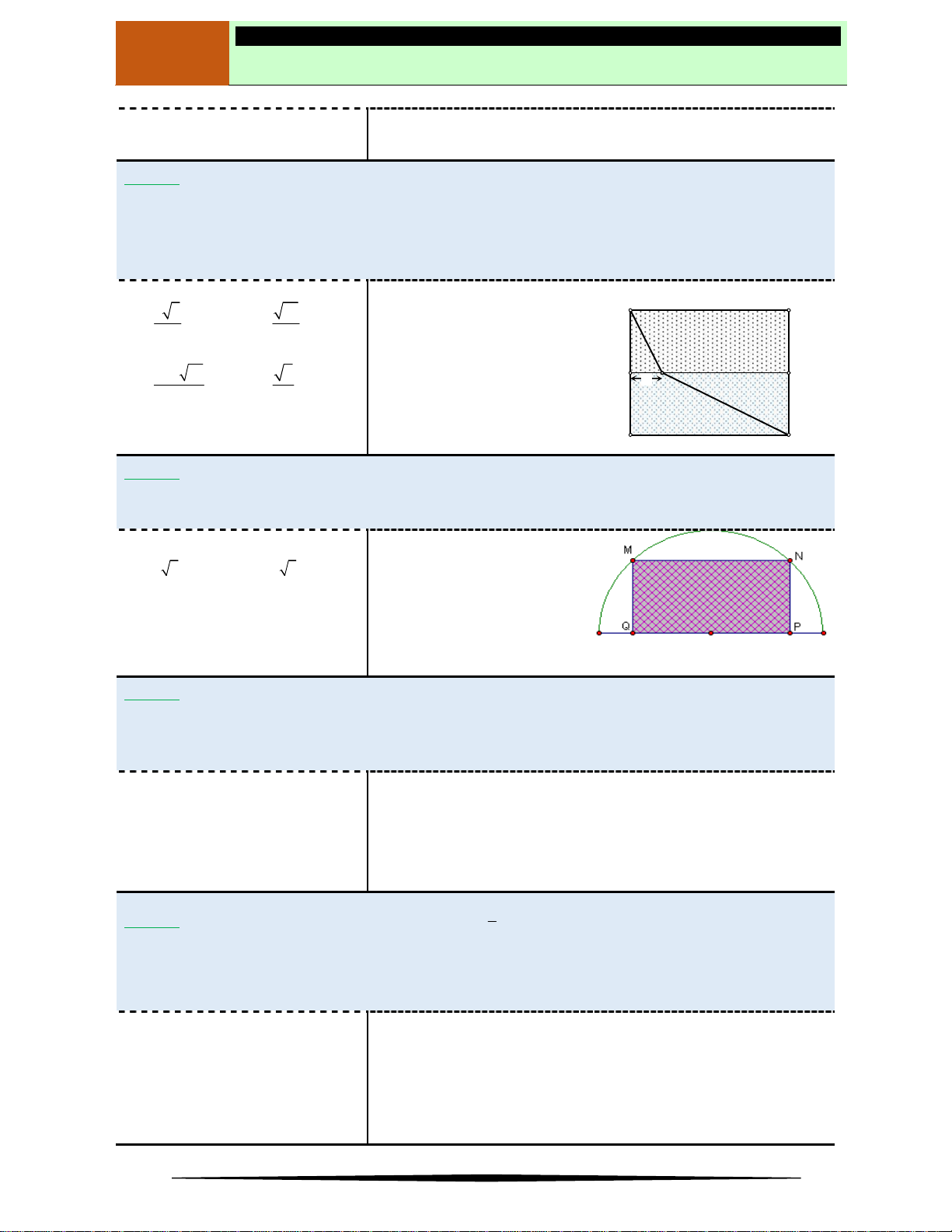
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 161

Ⓒ

15

con.

Ⓓ

13

con.

................................................................................................................................................................................................................................

................................

Ví dụ 6. Một vùng đất hình chữ nhật

ABCD

có

25 km,AB 

20 kmBC 

và

, M N

lần lượt là

trung điểm của

,AD

.BC

Một người cưỡi ngựa xuất phát từ

A

đi đến

C

bằng cách đi

thẳng từ

A

đến một điểm

X

thuộc đoạn

MN

rồi lại đi thẳng từ

X

đến

.C

Vận tốc của ngựa

khi đi trên phần

ABNM

là

15 km/h,

vận tốc của ngựa khi đi trên phần

MNCD

là

30 km/h.

Thời gian ít nhất để ngựa di chuyển từ

A

đến

C

là mấy giờ ?

Ⓐ

2 5

3



Ⓑ

41

4



Ⓒ

4 29

6





Ⓓ

5

3



................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 7. Từ một miếng tôn hình bán nguyệt có bán kính

3,R 

người ta muốn cắt ra một hình chữ

nhật (xem hình) có diện tích lớn nhất. Tìm diện tích lớn nhất có thể có của miếng tôn hình

chữ nhật.

Ⓐ

6 3.

Ⓑ

6 2.

Ⓒ

7.

Ⓓ

9.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 8. Một vật chuyển động theo quy luật

2 3

12 ,s t t 

với

t

(giây) là khoảng thời gian tính từ lúc

vật bắt đầu chuyển động và

s

(mét) là quãng đường vật đi được trong khoảng thời gian đó.

Trong khoảng thời gian

8

giây, kể từ lúc bắt đầu chuyển động, vận tốc

v

(m/s) của chuyển

động đạt giá trị lớn nhất tại thời điểm

t

(giây) bằng bao nhiêu ?

Ⓐ

4.t 

Ⓑ

3.t 

Ⓒ

6.t 

Ⓓ

2.t 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 9. Một vật chuyển động theo quy luật

3 2

1

9

2

s t t  

với

t

(giây) là khoảng thời gian tính từ

lúc bắt đầu chuyển động và

( 2) 22y  

(mét) là quãng đường vật đi được trong khoảng thời

gian đó. Hỏi trong khoảng thời gian

10

giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn

nhất của vật đạt được bằng bao nhiêu ?

Ⓐ

216 ( / ).m s

Ⓑ

30 ( / ).m s

Ⓒ

400 ( / ).m s

Ⓓ

54 ( / ).m s

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

25km

20km

15km/h

30km/h

N

M

A

B

D

C

X

x

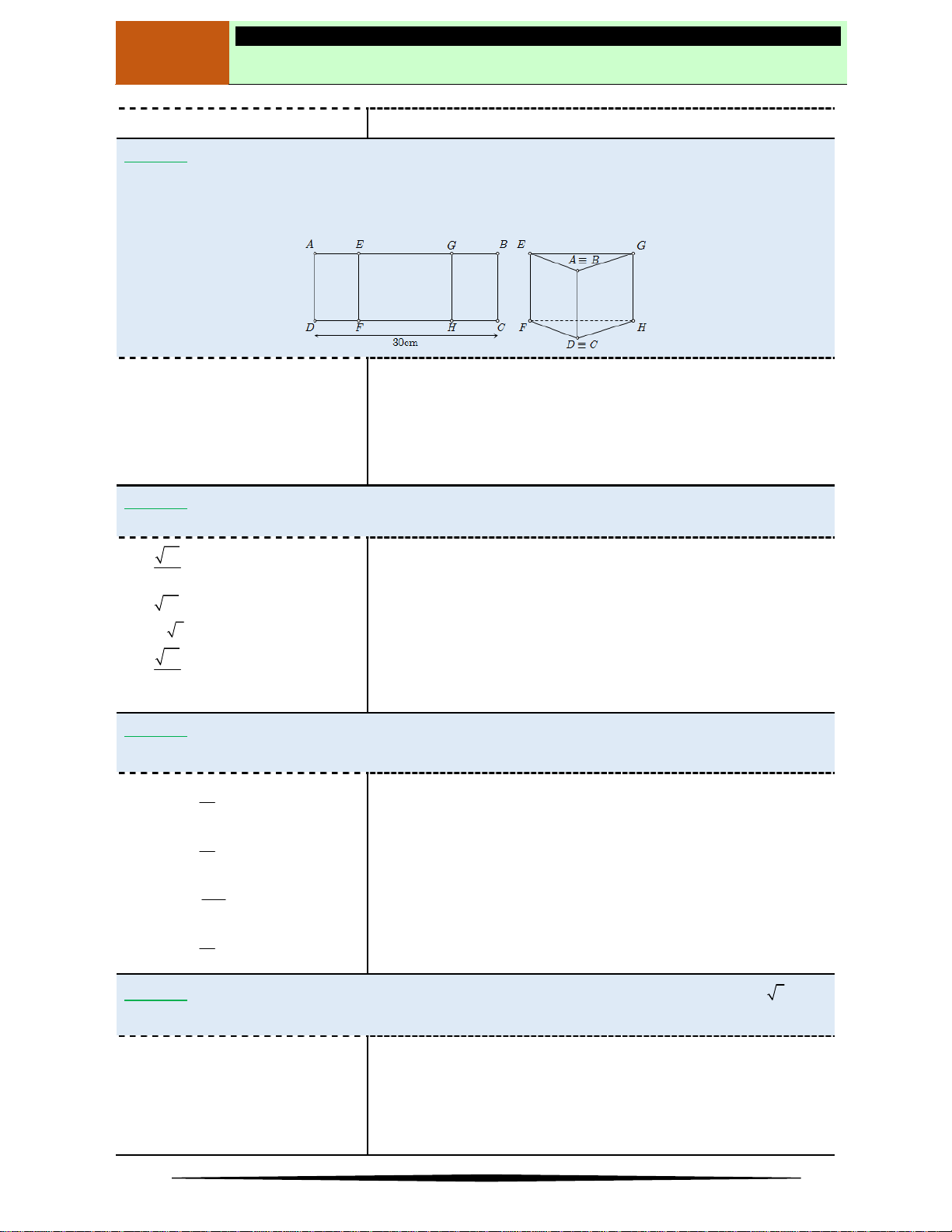
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 162

................................................................................................................................................................................................................................

................................

Ví dụ 10. Một tấm kẽm hình chữ nhật

ABCD

có cạnh

30AB 

(cm).

Người ta gập tấm kẽm theo hai

cạnh

EF

và

GH

cho đến khi

AD

và

BC

trùng nhau (như hình vẽ dưới đây) để được một

hình lăng trụ khuyết hai đáy. Tìm giá trị của

, ( )x x DF HC 

để thể tích khối lăng trụ

tương ứng đó lớn nhất ?

Ⓐ

9 (cm).

Ⓑ

10 (cm).

Ⓒ

8 (cm).

Ⓓ

12 (cm).

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 11. Một hình chóp tứ giác đều có tổng độ dài của đường cao và bốn cạnh đáy là

33.

Hỏi độ dài

cạnh bên ngắn nhất là bao nhiêu ?

Ⓐ

33

17



Ⓑ

33.

Ⓒ

11 3.

Ⓓ

33

2



................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 12. Khối chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

.a

Biết

,SA SB SC a  

cạnh

SD

thay đổi. Tính thể tích lớn nhất

max

V

của khối chóp

. .S ABCD

Ⓐ

3

max

8

a

V  

Ⓑ

3

max

4

a

V  

Ⓒ

3

max

3

8

a

V  

Ⓓ

3

max

2

a

V  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 13. Tìm

max

V

là giá trị lớn nhất của thể tích các khối hộp chữ nhật có đường chéo bằng

3 2cm

và

diện tích toàn phần bằng

2

18cm .

Ⓐ

3

max

6cm .V 

Ⓑ

3

max

5cm .V 

Ⓒ

3

max

4cm .V 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 163

Ⓓ

3

max

8cm .V 

Ví dụ 14. Cho phương trình

2 3 2

3 1 2 2 1x x x m    

với

m

là tham số thựⒸ Hỏi có bao nhiêu

giá trị nguyên của

m

để phương trình đã cho có nghiệm ?

Ⓐ

6.

Ⓑ

5.

Ⓒ

2.

Ⓓ

9.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 15. Cho phương trình

2 2

4 21 3 10x x x x m       

với

m

là tham số thựⒸ Hỏi có bao

nhiêu giá trị nguyên của

m

để phương trình có

2

nghiệm phân biệt ?

Ⓐ

6.

Ⓑ

5.

Ⓒ

2.

Ⓓ

9.

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 164

Daïng toaùn 4: Baøi toaùn tieäm caän lieân quan ñeán tham soá



Ví dụ 1.

Với giá trị nào của

m

thì đồ thị hàm số

1

2

mx

y

x m







có tiệm cận đứng là đường thẳng

1 ?x  

Ⓐ

2.m 

Ⓑ

1

2

m

 

Ⓒ

0.m 

Ⓓ

2.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 2.

Tìm tham số thực

m

để đồ thị hàm số

(2 1) 1m x

y

x m

 





có đường tiệm cận ngang là

3.y 

Ⓐ

2.m 

Ⓑ

3.m 

Ⓒ

1.m 

Ⓓ

0.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 3.

Tìm tham số thực

m

để đồ thị hàm số

3

mx

y

x m







có tiệm cận đứng là đường

1,x 

tiệm cận

ngang là đường

1.y 

Ⓐ

1.m 

Ⓑ

2.m 

Ⓒ

1.m  

Ⓓ

3.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 4.

Tìm giá trị thực của tham số

m

sao cho tiệm cận đứng của đồ thị hàm số

1

2

x

y

x m







đi qua

(1;2).A

Ⓐ

2.m 

Ⓑ

2.m  

Ⓒ

4.m 

Ⓓ

4.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 5.

Cho hàm số

2

1

mx m

y

x



 



Với giá trị nào của tham số

m

thì đường tiệm cận đứng, tiệm cận

ngang của đồ thị hàm số cùng hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng

8.

Ⓐ

2.m 

Ⓑ

1

2

m

  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 165

Ⓒ

4.m  

Ⓓ

2.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 6.

Biết rằng trong các tiệm cận của đồ thị hàm số

2

( ) 1

2

m n x mx

y

x mx n

  



  

có hai tiệm cận là trục

hoành và trục tung. Hãy tính tổng

.m n

Ⓐ

6.m n 

Ⓑ

4.m n 

Ⓒ

2.m n 

Ⓓ

8.m n 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 7.

Biết đồ thị của hàm số

2

( 2 ) 1

a b x bx

y

x x b

  



 

có tiệm cận đứng là

1x 

và tiệm cận ngang là

đường thẳng

0.y 

Tính

2 .a b

Ⓐ

2 6.a b 

Ⓑ

7.m n 

Ⓒ

8.m n 

Ⓓ

10.m n 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 8.

Cho hàm số

2

1

4 9

ax x

y

x bx

 



 

có đồ thị

( )C

( , a b

là các hằng số dương và

4).ab 

Biết rằng

( )C

có tiệm cận ngang

y c

và có đúng 1 tiệm cận đứng. Tính tổng

3 24 .T a b c  

Ⓐ

1.T 

Ⓑ

4.T 

Ⓒ

7.T 

Ⓓ

11.T 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 9.

Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

2

1

x

y

x mx





 

có hai đường

tiệm cận đứng ?

Ⓐ

( ; 2] [2; ).m     

Ⓑ

5

2

m

 

Ⓒ

( ; 2) (2; ).m     

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 166

Ⓓ

5

( ; 2) (2; ) \

2

m

 

 

     

 

 

 

................................................................................................................................................................................................................................

................................

Ví dụ 10.

Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

2

x x

y

x x m

 



 

có hai tiệm cận

đứng ?

Ⓐ

1m 

và

8.m 

Ⓑ

1m 

và

8.m  

Ⓒ

1m 

và

8.m  

Ⓓ

1.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 11.

Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

2 2

2( 1)

x

y

x m x m



  

có đúng

một đường tiệm cận đứng ?

Ⓐ

1

;0

2

m

 

 

  

 

 

 

Ⓑ

1

;0

2

m

 







  











 

Ⓒ

0.m 

Ⓓ

1

2

m

  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 12.

Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

2

3 2

x m

y

x x





 

có đúng hai đường

tiệm cận ?

Ⓐ

1, 4.m m 

Ⓑ

1.m 

Ⓒ

4.m 

Ⓓ

0.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 13.

Tìm tất cả các giá trị của tham số

a

để đồ thị hàm số

2

3 2

x

y

x

a

ax





có ba đường tiệm cận.

Ⓐ

0, 1.aa   

Ⓑ

0, 1.aa   

Ⓒ

1.0, a a  

Ⓓ

0.a 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 14.

Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị của hàm số

2

1

2

x

y

x mx m





 

có ba

tiệm cận.

Ⓐ

1m  

hoặc

0m 

và

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 167

1

3

m

 

Ⓑ

1m  

hoặc

0.m 

Ⓒ

1m  

và

1

3

m

 

Ⓓ

1 0m  

và

1

3

m

 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 15.

Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

2

2 3

x x m

y

x m

 





không có tiệm

cận đứng ?

Ⓐ

0.m 

Ⓑ

0, 1.m m 

Ⓒ

1.m 

Ⓓ Không có

.m

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 16.

Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị của hàm số

2

1

x

y

mx







có hai

tiệm cận ngang.

Ⓐ Không có

.m

Ⓑ

0.m 

Ⓒ

0.m 

Ⓓ

0.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 17.

Tìm tất cả các giá trị thực của tham số

m

sao cho đồ thị của hàm số

2

1

2 1

mx mx

y

x

 





có

hai tiệm cận ngang.

Ⓐ

0.m 

Ⓑ

0.m 

Ⓒ

0.m 

Ⓓ Không có

.m

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 18.

Tìm tất cả các giá trị thực của tham số

m

để đồ thị hàm số

2

3

x

y

x m







có ba tiệm cận.

Ⓐ

0m 

và

9.m 

Ⓑ

0.m 

Ⓒ

9m  

hoặc

0.m 

Ⓓ

0.m 

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 168

Ví dụ 19.

Tìm tất cả các giá trị thực của tham số

m

để tiệm cận ngang của đồ thị hàm số

2

4

(2 1) 3

1

m x

y

x

 





đi qua điểm

(1; 3).A 

Ⓐ

1m  

hoặc

1.m 

Ⓑ

2m  

hoặc

2.m 

Ⓒ

1.m 

Ⓓ

2.m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

Ví dụ 20.

Tìm các giá trị của tham số thực

m

để đồ thị hàm số

2

2y mx x x  

có đường tiệm cận

ngang.

Ⓐ

1.m 

Ⓑ

{ 2;2}.m  

Ⓒ

{ 1;1}.m  

Ⓓ

(0; ).m  

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

................................................................................................................................................................................................................................

................................

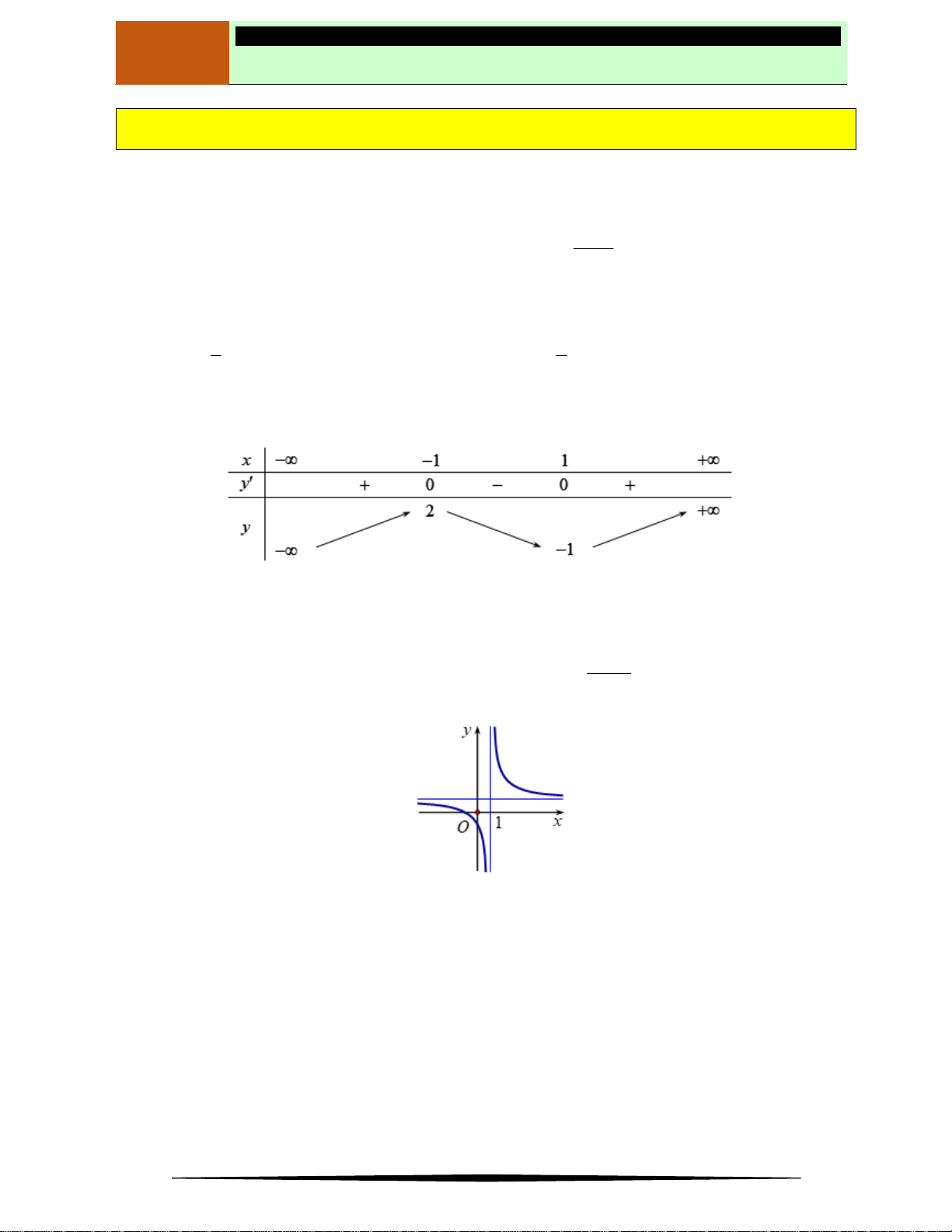
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 169

7.5: ĐỀ ÔN TẬP CHƯƠNG

ĐỀ ÔN TẬP CHƯƠNG SỐ 1

Câu 1. Trong các hàm số sau, hàm số nào đồng biến trên



.

Ⓐ

4 2

1

y x x

  

. Ⓑ

3

1

y x

 

. Ⓒ

4 1

2

x

y

x







. Ⓓ

tany x

.

Câu 2. Hàm số

4

2

y x

 

nghịch biến trên khoảng nào?

Ⓐ

1

;

2







 

 

. Ⓑ

 

;0



. Ⓒ

1

;

2







 

 

. Ⓓ

 

0;

.

Câu 3. Cho hàm số

 

y f x



xác định và liên tục trên khoảng

 

; , 

có bảng biến thiên như

hình sau:

Mệnh đề nào sau đây đúng ?

Ⓐ Hàm số nghịch biến trên khoảng

 

1;



. Ⓑ Hàm số đồng biến trên khoảng

 

; 2 

.

 

;1

. Ⓓ Hàm số đồng biến trên khoảng

 

1;

 

.

Câu 4. Đường cong ở hình dưới đây là đồ thị của hàm số







ax b

y

cx d

, với

, , ,a b c d

là các số thựⒸ

Mệnh đề nào dưới đây đúng?

Ⓐ

' 0, .   

y x

Ⓑ

' 0, 1.  

y x

Ⓒ

' 0, .   

y x

Ⓓ

' 0, 1.  

y x

Câu 5. Cho hàm số

 

f x

xác định trên



và có đồ thị hàm số

 

y f x





là đường cong trong

hình bên. Mệnh đề nào dưới đây đúng?

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 170

Ⓐ Hàm số

 

f x

nghịch biến trên khoảng

 

1;1

.

Ⓑ Hàm số

 

f x

đồng biến trên khoảng

 

1;2

.

 

f x

đồng biến trên khoảng

 

2;1

.

Ⓓ Hàm số

 

f x

nghịch biến trên khoảng

 

0; 2

.

Câu 6. Tìm tất cả các giá trị thực của tham số

m

để hàm số

3 2

1y x x mx   

đồng biến trên

 

;   

.

Ⓐ

4

3

m 

. Ⓑ

1

3

m 

. Ⓒ

1

3

m 

. Ⓓ

4

3

m 

.

Câu 7. Kết quả của

m

để hàm số sau

2

x m

y

x







đồng biến trên từng khoảng xác định là

Ⓐ

2m 

. Ⓑ

2m 

. Ⓒ

2m 

. Ⓓ

2m 

.

Câu 8. Tồn tại bao nhiêu số nguyên

m

để hàm số

2x

y

x m







đồng biến trên khoảng

 

; 1 

.

Ⓐ

3

. Ⓑ

4

. Ⓒ

2

. Ⓓ Vô số.

Câu 9. Điểm cực tiểu của đồ thị hàm số

3

3 5y x x  

là điểm ?

Ⓐ

 

3; 1Q

. Ⓑ

 

1; 3M

. Ⓒ

 

7; 1P 

. Ⓓ

 

1; 7N 

.

Câu 10. Cho

hàm

số

 

y f x

có bảng biến thiên sau:

Khẳng định nào sau đây là đúng?

Ⓐ Hàm số đạt cực đại tại

2.x 

Ⓑ Hàm số đạt cực đại tại

3.x 

2.x  

Ⓓ Hàm số đạt cực đại tại

4.x 

Câu 11. Cho hàm số

 

y f x

có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 171

Ⓐ Hàm số có giá trị cực tiểu bằng

2

.

Ⓑ Hàm số có giá trị lớn nhất bằng

2

và giá trị nhỏ nhất bằng

2

.

0

x



và cực tiểu tại

2

x



.

Ⓓ Hàm số có ba điểm cực trị.

Câu 12. Hàm số

3 2

3 2y x x mx   

đạt cực tiểu tại

2

x



khi:

Ⓐ

0

m



. Ⓑ

0

m



. Ⓒ

0

m



. Ⓓ

0

m



.

Câu 13. Tìm

m

để hàm số

 

3 2 2

1

1 1

3

y x mx m m x     

đạt cực trị tại 2 điểm

1 2

;x x

thỏa

mãn

1 2

4

x x

 

.

Ⓐ

2

m



. Ⓑ Không tồn tại

m

. Ⓒ

2

m

 

. Ⓓ

2

m

 

.

Câu 14. Cho hàm số:

 

4 2

1 2 1

y m x mx m

    

. Tìm

m

để đồ thị hàm số có đúng một cực trị

Ⓐ

0

m



. Ⓑ

0

m



hoặc

1

m



.

Ⓒ

0

m



hoặc

1

m



. Ⓓ

1

m



.

Câu 15. Tìm giá trị lớn nhất của hàm số

3

3 5y x x  

trên đoạn

 

0;2

.

Ⓐ

 

0;2

max 0.

y



Ⓑ

 

0;2

max 3.

y



Ⓒ

 

0;2

max 7.

y



Ⓓ

 

0;2

max 5.

y



Câu 16. Tìm giá trị

lớn

nhất và nhỏ nhất của hàm số

4 2

sin cos 2

xy x

  

.

Ⓐ

min 3

y



. Ⓑ

11

min

4

y



. Ⓒ

min 3

y

 

. Ⓓ

11

min

2

y



.

Câu 17. Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có

thể tích bằng

3

288m

. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công

để xây bể là

500000

đồng/

2

m

. Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí

thuê nhân công sẽ thấp nhất. Hỏi ông An trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu?

Ⓐ

108

triệu đồng. Ⓑ

54

triệu đồng. Ⓒ

168

triệu đồng. Ⓓ

90

triệu đồng.

Câu 18. Cho hàm số

 

f x

có đạo hàm trên



và có đồ thị của hàm

 





y f x

như hình vẽ. Biết

rằng

       

0 3 2 5

  f f f f

. Giá trị nhỏ nhất và giá trị lớn nhất của

 

f x

trên đoạn

 

0;5

lần lượt là:

Ⓐ

 

0

f

,

 

5f

. Ⓑ

 

2

f

,

 

0

f

. Ⓒ

 

1f

,

 

3f

. Ⓓ

 

2

f

,

 

5f

.

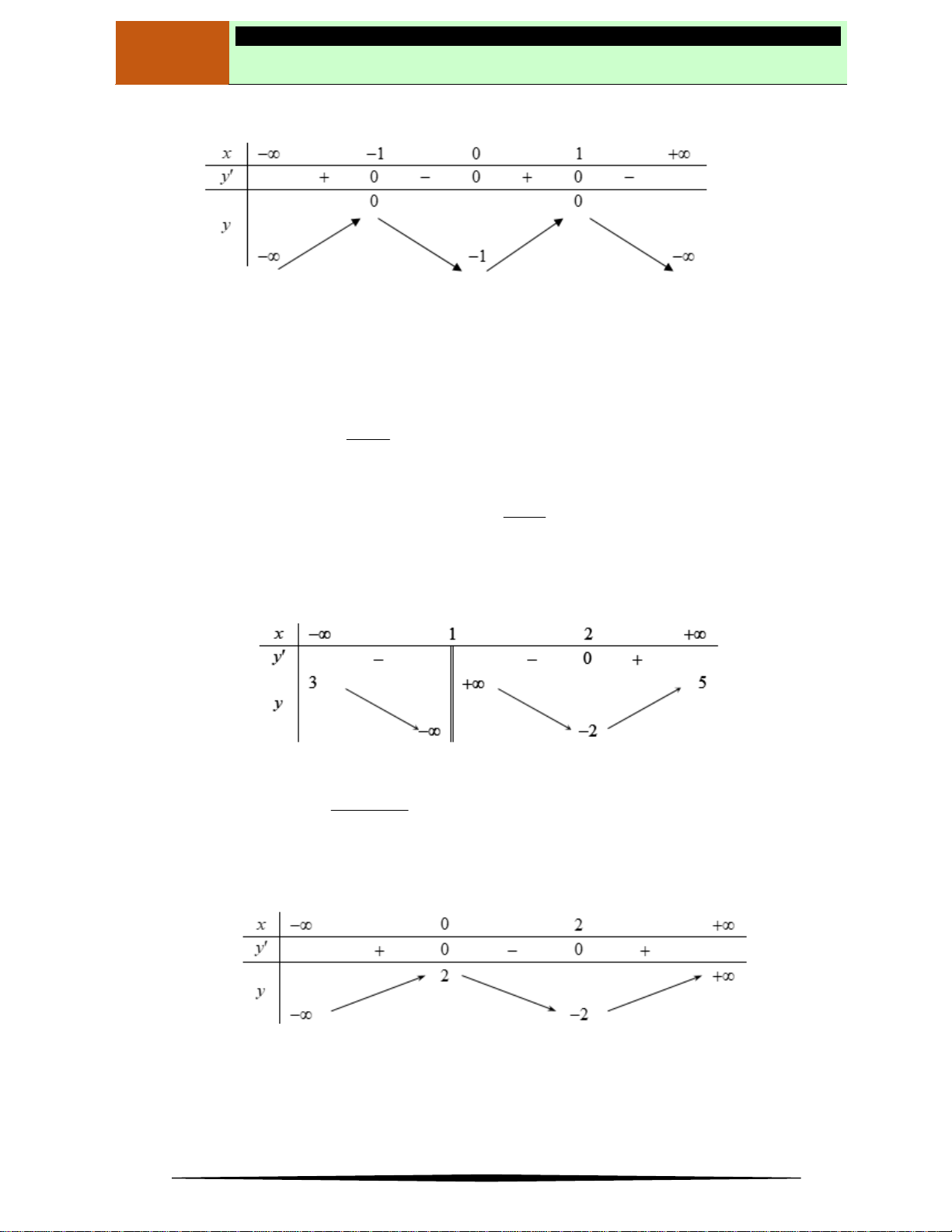
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 172

Câu 19. Cho bảng biến thiên của hàm số

 

y f x



. Mệnh đề nào sau đây sai?

Ⓐ Giá trị lớn nhất của hàm số

 

y f x



trên tập



bằng

0

.

Ⓑ Giá trị nhỏ nhất của hàm số

 

y f x



trên tập



bằng

1

.

 

y f x



nghịch biến trên

 

1;0



và

 

1;

 

.

Ⓓ Đồ thị hàm số

 

y f x



không có đường tiệm cận.

Câu 20. Đồ thị hàm số

2 3

1

x

y

x







có các đường tiệm cận đứng và tiệm cận ngang lần lượt là

Ⓐ

2

x



và

1y 

. Ⓑ

1x 

và

3

y

 

. Ⓒ

1

x

 

và

2

y



. Ⓓ

1x 

và

2

y



.

Câu 21. Tâm đối xứng

I

của đồ thị hàm số

2 1

1

x

y

x



 



là

Ⓐ

 

1; 2

I

. Ⓑ

 

1; 2 

I

. Ⓒ

 

1; 2

I

. Ⓓ

 

1; 2

I

.

Câu 22. Cho hàm số

 

y f x



xác định trên

 

\ 1

, liên tục trên mỗi khoảng xác định và có bảng

biến thiên như hình bên. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

Ⓐ

3

. Ⓑ

1

. Ⓒ

2

. Ⓓ

4

.

Câu 23. Cho hàm số

2 2 1

x m

y

x m

 





. Tìm tất cả các giá trị thực của tham số

m

để đường tiệm cận

đứng của đồ thị hàm số đi qua điểm

 

3;1

M

Ⓐ

1

m



. Ⓑ

3

m

 

. Ⓒ

3

m



. Ⓓ

2

m



.

Câu 24. Hàm số nào trong bốn hàm số sau có bảng biến thiên như hình vẽ sau?

Ⓐ

3 2

3 1.

y x x

   

Ⓑ

3 2

3 1.

y x x

  

Ⓒ

3

3 2.

y x x

  

Ⓓ

3 2

3 2.

y x x

  

Câu 25. Đường cong trong hình bên là đồ thị của một hàm số nào dưới đây.

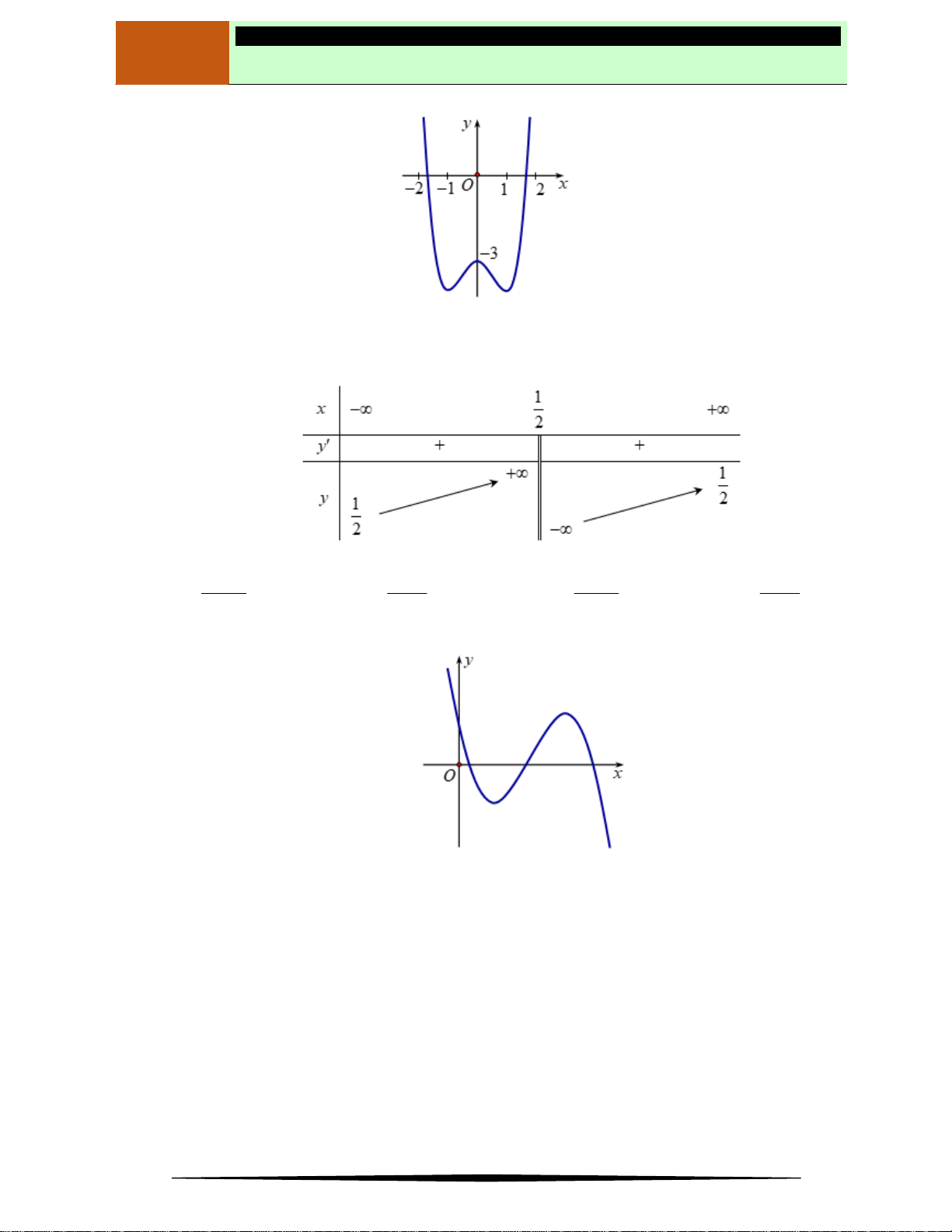
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 173

Ⓐ

4 2

2 3

y x x

   

. Ⓑ

4 2

2 3

y x x

  

. Ⓒ

4 2

3

y x x

  

. Ⓓ

4 2

2 3

y x x

  

.

Câu 26. Cho hàm số

 

y f x



có bảng biến thiên

Hỏi hàm số đó là hàm nào?

Ⓐ

2

2 1

x

y

x

 





. Ⓑ

2

2 1

x

y

x







. Ⓒ

2

2 1

x

y

x

 





. Ⓓ

2

2 1

x

y

x







.

Câu 27. Cho hàm số

3 2

y ax bx cx d   

có đồ thị như hình vẽ

Mệnh đề nào sau đây đúng?

Ⓐ

0, 0, 0, 0

a b c d

   

. Ⓑ

0, 0, 0, 0

a b c d

   

.

Ⓒ

0, 0, 0, 0

a b c d

   

. Ⓓ

0, 0, 0, 0

a b c d

   

.

Câu 28. Cho hàm số

 

y f x



có bảng biến thiên dưới đây.

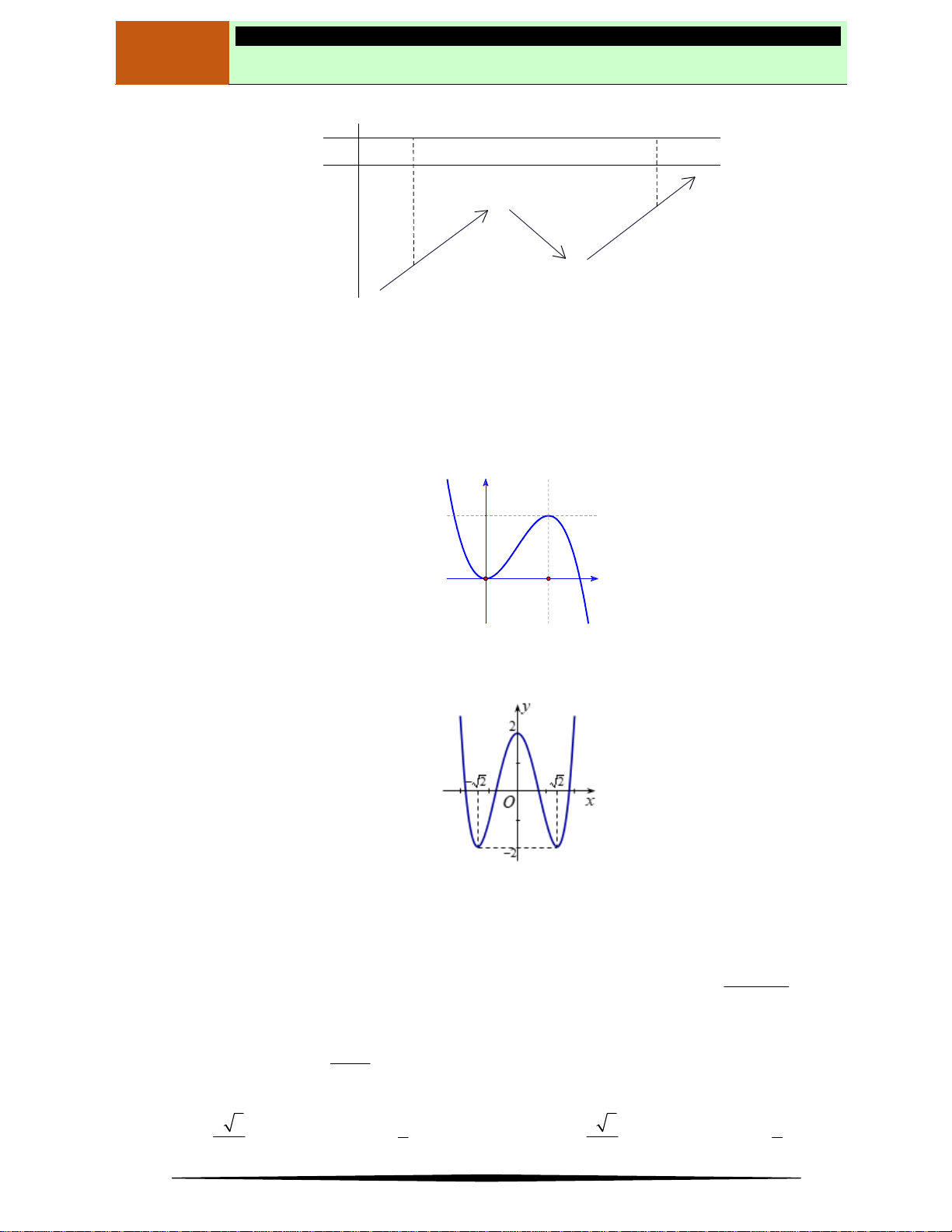
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 174

Tìm tất cả các giá trị thực của tham số

m

để phương trình

   

f x f m



có ba nghiệm phân

biệt.

Ⓐ

 

;

m  

2 2

. Ⓑ

   

; \ ;

m  

1 3 0 2

. Ⓒ

 

;

m  

1 3

.Ⓓ

 

 

; \ ;

m  

1 3 0 2

.

Câu 29. Cho đồ thị hàm số

 

y f x



có đồ thị như hình vẽ. Tìm số nghiệm của phương trình

 

f x x

.

Ⓐ

0

. Ⓑ

1

. Ⓒ

2

. Ⓓ

3

.

Câu 30. Cho hàm số

 

y f x



có đồ thị như hình bên dưới

Số nghiệm của phương trình

 

2 3 0

f x

 

là

Ⓐ

4

. Ⓑ

2

. Ⓒ

0

. Ⓓ

3

.

Câu 31. Đường thẳng

2 1y x 

có bao nhiêu điểm chung với đồ thị hàm số

2

1

x x

y

x

 





.

Ⓐ

3

. Ⓑ

1

. Ⓒ

0

. Ⓓ

2

.

Câu 32. Cho hàm số

2 1

1

x

y

x







có đồ thị

 

C

và đường thẳng

: 2 3d y x 

. Đường thằng

d

cắt

( )C

tại hai điểm

A

và

B

. Khoảng cách giữa

A

và

B

là

Ⓐ

2 5

5

AB 

. Ⓑ

5

2

AB



. Ⓒ

5 5

.

2

AB 

Ⓓ

2

.

5

AB



-2

2

+∞

-∞

++

-

00

-1

3

20

-∞

+∞

f'(x)

f(x)

x

y

1

O

1

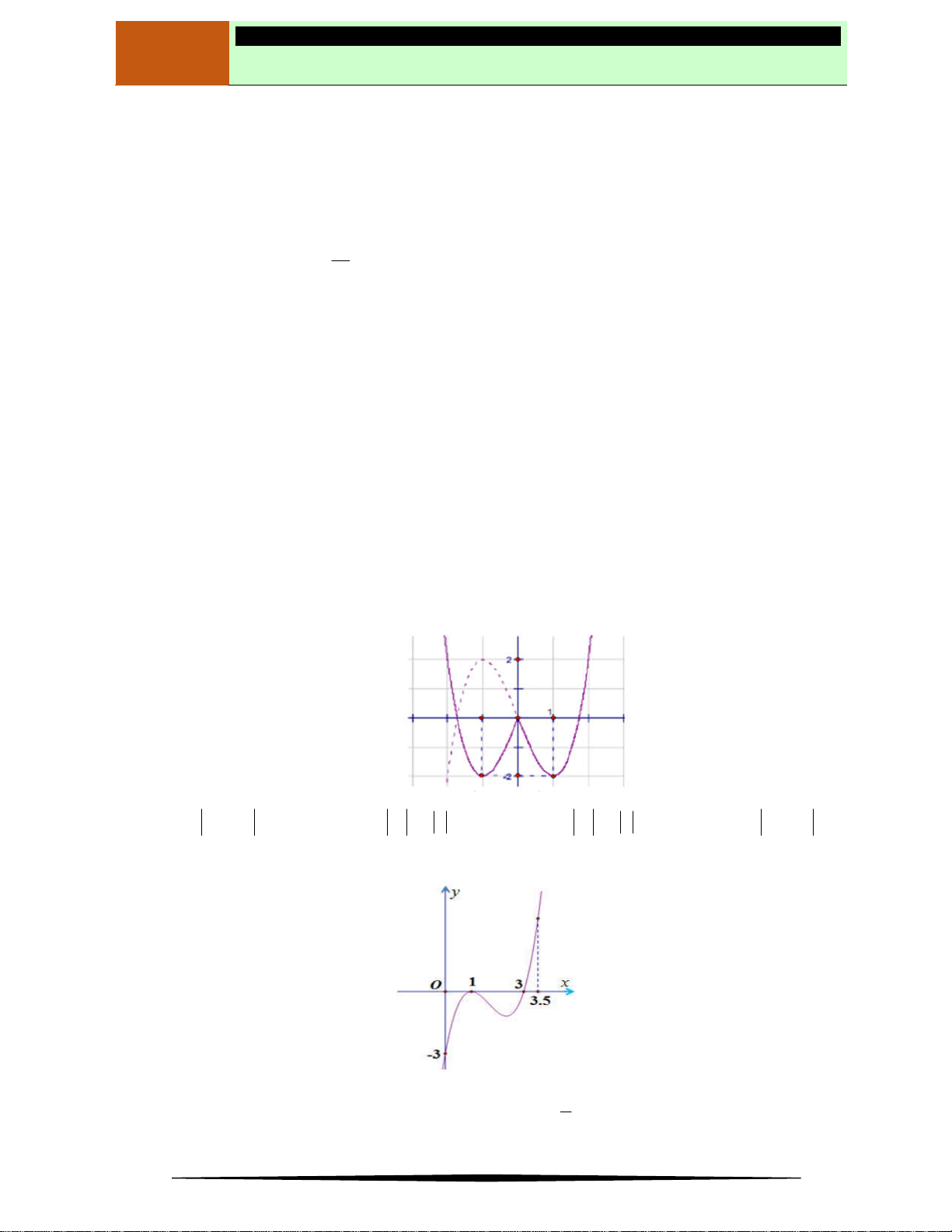
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 175

Câu 33. Tìm tọa độ giao điểm

I

của đồ thị hàm số

3

4 3y x x 

và đường thẳng

2y x  

:

Ⓐ

 

2; 2I

. Ⓑ

 

2;1I

Ⓒ

 

1;1I

Ⓓ

 

1; 2I

Câu 34. Phương trình tiếp tuyến của đồ thị hàm số

2

2y x x  

tại điểm có hoành độ

1x 

là

Ⓐ

2 0x y 

Ⓑ

2 4 0x y  

. Ⓒ

1 0x y  

. Ⓓ

3 0x y  

.

Câu 35. Cho hàm số

3

2

3 2

3

x

y x  

có đồ thị là

 

C

. Viết phương trình tiếp tuyến với đồ thị

 

C

biết tiếp tuyến có hệ số góc

9k  

.

Ⓐ

 

16 9 3y x   

. Ⓑ

 

16 9 3y x   

. Ⓒ

 

9 3y x  

. Ⓓ

 

16 9 3y x   

.

Câu 36. Cho hàm số

3 2

2 1y x x  

có đồ thị là

 

C

. Phương trình tiếp tuyến của

 

C

tại điểm

 

1; 4M

là:

Ⓐ

3 1y x 

. Ⓑ

7 3y x 

. Ⓒ

7 2y x 

. Ⓓ

5y x  

.

Câu 37. Cho hàm số

3 2

2y x x  

có đồ thị

 

C

. Có bao nhiêu tiếp tuyến của đồ thị

 

C

song

song với đường thẳng

y x

.

Ⓐ

2

. Ⓑ

3

. Ⓒ

1

. Ⓓ

4

.

Câu 38. Cho hàm số

3 2

3 2y x x   

có đồ thị

 

C

. Phương trình tiếp tuyến của

 

C

mà có hệ

số góc lớn nhất là

Ⓐ

3 1y x  

. Ⓑ

3 1y x  

. Ⓒ

3 1y x 

. Ⓓ

3 1y x 

.

Câu 39. Đồ thị hình bên là của hàm số nào?

Ⓐ

3

3y x x 

Ⓑ

3

3y x x 

Ⓒ

3

3y x x 

Ⓓ

3

3y x x 

Câu 40. Cho hàm số

 

y f x

có đồ thị hàm số

 

'y f x

như hình vẽ

Hàm số

 

y f x

đạt giá trị nhỏ nhất trên đoạn

7

0;

2

 

 

 

tại điểm

0

x

nào dưới đây?

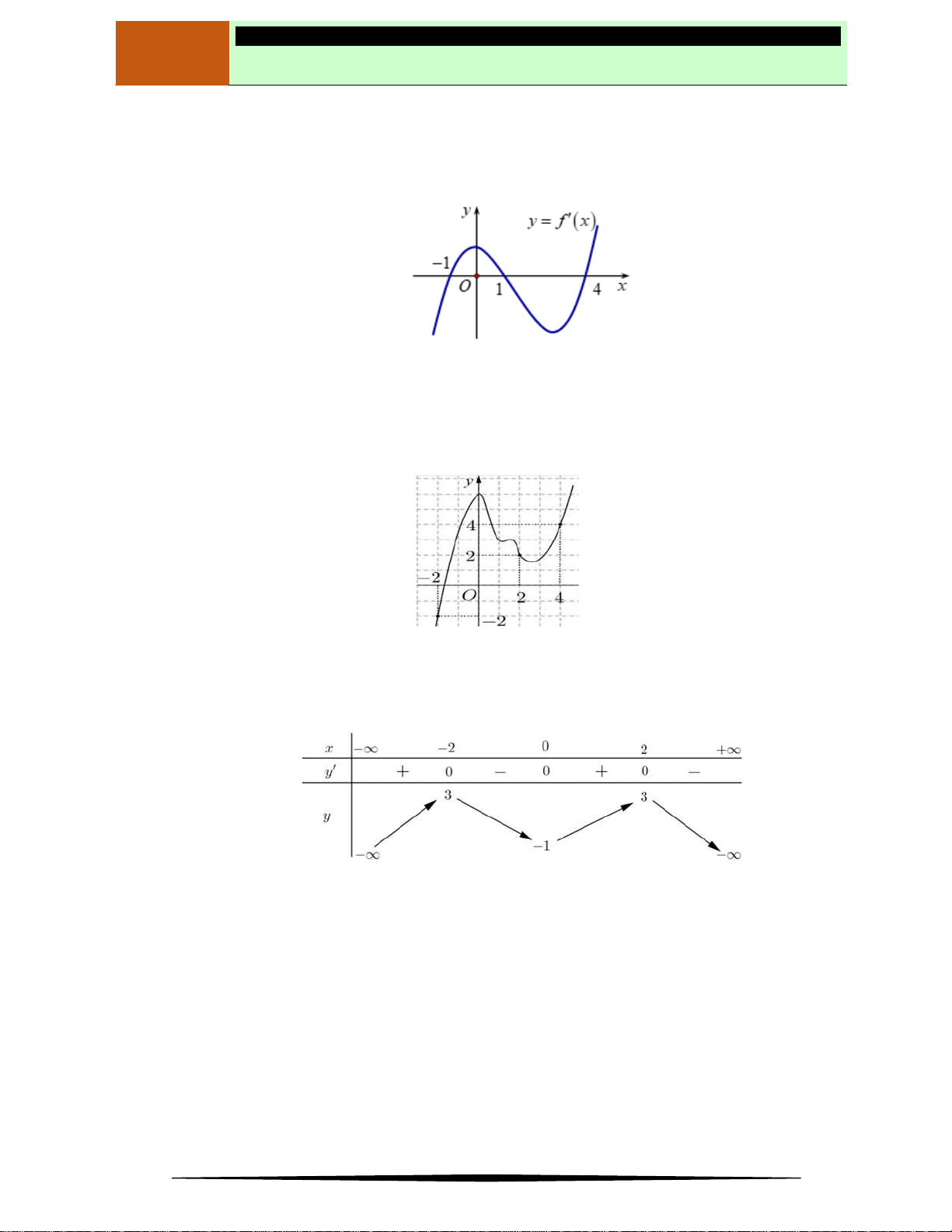
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 176

Ⓐ

0

0x 

.

Ⓑ

0

1x 

.

Ⓒ

0

2x 

.

Ⓓ

0

3x 

.

Câu 41. Cho hàm số

 

y f x

.Hàm số

 

y f x





có đồ thị như hình bên. Hàm số

 

2y f x 

đồng biến trên khoảng:

Ⓐ

 

1;3

. Ⓑ

 

2;

. Ⓒ

 

2;1

. Ⓓ

 

;2

.

Câu 42. Cho hàm số

( )y f x

. Đồ thị của hàm số

( )y f x





như hình vẽ. Đặt

( ) ( )h x f x x 

.

Mệnh đề nào dưới đây đúng?

Ⓐ

(1) 1 (4) (2)h h h  

. Ⓑ

(0) (4) 2 (2)h h h  

.

Ⓒ

( 1) (0) (2)h h h  

. Ⓓ

(2) (4) (0)h h h 

.

Câu 43. Cho hàm số

( )y f x

có bảng biến thiên như sau:

Hàm số

2

( 2) y f x

nghịch biến trên khoảng nào dưới đây ?

Ⓐ

 

; 2 

. Ⓑ

 

0; 2

. Ⓒ

 

2;

. Ⓓ

 

2;0

.

Câu 44. Hình vẽ bên là đồ thị của hàm số

 

y f x

.

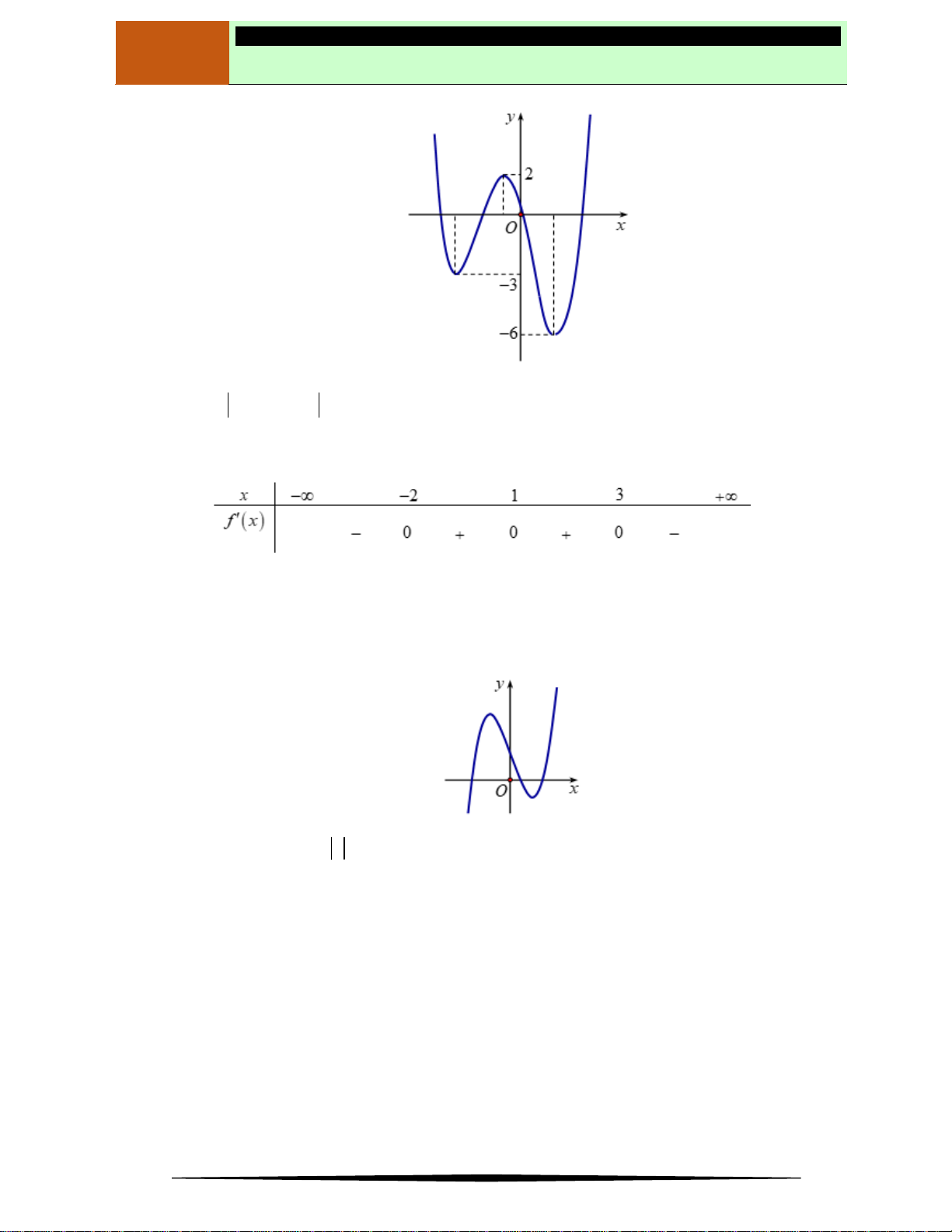
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 177

Gọi

S

là tập hợp các giá trị nguyên dương của tham số

m

để hàm số

 

1

y f x m  

có

5

điểm cực trị. Tổng giá trị tất cả các phần tử của

S

bằng

Ⓐ

9

. Ⓑ

12

. Ⓒ

18

. Ⓓ

15

.

Câu 45. Cho hàm số

 

y f x



có đạo hàm trên



và có bảng xét dấu

 

f x



như sau

Hỏi hàm số

 

2

2y f x x

 

có bao nhiêu điểm cực tiểu.

Ⓐ

1

. Ⓑ

2

. Ⓒ

3

. Ⓓ

4

.

Câu 46. Hàm số

 

f x

có đạo hàm

 

f x



trên



. Hình vẽ bên là đồ thị của hàm số

 

f x



trên



.

Hỏi hàm số

 

2018

y f x 

có bao nhiêu điểm cực trị?

Ⓐ

5

. Ⓑ

3

. Ⓒ

2

. Ⓓ

4

.

Câu 47. Cho hàm số

 

y f x



liên tục trên



có đồ thị

 

y f x





cho như hình dưới đây. Đặt

     

2

2 1

g x f x x

  

. Mệnh đề nào dưới đây đúng.

Ⓐ

 

   

3;3

min 1g x g





.

Ⓑ

 

   

3;3

max 1g x g





.

Ⓒ

 

   

3;3

max 3

g x g





.

Ⓓ Không tồn tại giá trị nhỏ nhất của

 

g x

trên đoạn

 

3;3



.

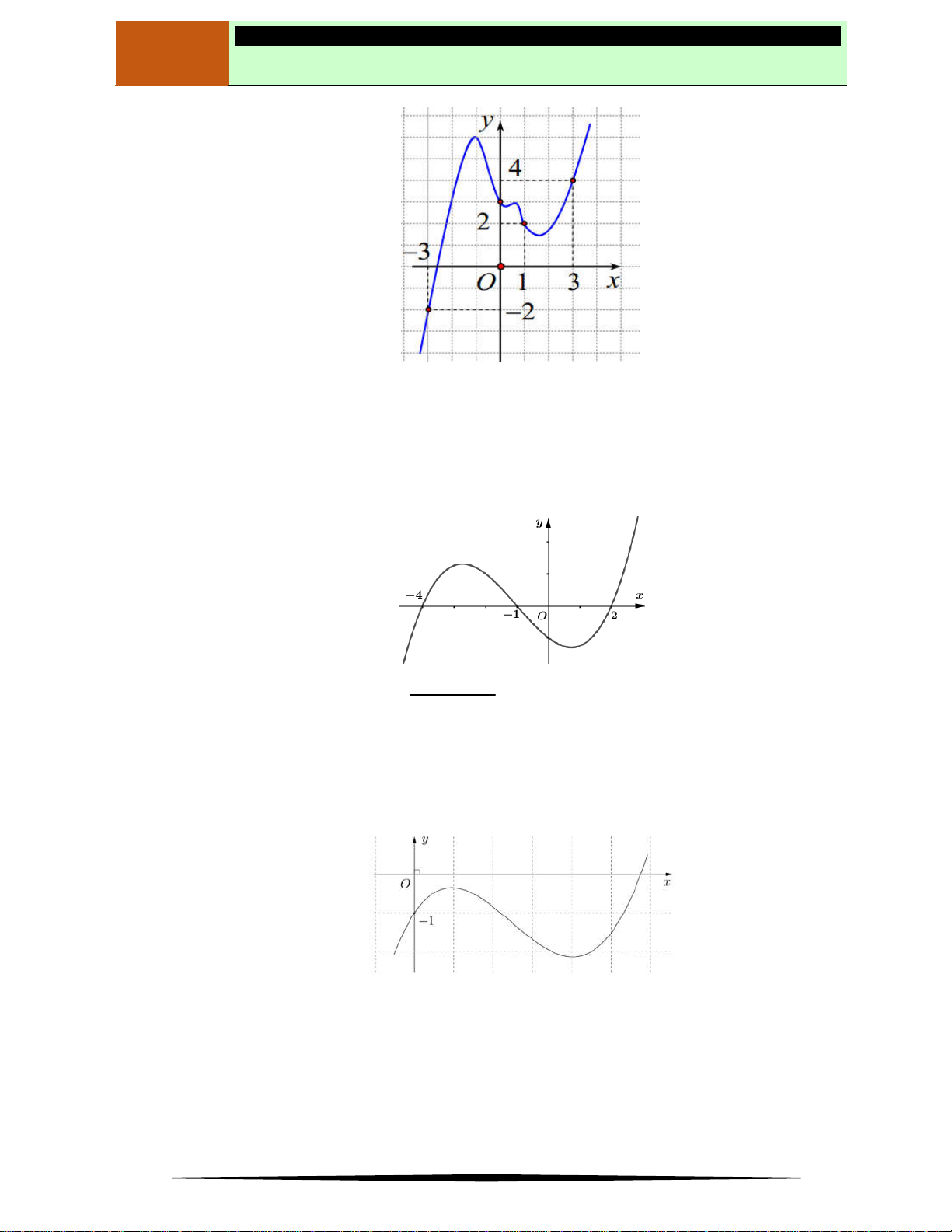
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 178

.

Câu 48. Tìm tọa độ điểm

M

có hoành độ dương thuộc đồ thị

 

C

của hàm số

2

x

y

x







sao cho

tổng khoảng cách từ

M

đến hai đường tiệm cận của đồ thị

 

C

đạt giá trị nhỏ nhất.

Ⓐ

 

1; 3M 

. Ⓑ

 

3;5M

. Ⓒ

 

0; 1M 

. Ⓓ

 

4;3M

Câu 49. Cho hàm số

3 2

( )    y f x ax bx cx d

có đồ thị như sau:

Hỏi đồ thị hàm số

 

2020 2x

y g x

f x



 

có bao nhiêu đường tiệm cận đứng ?

Ⓐ

4.

Ⓑ

1.

Ⓒ

3.

Ⓓ

2

.

Câu 50. Cho hàm số bậc ba

 

y f x

có đồ thị là đường cong trong hình bên. Số nghiệm thực

phân biệt của phương trình

 

3

1 0f x f x  

là

Ⓐ

6

. Ⓑ

4

. Ⓒ

8

. Ⓓ

5

.

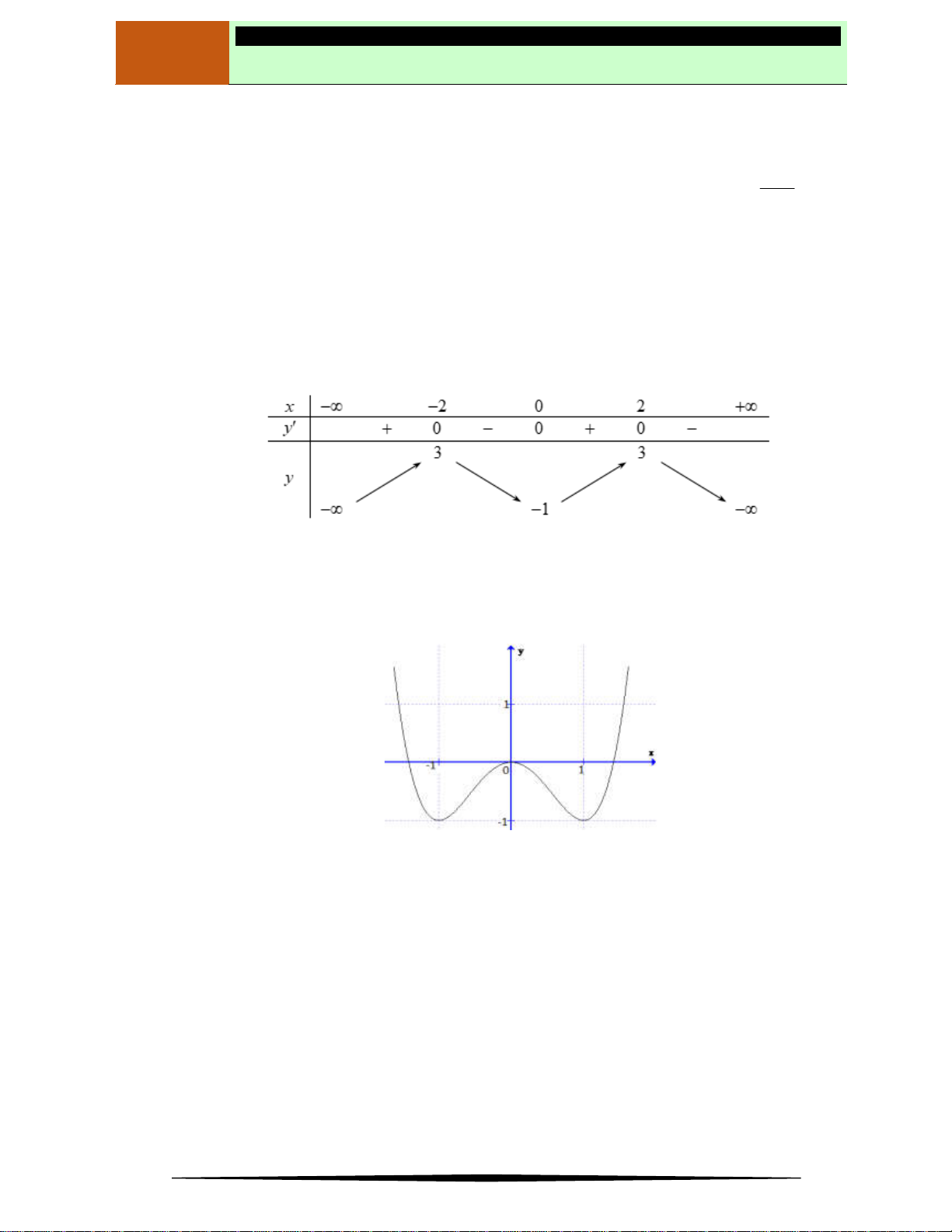
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 179

ĐỀ ÔN TẬP CHƯƠNG SỐ 02

Câu 1. Trong các hàm số sau, hàm số nào nghịch biến trên



?

Ⓐ

2

2y

x x  

. Ⓑ

4 2

y

x x 

. Ⓒ

3

1x x

y

   

. Ⓓ

4

3

y

x







Câu 2. Cho hàm số

3

3 .y x x

 

Mệnh đề nào dưới đây đúng?

Ⓐ Hàm số đồng biến trên khoảng

 

; 1 

và nghịch biến trên khoảng

 

1;



.

Ⓑ Hàm số đồng biến trên khoảng

( ; ). 

 

; 1 

và đồng biến trên khoảng

 

1;



Ⓓ Hàm số nghịch biến trên khoảng

 

1;1



.

Câu 3. Cho hàm số

 

y f x



có bảng biến thiên như sau

Hàm số

 

y f x



nghịch biến trên khoảng nào dưới đây?

Ⓐ

 

2; 0



. Ⓑ

 

; 2 

. Ⓒ

 

0; 2

. Ⓓ

 

0;

 

.

Câu 4. Cho đồ thị hàm số như hình vẽ.

Mệnh đề nào dưới đây đúng ?

Ⓐ Hàm số luôn đồng biến trên



. Ⓑ Hàm số nghịch biến trên

 

1;



.

 

1;

 

. Ⓓ Hàm số nghịch biến trên

 

; 1 

.

Câu 5. Cho hàm số

 

f x

có đạo hàm

       

2 3

1 1 2

f x x x x



   

. Hỏi hàm số đồng biến

trên khoảng nào dưới đây?

Ⓐ

 

2;



. Ⓑ

 

1; 2

. Ⓒ

 

; 1 

. Ⓓ

 

1;1



.

Câu 6. Tất cả các giá trị của

m

để hàm số

     

3 2

1 3 1 3 2 5

y m x m x m x m      

nghịch biến

trên



là

Ⓐ

1

m



. Ⓑ

1

m



. Ⓒ

1

m



. Ⓓ

4 1

m

  

.

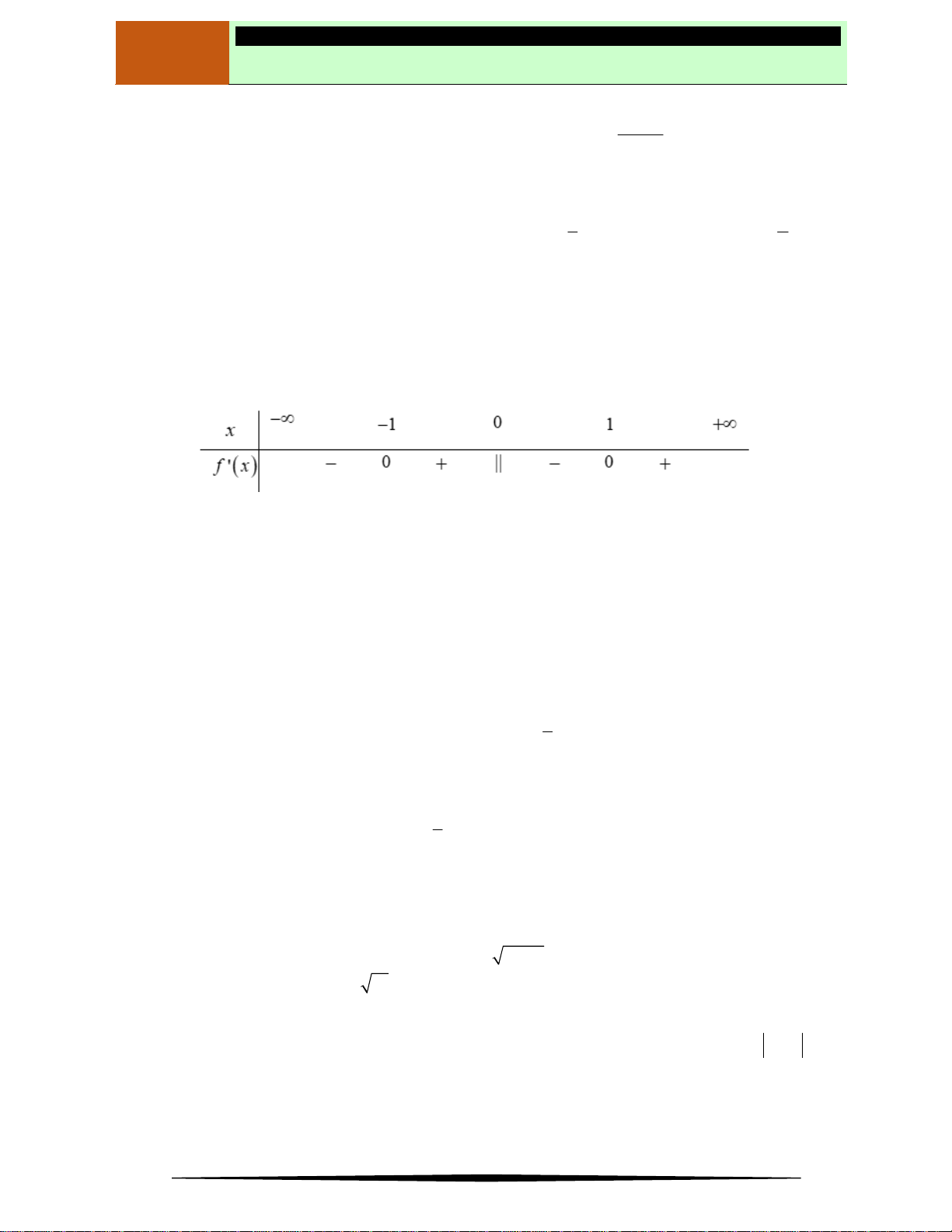
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 180

Câu 7. Có bao nhiêu giá trị nguyên của tham số

m

để hàm số

2

4

x m

y

x







đồng biến trên từng

khoảng xác định của nó?

Ⓐ

5

Ⓑ

3

Ⓒ

1

Ⓓ

2

Câu 8. Tìm tất cả các giá trị của tham số

m

để hàm số

   

3 2

1 2

1 2 3

3 3

y x m x m x

     

đồng

biến trên

 

1;



Ⓐ

2

m



. Ⓑ

2

m



. Ⓒ

1

m



. Ⓓ

1

m



.

Câu 9. Tìm giá trị cực đại

C

Đ

y

của hàm số

3

12 1  y x x

Ⓐ

17 

CĐ

y

. Ⓑ

2 

CĐ

y

. Ⓒ

45

CĐ

y

. Ⓓ

15

CĐ

y

.

Câu 10. Cho hàm số

 

y f x



liên tục trên



và có bảng xét dấu

 

'f x

như sau :

Khẳng định nào sau đây là đúng?

Ⓐ Hàm số đạt cực đại tại

0

x



.

Ⓑ Hàm số có đúng hai điểm cực trị.

0

và giá trị nhỏ nhất bằng

3

.

Ⓓ Hàm số có giá trị cực tiểu bằng

1

và

1

.

Câu 11. Cho hàm số

 



y f x

liên tục trên



, có đạo hàm

   

2

3

( ) 1 2



  

f x x x x

. Hỏi hàm số

 



y f x

có bao nhiêu điểm cực trị?

Ⓐ

3

. Ⓑ

1

. Ⓒ

0

. Ⓓ

2

.

Câu 12. Tìm giá trị thực của tham số

m

để hàm số

 

3 2 2

1

3

y x mx m m x

    

đạt cực đại tại

1x 

.

Ⓐ

2

m



. Ⓑ

3

m



. Ⓒ

m



. Ⓓ

0

m



.

Câu 13. Tìm tham số

m

để hàm số

 

3 2

1

2 2018

3

y x mx m x    

không có cực trị.

Ⓐ

1

m

 

hoặc

2

m



. Ⓑ

1

m

 

. Ⓒ

2

m



. Ⓓ

1 2

m

  

.

Câu 14. Tìm tất cả các giá trị của

m

để hàm số

   

4 2

1 2 2 1

y m x m x

    

có ba cực trị.

Ⓐ

1 2

m

  

. Ⓑ

2

m



. Ⓒ

1 2

m

  

. Ⓓ

1

m

 

.

Câu 15. Tìm giá trị lớn nhất của hàm số

2

5

y x x  

.

Ⓐ

5

. Ⓑ

10

. Ⓒ

6

. Ⓓ Một đáp án khá

Ⓒ

Câu 16. Cho hàm số

 

y f x



có đồ thị trên đoạn

 

2; 4



như hình vẽ bên. Tìm

 

 

2; 4

max

f x



.

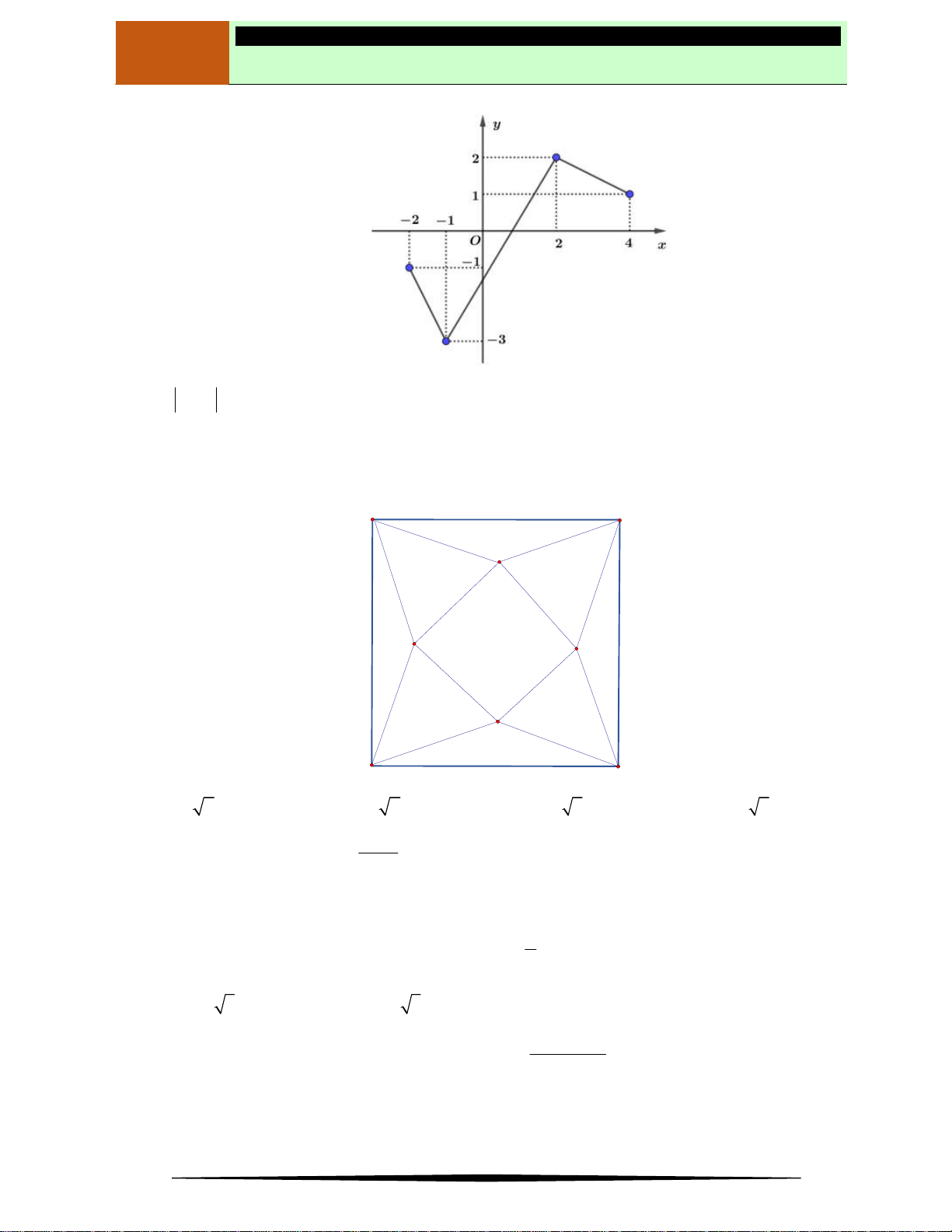
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 181

Ⓐ

 

0

f

. Ⓑ

2

. Ⓒ

3

. Ⓓ

1

.

Câu 17. Cho một tấm bìa hình vuông cạnh

50 cm

. Để làm một mô hình kim tự tháp Ai Cập,

người ta cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gấp lên,

ghép lại thành một hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của mô

hình bằng:

Ⓐ

20 2 cm

. Ⓑ

25 2 cm

. Ⓒ

15 2 cm

. Ⓓ

10 2 cm

.

Câu 18. Cho hàm số

 

1

x m

f x

x







, với

m

là tham số. Biết

 

 

 

 

0;3

min max 2

f x f x

  

. Hãy chọn

kết luận đúng.

Ⓐ

2

m



. Ⓑ

2

m



. Ⓒ

2

m

 

. Ⓓ

2

m

 

.

Câu 19. Tìm giá trị nhỏ nhất

m

của hàm số

3

y x

x

 

trên

 

0;



.

Ⓐ

4

4 3

m 

. Ⓑ

2 3

m 

. Ⓒ

4

m



Ⓓ

2

m



Câu 20. Tìm số tiệm cận đứng của đồ thị hàm số

2

3 2

4

x x

y

x

 





.

Ⓐ

1

. Ⓑ

2

. Ⓒ

3

. Ⓓ

4

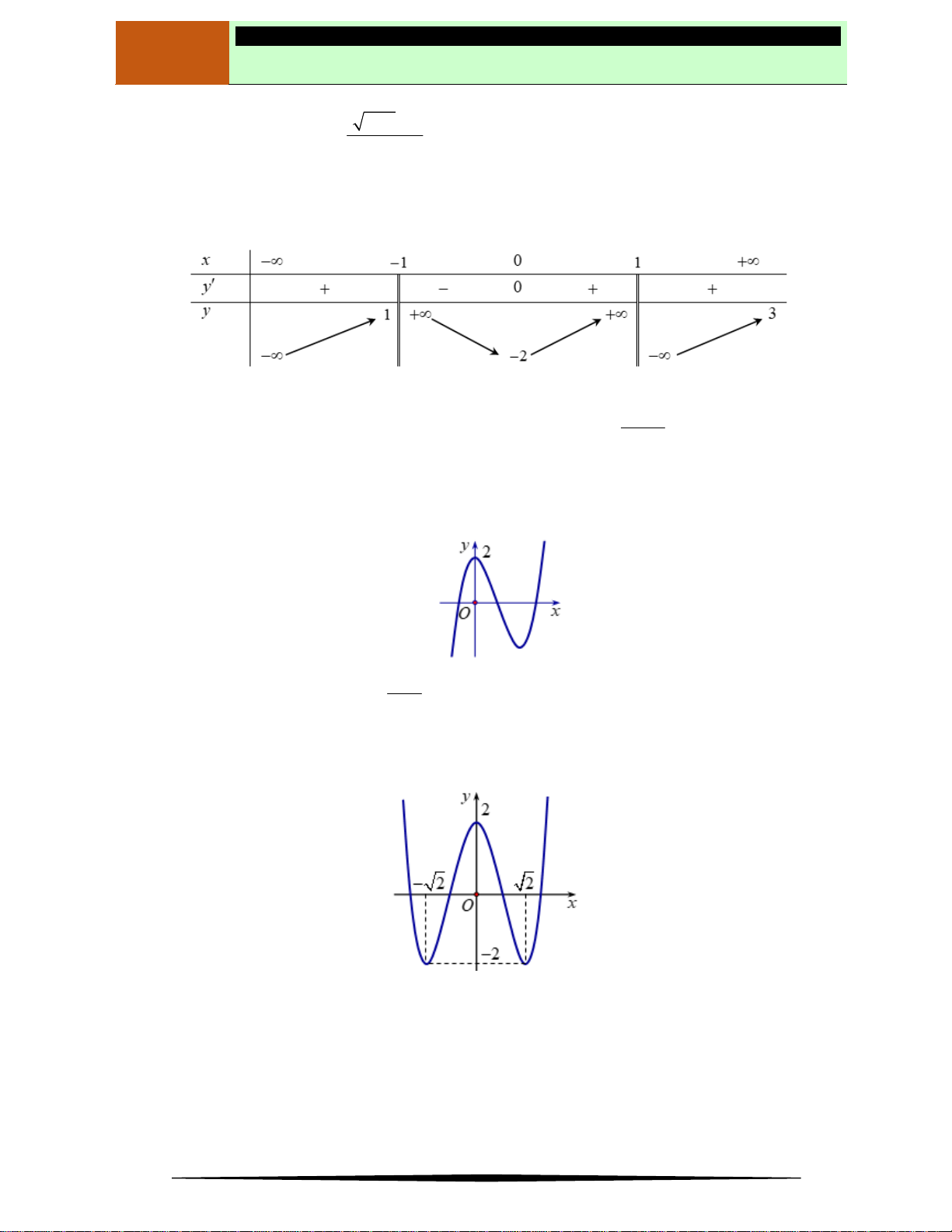
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 182

Câu 21. Đồ thị hàm số

2

1 1

4 5

 



 

x

y

x x

có tổng số bao nhiêu đường tiệm cận ngang và đứng?

Ⓐ

1

. Ⓑ

2

. Ⓒ

4

. Ⓓ

3

.

Câu 22. Cho hàm số

 

y f x



có bảng biến thiên như hình dưới. Hỏi đồ thị hàm số

 

y f x



có

bao nhiêu đường tiệm cận:

Ⓐ

3

. Ⓑ

4

. Ⓒ

2

. Ⓓ

1

.

Câu 23. Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

2 4

x

y

x m







có tiệm cận đứng.

Ⓐ

2

m

 

. Ⓑ

2

m

 

. Ⓒ

2

m

 

. Ⓓ

2

m

 

.

Câu 24. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm

số nào?

Ⓐ

3 2

y x x

  

. Ⓑ

2

1

x

y

x







. Ⓒ

3 2

y x x

   

. Ⓓ

4 3

2 2

y x x

  

.

Câu 25. Đường cong trong hình sau đây là đồ thị một hàm số nào trong bốn hàm số dưới đây?

Ⓐ

4 2

y x x

   

. Ⓑ

4 2

y x x

  

.

Ⓒ

4 2

y x x

  

. Ⓓ

4 2

y x x

  

.

Câu 26. Đồ thị sau là đồ thị của hàm số nào sau?

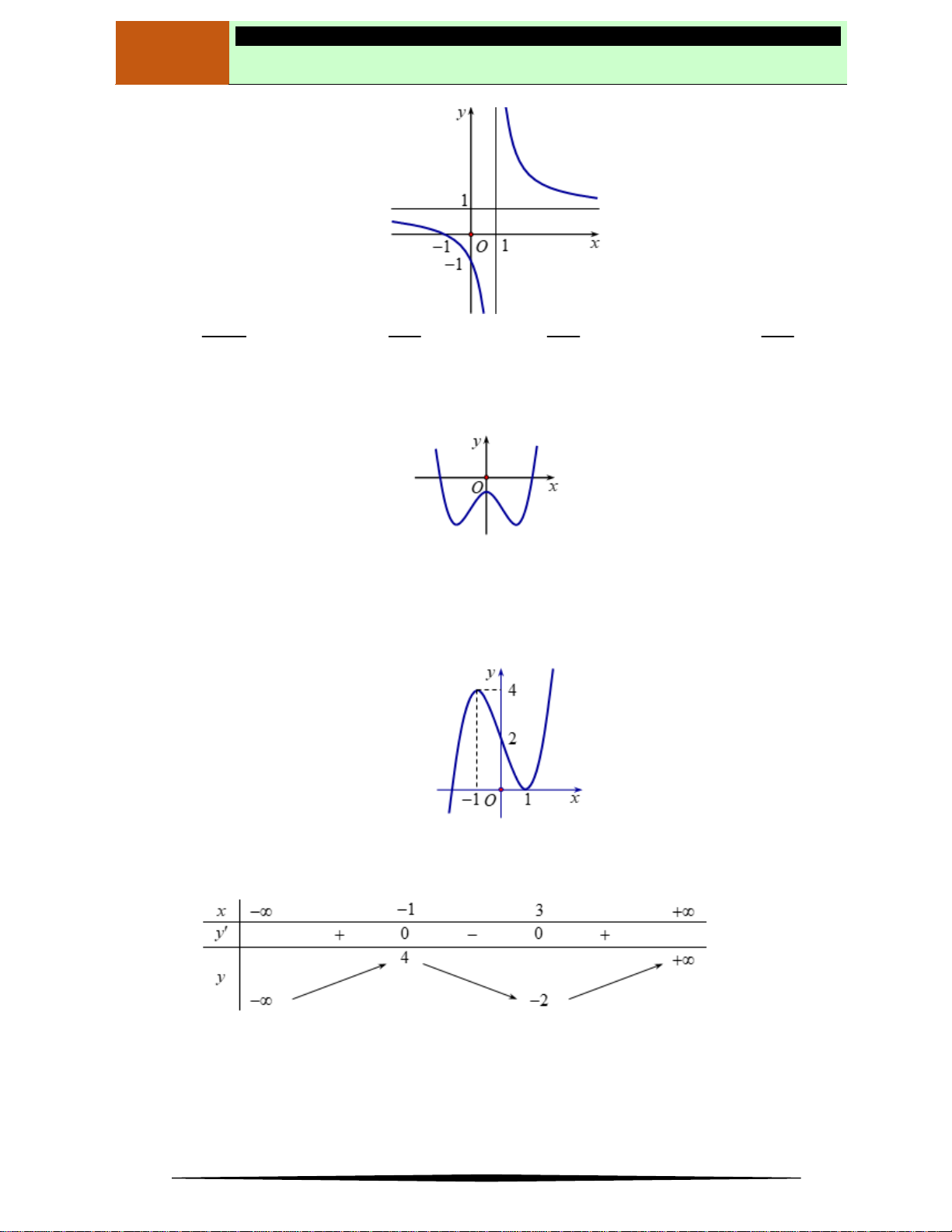
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 183

Ⓐ

2 3

2 2

x

y

x







. Ⓑ

1

x

y

x





. Ⓒ

1

x





. Ⓓ

1

x

y

x







.

Câu 27. Cho hàm số bậc bốn

 

4 2

0

y ax bx c a

   

có đồ thị như hình vẽ. Mệnh đề nào dưới

đây đúng?

Ⓐ

0, 0, 0

a b c

  

. Ⓑ

0, 0, 0

a b c

  

.

Ⓒ

0, 0, 0

a b c

  

. Ⓓ

0, 0, 0

a b c

  

.

Câu 28. Cho đồ thị hàm số

 

y f x



như hình vẽ. Tìm tất cả các giá trị thực

m

để phương trình

 

1

f x m 

có ba nghiệm phân biệt.

Ⓐ

0 5

m

 

. Ⓑ

1 5

m

 

. Ⓒ

1 4

m

  

. Ⓓ

0 4

m

 

.

Câu 29. Cho hàm số

 

y f x



có bảng biến thiên như sau

Số nghiệm của phương trình

 

2

4 0

f x

 

là

Ⓐ

3

. Ⓑ

5

. Ⓒ

1

. Ⓓ

2

.

Câu 30. Cho hàm số

 

y f x



xác định, liên tục trên



và có bảng biến thiên

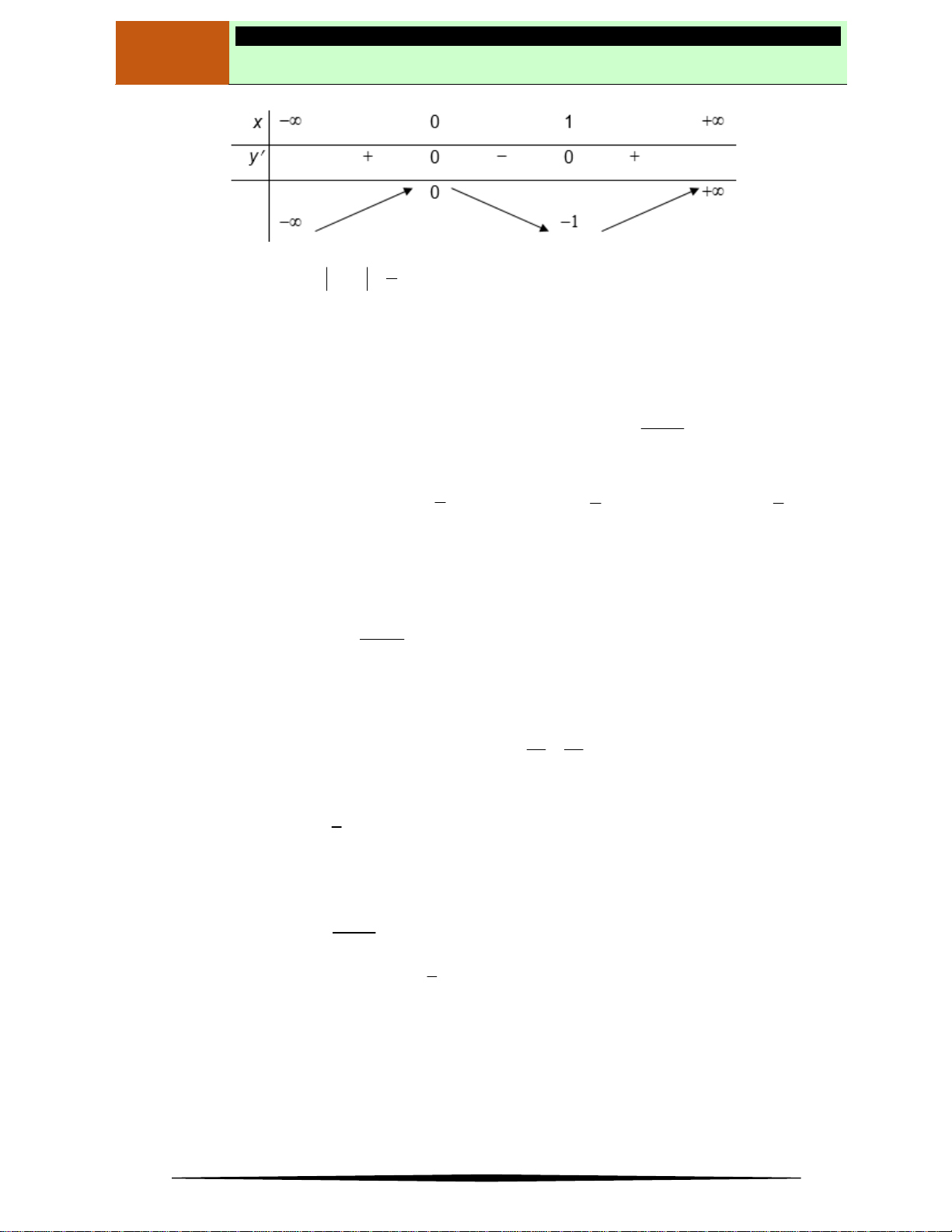
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 184

Hỏi phương trình

 

2

f x

e



có bao nhiêu nghiệm thực phân biệt

Ⓐ

4

. Ⓑ

2

. Ⓒ

3

. Ⓓ

1

.

Câu 31. Đồ thị hàm số

4 2

5 1

y x x

  

cắt trục hoành tại bao nhiêu điểm?

Ⓐ

1

. Ⓑ

4

. Ⓒ

3

. Ⓓ

2

.

Câu 32. Tìm

m

để đường thẳng

y x m 

 

d

cắt đồ thị hàm số

2 1

2

x

y

x







 

C

tại hai điểm phân

biệt thuộc hai nhánh của đồ thị

 

C

.

Ⓐ

m



. Ⓑ

1

\

2

m

 

 

 

 



. Ⓒ

1

2

m

 

. Ⓓ

1

2

m

 

.

Câu 33. Đồ thị hàm số

3 2

3 1

y x x

  

cắt đường thẳng

y m

tại ba điểm phân biệt thì tất cả các

giá trị tham số

m

thỏa mãn là

Ⓐ

1 .

m



Ⓑ

3 1 .

m

  

Ⓒ

3 1 .

m

  

Ⓓ

3.

m

 

Câu 34. Cho đồ thị

 

H

:

2 4

3

x

y

x







. Lập phương trình tiếp tuyến của đồ thị

 

H

tại giao điểm

của

 

H

và

Ox

.

Ⓐ

2y x

. Ⓑ

2 4y x  

. Ⓒ

2 4y x  

. Ⓓ

2 4

y x

 

.

Câu 35. Hệ số góc của tiếp tuyến của đồ thị hàm số

4 2

1

4 2

x x

y

  

tại điểm có hoành độ

0

1

x

 

bằng

Ⓐ

2

. Ⓑ Đáp số kháⒸ Ⓒ

2

. Ⓓ

0

.

Câu 36. Cho hàm số

3 2

1

3 7 2

3

y x x x

   

. Phương trình tiếp tuyến của đồ thị hàm số tại điểm

 

0;2

A

là

Ⓐ

7 2

y x

 

. Ⓑ

7 2y x  

. Ⓒ

7 2

y x

 

. Ⓓ

7 2y x  

.

Câu 37. Cho hàm số

2 1

2

x

y

x







có đồ thị

 

C

. Viết phương trình tiếp tuyến của

 

C

biết tiếp

tuyến vuông góc với đường thẳng

1

: 2 0

3

x y

    

là

Ⓐ

3 14

y x

 

. Ⓑ

3 14

y x

 

,

3 2

y x

 

.

Ⓒ

3 5y x 

,

3 8y x 

. Ⓓ

3 8y x 

.

Câu 38. Tìm số tiếp tuyến của đồ thị hàm số

3 2

4 6 1  

y x x

, biết tiếp tuyến đó đi qua điểm

 

1; 9 . 

M

Ⓐ

3

. Ⓑ

0

. Ⓒ

1

. Ⓓ

2

.

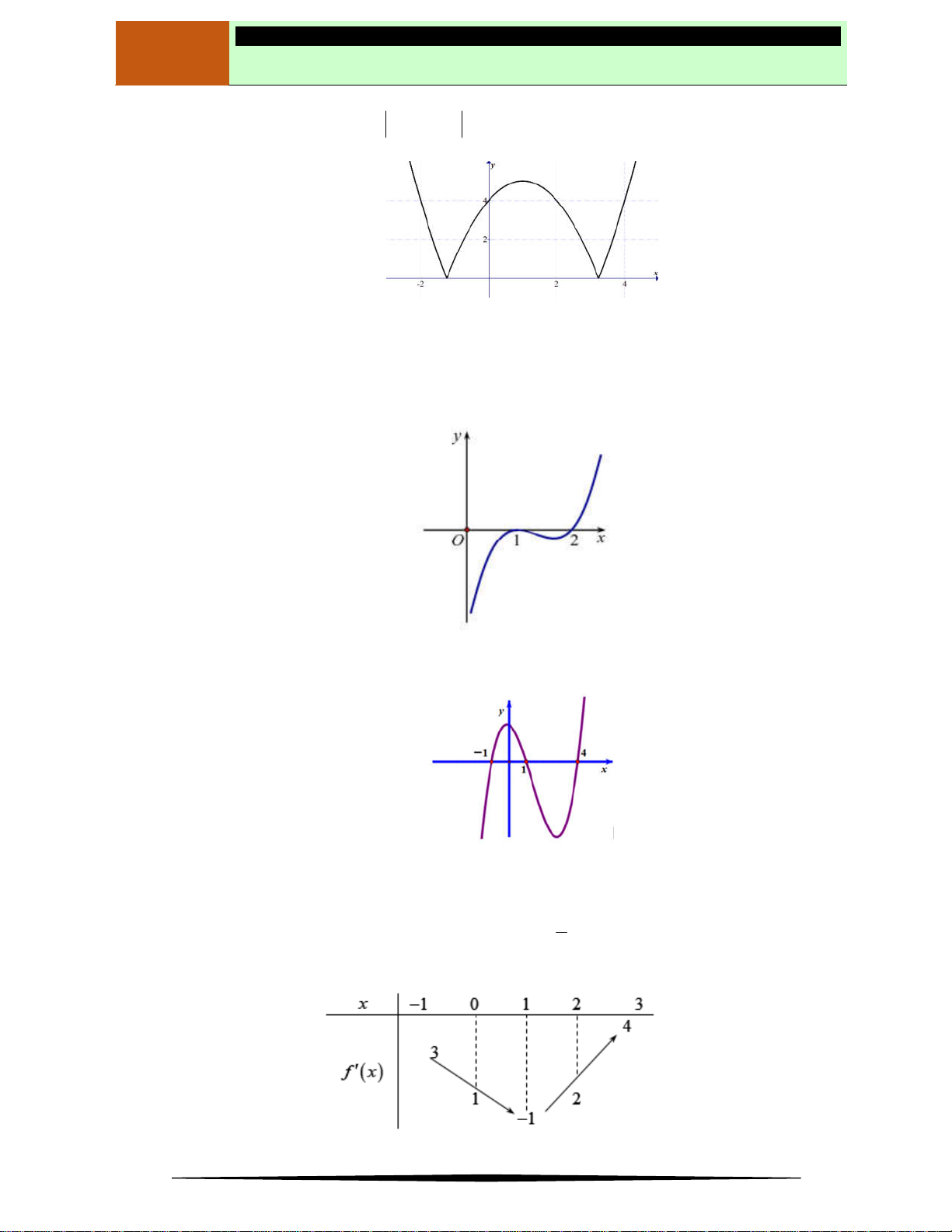
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 185

Câu 39. Cho hàm số

 

2

2 4   y f x x x

có đồ thị như hình vẽ. Đồ thị hàm số

 

y f x

có

bao nhiêu điểm cực trị?

Ⓐ

1

. Ⓑ

3

. Ⓒ

4

. Ⓓ

2

.

Câu 40. Hình dưới đây là đồ thị của hàm số

 

'

.y f x

Hỏi hàm số đồng biến trên khoảng nào

trong các khoảng dưới đây

Ⓐ

 

2;

. Ⓑ

 

0;1

. Ⓒ

 

1;2

. Ⓓ

 

;1

.

Câu 41. Cho hàm số

 

y f x

. Hàm số

 

y f x





có đồ thị như hình vẽ. Hàm số

 

3 2 2018y f x  

nghịch biến trên khoảng?

Ⓐ

 

1; 2

. Ⓑ

 

2;  

. Ⓒ

 

;1

. Ⓓ

 

1;1

.

Câu 42. Cho hàm số

 

y f x

có đạo hàm liên tục trên



. Bảng biến thiên của hàm số

 

y f x





được cho như hình vẽ bên. Hàm số

1

2

x

y f x

 

  

 

 

nghịch biến trên khoảng

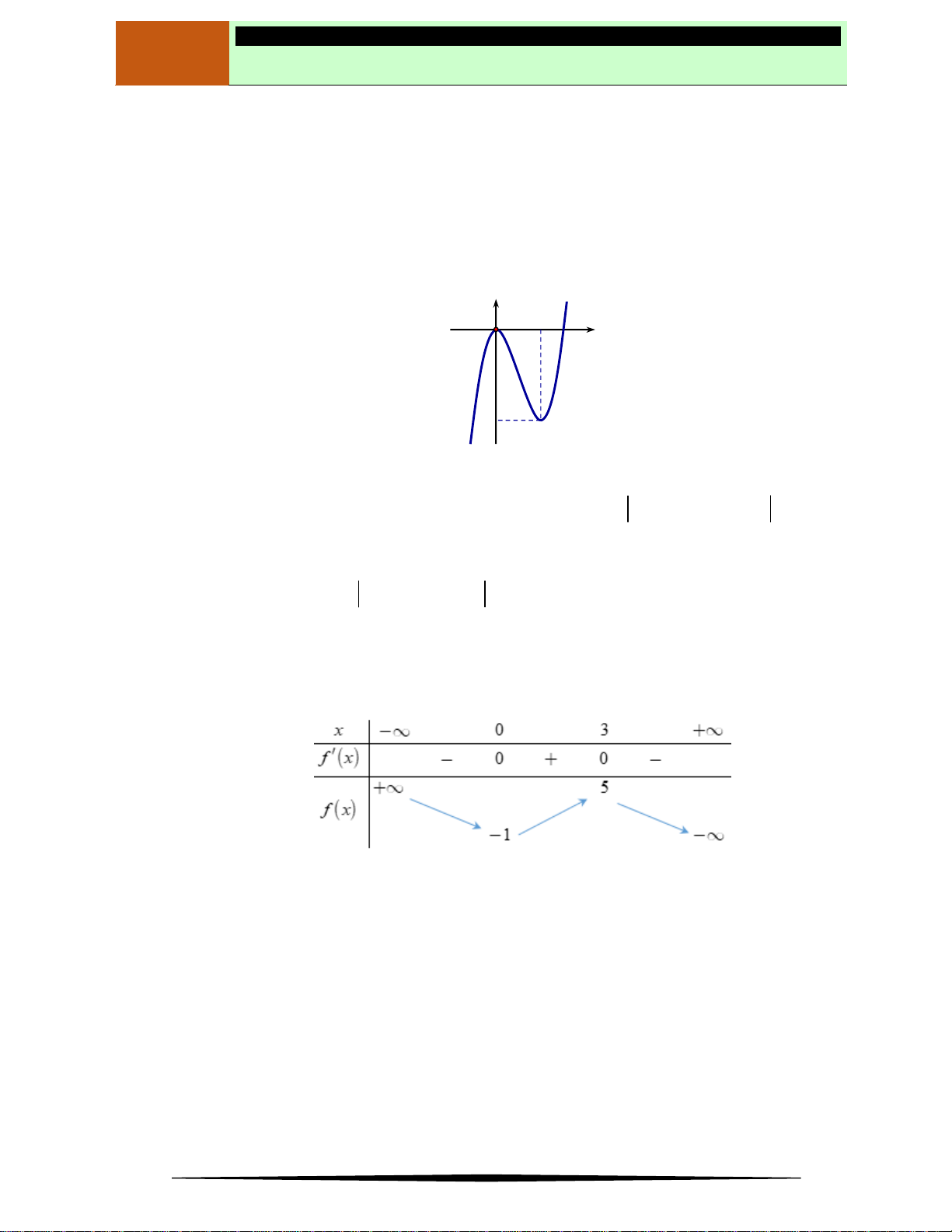
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 186

Ⓐ

 

2; 4

. Ⓑ

 

0; 2

. Ⓒ

 

2; 0

. Ⓓ

 

4; 2 

.

Câu 43. Cho hàm số

 

y f x

có đạo hàm

    

2

9 4f x x x x



  

. Khi đó hàm số

 

2

y f x

nghịch biến trên khoảng nào?

Ⓐ

 

2; 2

. Ⓑ

 

; 3 

. Ⓒ

 

3;0

. Ⓓ

 

3; 

.

Câu 44. Biết rằng hàm số

 

f x

có đồ thị được cho như hình vẽ bên. Tìm số điểm cực trị của hàm

số

 

y f f x

 

 

.

Ⓐ

5

. Ⓑ

3

. Ⓒ

4

. Ⓓ

6

.

Câu 45. Có bao nhiêu giá trị nguyên của tham số

m

để hàm số

4 3 2

3 4 12y x x x m   

có

7

điểm cực trị?

Ⓐ

3

. Ⓑ

5

. Ⓒ

6

. Ⓓ

4

.

Câu 46. Cho hàm số

 

4 3 2

4 4f x x x x a   

. Gọi

M

,

m

lần lượt là giá trị lớn nhất, giá trị nhỏ

nhất của hàm số đã cho trên đoạn

 

0;2

. Có bao nhiêu số nguyên

a

thuộc đoạn

 

3;3

sao cho

2M m

?

Ⓐ

3

. Ⓑ

7

. Ⓒ

6

. Ⓓ

5

.

Câu 47. Cho hàm số

 

f x

có bảng biến thiên như hình sau.

Hàm số

     

3 2

2 6 1g x f x f x  

có bao nhiêu điểm cực đại?

Ⓐ

3

. Ⓑ

4

. Ⓒ

6

. Ⓓ

8

.

Câu 48. Cho hàm số

 

y f x

liên tục trên



và có đồ thị như hình vẽ bên.

O

x

y

2

4

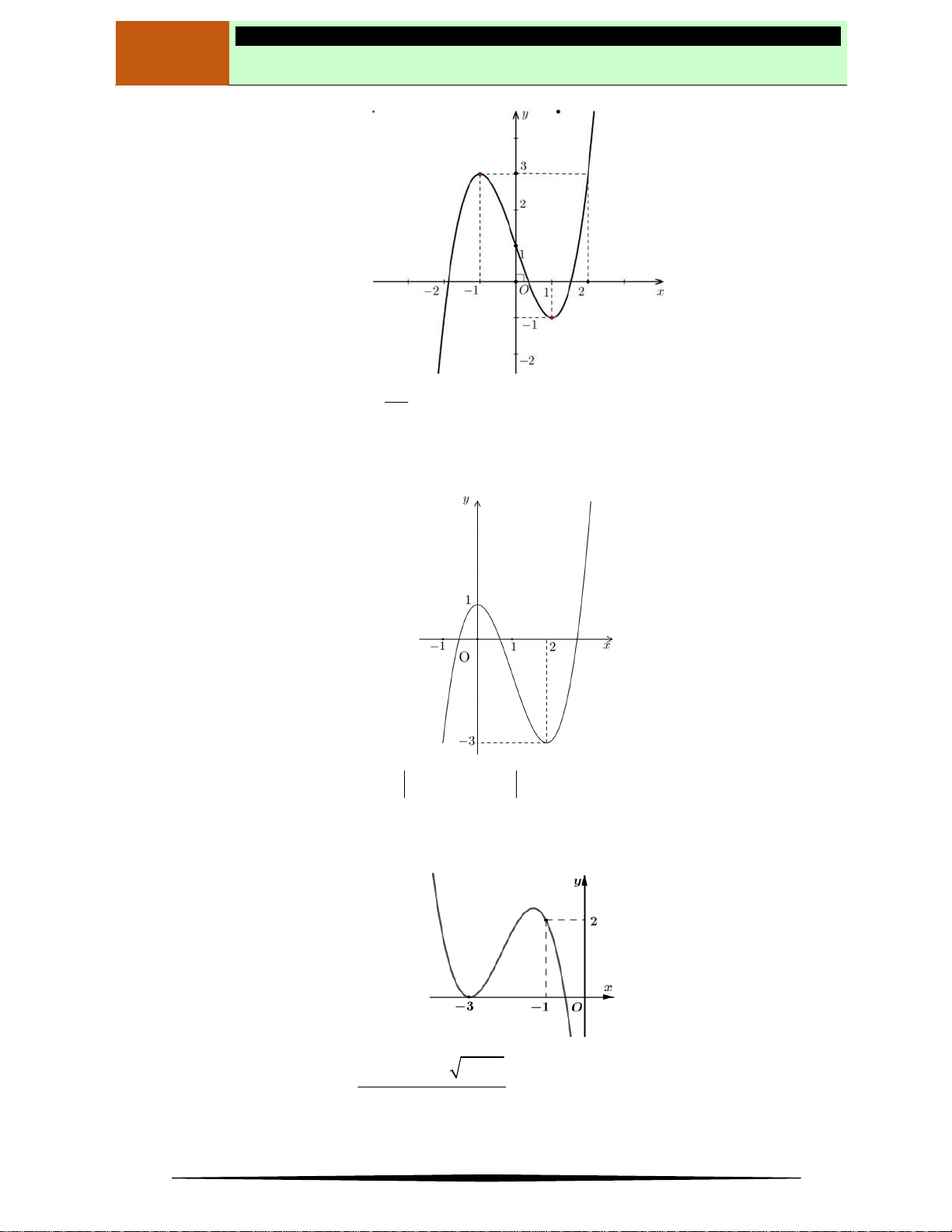
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 187

`

Số nghiệm thuộc đoạn

7

0;

2



 

 

 

của phương trình

 

cos 0f f x

là

Ⓐ

7

. Ⓑ

5

. Ⓒ

8

. Ⓓ

6

.

Câu 49. Cho hàm số

( )y f x

có đồ thị như hình vẽ

Số nghiệm của phương trình

 

3 2

3 2 1 0f x x   

là

Ⓐ

9

. Ⓑ

10

. Ⓒ

11

. Ⓓ

12

.

Câu 50. Cho hàm bậc ba

 

y f x

có đồ thị như hình vẽ bên.

Hỏi đồ thị hàm số

 

   

2 2

2

4 3

2

x x x x

y

x f x f x

  



 



 

có bao nhiêu đường tiệm cận đứng ?

Ⓐ

2

. Ⓑ

3

.

Ⓒ

4

. Ⓓ

6

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 188

 BẢNG ĐÁP ÁN CHƯƠNG I – ĐỀ 1

1B 2B 3B 4D 5D 6C 7C 8A 9B 10A

11C 12B 13C 14C 15C 16B 17A 18D 19B 20D

21B 22A 23B 24D 25D 26D 27A 28B 29D 30A

31D 32C 33C 34D 35D 36B 37C 38D 39B 40D

41C 42C 43C 44B 45A 46A 47B 48D 49D 50A

 BẢNG ĐÁP ÁN CHƯƠNG I – ĐỀ 2

1C 2D 3A 4D 5B 6B 7B 8D 9D 10A

11D 12B 13D 14A 15B 16C 17A 18B 19C 20A

21B 22A 23A 24A 25C 26D 27A 28B 29B 30A

31D 32A 33C 34B 35A 36A 37B 38D 39B 40A

41A 42D 43B 44C 45D 46D 47B 48A 49C 50C

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 189

§1. LŨY THỪA

A. TÓM TẮT LÝ THUYẾT

1. Định nghĩa lũy thừa:

Số mũ 

Cơ số a

Lũy thừa

a



*

n N



 

a



R

. ......

n

a a a a a



 

(n thừa số a)

0





0a 

0

1a a



 

*

( )n n N



  

0a 

1

n

a a

a





 

*

( , )

m

m Z n N

n



  

0a 

( )

m

n m n

n

a a a a b b a



    

*

lim ( , )

n n

r r Q n N



  

0a 

lim

n

r

a a





Chương

2

HÀM SỐ LŨY THỪA – HÀM SỐ

MŨ – HÀM SỐ LÔGARIT

1. LŨY THỪA

2. HÀM LŨY THỪA

3. LÔGARIT

4. HÀM SỐ MŨ, HÀM SỐ LOGARIT

5. PHƯƠNG TRÌNH MŨ

6. PHƯƠNG TRÌNH LÔGARIT

7. BẤT PHƯƠNG TRÌNH MŨ VÀ

BẤT PHƯƠNG TRÌNH LÔGARIT

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 190

2. Tính chất của lũy thừa:

 Với số mũ a > 0, b > 0 ta có:

.

. ; ; ( ) ; ( ) . ;

a a a

a a a a a a ab a b

a b b



 

            

 

 

 

    

 

 

 + a > 1 :

a a

 

  

+ 0 < a < 1 :

a a

 

  

 Với 0 < a < b ta có

+

0

m m

a b m

  

+

0

m m

a b m

  

Chú ý: + Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0.

+ Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương.

3. Định nghĩa và tính chất của căn thức:

 Căn bậc n của a là số b sao cho

n

b a

.

 Với a, b



0, m, n



N*, p, q



Z ta có:

.

n n n

ab a b



;

( 0)

n

a a

b

 

;

 

( 0)

p

n

p

n

a a a

 

;

m

n mn

a a



( 0)

n mp q

p q

Neáu thì a a a

n m

  

; Đặc biệt:

mn

m

n

a a



 + Nếu n là số nguyên dương lẻ và a < b thì

n n

a b

 .

+ Nếu n là số nguyên dương chẵn và 0 < a < b thì

n n

a b

 .

Chú ý:

+ Khi n lẻ, mỗi số thực a chỉ có một căn bậc n. Kí hiệu

n

a

.

+ Khi n chẵn, một số thực dương a có đúng hai căn bậc n là hai số đối nhau.

CÁC VÍ DỤ

Ví dụ 1: Thực hiện các phép tính sau:

a)

   

3 2

3

7 2 7

1 . . 7 .

8 7 14

A

     

     

     

     

b)

   

2 6

4

6 4

2

3 . 15 .8

9 . 5 . 6

B

 



 

--------------------------------------------------------------------------------------------------------------------------------

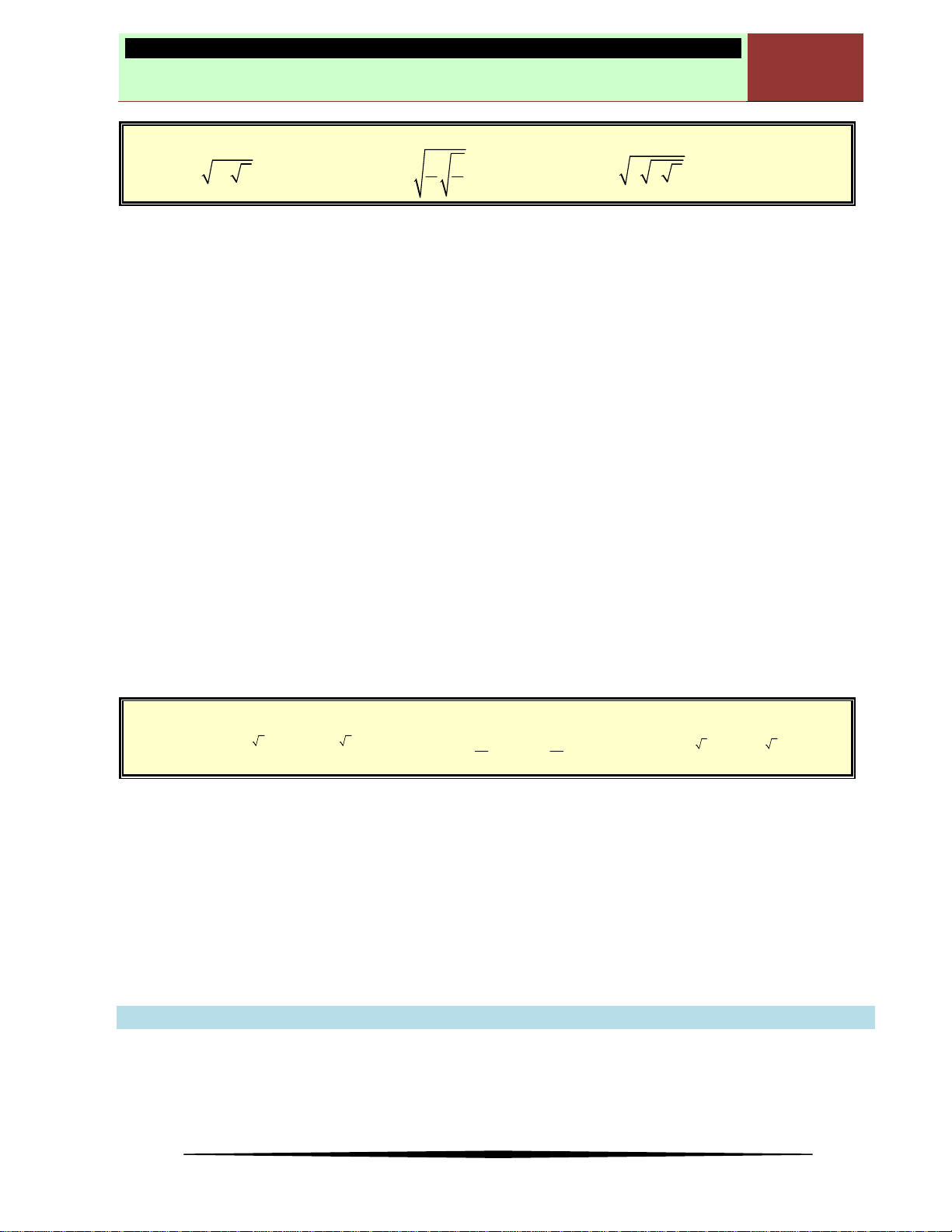
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 191

Ví dụ 2: Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:

a)

 

2

4

3

, 0

x x x



b)

 

5

3

, , 0

b a

a b



c)

5

3

2 2 2

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 3: So sánh các cặp số sau:

a)

 

2 2

0,01 vaø 10

 

b)

2 6

vaø

4 4

 

   

   

   

c)

2 3 3 2

5 vaø 5

 

--------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Bài 1: Thực hiện các phép tính sau:

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 192

a)

   

     

7 3

4

4 5 2

18 .2 . 50

25 . 4 . 27

E

 



  

b)

   

 

3 3

6

4

2

3

125 . 16 . 2

25 5

F

 



 



 

c)

 

   

2

3 1 3 4 2

0 3

3 2 2

2 .2 5 .5 0,01 .10

10 :10 0,25 10 0,01

G



  



  

 



 

d)

  

1 1 1 1 1

3 3 3 3 3

4 10 25 2 5

H    

Bài 2: Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:

a)

3

2 3 2

3 2 3

b)

4

3

8

a

c)

2

5

3

b b

Bài 3: Đơn giản các biểu thức sau :

a)

1,5 1,5

0,5 0,5

0,5

0,5 0,5

2

a b

b

a b

a b a b







 

b)

0,5 0,5 0,5

0,5 0,5

2 2 1

.

2 1 1

a a a

a a a a

 

  



 

  

 

c)

1 1 1 1 3 1

2 2 2 2 2 2

1 1 1 1

2 2 2 2

2

.

x y x y x y y

x y x y

xy x y xy x y

 

 

 

 

 

 

 

 

 

d)

   

1 2 2 1 2 4

3 3 3 3 3 3

. .

a b a a b b

  

Bài 4: Có thể kết luận gì về số a nếu:

a)

   

2 1

3 3

1 1

a a

 

  

b)

   

3 1

2 1 2 1

a a

 

  

c)

0,2

2

1

a



 



 

 

d)

   

1 1

3 2

1 1

a a

 

  

e)

   

3

2

4

2 2

a a

  

f)

1 1

2 2

1 1

a a



   



   

   

g)

3 7

a a



h)

1 1

17 8

a a

 



i)

0,25 3

a a

 



BÀI TẬP VỀ NHÀ

Câu 1. Với

a

là số thực dương tùy ý ,

2021

a

bằng

Ⓐ

1

2021

a

. Ⓑ

2021

a

. Ⓒ

2021

a

. Ⓓ

2021

a

.

Câu 2. Với

a

là số thực dương tùy ý,

 

10

2

3

:

p

q

a a a



với

,p q



và

p

q

là phân số tối giản.Giá trị của

p q

bằng

Ⓐ

2 3

. Ⓑ

7

. Ⓒ

8

. Ⓓ

19

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 193

Câu 3. Cho

0

x



.Biểu thức

5

.P x x



bằng

Ⓐ

7

5

x

. Ⓑ

6

5

x

. Ⓒ

1

5

x

. Ⓓ

4

5

x

.

Câu 4. Với

a

là số thực dương tùy ý,

3

1

a

bằng?

Ⓐ

3

a



. Ⓑ

3

2

a

. Ⓒ

1

6

a

. Ⓓ

3

2

a



.

Câu 5. Giá trị của biểu thức

2 1 2 1 2

3 .9 .27

 

bằng

Ⓐ

9

. Ⓑ

1

. Ⓒ

3

. Ⓓ

27

.

Câu 6. Cho

0

x



.Biểu thức

5

P x x



bằng

Ⓐ

6

5

x

. Ⓑ

1

5

x

. Ⓒ

4

5

x

. Ⓓ

7

5

x

.

Câu 7. Cho số thực

a

dương.Rút gọn biểu thức

1

4

P a a

ta được biểu thức nào sau đây?

Ⓐ

1

2

a

. Ⓑ

3

4

a

. Ⓒ

9

4

a

. Ⓓ

1

4

a

.

Câu 8. Một người gởi

150

triệu đồng vào ngân hàng với lãi suất

0,42% /

tháng.Biết rằng nếu không rút

tiền khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng tiếp

theo.Hỏi sau đúng 5 tháng người đó được lĩnh số tiền gần nhất với số tiền nào dưới đây,nếu trong thời gian

đó người đó không rút tiền ra và lãi suất không đổi?

Ⓐ

153.636.000

đồng. Ⓑ

153.820.000

đồng.

Ⓒ

152.836.000

đồng. Ⓓ

153.177.000

đồng.

Câu 9. Cho

a

là số thực dương và

,m n

là các số thực tùy ý.Mệnh đề nào sau đây đúng?

Ⓐ

.

m n m n

a a a



. Ⓑ

.

m n m n

a a a a 

. Ⓒ

 

. .

n

m n m

a a a a



. Ⓓ

.

m n m n

a a a





.

Câu 10. Một người gởi

150

triệu đồng vào ngân hàng với lãi suất

0,42% /

tháng.Biết rằng nếu không rút

tiền khỏi ngân hàng thì cứ sau mỗi tháng số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho tháng tiếp

theo.Hỏi sau đúng 5 tháng người đó được lĩnh số tiền gần nhất với số tiền nào dưới đây,nếu trong thời gian

đó người đó không rút tiền ra và lãi suất không đổi?

Ⓐ

153.636.000

đồng. Ⓑ

153.820.000

đồng.

Ⓒ

152.836.000

đồng. Ⓓ

153.177.000

đồng.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 194

Câu 11. Cho

,a b

là các số thực dương và thỏa mãn

5

x

a



,

3

x

b



.Giá trị của biểu thức

25 15 27

x x x

P   

bằng

Ⓐ

3 2

P a ab b  

. Ⓑ

2 2 2

P a b ab b  

.

Ⓒ

2 3

P a ab b  

. Ⓓ

3 2

P ab ab b  

.

Câu 12. Tính giá trị biểu thức

   

2020 2021

2 1 . 2 1 2

P    

Ⓐ

2 1

P

 

. Ⓑ

1P 

. Ⓒ

2 1

P

 

. Ⓓ

0

P



.

Câu 13. Cho

a

là số thực dương.Giá trị của biểu thức

4

3

P a a



bằng

Ⓐ

11

6

a

. Ⓑ

1

6

a

. Ⓒ

2

a

. Ⓓ

5

6

a

Câu 14. Cho biểu thức

2

4

3

P x x



,(

0

x



).Mệnh đề nào dưới đây đúng?

Ⓐ

8

12

P x



. Ⓑ

9

12

P x



. Ⓒ

1

6

P x

. Ⓓ

7

12

P x



.

Câu 15. Cho đẳng thức

4

2 2.

2

x



.Mệnh đề nào sau đây đúng?

Ⓐ

7

8

x



. Ⓑ

3

4

x



Ⓒ

3

4

x

 

. Ⓓ

7

8

x

 

.

Câu 16. Cho

   

2018 2019

5 2 6 5 2 6P   

.Ta có

Ⓐ

 

3;5

P 

. Ⓑ

 

5;7

P 

. Ⓒ

 

7;9

P 

. Ⓓ

 

9;11

P 

.

Câu 17. Tính giá trị biểu thức

3 3

3(3 3 )

x x

A



 

biết

3 3 4

x x

 

Ⓐ

12

. Ⓑ

192

. Ⓒ

3

. Ⓓ

156

.

Câu 18. Cho hàm số

 









1

3 4

3

1

8 8

3 1

8

a a a

f a

a a a







với

0, 1

a a

 

.Tính giá trị

 

2020

2021M f

Ⓐ

2020

1 2021

M  

. Ⓑ

1010

2021 1

M

  

.

Ⓒ

1010

2021 1

M

 

. Ⓓ

2019

2021 1

M

 

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 195

Câu 19. Rút gọn biểu thức

 

3 1 2 3

2 2

.a a

P

a

 







với

0

a



.

Ⓐ

5

a

. Ⓑ

2

a

. Ⓒ

3

a

. Ⓓ

a

.

Câu 20. Tập xác định của hàm số

   

1

3

2 2

5

2 4

y x x x



    

là

Ⓐ

 

\ 1;2

D  



. Ⓑ

 

2; 1

D

  

.

Ⓒ

   

2;2 \ 1

D

  

. Ⓓ

     

; 1 2; \ 2

D

     

.

Câu 21. Biết

 

10

3 3 3

0 1 2

1 2 2 4

a a a   

.Tính

2

a

.

Ⓐ

2

210

a 

. Ⓑ

2

342

a 

. Ⓒ

2

45

a



. Ⓓ

2

729

a 

.

Câu 22. Cho

a

là số thực dương.Giá trị của biểu thức

2

3

P a a



bằng

Ⓐ

2

3

a

. Ⓑ

5

6

a

. Ⓒ

7

6

a

. Ⓓ

5

a

.

Câu 23. Cho

a

là số thực dương tùy ý,

3

2

3

a

bằng

Ⓐ

2

9

a

. Ⓑ

2

a

. Ⓒ

11

3

a

. Ⓓ

7

3

a



.

Câu 24. Thu gọn biểu thức



4

3

.A a a

với

a

là số thực dương ta được ?

Ⓐ



3

4

A a

. Ⓑ



7

4

A a

. Ⓒ



5

2

A a

. Ⓓ



1

4

A a

.

Câu 25. Xét các số thực

,ba

sao cho

b 0a 

.Khẳng định nào sau đây là sai?

Ⓐ

3

6

ab ab



. Ⓑ

 

8

ab ab

. Ⓒ

6 6 6

.ab a b



. Ⓓ

 

1

5

ab ab



.

Câu 26. Cho

,a b

là các số thực dương.Rút gọi biểu thức





4

3 2

4

3

12 6

a b

P

a b



được kết quả là:

Ⓐ

2

P ab



. Ⓑ

2 2

P a b



. Ⓒ

2

P a b



. Ⓓ

P ab

.

Câu 27. Viết biểu thức

3

4

P x x



dưới dạng lũy thừa với số mũ hữu tỷ

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 196

Ⓐ

5

12

P x



. Ⓑ

1

7

P x

. Ⓒ

1

12

P x



. Ⓓ

5

4

P x

.

Câu 28. Với

a

là số thực dương tùy ý

7

4

a

bằng

Ⓐ

7

4

a

. Ⓑ

7

a

. Ⓒ

28

a

. Ⓓ

4

7

a

.

Câu 29. Với

,a b

là các số thực dương.Rút gọn của biểu thức

1 1

3 3

6 6

a b b a

A

a b







là

Ⓐ

3 3

a b

. Ⓑ

3

2 2

a b

. Ⓒ

3

ab

. Ⓓ

6

ab

.

Câu 30. Cho hai số thực dương

a

và

b

.Rút gọn biểu thức

1 1

3 3

6 6

a b b a

A

a b







.

Ⓐ

3

A ab



. Ⓑ

6

A ab



. Ⓒ

3

1

ab

. Ⓓ

6

1

ab

.

Câu 31. Cho

0

a



,viết biểu thức

3

P a a



về dạng

m

a

.Khi đó giá trị

m

bằng:

Ⓐ

2

3

. Ⓑ

7

10

. Ⓒ

5

6

. Ⓓ

1

12

.

Câu 32. Cho

b

là số thực dương.Biểu thức

2

5

3

.

b b b

b b

được viết dưới dạng lũy thừa với số mũ hữu tỉ là:

Ⓐ

1

2

b

Ⓑ

3

2

b

. Ⓒ

2

3

b

. Ⓓ

b

.

Câu 33. Rút gọn biểu thức

7

3 5

3

7

4 2

.

a a

A

a a





với

0

a



ta được kết quả

m

n

A a



,trong đó

*

,m n



và

m

n

là

phân số tối giản.Khẳng định nào sau đây đúng?

Ⓐ

2

3 2 2

m n

 

. Ⓑ

2 2

43

m n

 

. Ⓒ

2

2 15

m n

 

. Ⓓ

2 2

25

m n

 

.

Câu 34. Cho

x

là số thực dương và biểu thức

3

2

4

P x x x



.Viết biểu thức

P

dưới dạng lũy thừa của một

số với số mũ hữu tỉ.

Ⓐ

19

24

P x



. Ⓑ

58

63

P x



. Ⓒ

1

432

P x



. Ⓓ

1

4

P x

.

Câu 35. Cho

0

a



,viết biểu thức

3

P a a



về dạng

m

a

.Khi đó giá trị

m

bằng:

Ⓐ

2

3

. Ⓑ

7

10

. Ⓒ

5

6

. Ⓓ

1

12

.

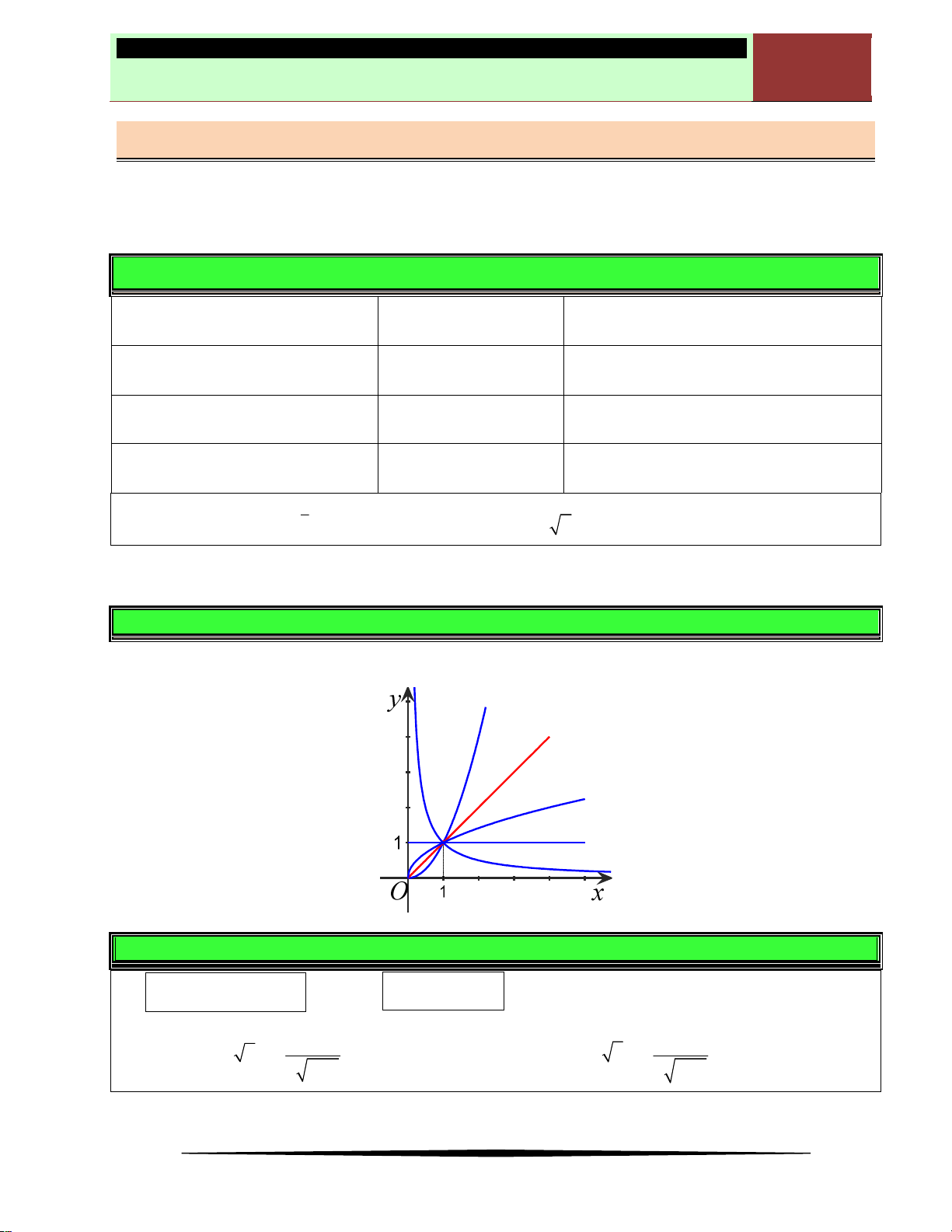
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 197

§2. HÀM LŨY THỪA

A. TÓM TẮT LÝ THUYẾT

1. Khái niệm hàm số lũy thừa :

y x





( là hằng số)

Số mũ 

Hàm số

y x





Tập xác định D

 = n (n nguyên dương)

n

y x

D = R

 = n (n nguyên âm hoặc n = 0)

n

y x

D = R \ {0}

 là số thực không nguyên

y x





D = (0; +)

Chú ý : Hàm số

1

n

y x



không đồng nhất với hàm số

( *)

n

y x n N

 

.

2. Đồ thị hàm số lũy thừa :

3. Đạo hàm:



 

1

( 0)

x x x





 

 



;

 

1

.u u u







 



Chú ý:

 

1

0

n

voi x neu n chan

x

voi x neu n le

n x







 



 



 

.

 

1

n

u

n u







  





  

 

 

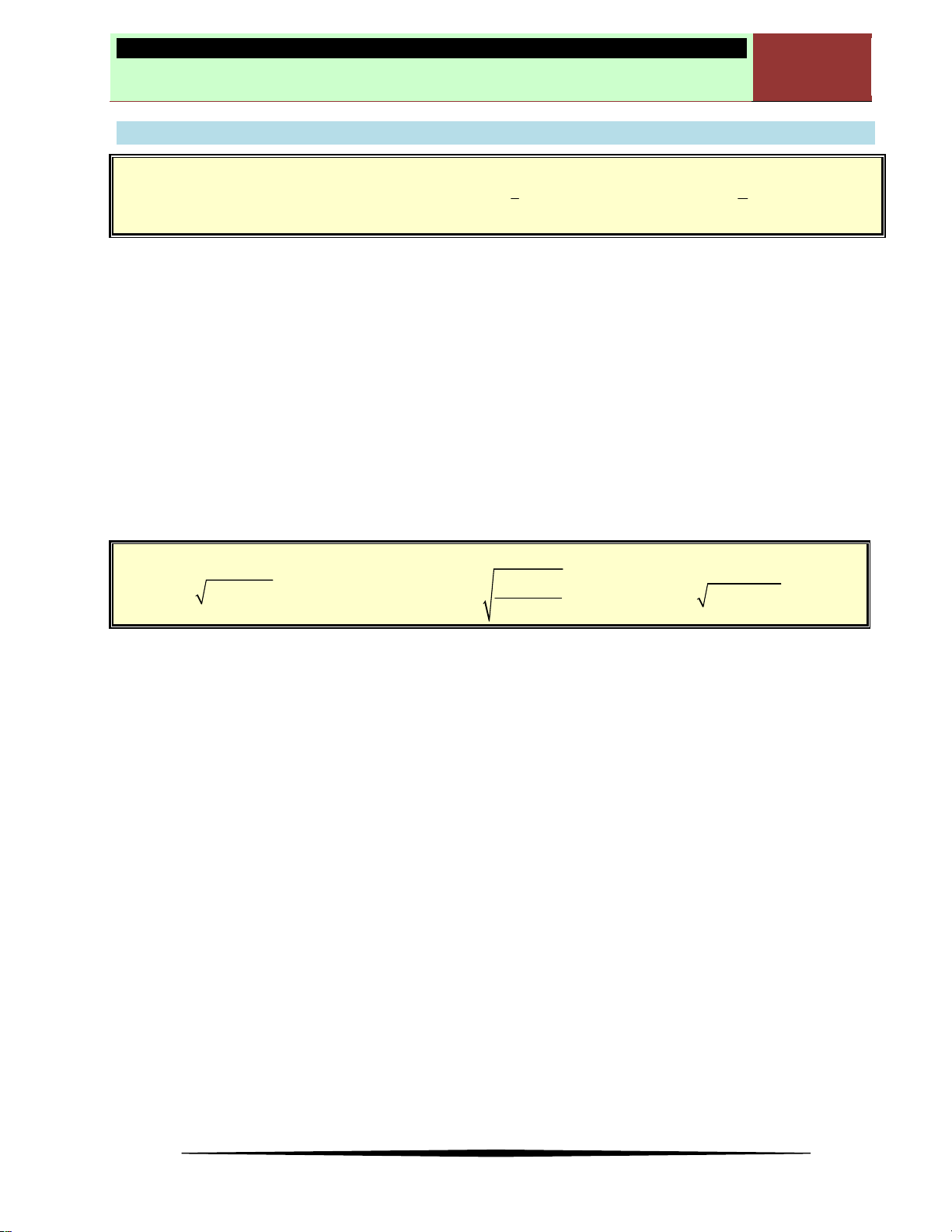
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 198

CÁC VÍ DỤ

Ví dụ 1: Tìm tập xác định của các hàm số sau:

a)

 



  

2

4 3

y x x

b)

 

  

2

3

6

y x x

c)

 



 

3

8

y x

--------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2 Tính đạo hàm của các hàm số sau:

a)

3

2

1

y x x

  

b)

2

4

2

1

x x

y

x x

 



 

c)

3

sin(2 1)

y x

 

--------------------------------------------------------------------------------------------------------------------------------

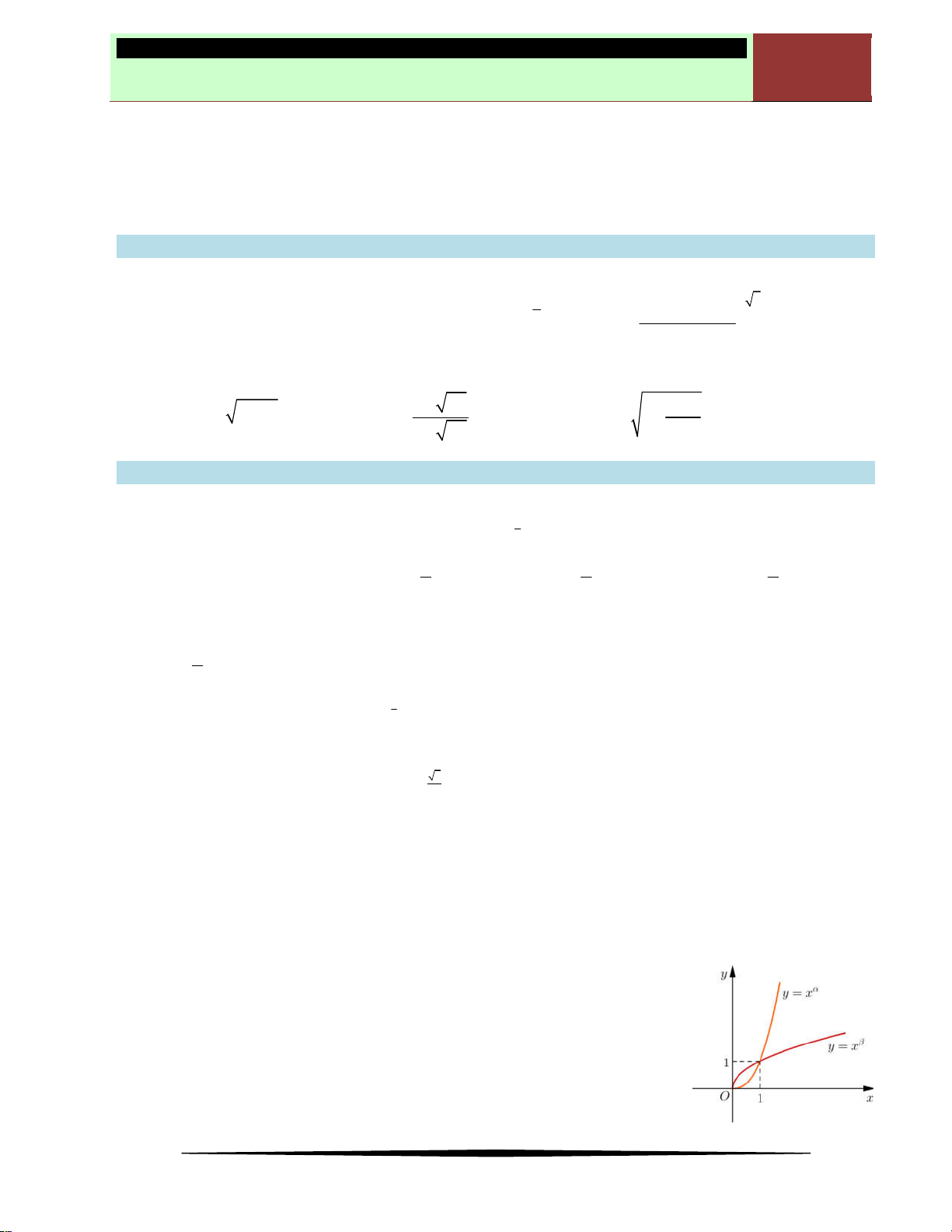
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 199

--------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Bài 1. Tìm tập xác định của các hàm số sau:

a)

 



  

4

3 2

6 9

y x x x

b)

 

  

1

3 2

4

3 2

y x x x

c)

 





 

  

 

5

2

2 1

7 10

x

y

x x

Bài 2. Tính đạo hàm của các hàm số sau:

a)

3

2

cot 1

y x

 

b)

3

1 2

x

y

x







c)

3

sin

4

x

y





BÀI TẬP TRẮC NGHIỆM

Câu 1. Tìm tập xác định

D

của hàm số

   

1

2

4 3

f x x 

.

Ⓐ

.

D

 

Ⓑ

3

\ .

4

D

 



 

 



Ⓒ

3

;

4

D

 

 





 

. Ⓓ

3

; .

4

D

 

 

 

 

Câu 2. Tập xác định của hàm số

 

2

2y x x





 

là

Ⓐ

1

0;

2

 

 

 

. Ⓑ

 

0;2

. Ⓒ

 

0;2

. Ⓓ

   

;0 2;

  

.

Câu 3. Tập xác định của hàm số

1

3

y x

là

Ⓐ



. Ⓑ

 

0;



. Ⓒ

 

\ 0

. Ⓓ





0;



.

Câu 4. Tập xác định của hàm số là:

Ⓐ Ⓑ Ⓒ Ⓓ .

Câu 5. Cho hàm số trong các kết luận sau kết luận nào sai?

Ⓐ Đồ thị hàm số nhận làm hai tiệm cận.

Ⓑ Đồ thị hàm số luôn đi qua

Ⓓ Tập xác định của hàm số là

Câu 6.

Cho là các số thựⒸ Đồ thị các hàm số , trên

khoảng được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?

Ⓐ

. Ⓑ .

2

3

( 2)

y x 





\ 2



( 2; ) 

(0; )

3e

y x





,Ox Oy

 

1,1 .

M

 

0, .

 

0, .

D

 

,

 

y x





y x





 

0; +

0 1

 

  

0 1

 

  

0 1

 

  

0 1

 

  

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 200

Câu 7. Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên?

Ⓐ Ⓑ Ⓒ Ⓓ

Câu 8. Đạo hàm của hàm số là

Ⓐ . Ⓑ .

Câu 9. Trong các khẳng định sau, khẳng định nào sai?

Ⓐ Nếu

, ,a b c

dương và

a b c 

thì

2016 2016 2016

a b c 

.

Ⓑ Hàm số

x

y x có đạo hàm là

1

' .

x

y x x



 .

Ⓒ

3 3

7 5 2 7 5 2   A

là một số tự nhiên.

Ⓓ Hàm

 

2

2y x x  

xác định với mọi

x

.

Câu 10. Hàm số y =

3

2

1 x

có tập xác định là

Ⓐ [-1; 1] Ⓑ (-; -1]  [1; +) Ⓒ R\{-1; 1} Ⓓ R

Câu 11. Hàm số y =

 

4

2

4x 1



có tập xác định là

Ⓐ R Ⓑ (0; +)) Ⓒ R\

1 1

;

2 2

 



 

 

Ⓓ

1 1

;

2 2

 



 

 

Câu 12. Hàm số y =

 

3

2

5

4 x

có tập xác định là

Ⓐ [-2; 2] Ⓑ (-: 2]  [2; +) Ⓒ R Ⓓ R\{-1; 1}

Câu 13. Hàm số y =

 

e

2

x x 1



 

có tập xác định là

Ⓐ R Ⓑ (1; +) Ⓒ (-1; 1) Ⓓ R\{-1; 1}

Câu 14. Hàm số y =

 

2

3

x 1

có đạo hàm là

Ⓐ y’ =

3

2

4x

3 x 1

Ⓑ y’ =

 

2

3

4x

3 x 1

3

2

2x x 1

Ⓓ y’ =

 

2

3

4x x 1

Câu 15. Hàm số y =

3

2

2x x 1 

có đạo hàm f’(0) là

Ⓐ

1

3



Ⓑ

1

3

.y x

4

.y x



1

5

.y x



.y x



 

1

2

3

5 2

y x x  

3 2

10 1

3 5 2

x

y

x x







 

 

2

3

10 1

5 2

x

y

x x







 

 

2

3

10 1

3 5 2

x

y

x x







 

 

2

3

1

3 5 2

y

x x





 

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 201

Câu 16. Cho hàm số y =

4

2

2x x

. Đạo hàm f’(x) có tập xác định là

Ⓐ R Ⓑ (0; 2) Ⓒ (-;0)  (2; +) Ⓓ R\{0; 2}

Câu 17. Hàm số y =

3

a bx



có đạo hàm là

Ⓐ y’ =

3

bx

3 a bx



Ⓑ y’ =

 

2

3

bx

a bx

3

2 3

3bx a bx



Ⓓ y’ =

2

3

3bx

2 a bx



Câu 18. Cho f(x) =

3

2 2

x x

. Đạo hàm f’(1) bằng

Ⓐ

3

8

Ⓑ

8

3

Câu 19. Cho f(x) =

3

x 2

x 1





. Đạo hàm f’(0) bằng

Ⓐ 1 Ⓑ

3

1

4

Ⓒ

3

2

Ⓓ 4

Câu 20. Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng nó xác định?

Ⓐ y = x

-4

Ⓑ y =

3

4

x



4

Ⓓ y =

3

x

Câu 21. Cho hàm số y =

 

2

x 2





. Hệ thức giữa y và y” không phụ thuộc vào x là

Ⓐ y” + 2y = 0 Ⓑ y” - 6y

2

= 0 Ⓒ 2y” - 3y = 0 Ⓓ (y”)

2

- 4y = 0

Câu 22. Cho hàm số y = x

-4

. Tìm mệnh đề sai trong các mệnh đề sau:

Ⓐ Đồ thị hàm số có một trục đối xứng. Ⓑ Đồ thị hàm số đi qua điểm (1; 1)

Câu 23. Trên đồ thị (C) của hàm số y =

2

x



lấy điểm M

0

có hoành độ x

0

= 1. Tiếp tuyến của (C) tại điểm

M

0

có phương trình là

Ⓐ y =

x 1

2





Ⓑ y =

x 1

2 2

 

 

x 1   

Ⓓ y =

x 1

2 2

 

  

Câu 24. Trên đồ thị của hàm số y =

1

2

x





lấy điểm M

0

có hoành độ x

0

=

2



. Tiếp tuyến của (C) tại điểm M

0

có hệ số góc bằng

Ⓐ  + 2 Ⓑ 2 Ⓒ 2 - 1 Ⓓ 3

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 202

§3. LÔGARIT

A. TÓM TẮT LÝ THUYẾT

1. Định nghĩa :

 Với a > 0, a



1, b > 0 ta có:

log

a

b a b  



Chú ý:

log

a

b

có nghĩa khi

0, 1

0

a a

b



 







 Logarit thập phân:

10

lg log log

b b b

 

 Logarit tự nhiên (logarit Nepe):

ln log

e

b b



(vôùi

1

lim 1 2,718281

n

e

n

 

  

 

 

)

2. Tính chất của lôgarit:



log 1 0

a



;

log 1

a

a 

;

log

b

a

a b

;

log

( 0)

a

b

a b b

 

 Cho a > 0, a



1, b, c > 0. Khi đó:

+ Nếu a > 1 thì

log log

a a

b c b c  

+ Nếu 0 < a < 1 thì

log log

a a

b c b c  

3. Các qui tắc tính lôgarit:

Với a > 0, a



1, b, c > 0, ta có:



log ( ) log log

a a a

bc b c

 



log log log

a a a

b

b c

c

 

 

 

 



log log

a a

b b





4. Đổi cơ số:

Với a, b, c > 0 và a, b



1, ta có:



log

a

b

a

c

b



hay

log .log log

a b a

b c c



TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 203



1

log

a

b

a





1

log log ( 0)

a

c c

 



CÁC VÍ DỤ

Ví dụ 1: Thực hiện các phép tính sau:

a)

2 1

4

log 4.log 2

b)

3

2

log 2

log 3

4 9

c)

3 81

2log 2 4log 5

9



--------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: So sánh các cặp số sau:

a)

3 4

1

log 4 ; log

3

b)

3

0,1 0,2

log 2 ; log 0,34

c)

3 5

4 2

2 3

log ; log

5 4

--------------------------------------------------------------------------------------------------------------------------------

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 204

--------------------------------------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------------------------------------

Ví dụ 3: Tính gía trị của biểu thức logarit theo các biểu thức đã cho:

a) Cho

2

log 14

a

. Tính

49

log 32

theo a.

b) Cho

15

log 3

a

. Tính

25

log 15

theo a.

--------------------------------------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------------------

----------------------------------------------------------------------------------------------------------------------------

---------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Bài 1. Thực hiện các phép tính sau:

a)

5 27

1

log .log 9

25

b)

3

log

a

c)

3 4

1/3

7

1

log .log

log

a a

a

a a

a

d)

3 8 6

log 6.log 9.log 2

e)

9 9

3

log 36 4log 7

log 5

81 27 3 

f)

3 81

2log 2 4log 5

9



g)

5 7

log 6 log 8

25 49

h)

5

3 2log 4

5



i)

6 8

1 1

log 3 log 2

9 4

Bài 2. Tính gía trị của biểu thức logarit theo các biểu thức đã cho:

a) Cho

lg3 0,477

. Tính

lg9000

;

lg0,000027

;

81

1

log 100

b). Cho

7

log 2

a

. Tính

1

2

log 28

theo a.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 205

Bài 3. Tính gía trị của biểu thức logarit theo các biểu thức đã cho:

a) Cho

25

log 7

a

;

2

log 5

b

. Tính

3

5

49

log

8

theo a, b.

b) Cho

30

log 3

a

;

30

log 5

b

. Tính

30

log 1350

theo a, b.

c) Cho

14

log 7

a

;

14

log 5

b

. Tính

35

log 28

theo a, b.

d) Cho

2

log 3

a

;

3

log 5

b

;

7

log 2

c

. Tính

140

log 63

theo a, b, c.

Bài 4. Chứng minh các đẳng thức sau (với giả thiết các biểu thức đã cho có nghĩa):

a)

log log

a a

c b

b c

b)

log log

log ( )

1 log

a a

ax

a

b x

bx

x







c)

log

1 log

log

a

ab

c

b

c

 

d)

1

log (log log )

3 2

c c c

a b



 

, với

2 2

7a b ab

 

.

e)

1

log ( 2 ) 2log 2 (log log )

2

a a a a

x y x y

   

, với

2 2

4 12x y xy

 

.

BÀI TẬP TRẮC NGHIỆM

Câu 1. Tính





1

2 lg 16

2

10x

Ⓐ

 20x

Ⓑ

 30x

Ⓒ

 10x

Ⓓ

 15x

Câu 2. Tính





4

1 log 9

2y

Ⓐ

 6y

Ⓑ

 9y

Ⓒ

 3y

Ⓓ

 4y

Câu 3. Tính

      lg tan 1 lg tan 2 ... lg tan 89A

Ⓐ

 0A

Ⓑ

 1A

Ⓒ

 2A

Ⓓ

 5A

Câu 4. Tính

   lg tan1 .lg tan 2 ...lg tan 89B

Ⓐ

 0B

Ⓑ

 10B

Ⓒ

 9B

Ⓓ

 6B

Câu 5. Khẳng định nào sau đây là đúng.

Ⓐ

 

12

8 5 log 54

b

Ⓑ

 

12

8 5 log 54

b

Ⓒ

 

12

8 5 log 54

b

Ⓓ

 

12

8 5 log 54

b

Câu 6. Cho



7

log 12

a

và



12

log 24

b

. Tính

54

log 168

theo a, b

Ⓐ

 







54

1

log 168

8 5

ab

a b

Ⓑ

 







54

1

log 168

8 5

ab

a b

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 206

Ⓒ

 







54

1

log 168

8 5

ab

a b

Ⓓ

 







54

1

log 168

8 5

ab

b a

Câu 7. Tính giá trị của biếu thức sau:



  

2

9 1

3

2 log 3

3 3

2 1

log 2 log 5

3

4

log 4 16 2log 27 3

3

A

Ⓐ



144

10

5 2

Ⓑ



144

10

5 2

Ⓒ



144

5 2

10

Ⓓ



144

5 2

10

Câu 8. Tính giá trị của biếu thức sau:

 



3

9 9

log 5

3

1

log 36 log 2401

5

2

4 81

15log

27 3

2 8

B

Ⓐ

1609

53

Ⓑ

1906

53

Ⓒ

1909

53

Ⓓ

1606

53

Câu 9. Ta có a, b là hai cạnh của một tam giác vuông có cạnh huyền c, khẳng định nào sau đây là

đúng:(với

    1; 1; 1a c b c b

)

Ⓐ

  

   

 log log 2 log log

c b c b c b c b

a a a a

Ⓑ

  

   

 log log 2 log log

c b c b c b c b

a a a a

Ⓒ

  

   

 log log 3 log log

c b c b c b c b

a a a a

Ⓓ

  

   

 log log 3 log log

c b c b c b c b

a a a a

Câu 10. Tính:

 

2 3

log log 81

Ⓐ

2.

Ⓑ

1

Ⓒ

3

Ⓓ

6

Câu 11. Tính:

 

3 2

log log 8

Ⓐ

1.

Ⓑ

16

Ⓒ

3

Ⓓ

6

Câu 12. Tính:

 

9 2

1

log log 8

3

Ⓐ

1

.

6

Ⓑ

1

.

8

Ⓒ

4

.

3

Ⓓ

3

.

4

Câu 13. Tính:

 



1

2

2 4

3log log 16 log 2

Ⓐ

2.

Ⓑ

16

Ⓒ

3

Ⓓ

6

Câu 14. Cho

 

30 30

log 3; log 5

a b

. Tính

30

log 1350

theo

,a b

Ⓐ

 2 1.a b

Ⓑ

 2 3.a b

Ⓒ

 2 1.a b

Ⓓ

 2 3.a b

Câu 15. Cho



15

log 3

m

. Tính

25

log 15

theo m.

Ⓐ

 



1

.

2 1

m

Ⓑ

 



1

.

2 1

m

Ⓒ

 



1

.

1

m

Ⓓ

 



1

.

1

m

Câu 16. So sánh các cặp số sau.

3

log 5

và

7

log 4

Ⓐ



3 7

log 5 log 4.

Ⓑ



3 7

log 5 log 4.

Ⓒ



3 7

log 5 log 4.

Ⓓ Không xác định

được

Câu 17. So sánh các cặp số sau.

0,3

log 2

và

4

log 3

Ⓐ



0,3 4

log 2 log 3.

Ⓑ



0,3 4

log 2 log 3.

Ⓒ



0,3 4

log 2 log 3.

Ⓓ Không xác định

được

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 207

Câu 18. So sánh các cặp số sau.

2

log 10

và

5

log 30

Ⓐ



2 5

log 10 log 30.

Ⓑ



2 5

log 10 log 30.

Ⓒ



2 5

log 10 log 30.

Ⓓ Không xác định

được

Câu 19. Đơn giản biểu thức sau:

 

1 1

lg lg 4 4 lg 2

8 2

Ⓐ

0.

Ⓑ

16

Ⓒ

3

Ⓓ

6

Câu 20. Đơn giản biểu thức sau:

 

4 1 3 9

lg lg 36 lg

9 2 2 2

Ⓐ



1

lg18 lg 2.

2

Ⓑ



1

lg18 lg 2.

2

Ⓒ



1

lg18 lg 4.

2

Ⓓ



1

lg18 lg 4.

2

Câu 21. Đơn giản biểu thức sau:

 

27

lg 72 2 lg lg 108

256

Ⓐ



5

20 lg 2 lg 3.

2

Ⓑ



5

20 lg 2 lg 3.

2

Ⓒ



5

lg 2 lg 6.

2

Ⓓ



5

lg 2 lg 6.

2

Câu 22. Đơn giản biểu thức sau:

 

1

lg lg 0,375 2 lg 0,5625

8

Ⓐ

lg 3 4 lg 2.

Ⓑ

lg 3 4 lg 2.

Ⓒ

lg 4 4 lg 2.

Ⓓ

lg 4 4 lg 2.

Câu 23. Tính:





3 81

2 log 4 4 log 2

9A

Ⓐ

1024.

Ⓑ

2048.

Ⓒ

128

Ⓓ

64.

Câu 24. Tính:

 

 



 

 

5

2 4

3

4

. .

log

a

a a a

B

a

Ⓐ

173

.

60

Ⓑ

177

.

50

Ⓒ

173

.

90

Ⓓ

173

.

30

Câu 25. Tính:



5

5 5

log log ... 5

C

(n dấu căn)

Ⓐ

 .n

Ⓑ

3 .n

Ⓒ

3 .n

Ⓓ

2 .n

Câu 26. Gọi

c

là cạnh huyền,

,a b

là hai cạnh góc vuông của môt tam giác vuông. Khẳng định nào sau đây

là đúng:

Ⓐ

   

 log log 2log .log

b c c b b c c b

a a a a

Ⓑ

   

 log log 2log .log

b c c b b c c b

a a a a

Ⓒ

   

 log log 2 log .log

b c c b b c c b

a a a a

Ⓓ

   

 log log log .log

b c c b b c c b

a a a a

Câu 27. Giả sử ta có hệ thức

  

2 2

7 ( , 0)

a b ab a b

. Hệ thức nào sau đây là đúng?

Ⓐ

  

2 2 2

2log ( ) log loga b a b

Ⓑ



 

2 2 2

2 log log log

3

a b

Ⓒ

 



 

2 2 2

log 2 log log

3

a b

Ⓓ



 

2 2 2

4 log log log

6

a b

Câu 28. Cho



 







2

log ; 0; #1

log (8 )

m

a m m m

A m

. Khi đó mối quan hệ giữa A và a là:

Ⓐ

3 a

a

Ⓑ

(3 )a a

Ⓒ

3

.

a

C

a

Ⓓ

(3 )a a

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. HÀM SỐ LŨY THỪA-HÀM SỐ MŨ-HÀM SỐ LOGARIT

GIẢI TÍCH

Trang: 208

Câu 29. Cho

log 0

a

b

. Khi đó phát biểu nào sau đây là đúng nhất?

Ⓐ

,a b

là các số thực cùng lớn hơn 1.

Ⓑ

,a b

là các số thực cùng nhỏ hơn 1.

Ⓒ

,a b

là các số thực cùng lớn hơn 1 hoặc cùng thuộc khoảng (0;1).

Ⓓ a là số thực lớn hơn 1 và b là số thực thuộc khoảng (0;1).

Câu 30. Phát biểu nào sau đây sai:

Ⓐ

 log log log

a a a

b c bc

với

, , 0a b c

. Ⓑ



2

1

log log

2

a

b b

với

 0, 1b a

.

Ⓒ



2

1

log log

2

a a

b b

với

  0,1 0b a

. Ⓓ



log

c

a

c

b

a

với các số dương

, ,a b c

và

 1a

.

Câu 31. Cho



3

log 15

a

,



3

log 10

b

. Tính

9

log 50

theo a và b, đáp án đúng là:

Ⓐ a+b-1 Ⓑ a-b Ⓒ a+b-5 Ⓓ a+2b

Câu 32. Rút gọn

 

3

2 log

2

5

3 log .log 25

a

B a

. Đáp án đúng là:

Ⓐ B=a

2

-4 Ⓑ B=a Ⓒ B=a-4 Ⓓ B=5

Câu 33. Tính giá trị của biểu thức:

   

 

  

3

4

log log . log

a

b

Q a b a b b

biết rằng a, b là các số thực

dương khác 1.

Ⓐ

 2Q

Ⓑ

 3Q

Ⓒ

 4Q

Ⓓ

 5Q

Câu 34. Cho các số thực dương

, ,a b c

và cùng khác

1

. Xét các khẳng định sau:

1-

log 1

abc

. 3-

 

log . log log

a a a

b c b c

.

2-



1

log log

2

a

c

b b

a

. 4-

 

log log log

a a a

bc b c

.

Số khẳng định đúng trong các khẳng định trên.

Ⓐ

1

. Ⓑ

2

. Ⓒ

3

. Ⓓ

4

.

Câu 35. Đặt



3

log 5

a

,



4

log 5

b

. Hãy biểu diễn

15

log 20

theo

a

và

b

.

Ⓐ

 







15

1

log 20

1

a a

b b

. Ⓑ

 







15

1

log 20

1

b b

a a

.

Ⓒ

 







15

1

log 20

1

b a

a b

. Ⓓ

 







15

1

log 20

1

a b

b a

.

Câu 36. Cho các số thực

,a b

thỏa

 1 a b

. Khẳng định nào sau đây đúng.

Ⓐ

 

1 1

1

log log

a b

b a

. Ⓑ

 

1 1

1

log log

a b

b a

.

Ⓒ

 

1 1

1

log log

a b

b a

. Ⓓ

 

1 1

1

log log

b a

a b

.

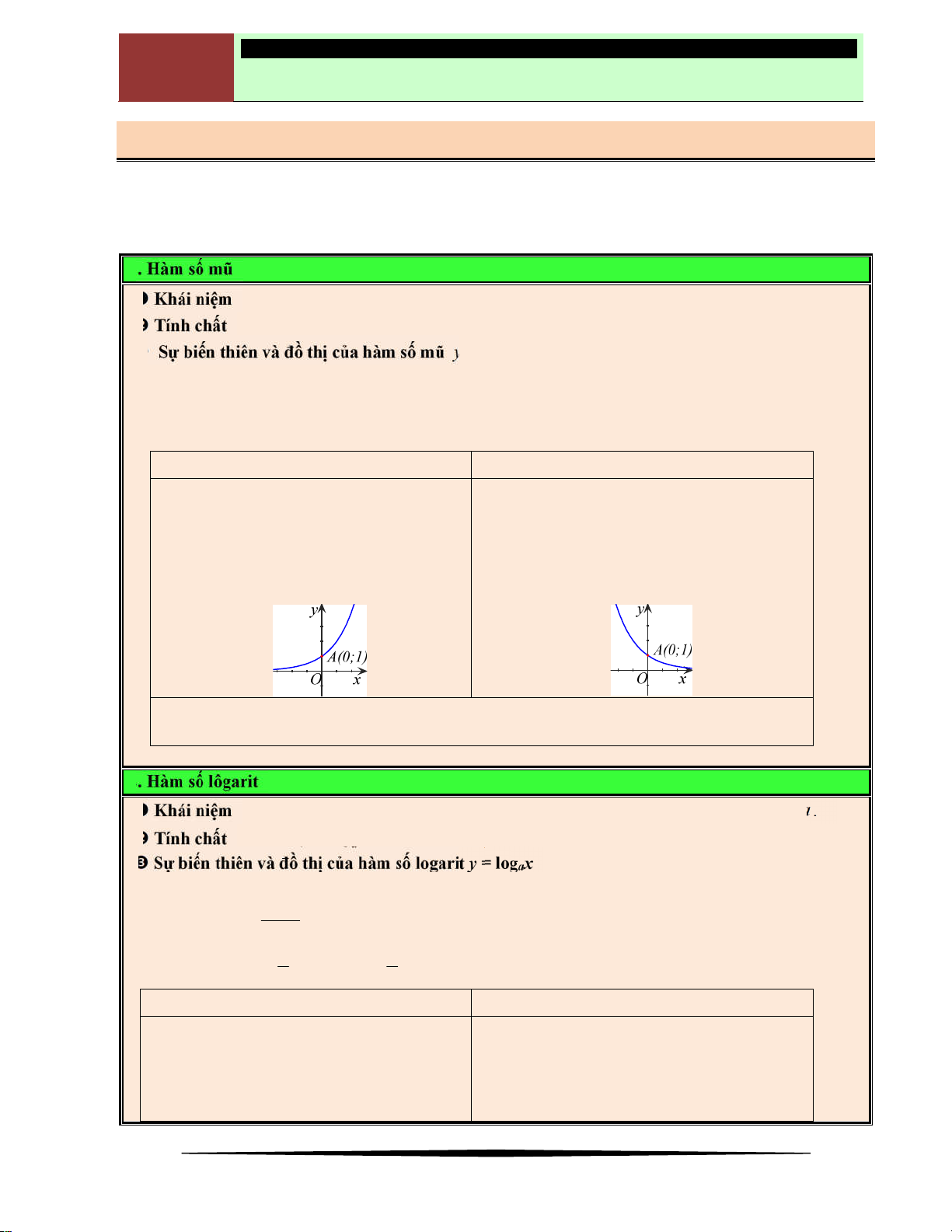
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 209

§4. HÀM SỐ MŨ – HÀM SỐ LÔGARIT

A. TÓM TẮT LÝ THUYẾT

1.

Hàm số mũ



Khái niệm

: Cho

0a 

và

1a 

. Hàm số dạng

x

y a được gọi là hàm số mũ cơ số

a

.



Tính chất

: Hàm số

x

y a liên tục trên





x

y a

Sự biến thiên và đồ thị của hàm số mũ

 Tập xác định là



. Tập giá trị là

(0; )

 ( ) .ln

x x

y a a a



 

Đặc biệt :

( )

x x

e e





;

( ) .

u u

e e u





Hàm số

x

y a ,

( 1)a 

Hàm số

x

y a ,

(0 1)a 



0,y x



   

 Hàm số đồng biến trên





lim

x

a



 

;

lim 0

x

a





 Tiệm cận ngang là

0y 

 Đồ thị :



0,y x



  

 Hàm số nghịch biến trên





lim 0

x

a





;

lim

x

a



 

 Tiệm cận ngang là

0y 

 Đồ thị :

Đồ thị hàm số

x

y a

luôn cắt trục tung tại điểm

(0;1)

và nằm phía trên trục

Ox

, nhận trục

Ox

làm tiệm cận ngang.

2.

Hàm số lôgarit



Khái niệm

: Cho

0a 

và

1a 

. Hàm số dạng log

a

y x



được gọi là hàm số lôgarit cơ số

a

.



Tính chất

: Hàm số log

a

y x liên tục trên

*







Sự biến thiên và đồ thị của hàm số logarit y = log

a

x

 Tập xác định là

(0; )

. Tập giá trị là





1

(log )

ln

a

y x

x a



 

Đặc biệt :

1

(ln )x

x





;

1

(ln )u u

u



 

Hàm số log

a

y x



( 1)a



Hàm số log

a

y x



(0 1)a

 



0, (0; )y x



   

 Hàm số đồng biến trên khoảng

(0; )



lim log

a

x



 

;

0

lim log

a

x





 

 Tiệm cận đứng là

0x 



0, (0; )y x



   

 Hàm số nghịch biến trên khoảng

(0; )



lim log

a

x



 

;

0

lim log

a

x





 

 Tiệm cận đứng là

0x 

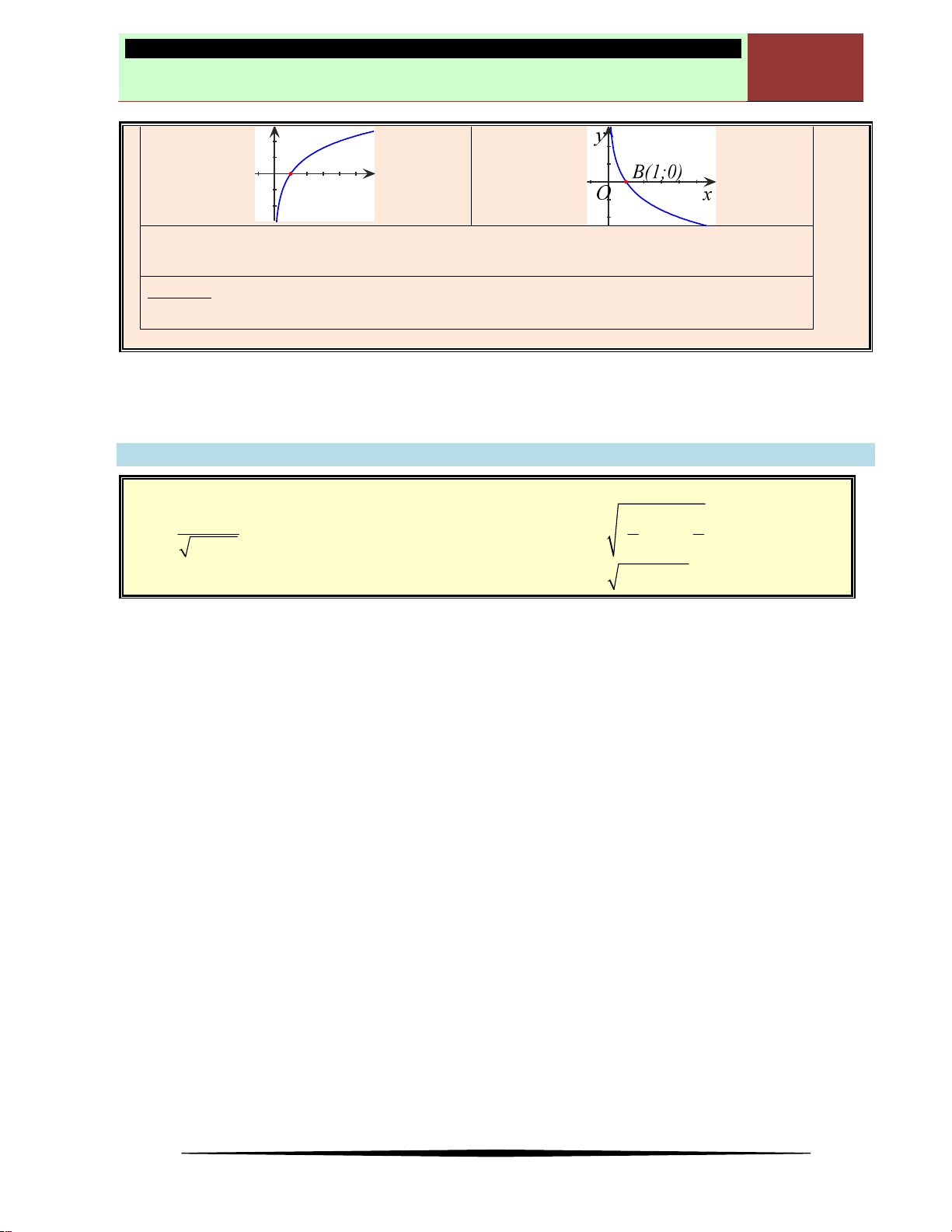
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 210

Đồ thị hàm số log

a

y x



cắt trục hoành tại điểm

(1;0)

và nằm bên phải trục

Oy

, nhận trục

Oy

làm tiệm cận đứng.

Nhận xét : Đồ thị hàm số

x

y a và đồ thị hàm số log

a

y x ( với

0, 1a a 

) đối xứng nhau

qua đường thẳng

y x

B. CÁC DẠNG TOÁN THƯỜNG GẶP

CÁC VÍ DỤ

Ví dụ 1: Tìm tập xác định của các hàm số sau:

a)

4

1

x

y

e e





b)

2

3

2 9

3 4

x x

y



 

 

 

 

c)

 

2

log 2y x x 

d)

 

2 lny ex 

--------------------------------------------------------------------------------------------------------------------------------

y

x

O

B(1;0)

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 211

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a)

e

x

y x



trên

 

2;0



b)

2

2lny x x

 

trên

1

e ;e



 

 

c)

2

3

1

x x

x

y e







trên đoạn

 

0;3

. d)

 

2

4ln 1

y x x  

trên đoạn

 

2;0



--------------------------------------------------------------------------------------------------------------------------------

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 212

Ví dụ 3. Cho

0, 1

a a

 

. Tìm mệnh đề đúng trong các mệnh đề sau.

Ⓐ Tập xác định của hàm số

x

y a

là khoảng

(0; )

.

Ⓑ Tập xác định của hàm số

y log

a

x

là



.

x

y a

là



.

Ⓓ Tập giá trị của hàm số

log

a

y x

là



.

Lời giải :......................................................................

......................................................................................

Ví dụ 4. Cho hàm số

2

logy x

. Mệnh đề nào dưới đây sai?

Ⓐ Tập xác định của hàm số là

 

;

 

Ⓑ Đồ thị hàm số nhận trục

Oy

làm tiệm cận

đứng.

1

ln 2

y

x





.

Ⓓ Hàm số đồng biến trên khoảng

 

0;



.

Lời giải :......................................................................

......................................................................................

Ví dụ 5. Tìm tập xác định

D

của hàm số

2

e

x x

y





.

Ⓐ

D  

.

Ⓑ

 

0;2

D 

.

Ⓒ

 

\ 0;2

D 



.

Ⓓ

D

 

.

Lời giải :......................................................................

......................................................................................

Ví dụ 6. Hàm số

 

2

5

log 4

y x x

 

có tập xác định là

Ⓐ

 

0;4

D 

Ⓑ

D  

Ⓒ

   

;0 4;D

    

Ⓓ

 

0;D

  

Lời giải :......................................................................

......................................................................................

Ví dụ 7. Tìm tất cả các giá trị thực của tham số

m

để hàm số

 

2

log 2 4

y x mx

  

có tập xác định là



Ⓐ

2

.

2

m







 



Ⓑ

2.

m



Ⓒ

2.

m



Ⓓ

2 2.

m

  

Lời giải :......................................................................

......................................................................................

Ví dụ 8. Tìm đạo hàm của hàm số

logy x

.

Ⓐ

1

y

x





Ⓑ

ln10

y

x





Ⓒ

1

ln10

y

x





Lời giải :......................................................................

......................................................................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 213

Ⓓ

1

10ln

y

x





Ví dụ 9. Hàm số nào dưới đây đồng biến trên



.

Ⓐ

1

5

x

y 

.

Ⓑ

4

x

y



 



 

 

.

Ⓒ

 

1

7 5

x

y 



.

Ⓓ

e

3

x

y

 



 

 

.

Lời giải :......................................................................

......................................................................................

Ví dụ 10. Cho hàm số

 

ln 1y x x  

. Mệnh đề nào sau đây đúng?

Ⓐ Hàm số đồng biến trên khoảng

 

1;0

Ⓑ Hàm số đạt cực đại tại

0x 

 

1;  

Ⓓ Hàm số đạt cực tiểu tại

0x 

Lời giải :......................................................................

......................................................................................

Ví dụ 11. Cho hàm số

ln x

y

x



. Mệnh đề nào sau đây đúng?

Ⓐ Hàm số có một cực đại.

Ⓑ Hàm số có một cực tiểu.

Ⓓ Hàm số không có cực trị.

Lời giải :......................................................................

......................................................................................

Ví dụ 12. Đường cong trong hình sau là đồ thị của hàm số nào

Ⓐ

 

2

x

y 

Ⓑ

 

2

log 2y x

Ⓒ 2

x

y 

Ⓓ

1

2

y x 

Lời giải :......................................................................

......................................................................................

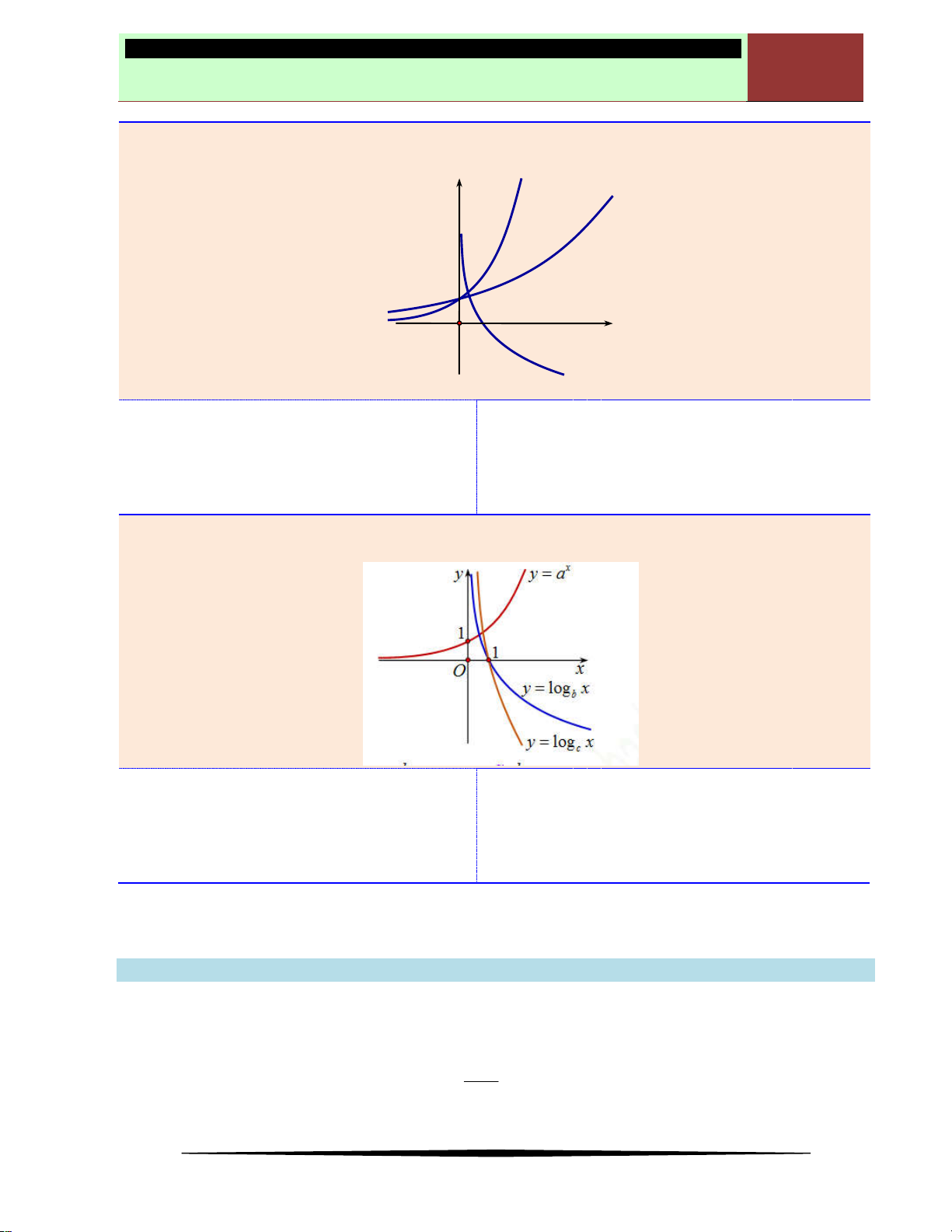
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 214

Ví dụ 13. Cho

a

,

b

,

c

là các số thực dương khác

1

. Hình vẽ bên là đồ thị các hàm số

, , log

x x

c

y a y b y x  

.

Mệnh đề nào sau đây đúng?

Ⓐ

.a b c 

Ⓑ

.c b a 

Ⓒ

.a c b 

Ⓓ

.c a b 

Lời giải :......................................................................

......................................................................................

Ví dụ 14. Cho ba số thực dương

a

,

b

,

c

khác

1

. Đồ thị các hàm số

x

y a

, log

b

y x , log

c

y x được

cho trong hình vẽ bên. Mệnh đề nào dưới đây là mệnh đề đúng ?

Ⓐ

b c a 

.

Ⓑ

c a b 

.

Ⓒ

b a c 

.

Ⓓ

c b a 

.

Lời giải :......................................................................

......................................................................................

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Tìm tập xác định của hàm số

2

2 3

5

x x

y

  



?

Ⓐ

 

1; 3 .

Ⓑ

.

Ⓒ

 

\ 1;3 .

Ⓓ

 

1;3 .

Câu 2. Tìm tập xác định

D

của hàm số

3

1

log

3

x

y

x







.

O

x

y

1

log

c

y x

x

y b

x

y a

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 215

Ⓐ

 

3;D

 

. Ⓑ

   

; 1 3;D

    

.

Ⓒ

 

; 1

D

  

. Ⓓ

 

1;3

D  

.

Câu 3. Trong các hàm số được cho dưới đây, hàm số nào có tập xác định là

D  

?

Ⓐ

 

2

ln 1

y x

 

Ⓑ

 

2

ln 1

y x

 

Ⓒ

 

2

ln 1

y x

 

Ⓓ

 

2

ln 1

y x

 

Câu 4. Hàm số

 

2

ln 2 4

y x mx

  

có tập xác định

D  

khi các giá trị của tham số

m

là:

Ⓐ

2

m



. Ⓑ

2

m

 

hoặc

2

m



. Ⓒ

2

m



. Ⓓ

2 2

m

  

.

Câu 5. Hàm số

 

2

log 4 2

x x

y m

  

có tập xác định là



khi

Ⓐ

1

4

m



. Ⓑ

0

m



. Ⓒ

1

4

m



. Ⓓ

1

4

m



.

Câu 6. Đạo hàm của hàm số

2

x

y



là

Ⓐ

2 ln 2

x

y





. Ⓑ

2

x

y





. Ⓒ

2

ln 2

x

y





. Ⓓ

1

2

x

y x







.

Câu 7. Đạo hàm của hàm số

2

x x

y e





là:

Ⓐ

 

2

2 1

x x

x e



. Ⓑ

 

2 2 1x

x x e



. Ⓒ

 

2 1

x

x e



. Ⓓ

 

2 1

x

x e



.

Câu 8. Tính đạo hàm của hàm số

1

4

x

y





Ⓐ

 

2

1 2 1 ln 2

'

2

 



x

y

Ⓑ

 

2

1 2 1 ln 2

'

2

x

y

 



Ⓒ

 

2

1 2 1 ln 2

'

2

x

y

 



Ⓓ

 

2

1 2 1 ln 2

'

2

x

y

 



Câu 9. Hàm số

 

2

log 2

 

f x x x

có đạo hàm

Ⓐ

 

2

ln 2

2







f x

x x

. Ⓑ

 

2

1

2 ln 2







f x

x x

.

Ⓒ

 

2

2 2 ln 2

2









x

f x

x x

. Ⓓ

 

2

2 2

2 ln 2









x

f x

x x

.

Câu 10. Tính đạo hàm của hàm số

 

y = ln 1+ x +1

.

Ⓐ

 

1

2 1 1 1

y

x x





  

Ⓑ

1

1 1

y

x





 

Ⓒ

 

1

1 1 1

y

x x





  

Ⓓ

 

2

1 1 1

y

x x





  

Câu 11. Hàm số nào dưới đây đồng biến trên tập xác định của nó?

Ⓐ

2

3

x

y

 



 

 

. Ⓑ

e

x

y



 



 

 

. Ⓒ

 

2

x

y 

. Ⓓ

 

0,5

x

y 

.

Câu 12. Giá trị cực tiểu của hàm số

 

2

3

x

y e x

 

là:

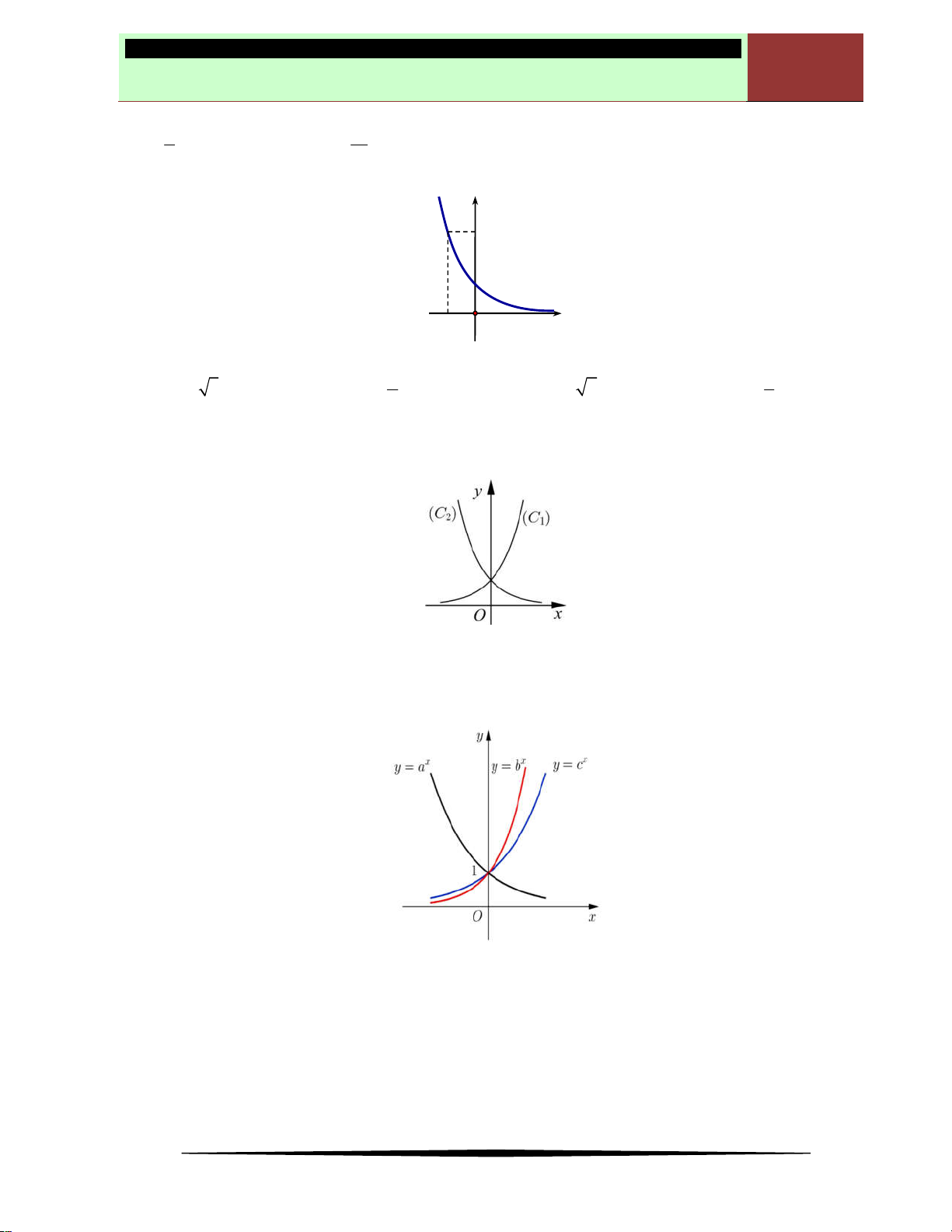
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 216

Ⓐ

6

e

. Ⓑ

3

6

e

. Ⓒ

3e

. Ⓓ

2e

.

Câu 13. Đồ thị hình bên là của hàm số nào?

Ⓐ

 

3

x

y  . Ⓑ

1

2

x

y

 



 

 

. Ⓒ

 

2

x

y  . Ⓓ

1

3

x

y

 



 

 

.

Câu 14. Cho hai hàm số

,

x x

y a y b 

với

,a b

là hai số thực dương khác 1, lần lượt có đồ thị là

1

( )C và

2

( )C như hình bên.

Mệnh đề nào dưới đây là đúng ?

Ⓐ

0 1a b  

Ⓑ

0 1b a  

Ⓒ

0 1a b  

Ⓓ

0 1b a  

Câu 15. Cho ba số thực dương

, ,a b c

khác

1

. Đồ thị các hàm số , ,

x x x

y a y b y c   được cho trong hình

vẽ bên

Mệnh đề nào dưới đây đúng?

Ⓐ

a b c 

Ⓑ

a c b 

Ⓒ

b c a 

Ⓓ

c a b 

Câu 16. Hình vẽ dưới đây vẽ đồ thị của các hàm số mũ

, ,

x x x

y a y b y c  

O

x

y

1

1

3

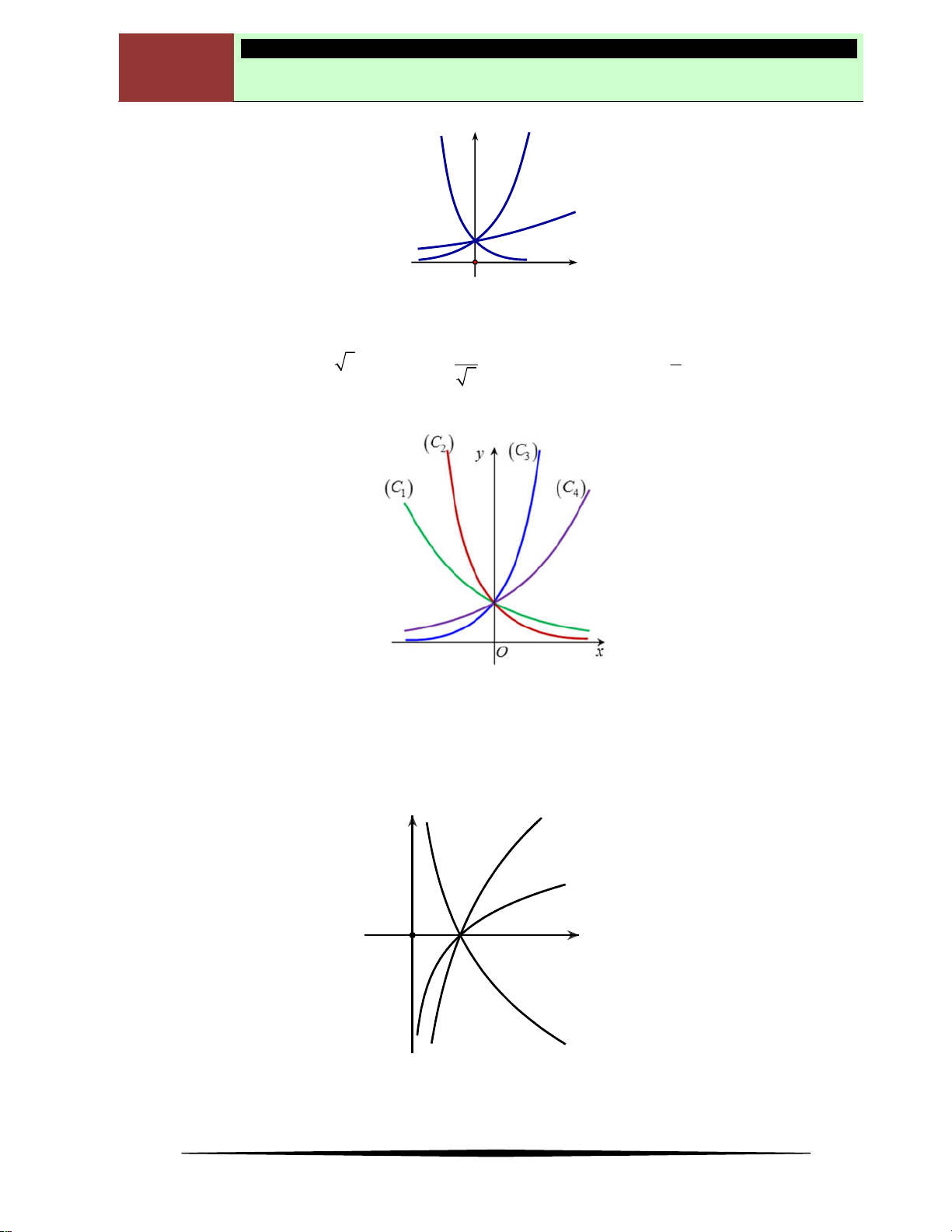
GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 217

Khẳng định nào dưới đây đúng?

Ⓐ

a b c 

. Ⓑ

1a c b  

. Ⓒ

1b c a  

. Ⓓ

b a c 

.

Câu 17. Cho bốn hàm số

 

3 1

x

y   ,

 

1

2

3

x

y

 



 

 



,

 

4 3

x

y  

,

 

1

4

x

y

 



 

 



và bốn đường cong

 

1

C

,

 

2

C

,

 

3

C

,

 

4

C

như hình vẽ bên. Đồ thị các hàm số

 

1

,

 

2

,

 

3

,

 

4

lần lượt là

Ⓐ

 

2

C

,

 

3

C

,

 

4

C

,

 

1

C

. Ⓑ

 

1

C

,

 

2

C

,

 

3

C

,

 

4

C

.

Ⓒ

 

4

C

,

 

1

C

,

 

3

C

,

 

2

C

. Ⓓ

 

1

C

,

 

2

C

,

 

3

C

,

 

4

C

.

Câu 18. Cho

a

,

b

,

c

là các số thực dương và khác

1

. Hình vẽ bên là đồ thị của ba hàm số log

a

y x ,

log

b

y x , log

c

y x . Khẳng định nào sau đây là đúng?

Ⓐ

b c a 

Ⓑ

c a b 

Ⓒ

a b c 

Ⓓ

b a c 

1

y=log

c

x

y=log

b

x

y=log

a

x

y

x

O

x

y

1

x

y b

x

y c

x

y a

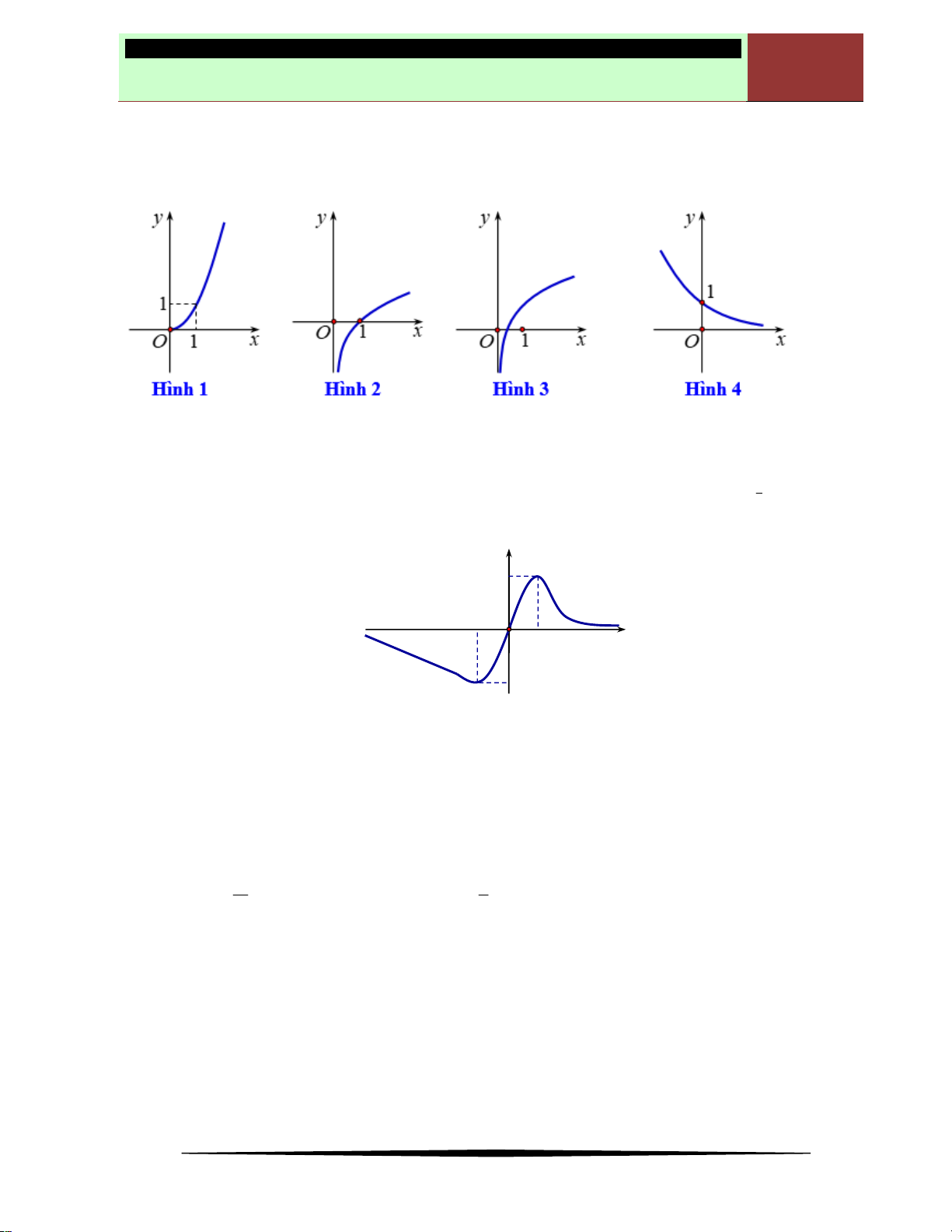
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 218

Câu 19. Cho hàm số

 

lnf x x x

. Một trong bốn đồ thị cho trong bốn phương án A, B, C, D dưới đây là

đồ thị của hàm số

 

y f x





. Tìm đồ thị đó?

Ⓐ Hình 1 Ⓑ Hình 2 Ⓒ Hình 3 Ⓓ Hình 4

Câu 20. Cho hàm số

 

y f x

liên tục trên



và có đồ thị như hình dưới. Biết rằng trục hoành là tiệm cận

ngang của đồ thị. Tìm tất cả các giá trị thực của tham số

m

để phương trình

 

1

2

4

m

f x





có hai nghiệm

phân biệt dương

Ⓐ

1m 

. Ⓑ

0 1m 

. Ⓒ

0m 

. Ⓓ

0 2m 

.

Câu 21. Tìm tập hợp tất cả các giá trị thực của tham số

m

để hàm số

 

2

y ln 1 1x mx   

đồng biến trên

khoảng

 

; 

Ⓐ





; 1 

Ⓑ

 

; 1 

Ⓒ

 

1;1

Ⓓ





1;

Câu 22. Có bao nhiêu giá trị nguyên của tham số

m

thuộc khoảng

 

2021; 2021

để hàm số

 

ln 4 1 2022

m

y x

x

   

đồng biến trên khoảng

1

;

3

 



 

 

là

Ⓐ

4040

. Ⓑ

2022

. Ⓒ

2021

. Ⓓ

4041

.

Câu 23. Gọi

,a b

lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số

 

2

log 2y x x  

trên đoạn

 

2;0

. Tổng

a b

bằng

Ⓐ

5

. Ⓑ

0

. Ⓒ

6

. Ⓓ

7

.

Câu 24. Giá trị nhỏ nhất của hàm số

2

2 2

log 4log 1y x x  

trên

 

1;8

là

Ⓐ

2

Ⓑ

1

Ⓒ

3

Ⓓ

2

O

x

y

1

1

2

2

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 219

Câu 25. Có bao nhiêu giá trị của

m

để giá trị nhỏ nhất của hàm số

 

2

e 4e

x x

f x m  

trên đoạn

 

0;ln 4

bằng

6

?

Ⓐ

3

. Ⓑ

4

. Ⓒ

1

. Ⓓ

2

.

BẢNG ĐÁP ÁN

1B 2B 3D 4D 5D 6A 7A 8A 9D 10A 11C 12D 13D 14C 15B

16B 17C 18A 19C 20C 21A 22B 23A 24C 25D

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 220

§5. PHƯƠNG TRÌNH MŨ

A. TÓM TẮT LÝ THUYẾT

Phương trình mũ

Với cơ số

0

a



,

1

a



, ta có :

 Phương trình mũ cơ bản có dạng :

x

a m

— Nếu

0

m



thì phương trình

x

a m

vô nghiệm

— Nếu

0

m



thì phương trình

log

x

a

a m x m

  

 Phương trình

( ) ( )

f x g x

a a f x g x

  

B. CÁC DẠNG TOÁN THƯỜNG GẶP

 Chú ý : Các cặp số có dạng :

1a a 

và

1a a 

(với

1

a



) là nghịch đảo của nhau

Ví dụ :

 

1

2 3 2 3



  

CÁC VÍ DỤ

Ví dụ 1: Giải các phương trình sau:

a)

2

3 4 1

2 4

x x x  



b)

10 5

10 15

16 0,125.8

x x

 

 



c)

2 2 2 2

1 2 1

2 2 3 3

x x x x

  

  

d)

1

6 2 3 2

x x x

  

--------------------------------------------------------------------------------------------------------------------------------

Dạng 1:

Biến đổi phương trình về cùng cơ số

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 221

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2. Phương trình

2

3 2

2 4

x x 



có 2 nghiệm là

1

x

;

2

x

. Hãy tính giá trị của

3 3

1 2

T x x 

.

Ⓐ

9

T



.

Ⓑ

1T 

.

Ⓒ

3

T



.

Ⓓ

27

T



.

Lời giải:

..........................................................................................................................................

.....................................................................................

Ví dụ 3. Giải phương trình

3 1

4

1

3

9

x



 



 

 

Ⓐ

6

7

x



.

Ⓑ

1

3

x



.

Ⓒ

1x 

.

Ⓓ

7

6

x



.

Lời giải:

..........................................................................................................................................

.....................................................................................

Ví dụ 4. Tìm số nghiệm thực của phương trình

3 1

3 9 .

x x





Ⓐ

2

.

Ⓑ

1.

Ⓒ

3

.

Ⓓ

0

.

Lời giải:

..........................................................................................................................................

.....................................................................................

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 222

Ví dụ 5. Tìm nghiệm của phương trình

1 2

3 3 2

x x x 

 

.

Ⓐ

2

log 3

x



.

Ⓑ

0

x



.

Ⓒ

2

3

x



.

Ⓓ

3

2

x



.

Lời giải:

..........................................................................................................................................

.....................................................................................

Ví dụ 6. Phương trình có hai nghiệm . Tính giá trị của .

Ⓐ

2P 

.

Ⓑ

4P 

.

Ⓒ

1P  

.

Ⓓ

3

P



.

Lời giải:

..........................................................................................................................................

.....................................................................................

Ví dụ 7. Tính tích

t

của tất cả các nghiệm của phương trình

   

2 3

2 2

3 2 2 3 2 2

x x x

  

  

.

Ⓐ

0t 

.

Ⓑ

2

t

 

.

Ⓒ

1

t

 

.

Ⓓ

1t 

.

Lời giải:

..........................................................................................................................................

.....................................................................................

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Tập nghiệm của phương trình

2

3 10

2 1

x x 



là:

Ⓐ

 

1;2

. Ⓑ

 

2;5

. Ⓒ

 

5; 2 

. Ⓓ

 

5;2



.

Câu 2. Giải phương trình

1 3 2

4 8

x x 



.

Ⓐ

11

8

x



. Ⓑ

4

3

x



. Ⓒ

1

8

x



. Ⓓ

8

11

x



.

Câu 3. Tập nghiệm của phương trình

2

2 3

1

7

x x

x

 



 



 

 

là

Ⓐ

 

1

. Ⓑ

 

1;2



. Ⓒ

 

1;4



. Ⓓ

 

2

.

 

2

2 2

2 3 7 4 3

x x 

  

1 2

,x x

1 2

P x x 

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 223

Câu 4. Tập nghiệm của phương trình

2

1

4

2

x

x x

 



 

 

là

Ⓐ

 

0;2

. Ⓑ

3

0;

2

 

 

 

. Ⓒ

2

0;

3

 

 

 

. Ⓓ

1

0;

2

 

 

 

.

Câu 5. Cho

a

,

b

là hai số thực khác

0

. Biết

 

2

4

3 10

3

1

625

125

a ab





 



 

 

. Tính tỉ số

a

b

?

Ⓐ

76

3

. Ⓑ

4

21

. Ⓒ

76

21

. Ⓓ

2

.

Câu 6. Tìm nghiệm của phương trình

1 2 1

4 2 5 0

x x 

  

.

Ⓐ

4

10

log

9

x 

. Ⓑ

10

ln

9

x 

. Ⓒ

10

9

4

x 

. Ⓓ

10

9

x



.

Câu 7. Phương trình

1 2 4 3

7.3 5 3 5

x x x x   

  

có nghiệm là

Ⓐ

1x 

. Ⓑ

1

x

 

. Ⓒ

2

x

 

. Ⓓ

2

x



.

Câu 8. Biết nghiệm của phương trình

1 3

2 .15 3

x x x 



được viết dưới dạng

2log logx a b 

, với

,a b

là

các số nguyên dương nhỏ hơn

10

. Tính

3 2

2017 2018S a b

 

.

Ⓐ

4009

S



. Ⓑ

2014982

S



. Ⓒ

1419943

S



. Ⓓ

197791

.

Câu 9. Tính tổng

T

của tất cả các nghiệm của phương trình

   

2 3

2 2

3 2 2 3 2 2

x x x

  

  

.

Ⓐ

0

T



. Ⓑ

2T  

. Ⓒ

1T  

. Ⓓ

1T 

.

BẢNG ĐÁP ÁN

1D 2A 3B 4B 5B 6A 7B 8A 9C

Ví dụ 1: Giải các phương trình sau:

a)

2 5 3

2 2 12

x x 

 

b)

   

5 24 5 24 10

x x

   

c)

1

5 5 4

x x

  

d)

2 1

36 4.30 5 0

x x x

  

--------------------------------------------------------------------------------------------------------------------------------

Dạng 2:

Giải phương trình bằng cách đặt ẩn phụ

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 224

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2. Giải phương trình

4 6.2 8 0

x x

  

. Ta có tập nghiệm bằng:

Ⓐ

 

1, 2



.

Ⓑ

 

1, 4

.

Ⓒ

 

2,4

.

Ⓓ

 

1, 2

.

Lời giải:

....................................................................................................................................

Ví dụ 3. Tổng tất cả các nghiệm của phương trình

2 1

2 5.2 2 0

x x

  

bằng bao nhiêu?

Ⓐ

1

.

Ⓑ

3

2

.

Ⓒ

5

2

.

Ⓓ

0

.

Lời giải:

....................................................................................................................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 225

Ví dụ 4. Tìm tổng các nghiệm của phương trình

2 2

3 3 30

x x 

 

.

Ⓐ

3

.

Ⓑ

10

3

.

Ⓒ

0

.

Ⓓ

1

3

.

Lời giải:

....................................................................................................................................

Ví dụ 5. Phương trình

9 3 3

x x

 

có bao nhiêu nghiệm?

Ⓐ

2

.

Ⓑ Vô nghiệm.

Ⓒ

1

.

Ⓓ

3

.

Lời giải:

....................................................................................................................................

Ví dụ 6. Cho phương trình

2 2

2 2 3

4 2 3 0

x x x x  

  

. Khi đặt

2

x x

t





, ta được phương trình nào dưới đây?

Ⓐ

2

8 3 0

t t

  

.

Ⓑ

2

2 3 0

t

 

.

Ⓒ

2

2 3 0

t t

  

.

Ⓓ

4 3 0

t

 

.

Lời giải:

....................................................................................................................................

Ví dụ 7. Tổng các nghiệm của phương trình

2

3 8.3 15 0

x

  

bằng.

Ⓐ

 

3

2 1 log 5 .



Lời giải:

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 226

Ⓑ

5

4log 3.

Ⓒ

3

3log 5.

Ⓓ

3

2 log 5.

....................................................................................................................................

Ví dụ 8. Phương trình

   

2 1 2 1 2 2 0

x x

    

có tích các nghiệm là :

Ⓐ

2

Ⓑ

1

Ⓒ

1

Ⓓ

0

Lời giải:

....................................................................................................................................

Ví dụ 9. Từ phương trình

   

3 2 2 2 2 1 3

x x

   

, đặt

 

2 1

x

t

 

ta thu được phương trình nào

sau đây?

Ⓐ

3

3 2 0

t t

  

.

Ⓑ

3 2

2 3 1 0

t t

  

.

Ⓒ

3

2 3 1 0

t t

  

.

Ⓓ

2

2 3 1 0

t t

  

.

Lời giải:

....................................................................................................................................

Ví dụ 10. Số nghiệm của phương trình

4 10 2.25

x x x

 

là:

Ⓐ

2.

Ⓑ

0.

Ⓒ

1.

Ⓓ

3

Lời giải:

....................................................................................................................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 227

....................................................................................................................................

Ví dụ 11. Tính tổng

T

tất cả các nghiệm của phương trình

4.9 13.6 9.4 0

x x x

  

.

Ⓐ

2T 

.

Ⓑ

3

T



.

Ⓒ

13

4

T



.

Ⓓ

1

4

T



.

Lời giải:

....................................................................................................................................

Ví dụ 12. Phương trình

   

3 5 3 5 3.2

x x

x

   

có hai nghiệm

1 2

,x x

. Tính

2 2

1 2

A x x 

.

Ⓐ

9

.

Ⓑ

13

.

Ⓒ

1

.

Ⓓ

2

.

Lời giải:

....................................................................................................................................

BÀI TẬP VỀ NHÀ

Câu 1. Tìm tập nghiệm

S

của phương trình

2 1

2 5.2 2 0

x x

  

.

Ⓐ

 

0;1

S 

Ⓑ

 

1;0

S  

. Ⓒ

 

1;1

S  

. Ⓓ

 

1

S 

.

Câu 2. Gọi

S

là tổng các nghiệm của phương trình

1

4 3.2 7 0

x x

  

. Tính

S

.

Ⓐ

2

log 28

S



. Ⓑ

28

S



. Ⓒ

2

log 7

S



. Ⓓ

12

S



.

Câu 3. Phương trình

2 1

3 4.3 1 0

x x

  

có nghiệm

1 2

,x x

trong đó

1 2

x x

. Chọn phát biểu đúng ?

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 228

Ⓐ

1 2

. 1

x x

 

. Ⓑ

1 2

2 0

x x

 

. Ⓒ

1 2

2 1

x x

  

. Ⓓ

1 2

2

x x

  

.

Câu 4. Cho phương trình

1

9 3 2 0

x x

  

có hai nghiệm

1 2

,x x

 

1 2

x x



. Tính giá trị của

1 2

2 3A x x 

.

Ⓐ

3

3log 2

A



. Ⓑ

2A 

. Ⓒ

0

A



. Ⓓ

2

4log 3

A



.

Câu 5. Tập nghiệm của phương trình

2 2

3 3 30

x x 

 

là

Ⓐ

 

1; 1

S

 

Ⓑ

 

3;1 .

S 

Ⓒ

1

3;

3

S

 



 

 

Ⓓ

 

1

S

 

Câu 6. Phương trình

2

2 2

1

9 10.3 1 0

x x

 

  

có tập nghiệm là:

Ⓐ

 

2; 1;0;1

 

. Ⓑ

 

1;0;2



. Ⓒ

 

2; 1;1;2

 

. Ⓓ

 

2;0;1;2



.

Câu 7. Cho phương trình

 

2 10 4

3 6.3 2 0 1

x x 

  

. Nếu đặt

 

5

3 0

x

t t



 

thì

 

1

trở thành phương trình

nào ?

Ⓐ

2

9 6 2 0.

t t

  

Ⓑ

2

2 2 0.

t t

  

Ⓒ

2

18 2 0.

t t

  

Ⓓ

2

9 2 2 0.

t t

  

Câu 8. Gọi

S

là tổng tất cả các nghiệm của phương trình:

2

1

2

3 5.3 18 0

x



  

. Tính

S

?

Ⓐ

2

1

2 log 3

2

S  

. Ⓑ

2

3

1 log 2

S  

. Ⓒ

3

2log 2

S



.

Ⓓ

 

3

2 1 log 2

S  

.

Câu 9. Phương trình

3.4 5.6 2.9 0

x x x

  

đương đương với phương trình nào sau đây?

Ⓐ

2

3 5 2 0

x x

  

. Ⓑ

2

0

x x

 

. Ⓒ

2

2 5 3 0

x x

  

. Ⓓ

2

2 5 3 0

x x

  

.

Câu 10. Phương trình

2 1

9 6 2

x



 

có bao nhiêu nghiệm âm?

Ⓐ

2

Ⓑ

3

Ⓒ

0

Ⓓ

1

Câu 11. Phương trình

   

7 4 3 3. 2 3 2 0

x x

    

có tập nghiệm là.

Ⓐ

 

0

. Ⓑ

 

1; 0

. Ⓒ

 

1; 2

.

Ⓓ

 

2;2



.

Câu 12. Tích tất cả các nghiệm của phương trình









2

5 21 5 21 5.2

x

x x

   

bằng:

Ⓐ

4

. Ⓑ

4

. Ⓒ

2

. Ⓓ

2

.

Câu 13. Cho phương trình









sinx sin

5 2 6 5 2 6 2

x

   

. Hỏi phương trình đã cho có bao nhiêu

nghiệm trong





0;4



?

Ⓐ

4

nghiệm. Ⓑ

3

nghiệm. Ⓒ

6

nghiệm. Ⓓ

5

nghiệm.

Câu 14. Tính tổng tất cả các nghiệm của phương trình

Ⓐ . Ⓑ . Ⓒ . Ⓓ .

Câu 15. Tích tất cả các nghiệm thực của phương trình

     

3 3 3

9 3 3 9 9 3 12

x x x x

     

bằng

Ⓐ

2

. Ⓑ

1

2

. Ⓒ

25

2

. Ⓓ

1

.

BẢNG ĐÁP ÁN

1C 2A 3C 4A 5A 6A 7B 8D 9B 10C 11A 12A 13A 14A 15D

T

4.9 13.6 9.4 0

x x x

  

2T 

3

T



13

4

T



1

4

T



GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 229

Ví dụ 1: Giải các phương trình sau:

a)

2

4 4

3 2

x x x 



b)

2

3 .2 1

x x



c)

1

3 .8 36

x

x



d)

5 3

(3) (5)

x x



--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Tìm tập nghiệm thực của phương trình

2

3 .2 1

x x



Ⓐ

 

0; log 6

S 

. Ⓑ

 

2

0; log 3

S 

. Ⓒ

2

1

0;log

3

S

 



 

 

. Ⓓ

 

0

S 

.

Câu 2. Gọi

1

x

,

2

x

là hai nghiệm của phương trình

2

1 1

5 2

x x

 



. Tính

  

1 2

1 1

P x x

  

.

Ⓐ

2

2log 5 1

. Ⓑ

2

log 25

. Ⓒ

0

. Ⓓ

2

2log 5 2

.

Câu 3. Giải phương trình

2

1

8 .5

8

x x 



Ⓐ

5

1; 1 log 8

x x

   

. Ⓑ

8

1; 1 log 5

x x

   

.

Ⓒ

5

1; 1 log 8

x x

   

. Ⓓ Kết quả kháⒸ

Dạng 3:

Giải phương trình bằng cách lôgarit hai vế

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 230

Câu 4. Tính tổng tất cả các nghiệm của phương trình

2

4 2

3 7

x x 



.

Ⓐ

3

4 log 7

. Ⓑ

3

log 7

. Ⓒ

3

log 7

. Ⓓ

3

2 log 7 

.

Câu 5. Phương trình

2

3 2 2

5 3

x x x  



có một nghiệm dạng

log

a

x b

với

a

,

b

là các số nguyên dương lớn

hơn

4

và nhỏ hơn

16

. Khi đó

2a b

bằng

Ⓐ

3 0

. Ⓑ

2 5

. Ⓒ

4 0

. Ⓓ

3 5

.

Câu 6. Biết phương trình

1

27 .2 72

x





có một nghiệm viết dưới dạng

log

a

x b 

, với

a

,

b

là các số

nguyên dương nhỏ hơn

8

. Khi đó tính tổng

2 2

S a b 

.

Ⓐ

25

S



. Ⓑ

1 3

S



. Ⓒ

34

S



. Ⓓ

29

S



.

Câu 7. Phương trình

 

8

log

log 4

4 4

x

x x

 

có tập nghiệm là

Ⓐ

 

2;8

. Ⓑ

1

;8

2

 

 

 

. Ⓒ

1 1

;

2 8

 

 

 

. Ⓓ

1

2;

8

 

 

 

.

Câu 8. Có bao nhiêu cặp số nguyên

( ; )a b

thỏa mãn

1 100

a b

  

để phương trình

x x

b a

a b



có nghiệm nhỏ

hơn

1

?

Ⓐ

4 7 5 1

. Ⓑ

46 56

. Ⓒ

2

. Ⓓ

47 50

.

Câu 9. Phương trình:

2 log

1000

x

 



có tập nghiệm là

Ⓐ

 

10; 100

Ⓑ

 

10; 20

Ⓒ

1

;1000

10

 

 

 

Ⓓ



BẢNG ĐÁP ÁN

1C 2B 3A 4B 5D 6B 7D 8A 9C

Định lý 1: Cho hai hàm số

 

y f x



và

 

y g x



liên tục trên

D

. Nếu hàm số

 

y f x



luôn đồng

biến (hoặc luôn nghịch biến) trên

D

thì số nghiệm của phương trình

 

f x k

trên

D

không nhiều

hơn một và

   

f x f y



khi và chỉ khi

x y

với mọi

,

x y D

.

Định lý 2: Cho hai hàm số

 

y f x



và

 

y g x



liên tục trên

D

. Nếu hàm số

 

y f x



luôn đồng

biến (hoặc luôn nghịch biến) và hàm số

 

y g x



luôn nghịch biến (hoặc luôn đồng biến) trên

D

thì

số nghiệm trên

D

của phương trình

   

f x g x



không nhiều hơn 1 .

Khi đó : nếu

0

x

là nghiệm của phương trình

   

f x g x



thì

0

x

là nghiệm duy nhất.

Dạng 4:

Sử dụng tính đơn điệu để giải phương tình mũ, lôgarit

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 231

CÁC VÍ DỤ

Ví dụ 1: Giải các phương trình sau:

a)

3 4 5

x x x

 

b)

6 2 32

x x

 

c)

3 4 0

x

  

d)

2

1 2

2 2 ( 1)

x x x

x

 

  

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2. Giải phương trình

4 6.2 8 0

x x

  

. Ta có tập nghiệm bằng:

Ⓐ

 

1, 2



.

Ⓑ

 

1, 4

.

Ⓒ

 

2, 4

.

Ⓓ

 

1, 2

.

Lời giải:

....................................................................................................................................

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 232

BÀI TẬP VỀ NHÀ

Câu 1. Nghiệm của phương trình:

3 4 5

x x x

 

là.

Ⓐ

3

. Ⓑ

1

. Ⓒ

4

. Ⓓ

2

.

Câu 2. Số nghiệm của phương trình

 

5

log 3

2

x





là:

Ⓐ

0

. Ⓑ

1

. Ⓒ

3

. Ⓓ

2

.

Câu 3. Phương trình

4 6 25 2

x x

x  

có tập nghiệm là

Ⓐ

 

0;1; 2

. Ⓑ

 

0

. Ⓒ

 

2

. Ⓓ

 

0; 2

.

Câu 4. Số nghiệm của phương trình

 

9 2 2 3 2 5 0

x x

    

?

Ⓐ

0

. Ⓑ

1

. Ⓒ

2

. Ⓓ

3

.

Câu 5. Nghiệm của phương trình

 

25 2 3 5 2 7 0

x x

    

nằm trong khoảng nào sau đây?

Ⓐ

 

5;10

. Ⓑ

 

0; 2

. Ⓒ

 

1;3

. Ⓓ

 

0;1

Câu 6. Có tất cả bao nhiêu cặp số nguyên chẵn

 

;x y

thỏa mãn

2 3 55

x y

 

?

Ⓐ

16

. Ⓑ

1

. Ⓒ

8

. Ⓓ

2

.

Câu 7. Gọi

0

3a b

x

c





là một nghiệm lớn hơn

1

của phương trình

 

1

2

1

2 3 1 2 1

3

x

x x



 

 

   

 

 

 

 

 

. Giá

trị của

P a b c  

là

Ⓐ

6

P



. Ⓑ

0

P



. Ⓒ

2P 

. Ⓓ

4P 

.

Câu 8. Số nghiệm của phương trình

 

2

2 2 3 5 8 3

5 2 8 3 .8 3 5 .8

x x x

x x x x x

  

      

là

Ⓐ

4

. Ⓑ

3

. Ⓒ

1

. Ⓓ

2

.

Câu 9. Xét hàm số

 

2

9

t

f t

m





với

m

S

là tập hợp tất cả các giá trị của

m

sao

cho

   

1

f x f y

 

với mọi số thực

,x y

thỏa mãn

 

x y

e e x y



 

.Tìm số phần tử của

S

.

Ⓐ Vô số Ⓑ

1

Ⓒ

2

Ⓓ

0

BẢNG ĐÁP ÁN

1D 2B 3D 4B 5B 6B 7D 8B 9C

CÁC VÍ DỤ

Ví dụ 1. Tìm tất cả các giá trị thực của

m

để phương trình

3

x

m

có nghiệm thựⒸ

Ⓐ

1

m



Lời giải:...................................................................... ...................

Dạng 5:

Phương trình mũ chứa tham số

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 233

Ⓑ

0

m



Ⓒ

0

m



Ⓓ

0

m



.......................................................................................................

Ví dụ 2. Tìm tất cả các giá trị thực của tham số

m

để phương trình

1

4 2 0

x x

m



  

có hai nghiệm

thực phân biệt

Ⓐ

 

;1

m

 

Ⓑ





0;1

m 

Ⓒ

 

0;1

m 

Ⓓ

 

0;m

 

Lời giải:...................................................................... ...................

.......................................................................................................

Ví dụ 3. Tìm giá trị của tham số

m

để phương trình

2

9 .3 9 0

x x

m m



  

có hai nghiệm phân biệt

1 2

,x x

thỏa mãn

1 2

3

x x

 

.

Ⓐ

3

m



.

Ⓑ

4

m



.

Ⓒ

1

m



.

Ⓓ

5

2

m



.

Lời giải:...................................................................... ...................

.......................................................................................................

Ví dụ 4. Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

1 2

4 2 2 6 0 (1)

x x

m m



   

có hai nghiệm phân biệt?

Ⓐ

3

.

Ⓑ

2

.

Ⓒ

1

.

Ⓓ

0

.

Lời giải:...................................................................... ...................

.......................................................................................................

Ví dụ 5. Tìm

m

để phương trình

1

4 2 2

x x

m



  

có nghiệm

 

1; 2

x  

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 234

Ⓐ

1 10

m

 

.

Ⓑ

1 10

m

 

.

Ⓒ

5

10

4

m

 

.

Ⓓ

5

10

4

m

 

.

Lời giải:...................................................................... ...................

.......................................................................................................

Ví dụ 6. Phương trình

   

3

7 3 5 7 3 5 2 (1)

x x

x

m



   

có nghiệm thực thì

m

bằng:

Ⓐ

16

m



.

Ⓑ

16

m



.

Ⓒ

16

m

 

.

Ⓓ

0

m



.

Lời giải:...................................................................... ...................

.......................................................................................................

Ví dụ 7. Để phương trình:

2 2

sin cos

2 2

x x

m 

có nghiệm, thì các giá trị cần tìm của tham số m là:

Ⓐ

1 2

m 

.

Ⓑ

2 2 2

m 

.

Ⓒ

2 2 3

m

 

.

Ⓓ

3 4

m

 

.

Lời giải:...................................................................... ...................

.......................................................................................................

Ví dụ 8. Tìm tập hợp các giá trị của tham số thực

m

để phương trình

 

6 3 2 0

x x

m m

   

có

nghiệm thuộc khoảng

 

0;1

.

Ⓐ

 

3; 4

.

Ⓑ

 

2; 4

.

Ⓒ

 

2; 4

.

Ⓓ

 

3; 4

.

Lời giải:...................................................................... ...................

.......................................................................................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 235

BÀI TẬP VỀ NHÀ

Câu 1. Biết rằng

0

m m

là giá trị của tham số

m

sao cho phương trình

   

9 2 2 1 3 3 4 1 0

x x

m m

    

có

hai nghiệm thực

1 2

,x x

thỏa mãn

  

1 2

2 2 12

x x

  

. Khi đó

0

m

thuộc khoảng nào sau đây

Ⓐ

 

9; + 

. Ⓑ

 

1; 3

. Ⓒ

 

2; 0



. Ⓓ

(3;9)

.

Câu 2. Giá trị của tham số

m

để phương trình

9 4.6 ( 3).4 0

x x x

m

   

có hai nghiệm phân biệt

Ⓐ

6 7

m

 

. Ⓑ

3 7

m

 

. Ⓒ

7

m



. Ⓓ

6 7

m

 

.

Câu 3. Gọi

S

là tập hợp các giá trị nguyên của tham số

m

sao cho phương trình

1 2

25 .5 7 7 0

x x

m m



   

có hai nghiệm phân biệt. Hỏi

S

có bao nhiêu phần tử.

Ⓐ

7

. Ⓑ

1

. Ⓒ

2

. Ⓓ

3

.

Câu 4. Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

 

16 2 1 4 3 8 0    

x x

m m

có hai

nghiệm trái dấu?

Ⓐ

3

Ⓑ

7

Ⓒ

0

Ⓓ

6

Câu 5. Phương trình

2 2

2

4 2 6

x x

m



  

có 3 nghiệm khi:

Ⓐ

2 3

m

 

. Ⓑ

2

m



. Ⓒ

2

m



. Ⓓ

3

m



.

Câu 6. Tập các giá trị của

m

để phương trình

   

4. 5 2 5 2 3 0     

x x

m

có đúng hai nghiệm âm

phân biệt là:

Ⓐ

 

; 3



. Ⓑ

 

7; 9

. Ⓒ

   

; 1 7;

   

. Ⓓ

 

7; 8

.

Câu 7. Tìm tập hợp tất cả các giá trị thực của tham số

m

để phương trình

 

2

4 1 3 2 2 0

x x

m m m

    

có

nghiệm.

Ⓐ

 

;

 

. Ⓑ

   

;1 1;

  

. Ⓒ

 

0;



Ⓓ

1

;

2

 



 

 

.

Câu 8. Tìm tập các giá trị thực của tham số

m

để phương trình

   

4 2 1 2 1 0

x x

m

    

có đúng hai

nghiệm âm phân biệt.

Ⓐ

 

5; 6

. Ⓑ

 

2; 4

. Ⓒ

 

3; 5

. Ⓓ

 

4;5

.

Câu 9. Tìm giá trị của

a

để phương trình

 

2 3 1 2 3 4 0

x x

a

     

có

2

nghiệm phân biệt

1 2

,x x

thỏa mãn:

1 2

2 3

log 3

x x



 

, ta có

a

thuộc khoảng:

Ⓐ

 

; 3 

Ⓑ

 

3;

 

Ⓒ

 

0;



Ⓓ

 

3;



Câu 10. Tìm tất cả các giá trị của tham số thực

m

để phương trình

 

4 2 2 5 0

x x

m m

    

có nghiệm

thuộc

 

1;1 .



Ⓐ





4; .

m

  

Ⓑ

13

4; .

3

m

 







 

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 236

Ⓒ



 



; 4 4; .

m

     

Ⓓ

25 13

; .

6 3

m

 



 

 

Câu 11. Tập các giá trị của

m

để phương trình

   

4 5 2 5 2 3 0

x x

m

     

có đúng hai nghiệm âm

phân biệt là:

Ⓐ

   

; 1 7;

   

. Ⓑ

 

7; 8

. Ⓒ

 

; 3



. Ⓓ

 

7; 9

.

BẢNG ĐÁP ÁN

1B 2B 3C 4D 5D 6D 7C 8C 9B 10B 11B

§6. PHƯƠNG TRÌNH LÔGARIT

A. TÓM TẮT LÝ THUYẾT

Phương trình lôgarit

Với cơ số

0

a



,

1

a



và điều kiện xác định của phương trình

log

a

x b

là

0

x



 Phương trình lôgarit cơ bản có dạng

log

b

a

x b x a  

 Phương trình

( ) 0

log ( ) log ( )

( ) ( )

a a

f x

f x g x





 







B. CÁC DẠNG TOÁN THƯỜNG GẶP

CÁC VÍ DỤ

Ví dụ 1: Giải các phương trình sau:

a)

2

log ( 1) 3

x

 

b)

3 9 27

log log log 11

x x x

  

c)

5 5 5

log log ( 6) log ( 2)

x x x

   

d)

2 8

log ( 2) 2 6 log 3 5

x x

   

--------------------------------------------------------------------------------------------------------------------------------

Dạng 1:

Biến đổi phương trình về cùng cơ số

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 237

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2. Tập nghiệm

S

của phương trình

 

3

log 1 2.

x

 

Ⓐ

 

6

S 

Ⓑ

 

7

S 

.

Ⓒ

 

9

S 

.

Ⓓ

 

10

S 

.

Lời giải:...................................................................... ....................

........................................................................................................

Ví dụ 3. Phương trình

 

log 1 2

x

 

có nghiệm là

Ⓐ

11

.

Ⓑ

9

.

Ⓒ

101

.

Ⓓ

9 9

.

Lời giải:...................................................................... ....................

........................................................................................................

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 238

........................................................................................................

Ví dụ 4. Tìm tập nghiệm của phương trình

 

2

log 3 2

x x

 

.

Ⓐ

 

1; 4

S

 

.

Ⓑ

 

1; 4

S 

.

Ⓒ

 

1

S 

.

Ⓓ

 

1; 4

S

  

.

Lời giải:...................................................................... ....................

........................................................................................................

Ví dụ 5. Tính số nghiệm của phương trình

 

2

2 3 log 3 0

x x x

   

.

Ⓐ

1

.

Ⓑ

2

.

Ⓒ

3

.

Ⓓ

0

.

Lời giải:...................................................................... ....................

........................................................................................................

Ví dụ 6. Tập nghiệm của phương trình

2 4 16

log log log 7

x x x

  

là:

Ⓐ

 

2

Ⓑ

 

16

Ⓒ

 

2 2

Ⓓ

 

4

Lời giải:...................................................................... ....................

........................................................................................................

Ví dụ 7. Số nghiệm của phương trình

 

2 2 2

log log 6 log 7

x x  

là

Ⓐ

1

.

Ⓑ

2

.

Ⓒ

0

.

Ⓓ

3

.

Lời giải:...................................................................... ....................

........................................................................................................

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 239

........................................................................................................

Ví dụ 8. Tổng tất cả các nghiệm thực của phương trình

   

2

4 4

2log 3 log 5 0

x x

   

là:

Ⓐ

8

.

Ⓑ

8 2



.

Ⓒ

8 2



.

Ⓓ

4 2



.

Lời giải:...................................................................... ....................

........................................................................................................

Ví dụ 9. Số nghiệm của phương trình:

   

4 2 2 4

log log log log 2

x x

 

là:

Ⓐ

0

.

Ⓑ

2

.

Ⓒ

3

.

Ⓓ

1

.

Lời giải:...................................................................... ....................

........................................................................................................

BÀI TẬP VỀ NHÀ

Câu 1. Tìm nghiệm của phương trình

 

25

1

log 1

2

x

 

.

Ⓐ

23

2

x 

. Ⓑ

6

x

 

. Ⓒ

4

x



. Ⓓ

6

x



.

Câu 2. Tổng bình phương các nghiệm của phương trình

 

2

1

2

log 5 7 0

x x

  

bằng

Câu 3. Nghiệm của phương trình

 

2 4

log log 1

x



là:

Ⓐ

4

x



. Ⓑ

2

x



. Ⓒ

8

x



. Ⓓ

16

x



.

Câu 4. Tích các nghiệm của phương trình

2 4 8 16

81

log log log log

24

x x x x   

là

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 240

Ⓐ

3.

Ⓑ

2.

Ⓒ

1

2

. Ⓓ

1.

Câu 5. 3: Nghiệm phương trình

   

4 2

log 7 log 1

x x

  

là ?

Ⓐ

6

. Ⓑ

1

. Ⓒ

6

. Ⓓ

2

.

Câu 6. Tìm nghiệm của phương trình

 

3 2

log log 1

x



.

Ⓐ

6

x



. Ⓑ

8

x



. Ⓒ

9

x



. Ⓓ

2

x



.

Câu 7. 2: Nghiệm của phương trình

 

2 2

log log 1 2

x x

  

là :

Ⓐ

1

. Ⓑ

1 17

2



. Ⓒ

1 17

2



. Ⓓ

4

.

Câu 8. Tập nghiệm

S

của phương trình

   

3 3

log 2 1 log 1 1

x x

   

là

Ⓐ

 

3

S 

. Ⓑ

 

1

S 

. Ⓒ

 

4

S 

. Ⓓ

 

2

S

 

.

Câu 9. Số nghiệm thực của phương trình

   

3

3 1

3

3log 1 log 5 3

x x

   

là

Ⓐ

3

Ⓑ

1

Ⓒ

2

Ⓓ

0

Câu 10. Phương trình

 

2

log 2 7 1 log

   

x x x

có tập nghiệm là.

Ⓐ

 

1

. Ⓑ

 

1;7

. Ⓒ

 

7

. Ⓓ

 

1;7

.

Câu 11. Phương trình

   

2

3 3 1

3

1

log 2 log 5 log 8 0

2

x x

    

có bao nhiêu nghiệm thực?

Ⓐ

1

. Ⓑ

2

. Ⓒ

3

. Ⓓ

4

.

BẢNG ĐÁP ÁN

1C 2B 3D 4D 5_ 6_ 7B 8B 9C

CÁC VÍ DỤ

Ví dụ 1: Giải các phương trình sau:

a)

2

3 3

2log 5log 9 3 0

x x

  

b)

2

2 4

log ( 1) 6 log 1 2 0

x x

    

c)

   

2

2 2

2 3 2 3

log 1 log 1 6

x x x x

 

     

d)

1

3 3

log (3 1).log (3 3) 6

x x 

  

--------------------------------------------------------------------------------------------------------------------------------

Dạng 2:

Giải phương trình bằng cách đặt ẩn phụ

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 241

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2. Số nghiệm của phương trình

   

2

5 25

log 5 log 5 3 0

x x 



là.

Ⓐ

2

. Ⓑ

0

. Ⓒ

1

. Ⓓ

3

.

Ví dụ 3. Biết phương trình

2

2 2

log 7log 9 0

x x

  

có hai nghiệm

1 2

,x x

. Giá trị

1 2

.x x

bằng

Ⓐ

128

Ⓑ

64

Ⓒ

9

Ⓓ

512

Ví dụ 4. Tổng bình phương các nghiệm của phương trình

 

2

2 2

log log 4

4

x

x x  



là

Ⓐ

0

. Ⓑ

4

. Ⓒ

65

4

. Ⓓ

17

4

.

Ví dụ 5. Số nghiệm của phương trình

 

2 2

3 5

log 2 log 2 2

x x x x

   

là.

Ⓐ

2

. Ⓑ

1

. Ⓒ

4

. Ⓓ

3

.

BÀI TẬP VỀ NHÀ

Câu 1. Tích hai nghiệm của phương trình

2

3 3

log 6 log 8 0

x x

  

bằng

Ⓐ

729

. Ⓑ

8

. Ⓒ

6

. Ⓓ

90

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 242

Câu 2. Tích tất cả các nghiệm của phương trình

2

2 2

log log 1 1

x x

  

Ⓐ

1

2

Ⓑ

1

Ⓒ

1 5

2



Ⓓ

1 5

2

 

Câu 3. Gọi

T

là tổng các nghiệm của phương trình

2

1 3

3

log 5log 6 0

x x

  

.Tính

T

.

Ⓐ

3

T

 

. Ⓑ

36

T



. Ⓒ

1

243

T 

. Ⓓ

5

T



.

Câu 4. Phương trình

2

log log 2 0

x x

  

có bao nhiêu nghiệm thuộc khoảng

 

1;100

?

Ⓐ

3

. Ⓑ

0

. Ⓒ

2

. Ⓓ

1

.

Câu 5. Tổng các nghiệm của phương trình

2

2 2 3

log log 9.log 3

x x

 

là:

Ⓐ

2

. Ⓑ

8

. Ⓒ

17

2

. Ⓓ

2

.

Câu 6. Số nghiệm của phương trình

 

2

3 3

log 4log 3 7 0

x x

  

là.

Ⓐ

3

. Ⓑ

1

. Ⓒ

2

. Ⓓ

0

.

Câu 7. Phương trình

2

2 4

log log 1 0

x x

  

có bao nhiêu nghiệm thực?

Ⓐ

1

. Ⓑ

4

. Ⓒ

2

. Ⓓ

3

.

Câu 8. Cho phương trình:

2

3

log 4log 1 0

x x

  

. Khi đó ta đặt

3

log

x t

thì ta có phương trình nào sau

đây?

Ⓐ

2

4 4 1 0

t t

  

. Ⓑ

2

2 4 1 0

t t

  

. Ⓒ

2

4 1 0

t t

  

. Ⓓ

2

1

4 1 0

2

t t

  

.

Câu 9. Cho phương trình

 

2

log log 8 3 0

x x

  

. Khi đặt

2

logt x

, phương trình đã cho trở thành

phương trình nào dưới đây?:

Ⓐ

2

8 2 3 0

t t

  

Ⓑ

2

4 0

t t

 

Ⓒ

2

4 3 0

t t

  

Ⓓ

2

8 2 6 0

t t

  

Câu 10. Tính tổng

T

các nghiệm của phương trình

 

2

log10 3log100 5

x x

  

Ⓐ

10

T



. Ⓑ

12T 

. Ⓒ

11T 

. Ⓓ

110

T



.

Câu 11. Phương trình

5 5

1 2

1

4 log 2 logx x

 

 

có nghiệm là.

Ⓐ

1

5

1

125

x













.

Ⓑ

1

5

1

25

x













. Ⓒ

125

25

x











.

Ⓓ

5

25

x











.

Câu 12. Phương trình

2

2 2

log 5log 4 0

x x

  

có 2 nghiệm

1 2

,x x

khi đó tích

1 2

.x x

bằng:

Câu 13. Biết rằng phương trình

2

2 2

3log log 1 0

x x

  

có hai nghiệm là

a

,

b

. Khẳng định nào sau đây đúng

?

Ⓐ

3

2

ab 

. Ⓑ

3

2

a b 

. Ⓒ

1

3

a b

 

. Ⓓ

1

3

ab

 

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 243

Câu 14. Tìm số nghiệm thực của phương trình

 

2 2 2

2 4

log log 4 5 0

x x

  

.

Ⓐ

3

. Ⓑ

2

. Ⓒ

4

. Ⓓ

1

.

Câu 15. Biết rằng phương trình

4

2

3 3

log log

3

x

 



 

 

có hai nghiệm là

a

,

b

. Khi đó

.a b 

?

Ⓐ

8

. Ⓑ

64

. Ⓒ

81

. Ⓓ

9

.

Câu 16. Tìm tập nghiệm của phương trình:

3

9

1

log 3

log

x

 

.

Ⓐ

 

3;9

. Ⓑ

1

;9

3

 

 

 

. Ⓒ

 

1;2

. Ⓓ

1

;3

3

 

 

 

.

Câu 17. Tích tất cả các nghiệm của phương trình

2

2 2

17

log log

4

x x

 

Ⓐ

17

4

. Ⓑ

1

4

. Ⓒ

3

2

. Ⓓ

1

2

.

Câu 18. Cho phương trình

   

1

2 4

log 2 1 .log 2 2 1,

x x

  

phát biểu nào sau đây đúng?

Ⓐ Phương trình chỉ có một nghiệm.

Ⓑ Phương trình có một nghiệm là

a

sao cho

2 3

a



.

Ⓓ Tổng hai nghiệm là

2

log 5

.

Câu 19. Cho phương trình

   

2

3 3

2 log 5log 9 3 0

x x

  

có các nghiệm

1 2

;x x

. Giá trị biểu thức

1 2

.P x x

là.

Ⓐ

27

5

P 

. Ⓑ

27 5

P 

. Ⓒ

9 3

P 

. Ⓓ

27 3

P 

.

Câu 20. Phương trình

3 3

3 log log 3 1 0

x x

  

có tổng các nghiệm bằng.

Ⓐ

84

. Ⓑ

3

. Ⓒ

78

. Ⓓ

81

.

Câu 21. Gọi

,x y

là các số thực dương thỏa mãn điều kiện

 

9 6 4

log log log

  x y x y

và

2

 



x a b

y

với

,a b

là các số nguyên dương. Tính

a b

.

Ⓐ

4

Ⓑ

6

Ⓒ

8

Ⓓ

11

Câu 22. Cho phương trình

 

3

4 2

2

log .log 4 log 0

2

x

x x

 

 

 

 

. Nếu đặt

2

logt x

, ta được phương trình nào

sau đây?

Ⓐ

2

14 2 0

t t

  

. Ⓑ

2

11 3 0

t t

  

. Ⓒ

2

14 4 0

t t

  

. Ⓓ

2

11 2 0

t t

  

.

Câu 23. Giải phương trình

2

2 2 2

2

log 3.log 2 log 2   

x x x

. Ta được mấy nghiệm.

Ⓐ

2

. Ⓑ

1

. Ⓒ

3

. Ⓓ

0

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 244

CÁC VÍ DỤ

Ví dụ 1: Giải các phương trình sau:

a)

 

5

log 5 4 1

x

x  

b)

 

2 1

log 25 2

x x

x



 

c)

2 2

log (9 7) 2 log (3 1)

x x 

   

d)

 

2 2

1

log 4 15.2 27 2log 0

4.2 3

x x

x

   



--------------------------------------------------------------------------------------------------------------------------------

Câu 3. Tổng tất cả các nghiệm của phương trình

 

2

log 3.2 1 2 1

x

x  

bằng

Ⓐ

0

.

Ⓑ

3

2

.

Ⓒ

1

2

.

Ⓓ

1

.

Lời giải:...................................................................... ...................

.......................................................................................................

Câu 13. Cho các số thực dương

,x y

thỏa mãn

 

6 9 4

log log log 2 2x y x y

  

. Tính tỉ số

x

y

?

Dạng 3:

Giải phương trình bằng cách mũ hóa hai vế

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 245

Ⓐ

2

3

x

y



.

Ⓑ

2

3 1

x

y





.

Ⓒ

2

3 1

x

y





.

Ⓓ

3

2

x

y



.

Lời giải:...................................................................... ...................

.......................................................................................................

Câu 41.Cho

x

,

y

là các số thực dương thỏa mãn

 

9 6 4

log log log 2

  x y x y

. Giá trị của

x

y

bằng

Ⓐ

2

.

Ⓑ

1

2

.

Ⓒ

2

3

log

2

 

 

 

.

Ⓓ

3

2

log 2

.

Lời giải:...................................................................... ...................

.......................................................................................................

Định lý 1: Cho hai hàm số

 

y f x



và

 

y g x



liên tục trên

D

. Nếu hàm số

 

y f x



luôn đồng

biến (hoặc luôn nghịch biến) trên

D

thì số nghiệm của phương trình

 

f x k

trên

D

không nhiều

hơn một và

   

f x f y



khi và chỉ khi

x y

với mọi

,

x y D

.

Định lý 2: Cho hai hàm số

 

y f x



và

 

y g x



liên tục trên

D

. Nếu hàm số

 

y f x



luôn đồng

biến (hoặc luôn nghịch biến) và hàm số

 

y g x



luôn nghịch biến (hoặc luôn đồng biến) trên

D

thì

số nghiệm trên

D

của phương trình

   

f x g x



không nhiều hơn 1 .

Khi đó : nếu

0

x

là nghiệm của phương trình

   

f x g x



thì

0

x

là nghiệm duy nhất.

CÁC VÍ DỤ

Ví dụ 1: Giải các phương trình sau:

a)

3 5

log ( 1) log (2 1) 2

x x

   

b)

 

2 2

3 3

log 2 3 7 log 1

x x x x x

      

c)

 

1009

2 3

log 1 2018logx x

 

d)

2

7

4 4 1

log 4 1 6

2

x x

x

 

 

  

 

 

--------------------------------------------------------------------------------------------------------------------------------

Dạng 4:

Sử dụng tính đơn điệu để giải phương tình mũ, lôgarit

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 246

--------------------------------------------------------------------------------------------------------------------------------

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 247

BÀI TẬP VỀ NHÀ

Câu 1. Biết phương trình

2018 2019

2 1 1

log 2log

2

x

x x

 

  

 

 

có nghiệm duy nhất

2x a b

 

trong

đó

a

,

b

là những số nguyên. Khi đó

a b

bằng

Ⓐ

1

Ⓑ

5

Ⓒ

1

Ⓓ

2

Câu 2. Số nghiệm của phương trình

 

3 2

log log 1 

x x

là

Ⓐ

1

. Ⓑ

2

. Ⓒ

0

. Ⓓ

3

.

Câu 3. Số nghiệm của phương trình

 

1

ln 1

2

x

 



là:

Ⓐ

2

. Ⓑ

0

. Ⓒ

3

. Ⓓ

1

.

Câu 4. Phương trình

 

2 2

3 3

log 2 3 7 log 1

x x x x x

      

có số nghiệm là

T

và tổng các nghiệm là

S

. Khi đó

T S

bằng

Ⓐ

1

. Ⓑ

2

. Ⓒ

4

. Ⓓ

3

.

Câu 5. Phương trình

 

2 2

3 3

log 2 3 7 log 1

x x x x x

      

có số nghiệm là

T

và tổng các nghiệm là

S

. Khi đó

T S

bằng

Ⓐ

2

. Ⓑ

4

. Ⓒ

3

. Ⓓ

1

.

Câu 6. Tìm tổng các nghiệm của phương trình:

 

3 3 2

4 2

log 2 7 log 1 4 7

x x x x x x

       

Ⓐ

9

. Ⓑ

11

. Ⓒ

17

. Ⓓ

2

.

Câu 7. Biết rằng phương trình

 

1009

2 3

log 1 2018logx x

 

có nghiệm duy nhất

0

x

. Khẳng định nào dưới

đây đúng?

Ⓐ

1 1

1008 1006

0

3 3

x 

. Ⓑ

2

1009

0

3

x 

. Ⓒ

1

1008

0

1 3

x 

. Ⓓ

1

1007

0

3 1

x

 

.

Câu 8. Biết

1

x

,

2

x

là hai nghiệm của phương trình

2

7

4 4 1

log 4 1 6

2

x x

x

 

 

  

 

 

và

 

1 2

1

2

4

x x a b

  

với

a

,

b

là hai số nguyên dương. Tính

.a b

Ⓐ

16

a b

 

. Ⓑ

11

a b

 

. Ⓒ

14

a b

 

. Ⓓ

13.

a b

 

Câu 9. Phương trình

   

3 2

2 log cot log cosx x



có bao nhiêu nghiệm trên khoảng

;2

6

 



 

 



?

Ⓐ

2

. Ⓑ

1

. Ⓒ

4

. Ⓓ

3

.

Câu 10. Cho

a

,

b

là hai số thực dương thỏa mãn

5

4 2 5

log 3 4

a b

 

 

  

 



 

. Tìm giá trị nhỏ nhất của

biểu thức

2 2

T a b 

Ⓐ

1

. Ⓑ

1

2

. Ⓒ

5

2

. Ⓓ

3

2

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 248

BẢNG ĐÁP ÁN

1B 2A 3A 4C 5B 6D 7B 8C 9B 10C

Câu 1. Tập hợp các giá trị

m

để phương trình

2020

log

x m

có nghiệm thực là

Ⓐ

 

;0



. Ⓑ

 

\ 1

. Ⓒ



. Ⓓ

 

0;



.

Câu 2. Gọi

S

là tập tất cả các giá trị nguyên của tham số m với

64

m



để phương trình

   

1 5

5

log log 2 0

x m x

   

có nghiệm. Tính tổng tất cả các phần tử của

S

.

Ⓐ

2018.

Ⓑ

2016.

2013.

Câu 3. Số các giá trị nguyên của tham số

a

để phương trình

   

3

log 1 log 8 0

x ax

   

có hai nghiệm

thực phân biệt là

Ⓐ

5

. Ⓑ

8

. Ⓒ

4

. Ⓓ

3.

Câu 4. Tìm các giá trị thực của tham số

m

để phương trình

2

3 3

log 3log 2 7 0   

x x m

có hai nghiệm

thực

1 2

;x x

thỏa mãn

  

1 2

3 3 72.

  x x

Ⓐ

61

2



m

. Ⓑ

3

m

9

2



m

.

Câu 5. Cho phương trình

2

log log 2 3 0

x m x m

   

. Tìm

m

để phương trình có

2

nghiệm phân biệt

1 2

,x x

sao cho

1 2

16

x x



.

Ⓐ

19

2

m 

. Ⓑ

2

m



. Ⓒ

4

m



. Ⓓ

8

m



.

Câu 6. Số các giá trị nguyên của tham số

m

để phương trình

2

log ( 1) log ( 8)  

x mx

có hai nghiệm

thực phân biệt là

Câu 7. Cho phương trình

   

3

36 2 log 0 1 .

mx x  

Có tất cả bao nhiêu giá trị nguyên của tham số

m

thuộc đoạn

 

100;100



để phương trình

 

1

có hai nghiệm phân biệt?

Ⓐ

197

. Ⓑ

196

. Ⓒ

97

. Ⓓ

96

.

Câu 8. Gọi

S

là tập tất cả các giá trị nguyên không dương của

m

để phương trình

   

1 5

5

log log 2 0

x m x

   

có nghiệm. Tập

S

có bao nhiêu tập con?

Ⓐ

4

. Ⓑ

2

. Ⓒ

3

. Ⓓ

1

.

Câu 9. Tìm các giá trị thực của tham số

m

để phương trình

2

3 3

log .log 2 7 0

x m x m

   

có hai nghiệm

thực

1

x

,

2

x

thỏa mãn

1 2

. 81

x x



.

Ⓐ

44

m



. Ⓑ

4

m

 

. Ⓒ

81

m



. Ⓓ

4

m



.

Dạng 5:

Phương trình logarit chứa tham số

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 249

Câu 10. Tìm tất cả các giá trị thực của tham số

m

sao cho phương trình:

2 2

3 3

log log 1 2 1 0

x x m

    

có ít nhất một nghiệm trên đoạn

3

1;3

 

 

?

Ⓐ

1 3

m

  

. Ⓑ

0 2

m

 

. Ⓒ

0 3

m

 

. Ⓓ

1 2

m

  

.

Câu 11. Tìm giá trị của tham số

m

để phương trình

2 2

log log 1 2 5 0

x x m

    

có nghiệm trên đoạn

3

1;3 .

 

 

.

Ⓐ



 



; 2 0;m

    

. Ⓑ

 

;0

m  

.

Ⓒ





2;

 

.

Ⓓ

 

2;0

m 

.

Câu 12. Tìm tất cả các giá trị của tham số

m

để phương trình

2

4 1

log

4 1

x

m







có nghiệm.

Ⓐ

1 1

m

  

. Ⓑ

1

m

 

. Ⓒ

1 0

m

  

. Ⓓ

0

m



.

Câu 13. Biết điều kiện cần và đủ của

m

để phương trình

   

2

1 1

2 2

1

log 2 4 5 log 8 4 0

2

x m m

x

     



Có nghiệm thuộc

5

;4

2

 

 

 

là

 

;m a b



.Tính

T a b 

Ⓐ

4T 

. Ⓑ

4T  

. Ⓒ

10

3

T





. Ⓓ

10

3

T 

.

Câu 14. Cho phương trình













2 2 2

2 5

log 1 .log 1 log 1 .

m

x x x x x x

      

Có bao nhiêu giá trị

nguyên dương khác

1

của

m

sao cho phương trình đã cho có nghiệm

x

lớn hơn

2

?

Ⓐ

2

. Ⓑ

1

. Ⓒ Vô số. Ⓓ

3

.

Câu 15. Tìm tập hợp tất cả các giá trị thực của

m

để phương trình

   

2 2

5 5

1 log 1 log 4

x mx x m    

có hai nghiệm phân biệt?

Ⓐ

 

\ 5

m



. Ⓑ

 

3;7

m

. Ⓒ

   

3;7 \ 5

m

. Ⓓ

m



.

Câu 16. Tìm tất cả các giá trị của

m

để phương trình

 

2

2 1

2

4 log log 0

x x m

  

có nghiệm thuộc

khoảng

 

0;1

.

Ⓐ

1

;

4

m

 

 





 

. Ⓑ

1

;

4

m

 

 





 

. Ⓒ





;0

m 

. Ⓓ

1

0;

4

m

 







 

.

Câu 17. Tìm

m

để phương trình :

     

2

1 1

2 2

1

1 log 2 4 5 log 4 4 0

2

m x m m

x

      



có nghiệm trên

5

,4

2

 

 

 

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 250

Ⓐ

7

3

m

  

. Ⓑ

m



. Ⓒ

m



. Ⓓ

7

3

m

  

.

Câu 18. Cho phương trình:

 

2

3 2 2 3 2 2

log 1 log 0

x m mx x

 

    

. Tìm

m

để phương trình có nghiệm

thực duy nhất.

Ⓐ

1

m



. Ⓑ

3

1

m

 









. Ⓒ

1

m



. Ⓓ

3 1

m

  

.

Câu 19. Tìm

m

để phương trình

 

ln 1 ln

m x x m  

có nghiệm

 

0;1

x 

.

Ⓐ

 

1;m e



. Ⓑ

 

0;m

 

. Ⓒ

 

;0

m 

. Ⓓ

 

; 1

m

  

.

Câu 20. Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

 

2

log 4 1

x

m x  

có đúng

2

nghiệm phân biệt?

Ⓐ

2

. Ⓑ

3

. Ⓒ

1

. Ⓓ

0

.

Câu 21. Tìm tất cả các giá trị của tham số

m

để phương trình

 

2

2 1

2

4 log log 0

x x m

  

có nghiệm

thuộc khoảng

 

0;1

.

Ⓐ

1

;

4

m

 

 





 

. Ⓑ

1

0;

4

m

 







 

. Ⓒ





;0

m 

. Ⓓ

1

;

4

m

 

 





 

.

Câu 22. Tìm tham số

m

để phương trình

   

2018

log 2 log

x mx

 

có nghiệm thực duy nhất.

Ⓐ

1.

m



Ⓑ

0.

m



Ⓒ

2.

m



Ⓓ

1 2.

m

 

Câu 23. Tất cả các giá trị của m để phương trình

2

0,5 2

log ( 6 ) log (3 2 ) 0

m x x x

    

có nghiệm duy nhất

là.

Ⓐ

m 18

. Ⓑ

3 m 18  

. Ⓒ

6 m 20  

. Ⓓ

6 m 18  

.

Câu 24. Tìm

m

để phương trình

2

2 2

log 2log 0

x x m

  

có nghiệm

Ⓐ

1

m

 

. Ⓑ

1

m



. Ⓒ

1

m

 

. Ⓓ

1

m



.

Câu 25. Tìm

m

để phương trình:

2

3 3

log log 9 0

x m x

  

có nghiệm duy nhất nhỏ hơn

1

.

Ⓐ

4

m

 

. Ⓑ

6

m

 

. Ⓒ

6

m

 

. Ⓓ Không tồn tại

m

.

Câu 26. Tất cả các giá trị của tham số

m

để phương trình

   

log 2log 1

mx x

 

có nghiệm là

Ⓐ

0

m



. Ⓑ

4

m



. Ⓒ

0

m



và

4

m



. Ⓓ

4

m



.

Câu 27. Cho phương trình

   

2

3 3

log 3 log 3 2 2 1 0

x m x m m

    

. Gọi

S

là tập hợp tất cả các số tự

nhiên

m

mà phương trình có hai nghiệm phân biệt

1

x

,

2

x

thỏa

1 2

10

3

x x 

. Tính tổng các phần tử của

S

.

Ⓐ

1

Ⓑ

0

Ⓒ

10

Ⓓ

6

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 251

§7. BẤT PHƯƠNG TRÌNH MŨ - LOGARIT

A. TÓM TẮT LÝ THUYẾT

Bất phương trình mũ , logarit

Cho

1

a





( ) ( )

f x g x

a a f x g x

  



( ) 0

log ( ) log ( )

( ) ( )

a a

g x

f x g x





 







Cho

0 1a 



( ) ( )

f x g x

a a f x g x

  



( ) 0

log ( ) log ( )

( ) ( )

a a

f x

f x g x





 







Nhận xét :

Với cơ số

0

a



,

1

a





 

( ) ( )

( 1). ( ) ( ) 0

f x g x

a a a f x g x

    



 

( ) 0, ( ) 0

log ( ) log ( )

( 1). ( ) ( ) 0

a a

f x g x

a f x g x

 





 



  





B. CÁC DẠNG TOÁN THƯỜNG GẶP

 Chú ý : Các cặp số có dạng :

1a a 

và

1a a 

(với

1

a



) là nghịch đảo của nhau

Ví dụ :

 

1

2 3 2 3



  

Câu 1. Tập nghiệm của bất phương trình

2 1

3 27

x



là:

Ⓐ

1

;

3

 



 

 

. Ⓑ

 

2;



. Ⓒ

1

;

2

 



 

 

. Ⓓ

 

3;



.

Câu 2. Tập nghiệm

S

của bất phương trình

2

4

1

8

2

x x

 



 

 

là:

Ⓐ

   

;1 3;S

   

. Ⓑ

 

1;3

S 

.

Ⓒ

 

;3

S  

. Ⓓ

 

1;S

 

.

Dạng 1:

Biến đổi bất phương trình về cùng cơ số

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 252

Câu 3. Giải bất phương trình:

1

2

4

x



Ⓐ

2

x



. Ⓑ

2

x

 

. Ⓒ

2

x



. Ⓓ

1x 

Câu 4. Tập nghiệm của bất phương trình

2

5 25

x x



là:

Ⓐ



. Ⓑ

 

2;



. Ⓒ

   

;1 2;

  

. Ⓓ

 

1;2



.

Câu 5. Tìm tập nghiệm

S

của bát phương trình

1

4 2

x x



Ⓐ

 

1;S

 

Ⓑ

 

;1

S

 

Ⓒ

 

0;1

S 

Ⓓ

 

;S

  

Câu 6. Tìm tập nghiệm

S

của bất phương trình

2

3

1 1

2 4

x x 

 



 

 

.

Ⓐ

 

2;S

 

Ⓑ

 

;1

S

 

Ⓒ

 

1;2

S



Ⓓ

 

1;2

S



Câu 7. Tập nghiệm của bất phương trình

2 1

1 1

3 3

x

 



 

 

là

Ⓐ





1;



. Ⓑ





;1

. Ⓒ





;0



. Ⓓ





0;1

.

Câu 8. Giải bất phương trình:

2 1 2

3 4

4 3

x x  

   



   

   

ta được nghiệm là:

Ⓐ

1x 

Ⓑ

1x 

Ⓒ

1x 

Ⓓ

1x 

Câu 9. Nghiệm của bất phương trình

2 1 3

3 3

x x 



là

Ⓐ

2

3

x

 

Ⓑ

3

2

x



Ⓒ

2

3

x



Ⓓ

2

3

x



Câu 10. Bất phương trình

2

2 10

3 4

1

2

x

x x



 

 



 

 

có bao nhiêu nghiệm nguyên dương?

Ⓐ

4

. Ⓑ

6

. Ⓒ

3

. Ⓓ

2

.

Câu 11. Tập nghiệm của bất phương trình

 

1

3

5 5

x







là

Ⓐ

 

0;



Ⓑ

 

;0



Ⓒ

 

; 5 

Ⓓ

 

5;

 

Câu 12. Nghiệm nguyên dương lớn nhất của bất phương trình:

1 2

4 2 3

x x 

 

là:

Ⓐ

3

. Ⓑ

4

. Ⓒ

1

. Ⓓ

2

.

Câu 13. Nếu

 

6 5 6 5

x

  

thì:

Ⓐ

1

x

 

. Ⓑ

1

x

 

. Ⓒ

1x 

. Ⓓ

1x 

.

Câu 14. Nghiệm của bất phương trình

   

1

5 2 5 2

x





  

là.

Ⓐ

3 1

x

   

. Ⓑ

1x 

.

Ⓒ

2 1

x

   

hoặc

1x 

. Ⓓ

2 1x  

.

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 253

Câu 15. Số nghiệm nguyên của bất phương trình

   

3 1

1 3

10 3 10 3

x x

 

  

là.

Ⓐ

0

. Ⓑ

3

. Ⓒ

2

. Ⓓ

1

.

Câu 16. Nếu

 

1

7 4 3 7 4 3

a

  

thì

Ⓐ

0

a



. Ⓑ

1

a



. Ⓒ

0

a



. Ⓓ

1

a



.

Câu 17. Tập nghiệm của bất phương trình

2

3 10 2

1 1

3 3

x x x  

   



   

   

là





;S a b



. Tính

b a

.

Ⓐ

9.

Ⓑ

21

.

2

Ⓒ

10.

Ⓓ

12.

Câu 18. Tìm tập nghiệm của bất phương trình

 

3

log 2 2

x

 

.

Ⓐ

 

;11



. Ⓑ

 

2;



. Ⓒ





11;



. Ⓓ

 

11;



.

Câu 19. Tập hợp nghiệm của bất phương trình

 

2

log 1 3

x

 

là:

Ⓐ

 

1;9

S 

Ⓑ

 

1;10

S 

Ⓒ

 

;10

S  

Ⓓ

 

;9

S  

Câu 20. Tìm số nghiệm nguyên của bất phương trình

 

2

log 9 3

x

 

.

Ⓐ

8

. Ⓑ

9

. Ⓒ

7

. Ⓓ

6

.

Câu 21. Tập nghiệm của bất phương trình

 

2

1

2

log 7 0

x x

  

là

Ⓐ

   

;2 3;

   

. Ⓑ

 

;2



. Ⓒ

 

2;3

. Ⓓ

 

3;

 

.

Câu 22. Tập nghiệm của của bất phương trình

1

3

1 2

log 0

x





là.

Ⓐ

1

0;

3

S

 



 

 

. Ⓑ

1 1

;

3 2

S

 



 

 

. Ⓒ

1

;

3

S

 

 

 

 

. Ⓓ

1

;

3

S

 

 

 

 

.

Câu 23. Tìm tập nghiệm

S

của bất phương trình

 

1 1

2 2

log 3 log 4

x  

.

Ⓐ





7;S

  

. Ⓑ

 

3; 7

S 

. Ⓒ





; 7

S  

. Ⓓ





3; 7

S 

.

Câu 24. Tìm tập nghiệm

S

của bất phương trình

 

0,5

log 1 2

x

 

.

Ⓐ

5

;

4

S

 

 

 

 

. Ⓑ

 

1;S

 

. Ⓒ

5

;

4

S

 

 

 

 

. Ⓓ

5

1;

4

S

 



 

 

.

Câu 25. Tìm tập nghiệm

S

của bất phương trình

 

2

log 1 2 3

x

 

.

Ⓐ

7 1

;

2 2

 







 

.

Ⓑ

5 1

;

2 2

 







 

. Ⓒ

7 1

;

2 2

 



 

 

. Ⓓ

7

;

2

 

 





 

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 254

Câu 26. Gọi

S

là tập hợp các nghiệm nguyên của bất phương trình

 

1

3

log 1 2

x

  

. Số phần tử của tập

hợp

S

là

Ⓐ

7

. Ⓑ

9

. Ⓒ

10

. Ⓓ

8

.

Câu 27. Tập nghiệm của bất phương trình

 

2

1 1

2 2

log log 2 2

x x x

  

Ⓐ

 

1;2

. Ⓑ

 

1;



. Ⓒ

 

1;2

. Ⓓ

   

1;2 2;

 

.

Câu 28. Giải bất phương trình

 

2

log 1 log 2x x

 

.

Ⓐ

x



. Ⓑ

0

1

x











. Ⓒ

0

x



. Ⓓ

1x 

.

Câu 29. Tập nghiệm của bất phương trình

 

2 2

log log 12 3x x

 

là:

Ⓐ

 

;3



. Ⓑ

 

0;3

. Ⓒ

 

0;6

. Ⓓ

 

3;



.

Câu 30. Bất phương trình

 

2

6 6

log log 6 

x x

có tập nghiệm là

Ⓐ

 

2;3

. Ⓑ

   

3;2 \ 0

. Ⓒ

   

; 2 3;

   

. Ⓓ

   

2;3 \ 0

.

Câu 31. Tập nghiệm của bất phương trình

 

2

log 1 3

x

 

là:

Ⓐ



 



; 2 2;

   

. Ⓑ

 

3;3



. Ⓒ

 

2;2



. Ⓓ



 



; 3 3;

   

.

Câu 32. Tập nghiệm của bất phương trình

 

1

2

log x 1 0 

là

Ⓐ





;2



. Ⓑ





2;



. Ⓒ

 

1;2

. Ⓓ





1;2

.

Câu 1. Xét bất phương trình

2 2

5 3.5 32 0

x x

  

. Nếu đặt

5

x

t



thì bất phương trình trở thành bất phương

trình nào sau đây?

Ⓐ

2

75 32 0

t t

  

. Ⓑ

2

16 32 0

t t

  

. Ⓒ

2

6 32 0

t t

  

. Ⓓ

2

3 32 0

t t

  

.

Câu 2. Bất phương trình

2

2 18.2 32 0

x x

  

có tập nghiệm là

Ⓐ



 



;2 4;

  

. Ⓑ



 



;1 16;

  

. Ⓒ



 



;2 16;

  

. Ⓓ



 



;1 4;

  

.

Câu 3. Tập hợp nghiệm của bất phương trình

3 2

1 2

3

27 3

x



 

là

Ⓐ

 

2;3 .

Ⓑ

 

0;1 .

Ⓒ

 

1;2 .

Ⓓ

1

.

3

 

 

 

Dạng 2:

Giải bất phương trình bằng cách đặt ẩn phụ

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 255

Câu 4. Nghiệm của bất phương trình

1 3

9 36.3 3 0

x x 

  

là.

Ⓐ

1 3

x

 

. Ⓑ

1x 

. Ⓒ

3

x



. Ⓓ

1 2

x

 

.

Câu 5. Số nghiệm nguyên của bất phương trình

3 9.3 10

x x

 

là

Ⓐ

2

. Ⓑ

0

. Ⓒ

1

. Ⓓ Vô số.

Câu 6. Bất phương trình

3.4 5.6 2.9 0

x x x

  

có tập nghiệm

 

;S a b



. Khi đó giá trị của

2 2

a b

bằng?

Ⓐ 1 Ⓑ

5

3

Ⓒ

13

4

Ⓓ

13

9

Câu 7. Tập nghiệm của bất phương trình

9 2.6 4 0

x x x

  

là

Ⓐ

 

\ 0

S 



. Ⓑ





0;S

 

. Ⓒ

 

0;S

 

. Ⓓ

S

 

.

Câu 8. Tập nghiệm của bất phương trình

2 2

1 2

9 10.3 1 0

x x x x   

  

là:

Ⓐ



 



; 2 1;

   

. Ⓑ

 

0;1

.

Ⓒ



   



; 2 1;0 1;

     

. Ⓓ

  



2; 1 1;

   

.

Câu 9. Nghiệm của bất phương trình là.

Ⓐ . Ⓑ .

.

Ⓓ hoặc .

Câu 10. Tập nghiệm của bất phương trình:

2

x

x 2x

1 2

0

2



 

là

Ⓐ





;0



Ⓑ





;1

Ⓒ





2;



Ⓓ

 

0;2

Câu 11. Bất phương trình

2 2

2.5 5.2 133. 10

x x x

 

 

có tập nghiệm là

 

;S a b



thì biểu thức

1000 4 1A b a  

có giá trị bằng

Ⓐ

1004

. Ⓑ

2017

. Ⓒ

3992

. Ⓓ

4008

.

Câu 12. Giải bất phương trình:

2 2

6 2 4.3 2

x x x x



  

có tập nghiệm là.

Ⓐ

( ;0] [2; )

x

   

. Ⓑ

[1; )

x

 

.

Ⓒ

 

0; 2

x 

. Ⓓ

( ; 1] [1; )

x

    

.

Câu 13. Số nghiệm nguyên không âm của bất phương trình

1 1

15.2 1 2 1 2

x x x 

   

bằng bao nhiêu?

Ⓐ

2

. Ⓑ

3

. Ⓒ

0

. Ⓓ

1

.

Câu 14. Tìm tập nghiệm

S

của phương trình

2

2 2

log 5log 4 0

x x

  

Ⓐ



 



; 2 16;S

   

. Ⓑ



 



0; 2 16;S

  

.

Ⓒ



 



;1 4;S

   

. Ⓓ

 

2;16

S 

.

5

2

x x

e e



 

ln 2 ln 2

x

  

1

2

x

 

1

2

x



2

x



ln 2

x

 

ln 2

x



TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 256

Câu 15. Bất phương trình

2

log 2019log 2018 0

x x

  

có tập nghiệm là

Ⓐ

2018

10;10S

 



 

. Ⓑ



2018

10;10S







. Ⓒ

 

1; 2018

S 

. Ⓓ

 

2018

10;10S 

.

Câu 16. Khi đặt

5

logt x

thì bất phương trình

 

2

5

log 5 3log 5 0

x x

  

trở thành bất phương trình nào

sau đây?

Ⓐ

  

2

6 4 0t t

. Ⓑ

  

2

6 5 0t t

. Ⓒ

  

2

4 4 0t t

. Ⓓ

  

2

3 5 0t t

.

Câu 17. Số các nghiệm nguyên nhỏ hơn

201 9

của bất phương trình

 

2

4

log 16 5 log 2 0

x

 

là:

Ⓐ

201 6

. Ⓑ

201 8

. Ⓒ

2 0 1 7

. Ⓓ

201 5

.

Câu 1. Tìm tập

S

của bất phương trình:

2

3 .5 1

x x



.

Ⓐ

 

5

log 3;0



. Ⓑ





5

log 3;0



. Ⓒ

 

3

log 5;0

. Ⓓ





3

log 5;0

.

Câu 2. Cho hàm số

 

2

5 .4

x x

f x 

. Khẳng định nào sau đây sai?

Ⓐ

 

25

f x

 

2

log5 2 log2 2log5

x x 

. Ⓑ

 

2

5

25 2 log 2 2

f x x x

   

.

Ⓒ

 

2

25 log 5 2 25

f x x x

   

. Ⓓ

 

2

2 2

25 2 log 5 2log 5

f x x x   

.

Câu 3. Bất phương trình

2 3

log log 1x x 

có nghiệm là.

Ⓐ

3

log 6

2x 

. Ⓑ

6

x



. Ⓒ

6

log 2

3x 

. Ⓓ

2

log 6

3x 

.

Câu 1. Tìm tập nghiệm của bất phương trình

7 10 3x

x

 

.

Ⓐ





1;



. Ⓑ





;1

. Ⓒ

 

1;



. Ⓓ



.

Câu 2. Nghiệm của bất phương trình

2.2 3.3 6 –1

x x x

 

là.

Ⓐ

3

x



. Ⓑ

2

x



. Ⓒ

3

x



. Ⓓ

2

x



.

Dạng 3:

Giải bất phương trình bằng cách lấy mũ (lôgarit) hai vế

Dạng 4:

Phương pháp đánh giá

GIẢI TÍCH

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

Trang: 257

Câu 3. Tập hợp tất cả các số thực

x

không thỏa mãn bất phương trình

 

2

4 2 2

9 4 .2019 1

x x

x

 

  

là

khoảng

 

;a b

. Tính

b a

.

Ⓐ

5

. Ⓑ

4

. Ⓒ

5

. Ⓓ

1

.

Câu 4. Tìm số nghiệm nguyên của bất phương trình

2 2

2 15 100 10 50 2

2 2 25 150 0

x x x x

x x

   

    

.

Ⓐ

3

. Ⓑ

6

. Ⓒ

4

. Ⓓ

5

.

Câu 5. Có bao nhiêu giá trị nguyên của

x

trong đoạn

 

0;2020

thỏa mãn bất phương trình sau

16 25 36 20 24 30

x x x x x x

    

.

Ⓐ

3

. Ⓑ

2000

. Ⓒ

1

. Ⓓ

1000

.

Câu 6. Số nghiệm nguyên thuộc đoạn

 

20; 20



của bất phương trình:

2 1 2

2 9.2 4 2 3 0

x x



    

là

Ⓐ

37

. Ⓑ

19

. Ⓒ

38

. Ⓓ

36

.

Câu 7. Tập hợp tất cả các số thực

x

không thỏa mãn bất phương trình

 

2

9 2 1

3 9 5 1

x x

x

 

  

là một

khoảng

 

;a b

. Tính

.b a

Ⓐ

6

. Ⓑ

3

. Ⓒ

4

. Ⓓ

8

.

Câu 8. Biết tập nghiệm của bất phương trình





 

2 2

3 5

log 4 1 2log 5 3

x x x x

      

là

 

;a b

. Khi đó

tổng

2a b

bằng

Ⓐ

4

. Ⓑ

2

. Ⓒ 1. Ⓓ

3

.

Câu 1. Tìm tất cả giá trị của

m

để bất phương trình

 

9 2 1 3 3 2 0

x x

m m

    

nghiệm đúng với mọi số

thực

x

.

Ⓐ

2

m



. Ⓑ

 

5 2 3; 5 2 3

m     

.

Ⓒ

3

2

m

 

. Ⓓ

3

2

m

 

.

Câu 2. Cho bất phương trình

 

   

1

.3 3 2 . 4 7 4 7 0

x x

x

m m



     

, với

m

là tham số. Tìm tất cả các

giá trị của tham số

m

để bất phương trình đã cho nghiệm đúng với mọi





;0

x 

.

Ⓐ

2 2 3

3

m





. Ⓑ

2 2 3

3

m



 

. Ⓒ

2 2 3

3

m





. Ⓓ

2 2 3

3

m





.

Câu 3. Tìm tất cả các giá trị thực của tham số

m

để bất phương trình

2

2 2

log 2log 3 2 0

x x m

   

có

nghiệm thựⒸ

Dạng 5:

Bất phương trình mũ, lôgarit chứa tham số

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

GIẢI TÍCH

Trang: 258

Ⓐ

2

3

m



. Ⓑ

1

m



. Ⓒ

1

m



. Ⓓ

0

m



.

Câu 4. Có bao nhiêu giá trị nguyên dương của tham số

m

để hàm số

2

2 2

4log 2log 3 2 0

x x m

   

có

nghiệm thực?

Ⓐ

2

. Ⓑ

1

. Ⓒ

0

. Ⓓ Vô số.

Câu 5. Gọi

S

là tập hợp tất cả các giá trị của tham số

m

để bất phương trình

 

2

1 1

3 3

log 3 log 1

x x m x

   

có tập nghiệm chứa khoảng

 

1;



. Tìm tập

S

.

Ⓐ

 

3;S

 

. Ⓑ





2;S

 

. Ⓒ

 

;0

S  

. Ⓓ





;1

S

 

.

Câu 6. Cho các bất phương trình

2 2

5 5

log ( 4 ) log ( 1) 1

x x m x

     

 

1

và

4 1 0

x x

   

 

2

.

Tổng tất cả các giá trị nguyên dương của

m

sao cho mọi nghiệm của bất phương trình

 

2

đều là nghiệm

của bất phương trình

 

1

là

Ⓐ

13

Ⓑ

21

Ⓒ

28

Ⓓ

11

Câu 7. Tìm tất cả các giá trị thực của tham số

m

để bất phương trình

 

2

2 2

4 log log 0

x x m

  

nghiệm

đúng mọi giá trị

 

1;64

x 

.

Ⓐ

0

m



. Ⓑ

0

m



. Ⓒ

0

m



. Ⓓ

0

m



.

Câu 8. Tìm số nguyên

m

nhỏ nhất để bất phương trình

 

2 3 2

3 3

log 1 2 3 log 1

x x x x x m

      

(ẩn

x

)

có ít nhất hai nghiệm phân biệt.

Ⓐ

3

m



. Ⓑ

2

m



. Ⓒ

1

m



. Ⓓ

1

m

 

.

Câu 9. Gọi

a

là số thực lớn nhất để bất phương trình

 

2 2

2 ln 1 0

x x a x x

     

nghiệm đúng với mọi

x



. Mệnh đề nào sau đây đúng?

Ⓐ





6;7

a 

. Ⓑ





6; 5

a

  

. Ⓒ





2;3

a 

. Ⓓ

 

8;a

  

.

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 259

§1. KHÁI NIỆM VỀ KHỐI ĐA DIỆN

A. TÓM TẮT LÝ THUYẾT

I. Khối đa diện, khối chóp, khối lăng trụ:

1. Định nghĩa hình đa diện:

Hình đa diện là hình được tạo bởi một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện:

a) Hai đa giác bất kỳ hoặc không có điểm chung, hoặc có một đỉnh chung,

hoặc có một cạnh chung.

b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.

Hình H gồm các đa giác đó được gọi là một hình đa diện, hoặc đa diện.

2. Định nghĩa khối chóp, khối lăng trụ:

Khối đa diện được gọi là khối chóp, khối chóp cụt nếu nó được giới hạn bởi

một hình chóp, hình chóp cụt (h.1a, 1b).

Tương tự, khối đa diện được gọi là khối lăng trụ nếu nó được giới hạn bởi một hình lăng trụ (h.1c).

Chương

1

KHỐI ĐA DIỆN

1. KHÁI NIỆM VỀ KHỐI ĐA DIỆN

2. KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA

DIỆN ĐỀU

3. KHÁI NIỆM VỀ THỂ TÍCH CỦA

KHỐI ĐA DIỆN

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 260

1a 1b 1c

3. Định nghĩa khối đa diện:

Hình H cùng với các điểm nằm trong H được gọi là khối đa diện giới hạn bởi hình H.

- Mỗi đa giác của hình H được gọi là một mặt của khối đa diện.

- Các đỉnh, các cạnh của mỗi mặt còn gọi là đỉnh, cạnh của khối đa diện.

4. Phân chia và lắp ghép khối đa diện:

Ví dụ 1:

Cho khối chóp tứ giác S.ABCD. Ta hãy xét hai

khối chóp tam giác S.ABC và S.ACD. Ta thấy

rằng:

1) Hai khối chóp đó không có điểm trong

chung, nghĩa là điểm trong của các khối chóp

này không phải là điểm trong của khối chóp kia.

2) Hợp của hai khối chóp S.ABC và S.ACD

chính là khối chóp S.ABCD

Ta nói rằng: Khối đa diện S.ABCD được phân chia thành hai khối đa diện S.ABC và S.ACD.

Ta cũng còn nói: Hai khối đa diện S.ABC và S.ACD được ghép lại thành khối đa diện S.ABCD.

Ví dụ 2:

1) Cắt khối lăng trụ ABC.A’B’C’ bởi mặt

phẳng (A’BC). Khi đó khối lăng trụ được phân

chia thành những khối đa diện nào?

2) Hãy phân chia khối lăng trụ ABC.A’B’C’

thành ba khối tứ diện.

Một cách tổng quát, mọi khối chóp và khối lăng trụ

luôn có thể phân chia được thành những khối tứ diện

A

B

C

D

E

F

F'

E'

D'

C'

B'

A'

C

D

A

B

S

M

N

... hình là phần vỏ

bọc bên ngoài. Khối

gồm phần vỏ bên

ngoài và phần ruột

đặc bên trong.

... hai điểm M, N

không phải là điểm

trong của khối

chóp.

A

B

C

D

S

C

C'

B'

A

B

A'

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 261

II. Phép đối xứng qua mặt phẳng và sự bằng nhau của các khối đa diện:

1. Phép biến hình trong không gian:

Phép biến hình F trong không gian là một quy tắc để với mỗi điểm M xác định được một điểm M’

duy nhất gọi là ảnh của điểm M qua phép biến hình F.

Ta còn nói F biến điểm M thành điểm M’ và kí hiệu M’ = F(M).

Qua phép biến hình F, mỗi hình H được biến thành hình H’ gồm tất cả các ảnh của các điểm thuộc

hình H.

Một phép biến hình F trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa

hai điểm bất kỳ.

Có nghĩa là nếu F biến hai điểm bất kỳ M, N lần lượt thành hai điểm M’, N’ thì M’N’ = MN.

2. Phép đối xứng qua mặt phẳng:

a. Định nghĩa:

Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính

nó và biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực

của MM’.

b. Định lý:

Nếu phép đối xứng qua mp (P) biến hai điểm M, N lần lượt thành hai điểm M’, N’

thì M’N’ = MN.

Như vậy: phép đối xứng qua mặt phẳng là phép biến hình bảo toàn khoảng cách giữa hai

điểm bất kì.

3. Mặt phẳng đối xứng của một hình:

a. Định nghĩa:

Nếu phép đối xứng qua mp (P) biến hình H thành chính nó thì (P) gọi là mặt phẳng đối xứng

của hình H.

b. Một số ví dụ:

Ví dụ 1: Mọi mặt phẳng đi qua tâm mặt cầu đều là mặt phẳng đối xứng của mặt cầu.

Ví dụ 2: Cho tứ diện đều ABCD . Gọi M là trung điểm của cạnh CD thì phép đối xứng qua mp

(ABM) biến A thành A, B thành B, C thành D, D thành C.

Như vậy, phép đối xứng đó biến tứ diện ABCD thành chính nó, suy ra mp (ABM) là mặt phẳng

đối xứng của tứ diện ABCD.

P

M

M'

p

M

M'

N

N'

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 262

Hình tứ diện đều ABCD có sáu mặt phẳng đối xứng . Đó là các mặt phẳng đi qua một cạnh và

trung điểm của cạnh đối diện.

Ví dụ 3: Xét hình lập phương ABCD. A’B’C’D’. Nếu (P) là mặt phẳng trung trực của cạnh AB

thì nó cũng là mặt phẳng trung trực của các cạnh CD, A’B’, C’D’, vì vậy nó là mặt phẳng đối

xứng của hình lập phương.

Tương tự, các mặt phẳng trung trực của các cạnh AD và AA’ cũng là các mặt phẳng đối xứng

của hình lập phương.

Gọi (Q) là mặt phẳng đi qua hai cạnh đối diện AB, C’D’ thì (Q) là mặt phẳng đối xứng của

hình lập phương vì phép đối xứng qua (Q) biến mỗi điểm A, B, C’, D’ thành chính nó và biến

A’ thành D, D thành A’, C thành B’ và B’ thành C.

B. CÁC DẠNG TOÁN THƯỜNG GẶP

— Bài toán. Cho các hình vẽ. Đưa ra kết luận xem hình nào là hình đa diện, khối đa diện.

— Phương pháp: Áp dụng định nghĩa hình đa diện và khối đa diện

Hình đa diện là hình được tạo bởi một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện:

a) Hai đa giác bất kỳ hoặc không có điểm chung, hoặc có một đỉnh chung,

hoặc có một cạnh chung.

b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.

Hình H gồm các đa giác đó được gọi là một hình đa diện, hoặc đa diện.

Hình H cùng với các điểm nằm trong H được gọi là khối đa diện giới hạn bởi hình H.

CÁC VÍ DỤ

Ví dụ 1:

Hình nào dưới đây không phải là hình đa diện ?

Dạng 1:

Nhận dạng hình đa diện, khối đa diện

M

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 263

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Vật thể nào dưới đây không phải là khối đa diện?

Ⓐ Ⓑ Ⓒ Ⓓ

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Trong các hình sau, có bao nhiêu hình được gọi là khối đa diện ?

Hình 4

Hình 3

Hình 2

Hình 1

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 264

Ⓐ

2

. Ⓑ

3

. Ⓒ

4

. Ⓓ

5

.

Câu 2. Cho một hình đa diện. Khẳng định nào sau đây sai ?

Ⓐ Mỗi mặt có ít nhất 3 cạnh. Ⓑ Mỗi đỉnh là đỉnh chung của ít nhất 3 cạnh.

Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng? Số các đỉnh hoặc các mặt của bất kì hình đa diện nào

cũng

Ⓐ Lớn hơn hoặc bằng

5

. Ⓑ Lớn hơn

4

.

4

. Ⓓ Lớn hơn

5

.

Câu 4. Trong một hình đa diện, mỗi cạnh là cạnh chung của đúng bao nhiêu mặt ?

Ⓐ Không có mặt nào. Ⓑ

3

mặt. Ⓒ

4

mặt. Ⓓ

2

mặt.

Câu 5. Có bao nhiêu hình đa diện trong bốn hình sau ?

Ⓐ

1

. Ⓑ

3

. Ⓒ

2

. Ⓓ

4

.

Câu 6. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt ?

Ⓐ

5

mặt. Ⓑ

3

mặt. Ⓒ

2

mặt. Ⓓ

4

mặt.

Câu 7. Hình đa diện bên dưới có bao nhiêu mặt ?

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 265

Ⓐ

11

. Ⓑ

7

. Ⓒ

12

. Ⓓ

10

.

Câu 8. Một hình đa diện có tối thiểu bao nhiêu đỉnh ?

Ⓐ

4

. Ⓑ

3

. Ⓒ

5

. Ⓓ

6

.

Câu 9. Hình lăng trụ có

4 5

cạnh có bao nhiêu mặt ?

Ⓐ

15

mặt. Ⓑ

2 0

mặt. Ⓒ

18

mặt. Ⓓ

17

mặt.

Câu 10. Số cạnh của một khối chóp bất kì luôn là:

Ⓐ Một số chẵn ớn hơn hoặc bằng

6

. Ⓑ Một số chẵn lớn hơn hoặc bằng

4

.

5

.

CÁC VÍ DỤ

Ví dụ 1: Cho khối đa diện

.

S ABC D

có đáy

ABCD

là hình bình hành. Chia khối đa diện

.

S ABC D

bởi hai mặt phẳng

 

SBD

và

 

SAC

, khi đó ta thu được bao nhiêu khối đa diện ?

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Nếu không sử dụng thêm điểm nào khác ngoài các đỉnh của hình lập phương thì có thể chia

hình lập phương thành:

Dạng 2:

Phân chia và lắp ghép khối đa diện

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 266

Ⓐ Bốn tứ diện đều và một hình chóp tam giác đều.

Ⓑ Năm hình chóp tam giác đều, không có tứ diện đều.

Ⓓ Năm tứ diện đều.

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Cho khối tứ diện

ABCD

. Lấy điểm

M

nằm giữa

A

và

B

, điểm

N

nằm giữa

C

và

D

. Bằng hai

mặt phẳng

 

CDM

và

 

ABN

, ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây ?

Ⓐ

MANC

,

BCDN

,

A M N D

,

ABND

. Ⓑ

MANC

,

B C M N

,

A M N D

,

MBND

.

Ⓒ

ABCN

,

ABND

,

A M N D

,

MBND

. Ⓓ

NAC B

,

B C M N

,

ABND

,

MBND

.

Câu 2. Cho khối lăng trụ

.

ABC A B C

  

. Gọi

M

là trung điểm của

BB



. Mặt phẳng (

MCA



) chia khối lăng

trụ đã cho thành những khối đa diện nào ?

Ⓐ Hai khối lăng trụ tam giác.

Ⓑ Một khối chóp tam giác và một khối chóp tứ giác.

Ⓓ Hai khối chóp tứ giác.

Câu 3. Cắt khối lăng trụ

.

M NP M N P

  

bởi các mặt phẳng

 

MN P

 

và

 

MNP



ta được những khối đa diện

nào ?

Ⓐ Hai khối tứ diện và hai khối chóp tứ giác. Ⓑ Một khối tứ diện và một khối chóp tứ giác.

Câu 4. Một hình lập phương có cạnh

4cm

Người ta sơn đỏ mặt ngoài của hình lập phương rồi cắt hình lập

phương bằng các mặt phẳng song song với các mặt của hình lập phương thành 64 hình lập phương nhỏ có

cạnh

1cm

Có bao nhiêu hình lập phương có đúng một mặt được sơn đỏ ?

Ⓐ

4 8

. Ⓑ

8

. Ⓒ

24

. Ⓓ

16

.

Câu 5. Có thể chia khối lập phương thành bao nhiêu khối tứ diện bằng nhau có các đỉnh là đỉnh của hình lập

phương ?

Ⓐ Vô số. Ⓑ

4

. Ⓒ

6

. Ⓓ

2

.

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 267

§2. KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU

B. TÓM TẮT LÝ THUYẾT

I. Khối đa diện lồi:

Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H).

Khi đó đa diện xác định (H) được gọi là đa diện lồi.

* Chú ý: Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía

đối với mỗi mặt phẳng chứa một mặt của nó.

II. Khối đa diện đều:

4. Định nghĩa:

Khối đa diện đều là khối đa diện lồi có tính chất sau đây:

a) Mỗi mặt của nó là một đa giác đều p cạnh.

b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.

Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.

5. Định lý:

Chỉ có năm loại khối đa diện đều. Đó là:

Khối đa diện đều Số đỉnh Số cạnh Số mặt Ký hiệu Mặt đối xứng

Tứ diện đều 4 6 4 {3 ; 3} 6

Khối lập phương 8 12 6 {4 ; 3} 9

Khối bát diện đều 6 12 8 {3 ; 4} 9

Khối thập nhị diện(12) đều 20 30 12 {5 ; 3} 15

Khối nhị thập diện(20) đều 12 30 20 {3 ; 5} 15

Chú ý: Loại {p; q} có Đ đỉnh, C cạnh, M mặt thì p.M = q.Đ = 2.C hoặc Đ + M = C + 2



TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 268

B. CÁC DẠNG TOÁN THƯỜNG GẶP

— Bài toán. Cho các hình vẽ. Đưa ra kết luận xem hình nào khối đa diện lồi.

— Phương pháp: Áp dụng định khối đa diện lồi

Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H).

Khi đó đa diện xác định (H) được gọi là đa diện lồi.

* Chú ý: Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một

phía đối với mỗi mặt phẳng chứa một mặt của nó

CÁC VÍ DỤ

Ví dụ 1: Hình nào dưới đây là khối đa diện lồi ?

Hình 1 Hình 2 Hình 3 Hình 4

--------------------------------------------------------------------------------------------------------------------------------

Dạng 1:

Nhận dạng khối đa diện lồi

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 269

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Trong các hình sau, hình nào không phải là khối đa diện lồi ?

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Số hình đa diện lồi trong các hình dưới đây là ?

Ⓐ

2

. Ⓑ

3

. Ⓒ

0

. Ⓓ

1

.

Câu 2. Một khối đa diện lồi với các mặt là tam giác thì:

Ⓐ

3 2M C

. Ⓑ

3 2M C

. Ⓒ

3 2M C

. Ⓓ Đáp số khác.

Câu 3. Có mấy khối đa diện lồi trong các hình sau ?

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 270

Ⓐ

0

. Ⓑ

3

. Ⓒ

2

. Ⓓ

1

.

Câu 4. Trong các mệnh đề sau, mệnh đề nào sai ?

Ⓐ Hình lập phương là đa diện lồi.

Ⓑ Hình tạo bởi hai tứ diện ghép với nhau là một hình đa diện lồi.

Ⓓ Tứ diện là đa diện lồi.

Câu 5. Có bao nhiêu hình đa diện lồi trong bốn hình sau ?

Ⓐ

1

. Ⓑ

3

. Ⓒ

2

. Ⓓ

4

.

CÁC VÍ DỤ

Ví dụ 1: Khối lập phương có bao nhiêu mặt phẳng đối xứng ?

Ⓐ

 

3; 4

. Ⓑ

 

3;3

. Ⓒ

 

3; 5

. Ⓓ

 

4; 3

.

--------------------------------------------------------------------------------------------------------------------------------

Dạng 2:

Nhận dạng các khối đa diện đều và các tính chất liên quan

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 271

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Khối đa diện đều loại

 

5;3

có bao nhiêu đỉnh ?

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Các mặt của khối tứ diện đều là

Câu 2. Cho đa diện đều loại

 

;p q

. Mệnh đề nào sau đây sai ?

Ⓐ Mỗi mặt của nó là một đa giác đều có đúng

p

cạnh.

Ⓑ Mỗi cạnh của nó là cạnh chung của đúng hai mặt.

q

mặt.

Ⓓ Mỗi mặt của nó là một tam giác đều.

Câu 3. Đa diện đều loại

 

3; 5

có:

Câu 4. Cho hình đa diện đều loại

 

4;3

có cạnh bằng

a

. Gọi

S

là tổng diện tích tất cả các mặt của hình đa

diện đó. Mệnh đề nào dưới đây đúng ?

Ⓐ

2

10S a



. Ⓑ

2

8S a



. Ⓒ

2

4S a



. Ⓓ

2

6S a



.

Câu 5. Khối đa diện đều loại

 

;p q

được sắp xếp theo thứ tự tăng dần của số đỉnh là:

Ⓐ

 

3; 3

,

 

3; 4

,

 

5; 3

,

 

4; 3

,

 

3; 5

. Ⓑ

 

3; 3

,

 

4; 3

,

 

3; 4

,

 

3; 5

,

 

5; 3

.

Ⓒ

 

3; 3

,

 

3; 4

,

 

4; 3

,

 

5; 3

,

 

3; 5

. Ⓓ

 

3; 3

,

 

3; 4

,

 

4; 3

,

 

3; 5

,

 

5; 3

.

Câu 6. Trong tất cả các loại hình đa diện đều sau đây, hình nào có số mặt nhiều nhất ?

Ⓐ Loại

 

3; 4

. Ⓑ Loại

 

5; 3

. Ⓒ Loại

 

4; 3

. Ⓓ Loại

 

3; 5

.

Câu 7. Khối mười hai mặt đều có số cạnh là:

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 272

Ⓐ

2 0

. Ⓑ

12

. Ⓒ

30

. Ⓓ

8

.

Câu 8. Có bao nhiêu loại khối đa diện đều mà mỗi mặt của nó là một tam giác đều ?

Ⓐ

1

. Ⓑ

3

. Ⓒ

5

. Ⓓ

2

.

Câu 9. Cho khối đa diện đều loại

 

3; 4

. Tổng các góc phẳng tại

1

đỉnh của khối đa diện bằng ?

Ⓐ

180

. Ⓑ

240

. Ⓒ

324

. Ⓓ

360

.

Câu 10. Cho khối đa diện đều có số mặt là M, số cạnh là

C

. Số đỉnh của khối đa diện đều là bao nhiêu? Biết

rằng

4 3

3 2 432M C 

.

Ⓐ

8

. Ⓑ

12

. Ⓒ

6

. Ⓓ

4

.

— Bài toán. Xác định tâm đối xứng, trục đối xứng và mặt phẳng đối xứng của một hình đa diện (nếu

có).

— Phương pháp: Áp dụng định nghĩa về tâm đối xứng, trục đối xứng, mặt phẳng đối xứng của một

hình.

+ Nếu phép đối xứng qua mp (P) biến hình H thành chính nó thì (P) gọi là mặt phẳng đối xứng của

hình H.

Mặt phẳng đối xứng của một số hình thường gặp:

1) Hình hộp chữ nhật có 3 kích thước khác nhau: Có 3 mặt phẳng đối xứng

2) Hình lăng trụ tam giác đều: Có 4 mặt phẳng đối xứng

Dạng 3:

Tính chất đối xứng của các khối đa diện

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 273

3) Hình chóp tam giác đều: Có 3 mặt phẳng đối xứng

4) Hình tứ diện đều: Có 6 mặt phẳng đối xứng

5) Hình chóp tứ giác đều: Có 4 mặt phẳng đối xứng

O

D

B

C

A

S

O

D

B

C

A

S

O

D

B

C

A

S

O

D

B

C

A

S

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 274

6) Hình bát diện đều: Có 9 mặt phẳng đối xứng

7) Hình lập phương: Có 9 mặt phẳng đối xứng

CÁC VÍ DỤ

Ví dụ 1: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng ? Vẽ các mặt phẳng đối xứng đó.

--------------------------------------------------------------------------------------------------------------------------------

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 275

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Số mặt phẳng đối xứng của đa diện đều loại

 

4;3

là:

Ⓐ

8

. Ⓑ

7

. Ⓒ

6

. Ⓓ

9

.

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng ?

Ⓐ

9

. Ⓑ

5

. Ⓒ

6

. Ⓓ

7

.

Câu 2. Hình đa diện nào dưới đây không có tâm đối xứng ?

Câu 3. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình vuông. Biết hai mặt phẳng

 

SAB

và

 

SAD

cùng

vuông góc với mặt đáy. Hình chóp này có bao nhiêu mặt phẳng đối xứng ?

Ⓐ

4

. Ⓑ

1

. Ⓒ

0

. Ⓓ

2

.

Câu 4. Hình hộp đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng ?

Ⓐ

4

. Ⓑ

1

. Ⓒ

3

. Ⓓ

2

.

Câu 5. Hình nào dưới nào dưới đây không có trục đối xứng ?

Câu 6. Khối chóp tam giác đều có cạnh đáy bằng

a

, cạnh bên bằng

3a

có bao nhiêu mặt phẳng đối xứng

?

Ⓐ

6

. Ⓑ

4

. Ⓒ

3

. Ⓓ

9

.

Câu 7. Hình đa diện nào sau đây không có tâm đối xứng?

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 276

Câu 8. Hình nào sau đây không có trục đối xứng ?

Câu 9. Số mặt phẳng đối xứng của hình bát diện đều là:

Ⓐ

3

. Ⓑ

4

. Ⓒ

9

. Ⓓ

6

.

Câu 10. Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng ?

Ⓐ

9

. Ⓑ

3

. Ⓒ

6

. Ⓓ

4

.

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 277

§3. KHÁI NIỆM VỀ THỂ TÍCH KHỐI ĐA DIỆN

A. TÓM TẮT LÝ THUYẾT

I. Thể tích khối hộp chữ nhật và khối lăng trụ:

5. Thể tích khối hộp chữ nhật:

Thể tích khối hộp chữ nhật bằng tích ba kích thước của nó.

Hình hộp chữ nhật có ba kích thước là a, b, c thì thể tích của nó là:

6. Thể tích khối lăng trụ:

Thể tích khối lăng trụ có diện tích đa giác đáy S

đ

và chiều cao h là:

II. Thể tích khối chóp và tỉ số thể tích:

6. Thể tích khối chóp:

Thể tích khối chóp có diện tích đáy S

đ

và chiều cao h là:

c

b

a

V

ABC.A'B'C'

= S

ABC

x h

S

ABC

h

C'

B'

A

C

B

A'

V

ABCD.A'B'C'D' =

S

ABCD

x

h

S

ABCD

H

h

C'

B'

D'

C

D

A

B

A'

V

S.ABCD

=

1

3

S

ABCD

x h

S

ABCD

h

A

D C

S

B

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 278

7. Tỉ số thể tích đối với khối chóp tam giác:

Cho hình chóp S.ABC. Trên các đoạn thẳng SA, SB, SC lần

lượt lấy ba điểm A', B', C' khác với S. Ta có tỉ số thể tích:

* Đặc biệt: Nếu A'  A ta có:

B. CÁC DẠNG TOÁN THƯỜNG GẶP

I. Thể tích khối chóp

— Bài toán. Tính thể tích khối chóp có cạnh bên vuông góc với đáy.

— Phương pháp: Chiều cao của khối chóp chình là độ dài cạnh bên vuông góc

với đáy.

Vd: Hình chóp S.ABC có cạnh bên SA vuông góc với đáy thì độ dài SA là chiều

cao của khối chóp

CÁC VÍ DỤ

Ví dụ 1: Cho hình chóp

.S ABC

có đáy

A B C

là tam giác vuông tại

.B

Cạnh bên

SA

vuông góc với

mặt phẳng đáy.

SA

=

AB

=

2 a

,

BC

=

3a

. Tính thể tích của

.S ABC

.

--------------------------------------------------------------------------------------------------------------------------------

SC

SB

SB '

.

'

V

S.ABC

C'B'S.A'



Dạng 1:

Khối chóp có cạnh bên vuông góc với đáy

S.A'B'C'

S.ABC

V

SA' SB' SC'

. .

V SA SB SC



A

C

B

S

A'

B'

C'

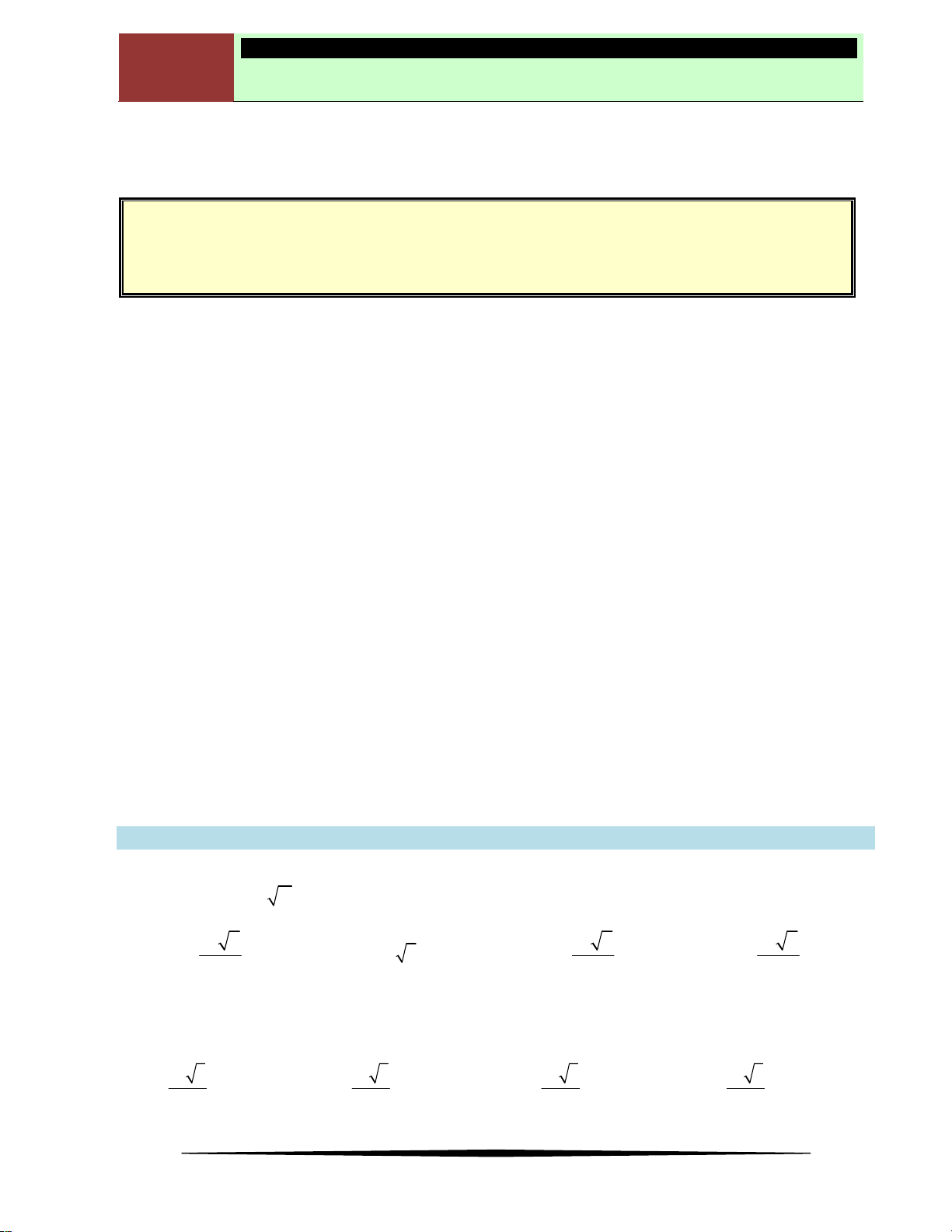
HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 279

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình chữ nhật có

, 2AB a BC a 

. Hai mặt phẳng

 

SAB

và

 

SAD

cùng vuông góc với mặt phẳng đáy, đường thẳng

SC

hợp với đáy một góc

60

. Thể

tích

V

của khối chóp

.

S ABC D

.

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình vuông cạnh

a

, cạnh bên

SA

vuông góc với mặt

phẳng đáy và

2

SA a

. Tính thể tích của khối chóp

.

S ABC D

là:

Ⓐ

3

2

3

a

V 

. Ⓑ

3

2

V a

. Ⓒ

3

2

6

a

V 

. Ⓓ

3

2

4

a

V 

.

Câu 2. Cho khối chóp

.

S ABC

có đáy

A B C

là tam giác đều cạnh

a

,

SA

vuông góc với mặt phẳng đáy và

2SA a

. Tính thể tích khối chóp

.

S ABC

.

Ⓐ

3

12

a

. Ⓑ

3

2

a

. Ⓒ

3

6

a

. Ⓓ

3

a

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 280

Câu 3. Cho hình chóp tam giác

.

S ABC

có đáy

A B C

là tam giác vuông tại

A

,

AB a

,

2AC a

, cạnh bên

SA

vuông góc với mặt đáy và

SA a

. Tính thể tích

V

của khối chóp

.

S ABC

.

Ⓐ

3

2

a

V 

. Ⓑ

3

V a

. Ⓒ

3

4

a

V 

. Ⓓ

3

a

V 

.

Câu 4. Cho khối chóp

.

S ABC D

có đường cao

SA

và đáy

ABCD

là hình thoi. Thể tích khối chóp đã cho

được tính theo công thức nào sau đây ?

Ⓐ

2

1

.

3

SA AB

. Ⓑ

1

. .

3

SA AC BD

. Ⓒ

1

. .

6

SA AC BD

. Ⓓ

2

1

.

2

SA AB

.

Câu 5. Cho khối chóp

.

S ABC

có

 

SA ABC



,

SA a

,

AB a

,

2AC a

và



120

BAC

 

. Tính thể tích

khối chóp

.

S ABC

?

Ⓐ

3

a

. Ⓑ

3

2

a

. Ⓒ

3

a . Ⓓ

3

6

a

.

Câu 6. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình thang vuông tại

A

và

B

. Biết

AB a

,

2 2AD BC a 

,

( )SA ABCD

và

SD

tạo với đáy một góc

0

60

. Thể tích khối chóp

.

S ABC D

bằng:

Ⓐ

3

a

. Ⓑ

3

2 3

a

. Ⓒ

3

2

a

. Ⓓ

3

a

.

Câu 7. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình vuông cạnh bằng

2 a

, cạnh

SB

vuông góc với đáy

và mặt phẳng

 

SAD

tạo với đáy một góc

60



. Thể tích

V

của khối chóp

.

S ABC D

bằng:

Ⓐ

3

3 3

4

a

V 

. Ⓑ

3

3 3

8

a

V 

. Ⓒ

3

4 3

3

a

V 

. Ⓓ

3

8 3

3

a

V 

.

Câu 8. Cho hình chóp

.

S ABC

có

, ,SA AB BC

đôi một vuông góc với nhau. Tính thể tích khối chóp

.

S ABC

, biết

3,

SA a AB BC a  

?

Ⓐ

3

9

a

V 

. Ⓑ

3

2

a

V 

. Ⓒ

3

6

a

V 

. Ⓓ

3

a

V 

.

Câu 9. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình chữ nhật với

AB a

,

3BC a



. Cạnh bên

SA

vuông góc với đáy và đường thẳng

SC

tạo với mặt phẳng

 

SAB

một góc

30

. Tính thể tích

V

của khối

chóp

.

S ABC D

theo

a

.

Ⓐ

3

2 6

3

a

V 

. Ⓑ

3

2

3

a

V 

. Ⓒ

3

3V a



. Ⓓ

3

a

V 

.

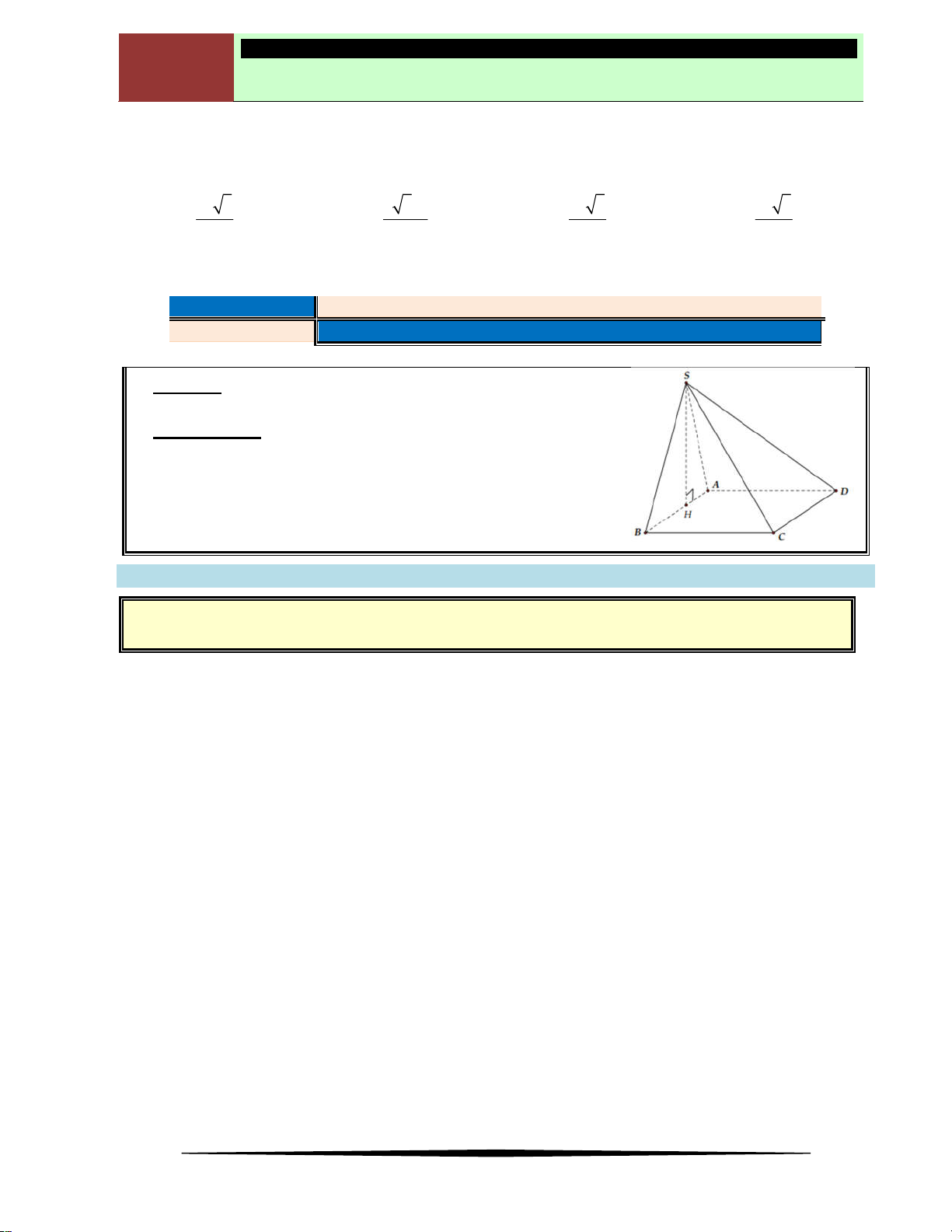
HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 281

Câu 10. Cho hình chóp

.S ABC

có đáy

A B C

là tam giác đều cạnh

a

, cạnh bên

SA

vuông góc với đáy

 

ABC

. Biết góc tạo bởi hai mặt phẳng

 

SBC

và

 

ABC

bằng

60

. Thể tích

V

của khối chóp

.S ABC

là:

Ⓐ

3

24



a

V

. Ⓑ

3

3 3

8



a

V

. Ⓒ

3

8



a

V

. Ⓓ

3

12



a

V

.

— Bài toán. Tính thể tích khối chóp có một mặt bên vuông góc với

đáy

— Phương pháp: Chiều cao của khối chóp là chiều cao của tam giác

chứa trong mặt bên vuông góc với đáy.

Vd: Hình chóp S.ABCD có mặt bên (SAB) vuông góc với đáy thì

chiều cao SH của tam giác SAB là chiều cao của khối chóp S.ABCD.

CÁC VÍ DỤ

Ví dụ 1: Cho hình chóp

.S A B C D

có đáy

ABCD

là hình vuông cạnh

a

. Mặt bên

SAB

là tam giác

đều nằm trong mặt phẳng vuông góc với mặt đáy

 

ABCD

. Thể tích khối chóp

.S A B C D

?

--------------------------------------------------------------------------------------------------------------------------------

Dạng 2:

Khối chóp có mặt bên vuông góc với đáy

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 282

Ví dụ 2: Cho hình chóp

.

S ABC

có đáy

A B C

là tam giác vuông cân;

AB AC a 

; mặt bên

SAB

là tam giác vuông cân tại

S

và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của khối chóp

.

S ABC

.

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Cho hình chóp

.

S ABC

có đáy là tam giác vuông cân tại

A

,

SB C

đều cạnh

a

và nằm trong mặt

phẳng vuông góc với đáy. Thể tích của khối chóp

.

S ABC

là:

Ⓐ

3

12

a

. Ⓑ

3

24

a

. Ⓒ

3

4

a

. Ⓓ

3

8

a

.

Câu 2. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình thang vuông tại

A

và

B

,

1

2

AB BC AD a  

.

Tam giác

SAB

đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp

.

S ACD

.

Ⓐ

3

.

2

S ACD

a

V 

. Ⓑ

3

.

3

S ACD

a

V 

. Ⓒ

3

.

2

6

S ACD

a

V 

. Ⓓ

3

.

3

6

S ACD

a

V 

.

Câu 3. Cho hình chóp

.

S ABC

có đáy là tam giác cân tại

A

,

AB AC a 

,



120

BAC

 

. Mặt bên

SAB

là

tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích

V

của khối chóp

.

S ABC

là :

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 283

Ⓐ

3

8

a

V 

. Ⓑ

3

V a

. Ⓒ

3

2

a

V 

. Ⓓ

3

2V a



.

Câu 4. Cho hình chóp

.

S ABC D

có đáy là hình vuông cạnh

a

, hình chiếu vuông góc của

S

lên mặt phẳng

 

ABCD

trùng với trung điểm của cạnh

AD

, cạnh

SB

hợp với đáy một góc

60

. Tính theo

a

thể tích

V

của khối chóp

.

S ABC D

?

Ⓐ

3

15

2

a

. Ⓑ

3

15

6

a

. Ⓒ

3

5

4

a

. Ⓓ

3

15

6 3

a

.

Câu 5. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình vuông, tam giác

SAD

cân tại

S

và nằm trong mặt

phẳng vuông góc với đáy

ABCD

. Biết

SD a

, gọi

K

là trung điểm của

AB

, góc giữa đường thẳng

SK

với

mặt phẳng đáy bằng

60

. Tính thể tích V của hình chóp

.

S ABC D

?

Ⓐ

3

4 42

49

a

V 

. Ⓑ

3

2 42

147

a

V 

. Ⓒ

3

2 42

49

a

V 

. Ⓓ

3

4 42

147

a

V 

.

Câu 6. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình chữ nhật, tam giác

SAD

vuông tại

S

và nằm trong

mặt phẳng vuông góc với mặt phẳng đáy. Cho biết

AB a

,

2SA SD

, mặt phẳng

 

SBC

tạo với mặt phẳng

đáy một góc

60

. Tính thể tích của khối chóp

.

S ABC D

?

Ⓐ

3

5

2

a

. Ⓑ

3

5a

. Ⓒ

3

15

2

a

. Ⓓ

3

2

a

.

Câu 7. Cho hình chóp

S.

ABC

có đáy

A B C

là tam giác đều cạnh bằng

a

, tam giác

SAB

cân tại

S

và nằm

trong mặt phẳng vuông góc với đáy,

SC

hợp với đáy một góc

30

,

M

là trung điểm của

.AC

Tính thể tích

khối chóp

.

S BCM

?

Ⓐ

3

48

a

. Ⓑ

3

16

a

. Ⓒ

3

96

a

. Ⓓ

3

24

a

.

Câu 8. Cho hình chóp

.

S ABC

có tam giác

A B C

vuông cân tại

B

,

2,

AC a

mặt phẳng

 

SAC

vuông

góc với mặt đáy

 

ABC

. Các mặt bên

 

SAB

,

 

SBC

tạo với mặt đáy các góc bằng nhau và bằng

60

. Tính

theo

a

thể tích

V

của khối chóp

.

S ABC

?

Ⓐ

3

2

a

V 

. Ⓑ

3

4

a

V 

. Ⓒ

3

6

a

V 

. Ⓓ

3

12

a

V 

.

Câu 9. Cho hình chóp

.

S ABC D

có đáy là hình thang vuông tại

A

và

B

. Hình chiếu vuông góc của

S

trên

mặt đáy

 

ABCD

trùng với trung điểm

AB

. Biết

AB a

,

2B C a

,

10

BD a

. Góc giữa hai mặt phẳng

 

SBD

và mặt phẳng đáy là

60

. Tính thể tích

V

của khối chóp

.

S ABC D

theo

a

?

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 284

Ⓐ

3

3 30

8

a

V 

. Ⓑ

3

30

4

a

V 

. Ⓒ

3

30

12

a

V 

. Ⓓ

3

30

8

a

V 

.

Câu 10. Cho hình chóp

.S ABC

có mặt phẳng

 

SAC

vuông góc với mặt phẳng

 

ABC

,

SAB

là tam giác

đều cạnh 3a , 3BC a đường thẳng

SC

tạo với mặt phẳng

 

ABC

góc

60

. Thể tích của khối chóp

.S ABC

bằng:

Ⓐ

3

a

. Ⓑ

3

6

2

a

. Ⓒ

3

6

a

. Ⓓ

3

2 6a .

— Bài toán. Tính thể tích khối chóp đều.

— Phương pháp: Khối chóp đều là khối chóp có hình chiếu có đỉnh

trùng với tâm của đa giác đáy.

Khi đó: Chiều cao của khối chóp là độ dài đoạn thẳng nối từ đỉnh đến

tâm của đa giác đáy.

Vd: Khối chóp đều S.ABCD có chiều cao chiều chính là độ dài của

đoạn thẳng SO.

CÁC VÍ DỤ

Ví dụ 1: Cho hình chóp tam giác đều có cạnh đáy bằng

3a

và cạnh bên tạo với đáy một góc

60

.

Tính thể tích của khối chóp đó.

--------------------------------------------------------------------------------------------------------------------------------

Dạng 3:

Khối chóp đều

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 285

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Tính thể tích khối bát diện đều cạnh

a

?

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Cho khối chóp tứ giác đều

.

S ABC D

có cạnh đáy bằng

a

và cạnh bên bằng

3a

. Tính thể tích

V

của khối chóp đó theo

a

?

Ⓐ

3

2

3

a

. Ⓑ

3

2

6

a

. Ⓒ

3

10

6

a

. Ⓓ

3

2

a

.

Câu 2. Cho hình chóp đều

.

S ABC D

có cạnh đáy bằng

a

, cạnh bên hợp với mặt đáy một góc

60

. Tính

theo

a

thể tích

V

của khối chóp

.

S ABC D

?

Ⓐ

3

6

a

V 

. Ⓑ

3

6

2

a

V 

. Ⓒ

3

6

3

a

V 

. Ⓓ

3

a

V 

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 286

Câu 3. Cho hình chóp đều

.

S ABC D

có

2AC a

, góc giữa mặt phẳng

 

SBC

và mặt phẳng

 

ABCD

bằng

45

. Tính thể tích

V

của khối chóp

.

S ABC D

theo

a

?

Ⓐ

3

2

3

a

V 

. Ⓑ

3

2 3

3

a

V 

. Ⓒ

3

2

V a

. Ⓓ

3

2

a

V



.

Câu 4. Thể tích của khối tứ diện đều có cạnh bằng

3

là:

Ⓐ

2

. Ⓑ

2 2

. Ⓒ

4 2

9

. Ⓓ

9 2

4

.

Câu 5. Cho khối chóp tam giác đều

.

S ABC

có cạnh đáy bằng

a

,

3SA a

 . Tính thể tích

V

của khối chóp

.

S ABC

?

Ⓐ

3

35

24

a

V 

. Ⓑ

3

6

a

V 

. Ⓒ

3

2

6

a

V 

. Ⓓ

3

2

a

V 

.

Câu 6. Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng

25 00

năm trước Công nguyên. Kim tự tháp

này là một khối chóp tứ giác đều có chiều cao

147m

, cạnh đáy dài

230m

. Thể tích của nó là:

Ⓐ

7776300

3

m

. Ⓑ

3888 1 50

3

m

. Ⓒ

2592100

3

m

. Ⓓ

2592100

2

m

.

Câu 7. Tính thể tích khối chóp tứ giác đều có cạnh đáy bằng

2 a

và diện tích của một mặt bên là

2

a

?

Ⓐ

3

4 2

3

a

. Ⓑ

3

4

3

a

. Ⓒ

3

4a

. Ⓓ

3

4 3

3

a

.

Câu 8. Cho hình chóp tam giác đều

.

S ABC

đỉnh

S

, độ dài cạnh đáy là

a

, cạnh bên bằng

2 a

. Gọi

I

là

trung điểm của cạnh

BC

. Tính thể tích

V

của khối chóp

.

S A B I

?

Ⓐ

3

11

12

a

. Ⓑ

3

11

24

a

. Ⓒ

3

11

8

a

. Ⓓ

3

11

6

a

.

Câu 9. Cho chóp tứ giác đều

.

S ABC D

, có

O

là tâm của đáy. Khoảng cách từ tâm

O

đến mặt bên bằng 1.

Góc giữa mặt bên với đáy bằng

0

45

. Thể tích của hình chóp đã cho là:

Ⓐ

4 2

3

. Ⓑ

8 2

3

. Ⓒ

4 3

3

. Ⓓ

2 3

.

Câu 10. Trong các khối chóp tứ giác đều

.

S ABC D

mà khoảng cách từ

A

đến mp

( )SBC

bằng

2 a

, khối

chóp có thể tích nhỏ nhất bằng:

Ⓐ

3

2 3a

. Ⓑ

3

2a

. Ⓒ

3

3 3a

. Ⓓ

3

4 3a

.

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 287

CÁC VÍ DỤ

Ví dụ 1: Một khối chóp tam giác có đáy là một tam giác đều cạnh

6cm

. Một cạnh bên có độ dài bằng

3cm

và tạo với đáy một góc

60

. Tính thể tích của khối chóp đó.

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình vuông cạnh

a

. Hình chiếu của

S

lên mặt

phẳng đáy trùng với trọng tâm của tam giác

ABD

. Cạnh

SD

tạo với đáy một góc

60

. Tính thể tích

của khối chóp

.

S ABC D

?

--------------------------------------------------------------------------------------------------------------------------------

Dạng 4:

Khối chóp khác

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 288

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Cho khối chóp

.

S ABC D

có đáy là hình thoi tâm

O

cạnh

a

, tam giác

ABD

đều,

SO

vuông góc

với mặt phẳng

 

ABCD

và

2SO a

. Thể tích của khối chóp

.

S ABC D

bằng:

Ⓐ

3

6

a

. Ⓑ

3

a

. Ⓒ

3

12

a

. Ⓓ

3

a

.

Câu 2. Cho hình chóp tam giác đều có cạnh đáy bằng

a

và cạnh bên tạo với đáy một góc



. Thể tích của

khối chóp đó bằng:

Ⓐ

3

tan

12

a



. Ⓑ

3

cot

12

a



. Ⓒ

3

tan

6

a



. Ⓓ

3

cot

6

a



.

Câu 3. Cho hình chóp đều

.

S ABC D

có

2AC a

, góc giữa mặt phẳng

 

SBC

và mặt phẳng

 

ABCD

bằng

45

. Tính thể tích

V

của khối chóp

.

S ABC D

theo

a

?

Ⓐ

3

2

3

a

V 

. Ⓑ

3

2 3

3

a

V 

. Ⓒ

3

2

V a

. Ⓓ

3

2

a

V



.

Câu 4. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình thoi tâm

O

cạnh

a

, góc



30

BCA

 

,

 

SO ABCD



và

3

4

a

SO 

. Khi đó thể tích của khối chóp là:

Ⓐ

3

2

4

a

. Ⓑ

3

8

a

. Ⓒ

3

2

8

a

. Ⓓ

3

4

a

.

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 289

Câu 5. Cho khối chóp tam giác

.

S ABC

có thể tích bằng

16

. Gọi

, ,M N P

lần lượt là trung điểm các cạnh

, ,AB BC CA

. Khi đó thể tích khối chóp

.

S M N P

bằng:

Ⓐ

2

. Ⓑ

8

. Ⓒ

4

. Ⓓ

16

.

Câu 6. Cho lăng trụ

.

ABC A B C

  

có đáy là tam giác vuông cân tại

A

,

AB a

. Gọi

G

là trọng tâm tam giác

A B C

. Biết

A G



vuông góc với mặt phẳng

 

ABC

và

A B



tạo với đáy một góc

45

. Tính thể tích khối

chóp

.

A BCC B

  

?

Ⓐ

3

5

9

a

. Ⓑ

3

5

6

a

. Ⓒ

3

5

3

a

. Ⓓ

3

5

4

a

.

Câu 7. Cho hình lập phương

. ' ' ' 'ABCD A B C D

cạnh

a

. Gọi

M

,

N

,

P

lần lượt là trung điểm

CD

,

' 'A B

,

' 'A D

. Thể tích khối tứ diện

'

A MNP

bằng :

Ⓐ

3

16

a

. Ⓑ

3

32

a

. Ⓒ

3

12

a

. Ⓓ

3

24

a

.

Câu 8. Cho hình chóp tam giác đều

.

S ABC

có cạnh đáy bằng

a

và cạnh bên là

2 a

.

M

thuộc cạnh

SA

sao cho

2

MS MA

. Tính thể tích

V

của tứ diện

MABC

?

Ⓐ

3

11

12

V a



. Ⓑ

3

11

14

V a



. Ⓒ

3

11

16

V a



. Ⓓ

3

11

18

V a



.

Câu 9. Cho tứ diện

OA BC

có ba cạnh

OA

,

OB

,

O C

đôi một vuông góc với nhau,

2

a

OA 

,

OB OC a 

. Gọi

H

là hình chiếu của điểm

O

trên mặt phẳng

 

ABC

. Tính thể tích khối tứ diện

OABH

?

Ⓐ

3

2

6

a

. Ⓑ

3

2

12

a

. Ⓒ

3

2

24

a

. Ⓓ

3

2

48

a

.

Câu 10. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình thoi cạnh

a

, góc



BAD

bằng

60

, gọi

I

là giao

điểm của

A C

và

BD

. Hình chiếu vuông góc của

S

trên mặt phẳng

 

ABCD

là trung điểm

H

của

BI

.

Góc giữa

SC

và

 

ABCD

bằng

45

. Thể tích của khối chóp

.

S ABC D

là:

Ⓐ

3

39

24

a

. Ⓑ

3

39

12

a

. Ⓒ

3

39

8

a

. Ⓓ

3

39

48

a

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 290

— Bài toán. Tính thể tính của khối chóp bằng cách vận dụng tỉ số thể tích.

— Phương pháp: Vận dụng tỉ số thể tích của khối chóp tam giác.

Cho hình chóp S.ABC. Trên các đoạn thẳng SA, SB, SC lần

lượt lấy ba điểm A', B', C' khác với S. Ta có tỉ số thể tích:

* Đặc biệt: Nếu A'  A ta có:

CÁC VÍ DỤ

Ví dụ 1: Cho khối chóp

.

S ABC

, trên ba cạnh

SA

,

SB

,

SC

lần lượt lấy ba điểm

A



,

B



,

C



sao cho

1

2

SA SA





,

1

3

SB SB





,

1

4

SC SC





. Gọi

V

và

V



lần lượt là thể tích của các khối chóp

.

S ABC

và

.

S A B C

  

. Tính tỉ số

V



.

--------------------------------------------------------------------------------------------------------------------------------

SC

SB

SB '

.

'

V

S.ABC

C'B'S.A'



Dạng 5:

Tỉ số thể tích

S.A'B'C'

S.ABC

V

SA' SB' SC'

. .

V SA SB SC



A

C

B

S

A'

B'

C'

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 291

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Cho hình chóp

.

S ABC

có

A



và

B



lần lượt là trung điểm của

SA

và

SB

. Biết thể tích khối

chóp

.

S ABC

bằng

24

. Tính thể tích

V

của khối chóp

.

S A B C

 

?

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Cho khối chóp

.

S ABC

. Gọi

A



,

B



,

C



lần lượt là trung điểm của các cạnh

SA

,

SB

,

SC

. Tỉ số

.

S A B C

S ABC

V

  

bằng

Ⓐ

8

. Ⓑ

2

. Ⓒ

1

8

. Ⓓ

1

2

.

Câu 2. Cho khối tứ diện

ABCD

có thể tích

V

và điểm

E

trên cạnh

AB

sao cho

3AE EB

. Tính thể tích

khối tứ diện

EBCD

theo

.V

Ⓐ

4

V

. Ⓑ

3

V

. Ⓒ

2

V

. Ⓓ

5

V

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 292

Câu 3. Cho hình chóp

.

S ABC D

có đáy

ABCD

là hình vuông. Gọi

E

,

F

lần lượt là trung điểm của

SB

,

SD

. Tỉ số

.

S AEF

S ABCD

V

bằng:

Ⓐ

1

4

. Ⓑ

3

8

. Ⓒ

1

8

. Ⓓ

1

2

.

Câu 4. Cho lăng trụ tam giác đều . Lấy ,

lần lượt là tâm của hình chữ nhật và

,

là trung điểm của . Tính tỉ số thể tích của tứ diện

và tứ diện ?

Câu 5. Cho hình chóp tứ giác đều

.

S ABC D

, đáy

ABCD

là hình vuông cạnh

,a

cạnh bên tạo với đáy góc

60

. Gọi

M

là trung điểm

SC

. Mặt phẳng đi qua

AM

và song song với

BD

, cắt

SB

tại

E

và cắt

SD

tại

F

. Tính thể tích khối chóp

.

S AEM F

?

Ⓐ

3

6

12

a

. Ⓑ

3

6

27

a

. Ⓒ

3

6

36

a

. Ⓓ

3

6

18

a

.

Câu 6. Cho tứ diện

ABCD

có các cạnh

AB

,

A C

,

AD

vuông góc với nhau từng đôi một và

3AB a

,

6AC a

,

4AD a

. Gọi

M

,

N

,

P

lần lượt là trung điểm các cạnh

BC

,

CD

,

BD

. Tính thể tích khối đa

diện

AMNP

.

Ⓐ

3

3a

. Ⓑ

3

12a

. Ⓒ

3

a

. Ⓓ

3

2a

.

Câu 7. Cho hình chóp

.

S ABC

có đáy là

AB C

vuông cân ở

,B

2,

AC a

 

,SA ABC



.SA a

Gọi

G

là trọng tâm của

SB C

,

 

mp



đi qua

AG

và song song với

BC

chia khối chóp thành hai phần. Gọi

V

là

thể tích của khối đa diện không chứa đỉnh

S

. Tính

.V

Ⓐ

3

4

9

a

. Ⓑ

3

4

27

a

. Ⓒ

3

5

54

a

. Ⓓ

3

2

9

a

.

Câu 8. Cho hình chóp

.

S ABC

có

2SC a

và

( )SC ABC

. Đáy

A B C

là tam giác vuông cân tịa

B

và

2AB a

. Mặt phẳng

 



qua

C

và vuông góc với

SA

,

 



cắt

SA

,

SB

lần lượt tại

D

,

E

.Tính thể tích

khối chóp

ABCDE

.

Ⓐ

3

4

9

a

. Ⓑ

3

2

9

a

. Ⓒ

3

8

9

a

. Ⓓ

3

19

27

a

.

Câu 9. Cho khối chóp

.

S ABCD

có đáy

ABCD

là hình bình hành và có thể tích

12

V



. Gọi

,M N

lần lượt

trung điểm

, ;SA SB P

là điểm thuộc cạnh

SC

sao cho

2

PS PC

. Mặt phẳng

 

MNP

cắt cạnh

SD

tại

Q

. Tính

thể tích khối chóp

.

SMNPQ

:

.

ABC A B C

  

H

G

BC C B

 

A C C A

 

I

C C



C H G I

CB A C

  

1

8

4

5

30

8

15

2

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 293

Ⓐ

5

18

. Ⓑ

7

3

. Ⓒ

4

3

. Ⓓ

12

25

.

Câu 10. Cho hình chóp đáy là hình vuông cạnh , có

và vuông góc với mặt đáy. Gọi

, lần lượt là trọng tâm của tam giác , . Tính thể tích khối tứ diện ?

II. Thể tích khối lăng trụ

— Bài toán. Tính thể tích khối lăng trụ đứng.

— Phương pháp: Lăng trụ đứng là lăng trụ có cạnh bên vuông góc với đáy.

Khi đó chiều cao của lăng trụ là độ dài cạnh bên của lăng trụ đó.

Vd: Hình chóp S.ABC có cạnh bên SA vuông góc với đáy thì độ dài SA là

chiều cao của khối chóp

CÁC VÍ DỤ

Ví dụ 1: Cho hình lăng trụ đứng

D.

AB C A B C D

   

có đáy

DABC

là hình vuông với đường chéo bằng

3 2a

. Diện tích xung quanh của hình lăng trụ đứng

D. ' ' ' 'ABC A B C D

bằng

2

6a

. Tính thể tích của

khối lăng trụ đã cho.

--------------------------------------------------------------------------------------------------------------------------------

.

S A B C D

a

2SA a

M

N

SAB

S C D

.

S M N C

3

1

27

a

3

2

27

a

3

1

13

a

3

2

13

a

Dạng 1:

Khối lăng trụ đứng

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 294

Ví dụ 2: Cho lăng trụ đều

.

A B C A B C

  

có cạnh đáy bằng

2 a

. Góc giữa đường thẳng

A B



và mặt

đáy là

60

. Tính theo

a

thể tích khối lăng trụ

.

A B C A B C

  

.

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Thể tích khối lăng trụ đứng tam giác

.

ABC A BC

  

có tất cả các cạnh bằng

a

là:

Ⓐ

3

4

a

. Ⓑ

3

6

a

. Ⓒ

3

a

. Ⓓ

3

4

a

.

Câu 2. Cho hình hộp chữ nhật

.

ABC D A B C D

   

có

AB a

,

B C a

,

2AA a





. Thể tích khối

ABCDB C D

  

:

Ⓐ

3

2a

. Ⓑ

3

5

3

a

. Ⓒ

3

10

3

a

. Ⓓ

3

5

2

a

.

Câu 3. Nếu một khối hộp chữ nhật có độ dài các đường chéo của các mặt lần lượt là

5

,

10

,

13

thì thể

tích khối hộp đó bằng :

Ⓐ

8

. Ⓑ

4

. Ⓒ

6

. Ⓓ

5

.

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 295

Câu 4. Cho lăng trụ tam giác đều

.

ABC A B C

  

có cạnh đáy bằng

a

và

AB BC

 



. Tính thể tích

V

của khối

lăng trụ đã cho ?

Ⓐ

3

7

8

a

V 

. Ⓑ

3

6

V a

. Ⓒ

3

6

8

a

V 

. Ⓓ

3

6

4

a

V 

.

Câu 5. Tính thể tích

V

của khối lăng trụ tứ giác đều

.

   

ABC D A B C D

biết độ dài cạnh đáy của lăng trụ

bằng

2

đồng thời góc tạo bởi



A C

và đáy

 

ABCD

bằng

30

?

Ⓐ

8 6

3

V

. Ⓑ

24 6

V . Ⓒ

8 6

V . Ⓓ

8 6

9

V

.

Câu 6. Lăng trụ đều

.

ABC A B C

  

có

2AB a

, góc giữa hai mặt phẳng

 

’

C AB

và

 

CAB

bằng

60

. Thể

tích khối lăng trụ đó bằng:

Ⓐ

3

3 3

a . Ⓑ

3

a . Ⓒ

3

3 3

4

a

. Ⓓ

3

9

8

a

.

Câu 7. Cho hình lăng trụ đứng

.

ABC A B C

  

, biết đáy

A B C

là tam giác đều cạnh

a

. Khoảng cách từ tâm

O

của tam giác

A B C

đến mặt phẳng

 

A BC



bằng

6

a

. Tính thể tích khối lăng trụ

.

ABC A B C

  

?

Ⓐ

3

3 2

8

a

. Ⓑ

3

3 2

28

a

. Ⓒ

3

3 2

4

a

. Ⓓ

3

3 2

16

a

.

Câu 8. Cho khối lăng trụ đứng

.

  

ABC A B C

có đáy

A B C

là tam giác cân với

 AB AC a

,



120 

BAC

,

mặt phẳng

 

A BC

 

tạo với đáy một góc

60

. Tính thể tích

V

của khối lăng trụ đã cho ?

Ⓐ

3

8



a

V

. Ⓑ

3

9

8



a

V

. Ⓒ

3

8

a

V 

. Ⓓ

3

3 3

8



a

V

.

Câu 9. Cho lăng trụ đứng

.

ABC D A B C D

   

có đáy

ABCD

là hình bình hành. Các đường chéo

DB



và

AC



lần lượt tạo với đáy các góc

45

và

30

. Biết chiều cao của lăng trụ là

a

và



60

BAD

 

. Hãy tính thể tích

V

của khối lăng trụ này.

Ⓐ

3

2

3

a

V 

. Ⓑ

3

V a

. Ⓒ

3

2

a

V 

. Ⓓ

3

2

a

V 

.

Câu 10. Cho lăng trụ đứng

.

ABC A B C

  

có



0

, 2 , 120

AC a BC a ACB  

và đường thẳng

A C



tạo với mặt

phẳng

 

ABB A

 

một góc

0

30

. Thể tích khối lăng trụ

.

ABC A B C

  

là :

Ⓐ

3

105

28

a

. Ⓑ

3

35

27

a

. Ⓒ

3

105

7

a

. Ⓓ

3

105

14

a

.

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 296

— Bài toán. Tính thể tích khối lăng trụ xiên

— Phương pháp: Chiều cao của khối lăng trụ xiên là khoảng các

từ một đỉnh bất kì của lăng trụ đến mặt đáy không chứa đỉnh đó.

Vd: Cho lăng trụ

.

ABC D A B C D

   

. Khi đó khoảng cách từ

A



đến mp

 

ABCD

là chiều cao của khối lăng trụ

.

ABC D A B C D

   

CÁC VÍ DỤ

Ví dụ 1: Cho hình lăng trụ

.

ABC A B C

  

có tất cả các cạnh bằng

a

, các cạnh bên tạo với đáy góc

60

.

Tính thể tích khối lăng trụ

.

ABC A B C

  

.

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2: Cho lăng trụ

.

ABC D A B C D

   

có đáy

ACBD

là hình thoi cạnh

a

, biết

.

A A BC



là hình chóp

đều và

A D



hợp với mặt đáy một góc

45

. Thể tích khối lăng trụ

.

ABC D A B C D

   

.

--------------------------------------------------------------------------------------------------------------------------------

Dạng 2:

Khối lăng trụ xiên

V

ABCD.A'B'C'D' =

S

ABCD

x

h

S

ABCD

H

h

C'

B'

D'

C

D

A

B

A'

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

Trang: 297

--------------------------------------------------------------------------------------------------------------------------------

BÀI TẬP VỀ NHÀ

Câu 1. Cho hình lăng trụ

.

ABC A B C

  

có đáy là tam giác vuông cân đỉnh

,A

,AB a

2 ,AA a





hình chiếu

vuông góc của

A



lên mặt phẳng

 

ABC

là trung điểm

H

của cạnh

.B C

Thể tích của khối lăng trụ

.

ABC A B C

  

bằng:

Ⓐ

3

14

2

a

. Ⓑ

3

14

4

a

. Ⓒ

3

7

4

a

. Ⓓ

3

2

a

.

Câu 2. Cho lăng trụ tam giác

.

ABC A B C

  

có đáy

A B C

là tam giác đều cạnh

a

và điểm

A



cách đều

A

,

B

,

C

biết

3

2 3

AA

a





. Thể tích lăng trụ là:

Ⓐ

3

10

4

a

. Ⓑ

3

4

6

a

. Ⓒ

3

4

5

a

. Ⓓ

3

4

3

a

.

Câu 3. Cho hình hộp

.

ABC D A B C D

   

có đáy là hình chữ nhật, các cạnh

AB a

,

2AD a

,

6AA a





, góc

giữa

AA



và mặt phẳng

 

ABCD

là

30

. Thể tích của khối tứ diện

ACB D

 

là:

Ⓐ

3

2 3a

. Ⓑ

3

6a

. Ⓒ

3

2a

. Ⓓ

3

6 3a

.

Câu 4. Cho lăng trụ

.

ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên

mặt phẳng

 

ABC

trùng với trọng tâm tam giác

A B C

. Biết khoảng cách giữa hai đường thẳng

AA



và

BC

bằng

3

4

a

. Khi đó thể tích của khối lăng trụ là:

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG I. KHỐI ĐA DIỆN

HÌNH HỌC

Trang: 298

Ⓐ

3

12

a

. Ⓑ

3

6

a

. Ⓒ

3

a

. Ⓓ

3

24

a

.

Câu 5. Cho hình lăng trụ

.

ABC A BC

  

có đáy

A B C

là tam giác đều cạnh

a

, hình chiếu vuông góc của

điểm

A



lên mặt phẳng

 

ABC

là trung điểm của

AB

. Mặt bên

 

ACC A

 

tạo với mặt phẳng đáy một góc

0

45

. Tính thể tích của khối lăng trụ

.

ABC A BC

  

.

Ⓐ

3

16

a

. Ⓑ

3

a

. Ⓒ

3

16

a

. Ⓓ

3

2 3

3

a

.

Câu 6. Cho lăng trụ

.

ABC D A B C D

   

có đáy

ABCD

là hình thoi cạnh

a

, tâm

O

và



120

ABC

 

. Góc giữa

cạnh bên

AA



và mặt đáy bằng

60

. Đỉnh

A



cách đều các điểm

A

,

B

,

D

. Tính theo

a

thể tích

V

của

khối lăng trụ đã cho.

Ⓐ

3

2

a

V 

. Ⓑ

3

6

a

V 

. Ⓒ

3

2

a

V 

. Ⓓ

3

V a .

Câu 7. Cho lăng trụ

1 1 1

.

ABC A B C

có diện tích mặt bên

1 1

ABB A

bằng

4

; khoảng cách giữa cạnh

1

CC

và

mặt phẳng

 

1 1

ABB A

bằng 7. Tính thể tích khối lăng trụ

1 1 1

.

ABC A B C

.

Ⓐ

14

. Ⓑ

28

3

. Ⓒ

14

3

. Ⓓ

2 8

.

Câu 8. Cho hình lăng trụ

.

  

ABC A B C

có độ dài tất cả các cạnh bằng

a

và hình chiếu vuông góc của đỉnh

C

lên mặt phẳng

 

 

ABB A

là tâm của hình bình hành

 

ABB A

. Thể tích khối lăng trụ

.

  

ABC A B C

tính

theo a là:

Ⓐ

3

2

4

a

. Ⓑ

3

2

12

a

. Ⓒ

3

a . Ⓓ

3

4

a

.

Câu 9. Cho lăng trụ

.

ABC A B C

  

có đáy là tam giác vuông cân tại

B

,

3AB a



. Hình chiếu vuông góc

của

A



lên mặt phẳng

 

ABC

là điểm

H

thuộc cạnh

A C

sao cho

2

HC HA

. Mặt bên

 

ABB A

 

tạo với

đáy một góc

60

. Thể tích khối lăng trụ là:

Ⓐ

3

6

a

. Ⓑ

3

a

. Ⓒ

3

5

a

. Ⓓ

3

2

a

.

Câu 10. Cho lăng trụ

.

ABC D A B C D

   

có đáy

ABCD

là hình chữ nhật với

6

AB 

,

3

AD 

,

3

A C





và mặt phẳng

 

AA C C

 

vuông góc với mặt đáy. Biết hai mặt phẳng

 

AA C C

 

,

 

AA B B

 

tạo với nhau

góc



có

3

tan

4





. Thể tích của khối lăng trụ

.

ABC D A B C D

   

là:

Ⓐ

12

V



. Ⓑ

6

V



. Ⓒ

10

V



. Ⓓ

8

V



.

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 299

§1. KHÁI NIỆM VỀ MẶT TRÒN XOAY

A. TÓM TẮT LÝ THUYẾT

1. Sự tạo thành mặt tròn xoay:

Trong không gian cho mp(P) chứa đường thẳng  và

đường cong

C

. Khi quay mp(P) quanh  một góc 360

0

thì mỗi điểm M trên

C

vạch ra một đường tròn có tâm O

thuộc  và nằm trên mặt phẳng vuông góc với . Như

vậy khi quay mặt phẳng (P) quanh đường thẳng  thì

đường

C

sẽ tạo nên một hình được gọi là mặt tròn xoay.

 Đường

C

được gọi là đường sinh của mặt tròn xoay.

 Đường thẳng  được gọi là trục của mặt tròn xoay.

2. Mặt nón tròn xoay:

Trong mặt phẳng (P) cho hai đường thẳng d và  cắt nhau và

tạo thành một góc



với

0 0

0 90



 

. Khi quay mặt phẳng

(P) xung quanh  thì đường thẳng d sinh ra một mặt tròn xoay

được gọi là mặt nón tròn xoay đỉnh O, gọi tắt là mặt nón.

 Đường thẳng  gọi là trục.

 Đường thẳng d gọi là đường sinh.

 Góc

2



gọi là góc ở đỉnh của mặt nón.

Chương

2

MẶT NÓN – MẶT TRỤ – MẶT CẦU

1. MẶT TRÒN XOAY - MẶT NÓN TRÒN

XOAY - MẶT TRỤ TRÒN XOAY

2. MẶT CẦU

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 300

3. Hình nón:

Cho tam giác

OAC vuông tại O.

Khi quay tam giác

đó xung quanh

cạnh góc vuông

AO thì đường gấp

khúc OAC tạo

thành một hình được gọi là hình nón tròn xoay, gọi tắt là hình nón.

 Hình tròn tâm O sinh bởi các điểm thuộc cạnh OC khi OC quay quanh trục AO được gọi là mặt đáy

của hình nón. (OC = r gọi là bán kính hình tròn đáy)

 Điểm A gọi là đỉnh của hình nón.

 Độ dài đoạn AO = h gọi là độ dài chiều cao của hình nón (AO = khoảng cách từ A đến mặt đáy).

 Độ dài đoạn AC = l gọi là độ dài đường sinh của hình nón.

 Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh AC khi quay quanh trục AO gọi là mặt xung

quanh của hình nón đó.

Diện tích xung quanh, diện tích toàn phần của hình nón:

4. Khối nón:

Khối nón tròn xoay là phần không gian được

giới hạn bởi một hình nón tròn xoay kể cả hình

nón đó. Khối nón tròn xoay gọi tắt là khối nón.

Đỉnh, mặt đáy, đường sinh của một hình nón

cũng là đỉnh, mặt đáy, đường sinh của khối

nón tương ứng.

Thể tích của khối nón:

xq

S rl





2

( )

tp xq đ

S S S rl r r l r

  

     

* Lưu ý:

2 2 2

l r h 

2

1 1

.

3 3

đ

V S h r h



 

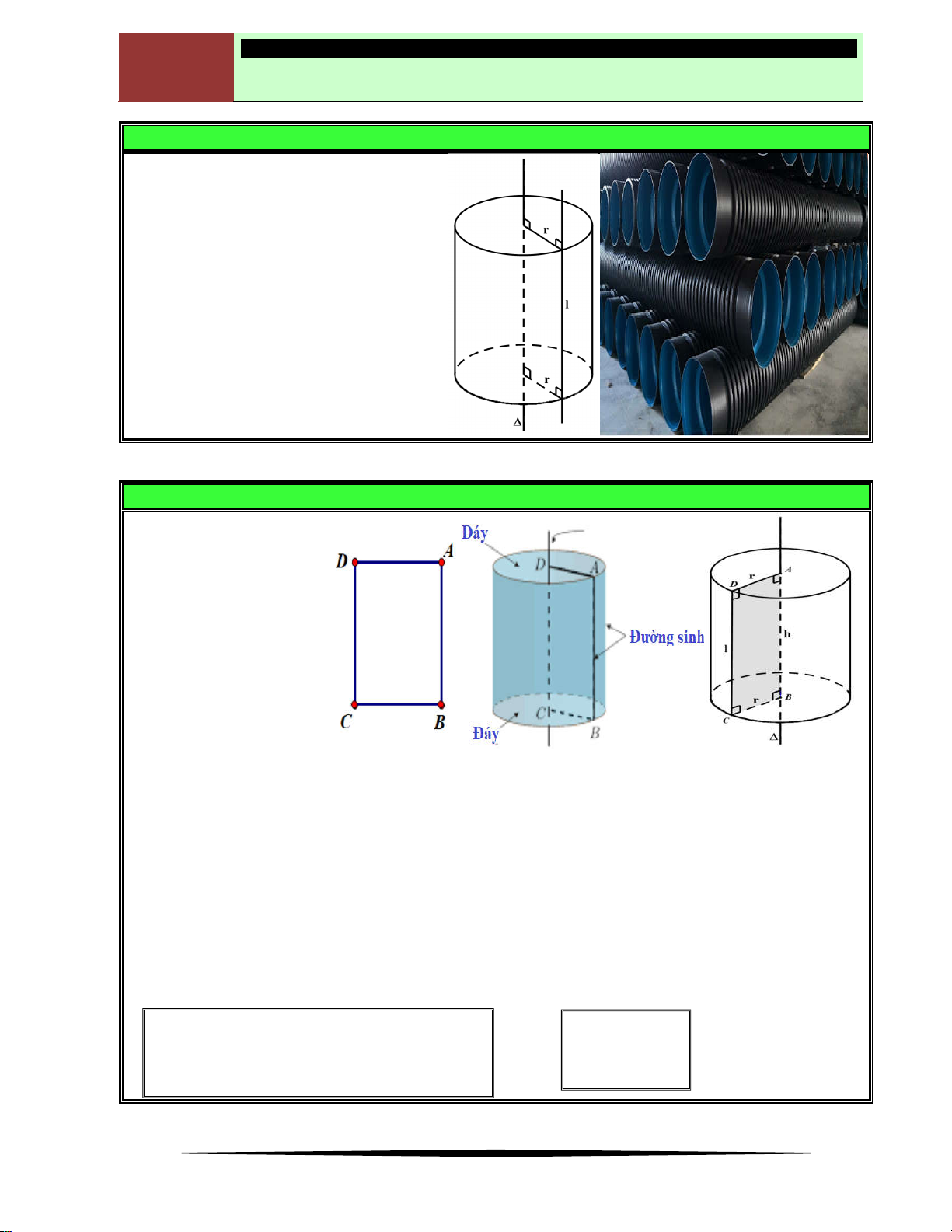
HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 301

5. Mặt trụ tròn xoay:

Trong mặt phẳng (P) cho hai đường thẳng

và l song song với nhau, cách nhau một

khoảng bằng r. Khi quay mặt phẳng (P)

xung quanh thì đường thẳng l sinh ra một

mặt tròn xoay được gọi là mặt trụ tròn xoay,

gọi tắt là mặt trụ.

 Đường thẳng gọi là trục.

 Đường thẳng l là đường sinh.

 r là bán kính của mặt trụ đó.

6. Hình trụ:

Xét hình chữ nhật

ABCD. Khi quay hình

chữ nhật ABCD xung

quanh đường thẳng chứa

một cạnh nào đó, chẳng

hạn cạnh AB thì đường

gấp khúc ADCB sẽ tạo

thành một hình gọi là

hình trụ tròn xoay, hay gọi tắt là hình trụ.

 Khi quay quanh AB, hai cạnh AD và BC sẽ vạch ra hai hình tròn bằng nhau gọi là hai đáy của hình

trụ, bán kính của chúng gọi là bán kính của hình trụ. (r = AD = CB)

 Độ dài đoạn CD = l gọi là độ dài đường sinh của hình trụ.

 Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh CD khi quay xung quanh AB gọi là mặt xung

quanh của hình trụ.

 Khoảng cách AB = h giữa hai mặt phẳng song song chứa hai đáy là chiều cao của hình trụ.

Diện tích xung quanh, diện tích toàn phần của hình trụ:



2

xq

S rl





2

2 2 2 2 ( )

tp x đq

S S S rl r r l r

  

     

* Lưu ý:

l h

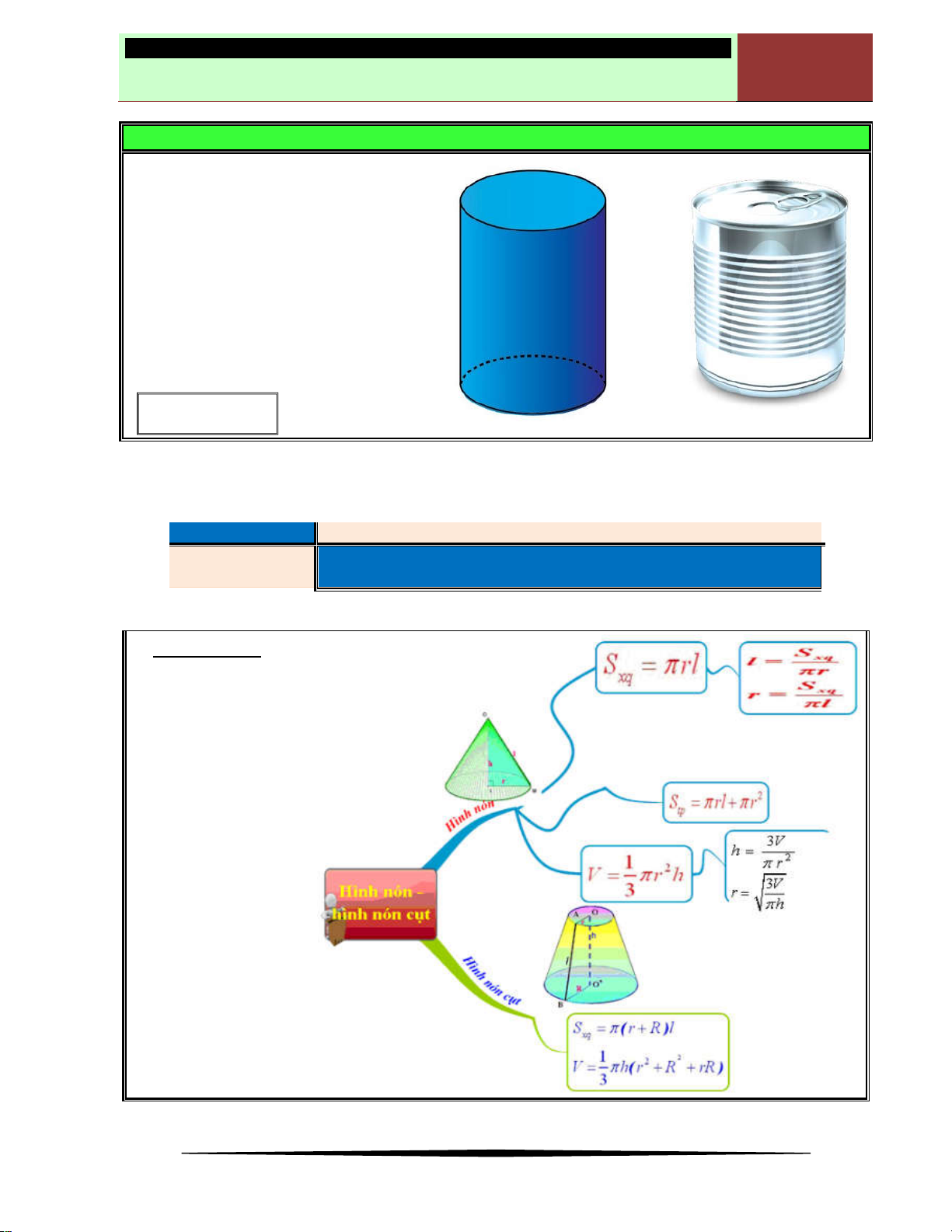
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 302

7. Khối trụ:

Khối trụ tròn xoay hay khối trụ là phần

không gian được giới hạn bởi một hình

trụ tròn xoay kể cả hình trụ tròn xoay đó.

Mặt đáy, chiều cao, đường sinh, bán kính

của một hình trụ cũng là mặt đáy, chiều

cao, đường sinh, bán kính của khối trụ

tương ứng.

Thể tích của khối trụ:

B. CÁC DẠNG TOÁN THƯỜNG GẶP

— Phương pháp:

Dạng 1:

Tính diện tích xung quanh, diện tích toàn phần và thể tích của

hình nón – khối nón.

2

.

đ

V S h r h



 

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 303

CÁC VÍ DỤ

Ví dụ 1. Cho hình nón có đường cao h = 20cm, bán kính đáy r = 25cm.

a) Tính diện tích xung quanh, diện tích toàn phần của hình nón.

b) Tính thể tích của khối nón.

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2. Cho hình nón có bán kính đáy bằng 3 cm, chiều cao bằng 4 cm. Diện tích xung quanh của hình

nón là

Ⓐ

2

30

cm



Ⓑ

2

15

cm



.

Ⓒ

2

12

cm



Ⓓ

2

9

cm



Lời giải :....................................................................

......................................................................................

Ví dụ 3. Cho một hình nón có góc ở đỉnh bằng 60

0

, độ dài đường sinh bằng 2a. Diện tích xung quanh

xq

S

của hình nón là

Ⓐ

2

S 4

xq

a





Ⓑ

2

S

xq

a





Ⓒ

2

S 3

xq

a





Ⓓ

2

S 2

xq

a





.

Lời giải:.....................................................................

......................................................................................

Ví dụ 4. Cho tam giác ABC vuông tại B,

;AB a

góc A bằng 60

o

. Quay tam giác quanh cạnh AB ta

được 1 hình nón. Diện tích xung quanh hình nón đó là

Ⓐ

2

2 3

xq

S a





. Ⓑ

2

xq

S a





Ⓒ

2

4

xq

S a





Ⓓ

2

4 3

xq

S a





Lời giải:.....................................................................

......................................................................................

Ví dụ 5. Cho hình nón có bán kính đáy là 4a, chiều cao là 3a. Diện tích toàn phần hình nón là

Ⓐ

2

S 36

tp

a





. Ⓑ

2

S 30

tp

a





Ⓒ

2

S 38

tp

a





Ⓓ

2

S 32

tp

a



Lời giải:.....................................................................

......................................................................................

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 304

BÀI TẬP

Câu 1. Cho hình nón có bán kính đáy là 4a, chiều cao là 3a Diện tích xung quanh hình nón là

Ⓐ

2

20



a

Ⓑ

2

40



a

Ⓒ

2

24



a

Ⓓ

2

12



a

Câu 2. Cho hình nón có bán kính đáy là 3a, chiều cao là 4a.Thể tích của hình nón là

Ⓐ

3

12



a

Ⓑ

3

36



a

Ⓒ

3

15



a

Ⓓ

3

12



a

Câu 3. Cho hình nón có bán kính đáy là 4a, chiều cao là 3a. Diện tích toàn phần hình nón là

Ⓐ

2

36



a

Ⓑ

2

30



a

Ⓒ

2

38



a

Ⓓ

2

32



a

......................................................................................

Ví dụ 6. Hình nón có thiết diện qua trục là tam giác vuông, đường sinh có độ dài bằng 2a, diện tích toàn

phần của hình nón là

Ⓐ

2

4

3

tp

S a





Ⓑ

2

tp

S a





Ⓒ

2

6

tp

S a





Ⓓ

2

3

tp

S a





Lời giải :....................................................................

......................................................................................

Ví dụ 7.

Hình nón có đường sinh l = 2a và hợp với đáy góc 60

0

. Diện tích toàn phần của hình nón bằng:

Ⓐ

2

S 4

tp

a





Ⓑ

2

S 3

tp

a





Ⓒ

2

S 2

tp

a





Ⓓ

2

S

tp

a





Lời giải:.....................................................................

......................................................................................

Ví dụ 8. Một khối nón tròn xoay có độ dài đường sinh l = 13 cm và bán kính đáy

5r cm

. Khi đó thể

tích khối nón là:

Ⓐ

3

100

V cm





. Ⓑ

3

300

V cm





Ⓒ

3

325

3

V cm





Ⓓ

3

20

V cm





Lời giải:.....................................................................

......................................................................................

Ví dụ 9. Cho hình nón có độ dài đường sinh

l 2a

, góc ở đỉnh của hình nón

0

2 60

 

. Tính thể tích V

của khối nón đã cho:

Ⓐ

3

V a





Ⓑ

3

2

a

V





Ⓒ

3

V a





Ⓓ

3

V a





Lời giải:.....................................................................

......................................................................................

Ví dụ 10. Cho



ABC vuông tại A, AB = 3a, AC = 2a, khi quay tam giác xung quanh cạnh AB ta được

khối nón có thể tích bằng:

Ⓐ

3

12

V a





Ⓑ

3

4

V a





.

Ⓒ

3

4V a



Ⓓ

3

8

V a





Lời giải :....................................................................

......................................................................................

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 305

Câu 4. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa một mặt bên và đáy bằng

0

60

, diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp tam giác ABC là

Ⓐ

2

6



a

Ⓑ

2

4



a

Ⓒ

2

3



a

Ⓓ

2

5

6



a

Câu 5. Cho hình hóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a, diện tích xung quanh

của hình nón đỉnh S và đáy là hình tròn nội tiếp ABCD là

Ⓐ

2

17

4



a

Ⓑ

2

15

4



a

Ⓒ

2

17

6



a

Ⓓ

2

17

8



a

Câu 6. Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng a. Diện

tích xung quanh của hình nón là

Ⓐ

2



a

Ⓑ

2

3



a

Ⓒ

2



a

Ⓓ

2

4



a

Câu 7. Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh huyền 2a. Thể tích của

khối nón bằng

Ⓐ

3



a

Ⓑ

3

2

3



a

Ⓒ

3



a

Ⓓ

3

2



a

Câu 8. Diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đường sinh bằng

3

và thiết

diện qua trục là tam giác đều là

Ⓐ

8 3

3

Ⓑ

8 2

3

Ⓒ

4 2

3

Ⓓ

8 6

3

Câu 9. Cho hình nón có đường sinh l, góc giữa đường sinh và mặt phẳng đáy là

0

30

. Diện tích xung

quanh của hình nón này là

Ⓐ

2

3

2



l

Ⓑ

2

3

4



l

Ⓒ

2

3

6



l

Ⓓ

2

3

8



l

Câu 10. Thể tích V của khối nón (N) có chiều cao bằng a và độ dài đường sinh bằng

5a

là

Ⓐ

3

4

3





V a

Ⓑ

3

4





V a

Ⓒ

3

2

3





V a

Ⓓ

3

5

3





V a

Câu 11. Cho hình nón có thiết diện qua trục là tam giác đều cạnh 2a. Thể tích và diện tích xung quanh của

hình nón là

Ⓐ

3 2

3; 2

 

 

xq

V a S a

Ⓑ

3 2

3; 2

 

 

xq

V a S a

Ⓒ

3

2

3

; 2

6



 

xq

a

V S a

Ⓓ

3

2

3

; 4

3



 

xq

a

V S a

Câu 12. Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng a. Một

thiết diện qua đỉnh tạo với đáy một góc

0

60

. Diện tích của thiết diện này bằng

Ⓐ

2

3

a

Ⓑ

2

a

Ⓒ

2

2a

Ⓓ

2

4

a

Câu 13. Hình nón có đường cao 20cm, bán kính đáy 25cm. Một mặt phẳng (P) qua đỉnh của hình nón và

có khoảng cách đến tâm là 12cm. Diện tích thiết diện tạo bởi (P) và hình nón là

Ⓐ

2

500( )cm

Ⓑ

2

600( )cm

Ⓒ

2

550( )cm

Ⓓ

2

450( )cm

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 306

Câu 14. Khối nón (N) có chiều cao bằng

3a

. Thiết diện song song và cách mặt đáy một đoạn bằng a, có

diện tích bằng

2

64

9



a

. Khi đó, thể tích của khối nón (N) là

Ⓐ

3

16



a

Ⓑ

3

25

3



a

Ⓒ

3

48



a

Ⓓ

3

16

3



a

Câu 15. Một hình nón có thiết diện qua trục là một tam giác đều. Gọi

1 2

,V V

lần lượt là thể tích của khối cầu

ngoại tiếp và nội tiếp khối nón trên. Khi đó, tỉ số

1

2

V

bằng

Câu 16. Khối nón (N) có chiều cao là h và nội tiếp trong khối cầu có bán kính R với

2h R

. Khi đó thể

tích của khối nón (N) theo h và R là

Ⓐ

 

2

1

2

3



h R h

Ⓑ

 

2

4

2

3



h R h

Ⓒ

 

2



h R h

Ⓓ

 

1

2

3



h R h

Câu 17. Diện tích xung quanh của một hình nón có bán kính đáy bằng 3 và chiều cao bằng 4 là

Ⓐ

15



Ⓑ

30



Ⓒ

36



Ⓓ

12



Câu 18. Một hình nón có đường kính của đường tròn đáy bằng

 

6

m

, chiều cao bằng

 

4

m

. Thể tích của

khối nón này là

Ⓐ

 

3

12



m

Ⓑ

 

3

36



m

Ⓒ

 

3

48



m

Ⓓ

 

3

15



m

Câu 19. Cho hình nón có đường kính của đường tròn đáy bằng

 

8

cm

, đường cao

 

3

cm

, diện tích xung

quanh của hình nón này là

Ⓐ

 

2

20



cm

Ⓑ

 

2

40



cm

Ⓒ

 

2

16



cm

Ⓓ

 

2

12



cm

Câu 20. Một khối nón có thể tích bằng

4



và chiều cao là

3

. Bán kính đường tròn đáy của hình nón là

Ⓐ 2 Ⓑ

2 3

3

Ⓒ

4

3

Ⓓ 1

Câu 21. Một hình nón có chiều cao

6

và bán kính đường tròn đáy là

8

. Diện tích toàn phần của hình nón

là

Ⓐ

144



Ⓑ

188



Ⓒ

96



Ⓓ

112



Câu 22. Cho khối nón có chu vi đường tròn đáy là

6



, chiều cao bằng

7

. Thể tích của khối nón là

Ⓐ

3 7



Ⓑ

9 7



Ⓒ

12



Ⓓ

36



Câu 23. Cho hình nón có diện tích xung quanh

25



, bán kính đường tròn đáy bằng

5

. Độ dài đường sinh

bằng

Ⓐ

5

Ⓑ

5

2

Ⓒ

1

Ⓓ

3

Câu 24. Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh huyền bằng

2 3

. Thể

tích của khối nón này là

Ⓐ

3



Ⓑ

3 3



Ⓒ

3



Ⓓ

3 2



Câu 25. Thiết diện qua trục của một hình nón là một tam giác vuông cân có diện tích bằng

4

. Diện tích

xung quanh của hình nón là

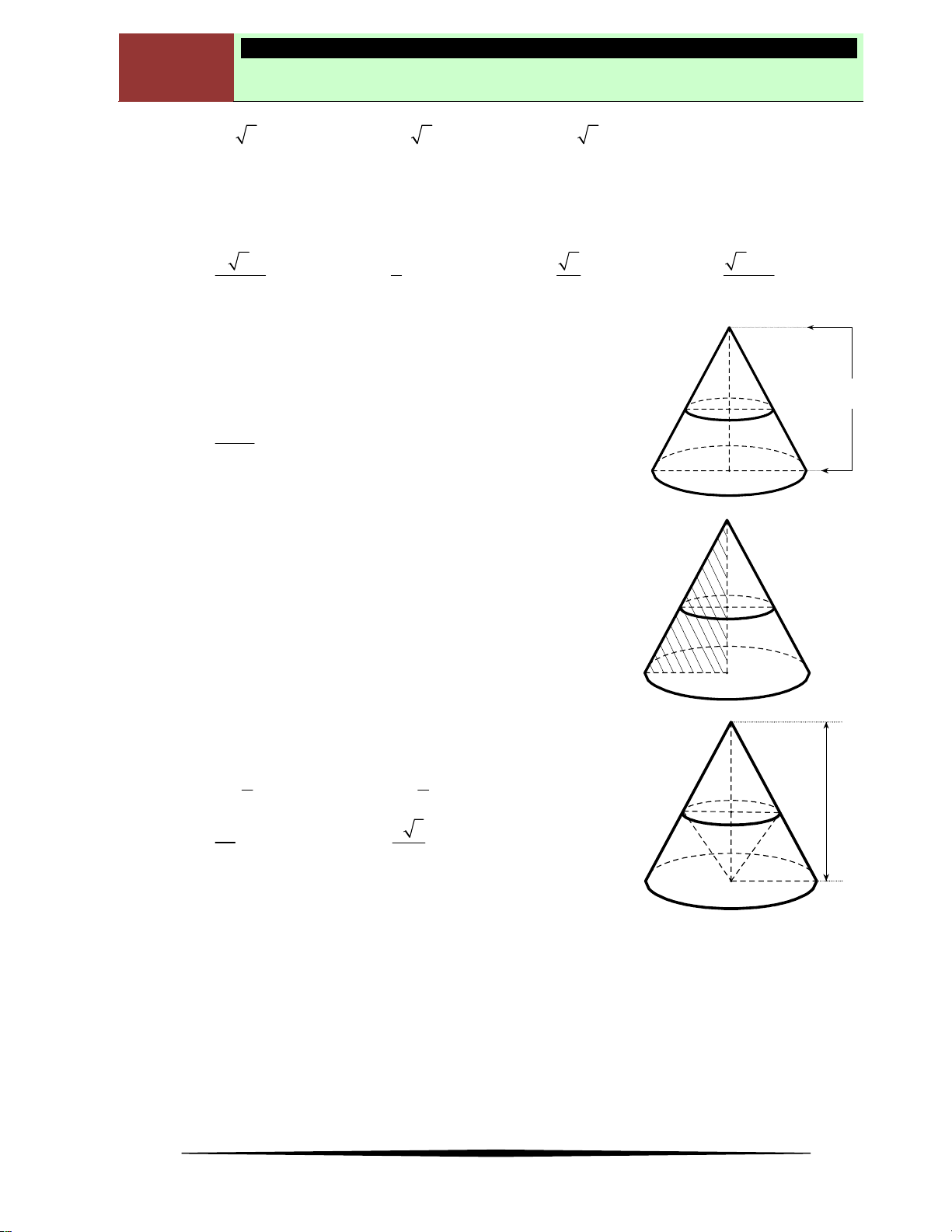
HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 307

Ⓐ

4 2



Ⓑ

8 2



Ⓒ

2 2



Ⓓ

8



Câu 26. Một khối nón có thể tích bằng

30



, nếu giữ nguyên chiều cao và tăng bán kính khối nón đó lên

2 lần thì thể tích của khối nón mới bằng

Ⓐ

120



Ⓑ

60



Ⓒ

40



Ⓓ

480



Câu 27. Thể tích khối nón ngoại tiếp hình chóp tứ giác đều có các cạnh đều bằng a là

Ⓐ

3

2

12



a

Ⓑ

3

1

6



a

Ⓒ

3

2

6



a

Ⓓ

3

2

9



a

Câu 28. Cho hình nón có đáy là đường tròn có đường kính

10

. Mặt

phẳng vuông góc với trục cắt hình nón theo giao tuyến là một

đường tròn như hình vẽ. Thể tích của khối nón có chiều cao

bằng 6 là

Ⓐ

8



Ⓑ

24



Ⓒ

00

9





Ⓓ

96



Câu 29. Cho hình nón

 

N

có bán kính đáy bằng 10, mặt phẳng vuông

góc với trục của hình nón cắt hình nón theo một đường tròn

có bán kính bằng 6, khoảng cách giữa mặt phẳng này với mặt

phẳng chứa đáy của hình nón

 

N

là 5. Chiều cao của hình

nón

 

N

là

Ⓐ

12,5

Ⓑ 10

Câu 30. Cho hình nón đỉnh O, chiều cao là h. Một khối nón khác có

đỉnh là tâm của đáy và đáy là một thiết diện song song với

đáy của hình nón đã cho. Chiều cao x của khối nón này là

bao nhiêu để thể tích của nó lớn nhất, biết

0

 x h

Ⓐ

3



h

x

Ⓑ

2



h

x

Ⓒ

2

3

h

Ⓓ

3

h

10

15

9

6

P

O

x

10

5

6

h

x

O

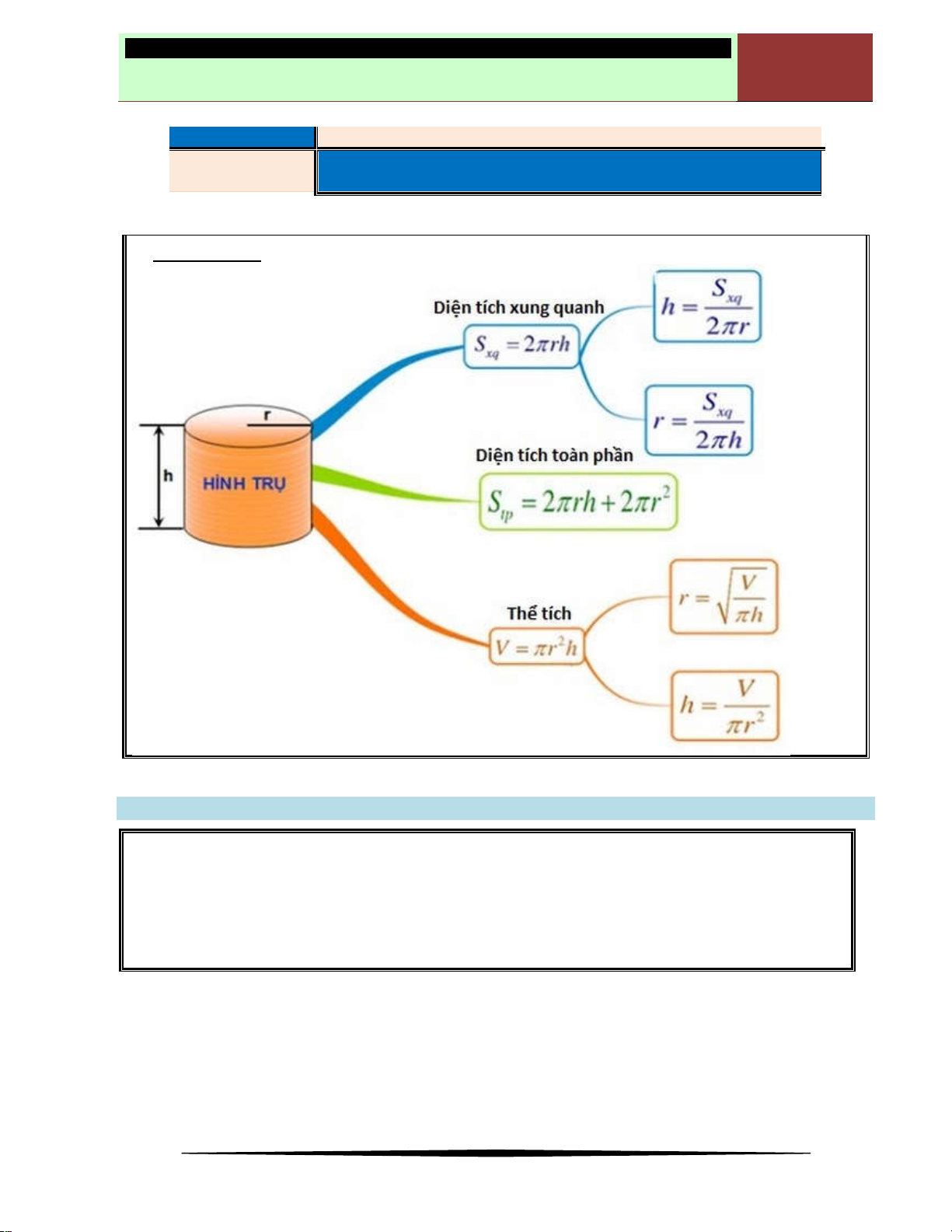
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 308

— Phương pháp:

CÁC VÍ DỤ

Ví dụ 1. Cho hình trụ có đường cao h = 10cm, bán kính đáy r = 5cm.

a) Tính diện tích xung quanh, diện tích toàn phần của hình trụ.

b) Tính thể tích của khối trụ.

--------------------------------------------------------------------------------------------------------------------------------

Dạng 2:

Tính diện tích xung quanh, diện tích toàn phần và thể tích của

hình trụ – khối trụ.

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 309

Ví dụ 2. Một hình trụ có bán kính đáy

a

, có thiết diện qua trục là một hình vuông. Diện tích xung quanh

của hình trụ là:

Ⓐ

2

S 4

xq

a





. Ⓑ

2

S

xq

a





Ⓒ

2

S 3

xq

a





Ⓓ

2

S 2

xq

a





Lời giải :....................................................................

......................................................................................

Ví dụ 3. Cho hình vuông ABCD cạnh 8cm. Gọi M, N lần lượt là trung điểm của

AB

và

CD

. Quay

hình vuông ABCD xung quanh MN. Diện tích xung quanh của hình trụ tạo thành là:

Ⓐ

2

96 ( )

xq

S cm





Ⓑ

2

126 ( )

xq

S cm





Ⓒ

2

64 ( )

xq

S cm





. Ⓓ

2

32 ( )

xq

S cm





Lời giải:.....................................................................

......................................................................................

Ví dụ 4. Cho hình chữ nhật ABCD có

AB a

và góc

0

30

BDC 

. Quay hình chữ nhật này xung quanh

cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là:

Ⓐ

2

2 3

xq

S a





Ⓑ

2

xq

S a





Ⓒ

2

3

xq

S a





. Ⓓ

2

3

xq

S a





Lời giải:.....................................................................

......................................................................................

Ví dụ 5. Một hình trụ có bán kính đáy

r a

, đồ dài đường sinh

2l a

. Diện tích toàn phần của hình

trụ này là:

Ⓐ

2

S 6

tp

a





. Ⓑ

2

S 2

tp

a





Ⓒ

2

S 4

tp

a





Ⓓ

2

S 5

tp

a



Lời giải:.....................................................................

......................................................................................

Ví dụ 6. Trong không gian, cho hình chữ nhật

ABCD

có

1AB 

và

2AD 

. Gọi M, N lần lượt là

trung điểm của

AD

và

BC

. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Diện tích

toàn phần của hình trụ đó là:

Ⓐ

4

tp

S





. Ⓑ

2

tp

S





Ⓒ

6

tp

S





Ⓓ

10

tp

S





Lời giải :....................................................................

......................................................................................

Ví dụ 7. Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện

tích bằng

2

30

cm

và chu vi bằng

26cm

. Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy

của hình trụ (T). Diện tích toàn phần của (T) là

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 310

BÀI TẬP

Câu 1. Cho hình trụ có bán kính đáy 5 cm chiều cao 4 cm. Diện tích toàn phần của hình trụ này là

Ⓐ

2

90 ( )



cm

Ⓑ

2

92 ( )



cm

Ⓒ

2

94 ( )



cm

Ⓓ

2

96 ( )



cm

Câu 2. Cho hình trụ có bán kính đáy 3 cm, đường cao 4cm, diện tích xung quanh của hình trụ này là

Ⓐ

2

24 ( )



cm

Ⓑ

2

22 ( )



cm

Ⓒ

2

26 ( )



cm

Ⓓ

2

20 ( )



cm

Câu 3. Một hình trụ có bán kính đáy 6 cm, chiều cao 10 cm. Thể tích của khối trụ này là

Ⓐ

3

360 ( )



cm

Ⓑ

3

320 ( )



cm

Ⓒ

3

340 ( )



cm

Ⓓ

3

300 ( )



cm

Câu 4. Thể tích V của khối trụ có chiều cao bằng a và đường kính đáy bằng

2a

là

Ⓐ

3

1

2





V a

Ⓑ

3

1

3





V a

Ⓒ

3

2

3





V a

Ⓓ

3

1

6





V a

Câu 5. Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết

2 2



AC a

và



0

45

ACB

. Diện tích toàn phần

tp

S

của hình trụ(T) là

Ⓐ

2

16





tp

S a

Ⓑ

2

10





tp

S a

Ⓒ

2

12





tp

S a

Ⓓ

2

8





tp

S a

Ⓐ

2

69

( )

2

tp

S cm





. Ⓑ

2

69 ( )

tp

S cm





Ⓒ

2

23 ( )

tp

S cm





Ⓓ

2

23

( )

2

xq

S cm





Lời giải:.....................................................................

......................................................................................

Ví dụ 8. Quay hình vuông ABCD cạnh

a

xung quanh một cạnh. Thể tích của khối trụ được tạo thành

là

Ⓐ

3

V a





. Ⓑ

3

2

a

V





Ⓒ

3

2

V a





Ⓓ

3

V a





Lời giải:.....................................................................

......................................................................................

Ví dụ 9. Một hình trụ có diện tích xung quanh bằng

4



và có thiết diện qua trục là hình vuông. Thể

tích khối trụ tương ứng bằng

Ⓐ

3

V a





Ⓑ

3

2

V a





.

Ⓒ

3

V a





Ⓓ

3

4

V a





Lời giải:.....................................................................

......................................................................................

Ví dụ 10. Cắt hình trụ (T) bằng một mặt phẳng song song với trục và cách trục một khoảng bằng 2cm

được thiết diện là một hình vuông có diện tích bằng

2

16

cm

. Thể tích của (T) là

Ⓐ

3

8

V cm





Ⓑ

3

16

V cm





Ⓒ

3

32

V cm





. Ⓓ

3

64

V cm





Lời giải :....................................................................

......................................................................................

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 311

Câu 6. Gọi

, , l h R

lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Đẳng thức luôn

đúng là

Ⓐ

l h

Ⓑ

R h

Ⓒ

2 2 2

 l h R

Ⓓ

2 2 2

 R h l

Câu 7. Gọi

, , l h R

lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ (T). Diện tích

xung quanh

xq

S

của hình trụ (T) là

Ⓐ

2





xq

S Rl

Ⓑ





xq

S Rh

Ⓒ





xq

S Rl

Ⓓ

2





xq

S R h

Câu 8. Gọi

, , l h R

lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ (T). Diện tích

toàn phần

tp

S

của hình trụ (T) là

Ⓐ

2

2 2

 

 

tp

S Rl R

Ⓑ

2

 

 

tp

S Rl R

Ⓒ

2

 

 

tp

S Rl R

Ⓓ

2

 

 

tp

S Rh R

Câu 9. Gọi

, ,l h R

lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của khối trụ (T). Thể tích V

của khối trụ (T) là

Ⓐ

2





V R h

Ⓑ

2

1

3





V R l

Ⓒ

3

4





V R

Ⓓ

2

4

3





V R h

Câu 10. Cho hình trụ có bán kính đáy 3 cm, đường cao 4cm, diện tích xung quanh của hình trụ này là

Ⓐ

2

24 ( )



cm

Ⓑ

2

22 ( )



cm

Ⓒ

2

26 ( )



cm

Ⓓ

2

20 ( )



cm

Câu 11. Cho hình trụ có bán kính đáy 5 cm chiều cao 4 cm. Diện tích toàn phần của hình trụ này là

Ⓐ

2

90 ( )



cm

Ⓑ

2

92 ( )



cm

Ⓒ

2

94 ( )



cm

Ⓓ

2

96 ( )



cm

Câu 12. Một hình trụ có bán kính đáy 6 cm, chiều cao 10 cm. Thể tích của khối trụ này là

Ⓐ

3

360 ( )



cm

Ⓑ

3

320 ( )



cm

Ⓒ

3

340 ( )



cm

Ⓓ

3

300 ( )



cm

Câu 13. Thể tích V của khối trụ có chiều cao bằng a và đường kính đáy bằng

2a

là

Ⓐ

3

1

2





V a

Ⓑ

3

1

3





V a

Ⓒ

3

2

3





V a

Ⓓ

3

1

6





V a

Câu 14. Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết

2 2



AC a

và



0

45

ACB

. Diện tích toàn phần

tp

S

của hình trụ (T) là

Ⓐ

2

16





tp

S a

Ⓑ

2

10





tp

S a

Ⓒ

2

12





tp

S a

Ⓓ

2

8





tp

S a

Câu 15. Cho hình trụ có bán kính đáy bằng R và chiều cao bằng

3

2

R

. Mặt phằng

 



song song với trục

của hình trụ và cách trục một khoảng bằng

2

R

. Diện tích thiết diện của hình trụ với mp

 



là

Ⓐ

2

3 3

2

R

Ⓑ

2

2 3

3

R

Ⓒ

2

3 2

2

R

Ⓓ

2

2 2

3

R

Câu 16. Cho lăng trụ đứng ABC.A’B’C’ có cạnh bên AA’ = 2A. Tam giác ABC vuông tại A có

2 3



BC a

. Thề tích của hình trụ ngoại tiếp khối lăng trụ này là

Ⓐ

3

6



a

Ⓑ

3

4



a

Ⓒ

3

2



a

Ⓓ

3

8



a

Câu 17. Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a, mặt bên là các hình vuông. Diện tích

toàn phần của hình trụ ngoại tiếp khối lăng trụ là

Ⓐ

2

( 3 1)

3





a

Ⓑ

2

4



a

Ⓒ

2



a

Ⓓ

2

3

2



a

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 312

Câu 18. Cho hình trụ có có bán kính R. AB, CD lần lượt là hai dây cung song song với nhau và nằm trên

hai đường tròn đáy và cùng có độ dài bằng

2

R

. Mặt phẳng (ABCD) không song song và cũng

không chứa trục của hình trụ. Khi đó tứ giác ABCD là hình gì

Câu 19. Cho hình lăng trụ tam giác đều có cạnh đáy bằng a và chiều cao bằng h. Khi đó thể tích của khối

trụ nội tiếp lăng trụ sẽ bằng

Ⓐ

2

12



ha

Ⓑ

2

3



ha

Ⓒ

2

9



ha

Ⓓ

2

4

3



ha

Câu 20. Thiết diện qua trục của hình trụ (T) là một hình vuông có cạnh bằng a. Diện tích xung quanh

xq

S

của hình trụ (T) là

Ⓐ

2





xq

S a

Ⓑ

2

1

2





xq

S a

Ⓒ

2





xq

S a

Ⓓ

2



xq

S a

Câu 21. Một hình trụ

 

T

có diện tích xung quanh bằng

4



và thiết diện qua trục của hình trụ này là một

hình vuông. Diện tích toàn phần của

 

T

là

Ⓐ

6



Ⓑ

12



Ⓒ

10



Ⓓ

8



Câu 22. Cho lăng trụ lục giác đều ABCDEF có cạnh đáy bằng a. Các mặt bên là hình chữ nhật có diện tích

bằng

2

2a

. Thề tích của hình trụ ngoại tiếp khối lăng trụ là

Ⓐ

3

2



a

Ⓑ

3

4



a

Ⓒ

3

6



a

Ⓓ

3

8



a

Câu 23. Một hình trụ có bán kính 5cm và chiều cao 7cm. Cắt khối trụ bằng một mặt phẳng song song với

trục và cách trục 3cm. Diện tích thiết diện tạo bởi khối trụ và mặt phẳng bằng

Ⓐ

2

56

cm

Ⓑ

2

54

cm

Ⓒ

2

52

cm

Ⓓ

2

58

cm

Câu 24. Cho hình trụ có có bán kính R; AB, CD lần lượt là hai dây cung song song với nhau, nằm trên hai

đường tròn đáy và cùng có độ dài bằng

2

R

. Mặt phẳng (ABCD) không song song và cũng không

chứa trục của hình trụ, góc giữa (ABCD) và mặt đáy bằng

0

30

. Thể tích khối trụ bằng

Ⓐ

3

6

3



R

Ⓑ

3

6

2



R

Ⓒ

3

6



R

Ⓓ

3

2

3



R

Câu 25. Khối trụ (T) có bán kính đáy là R và thiết diện qua trục là một hình vuông. Thể tích của khối lăng

trụ tứ giác đều nội tiếp khối trụ (T) trên tính theo R bằng

Ⓐ

3

4R

Ⓑ

3

3R

Ⓒ

3

2R

Ⓓ

3

5R

Câu 26. Một hình trụ có chu vi của đường tròn đáy

4



a

, chiều cao

a

. Thể tích của khối trụ này bằng

Ⓐ

3

4



a

Ⓑ

3

2



a

Ⓒ

3

16



a

Ⓓ

3

4

3



a

Câu 27. Một hình trụ có chiều cao

5m

và bán kính đường tròn đáy

3m

. Diện tích xung quanh của hình trụ

này là

Ⓐ

 

2

30



m

Ⓑ

 

2

15



m

Ⓒ

 

2

45



m

Ⓓ

 

2

48



m

Câu 28. Hình trụ có bán kính đáy bằng

2 3

và thể tích bằng

24



. Chiều cao hình trụ này bằng

Ⓐ 2 Ⓑ 6 Ⓒ

2 3

Ⓓ 1

Câu 29. Một hình trụ có chu vi của đường tròn đáy là

c

, chiều cao của hình trụ gấp 4 lần chu vi đáy. Thể

tích của khối trụ này là

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 313

Ⓐ

3



c

Ⓑ

3

2



c

Ⓒ

3

4



c

Ⓓ

2



c

Câu 30. Một khối trụ có thể tích là

20

. Nếu tăng bán kính lên 2 lần thì thể tích của khối trụ mới là

Câu 31. Thiết diện qua trục của một hình trụ là hình vuông có cạnh

2a

. Diện tích xung quanh của hình trụ

này bằng

Ⓐ

2

4



a

Ⓑ

2



a

Ⓒ

2

8



a

Ⓓ

2

6



a

Câu 32. Cho khối trụ có thể tích bằng

24



. Nếu tăng bán kính đường tròn đáy lên 2 lần thì thể tích khối

trụ mới là

Ⓐ

96



Ⓑ

48



Ⓒ

32



Ⓓ

192



Câu 33. Một hình trụ có đường kính của đáy bằng với chiều cao của nó. Nếu thể tích của khối trụ bằng

2



thì chiều cao của hình trụ là

Ⓐ

2

Ⓑ

3

24

Ⓒ

2

Ⓓ

3

4

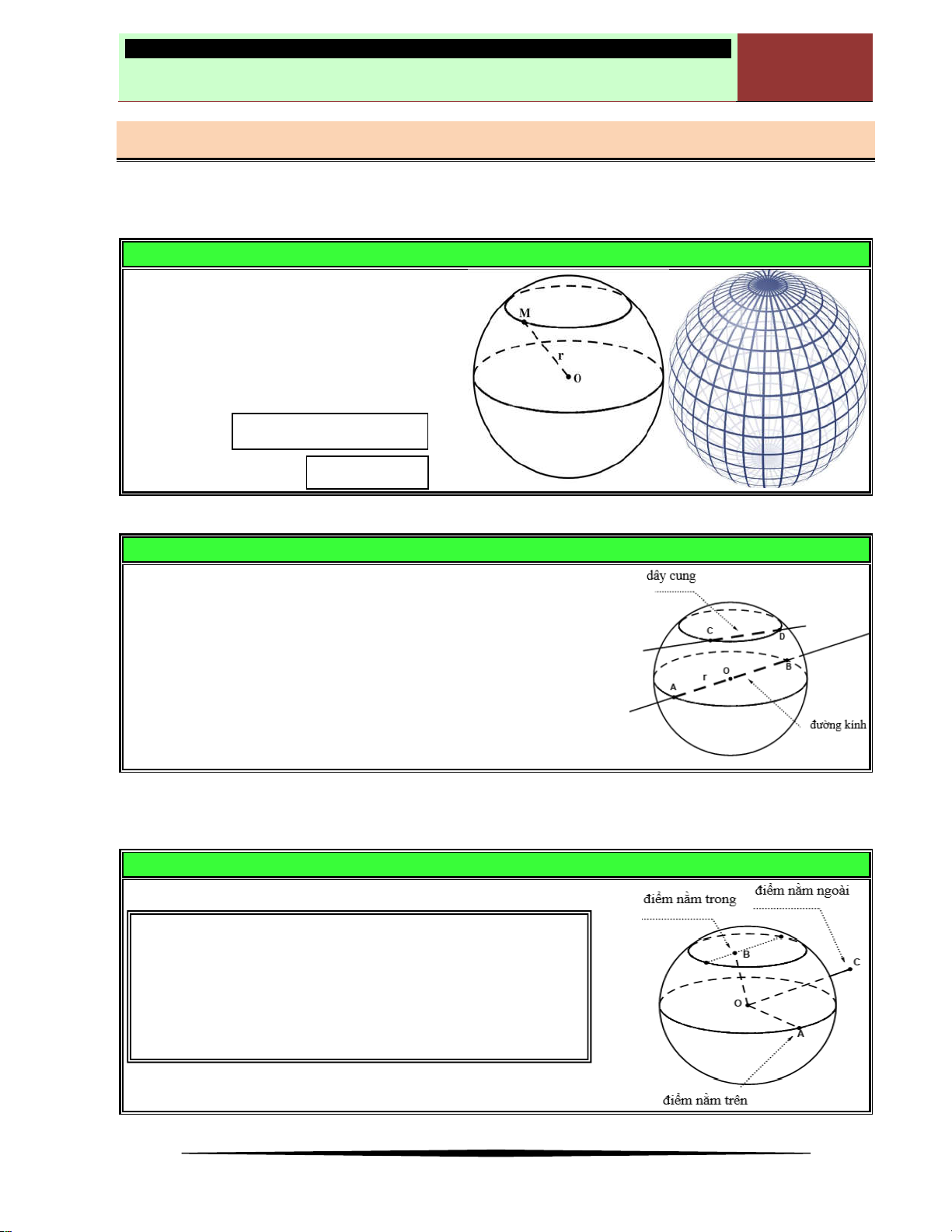
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 314

§2. MẶT CẦU

A. TÓM TẮT LÝ THUYẾT

1. Mặt cầu:

Tập hợp những điểm M trong không gian cách

điểm O cố định một khoảng không đổi bằng r

(r > 0) được gọi là mặt cầu tâm O bán kính r.

 Mặt cầu tâm O, bán kính r được kí hiệu:

S(O; r) hay viết tắt là (S).

 Vậy:

 Diện tích mặt cầu:

2. Khái niệm dây cung, đường kính mặt cầu:



Nếu hai điểm CD nằm trên mặt cầu S(O; r) thì đoạn thẳng CD

được gọi là dây cung của mặt cầu đó.

 Dây cung AB đi qua tâm O được gọi là một đường kính của mặt

cầu. Khi đó AB = 2r.

3. Điểm nằm trong, nằm ngoài mặt cầu:

Cho mặt cầu S(O; r) và một điểm A bất kì trong không gian.

S(O; r) = {M  OM = r}

2

4

mc

S r





 Nếu OA = r thì ta nói điểm A nằm trên mặt cầu S(O; r)

 Nếu OA < r thì ta nói điểm A nằm trong mặt cầu S(O; r)

 Nếu OA > r thì ta nói điểm A nằm ngoài mặt cầu S(O; r)

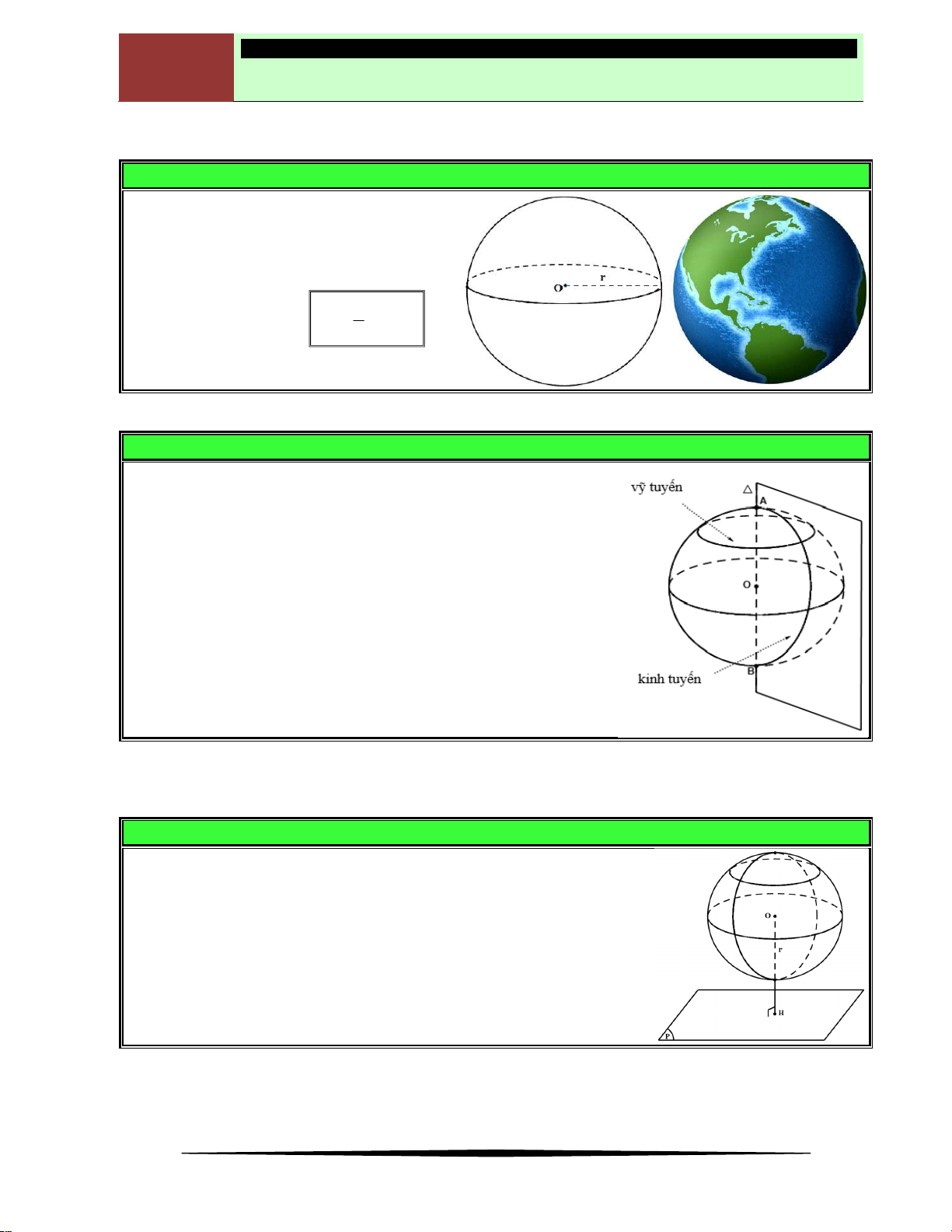
HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 315

4.Khối cầu:

Tập hợp các điểm thuộc mặt cầu S(O; r) cùng

với các điểm nằm trong mặt cầu đó được gọi

là khối cầu hoặc hình cầu tâm O bán kính r.

 Thể tích khối cầu:

5. Đường kinh tuyến, vỹ tuyến của mặt cầu:

Ta có thể xem mặt cầu là một mặt tròn xoay tạo nên bởi nửa đường

tròn quay quanh trục chứa đường kính của nửa đường tròn đó.

 Giao tuyến của mặt cầu với nửa mặt phẳng có bờ là trục của mặt

cầu được gọi là kinh tuyến.

 Giao tuyến (nếu có) của mặt cầu với các mặt phẳng vuông góc

với trục được gọi là vĩ tuyến của mặt cầu.

 Hai giao điểm của mặt cầu với trục được gọi là hai cực của mặt

cầu.

6. Giao của mặt cầu và mặt phẳng:

Cho mặt cầu (S) tâm O, bán kính r và mặt phẳng (P). Ta có:

 Mặt cầu (S) và mp(P) không có điểm chung.



( ) [ ,( )]S P d O P r    

3

4

3

V r





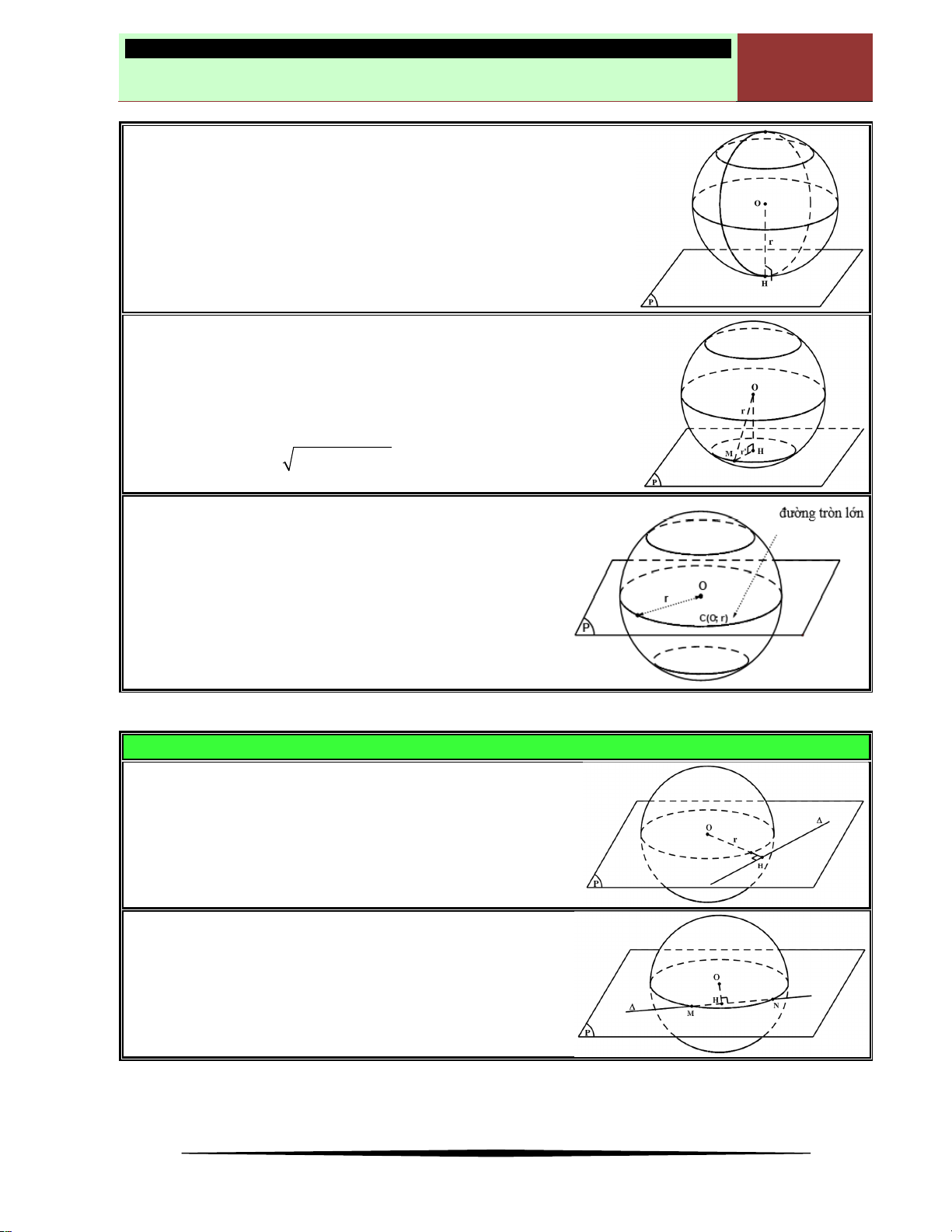
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 316

 Mặt cầu (S) và mp(P) có 1 điểm chung. (hay còn gọi mặt phẳng

(P) tiếp xúc với mặt cầu (S))



( ) ( ) {H} [ ,( )] = OH = S P d O P r  

 Khi đó: (P) gọi là tiếp diện của mặt cầu (S), H gọi

là tiếp điểm.

 Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C)

tâm H, bán kính r'.



( ) ( ) ( ; ') [ ,( )] = OH < S P C H r d O P r  

.

 Tâm H là hình chiếu của O trên mp(P).

 Bán kính

2 2

' [O,(P)]r r d 

 Mặt phẳng (P) đi qua tâm O của mặt cầu.



( ) ( ) ( ; ) [ ,( )] = 0S P C O r d O P  

 Khi đó giao tuyến của mp(P) và S(O; r) là đường

tròn C(O; r) gọi là đường tròn lớn.

7. Giao của mặt cầu và đường thẳng:

Cho mặt cầu (S) tâm O, bán kính r và đường thẳng . Ta có:

 Đường thẳng  không cắt mặt cầu (S).



( ) ( , ) > rS d O     

 Đường thẳng  cắt mặt cầu (S) tại 2 điểm.



( ) {M;N} ( , ) < rS d O    

 MN là dây cung của mặt cầu.

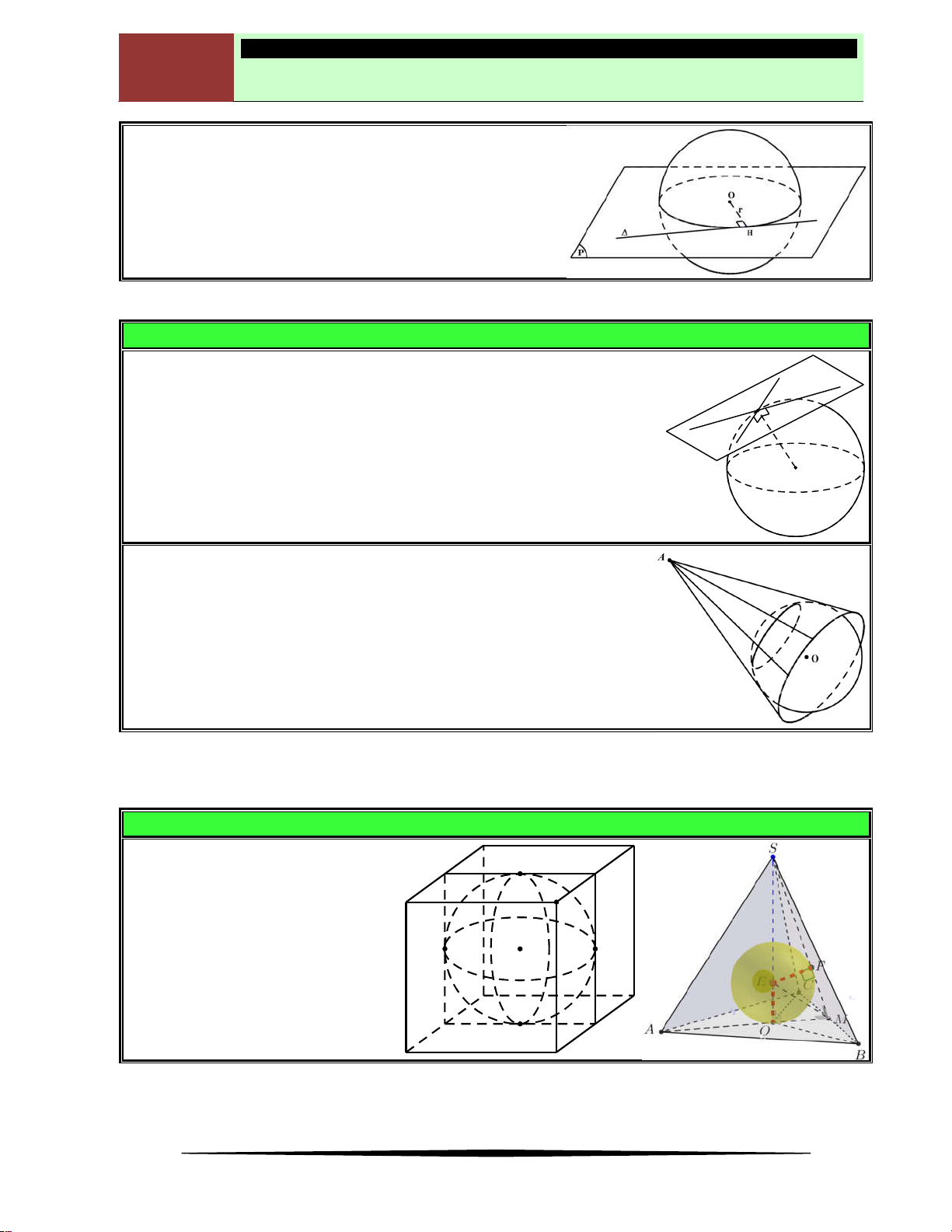
HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 317

 Đường thẳng  tiếp xúc mặt cầu (S) tại H.



( ) {H} ( , ) = OH = rS d O    

 Khi đó:  gọi là tiếp tuyến của mặt cầu (S), H gọi là

tiếp điểm.

8. Nhận xét:

 Qua một điểm A nằm trên mặt cầu S(O; r) có vô số tiếp tuyến của mặt

cầu. Tất cả các tiếp tuyến này đều vuông góc với bán kính OA của mặt

cầu tại A và đều nằm trên tiếp diện của mặt cầu tại A.

 Qua một điểm A nằm ngoài mặt cầu S(O; r) có vô số tiếp tuyến với

mặt cầu. Các tiếp tuyến này tạo thành mặt nón đỉnh A. Khi đó độ dài

các đoạn thẳng kẻ từ A đến các tiếp điểm đều bằng nhau.

9. Mặt cầu nội tiếp, ngoại tiếp hình đa diện:

 Mặt cầu nội tiếp hình đa diện nếu

mặt cầu đó tiếp xúc với tất cả các

mặt của hình đa diện. Người ta

còn gọi hình đa diện ngoại tiếp

mặt cầu.

A

O

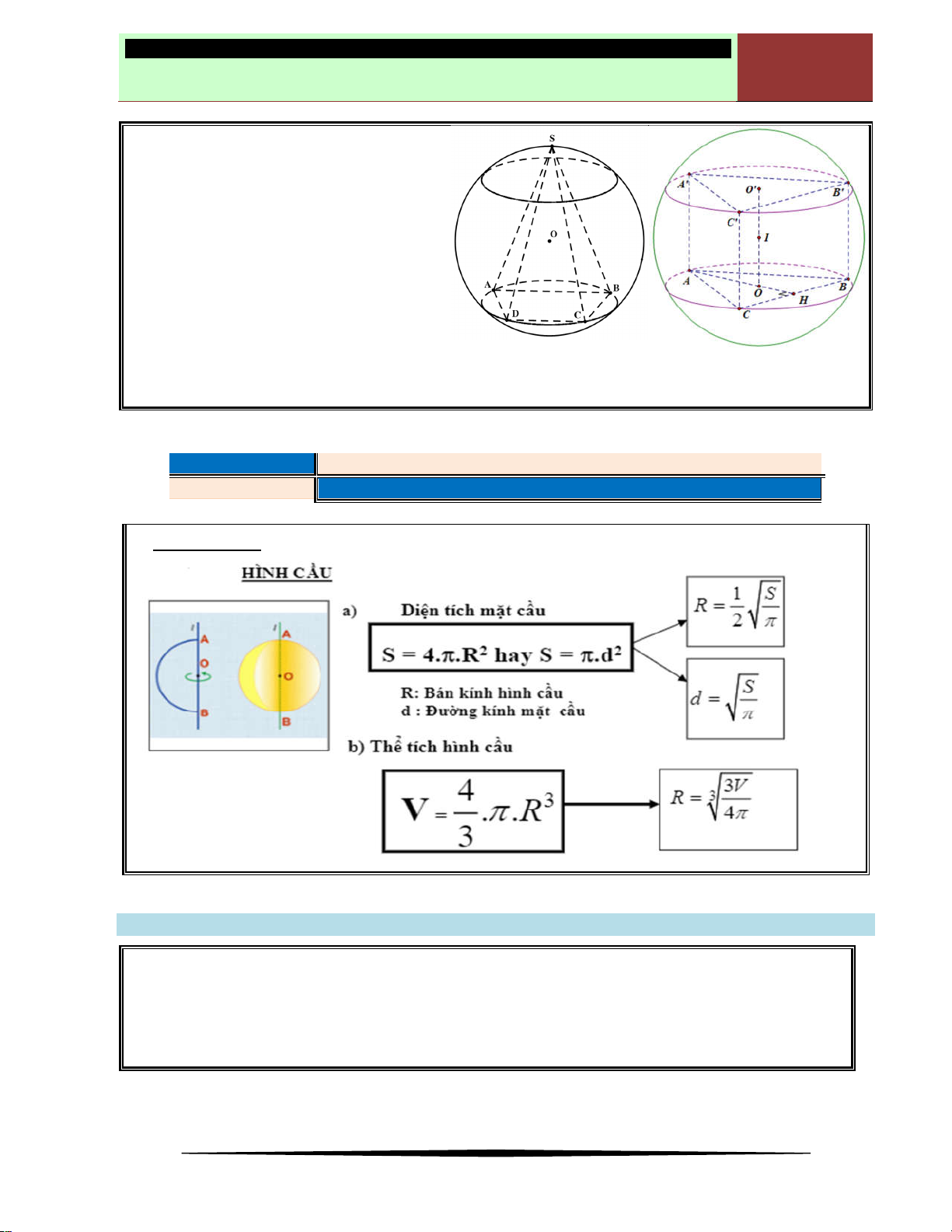
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 318

 Mặt cầu ngoại tiếp hình đa diện nếu tất

cả các đỉnh của hình đa diện đều nằm

trên mặt cầu. Còn nói hình đa diện nội

tiếp mặt cầu.

 Mặt cầu tâm O bán kính r ngoại tiếp

hình chóp S.ABCD khi và chỉ khi

OA = OB = OC = OD = OS = r

 Mặt cầu tâm I bán kính r ngoại tiếp

hình lăng trụ ABC.A’B’C’ khi và chỉ khi IA = IB = IC = IA’ = IB’ = IC’ = r

— Phương pháp:

CÁC VÍ DỤ

Ví dụ 1. Cho mặt cầu có đường kính bằng 4.

a) Tính diện tích mặt cầu.

b) Tính thể tích của khối cầu.

--------------------------------------------------------------------------------------------------------------------------------

Dạng 1:

Tính diện tích mặt cầu, thể tích khối cầu.

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 319

--------------------------------------------------------------------------------------------------------------------------------

Ví dụ 2. Cho mặt cầu có diện tích bằng

2

8

3

a



. Khi đó, bán kính mặt cầu bằng:

Ⓐ

6

3

a

Ⓑ

3

a

Ⓒ

6

2

a

Ⓓ

2

3

a

Lời giải :....................................................................

......................................................................................

Ví dụ 3. Cho hình lăng trụ tam giác đều có cạnh đáy và cạnh bên cùng bằng a. Diện tích của hình cầu

ngoại tiếp hình lăng trụ này bằng:

Ⓐ

2

7

3

a



Ⓑ

2

7

36

a



Ⓒ

2

7

12

a



Ⓓ

2

7

9

a



Lời giải:.....................................................................

......................................................................................

Ví dụ 4. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng

0

45

. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD bằng:

Ⓐ

2

9

4

a



Ⓑ

2

4

3

a



Ⓒ

2

3

4

a



Ⓓ

2

3

a



Lời giải:.....................................................................

......................................................................................

Ví dụ 5. (S) là mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a. Thể tích của khối cầu tạo bởi mặt cầ

u (S)

là:

Ⓐ Ⓑ

Ⓒ Ⓓ

Lời giải:.....................................................................

......................................................................................

Ví dụ 6. Cho hình chóp đều SABCD có cạnh đáy bằng a, cạnh bên SA = a; Gọi (S) là mặt cầu ngoại

tiếp hình chóp SABCD. Thể tích của khối cầu tạo nên bởi mặt cầu (S) bằng:

Ⓐ Ⓑ

Ⓒ Ⓓ

Lời giải :....................................................................

......................................................................................

Ví dụ 7. Cho hình chóp SABCD có AB = SA = a, SA (ABCD), đáy ABCD là hình vuông. Thể

tích của khối cầu ngoại tiếp hình chóp SABCD là:

3

a

V

4





3

3 a

V

4





3

3 a

V

4





3

5 a

V

4





3

2 2 a

3



3

3 a

2



3

2 a

3



3

2 a

3





TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 320

BÀI TẬP

Câu 1. Cho mặt cầu

 

1

S

có bán kính

1

R

, mặt cầu

 

2

S

có bán kính

2

R

và

2 1

2R R

. Tỉ số diện tích của

mặt cầu

 

2

S

và mặt cầu

 

1

S

bằng

Ⓐ

1

2

Ⓑ

2

Ⓒ

1

4

Ⓓ

4

Câu 2. Gọi

 

S

là mặt cầu có tâm

O

và bán kính

R

;

d

là khoảng cách từ

O

đến mặt phẳng (P) , với

d R

. Khi đó, có bao nhiêu điểm chung giữa (S) và (P)?

Câu 3. Cho mặt cầu có diện tích bằng

2

8

3

a



. Khi đó, bán kính mặt cầu bằng

Ⓐ

6

3

a

Ⓑ

3

a

Ⓒ

6

2

a

Ⓓ

2

3

a

Câu 4. Cho khối cầu có thể tích bằng

3

8 6

27

a



. Khi đó, bán kính mặt cầu bằng

Ⓐ

6

3

a

Ⓑ

3

a

Ⓒ

6

2

a

Ⓓ

2

3

a

Câu 5. Cho tứ diện

DABC

, đáy

ABC

là tam giác vuông tại B,

DA

vuông góc với mặt đáy. Biết AB =

3a, BC = 4a, DA = 5a. Bán kính mặt cầu ngoại tiếp hình chóp DABC có bán kính bằng

Ⓐ

5 2

2

a

Ⓑ

5 2

3

a

Ⓒ

5 3

2

a

Ⓓ

5 3

3

a

Câu 6. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng

a

. Diện tích của mặt

cầu ngoại tiếp hình chóp S.ABCD bằng

Ⓐ

2

a



Ⓑ

2

4

a



Ⓒ

2

a



Ⓓ

2

6

a



Câu 7. Cho tứ diện đều ABCD cạnh a. Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng

Ⓐ

3

6

8

a



Ⓑ

3

6

a



Ⓒ

3

6

4

a



Ⓓ

3

3 6

8

a



Ⓐ

3

a



Ⓑ

3

2

a



.

Ⓒ

3

6

2

a



Ⓓ

3

2

a



Lời giải:.....................................................................

......................................................................................

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 321

Câu 8. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng

0

45

.

Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD bằng

Ⓐ

2

9

4

a



Ⓑ

2

4

3

a



Ⓒ

2

3

4

a



Ⓓ

2

3

a



Câu 9.

Một hình hộp chữ nhật có ba kích thước là

, ,a b c

Khi đó mặt cầu ngoại tiếp hình hộp chữ nhật

có bán kính

R

bằng:

Ⓐ

2 2 2

R a b c  

Ⓑ

2 2 2

1

2

R a b c  

Ⓒ

2 2 2

1

3

R a b c  

Ⓓ

2 2 2

2( )R a b c

  

Câu 10.

Một hình hộp chữ nhật có 3 kích thước 20cm, 20

3

cm, 30cm . Thể tích khối cầu ngoại tiếp

hình hộp đó bằng:

Ⓐ

3

32

dm

3



Ⓑ

3

3200

cm

3



Ⓒ

3

62,5

dm

3



Ⓓ

3

625000

dm

3



Câu 11. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc nhau và

; ;

OA a OB b OC c  

. Bán

kính của mặt cầu (S) ngoại tiếp tứ diện OABC bằng:

Ⓐ

2 2 2

1

2

R a b c  

Ⓑ

2 2 2

1

3

R a b c  

Ⓒ

2 2 2

2( )R a b c

  

Ⓓ

2 2 2

R a b c  

Câu 12.

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc nhau và OA = a, OB = 2a, OC= 3a.

Diện tích của mặt cầu (S) ngoại tiếp hình chóp S.ABC bằng:

Ⓐ

2

S 14 a 

Ⓑ

2

S 8 a 

Ⓒ

2

S 12 a 

Ⓓ

2

S 10 a 

Câu 13. Cho hình chóp tứ giác đều S. ABCD có cạnh đáy và cạnh bên cùng bằng a. Bán kính của mặt cầu

ngoại tiếp hình chóp này bằng

Ⓐ

2a

Ⓑ

2

a

Ⓒ

3a

Ⓓ

3

a

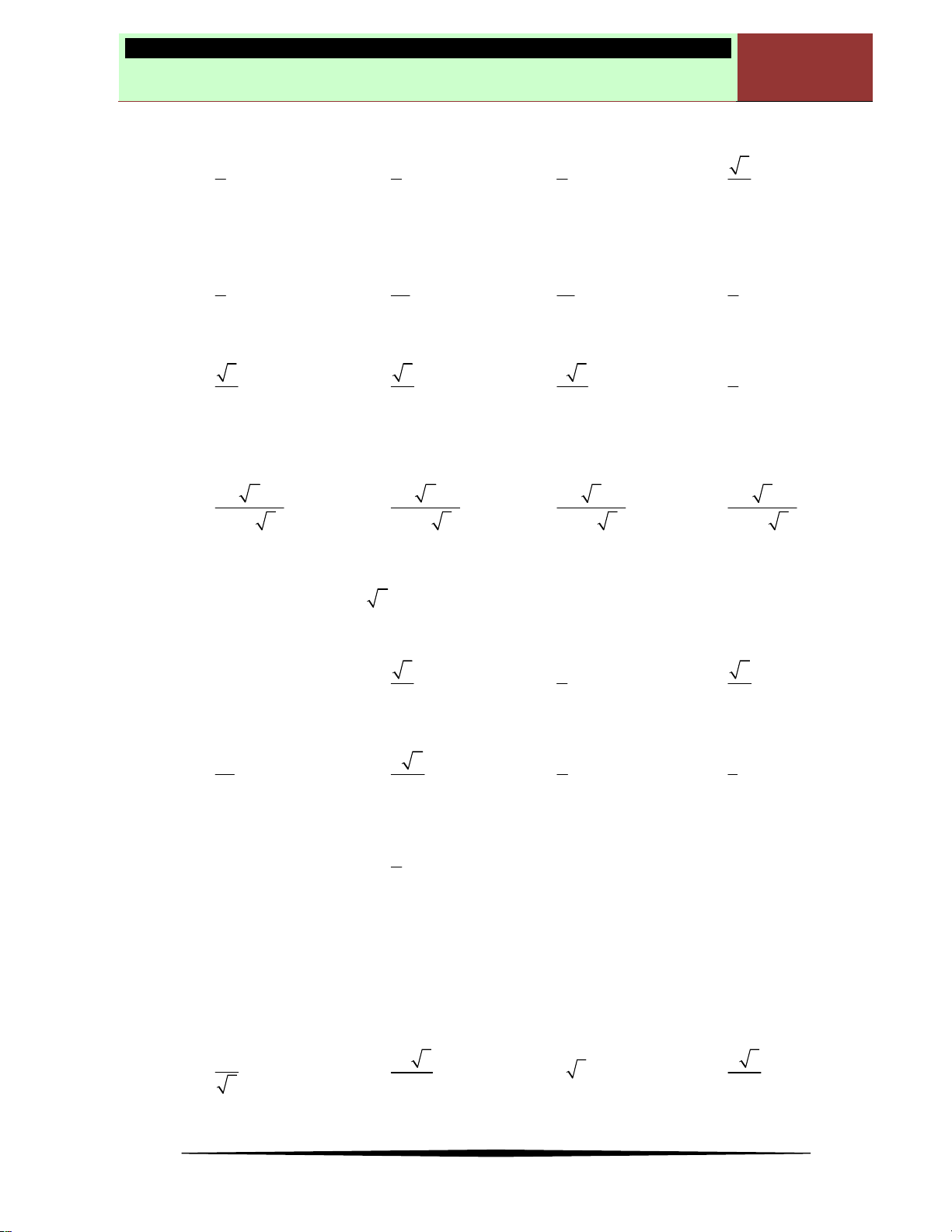
TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 322

Câu 14. Thể tích của khối cầu nội tiếp khối lập phương có cạnh bằng a là

Ⓐ

3

1

2

a



Ⓑ

3

2

9

a



Ⓒ

3

2

3

a



Ⓓ

3

6

a



Câu 15. Cho hình lăng trụ tam giác đều có cạnh đáy và cạnh bên cùng bằng a. Diện tích của hình cầu

ngoại tiếp hình lăng trụ này bằng

Ⓐ

2

7

3

a



Ⓑ

2

7

36

a



Ⓒ

2

7

12

a



Ⓓ

2

7

9

a



Câu 16. Thể tích của khối cầu ngoại tiếp khối lập phương có cạnh bằng a là

Ⓐ

3

2

a



Ⓑ

3

8

a



Ⓒ

3

3 3

2

a



Ⓓ

3

1

6

a



Câu 17. Cho hình chóp tứ giác đều S. ABCD có cạnh đáy và cạnh bên cùng bằng a. Bán kính của mặt cầu

nội tiếp hình chóp này bằng

Ⓐ

 

2

2 1 3

a



Ⓑ

 

2

4 1 3

a



Ⓒ

 

3

2 1 3

a



Ⓓ

 

3

4 1 3

a



Câu 18. Cho hình chóp S.ABCD có đáy là hình thang vuông với đường cao

AB BC a 

,

2AD a

,

 

SA ABCD



và

2SA a



. Gọi E là trung điểm của AD. Kẻ

EK SD

tại K. Bán kính mặt cầu

đi qua sáu điểm S, A, B, C, E, K bằng

Ⓐ

a

Ⓑ

3

2

a

Ⓒ

1

2

a

Ⓓ

6

2

a

Câu 19. Giá trị lớn nhất của thể tích khối nón nội tiếp trong khối cầu có bán kính R bằng

Ⓐ

3

32

81

R



Ⓑ

3

4 2

9

R



Ⓒ

3

4

3

R



Ⓓ

3

1

3

R



Câu 20. Một mặt cầu có diện tích

2

36 (m )



. Thể tích của khối cầu này bằng

Ⓐ

 

3

36

m



Ⓑ

 

3

4

3

m



Ⓒ

 

3

72

m



Ⓓ

 

3

108

m



Câu 21. Một khối cầu có thể tích là

 

3

288

m



. Diện tích của mặt cầu này bằng

Ⓐ

 

2

144

m



Ⓑ

 

2

72

m



Ⓒ

 

2

288

m



Ⓓ

 

2

36

m



Câu 22. Một lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Bán kính mặt cầu ngoại tiếp

lăng trụ này bằng

Ⓐ

2

3

a

Ⓑ

2 3

5

a

Ⓒ

3a

Ⓓ

3

2

a

HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 323

Câu 23. Một hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng 2x. Điều kiện cần và đủ của x để

tâm mặt cầu ngoại tiếp hình chóp ở ngoài hình chóp là

Ⓐ

2

2 2

a a

x

 

Ⓑ

2

2 2

a a

x 

Ⓒ

2

a

x



Ⓓ

2

a

x



Câu 24. Một lăng trụ tứ giác đều có cạnh đáy bằng 4 nội tiếp mặt cầu có diện tích là

64



. Chiều cao của

hình lăng trụ này bằng

Ⓐ

4 2

Ⓑ

3 2

Ⓒ

4

Ⓓ

6 2

Câu 25. Số mặt cầu chứa một đường tròn cho trước là:

Câu 26.

Cho mặt cầu có bán kính là a, ngoại tiếp hình nón. Thiết diện qua trục của hình nón là tam giác

đều. Thể tích của khối nón là:

Ⓐ

3

4

V a





Ⓑ

3

4

V a





Ⓒ

3

1

8

V a





Ⓓ

3

8

V a





Câu 27.

Hình nón có bán kính của đường tròn đáy bằng a, thiết diện qua trục là tam giác đều. Thế tích

của khối cầu ngoại tiếp hình nón là:

Ⓐ

3

32 3

12

V a





Ⓑ

3

32 3

9

V a





Ⓒ

3

32 3

27

V a





Ⓓ

3

32 3

3

V a





Câu 28.

Trong các mệnh đề sau đây, mệnh đề nào sai?

Ⓐ

Bất kì một hình tứ diện nào cũng có mặt cầu ngoại tiếp

Ⓑ

Bất kì một hình hộp chữ nhật nào cũng có một mặt cầu ngoại tiếp

Ⓒ

Bất kì một hình hộp nào cũng có một mặt cầu ngoại tiếp.

Ⓓ

Bất kì một hình chóp đều nào cũng có một mặt cầu ngoại tiếp

Câu 29.

Một hình trụ có thiết diện qua trục là hình vuông, đường chéo của hình vuông bằng

a 2

. Thể

tích của khối cầu nội tiếp hình trụ là:

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 324

Ⓐ

3

1

3

V a





Ⓑ

3

1

6

V a





Ⓒ

3

1

4

V a





Ⓓ

3

1

2

V a





Câu 30.

Một đường thẳng cắt mặt cầu tâm O tại hai điểm A,B sao cho tam giác OAB vuông cân tại O và

AB a 2



. Thể tích khối cầu là:

Ⓐ

3

4V a





Ⓑ

3

V a 

Ⓒ

3

4

3

V a





Ⓓ

3

2

3

V a





Câu 31.

Cho hình lập phương cạnh a nội tiếp trong một mặt cầu . Bán kính đường tròn lớn của mặt cầu

đó bằng

Ⓐ

3

2

a

Ⓑ

a

Ⓒ

2a

Ⓓ

2

a

Câu 32. Cho hình trụ nội tiếp trong hình lập phương có cạnh bằng

x

. Tỷ số thể tích của khối trụ và khối

lập phương trên là

Ⓐ

4



Ⓑ

2



Ⓒ

12



Ⓓ

2

3

Câu 33. Một hình trụ có chiều cao bằng 6 nội tiếp trong hình cầu có bán kính bằng 5 như hình vẽ. Thể

tích của khối trụ này bằng

Ⓐ

96



Ⓑ

36



Ⓒ

192



Ⓓ

48



ĐỀ KIỂM TRA 45 PHÚT

Câu 1. Gọi

, ,l h R

lần lượt là độ dài đường sinh,chiều cao và bán kính đáy của khối nón (N).Thể tích V của

khối nón (N)là

Ⓐ

2

V R h





Ⓑ

2

1

3

V R h





Ⓒ

2

V R l





Ⓓ

2

1

3

V R l





Câu 2. Cho hình nón có bán kính đáy là 4a,chiều cao là 3a . Diện tích xung quanh hình nón là:

Ⓐ

2

20

a



Ⓑ

2

40

a



Ⓒ

2

24

a



Ⓓ

2

12

a



Câu 3. Cho hình nón có bán kính đáy là 3a,chiều cao là 4a . Thể tích của hình nón là:

Ⓐ

3

15

a



Ⓑ

3

36

a



Ⓒ

3

12

a



Ⓓ

3

12

a



HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 325

Câu 4. Cho hình nón có bán kính đáy là 4a,chiều cao là 3a . Diện tích toàn phần hình nón là:

Ⓐ

2

32

a



Ⓑ

2

30

a



Ⓒ

2

38

a



Ⓓ

2

36

a



Câu 5. Gọi

, ,l h R

lần lượt là độ dài đường sinh,chiều cao và bán kính đáy của hình trụ (T).Diện tích toàn

phần

tp

S

của hình trụ (T)là:

Ⓐ

2

tp

S Rl R

 

 

Ⓑ

2

2 2

tp

S Rl R

 

 

Ⓒ

2

tp

S Rl R

 

 

Ⓓ

2

tp

S Rh R

 

 

Câu 6. Cho hình trụ có bán kính đáy 3 cm,đường cao 4cm,diện tích xung quanh của hình trụ này là:

Ⓐ

2

24 ( )cm



Ⓑ

2

22 ( )cm



Ⓒ

2

26 ( )cm



Ⓓ

2

20 ( )cm



Câu 7. Một hình trụ có bán kính đáy 6 cm,chiều cao 10 cm.Thể tích của khối trụ này là:

Ⓐ

3

360 ( )cm



Ⓑ

3

320 ( )cm



Ⓒ

3

340 ( )cm



Ⓓ

3

300 ( )cm



Câu 8. Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng

2a

.Khi đó thể tích khối trụ là:

Ⓐ

3

a

Ⓑ

3

2 a

Ⓒ

3

8 a

Ⓓ

3

4 a

Câu 9. Gọi

R

bán kính,S là diện tích và

V

là thể tích của khối cầu.Công thức nào sau sai?

Ⓐ

3

4

3

V R





Ⓑ

2

4

S R





Ⓒ

2

S R





Ⓓ

3 .V S R

Câu 10. Cho mặt cầu

 

1

S

có bán kính

1

R

,mặt cầu

 

2

S

có bán kính

2

R

và

2 1

2R R



.Tỉ số diện tích của mặt

cầu

 

2

S

và mặt cầu

 

1

S

bằng:

Ⓐ

1

2

Ⓑ

2

Ⓒ

1

4

Ⓓ

4

Câu 11. Gọi

 

S

là mặt cầu có tâm

O

và bán kính

R

;

d

là khoảng cách từ

O

đến mặt phẳng (P),với

d<R.Khi đó có bao nhiêu điểm chung giữa (S)và (P)?

Câu 12. Cho khối cầu có thể tích bằng

3

8 6

27

a



,khi đó bán kính mặt cầu là:

Ⓐ

6

3

a

Ⓑ

3

a

Ⓒ

6

2

a

Ⓓ

2

3

a

Câu 13. Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh huyền bằng

2 3

.Thể

tích của khối nón này là:

Ⓐ

3



Ⓑ

3 3



Ⓒ

3



Ⓓ

3 2



Câu 14. Một hình nón ngoại tiếp hình tứ diện đều với cạnh bằng 3 có diện tích xung quanh bằng bao nhiêu

?

Ⓐ

3 3

2



Ⓑ

3 3

Ⓒ

2 3

Ⓓ

9 3

2



Câu 15. Một khối nón có thể tích bằng

30



,nếu giữ nguyên chiều cao và tăng bán kính khối nón đó lên 2

lần thì thể tích của khối nón mới bằng:

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

HÌNH HỌC

Trang: 326

Ⓐ

40



Ⓑ

60



Ⓒ

120



Ⓓ

480



Câu 16. Một hình trụ có chu vi của đường tròn đáy là

c

,chiều cao của hình trụ gấp 4 lần chu vi đáy.Thể

tích của khối trụ này là:

Ⓐ

2

2c



Ⓑ

3

2c



Ⓒ

3

4

c



Ⓓ

3

c



Câu 17. Một khối trụ có thể tích là

20

(đvtt).Nếu tăng bán kính lên 2 lần thì thể tích của khối trụ mới là:

400

(đvtt)

Câu 18. Một hình trụ ngoại tiếp hình lăng trụ tam giác đều với tất cả các cạnh bằng a có diện tích xung

quanh bằng bao nhiêu ?

Ⓐ

2

2 3

3

a



Ⓑ

2

3

a



Ⓒ

2

4 3

3

a



Ⓓ

2

3

a



Câu 19. Cho mặt cầu có diện tích bằng

2

8

3

a



,khi đó bán kính mặt cầu là:

Ⓐ

6

2

a

Ⓑ

3

a

Ⓒ

6

3

a

Ⓓ

2

3

a

Câu 20. Cho hình chóp tam giác đều S.ABC có cạnh đáy là a và cạnh bên là 2Ⓐ Bán kính của mặt cầu

ngoại tiếp hình chóp S.ABC là:

Ⓐ Ⓑ Ⓒ Ⓓ

Câu 21. Cho mặt cầu S(O; R)và mặt phẳng (P)cách O một khoảng bằng

2

R

.Khi đó (P)cắt mặt cầu theo

giao tuyến là một đường tròn có bán kính bằng:

Ⓐ

3

4

R

Ⓑ

2 3

3

R

Ⓒ

2

R

Ⓓ

3

2

R

Câu 22. Cho tam giác

ABC

vuông tại

B

có

2 ;AC a BC a 

; khi quay tam giác

ABC

quanh cạnh

góc vuông

AB

thì đường gấp khúc

ABC

tạo thành một hình nón tròn xoay có diện tích xung quanh bằng:

Ⓐ

2

a

Ⓑ

2

4 a

Ⓒ

2

2 a

Ⓓ

2

3 a

Câu 23. Trong không gian cho tam giác vuông tại ,góc và cạnh .Khi quay tam

giác quanh cạnh góc vuông thì đường gấp khúc tạo thành một hình nón tròn xoay.Khi đó

diện tích xung quanh của hình nón tròn xoay đó là

Ⓐ Ⓑ Ⓒ Ⓓ

Câu 24. Cho lăng trụ đứng AB

Ⓒ

A’B’C’ có cạnh bên AA’ = 2

Ⓐ

Tam giác ABC vuông tại A có

.Thề tích của hình trụ ngoại tiếp khối lăng trụ này là:

Ⓐ Ⓑ Ⓒ Ⓓ

2 33

11

a

11

a

33

a

33

11

a

OIM

I



0

45

IOM 

IM a

OIM

OI

OMI

2

a



2

a



2

3

a



2

a



2 3BC a



3

6

a



3

4

a



3

2

a



3

8

a



HÌNH HỌC

TỔ TOÁN TRƯỜNG THPT NGUYỄN DU

CHƯƠNG II. MẶT NÓN – MẶT TRỤ – MẶT CẦU

Trang: 327

Câu 25. Cắt hình trụ có bán kính r = 5 và chiều cao bởi một mặt phẳng song song với trục và cách

trục 3cm.Hãy tính diện tích của thiết diện được tạo nên

Ⓐ Ⓑ Ⓒ Ⓓ

Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a,SA vuông góc với mặt phẳng

(ABCD), .Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD là:

Ⓐ Ⓑ Ⓒ Ⓓ

Câu 27. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là a và cạnh bên là 2Ⓐ Thể tích của khối cầu

ngoại tiếp hình chóp S.ABCD là:

Ⓐ Ⓑ Ⓒ Ⓓ

Câu 28. Cho hình nón đỉnh

S

,đường cao

SO

;

;A B

là 2 điểm nằm trên đường tròn đáy hình nón sao cho

khoảng các từ

O

đến

AB

bằng

a

.Góc



0 0

30 ; 60

SAO SAB 

.Khi đó độ dài đường sinh

l

của hình

nón là:

Ⓐ

a

Ⓑ

2a

Ⓒ

2a

Ⓓ

2 2a

Câu 29. Một hình trụ có chiều cao bằng 6 nội tiếp trong hình cầu có bán kính bằng 5 như hình vẽ.Thể tích

của khối trụ này bằng:

Ⓐ

36



Ⓑ

96



Ⓒ

192



Ⓓ

48



Câu 30. Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình

tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính bóng bàn.Gọi là tổng diện tích của ba

quả bóng bàn, là diện tích xung quanh của hình trụ.Tỉ số bằng:

ĐÁP ÁN

1.B 2.A 3.C 4.D 5.B 6.A 7.A 8.B 9.C 10.D

11.A 12.A 13.C 14.B 15.C 16.D 17.B 18.A 19.C 20.A

21.D 22.C 23.D 24.A 25.D 26.B 27.C 28.B 29.B 30.A

5 3

h 

3

100 3

cm

3

20 3

cm

2

80 3

cm

2

40 3

cm

2SA a

2

6

a



2

12

a



2

36

a



2

3

a



3

16 14

49

a



3

2 14

7

a



3

64 14

147

a



3

64 14

49

a



1

S

2

S

1

2

S

Đề cương học kỳ 1 Toán 12 năm 2021 – 2022 trường THPT Nguyễn Du – TP HCM

Đề HK1 Toán 12 458 tài liệu

Toán 12 3.8 K tài liệu

Bình luận

Đề cương học kỳ 1 Toán 12 năm 2021 – 2022 trường THPT Nguyễn Du – TP HCM