Đề cương kiểm tra giữa kì I môn Toán 8 năm học 2025 – 2026

Họ và tên: ...................................................................................
ĐỀ CƯƠNG KIỂM TRA GIỮA KÌ I TOÁN 8
Năm học 2025 – 2026 1. Trắc nghiệm:
Câu 1. Kết quả của phép nhân là: A. , B. , C. , D. .
Câu 2. Thực hiện phép nhân được A. B. C. D.
Câu 3. Hằng đẳng thức
được khai triển có dạng A. , B. , C. , D. . Câu 4. Tích
là dạng khai triển của hằng đẳng thức A. , B. , C. , D. Câu 5: A. B. C. D.
Câu 6. Giá trị của biểu thức tại là: A. 2 , B. 0 , C. 1 , D. - 1 . Câu 7.Tìm x biết: A. x = 2 B. x = 2 C. x = 4 D. x = -23
Câu 8 : Viết đa thức x2 + 6x + 9 dưới dạng bình phương của một tổng ta được kết quả nào sau đây: A. (x + 3)2 B. (x - 3)2 C. (x + 9)2 D. (x - 9)2
Câu 9 : Cho (3x – y)2 = … - 6xy + y2. Đơn thức thích hợp điền vào dấu “…” là A.3x2 B. 6x2 C. 9x2 D.4x2
Câu 10. Trong các biểu thức sau, biểu thức nào là đơn thức? A. B. C. . D.
Câu 11. Đơn thức đồng dạng với đơn thức là: A. . B. . C. . D. .
Câu 12. Biểu thức nào là đa thức? A. B. C. D. .
Câu 13. Giá trị của biểu thức tại x = 1 và y = -1 là A. 2. B. -3. C. 6. D. -6.
Câu 14. Cho tứ giác ABCD có . Số đo góc D bằng A. . B. . C. . D.
Câu 15. Cho hình thang cân ABCD (AB/ CD), = . Số đo của góc D là A. . B. . C. . D. .
Câu 16 : Tứ giác ABCD có A = 60o, B = 110o, C = 71o. Số đo góc D là A. 119o. B. 109o. C. 69o. D. 129o.
Câu 17 : Hình bình hành là tứ giác có: A. Các góc bằng nhau B. Hai cạnh song song C. Hai cạnh bằng nhau
D. Các cạnh đối song song
Câu 18 . Hình bình hành có một góc vuông là: A.Hình chữ nhật
B.Hình thoi C.Hình vuông D.Hình thang
Câu 19 : Khẳng định nào sau đây là đúng
A. Hình thang có 2 cạnh đối bằng nhau là hình thang cân.
B. Hình thang cân là tứ giác có 2 đường chéo bằng nhau.
C. Hình thang cân là tứ giác có 2 cạnh bên bằng nhau.
D. Hình thang có 2 góc kề 1 đáy bằng nhau là hình thang cân .
Câu 20 : Tứ giác có bốn cạnh bằng nhau và có một góc vuông là hình gì? A. Hình bình hành B. Hình chữ nhật C. Hình vuông D. Hình thoi
Câu 21 : Tứ giác dưới đây là hình thoi theo dấu hiệu nào?
A. Tứ giác có hai đường chéo vuông góc.
B. Tứ giác có bốn cạnh bằng nhau.
C. Hình bình hành có hai đường chéo bằng nhau.
D. Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường.
Câu 22: Tứ giác có bốn góc bằng nhau, thì số đo mỗi góc là A. 900. B. 3600. C. 1800. D. 600.
Câu 23: Tứ giác có hai cạnh đối song song và bằng nhau là A. Hình thang cân.
B. Hình bình hành. C. Hình chữ nhật. D. Hìnhthang vuông.
Câu 24: Hình bình hành có một góc vuông là A. Hình thang cân.
B. Hình bình hành. C. Hình chữ nhật. D. Hìnhthang vuông.
Câu 25: Hình bình hành có hai đường chéo bằng nhau là A. Hình thang cân.
B. Hình bình hành. C. Hình chữ nhật. D. Hìnhthang vuông
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Câu 1: Cho đa thức: a) là đa thức một biến.
b) Bậc của đa thức là 2. c) Biết . Đa thức là:
d) Giá trị của đa thức khi là .
Câu 2: Cho các đa thức sau: ; ; ; .
a) Bậc của đa thức N là 3
b) Đa thức P có bậc là 2
c) Giá trị của đa thức M tại 𝑥 = 1;𝑦 = 2 bằng -1 6 5
d) Trong bốn đa thức đã cho, đa thức Q có bậc lớn nhất và giá trị của đa thức Q tại x=-2, y =5 bằng 195 Câu 3: Cho đa thức:
a) Hạng tử tự do của đa thức là 2.
b) Bậc của đa thức A là 3.
c) Giá trị của đa thức tại x = 3; y = 2 là 26.
d) Đa thức A luôn nhận giá trị dương với mọi giá trị của x, y.
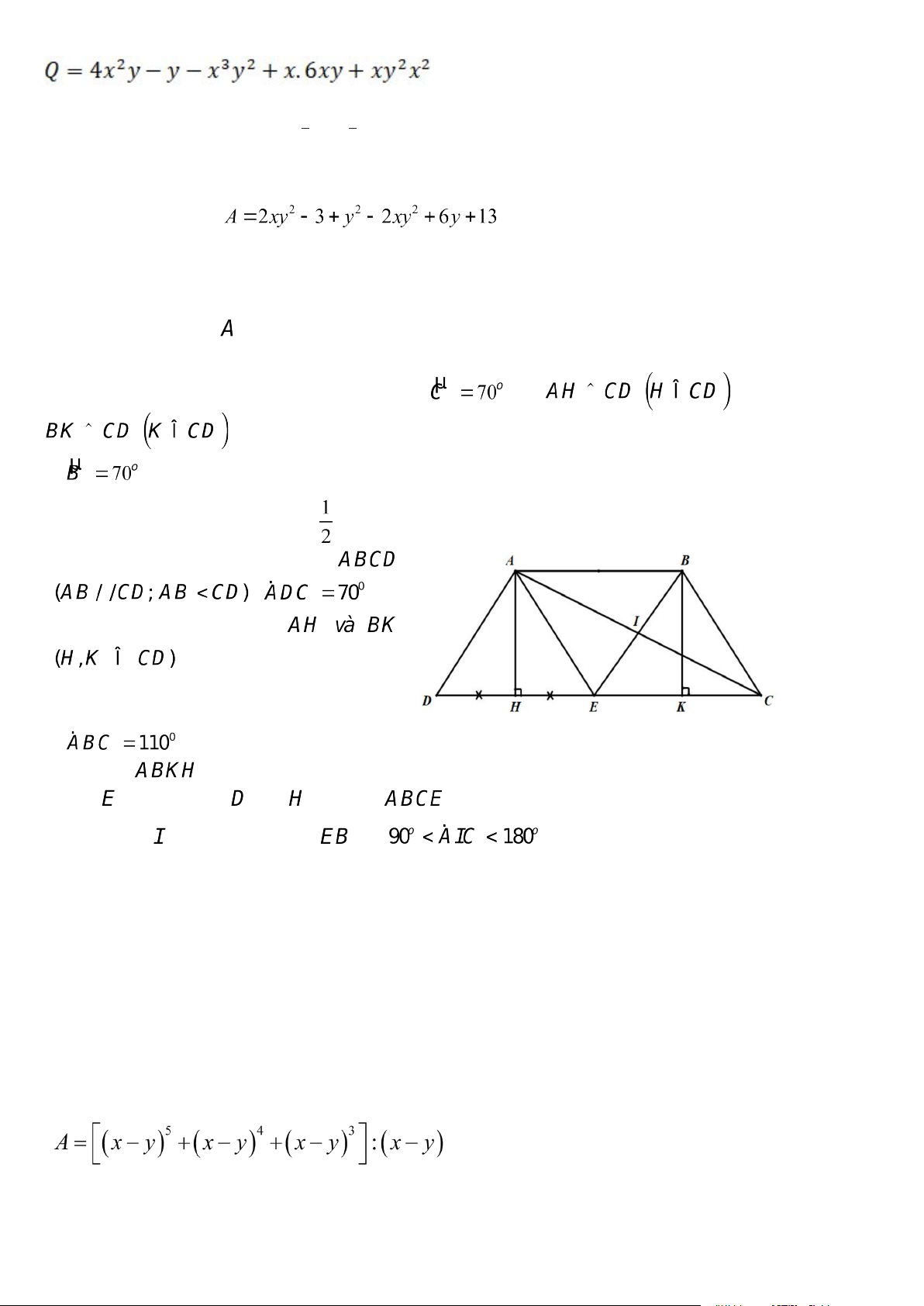
Câu 4. Cho hình thang cân ABCD (AB / CD); . Kẻ ;
. Gọi O là giao điểm của AK và BH. Khi đó: a)
b) Tứ giác ABKH là hình chữ nhật c) DH = KC d) AO = BK.
Câu 5: Cho hình thang cân , . Kẻ các đường cao . a) b) Tứ giác là hình vuông.
c) Gọi đối xứng với qua . Khi đó là hình bình hành.
d) Nếu điểm là trung điểm của thì .
Câu 6 . Cho hai hình bình hành MNBA và MNCB, ta có:
a) Ba điểm A,B,C thẳng hàng b) AB = CB
c) Để MNCA là một hình thang cân thì tam giác MAB phải là tam giác đều
d) Lấy điểm D để tứ giác MNDC là hình bình hành. Khi đó, để MNDA là một hình thang cân thì tam giác MAB là tam giác cân
Phần 3.Câu hỏi trắc nghiệm trả lời ngắn
Các câu từ 15 đến 18, hãy viết đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 1. Giá trị của biểu thức A tại x = 3; y = 4 là bao nhiêu?
Câu 2 . Viết biểu thức 4𝑥2 + 4𝑦2 − 8𝑥𝑦 dưới dạng bình phương của một tổng hoặc của một hiệu.
Câu 3 Một tứ giác có tổng bốn góc trong bằng bao nhiêu độ?
Câu 4 . Cho hình thang cân ABCD có AB / CD. Gọi M là giao điểm của AC và BD. Tam giác MCD là tam giác gì?
Câu 5. Kết quả rút gọn của biểu thức là bao nhiêu? Câu 6. Cho đa thức . Tìm giá trị của x khi ? Câu 7. Cho tứ giác , trong đó . Tổng bằng bao nhiêu độ?
Câu 8. Có bao nhiêu hình bình hành trong hình vẽ bên. Biết B. TỰ LUẬN
Bài 1 a) Xác định đa thức biết
b) Tính giá trị của biểu thức tại
Bài 2. Cho các đa thức a. Thu gọn các đa thức A
b)Tính giá trị của B tại
Bài 3: Thực hiện phép tính:
Bài 4: Thực hiện phép tính:
Bài 4: Khai triển các biểu thức: Bài 5: Tính nhanh:
Bài 6 : Sử dụng HĐT để tính nhanh giá trị các biểu thức: a) tại x = 15 b) tại c) tại
Bài 7 Rút gọn biểu thức sau : a) (x + 1)2 + (x - 1)2;
b) 3(x - y)(x + y) +2(x - y)2 + (x + y)2;:
c) 3(x - y)2 - 2(x + y)2 – ( x – y) ( x + y) ;
d) ( x - 2y) 2 – 2(x -1) ( x-3) + ( 2x + 3)2
e) ( x + 3)2 + 5 (x +3) ( x – 3) + ( x – 3)2
Bài 8 : Rút gọn biểu thức
a. (x + 3)2 + (x – 3)2 – 2(3 + x)(x – 3) b . x(2x2 – 3) – x2(5x + 1) + x2.
c . 2x(x – 2) – 5x(1 – x) – 7(x2 – 3)
Bài 9 . Tìm x biết : a) (2x + 1)2 - 4(x + 2)2 = 9;
b) (x + 2)2 - (x - 3)( x + 3) = 10;
c) 3(x - 2)2 + (2x – 3 )2 - 7(x + 1)(x - 1) = 16; Hình học
Bài 1: a)Tính các góc của hình thang cân ABCD (AB / CD), biết A = 1200 .
b)Tính các góc của hình bình hành MNPQ, biết 𝑁 = 45°.
Bài 2 :Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC. Trên
tia đối của tia IM lấy điểm K sao cho IK = IM.
a) Chứng minh tứ giác AKCM là hình chữ nhật.
b) Tứ giác AKMB là hình gì? Vì sao?
c) Tìm điều kiện của tam giác ABC để tứ giác AKCM là hình vuông.
Bài 3 : Cho tam giác ABC vuông tại A (AB < AC). Gọi I là trung điểm của cạnh BC. Qua I vẽ
IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a. Tứ giác AMIN là hình gì? Vì sao?
b.Trên tia đối của tia IM lấy điểm K sao cho I là trung điểm của MK, Chứng minh rằng : MC = BK
Bài 4: Cho tam giác ABC vuông tại A (AB < AC). Lấy điểm M là trung điểm của BC. Gọi D, E lần
lượt là chân các đường vuông hạ từ M đến AB và AC.
a) Chứng minh tứ giác ADME là hình chữ nhật.
b) Vẽ AH vuông góc với BC. Chứng minh tứ giác MHDE là hình thang cân
c) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.
Bài 5: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Từ M kẻ các đường thẳng vuông góc
với AB, AC lần lượt tại D và E.
a) Tứ giác ADME là hình gì? Vì sao?
b) Gọi O là trung điểm của MD. Chứng minh DE = BM và B, E, O thẳng hàng.
Bài 6: Cho vuông tại . Gọi là trung điểm của Trên tia đối của tia lấy điểm sao cho a) Tứ giác là hình gì ? b) Lấy điểm sao cho là trung điểm của . So sánh độ dài đoạn và
Bài 7: Cho tam giác ABC. Đường thẳng qua B song song với AC cắt đường thẳng qua C song song với AB ở D.
a) Chứng minh rằng tứ giác ABDC là hình bình hành.
b) Gọi M là trung điểm cạnh BC. Chứng minh rằng ba điểm A, M, D thẳng hàng.
Một số bài tập nâng cao
Bài 1: Chứng minh rằng với mọi thì a) b)
Bài 2. Tìm giá trị nhỏ nhất của các biểu thức sau 1) 2) 3) 4) 5) 6)
Bài 3. Tìm giá trị lớn nhất của các biểu thức sau 1) 2) 3) 4) 5) 6) Bài 4: Cho
. Tính giá trị của biểu thức Cho
. Tính giá trị của biểu thức Bài 5: Cho
. Tính giá trị của biểu thức
Bài 6: Chứng minh rằng nếu chia hết cho thì Bài 7: Cho đa thức ( là biến) .
Tính giá trị của biểu thức Khi thì . Khi thì Khi thì