Đề ôn tập số 14 - tham khảo học kỳ I Năm học: 2025 – 2026 Môn: Toán 8

ĐỀ ÔN TẬP SỐ 14 - THAM KHẢO HỌC KỲ I
NĂM HỌC: 2025 – 2026 MÔN: TOÁN 8
I. TRẮC NGHIỆM:
Câu 1. Biểu thức nào sau đây không phải là đa thức bậc 4? 3 A. 2 2x yz B. 4 3 2 x  x y C. 2 x y  xyzt D. 4 5 x  2 2
Câu 2. Biểu thức nào sau đây đồng dạng với đơn thức 3 2  x y ? 1 A. 2 x yz B. 3 2x yz C. 3 2  x z D. 3 3xy 3
Câu 3. Biểu thức nào sau đây không phải là phân thức? 3xy x x  y A. 2 x y  y B. C. D. 2z 2 x  y x 1
Câu 4. Với điều kiện nào của x thì phân thức có nghĩa? 2 (x  2)
A. x  2 . B. x  1. C. x  2 . D. x  2  . A C
Câu 5. Hai phân thức và bằng nhau nếu : B D A. . A C  . B D B. . A D  . B C C. . A B  . C D
D. A : D  B : C
Câu 6. Tổng số đo bốn góc của một tứ giác bằng: A. 900 . B. 1800. C. 2700. D. 3600.
Câu 7. Hình bình hành có hai đường chéo bằng nhau là:
A. Hình vuông. B. Hình chữ nhật. C. Hình thang. D. Hình thoi.
Câu 8. Trong các khẳng định sau, khẳng định nào đúng?
A. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.
B. Hình thoi có hai đường chéo vuông góc là hình vuông.
C. Hình thoi có một góc vuông là hình vuông.
D. Hình chữ nhật có một góc vuông là hình vuông. I. TỰ LUẬN
Câu 1. Thực hiện phép tính: a)  x  2 2 1  x ; x 3 6x f)   2 x  2 x  2 4  x 2 2 3
b)  x  2yx  2xy  4y  8y .  3 5  7 g)    
 x  2 x  2  2x 1 c) 2
(3x 1)  3x(4  3x) x 3 6  7x d)   2 x  2 x  2 x  4
e) (x – y)2 + 3x ( x – 2y)
Câu 2. Phân tích đa thức sau thành nhân tử: a) 2 2x y  6xy g) 2 2
2x y  4xy  8xy b) 2 x  6x  9 h) 2 2 x 6x y 9
c) x x  y 12x 12y m) 9x2 – 15xy. n) x2 +4x +4 – y2. d) 2
y  6 y  9 ; i) x3 – 3x – y3 + 3y. e) 3 3 64x  27 y ; f)*  2
x  x   2 3
1 x  3x  2  6 .
Câu 3.1. Để đảm bảo kì thi cuối HKI lớp 8 một cách khách quan nhà trường chia thành các
phòng. Lớp 8 có 105 học sinh được chia thành 5 phòng. Bảng thống kê số học sinh ở mỗi phòng như sau: Phòng Số học sinh 1 21 2 21 3 20 4 22 5 22
Theo em số liệu đã cho trong bảng thống kê trên có hợp lí không? Vì sao?
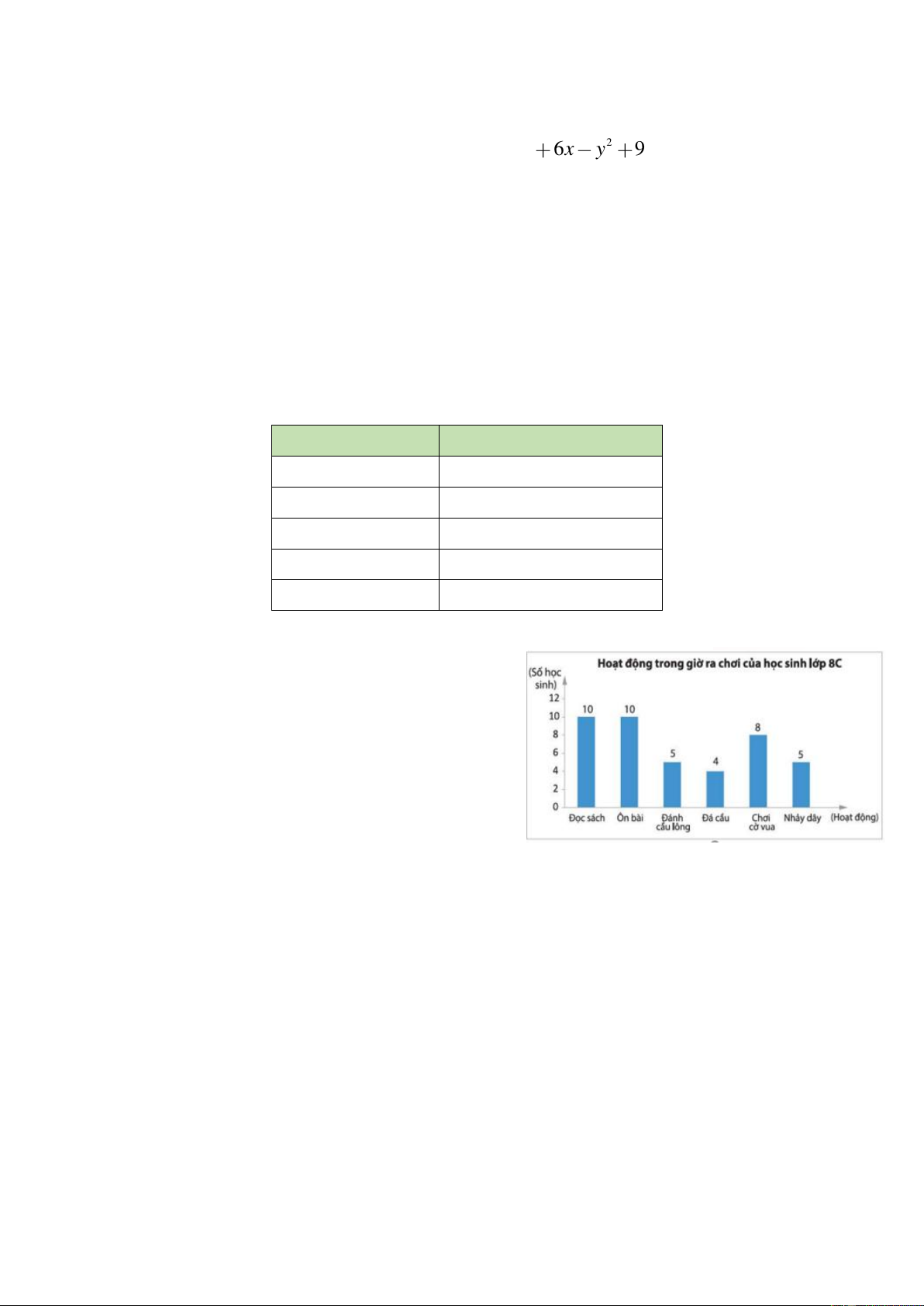
Bài 3.2. Hoạt động giờ ra chơi của các bạn lớp 8A được
biểu diễn trong biểu đồ sau (hình bên).
a) Lập bảng thống kê tương ứng với biểu đồ bên.
b) Hãy cho biết tỉ lệ các em đọc sách chiếm
bao nhiêu phần trăm (kết quả làm tròn đến hàng phần mười).
Câu 5.1. Cho  ABC vuông tại A, đường cao AH. Từ H kẻ HE vuông góc với AB, HF vuông
góc với AC (E thuộc AB; F thuộc AC).
a) Tứ giác AEHF là hình gì? Vì sao?
b) Vẽ điểm D đối xứng với A qua E. Chứng minh tứ giác DHFE là hình bình hành.
c) Vẽ điểm K đối xứng H qua E. Chứng minh tứ giác AHDK là hình thoi.
Bài 5.2. Cho tam giác ABC vuông tại A, đường trung tuyến AD. Từ D vẽ DE  AB, DF  AC ( .
a) Chứng minh tứ giác AEDF là hình chữ nhật.
b) Gọi H đối xứng với D qua E.Chứng minh tứ giác ADBH là hình thoi.
c) Gọi K đối xứng với D qua F. Chứng minh H, A, K thẳng hàng.
Bài 5.3. Cho ABC vuông tại A. Gọi AM là đường trung tuyến của ABC. Vẽ MD vuông
góc với AB tại D, ME vuông góc với AC tại E (D, E thuộc AB, AC)
a) Chứng minh: tứ giác ADME là hình chữ nhật
b) Gọi I là trung điểm của AM. Chứng minh: 3 điểm D, I, E thẳng hàng.
c) Chứng minh: tứ giác BDEM là hình bình hành
Câu 6.1* Cho x và y thỏa mãn: 2 2
x  4xy 13y  6y 1  0 .
Tính giá trị biểu thức B  2023x  2024y .
Câu 6.2* Cho a, b, c thỏa mãn abc = 2. Tính giá trị biểu thức: 2a b c A    . ab  2a  2 bc  b  2 ac  c 1
Câu 6.3* Cho x, y thỏa mãn: 2 2
5x  5y  8xy  2x  2y  2  0
Tính giá trị biểu thức: M  x  y2024  x  2025   y  2026 2 1
Câu 6.4* Tìm x 
để N đạt giá trị nguyên, biết: 9  N 2x  1 x 
Câu 6.5* Tìm x 
để M đạt giá trị nguyên, biết: 3 2  M x  1 ---HẾT---