ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
ĐỀ CƯƠNG KIỂM TRA HỌC KỲ
TRƯỜNG ĐẠI HỌC KHOA HỌC XÃ HỘI
Môn: LOGIC HỌC ĐẠI CƯƠNG VÀ NHÂN VĂN
CÂU 1. TRÌNH BÀY ĐỐI TƯỢNG VÀ Ý NGHĨA CỦA LOGIC HỌC?
1. Đối tượng của Logic học
- Logic học là khoa học nghiên cứu các hình thức, quy luật của tư duy trong quá trình xác
lập các giá trị chân lý của tư tưởng.
2. Ý nghĩa của Logic học Giúp con người:
- Thiết lập và sử dụng các khái niệm, phán đoán, suy luận một cách mạch lạc, hợp lý.
- Tự giác biết được lập luận đúng, sai, phát hiện được những lập luận ngụy biện của người khác.
- Có cơ sở phương pháp luận để tiếp cận và giải quyết vấn đề một cách hiệu quả nhất trong
nghiên cứu khoa học cũng như trong nghiệp vụ chuyên môn của thực tiễn cuộc sống.
CÂU 2. TRÌNH BÀY CÁC THAO TÁC ĐỊNH NGHĨA, PHÂN CHIA, MỞ RỘNG VÀ THU HẸP KHÁI NIỆM?
1. Định nghĩa khái niệm a) Định nghĩa
- Định nghĩa khái niệm là thao tác logic nhằm xác lập nội hàm và ngoại diên của khái niệm đó.
- Cấu trúc A ≡ B
Ví dụ: Danh từ (A) là từ dùng để chỉ tên người và vật (B).
- Mỗi định nghĩa thường có 2 phần: khái niệm được định nghĩa và khái niệm dùng để định
nghĩa. Giữa 2 phần được kết nối với nhau bởi liên từ “là”.
Ví dụ: Hình vuông là hình chữ nhật có 4 cạnh bằng nhau. Trong đó:
+ Khái niệm được định nghĩa: hình vuông.
+ Khái niệm dùng để định nghĩa: hình chữ nhật có 4 cạnh bằng nhau.
- Khi khái niệm dùng để định nghĩa đặt trước khái niệm được định nghĩa thì từ “là” được
thay bằng “được gọi là”.
Ví dụ: Hình chữ nhật có 4 cạnh bằng nhau được gọi là hình
vuông. b) Các loại định nghĩa
- Định nghĩa chính thức:
+ Định nghĩa thông qua loại và hạng.
Ví dụ: Cá là loài động vật có xương sống, sống ở nước, thở bằng mang, bơi bằng vây.
+ Định nghĩa thông qua nguồn gốc phát sinh.
Ví dụ: Tam giác là hình được tạo bởi 3 đoạn thẳng gấp khúc khép kín.
+ Định nghĩa thông qua quan hệ với cái đối lập.
Ví dụ: Vật chất là những gì tồn tại không phụ thuộc vào ý thức con người.
+ Định nghĩa thông qua chức năng.
Ví dụ: Bệnh viện là cơ sở khám, chữa bệnh.
+ Định nghĩa ngoại diên.
Ví dụ: Thành phố trực thuộc trung ương của Việt Nam là Hà Nội, Thành phố Hồ Chí Minh,
Hải Phòng, Đà Nẵng, Cần Thơ.
- Định nghĩa không chính thức:
+ Định nghĩa thông qua từ tương đương. Lê Trần Quang Khang lOMoAR cPSD| 41487872
Ví dụ: Tứ giác là hình có 4 góc. + Định nghĩa mô tả.
Ví dụ: Cọp là loài thú dữ ăn thịt, cùng họ với mèo, lông màu vàng, có vằn đen.
+ Định nghĩa so sánh.
Ví dụ: Tối như đêm ba mươi.
+ Định nghĩa trực quan (trỏ ra).
Ví dụ: Đây là bông hồng (Đưa bông hồng ra).
+ Định nghĩa duy danh.
Ví dụ: x là dấu nhân.
c) Các quy tắc định nghĩa khái niệm.
- Quy tắc 1: Định nghĩa phải cân đối, đầy đủ.
+ Tránh định nghĩa quá rộng.
+ Tránh định nghĩa quá hẹp.
- Quy tắc 2: Định nghĩa phải rõ ràng.
+ Tránh dùng từ mơ hồ.
+ Không dùng từ chưa biết để định nghĩa cho từ chưa biết khác.
- Quy tắc 3: Định nghĩa phải ngắn gọn.
+ Chỉ nêu ra vừa đủ những tính chất cơ bản của đối tượng.
+ Không nêu những thuộc tính mà tất yếu suy ra được từ những thuộc tính đã nêu.
- Quy tắc 4: Định nghĩa không được phủ định.
2. Phân chia khái niệm a) Định nghĩa
- Phân chia khái niệm là thao tác logic vạch ra các khái niệm cấp hạng nằm trong khái niệm
cấp loại được phân chia.
- Khái niệm đem phân chia (loại) gọi là khái niệm bị phân chia.
- Khái niệm được chỉ ra (hạng) gọi là khái niệm phân chia hay thành phần phân chia.
- Thuộc tính dùng để phân chia khái niệm gọi là cơ sở phân chia.
Ví dụ: Người gồm người da trắng, người da vàng, người da đen. Trong đó:
+ Khái niệm bị phân chia (loại): người
+ Khái niệm phân chia (hạng): người da trắng, người da vàng, người da đen.
+ Cơ sở phân chia: màu da.
b) Quy tắc phân chia khái niệm
- Quy tắc 1: Phân chia phải cân đối.
+ Tránh phân chia thiếu.
+ Tránh phân chia thừa.
- Quy tắc 2: Phân chia phải nhất quán 1 tiêu chí.
+ Phải xác định 1 tiêu chí nhất định.
+ Một phép phân chia chỉ được sử dụng 1 tiêu chí.
- Quy tắc 3: Phân chia phải liên tục và không vượt cấp.
+ Tránh phân chia khái niệm thành phần không đồng hạng.
+ Tránh bỏ qua bước trung gian.
- Quy tắc 4: Phân chia phải tránh trùng lắp. Lê Trần Quang Khang Trang 2
Khoa Lịch sử - HCMUSSH lOMoAR cPSD| 41487872
3. Mở rộng khái niệm
- Mở rộng khái niệm là thao tác logic chuyển từ khái niệm có ngoại diên hẹp, nội hàm sâu
sang khái niệm có ngoại diên rộng, nội hàm cạn.
- Giới hạn của thao tác mở rộng khái niệm là phạm trù.
Ví dụ: Người → Động vật → Sinh vật → Vật chất. 4. Thu hẹp khái niệm
- Thu hẹp khái niệm là thao tác logic chuyển từ khái niệm có ngoại diên rộng, nội hàm cạn
sang khái niệm có ngoại diên hẹp, nội hàm sâu
- Giới hạn của thao tác thu hẹp khái niệm là khái niệm đơn nhất.
Ví dụ: Số thực → Số hữu tỷ → Số tự nhiên → Số tự nhiên chẵn → Số 2.
CÂU 3. DÙNG SƠ ĐỒ THỂ HIỆN MỐI QUAN HỆ GIỮA CÁC KHÁI NIỆM?
1. Quan hệ đồng nhất
- Hai khái niệm đồng nhất là 2 khái niệm có cùng ngoại diên (ngoại diên của 2 khái niệm này cùng
phản ánh 1 đối tượng).
- Kí hiệu: A ≡ B
Ví dụ: Số chẵn (A) và số chia hết cho 2 (B) 2. Quan hệ bao hàm
Quan hệ bao hàm là quan hệ giữa 2 khái niệm mà ngoại diên của 2 khái niệm này chứa trong nó - ⊂
ngoại diên của khái niệm khác.
- Kí hiệu: B A (A bao hàm B hay B thuộc A)
Ví dụ: Cây (B) và thực vật (A) 3. Quan hệ giao nhau
- Hai khái niệm giao nhau là 2 khái niệm mà ngoại diên của chúng có 1 số đối tượng
chung. - Kí hiệu: A ∩ B (A giao với B)
Ví dụ: Đoàn viên (A) và sinh viên (B)
4. Quan hệ ngang hàng
- Quan hệ ngang hàng là quan hệ giữa các khái niệm hạng mà ngoại diên của chúng tách rời nhau và cùng lệ thuộc ngoại diên của k hái niệm loại.
- Kí hiệu: (A1 ∪ A2 ∪ A3 ... ∪ An) ⊂ A Lê Trần Quang Khang Trang 3
Khoa Lịch sử - HCMUSSH lOMoAR cPSD| 41487872
Ví dụ: Hà Nội (A1), Seoul (A2), Bắc Kinh (A3), Thành phố (A)
5. Quan hệ mâu thuẫn
- Quan hệ mâu thuẫn là quan hệ giữa các khái niệm có nội hàm không chỉ trái ngược mà còn loại trừ nhau và tổng∪ ngoại diên của chúng đúng bằng ngoại diên của 1 khái niệm khác. - Kí hiệu: A B = C
Ví dụ: Số chẵn (A) và số lẻ (B)
6. Quan hệ đối chọi
- Quan hệ đối chọi là quan hệ giữa các khái niệm mà nội hàm của chúng có những dấu hiệu trái ngược nhau nhưng tổng ngoại diên của chúng
bao giờ cũng nhỏ hơn ngoại diên của khái niệm loại chung của chúng∪. ⊂ - Kí hiệu: (A B) C
Ví dụ: Màu trắng (A) và màu đen (B)
CÂU 4. XÁC ĐỊNH GIÁ TRỊ CỦA PHÁN ĐOÁN. TỪ GIÁ TRỊ PHÁN ĐOÁN ĐÃ XÁC
ĐỊNH, CHO BIẾT NỘI DUNG VÀ GIÁ TRỊ CÁC PHÁN ĐOÁN CÒN LẠI TRONG HÌNH V UÔNG LOGIC?
- Phán đoán là hình thức của tư duy trừu tượng, khẳng định hay phủ định một tình trạng
xác định nào đó ở các sự vật và hiện tượng.
Ví dụ: Trái Đất quay xung quanh Mặt
Trời. Mọi kim loại đều dẫn điện.
- Phán đoán thuộc tính đơn là phán đoán chỉ có 1 mệnh đề, trong đó gồm 1 chủ từ, 1 hệ từ và 1 thuộc từ.
- Cấu trúc của phán đoán thuộc tính đơn có 4 thành phần:
+ Chủ từ S (chủ ngữ): từ nêu đối tượng mà phán đoán nói về.
+ Thuộc từ P (tân ngữ, vị ngữ, vị từ): từ nêu tính chất mà phán đoán khẳng định hoặc phủ
định về đối tượng.
+ Hệ từ (là, không là):∀ từ hoặc cấu∃ trúc câu nêu sự khẳng định hoặc phủ định của phán đoán.
+ Lượng từ (với mọi , tồn tại ): từ hoặc cấu trúc câu đặc trưng về lượng của phán đoán.
Ví dụ: Mọi sinh viên đều tham gia nghiên cứu khoa học. Trong đó:
+ Chủ từ S: sinh viên. Lê Trần Quang Khang Trang 4
Khoa Lịch sử - HCMUSSH lOMoAR cPSD| 41487872
+ Thuộc từ P: đều tham gia nghiên cứu khoa học. +
Hệ từ: là. ∀ + Lượng từ:
- Phân loại phán đoán thuộc tính đơn theo chất và lượng:
+ Phán đoán khẳng định toàn thể (phán đoán A) - SaP: Mọi S đều là P.
Ví dụ: Mọi kim loại đều dẫn điện.
+ Phán đoán khẳng định bộ phận (phán đoán I) - SiP: Có S là P.
Ví dụ: Một số sinh viên là đoàn viên.
+ Phán đoán phủ định toàn thể (phán đoán E) - SeP: Mọi S đều không là P.
Ví dụ: Tất cả cá đều không sống trên cạn.
+ Phán đoán phủ định bộ phận (phán đoán O) - SoP: Có S không là P.
Ví dụ: Một số sinh viên không học logic.
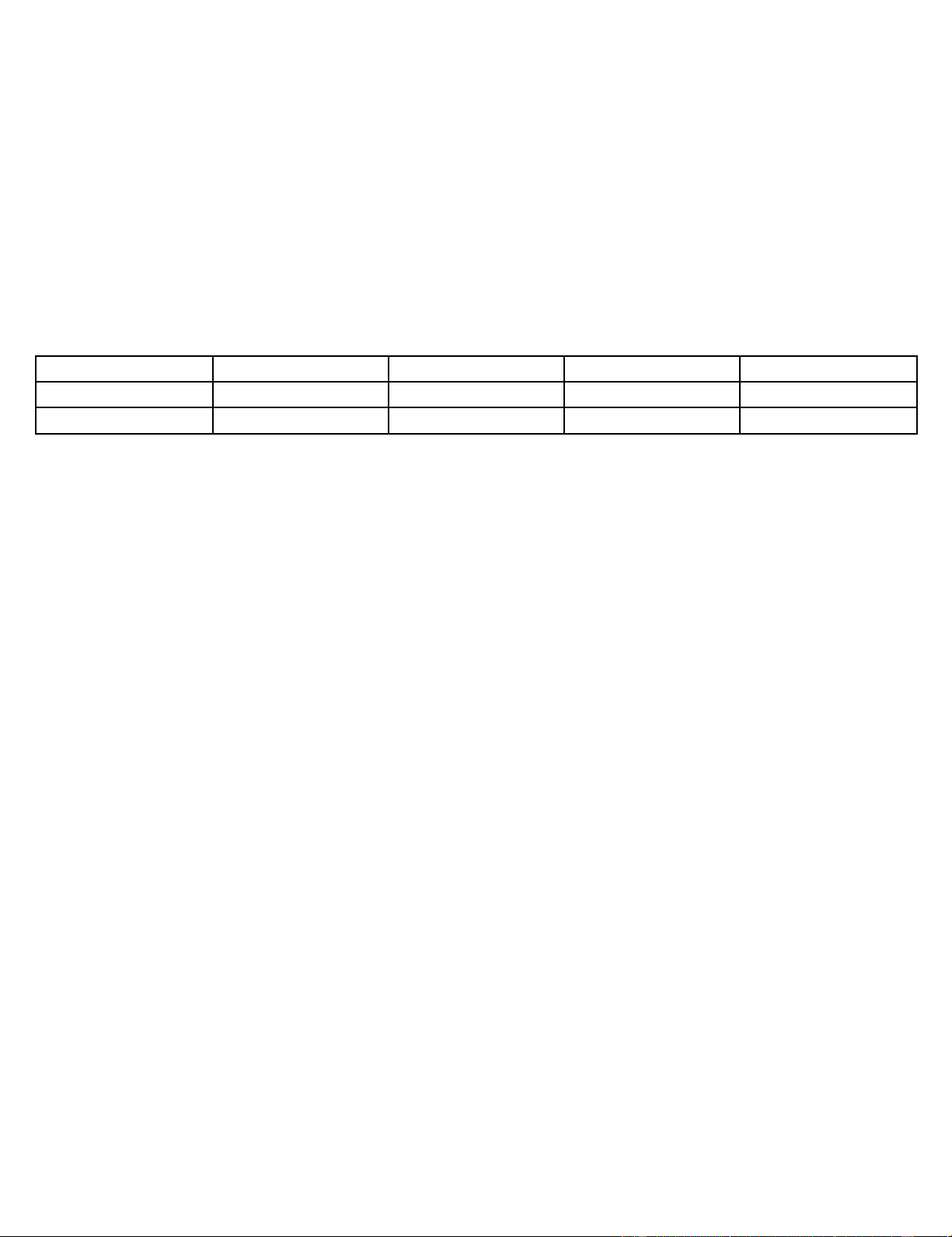
- Tính chu diên của chủ từ S, thuộc từ P trong phán đoán. Phán đoán A Phán đoán I Phán đoán E Phán đoán O Chủ từ S + - + - Thuộc từ P - - + + Lưu ý:
+ Trong phán đoán toàn thể (A, E): S luôn luôn chu diên (S+).
+ Trong phán đoán bộ phận (I, O): S luôn luôn không chu diên (S-).
+ Trong phán đoán A: P thường không chu diên (P ) trừ trường hợp ngoại diên S ≡ - ⊂ P thì P chu diên (P+).
+ Trong phán đoán I: P thường không chu diên (P-) trừ trường hợp ngoại diên P S thì P chu diên (P+).
+ Trong phán đoán phủ định (E, O): P luôn luôn chu diên (P+). - Hình vuông logic.
Ví dụ: Cho phán đoán “Cá sống dưới nước”.
Phán đoán trên là phán đoán gì? Đúng hay sai? Từ giá trị đã xác định, hãy cho biết nội
dung và giá trị của các phán đoán còn lại trong hình vuông logic? Giải
- Phán đoán “Cá sống dưới nước” là phán đoán khẳng định toàn thể (phán đoán A). Phán
đoán A là phán đoán đúng.
Ađ: Cá sống dưới nước.
- Nội dung và giá trị của các phán đoán còn lại trong hình vuông logic:
Es: Cá không sống dưới nước.
Iđ: Có loài cá sống dưới nước.
Os: Có loài cá không sống dưới nước. Lê Trần Quang Khang Trang 5
Khoa Lịch sử - HCMUSSH lOMoAR cPSD| 41487872
CÂU 5. VIẾT CÔNG THỨC PHÂN BIỆT ĐIỀU KIỆN CẦN, ĐIỀU KIỆN ĐỦ, ĐIỀU KIỆN CẦN VÀ ĐỦ? ⊃ B.
1. Điều kiện cần - Xét phán đoán ~A
~B, nếu không có A thì không có B, khi đó A được gọi là điều kiện cần của
- Công thức: ~A (điều kiện cần) ~B
Ví dụ: Nếu không tốt nghiệp đại học loại giỏi (A) thì không được học chuyển tiếp bậc cao học (B). ⊃
2. Điều kiện đủ
- Điều kiện đủ là điều kiện có nó thì đủ để biết có kết quả. Xét phán đoán A ⊃ B, khi có A thì B
có, khi đó A được gọi là điều kiện đủ của B.
- Công thức: A (điều kiện đủ) B (kết quả)
thì em được thư ởng (B).
Ví dụ: Nếu em học giỏi (A) ⊃
3. Điều kiện cần và đủ
- Điều kiện cần và đủ là điều kiện duy nhất có kết quả. - Công thức: (B A) (~B ~A) ⊃ ∧ ⊃ (A B) (~A ~B)
chia hết cho 3 khi và chỉ khi tổng các chữ số của nó chia hết cho 3.
Ví dụ: Một số ⊃ ∧ ⊃
CÂU 6. TAM ĐOẠN LUẬN ĐƠN 1. Định nghĩa
Tam đoạn luận đơn là hình thức suy luận diễn dịch gián tiếp, từ 2 phán đoán đơn làm tiền
đề, được sắp xếp theo các quy tắc nhất định để rút ra một phán đoán mới. 2. Cấu trúc
Mỗi tam đoạn luận có: - 3 thuật ngữ: + Tiểu từ S. + Đại từ P. + Trung từ M. - 3 mệnh đề:
+ Đại tiền đề: P & M.
+ Tiểu tiền đề: S & M.
+ Kết luận: S - P
Ví dụ: Mọi khoa học đều có phương pháp của mình.
Logic học là khoa học.
Vậy, Logic học có phương pháp của mình. Trong đó:
+ Tiểu từ S: Logic học.
+ Trung từ M: khoa học.
+ Đại từ P: có phương pháp của mình.
+ Đại tiền đề: Mọi khoa học đều có phương pháp của mình.
+ Tiểu tiền đề: Logic học là khoa học.
+ Kết luận: Vậy, Logic học có phương pháp của mình.
3. Hình và kiểu của tam đoạn luận đơn Lê Trần Quang Khang Trang 6
Khoa Lịch sử - HCMUSSH lOMoAR cPSD| 41487872
TRÌNH BÀY CÁC PHƯƠNG PHÁP STUART MILL VÀ CHO VÍ DỤ MINH HỌA?
1. Phương pháp tương đồng
Nếu hai hay nhiều trường hợp của hiện tượng nghiên cứu chỉ có một sự kiện chung thì sự
kiện chung đó có thể là nguyên nhân của hiện tượng ấy.
2. Phương pháp khác biệt
Nếu hiện tượng xuất hiện và không xuất hiện trong những trường hợp khác nhau có những
điều kiện như nhau, trừ điều kiện, thì điều kiện bị loại trừ đó có thể là nguyên nhân (hay
một phần nguyên nhân) của hiện tượng ấy.
3. Phương pháp đồng biến
Nếu một hiện tượng nào đó xuất hiện hay biến đổi thì một hiện tượng khác cũng xuất hiện
hay biến đổi tương ứng – thì hiện tượng thứ nhất là nguyên nhân của hiện tượng thứ hai.
4. Phương pháp thặng dư
Nếu biết những điều kiện cần thiết của hiện tượng nghiên cứu, trừ một điều kiện không là
nguyên nhân của nó thì điều kiện bị loại trừ có thể là nguyên nhân của hiện tượng còn lại.
* Nhận xét về suy luận quy nạp khoa
học - Cho kết luận khái quát và mới.
- Giúp hình thành giả thuyết khoa học.
- Tuy nhiên kết luận chỉ có tính xác suất.
CHỨNG MINH LÀ GÌ? NÊU CẤU TRÚC VÀ QUY TẮC CHỨNG MINH? CÁC
PHƯƠNG PHÁP CHỨNG MINH? CHO VÍ DỤ MINH HỌA? 1. Định nghĩa
Chứng minh là thao tác logic sử dụng những tri thức đã biết, những chứng cứ đã được kiểm
tra để làm rõ tính đúng đắn của một mệnh đề. 2. Cấu trúc
- Luận đề: chứng minh cái gì?
- Luận cứ: chứng minh dựa trên cơ sở nào?
- Luận chứng: chứng minh bằng phương pháp nào? 3. Quy tắc
- Quy tắc 1: Luận đề phải rõ ràng, nhất quán và khả chứng.
- Quy tắc 2: Luận cứ phải chân thực, có giá trị logic, độc lập với luận đề và làm sáng tỏ luận đề.
- Quy tắc 3: Luận chứng phải hợp logic.
4. Các phương pháp chứng minh
- Chứng minh trực tiếp: là phép chứng minh trong đó từ tính chân thực của các luận cứ rút
ra tính chân thực của luận đề mà không dùng đến phản luận đề.
Ví dụ: Để chứng minh một kẻ nào đó là thủ phạm trong một vụ án, người ta dựa vào các
dấu vết tin cậy của kẻ đó để lại tại hiện trường gây án.
- Chứng minh gián tiếp: là phép chứng minh trong đó từ tính chân thực của các luận cứ rút
ra tính giả dối của phản luận đề, rồi từ đó rút ra tính chân thực của luận đề.
Có hai loại chứng minh gián tiếp:
+ Chứng minh phản chứng: vạch ra tính giả dối, sai lầm của phản đề.
Ví dụ: Công tác quy hoạch đất đai không ổn định khiến cuộc sống người dân bị xáo trộn.
Do đó, chính quyền địa phương cần phải sớm quy hoạch đất đai ổn định.
+ Chứng minh loại trừ: vạch ra tính giả dối, sai lầm của tất cả các thành phần trong phán
đoán lựa chọn, trừ luận đề. Lê Trần Quang Khang Trang 7
Khoa Lịch sử - HCMUSSH lOMoAR cPSD| 41487872
Ví dụ: Ta đang ủi quần áo thì thấy bàn ủi không có điện vào. Kiểm tra thấy không phải do
điện bị cắt, không phải ổ cắm điện bị lỏng, cũng không phải do cầu chì bị đứt. Vậy thì phải
có một bộ phận nào đó của bàn ủi bị hỏng.
NGỤY BIỆN LÀ GÌ? TRÌNH BÀY KHÁI QUÁT CÁC LOẠI NGỤY BIỆN VÀ PHƯƠNG
PHÁP BÁC BỎ? CHO VÍ DỤ MINH HỌA? 1. Định nghĩa
Ngụy biện là sự cố ý vi phạm các quy tắc trong suy luận nhằm mục đích đánh lạc hướng
làm cho người khác nhầm tưởng.
2. Các loại ngụy biện
- Căn cứ vào cấu trúc của phép chứng minh
+ Ngụy biện liên quan đến luận đề.
+ Ngụy biện liên quan đến luận cứ.
+ Ngụy biện liên quan đến luận chứng.
- Căn cứ vào các thủ pháp: dựa vào uy tín cá nhân, đám đông, dư luận, sức mạnh, đánh vào
tình cảm, đánh tráo luận đề, ngẫu nhiên, đen - trắng, nhân quả sai, sự kém cỏi, lập luận
vòng quanh, khái quát hóa vội vã, câu hỏi phức hợp, sử dụng những phương pháp suy luận
có tính xác suất, diễn đạt mập mờ.
3. Phương pháp bác bỏ ngụy biện
- Phương pháp chung bác bỏ ngụy biện là làm ngược lại những thủ pháp mà nhà ngụy biện sử dụng.
Ví dụ: nhà ngụy biện hành văn mập mờ thì ta đòi hỏi phải hành văn rõ ràng, nhà ngụy biện
đánh tráo luận đề, đánh tráo khái niệm thì ta đòi hỏi phải xác định lại.
- Nghiên cứu thật nhiều các dạng ngụy biện và các ví dụ ngụy biện, để khi gặp ngụy biện có
thể nhận ra chúng và bác bỏ.
- Nói chung, nắm được các quy tắc logic thì ta dễ dàng vạch ra được sự ngụy biện trong suy luận.
* Phương pháp bác bỏ một mệnh đề
- Bác bỏ bằng cách chứng minh mệnh đề sai.
- Bác bỏ bằng cách chỉ ra rằng lập luận đưa đến (tức là phép chứng minh) mệnh đề đó thiếu cơ sở. Lê Trần Quang Khang Trang 8
Khoa Lịch sử - HCMUSSH