Đề cương môn đại số tuyến tính- Trường Đại học bách khoa - Đại học đà nẵng.

ĐẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
🙥🞗 🞗 🟔🞗 🞗 🙧
BÀI TẬP LỚN HỌC PHẦN ĐẠI SỐ TUYẾN TÍNH ĐỀ TÀI: MÃ HAMMING (7,4)
LỚP L04 - NHÓM 10 – HK 241
Giảng viên hướng dẫn: TS. Nguyễn Xuân Mỹ
Sinh viên thực hiện
Mã số sinh viên Điểm số Chữ ký Phan Anh Khôi 2411717 Phan Duy Đan 2410643 Phan Phú Trọng 2413684 Phan Thái Nhân 2412434 Phan Thị Như Quỳnh 2412982 Phan Trần Bảo Long 2411936 Phan Văn Quyết 2412954 Tạ Thành Khang 2411474 Tô Hoài Anh 2410145 1 MỤC LỤC
LỜI MỞ ĐẦU ............................................................................................................ 3
PHẦN 1: YÊU CẦU ................................................................................................... 4
PHẦN 2: GIỚI THIỆU MÃ HAMMING ................................................................... 5
1. Thế nào là mã Hamming? ................................................................................. 5
2. Cơ sở lý thuyết của mã Hamming .................................................................... 5
2.1 Dữ liệu và bit kiểm tra ................................................................................ 5
2.2 Số bit kiểm tra và dữ liệu ............................................................................ 6
2.3 Đặc điểm cơ bản ......................................................................................... 6
2.4 Phương pháp kiểm tra và sửa lỗi ................................................................. 7
2.5 Ví dụ mã Hamming: mã Hamming (7,4) .................................................... 7
3. Ứng dụng của mã Hamming ............................................................................. 8
PHẦN 3: CƠ SỞ LÝ THUYẾT CỦA MÃ HAMMING (7,4) VÀ GIẢI THÍCH MA
TRẬN TẠO MÃ VÀ MA TRẬN KIỂM TRA ........................................................... 9
1. Mã Hamming (7,4) ......................................................................................... 10
2. Ma trận tạo mã ................................................................................................ 10
2.1 Thế nào là ma trận tạo mã? ........................................................................ 10
2.2 Cách sử dụng ma trận tạo mã ..................................................................... 11
3. Ma trận kiểm tra .............................................................................................. 11
3.1 Thế nào là ma trận kiểm tra? ..................................................................... 11
3.2 Cách sử dụng ma trận kiểm tra .................................................................. 12
4. Mã Hamming bổ sung để kiểm tra trường hợp 2 lỗi ...................................... 12
4.1 Mã Hamming bổ sung ............................................................................... 12
4.2 Mã Hamming bổ sung để kiểm tra trường hợp 2 lỗi ................................ 13
PHẦN 4: CÁCH THIẾT LẬP MÃ HAMMING (7,4) .............................................. 13
1. Tạo mã Hamming (7,4) .................................................................................. 13
2. Kiểm tra, tìm lỗi sai, cách sửa lỗi .................................................................... 14
PHẦN 5: CHƯƠNG TRÌNH MATLAB .................................................................. 15
1. Tổng quan về Matlab ...................................................................................... 15
2. Các lệnh cơ bản .............................................................................................. 15
3. Đoạn code về mã Hamming (7,4) ................................................................... 16
TÀI LIỆU THAM KHẢO ........................................................................................ 18 2 LỜI MỞ ĐẦU
Trong các hệ thống kỹ thuật số, dữ liệu được truyền qua các kênh giao tiếp thường
xuyên đối diện với nguy cơ bị hỏng do nhiễu bên ngoài và các yếu tố vật lý khác.
Khi dữ liệu nhận được không khớp với dữ liệu ban đầu, nó sẽ bị coi là 'lỗi'. Dữ liệu
trong hệ thống kỹ thuật số thường được mã hóa dưới dạng các bit (0 và 1), và khi
một bit bị thay đổi, chẳng hạn từ '1' thành '0' hoặc ngược lại, thì đó được gọi là lỗi
bit. Những lỗi bit này có thể dẫn đến việc mất mát hoặc sai lệch dữ liệu quan trọng,
gây ra các hậu quả nghiêm trọng, đặc biệt trong các ứng dụng yêu cầu tính chính xác cao.
Có nhiều loại lỗi có thể xảy ra trong hệ thống truyền thông, bao gồm lỗi bit đơn, lỗi
bit kép, hay lỗi trong một nhóm các bit liên tiếp (lỗi cụm). Để giải quyết vấn đề này,
các kỹ thuật mã hóa và sửa lỗi ra đời, giúp phát hiện và sửa chữa những lỗi này. Một
trong những phương pháp mã hóa đơn giản nhưng rất hiệu quả là mã Hamming,
trong đó mã Hamming (7,4) là một trong các dạng cơ bản. Mã Hamming (7,4) có
khả năng phát hiện và sửa chữa lỗi bit đơn, giúp duy trì tính toàn vẹn của dữ liệu
trong quá trình truyền tải.
Ngày nay, với sự phát triển của công nghệ và ứng dụng của toán học vào các bài
toán xử lý số, việc sử dụng phần mềm để giải quyết các vấn đề này đã trở nên dễ
dàng và phổ biến. Một trong những phần mềm được sử dụng rộng rãi là MATLAB,
môi trường tính toán mạnh mẽ hỗ trợ lập trình và giải quyết các bài toán toán học
phức tạp. Bài báo cáo này sẽ trình bày phương pháp mã hóa và giải mã dữ liệu bằng
mã Hamming (7,4), dựa trên các cơ sở lý thuyết và việc triển khai thực tế thông qua phần mềm MATLAB.
Trong quá trình thực hiện đề tài, nhóm chúng em nhận thức rằng kiến thức của mình
còn hạn chế và không thể tránh khỏi những thiếu sót trong quá trình tìm hiểu, triển
khai và trình bày. Vì vậy, rất mong nhận được sự đóng góp và góp ý từ các thầy cô
để đề tài có thể hoàn thiện và mang lại giá trị thực tiễn hơn. 3 PHẦN 1: YÊU CẦU 1. Yêu cầu.
Có kiến thức cơ bản về ma trận, mã Hamming và biết sử dụng các hàm, câu lệnh
trong matlab để xử lí vấn đề, các ví dụ được nêu ra. 2. Điều kiện.
Nêu ra được các ví dụ về sử dụng mã Hamming, chương trình matlab để giải các ví
dụ và chạy thành công đoạn mã sửa lỗi của mã Hamming.
3. Hướng giải quyết vấn đề.
- Nêu cơ sở lý thuyết của mã Hamming (7,4); ma trận tạo mã và ma trận kiểm tra.
- Nêu cơ sở lý thuyết giải thích ma trận tạo mã và ma trận kiểm tra.
(Thêm: tham khảo mã Hamming bổ sung để kiểm tra trường hợp 2 lỗi)
- Cho một đoạn mã. Nêu rõ cách tạo mã và kiểm tra một mã có bị lỗi hay không; cách sửa lỗi.
- Sản phẩm là phần mềm mô phỏng quá trình:
Một đoạn mã đi vào (một chuỗi ký tự) - mã hoá thành chuỗi nhị phân - gây nhiễu -
phát hiện lỗi - sửa lỗi - xuất ra chuỗi ký tự. 4
PHẦN 2: GIỚI THIỆU MÃ HAMMING
1. Thế nào là mã Hamming ?
Trong viễn thông (telecommunication), mã Hamming là một mã sửa lỗi tuyến tính
(linear error-correcting code), được đặt tên theo tên của người phát minh ra nó, Richard Hamming (1915-1998)
Mã Hamming hoạt động bằng cách sử dụng các bit kiểm tra (hoặc parity bits) được
chèn vào trong dãy bit dữ liệu để có thể phát hiện và sửa chữa lỗi. Một trong những
đặc điểm của mã Hamming là khả năng phát hiện lỗi đơn và sửa chữa lỗi đơn trong
khi chỉ thêm một số bit kiểm tra vào thông điệp gốc.
2. Cơ sở lý thuyết của mã Hamming.
2.1 Dữ liệu và bit kiểm tra.
2.1.1 Cấu trúc của mã Hamming.
Khi mã hóa một chuỗi dữ liệu bằng mã Hamming, các bit kiểm tra được chèn vào
các vị trí có chỉ số là các số lũy thừa của 2 (tức là các vị trí 1, 2, 4, 8,...). Các bit dữ
liệu được đặt ở các vị trí còn lại.
Mã Hamming sử dụng các bit kiểm tra (parity bits) được chèn vào các vị trí đặc biệt
trong chuỗi dữ liệu. Số lượng bit kiểm tra r được xác định bằng công thức:
2𝑟 ≥ m + r + 1 Trong đó:
m: số lượng bit dữ liệu.
r: số lượng bit kiểm tra.
m + r: tổng số bit trong mã Hamming, bao gồm cả số bit kiểm tra và bit dữ liệu.
2.1.2 Số bit kiểm tra và dữ liệu.
2.1.2.1 Các bit kiểm tra.
Mỗi bit kiểm tra pk được tính sao cho đảm bảo số bit 1 trong một nhóm bit xác định
phải chẵn (hoặc lẻ, tùy thuộc vào quy ước). Cụ thể:
Bit kiểm tra ở vị trí 1 (p1) sẽ kiểm tra các bit có chỉ số lẻ (1, 3, 5, 7, ...). 5
Bit kiểm tra ở vị trí 2 (p ) sẽ kiểm 2
tra các bit có chỉ số dạng 2, 3, 6, 7, ... (tức là các
chỉ số có bit thứ 2 là 1 trong mã nhị phân).
Bit kiểm tra ở vị trí 4 (p3) sẽ kiểm tra các bit có chỉ số 4, 5, 6, 7, ...
Các bit kiểm tra được tính toán sao cho tổng số bit 1 trong mỗi nhóm mà nó kiểm
tra phải chẵn. Nếu có lỗi trong quá trình truyền, các bit kiểm tra sẽ phát hiện và giúp
xác định vị trí của bit bị lỗi.
2.1.2.2 Các bit dữ liệu:
Các bit dữ liệu sẽ được chèn vào những vị trí không phải là lũy thừa của 2 (tức là
không phải các vị trí 1, 2, 4, 8, 16, ...), trong khi các bit kiểm tra sẽ được đặt ở các
vị trí có chỉ số là các số lũy thừa của 2 (như 1, 2, 4, 8, ...). Ký hiệu: Dk Ví dụ: Vị trí bit 1 2 3 4 5 6 7 Số vị trí 0001 0010 0011 0100 0101 0110 0111 Bit dữ liệu D1 D2 D3 D4 Bit kiểm tra p1 p2 p3 2.2 Đặc điểm cơ bản.
2.2.2 Khả năng phát hiện và sửa lỗi đơn (lỗi 1 bit).
Mã Hamming có khả năng phát hiện một lỗi đơn (single-bit error) trong quá trình
truyền tải. Mã Hamming không chỉ phát hiện mà còn có thể sửa lỗi đơn (có thể sửa
một bit bị lỗi trong dữ liệu). Nhưng mã Hamming không thể sửa được lỗi khi có hai
bit bị lỗi đồng thời (lỗi kép), nhưng có thể phát hiện lỗi kép.
2.2.3 Sử dụng các bit kiểm tra.
Các bit kiểm tra được chèn vào dãy dữ liệu để đảm bảo tính toàn vẹn của thông tin.
Số lượng bit kiểm tra cần thiết phụ thuộc vào số bit dữ liệu và được tính toán theo công thức: 2𝑟 − 1 ≥ 𝑚 + 𝑟.
2.2.4 Xác định lỗi bằng các bit kiểm tra. 6
Mỗi bit kiểm tra chịu trách nhiệm kiểm tra tính chẵn lẻ của một nhóm bit trong mã.
Khi một bit bị lỗi, các bit kiểm tra sẽ tạo thành một số nhị phân xác định vị trí của
bit lỗi đó trong dãy mã.
2.2.5 Cơ chế kiểm tra và sửa lỗi đơn giản.
Mã Hamming có một quy trình kiểm tra và sửa lỗi đơn giản, dễ thực hiện. Nếu tìm
thấy lỗi, hệ thống sẽ xác định vị trí của lỗi đó và đảo ngược bit lỗi để khắc phục lại dữ liệu ban đầu.
2.2.6 Hiệu quả mã hoá.
Mã Hamming là một dạng mã sửa lỗi có hiệu quả cao vì nó sử dụng ít bit kiểm tra
hơn so với nhiều mã sửa lỗi khác cho cùng mục đích. Do đó giảm thiểu chi phí lưu
trữ và băng thông khi truyền dữ liệu.
2.3 Phương pháp kiểm tra và sửa lỗi.
2.3.1 Nhận dữ liệu và kiểm tra các bit kiểm tra.
Khi nhận một chuỗi bit của mã Hamming, dùng các bit kiểm tra để phát hiện lỗi.
Các bit kiểm tra được tính toán dựa trên dữ liệu nhận được và so sánh và so sánh các bit kiểm tra ban đầu
2.3.2 Xác định vị trí lỗi.
Mỗi bit kiểm tra trong mã Hamming kiểm tra tính chẵn lẻ của một nhóm bit trong
mã. Khi các bit kiểm tra không khớp với dự liệu dự kiến, ta xác định vị trí của lỗi
dựa vào tổ hợp của các bit kiểm tra sai:
Mỗi bit kiểm tra mang giá trị 0 (không lỗi) hoặc 1 (lỗi)
Số nhị phân tạo thành từ các bit kiểm trac ho biết vị trí của bit sai
Ví dụ: Nếu tất cả các bit kiểm tra đều đúng 0, tức là không lỗi.
Nếu các bit kiểm tra cho kết quả 1 ở các vị trí tạo thành một số nhị phân khác
0, số đó chính là vị trí của bit lỗi trong dãy mã.
2.4 Ví dụ mã Hamming: mã Hamming (7,4)
Giả sử cho dữ liệu “1101”
Bước 1: Tính số bit kiểm tra.
Với m = 4 (số bit dữ liệu), ta áp dụng bất đẳng thức để tìm số bit kiểm tra: 2𝑟 − 1 ≥ 𝑚 + 𝑟
r = 3 thoả mãn (7 ≥ 7) 7
Vậy cần 3 bit kiểm tra cho 4 bit dữ liệu.
Bước 2: Đặt các bit dữ liệu và bit kiểm tra vào vị trí thích hợp.
Gọi các bit kiểm tra được đặt ở vị trí luỹ thừa 2 lần lượt: p1, p2, p3 (ở vị trí 1, 2, 4)
Gọi các bit dữ liệu lần lượt: D1, D2, D3, D4 (ở vị trí 3, 5, 6, 7) Vị trí bit 1 2 3 4 5 6 7 Số vị trí 0001 0010 0011 0100 0101 0110 0111 Bit dữ liệu 1 1 0 1 Bit kiểm tra ? ? ?
Bước 3: Tính các bit kiểm tra.
Các bit kiểm tra p1, p2, p3 được tính theo nguyên tắc chẵn lẻ sao cho mỗi nhóm bit
mà chúng kiểm tra phải có tính tổng chẵn (hoặc lẻ) tuỳ theo mã hoá. Tính p1:
p1 sẽ kiểm tra p1, D1, D2, D4.
Các bit ở vị trí này là p1, 1, 1, 1.
Tổng là: 1 + 1 + 1 = 3 (lẻ), nên p1 = 1. Tính p2:
p2 sẽ kiểm tra p2, D1, D3, D4.
Các bit ở vị trí này là 1, 0, 1.
Tổng là: 1 + 0 + 1 = 2 (chẵn), nên p2 = 0. Tính p3:
p3 sẽ kiểm tra p3, D2, D3, D4.
Các bit ở vị trí này là: 1, 0, 1.
Tổng là: 1 + 0 + 1 = 2 (chẵn), nên p3 = 0.
Bước 4: Hoàn thành mã Hamming. Vị trí bit 1 2 3 4 5 6 7 Số vị trí 0001 0010 0011 0100 0101 0110 0111 Bit dữ liệu 1 1 0 1 Bit kiểm tra 1 0 0
 Vậy mã Hamming cho dãy “1101” là “1010101”.
3. Ứng dụng của mã Hamming. 8
Mã Hamming được dùng rộng rãi trong nhiều lĩnh vực, đặc biệt là trong các hệ thống
truyền thông và lưu trữ dự liệu, nhờ khả năng phát hiện và sửa lỗi 1 bit. Dưới đây là
một số ứng dụng phổ biến của mã Hamming.
3.1 Bộ nhớ máy tính (ECC RAM).
ECC (Error-Correcting Code) RAM sử dụng mã Hamming để phát hiện và sửa lỗi
các bit dữ liệu. Điều này đảm bảo dữ liệu lưu trữ trong bộ nhớ chính xác, giảm thiểu
các lỗi xảy ra trong quá trình lưu trữ và truy xuất, đặc biệt quan trọng trong các hệ
thống máy chủ và các ứng dụng quan trọng đòi hỏi tính toàn vẹn dữ liệu cao
3.2 Truyền thông dữ liệu.
Trong các hệ thống truyền thông như mạng máy tính, truyền dữ liệu qua vệ tinh, mã
Hamming giúp phát triển và sửa lỗi đơn bit, đảm bảo dữ liệu được truyền chính xác.
Điều này đặc biệt hữu ích trong các môi trường có tỷ lệ nhiễu thấp nhưng vẫn có
nguy cơ gặp lỗi trong quá trình truyền tải. VD: truyền dữ liệu qua mạng LAN hoặc Wifi
3.3 Hệ thống viễn thông.
Các hệ thống viễn thông như điện thoại di động, truyền hình vệ tinh, và hệ thống
truyền phát qua cap sử dụng mã Hamming để kiểm tra và sửa lỗi trong quá trình
truyền tín hiểu. Điều này giúp cải thiện chất lượng dịch vụ và giảm tỷ lệ mất tín hiệu
hoặc méo tín hiệu do nhiễu 3.4 Lưu trữ dữ liệu.
Mã Hamming được sử dụng trong các thiết bị lưu trữ như ổ cứn (HDD), ổ đĩa quang
(CD, DVD), và ổ lưu trữ thể rắn (SSD) để phát hiện và sửa lỗi một bit trong quá
trình đọc và ghi dữ liệu. Điều này đảm bảo dữ liệu được dữ liệu được lưu trữ an toàn
và có thể được khôi phục chính xác ngay cả khi có lỗi nhỏ xảy ra trong quá trình sử dụng 3.5 Các thiết bị mạng.
Trong các thiết bị chuyển mạch và định tuyến mạng, mã Hamming được dung để
đảm bảo các gói dữ liệu truyền đi không bị lỗi. Các gói dữ liệu sẽ được mã hoá và
kiểm tra trước khi truyền tải, giúp phát hiện lỗi sớm và giảm thiểu khả năng lỗi lan rộng qua các nút mạng
3.6 Giao tiếp giữa vi xử lý và các thiết bị ngoại vi.
Mã Hamming được dung để kiểm tra tính toàn vẹn dữ liệu trong giao tiếp giữa vi xử
lý và các thiết bị ngoại vi (như cảm biến, bộ điều khiển) trong các hệ thống nhúng 9
và thiết bị IoT. Việc này đảm bảo rằng dữ liệu được truyền giữa các thiết bị là chính
xác, tránh các lỗi không mong muốn có thể gây ảnh hưởng đến quá trình điều khiển
3.7 Hệ thống truyền hình và phát thanh.
Trong các hệ thống truyền hình kỹ thuật số và phát thanh, mã Hamming giúp phát
hiện và sửa lỗi khi truyền tải các tín hiệu âm thanh và hình ảnh, đảm bảo chất lượng
tín hiệu nhận được là tốt nhất có thể, ngay cả khi có những nhiễu nhỏ trong quá trình truyền
3.8 Truyền tải dữ liệu trong không gian.
Trong các nhiệm vụ không gian, mã Hamming được sử dụng để truyền tải dữ liệu
giữa các vệ tinh hoặc tàu vũ trụ và các trạm mặt đất. Dữ liệu truyền trong không gian
có thể bị ảnh hưởng bởi nhiễu từ môi trường ngoài vũ trụ, vì vậy mã Hamming được
sử dụng để sửa lỗi và duy trì tính toàn vẹn dữ liệu.
PHẦN 3: CƠ SỞ LÝ THUYẾT CỦA MÃ HAMMING (7,4) VÀ GIẢI THÍCH
MA TRẬN TẠO MÃ VÀ MA TRẬN KIỂM TRA. 1. Mã Hamming (7,4).
Mã Hamming (7,4) là một loại mã phát hiện và sửa lỗi do Richard Hamming phát
triển vào năm 1950. Đây là mã có độ dài 7 bit, trong đó có 4 bit chứa thông tin dữ
liệu và 3 bit dùng để kiểm tra lỗi. Mã Hamming (7,4) là một ví dụ điển hình của mã
Hamming nói chung, sử dụng lý thuyết cơ bản về khoảng cách Hamming để xác định và sửa lỗi.
Phương pháp tính các bit kiểm tra:
Các bit kiểm tra được tính toán để đảm bảo tính chẵn lẻ (parity) trên các nhóm bit mà chúng kiểm soát.
Bit kiểm tra p1: kiểm tra tính chẵn lẻ của các bit tại các vị trí 1, 3, 5, 7.
Công thức: p1 = D1 + D2 + D4
Bit kiểm tra p2: kiểm tra tính chẵn lẻ của các bit tại các vị trí 2, 3, 6, 7.
Công thức: p2 = D1 + D3 + D4
Bit kiểm tra p3: kiểm tra tính chẵn lẻ của các bit tại các vị trí 4, 5, 6, 7.
Công thức: p3 = D2 + D3 + D4
2. Ma trận tạo mã.
2.1 Thế nào là ma trận tạo mã? 10
Ma trận tạo mã Hamming (7,4) là ma trận dùng để mã hóa dữ liệu (4 bit) thành mã
Hamming (7 bit) thông qua phép nhân ma trận. Ma trận này có kích thước 4×7, trong
đó mỗi hàng của ma trận tương ứng với một bit kiểm tra và bit dữ liệu, và việc nhân
với một vector dữ liệu sẽ tạo ra chuỗi mã hóa 7 bit.
Ma trận tạo mã hamming (7,4) có dạng sau: 1 0 0 0 1 1 0 G = ( 0 1 0 0 1 0 1 ) 0 0 1 0 0 1 1 0 0 0 1 1 1 1
Giải thích cấu trúc ma trận:
Cột 1 đến cột 4: các bit dữ liệu D1, D2, D3, D4.
Cột 5 đến cột 7: chứa các bit kiểm tra p1, p2, p3 được tính từ các bit dữ liệu theo các quy tắc XOR.
2.2 Cách sử dụng ma trận tạo mã để mã hóa.
Giả sử dữ liệu cần mã hóa là D = [D
], với 4 bit dữ liệu. Để mã hóa, ta
1, D2, D3, D4
nhân ma trận nhân tạo G với vecto dữ liệu D (dưới dạng ma trận hang 1×4)
Ví dụ: mã hóa dữ liệu D = [1, 0, 1, 1]
Nhân ma trận G với vecto dữ liệu D theo phép nhân ma trận như sau: 1 1 0 0 0 1 1 0 0 0 1 0 0 1 0 1 Mã hóa = D × G= [ ] × [ ] 1 0 0 1 0 0 1 1 1 0 0 0 1 1 1 1
Sau phép nhân ma trận ta sẽ có chuỗi mã hóa 7 bit: [1, 0, 1, 1, 0, 1, 1]
3. Ma trận kiểm tra.
3.1 Thế nào là ma trận kiểm tra?
Ma trận kiểm tra (parity-check matrix) của mã Hamming (7,4) được sử dụng để kiểm
tra và phát hiện lỗi trong mã Hamming (7,4). Nó có tác dụng xác định xem một chuỗi
mã hóa có hợp lệ hay không và nếu có lỗi xảy ra trong quá trình truyền tải dữ liệu,
ma trận kiểm tra sẽ giúp xác định vị trí lỗi.
Ma trận kiểm tra mã hamming (7,4) có kích thước 3×7 (3 hàng, 7 cột) và có dạng sau: 11 1 1 1 0 0 0 1 H=[ 1 0 1 1 0 0 0] 1 0 0 1 1 0 0
Giải thích cấu trúc ma trận:
Cột 1 đến cột 4: Liên quan đến các bit dữ liệu D1, D2, D3, D4.
Cột 5 đến cột 7: Liên quan đến các bit kiểm tra p1, p2, p3.
3.2 Cách sử dụng ma trận kiểm tra.
Ma trận kiểm tra được sử dụng để kiểm tra xem một chuỗi mã hóa có hợp lệ hay
không. Để kiểm tra tính hợp lệ của một chuỗi mã hóa nhận được, ta thực hiện phép
nhân ma trận kiểm tra với chuỗi mã hóa.
Giả sử chuỗi mã hóa nhận được là C = [C1, C2, C3, C4, C5, C6, C7].
Để kiểm tra ta nhân ma trận kiểm tra H với chuỗi mã hóa C: H × 𝐶𝑇
Nếu kết quả là vector 0 (tức là tất cả các phần từ đều bằng 0), thì chuỗi mã hóa không có lỗi.
Nếu kết quả là một vector khác vector 0, thì chuỗi mã hóa có lỗi, và vị trí lỗi có
thể được xác định từ vector này.
Ví dụ: Kiểm tra mã hamming (7,4)
Giả sử ta nhận được chuỗi mã hóa là 0110011 (tương ứng với dữ liệu D = 1011)
Ta thực hiện phép tính H × 𝐶𝑇 như sau: 0 ⎡1⎤ ⎢ 1 1 1 0 0 0 1 1⎥ ⎢ ⎥ ] × 0 H × 𝐶𝑇=[1 0 1 1 0 0 0 ⎢ ⎥ 1 0 0 1 1 0 0 ⎢0⎥ ⎢1⎥ [1] 0
Kết quả phép nhân là: [0] 1
Vì vector này khác với vector [0,0,0], điều này cho thấy chuỗi mã hóa có lỗi, và vị
trí của lỗi được xác định là bit thứ 7 (vì vector lỗi [0,0,1] tương ứng với vị trí bit 7). 12
4. Mã Hamming bổ sung để kiểm tra trường hợp 2 lỗi. 4.1 Mã Hamming bổ sung.
Mã Hamming bổ sung (hay mã Hamming có khả năng phát hiện và sửa được 2 lỗi)
là một dạng cải tiến, nơi mà các bit kiểm tra không chỉ kiểm tra các bit dữ liệu mà
còn đảm bảo khả năng phát hiện khi có 2 lỗi xảy ra trong quá trình truyền tín hiệu.
Phương pháp này được gọi là mã Hamming sửa lỗi đôi.
4.2 Mã Hamming bổ sung kiểm tra trường hợp 2 lỗi.
Để mã Hamming có thể sửa được 2 lỗi, yêu cầu là phải tăng thêm các bit kiểm tra,
từ đó cho phép phát hiện và sửa được nhiều lỗi hơn. Việc mở rộng này không còn là
mã Hamming (7,4) nữa, mà thay vào đó là một dạng mã có nhiều bit kiểm tra hơn,
có thể là mã Hamming (15,11) hoặc tương tự, tùy thuộc vào mục tiêu và yêu cầu sử dụng.
PHẦN 4: CÁCH THIẾT LẬP MÃ HAMMING (7,4).
1. Tạo mã Hamming (7,4).
Các bước tạo mã Hamming (7,4):
Bước 1: Xác định vị trí của các bit kiểm tra
Trong mã Hamming (7,4), ta sử dụng 7 bit để truyền dữ liệu, trong đó 4 bit là bit dữ liệu (D
) và 3 bit là bit kiểm tra (
). Vị trí các bit trong chuỗi 7
1, D2, D3, D4
p1, p2, p3
bit được sắp xếp như sau:
Vị trí 1, 2, 4 là các bit kiểm tra (p1, p2, p3).
Vị trí 3, 5, 6, 7 là các bit dữ liệu (D1, D2, D3, D4).
Bước 2: Tính giá trị các bit kiểm tra.
Ví dụ: Cho dữ liệu [D1, D2, D3, D4]
Các bit kiểm tra (p1, p2, p3) được tính dựa trên các bit dữ liệu theo quy tắc sau:
p1 = D1 ⊕ D2 ⊕ D4
p2 = D1 ⊕ D3 ⊕ D4
p3 = D2 ⊕ D3 ⊕ D4 Trong đó:
⊕: là phép XOR (phép cộng modulo 2, tức là chỉ trả về 1 nếu số lượng bit 1 là lẻ).
Bước 3: Đặt các bit vào chuỗi mã Hamming 13
Sau khi tính xong các bit kiểm tra, ta sắp xếp các bit vào đúng vị trí của chúng để
tạo thành chuỗi 7 bit có dạng: [p1, p2, D1, p3, D2, D3, D4].
2. Kiểm tra, tìm lỗi, cách sửa lỗi: Ví dụ:
Truyền đi dữ liệu M bằng mã Hamming (7,4), mã nhận được là: X = (1 1 1 0 1 0 1).
Kiểm tra mã và sửa lỗi nếu có. Dữ liệu nhận được là gì? Cách giải:
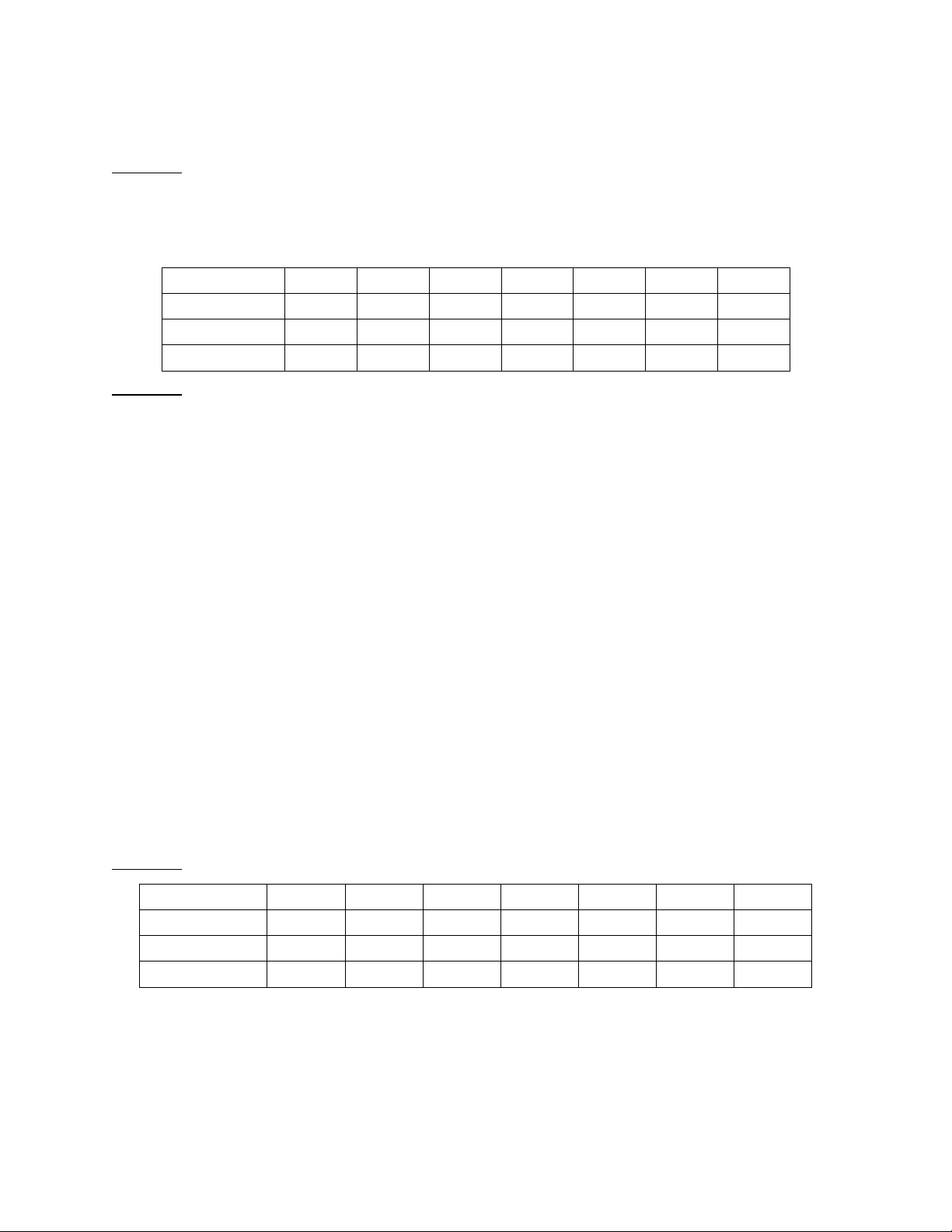
Bước 1: Lập ma trận kiểm tra.
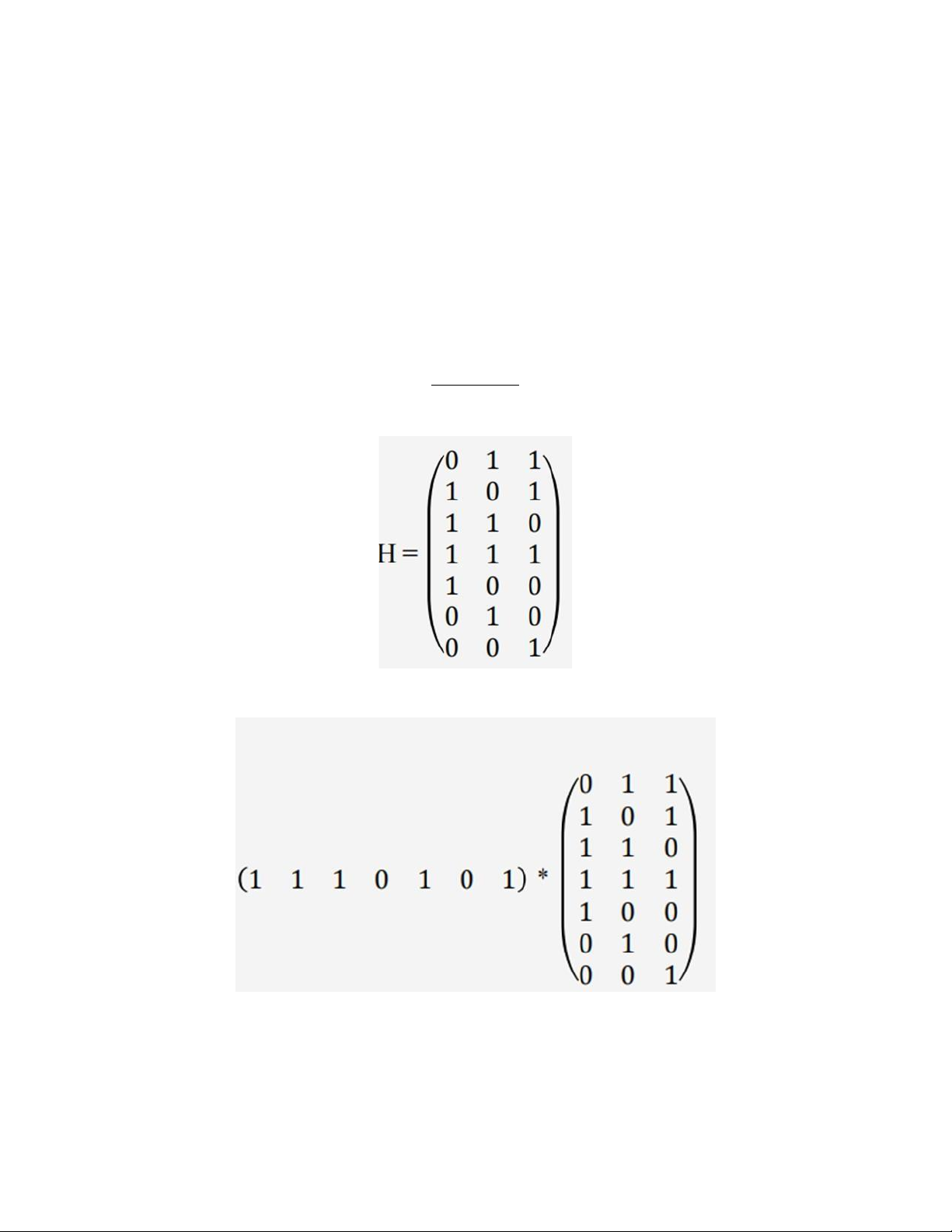
Bước 2: Kiểm tra bằng cách lấy X × H: = (1 0 1) = h2
 Mã nhận được bị lỗi tại bit thứ 2.
 Thay bit thứ hai từ 1 sang 0 ta được: 14 X1 = (1 0 1 0 1 0 1) Bước 3: Kiểm tra lại. X1 × H = (1 0 1 0 1 0 1) × = (0 0 0)  Mã X1 hợp lệ.
PHẦN 5: CHƯƠNG TRÌNH MATLAB.
1. Tổng quan về Matlab.
Matlab (viết tắt của matrix laborary) là một ngôn ngữ lập trình bậc cao bốn thế hệ,
môi trường để tính toán số học, trực quan và lập trình. Được phát triển bởi MathWorks.
Nó cho phép thao tác với ma trận, vẽ biểu đồ với hàm và số liệu, hiện thực thuật
toán, tạo ra giao diện người dùng, bao gồm C, C+, Java và Fortran; phân tích dữ liệu,
phát triển thuật toán, tạo các kiểu mẫu và ứng dụng.
2. Các lệnh cơ bản. Lệnh Ý nghĩa ~
Toán tử logic: không (not) Clear Xoá biến khỏi bộ nhớ =[A ; B ; C]
Lập ma trận có các hàng A,B, các
phần tử trên mỗi hàng được cách
nhau bởi 1 phím Space(phím cách) eye(n)
Tạo một ma trân đơn vị cấp n
Mod( số/ biến chia, số bị chia)
Toán tử modulo ( dùng để lấy phần dư )
for=trị đầu>:tăng>: If....else. ... end
Nếu....thì .... nếu không thì.. 15 Disp
Hiển thị giá trị chuỗi num2str
Viết tắt của “Number to string”:
Chuyển dữ liệu từ kiểu số sang kiểu chuỗi
3. Đoạn code về mã Hamming (7,4). >> clear >> n = 7 n = 7 >> k = 4 k = 4
>> A = [1 1 1;1 1 0;1 0 1;0 1 1]; >> G = [ eye(k) A ]
G = 1 0 0 0 1 1 1 0 1 0 0 1 1 0 0 0 1 0 1 0 1 0 0 0 1 0 1 1 >> H = [ A' eye(n-k) ]
H = 1 1 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 1 0 0 1 >> msg = [ 1 1 1 1 ] msg = 1 1 1 1 >> code = mod(msg*G,2) code = 1 1 1 1 1 1 1 >> code(2)= ~code(2) code = 1 0 1 1 1 1 1 >> recd = code recd = 1 0 1 1 1 1 1
>> syndrome = mod(recd * H',2) syndrome = 1 1 0 >> find = 0; >> for ii = 1:n if ~find errvect = zeros(1,n); errvect(ii) = 1; search = mod(errvect * H',2); if search == syndrome 16 find = 1; index = ii; end end end
>> disp(['Position of error in codeword=',num2str(index)]);
Position of error in codeword=2
>> correctedcode = recd;
>> correctedcode(index) = mod(recd(index)+1,2) correctedcode = 1 1 1 1 1 1 1
>> msg_decoded=correctedcode;
>> msg_decoded=msg_decoded(1:4) msg_decoded = 1 1 1 1 >> 17
TÀI LIỆU THAM KHẢO
1. https://drive.google.com/file/d/1JExRyxYQcP4sspD4K_Ssjy ME6sZYpr/view
2. https://www.guru99.com/vi/hamming-code-error-correction-example.html
3. https://tongquanvienthong.blogspot.com/2012/03/ma-hamming.html.
4. https://youtu.be/xXeXijCTn44?si=3gYoT4aItZaK2fAb
5. https://en.wikipedia.org/wiki/Hamming(7,4)
6. https://www.studocu.com/vn/document/dai-hoc-bach-khoa-tphcm/dai-so-tuyen-
tinh/ma-hamming-74-ma-hamming/77580828
7. https://vi.wikipedia.org/wiki/M%C3%A3_Hamming
8.https://www.voer.edu.vn/m/ma-hamming/1dda7d8
9. Trang chủ bách khoa cncp
10. Giáo trình Đại số tuyến tính- Đặng Văn Vinh 18