





Preview text:
Họ và tên sinh viên:.......................................
ĐỀ ÔN TẬL ĐỊNH KỲ LẦN I
Trường:.............................................................
Học phần: XÁC SUẤT THỐNG KÊ Tổng điểm
Thời gian: 60 phút Mã đề: 01
(Đề gồm 15 câu)
Chú ý: Thí sinh không được phép sử dụng tài liệu.
Trắc nghiệm một đáp án đúng
Câu 1: Bốc ngẫu nhiên một số viên bi từ hộp có số bi nhiều hơn số cần bốc . Để tính được số cách
bốc ta sử dụng phép toán: A. Tổ hợp B. Chỉnh hợp C. Hoán vị D. Giai thừa
Hướng dẫn giải
Bốc không quan tâm đến thứ tự , ta chọn tổ hợp
Câu 2: Xác suất làm việc của một hệ thống trong khoảng thời gian xác định nào đó được gọi là xác
suất tin cậy (XSTC) của hệ thống đó. Tính XSTC của một mạng gồm 2 linh kiện mắc nối tiếp cùng có XSTC là 0,95 . A. 0, 9 B. 0,9025 C. 0, 25 D. 0, 925
Hướng dẫn giải
Gọi A = { Linh kiện i hoạt động tốt },i = 1, 2 i
Gọi A = { Mạng làm việc tốt }
P (A) = A A P (A) = P (A A ) = P (A )P (A ) = 0,95.0,95 = 0,9025 (do tính độc lập) 1 2 1 2 1 2
Câu 3: Trong tủ quần áo của Hoa có 3 chiếc áo , 4 đôi giày , 5 chiếc quần. Hôm nay bạn cần chọn
một bộ gồm 1 quần, 1 áo, 1 đôi giày để đi học. Bạn ấy có bao nhiêu cách chọn ? A. 12 B. 60 C. 3 D. 1
Hướng dẫn giải
Dùng phép nhân : 3 cách chọn áo , 4 cách chọn giày , 5 cách chọn quần => 3.4.5 = 60 cách
Câu 4: Cho phương trình x + y + z = 100 . Phương trình đã cho có bao nhiêu nghiệm nguyên dương 3 A. C B. C 2 3 C. C D. C 2 99 100 100 99
Hướng dẫn giải
Ta đánh dấu trên trục số từ số 1 đến 100 bởi 100 số 1 cách đều nhau 1 đơn vị. Khi đó, ta có 99 khoảng giữa 2 số 1 liên tiếp.
Nếu chia đoạn thẳng 1,100 này bởi 2 diểm chia nằm trong đoạn thì ta sẽ có 3 phần có độ dài ít nhất là 1.
Có thể thấy rằng ta có song ánh giữa bài toán chia đoạn này với bài toán tìm nghiệm nguyên dương
của phương trình x + y + z = 100 .
Như vậy, số nghiệm của phương trình này bằng số cách chia, và bằng C 2 99
Câu 5: Ba nữ nhân viên phục vụ A, B và C thay nhau rửa dĩa chén và giả sử ba người này đều
"khéo léo" như nhau. Trong một tháng có 4 chén bị vỡ. Tìm xác suất để một trong ba người dánh vỡ 3 chén. A. 0.263 B. 0.29 C. 0.2963 D. 0.23
Hướng dẫn giải
Chọn một người đánh vỡ 3 chén, và một trong 2 người còn lại đánh vỡ 1 chén. C1C3C11
Suy ra P (B) = 3 4 2 0.2963 34
Câu 6: Đội A có 3 người và đội B có 3 người tham gia vào một cuộc chạy thi, 6 người có khả năng
như nhau và xuất phát cùng nhau. Tính xác suất để 3 người đội A về vị trí nhất, nhì, ba. 2 A. 0.01 B. 0.03 C. 0.05 D. 0.04
Hướng dẫn giải
Vì chỉ có 3 giải nhất, nhì, ba và mỗi giải chỉ có thể trao cho 1 trong 6 người, nên số kết cục đồng khả
năng là A3 = 20 . 6
Mặt khác, với mỗi cách trao giải cho 3 người đội A , ta có một hoán vị của 'nhất, nhì, ba' nên số kết cục thuận lợi là 3!. 3!
Tóm lại, xác suất cần tính P = = 0.05 3 A 6
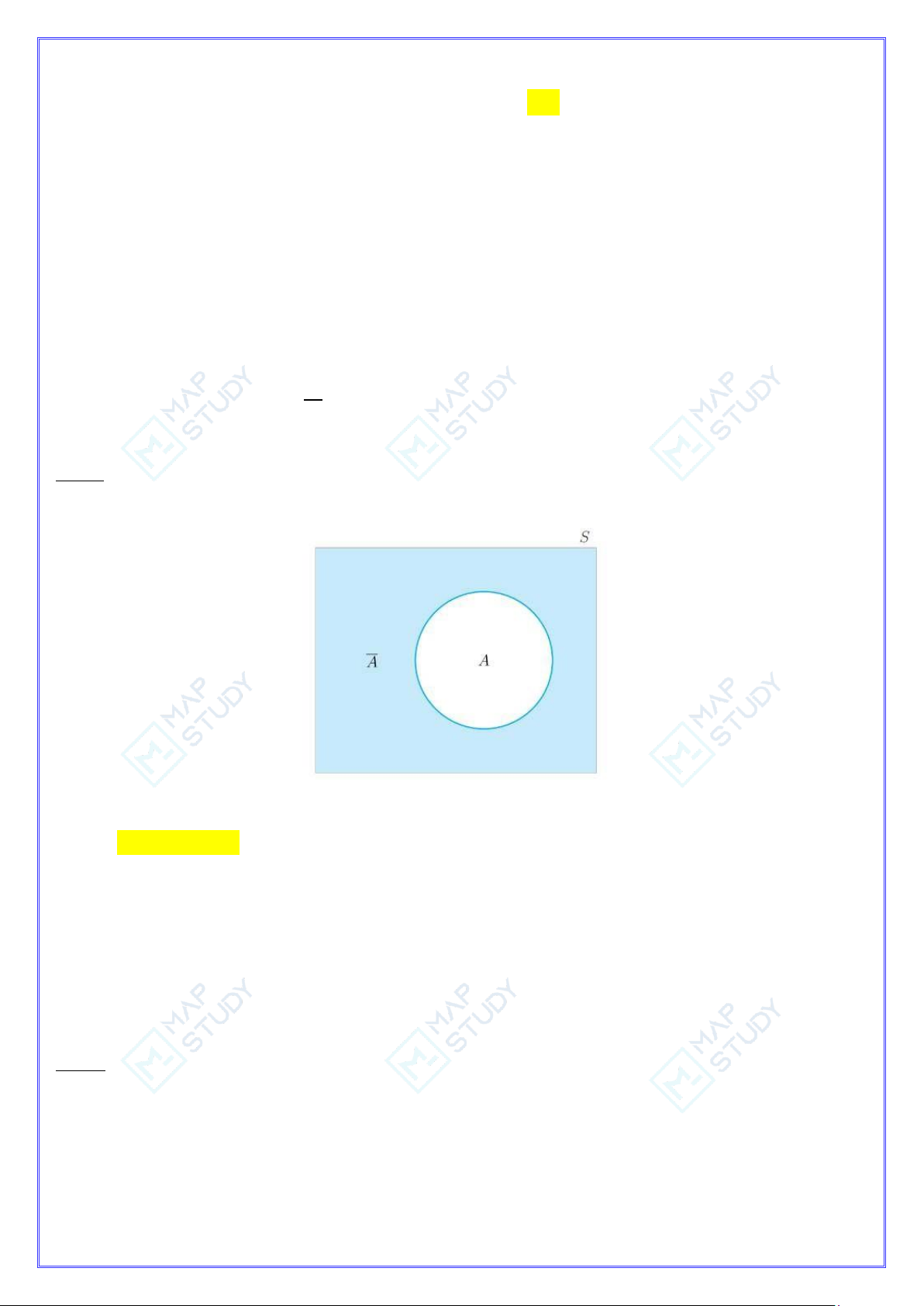
Câu 7: Hình sau đề cập chính xác nhất tới phép toán nào của sự kiện : A. Sự kiện đối lập B. Hiệu 2 sự kiện C. Giao của 2 sự kiện
D. Chưa có kết luận cụ thể
Hướng dẫn giải
Đây là 2 sự kiện đối lập (xem lại lý thuyết)
Câu 8: Một lô hàng có 15 sản phẩm gồm 6 loại A, 5 loại B và 4 loại C . Chọn ngẫu nhiên (không
hoàn lại) ra 4 sản phẩm. Biết trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại A . Tính xác suất
để trong 4 sản phẩm đó có đúng 1 sản phẩm loại C . A. 5 B. 5 C. 7 D. 5 9 8 9 7
Hướng dẫn giải
Gọi A = { Trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại A}
Số kết cục thuận lợi cho A là: p = C2 C2 = 540 cách 6 9 540
P ( A) = p = = 36 n 1365 91
Gọi H = TTrong 4 sản phẩm đó có dúng 1 sản phẩm loại C} Xác suất cần tính là: P ( AH )
P (H∣ A) = P ( A)
C2 C1 C1 20
P ( AH ) 20 91 5
trong đó: P ( AH ) = 6 4 5 =
P (H∣ A) = = = 4 C 91 P ( A) 36 9 15 91
Trắc nghiệm nhiều đáp án đúng (sinh viên phải chọn được tất cả các đáp án đúng) 1 1
Câu 9: Cho các sự kiện A, B với P ( A) = P (B) = ; ( P )
AB = . Giá trị của P (A + B); P (AB) là : 2 8
A. P (A + B)= 0.625
D. P (A + B) = 0.25 G.
B. P (AB) = 0.15
E. P (A + B)= 0.62
C. P (AB) = 0.12
F. P (A + B)= 0.725
Hướng dẫn giải
P (A + B) = 1− P (AB) = 1− P (A) + P (AB) = 0.625
P (AB) = P (B) − P (AB) = P (B) − P (A) + P (AB) = 0.125
Câu 10: Có 6 khẩu súng cũ và 4 khẩu súng mới, trong đó xác suất trúng khi bắn bằng súng cũ là 0,8
, còn súng mới là 0,95 . Bắn hú họa bằng một khẩu súng vào một mục tiêu thì thấy trúng. Giả sử ,
gọi M là "bắn bằng khẩu mới" và Gọi T là "bắn trúng' chọn các khẳng định đúng ц 0.8
A. P (MlT ) = 0.38
P (T∣ M ) = E. C. P (T ) 0.38 0.8
P (M∣ T ) = F. 0.6
P (M∣ T ) = D. P (M ) B. P (T )
P (M∣ T ) = P (T )
Hướng dẫn giải
M là "bắn bằng khẩu mới" thì M là "bắn bằng khẩu cũ".
Có P (M ) = 0.4 và P (M) = 0.6 .
theo đề bài, ta có P (T∣ M ) = 0.95 và P (T∣ M) = 0.8 .
Áp dụng công thức xác suất điều kiện suy ra
P (M ) P (T∣ M ) 0.38 0.48
P (M∣ T ) = =
P (M )P (T∣ M )
, P (M∣ T ) = = P (T ) P (T ) P (T ) P (T )
Câu 11: Theo thống kê xác suất để hai ngày liên tiếp có mưa ở một thành phố vào mùa hè là 0,5 ;
còn không mưa là 0,3 . Biết các sự kiện có một ngày mưa, một ngày không mưa là đồng khả năng.
Gọi A là "ngày đầu mưa" và B là 'ngày thứ hai mưa". A.
C. P (B∣ A) = 0.25 E. B.
D. P (B∣ A) = 0.3
F. P (B∣ A) = 0.25
Hướng dẫn giải
Gọi A là "ngày đầu mưa" và B là 'ngày thứ hai mưa" thì ta có P (AB) = 0.5, P (AB) = 0.3 . Vì các sự
kiện có một ngày mưa, một ngày không mưa là đồng khả năng nên
P (AB) = P (AB) = 1− 0.5 − 0.3 = 0.1 2
P (BA) P (BA) 0.1
+) P (B∣ A) = = = = 0.25
P (A) P (AB)+ P (AB) 0.1+ 0.3
Câu 12: Ở một địa phương đàn ông chiếm 55% dân số. Theo thống kê tỷ lệ đàn ông bị bạch tạng là
0, 4% , còn tỷ lệ trên của đàn bà là 0, 32% . Gọi A = { Gặp được đàn ông }; A = { Gặp được đàn bà } 1 2
.Gọi A = { Gặp dược người bị bạch tạng}. Chọn các khẳng định đúng
A. P ( A) = 0, 364
B. P (A∣ A ) = 0, 32 1
C. P (A ∣ A) = 0,6044 P ( A A) D. = 1 0, 44 P ( A)
E. P (A) = P (A ) P (A∣ A ) + P (A )P (A∣ A ) 1 1 1 2
Hướng dẫn giải
Gọi A = { Gặp được đàn ông }; A = { Gặp được đàn bà } 1 2 Hệ A
tạo thành hệ đầy đủ với: 1 ; A2
P (A ) = 0, 55; P (A ) = 0, 45 1 2
a) Gọi A = { Gặp dược người bị bạch tạng}
Áp dụng công thức xác suất đầy đủ: P (A) = P (A ) P (A∣ A ) + P (A )P (A∣ A ) 1 1 2 2
trong đó: P (A∣ A ) = 0, 4; P (A∣ A ) = 0, 32 P (A) = 0, 55.0, 4 + 0, 45.0, 32 = 0, 364 1 2
b) Xác suất cần tính là:
P ( A A) P ( A ) P ( A∣ A ) 0, 55.0, 4 1 1
P ( A ∣ A) = 1 = = = 0,6044 1 P ( A) P ( A) 0, 364
Hoàn thiện các tính toán và các phát biểu sau
Câu 13: Có một nhóm 4 sinh viên, mỗi người có một chiếc mũ giống hệt nhau để trên giá. Khi ra
khỏi phòng, mỗi người lấy ngẫu nhiên một chiếc mũ để đội. Tính xác suất để sinh viên thứ nhất và
sinh viên thứ ba lấy đúng mũ của mình. 6
Hướng dẫn giải
Xét phép thử mỗi người lấy ngẫu nhiên một chiếc mũ để đội.
• Số kết cục dồng khả năng là: n = 4 ! = 24 cách
• Gọi A = {Sinh viên thứ nhất và thứ ba lấy dúng mũ của mình }
• Số kết cục thuận lợi cho A là: m = 11 2 . = 2 cách 2 1
P ( A) = m = = n 24 12
Câu 14: Có ba hộp I, II, III đựng bóng đèn. Hộp I có 8 bóng đèn màu đỏ, 2 bóng đèn màu xanh; hộp
II có 7 bóng đèn màu đỏ, 3 bóng đèn màu xanh; hộp III có 6 bóng đèn màu đỏ, 4 bóng đèn màu
xanh. Lấy ngẫu nhiên ra một hộp rồi từ đó lấy ngẫu nhiên ra 3 bóng đèn thì được 2 bóng màu đỏ, 1
bóng màu xanh. Tính xác suất dể các bóng đèn này được lấy từ hộp I .
Hướng dẫn giải
Gọi A = {Số bóng lấy ra được lấy từ hộp i, i = 1, 2, 3 . i
Hệ A tạo thành hệ đầy đủ với: P ( A ) = P (A ) = P (A ) = 1 i 1 2 3 3
Gọi B = {Lấy ra được 2 bóng màu đỏ, 1 bóng màu xanh } Áp dụng công thức xác suất đầy đủ:
P (B) = P (A ) P (B∣ A ) + P (A )P (B∣ A ) + P (A )P (B∣ A ) 1 1 2 2 3 3 C2 2 C2 3 C2 4
với: P (B∣ A ) = 8 = 7 P (B∣ A ) = 7 = 21 P (B∣ A ) = 6 = 1 1 2 3 C3 15 C3 40 C3 2 10 10 10 1 7 P (B) =
+ 1 21 + 1 1 = 0, 4972
3 15 3 40 3 2 7
P ( A B) P ( A ) P (B∣ A ) 1 1 1
Xác suất cần tính là: P ( A ∣ B) = 1 = 1 P (B) P (B)
= 3 15 = 0, 3129 0, 4972
Câu 15: Trong một kho rượu, số lượng rượu loại A và loại B bằng nhau. Người ta chọn ngẫu nhiên
một chai và đưa cho 5 người nếm thử. Biết xác suất đoán đúng của mỗi người là 0,8 . Có 3 người
kết luận rượu loại A, 2 người kết luận rượu loại B . Hỏi khi đó xác suất chai rượu đó thuộc loại A là bao nhiêu?
Hướng dẫn giải
Gọi A là "chai rượu thuộc loại A " thì A, A tạo thành hệ đầy đủ và P ( A) = P (A) = 1 . 2
Gọi H là "có 3 người kêt luận rượu loại A và 2 người kết luận rượu loại B ".
Theo công thức đẩy đủ = 5 5
P (H ) P (A)P (H∣ A) + P (A)P (A∣ H )= 0.5 0.83 0.22 + 0.5 0.82 0.23 = 0.128 3 2
P ( A) P (H∣ A) 0.5 C3 0.83 0.22
Xác suất cần tính là P ( A∣ H ) = = 5 = 0.8 P (H ) 0.128 HẾT k



