Chương 4: Tích phân ậ Tp bất đ nh
Nguyên hàm: Hàm F(x) được gọi là nguyên hàm c a hàm f(x)
trong khỏang (a,b) nếu tại mọi điểm x thu c (a,b) ta đều có F’(x) = f(x)
Từ đ nh nghĩa nguyên hàm ta suy ra:
1. Nếu F(x) là m t nguyên hàm c a f(x) thì F(x)+C cũng là nguyên hàm c a hàm f(x)
2. Mọi nguyên hàm c a f(x) đều có dạng F(x)+C
Đ nh lỦ: Mọi hàm liên t c trên [a,b] (liên t c trong khoảng (a,b)
và liên t c trái tại b, liên t c phải tại a) thì có nguyên hàm trên [a,b]
Chương 4: Tích phân ậ Tp bất đ nh
Đ nh nghĩa tích phân bất đ nh : Nếu hàm F(x) là m t nguyên
hàm c a hàm f(x) thì F(x)+C (C: hằng số) được gọi là tích
phân bất đ nh c a hàm f(x), kí hiệu f (x)dx 
 F(x) C Tính chất: f (
  x)dx  f (x)C d f (x)dx   f (x) dx . a f (x)dx   . a f (x)dx 
 f (x)  g(x)dx  f (x)dx 
 g(x)dx 
Chương 4: Tích phân ậ Tp bất đ nh
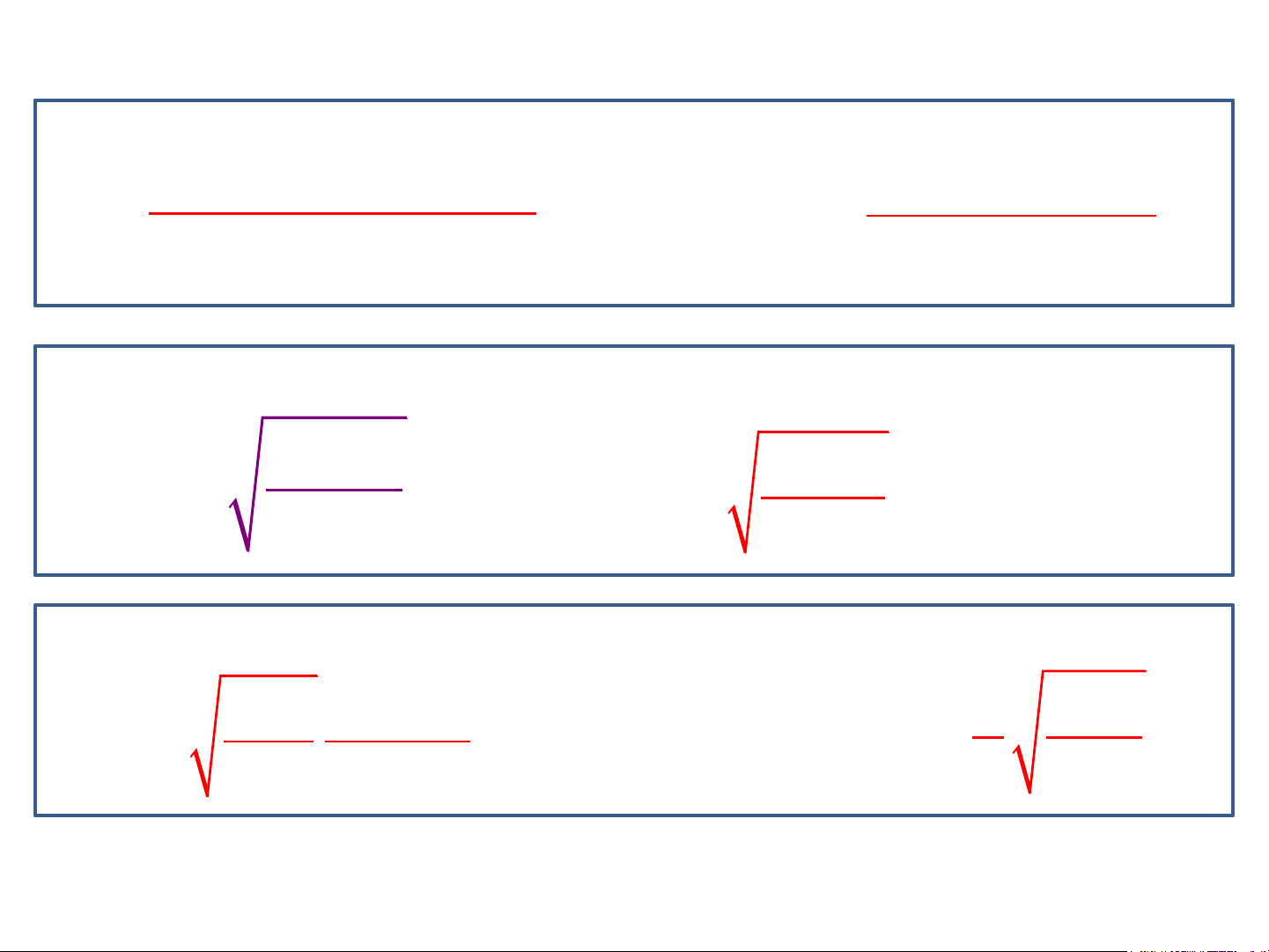
Bảng tích phân các hàm cơ bản  1 x   1 x dx   C,  1 dx   tan x  C    2 1 cos x 1 1 dx   ln x C dx 
 cot x  c 2 x sin x x 1 1 x x a a dx   C dx   arctan  C 2 2 ln a a  x a a sin xdx 
 cos x C 1 1 x  a dx   ln  C 2 2 cos xdx   sin x  c a  x 2a x  a dx x      dx x ln tan  C 
 ln tan   C sin x 2 cos x 2 4  
Chương 4: Tích phân ậ Tp bất đ nh
Bảng tích phân các hàm cơ bản 1 x dx   arcsin  c 2 2 a a  x 1 2 2 dx 
 ln x  x  a C 2 2 x  a 2 2 2 2 2 a x x a  x a   x dx  arcsin  C 2 a 2 dx shxdx   chx  C   thx  C 2 ch x chxdx   shx  C dx 
 cthx  C 2 sh x
Chương 4: Tích phân ậ Tp bất đ nh
Phương pháp đổi biến: Định lý: V i φ(t) là hàm khả vi
Nếu: f (x)dx 
 F(x) C Thì: f (
 (t)) (t)dt  F((t)) C
Phương pháp đổi biến 1: Đ t x = φ(t), φ(t) là hàm khả vi và
có hàm ngược t= φ-1(x) thì f (x)dx   f (
 (t)) (t)dt Gsử nguyên hàm c a 1      
f(φ(t))φ’(t) là G(t) thì f (x)dx G(t) C G( (x)) C
Phương pháp đổi biến 2: Đ t u = φ(x), du=φ’(x)dx và giả sử f (x)dx   g(
 (x)) (x)dx v i g(x)dx 
 G(x) C
Thì f (x)dx 
 G((x)) C
Chương 4: Tích phân ậ Tp bất đ nh
Ví d : Tính các tích phân 2 I  1   x dx x  4 x I e   e dx 1 3 dx dx I  I  2   2 2 4 x  a 2x 1
Phương pháp tích phân từng phần:
Định lý: Cho các hàm u(x), v(x) khả vi và u(x), v’(x) có
nguyên hàm trên (a,b). Khi ấy hàm u’(x), v(x) cũng có
nguyên hàm trên (a,b) và ta có u (
  x)v(x)dx  u(x)v(x)  u(x)v (   x)dx
Ta còn viết CT trên ở dạng udv   uv  vdu 
Ví d : Tính các tích phân I  arcsin xdx I  x ln xdx 5  2 6 
Chương 4: Tích phân ậ Tp bất đ nh
Tích phân các hàm hữu tỉ
1. Tích phân phân th c đơn giản lọai 1: M k M dx  b  x   C 1  a a k 1 1
(ax  b)k
2. Tích phân phân th c đơn giản lọai 2: v i ax2+bx+c là tam
th c b c 2 không có nghiệm thực Mx  N du du dx   ,   2 k 2 2 k
(ax  bx  c)k u (u  a )
Biến đổi để đưa tp trên thành tổng c a 2 tp cơ bản dạng
Ví d : Tính các tích phân x 1 2x  3 I  dx I   dx 7 2  2 2 2x  4x  5 (x  x 1)
Chương 4: Tích phân ậ Tp bất đ nh
Tích phân hàm hữu tỉ tổng quát P (x) : f (x) n  Q (x) m
Trường hợp 1: n < m Phân tích hàm thành tổng các phân th c đơn giản M M  j x N j i  , l k i 2 (a x  b ) i i
(c x  d x  e ) j j j j
Trường hợp 2: n ≥ m
Ta chia đa th c : P (x)  Q (x).T (x)  R (x),l  m n m k l
Rồi đưa về trường hợp 1
Ví d : Tính các tích phân 2x  3 3 x  x 1 I  dx  8  I dx  3 2 9
x  5x  6x 2 x  5x  4
Chương 4: Tích phân ậ Tp bất đ nh
Ví d : Tính các tích phân 2x 1 3x 1 I  dx  I  dx 10 2  2 2
x  2x  3 x 1 (x   2 1)(x 1)
Tích phân 1 số hàm vô tỉ ax  b n  1. f ( , x )dx  Đ t: ax b n t  cx  d cx  d
Ví d : Tính các tích phân x 1 dx 1 x  1 3 I  I  dx  11  3 12 x 1 (x 1) x x  1
Chương 4: Tích phân ậ Tp bất đ nh
Tích phân 1 số hàm vô tỉ mx  n 2. f dx  Tính như tp hàm hữu t 2
ax  bx  c 1 3. f dx 
Đ t (x-α)=1/t để đưa về x  m 2
ax  bx  c dạng trên
Ví d : Tính các tích phân dx x    1 dx I  13 I   14  x   2 1 x  x  1 2 x  2x  3 (x  1)dx  15 I  2
(x  1) x  1
Chương 4: Tích phân ậ Tp bất đ nh
Tích phân hàm lượng giác
f cos x,sin xdx  2 x 2dt 1  t 2t
t  tan  dx  ,cos x  ,sin x  2 2 2 2 1  t 1  t 1  t
Ví d : Tính các tích phân dx 
3sin x  4cos x  16 I  I dx 
4sin x  3cos x  5 17
2cos x  5sin x
Chương 4: Tích phân ậ Tp bất đ nh Tính các tp dx I   x  8
4cos x  3sin x  5 1 I e dx  arcsin x dx I  I   2 dx  9 2 x 3 cos x sin x dx dx I  3  I   2 10 2x  4x  5 2 2
4sin x  7cos x cos x I  1 x 1 4 dx  x I  dx e 11  x x 1 arcsin x x 1 I  5 dx  I  dx  1  x 12 2 1  2x  x xdx I  2 6  4 2 I  x x   4dx x  6x 13 13 4 3 2 dx
x  3x  3x  5 I  I  14  7    2x 9 2 x   dx 3 1 16  x
Chương 4: Tích phân ậ Tp xác đ nh
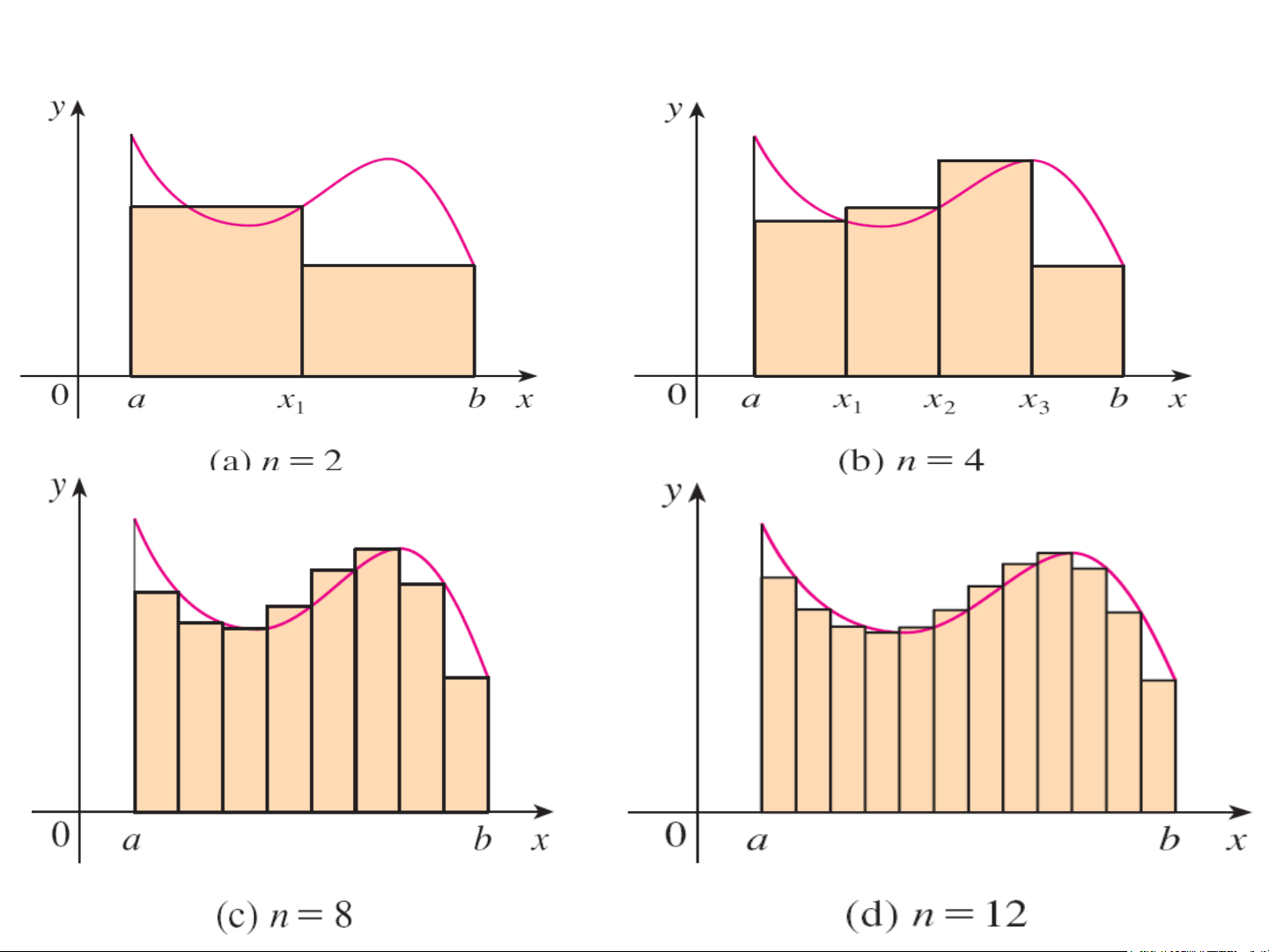
Đ nh nghĩa tích phân xác đ nh: Cho hàm f(x) xác đ nh
trên [a,b]. Chia [a,b] thành n-phần tùy Ủ bởi các điểm chia (ta
gọi là m t phân hoạch c a đoạn [a,b]) a  0 x  1 x  ...  n x  b
Lấy điểm bất kỳ M x , k k k x 1
  , l p tổng tích phân: n 1 
S   f (M ). x  , n k k  k x  k x 1   k x (Tổng Riemann) k 0 Ta cho max 0 k x
  , nếu Sn tiến đến m t gi i hạn hữu
hạn mà không ph thu c cách chia [a,b] và cách lấy điểm Mk
thì gi i hạn đó được gọi là tích phân xác đ nh c a hàm f(x)
trên [a,b] và kí hiệu là b
Khi ấy, ta nói hàm f(x) khả tích trên [a,b] f (x)dx a
Chương 4: Tích phân ậ Tp xác đ nh
Chương 4: Tích phân ậ Tp xác đ nh
Tính chất c a tích phân xác đ nh
Định lý 1: Hàm liên t c trên [a,b] thì khả tích trên [a,b]
Định lý 2: Hàm có hữu hạn điểm gián đoạn trên [a,b] thì khả tích trên [a,b]
Trong các tính chất dư i đây, đều có f(x), g(x) là các hàm khả tích trên [a,b] b b b 1 / dx   b  a 2 / . c f (x)dx 
 .c f (x)dx  a a a b b b
3 /   f (x)  g(x)dx  f (x)dx 
 g(x)dx  a a a
Chương 4: Tích phân ậ Tp xác đ nh b a 4 / f (x)dx 
  f (x)dx  a b b b 5 / f (x)dx 
 g(x)d ,x f (x) 
 g(x) x  [a,b] a a b c b 6 / f (x)dx 
 f (x)dx 
 f (x)dx  f(x) khả tích trên [a,c], [c,b], [a,b] a a c b b 7 / f (x)dx 
 f (x) dx  a a 0
 , f (x) là hàm lẻ a  8 / f (x) a dx 
 2 f (x)dx, f (x)  là hàm ch n a    0
Chương 4: Tích phân ậ Tp xác đ nh a T  a 9 / f (x)dx 
 f (x)dx, f (x) 
là hàm tuần hoàn chu kỳ T a 0 b M, m là GLNN, GTNN c a 7 / (
m b  a)  f (x)dx 
 M (b  a) f(x) trên [a,b] a
Định lý giá trị trung bình: Cho hàm f(x) liên t c trên [a,b], tồn
tại điểm c trong [a,b] sao cho b f (x)dx 
 (b  a) f (c) a
Ta gọi f(c) là giá tr trung bình c a hàm f(x) trên [a,b] 1 b f (c)  f (x)dx  b  a a
Chương 4: Tích phân ậ Tp xác đ nh
Công th c đạo hàm dư i dấu tích phân  b(x)   f (t)dt 
  f (b(x)).b (x)  f (a(x)).a (x)   a(x)  
Ví d : Tính đạo hàm theo x c a cos x 2 f (x)  cos(t )dt  sin x x 2 (arctan t) dt  Ví d : Tính gi i hạn 0 lim x 2  x 1
Chương 4: Tích phân ậ Tp xác đ nh Phương pháp đổi biến
 f (x) liên t c trên [a,b]  Nếu (t) 
khả vi, liên t c trên [t1,t2]    [     1
t ,t2] [a,b], ( 1t) , a (t2)  b b t2 Thì f (x)dx   f (
 (t)) (t)dt a 1 t 6 Ví d : Tính dx  1 3x2 1
Chương 4: Tích phân ậ Tp xác đ nh
Phương pháp tích phân từng phần
Nếu 2 hàm u(x), v(x) khả vi, liên t c trên [a,b] thì b b b u(x)v ( 
 x)dx  u(x)v(x)  u (
  x)v(x)dx a a a Ví d : Tính 1 arcsin xdx 0 1 x