Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.

GIẢI TÍCH TRONG KINH DOANH (MT1017).
Chương 2: Giới hạn. Liên Tục. Toán Tài chính (Tóm tắt). TS. Nguyễn Quốc Lân
Trong chương này, ta nhắc lại 2 khái niệm Giới hạn - Liên tục đã gặp ở Phổ thông. Để tìm Giới
hạn, chúng ta chỉ xét một số dạng vô định đơn giản. Với Toán tài chính, chúng ta nhắc lại khái niệm
Lãi kép đã gặp ở Phổ thông. Sử dụng công thức lãi kép, chúng ta sẽ đề cập đến 2 khái niệm cơ bản:
Giá trị hiện tại ròng và Tỷ suất sinh lợi nội tại vốn thường xuyên xuất hiện trong các bản phân tích,
đánh giá đầu tư dự án chẳng hạn như đoạn trích sau đây Bản cáo bạch trên Sàn chứng khoán London
ngày 21/05/2019 (Nguồn: puregoldmining.ca): "Công bố tiền khả thi về dự án Madsen Red Lake Gold
cho thấy chi phí ban đầu tương đối thấp với 95 triệu đôla canadia và khía cạnh tài chính hấp dẫn với
GIÁ TRỊ HIỆN TẠI RÒNG (net present value) hậu thuế 12.35 triệu đôla cũng như TỶ SUẤT SINH
LỢI NỘI TẠI (internal rate of return) là 36% sau 12 năm".
1 Ý tưởng đơn giản về Giới hạn (Hoffmann, Sec. 1.5, page 63)
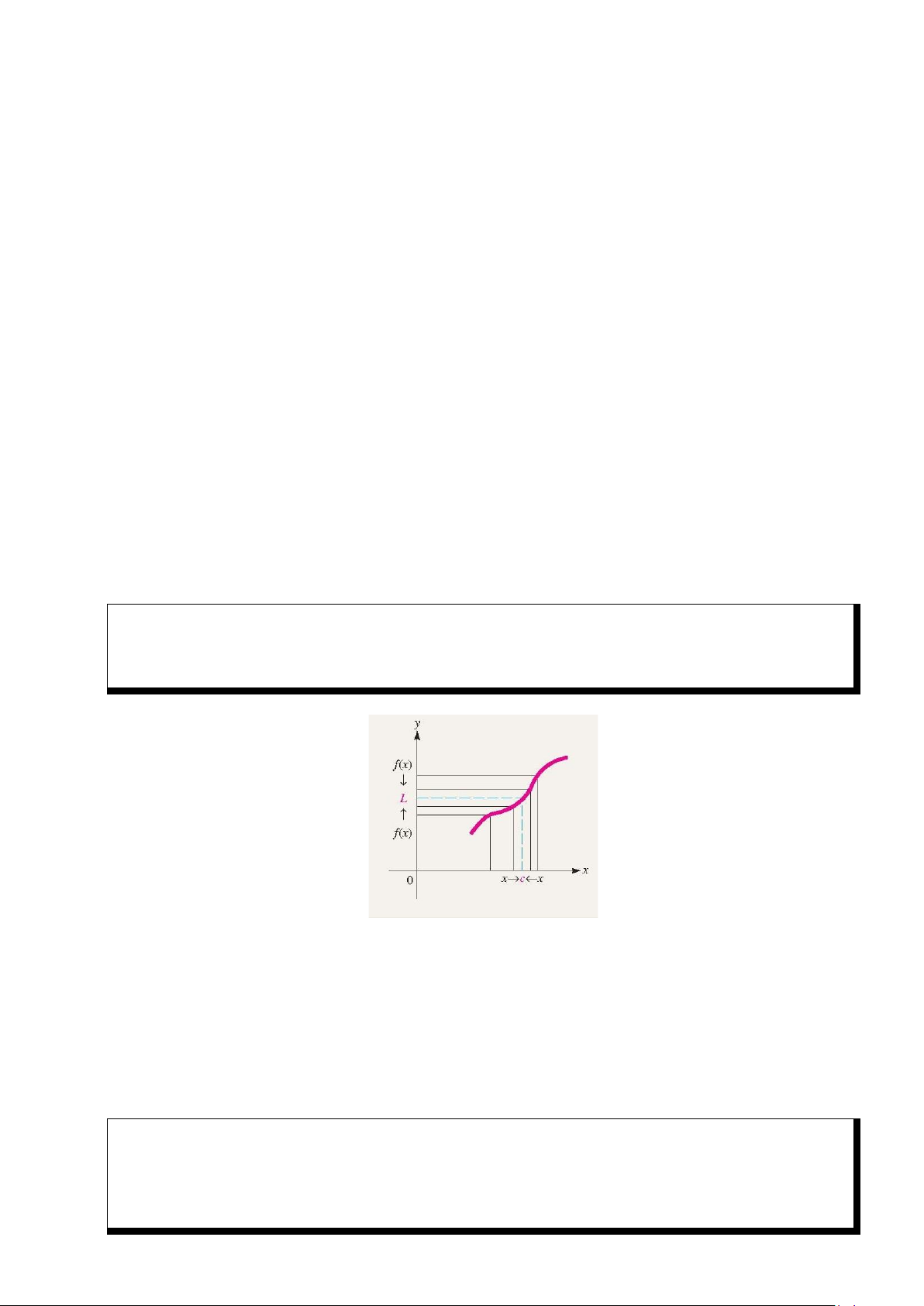
Định Nghĩa 1. (Giới hạn của hàm số) Giá trị L được gọi là giới hạn của hàm f(x) khi x tiến
về c nếu giá trị f(x) gần L tùy ý khi ta chọn x rất gần c. Khi đó ta viết lim f (x) = L. x→c
Hình 1: Minh họa hình học: Khi lim f (x) = L, cao độ của đồ thị y = f (x) tiến về L khi x tiến về c. x c →
2 Kỹ thuật tính Giới hạn
Với các hàm đơn giản trong chương trình, ta có ngay
Mệnh Đề 1. (Nguyên lý thay vào trực tiếp) Nếu f là hàm sơ cấp (tức f được xác định bởi
1 công thức - đã định nghĩa ở chương 1) và c thuộc miền xác định của f (tức f (c) có nghĩa), khi
đó lim f (x) = f (c). x→c
3 LIÊN TỤC (HOFFMANN, PHẦN 1.6, TRANG 78) 2
Nói vắn tắt, để tìm giới hạn của hàm sơ cấp ta chỉ cần thay vào nếu kết quả thu được là có nghĩa. √ 3x + 1 √ 4 Ví Dụ 1. lim
x2 + x + 1 + sin = 3 + sin x→1 log2 x + 3 3
Khi thay vào mà kết quả chưa xác định, ta có Dạng vô định. 0
Ví Dụ 2. (Hàm phân thfíc hữu tỷ, : Phân tích ra thừa số) 0 x2 − 1
(x − 1)(x + 1) x + 1 lim 2 = lim = lim = −2.
x→1 x − 3x + 2
x→1 (x − 1)(x − 2) x→1 x − 2 0
Ví Dụ 3. (Phân thfíc chfía căn, : Nhân lượng liên hợp) 0 √ √ √ 2x + 7 − 3 ( 2x + 7 − 3 √ )( 2x + 7 + 3) 1 lim x→1 x − 1 = lim x→1 = (x − 1)( 3) 3 2x + 7 + ∞
Ví Dụ 4. (Hàm phân thfíc hữu tỷ,
: Chia tử và mẫu cho lũy thừa bậc cao nhất.) ∞ 2x2 + 3x + 1 2 + 3 + 1 2 lim = lim x x2 = .
x→+∞ 3x2 − 5x + 2 x→∞ 3 − 5 + 2 3 x x2
Chú ý 1. Ở dạng bài này, trong thực tế sinh viên có thể sử dụng qui tắc sau (Dạng phân 2 ∞ 2x + 3x + 1 thfíc,
) : Chỉ giữ lại số hạng bậc cao nhất) để có lời giải siêu gọn: lim = ∞
x→+∞ 3x2 − 5x + 2 2x2 2 lim x 2 = . →+∞ 3x 3 a x 2x + 3 5x+2 ∞ a
Ví Dụ 5. Dùng Giới hạn hàm mũ 1 : lim 1 + = e , tính lim . x→+∞ x x→+∞ 2x − 1 Giải. " # 5x+2 5x+2 2x−1 2x + 3 4 2x−1 5 lim = lim 1 +
= e4 2 = e10. x→+∞ 2x − 1 x→∞ 2x − 1
Sinh viên có thể nghiên cứu đầy đủ hơn về kỹ thuật xử lý dạng vô định trong [1].
Ví dụ Kinh tế 1. Nghiên cứu cho thấy trong vòng t năm nữa, dân số một quốc gia sẽ là √
P (t) = 0.2t + 1500 ngàn người, và GNP là E(t) = 9t2 + 0.5t + 179. triệu đôla. Tính thu nhập
bình quân đầu người của quốc gia này trong dài hạn?
3 Liên tục (Hoffmann, Phần 1.6, Trang 78)
Định Nghĩa 2. Hàm f được gọi là liên tục tại c khi lim f (x) = f (c). x→c 4 TOÁN TÀI CHÍNH 3
Với hàm sơ cấp, tính liên tục tại x = c đơn giản chỉ là c ∈ miền xác định D của hàm số. √
ln x + 25 − x2
Ví Dụ 6. Tìm tất cả các điểm tại đó f (x) = liên tục. x2 − 1  x > 0
Giải. f (x) xác định khi
25 − x2 ≥ 0 ⇔ x ∈ D = (0; 1) ∪ (1, 5]. Vì f (x) sơ cấp, tập các điểm  x2 − 1 /= 0
cần tìm (0, 1) và (1, 5].
Khi hàm không sơ cấp - chẳng hạn hàm xác định từng khúc, ta phải dùng giới hạn một phía. (
x + 1, if x < 1
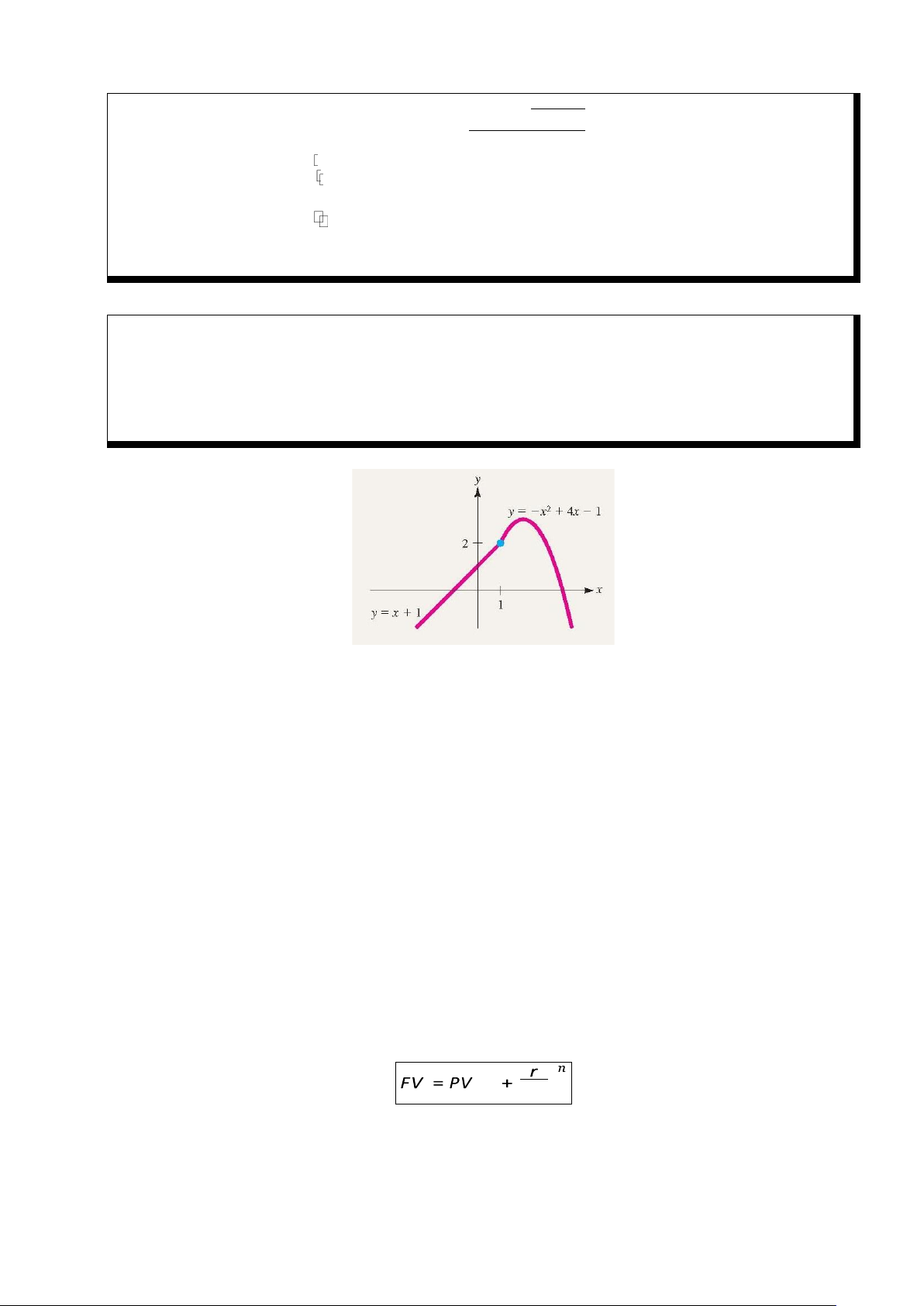
Ví Dụ 7. Tìm a để hàm f (x) =
liên tục tại x = 1.
−x + ax − 1, if x ≥ 1 2
Giải. lim f (x) = lim f (x) = f (1) ⇒ 2 = a − 2 ⇒ a = 4. x→1− x→1+
Hình 2: Đồ thị f (x) khi a = 4. 4 Toán Tài Chính
Một trong những nguyên tắc cơ bản nhất của giới đầu tư: Tiền đẻ ra tiền. Thật ra giới đầu tư
không chỉ quan tâm đến tiền đẻ ra tiền mà còn quan tâm đến hiệu suất "sinh sản" của tiền! Chẳng
hạn một nhà đầu tư có 50 triệu đồng. Liệu nhà đầu tư này sẽ tham gia đầu tư một dự án hứa hẹn
hoàn lại cho họ 60 triệu sau 2 năm, hay nên gửi ngân hàng với lãi suẩt 10%/năm? Để giúp nhà đầu tư
đưa ra quyết định đúng đắn, chúng ta sẽ đề cập đến 3 khái niệm: Lãi kép - Giá trị hiện tại ròng - Tỷ
suất sinh lợi nội tại. 4.1 Lãi kép
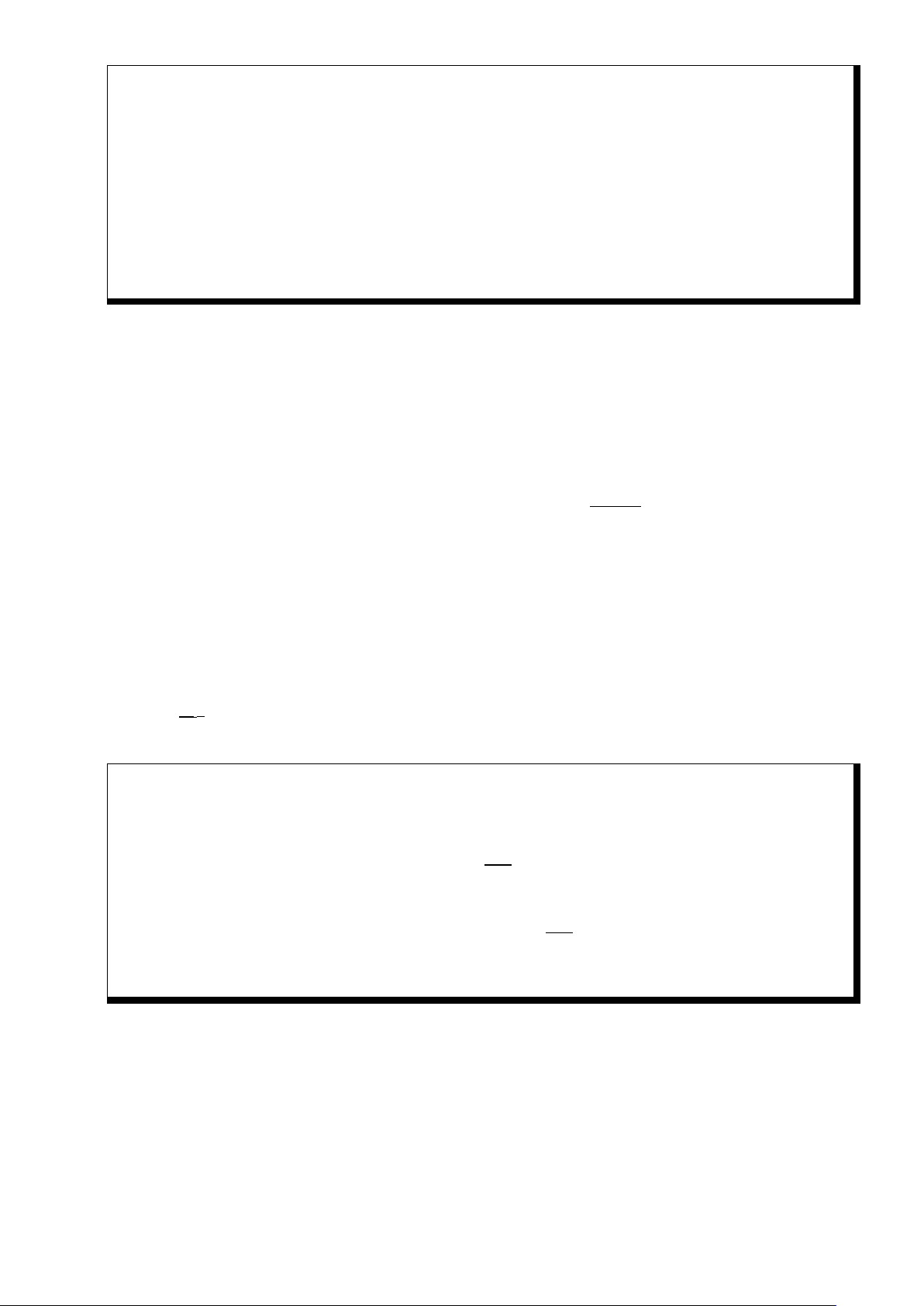
Công thức sau đây đã biết ở Phổ thông: Gửi PV đồng vào Ngân hàng với lãi suất r% năm theo
hình thức lãi kép, sau n năm ta sẽ có số tiền FV xác định qua công thức 1 (1) 100
4.2 Đánh giá dự án đầu tư 4
Ví dụ Kinh tế 2. Tìm số tiền nhận được sau khi gửi tiết kiệm 4 năm số tiền 10000 đồng vào
ngân hàng có lãi suất 5%/năm theo hình thức lãi kép. 4 5 Giải. FV = 10000 1 + = 12155.06 đồng. 100
Công thức (1) cũng cho thấy nếu biết 3 trong 4 đại lượng r, n, PV và FV , ta dễ dàng suy ra giá trị còn lại.
Ví dụ Kinh tế 3. Gửi 25 000 đồng vào Ngân hàng lãi suất 12%/năm theo hình thức lãi kép. Sau
bao nhiêu năm số tiền gửi sẽ vượt quá 250000 đồng? n 12
Giải. Giải phương trình 250000 = 25000 1 +
⇒ n = 20.3. Chú ý vì n là số nguyên và yêu 100
cầu vượt quá nên đáp số phải là 21 năm. Thật vậy sau 20 năm FV = 25000(1.12)20 = 241157.33
đồng, còn sau 21 năm FV = 25000(1.12)21 = 270096.21.
Ví dụ Kinh tế 4. Một giáo viên muốn gửi tiếp kiệm 50000 đồng theo hình thức lãi kép để nhận
được 60000 đồng sau 5 năm. Hãy tính lãi suất hàng năm của ngân hàng để giáo viên này đạt được mục tiêu. r n Giải. Giải = 3.7% . 50000 1 + = 60000 ⇒ r 100
Nếu chia nhỏ định kỳ thời gian gửi (đồng thời cũng chia nhỏ lãi suất) ta được lãi kép liên tục.
Như thế ta có 2 cách tính lãi kép khác nhau. r n
Khái niệm Kinh tế 1. (i) Lãi kép rời rạc:
với là số định kỳ gửi. FV = PV 1 + n 100 rt
(ii) Lãi kép liên tục: FV = PV e 100 với t là số năm.
4.2 Đánh giá dự án đầu tư
Khi biết giá trị FV trong tương lai, lãi suất r và số năm t, ta dễ dàng tính được khoản tiền ban
đầu cần đầu tư PV .
Khái niệm Kinh tế 2. Công thức tính khoản ban đầu FV r −t Lãi kép rời rạc: (2) PV = = FV 1 + t 1 + r 100 100 FV
Lãi kép liên tục: PV = = FV e− rt (3) 100 rt e 100
4.2 Đánh giá dự án đầu tư 5
Ví dụ Kinh tế 5. Tìm khoản tiền cần gửi ban đầu để có được 1000 đồng sau 4 năm với lãi suất 10%/năm
(a) Định kỳ nửa năm, hình thức lãi kép rời rạc.
(b) Định kỳ nửa năm, hình thức lãi kép liên tục.
Giải. (a) Nửa năm, vậy r = 5 ⇒ PV = 1000(1.05)−8 ≈ 676.84 đồng. −0.4
(b) r = 10, t = 4 ⇒ PV = 1000e ≈ 670.32 đồng.
Ở ví dụ trên, giả sử người định gửi tiền nhận được lời mời đầu tư 600 đồng vào một dự án với
bảo đảm sẽ được hoàn lại 1000 đồng sau 4 năm, liệu người gửi tiền sẽ chọn lựa việc đầu tư hay vẫn
gửi tiền tiết kiệm? Ta đã thấy nếu chọn hình thức tiết kiệm, người gửi phải cần đến 676.84 đồng để
có 1000 đồng sau 4 năm. Vì 676.84 > 600 nên việc tham gia đầu tư sẽ có lợi hơn cho người gửi. Cụ
thể mức lợi là 676. —
84 600 = 76.84 đồng. Đại lượng này được gọi là Giá trị hiện tại ròng (Net Present Value - NPV)
Nói chung, một dự án đầu tư sẽ được đánh giá đáng đầu tư khi NPV nhận giá trị dương. Thêm
nữa, giữa 2 dự án đầu tư, dự án nào có NPV lớn hơn sẽ đáng được đầu tự hơn. Thật ra trong thực
tế, những yếu tố khác như độ an toàn cũng phải được tính đến. 676.84
Thay vì xét hiệu 2 giá trị, ta cũng có thể xét tỷ số 2 giá trị
≈ 1.13 > 1. Tỷ số này được 600
gọi là Tỷ suất lợi nhuận và chi phí - BCR (benefit cost ratio) BCR (hay BC). Ở đây BCR
của dự án này là 1.13. Tương tự NPV, một dự án đầu tư sẽ được đánh giá đáng đầu tư khi lớn hơn
1. Giữa 2 dự án đầu tư, dự án nào có NPV lớn hơn sẽ nên được ưu tiên xem xét hơn.
Một cách đánh giá dự án đầu tư nữa dựa trên Tỷ suất sinh lợi nội tại (IRR - internal
rate of return). Đó là tỷ suất ri tính theo công thức lãi kép bảo đảm cho khoảng tiền đầu tư ban
đầu đem lại cùng một giá trị tương lai như dự án. Nói cách khác, ta xem tham gia dự án tương
tự như gửi ngân hàng theo hình thức lãi kép, và ta tính lãi suất ri của ngân hàng "nội tại" này để
so sánh với lãi suất r trên thị trường của các ngân hàng "công cộng" khác. Ở ví dụ đang xét, giải ri 4
600 1 + 100 = 1000 ⇒ ri ≈ 13.62, vậy IRR = 13.62%. Dự án này đáng được quan tâm vì IRR tốt
hơn lãi suất 10% của ngân hàng ban đầu người gửi dự định chọn.
Khái niệm Kinh tế 3. Tổng quát xét dự án với khoản đầu tư ban đầu C đồng trên thị trường
có lãi suất r% theo hình thức lãi kép rời rạc. Nếu dự án này bảo đảm giá trị FV đồng sau n định kỳ, khi đó r −n
(i) Giá trị hiện tại ròng (NPV) =
. Dự án đáng được xem xét nếu NPV FV 1 + − C 100 > 0. r n
(iii) Tỷ suất sinh lợi nội tại (IRR) = , với i
. Dự án đáng được xem xét ri C 1 + = FV 100 nếu ri > r.
Ví dụ sau đây minh họa phương pháp NPV và IRR khi đánh giá dự án đầu tư
4.3 Phân tích bổ sung 6
Ví dụ Kinh tế 6. Một dự án chào mời đầu tư 15000 đồng và bảo đảm hoàn lại 20000 đồng sau
3 năm. Sử dụng phương pháp
(a) Giá trị hiện tại ròng
(b) Tỷ suất sinh lợi nội tại
với công thức lãi suất kép rời rạc để tư vấn nhà đầu tư biết lãi suất trên thị trường là 5%/năm.
Phương án tư vấn có cần điều chỉnh không khi lãi suất thị trường là 12%? r −n Giải. (a) = 20 000, = 3, 17276.75 đồng. Vậy NPV = FV t
r = 5 ⇒ PV = FV 1 + ≈ 100
17276.75 − 15000 = 2276.75 > 0. Dự án đáng được đầu tư r 3 (b) Tương tự: i r
10% > 5%: Dự án đáng được đầu tư. 15000 1 + = 20000 ⇔ i ≈ 100
Trường hợp r = 12%: Sinh viên tự giải. 4.3 Phân tích bổ sung
Ví dụ trên có thể gây ấn tượng phương pháp IRR tốt hơn vì cho phép kết luận nhanh hơn với biến
động lãi suất trên thị trường, hay khi phải so sánh với nhiều ngân hàng áp dụng nhiều lãi suất khác
nhau. Thực tế, phương pháp IRR đôi khi đưa ra kết luận sai lầm khi ta cần so sánh nhiều dự án đầu tư.
Ví dụ Kinh tế 7. Có hai dự án đầu tư: Dự án A đầu tư 1000 đồng để được 1200 đồng sau 4
năm. Dự án B đầu tư 30000 đồng để được 35000 đồng sau 4 năm. Dự án nào được ưu tiên hơn
nếu lãi suất thị trường là 3%/năm?
Giải. Phương pháp NPV: NPV của dự án A: 66.18 đồng. NPV của dự án B: 1097.05 đồng. Vậy B đáng quan tâm hơn.
Thật vậy, nếu ta đầu tư A và phần tiền còn lại (trong số 30000 đồng để tham gia B) gửi tiết kiệm,
ta sẽ nhận lại sau 4 năm (sinh viên tự tính!) khoản tiền nhỏ hơn khoản tiền B mang đến.
Tuy nhiên, phương pháp IRR lại cho kết quả ngược lại khi IRR của A là 4.7%, còn của B là 3.9%
(Tại sao? Sinh viên tự tính!)
Lời giải thích ở đây là tỷ lệ phần trăm dù cao nhưng của một khoản tiền khiêm tốn vẫn chỉ cho
tổng giá trị thấp hơn tỷ lệ phần trăm nhỏ nhưng của khoản đầu tư đáng kể.
Sinh viên có thể tìm đọc Nghiên cứu sâu hơn quanh NPV và IRR trong [5], Phần 3.4, trang 220. TÀI LIỆU 7 Tài liệu
[1] Nguyễn Đình Huy (chủ biên), Giáo trình Giải tích 1, ĐHQG TPHCM - Trường ĐHBK, NXB ĐHQG TP HCM 2018.
[2] Nguyễn Quốc Hưng, Toán Cao Cấp C1 và một số ứng dụng trong kinh doanh, NXB ĐHQG TP HCM.
[3] Hoffmann, Calculus for business, economics and social life, Brief edition.
[4] James Stewart, Calculus Early Transcendentals, Brooks/Cole, 2012.
[5] Ian Jacques, Mathematics for Economics and business, Fifth editions, Prentice Hall, 2006.