Đề cương môn giải tích 2- Trường Đại học bách khoa - Đại học đà nẵng.

THANG ĐIỂM MÔN GIẢI TÍCH 2_Đại trà
Đưa được về dạng chính tắc 0,5 điểm
Giải được PTVP thuần nhất 1,0 điểm điểm
Câu 1: (2,5 điểm)
Biến thiên hằng số đúng 0,5 điểm Kết luận nghiệm đúng 0,5 điểm Tìm được y 1,0 điểm
Câu 2: (2,5 điểm)
Viết được dạng y * 0,5 điểm Tìm được y * 0,5 điểm Kết luận: 0,5 điểm
Biến đổi số hạng tổng quát của 0,5 điểm
chuỗi về dạng giới hạn đặc biệt
Câu 3: (1,0 điểm)
Tính được giới hạn và kết luận 0,5 điểm đúng
Đổi biến và viết được công thức 0,5 điểm
Câu 4: (2,5 điểm) Tìm được BKHT 1,0 điểm
Xét hai đầu mút và kết luận 1,0 điểm Vẽ hình 0,5 điểm
Câu 5: (1,5 điểm)
Đưa về được tích phân 2 lớp 0,5 điểm
Tính được kết quả đúng 0,5 điểm
TRƯỜNG ĐẠI HỌC BÁCH KHOA ĐÀ NẴNG KHOA TOÁN BỘ MÔN: GIẢI TÍCH
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên học phần: Giải tích 2 (Đại trà) Mã học phần: 3190121
Hình thức thi: Tự luận Đề số: 01
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Không được sử dụng tài liệu, điện thoại khi làm bài.
Câu 1: (2,5 điểm)
Giải phương trình vi phân cấp 1: (xex2 + y )dx+ ( y cos y + x)dy = 0.
Câu 2: (2,5 điểm)
Giải phương trình vi phân cấp 2:
y' + y'− 2 y = 20x sin x −18 cosx.
Câu 3: (1,0 điểm)  1
Khảo sát sự hội tụ của chuỗi số:  . 2ln n n=1
Câu 4: (2,5 điểm) + (1 + x)2n
Tìm miền hội tụ của chuỗi hàm:  . n=1 2n + 2
Câu 5: (1,5 điểm)
Tính tích phân mặt loại 2:
I =  x2 y2 zdxdy, S
trong đó S là phần mặt z = −(x2 + y2 ) nằm trong miền: x  0, y  0, z  −2, lấy hướng phía trên.
Tổng cộng có: 05 câu.
Đáp án - Đề số 01_Đại trà Câu 1: ĐS
1 ex2 + xy + y sin y + cos y = C. 2 Câu 2: Phương trình đặc trưng
𝑟2 + 𝑟 − 2 = 0, 𝑟 = 1, 𝑟 = −2
Nghiệm tổng quát của phương trình thuần nhất
𝑦 = 𝐶1𝑒𝑥 + 𝐶2𝑒−2𝑥 Nghiệm riêng dạng
𝑦𝑟 = (𝐴𝑥 + 𝐵)𝑐𝑜𝑠 𝑥 + (𝐶𝑥 + 𝐷)𝑠𝑖𝑛 𝑥
Nghiệm tổng quát của phương trình ban đầu
𝑦 = 𝐶1𝑒𝑥 + 𝐶2𝑒−2𝑥 + (1 − 2𝑥)𝑐𝑜𝑠 𝑥 − (1 + 6𝑥)𝑠𝑖𝑛 𝑥 Câu 3: 1 1 1 u = = = n
2ln n eln 2.ln n nln 2
Do ln2<1 nên suy ra chuỗi đã cho PHÂN KỲ.
Câu 4: MHT: −2  x  0  Câu 5: − 8
TRƯỜNG ĐẠI HỌC BÁCH KHOA ĐÀ NẴNG KHOA TOÁN BỘ MÔN: GIẢI TÍCH
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên học phần: Giải tích 2 (Đại trà) Mã học phần: 3190121
Hình thức thi: Tự luận Đề số: 02
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Không được sử dụng tài liệu, điện thoại khi làm bài.
Câu 1: (2,5 điểm)
Giải phương trình vi phân cấp 1: (x
+ y )dx+ ( y sin y + x)dy = 0.
Câu 2: (2,5 điểm)
Giải phương trình vi phân cấp 2:
y' − y'− 2 y = 26 sin x + 40x cos x.
Câu 3: (1,0 điểm)  1
Khảo sát sự hội tụ của chuỗi số:  . 3ln n n=1
Câu 4: (2,5 điểm) + (−1)n
Tìm miền hội tụ của chuỗi hàm:  .
n=1 (3n+ 1)(x−1)n
Câu 5: (1,5 điểm)
Tính tích phân mặt loại 2:
I =  x3 z dxdy, S
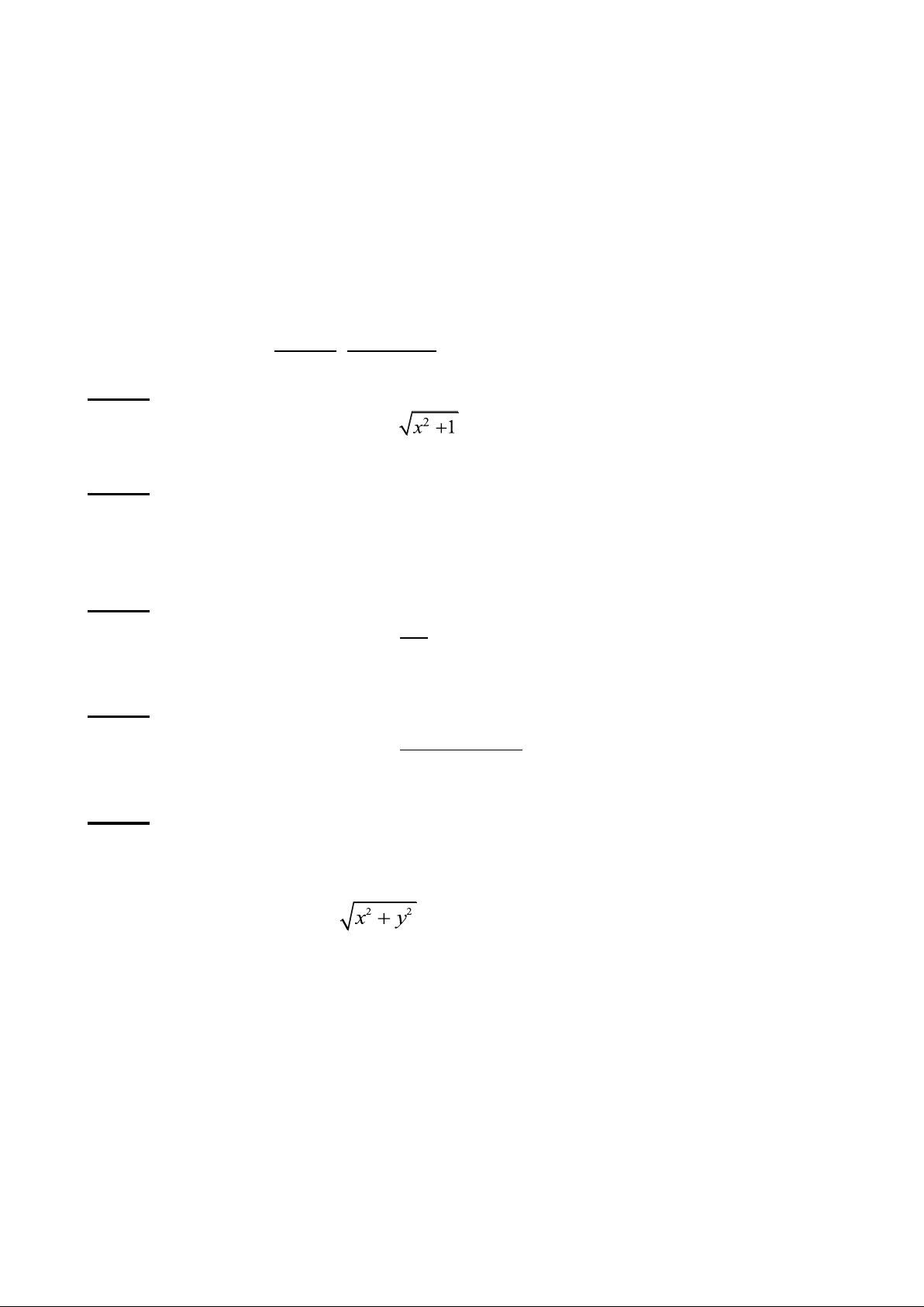
trong đó S là phần mặt z =
nằm trong miền: x  0, y  0, z  3, lấy hướng phía dưới.
Tổng cộng có: 05 câu.
Đáp án - Đề số 02_Đại trà Câu 1: ĐS 1
(x2 +1) x2 +1 + xy − y cosy+ siny = C. 3 Câu 2: Phương trình đặc trưng
𝑟2 − 𝑟 − 2 = 0, 𝑟 = −1, 𝑟 = 2
Nghiệm tổng quát của phương trình thuần nhất
𝑦 = 𝐶1𝑒−𝑥 + 𝐶2𝑒2𝑥 Nghiệm riêng dạng
𝑦𝑟 = (𝐴𝑥 + 𝐵)𝑐𝑜𝑠 𝑥 + (𝐶𝑥 + 𝐷)𝑠𝑖𝑛 𝑥
Nghiệm tổng quát của phương trình ban đầu
𝑦 = 𝐶1𝑒−𝑥 + 𝐶2𝑒2𝑥 + (1 − 12𝑥)𝑐𝑜𝑠 𝑥 + (1 − 4𝑥)𝑠𝑖𝑛 𝑥 Câu 3: 1 1 1 u = = = n
3ln n eln 3.ln n nln 3
Do ln3>1 nên suy ra chuỗi đã cho HỘI TỤ.  x  2 Câu 4: MHT:   x  0 Câu 5: -81
TRƯỜNG ĐẠI HỌC BÁCH KHOA ĐÀ NẴNG KHOA TOÁN BỘ MÔN: GIẢI TÍCH
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên học phần: Giải tích 2 (Đại trà) Mã học phần: 3190121
Hình thức thi: Tự luận Đề số: 03
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Không được sử dụng tài liệu, điện thoại khi làm bài.
Câu 1: (2,5 điểm)
Giải phương trình vi phân cấp 1: (ex sin(ex +1) + y)dx+ ( yey + x)dy = 0.
Câu 2: (2,5 điểm)
Giải phương trình vi phân cấp 2:
y' − 3 y'+ 2 y = (36 − 40 x) sin 2 x.
Câu 3: (1,0 điểm)  2ln n
Khảo sát sự hội tụ của chuỗi số:  . n=1 5 ln n
Câu 4: (2,5 điểm) + (−1)n
Tìm miền hội tụ của chuỗi hàm:  .
n=1 (n+ 1)2 (3x + 1)n
Câu 5: (1,5 điểm)
Tính tích phân mặt loại 2:
I =  y3 (3 − z) dxdy, S
trong đó S là phần mặt z = 3 − (x2 + y2 ) nằm trong miền: x  0, y  0, z  0, lấy hướng phía trên.
Tổng cộng có: 05 câu.
Đáp án - Đề số 03_Đại trà Câu 1: ĐS
xy − cos(ex + 1) + yey − ey = C. Câu 2: Phương trình đặc trưng
𝑟2 − 3𝑟 + 2 = 0, 𝑟 = 1, 𝑟 = 2
Nghiệm tổng quát của phương trình thuần nhất
𝑦 = 𝐶1𝑒𝑥 + 𝐶2𝑒2𝑥 Nghiệm riêng dạng
𝑦𝑟 = (𝐴𝑥 + 𝐵)𝑐𝑜𝑠 2𝑥 + (𝐶𝑥 + 𝐷)𝑠𝑖𝑛 2𝑥
Nghiệm tổng quát của phương trình ban đầu
𝑦 = 𝐶1𝑒𝑥 + 𝐶2𝑒2𝑥 + (4 − 6𝑥)𝑐𝑜𝑠 2𝑥 + (2𝑥 + 3)𝑠𝑖𝑛 2𝑥 Câu 3: 2ln n  2 lnn 1 1 u = n 5ln n =   5 = lnn = nln(5/2)    5     2 
Do ln5/2<1 nên suy ra chuỗi đã cho PHÂN KỲ.  x  0  Câu 4: MHT: −2  x   3 18 3 Câu 5: 7
TRƯỜNG ĐẠI HỌC BÁCH KHOA ĐÀ NẴNG KHOA TOÁN BỘ MÔN: GIẢI TÍCH
ĐỀ THI KẾT THÚC HỌC PHẦN
Tên học phần: Giải tích 2 (Đại trà) Mã học phần: 3190121
Hình thức thi: Tự luận Đề số: 04
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Không được sử dụng tài liệu, điện thoại khi làm bài.
Câu 1: (2,5 điểm)
Giải phương trình vi phân cấp 1: (ex
+ y )dx+ (sin y cos y + x)dy = 0.
Câu 2: (2,5 điểm)
Giải phương trình vi phân cấp 2:
y' + 3 y'− 4 y = (34 x−18) cosx.
Câu 3: (1,0 điểm)  3ln n
Khảo sát sự hội tụ của chuỗi số:  . n=1 7 ln n
Câu 4: (2,5 điểm) + (−1)n
Tìm miền hội tụ của chuỗi hàm:  .
n=2 (n−1)2 (2 x−1)2n
Câu 5: (1,5 điểm)
Tính tích phân mặt loại 2:
I =  xy3 (z + 2)dxdy, S
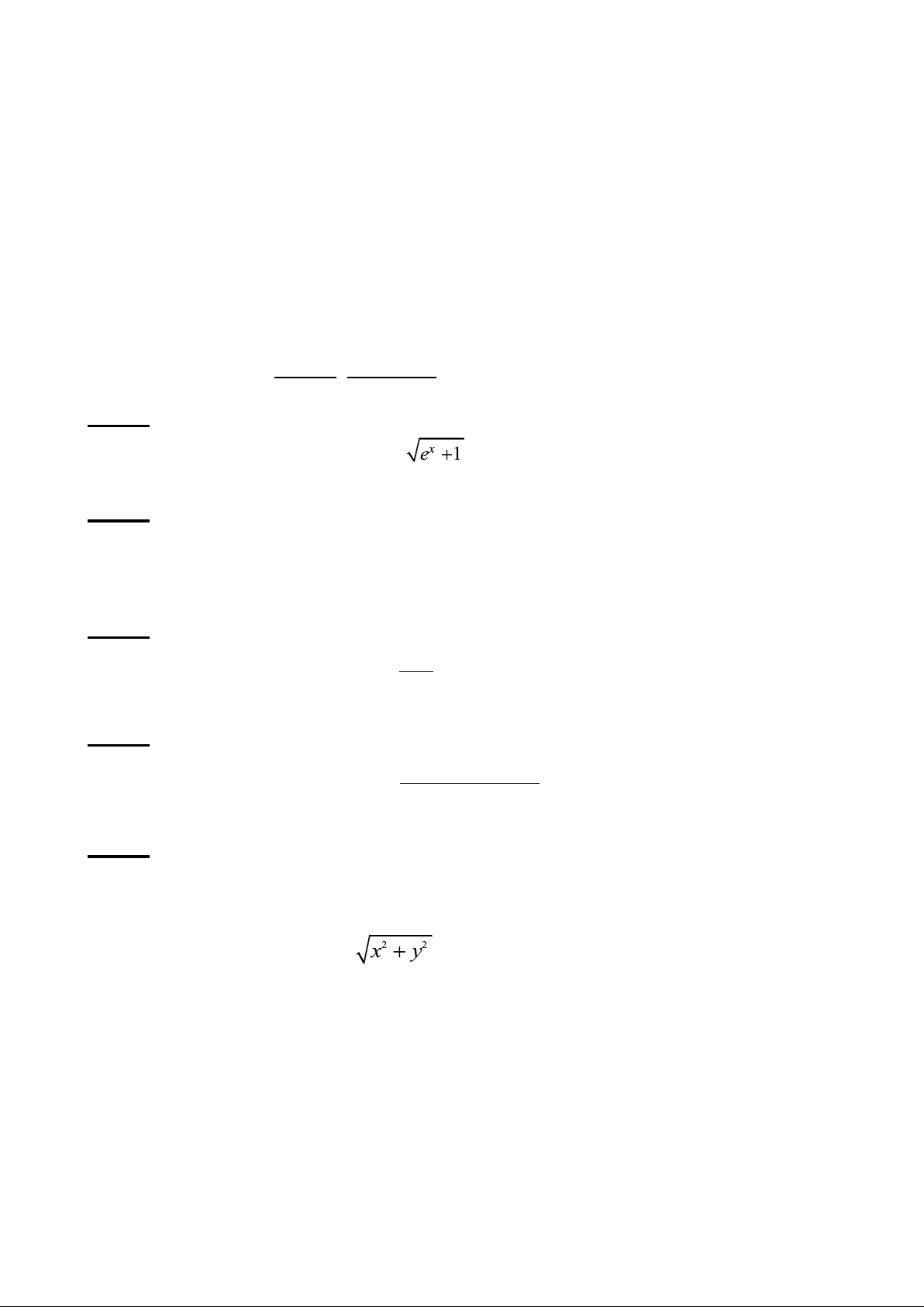
trong đó S là phần mặt z =
− 2 nằm trong miền: x  0, y  0, z  0, lấy hướng phía dưới.
Tổng cộng có: 05 câu.
Đáp án - Đề số 04_Đại trà Câu 1: ĐS 2 1
(ex +1) ex +1 + xy − cos 2 y = C. 3 4 Câu 2: Phương trình đặc trưng
𝑟2 + 3𝑟 − 4 = 0, 𝑟 = 1, 𝑟 = −4
Nghiệm tổng quát của phương trình thuần nhất
𝑦 = 𝐶1𝑒𝑥 + 𝐶2𝑒−4𝑥 Nghiệm riêng dạng
𝑦𝑟 = (𝐴𝑥 + 𝐵)𝑐𝑜𝑠 𝑥 + (𝐶𝑥 + 𝐷)𝑠𝑖𝑛 𝑥
Nghiệm tổng quát của phương trình ban đầu
𝑦 = 𝐶1𝑒𝑥 + 𝐶2𝑒−4𝑥 + (3 − 5𝑥)𝑐𝑜𝑠 𝑥 + (3𝑥 + 2)𝑠𝑖𝑛 𝑥 Câu 3: 3ln n  3 lnn 1 1 u = n 7ln n =   7 = lnn = nln(7/3)    7     3 
Do ln(7/3)<1 nên suy ra chuỗi đã cho PHÂN KỲ.  x  1 Câu 4: MHT:   x  0 Câu 5: 32/7