Đề cương môn Giải tích - Trường Đại học lao động -  xã hội.

I. Lời mở đầu
Giải tích là một nhánh quan trọng của toán học, tập trung vào việc nghiên cứu các
khái niệm như giới hạn, đạo hàm và tích phân. Vai trò của giải tích không chỉ nằm
ở việc cung cấp công cụ để giải quyết các bài toán trong toán học thuần túy, mà
còn ứng dụng rộng rãi trong các lĩnh vực như vật lý, kỹ thuật, kinh tế, khoa học máy tính…
Tích phân suy rộng là một công cụ quan trọng trong giải tích, cho phép chúng ta
đánh giá các tích phân mà không thể được xác định bằng các phương pháp tích
phân thông thường do tính vô hạn của hàm.
Trong khuôn khổ bài báo cáo này, chúng tôi sẽ trình bày cơ sở lý thuyết, các ứng
dụng của tích phân suy rộng cùng với đó là xử lý chi tiết một ví dụ. Dù đã có sự
chuẩn bị, thì việc thiếu sót và sai sót là không thể tránh khỏi. Vì thế, chúng tôi rất
mong nhận được những đánh giá và đóng góp khách quan, mang tính xây dựng từ
phía giáo viên cũng như các bạn đọc. Xin chân thành cảm ơn. II.
Cơ sở lý thuyết về các ứng dụng của tích phân suy rộng
Tích phân suy rộng là một mở rộng của tích phân thông thường, được định nghĩa
để giải quyết các trường hợp mà hàm số cần tích phân không bị chặn hoặc miền
tích phân không giới hạn. Nó đóng vai trò quan trọng trong nhiều lĩnh vực toán học và ứng dụng thực tế.
1. Định nghĩa tích phân suy rộng
Tích phân suy rộng được chia thành hai loại chính:
 Tích phân trên miền không giới hạn: Khi một hoặc cả hai cận của miền
tích phân là vô cực, tích phân suy rộng được định nghĩa như sau: hoặc Ví dụ:
 Tích phân trên miền hữu hạn với hàm không bị chặn: Khi hàm
không xác định hoặc có điểm kỳ dị trong miền tích phân, nó được xác định bằng giới hạn:
với c là điểm kỳ dị. Ví dụ:
2. Các ứng dụng của tích phân suy rộng
Tích phân suy rộng có nhiều ứng dụng trong cả lý thuyết và thực tiễn, bao gồm:
2.1.1 Trong giao thông: Dự đoán khả năng/xác suất
Giả sử tại một ngã tư đông đúc, tai nạn giao thông xảy ra với tần suất trung bình là
một vụ trong ba tháng. Sau khi người dân phàn nàn, người ta đã tăng cường an
ninh giao thông ở khu vực ngã tư. Tám tháng trôi qua kể từ khi an ninh giao thông
được cải thiện và không có tai nạn nào xảy ra. Việc tăng cường này có hiệu quả
không hay tám tháng không có tai nạn tăng là ngẫu nhiên, tình cờ? Biết: Với: Trong đó:
 P là khả năng/xác suất xảy ra tai nạn
 k là tần suất trung bình
 x là khoảng thời gian xảy ra các vụ tai nạn, giữa thời điểm a và thời điểm b, tính theo tháng Giải:
Ta cần phải tính tích phân:
và xác định xem nếu tình hình giao thông
không được cải thiện thì xác suất việc 8 tháng trôi qua mà không xảy ra tai nạn xảy ra có cao không Giá trị
biểu thị xác suất không có tai nạn nào trong 8 tháng nếu các điều
kiện giao thông không được cải thiện. Vì xác suất này là rất, rất nhỏ nên ta có thể
thấy việc tám tháng không xảy ra tai nạn không thể là ngẫu nhiên, mà là kết quả
của việc tăng cường an ninh giao thông.
2.1.2 Trong kinh tế: Tính giá trị vốn hóa (capital value)
Tích phân xác định thường được sử dụng để xác định tổng thu nhập trong một số
năm cố định từ một dòng thu nhập liên tục. Khi ta thay đổi cận của tích phân giới
hạn để tính tích phân suy rộng của luồng thu nhập này, ta đang đi tìm giá trị vốn hóa của nó: trong đó: 
: tốc độ thay đổi thường niên của dòng tiền tại thời điểm t
 r: tỉ lệ lãi suất kép hằng năm
Tích phân xác định thường được sử dụng để xác định tổng thu nhập trong một số
năm cố định từ một dòng thu nhập liên tục. Nó cũng được sử dụng để tìm giá trị
xác định của một luồng thu nhập liên tục thay đổi trong tương lai. Khi chúng ta
Ta lấy một ví dụ cụ thể hơn: Giả sử hội cựu sinh viên của một trường đại học muốn
hỗ trợ cho trường bằng cách tài trợ một khoản tiền: Mỗi năm họ sẽ trích ra 20.000
Rupee từ khoản tiền đó để cung cấp sách giáo khoa miễn phí cho những sinh viên
có nhu cầu. Giả sử lãi suất hàng năm là 10% được tính gộp liên tục, hãy tìm số tiền
mà hội cựu sinh viên phải trả cho trường. Ta tính:
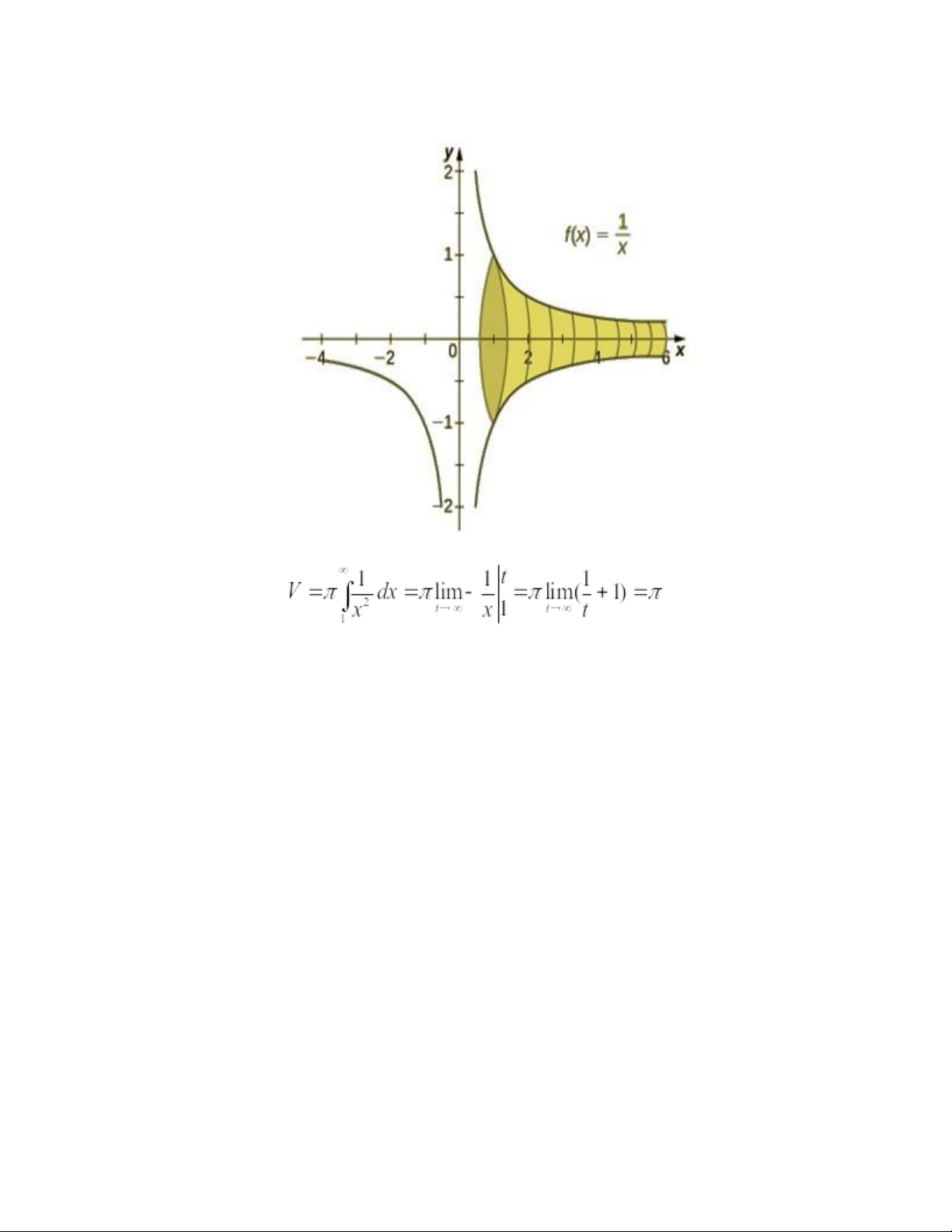
2.1.3 Tính thể tích vật rắn 2.2.1 Vật lý
 Tính diện tích, thể tích và các đại lượng liên tục: Tích phân suy rộng
được sử dụng để tính các đại lượng trên miền không giới hạn. Ví dụ:
o Diện tích dưới một hàm suy giảm vô hạn.
o Thể tích của vật thể quay quanh một trục (phương pháp vỏ trụ hoặc mặt cắt).
 Điện học và cơ học lượng tử:
o Mô tả trường điện từ và thế năng trong không gian vô hạn.
o Hàm sóng lượng tử trong cơ học lượng tử thường liên quan đến tích
phân suy rộng để tính xác suất.
2.2.2 Xác suất và thống kê
 Hàm mật độ xác suất (PDF): Các hàm mật độ xác suất liên tục như phân
phối chuẩn, phân phối mũ thường được tính thông qua tích phân suy rộng trên miền vô hạn
 Kỳ vọng và phương sai: Tích phân suy rộng được dùng để tính kỳ vọng và
phương sai của các biến ngẫu nhiên. 2.2.3 Kỹ thuật
 Xử lý tín hiệu: Trong phân tích Fourier, các tín hiệu vô hạn thường được
biểu diễn qua tích phân suy rộng.
 Mạch điện: Tính toán đáp ứng của mạch RC, RLC với các hàm đầu vào
phức tạp liên quan đến miền thời gian vô hạn. 2.2.4 Toán học
 Chuỗi số và hàm đặc biệt: Tích phân suy rộng xuất hiện trong việc định
nghĩa và tính giá trị của các hàm đặc biệt như hàm gamma ( )hoặc hàm zeta Riemann ( )
 Giải tích hàm: Tích phân suy rộng được sử dụng trong nghiên cứu các không gian hàm như
hoặc trong lý thuyết phổ.
2.2.5 Kinh tế và tài chính
 Mô hình hóa rủi ro: Các mô hình phân phối xác suất trong tài chính (như
phân phối log-normal) thường sử dụng tích phân suy rộng để tính xác suất
hoặc kỳ vọng lợi nhuận.
 Định giá tài sản: Tích phân suy rộng giúp định giá các công cụ tài chính
dựa trên các giả định liên tục. III. Kết luận
Tích phân suy rộng không chỉ là công cụ lý thuyết quan trọng trong toán học mà
còn có nhiều ứng dụng trong các ngành khoa học tự nhiên và kỹ thuật. Việc hiểu rõ
định nghĩa, tính chất và ứng dụng của nó giúp giải quyết hiệu quả các bài toán trong thực tế.
Document Outline

• I. Lời mở đầu
• II. Cơ sở lý thuyết về các ứng dụng của tích phân suy rộng
• 1. Định nghĩa tích phân suy rộng
•  Tích phân trên miền hữu hạn với hàm không bị chặn: Khi hàm
• 2. Các ứng dụng của tích phân suy rộng
• 2.1.1 Trong giao thông: Dự đoán khả năng/xác suất
• 2.1.2 Trong kinh tế: Tính giá trị vốn hóa (capital value)
• 2.1.3 Tính thể tích vật rắn
•  Điện học và cơ học lượng tử:
• 2.2.2 Xác suất và thống kê
• 2.2.3 Kỹ thuật
• 2.2.4 Toán học
• 2.2.5 Kinh tế và tài chính
• III. Kết luận