Đề cương môn Toán cao cấp- Trường Đại học bách khoa - Đại học đà nẵng.

12/4/2022
TOÁN CAO CẤP HỌC PHẦN I
CHƯƠNG 1. KHÔNG GIAN VÉC TƠ ℝn
CHƯƠNG 2. MA TRẬN - ĐỊNH THỨC
CHƯƠNG 3. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
CHƯƠNG 4. DẠNG TOÀN PHƯƠNG CHƯƠNG 1
KHÔNG GIAN VÉC TƠ 𝒏 1 12/4/2022 BÀI 1 KHÔNG GIAN
VÉC TƠ n CHIỀU 𝒏 1. Định nghĩa 1
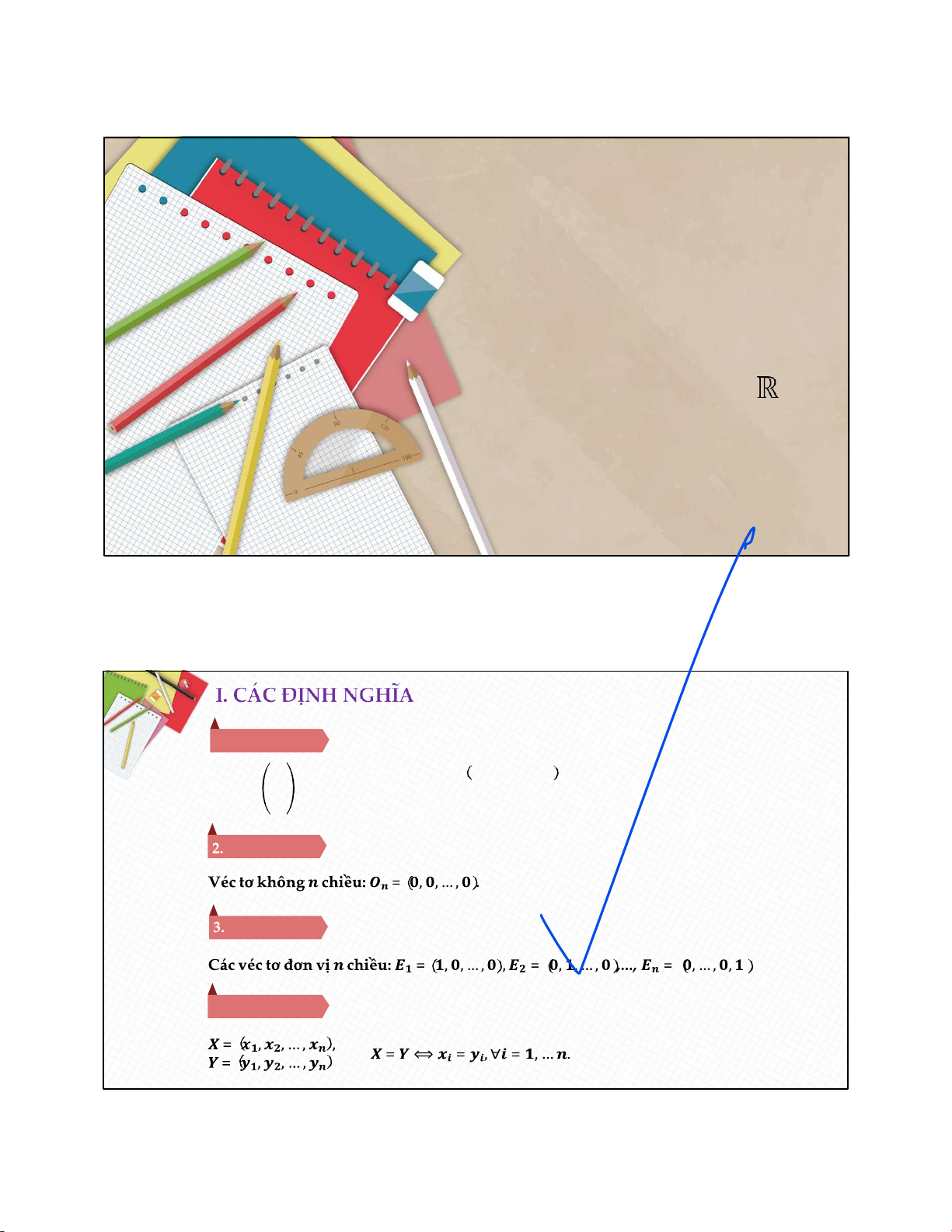
Mỗi bộ gồm 𝒏 số thực 𝒙𝟏, 𝒙𝟐, … , 𝒙𝒏 được xếp có thứ tự viết dạng cột 𝒙𝟏 𝒙
hoặc dạng hàng 𝒙𝟏, 𝒙𝟐, … , 𝒙𝒏 gọi là một véc tơ 𝒏 chiều, 𝟐 … trong đó 𝒙 𝒙
𝒊 là tọa độ thứ 𝒊 của véc tơ đó. 𝒏
Các véc tơ thường kí hiệu bằng các chữ cái in hoa như 𝑿, 𝒀, 𝑨, 𝑩, … Định nghĩa 2 Định nghĩa 3 4. Định nghĩa 4
Hai véc tơ cùng 𝒏 chiều bằng nhau 2 12/4/2022
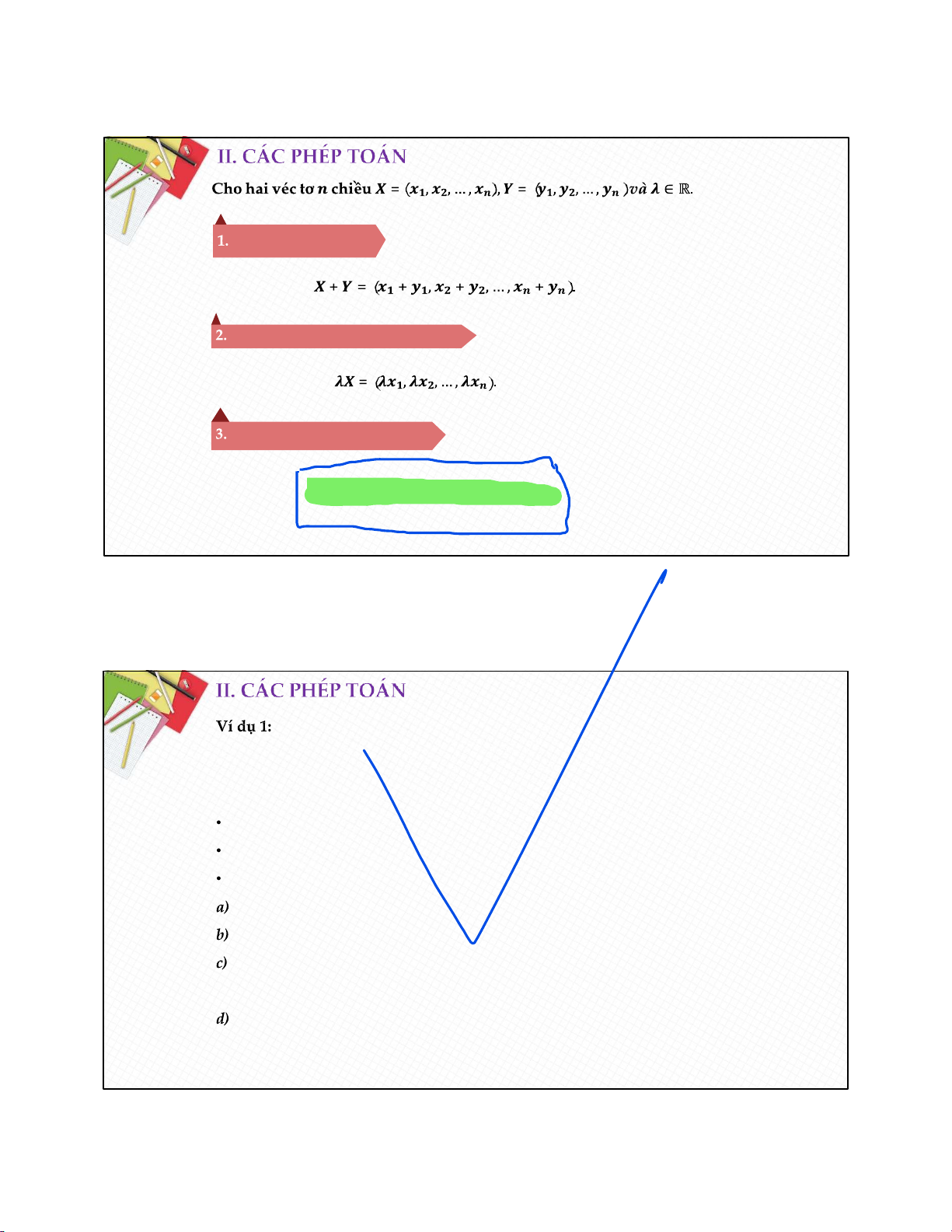
Phép cộng hai véc tơ
Phép nhân véc tơ với một số thực
Tích vô hướng của hai véc tơ
Một nhà máy sản xuất 4 loại sản phẩm I, II, III, IV.
Số đơn vị sản phẩm các loại I, II, III, IV nhà máy sản xuất được trong:
tháng 1 lần lượt là 10, 12, 14, 13.
tháng 2 lần lượt là 11, 13, 15, 16.
tháng 3 lần lượt là 11, 13, 15, 16.
Biểu diễn dưới dạng véc tơ sản lượng mỗi tháng của nhà máy.
Sử dụng phép cộng hai véc tơ biểu diễn tổng sản lượng của tháng 1 và tháng 2.
Sử dụng phép nhân véc tơ với một số thực biểu diễn dưới dạng véc tơ tổng sản
lượng của tháng 2 và tháng 3.
Cho giá của mỗi đơn vị sản phẩm loại I, II, III, IV lần lượt là 5, 6, 7, 9 tỷ đồng.
Biểu diễn doanh thu tháng 1 dưới dạng tích vô hướng hai véc tơ. 3 12/4/2022
Định nghĩa: Tập hợp tất cả các véc tơ n chiều cùng với hai phép toán cộng 2 véc tơ và
nhân véc tơ với một số thực được gọi là một không gian véc tơ n chiều. Kí hiệu: ℝ𝒏. BÀI 2 CÁC MỐI LIÊN HỆ
TUYẾN TÍNH TRONG 𝒏 4 12/4/2022 1. Định nghĩa 1
Cho hệ véc tơ 𝑺 = 𝑨𝟏, 𝑨𝟐, … , 𝑨𝒎 ⊂ ℝ𝒏, 𝝀𝒊 ∈ ℝ, ∀𝒊 = 𝟏, 𝒎.
Biểu thức có dạng
𝝀𝟏𝑨𝟏 + 𝝀𝟐𝑨𝟐 + ⋯ + 𝝀𝒎𝑨𝒎
được gọi là một tổ hợp tuyến tính của hệ 𝑺. Nhận xét:
• Mỗi tổ hợp tuyến tính của hệ 𝑺 là một véc tơ 𝒏 chiều.
• Có vô số tổ hợp tuyến tính của hệ 𝑺 cho trước. 2. Định nghĩa 2
Véc tơ 𝒏 chiều 𝑿 được gọi là biểu diễn tuyến tính qua hệ 𝑺 hay còn gọi véc tơ 𝑿 là tổ hợp
tuyến tính của hệ 𝑺 nếu tồn tại các số thực 𝝀𝟏, 𝝀𝟐, … , 𝝀𝒎 sao cho: Nhận xét:
• Véc tơ 𝑶𝒏 luôn biểu diễn tuyến tính qua mọi hệ véc tơ 𝒏 chiều.
• Véc tơ 𝒏 chiều 𝑿 luôn biểu diễn tuyến tính qua hệ n véc tơ đơn vị 𝒏 chiều.
Nếu véc tơ 𝒏 chiều 𝑿 biểu diễn tuyến tính qua hệ 𝑺 thì véc tơ X luôn biểu thị tuyến tính qua
mọi hệ chứa hệ 𝑺. 5 12/4/2022 Ví dụ 1:
Xét xem véc tơ 𝑿 = 𝟑, 𝟓, 𝟏𝟎 có được biểu diễn tuyến tính qua hệ véc tơ trên không? Định nghĩa 3
Hệ 𝑺 được gọi là độc lập tuyến tính (ĐLTT) nếu
Hệ 𝑺 được gọi là phụ thuộc tuyến tính (PTTT) nếu sao cho 6 12/4/2022 Ví dụ 2:
Một số tính chất
Tính chất 2: Nếu một hệ ĐLTT thì hệ đó không chứa véc tơ 𝟎𝒏.
Hệ quả: Nếu hệ có chứa véc tơ 𝟎𝒏 thì hệ đó PTTT.
Tính chất 3: Nếu một hệ véc tơ PTTT thì mọi hệ chứa nó cũng PTTT.
Hệ quả: Nếu một hệ ĐLTT thì mọi hệ con khác rỗng của nó cũng ĐLTT. 7 12/4/2022
3. Một số định lý
Định lý 2. Một véc tơ biểu diễn tuyến tính qua một hệ ĐLTT thì sự biểu diễn đó là duy nhất.
Định lý 3. Trong không gian ℝ𝒏cho hai hệ véc tơ:
Hệ (1): 𝑨𝟏, 𝑨𝟐, . . . , 𝑨𝒎 và hệ (2): 𝑩𝟏, 𝑩𝟐, . . . , 𝑩𝒌
Nếu mỗi véc tơ của hệ (1) đều biểu diễn tuyến tính qua các véc tơ của hệ (2) và 𝒎 > 𝒌
thì hệ (1) PTTT. 𝟎 𝟑 𝟕
Véc tơ 𝑿 có biểu diễn tuyến tính qua hệ 𝑺 hay không?
Sự biểu diễn tuyến tính ở câu a) có duy nhất không? 𝟐 𝟓 𝟔
Ví dụ 4: Cho hệ véc tơ 𝑺 = 𝑨𝟏 = 𝟏 𝟎
Véc tơ 𝑿 có biểu diễn tuyến tính qua hệ 𝑺 hay không?
Sự biểu diễn tuyến tính ở câu a) có duy nhất không? 8 12/4/2022
Ví dụ 15: Một nhà máy sử dụng 3 loại vật liệu để sản xuất 4 loại sản phẩm. Biết 𝟏 𝟏 𝟐 𝟏 𝟏 𝟐 𝟑 𝟐
là các véc tơ định mức vật liệu cho mỗi đơn vị sản phẩm tương ứng.
Tìm biểu diễn tuyến tính của 𝑨𝟒 qua hệ véc tơ 𝑨𝟏, 𝑨𝟐, 𝑨𝟑 và nêu ý nghĩa kinh tế của kết quả đó.
Xác định số lượng vật liệu vừa đủ để sản xuất được 4 đơn vị sản phẩm loại 1, 5 đơn vị sản phẩm
loại 2, 3 đơn vị sản phẩm loại 3 và 0 đơn vị sản phẩm loại 4.
Với điều kiện sử dụng vừa hết vật liệu đã có ở ý b), nếu nhà máy muốn sản xuất thêm 1 đơn vị
sản phẩm loại 4 thì sản lượng các loại sản phẩm khác là bao nhiêu?
Với điều kiện sử dụng vừa hết vật liệu ở ý b), nhà máy có thể sản xuất được tối đa bao nhiêu đơn
vị sản phẩm loại 4? BÀI 3
CƠ SỞ CỦA KHÔNG GIAN VÉC TƠ 𝒏 9 12/4/2022
I. HỆ VÉC TƠ ĐỘC LẬP TUYẾN TÍNH CỰC ĐẠI TRONG ℝ𝒏 Định nghĩa 1
Cho hệ 𝒎 véc tơ 𝒏 chiều 𝑨𝟏, 𝑨𝟐, . . . , 𝑨𝒎 𝟏 .
Hệ (1) được gọi là hệ véc tơ độc lập tuyến tính cực đại (ĐLTTCĐ) trong không gian ℝ𝒏 nếu
hệ đó đồng thời thỏa mãn hai điều kiện: Hệ (1) ĐLTT.
Nếu thêm bất kỳ một véc tơ nào của không gian ℝ𝒏 vào hệ đã cho thì hệ mới PTTT.
Chú ý: Điều kiện thứ hai còn tương đương với điều kiện sau đây:
∀𝑿 ∈ ℝ𝒏 đều biểu diễn tuyến tính qua hệ (1).
I. HỆ VÉC TƠ ĐỘC LẬP TUYẾN TÍNH CỰC ĐẠI TRONG ℝ𝒏 Ví dụ 1:
Các hệ véc tơ sau có phải là hệ ĐLTTCĐ trong không gian ℝ𝒏 không? a) b) 10
Downloaded by giang le (nguyengiang1990@gmail.com) 12/4/2022
I. HỆ VÉC TƠ ĐỘC LẬP TUYẾN TÍNH CỰC ĐẠI TRONG ℝ𝒏 Nhận xét:
Trong không gian 𝒏 chiều có vô số hệ véc tơ ĐLTTCĐ nhưng mọi hệ véc tơ ĐLTTCĐ
đều có số véc tơ bằng nhau và bằng 𝒏 (𝒏 là số chiều của mỗi véc tơ).
Trong không gian ℝ𝒏:
Mọi hệ véc tơ có số véc tơ lớn hơn 𝒏 đều PTTT.
Mọi hệ ĐLTT chứa không quá 𝒏 véc tơ.
Mọi hệ ĐLTT chứa đúng 𝒏 véc tơ đều là hệ véc tơ ĐLTTCĐ.
II. CƠ SỞ CỦA KHÔNG GIAN ℝ𝒏 Định nghĩa 2
Trong không gian ℝ𝒏 mỗi hệ gồm 𝒏 véc tơ ĐLTT được gọi là một cơ sở của không gian ℝ𝒏. Ví dụ 2:
Hệ véc tơ nào sau đây là cơ sở của KGVT ℝ𝟑? 11 12/4/2022
II. CƠ SỞ CỦA KHÔNG GIAN ℝ𝒏 2. Tính chất
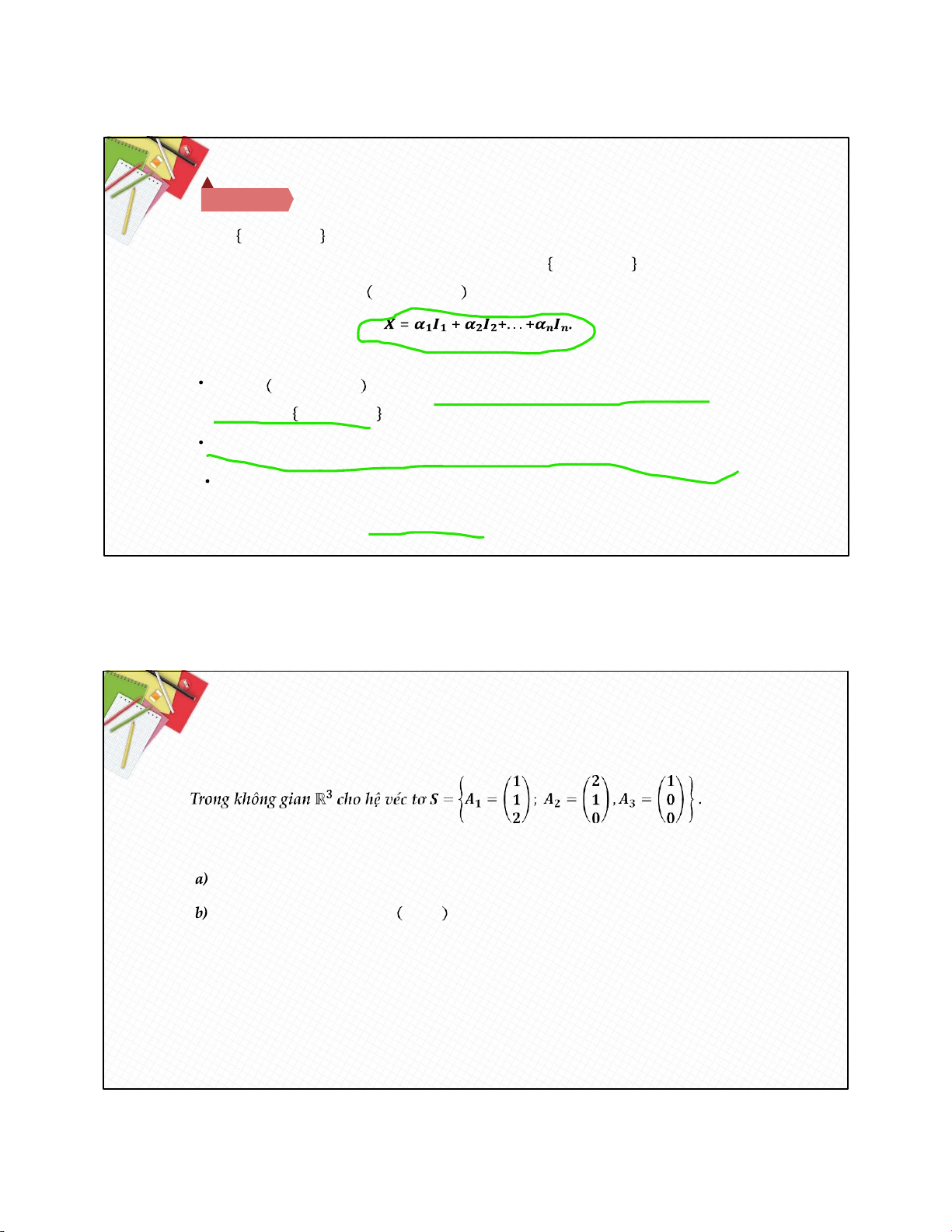
Cho 𝑰𝟏, 𝑰𝟐, . . . , 𝑰𝒏 là 1 cơ sở của không gian ℝ𝒏, khi đó mọi véc tơ 𝑿 ∈ ℝ𝒏
đều được biểu diễn tuyến tính duy nhất qua cơ sở 𝑰𝟏, 𝑰𝟐, . . . , 𝑰𝒏 , nghĩa là tồn
tại duy nhất bộ số thực 𝜶𝟏, 𝜶𝟐, . . . , 𝜶𝒏 sao cho Chú ý:
Bộ số 𝜶𝟏, 𝜶𝟐, . . . , 𝜶𝒏 được gọi là hệ số phân tích (tọa độ) của véc tơ 𝑿
theo cơ sở 𝑰𝟏, 𝑰𝟐, . . . , 𝑰𝒏 .
Hệ số phân tích của véc tơ 𝑿 theo các cơ sở khác nhau của ℝ𝒏 thì khác nhau.
Việc tìm hệ số phân tích (tọa độ) của véc tơ 𝑿 qua cơ sở của không gian
ℝ𝒏 thực chất là việc đi giải hệ và ta sẽ gặp bài toán này ở chương 3.
II. CƠ SỞ CỦA KHÔNG GIAN ℝ𝒏 Ví dụ 3:
Chứng minh 𝑺 là một cơ sở của ℝ𝟑.
Tìm tọa độ của véc tơ 𝑿 = 𝟓, 𝟑, 𝟐 qua cơ sở 𝑺. 12 12/4/2022 BÀI 4
CƠ SỞ VÀ HẠNG CỦA HỆ VÉC TƠ
I. CƠ SỞ CỦA HỆ VÉC TƠ
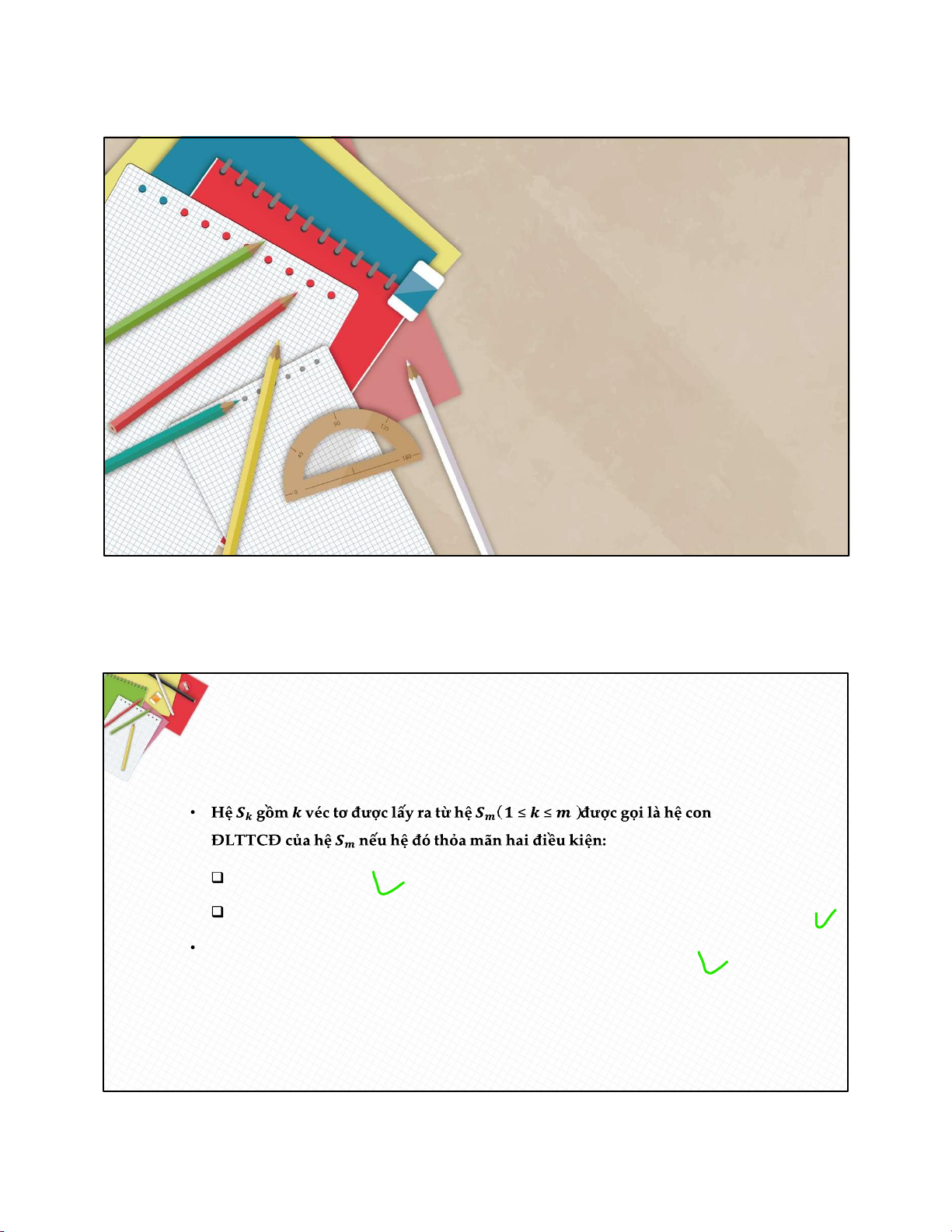
Cho hệ 𝑺𝒎 gồm 𝒎 véc tơ 𝒏 chiều (hệ này chứa ít nhất một véc tơ khác véc tơ 𝑶𝒏).
Hệ 𝑺𝒌 là hệ ĐLTT. (*)
Nếu thêm bất kỳ một véc tơ nào của hệ 𝑺𝒎 vào hệ 𝑺𝒌 thì thu được hệ PTTT. (**)
Mỗi hệ con ĐLTTCĐ của hệ véc tơ được gọi là một cơ sở của hệ đó.
Chú ý: Điều kiện (**) tương đương với điều kiện: mọi véc tơ của hệ 𝑺𝒎 đều biểu
diễn tuyến tính qua hệ 𝑺𝒌. 13 12/4/2022
I. CƠ SỞ CỦA HỆ VÉC TƠ Ví dụ 1: 𝟏 𝟐 𝟏 𝟐 𝟐 ; 𝑨 𝟒 𝟐 = ; 𝑨 𝟎 𝟑 = ; 𝑨 𝟐 . 𝟒 = 𝟎 𝟎 𝟑 𝟑
CMR hệ 𝑨𝟏, 𝑨𝟑 là một hệ con ĐLTTCĐ của hệ 𝑺.
Chỉ ra một hệ con ĐLTTCĐ khác của hệ 𝑺 (nếu có).
Nhận xét: Qua ví dụ trên ta thấy trong một hệ véc tơ có thể có rất nhiều
hệ con ĐLTTCĐ nhưng mọi hệ con ĐLTTCĐ đều có số véc tơ bằng nhau.
Chứng minh 𝑬𝟏, 𝑬𝟐 là một cơ sở của 𝑺.
II. HẠNG CỦA HỆ VÉC TƠ
Cho hệ 𝒎 véc tơ 𝒏 chiều 𝑨𝟏, 𝑨𝟐, ....... , 𝑨𝒎
∃𝒊 ∈ 𝟏, 𝟐, … , 𝒎 : 𝑨𝒊 𝟎𝒏 .Ta
gọi số véc tơ của hệ con ĐLTTCĐ của hệ 𝑨𝟏, 𝑨𝟐, . . . . . , 𝑨𝒎 là hạng của hệ
đó và ký hiệu là 𝒉 𝑨𝟏, 𝑨𝟐, . . . , 𝑨𝒎 . 14 12/4/2022
II. HẠNG CỦA HỆ VÉC TƠ Ví dụ 3: Ví dụ 4:
Trong không gian véc tơ ℝ𝟑, cho hệ 𝟏 𝟐 𝟐 𝟑 𝟏
; 𝑨𝟑 = 𝟐 ; 𝑨𝟒 = 𝟎 . 𝟐 𝟎 𝟒 𝟐
Chứng minh rằng 𝑨𝟏, 𝑨𝟐 là một cơ sở của 𝑺 và tìm 𝒉 𝑺 .
II. HẠNG CỦA HỆ VÉC TƠ Nhận xét:
𝑨𝟏, 𝑨𝟐, . . . , 𝑨𝒎 . 15 12/4/2022
II. HẠNG CỦA HỆ VÉC TƠ
2. Một số tính chất Ví dụ 5:
Tác động lên véc tơ
Đổi chỗ hai véc tơ trong hệ.
Nhân một số thực 𝝀 ≠ 𝟎 vào một véc tơ trong hệ.
Nhân số thực 𝝀 vào một véc tơ rồi cộng với một véc tơ khác trong hệ.
Tác động lên tọa độ
Đổi chỗ hai tọa độ tương ứng của các véc tơ trong hệ.
Nhân một số thực 𝝀 ≠ 𝟎 vào tọa độ thứ 𝒊 của các véc tơ trong hệ.
Nhân một số thực 𝝀 vào tọa độ thứ 𝒊 rồi cộng vào tọa độ thứ 𝒋 của các véc tơ trong hệ. 16 12/4/2022 Ví dụ 4: 𝟏 𝟏 𝟐
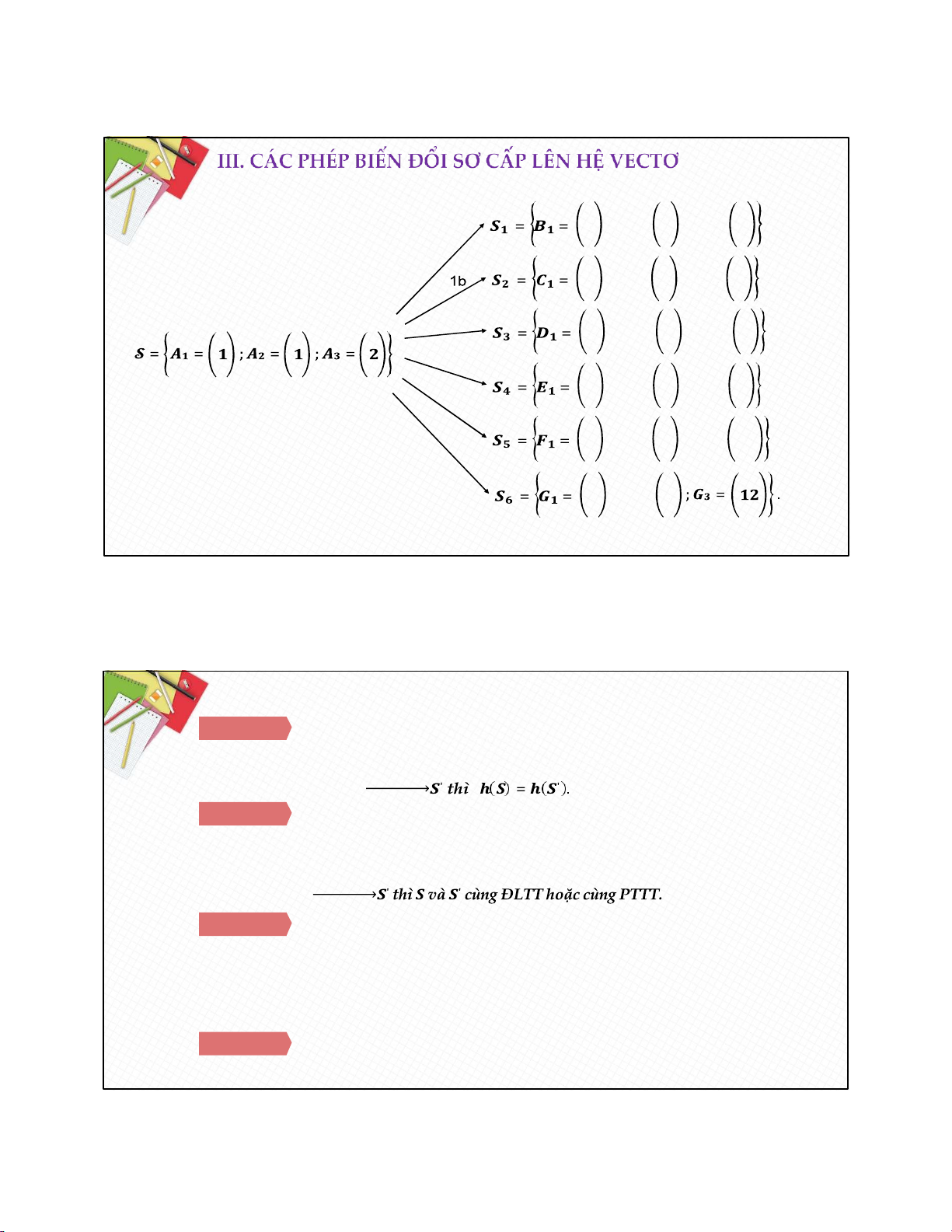
𝟏 ; 𝑩𝟐 = 𝟏 ; 𝑩𝟑 = 𝟐 . 𝟐 𝟏 𝟑 1a 𝟐 𝟏 𝟐
𝟐 ; 𝑪𝟐 = 𝟏 ; 𝑪𝟑 = 𝟐 . 𝟐 𝟐 𝟑 𝟐 𝟏 𝟐 1c 𝟏 𝟐 𝟐 ; 𝑫 𝟏 ; 𝑫 𝟐 . 𝟏 𝟐 = 𝟑 = 𝟑 𝟐 𝟑 𝟏 𝟐 𝟑 2a 𝟏 𝟏 𝟐 𝟏 ; 𝑬 𝟐 𝟑 . 𝟐 = ; 𝑬𝟑 = 2b 𝟏 𝟏 𝟐 𝟓 𝟓 𝟏𝟎
𝟏 ; 𝑭𝟐 = 𝟏 ; 𝑭𝟑 = 𝟐 . 2c 𝟏 𝟐 𝟑 𝟏 𝟏 𝟐 𝟔 ; 𝑮𝟐 = 𝟔 𝟏 𝟐 𝟑 IV. CÁC ĐỊNH LÝ 1. Định lý 1
Hạng của hệ véc tơ không thay đổi qua các phép biến đổi sơ cấp nghĩa là: BĐSC nếu 𝑺 2. Định lý 2
Các phép BĐSC khi thực hiện lên hệ véc tơ sẽ không làm thay đổi tính ĐLTT
hay PTTT của hệ véc tơ đó nghĩa là: BĐSC nếu 𝑺 3. Định lý 3
Cho hệ véc tơ S và B là một hệ con của S. Sau khi thực hiện các phép biến đổi
sơ cấp vào các thành phần của các véc tơ của hệ S ta nhận được hai hệ mới
tương ứng là S’ và B’. Hệ B là cơ sở của hệ S khi và chỉ khi B’ là cơ sở của S’. 4. Định lý 4
Nếu 𝑷 là hệ con của 𝑺 và 𝑷 là một cơ sở của không gian ℝ𝒏 thì 𝑷 là cơ sở của 𝑺. 17 12/4/2022 KẾT THÚC CHƯƠNG 1 18