







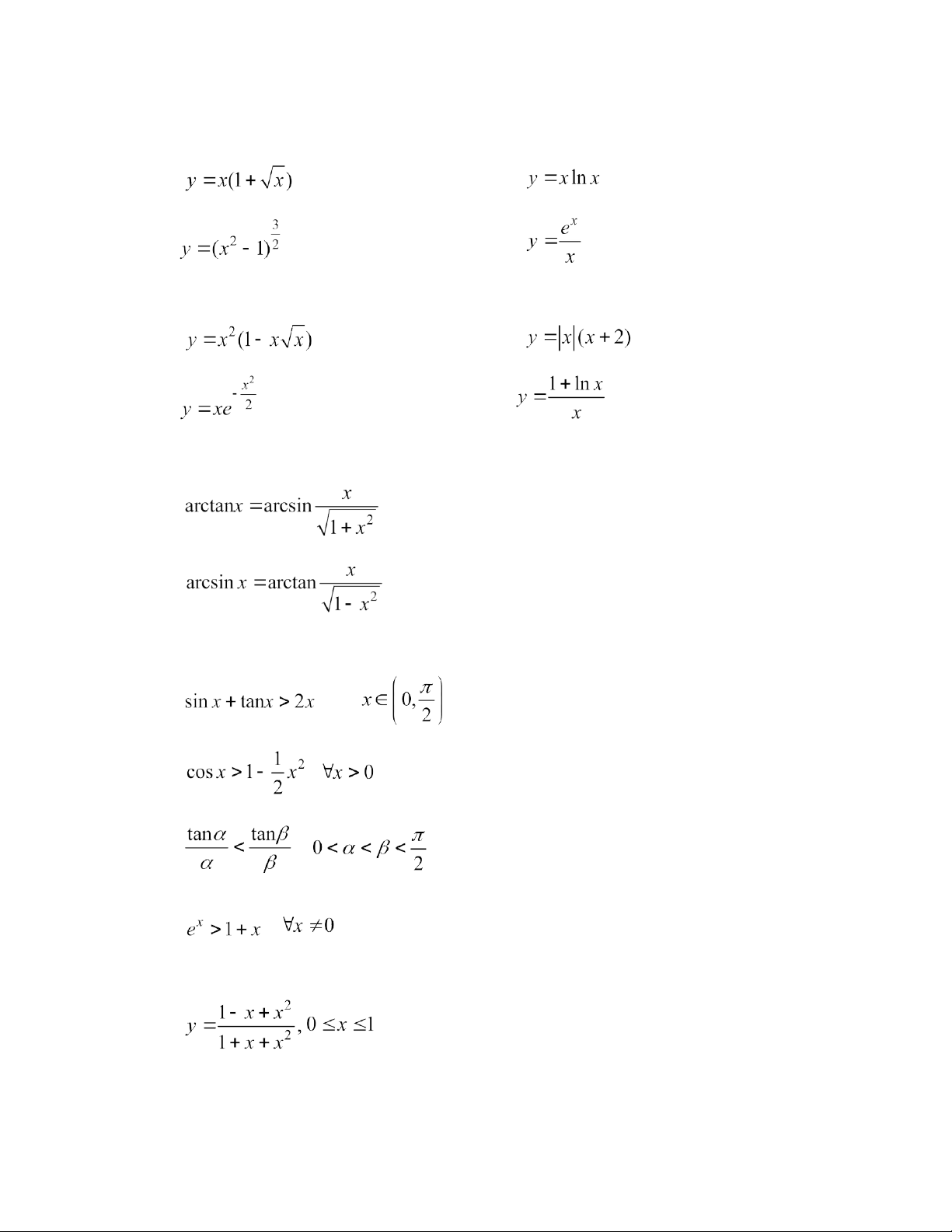











Preview text:
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ
BÀI TẬP TOÁN CAO CẤP I CHO CÁC LỚP TÍN CHỈ
CHƯƠNG 1. HÀM SỐ VÀ GIỚI HẠN
1.1. Tìm giới hạn của các dãy có số hạng tổng quát sau: a) ; b) ; c) ; d) . 1.2. Cho dãy với , = 1. a) Chứng minh
không có giới hạn hữu hạn; b) Chứn minh .
1.3. Chứng tỏ rằng các dãy số sau có giới hạn hữu hạn: a) ; b) .
1.4. Chứng tỏ các dãy số sau có giới hạn là + a) ; b) . 1.5. Cho hàm số . Tính .
1.6. Tìm miền xác định của các hàm số: ; b) a) c) d)
1.7. Tìm miền giá trị của các hàm số:
Giảng viên soạn: Lê Văn Ngọc 1
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ a) ; b) ; c) ; d) . 1.8. Tìm hàm số biết a) ; b) ; c) .
1.9. Xét tính chẵn, lẻ của các hàm số: a) ; b) ; c) ; d) .
1.10. Tìm hàm ngược của các hàm số sau: a) ; b) ; c) d) .
1.11. Tìm các giới hạn a) b) ; c)
1.12. Tìm các giới hạn
Giảng viên soạn: Lê Văn Ngọc 2
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ b) a)
1.13. Tìm các giới hạn a) ; b) .
1.14. Tìm các giới hạn a) ; b) ; c) ; d) .
1.15. Tìm các giới hạn a) ; b) .
1.16. Tìm các giới hạn a) ; b) ; c) ; d) .
1.17. Tính các giới hạn a) ; b) ; c) .
1.18. Tính các giới hạn
Giảng viên soạn: Lê Văn Ngọc 3
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ a) ; b) c) ; d) .
1.19. Xét sự liên tục của các hàm số sau: a) ; b) ; c) d)
1.20. Tìm A để hàm số sau liên tục trên khoảng .
CHƯƠNG 2. ĐẠO HÀM VÀ VI PHÂN
2.1. Dùng định nghĩa, hãy tính đạo hàm của các hàm số: a) b) ; c) .
2.2. Tính đạo hàm của các hàm số a) b) ;
Giảng viên soạn: Lê Văn Ngọc 4
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ c) ; d)
2.3. Chứng tỏ rằng nếu khả vi tại thì .
2.4. Chứng minh rằng hàm số trong đó
là hàm số liên tục và không khả vi tại .
2.5. Tính các đạo hàm và
của các hàm số sau đây: a) ; b) .
2.6. Tính đạo hàm của các hàm số: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) ; i) ; j) ; k) ; l) ;
Giảng viên soạn: Lê Văn Ngọc 5
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ m) ; n) .
2.7. Tính đạo hàm của các hàm số sau bằng phương pháp đạo hàm lôgarit: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h)
2.8. Tính vi phân của các hàm số a) ; b) tại c) tại và . 2.9. Tính đạo hàm
của các hàm cho theo tham số: a) , ; b) , .
2.10. Chứng minh các hệ thức sau: a) Cho . Chứng minh ; b) Cho . Chứng minh ;
Giảng viên soạn: Lê Văn Ngọc 6
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ c) Cho . Chứng minh .
2.11. Tính đạo hàm cấp n của các hàm số: a) ; b) ; c) ; d) ; e) .
2.12. Tính các đạo hàm cấp cao sau: a) , tính ; b) , tính ; c) , tính .
2.13. Áp dụng các phép tính đạo hàm, hãy tìm các tổng sau: a) b) .
2.14. Chứng minh rằng với mọi , phương trình
không thể có 2 nghiệm khác nhau trong [0,1].
2.15. Chứng tỏ rằng phương trình
có 3 nghiệm thực biết rằng
2.16. Không cần tính đạo hàm của hàm số
, hãy cho biết số nghiệm của phương trình
và chỉ ra các khoảng chứa nghiệm đó.
2.17. Chứng minh các bất đẳng thức sau đây:
Giảng viên soạn: Lê Văn Ngọc 7
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ a) ; b) ; c) ; d) .
2.18. Dùng qui tắc L’Hospital tìm các giới hạn sau: a) ; b) ; c) ; d) ; e) ; f) .
2.19. Tìm các giới hạn sau: ; b) ; a) c)
2.20. Tìm các giới hạn sau: a) ; b) ; c) ; d)
Giảng viên soạn: Lê Văn Ngọc 8
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ
2.21. Tìm các khoảng tăng, giảm và cực trị của các hàm số sau: a) ; b) ; c) ; d) .
2.22. Tìm cực trị của các hàm số sau: a) ; b) ; c) ; d) .
2.23. Chứng minh các đẳng thức sau: a) ; b) .
2.24. Chứng minh các bất đẳng thức sau: a) với ; b) , ; c) , ; d) , .
2.25. Tìm giá trị lớn nhất, nhỏ nhất của các hàm số: a) ;
Giảng viên soạn: Lê Văn Ngọc 9
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ b) ; c) ; d) .
CHƯƠNG 3. PHÉP TÍNH TÍCH PHÂN
3.1. Biến đổi về các tích phân đơn giản để tính các tích phân sau: b) c) a) d) ; e) f) ; g) h) i) j) ; k) ; l) m) ; n) ; o) ; p) q)
3.2. Dùng phương pháp đổi biến để tính các tích phân sau: b) c) a) d) ; e) ; f) ;
Giảng viên soạn: Lê Văn Ngọc 10
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ g) ; h)
3.3. Dùng phương pháp tích phân từng phần để tính các tích phân sau: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) ; i) ; j) k) ; l) ; m) n)
3.4. Tính tích phân các phân thức hữu tỉ: b) c) a) d) e) f ) ; g)
3.5. Tích phân các hàm lượng giác: b) c) a) d) ; e) .
3.6. Tính các đạo hàm:
Giảng viên soạn: Lê Văn Ngọc 11
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ b) c) a)
3.7. Sử dụng công thức Newton-Leibnitz, tính các tích phân sau: a) ; b) ; c) ; d) .
3.8. Tính các tích phân sau bằng phép đổi biến: a) ; b) c) ; d) ; e) ; f) ; g) ; h) .
3.9. Tính các tích phân sau bằng phương pháp tích phân từng phần: a) b) ; c) d)
3.10. Tính các tích phân sau bằng cách sử dụng hỗn hợp các phương pháp:
Giảng viên soạn: Lê Văn Ngọc 12
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ a) b) ; c) ; d) e) ; f) ; g) h)
3.11. Tính diện tích hình phẳng giới hạn bởi các đường cong trong hệ toạ độ Descartes vuông góc: a) và ; b) và ; c)
3.12. Tính các tích phân suy rộng sau: a) b) ; c) ; e) ; f) d) g) h)
Giảng viên soạn: Lê Văn Ngọc 13
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ
CHƯƠNG 4. HÀM SỐ NHIỀU BIẾN SỐ
4.1. Tìm miền xác định của các hàm số sau: a) ; b) ; c) ; d) .
4.2. Tìm các giới hạn sau: a) ; b) ; c) ; d)
4.3. Tính đạo hàm riêng của các hàm số sau: a) ; b) ; c) ; d)
4.4. Xét sự liên tục của hàm số sau:
4.5. Chứng minh các hệ thức sau: a) , với ; b) , với , có đạo hàm liên tục.
4.6. Tính đạo hàm riêng của các hàm số hợp sau: a)
Giảng viên soạn: Lê Văn Ngọc 14
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ b)
4.7. Bằng phép đổi biến số , tìm hàm số thỏa mãn phương trình .
4.8. Tìm vi phân toàn phần của các hàm số sau: a) ; b) c) d)
4.9. Tính gần đúng các số sau đây: a) ; b)
4.10. Tính đạo hàm của các hàm số ẩn xác định bởi các phương trình: a) tính ( ); b) , tính c) , tính ; d) , tính 4.11. Cho
là hàm số ẩn xác định từ phương trình Hãy tính gần đúng 4.12. Cho hàm số
trong đó là hàm số ẩn của
xác định từ hệ thức Tính .
4.13. Tính các đạo hàm riêng cấp hai của các hàm số sau:
Giảng viên soạn: Lê Văn Ngọc 15
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ a) ; b) ; c) ; d) .
4.14. Chứng minh các hệ thức sau đây: a) , với ,
có đạo hàm cấp hai liên tục; b) , với ; c) , với 4.15. Tìm hàm số biết .
4.16. Tính vi phân cấp hai của các hàm số a) ; b) c)
4.17. Tìm cực trị của các hàm số a) ; b) ; c) ;
Giảng viên soạn: Lê Văn Ngọc 16
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ d) e) ; f) ; g) với h)
4.18. Tìm GTLN, GTNN của các hàm số sau: a) trên miền ; b) trên miền ; c)
trên miền tam giác giới hạn bởi các đường thẳng ; d) trên miền
CHƯƠNG 5. PHƯƠNG TRÌNH VI PHÂN
5.1. Giải các phương trình có biến số phân li sau: a) ; b) ; c) ; d) ; e) ; f) .
5.2. Giải các bài toán Cauchy: a) b)
Giảng viên soạn: Lê Văn Ngọc 17
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ
5.3. Giải các phương trình vi phân đẳng cấp sau: a) ; b) .
5.4. Giải các phương trình vi phân tuyến tính cấp 1: a) ; b) ; c) .
5.5. Giải các bài toán Cauchy: a) ; b)
5.6. Giải các phương trình: a) ; b) .
5.7. Giải các phương trình vi phân toàn phần: a) ; b) ; c) ; d)
Giảng viên soạn: Lê Văn Ngọc 18
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ
5.8. Giải phương trình vi phân sau:
, biết rằng nó có một nghiệm riêng dạng
5.9. Giải phương trình
biết phương trình thuần nhất tương ứng có một nghiệm
5.10. Giải các phương trình: a) ; b) ; c)
5.11. Giải các phương trình: a) ; b) ; c) ; d) ; e) ; f) .
5.12. Giải các bài toán Cauchy a) b)
5.13. Giải phương trình: a)
bằng cách đổi biến số ; bằng cách đổi hàm b)
Giảng viên soạn: Lê Văn Ngọc 19
Bộ môn Toán – HVCNBCVT
Bài tập môn toán cao cấp 1 – Dùng cho các lớp tín chỉ
5.14. Cho hàm cung và hàm cầu của một mặt hàng như sau:
là giá của mặt hàng, p phụ thuộc biến thời gian t)
Tại thời điểm bắt đầu khảo sát ta có: và
Tìm quy luật biến động giá theo thời gian với giả thiết hàng được bán hết tại mọi thời điểm.
Giảng viên soạn: Lê Văn Ngọc 20



