Đề cương môn Toán rời rạc - Trường Đại học lao động -  xã hội

Ôn tập TOÁN RỜI RẠC – MTH254 (DD, BB)
Nguyen Minh Nhật, 10/03/2024
PHẦN 1: LOGIC VÀ TẬP HỢP
Câu 1: Tập nào dưới đây là tập con của {1, 2, 3, 4}? A. {1, 2} B. {1, 2, 3} C. {1} D. Tất cả đều đúng
Câu 2: Nếu tập A = {1, 2} và tập B = {a, b} thì tích Cartesian của hai tập A và B là:
A. {(1, a), (1, b), (2, a), (b, b)}
B. {(1, 1), (2, 2), (a, a), (b, b)}
C. {(1, a), (2, a), (1, b), (2, b)}
D. {(1, 1), (a, a), (2, a), (1, b)}
Câu 3: Cho tập S = {a, b, c}. Số tập con của tập S là: A. 3 B. 9 C. 6 D. 8
Câu 4: Số số nguyên dương không lớn hơn 1000 chia hết cho 7 hoặc 11 là: A. 232 B. 230 C. 220 D. Tất cả đều sai Giải: Số số chia hết cho 7: 1000/7 = 142.857… lấy 142 Số số chia hết cho 11:
1000/11 = 90.909090… lấy 90
Số số chia hết cho cả 7 và 11: 7*11 = 77 1000/77 = 12.987… lấy 12
Áp dụng công thức bao hàm loại trừ: 142 + 90 – 12 = 220
PHẦN 2: BÀI TOÁN ĐẾM – ĐỘ PHỨC TẠP CỦA THUẬT TOÁN
Câu 5. Một bình đựng 5 viên bi xanh và 4 viên bi đỏ. Lần thứ nhất lấy ngẫu nhiên một viên
bi và không bỏ vào lại bình, lần thứ hai lấy ngẫu nhiên một viên bi. Xác suất để lần đầu lấy
1 bi xanh và lần hai lấy 1 bi đỏ là: A. 0.2996 B. 0.3124 C. 0.2778 D. 0.3112 Giải: 1 | 13
Xác suất để lấy bi xanh ban đầu: 5/9 = 0,5555…
Xác suất để lấy bi đỏ sau đó là : 4/8 = 0.5
Xác suất để hai sự kiện xảy ra: 5/9 * 4/8 = 0.2778
Câu 6: Phương trình sau có bao nhiêu nghiệm nguyên không âm?x + y + z = 11 A. 33 B. 78 C. 190 D. A, B, C đều sai Giải:
Theo phương pháp chia kẹo Euler ta có:
C(n + k - 1, k - 1) = C(n + k - 1, n)
➔ C(11 + 3 – 1, 3 – 1) = C(13,2) = 78
Câu 7: Số xâu nhị phân độ dài 10 bắt đầu bằng 3 bit 0 hoặc kết thúc bằng 2 bit 0 là: A. 352 B. 1024 C. 512 D. A, B, C đều sai Giải:
Số xâu bắt đầu bằng 3 bit 0: 2^7 = 128
Số xâu kết thúc bằng 2 bit 0: 2^8 = 256
Số xâu bắt đầu bằng 3 bit 0 và kết thúc bằng 2 bit 0: 2^5 = 32
Áp dụng nguyên lí bù trừ: 128 + 256 – 32 = 352
Câu 9: Phương trình x + y + z = 15 có số nghiệm nguyên không âm và x>=1 là: A. 100 B. 136 C. 120 D. 45 Giải:
Vì x ≥ 1, ta đặt x' = x - 1, suy ra x = x' + 1. Khi đó, x' ≥ 0.
Thay x = x’ + 1 vào x + y + z = 15 ta có: x’ + 1 + y + z =15 x’ + y + z = 14
➔ C(14 + 3 - 1, 3 - 1) = C(16, 2) = 120
Câu 10: Mỗi thành viên trong câu lạc bộ thể thao có quê ở 1 trong 20 tỉnh thành. Hỏi cần
phải tuyển bao nhiêu thành viên để đảm bảo có ít nhất 4 người cùng quê? A. 81 B. 80 C. 101 D. A, B sai Giải:
Số người cần tuyển là: (số người cùng quê - 1) * (số tỉnh thành) + 1
(4 - 1) * 20 + 1 = 3 * 20 + 1 = 61. Điều kiện: n/20 > 3 ➔ Cần tuyển n + 1 = 61
Câu 11: Số xâu gồm ba chữ số thập phân, bắt đầu chữ số lẻ là: 2 | 13 A. 1000 B. 550 C. 500 D. A, B, C đều sai 1,3,5,7,9 5*10*10 = 500
Câu 13: Một hộp đựng 4 bi xanh và 5 bi đỏ. Xác suất lấy ngẫu nhiên 1 viên bi xanh từ hộp là: A. 4/5 B. 5/9 C. 4/9 D. Tất cả đều sai
Câu 14: Sắc số (số màu tối thiểu để tô các đỉnh) của đồ thị dưới đây là: A. 2 B. 3 C. 4 D. 6
Đạt kêu chỉ cần có 3 màu sẽ vẽ được bản đồ tG.
Câu 15: Số hàm đơn ánh từ tập có 5 phần tử đến tập có 7 phần tử là: A. 35 B. 78125 C. 16807 D. 2520 Giải: 7A5
Câu 16: Phải chọn ít nhất bao nhiêu quân bài trong bộ bài để luôn có được 3 quân bài cùng
nước (cơ, rô, chuồn, bích)? A. 3 B. 9 C. 7 D. 13 Giải:
Trường hợp xấu nhất chỉ chọn được 2 lá đồng chất 2 cơ, 2 rô, 2 chuồn, 2 bích = 2*4 = 8
Thì chỉ cần ít nhất một lá nữa sẽ có 3 quân đồng chất -> 8 + 1 = 9
Câu 17. Cho biết độ phức tạp của đoạn chương trình sau:for (i= 1;i<=n;i++) { for (u= 1;u<=m;u++)
for (v= 1;v<=n;v++)//lệnh;for j:= 1 to x dofor k:= 1 to z do//lệnh;} A. O() B. O() C. O(n*max(m*n, x*z)) D. O(max(n, m*n, x*z)) Câu 18.
PHẦN 3: NGUYÊN LÝ BÙ TRỪ - HỆ THỨC TRUY HỒI
Câu 19: Công thức nào sau đây có thể tạo ra chuỗi 5, 9, 13, 17, 21, . . . A. an = 2n + 1. B. an = 4n + 1. 3 | 13 C. an = 4n + 3. D. an = 4n - 1.
Câu 20: Phương trình sau có bao nhiêu nghiệm nguyên không âm?x + y + z = 11 A. 33 B. 78 C. 190 D. A, B, C đều sai
PHẦN 4: BÀI TOÁN TỒN TẠI – BÀI TOÁN LIỆT KÊ
Câu 21: Chuỗi nhị phân liền sau chuỗi 11011111 là: A. 11011110 B. 10111111 C. 11111111 D. 11100000 Giải: Bấm máy MENU 3
Màn hình hiện BIN nhập 11011111
Bấm x2 để chuyển qua thập phân Kết quả bằng 223 ➔ Liền sau là 224
Chuyển 224 thành số nhị phân ➔ 11100000
Câu 22: Hoán vị kế tiếp của dãy 5 4 6 3 2 1 là: A. 4 5 6 3 2 1 B. 5 6 4 3 2 1 C. 5 6 1 2 3 4 D. 6 5 1 2 3 4 Giải:
Ta thấy dãy giảm dần từ 6321 ta chọn số trước nó là 4
Đổi 4 với số lớn hơn và nhỏ nhất của dãy sau nó(6): 564321
Sau đó sắp xếp lại theo thứ tự tăng dần sau đó: 561234
PHẦN 5: LÝ THUYẾT ĐỒ THỊ
Câu 23: Đồ thị G liên thông, gồm n đỉnh thì số thành phần liên thông của đồ thị là: A. n B. 0 C. 1 D. Tất cả đều sai
Câu 24: Dùng thuật toán Prim, chúng ta có thể:
A. Tìm cây khung nhỏ nhất của đồ thị
B. Tìm được đường đi ngắn nhất giữa các đỉnh trong đồ thị - Dijkstra
C. Kiểm tra tính liên thông của đồ thị D. Câu A và câu C đúng
Câu 25: Số đỉnh bậc lẻ trong đồ thị luôn là: A. 2 B. 4 C. Số chẵn 4 | 13 D. Tất cả đều sai
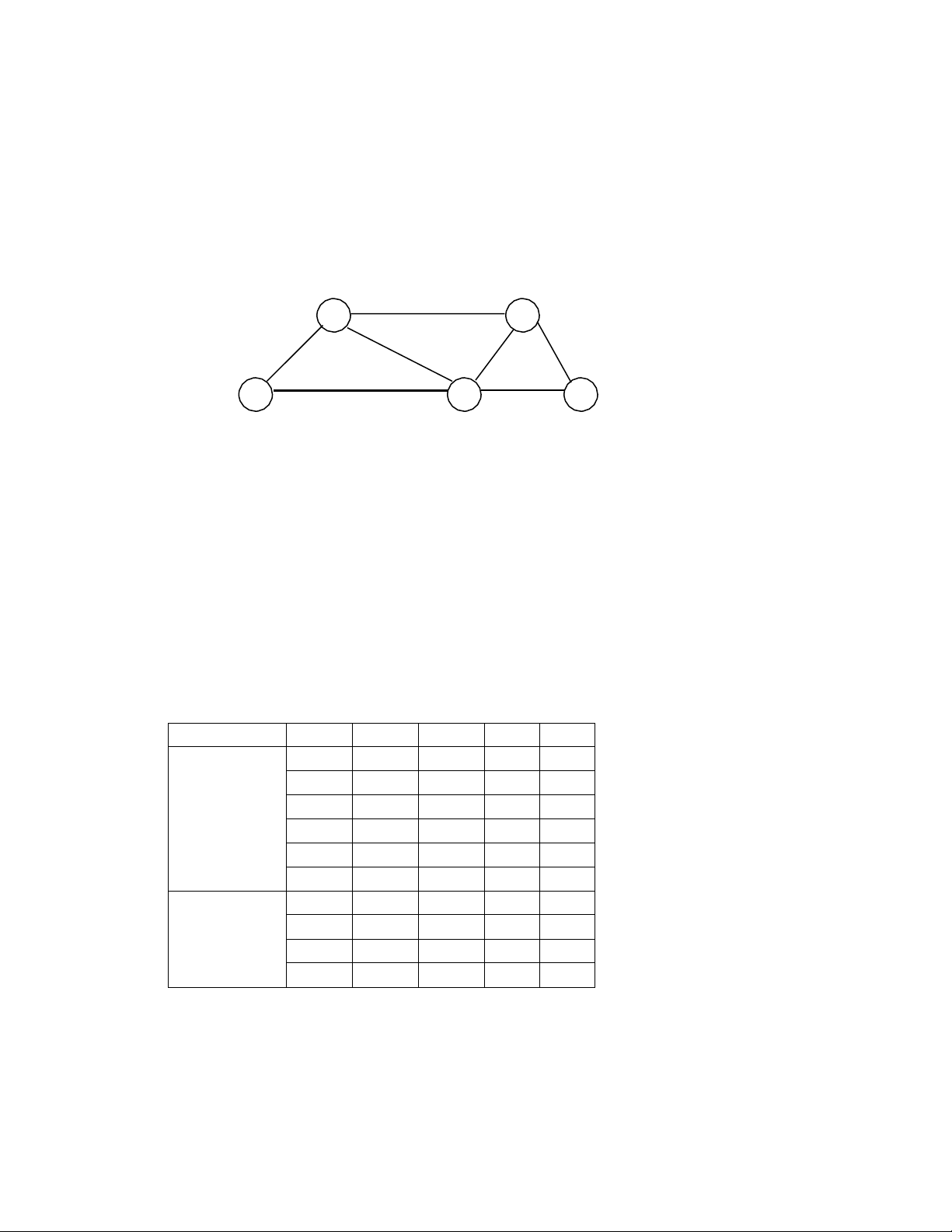
Câu 26: Giả sử các đỉnh được duyệt ưu tiên theo thứ tự đỉnh từ 1 đến n. Kết quả duyệt đồ
thị dưới đây theo chiều rộng, xuất phát từ đỉnh 1 là: A. 1 2 3 4 5 6 B. 1 2 3 4 6 5 C. 1 2 3 5 4 6 D. 1 2 5 3 4 6 CÂU HỎI NGẮN
Câu 1: Có bao nhiêu cách chia 8 bánh cho 3 em nhỏ
Vậy có 8!/(3!5!) = 56 cách đáp ứng yêu cầu.
Câu 2: Có bao nhiêu bộ nghiệm thỏa mãn phương trình X1+X2 + X3 + X4 = 6.
Mỗi bộ nghiệm của phương trình là một tổ hợp lặp chập 6 của 4 phần tử thuộc loại X1, X2, X3, X4
Vậy, số nghiệm là C(6 + 4 - 1, 4 - 1) = C(9, 3) = 84.
Câu 3: Giải hệ thức truy hồi sau: an = 4an-1 – 4an-2 (1)
, với a0 = 4, a1 = 2 và n > 1. Giải:
Đặt rn = an (rn ≠ 0)
-> rn = 4an-1 – 4an-2
rn – 4rn-1 + 4rn-2 rn-2(r2 – 4r + 4)
Vì rn-2 > 0 -> r2 - 4r + 4 = 0 ➔ r = 2
Nghiệm bị lặp, nên nghiệm tổng quát của hệ là: An = b1r0n + b2nr0n ➔ an = b1*2n + b2*n*2n (2)
Thay a0 = 4, a1 = 2 vào (2) ta có: 4=b 1 { } 2=2 b 1+2 b 2 ➔ { b1=4 b 2=−3 } ⇨ An = 4*2n + (-3) * n * 2n ⇨ An = 2n(4 – 3n)
Câu 4: Tìm số nghiệm nguyên không âm của phương trình x + y + z = 20, trong trường hợp: x= 0, y= 2, z=3. Giải: TH1: x=0 Thì y + z = 20
C(20 + 2-1, 2-1) = C(21,1) = 21 nghiệm TH2: y=2 Thì x + z = 20 – 2 =18
C(18 + 2-1, 2-1) = C(19,1) = 19 nghiệm TH3: z = 3 Thì x + y = 20 – 3 =17 5 | 13
C(17 + 2-1, 2-1) = C(18,1) = 18 nghiệm
Câu 5: Cho đồ thị G= (V, E) như hình vẽ sau đây:
a. Biểu diễn đồ thị trên dưới dạng ma trận trọng số. 0 1 1 0 0 0 1 0 1 1 1 0 1 1 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0
b. Duyệt đồ thị ở câu G theo chiều sâu và chiều rộng với đỉnh xuất phát là đỉnh số 1. DFS: 1-2-4-5-6-3 ĐẠt lỏ: DFS: 1-2-3-4-6-5 BFS: 1-2-3-4-5-6
Câu 6: Chứng minh: AB+ A C ̅ +BC=AB+ A C ̅ Giải: VT = AB+ A C ̅ +BC
Áp dụng định luật đồng thuận trong đại số Boolean ta có: XY + X̅Z + YZ = XY + X̅Z
Trong trường hợp này: X = A, Y = B, Z = C.
⇨ BC có thể được loại bỏ ⇨ VT = AB + A̅C
So sánh với vế phải => bằng nhau.
Câu 7: Khử phép kéo theo cho biểu thức logic α = (P --> Q) -->R
P -> Q ≡ ¬P∨Q ¬P∨Q →R
Áp dụng định nghĩa kéo theo: A -> B ≡¬ A ∨B
➔ (¬ P∨Q ) →R≡¬ (¬ P ∨Q )∨ R (P V ¬Q) ∨R TỰ LUẬN
Câu 1: Chứng minh các mệnh đề sau tương đương logic a. Ø (p ↔ q) và Øp ↔ q b. Øp ↔ q và p ↔ Øq Hướng dẫn a. Ø (p ↔ q) và Øp ↔ q Ø (p ↔ q) - Ø(p ⟶q) Ø(q ⟶ p) 6 | 13 - Ø(Ø p q) Ø( Ø q p) -(p ˄ Ø q) (q ˄ Ø p) Ø p↔ q
- (Ø p ⟶ q) ˄ (q ⟶ Ø p) - (p q) ˄ (Ø q Ø p) (1)
- [(p q) ˄ Ø q] [(p q) ˄ Ø p] - (p ˄ Ø q) (q ˄ Ø p)
Vậy Ø (p ↔ q) - Øp ↔ q
b. Øp ↔ q và p ↔ Øq
p ↔ Øq - (p ⟶ Ø q) ˄ (Ø q ⟶ p) -(Ø p Ø q) ˄ (q p) -(p q) ˄ (Ø p Ø q) (2)
Từ (1) và (2) suy ra Øp ↔ q - p ↔ Øq Câu 2:
a. Giải hệ thức truy hồi sau: ao = 5, a1 = 8... an=3an-1 - 2an-2 An = 2 + 3 * 2n
b. Giải hệ thức truy hồi sau: an = 4an-1 – 4an-2, với a0 = 4, a1 = 2 và n > 1.
c. Tìm nghiệm của hệ thức truy hồi sau: an = 2an-1 – an-2 n³ 2 với các điều kiện
đầu là a0 = 2, a1 = 3. Hướng dẫn
Đặt an = rn, thay vào hệ thức truy hồi đã cho, ta có được phương trình đặc trưng như sau: r2 – 2r + 1 = 0 - (r – 1)2 = 0 - r = 1 (
Do đó nghiệm của hệ thức truy hồi có dạng an = b1. 1n + b2.n.1n. Từ điều kiện đầu ta có được 2 phương trình: b =2 b =2 1 1 { {
b +b =3 b =1 1 2 2
Từ đó ta suy ra được b1 = 2 và b2 = 1. Do đó nghiệm của hệ thức truy hồi đã cho là: a n = 2. 2n +n.2n.
d. Giải hệ thức truy hồi sau: an = 2an-1 +1, với a1 = 1. Tính a7 an= 2.a(n – 1) + 1 = 2.(2.a(n – 2) + 1) + 1 = 22.a(n – 2) + 21 + 20
= 23. a(n – 3) + 22 + 21+ 20 = …
= 2n-1.a(1) + 2n-2 + … + 21 + 20 = 2n – 1. 1.0 Với a1 = 1, a7 = 127
Câu 3: Tại thành phố Đà Nẵng, các biển số xe theo quy định mới có dạng 43- XN1 -
NNN.NN, trong đó X là một chữ cái từ A → Z, N1 là một chữ số từ 1 → 9, N là một 7 | 13
chữ số từ 0 → 9 ( ngoại trừ các biển số dạng 43 – XN1 - 000.00). Hỏi có thể đăng ký
cho tối đa là bao nhiêu xe trên toàn địa bàn thành phố? Hướng dẫn
- Có 26 cách chọn 1 chữ cái cho vị trí X
- Có 9 cách chọn 1 chữ số cho vị trí N1
- Có 10 cách chọn 1 chữ số cho vị trí N
Vậy có tổng cộng là 26 x 9 x 105 = 23400000 biển số xe theo quy định, tuy
nhiên loại trừ những biển số dạng XN1- 000.00 (có 234 biển số dạng như vậy).
Vậy kết quả có 234000000-234 = 23399766 biển số có thể đăng ký được trên toàn địa bàn thành phố.
Câu 4: Chỉ ra rằng 7 số chọn từ 10 số nguyên dương đầu tiên nhất thiết có ít nhất 2
cặp số có tổng bằng 11. Hướng dẫn
Với 10 số nguyên dương đầu tiên 1, 2, 3, …, 10 thì có thể chia thành 5 cặp số mà có tổng
là 11, gọi 5 cặp số đó lần lượt là G1, G2, G3, G4, G5. Để chọn 7 số từ 10 số này thì cũng
là chọn 7 số từ 5 cặp số G1 …G5, theo nguyên lý Dirichlet phải có ít nhất 2 cặp số được
chọn thuộc cùng 1 nhóm tức là có tổng là 11.
Câu 5: Có 3 hộp đựng bi xanh, đỏ, trắng. Mỗi hộp chỉ chứa các viên bi cùng màu và
mỗi hộp có ít nhất là 8 bi. Có bao nhiêu cách chọn ra 8 viên bi trong đó có ít nhất mỗi loại một viên bi? Giải:
Ta chọn mỗi loại một viên bi -> ta đã chọn 3 viên có đủ Đ, X, T
Chọn 5 viên bi còn lại có thể chọn bất kì từ 3 hộp.
Áp dụng chia keo Euler: C(5 + 3 – 1, 3 – 1) = C(7, 2) = 21 cách.
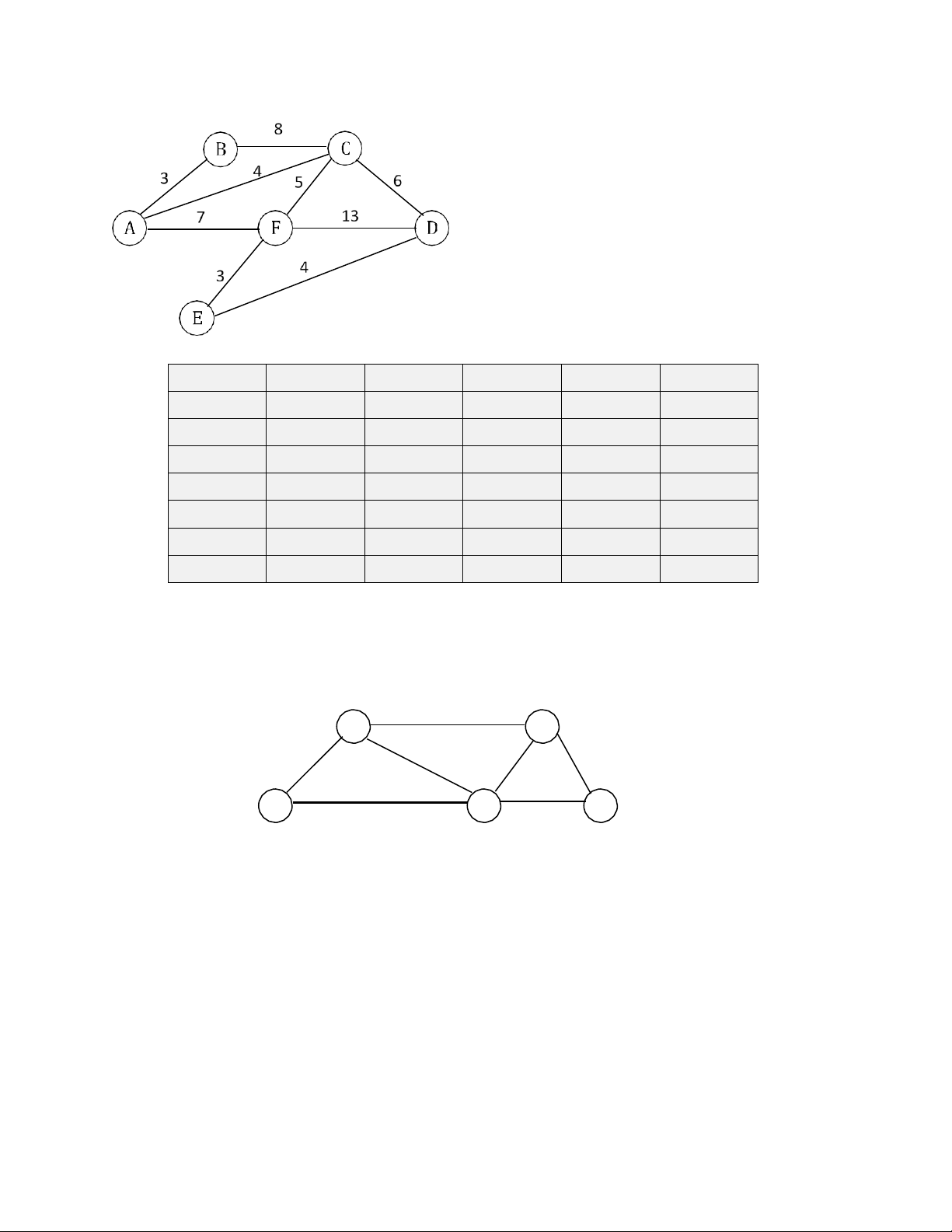
Câu 6: Cho đồ thị như hình vẽ: 8 | 13
a) Tìm đường đi ngắn nhất từ đỉnh A đến đỉnh D T A B C D E F L 0 ∞ ∞ ∞ ∞ ∞ X 3 4 ∞ ∞ 7 X 4 ∞ ∞ 7 X 10 ∞ 7 10 10 X X F A A // // A A A // // A A A C // A A A C F A
Vậy đường đi từ A đến D là A->C->D với độ dài là 10 Vòng lặp A B C D E F Khởi tạo 0 ∞ ∞ ∞ ∞ ∞ 1 (A) 0 3 4 ∞ ∞ 7 2 (B) 0 3 7 ∞ ∞ 7 3 (C) 0 3 4 10 ∞ 7 4 (F) 0 3 4 10 10 7 5 (E) 0 3 4 14 10 7 6 (D) 0 3 4 10 10 7 Vòng lặp A B C D E F Khởi tạo A // // // // // 1 (A) A A A // // A 2 (B) A A B // // A 3 (C) A A C C // A 4 (F) A A C C F A 5 (E) A A C E F A 6 (D) A A C C F A
b) Tìm cây khung nhỏ nhất 9 | 13 A B C D E F [0,0] [0, ∞] [0, ∞] [0, ∞] [0, ∞] [0, ∞] * [A,3] [A,4] [0, ∞] [0, ∞] [A,7] * [A,4] [0, ∞] [0, ∞] [A,7] * [C,6] [0, ∞] [C,5] [C,6] [F,3] * [E,4] * *
Vậy cây khung nhỏ nhất của đồ thị là:{AB, AC, FC, EF, ED} tổng trọng số cây khung là 19
Câu 7: Cho đồ thị G= (V, E) như hình vẽ sau đây: a b 12 4 10 14 3 3 11 c d e
a) Biểu diễn đồ thị trên dưới dạng ma trận trọng số. 00 12 04 10 00 12 00 00 14 03 04 00 00 03 00 10 14 03 00 11 00 03 00 11 00
b) Chỉ ra 2 đường đi bất kỳ từ đỉnh a đến đỉnh e của đồ thị trên. 10 | 13 a-c-d-b-e a-c-d-e
c) Dùng thuật toán Dijkstra, tìm đường đi ngắn nhất từ đỉnh a đến các đỉnh
khác của đồ thị. Hướng dẫn Đồ thị đã cho: a b 12 4 10 14 3 3 11 c d e
a. Biểu diễn đồ thị dưới dạng ma trận trọng số. 0 12 4 10 0 12 0 0 14 3 ∣ 4 0 0 3 0 ∣ 10 14 3 0 11 0 3 0 11 0 b. Chỉ
ra 2 đường đi bất kỳ từ a đến e:
(a,b),(b,e) : chiều dài đường đi là 15
(a,c), (c,d), (d,e): chiều dài đường đi là 18.
c. Dùng thuật toán Dijkstra, tìm đường đi ngắn nhất từ đỉnh a đến các đỉnh khác của đồ thị trên. T a b c d e 0 ∞ ∞ ∞ ∞ x 12 4 10 ∞ x 12 x 7 ∞ L x 12 x x 18 x x x x 15 x x x x x a a a // Trươc a a c // a a c d a a c b
Kết luận: đường đi ngắn nhất từ đỉnh a đến các đỉnh: B: a ⟶b độ dài: 12 C:a ⟶ c độ dài: 4 D:a ⟶ c⟶ d độ dài: 7
E: a ⟶b ⟶ e độ dài: 15 11 | 13
Câu 8. Cho đồ thị sau:
https://hfs2.duytan.edu.vn/ndJK184IUkdfn23df675/TestBank/
230318_Dothi01_4523_8815A_101141.png
a. Biểu diễn đồ thị dưới dạng ma trận trọng số. 0 1 0 0 0 3 1 0 2 0 3 1 0 2 0 2 1 0 0 0 2 0 3 0 0 3 1 3 0 2 3 1 0 0 2 0
b. Dùng thuật toán Dijkstra, tìm đường đi ngắn nhất từ đỉnh a đến các đỉnh khác của đồ thị. T a b c d e f L 0 i i i i i x 1 i i i 3 x 3 i 4 2 3 i 4 x Trước
c. Giải hệ thức truy hồi sau: an = an-1+an-2 với a0 = 0, a1 = 1.
Câu 9: Tìm dạng cực tiểu của hàm Boole sau:
x y z+ x y z+x yz+x y z+ x y z F(x,y,z)= Hướng dẫn 11 10 00 01
x y z+ x y z+x yz+x y z+ x y z x 12 | 13
Cực tiểu của biểu thức x y z +x y z+ x yz + x y z +x y z là y+x z
Câu 10: Rút gọn hàm bool sau bằng 2 cách
- Phép biến đổi tương đương
- Bìa Karnaugh, và vẽ mạch kết quả. ---o0o--- 13 | 13
Document Outline

• PHẦN 1: LOGIC VÀ TẬP HỢP
• PHẦN 2: BÀI TOÁN ĐẾM – ĐỘ PHỨC TẠP CỦA THUẬT TOÁN
• PHẦN 3: NGUYÊN LÝ BÙ TRỪ - HỆ THỨC TRUY HỒI
• PHẦN 4: BÀI TOÁN TỒN TẠI – BÀI TOÁN LIỆT KÊ
• DFS: 1-2-4-5-6-3
• BFS: 1-2-3-4-5-6
• Hướng dẫn
• Hướng dẫn (1)
• Hướng dẫn (2)
• Hướng dẫn (3)
• Hướng dẫn (4)