Đề cương môn Toán rời rạc - Trường Đại học lao động -  xã hội.

ĐỀ CƯƠNG TOÁN RỜI RẠC I. LÝ THUYẾT
1. CÁC CẤU HÌNH TỔ HỢP
2. TÌM KIẾM THEO CHIỀU SÂU, RỘNG
3. CÂY KHUNG CỰC TIỂU PRIM, KRUSKAL
4. QUAN HỆ TƯƠNG ĐƯƠNG, QUAN HỆ THỨ TỰ
5. DÙNG BẢNG KARNAUGH TỐI THIỂU HÓA HÀM LOGIC II. BÀI TẬP
1. Một nhóm học sinh gồm 8 nam và 3 nữ. Có bao nhiêu cách sắp xếp nhóm
học sinh này thành hàng dọc sao cho có 5 học sinh nam luôn đứng cạnh nhau
Đáp án: A5 .7 !
=C5.5 ! .7 ! 8 8
Gđ 1: chọn 5 bạn nam từ 8 bạn có sắp thứ tự có : A5 cách 8
Gđ 2: hoán vị của 5 bạn nam và 6 bạn còn lại có: 7!
2. Một nhóm gồm 6 học sinh. Có bao nhiêu cách sắp xếp nhóm hs theo hàng
dọc sao cho A luôn đứng cạnh B. Đáp án: 2.5!
Coi AB là 1 vị trí, có 5! Cách xếp AB với 4 hs còn lại
Có 2 cách để A đứng cạnh B (AB, BA)
3. Một nhóm gồm 6 học sinh nam và 4 học sinh nữ được xếp vào 10 chỗ ngồi.
Hỏi có bao nhiêu cách sắp xếp để không có học sinh nữ nào ngồi cạnh nhau?
Đáp án: A4.6 ! 7
Có 6! Cách xếp 6 bạn nam; giữa các bạn có 7 vị trí có thể xếp 4 bạn nữ, vậy
có A4 cách xếp 4 bạn nữ, theo ngly nhân có A4.6 ! cách xếp 7 7
4. Có bao nhiêu hoán vị của các số 1,2,...,9 mà trong đó 4 số 3, 4, 5, 6 không
đứng cạnh nhau theo thứ tự tăng dần.
Đáp án: 9!-6! (coi 3456 là 1 vị trí, số cách xếp 3456 đứng cạnh nhau tăng
dần là hoán vị của 3456 và 5 số còn lại: có 6! Cách)
5. Trong không gian Oxyz cho 9 điểm có tọa độ nguyên. Chứng minh rằng
luôn tìm được 2 điểm mà trung điểm của nó cũng có tọa độ nguyên
Đáp án: Trung điểm của 2 điểm có tọa độ nguyên nếu các tọa độ cùng chẵn hoặc cùng lẻ
A(x1,y1,z1) ; B(x2,y2,z2) C là tđ C((x1+x2)/2; (y1+y2)/2; (z1+z2)/2)
Gs 1 điểm có tọa độ (x,y,z); mỗi x,y,z có thể là số chẵn hoặc lẻ, có 23 =8
trường hợp có thể xảy ra với mỗi điểm có tọa độ (x,y,z); có 9 điểm, theo
dirichlet có ít nhất 2 điểm thuộc cùng 1 trường hợp, tức là tọa độ (x,y,z)
cùng tính chẵn lẻ, suy ra trung điểm của chúng có tọa độ nguyên. Gs chẵn là 1, lẻ là 0 x y z (x,y,z) ví dụ A( 3, 5, 7) B(1,9, 11) C=(2,7,9) 1 1 1 (1,1,1)
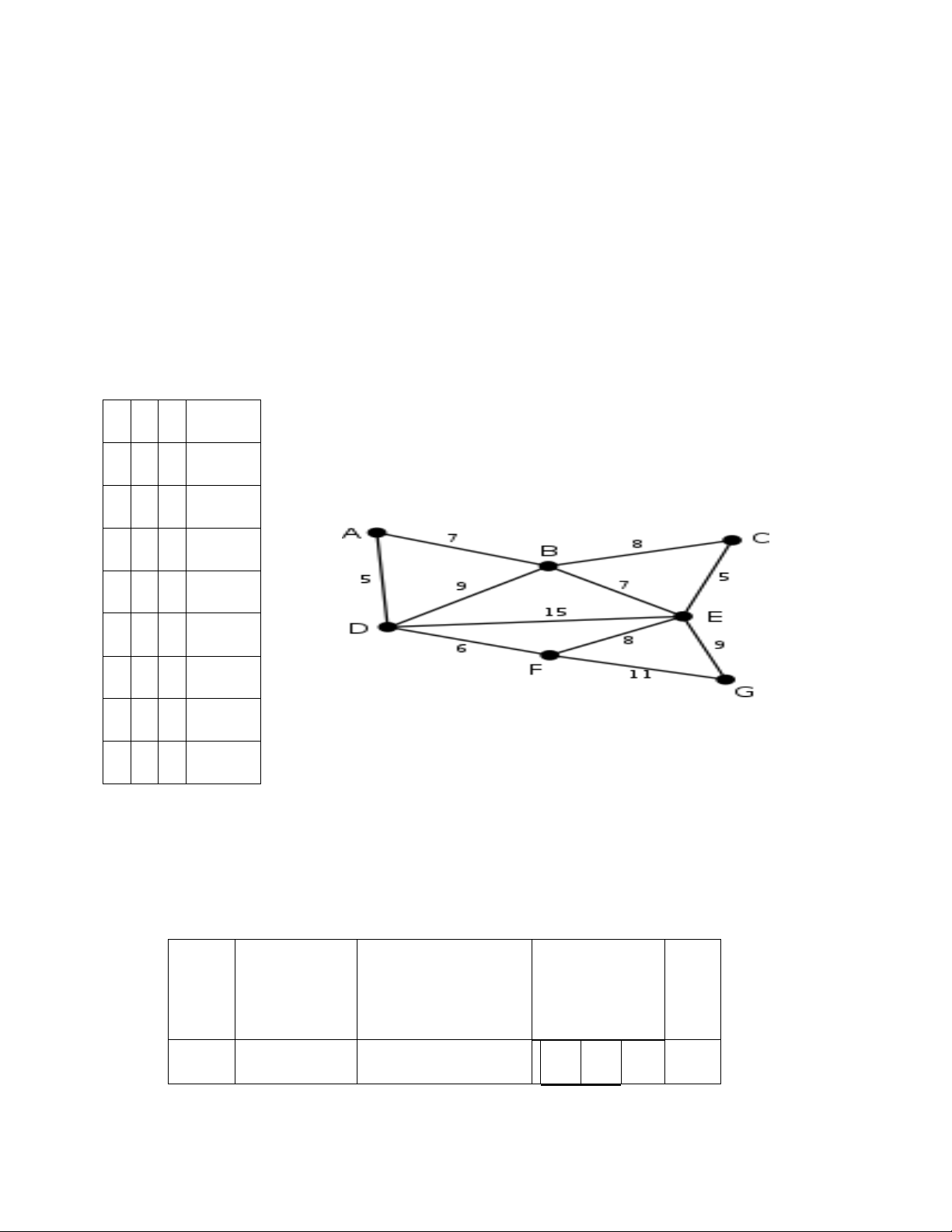
X(2,4,1) Y(4,6,7) => Z(3,5,4) 6. Cho đồ thị 1 1 0 (1,1,0) 1 0 1 (1,0,1) 1 0 0 (1,0,0) 0 1 1 (0,1,1) 0 1 0 (0,1,0) 0 0 1 (0,0,1) 0 0 0 (0,0,0)
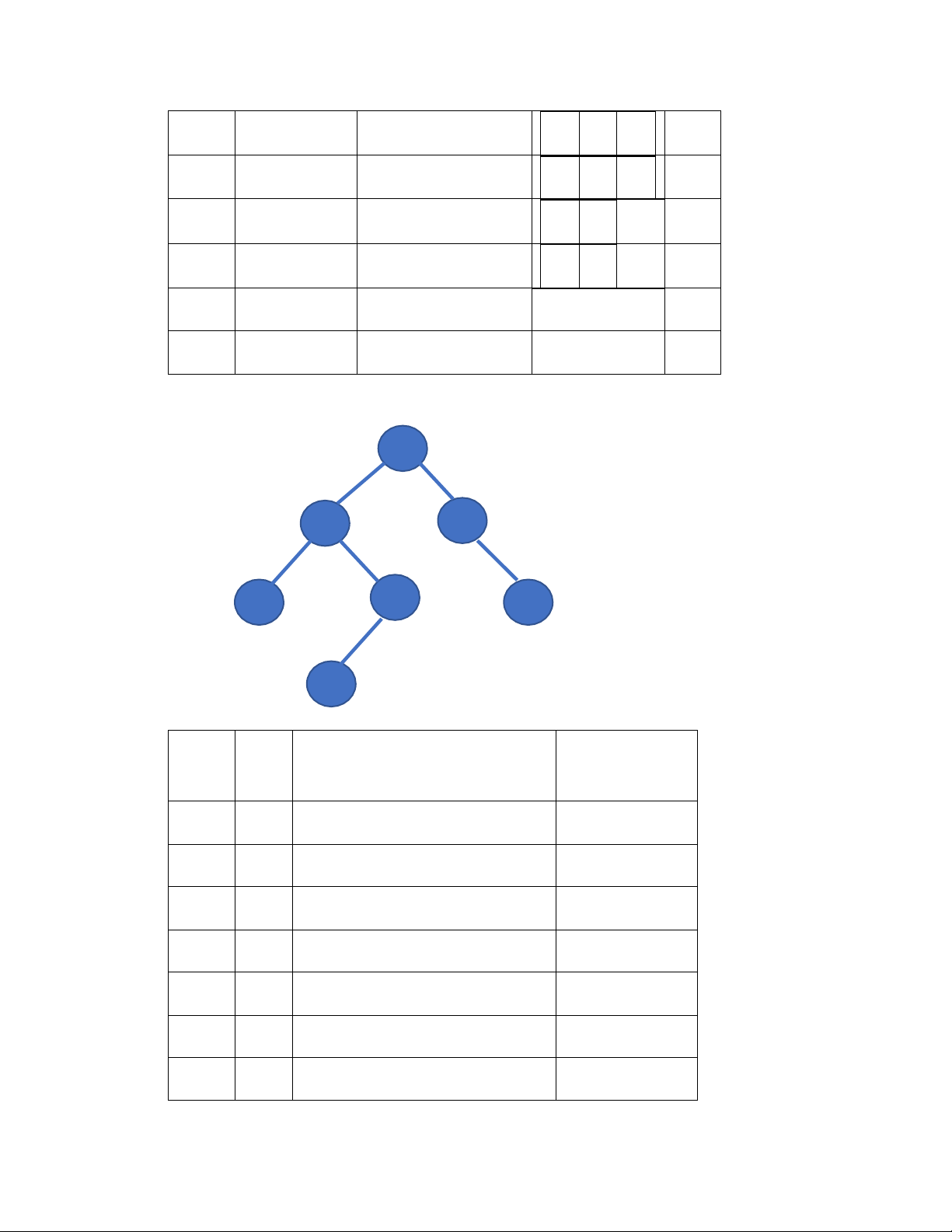
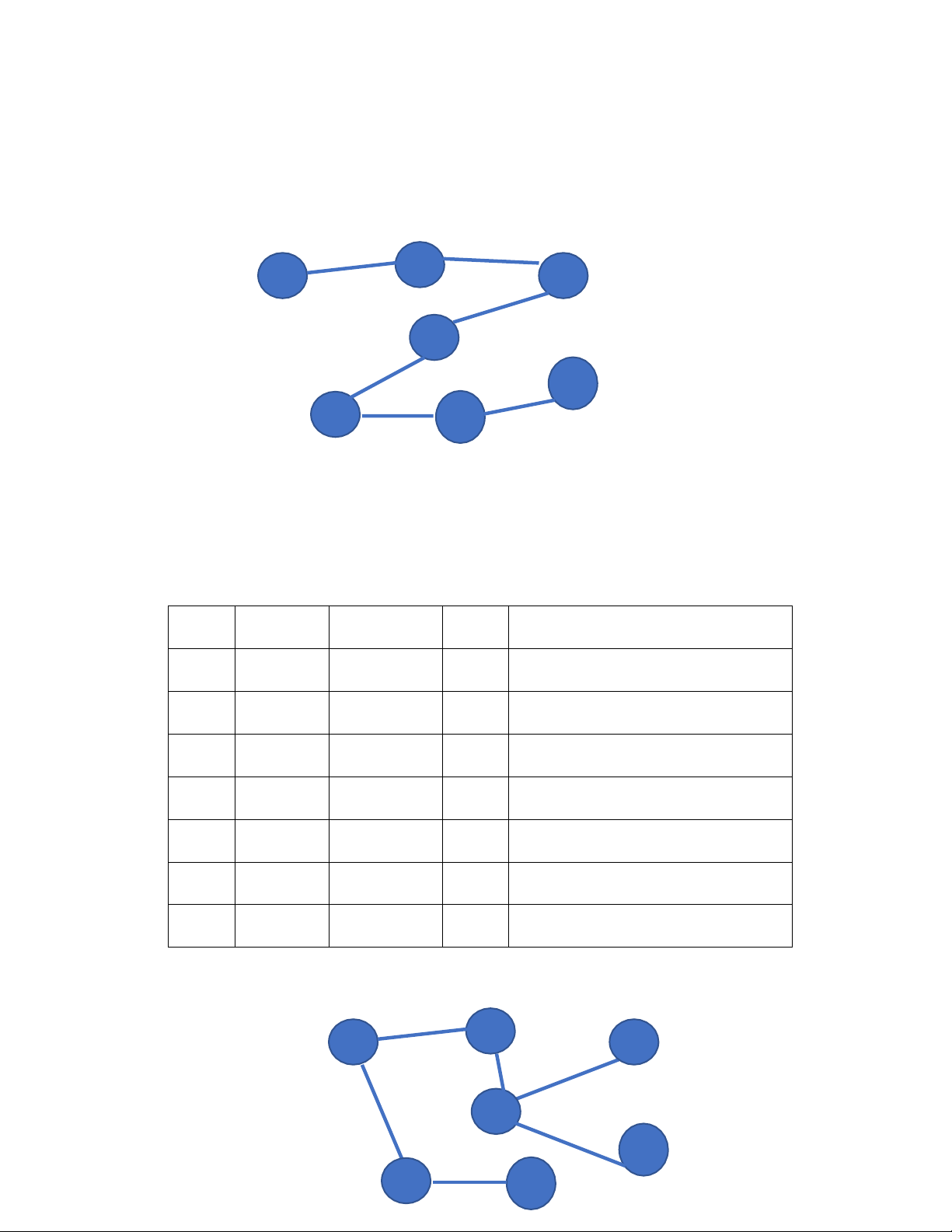
Duyệt theo chiều rộng, sâu xuất phát từ A Duyệt chiều rộng:
Khởi tạo: Đưa A vào hàng đợi, đánh dấu A đã thăm Các bước lặp
Bước Đỉnh lấy ra Đỉnh kề chưa xét Hàng đợi Đã /Đỉnh xét thăm 1 A B,D D B B,D 2 B C,E E C D C,E 3 D F F E C F 4 C Ko có F E 5 E G G F G 6 F Ko có G 7 G Ko có Rỗng. KT
Trình tự duyệt theo chiều rộng: ABDCEFG A B D C E F G Duyệt chiều sâu: Bước DF
Đỉnh kề chưa xét Đỉnh đã xét S 1 A B,D A 2 B C,D,E B 3 C E C 4 E D,G,F E 5 D F D 6 F G F 7 G
Ko còn đỉnh chưa xét. Dừng G
Trình tự duyệt theo chiều sâu: ABCEDFG B A C E G D F
Tìm cây khung cực tiểu bằng thuật toán Prim: Xuất phát từ 1 đình, sau
đó chọn cạnh thỏa mãn 2 đk: 1.
1 đỉnh thuộc VT, 1 đỉnh thuộc VG 2.
Có trọng số nhỏ nhất Bước ET Trọng số VT VG 0 ∅ A B, C, D, E, F, G 1 AD 5 D B, C, E, F, G 2 DF 6 F B, C, E, G 3 AB 7 B C, E, G 4 BE 7 E C,G 5 EC 5 C G 6 EG 9 G Rỗng. Dừng
Cây khung: Tổng trọng số: 39 7 B A C 7 5 5 E 9 G 6 D F
Tìm cây khung cực tiểu bằng thuật toán Kruskal
Bước 1: sắp xếp các cạnh theo chiều không giảm của trọng số Cạnh AD EC DF AB BE BC EF EG FG ED Trọng 5 5 6 7 7 8 9 9 11 15 số
Bước 2: Chọn các cạnh thêm vào cây khung T theo nguyên tắc: Trọng số
nhỏ, cạnh thêm không tạo thành chu trình với các cạnh đã chọn Bước ET Trọng số Cây khung 2.1 AD 5 7 B A C 2.2 EC 5 7 5 2.3 DF 6 5 E 9 2.4 AB 7 G 6 2.5 BE 7 D F 2.6 EG 9 Tổng TS 39
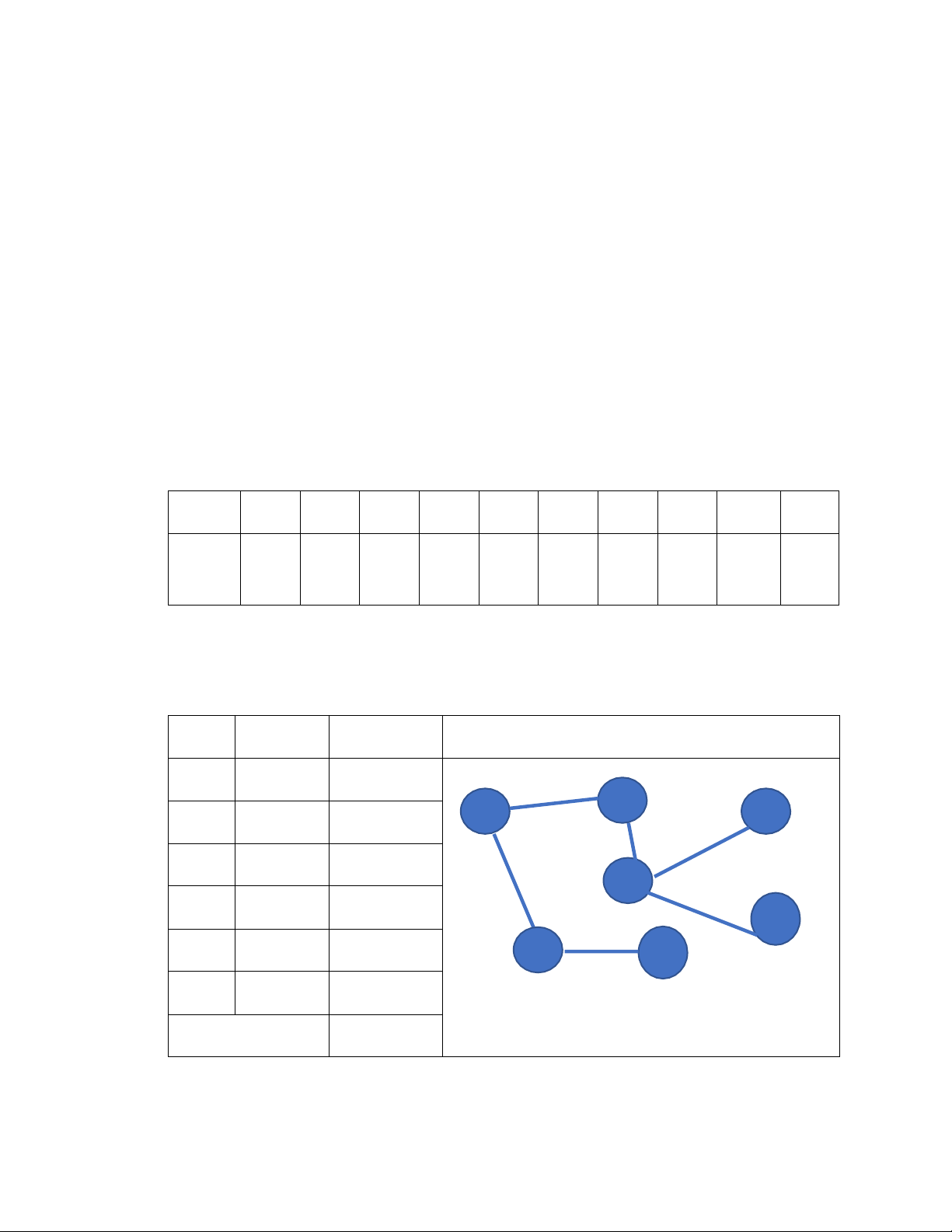
7. Cho đồ thị có ma trận trọng số sau: A B C D E F 0 4 0 0 1 0 4 0 3 0 1 0 0 3 0 5 6 3 0 0 5 0 2 0 1 1 6 2 0 1 0 0 3 0 1 0
Vẽ đồ thị tương ứng với ma trận trên.
Tìm cây khung cực tiểu bằng thuật toán Prim, Kruskal
8. R = {((a , b) , (c , d) ) ∈ R2 x R2 | a +c = b+ d} có phải quan hệ tương đương
(thứ tự) không? (giải thích)
- a+a ≠b+b nếu a≠b nên R không có tính phản xạ. Vậy R không phải
quan hệ tương đương hay thứ tự
9. Cho E là 1 tập hợp. P( E ) là tập các tập con được sinh bởi E. Xét quan hệ
R = {(A, B) ∈ P(E)x P(E) | A⊂ B}. (A là tập con của B) Chứng minh rằng R là quan hệ thứ tự.
- A⊂A vậy A R A , R có tính phản xạ - A R B : A⊂B ⇨ B R A : B⊂A
A =B. Vậy R có tính phản xứng - A R B : A⊂B
⇨ A⊂C => A R C. Vậy R có tính bắc cầu B R C : B⊂C
KL: R là quan hệ thứ tự
10. Dùng bảng Karnaugh để tối thiểu hóa hàm logic sau
a. f(α ,y,a) = αȳā+ āy + aȳ + ᾱāȳ Biểu đồ Karnaugh Các tế bào lớn: α α α ᾱ α ᾱ ᾱ ᾱ a a ā ā ȳ ȳ y y ȳ y y ȳ ā ȳ
Đa thức tối tiểu: ā+ ȳ
b. f(α ,y,a) = αȳā+ āy + aȳ + ya Biểu đồ Karnaugh α α ᾱ ᾱ a ā ȳ y y ȳ Các tế bào lớn: α α ᾱ ᾱ α α ᾱ ᾱ α α ᾱ ᾱ a a a ā ā ā ȳ y y ȳ ȳ y y ȳ ȳ y y ȳ y α a
Đa thức tối tiểu: a +y+α
Document Outline

• I. LÝ THUYẾT
• II. BÀI TẬP