





















Preview text:
1/ 26 Nhóm Toán THCS Toán học là đam mê
Trường THCS Trưng Vương Năm học: 2017-2018
ĐỀ CƯƠNG ÔN TẬP KIỂM TRA HỌC KỲ II MÔN: TOÁN 7 A. LÝ THUYẾT:
1. Đại số: Trả lời các câu hỏi 1,2 SGK trang 22. Câu 1,2,3,4 SGK trang 49. 2. Hình học:
- Nêu định nghĩa, tính chất, các cách nhận biết tam giác cân, đều, vuông, vuông cân?
- Nêu các trường hợp bằng nhau của hai tam giác, trường hợp bằng nhau đặc biệt của 2 tam giác vuông.
- Phát biểu, vẽ hình, ghi giả thiết, kết luận của các định lí.
+ Quan hệ giữa cạnh và góc đối diện trong tam giác.
+ Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu.
+ Quan hệ giữa 3 cạnh trong tam giác.
+ Tính chất tia phân giác của một góc, đường trung trực của đoạn thẳng.
+ Tính chất đường trung tuyến, 3 đường phân giác, 3 đường trung trực, 3 đường cao trong tam giác.
B. BÀI TẬP THAM KHẢO:
Bài 1. Thu gọn các đơn thức sau rồi chỉ ra bậc của đơn thức: a) 2 3 5x( 2 − xy ).3xyz b) 2 3 2 3 2 3 ( 2
− x yz ) .(3x y z) 3 3 c) 2 2 2 (4xy x) . x yz 4 2 2 1 1 5 d) 2 2 − x x y . y 25 3 2 2 2 1 1 5 e) 3 3 3 3
− x y .1 x y . − xy 2 5 3 2 1 f) 4abx − xy . (−ay)2 3 2 ( , a b là hằng số). 2 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 2/ 26 Nhóm Toán THCS Toán học là đam mê
Bài 2. Cho các đa thức: 2 2 2 2
A = −x y + 7x − 3x y + 4xy + 2yx − 5x − 4 2 2
B = 2xy + 3 − 6x y − 3xy + 2x +1− (xy) 2 2
C = 4(x −1) + 2x(xy − y) + y(x − x) − x(xy + 3)
a) Thu gọn và tìm bậc của , A , B C .
b) Tính A + B + C; A + B − C;2A − B + . C
c) Tính giá trị biểu thức C với x = 2, y = 2 − .
Bài 3. Tìm đa thức A biết: a) 2 2 3 2 2 2 3
A + (2xy − 3x y + y ) =5x y + 4x y + 4y . b) 2 2 2
A − (4xy − 3y ) = x − 7xy + 8y . c) 2 2 3 2 3
(25x y −13xy + x ) − A = 11x y − 2x . d) 2 2 2 3 3
(3x y − xy + 2x y ) − A .
Bài 4. Cho 2 đa thức: P ( x) 5 2 5 2 = 5
− x − 6x + 5x − 5x − 2 + 4x và Q ( x) 4 3 2 3 3 = 2
− x − 5x +10x −17x + 4x − 5 + x
a) Thu gọn mỗi đa thức trên rồi sắp xếp theo lũy thừa giảm dần của biến.
b) Tính P ( x) + Q ( x); P ( x) − Q ( x) . c) Chứng tỏ x = 2
− là nghiệm của P(x) nhưng không phải là nghiệm của Q(x) .
Bài 5. Cho 2 đa thức: A( x) 3 = x (x + ) 3
2 − 5x + 9 + 2x ( x − ) 1 và B ( x) = ( 2
x − x + ) − ( 4 3 2 3 1
3x + 2x − 3x + 4)
a) Thu gọn rồi sắp xếp theo lũy thừa tăng dần của biến.
b) Tính A( x) + B ( x) ; A( x) − B ( x) .
c) Tìm nghiệm của C ( x) = A( x) + B ( x).
d) Chứng tỏ đa thức H ( x) = A( x) + 5x vô nghiệm.
Bài 6. Cho hai đa thức: A( x) = ( 2
3 x + 2 − 4x) − 2x ( x − 2) +17 và B ( x) 2
= x − x + − ( 2 3 7
3 3 x − 2x + 4). Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 3/ 26 Nhóm Toán THCS Toán học là đam mê
a) Thu gọn A( x), B ( x) . Sắp xếp các đa thức theo lũy thừa giảm của biến. Tìm hệ số
cao nhất, hệ số tự do của 2 đa thức đó.
b) Tìm N ( x) sao cho N ( x) − B ( x) = A( x).
và M ( x) sao cho A( x) − M ( x) = B ( x).
c) Chứng minh: x = 2 là một nghiệm của N ( x). Tìm một nghiệm nữa của N ( x). 2
d) Tính nghiệm của A( x) tại x = . 3
Bài 7. Tìm nghiệm của các đã thức a) A( x) = 4 − x − 5 g) H ( x) 1 1 = x − 3 − 2 2
b) B ( x) = 3(2x − ) 1 − 2( x + ) 1
h) K ( x) = 3x − 2 + 4 − 6x c) C ( x) = ( 2 x − )( 2 2 8 −x + ) 1
i) M ( x) = x − + ( x − )2 2 1 1 d) D ( x) 3 = 3x − x j) N ( x) 2 = 4x − 3x + 7 e) E ( x) 3 = 2x + 4x k) P ( x) 2
= 7x − 2x − 9 f) G ( x) 3 2
= x − x + x −1 l) Q ( x) 2 = 5x −11x + 6
Bài 8*. (Dành cho HS giỏi)
a) Tìm giá trị nhỏ nhất của các biểu thức đại số: 2 2 A = ( x + )2 2 B = ( x − ) 1 + ( y + 5) +1
C = x − 2014 + x − 2015 D = ( x − )4 2 9 + y − 2 −1
b) Tìm giá trị lớn nhất của các biểu thức: 1 B = − ( x + )2 5 1 2
C = 9 − x − 5 D = 2 x + 2
c) Tìm các giá trị nguyên của biến x để: 2 8 − x 1) A = B = 6 − có giá trị lớn nhất. 2) x
x − có giá trị nhỏ nhất. 3 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 4/ 26 Nhóm Toán THCS Toán học là đam mê
Bài 9*. (Dành cho HS giỏi) Tính giá trị các biểu thức sau: 2a − 5b 4a + b a 3 a) A = − = a − 3b 8a − biết 2b b 4
b) B = ( x + y)( y + z)( x + z) biết xyz = 2 và x + y + z = 0 c) f ( x) 17 16 15 14
= x − 2015x + 2015x − 2015x +....+ 2015x −1. Tính f (2014)
Bài 10. Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm.
a) Tam giác ABC là tam giác gì? Vì sao?
b) Kẻ AH vuông góc với BC ( H BC ). Gọi AD là phân giác BAH ( D BC ). Qua A
vẽ đường thẳng song song với BC, trên đó lấy E sao cho AE = BD (E và C cùng phía đối
với AB). CMR: AB = DE. c) CMR: A DC cân.
d) Gọi M là trung điểm AD, I là giao điểm của AH và DE. CMR: C, I, M thẳng hàng.
Bài 11. Cho tam giác ABC vuông tại A, phân giác BD, kẻ DE vuông góc với BC tại E. Trên
tia đối của tia AB lấy F sao cho AF = CE. CMR: a) A BD = E BD
b) BD là đường trung trực của AE. c) AD < DC.
d) E, D, F thẳng hàng và BD ⊥ CF . e) 2(AD + AF) > CF. Bài 12. Cho ABC có 0
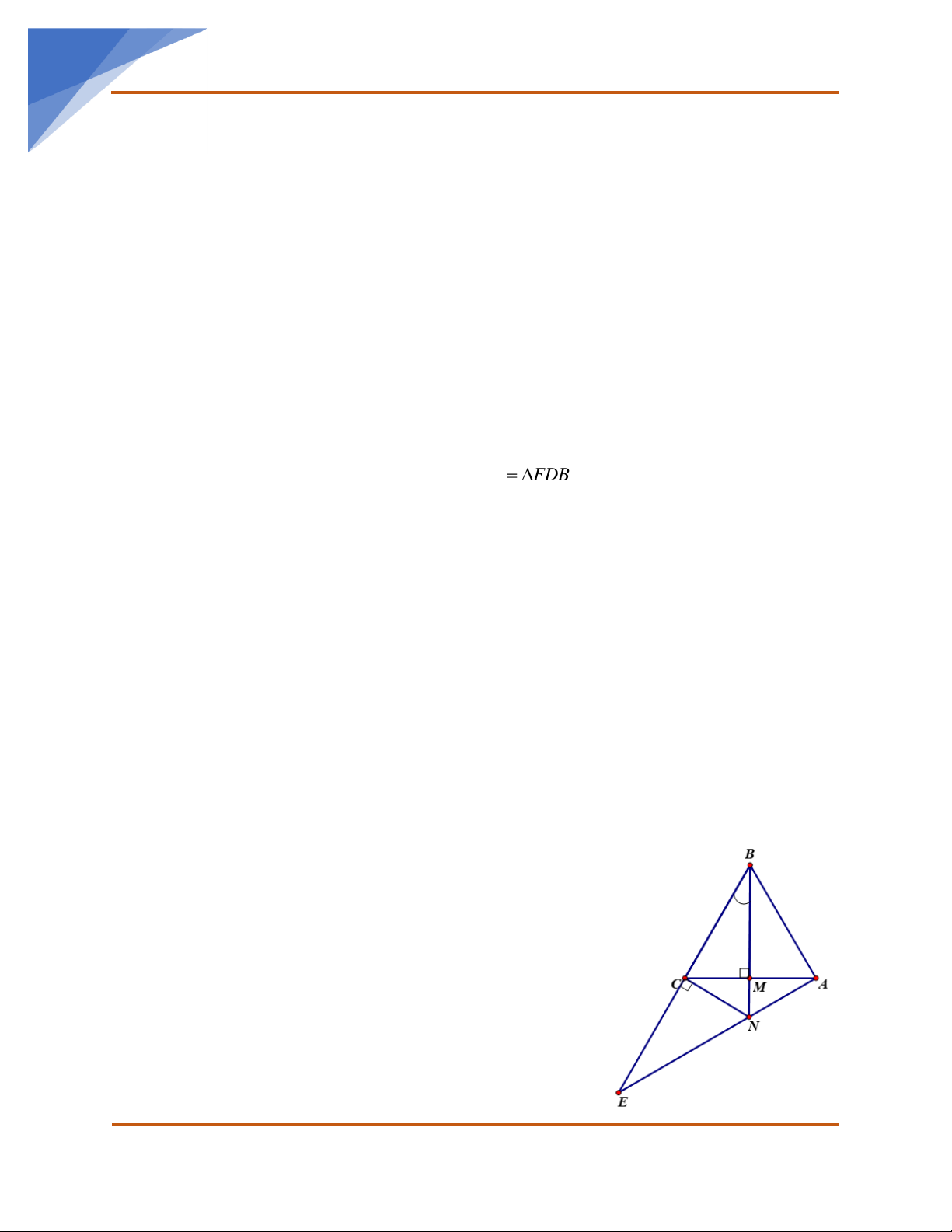
A = 90 và AC AB . Kẻ AH ⊥ BC . Trên tia HC lấy điểm D sao
cho HD = HB . Kẻ CE ⊥ AD kéo dài ( E thuộc tia AD ). Chứng minh: a) ABD cân. b) DAH = ACB
c) CB là tia phân giác của ACE
d) Kẻ DI ⊥ AC ( I AC ) , chứng minh 3 đường thẳng AH, I , D CE đồng quy.
e) So sánh AC và CD .
f) Tìm điều kiện của ABC
để I là trung điểm AC . Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 5/ 26 Nhóm Toán THCS Toán học là đam mê Bài 13. Cho ABC
cân tại A ( A 90 ). Trên cạnh BC lấy 2 điểm D , E sao cho
BD = DE = EC . Kẻ BH ⊥ AD, CK ⊥ AE ( H AD, K AE ), BH cắt CK tại G . Chứng minh rằng: a) ADE cân. b) BH = CK .
c) Gọi M là trung điểm của BC . Chứng minh ,
A M , G thẳng hàng. d) AC AD .
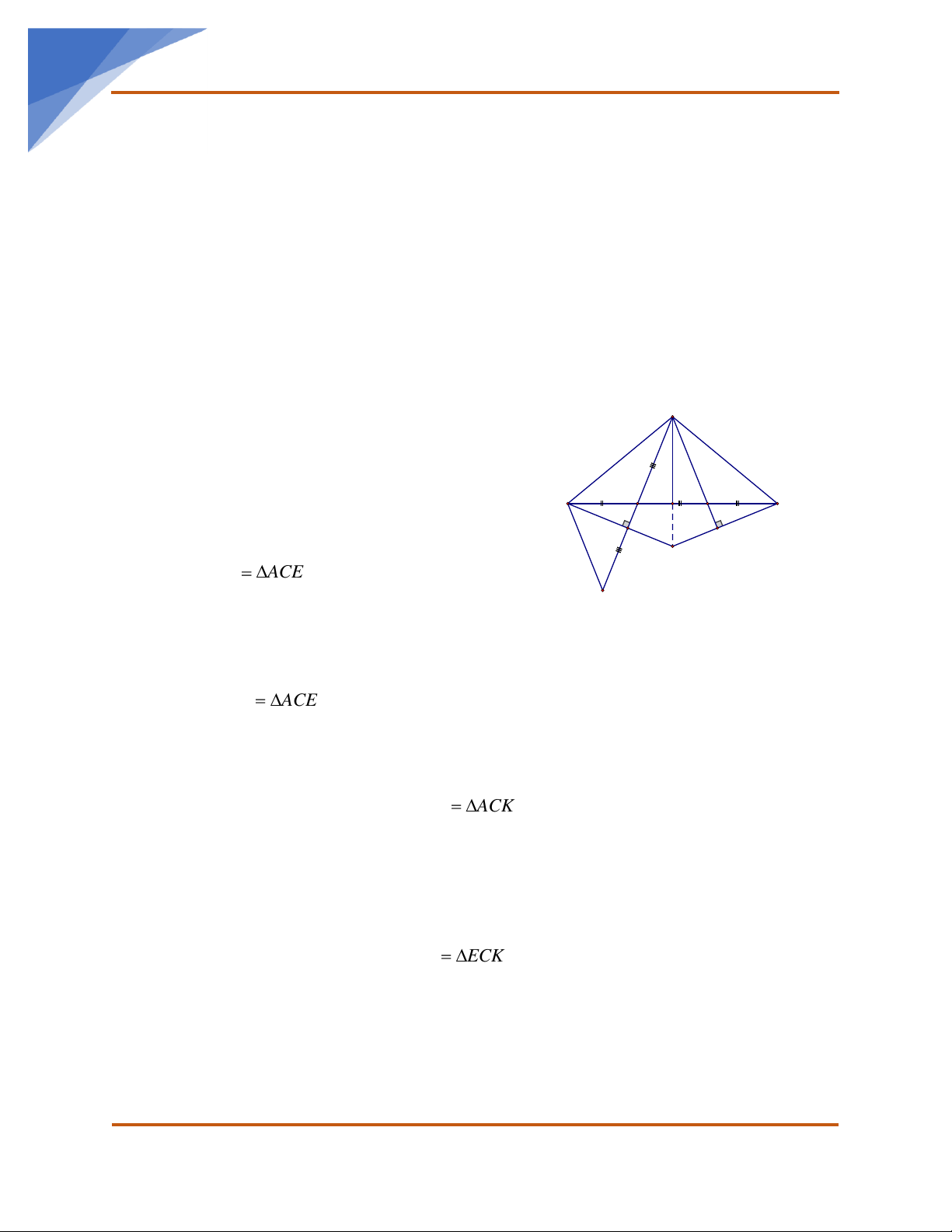
e) DAE DAB . Bài 14. Cho ABC
đều. Tia phân giác góc B cắt AC tại M. Từ A kẻ đường thẳng vuông
góc với AB cắt BM , BC tại N, E. Chứng minh: a) A NC cân. b) NC ⊥ B . C
c) Xác định dạng của tam giác B N . E
d) NC là trung trực của BE. e) Cho AB =10c .
m Tính diện tích B NE và chu vi . ABE Bài 15. Cho ABC có 0
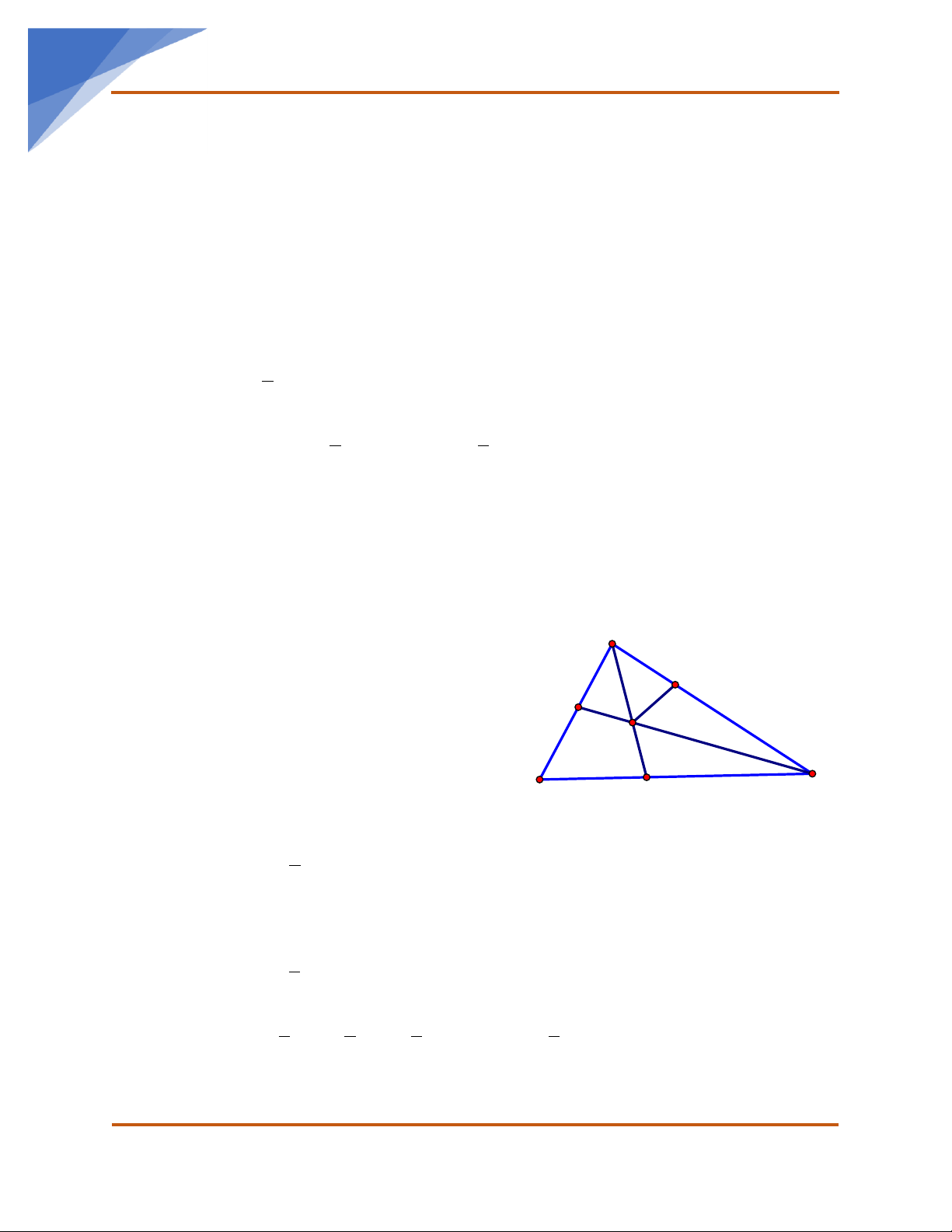
A = 90 ( AB AC ), đường cao AH , AD là phân giác của A HC .
Kẻ DE ⊥ AC .
a) Chứng minh: DH = D . E
b) Gọi K là giao điểm của DE và AH . Chứng minh A KC cân. c) Chứng minh K HE = C EH . d) Cho BH = 8c , m CH = 32c . m Tính AC. e) Giả sử ABC có 0
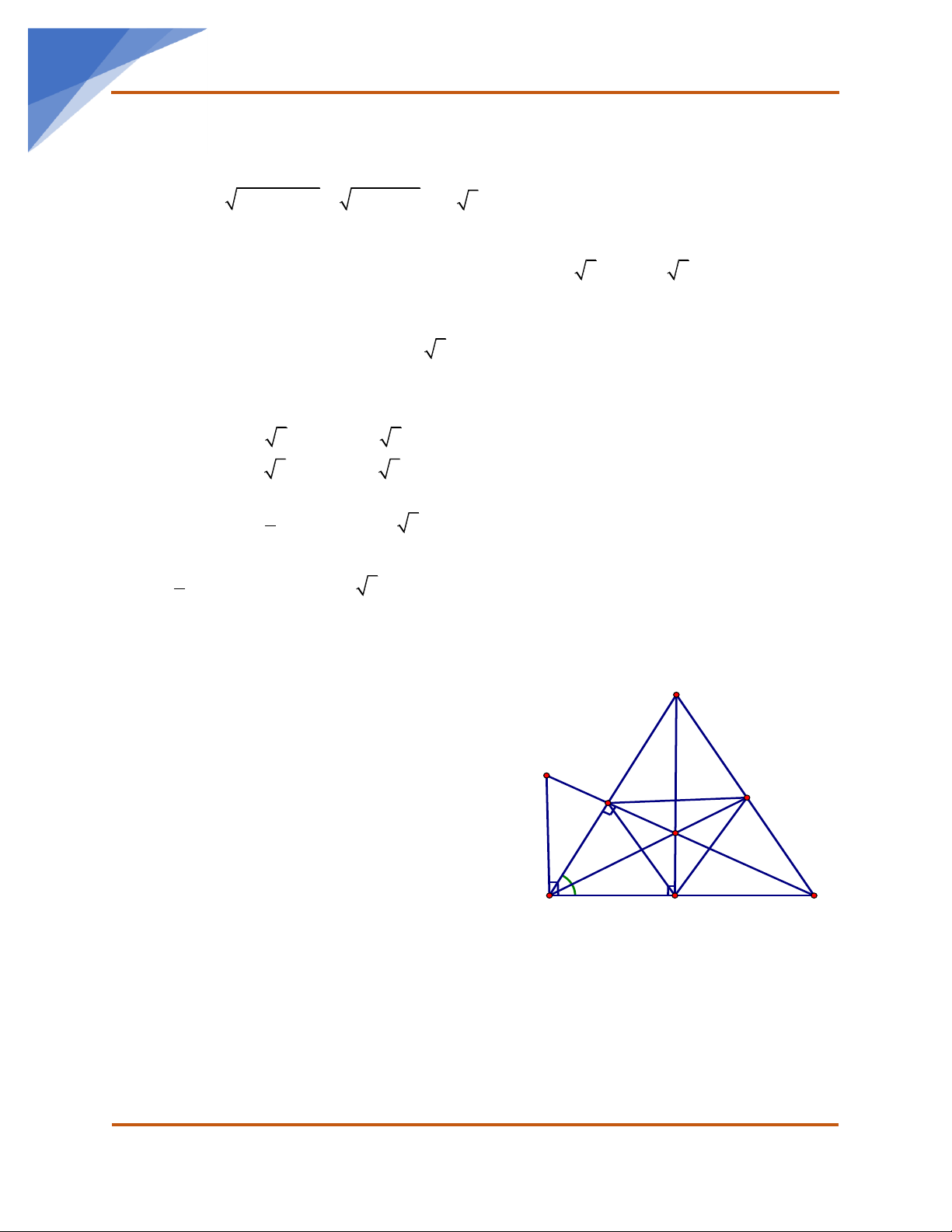
C = 30 , AD cắt CK tại P . Chứng minh HEP đều. Bài 16. Cho ABC có 60o A =
. Các tia phân giác của góc B và C cắt nhau ở I , cắt cạnh
AC, AB ở D và E. Tia phân giác góc BIC cắt BC ở F. a) Tính góc BIC
b) Chứng minh: ID = IE = IF . c) Chứng minh: D EF đều.
d) Chứng minh: I là giao điểm các đường phân giác của hai tam giác ABC và D EF Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 6/ 26 Nhóm Toán THCS Toán học là đam mê
Hướng dẫn giải: Bài 1. a) 2 3 3 3 3 5x( 2
− xy ).3xyz = 3 − 0x y z ; Bậc 9 b) 2 3 2 3 2 3 13 8 9 ( 2
− x yz ) .(3x y z) =12x y z ; Bậc 30 3 3 27 c) 2 2 2 10 7 3 (4xy x) . x yz = x y z ; Bậc 20 4 4 2 2 1 1 5 1 − d) 2 2 5 6 − x x y . y = x .y ; Bậc 11 25 3 2 36 2 2 1 1 5 5 e) 3 3 3 3 11 11
− x y .1 x y . − xy = x y ; Bậc 11 2 5 3 6 2 1 f) 4abx − xy . (−ay)2 3 2 3 5 6 = a . b x .y ; Bậc 11 2 Bài 2. a) Thu gọn và tìm bậc: 2 2 2
A = −x y − x y + 4xy + 2x − 4 ; Bậc 4 2 2 2
B = −x y − 6x y − xy + 2x + 4 ; Bậc 4 2 2
C = 2x y − 3xy + x − 4 ; Bậc 4 b) Tính: 2
A + B + C = 7
− x y + 5x − 4 2 2 2
A + B − C = 4
− x y − 7x y + 6xy + 3x + 4 2 2 2
2A − B + C = x y + 4x y + 6xy + 3x −16
c) Tính giá trị biểu thức C với x = 2, y = 2 − 2 2 C = 2.2 .( 2 − ) − 3.2.( 2 − ) + 2 − 4 = 42 Bài 3. Tìm A a) 2 2 3 2 2 2 3
A + (2xy − 3x y + y ) =5x y + 4x y + 4y 2 2 2 3 2 2 3
A = 5x y + 4x y + 4y − (2xy − 3x y + y ) 2 2 2 3 2 2 3
A = 5x y + 4x y + 4y − 2xy + 3x y − y 2 2 2 3 2
A = 5x y + 7x y + 3y − 2xy b) 2 2 2
A − (4xy − 3y ) = x − 7xy + 8y Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 7/ 26 Nhóm Toán THCS Toán học là đam mê 2 2 2
A = x − 7xy + 8y + 4xy − 3y 2 2
A = x − 3xy + 5y 2 2 3 2 3
(25x y −13xy + x ) − A = 11x y − 2x c) 2 2 3 2 3
A = (25x y −13xy + x ) − (11x y − 2x ) 2 2 3 2 3
A = 25x y −13xy + x −11x y + 2x 2 2 3
A =14x y −13xy + 3x d) 2 2 2 3 3
(3x y − xy + 2x y ) − A = 0 2 2 2 3 3
A = 3x y − xy + 2x y Bài 4.
a) Thu gọn mỗi đa thức trên rồi sắp xếp theo lũy thừa giảm dần của biến: P ( x) 5 2 5 2 = 5
− x − 6x + 5x − 5x − 2 + 4x = ( 5 5 − x + x ) + ( 2 2 − x + x ) 2 5 5 6 4 − 5x − 2 = 2
− x − 5x − 2 Q ( x) 4 3 2 3 3 4 3 3 3 2 = 2
− x − 5x +10x −17x + 4x − 5 + x = 2 − x + ( 5
− x + 4x + x ) −17x +10x − 5 4 2 = 2
− x −17x +10x −5
b) Tính P ( x) + Q ( x); P ( x) − Q ( x)
+) P ( x) + Q( x) 2 4 2 = 2
− x − 5x − 2 − 2x −17x +10x − 5
P ( x) + Q ( x) 4 = − x + ( 2 2 2 2
− x −17x ) + ( 5
− x +10x) + ( 2 − − 5)
P ( x) + Q ( x) 4 2 = 2
− x −19x + 5x − 7
+) P ( x) − Q ( x) 2
= − x − x − − ( 4 2 2 5 2 2
− x −17x +10x − 5)
P ( x) − Q ( x) 2 4 2 = 2
− x − 5x − 2 + 2x +17x −10x + 5
P ( x) − Q ( x) 4 = x + ( 2 2 2 2
− x +17x ) + ( 5
− x −10x) + ( 2 − + 5)
P ( x) − Q ( x) 4 2 = 2x + 1 + 5x −15x + 3 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 8/ 26 Nhóm Toán THCS Toán học là đam mê c) Chứng tỏ x = 2
− là nghiệm của P(x) nhưng không phải là nghiệm của Q(x) +) Thay x = 2
− vào P(x) , ta có: P(x) 2 = 2
− x − 5x − 2 2 Suy ra P ( 2 − ) = 2 − ( 2 − ) − 5( 2 − ) − 2 P( 2 − ) = 8 − +10 − 2 P( 2 − ) = 0 Hay x = 2
− là nghiệm của P(x) . +) Thay x = 2
− vào Q(x) , ta có: 4 2 Q(x) = 2
− x −17x +10x −5 4 2 Suy ra Q ( 2 − ) = 2 − .( 2 − ) −17.( 2 − ) +10.( 2 − ) −5 Q( 2 − ) = 3 − 2 + 68 − 20 − 5 Q ( 2 − ) = 1 − 1 0 Hay x = 2
− không phải là nghiệm của Q(x) . Vậy x = 2
− là nghiệm của P(x) nhưng không phải là nghiệm của Q(x) . Bài 5.
a) Thu gọn và sắp xếp theo lũy thừa giảm
A(x)= 𝑥3(𝑥 + 2) − 5𝑥 + 9 + 2𝑥3(𝑥 − 1)
= 𝑥4 +2𝑥3 − 5𝑥 + 9 + 2𝑥4 − 2𝑥3
=3𝑥4 − 5𝑥 + 9
B(x)= 2(𝑥2 − 3𝑥 + 1) − (3𝑥4 + 2𝑥2 − 3𝑥 + 4)
=2𝑥2 − 6𝑥 + 2 − 3𝑥4 − 2𝑥2 + 3𝑥 − 4
=−3𝑥4 − 3𝑥 − 2
b) Tính A(x)+B(x); A(x)-B(x)
A(x)= 3𝑥4 − 5𝑥 + 9 +
B(x)= −3𝑥4 − 3𝑥 − 2 A(x)+B(x)= −8𝑥 + 7 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 9/ 26 Nhóm Toán THCS Toán học là đam mê
A(x)= 3𝑥4 − 5𝑥 + 9 −
B(x)= −3𝑥4 − 3𝑥 − 2
A(x)−B(x)= 6𝑥4 − 2𝑥 + 11
c) Tìm nghiệm của C(x)=A(x) +B(x) 7
C(x)=−8𝑥 + 7=0 −8𝑥 = −7 x= 8 7
Vậy nghiệm của C(x)= −8𝑥 + 7 là x= 8
d) Chứng tỏ rằng H(x)=A(x)+5x vô nghiệm
H(x)= 3𝑥4 − 5𝑥 + 9 + 5𝑥 = 3𝑥4 + 9
H(x)=0 3𝑥4 + 9 = 0 3𝑥4 = −9 𝑥4 = −3 (vô lí)
Nên không có giá trị nào của x để H(x)=0
Vậy H(x) vô nghiệm. Bài 6. a) Thu gọn và sắp xếp
A(x)=3(𝑥2 + 2 − 4𝑥) − 2x(x − 2) + 17
=3𝑥2 + 6 − 12𝑥 − 2𝑥2 + 4x + 17 =𝑥2 − 8𝑥 + 23
Hệ số cao nhất: 1, hệ số tự do 23
B(x) = 3𝑥2 − 7𝑥 + 3 − 3(𝑥2 − 2𝑥 + 4)
= 3𝑥2 − 7𝑥 + 3 − 3𝑥2 + 6𝑥 − 12 = −𝑥 − 9
Hệ số cao nhất: -1, hệ số tự do -9 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 10/ 26 Nhóm Toán THCS Toán học là đam mê b) N(x)-B(x)=A(x) N(x)=B(x)+A(x)
A(x)= 𝑥2 − 8𝑥 + 23 + B(x) = − 𝑥 − 9
N(x) = 𝑥2 − 9𝑥 + 14 A(x)-M(x)=B(x) M(x)=A(x)-B(x)
A(x)= 𝑥2 − 8𝑥 + 23 − B(x) = −𝑥 − 9
M(x) = 𝑥2 − 7𝑥 + 32
c) Chứng minh 2 là nghiệm của N(x).Tìm một nghiệm nữa của N(x)
N(2)= 22−9.2 + 14 = 4 − 18 + 14 = 0
Vậy 2 là nghiệm của N(x)
N(x)= 𝑥2 − 9𝑥 + 14 = (𝑥 − 2)(𝑥 + 𝑎)
𝑥2 − 9𝑥 + 14 = 𝑥2 + (𝑎 − 2)𝑥 − 2𝑎 −9 = 𝑎 − 2 𝑎 = −7 { { (thỏa mãn) 14 = −2𝑎 𝑎 = −7
Vậy a=−7 là một nghiệm nữa của N(x) 2
d) Tính giá trị của A(x) tại x= 3 2
Thay x = vào biểu thức A(x)= 𝑥2 − 8𝑥 + 23 3 2 2 2 4 16 163
Ta được A ( )= ( )2 − 8. + 23= − + 23 = 3 3 3 9 3 9 2 163
Vậy tại x = thì giá trị của biểu thức A(x) bằng 3 9 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 11/ 26 Nhóm Toán THCS Toán học là đam mê Bài 7. 5 − a) Ta có 4
− x − 5 = 0 x = . 4 5
Vậy nghiệm của đa thức là x = − . 4
b) Ta có ( x − ) − ( x + ) 5 3 2 1 2
1 = 0 4x − 5 = 0 x = . 4 5
Vậy nghiệm của đa thức là x = . 4 2x −8 = 0 x = 4 x = 2
c) Ta có (2x − 8)(−x + ) 2 2 2 2 1 = 0 . 2 2 −x +1 = 0 x = 1 x = 1
Vậy tập nghiệm của đa thức là S = 2 − ; 1 − ;1; 2 . x = 0 x = 0 d) Ta có 3
3x − x = 0 x ( 2 3 − x ) = 0 . 2 x = 3 x = 3
Vậy tập nghiệm của đa thức là S = − 3;0; 3 . x = 0 e) Ta có 3
2x + 4x = 0 2x ( 2 x + 2) = 0 . 2 x = 2 − Vì 2
x 0 với mọi x nên 2 x = 2 − vô nghiệm.
Vậy nghiệm của đa thức là x = 0 . f) Ta có 3 2 2
x − x + x − =
x (x − ) + (x − ) = (x − )( 2 1 0 1 1 0 1 x + ) 1 = 0 . x −1 = 0 x =1 . 2 2 x +1 = 0 x = 1 − Vì 2
x 0 với mọi x nên 2 x = 1 − vô nghiệm.
Vậy nghiệm của đa thức là x =1. 1 1 1 7 x − 3 = x = 1 1 1 1 x = 7 2 2 2 2 g) Ta có: x − 3 − = 0 x − 3 = . 2 2 2 2 1 1 1 5 x = 5 x − 3 = − x = 2 2 2 2
Vậy tập nghiệm của đa thức là S = 5; 7 .
h) Ta có 3x − 2 + 4 − 6x = 0 . Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 12/ 26 Nhóm Toán THCS Toán học là đam mê 3x − 2 0 Vì
nên 3x − 2 + 4 − 6x 0 . 4 − 6x 0 3x − 2 = 0 3 x − 2 = 0 2 Dấu “=” xảy ra khi x = . 4 − 6x = 0 4 − 6x = 0 3 2
Vậy nghiệm của bất phương trình là x = . 3
i) Ta có x − + ( x − )2 2 1 1 = 0. x −1 0 Vì (
nên x − + ( x − )2 2 1 1 0 . x − )2 2 1 0 x =1 x −1 = 0 x −1 = 0
Dấu “=” xảy ra khi ( = = . x − ) x 1 x 1 2 2 2 1 = 0 x −1 = 0 x = 1 −
Vậy nghiệm của đa thức là x =1. j) Ta có: 2
4x − 3x + 7 = 0 3 3 9 103 2
4x − x − x + + = 0 2 2 16 16 3 3 3 103 2x 2x − − 2x − + = 0 4 4 4 16 3 3 103 2x − 2x − + = 0 4 4 16 2 3 1 − 03 2x − = . 4 16 2 2 3 3 103 Vì 2x − 0
với mọi x nên suy ra 2x − = − vô nghiệm. 4 4 16 k) Ta có 2 2
7x − 2x − 9 = 0 7x + 7x − 9x − 9 = 0 7x ( x + ) 1 − 9 ( x + ) 1 = 0 x = 1 − x +1 = 0 ( x + ) 1 (7x − 9) = 0 9 . 7x − 9 = 0 x = 7 9
Vậy tập nghiệm của đa thức là S = 1 − ; 7 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 13/ 26 Nhóm Toán THCS Toán học là đam mê l) Ta có 2 2
5x −11x + 6 = 0 5x − 5x − 6x + 6 = 0 5x ( x − ) 1 − 6( x − ) 1 = 0 ( − = = x − )( x − ) x 1 0 x 1 1 6 = 0 . x − 6 = 0 x = 6
Vậy tập nghiệm của đa thức là S = 1; 6 . Bài 8.
a) Tìm giá trị nhỏ nhất của các biểu thức đại số: +) A = ( x + )2 2 Vì ( x + )2 2 0, x
; dấu “=” xảy ra khi (x + )2 2
= 0 x + 2 = 0 x = −2
Vậy GTNN của A là 0 khi x = 2 − 2 2 +) B = ( x − ) 1 + ( y + 5) +1 Ta có: ( x − )2 1
0 với mọi x, ( y + )2 5 0 với mọi y 2 2 Suy ra: ( x − )
1 + ( y + 5) +1 0 + 0 +1 = 1 ( x − )2 1 = 0 x =1 Dấu “=” xảy ra khi ( y + )2 = y = 5 5 0 −
Vậy GTNN của B là 1 khi x = 1; y = 5 −
+) C = x − 2014 + x − 2015
Ta có: C = x − 2014 + x − 2015 = x − 2014 + 2015 − x
Mà: x − 2014 + 2015 − x x − 2014 + 2015 − x = 1 = 1
Dấu “=” xảy ra khi ( x − 2014)(2015 − x) 0 2014 x 2015
Vậy GTNN của C là 1 khi 2014 x 2015
+) E = ( x − )4 2 9 + y − 2 −1 Vì: ( x − )4 2 9
0 ; y − 2 0 với mọi x,y
Suy ra: D = ( x − )4 2 9
+ y − 2 −1 0 + 0 −1= 1 − Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 14/ 26 Nhóm Toán THCS Toán học là đam mê (x − )4 2 9 = 0 x = 3
Dấu “=” xảy ra khi: − = y = 2 y 2 0
Vậy GTNN của D là 1 − khi ( ;
x y) = (3; 2) hoặc ( ; x y) = ( 3 − ;2)
b) Tìm giá trị lớn nhất của các biểu thức:
+) B = − ( x + )2 5 1 2 2 Vì: ( x + ) 1
0 B = 5 − (x + ) 1
5 với mọi x, dấu “=” xảy ra khi: (x + )2 1 = 0 x = 1 −
Vậy GTLN của B là 5 khi x = 1 − +) 2
C = 9 − x − 5 Vì: 2 2 x − 5 0 x
C = 9 − x − 5 9 − 0 = 9 với mọi x Dấu “=” xảy ra khi: 2 2 2
x − 5 = 0 x − 5 = 0 x = 5 x = 5
Vậy GTLN của C là 9 khi x = 5 1 +) D = 2 x + 2 1 1 Vì 2
x + 2 2 D = 2 x + với mọi x 2 2 Dấu “=” xảy ra khi: 2 x = 0 x = 0 1 Vậy GTLN của D là khi x = 0 2
c) Tìm các giá trị nguyên của biến x để: 2
1) A = 6− có giá trị lớn nhất x
ĐK để A có nghĩa là x 6 2
Với x 6 6 − x 0 A = 0 6 − x Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 15/ 26 Nhóm Toán THCS Toán học là đam mê 2
Với x 6 6 − x 0 A = 0 6 − x
Do đó đề A lớn nhất thì A 0 trong trường hợp x 6
Mặt khác tử số của A không đổi nên A lớn nhất khi mẫu 6 − x bé nhất
Suy ra x là số nguyên lớn nhất mà x 6 nên x = 5 2 2 Khi đó A = = = 2 6 − x 6 − 5
Vậy khi x = 5 thì A đạt GTLN là 2 8 − x
2) B = x − có giá trị nhỏ nhất 3
ĐK để B có nghĩa là x 3 8 − x 5 − (x − 3) 5 Ta có: B = = = −1 x − 3 x − 3 x − ; 3 5
Suy ra B nhỏ nhất khi x − nhỏ nhất 3 5
Với x 3 x − 3 0 0 x − 3 5
Với x 3 x − 3 0 0 x − 3 5 5 Do đó đề 0 x
x − nhỏ nhất thì 3 x − trong trường hợp 3 3 5 5 Mặt khác tử số của x − lớn nhất
x − không đổi nên 3
x − nhỏ nhất khi mẫu 3 3
Suy ra x là số nguyên lớn nhất mà x 3 nên x = 2 5 5 Khi đó B = −1 = −1 = 6 − x − 3 2 − 3
Vậy khi x = 2 thì B đạt GTNN là 6 − .
Bài 9*. (Dành cho HS giỏi) a 3 a b a b a) Ta có
= = . Đặt = = k . Suy ra a = 3k;b = 4k b 4 3 4 3 4 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 16/ 26 Nhóm Toán THCS Toán học là đam mê
Khi đó biểu thức A trở thành: 2.3k − 5.4k 4.3k + 4k 6k − 20k 12k + 4k 1 − 4k 16k 14 5 5 A = − = − = − = −1 = 1 −1 = 3k − 3.4k 8.3k − 2.4k 3k −12k 24k − 8k 9 − k 16k 9 9 9 5 Vậy A = . 9
b) Ta có x + y + z = 0 , suy ra x + y = − ;
z y + z = −x và x + z = −y
Thay vào biểu thức B, ta được:
B = (−z)(−x)(− y) = −xyz , mà xyz = 2 nên B = 2 − Vậy B = 2 − .
c) Xét với x = 2014 x +1 = 2015. Khi đó ta được f ( ) 17
= x − (x + ) 16 x + ( x + ) 15 x − ( x + ) 14 2014 1 1
1 x + .... + ( x + ) 1 x −1 17 = x − ( 17 16 x + x ) + ( 16 15 x + x ) − ( 15 14 x + x ) + + ( 2 ... x + x) −1 17 17 16 16 15 15 14 2
= x − x − x + x + x − x − x +...+ x + x −1
= x −1 = 2014 −1 = 2013 Vậy f (2014) = 2013 Bài 10. a) Do 2 2 2
AB + AC = BC nên ABC vuông tại A. C b) Do E AD = B D (
A cgc) nên ED = AB . c) : =180o − ( + ) = 90o AHD ADH HAD AHD − HAD = H 90o CAD − DAB E I D
Mà AD là phân giác BAH M A Nên B
HAD = DAB → CAD = ADH Vậy A DC cân tại C. d) A
DC cân tại C, M là trung điểm AD nên CM ⊥ AD . Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 17/ 26 Nhóm Toán THCS Toán học là đam mê Do E AD = B D ( A cgc) (c/m ở b)
nên EDA = DAB → ED / / AB
Mà AB ⊥ AC → DE ⊥ CA → I = AH DE
Do đó I là trực tâm A
DC → I CM Vậy C, I, M thẳng hàng. Bài 11.
a) Vì BD là phân giác ABC F
Suy ra ABD = DBE Do đó A BD = E
BD (góc nhọn – cạnh huyền). A H b) Ta có: A BKI = E BK (c-g-c) D K
nên BD ⊥ AE = K và K là trung điểm AE. B C
Vậy BD là đường trung trực của AE. E c) Ta có: A BD = E
BD nên AD = DE mà E
DC vuông tại E nên DE DC → AD DC . d) Ta có: F AD = C
ED(c − g − c)
Suy ra: FAD = CDE do đó FAD + ADE = ADE + EDC
Mà A, D, C thẳng hàng nên E, D, F thẳng hàng. Trong B
EC :CA ⊥ BE, FE ⊥ BC,CA FE = D nên D là trực tâm B
EC → BD ⊥ CF . e) Ta có: F
AD: AF + AD FD và E
CD : DE + EC DC
Mà AF = CE, AD = DE Suy ra (AF + A )
D + (DE + EC) FD + DC
Hay 2(AD + AF) FD + DC Xét D
EFC : DF + DC FC
Do đó 2(AD + AF) F . C Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 18/ 26 Nhóm Toán THCS Toán học là đam mê Bài 12. a) Ta có:
+ AH ⊥ BC AH là đường cao của ABD
+ HD = HB AH là trung tuyến của ABD
ABD có AH vừa là đường cao vừa là đường
trung tuyến nên ABD cân tại A .
b) + ABD cân tại A nên: ADH = ABH (1) + ADH vuông tại H nên: 0
DAH + ADH = 90 (2) + ABC vuông tại A nên: 0
ACB + ABH = 90 (3)
Từ (1), (2), (3) suy ra: DAH = ACB (đpcm). c) Ta có: + D
CE vuông tại E nên: 0 DCE + CDE = 90 (4)
+ Mà: CDE = ADH (đối đỉnh) (5)
Từ (2), (4), (5) suy ra: DCE = ACB
CB là tia phân giác của ACE
d) Ta có: + AH ⊥ BC AH ⊥ DC + ID ⊥ AC + CE ⊥ AD AH, I ,
D CE là 3 đường cao của B
CD nên đồng quy tại một điểm.
e) Vì AH ⊥ BC nên H ,
B HC lần lượt là hình chiếu của A , B AC trên BC
Mà: AC AB (gt)
HC HB(quan hệ giữa đường xiên và hình chiếu)
Mà: HD = HB (điểm D tia HC )
Nên: điểm D thuộc đoạn thẳng HC
Do đó: CD CH
Lại có: CH AC (quan hệ giữa đường xien và đường vuông góc)
Vâỵ: CD AC .
f) Nếu I là trung điểm của AC thì: DI là đường trung tuyến của A DC Mà: DI ⊥ AC Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 19/ 26 Nhóm Toán THCS Toán học là đam mê A
DC có DI vừa là đường trung tuyến vừa là đường cao nên A
DC cân tại D DAC = DCA
Lại có: ADB = 2DCA ( tính chất góc ngoài của tam giác) Mà:
ADB = ABC (vì ABD cân tại A )
Do đó: ABC = 2DCA Mà: 0
ABC + DCA = 90 Suy ra: 0 0
ABC = 60 ; DCA = 30 Vậy ABC có thêm điều kiện 0 ABC = 60 (hoặc 0
ACB = 30 ) thì I là trung điểm AC . Bài 13.
a) Xét ABD và A CE có: A
+ AB = AC ( ABC cân)
+ ABC = ACE ( ABC cân) D E B C M
+ BD = CE (Giả thiết) H K G A BD A
CE ( .cg.c) F
AD = AE (2 cạnh tương ứng) A DE cân (đpcm). b) Vì A BD A
CE (cmt) BAH = CAK (2 góc tương ứng) Xét ABH và A CK có: AHB AKC ( 90 ) + = = A BH A CK ch − gn
+ AB = AC ( A BC can) ( )
BH = CK
(2 canh tuong ung)
+ BAH = CAK (cmt) c) Xét DBH và E CK có:
+ DHB = EKC (= 90) D BH E
CK (ch − cgv)
+ BD = CE (gt)
DBH = ECK goc tuong ung
+ BH = CK (cmt) (2 ) G
BC cân tại G , lại có GM là trung tuyến
GM là đường trung trực
G đường trung trực của BC ( ) 1 Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 20/ 26 Nhóm Toán THCS Toán học là đam mê Vì ABC cân tại A (gt)
A đường trung trực của BC (2)
Do M là trung điểm của BC (gt)
M đường trung trực của BC (3) Từ ( ) 1 , (2) và (3) ,
A M , G thẳng hàng. d) Xét A
ME có: AEC = AME + MAE = 90 + MAE 90 AEC là góc tù. Xét A
CE có: AC đối diện góc tù AEC AC AE (quan hệ góc và cạnh đối diện)
Mà AD = AE (cmt) AC AD (đpcm)
e) Trên tia đối của tia DA lấy điểm F sao cho DF = DA .
Xét ADE và FDB có:
+ DE = DB (gt) A DE F
DB ( .cg.c)
+ ADE = FDB (2 goc doi dinh) + AE = BF
(2 canh tuong ung)
+ DA = DF (cach ve) + DAE = DFB
(2 goc tuong ung)
Xét ABD có: ADB ACE = ABD (t/c góc ngoài tam giác)
AB AD (quan hệ góc và cạnh đối diện trong tam giác)
Mà AD = BF (= AE) nên AB BF . Xét ABF
có: AB BF (cmt )
AFB DAB (quan hệ góc và cạnh đối diện trong tam giác)
Lại có AFB = DAE (cmt ) DAE DAB (đpcm). Bài 14. a) ABC đều (giả thiết)
Mà BM là phân giác của ABC (giả thiết)
BM là đường trung trực của ABC CM = M ;
A BM ⊥ AC (tính chất đường trung trực) C M = MA Trong CNA
có: NM ⊥ AC (BM ⊥ AC) Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 21/ 26 Nhóm Toán THCS Toán học là đam mê Suy ra CNA cân tại N (đpcm)
ACN = NAC (tính chất tam giác cân)
BCA = BAC(gt)
b) Ta có: ACN = NAC (cmt)
BCA+ ACN = BAC + NAC BCN = BAN Do 0 BAN = (gt) 0 90
BCN = 90 NC ⊥ BC. c) Xét B CN và BAN có: 0 BCN = BAN = 90 BN chung BC = B ( A gt) B CN = B
AN (Cạnh huyền – Cạnh góc vuông)
BNC = BNA (Góc tương ứng bằng nhau) Trong B CN có: 0 0
BCN = 90 (cmt) BNC + CBN = 90 1 1 Mà: 0 0 CBN = NBA = CBA = .60 = 30 (gt) 2 2 0 0 0 0
CNB = 90 − CBN = 90 −30 = 60 0
CNB = BNA = 60 Ta có: 0
CNB + BNA + CNE = 180 0 0 0 0 0
CNE =180 − CNB − BNA =180 − 60 − 60 = 60 0
CNE = CNB = 60 .
NC là tia phân giác của BNE Mà NC ⊥ BC B
NE cân tại N . d) Ta có: B
NE cân tại N
mà NC ⊥ BC hay NC là đường cao của B NE
NC là đường trung trực của B
NE (t/c tam giác cân)
NC là đường trung trực của BE Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 22/ 26 Nhóm Toán THCS Toán học là đam mê e) Ta có : 0 BAE = 90 2 2 2
AE = BE + AB 2 2 2 2
AE = BE + AB = 20 +10 =10 5
Ta lại có : BC = CE =10cm BE = 20cm
Chu vi tam giác ABE là : AB + BE + EA = 10 + 20 +10 5 = 30 +10 5 Đặt NA = ;
x NE = y NB = y
Ta có : NA + NE = AE x + y =10 5 Mà : 2 2 2 2 2
BN = NA + AB y = x +10 y = 6 5 NE = 6 5 Suy ra . x = 2 5 NA = 2 5 1 Ta có: 2 S
= .NC.BE.10 = 20 5(cm ) . BNE 2 1 = .2 NA .BC = . NA BC = 2 5 2 Bài 15.
a) Chứng minh: DH = D . E K Cách 1: Xét A
HD và AED , có: B 0 AHD = AED = 90 H P
AD là cạnh huyền chung D
HAD = EAD ( AD là phân giác HAC ) Do đó A HD = A
ED (Cạnh huyền – góc nhọn) A C E
DH = DE (2 cạnh tương ứng). Cách 2: DH ⊥ AH
Ta có: DE ⊥ AE
Mà D thuộc đường phân giác HAE
DH = DE (Tính chất của điểm thuộc tia phân giác). Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 23/ 26 Nhóm Toán THCS Toán học là đam mê b) Chứng minh A KC cân.
Do D là giao điểm của hai đường cao KE và CH nên D là trực tâm của A KC AD ⊥ CK Xét A
KC có AD là đường cao đồng thời là đường phân giác Do đó: A KC cân tại A. c) Chứng minh K HE = C EH .
Xét AEK và A HC có:
AK = AC (Do A KC cân) A chung Do đó: A EK = A
HC (Cạnh huyền – góc nhọn)
HKE = ECH (2 góc tương ứng)
và KE = HC (2 cạnh tương ứng). Lại có:
+) AH = AE (Do A HD = A ED ) +) AK = AC (Do A KC cân)
+) AC = AE + EC
+) K = AH + HK Suy ra HK = EC Xét K HE và ΔCEH có:
HK = EC (Chứng minh trên)
HKE = ECH (Chứng minh trên)
KE = HC (Chứng minh trên) Do đó: K HE = C
EH (c - g -c) d) Tính AC .
Áp dụng định lí Py-ta-go cho A
BC vuông tại A có: 2 2 2
AB + AC = BC (1)
Áp dụng định lí Py-ta-go cho A
HB vuông tại H có: 2 2 2
AB = AH + BH (2)
Áp dụng định lí Py-ta-go cho A
HC vuông tại H có: 2 2 2
AC = AH + CH (3) Từ (1), (2), (3) Suy ra: 2 2 2 2 2 2
BC − BH − CH 50 −18 − 32 2 2 2 2 2
BC = 2 AH + BH + CH AH = = = 576 AH = 24 2 2
Thay vào (3), ta tính được AC = 30c . m
e) Chứng minh HEP đều Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 24/ 26 Nhóm Toán THCS Toán học là đam mê Khi 0 0
BCA = 30 KAC = 60 Xét A
KC cân tại A, có 0 KAC = 60 A KC đều
Do đó AK = AC = KC(4) Lại có: A ,
D KE, AP là các đường cao đồng thời là trung tuyến
E, H, P lần lượt là trung điểm của AC, AK,CK . Xét A
HC vuông tại H , trung tuyến HE ứng với cạnh huyền AC . 1 Suy ra HE =
AC(5) (Tính chất trung tuyến trong tam giác vuông) 2 1 1
Tương tự ta có: HP = AK (6) và EP = CK (7) 2 2
Từ (4), (5), (6), (7) suy ra: HE = HP = EP Vậy H
EP đều (Điểu phải chứng minh). Bài 16. a) Xét ABC có: B o ABC + ACB + BAC = 180 F E o o ABC + ACB + 60 = 180 I o ABC + ACB = 120 60° C A D
Ta có: CI là tia phân giác của góc ACB 1 BCI = ACI = ACB 2
BI là tia phân giác của góc ABC 1 CBI = ABI = ABC 2 1 1 1 1 o o
BCI + CBI= ACB+ ABC= (ACB + ABC)= .120 =60 2 2 2 2 Xét BIC có: Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 25/ 26 Nhóm Toán THCS Toán học là đam mê o BIC + CBI + BIC = 180 o o 60 + BIC = 180 o BIC = 120 b) Ta có: o EIB + BIC = 180 o o EIB + 120 = 180 o EIB = 60 . Ta có: o DIC + BIC = 180 o o DIC + 120 = 180 o DIC = 60 . O
Ta có: IF là tia phân giác của BIC BIF = FIC = 60 . Xét I FC và I DC có:
ICF = ICD (vì CI là phân giác của BCA ). Cạnh CI chung = (= 60O CIF CID ) ΔIFC = ΔIDC (g-c-g) IF = ID (1)
Xét IFB và IEB có:
IBF = IBE (vì BI là phân giác của CBA ) Cạnh IB chung = (= 60O BIF BIE ) I FB = I
EB (g − c − g) IF = IE (2)
Từ (1) và (2) IF = IE = ID . Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/ 26/ 26 Nhóm Toán THCS Toán học là đam mê c) Ta có: = +
= 60o + 60o =120o EIF EIB FIB = +
= 60o + 60o =120o DIF DIC FIC Xét E IF và DI F có IF là cạnh chung = (=120o EIF DIF ) IE = ID (cmt) E IF = D
IF (c-g-c) EF = DF (3)
Chứng minh tương tự: E IF = E
ID EF = ED (4)
TỪ (3) VÀ (4) ta có: EF = DE = DF . D
EF là tam giác đều d) E IF = D
IF IFE = IFD FI là phân giác của EFD E IF = E
ID IEF = IED EI là phân giác của FED
I là giao điểm của 3 đường phân giác trong tam giác DEF .
Tam giác ABC có: CI là phân giác của ACB
BI là phân giác của ABC
I là giao điểm của 3 đường phân giác trong tam giác ABC
Vậy I là giao điểm các đường phân giác của hai tam giác ABC và tam giác DEF. Nhóm Toán THCS:
https://www.facebook.com/groups/606419473051109/




