

















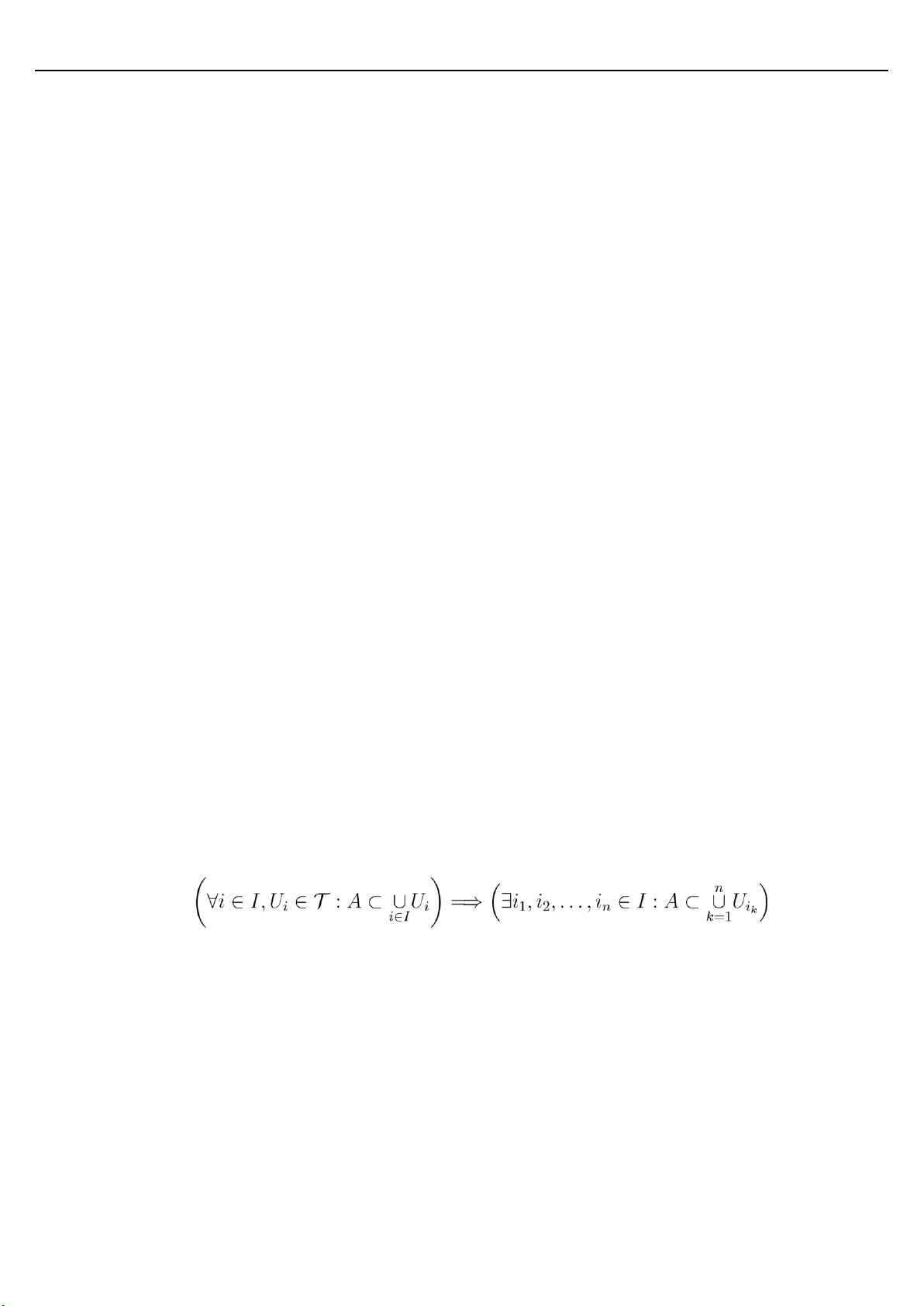











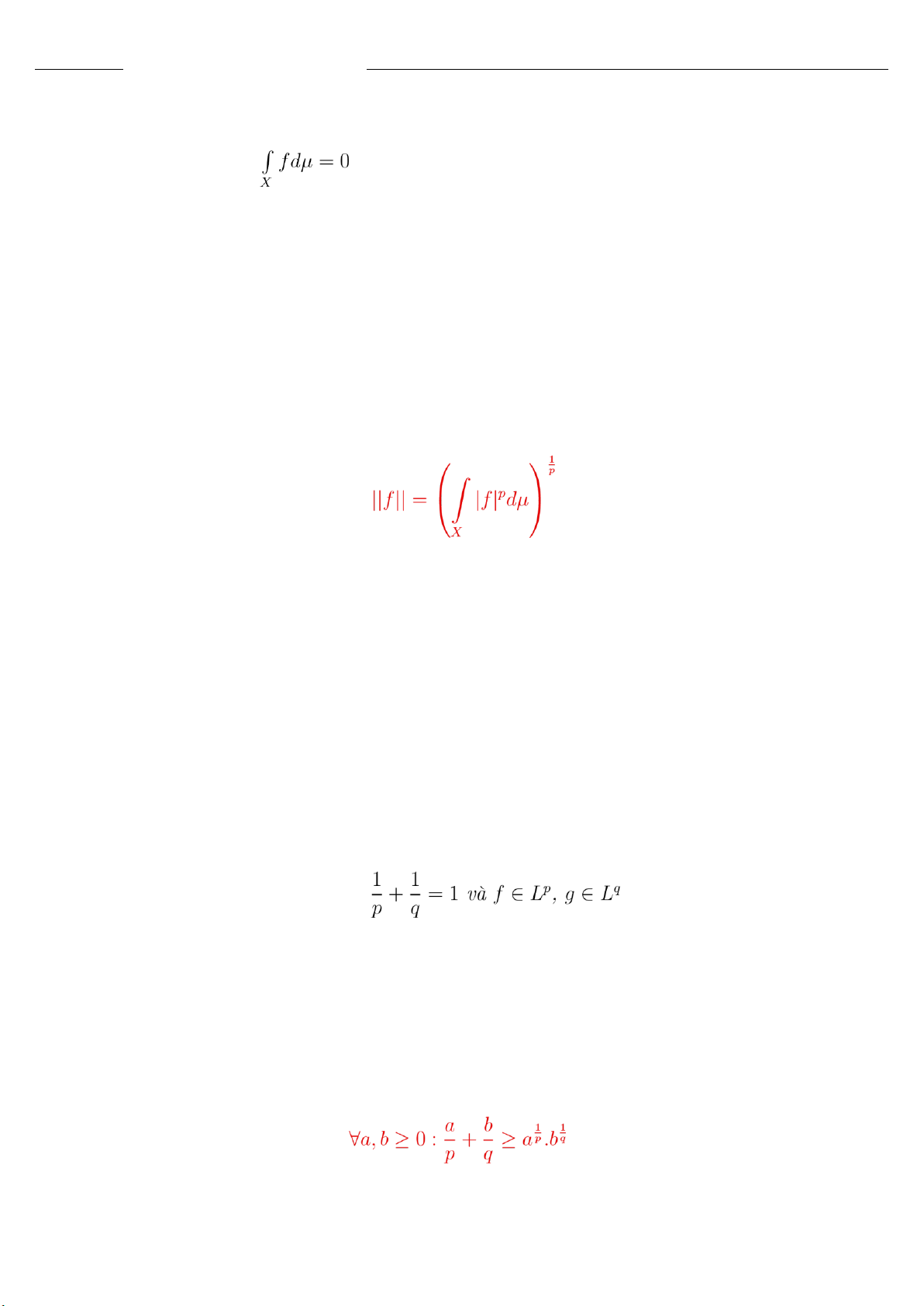




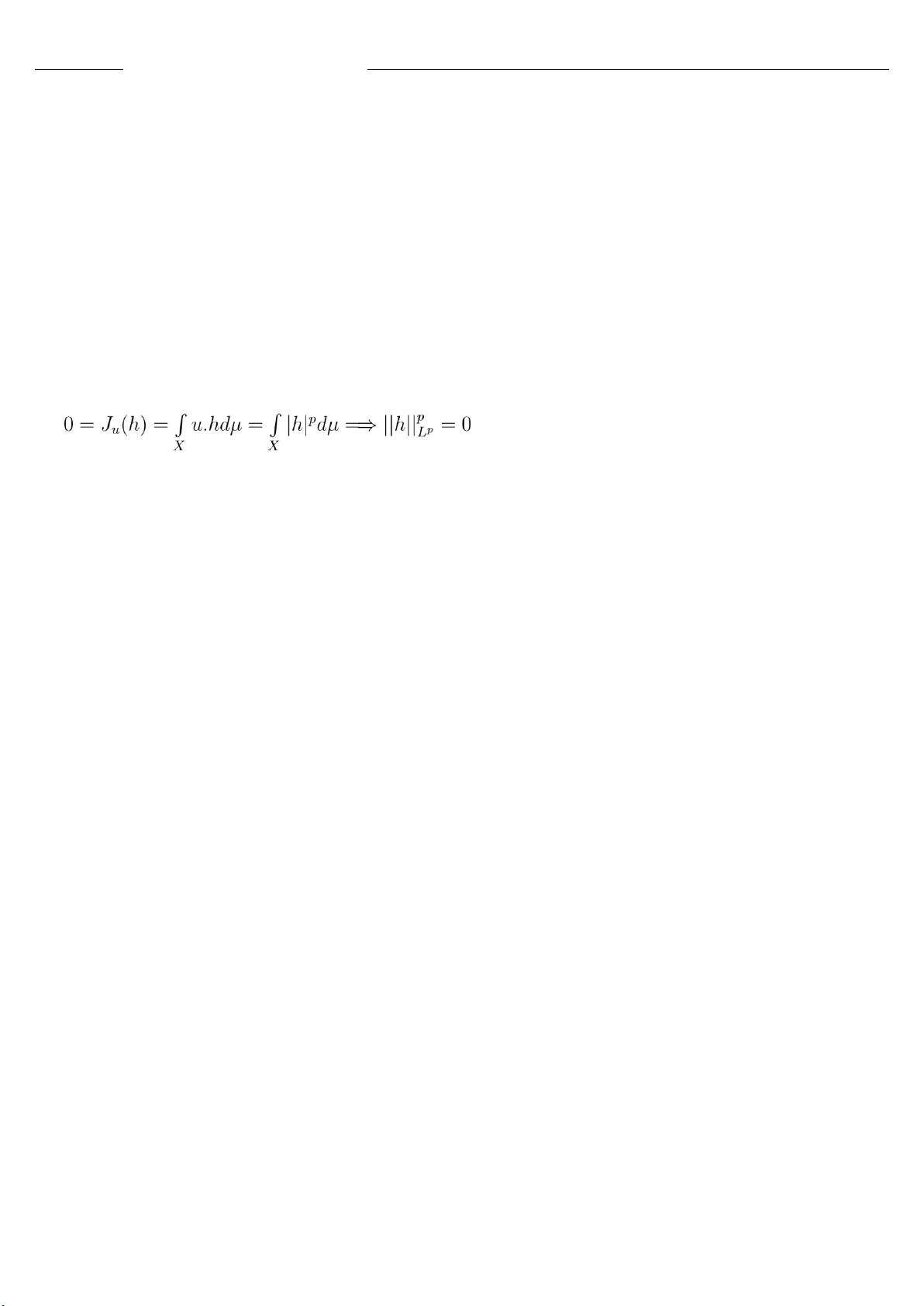













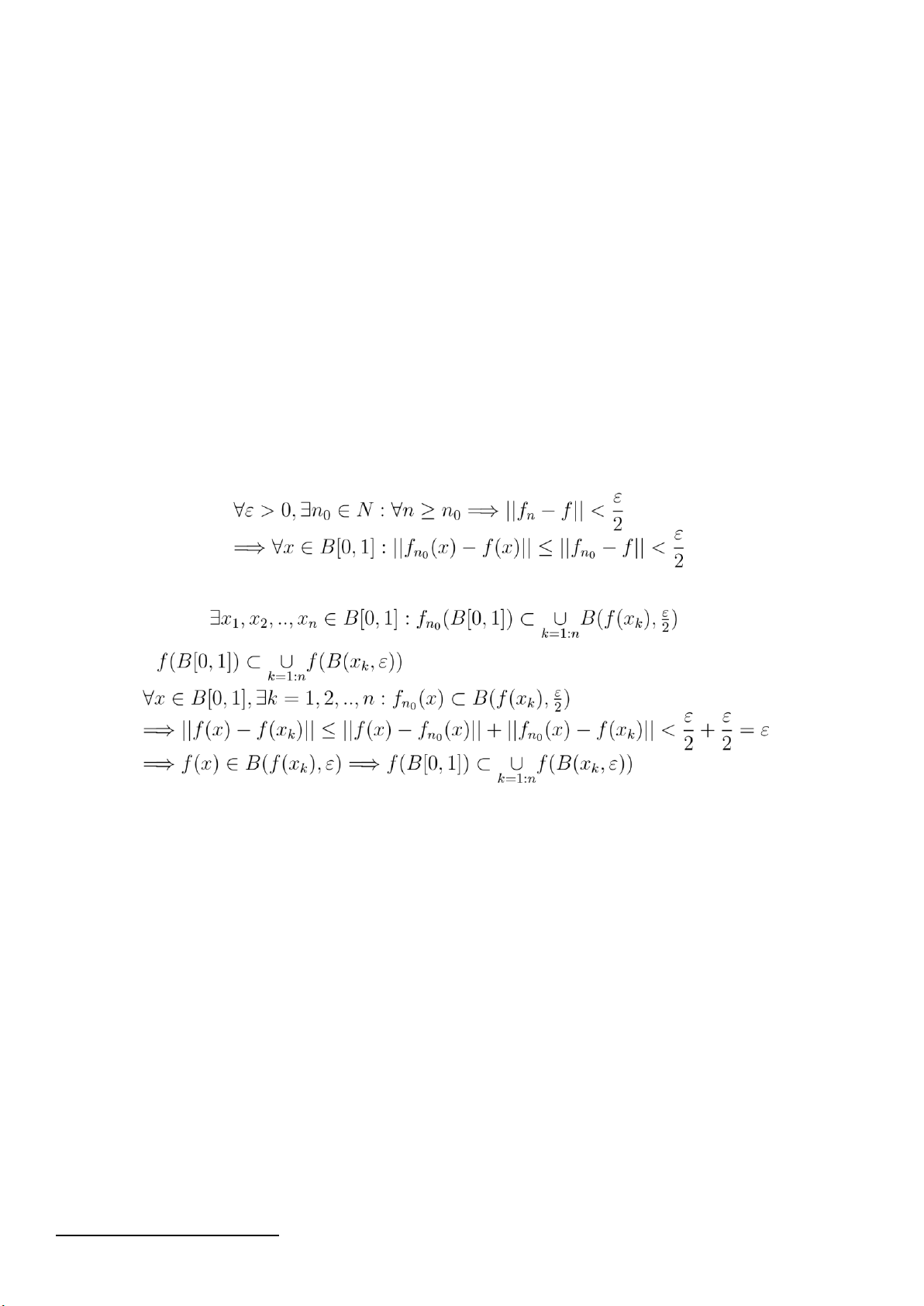


















Preview text:
lOMoARcPSD| 36782889 Mục lục
1 Tài liệu tham khảo ............................................................................................................................................................. 2
1 CÁC ĐỊNH LÝ CƠ BẢN GIẢI TÍCH HÀM .......................................................................................................................... 3
1 Định lý Hahn-Banach ......................................................................................................................................................... 3
2 Định lý tách tập lồi ............................................................................................................................................................. 6
3 Nguyên lý bị chặn đều .................................................................................................................................................... 10
4 Định lý ánh xạ mở và định lý đồ thị đóng .................................................................................................................. 12
5 Các định lý quan trọng khác .......................................................................................................................................... 13
2 TÔ PÔ YẾU và KHÔNG GIAN PHẢN XẠ ....................................................................................................................... 14
1 Nhắc lại một số khái niệm về tô pô ............................................................................................................................. 14
1.1 Không gian tô pô ........................................................................................................................................................... 14
1.2 Cơ sở tô pô ..................................................................................................................................................................... 14
1.3 T2 không gian ................................................................................................................................................................. 15
1.4 Phần trong và bao đóng của một tập hợp ............................................................................................................. 15 1.5
Sự hội tụ trong không gian tô pô
. . . . . . . . . . . . . . . . . . . . . . . . 14 1.6
Ánh xạ liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 1.7 Tập compact
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 2
Tô pô yếu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 2.1
Xây dựng tô pô yếu σ(E,E∗)
. . . . . . . . . . . . . . . . . . . . . . . . . . 17 2.2
Các tính chất tô pô yếu
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 3
Không gian phản xạ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 4
Tô pô yếu * . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 lOMoAR cPSD| 36782889 3 KHÔNG GIAN Lp 23
1 Nhắc lại về tích phân Lebesgue
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 2 Không gian Lp(1 ≤ p <
∞) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25 3 Các tính chất không của không gian Lp . . . . . . . . . .
. . . . . . . . . . . . . . . 28 4 KHÔNG GIAN HILBERT 31 1
Tích vô hướng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 1 lOMoARcPSD| 36782889 Các định lý cơ bản PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng 2
Góc và các tính chất không gian tiền Hilbert . . . . . . . . . . . . . . . . . . . . . . 33 3
Không gian Hilbert . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 4
Cơ sở trực chuẩn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 5
Định lý Stampacchia và Lax-MilGram
. . . . . . . . . . . . . . . . . . . . . . . . . 39
5 PHỔ CỦA TOÁN TỬ TRONG KHÔNG GIAN BANACH 41 1
Toán tử trong không gian banach . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 2
Toán tử hữu hạn chiều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 3
Phổ của toán tử trong không gian banach
. . . . . . . . . . . . . . . . . . . . . . . 43 3.1
Hàm giải tích vào không gian banach . . . . . . . . . . . . . . . . . . . . . . 43 3.2
Phổ của toán tử trong không gian banach
. . . . . . . . . . . . . . . . . . . 44 3.3
Phổ của toán tử compact . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 6 GIẢI TÍCH ĐA TRỊ 52 1
Ánh xạ đa trị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 2
Khoảng cách Hausdorff . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 1 Tài liệu tham khảo
1) Haim BreZis, Giải Tích Hàm - Lý thuyết và ứng dụng, nhà xuất bản Đại học Quốc gia.
2) Hoàng Tụy. Giải tích hiện đại, tập 1,2,3. NXB Giáo dục, 1978.
3) Nguyễn Xuân Liêm, Giải Tích Hàm, nhà xuất bản Giáo dục.
4) Nguyễn Xuân Liêm, Bài Tập Giải Tích Hàm, nhà xuất bản Giáo dục.
5) Đậu thế cấp, Giải Tích Hàm, nhà xuất bản Giáo dục, 2009. 6) Dương Minh Đức, Giải Tích Hàm, Nhà
xuất bản Đại học Quốc Gia. lOMoARcPSD| 36782889 trang 2 Chương 1
CÁC ĐỊNH LÝ CƠ BẢN GIẢI TÍCH HÀM 1 Định lý Hahn-Banach
Định nghĩa 1.1 (Sơ chuẩn) Cho X là không gian định chuẩn (KGĐC) trên trường số K.
p : X −→ R
gọi là một sơ chuẩn nếu thỏa
i) p(λx) = λp(x),∀λ ∈ R,λ ≥ 0,∀x ∈ X.
ii) p(x + y) ≤ p(x) + p(y).
Từ điều kiện (i), ta có p(0) = p(0.x) = 0.p(x) = 0.
Xét p : X −→ R thỏa p(λx) = |λ|p(x) và p(x + y) ≤ p(x) + p(y). Rõ ràng p là một sơ chuẩn.
Đặc biệt p(x) = ||x|| là một sơ chuẩn.
Định lý 1.1 (Định lý Hahn-Banach cho KGVT) .
Cho X0 là không gian con của KGVT X trên R. f : X0 −→ R là một phiếm hàm tuyến tính
Giả sử tồn tại sơ chuẩn p thỏa f(x) ≤ p(x),∀x ∈ X0.
Khi đó tồn tại phiếm hàm tuyến tính F : X −→ R thỏa
i) F|X0 = f.
ii) F(x) ≤ p(x),∀x ∈ X. 3 lOMoARcPSD| 36782889
Nhận xét: Định lý Hanh-Banach thác triển một phiếm hàm tuyến tính từ không gian con X0 ra không gian
lớn hơn X mà vẫn đảm bảo bị chặn bởi một sơ chuẩn.
Định lý 1.2 (Định lý Hahn-Banach cho KGĐC) .
Cho X0 là không gian con của KGĐC X trên R. f : X0 −→ R là một phiếm hàm tuyến tính liên tục
Khi đó tồn tại phiếm hàm tuyến tính liên tục F : X −→ R thỏa
i) F|X0 = f.
ii) ||F|| = ||f||.
Nhận xét: Định lý Hanh Banach thác triển một phiếm hàm ttlt từ một không gian con ra một không gian
lớn hơn. Nhìn chung, F là không duy nhất. Điều kiện để F duy nhất là X0 trù mật trong X. Chứng minh:
Trước hết ta xét p(x) = ||f||.||x|| là một sơ chuẩn trên X (dễ dàng kiểm chứng).
Vì f tuyến tính liên tục nên |f(x)| ≤ ||f||.||x|| = p(x),∀x ∈ X0. Theo
(1.1), tồn tại phiếm hàm tuyến tính F trên X thỏa F|X0 = f và F(x) ≤
p(x) = ||f||.||x||,∀x ∈ X.
Suy ra F liên tục trên X và ||F|| ≤ ||f|| (1.1) 1 Mặt khác ta có: (1.2)
Từ (1.1) và (1.2) suy ra ||F|| = ||f||. Ta có điều phải chứng minh. Các kết quả suy ra từ định lý Hahn-Banach
rất đa đạng. Sau đây là một hệ quả của nó.
Hệ quả 1.3 Cho KGĐC X trên R và x0 6= 0..
f(x0) = ||x0||
Khi đó ∃f ∈ X∗ thỏa mãn ||f|| = 1 Chứng minh 1 f ttlt thì
tuyến tính và f(x) ≤ M.||x|| thì f liên tục và ||f|| ≤ M.
X∗ là tập tất cả các phiếm hàm tuyến tính liên tục trên X. Cùng với chuẩn sup ở trên, X∗ cũng là một không gian định chuẩn. lOMoAR cPSD| 36782889
Đặt X0 =< x0 >= {λx : λ ∈ R} (Không gian con sinh bởi x0) lOMoARcPSD| 36782889 Các định lý cơ bản PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Xét g : X0 −→ R thỏa g(λx0) = λ||x0||.
Rõ ràng g tuyến tính trên X0 và dim(X0) = 1 nên g liên tục trên X0 và ||g|| = 1.
Áp dụng định lý Hahn Banach: . 2 Định lý tách tập lồi
Định nghĩa 2.1 (Phiếm hàm Mincowski) Cho C là tập lồi 2 , mở chứa 0 trong KGĐC X. Xét ánh xạ p : X −→ R thỏa . (1.3)
p được gọi là dung lượng tập lồi hay phiếm hàm Mincowski
Tính Chất 2.1 [Tính chất phiếm hàm Mincowski].
i) ∃M > 0 : 0 ≤ p(x) ≤ M||x||,∀x ∈ X.
ii) C = {x ∈ X : p(x) < 1}.
iii) p là một sơ chuẩn trên X. Chứng minh
i) Vì C mở chứa 0 nên ∃r > 0 : B¯(0,r) ⊂ C 3 Nếu Ta chọn .
∀x 6= 0 : p(x) ≤ M.||x||.
Nếu x = 0 thì có ngay p(0) = 0 = M.||x||
ii) Xét x ∈ C. Ta sẽ chứng minh p(x) < 1.
Vì C mở nên tồn tại ε > 0 đủ bé thỏa (1 + ε)x ∈ C. Theo định
nghĩa phiếm hàm Mincowski, ta có
2 C gọi là tập lồi nếu ∀x,y ∈ C,∀α ∈ (0,1) : αx + (1 − α)y ∈ C. {z = αx + (1 − α)y : α ∈ (0,1)} gọi là đoạn thẳng x,y. 3B¯(0,r) = {x ∈ X :
||x|| ≤ r}. lOMoARcPSD| 36782889 Các định lý cơ bản PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Ngược lại, giả sử p(x) < 1. Ta sẽ chứng minh x ∈ C Vì . Vì C lồi và
iii) Xét λ > 0. Ta chứng tỏ p(λx) = λp(x) 1
∀x,y ∈ X. Ta cần
chứng tỏ p(x + y) ≤ p(x) + p(y). x Theo (ii), ta có.
Vì C lồi nên t. Chọn Ta được
Cuối cùng, cho ε → 0+ ta được
p(x + y) ≤ p(x) + p(y) Ta có điều phải chứng minh.
Định nghĩa 2.2 (Siêu phẳng tách) 3 Cho KGĐC X. f ∈ X∗
i) Tập H[f = α] = {x ∈ X : f(x) = α} gọi là một siêu phẳng. 3 Tham khảo Haim Brezis lOMoARcPSD| 36782889 Các định lý cơ bản PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
ii) Giả sử A,B ⊂ X thỏa
, thì ta nói siêu phẳng H[f = α] tách 2 tập A,B.
iii) Giả sử A,B ⊂ X thỏa
, thì ta nói siêu phẳng H[f = α] tách chặt 2 tập A,B.
Định lý 2.2 (Định lý tách tập lồi) Cho 2 tập con A,B trong KGĐC X thỏa i)
A,B lồi, khác rỗng. ii)
A ∩ B = ∅. iii) A mở (hoặc B mở).
Khi đó tồn tại một siêu phẳng H[f = α] tách 2 tập A,B. Chứng minh
a) Xét trường hợp B = {y0}.
Ta có thể giả sử 0 ∈ A
(Nếu 0 ∈/ A thì ta có thể đặt A0 = A \ x0,B0 = B \ x0 với x0 ∈ A.) Gọi p là phiếm
hàm Mincowski của A.
Xét phiếm hàm tuyến tính g : X0 =< y0 >−→ R thỏa g(λy0) = λ.
Vì A ∩ B = ∅ =⇒ y0 ∈/ A =⇒ p(y0) ≥ 1.
∀λ > 0 : p(λy0) = λp(y0) > λ = g(λy0).
∀λ ≤ 0 : p(λy0) ≥ 0 ≥ g(λy0) = λ. Vậy
p(y) ≥ g(y),∀y ∈ X0. ∗
( thỏaf(x) = g(x),∀x ∈ X0
Theo định lý Hahn Banach, tồn tại f ∈ X
f(x) ≤ p(x).
Ta có ∀x ∈ A : f(x) ≤ p(x) < f(y0).
b) Xét B lồi tùy ý thỏa giả thiết.
Ta đặt A0 = A − B,B0 = {0}. Rõ ràng A0,B0 thỏa giả thiết và trường hợp a).
Như vậy, tồn tại f ∈ X∗ : f(z) < f(0) = 0.
∀x ∈ A,∀y ∈ B =⇒ z = x − y ∈ A0 Ta có: f(z) = f(x) − f(y) < 0 =⇒ f(x) <
f(y),∀x ∈ A,∀y ∈ B. Ta suy ra điều phải chứng minh.
Định lý 2.3 (Định lý tách chặt tập lồi) Cho 2 tập con A,B trong KGĐC X thỏa lOMoARcPSD| 36782889 Các định lý cơ bản PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
i) A,B lồi, khác rỗng.
ii) A ∩ B = ∅.
iii) A đóng, B compact.
Khi đó tồn tại một siêu phẳng H[f = α] tách chặt 2 tập A,B. Chứng minh
Theo giả thiết, A đóng , B compact nên d(A,B) > 0 4
Đặt d(A,B) = 2ε > 0,A0 = A + B(0,ε),B0 = B + B(0,ε). Lúc này ta được A0,B0 là 2 tập mở và A0 ∩ B0 = ∅ 5
Áp dụng định lý tách tập lồi (2.3) cho 2 tập A0 và B0:
∃f ∈ X∗ : f(x) < f(y),∀x ∈ A0,y ∈ B0 =⇒ f(x) < f(y),∀x ∈ A0,y ∈ B
Rõ ràng f 6= 0 =⇒ ∃x0 ∈ B(0,ε) : f(x0) > 0. (nếu f(x0)
< 0 thì ta chọn lại −x0 : f(−x0) > 0.) Do đó:
f(x + x0) < f(y),∀x ∈ A,y ∈ B (Chú ý: A + x0 ⊂ A0).
=⇒ f(x) + f(x0) < f(y),∀x ∈ A,y ∈ B
=⇒ supf(x) + f(x0) ≤ inff(y) x∈A y∈B
=⇒ supf(x) < inff(y) x∈A y∈B
Ta có điều phải chứng minh.
Định lý 2.4 Cho X0 là không gian con của KGĐC X. Các mệnh đề sau tương đương
i) x ∈ X0. ii) ∀f ∈ X∗ : f|X0 = 0 =⇒ f(x) = 0. Chứng minh
i) −→ ii) khá dễ dàng.
4 d(A,B) = inf{d(x,y) : x ∈ A,y ∈ B}
Nếu A đóng, B compact thì ∃x0 ∈ A,y0 ∈ B : d(x0,y0) = d(A,B).
5 Cho tập U tùy ý, V mở thì U + V mở. Tập đóng không có tính chất này. Chứng minh ? lOMoARcPSD| 36782889 Các định lý cơ bản PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Từ ii) −→ i) bằng cách dùng phản chứng để áp dụng định lý tách tập lồi. Cụ thể xem như bài tập. 3
Nguyên lý bị chặn đều
Bổ đề 3.1 ( Baire) Cho X là không gian mê tríc đầy đủ và . Khi đó
∃n0,∃B(x0,r) : B¯(x0,r) ⊂ X¯n0. Ghi chú:
• Bổ đề Baire có thể phát biểu nhiều cách khác nhau. Có thể tham khảo thêm trong sách Haim Brezis.
• Ý nghĩa bồ đề Baire: mọi kgmt đầy đủ không thể tách thành hợp đém được các tập không đáng kể
(tập có độ đo bằng 0.)
• Việc chứng minh bổ đề Baire không quan trọng mà người ta thường quan tâm đến việc áp dụng Bổ
đề Baire như thế nào. Có thể tham khảo cách chứng minh trong sách Haim Brezis (trang 34), xem như bài tập.
Định lý 3.2 (Nguyên lý bị chặn đều) Giả sử
i) X là không gian Banach, Y là không gian định chuẩn ii) thỏa
sup||Ai(x)|| < +∞,∀x ∈ X i∈I Khi đó
sup||Ai|| < +∞ i∈I Chú ý:
• ||Ai(x)|| là chuẩn trong không gian Y , còn ||Ai|| là chuẩn trong không gian L(X,Y ). . lOMoARcPSD| 36782889 Các định lý cơ bản PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
• Định lý này nói rằng: Ai bị chặn điểm (chặn trong Y ) thì bị chặn đều (chặn trong L(X,Y )).
7L(X,Y) là tập các toán tử ttlt từ X vào Y . Nếu X ≡ Y thì L(X,X) ≡ L(X). Khi Y ≡ R thì L(X,Y ) ≡ X∗ . lOMoARcPSD| 36782889 Các định lý cơ bản PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng Chứng minh Đặt là các tập đóng.
Theo giả thiết ii), ta có Áp dụng bổ đề Baire:
∃n0,∃B(x0,r) : B¯(x0,r) ⊂ X¯n0 = Xn0 Xét x ∈
X,||x|| = 1, ta có
Lấy sup theo x 2 vế
Ta có điều phải chứng minh. 4
Định lý ánh xạ mở và định lý đồ thị đóng
Định lý 4.1 (Định lý ánh xạ mở) Cho X,Y là 2 không gian Banach và A là một toàn ánh tuyến tính liên tục
từ X −→ Y . Khi đó A là ánh xạ mở (biến một tập mở trong X thành tập mở trong Y ).
Định lý 4.2 (Định lý ánh xạ ngược) Cho X,Y là không gian Banach. A : X −→ Y song ánh, tuyến tính, liên tục.
Khi đó f−1 cũng liên tục.
Định lý 4.3 (Định lý đồ thị đóng) Cho X,Y là không gian Banach. A : X −→ Y là ánh xạ tuyến tính có đồ thị
GA = {(x,A(x)) : x ∈ X} là tập đóng trong X × Y
Khi đó: A liên tục.
Chứng minh 3 định lý này xem như bài tập. trang 10 lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng 5
Các định lý quan trọng khác
Bổ đề 5.1 (Riesz) Cho E là không gian định chuẩn và M là không gian con đóng thật sự của E. Khi đó
Định lý này cho ta một tính chất rất hay của không gian định chuẩn. Trong không gian Hilbert thì ε có thể
bằng 0. Trong không gian định chuẩn bất kỳ thì nhìn chung ε > 0. Chứng minh
Vì M là tập con thật sự của E nên ∃u ∈ E \ M
=⇒ d(u,M) = inf||u − y|| : y ∈ M > 0 (vì M đóng) .
Theo định nghĩa inf thì Ta đặt
Khi đó ∀y ∈ M, ta có
Định lý 5.2 (điểm bất động Banach) Cho (X,d) là không gian metric đầy đủ. f : X −→ X là ánh xạ co, tức là
∃c < 1 : d(f(x),f(y)) ≤ c.d(x,y),∀x,y ∈ X
Khi đó tồn tại duy nhất x∗ ∈ X : x∗ = f(x∗) Ghi chú
Nếu c > 0 tùy ý thì f gọi là ánh xạ lipchitz.
Đây là định lý rất nổi tiếng và được ứng dụng rất nhiều trong nội tại môn học cũng như trong bài toán
đạo hàm riêng và rất nhiều lĩnh vực khác. Các nhà toán học cũng nghiên cứu nhiều các lĩnh vực mà định
lý này có thể áp dụng.
Chứng minh xem như bài tập. Chương 2 trang 13 lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
TÔ PÔ YẾU và KHÔNG GIAN PHẢN XẠ 1
Nhắc lại một số khái niệm về tô pô 1.1 Không gian tô pô
Định nghĩa 1.1 (Tô pô) Cho tập X 6= ∅ và T ⊂ P(X) thỏa i) ∅,X ∈ T . ii) .
iii) V1,V2 ∈ T =⇒ V1 ∩ V2 ∈ T . Ta nói T là một tô pô.
(X,T ) gọi là không gian tô pô.
Một tập thuộc T gọi là tập mở.
W gọi là tập đóng nếu X \ W ∈ T .
Ghi chú: Tô pô được đặc trưng là kín với phép toán hợp bất kỳ và giao hữu hạn. Các tập đóng thì kín với
phép toán giao bất kỳ và hợp hữu hạn.
Tính Chất 1.1 (chứng minh tập mở) Cho không gian tô pô (X,T ). Tập W mở nếu
∀x ∈ W,∃U ∈ T : x ∈ U ⊂ W.
Tính chất này thường được sử dụng để chứng minh một tập là mở. Chứng minh 12
Định nghĩa 1.2 Cho T1,T2 là 2 tô pô trên X. Nếu T1 ⊂ T2 thì ta nói _T1 yếu hơn (thô hơn) T2 hay T2 mạnh hơn (mịn hơn) T1. 1.2 Cơ sở tô pô
Định nghĩa 1.3 (Cơ sở tô pô) Cho không gian tô pô (X,T ). Họ σ ⊂ T gọi là cơ sở tô pô nếu trang 14 lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng Ví dụ 1.1 .
Trong không gian mê tríc, tập các quả cầu mở
σ = {B(x,r) : x ∈ X,r > 0} là cở sở tô pô.
Hay nói cách khác, tô pô của không gian mê tríc được sinh bởi các quả cầu mở.
Đặt biệt tô pô trên R sinh bởi các khoảng (a,b) với khoảng cách d(a,b) = |b − a|.
Chú ý: Một tô pô có thể có nhiều cơ sở (bản thân tô pô T là cơ sở của chính nó), thông thường ta xét cơ
sở có ít tập mở nhất. Mỗi cơ sở chỉ sinh ra đúng một tô pô. 1.3 T2 không gian
Định nghĩa 1.4 (Không gian Hausdoff) Không gian tô pô (X,T ) gọi là T2 không gian (hay không gian hausdoff) nếu
Trong không gian T2, giới hạn một dãy (hay một lưới) nếu có là duy nhất. 1.4
Phần trong và bao đóng của một tập hợp
Định nghĩa 1.5 Cho không gian tô pô (X,T ) và tập A ⊂ X.
• Phần trong của A là tập mở lớn nhất chứa trong A, ký hiệu là .
IntA là hợp tất cả các tập mở chứa trong A. x ∈
IntA thì ta nói x là điểm trong của A. trang 15 lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
• Bao đóng của A là tập đóng nhỏ nhất chứa A hay là giao của tất cả các tập đóng chứa A, ký hiệu là A¯.
x ∈ A¯ thì ta nói x là điểm dính của A
Tính Chất 1.2 Cho không gian tô pô (X,T ) và tập A ⊂ X.
i) IntA ⊂ A ⊂ A¯ ii) A mở
⇐⇒ A ≡ IntA.
iii) x ∈ IntA ⇐⇒ ∃U ∈ T : x ∈ U ⊂ A. iv) A
đóng ⇐⇒ A ≡ A¯.
v) x ∈ A¯ ⇐⇒ ∀U ∈ T ,U 3 x : U ∩ A =6 ∅.
Chứng minh xem như bài tập. 1.5
Sự hội tụ trong không gian tô pô
Định nghĩa 1.6 (Hội tụ) Cho không gian tô pô (X,T ) và lưới {xi}i∈I ⊂ X. Ta nói {xi} hội tụ về a ∈ X nếu
∀U ∈ T ,U 3 x,∃i0 ∈ I : ∀i ≥ i0 =⇒ xi ∈ U
Ký hiệu limxi = a hay xi → a. i
Tính Chất 1.3 Cho không gian tô pô (X,T ). Ta có
• Giới hạn của một lưới trong T2 nếu có là duy nhất.
• Nếu xi → a thì mọi lưới con của nó cũng hội tụ về a.
• x ∈ A¯ ⇐⇒ ∃{xi} ⊂ A : xi → x. • A đóng lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Chứng minh xem như bài tập. 1.6 Ánh xạ liên tục
Định nghĩa 1.7 (Ánh xạ liên tục) Cho 2 không gian tô pô X,Y . Ánh xạ f : X −→ Y . f gọi là liên tục tại x0 ∈ X nếu
∀V 3 f(x),∃U 3 x : f(U) ⊂ V .
f liên tục tại ∀x ∈ A thì ta nói f liên tục trên A.
Định lý 1.4 (liên tục) Cho 2 không gian tô pô X,Y . Ánh xạ f : X −→ Y . Các mệnh đề sau tương đương i)
f liên tục trên X. ii)
∀{xi} ⊂: xi → x =⇒ f(xi) → f(x). iii) V mở trong Y thì f−1(V ) mở trong X.
iv) V đóng trong Y thì f−1(V ) đóng trong X
Định lý này thường được sử dụng trong các bài toán liên tục Chứng minh
định lý này xem như bài tập. 1.7 Tập compact
Định nghĩa 1.8 (Tập compact) Trong không gian Tô pô (X,T ).
• Tập A gọi là compact nếu mọi phủ mở của A đều tồn tại phủ con hữu hạn
• A gọi là compact tương đối nếu A¯ compact. Tính Chất 1.5 Trong không gian Tô pô (X,T )
i) Tập compact trong không gian T2 là đóng
(A compact,X − T2KG) =⇒ A đóng
ii) Đóng trong compact là compact lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
A compact,B đóng : compact.
iii) Tính compact bảo toàn qua ánh xạ liên tục
f : X → Y liên tục, A compact =⇒ f(A) compact
iv) Trong không gian Banach: một tập là compact khi và chỉ khi nó đóng và bị chặn.
Chứng minh xem như bài tập
Định lý 1.6 i) A compact khi và chỉ khi mỗi lưới của A đều tồn tại lưới con hội tụ về phần tử thuộc A. ii)
Cho (X,d) là không gian định chuẩn : A compact tương đối khi và chỉ khi A hoàn toàn bị chặn.
iii) Trong không gian metric, tập compact khi và chỉ khi đóng và hoàn toàn bị chặn.
Trong KGMT, tập A gọi là hoàn toàn bị chặn nếu cho trước bán kính ε > 0 tùy ý, luôn tồn tại hữu hạn quả
cầu mở bán kính ε phủ A.
Một tập gọi là bị chặn nếu nó nằm trong một quả cầu nào đó.
Tập hoàn toàn bị chặn thì bị chặn.
Ngược lại ngược lại chỉ đúng trong không gian hữu hạn chiều.
Trong không gian vô hạn chiều, luôn tồn tại vô số quả cầu bán kính bằng chứa trong quả cầu đơn vị.
Kiểm chứng xem như bài tập 2 Tô pô yếu
Cho không gian tô pô X . Xét một phiếm hàm f : X −→ R. Trên X, ta có thể xét nhiều tô pô khác nhau, trong
đó f có thể liên tục với tô pô này nhưng không liên tục với tô pô khác.
Nếu ta xét tô pô rời rạc T ≡ P(X) thì mọi phiếm hàm trên X đều liên tục (kiểm tra xem như bài tập).
Một tô pô càng nhiều tập mở thì f càng dễ liên tục và ngược lại. Tô pô càng ít tập mở (yếu hơn) thì càng
làm một ánh xạ khó liên tục hơn. Tuy nhiên, tô pô yếu hơn lại có những tính chất rất quan trọng mà tô pô ban đầu không có.
Bây giờ, ta xét E là một không gian Banach và E∗ là tập các phiếm hàm tuyến tính liên tục trên E. Trong
phần này ta sẽ xây dựng một cấu trúc tô pô yếu nhất (ít tập mở nhất) mà vẫn đảm bảo các phiếm hàm
tuyến tính liên tục ban đầu vẫn còn liên tục, gọi là tô pô yếu trên E. 2.1
Xây dựng tô pô yếu σ(E,E∗) lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Định nghĩa 2.1 (Tô pô yếu) Tô pô yếu nhất trên E sao cho mọi phiếm hàm f ∈ E∗ liên tục gọi là tô pô yếu
trên E. Ký hiệu là σ(E,E∗).
Xét f ∈ E∗ : (E,σ(E,E∗)) −→ R.
Điều kiện cần và đủ để f liên tục là f−6(B) ∈ σ(E,E∗),∀B mở trong R.
Ta chú ý rằng, tô pô trong R được sinh bởi các khoảng mở. Do đó, ta có thể chọn B = (a,b)
f−1(B) = {x ∈ X : a < f(x) < b} := U(f,a,b) := Uα,α ∈ I (2.1)
ở đây, {Uα : α ∈ I} bao gồm tất cả các tập ở (2.1) với f chạy tùy ý trên E∗ và a,b tùy ý trên R.
Do vậy, tô pô yếu σ(E,E∗) phải được sinh bởi các tập {Uα : α ∈ I}. Hay nói cách khác, họ
{Uα : α ∈ I} là một cơ sở của tô pô yếu. 1
Định lý 2.1 Tô pô yếu σ(E,E∗) gồm các tập hợp bất kỳ của giao hữu hạn các tập {Uα : α ∈ I}
Chú ý: để thành lập các tập của σ(E,E∗), trước hết ta lấy giao hữu hạn các tập {Uα : α ∈ I}, sau đó lấy hợp
bất kỳ các tập vừa tạo ra. Ta không thể thay đổi thứ tự lấy hợp trước và giao sau, vì như thế không thể
tạo ra một không gian tô pô. Việc kiểm chứng khả dễ dàng dựa vào tính chất tô pô và cơ sở, xem như bài tập.
Rõ ràng, tô pô mạnh (tô pô ban đầu) chứa tô pô yếu nên một tập mở yếu thì mở mạnh. Điều người lại
không đúng. Bây giờ ta tìm điều kiện để một tập là mở yếu 2.2
Các tính chất tô pô yếu
Định lý 2.2 (Điều kiện tập mở yếu) Trong không gian Banach E, tập W là mở yếu khi và chỉ khi
Vx := {y ∈ E : |fi(y) − fi(x)| < ε,∀i = 1,2,. ,p} ⊂ W.
Ghi chú: Định lý này cho ta nhìn nhận rõ hơn về tập mở yếu. Nó được biểu diễn qua fi ∈ E∗. Ta có thể hình
dung tập V như một chiếc đĩa bay rộng vô hạn, càng ra xa thì khoảng cách càng nhỏ dần. Phần dày nhất
6 Không phải một họ các tập con đều có thể làm cơ sở tô pô. Điều kiện cần và đủ để một họ σ = {Wα,α ∈ I} là cơ sở tô pô là
Chứng minh điều này và kiểm tra họ {Uα : α ∈ I} ở (2.1) thỏa điều kiện cơ sở là khá thú vị được dành cho riêng cho các bạn. lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
của đĩa bay bằng 2ε chính là theo phương x. Ta còn nhìn thấy rằng, trong không gian vô hạn chiều, các
quả cầu mở không còn mở trong tô pô yếu nữa. Chứng minh
Trước hết ta thấy rằng
đo đó Vx mở yếu và chứa x. (⇐=)
∀x ∈ W,∃Vx ⊂ W nên W mở yếu (Chú ý Vx mở yếu chứa x). (=⇒)
Giả sử W mở yếu chứa x. Từ định lý 2.
(W bằng hợp của những tập giao hữu hạn nên có ít nhất một cái giao hữu hạn chứa x.)
Mặt khác, x ∈ Uαi = fi−1(ai,bi) =⇒ fi(x) ∈ (ai,bi),∀i = 1 : p.
Ta có thể chọn ε > 0 đủ bé sao cho B(fi(x),ε) ⊂ (ai,bi),∀i = 1 : p. Ta được
Ta có điều phải chứng minh.
Bây giờ, ta tìm hiểu tính hội tụ của dãy (hoặc lưới) trong tô pô yếu. Ta ký hiệu xn → x là sự hội tụ trong tô
pô mạnh, và xn →−y x là sự hội tụ trong tô pô yếu. Mệnh đề 2.3
i) Nếu xn → x thì xn →−y x.
ii) xn →−y x khi và chỉ khi f(xn) −→ f(x),∀f ∈ E∗.
iii) Nếu xn →−y x thì ||xn|| bị chặn. y xn →− x iv)
=⇒ fn(xn) −→ f(x) fn −→ f
Mệnh đề này cho ta một cách nhìn về sự hội tụ trong tô pô yếu. Chứng minh
i) ∀V 3 x mở yếu, suy ra V 3 x mở mạnh . Vì xn −→ x nên lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
∃n0 : ∀n > n0 =⇒ xn ∈ V
suy ra xn →−y x.
ii) Giả sử xn →−y x. ∀f ∈ E∗,∀ε > 0
Ta có Vf = {y ∈ E : |f(y) − f(x)| < ε} mở yếu chứa x. Do đó
∃n0 : ∀n > n0 =⇒ xn ∈ V ⇐⇒ |f(xn) − f(x)| < ε =⇒ f(xn) −→ f(x),∀f ∈ E∗
Ngược lại, f(xn) −→ f(x),∀f ∈ E∗
Lấy tùy ý V = {y ∈ E : |fi(y) − fi(x)| < ε,i = 1 : p} là tập mở yếu chứa x. Vì fi(xn) −→
fi(x),∀i = 1 : p nên y
∃n0 : ∀n > n0 =⇒ |fi(xn) − fi(x)| < ε,∀i = 1 : p =⇒ xn ∈ V =⇒ xn →− x
iii) Trước hết, ta chứng minh ||x|| = sup |f(x)|. ||f||=1 Thật vậy: Xét .
Giả sử x 6= 0 (trường hợp bằng 0 là tầm thường). Theo hệ quả (1.3) của định lý Hanh banach
∃f ∈ E∗ : f(x) = ||x||,||f|| = 1 =⇒ sup |f(x)| ≥ ||x|| ||f||=1
Từ đó ta có ||x|| = sup |f(x)|. ||f||=1
Quay lại bài toán, giả sử xn →−y x =⇒ f(xn) −→ f(x),∀f ∈ E∗. Mọi dãy hội
tụ trong R là bị chặn nên {f(xn)} bị chặn.
Xét phiếm hàm gx : E∗ −→ R thỏa g(f) = f(x),∀f ∈ E∗. Dễ dàng kiểm
tra g tuyến tính liên tục trên E∗.
Theo nguyên lý bị chặn đều, {gxn(f) = f(xn)} bị chặn nên {gxn} bị chặn
=⇒ ||xn|| = sup |f(xn)| = sup |gxn(f)| = ||gxn|| < ∞ ||f||=1 ||f||=1 iv) Ta có:
|fn(xn) − f(x)| ≤ |fn(xn) − f(xn)| + |f(xn) − f(x)|
≤ ||fn − f||.||xn|| + |f(xn) − f(x)| −→ 0
(Chú ý ||xn|| bị chặn và f(xn) −→ f(x).)
Mệnh đề 2.4 Trong không gian hữu hạn chiều, tô pô yếu trùng với tô pô mạnh. lOMoAR cPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng Chứng minh
Tập mở yếu thì hiển nhiên mở mạnh. Ta cần chứng minh điều ngược lại.
Xét W là tập mở mạnh và x ∈ W. Ta cần chỉ ra một tập mở yếu V : x ∈ V ⊂ W. Thật vậy, tồn tại
ε > 0 : B(x,ε) ⊂ W.
Vì dim(E) = n =⇒ x = (x1;x2;...;xn)
(ta xét trong một cơ sở trực chuẩn tùy ý. Các chuẩn trong không gian hữu hạn chiều tương đương nhau
nên ở đây ta có thể chọn chuẩn tổng).
Xét các phép chiếu xuống các trục tọa độ fi : E −→ R,fi(x) = xi,i = 1 : n là các phiếm hàm tuyến tính liên tục. lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng là tập mở yếu
Ta có điều phải chứng minh. Ghi chú:
• Trong không gian hữu hạn chiều, tô pô yếu và mạnh là đồng nhất nên sự hội tụ yếu và mạnh cũng như nhau.
• Tập B(0,1) = {x ∈ E : ||x|| < 1} mở mạnh và ∂B(0,1) = {x ∈ E : ||x|| = 1} là đóng mạnh. Tuy nhiên, cả
2 tính chất này không còn đúng đối với tô pô yếu trong không gian vô hạn chiều. Mọi tập mở yếu,
khác rỗng trong không gian vô hạn chiều luôn chứa vô số đường thẳng (thậm chí chứa cả một không
gian afin "khổng lồ" vô hạn chiều), suy ra mở yếu luôn không bị chặn.
• Trong không gian vô hạn chiều, người ta luôn tìm được dãy (lưới) hội tụ yếu nhưng không hội tụ mạnh.
• Tô pô yếu vô hạn chiều luôn không khả mê tríc, tức là không có một mê tríc nào có thể sinh ra tô pô yếu.
Các tính chất trên nêu lên sự khác biệt giữa tô pô mạnh và yếu. Sẽ thú vị hơn nếu ta có thời gian chứng
minh đầy đủ tính chất này. 3 Không gian phản xạ
Xét ánh xạ J : E −→ E∗∗ thỏa mãn
Jx(f) := J(x)(f) = f(x) (2.2) 2
Định lý 3.1 Ánh xạ J ở (2.2) là đơn ánh, tuyến tính, liên tục, đẳng cự từ E vào E∗∗ Chứng minh
2Jx là cách viết tắt của J(x) ∈ E∗∗ là phiếm hàm tuyến tính liên tục trên E∗, nó tác động vào f ∈ E∗ và nhận giá trị trên R. lOMoAR cPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
a) Tính tuyến tính là dễ thấy.
b) Tính liên tục: |Jx(f)| = |f(x)| ≤ ||f||.||x|| =⇒ ||Jx|| ≤ ||x|| suy ra J liên tục c) Tính đơn ánh. Xét Jx1 = Jx2
⇐⇒ Jx1(f) = Jx2(f),∀f ∈ E∗
⇐⇒ f(x1) = f(x2),∀f ∈ E∗
⇐⇒ f(x1 − x2) = 0,∀f ∈ E∗ ⇐⇒ x1 = x2 d) Tính đẳng cự.
||Jx|| = sup |Jx(f)| = sup |f(x)| = ||x||. ||f||=1 ||f||=1 Ghi chú:
• Ánh xạ J là một phép nhúng chính tắc (đơn ánh, đẳng cự) từ E vào E∗∗.
• Ta có thể đồng nhất Jx ≡ x, viết x(f) ≡ Jx(f) = f(x). Và không sợ nhầm lẫn, ta có thể viết < f,x > thay
cho f(x) hay x(f).
• J(E) là một không gian con của E∗∗ (dễ dàng kiểm tra), nhìn chung là không trùng với E∗∗.
• Trong trường hợp J toàn ánh thì nó trở thành đẳng cấu đẳng cự. Lúc này, E gọi là không gian phản xạ.
Định nghĩa 3.1 (Không gian phản xạ) Không gian Banach E gọi là không gian phản xạ nếu ánh xạ J là đẳng cấu đẳng cự
Khi E là không gian phản xạ, ta có thể đồng nhất E và E∗∗.
Hầu hết những không gian chúng ta xét đều phản xạ, những không gian không phản xạ rất ít gặp và không
được ứng dụng nhiều. Ngoài ra, không gian phản xạ có những tính chất quan trọng (tham khảo thêm tài
liệu về tính khả ly, lồi đều và tính phản xạ của không gian đối ngẫu). Bởi vậy, chứng minh một không gian
là phản xạ đóng vài trò quan trọng trong giải tích hàm cũng như ứng dụng. 4 Tô pô yếu *
Định nghĩa 4.1 (Tô pô yếu *) Cho E là không gian Banach, tô pô yếu nhất trên E∗ sao cho
Jx,∀x ∈ E liên tục gọi là tô pô yếu *. Ký hiệu là σ(E∗,E).
Với E là không gian Banach thì E∗ cũng là không gian Banach.
Tô pô yếu trên E∗ là tô pô yếu nhất mà vẫn đảm bảo mọi g ∈ E∗∗ liên tục, ký hiệu là σ(E∗,E∗∗).
Tô pô yếu * σ(E∗,E) nhìn chung là yếu hơn tô pô yếu σ(E∗,E∗∗). lOMoARcPSD| 36782889 Tô pô yếu PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Trong trường hợp E phản xạ thì E ≡ E∗∗ nên tô pô yếu * trùng với tô pô yếu.
Nếu E hữu hạn chiều thì dim(E) = dim(E∗) = dimE∗∗, do đó E phản xạ.
Tương tự như cách xây dựng tô pô yếu, ta có các tính chất sau Tính Chất 4.1
i) Cơ sở tô pô σ(E∗,E) gồm các tập dạng
V (f,x,ε) = {g ∈ E∗ : |g(x) − f(x)| < ε} := Vα
Các tập của tô pô yếu * là hợp bất kỳ của giao hữu hạn các tập Vα. ii) Dãy
{fn} hội tụ về f trong σ(E∗,E), ký hiệu là fn →−∗ f. Ta có
fn →−∗ f ⇐⇒ fn(x) −→ f(x),∀x ∈ E
iii) (fn −→ f) =⇒ (fn →−y f) =⇒ fn →−∗ f. iv) fn →−∗
f thì {fn} bị chặn trong E∗. ∗ fn →− f v)
=⇒ fn(xn) −→ f(x). xn −→ x
Chứng minh các tính chất này tương tự như tô pô yếu, xem như bài tập.
Định lý 4.2 (Banach - Alaoglu) Tập B = {f ∈ E∗ : ||f|| ≤ 1} compact trong σ(E∗,E).
Ta biết B compact trong tô pô mạnh khi và chỉ khi hữu hạn chiều. Định lý này cho thấy tầm quan trọng
của tô pô yếu *, nó có tầm quan trọng trong việc nhận dạng một không gian phản xạ thông qua định lý
Kakutani (tham khảo Haim Brezis).
Chứng minh xem như bài tập. lOMoARcPSD| 36782889 Chương 3 KHÔNG GIAN Lp
Trong chương này, ta xem X là tập con của Rn. 1
Nhắc lại về tích phân Lebesgue
Định nghĩa 1.1 ( đại số) Cho X là tập khác rỗng , M ⊂ P(X) là họ các tập con của X.
M gọi là σ−đại số trên X nếu thỏa
i) X,∅ ∈ M. ii) A ∈ M =⇒ X \ A ∈ M. iii) .
Các tập thuộc M gọi là các tập đo được.
(X,M) gọi là không gian đo được.
Nhận xét: σ−đại số kín với phép hợp hữu hạn và giao đém được.
Định nghĩa 1.2 (Độ đo) Cho M là σ−đại số trên tập X.
Ánh xạ µ : M −→ [0,+∞] gọi là một độ đo trên M nếu thỏa
i) µ(∅) = 0. ii) Cho {An,n ∈ N} là họ các tập đo được rời nhau thì . 23
(X,M,µ) gọi là không gian độ đo. µ gọi là độ đo đủ nếu mọi tập con của
tập có độ đo 0 luôn đo được. Ghi chú: lOMoARcPSD| 36782889 Không gian Lp PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
• Điều kiện thứ 2 của độ đo gọi là tính chất σ−cộng tính.
• Độ đo là một hàm toán học tương ứng với chiều dài, diện tích, thể tích hoặc một xác xuất của một họ các tập hợp.
• Các tập đo được thông thường trên R sinh bởi các khoảng mở và đóng. Độ đo trên R là độ dài các
khoảng đó. Ví dụ µ((a,b]) = b − a là độ dài khoảng (a,b]. 1, nếu x ∈ A
Hàm số XA(x) =gọi là hàm đặc trưng của tập A. (
0, nếu x /∈ A
Cho {Ai,i = 1,2,. ,n} là các tập rời nhau. Hàm số gọi là hàm đơn giản.
Định nghĩa 1.3 (Tích phân lebesgue) Trong không gian độ đo (X,M,µ), E ∈ M. Tích phân lebesgue của hàm
f xác định trên X ký hiệu là
được định nghĩa như sau:
i) Nếu f là hàm đơn giản: thì .
ii) Nếu f là hàm đo được không âm. Lúc này tồn tại một dãy tăng các hàm đơn giản fn −→ f. Ta có X XR fdµ = lim fndµ. n→∞ R
iii) Nếu f là hàm đo được bất kỳ.
Ta đặt f+(x) = max{f(x),0},f− =
max{−f(x),0} là các hàm đo được không âm và thỏa f = f+
− f−. Tích phân của f trên X được định nghĩa
Với quy ước: nếu cả 2 tích phân
đều bằng +∞ thì nói f không khả tích trên X.
Định nghĩa 1.4 (Hầu khắp nơi) Trong không gian độ đo, cho mệnh đề P(x),x ∈ X. Mệnh đề P(x) gọi là đúng
hầu khắp nơi(hkn) nếu P(x) chỉ không đúng khi x thuộc một tập có độ đo bằng 0. lOMoARcPSD| 36782889 Không gian Lp PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Ghi chú: khái niệm hkn thường được dùng trong phần này như : 2 hàm bằng nhau hkn, liên tục hkn, bị chặn hkn,...
Hàm f = 0 hkn khi và chỉ khi 2
Không gian Lp(1 ≤p<∞)
Định nghĩa 2.1 Cho không gian độ đo (X,M,µ) và p ∈ [1,+∞).
Tập tất cả các hàm f đo được trên X sao cho |f|p khả tích lebesgue tạo ra một không gian vec tơ, ký hiệu là Lp. Trên Lp, ta xét (3.1)
là một chuẩn trên Lp.
Chú ý trong không gian Lp, 2 hàm bằng nhau theo nghĩa hầu khắp nơi. Như vậy, mỗi hàm trong Lp là một
lớp các hàm bằng nhau hầu khắp nơi. Chứng minh
Dễ dàng kiểm tra ||.|| trong (3.1) thỏa 2 điều kiện đầu của chuẩn (Chú ý sự bằng nhau của 2 hàm theo nghĩa hkn).
Để kiểm tra điều kiện thứ 3, ta cần chứng minh các bất đẳng thức sau
Định lý 2.1 (BĐT Holder) Cho p,q > 0 thỏa .
Khi đó f.g ∈ L1 và
||f.g||L1 ≤ ||f||Lp.||g||Lq. (3.2) Chứng minh
Trước hết ta chứng minh bất đẳng thức . (3.3)
Ta chỉ cần xét a,b > 0. lOMoARcPSD| 36782889 Không gian Lp PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng . Xét hàm là hàm lồi. .
" Nếu||f||LLqp = 0 ⇐⇒ XRR |f|qpdµ = 0 =⇒ " f = 0 h kn trên X ||g|| = 0 |g| dµ = 0 g = 0 h kn trên X
X =⇒ f.g = 0 h kn trên X =⇒ ||f.g||L1 = |f.g|dµ = 0 XR Do đó (3.3) đúng. Nếu ||f|| .
Lp 6= 0 6= ||g||Lq. Ta đặt A = ||f||Lp,B =p ||g||Lq q
Áp dụng bất đẳng thức (3.3) cho , ta được
Lấy tích phân 2 vế trên X
Ta có điều phải chứng minh. Tiếp theo ta sẽ chứng minh điều kiện thứ 3 của chuẩn bằng bất đẳng thức MinKowski
Định lý 2.2 (Bất đẳng thức Minkowski) Cho f,g ∈ Lp. Khi đó
||f + g||Lp ≤ ||f||Lp + ||g||Lq. (3.4)
Chứng minh Nếu p = 1. Ta có |f(x) + g(x)| ≤ |f(x)| + |g(x)|,∀x
∈ X. Bằng cách lấy tích phân 2 vế trên X ta suy ra (3.4) Ta có: lOMoARcPSD| 36782889 Không gian Lp PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
|f(x)+g(x)|p = |f(x)+g(x)|p−1.|f(x)+g(x)| ≤ |f(x)+g(x)|p−1.|f(x)|+|f(x)+g(x)|p−1.|g(x)| (3.5)
Nếu p > 1. Chọn
(|f + g|p−1)q = |f + g|(p−1)q = |f + q|p khả tích (vì f,g) khả tích. Do đó: |f +
g|p−1 ∈ Lq.
Áp dụng bất đẳng thức Holder cho |f(x)| và |f(x) + g(x)|p−1 Tượng tự
Lấy tích phân (3.5) trên X
Như vậy ta chứng minh được điều kiện thứ 3 của chuẩn Lp do đó (3.1) xác định một chuẩn trên
Lp(0 < p < 1). Trường hợp p = 1 và p = +∞ tương tự (tham khảo tài liệu).
Ta có 2 định lý hội tụ đơn điệu và hội tụ bị chặn trong L1 như sau
Định lý 2.3 (Hội tụ đơn điệu) Cho {fn} là dãy tăng các hàm trong L1 thỏa
Khi đó {fn} hội tụ trong L7
Định lý 2.4 (Hội tụ bị chặn) Cho dãy {fn} ⊂ L1 và g ∈ L1 sao cho |f(x)| ≤ g(x) hkn trên X.
Khi đó: nếu fn(x) → f(x) hkn trên X thì fn → f trong L1. 3
Các tính chất không của không gian Lp
Ta đã chứng minh được ||.||p là một chuẩn trên Lp. Bây giờ ta cần chứng minh tích đầy đủ của chuẩn này.
7 Không gian định chuẩn là không gian Banach (đầy đủ) khi và chỉ khi mọi chuỗi hội tụ tuyệt đối thì hội tụ lOMoARcPSD| 36782889 Không gian Lp PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Định lý 3.1 (Tính đầy đủ) Không gian Lp với chuẩn là một không gian Banach. Chứng minh
Xét dãy hàm {fn : n ∈ N} ⊂ Lp thỏa . Ta cần chứng minh
hội tụ trong Lp 1. n=1 n Đặt gn(x) =
|fk(x)|,g(x) = lim gn(x) ,(g(x) có thể bằng +∞) kPn→+∞ Ta sẽ chứng tỏ Ta có: .
(chuyển giới hạn qua dấu tích phân theo định lý hội tụ đơn điệu)
=⇒ g ∈ Lp do đó g(x) bị chặn hkn hay hkn trên X.
Với mỗi x ∈ X,fk(x) ∈ R. Trên R mỗi chuỗi hội tụ tuyệt đối thì hội tụ do đó, chuỗi
+∞ hội tụ hkn trên X. +∞
fk(x) = lim Sn(x), nếu chuỗi
hội tụ Ta đặt f(x) = kP=1 n→∞ 0,
nếu chuỗi phân kỳ. Ta sẽ chứng minh Sn −→ f. Thật vậy
Ta có |f(x)| ≤ g(x),∀x ∈ X =⇒ f ∈ Lp ( vì g ∈ Lp)
=⇒ Sn − f ∈ Lp
lim ||Sn − f||p = lim
|Sn(x) − f(x)|pdµ =
lim |Sn(x) − f(x)|pdµ = 0 n→∞ n→∞XR XR n→∞
(Theo định lý hội tụ bị chặn) lOMoARcPSD| 36782889 Không gian Lp PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Vậy {Sn,n ∈ N} hội tụ và do đó Lp là một không gian Banach. Ta có điều phải chứng minh.
Tiếp theo, ta đưa ra một kết quả rất thú vị về không gian đối ngẫu của Lp.
Định lý 3.2 (Không gian đối ngẫu) Cho p ∈ (0,+∞) và ∀ϕ ∈ (Lp)∗.
Khi đó, tồn tại duy nhất thỏa
ϕ(f) = Z u.fdµ. (3.6) X Chú ý rằng, ánh xạ
tuyến tính liên tục. Cùng với định lý, ta thấy rằng, mỗi phiếm hàm tuyến
tính liên tục trên Lp tương ứng với một hàm u ∈ Lq và ngược lại. Do đó, ta có thể đồng nhất (Lp)∗ ≡ Lq.
Thông thường, một phiếm hàm tuyến tính liên tục trên một không gian định chuẩn khó có thể viết được
dưới dạng tường minh. Định lý này chỉ ra không gian đối ngẫu của Lp chính là Lq, rất tiện lợi cho việc
nghiên cứu những tính chất khác của không gian Lp.
Đặc biệt nếu p = 2 thì đối ngẫu của L2 là chính nó gọi là không gian tự liên hợp. Đây là cơ sở của lý thuyết
biến phân và phương pháp phần tử hữu hạn rất quan trọng. Chứng minh Xét ánh xạ tuyến tính
J : Lq −→ (Lp)∗,u 7→ Ju := J(u),∀u ∈ Lq được xác định bởi
Để đồng nhất được (Lp)∗ với Lq, ta cần chứng minh ánh xạ J là đẳng cấu đẳng cự. Thật vậy
a) Chứng minh J liên tục và đẳng cự
Ta có =⇒ Ju liên tục trên Lp và ||Ju|| ≤ ||u||Lq,∀u ∈ Lq
=⇒ J liên tục trên (Lq)∗ ||f||Lp=1
||f||Lp=1XR ||Ju|| = sup |Ju(f)| = sup
|f.u|dµ = ||u||Lq
cũng là phiếm hàm tuyến tính liên tục trên Lq theo bất đẳng thức Holder.) lOMoARcPSD| 36782889 Không gian Lp PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
b) J tuyến tính đẳng cự do đó đơn ánh. Cuối cùng, để chứng minh J song ánh, ta cần chứng minh J toàn
ánh. Điều này tương đương với J(Lq) đóng và trù mật trong (Lp)∗.
Xét dãy {Jun : un ∈ Lq,n ∈ N} thỏa Jun −→ ϕ ∈ (Lp)∗.
Jun hội tụ nên là dãy cauchy. Vì J đẳng cự nên (un) cũng là dãy cauchy trong Lq do đó (un) hội tụ
un −→ u ∈ Lq
Và do J liên tục nên Jun −→ Ju ≡ ϕ.
Vậy J(Lq) đóng trong (Lp)∗.
Tiếp theo, ta giả sử Ju(h) = 0,∀Ju ∈ T(Lq). Ta cần chỉ ra chỉ ra h = 0 trong Lp. Thật vậy
Chọn u = |h|p−2.h =⇒ |u|q = |h|q(p−1) = |h|p khả tích =⇒ u ∈ Lq. Ta có:
Ta có điều phải chứng minh. Ghi chú:
• Từ định lý này, ta thấy đối ngẫu của đối ngẫu của Lp(1 < p < +∞) là chính nó, suy ra Lp là không gian phản xạ.
• Tuy nhiên, L1 thì không phải không gian phản xạ, người ta chứng minh được rằng J(L1) là không gian
con thật sự của L∞.
• Ngoài ra, Lp(1 < p < ∞) còn là không gian khả ly và lồi đều. Để thấy được tầm quan trọng của không
gian Lp trong ứng dụng, ta cần tham khảo tích chập (được dùng trong các phương trình đạo hàm
riêng cũng như ứng dụng trong mạch điện) và định lý Ascoli về tiêu chuẩn compact mạnh trong
không gian mê tric compact, tham khảo trong Haim Bresiz. Chương 4 KHÔNG GIAN HILBERT
Trên một tập điểm, người ta xây dựng cấu trúc tô pô để thành lập không gian tô pô. Tiếp đó, người ta
định nghĩa khoảng cách giữa các điểm và thành lập không gian mê tric. Không gian mê tric là không gian
tô pô được sinh bởi các quả cầu mở. Không gian định chuẩn không còn định nghĩa trên tập hợp điểm nữa
mà định nghĩa trên một không gian véc tơ, trên đó người ta định nghĩa độ dài của một véc tơ. Không gian
định chuẩn cũng là không gian mê tríc với khoảng cách giữa 2 véc tơ là độ dài của véc tơ hiệu. Trong
không gian định chuẩn chưa có khái niệm về góc và quan hệ vuông góc.
Trong chương này, người ta bắt đầu định nghĩa tích vô hướng và từ đó xây dựng góc và quan hệ vuông
góc giữa 2 véc tơ, gọi là không gian tiền Hilbert. Một không gian tiền Hilbert cũng là không gian định chuẩn
với chuẩn được sinh bởi tích vô hướng đó. lOMoARcPSD| 36782889
Không gian tiền Hilbert với chuẩn sinh bởi tích vô hướng đầy đủ gọi là không gian Hilbert. Chuẩn sinh bởi
tích vô hướng trong không gian Hilbert đặc biệt thỏa mãn đẳng thức hình bình hành mà không gian định
chuẩn thông thường không có. Một đều đặc biệt nữa của không gian Hilbert là phép phân tích Riesz rất
quan trọng trong chương này. 1 Tích vô hướng
Định nghĩa 1.1 (Tích vô hướng) Cho H là KGVT trên C. Một tích vô hướng trên H là một ánh xạ
ϕ : H × H −→ C (x,y) 7−→ ϕ(x,y)
thỏa mãn các tích chất sau i)
ϕ(x,x) > 0,∀x 6= 0 và ϕ(0,0) = 0. 31 ii)
ϕ(x,y) = ϕ(y,x),∀x,y ∈ H. iii) ϕ(λx,y) = λϕ(x,y),∀x,y ∈ H,λ ∈ C. iv) ϕ(x +
y,z) = ϕ(x,z) + ϕ(y,z),∀x,y,z ∈ H.
Khi ánh xạ ϕ là một tích vô hướng trên H, ta có thể ký hiệu hx,yi ≡ ϕ(x,y).
Không gian H với tính vô hướng h.,.i gọi là không gian tiền Hilbert. Hay đơn giản, H là không tiền Hilbert.
Từ định nghĩa ta suy ra tính chất sau:
i) hx,λyi = λhx,yi,∀x,y ∈ H,λ ∈ C ii) ϕ(x,y + z) =
ϕ(x,y) + ϕ(x,z),∀x,y,z ∈ H.
iii) h0,xi = hx,0i = 0
Trong trường hợp E là không gian định chuẩn trên R thì điều kiện tích vô hướng trở thành i)
ϕ(x,x) > 0,∀x 6= 0 và ϕ(0,0) = 0.
ii) ϕ(x,y) = ϕ(y,x),∀x,y ∈ H. iii) ϕ(λx,y) = λϕ(x,y),∀x,y ∈ H. iv) ϕ(x + y,z) =
ϕ(x,z) + ϕ(y,z),∀x,y,z ∈ H.
Mệnh đề 1.1 (Bất đẳng thức Cauchy-Schwartz) Trong không gian tiền Hilbert H ta luôn có lOMoARcPSD| 36782889
|hx,yi|2 ≤ hx,xi.hy,yi,∀x,y ∈ H. (4.1) Chứng minh
Trường hợp y = 0 là tầm thường. Ta xét y 6= 0.
∀t ∈ C, ta có Chọn , ta được lOMoARcPSD| 36782889 Không gian Hilbert PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Ta có điều phải chứng minh
Mệnh đề 1.2 (Bất đẳng thức Mincowski- tam giác) Trong không gian tiền Hilbert H, ta luôn có
phx + y,x + yi ≤ phx,xi + phy,yi,∀x,y ∈ H. (4.2)
Chứng minh ∀x,y ∈ H, ta có theo Cauchy-Schwartz
Trong không gian véc tơ H với tích vô hướng h.,.i, xét ||x|| = phx,xi (4.3)
Ta có ||x|| > 0,∀ 6= 0 và ||0|| = 0. ||λx|| = hλx,λxi =
λ.λ¯ hx,xi = |λ|
hx,xi = |λ|.||x||.
||x + y|| ≤ ||p x|| + ||y||ptheo bất đẳng thức Mincowski.p
Như vậy ||.|| là một chuẩn trên H, gọi là chuẩn sinh bởi tích vô hướng h.,.i. Do đó ta có thể xem không
gian tiền Hilbert là không gian định chuẩn. Lúc này, bất đẳng thúc Cauchy Schwartz được viết lại
|hx,yi| ≤ ||x||.||y||
Và bất đẳng thức Mincowski trở thành bất đẳng thức tam giác. 2
Góc và các tính chất không gian tiền Hilbert lOMoARcPSD| 36782889 Không gian Hilbert PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Trong không gian tiền Hilbert H ta định nghĩa góc giữa 2 véc tơ là . (4.4)
x ⊥ y ⇐⇒ hx,yi = 0 gọi là x vuông góc với y hay x trực giao với y. x ⊥ M ⇐⇒
x ⊥ y,∀y ∈ M.
M ⊥ N ⇐⇒ x ⊥ N,∀x ∈ M
Không gian bù vuông góc M⊥ = {x ∈ H : x ⊥ M} là không gian con đóng (?).
Mệnh đề 2.1 (Đẳng thức Pithagore) Trong không không gian tiền Hilbert H, ta có
i) x ⊥ y ⇐⇒ ||x + y||2 = ||x||2 + ||y||2.
ii) Họ véc tơ {x1,x2,. .,xn} ⊂ H trực giao đôi một thì . Chứng minh
ii) được suy từ i) nên ta chỉ cần chứng minh i)
Ta có ||x + y||2 = hx + y,x + yi = hx,xi + hx,yi + hy,xi + hy,yi
Do đó x ⊥ y ⇐⇒ hx,yi = 0 ⇐⇒ ||x + y||2 = ||x||2 + ||y||2
Mệnh đề 2.2 (Đẳng thức hình bình hành) Trong không gian tiền Hilbert H, ta luôn có
||x + y||2 + ||x − y||2 = 2(||x||2 + ||y||2). (4.5)
Ghi chú: Giả sử x,y là 2 cạnh của một hình bình hành. Khi đó ||x + y|| và ||x − y|| là 2 đường chéo của hình
bình hành đó. Đẳng thức trên có thể phát biểu bằng lời: Trong hình bình hành, tổng bình phương 2 đường
chéo bằng tổng bình phương các cạnh.
Đẳng thức hình bình hành là đặc trưng của chuẩn sinh bởi tích vô hướng. Người ta có thể chứng minh
một chuẩn thỏa mãn đẳng thức hình bình hành thì phải được sinh bởi một tích vô hướng nào đó.
Chứng minh đẳng thức dễ dàng từ định nghĩa ||x + y|| và ||x − y||. 3 Không gian Hilbert lOMoARcPSD| 36782889 Không gian Hilbert PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Định nghĩa 3.1 (Không gian Hilbert) Không gian tiền Hilbert H gọi là không gian Hilbert nếu H cùng với
chuẩn sinh bởi tích vô hướng là không gian Banach.
Định nghĩa 3.2 (Họ trực giao) i) Một họ véc tơ {xα : α ∈ I} gọi là họ trực giao nếu trực giao đôi một.
ii) Một họ trực giao có các véc tơ có độ dài bằng 1 gọi là họ trực chuẩn.
Một họ trực giao thì luôn luôn độc lập tuyến tính (dựa vào đẳng thức Pithagore). Ngược lại, một họ độc
tuyến tính luôn có thể trực chuẩn được bằng thuật toán Gram-Smith.
Định lý 3.1 (Phép phân tích trực giao) Cho M là không gian con đóng của không gian Hilbert H. Khi đó
∀x ∈ H,∃!y ∈ M,z ∈ M⊥ : x = y + z. (4.6)
y gọi là hình chiếu vuông góc của x xuống M : y = PM(x). Chứng minh
Xét x ∈ H tùy ý. Ta đặt d = d(x,M) =⇒ {yn : n ∈ N} ⊂ M : d(yn,x) −→ d.
Ta có đẳng thức hình bình hành .
{yn : n ∈ N} là dãy Cauchy trong không gian Hilbert H do đó hội tụ.
=⇒ yn −→ y ∈ M (vì M) đóng.
Đặt z = x − y =⇒ ||z|| = ||x − y|| = lim||x − yn|| = d.
Ta sẽ chứng minh z ∈ M⊥. Thật vậy
∀u ∈ M, ta có ,
( Vì y + tu ∈ M nên ||x − (y + tu)|| ≥ d) Ta có thể giả sử u 6= 0 và chọn , ta được
Vậy z ∈ M⊥. lOMoARcPSD| 36782889 Không gian Hilbert PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Ta sẽ chứng minh sự phân tích x = y + z,y ∈ M,z ∈ m⊥ là duy nhất.
Giả sử ta có 2 sự phân tích
x = y + z = y0 + z0,;y,y0 ∈ M;z,z0 ∈ M⊥
=⇒ y − y0 = z − z0 ∈ M ∩ M⊥ = {0}
=⇒ y = y0,z = z0
Ta có điều phải chứng minh.
Mệnh đề 3.2 Cho không gian tiền Hilbert H và a ∈ H.
Phiếm hàm tuyến tính f(x) = hx,ai,∀x ∈ H là tuyến tính liên tục và ||f|| = ||a|| Chứng minh
Ta có |f(x)| = |hx,ai| ≤ ||x||.||a|| suy ra f
liên tục và ||f|| ≤ ||a||
Mặt khác |f(a)| = ||a||2 =⇒ ||f|| = ||a||
Định lý 3.3 (Định lý Riesz) Cho không gian Hilbert H và f ∈ H∗.
Khi đó tồn tại duy nhất a ∈ H : f(x) = hx,ai,∀x ∈ H
Định lý này cho ta thấy liên hợp của không gian Hilbert là chính nó và do đó không gian Hilbert là không
gian phản xạ. Chứng minh i) Sự tồn tại
Với f ≡ 0 thì ta chọn a = 0. Với f 6= 0.
Đặt M = ker(f) = {x ∈ H : f(x) = 0} = f−1{0} 6= X là không gian con đóng của X.
Xét x0 ∈/ M : x0 = y0 + z0,y0 ∈ M,z0 ∈ M⊥. =⇒ z0 = 06. f f lOMoARcPSD| 36782889 Không gian Hilbert PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng Đặt , ta có
∀x ∈ H : f(x) = hx,ai.
ii) Tính duy nhấtGiả sử f(x) = hx,ai = hx,a0i,∀x ∈ H =⇒ hx,a − a0i =
0,∀x ∈ H =⇒ a ≡ a0
Định lý 3.4 Cho hệ trực chuẩn
và dãy {λn,n ∈ N} ∈ C. Xét chuỗi (4.7) Ta có
i) Chuỗi (4.7) hội tụ khi và chỉ khi hội tụ.
+∞ ii) Đặt x = λnen. Ta luôn có nP=1 Chứng minh i) Đặt
Do đó {Sn} là dãy Cauchy khi và chỉ khi {tn} là dãy Cauchy.
Ta có điều phải chứng minh. +∞ x = λnen = lim Sn nP=1 n→∞ n
ii) =⇒ ||x||2 = lim ||Sn||2 = lim |λk|2 n→∞ n→∞ kP=1 ∞ =⇒
||x||2 = |λk|2. kP=1
hx,emi = lim hSn,emi = λm,∀m ∈ N m→∞
Định lý 3.5 (Bất đẳng thức Bessel) .
Trong không gian Hilbert H, Cho hệ trực chuẩn {en.n ∈ N}. Ta có Chuỗi
hội tụ, ∀x ∈ H. lOMoARcPSD| 36782889 Không gian Hilbert PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng Và . (4.8) Chứng minh Đặt
Ta có: x = Sn + (x − Sn) nên theo Pithagore 4 Cơ sở trực chuẩn
Định nghĩa 4.1 (Cơ sở trực chuẩn đầy đủ) Họ trực chuẩn {eα,α ∈ I} gọi là họ trực chuẩn đầy đủ (hay cơ sở
trực chuẩn đém được) nếu (x ∈ X,x ⊥ eα,∀α ∈ I) =⇒ x = 0.
Định nghĩa trên tương đương với không gian con M = Span{eα,α ∈ I} trù mật trong H hay M⊥ = {0}.
Nếu họ {eα,α ∈ I} đém được thì ta có cơ sở trực chuẩn đém được. Điều này chỉ tồn tại khi và chỉ khi H là
không gian khả ly (điều này được suy ra từ tính chất C khả ly).
Định lý 4.1 {en,n ∈ N} là hệ trực chuẩn đém được. Ta có các mệnh đề sau tương đương i) {en,n ∈ N} đầy đủ.
ii) Không gian con hen,n ∈ Ni trù mật trong H. iii) . iv) lOMoARcPSD| 36782889 Không gian Hilbert PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Chứng minh dễ dàng xem như bài tập
Định lý 4.2 Không gian Hilbert H có hệ trực chuẩn đém được khi và chỉ khi H khả ly. 5
Định lý Stampacchia và Lax-MilGram
2 định lý này được ứng dụng rất nhiều trong bài toán tối ưu và các lĩnh vực khác. Nó là một hướng nghiên
cứu lớn trong không gian Hilbert. Các dạng phi tuyến của định lý Stampacchia và Lax-MilGram và ứng
dụng đã được GS.Dương Minh Đức nghiên cứu nhiều năm 2006.
Định nghĩa 5.1 Cho H là không gian Hilbert và dạng song tuyến tính 8 a(.,.) : H × H −→ R. i) a gọi là đối xứng nếu
a(x,y) = a(y,x),∀x,y ∈ H.
ii) a gọi là liên tục nếu
∃C > 0 : |a(x,y)| ≤ C||x||.||y||,∀x,y ∈ H.
iii) a gọi là cưỡng bức nếu
∃α > 0 : a(x,x) ≥ α.||x||2,∀x ∈ H.
Định lý 5.1 (Stampacchia) Cho a là dạng song tuyến tính, liên tục, cưỡng bức trên không gian
Hilbert H. K là tập lồi, đóng khác rỗng. Khi đó
∀x ∈ H,∃!u ∈ K : a(u,y − u) ≥ (x,y − u),∀v ∈ K
Hơn nữa nếu a đối xứng thì
8 Dạng song tuyến tính ánh xạ trên H × H mà khi cố định một biến thì nó tuyến tính theo biến còn lại. lOMoARcPSD| 36782889 Không gian Hilbert PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng .
Định lý 5.2 (Lax-MilGram) ho a là dạng song tuyến tính, liên tục, cưỡng bức trên không gian Hilbert H. Khi đó lOMoARcPSD| 36782889 Không gian Hilbert PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
∀x ∈ H,∃!u ∈ H : a(u,y) = (x,y),∀y ∈ H
Hơn nữa nếu a đối xứng thì .
Chứng minh 2 định lý này xem như bài tập. lOMoAR cPSD| 36782889 Chương 5
PHỔ CỦA TOÁN TỬ TRONG KHÔNG GIAN BANACH 1
Toán tử trong không gian banach
Định nghĩa 1.1 (Toán tử compact) Cho E,F là 2 không gian định chuẩn. Toán tử f : E −→ F gọi là toán tử
compact nếu ảnh của quả cầu đơn vị đóng compact tương đối trong F
f(B[0,1]) = {f(x) : ||x|| ≤ 1} compact tương đối.
Nếu f compact tức là f(B[0,1]) compact tương đối do đó bị chặn trong F : ||f(x)|| ≤ M,∀x ∈ B[0,1]. Từ đó
cho thấy f là toán tử tuyến tính liên tục từ E vào F hay f ∈ L(E,F).
Vì f(B[0,1]) compact tương đối nên ảnh của mọi tập bị chặn trong E cũng compact tương đối trong F.
Nếu E hữu hạn chiều thị mọi toán tử trên E đều liên tục và compact.
Nếu E vô hạn chiều và f là toán tử đồng nhất từ E vào E thì f không là toán tử compact. Vì quả cầu đóng
đơn vị trong không gian định chuẩn vô hạn chiều không phải compact.
Ta cũng dễ dàng kiểm chứng nếu f,g là 2 toán tử compact thì αf + βg cũng là toán tử compact.
Hệ quả 1.1 Cho E,F,G là các không gian định chuẩn và f ∈ L(E,F),g ∈ L(F,G). Nếu f hoặc g compact thì g ◦
f là toán tử compact từ E vào G. Chứng minh Giả sử f compact. 41
Xét {xn,n ∈ N} ⊂ B[0,1] ⊂ E =⇒ {f(xn),n ∈ N} ⊂ f(B[0,1]) compact tương đối trong F.
Suy ra tồn tại dãy con {f(xnk),k ∈ N} hội tụ: f(xnk) −→ y ∈ F.
Vì g liên tục nên g ◦ f(xnk) −→ g(y) ∈ G =⇒ g ◦ f compact.
Bây giờ ta giả sử g compact. lOMoARcPSD| 36782889
Xét {xn,n ∈ N} ⊂ B[0,1] ⊂ E =⇒ {g ◦ f(xn),n ∈ N} ⊂ g ◦ f(B[0,1]) Vì f liên tục
nên f(B[0,1]) bị chặn.
Và vì g compact nên g◦f(B[0,1]) compact tương đối trong G, do đó tồn tại dãy con g◦f(xnk) −→ z ∈ G.
Vậy g ◦ f compact.
Định lý 1.2 Cho {fn,n ∈ N} là dãy các toán tử compact từ không gian banach E vào không gian banach F và
fn −→ f ∈ L(E,F).
Khi đó f cũng là toán tử compact. Chứng minh
Vì F đầy đủ nên ta chỉ cần chứng minh f(B[0,1]) hoàn toàn bị chặn 9Ta có fn −→ f :
Vì fn0(B[0,1]) compact tương đối trong F nên Ta chứng minh
Vậy f(B[0,1]) hoàn toàn bị chặn do đó compact tương đối trong F hay f compact. 2
Toán tử hữu hạn chiều
Định nghĩa 2.1 (Toán tử hữu hạn chiều) Toán tử tuyến tính f từ không gian định chuẩn E vào không gian
định chuẩn F gọi là hữu hạn chiều nếu Im(f) là không gian hữu hạn chiều trong F.
9 Trong không gia đầy đủ: tập compact là tập hoàn toàn bị chặn và ngược lại lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Mệnh đề 2.1 Mọi toán tử tuyến tính liên tục hữu hạn chiều là toán tử compact.
Chứng minh Giả sử f : E −→ F là toán tử tuyến tính liên tục hữu hạn chiều.
Ta có f liên tục nên f(B[0,1]) bị chặn trong không gian hữu hạn chiều Im(f) nên compact tương đối trong Im(f).
Vì Im(f) là không gian con hữu hạn chiều nên đóng trong F.
Vậy f(B[0,1]) compact tương đối trong F, hay f là toán tử compact. Nhận xét
Nếu E hoặc F hữu hạn chiều thì mọi toán tử tuyến tính liên tục là toán tử compact (Vì f ∈ L(E,F) thì f(E) hữu hạn chiều.)
Mệnh đề 2.2 Cho E,F là không gian banach và f ∈ L(E,F).
f hữu hạn chiều khi và chỉ khi tồn tại u1,u2,..,un ∈ E∗ và y1,y2,..,yn ∈ F thỏa Chứng minh
Chiều ngược lại là hiển nhiên.
Ta chứng minh chiều thuận
Giả sử f hữu hạn chiều. Gọi {y1,y2,..,yn} là cơ sở của Im(f).
∀x ∈ E,y = f(x) ∈ Im(f) thì y biểu diễn duy nhất ở dạng
Lúc này, dễ dàng kiểm tra các phép chiếu uk(x) 7→ ak là các phiếm hàm tuyến tính liên tục trên E.
Ta có điều phải chứng minh.
3 Phổ của toán tử trong không gian banach 3.1
Hàm giải tích vào không gian banach
Trước hết ta xét E là không gian banach. Dễ dàng kiểm chứng L(E) là một vành có đơn vị với phép toán
cộng 2 hàm thông thường và phép nhân theo nghĩa hợp 2 hàm.
Phần tử đơn vị 1E chính là ánh xạ đồng nhất trên E.
Phần tử không 0E là ánh xạ không trên từ E vào E. lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Định nghĩa 3.1 (hàm giải tích) Cho E là không gian banach trên K và D là tập mở trên K. Hàm f : D −→ E
gọi là giải tích tại λ0 ∈ K nếu
f giải tích trên D nếu nó giải tích mọi λ ∈ D
Nếu K = C thì hàm giải tích gọi là hàm chỉnh hình.
Như vậy, hàm giải tích là hàm có thể viết được chuỗi lũy thừa với hệ tử trên E.
Dễ dàng kiểm tra tính giải tích được bảo toàn qua một toán tử tuyến tính liên tục T ∈ L(E,F) bằng cách
lấy T 2 vế chuỗi lũy thừa.
Ta có định lý khá hay về hàm chỉnh hình sau
Định lý 3.1 (Liouville) f : C −→ E chỉnh hình và bị chặn trên C thì f là hàm hằng. Chứng minh
Tính chất này được suy ra từ giải tích phức là: mọi hàm số chỉnh hình và bị chặn trên C thì là hàm hằng.
Ta giả sử ∃z1,z2 : f(z1) 6= f(z2). Theo hệ quả định lý Hahn-Banach
∃u ∈ E∗ : u(f(z1) − f(z2)) = ||f(z1) − f(z2)|| =⇒ u(f(z1)) 6= u(f(z2))
Vì u liên tục và f(C) bị chặn nên u ◦ f(C) bị chặn.
Mặt khác u tuyến tính liên tục từ E vào C nên u ◦ f : C −→ C giải tích.
Do đó u ◦ f là hàm hằng. Điều này mâu thuẩn với u(f(z1)) 6= u(f(z2)). Vậy ta có điều phải chứng minh. 3.2
Phổ của toán tử trong không gian banach
Định nghĩa 3.2 (Phổ và chính quy) Cho E là không gian định chuẩn trên K và f ∈ L(E).
• λ ∈ K gọi là giá trị chính quy của f nếu λ.1E − f khả nghịch trong L(E).
Tập tất cả các giá trị chính quy ký hiệu là s(f).
• λ ∈ K gọi là giá trị phổ của f nếu λ.1E − f không khả nghịch trong L(E).
Tập tất cả các giá trị phổ ký hiệu là σ(f).
rf = {|λ| : λ ∈ σ(f)} gọi là bán kính phổ của f. Nhận xét. lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
1. K = s(f) ∪ σ(f).
2. λ ∈ s(f) khi và chỉ khi λ − f := λ.1E − f là một tự đẳng cấu trên E.
3. Trong trường hợp σ(f) = ∅ thì ta quy ước rf = −∞.
Sau đây là định lý cơ bản về đặc trưng phổ của toán tử tuyến tính liên tục trong không gian banach.
Định lý 3.2 (phổ của không gian banach) Cho E là không gian banach trên K. Ta có i)
σ(f) là tập compact trong K. ii)
Hàm λ 7→ (λ − f)−1 giải tích trên s(f). iii) Nếu K = C thì σ(f) 6= ∅. Chứng minh
i) Ta chứng minh σ(f) đóng và bị chặn trong K.
• Chứng minh σ(f) bị chặn bởi ||f||. Tức là ∀λ : |λ| > ||f|| =⇒ λ ∈ s(f). Thật vậy do đó chuỗi hội tụ.
Mặt khác, E banach nên L(E) banach nên mọi chuỗi hội tụ tuyệt đối thì hội tụ. Ta đặt . Ta cần chứng minh λ có nghịch đảo là g(λ). 2 .
Bởi tính giao hoán của fn với λ.1E − f nên ta cũng có ∞ 2Chú ý
hội tụ thì un → 0
[(λ − f)g(λ)](x) = 1E(x),∀x ∈ E Do đó λ
− f có nghịch đảo là g(λ). lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
• Tiếp theo ta chứng minh σ(f) đóng bằng cách chứng minh s(f) mở.
Thật vậy, xét λ0 ∈ s(f). Đặt . Ta cần chứng minh
∀λ ∈ B(λ0,δ) =⇒ α = ||(λ0 − f)−1||.|λ − λ0| < 1 Do đó chuỗi hội tụ Tức là chuỗi
hội tụ tuyệt đối trên L(E) do đó hội tụ. Ta đặt
λ0)n+1](x) = x = 1E(x). Như vậy λ − f khả nghịch .
Hay B(λ,δ) ⊂ s(f). ii) Theo chứng minh trên, hàm g(λ) = (λ − f)−1 viết được dưới dạng chuỗi lũy
thừa trên s(f) nên giải tích trên s(f)
iii) Với K = C. Giả sử σ(f) = ∅ =⇒ s(f) = C Theo chứng minh trên, hàm g(λ) = (λ − f)−1 viết được ở dạng
chuỗi lũy thừa nên chỉnh hình trên C. Mặt khác
Như vậy hàm g(λ) chỉnh hình và bị chặn trên C do đó là hàm hằng.
Hơn nữa lim g(λ) = 0 =⇒ g(λ) ≡ 0 ∈ L(E). λ→∞
Điều này mâu thuẩn với g(0) = f−1.
Vậy σ(f) 6= ∅.
Chú ý: Theo chứng minh trên, ta thấy rằng: λ ∈ σ(f) =⇒ |λ| ≤ ||f||
Định lý 3.3 Cho E là không gian banach trên C và f ∈ L(E). Khi đó bán kính phổ là rf ≤ lim ||fn||. n→∞ pn lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng Chứng minh
a) Trước hết ta chứng minh giới hạn tồn tại bằng cách chứng minh dãy { n ||fn||} là dãy giảm.
Thật vậy, giả sử ∀n ∈ N∗. Ta có p
b) Bây giờ ta chứng minh rf ≤ n ||fn||.
Xét λ ∈ σ(f) ta sẽ chứng minhpλn ∈ σ(fn).
Thật vậy. Giả sử λn ∈/ σ(fn) =⇒ λn ∈ s(fn).
Đặt h = (λn−fn)−1 =⇒ (λn−fn)◦h = 1E =⇒ (λ−f)(λn−1+λn−2f+...+λfn−2+fn−1)◦h = 1E
Do đó (λ − f) khả nghịch phải. Và bởi tính giao hoán của λ và f nên λ − f cũng khả nghịch trái và do đó khả nghịch.
Điều này suy ra λ /∈ σ(f).
Vậy nếu λ ∈ σ(f) thì λn ∈ σ(fn). 3.3
Phổ của toán tử compact
Định lý 3.4 Cho E là không gian banach và A ∈ L(E) là toán tử compact. Khi đó
i) Với λ 6= 0 thì Nλ = ker(λ − A) là không gian hữu hạn chiều. ii) Rλ =
Im(λ − A) là không gian con đóng. Chứng minh
Sau đây ta ký hiệu BE là quả cầu đóng trong E.
i) Ta cần chứng tỏ quả đơn vị BNλ = {x ∈ Nλ : ||x|| ≤ 1} là compact hay là đóng trong một tập compact. 10
Ta có λ − A liên tục nên Nλ đóng, do đó BNλ = Nλ ∩ BE đóng. 1
10 Nhớ lại rằng, một không gian hữu hạn chiều khi và chỉ khi quả cầu đơn vị là compact lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Vì A là toán tử compact nên A(BE) compact tương đối trên E. Vậy BNλ
compact do đó Nλ là không gian con hữu hạn chiều. ii) Ta xây dựng ánh
xạ chiếu P xuống Nλ như sau.
Giả sử {e1,e2,..,em} là cơ sở của .
Ánh xạ fk : x 7→ ak là phiếm hàm tuyến tính liên tục trên Nλ. Theo Hanh-banach, tồn
tại thác triển gk của fk lên E vào C
gk tuyến tính tục trên E
,k = 1,2,. ,m (
gk(x) = ak,∀x ∈ Nλ
Xét ánh xạ P : E −→ E thỏa
là ánh xạ chiếu xuống Nλ. Tức là
∀x ∈ E : x = x − P(x) + P(x), trong đó P(x) ∈ Nλ và P(x − P(x)) = P(x) − P(P(x)) = P(x) − P(x) = 0
=⇒ x − P(x) ∈ kerP := M
=⇒ E = M + Nλ
Hơn nữa x ∈ M ∩ Nλ =⇒ x = P(x) = 0 =⇒ M ∩ Nλ = {0}
=⇒ E = M ⊕ Nλ
Áp dụng tính chất trên ta chứng minh Rλ đóng như sau
Xét dãy {yn = (λ − A) ◦ xn,xn ∈ E} ⊂ Rλ thỏa yn → y0 ∈ E.
Vì E = M ⊕ Nλ nên ta có thể giả sử xn ∈ M,∀n.
Ta cần chứng tỏ y0 ∈ Rλ.
Vì {yn} hội tụ nên bị chặn: ∃a ∈ R : ||yn|| ≤ a,∀n.
Ta chứng tỏ {xn} cũng bị chặn. Thật vậy, giả sử {xn} không bị chặn. Tức là tồn tại dãy con
{xnk} sao cho ||xnk|| ≥ k.a,∀k. Ta lại có compact tương đối, Do đó tồn tại dãy con
sao cho A(zkj) → z0. Ta viết lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng . Vì là đóng). Hơn nữa,
(chú ý zkj là dãy con của
Điều này chứng tỏ z0 ∈ Nλ =⇒ z0 ∈ Nλ ∩ M =⇒ z0 = 0.
Mâu thuẩn với ||z0|| 6= 0.
Do vậy dãy {xn} bị chặn, tức là ∃b > 0 : ||xn|| ≤ b ⇐⇒ xn ∈ b.BE
Vì A compact nên A(b.BE) compact tương đối nên tồn tại dãy con {xnk} thỏa
A(xnk) → z0 ∈ E. Ta viết Do đó
(λ − A)(xnk) → y0 = (λ − A)(x0) =⇒ y0 ∈ Rλ.
Vậy Rf là không gian con đóng.
Định nghĩa 3.3 (tri riêng) Cho A ∈ L(E). λ ∈ K gọi là trị riêng (TR) nếu ∃x = 0 :6 Ax = λx.
Véc tơ x gọi là Véc tơ riêng (VTR) của A ứng với TR λ.
Không gian Nλ = ker(λ − A) gọi là không gian con riêng ứng với TR λ.
Số chiều của Nλ gọi là bội hình học (BHH) của TR λ.
• Trị riêng ở đây được định nghĩa giống như trong đại số tuyến tính.
• λ là TR khi và chỉ khi λ − A không đơn ánh.
• Các VTR ứng với các TR khác nhau thì độc lập tuyến tính. Tính chất này hoàn toàn giống trong đại số
tuyến tính. Việc kiểm chứng chỉ là một phép quy nạp tầm thường.
Định lý sau cho ta mối liên hệ giữa tập TR và phổ.
Định lý 3.5 Cho A ∈ L(E). Ta có tập TR là con tập phổ.
Hơn nữa nếu E hữu hạn chiều thì tập TR và phổ trùng nhau. lOMoAR cPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng Chứng minh
Nếu λ là trị riêng thì ∃x 6= 0 : (λ − A)x = 0.
Điều này chứng tỏ λ − A không đơn ánh nên không khả nghịch, do đó λ là giá trị phổ.
Nếu E hữu hạn chiều thì đơn ánh và toàn ánh là như nhau nên TR cũng là phổ.
Định lý 3.6 Cho E là không gian banach và A ∈ L(E) là toán tử compact. Khi đó lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
i) Nếu E vô hạn chiều thì 0 là một giá trị phổ.
ii) Mọi giá trị phổ khác 0 là trị riêng.
iii) Tập phổ là một tập hữu hạn hoặc là một dãy tiến về 0.
Chứng minh dựa vào định lý Riesz (??)
i) Giả sử 0 ∈/ σ(A), tức là A khả nghịch.
Vì A compact nên I = A ◦ A−1 compact, tức là BE = I(BE) compact. Điều này chứng tỏ E hữu hạn chiều.
ii) Giả sử ngược lại ∃λ 6= 0 là giá trị phổ mà không phải trị riêng.
Điều này tương đương λ − A đơn ánh nhưng không song ánh.
Đặt E1 = (λ − A)(E) ⊂ E,E1 6= E
Đặt E2 = (λ − A)(E1) ⊂ (λ − A)(E) = E1
Hơn nữa ∃x ∈ E \ E1 =⇒ (λ − A)(x) ∈ E1 \ E2. Tức là E2 là
không gian con thật sự của E1.
Hơn nữa, theo định lý (3.4), E1 = RA và E2 = RA(E1) là các không gian con đóng.
Tương tự như trên, ta xây dựng được một dãy các không gian con đóng giảm thật sự
{En = (λ − A)n(E),n ∈ N∗}
Theo bổ đề Riesz, với mỗi n ∈ N∗ .
Ta lại có A(BE) compact tương đối nên dãy {A(xn)} ⊂ A(BE) có dãy con là dãy cauchy.
Xét n,m ∈ N∗ : n < m, ta có Trong đó .
Điều nay mâu thuẩn với dãy {A(xn)} có dãy con cauchy.
Ta có điều phải chứng minh.
iii) Để chứng minh tập phổ hữu hạn hoặc là một dãy dần về 0, ta cần chứng minh lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng trang 50
với mọi ε > 0 thì {λ ∈ σ(A) : |λ| > ε} là tập hữu hạn.
Thật vậy. Giả sử tồn tại ε > 0 sao cho {λ ∈ σ(A) : |λ| > ε} vô hạn.
Lúc này tồn tại {λn} ∈ {λ ∈ σ(A) : |λ| > ε} hội tụ hoặc dần ra vô cực.
Gọi un là các VTR tương ứng với λn.
Khi đó tập {uk : k = 1,2,. ,n} độc lập tuyến tính, ∀n ∈ N∗.
Đặt En =< u1,u2,..,un > là dãy các không gian con hữu hạn chiều tăng thật sự.
Theo bổ đề Riesz, tồn tại xn ∈ En thỏa
A compact nên dãy {A(xn)} tồn tại một dãy con cauchy {xnk}.
Xét n,m ∈ N∗ : n < m, ta có
Nếu λn → ∞. A(xn) ⊂ A(BE) bị chặn nên vế trái dần về 0.
Nếu λn → λ ∈ K. Dãy A(xn) ⊂ A(BE) có một dãy con {xnk} là dãy cauchy 1 1 1 ||
(A(xnk) − A(xnk0)) + ( −
)A(xnk0)|| → 0 λnk λnk λnk0
Điều này mâu thuẩn với đẳng thức .
Vậy ta có điều phải chứng minh. Chương 6 GIẢI TÍCH ĐA TRỊ
Chương này ta sẽ giới thiệu về ánh xạ đa trị, các khái niệm liên quan cơ bản về ánh xạ đa trị. Nhìn chung,
đây là một khái niệm mở rộng của ánh xạ bình thường (ánh xạ đơn trị). Xây dựng một metric trên tập các
tập hợp con đóng, từ đó định nghĩa tính độ đo và tích phân trên đó. Lý thuyết giải tích đa trị được ứng
dụng mạnh mẻ trong toán học hiện đại, đặc biệt là những ứng dụng của nó trong phương trình vi phân
và lý thuyết điều khiển.
Cũng bởi thời gian nghiên cứu của chúng ta có giới hạn nên ở đây chúng ta chỉ giới thiệu những khái niệm
và tính chất cơ bản của giải tích đa trị, từ đó tạo một nền tảng để học viên có thể tự nghiên cứu về sau. 1 Ánh xạ đa trị lOMoARcPSD| 36782889 Lý thuyết phổ PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Cho X,Y là 2 tập hợp khác rỗng. 2Y là tập các tập hợp con của Y .
Định nghĩa 1.1 (Ánh xạ đa trị) Ánh xạ F cho tương ứng mỗi giá trị x ∈ X thành một tập còn của Y gọi là một
ánh xạ đa trị từ X vào Y . Ký hiệu là
F : X ⇒ Y
x 7−→ F(x) ∈ 2Y (Y )
F(x) có thể là tập rỗng.
Nếu mỗi x;∈ X thì F(x) đúng 1 phần tử trong Y thì F trở thành ánh xạ đơn trị bình thường và ta ký hiệu là
F : X −→ Y .
Ví dụ 1.1 Xét ánh xạ F xác định trên Rn+1 được xác định như sau.
Mỗi x = (a0,a1,..,an) ∈ Rn+1 thì F(x) là tập nghiệm của phương trình 52 lOMoAR cPSD| 36782889 Giải tích đa trị PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
a0 + a1x + a2x2 + . . + anxn = 0
Khi đó F là một ánh xạ đa trị từ Rn+1 vào C. Định nghĩa
1.2 Cho ánh xạ đa trị F : X ⇒ Y
• Miền xác định của F được định nghĩa
D(f) = {x ∈ X : F(x) 6= ∅} • Đồ
thị của F được định nghĩa
G(f) = {(x,y) ∈ X × Y : y ∈ F(x)} • Miền
ảnh của F được định nghĩa
R(f) = {y ∈ Y : ∃x ∈ X sao cho y ∈ F(x)}
• Ánh xạ ngược của F là F −1 : Y ⇒ X
F −1 = {x ∈ X : y ∈ F(x)} Định nghĩa 1.3 Cho
X,Y là không gian tô pô và Ánh xạ đa trị F : X ⇒ Y
• Nếu ∀x ∈ X : F(x) đóng thì F gọi là ánh xạ có giá trị đóng.
• F gọi là ánh xạ đóng nếu đồ thị G(F) đóng trong X × Y .
• Nếu Y là không gian tô pô tuyến tính (KGVT tô pô) và F(x) lồi với mọi x ∈ X thì F gọi là ánh xạ có giá trị lồi.
• Nếu X,Y là các không gian tô pô tuyến tính.
F gọi là ánh xạ lồi nếu đồ thị G(F) là tập lồi trong X × Y .
Định nghĩa 1.4 (Nửa liên tục trên) Cho X,Y là 2 không gian tô pô và F : X ⇒ Y . lOMoARcPSD| 36782889 Giải tích đa trị PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
F gọi là nửa liên tục trên tại x ∈ D(f) nếu
∀Vmở ⊃ F(x),∃Umở 3 x : F(U) ⊂ V
Ở đây F(U) được định nghĩa .
Định nghĩa 1.5 (Nửa liên tục dưới) Cho X,Y là 2 không gian tô pô và F : X ⇒ Y .
F gọi là nửa liên tục trên tại x ∈ D(f) nếu
(∀Vmở : V ∩ F(x) 6= ∅) =⇒ (∃Umở 3 x : F(y) ∩ V =6 ∅,∀y ∈ U ∩ D(f)).
Định nghĩa 1.6 (Liên tục) Ánh xạ đa trị F gọi là liên tục tại x ∈ D(f) nếu nó đồng thời nửa liên tục trên và
nửa liên tục dưới tại x.
Nếu F liên tục tại mọi x ∈ X thì ta nói F liên tục trên X. Ví dụ 1.2 .
Xét ánh xạ đa trị F : R ⇒ R như sau
Bằng cách chia 3 trường hợp dễ dàng chứng minh được F nửa liên tục trên trên R.
Tuy nhiên F chỉ nửa liên tục dưới trên R \ {0}.
Ta kiểm tra tại x0 bằng cách xét .
Lúc này không tồn tại một lân cận U nào của 0 thỏa điều kiện nửa liên tục dưới. Ví dụ 1.3 .
Xét ánh xạ đa trị F : R ⇒ R như sau
Hãy kiểm tra F nửa liên tục dưới chứ không nửa liên tục trên tại 0. Nhận xét lOMoARcPSD| 36782889 Giải tích đa trị PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
• Xét F là ánh xạ đơn trị trên R. Hàm F gọi là nửa liên tục trên nếu đồ thị trên của F là đóng. Ngược
lại F gọi là nửa liên tục dưới nếu đồ thị dưới của F là đóng. 11
• Qua các ví dụ ta thấy trong trường hợp f đơn trị trên R thì định nghĩa nửa liên tục trên và dưới là giống nhau. 2 Khoảng cách Hausdorff
Định nghĩa 2.1 (Hàm excess) Cho (X,d) là không gian metric và A,B ⊂ X.
Hàm excess từ A đến B được định nghĩa
e(A,B) = sup{d(x,B) : x ∈ A} Ta quy ước
e(A,∅) = +∞,∀A 6= ∅ e(∅,B) =
0,∀B 6= ∅.
Chú ý e(A,B) và e(B,A) nhìn chung không bằng nhau.
Tính Chất 2.1 Cho e là hàm excess như trên. Ta có
i) e(A,B) = 0 ⇐⇒ A ⊂ B¯
ii) e(A,C) ≤ e(A,B) + e(B,C),∀A,B,C ⊂ X Chứng minh
i) Nếu A ⊂ B¯ =⇒ d(x,B) = 0,∀x ∈ A =⇒ e(A,B) = 0.
Ngược lại e(A,B) = 0 =⇒ d(x,B) = 0,∀x ∈ A =⇒ x ∈ B,¯ ∀x ∈ A =⇒ A ⊂ B.¯ ii) ∀x ∈ A,y ∈
B,z ∈ C, ta có
d(x,z) ≤ d(x,y) + d(y,z)
11 Đồ thị trên của y = f(x) là phần phía trên của đồ thị tính cả đồ thị của f. Tương tự cho đồ thị dưới.
Hàm y = f(x) liên tục nếu nó vừa nửa liên tục trên, vừa nửa liên tục dưới.
Tham khảo thêm tính nửa liên tục trên và dưới của hàm đơn trị trên R lOMoARcPSD| 36782889 Giải tích đa trị PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Lấy inf theo z ∈ C 2 vế ta được
d(x,C) ≤ d(x,y) + d(y,C) ≤ d(x,y) + e(B,C)
Lấy inf theo y ∈ B ta được
d(x,C) ≤ d(x,B) + e(B,C)
Cuối cùng lấy sub theo x ∈ A 2 vế ta có điều phải chứng minh.
Định nghĩa 2.2 (Khoảng cách Hausdorff) Cho không gian metric (X,d). P(X) là tập hợp tất cả các tập con đóng của X.
Khi đó ∀A,B ∈ P(X), hàm
h(A,B) = max{e(A,B),e(B,A)}
là một me tric trên P(X) gọi là khoảng cách Hausdorff trên X. Chứng minh i)
ii) h(A,B) = h(B,A) là hiển nhiên.
iii) ∀A,B,C ∈ P(X), ta cần chứng tỏ h(A,C) ≤ h(A,B) + h(B,C) Ta có: e(A,C) ≤ e(A,B) +
e(B,C) ≤ h(A,B) + h(B,C) (
=⇒ h(A,C) ≤ h(A,B) + h(B,C)
e(C,A) ≤ e(C,B) + e(B,A) ≤ h(C,B) + h(B,A)
Vậy h(.,.) là một mê tric trên P(X). Định lý sau xem xét sự hội tụ trong P(X).
Định lý 2.2 Cho An → A trong P(X). Khi đó ta có i) ii) Chứng minh lOMoARcPSD| 36782889 Giải tích đa trị PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng i) Đặt
. Ta chứng minh A = B.
(a) Chứng minh A ⊂ B. Xét x ∈ A
∀n ∈ N∗. Vì An → A nên ∀ε > 0,∃m ≥ n : h(Am,A) < ε
Vậy ta có A ⊂ B
(b) Xét x ∈ B. Để chỉ ra x ∈ A ta chỉ cần chứng tỏ d(x,A) = 0 (vì A đóng). Điều này tương đương với
∀ε > 0 : d(x,A) < ε.
Cho n → ∞ : Amn → A suy ra
d(x,A) ≤ ε,∀ε > 0 =⇒ x ∈ A¯ = A Vậy B ⊂ A ii) Đặt .
(a) Ta chứng tỏ A ⊂ B.
∀x ∈ A =⇒ d(x,Am) ≤ e(A,Am) ≤ h(A,Am) → 0 Điều này tương đương với (b) Xét lOMoARcPSD| 36782889 Giải tích đa trị PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng Cho m → ∞
=⇒ d(x,A) ≤ ε,∀ε > 0 =⇒ x ∈ A¯ = A
Ta có điều phải chứng minh.
Định lý 2.3 Nếu (X,d) là không gian metric đầy đủ thì (P(X),h) cũng là không gian metric đầy đủ. Chứng mịnh
Xét {An,n ∈ n∗} là dãy cauchy trong P(X). Khi đó ∃n "
0 :An = ∅,∀n ≥ n0
An 6= ∅,∀n ≥ n0
Trường hợp 1 thì hiển nhiên An → ∅. Xét trường hợp 2 . Trước hết ta chứng tỏ .
Thật vậy. Vì {An,n ∈ N∗} là dãy cauchy nên ∀ε > 0
Từ tính chất này ta có thể chọn được dãy {xk,k ∈ K} thỏa
Điều này chứng tỏ dãy {xk,k ∈ K} là dãy cauchy trong X do đó hội tụ xk → x0
Với mỗi n ∈ N và k ≥ n thì xk ∈ Ank. Do đó Vậy A 6= ∅
Để chứng minh An → A, ta cần chứng minh e(An,A) → 0 và e(A,An) → 0.
i) Chứng minh e(An,A) → 0. ∀ε > 0. lOMoARcPSD| 36782889 Giải tích đa trị PGS.TS.Nguyễn Đình Huy Bộ môn Toán Ứng dụng
Khi đó ∃n0 : ∀n ≥ n0 thỏa mãn ∀x ∈ An, tồn tại dãy {xk} (cách xây dựng giống như trên) sao cho
Từ đó suy ra {xn} là dãy cauchy nên hội tụ: xn → y ∈ A Hơn nữa
Lấy sup theo x ∈ An ta được
e(An,A) < 2ε,∀n ≥ n0
Điều này chứng tỏ e(An,A) → 0
ii) Chứng minh e(A,An) → 0. ∀ε > 0.
Xét x ∈ A tùy ý.
Vì {An} là dãy cauchy nên
∃n0 : ∀n,m ≥ n0 =⇒ h(An,Am) < ε Ta cố định n. Vì nên
∃m ≥ n : d(x,Am) < ε
=⇒ d(x,An) ≤ d(x,Am) + h(An,Am) < 2ε,∀x ∈ A
Lấy sup 2 vế theo x ∈ A ta được
e(A,An) < 2ε,∀ε > 0 =⇒ e(A,An) → 0
Chứng minh được hoàn thành.




