Đề cương ôn tập từng chương môn Kinh tế vi mô | Trường Đại học Kinh Tế Quốc Dân

g ự ọ g ệ Câu 1:
Năm 2015 Iphone 5S cũ trên thị trường được chi thành 2 loại: chất lượng cao và chất lượng thấp. Giả sử
một nửa số Iphone 5S cũ có chất lượng thấp. Mức giá đúng của Iphone 5S cũ chất lượng cao là 7 triệu
đồng và Iphone 5S cũ chất lượng cao là 4 triệu đồng. a, Khi không thể xác định được chất lượng của
Iphone 5S cũ thì người mua Iphone 5S cũ sẽ trả mức giá tối đa là bao nhiêu? Giải thích?
b, Bạn là người đang muốn bán Iphone 5S cũ chất lượng cao, nếu thời gian bảo hành có thể thuyết phục
người mua tin tưởng vào chất lượng để bán đúng giá và việc bảo hành 1 năm sẽ mất phí là 1500 nghìn
đồng thì thời hạn tối đa bạn sẽ bảo hành cho Iphone 5S cũ của mình bán là bao lâu? Giải thích? c, Để
không mua phải Iphone 5S cũ có chất lượng thấp thì người mua sẵn sang trả tối đa bao nhiêu để thợ kiểm
tra? d, Theo bạn sẽ có bao nhiêu Iphone 5S cũ có chất lượng cao được bán? Đáp án:
a, Mức giá người mua Iphone 5S cũ sẵn sàng trả tối đa là 7 triệu đồng, vì trong những người mua Iphone
sẽ có những người muốn mua Iphone 5S muốn mua hàng chất lượng cao. Họ biết rằng họ trả thấp hơn 7
triệu đồng thì người bán sẽ không bán vì giá không tương xứng.
b, Nếu không tiền hành bảo hành thì hãng sẽ thu được sổ tiền bình quân khi bán Ịphone 5S cũ là: 0,5 * 7 + 0,5 * 4 = 5,5 (triệu)
Gọi thời gian bảo hành là x(năm), chi phí bảo hành sẽ do người bán chịu. Do đó số tiền hãng thu được sau
khi tiến hành bán và bán Iphone 5S CLC đúng giá là 7 - 1,5x (triệu)
Người bán sẽ tiến hành bảo hành nếu thấy có lợi hơn so với khi bán không kèm bảo hành, tức là 7 -
1,5x > 5,5 ⬄ x < 1 (năm)
Vậy thời gian bảo hành nhỏ hơn 1 năm. c, Việc hãng thuê thợ kiểm tra chính là hành vi mua thông tin.
Việc thợ kiểm tra chính xác sẽ giúp chọn được Iphone 5S cũ CLC ngay khi mua.
Giá trị của thông tin hoàn hảo là 7 triệu.
Giá trị kỳ vọng hiện có của người mua về Iphone 5S cũ là EI = 0,5 * 7 + 0,5 * 4 = 5,5 (triệu) Như vậy
người này sẽ trả tối đa cho việc thuê thợ là 7 – 5,5 = 1,5 triêu
d, Do số có ½ số Iphone 5S chất lượng cao được bán và ½ số Iphone 5S chất lượng thấp được bán ra thị
trường nên xác suất bán được Iphone 5S chất lượng cao là 0,5. Câu 2:
Chị Hương có hàm lợi ích phụ thuộc vào thu nhập là: U = I0,5
a, Thái độ của chị Hương với rủi ro là gì? Vì sao?
b, Giả sử chị Hương đang làm 1 công việc mà nhận được thu nhập 6 triệu với xác suất 60% hoặc 16 triệu
đồng với xác suất 40%. Hãy tính thu nhập kì vọng cho chị Hương.
c, Tính lợi ích kỳ vọng của công việc này cho chị Hương.
d. Nếu có bảo hiểm thì phí bảo hiểm nằm trong khoảng nào để đảm bảo rằng chị Hương sẽ mua và công ty bảo hiểm có lãi?
a, U = I0,5 ⇨ MU = 0,5I-0,5 ⇨ MU’ = - 0,25I-1,5 < 0
⇨ Chị Hương có lợi ích cận biên giảm dần ⇨ Chị Hương ghét rủi ro. b, Xét 2 trường hợp:
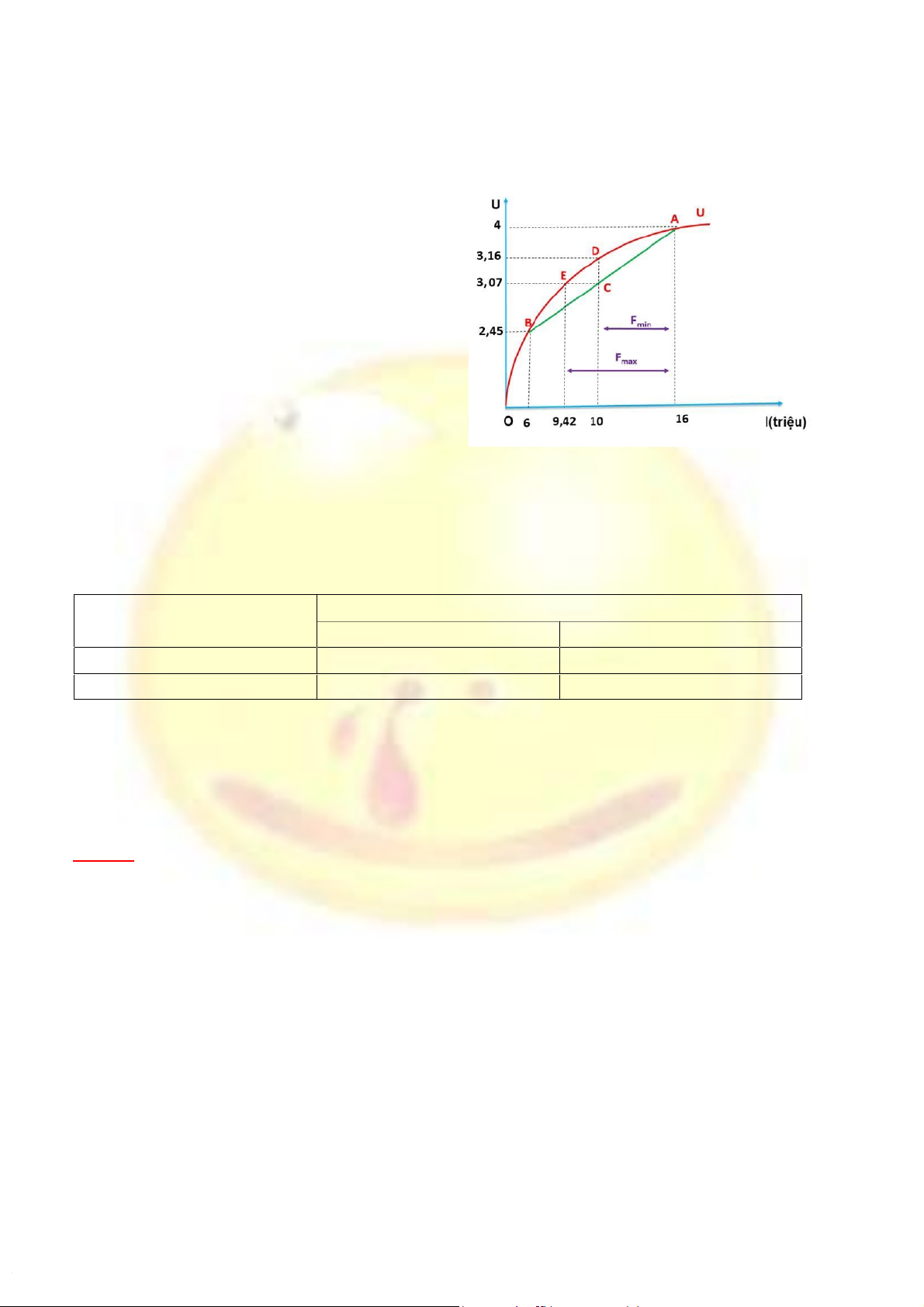
+ TH1: Chị Hương có thu nhập cao nhất: p1 = 0,4; I1 = 16 (triệu) ⇨ U1 = 4
+ TH2: Chị Hương có thu nhập cao nhất: p2 = 0,6; I2 = 6 (triệu) ⇨ U2 = 2,45
Thu nhập kì vọng của chị Hương: EI = p1I1 + p2I2 = 0,4*16 + 0,6*6 = 10(triệu) 1
c, Lợi ích kỳ vọng của chị Hương: EU = p1U1 + p2U2 = 0,4* 4 + 0,6*2,45 = 3,07
Gọi I0 là tương đương chắc chắn cho c
ông việc này. Ta có U(I0) = EU ⬄ I00,5 = 3,07 ⇨ I0 = 9,42(triệu) d,
Nếu chị Hương không mua bảo hiểm thì chị có lợi ích là EU = 3,07
Gọi phí bảo hiểm là F. Nếu chị Hương mua bảo hiểm thì chị chắc chắn có được thu nhập là 16 - F
Khi đó chị sẽ có lợi ích là U = (16 - F)0,5
Chị Hương sẽ mua bảo hiểm nếu thấy việc mua bảo
hiểm đem lại lợi ích cao hơn lợi ích kỳ vọng khi
không mua, Tức là khi đó (16 - F)0,5 > 3,07 ⇨ F < 6,58 (triệu) (1)
Nhà bảo hiểm phải đền bù thiệt hại 1 lượng bình quân là I1 E – I = 16
– 10 = 6 (triệu) , do đó để họ có
lãi thì mức phí bảo hiểm phải cao hơn lượng đền bù
nói trên, tức F > 6 (triệu) (2)
Từ (1) và (2) ⇨ Khoảng bảo hiểm cần tìm là: 6 < F < 6,58 (triệu) Câu 3:
Giám đốc công ty ABC có hàm lợi ích U = 150M – M2. Ông ấy đang cân nhắc 2 phương án cung cấp sản
phẩm: tự sản xuất và thuê bên ngoài làm. Lợi nhuận (tính bằng tỷ đồng) từ 2 phương án được cho bởi bảng dưới đây: Tình hình kinh tế Phương án Tốt (p = 0,4) Xấu (p = 0,6) Tự làm 2 5 Thuê ngoài làm 6 1
a, Thái độ của giám đốc công ty này với rủi ro là gì?
b, Tính lợi ích kì vọng của mỗi phương án kinh doanh cho giám đốc công ty này.
c, Tính tương đương chắc chắn của mỗi phương án kinh doanh cho giám đốc công ty này?
d. Giám đốc công ty này ra quyết định lựa chọn theo tiêu thức tương đương chắc chắn. phương án nào sẽ
được ông ấy chọn? Giải thích? Đáp án: a, U = 150M M – 2 ⇨ MU = 150 2M – ⇨ MU’ = - 2 < 0
=>Giám đốc công ty này có lợi ích cận biên giảm dần ⇨ Ông ta là người ghét rủi ro.
b, Tính toán cho các phương án: - Tự làm:
+ Tốt: pT = 0,4 ; MT = 2 (tỷ) ⇨ UT = 296
+ Xấu: pX = 0,4 ; MX = 5 (tỷ) ⇨ UX = 725
=>Lợi ích kì vọng của phương án tự làm: EU = pTUT + pXUX = 0,4*296 + 0,6*725 = 553,4 - Thuê ngoài làm:
+ Tốt: pT = 0,4 ; MT = 6 (tỷ) ⇨ UT = 864
+ Xấu: pX = 0,4 ; MX = 1 (tỷ) ⇨ UX = 149
=>Lợi ích kì vọng của phương án tự làm: EU = pTUT + pXUX = 0,4*864 + 0,6*149 = 435 2
c, Gọi M0 là tương đương chắc chắn của các hoạt động. Ta có: U(M0) = EU ⬄ 150M0 M – 02 = EU - Tự làm: 150M0 M – 02 = 553,4 ⇨
Vậy tương đương chắc chắn của phương án tự làm là M0 = 3,175 (tỷ) (1)
- Thuê ngoài làm: 150M0 – M
Vậy tương đương chắc chắn của phương án thuê ngoài làm là M0 = 2,958 (tỷ) (2)
d, Do giám đốc công ty là người ghét rủi ro nên ông ta sẽ chọn phương án có tương đương chắc chắn cao
hơn (đồng nghĩa với lợi ích kỳ vọng cao hơn).
Từ (1) và (2) ⇨ Phương án tự làm sẽ được chọn. Câu 4:
Doanh nhân A có hàm lợi ích là U = W0,5 trong đó W là của cải.
a, Doanh nhân này có phải là người ghét rủi ro không? Giải thích
b, Doanh nhân A có tổng tài sản giá trị 3,5 tỷ đồng (trong đó có một ô tô trị giá 500 triệu đồng). Ô tô có
thể bị mất trộm với xác suất là 15%. Hãy tính giá trị kỳ vọng của của cải và lợi ích kỳ vọng cho doanh nhân A này.
c, Để giảm rủi ro có thể mua bảo hiểm ô tô. Phí bảo hiểm thực tế mà công ty bảo hiểm đòi phải nằm trong
khoảng nào thì doanh nhân A mới mua bảo hiểm ô tô? d, Vẽ đồ thị minh họa các kết quả. Đáp án:
a, U = W0,5 ⇨ MU = 0,5W0,5 ⇨ MU’ = - 0,25W-0,5 < 0
⇨ Doanh nhân A có lợi ích cận biên giảm dần khi của cải tăng ⇨ A là người ghét rủi ro. b, Xét 2 khả năng:
+ TH1: Ô tô không bị mất: p1 = 0,85; W1 = 3,5 (tỷ) ⇨ U1 = 1,871
+ TH2: Ô tô bị mất: p2 = 0,15; W2 = 3 (tỷ) ⇨ U2 = 1,732
Thu nhập kì vọng của ông A là: EW = p1W1 + p2W2 =
0,85*3,5 + 0,15*3 = 3,425 (tỷ)
Lợi ích kì vọng của ông A: EU = p1U1 + p2U2 = 0,85*1,871 + 0,15*1,732 = 1,85
c, Nếu ông A không mua bảo hiểm thì chị có lợi ích kỳ vọng là EU = 1,85
Gọi phí bảo hiểm là F. Nếu ông A mua bảo hiểm thì chị chắc chắn có được thu nhập là 3,5 – F
Khi đó lợi ích của ông A là (3,5 – F)0,5 > 1,85
Ông A chỉ mua bảo hiểm nếu thấy có lợi hơn tức (3,5 – F)0,5 > 1,85 ⬄ F < 0,0775 (tỷ) (1)
Nhà bảo hiểm phải đền bù thiệt hại 1 lượng bình quân là W1 – EW = 3,5 –
425 = 0,075, do đó để họ có 3.,
lãi thì mức phí bảo hiểm phải cao hơn lượng đền bù nói trên, tức F > 0,075 (tỷ) (2)
Từ (1) và (2) ⇨ Khoảng bảo hiểm cần tìm là 0,075 < F < 0,0775 (tỷ). d, Đồ thị: 3 Câu 5:
Thắng vừa tốt nghiệp đại học và đang tìm việc làm. Công ty tổ chức sự kiện đang tuyển người với mức
lương phụ thuộc vào kết quả hoạt động: 13 triệu đồng nếu kết quả hoạt động cao với xác suất là 0,3 và 4
triệu nếu kết quả hoạt động thấp với xác suất là 0,7. Thắng có hàm lợi ích phụ thuộc vào thu nhập là U = 10I 0,1I – 2.
a. Nếu Thắng được tuyển vào công ty này thì thu nhập kỳ vọng của Thắng là bao nhiêu?
b. Tính lợi ích kỳ vọng cho Thắng nếu được nhận vào công ty.
c. Mức lương chắc chắn ít nhất phải là bao nhiêu sẽ làm Thắng thỏa mãn như mức lương rủi ro hiện thời?
d. Vẽ đồ thị minh họa các kết quả trên. Đáp án:
Khi Thắng được nhận vào công ty, sẽ có 2 khả năng xảy ra:
- TH1: Kết quả hoạt động cao:
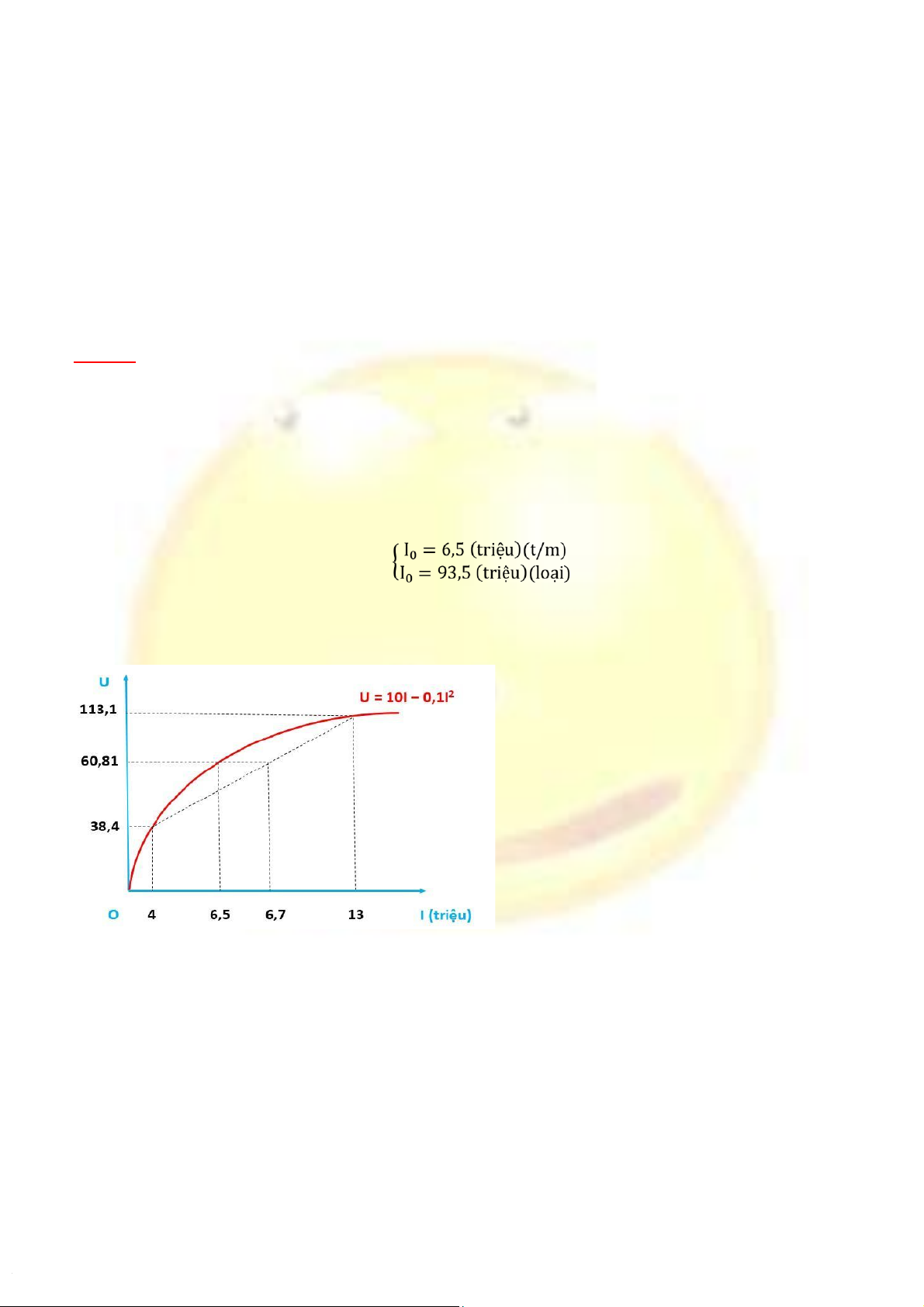
p1 = 0,3; I1 = 13 (triệu) ⇨ U1 = 113,1
- TH2 : Kết quả hoạt động thấp: p2 = 0,7; I2 = 4 (triệu) ⇨ U2 = 38,4
a, Thu nhập kỳ vọng của Thắng: EI = 0,3*13 + 0,7*4 = 6,7 (triệu)
b, Lợi ích kỳ vọng của Thắng: EU = 0,3*113,1 + 0,7*38,4 = 60,81 c, Gọi mức lương chắc chắn cần tìm là I0.
Ta có U(I0) = EU ⬄ 10I0 – 0,1I02 = 60,81 ⇨
Vậy mức lương chắc chắn ít nhất phải là bao nhiêu sẽ làm Thắng thỏa mãn như mức lương rủi ro hiện
thời là 6,5 triệu đồng. d, Đồ thị: Câu 6:
Một khách hàng của mạng điện thoại di động có hàm lợi ích U = 15000M – M2, trong đó M là lượng tiền.
Khách hàng này đang phải quyết định nhận quà tri ân của nhà mạng là 1 hàng có giá 10$ hoặc 1 phiếu rút
thăm trúng thưởng có giải thưởng 100$ vs xác suất trúng là 0,005.
a. Khách hàng này là người thích hay ghét rủi ro? Giải thích?
b. Tính lợi ích kỳ vọng cho cá nhân này khi nhận phiếu thăm trúng thưởng?
c. Người này nhận món hàng hay nhận phiếu rút thăm trúng thưởng? Giải thích? 4
d. Vẽ đồ thị minh họa các kết quả trên. Đáp án: a, U = 15000M M –
2 ⇨ MU = 15000 – 2M ⇨ MU’ = - 2 < 0 ⇨ Người này có lợi ích cận biên giảm dần ⇨
Người này ghét rủi ro. b, Khi nhận phiếu rút thăm trúng thưởng xảy ra 2 trường hợp sau:
+ TH1: Trúng thưởng p1 = 0,005; M1 =100($) ⇨ U1 = 1490000
+ TH2: Không trúng thưởng p2 = 0,995; M2 = 0 ⇨ U2 = 0
⇨ Lợi ích kỳ vọng khi bốc thăm: EU = 0,005*1490000 + 0,995*0 = 7450 (1) c, Khi nhận quà tri ân: M = 10($) ⇨ U = 149900 (2)
Từ (1) và (2) ⇨ Việc nhận quà tri ân sẽ có lợi hơn
⇨ Người này sẽ chọn nhận quà tri ân d, Đồ thị
Khi nhận phiếu rút thăm người này có số tiền kỳ vọng EM = 0,005 * 100 + 0,995*0 = 0,5 ($) và có lợi ích
kỳ vọng EU = 7450 được biểu diễn ở C.
Khi nhận quà tri ân người này có số tiền là M = 10 ($) và có lợi ích tương ứng là U = 149900 được biểu diễn ở D.
Chương 2: Lý thuyết cầu Câu 1:
Cho hàm lợi ích của 1 người tiêu dùng có dạng: U = 0,5lnX + 0,5lnY
a, Hãy sử dụng phương pháp nhân tử Lagrange để viết phương trình đường cầu Marshall cho người tiêu
dùng này? (Giá hàng hóa ký hiệu là Px và Py, thu nhập là I)
b, Áp dụng bằng số cho biết kết quả câu a với Px = 1$, Py = 2$ và I
= 100$. Hãy cho biết giá trị nhân tử λ là bao nhiêu?
c, Khi thu nhập tăng lên I = 101$ (các yếu tố khác không đổi) thì mức thỏa mãn của người tiêu dùng tăng
lên bao nhiêu? X và Y là hàng hóa thông thường hay cấp thấp?
d, Minh họa các kết quả trên cùng 1 đồ thị. Đáp án: a, U = 0,5lnX + 0,5lnY
Xây dựng hàm Lagrange: Ω = 0,5lnX + 0,5lnY + λ(I − pxX − pyY) 5 U Từ (1) và (2) ⇨ Thế vào (3) ta có
⇨ Hàm cầu Marshall về X và Y:
b, Với Px = 1$, Py = 2$ và I = 100$, thay vào (4)
⇨ ⇨ U = 0,5(ln 50 + ln 25) = 3,565 Khi đó nhân tử
c, Với Px = 1$, Py = 2$ và I = 101$, thay vào (4)
⇨ ⇨ U = 0,5(ln 50,5 + ln 25,25) = 3,575
Nhận thấy việc thu nhập tăng làm lượng tiêu dùng về X và Y đều tăng ⇨ Cả X và Y đều là hàng hóa thông thường. d, Đồ thị: Câu 2:
Một hãng có hàm sản xuất dạng Cobb - Douglas Q = K0,5L0,5 (Q: sản lượng/tuần)
Giá các đầu vào là: Lao động 100$/tuần Tư bản: 200$/tuần
a. Quá trình sản xuất của hãng có hiệu suất thế nào theo quy mô? Giải thích?
b. Để sản xuất ra 500 đơn vị sản phẩm với chi phí ít nhất thì K và L phải là bao nhiêu?
c. Cũng hỏi như câu b nhưng số lượng sản phẩm là 750 đơn vị?
d. Minh họa các kết quả trên đồ thị. Viết phương trình đường phát triển của hãng. 6 Đáp án:
a. Xét hàm sản xuất Q = K0,5L0,5
Giả sử các yếu tố đầu vào tăng lên n lần (n > 1), lúc này lượng yếu tố đầu vào sản xuất là: K1 = nK và L1 = nL
Ta có: Q1 = K10,5L10,5 = (nK)0,5(nL)0,5 = nK0,5L0,5 = nQ
⇨ Q tăng đúng n lần ⇨ Hàm sản xuất có hiệu suất không đổi theo quy mô.
b. Với giá của các đầu vào Lao động: w = 100$/tuần; Tư bản: r = 200$/tuần, ta có hàm chi phí sản xuất TC = rK + wL = 200K + 100L
Xét hàm Lagrange với mục tiêu là tối thiểu hóa chi phí tại 1 mức sản lượng Q0 cho trước:
Ω = 200K + 100L + λ(Q0 - K0,5L0,5) TC
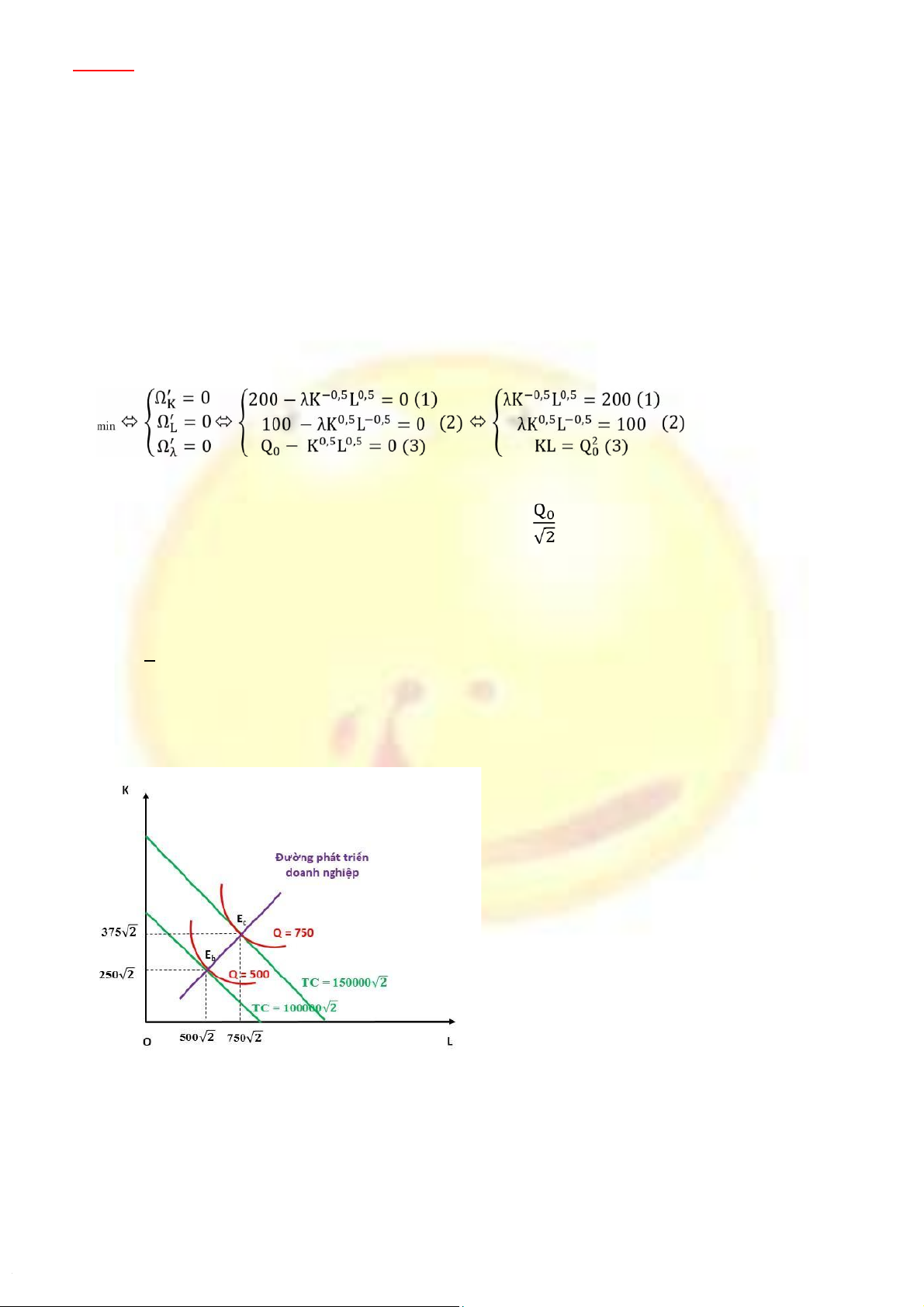
Chia 2 vế của (2) cho 2 vế của (1), ta có: K/L = 0,5 ⬄ K = L/2
Thay vào K = L/2 vào (3) ta có: L2/2= Q20 ⇨ L = √2Q0 ⇨ K =
+ Với mức sản lượng Q0 = 500 ta có mức kết hợp đầu vào tối ưu là: K = 250√2 và L = 500√2
⇨ Lúc này TC = 200*250√2 + 100*500√2 = 100000√2 = 141421,356 ($) c. Với
mức sản lượng Q0 = 750 ta có mức kết hợp đầu vào tối ưu là: K=375√2 và L = 750√2
⇨ Lúc này TC = 200*375√2 + 100*750√2 = 150000√2 = 212132,034 d. Đồ thị:
Giả định đường phát triển doanh nghiệp có dạng tuyến tính, khi đó nó có phương trình là
K = a1+ a2*L. Thay 2 cặp giá trị cặp cây b và c, ta sẽ tìm được: a1 = 0 và a2 = 0,5 7
⇨ Phương trình đường phát triển doanh nghiệp này là K = 0,5L.
Chương 6: Cạnh tranh không hoàn hảo Câu 1:
Thị trường sản phẩm X bao gồm 1 doanh nghiệp lớn chi phối thị trường và 10 doanh nghiệp nhỏ có quy
mô nhỏ hành động theo khuynh hướng chấp nhận giá do doanh nghiệp lớn đặt ra,
Đường cầu về sản phẩm X là: Q = 5000 – 0,25P
Hàm tổng chi phí cận biên của doanh nghiệp chi phối thị trường là MCL = 5000 + 5QL
Hàm cung sản phẩm của cả 10 doanh nghiệp nhỏ là QF = 0,25P – 500
a, Hãy xác định giá bán sản phẩm và sản lượng của doanh nghiệp lớn.
b, Hãy xác định giá bán sản phẩm và sản lượng của 10 doanh nghiệp nhỏ.
c, Nếu thị trường này hoạt động theo nguyên tắc cạnh tranh hoàn hảo thay vì hiện tượng chỉ đạo giá của
doanh nghiệp lớn thì mức giá bán và sản lượng trên thị trường là bao nhiêu?
d, Minh họa các kết quả bằng đồ thị. Đáp án:
Hàm cung của các hãng nhỏ: QF = 0,25P – 500 ⬄ P = 2000 + 4QF
Hàm cầu thị trường là QD = 5000 – 0,25P ⬄ P = 20000 – 4Q
- Phân tích thị trường:
+ Với P ≤ 2000, các hãng nhỏ không tham gia bán hàng nên hàm cầu về sản phẩm của hãng lớn là: QL = 5000 0,25P – ⬄ P = 20000 – 4Q
+ Với P = 2000 thì Qtt = 4500
+ Với P > 2000, thị trường có cả các hãng nhỏ bán hàng nên hàm cầu về sản phẩm của hãng lớn là:
QL = Qtt – QF = (5000 – 0,25P) – (0,25P – 500) = 5500 – 0,5P ⬄ P = 11000 – 2QL
- Hàm cầu về sản phẩm của hãng lớn:
⇨ Hàm doanh thu biên của hãng lớn:
a, Hãng lớn tối đa hóa lợi nhuận khi MRL = MCL ⬄
Vậy sản lượng hãng lớn là QL = 666,67 ⇨ Giá thị trường là P* = 9666,67
b, Các hãng nhỏ phải chấp nhận giá P* = 9666,67 do hãng lớn áp đặt, do đó tổng sản lượng của họ là: QF = 0,25*9666,67
– 500 = 1916,67 Sản lượng của 1 hãng nhỏ là QF/10 = 191,667
c, Nếu thị trường hoạt động theo nguyên tắc cạnh tranh hoàn hảo (không có hãng lớn).
Hàm cung thị trường là QS = 0,25P 500 –
Hàm cầu thị trường là: QD = 5000 – 0,25P
Thị trường cân bắng khi QS = QD ⬄ 5000 – 0,25P = 0,25P – 500 ⇨ P = 11000 ⇨ Q = 2250 d, Đồ thị: 8 Câu 2:
Thị trường sản phẩm X bão gồm 1 hãng lớn và nhiều hãng nhỏ chấp nhận giá do hãng lớn đặt ra. Đường
cầu thị trường về sản phẩm X là: DTT: P = 18 – 0,1Q.
Hàm tổng chi phi phí của hãng lớn là TCL = 7Q + 0,05Q2. Hàm cung sản phẩm của các hãng nhỏ được chơ bởi: P = 4 + 0,1Q.
a. Xác định giá bán sản phẩm và sản lượng của hãng lớn.
b. Xác định giá bán và sản lượng của các hãng nhỏ trên thị trường
c. Nếu thị trường này hoạt động theo nguyên tắc cạnh tranh hoàn hảo thay vì hãng lớn chỉ đạo giá thì mức
giá và sản lượng trên thị trường là bao nhiều?
d. Minh họa các kết quả trên đồ thị. Đáp án:
TCL = 7Q + 0,05QL2 ⇨ MCL = 7 + 0,1Q
Hàm cung của các hãng nhỏ là P = 4 + 0,1QF ⬄ QF = 10P - 40
Hàm cầu thị trường P = 18 – 0,1Q ⬄ Qtt = 180 - 10P
- Phân tích thị trường:
+ Với P ≤ 4, các hãng nhỏ không bán hàng nên hàm cầu về sản phẩm của hãng lớn là:
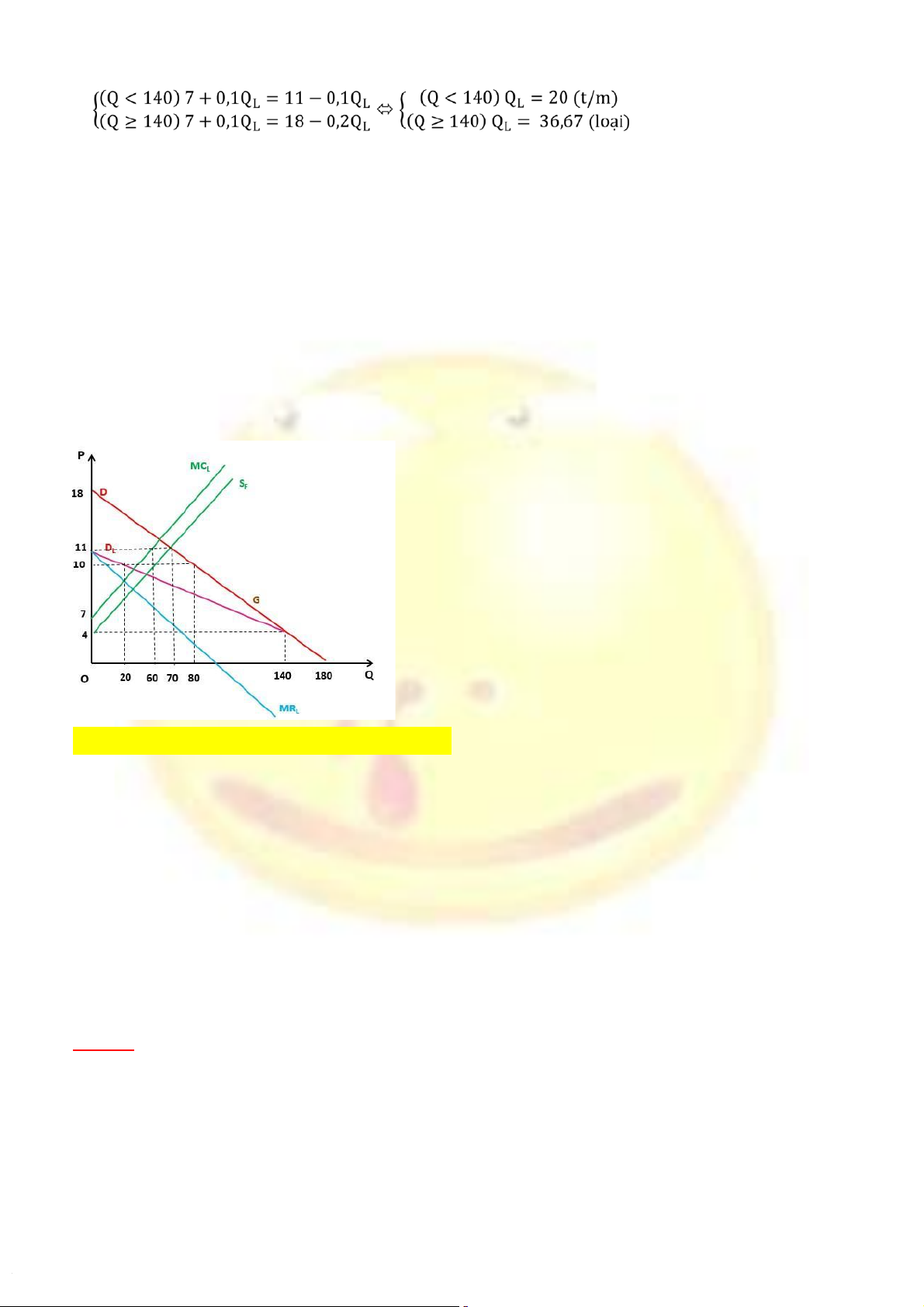
QL = Qtt = 180 – 10P ⬄ P = 18 – 0,1QL + Với P = 4 ⇨ Qtt = 140
+ Với P > 4, thị trường có cả hãng nhỏ bán hãng nên hàm cầu về sản phẩm của hãng lớn là:
QL = Qtt – QF = (180 – 10P) – (10P - 40) = 220 – 20P ⬄ P = 11 – 0,05QL
- Hàm cầu về sản phẩm của hãng lớn:
⇨ Hàm doanh thu biên của hãng lớn: 9
b, Hãng lớn tối đa hóa lợi nhuận khi MRL = MCL ⬄
Vậy sản lượng tối ưu hãng lớn là QL = 20 ⇨ Giá tối ưu hãng lớn đặt là P* = 10
Các hãng nhỏ phải chấp nhận giá mà các hãng lớn đã áp đặt P = 10, khi đó sản lượng hãng nhỏ là QF = 10*10 – 40 = 60
Tổng sản lượng thị trường là Qtt = QL + QF = 20 + 60 = 80
c, Nếu thị trường hoạt động theo nguyên tắc cạnh tranh hoàn hảo (không bao gồm hãng lớn), thị trường
cân bằng khi PS = PD ⬄ 18 – 0,1Q = 4 + 0,1Q ⇨ Q = 70 ⇨ P = 11 d, Đồ thị:
Chương 5: Cạnh tranh và độc quyền Câu 1:
Một hãng độc quyền có chi phí biên MC = 2Q + 5 và chi phí cố định FC = 1000. Hãng gặp cầu về 2 nhóm
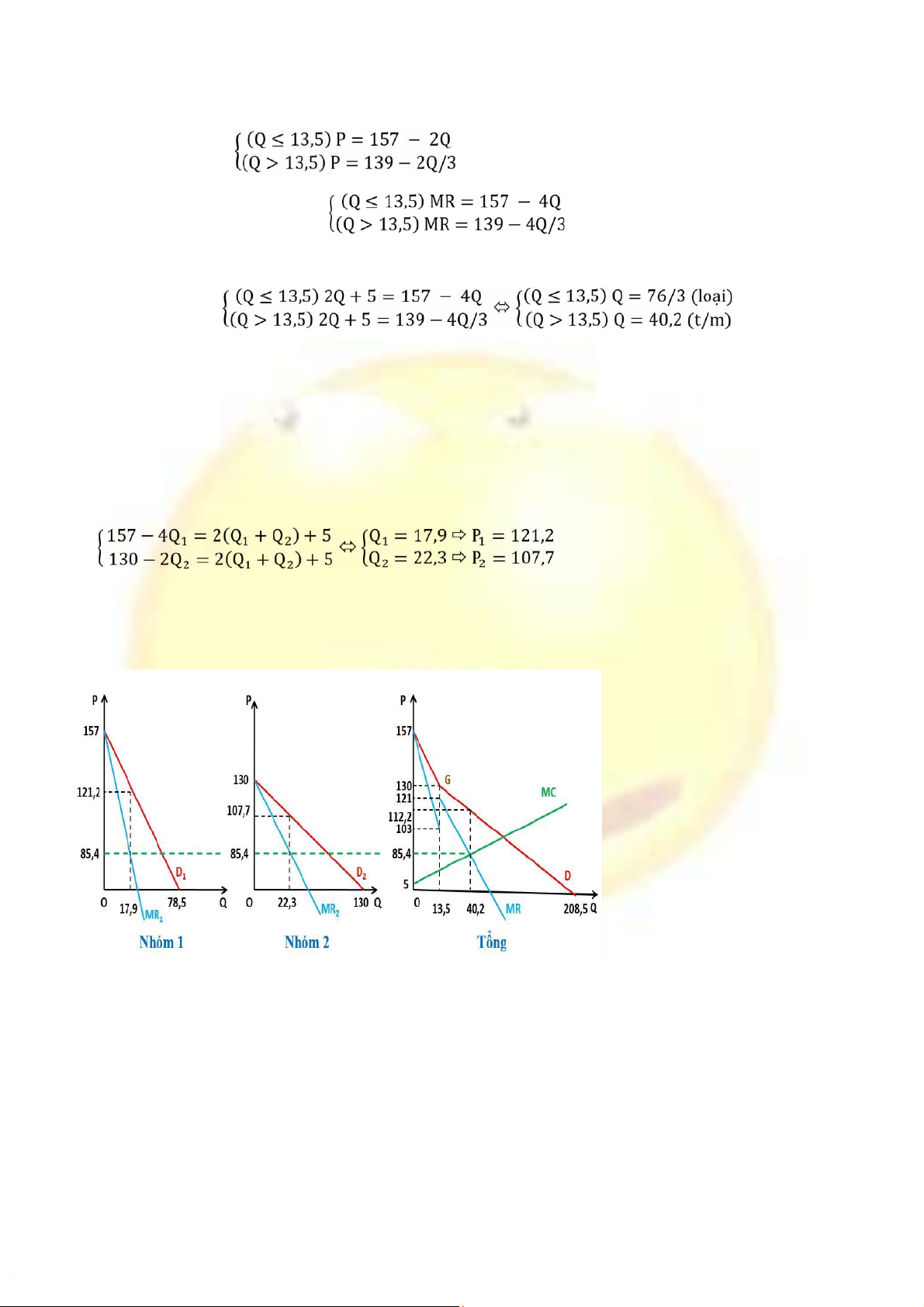
khách hàng như sau: P1 = 157 – 2Q1 và P2 = 130 – Q2
a, Viết phương trình đường cầu tổng cộng và doanh thu cận biên tổng cộng cho hãng này.
b, Nếu Chính phủ cấm phân biệt giá thì hãng sẽ bán trên 1 hay 2 thị trường? Mỗi thị trường sẽ tiêu thụ
bao nhiêu? Lợi nhuận khi đó của hãng là bao nhiêu?
c, Nếu có thể phân biệt giá thì hãng sẽ bán trên mỗi thị trường với giá như thế nào. Lợi nhuận của hãng khi đó là bao nhiêu?
d. Vẽ đồ thị minh họa các kết quả trên. Đáp án:
MC = 2Q + 5 và FC = 1000 ⇨ TC = VC + FC = Q2 + 5Q + 1000 P1 = 157 - 2Q1 ⇨ Q1 = 78,5 P
– /2 P2 = 130 - Q2 ⇨ Q2 = 130 P – a, - Phân tích cầu:
+ Với P ≥ 130, chỉ có nhóm 1 mua hàng nên hàm cầu tổng cộng là: Q = Q1 = 78,5 P – /2 ⬄ P = 157 2Q – 10 + Với P = 130 ⇨ Q1 = 13,5
+ Với P < 130, có 2 nhóm cùng mua hàng nên cầu tổng cộng là: Q = Q1 + Q2 = 78,5 – P/2 + 130 – P = 208,5 3P – /2 ⬄ P = 139 2Q – /3 - Hàm cầu tổng cộng:
⇨ Hàm doanh thu biên tổng cộng:
b, Khi bị cấm phân biệt giá thì hãng sẽ tối đa hóa lợi nhuận: πmax⬄M R=MC ⬄
Q* = 40, 2 ⇨ P* = 112,2 => Lúc này hãng sẽ bán trên cả 2 thị trường với Q1 = 22,4 và Q2 = 17,8
Lợi nhuận của hãng: π = 112,2*40,2 – 40,22 - 5*40, 2 – 1000 = 1693,4 c, MC = 2Q + 5 = 2(Q1+ Q2) +5
Nhóm 1: P1 = 157 - 2Q1 ⇨ MR1 = 157 – 4Q1 Nhóm 2: P2 = 130 Q – 2 ⇨ MR2 = 130 – 2Q2
Khi phân biệt giá hãng sẽ tối đa hóa lợi nhuận: πmax⬄M R1=MR2=MCn ⬄
Q = Q1 + Q2 = 40,2 Lợi nhuận của hãng lúc này:
π = 121,2*17,9 + 107,7*20,3 - 40,22 - 5*40, 2 – 1000 = 1754,15 d, Đồ thị: Câu 2:
Một hãng độc quyền bán hàng tại 2 thị trường tách biệt với hàm cầu tương ứng là
Nhóm 1: P1 = 24 - Q1 và P2 = 12 - 0,5Q2. Giả sử nhà độc quyền có chi phí bình quân không đổi là 6.
a, Nếu nhà độc quyền thực hiện phân biệt giá cấp 3 thì sản lượng, giá bán của mỗi thị trường là bao
nhiêu? Tính lợi nhuận tối đa của nhà độc quyền?
b, Tính phần mất không xã hội do nhà độc quyền gây ra khi phân biệt giá? 11
c, Nếu Chính phủ cấm phân biệt giá giữa 2 thị trường thì quyết định của nhà độc quyền là gì? Tính lợi
nhuận thu được trong trường hợp này?
d, Xác định phần mất không xã hội do nhà độc quyền gây ra cho xã hội ở câu c, Đáp án:
ATC = 6 ⇨ TC = 6Q ⇨ MC = 6
P1 = 24 - Q1 ⬄ Q1 = 24 – P1
P2 = 12 - 0,5Q2 ⬄ Q2 = 24 - 2P2
a, Nhóm 1: P1 = 24 - Q1 ⇨ MR1 = 24 - 2Q1
Nhóm 2: P2 = 12 - 0,5Q2 ⇨ MR2 = 12 - Q2
Nếu thực hiện phân biệt giá cấp 3, hãng sẽ tối đa hóa lợi nhuận: πmax ⬄ MR1 = MR2 = MC ⬄
Q = Q1 + Q2 = 15 π = 15*9 + 9*6 – 6*15 = 99
b, Phần mất không do độc quyền gây ra khi phân biệt giá là: DWL = SA1B1C1+ SA2B2C2= (15 6)
– (18 - 9)/2 + (9 – 6)(12 6) – /2 = 49,5 c, - Phân tích cầu:
+ Với P ≥ 12, chỉ có hãng 1 mua hàng nên hàm cầu tổng cộng là: Q = Q1 = 24 P – ⬄ P = 24 - Q + Với P = 12 ⇨ Q1 = 12
+ Với P < 12, có 2 nhóm cùng mua hàng nên cầu tổng cộng là: Q = Q1 + Q2 = 24 P – + 24 2P – = 48 – 3P ⬄ P = 16 Q – /3 - Hàm cầu tổng cộng:
⇨ Hàm doanh thu biên tổng cộng:
Nếu không thực hiện phân biệt giá, hãng sẽ tối đa hóa lợi nhuận: πmax ⬄ MR = MC ⬄ - Xét các trường hợp:
+ Q = 9 ⇨ P = 15 ⇨ π = 15*9 – 6*9 = 81 (1)
+ Q = 15 ⇨ P = 11 ⇨ π = 11*15 – 6*15 =75 (2)
Từ (1) và (2) ⇨ giá và sản lượng tối ưu là P* = 15 và Q* = 9
⇨ Hãng chỉ bán hàng cho nhóm 1, tức Q1 = 9 và Q2
= 0 Lúc này lợi nhuận của hãng là:
π = P*Q - TC = 15*9 - 6*9 = 81
d, Phần mất không do độc quyền gây ra khi không phân biệt giá là:
DWL = SAGCB = SAGEB + SGEC = (12 - 9)( 12 - 6 +15 - 6)/2 + (30 12) – (12 - 6)/2 = 76,5 12 Câu 3:
Một ngành sản xuất X bao gồm 2 doanh nghiệp hoạt động A và B với hàm chi phí cận biên như sau: MCA = 4QA + 30 MCB = 6QA + 50
Các hãng đều có chi phí cố định bằng 0.
Đường cầu về sản phẩm của ngành là Q = 150 – P
Trong đó Q tính bằng đơn vị sản phẩm, MC và P tính bằng USD/đơn vị sản phẩm.
a, Hãy xác định trạng thái cân bằng của thị trường theo mô hình Cournot
b, Lợi nhuận của mỗi doanh nghiệp là bao nhiêu?
c, Trạng thái cân bằng sẽ thay đổi như thế nào nếu doanh nghiệp A là người hành động trước?
d, Minh họa các kết quả tính toán trên. Đáp án:
Hàm cầu thị trường: Q = 150 – P ⬄ P = 150 – Q = 150 – QA – QB
MCA = 4QA + 30, FCA = 0 ⇨ TCA = 2QA2 + 30QA MCB = 6QB + 50, FCB = 0 ⇨ TCB = 3QB2 + 50QB a, - Xét doanh nghiệp A:
Doanh thu doanh nghiệp A: TRA = PQA = (150 – QA – QB)QA = 150QA - QA2 - QAQB
Lợi nhuận doanh nghiệp A: πA = TRA – TCA = 150QA - QA2 - QAQB - 2QA2 - 30QA = 120QA - 3QA2 - QAQB
Doanh nghiệp A tối đa hóa lợi nhuận: = 0 ⬄ 120 6Q – A Q – B = 0 ⬄ QA = (120 Q – B)/6 (1) - Xét doanh nghiệp B:
Doanh thu doanh nghiệp B: TRB = PQB = (150 – QA – QB)QB = 150QB Q – B2 - QAQB
Lợi nhuận doanh nghiệp B: πB = TRB – TCB = 150QB – QB2 - QAQB 3Q – B2 - 50QB = 100QB - 4QB2 - QAQB
Doanh nghiệp B tối đa hóa lợi nhuận: = 0 ⬄ 100 8Q – B – QA = 0 ⬄ QB = (100 Q – A)/8 (2)
Từ (1) và (2) ta sẽ có kết quả của cân bằng Cournot:
⇨ Q = 1340/47 ⇨ P = 5710/47 13
b, Lợi nhuận mỗi hãng là:
πA = 120*860/47 – 3*(860/47)2 –
860/47*480/47 = 1004,436 πB = 100*480/47 – 4*(480/47)2 – 860/47*480/47 = 417,202
c, Nếu doanh nghiệp A là người hành động trước
Thay (2) vào hàm lợi nhuận của A, ta có: πA = 120QA - 3QA2 - QA(100 Q – A)/8 = - 2,875QA2 + 107,5QA
Doanh nghiệp A tối đa hóa lợi nhuận:
= 0 ⬄ - 5,75QA + 107,5 = 0 ⇨ QA = 430/23 ⇨ QB = 935/92
⇨ Q = 2655/92 ⇨ P = 11145/92 d, Đồ thị: Câu 4:
Thị trường độc quyền tập đoàn gồm 2 hãng với hàm chi phí như sau: TC1 = 30Q1 và TC2 = 30Q2
Đường cầu về sản phẩm của thị trường là (D): Q = 150 – P
a, Viết phương trình đường phản ứng của mỗi hãng. Vẽ đồ thị minh họa
b, Ở cân bằng Cournot, sản lượng và lợi nhuận của mỗi hãng là bao nhiêu?
c, Nếu hãng 1 là người hành động trước, ở cân bằng Stackelberg sản lượng và lợi nhuận của mỗi hãng là bao nhiêu?
d, Cũng hỏi như câu c nhưng hãng 2 là người hành động trước. Đáp án
a, Hàm cầu thị trường: Q = 150 – P ⬄ P = 150 – Q = 150 – Q1 – Q2 - Hãng 1: Doanh thu TR1 = PQ1 = 150Q1 Q – 12 Q – 1Q2
Tổng chi phí: TC1 = 30Q1 Lợi nhuận: π1 = 120Q1 – Q12 Q
– 1Q2 π1max ⬄ π1′Q1= 0 ⬄ 120 2Q – 1 Q
– 2 = 0 ⬄ Q1 = 60 – 0,5Q2 (hàm phản ứng hãng 1) (1) - Hãng 2: Doanh thu: TR2 = PQ2 = 150Q2 Q – 22 Q – 1Q2 Tổng chi phí: TC2 = 30Q2
Lợi nhuận: π2 = 120Q2 – Q22 – Q1Q2 = 0 ⬄ 120 2Q – 2 – Q1 = 0 ⬄ Q2 = 60 0,5Q –
1 (hàm phản ứng hãng 2) (2)
b, Kết hợp (1) và (2) ta sẽ có kết quả của cân bằng Cournot: 14 ⇨ Q = 80 ⇨ P = 70
Lợi nhuận 2 hãng là: π1 = π2 = 70* 40 – 30*40 = 1600 c, Nếu hãng 1 là người hành động trước, thay (2)
vào hàm lợi nhuận hãng 1, ta có: π1 = 120Q1 – Q12 Q
– 1( 60 - 0,5Q1 ) = 60Q1 0,5Q – 12 π1max ⬄ π1′Q1= 0
⬄ 60 – Q1 = 0 ⬄ Q1 = 60 ⇨ Q2 = 60 0,5*60 = – 30 ⇨ Q = 90 ⇨ P = 60
Lúc này, lợi nhuận của mỗi hãng là:
π1 = 60*60 – 30*60 = 1800 π2 = 60*30 – 30*30 = 900
d, Nếu hãng 2 là người hành động trước, thay (1) vào
hàm lợi nhuận hãng 2, ta có:
π2 = 120Q2 – Q22 – Q2( 60 - 0,5Q2 ) = 60Q2 – 0,5Q22
= 0 ⬄ 60 – Q2 = 0 ⬄ Q2 = 60 ⇨ Q1 = 60 0,5*60 = – 30 ⇨ Q = 90 ⇨ P = 60
Lúc này, lợi nhuận của mỗi hãng là: π1 = 60*30 – 30*30 = 900 π2 = 60*60 – 30*60 = 1800 Câu 5:
Trên 1 thị trường có 2 hãng có hàm chi phí tương ứng là:
TC1 = 10 + 5Q1 + Q12 và TC2 = 5 + Q2 + Q22
Hàm cầu về sản phẩm của cả thị trường được cho bởi P = 100 – Q (trong đó P tính bằng nghìn đồng và Q tính bằng nghìn chiếc).
a. Giả sử 2 hãng hoạt động theo mô hình Cournot, xác định hàm phản ứng của mỗi hãng.
b. Xác định giá thị trường, sản lượng và lợi nhuận của mỗi hãng
c. Nếu 2 hãng cấu kết thành 1 cartel thì giá, sản lượng và lợi nhuận của mỗi hãng là bao nhiêu?
d. Minh họa kết quả trên đồ thị. Đáp án:
a, Ta có hàm cầu về thị trường ghế là: P = 100 – Q = 100 – Q1 –Q2
- Xét hành vi của hãng 1:
+ Doanh thu: TR1 = P*Q1 = (100 Q – 1 Q – 2) Q1 = 100Q1 Q – 12 Q – 2Q1
+ Chi phí: TC1 = 10 + 5Q1 + Q12
⇨ Lợi nhuận: π1 = 95Q1 2Q – 12 Q – 2Q1 - 10 = 0 ⬄ 95 4Q – 1 Q – 2 = 0 ⬄ Q1 = (95 Q
– 2)/4 (hàm phản ứng của hãng 1)(1)
- Xét hành vi của hãng 2
+ Doanh thu: TR2 = P*Q2 = (100 Q – 1 Q – 2) Q2 = 100Q2 Q – 22 Q – 2Q1 15
+ Chi phí: TC2 = 5 + Q2 + Q22
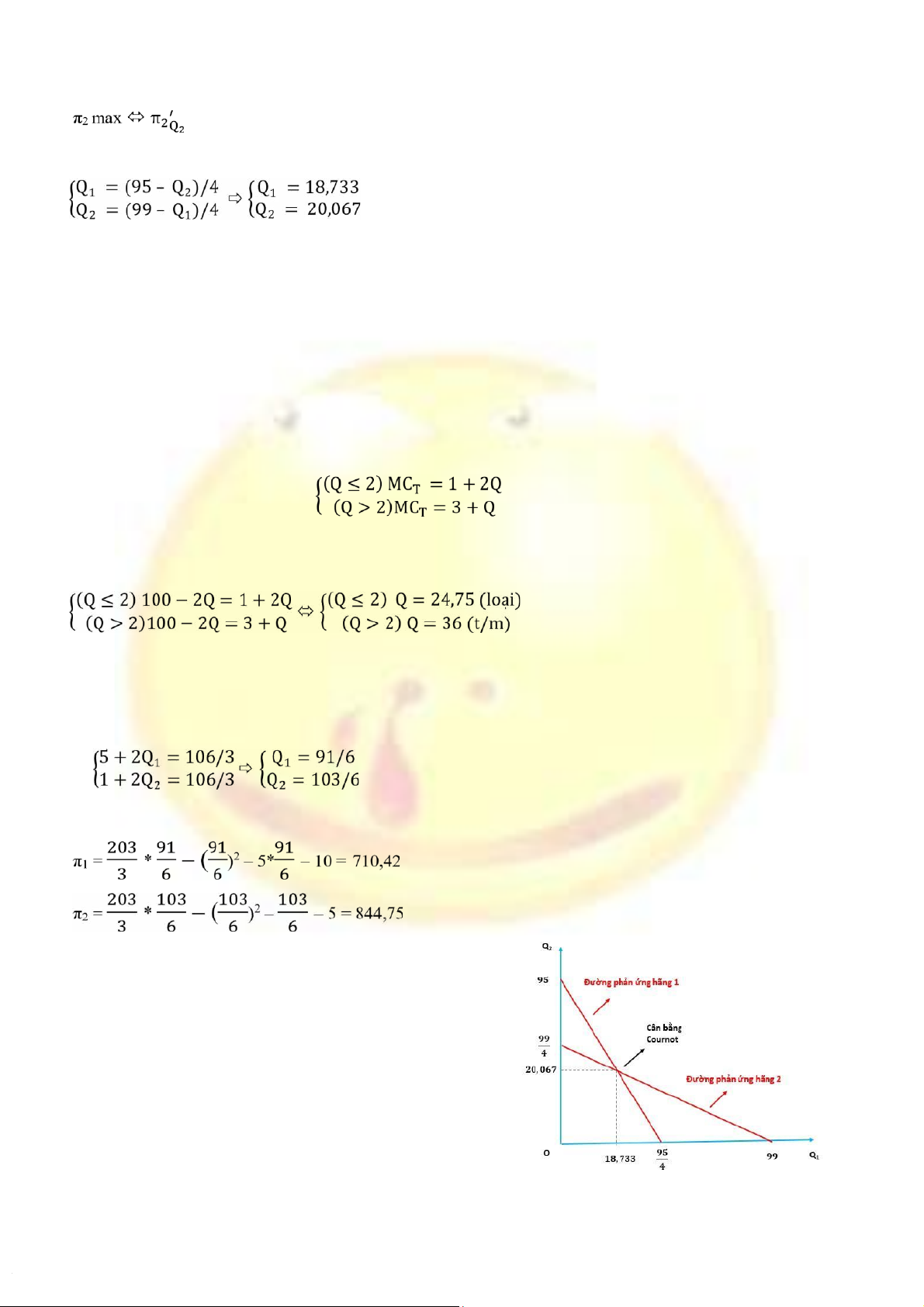
⇨ Lợi nhuận: π2 = 99Q2 2Q – 22 Q – 2Q1 – 5 = 0 ⬄ 99 4Q – 2 Q – 1 = 0 ⬄ Q2 = (99 Q
– 1)/4 (hàm phản ứng của hãng 2)(2)
b, Từ (1) và (2) ⇨ Cân bằng Cournot: ⇨ Q = 38,8 ⇨ P=61,2
Khi đó, lợi nhuận mỗi hãng là:
π1 = 61,2*18,733 - 18,7332 – – 5*18,733 10 = 691,869
π2 = 61,2*20,067 – 20,0672 – – 20,067 5 = 800,349
c, TC1 = 10 + 5Q1 + Q12 ⇨ MC1 = 5 + 2Q1 ⇨ Q1 = (MC 5) – /2
TC2 = 5 + Q2 + Q22 ⇨ MC2 = 1 + 2Q2 ⇨ Q2 = (MC – 1)/2 - Khi 2 hãng cấu kết thành 1 Cartel:
+ Với MC ≤ 5, chỉ có hãng 2 sản xuất, Q = Q2 = (MC 1) – /2 ⇨ MCT = 1 + 2Q
+ Với MC = 5, hãng 2 đã sản xuất được Q2 = 2
+ Với MC > 5, có cả 2 hãng cùng tham gia sản xuất nên Q = Q1 + Q2 = MC – 3 ⇨ MCT = 3 + Q
- Hàm chi phí biên của Cartel là:
- Hàm cầu của Cartel: P = 100 – Q ⇨ Doanh thu biên của Cartel: MR = 100 – 2Q
Cartel tối đa hóa lợi nhuận khi MR = MC ⬄ Q* = 97/3 ⇨ P* = 203/3 Q* = 97/3 ⇨ MCT* = 106/3
Hai hãng sẽ phân chia sản lượng theo nguyên tắc MC1 = MC2 = MCT* = 106/3 ⬄
Khi đó, lợi nhuận mỗi hãng là: d, Đồ thị:
- Khi 2 hãng phản ứng theo mô hình Cournot: 16
- Khi 2 hãng cấu kết thành Cartel: Câu 6:
Một hãng độc quyền sản xuất ở hai nhà máy với các chi phí tương ứng là: TC1 = 100Q1 + Q12 TC2 = 60Q2 + Q22
Đường cầu về sản phẩm của hãng độc quyền được cho bởi: Q = 800 – P
a, Viết phương trình đường chi phí cận biên tổng của hãng độc quyền
b, Xác định mức sản lượng và giá bán để hãng độc quyền tối đa hóa lợi nhuận
c, Hãng độc quyền này sẽ phân chia cho mỗi nhà máy sản xuất bao nhiêu sản phẩm để tối thiểu hóa tổng
chi phí sản xuất ở mức sản lượng trong câu b?
d, Minh họa các kết quả trên một đồ thị. Đáp án:
TC1 = 100Q1 + Q12 ⇨ MC1 = 100 + 2Q1 ⇨ Q1 = (MC - 100)/2
TC2 = 60Q2 + Q22 ⇨ MC2 = 60 + 2Q2 ⇨ Q1 = (MC - 60)/2
Hàm cầu của nhà độc quyền Q = 800 – P ⬄ P = 800 – Q
⇨ Doanh thu biên của nhà độc quyền: MR = 800 – 2Q
a, Phân tích hoạt động của nhà độc quyền:
+ Với chi phí MC ≤ 100, chỉ có nhá máy 2 sản xuất, lúc này
Q = Q2 = (MC - 60)/2 nên chi phí biên của hãng độc quyền là
MCT = 60 + 2Q + Tại MC = 100 thì Q2 = 20
+ Với MC > 100 thì có cả 2 nhà máy cùng sản xuất: Q = Q1 + Q2 = MC
– 80 nên chi phí biên của hãng độc quyền là MCT = Q + 80
Vậy ta có thể viết gọn hàm chi phí biên của nhà độc quyền là:
b, Nhà độc quyền tối đa hóa lợi nhuận khi MR = MCT ⬄
Vậy sản lượng tối ưu là Q* = 240 ⇨ Giá tối ưu P* = 560
Lúc này chi phí phiên tại sản lượng tối ưu MCT(Q*) = 320
c, Nhà độc quyền phân chia sản lượng cho các nhà máy theo nguyên tắc tối thiểu hóa tổng chi phí
nên MC1 = MC2 = MCT(Q*) = 320 ⬄ d, Đồ thị: 17 Câu 7:
Một thị trường gồm 2 hãng với chi phí tương ứng là:
TC1 = 12 + 0,1Q12 và TC2 = 6 + 0,1Q22.
Cầu về sản phẩm của thị trường là P = 18 – 0,1Q
Trong đó giá và chi phí tính bằng triệu đồng/đơn vị, sản lượng tính bằng nghìn đơn vị.
a. Nếu 2 hãng cấu kết với nhau để hình thành 1 cartel, thì cartel sẽ quyết định mức giá và sản lượng tối đa
hóa lợi nhuận là bao nhiêu?
b. Để tối thiểu hóa tổng chi phí cho mức sản lượng trên, cartel sẽ phân chia sản lượng cho mỗi thành viên
là bao nhiêu sản phẩm. Xác định lợi nhuận của mỗi thành viên.
c. Nếu không có sự cấu kết giữa các hãng và hãng 1 là người quyết định sản lượng trước, khi đó sản
lượng, giá bán sản phẩm và lợi nhuận của mỗi thành viên là bao nhiêu?
d. Vẽ đồ thị minh họa các kết quả trên. Đáp án:
a. TC1 = 12 + 0,1Q12 ⇨ MC1 = 0,2Q1 ⇨ Q1 = 5MC
TC2 = 6 + 0,1Q22 ⇨ MC2 = 0,2Q2 ⇨ Q2 = 5MC
Q = Q1 + Q2 = 10MC ⇨ Chi phí biên của Cartel là MCT = 0,1Q
Hàm cầu của Cartel: P = 18 – 0,1Q
⇨ Doanh thu biên của Cartel: MR = 18 – 0,2Q
Cartel tối đa hóa lợi nhuận khi MR = MCT
⬄ 18 − 0,2Q = 0,1Q ⇨ Q* = 60 ⇨ P* = 12
Vậy sản lượng tối ưu là Q* = 60 ⇨ Giá tối ưu P* = 12
Lúc này chi phí phiên tại sản lượng tối ưu MCT(Q*) = 6
b. Cartel quyền phân chia sản lượng cho các hãng theo nguyên tắc tối thiểu hóa tổng chi phí: MC1 = MC2 = MCT(Q*) ⬄
Lợi nhuận của mỗi nhà máy là: π1 = 12*30 – 0,1*302 - 12 = 258 π2 = 12*30 0,1*30 – 2 - 6 = 264
c. Hàm cầu thị trường: P = 18 - 0,1Q = 18 – 0,1(Q1 + Q2)
Nếu không có sự cấu kết giữa các hãng và hãng 1 là người quyết định sản lượng trước, khi đó hãng
2 vẫn phản ứng như mô hình Cournot còn hãng 1 dựa trên hàm phản ứng của hãng 2 để tối đa hóa lợi
nhuận cho mình. Xét hành vi của hãng 2:
- Doanh thu: TR2 = PQ2 = 18Q2 – 0,1Q22 0,1Q – 1Q2 18 - Chi phí: TC2 = 6 + 0,1Q22
⇨ Lợi nhuận: π2 = 18Q2 0,2Q – 22 0,1Q – 1Q2 - 6 = 0 ⬄ 18 – 0,4Q2 0,1Q – 1 = 0 ⬄ Q2 = 45 0,25Q –
1 (hàm phản ứng hãng 2) Xét hành vi của hãng 1:
- Doanh thu: TR2 = PQ2 = 18Q2 – 0,1Q12 0,1Q – 1Q2 - Chi phí: TC1 = 12 + 0,1Q22
⇨ Lợi nhuận: π1 = 18Q1 0,2Q – 12 0,1Q – 1Q2 12 –
Thay hàm phản ứng của hãng 2 vào hàm lợi nhuận hãng 1 ta có:
π1 = 18Q1 – 0,2Q12 – 0,1Q1(45 0,25Q – 1) – 12 = 13,5Q1 0,175Q – 12 12 –
π1max ⬄ π1′Q1= 0 ⬄ 13,5 – 0,35Q1 = 0 ⇨ Q1 = 38,57 ⇨ Q2 = 35,36 ⇨ Q = 73,93 ⇨ P = 10,61 d, Đồ thị:
- Khi 2 hãng cấu kết thành Cartel:
- Khi 2 hãng hoạt động theo mô hình Stackelberg với hãng 1 quyết định sản lượng trước: Câu 8:
Thị trường sản phẩm X bao gồm 2 doanh nghiệp với giả định sản phẩm của 2 doanh nghiệp là hoàn toàn
giống nhau. Đường cầu thị trường sản phẩm được cho bởi: DTT: P = 200 – Q
Trong đó P là giá bán sản phẩm (USD/1 đơn vị sản phẩm) và Q là tổng số lượng sản phẩm của 2 doanh nghiệp A và B cung ứng.
Chi phí của 2 doanh nghiệp này là:
MCA = 55 + 2QA, FCA = 500 MCB = 20 + 2QB, FCB = 200
Để tránh sự cạnh tranh, 2 doanh nghiệp cấu kết hình thành 1 cartel. 19
a. Hãy xác định mức giá bán và sản lượng tối ưu của cartel.
b. Sản lượng của mỗi doanh nghiệp là bao nhiêu để tối thiểu hóa tổng chi phí cho cả cartel?
c. Nếu không có sự cấu kết, 2 doanh nghiệp hoạt động theo mô hình Cournot thì mức giá và sản lượng
của mỗi doanh nghiệp là bao nhiêu?
d. Minh họa các kết quả bằng đồ thị. Đáp án:
Hàm cầu thị trường P = 200 – Q = 200 – QA – QB
MCA = 55 + 2QA, FCA = 500 ⇨ TCA = QA2 + 55QA + 500
MCB = 20 + 2QB, FCB = 200 ⇨ TCB = QB2 + 20QB + 200
MCA = 55 + 2QA ⇨ QA = (MC – 55)/2 MCB = 20 + 2QB ⇨ QB = (MC – 20)/2 a, Khi 2 hãng cấu kết thành 1 Cartel:
+ Với MC ≤ 55, chỉ có hãng B sản xuất, Q = QB = (MC 20) – /2 ⇨ MCT = 20 + 2Q
+ Với MC = 55, hãng 2 đã sản xuất được Q2 = 17,5
+ Với MC > 55, có cả 2 hãng cùng tham gia sản xuất nên Q = QA + QB = MC – 37,5 ⇨ MCT = 37,5 + Q
- Hàm chi phí biên của Cartel là:
- Hàm cầu của Cartel: P = 200 – Q ⇨ Doanh thu biên của Cartel: MR = 200 – 2Q
Cartel tối đa hóa lợi nhuận khi MR = MC ⬄ ⬄
Q* = 325/6 ⇨ P* = 875/6 Q* = 325/6 ⇨ MCT* = 275/3
b, Cartel tối thiểu hóa tổng chi phí khi MCA = MCB = MCT* = 275/3 ⬄ c, - Xét doanh nghiệp A:
Doanh thu doanh nghiệp A: TRA = PQA = (200 – QA – QB)QA = 200 QA - QA2 - QAQB
Lợi nhuận doanh nghiệp A: πA = TRA – TCA = 200QA - QA2 - QAQB - QA2 - 55QA 500 = – 145QA - 2QA2 - QAQB – 500 (*)
Doanh nghiệp A tối đa hóa lợi nhuận: = 0 ⬄ 145 4Q – A Q – B = 0 ⬄ QA = (145 Q
– B)/4 (hàm phản ứng doanh nghiệp A) (1) - Xét doanh nghiệp B:
Doanh thu doanh nghiệp B: TRA = PQB = (200 – QA – QB)QB = 200 QA – QB2 - QAQB
Lợi nhuận doanh nghiệp B: πB = TRB – TCB = 200QB – QB2 - QAQB – QB2 - 20QAB 200 = – 180QA - 2QB2 - QAQB - 200
Doanh nghiệp B tối đa hóa lợi nhuận: = 0 ⬄ 180 4Q – B – QA = 0 ⬄ QB = (180 Q
– A)/4 (hàm phản ứng doanh nghiệp B) (2)
Nếu hành vi của các doanh nghiệp tuân theo mô hình Cournot, cân bằng thị trường xảy ra khi 2 doanh
nghiệp đồng thời. Kết hợp (1) và (2) ta sẽ có kết quả của cân bằng Cournot: 20