Đề Cương Ôn Thi Giữa HK2 Toán 8 CTST 2025-2026

ĐỀ CƯƠNG ÔN TẬP GIỮA HỌC KÌ 2- TOÁN 8 I. TRẮC NGHIỆM:
Câu 1. Công thức biểu diễn số tiền phải trả y khi mua 26 quyển vở, giá của một quyển vở là x đồng là 26 26
A. y = 26x
B. x = 26 y C. y = D. x = x y
Câu 2. Cho hai đường thẳng y = 5
− x + 5 và y = 5x +10 . Hai đường thẳng đã cho: A. song song B. cắt nhau C. trùng nhau D. vuông góc
Câu 3. Đường thẳng y = 3x + 2 song song với đường thẳng nào dưới đây?
A. y = 6x − 3 B. y = 3 − x + 2
C. y = 3x + 4 D. y = 3 − x + 6
Câu 4. Hai đường thẳng y = −5x + 3 và y = 5x + 6 có đồ thị sẽ: A. cắt nhau B. song song C. trùng nhau D. vuông góc
Câu 5. Đường thẳng y = x −1 có hệ số góc là A. 1 B. 0 C. 1 − D. Đáp án khác
Câu 6. Cho hàm số y = f (x) = 2x + 3 . Tính f (0) ? A. 5 B. 3 C. −4 D. 3 −
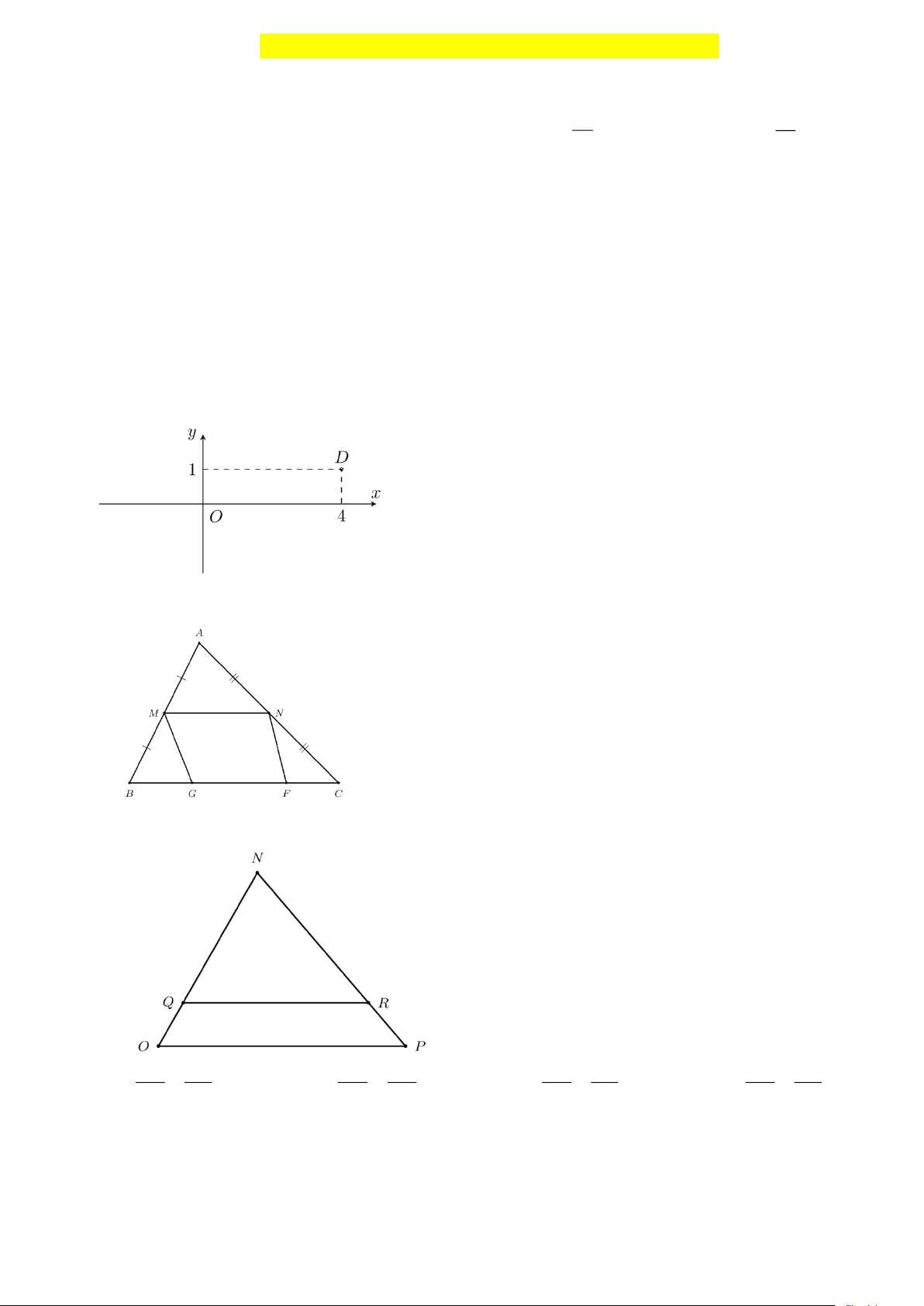
Câu 7. Trong hình bên, tọa độ của điểm D là A. (0; ) 1 B. (1;4) C. (4;0) D. (4; ) 1
Câu 8. Cho hình vẽ. Đoạn thẳng nào dưới đây là đường trung bình của ABC ? A. MN B. MG C. GF D. NF
Câu 9. Cho NOP có QR//OP với Q  NO , R  NP (như hình vẽ). Theo định lí Thales ta có NQ NR NQ OQ NQ NR NQ PR A. = B. = C. = D. = NO NP NO NP NO RP NO NP
Câu 10. Cho ABC có E , F lần lượt là trung điểm của AB , AC . Biết BC = 6cm . Tính độ dài đoạn thẳng EF ?
A. EF = 12cm
B. EF = 6cm
C. EF = 1.5cm D. EF = 3cm Trang 1
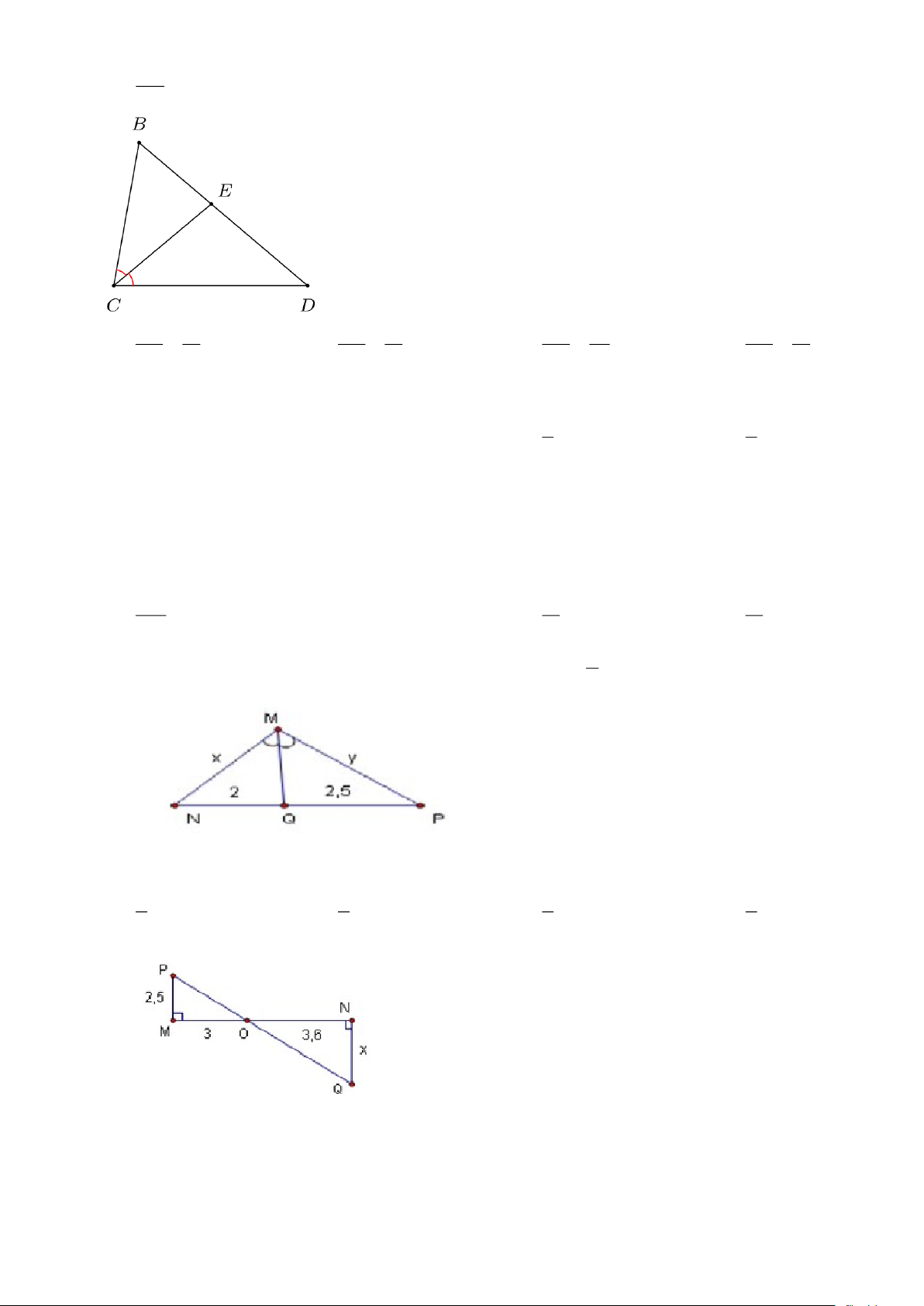
Câu 11. Cho BCD có CE là tia phân giác của BCD với E  BD . Giả sử CB = 13cm ; CD = 15cm . EB Khi đó =? ED EB 15 EB 13 EB 13 EB 13 A. = B. = C. = D. = ED 13 ED 11 ED 28 ED 15
Câu 12. Nếu tam giác IJK đồng dạng với tam giác LMN theo tỉ số đồng dạng là 2 thì tam giác
LMN đồng dạng với tam giác IJK với tỉ số: 1 1 A. 2 B. 4 C. D. 4 2
Câu 13. Nếu ABC và DEF có A = 80 ;  C = 60 ;  E = 40 ;
 F = 80 . Thì khi đó ta có:
A. ABC dồng dạng với FED
B. ACB đồng dạng với FED
C. ABC đồng dạng với DEF
D. ABC đồng dạng với DFE
Câu 14. ABC đồng dạng với DEF theo tỉ số đồng dạng k , DEF dồng dạng với MNP theo 1
tỉ số đồng dạng k .MNP dồng dạng với ABC theo tỉ số đồng dạng nào? 2 1 k k A. B. k k C. 1 D. 2 k k 1 2 k k 1 2 2 1 x
Câu 15. Trong hình biết MQ là tia phân giác NMP . Tỷ số là: y 5 5 2 4 A. B. C. D. 2 4 5 5
Câu 16. Độ dài x trong hình bên là: A. 2,5 B. 3 C. 2,9 D. 3,2
Câu 17. Cho ABC có A = 60 ,
 AB = 4cm, AC = 6cm;MNP có N = 60 ;
 NM = 3cm , NP = 2cm .
Cách viết nào dưới đây đúng ? Trang 2
A. ABC ~ MNP
B. ABC ~ NMP
C. BAC ~ PNM
D. BAC ~ MNP
Câu 18. Tam giác ABC và MNP có AB = 4, BC = 5, AC = 6, MN = 8, NP = 12 , MP = 10 . Trong
các cách viết sau thì cách viết đúng là :
A. MPN ~ ABC .
B. MPN ∽ ACB .
C. MNP ∽ BAC .
D. MNP ∽ CBA .
Câu 19. Cho tam giác ABC đồng dạng với tam giác 
A BC . Biết AB = 3 
A B . Kết quả nào sau đây là sai 1 AC  A C AB AC BC
A. A = A ; B = B B. 
A C = AC C. = = 3 D. = = 3 BC  B C  A  B  A C  B C II. TỰ LUẬN Hàm số và đồ thị
1. Tính giá trị của hàm số
a) Cho hàm số y = f(x) = 2x +1
Tính f(-1); f(0); f(1); f(2023)
b) Cho hàm số y = f(x) = x -2023
Tính f(-2); f(0); f(2); f(2024)
c) Cho hàm số y = f(x) = 3x -2023
Tính f(-2); f(0); f(1); f(2022) 2. Vẽ đồ thì hàm số: a) y = 2x b) y = 3x 1 x c) y = 2 d) y = 2x - 1 e) y = 3x + 2 1 x f) y = 2 -2
3. Cho hàm số bậc nhất: y = ax + 2 ( a  0 ) (d1)
a. Tìm a để đồ thị hàm số y = ax + 2 ( a  0 ) song song với đồ thị hàm số y = 2x.
b. Vẽ đồ thị hàm số ( d ) với a vừa tìm được. 1
c. Cho hàm số y = (2m + 3)x – 5 (d2). Tìm m để d2 song song với d1.
4. Cho hàm số bậc nhất: y = ax + b ( a  0 ) (d)
a. Tìm a;b để đồ thị hàm số y = ax + b ( a  0 ) song song với đồ thị hàm số
y = -2x và đi qua điểm A(2; 1).
b. Vẽ đồ thị hàm số (d) với a;b vừa tìm được.
c. Cho hàm số y = (2m -1)x +3 (d’). Tìm m để d cắt d’.
5. Cho hàm số bậc nhất: y = ax + b ( a  0 ) (d)
a. Tìm a;b để đồ thị hàm số y = ax + b ( a  0 ) song song với đồ thị hàm số y = 3x và đi qua điểm M(1; 1).
b. Vẽ đồ thị hàm số (d) với a;b vừa tìm được.
c. Cho hàm số y = 2mx - 3 (d1). Tìm m để: 1) d song song với d1 2) d cắt d1 HÌNH HỌC
Bài 1. Cho tứ giác ABCD có AC và BD cắt nhau tại O. Qua O, kẻ đường thẳng song
song với BC cắt AB tại E, kẻ đường thẳng song song với CD cắt AD tại F. Trang 3 a. Chứng minh EF // BD
b. Từ O kẻ đường thẳng song song với AB cắt BC tại G và đường thẳng song song với
AD cắt CD tại H. Chứng minh rằng: CG. DH = BG. CH
Bài 2. Cho ABC vuông tại A có AB = 3cm, AC = 4cm , đường phân giác góc A cắt BC tại D. a) Tính BC,BD,DC
b) Vẽ đường cao AH. Tính AH, HD và AD.
Bài 3. Cho ABC có trung tuyến AM. Đường phân giác của góc AMB cắt AB tại D
và đường phân giác của góc AMC cắt AC tại E. Chứng minh: DE //BC
Bài 4. Cho ABC có trung tuyến AM. Đường phân giác của góc AMB cắt AB tại D
và đường phân giác của góc AMC cắt AC tại E. Biết MA = 5 cm, MB = 3 cm. a) Tính tỉ số DA và DB. b) Chứng minh: DE //BC
Bài 5. Cho ABC có trung tuyến AM. Đường phân giác của góc AMB cắt AB tại D
và đường phân giác của góc AMC cắt AC tại E. Biết MA = 5 cm, MB = 3 cm. a) Tính tỉ số DA và DB. b) Chứng minh: DE //BC
c) Gọi I là trung điểm của DE. Chứng minh: I,M,A thẳng hàng.
Bài 6. Cho tứ giác ABCD có AC và BD cắt nhau tại O. Qua O, kẻ đường thẳng song
song với BC cắt AB tại E, kẻ đường thẳng song song với CD cắt AD tại F. AE AO = a) EB OC b) Chứng minh EF // BD
c) Từ O kẻ đường thẳng song song với AB cắt BC tại G và đường thẳng song song với
AD cắt CD tại H. Chứng minh rằng: CG. DH = BG. CH
Bài 7. Cho tứ giác ABCD có AC và BD cắt nhau tại O. Qua O, kẻ đường thẳng song
song với BC cắt AB tại E, kẻ đường thẳng song song với CD cắt AD tại F. AF AO = a. FD OC b. Chứng minh EF // BD
c. Từ O kẻ đường thẳng song song với AB cắt BC tại G và đường thẳng song song với
AD cắt CD tại H. Chứng minh rằng: CG. DH = BG. CH
HÌNH HỌC NỘI DUNG THỰC TẾ
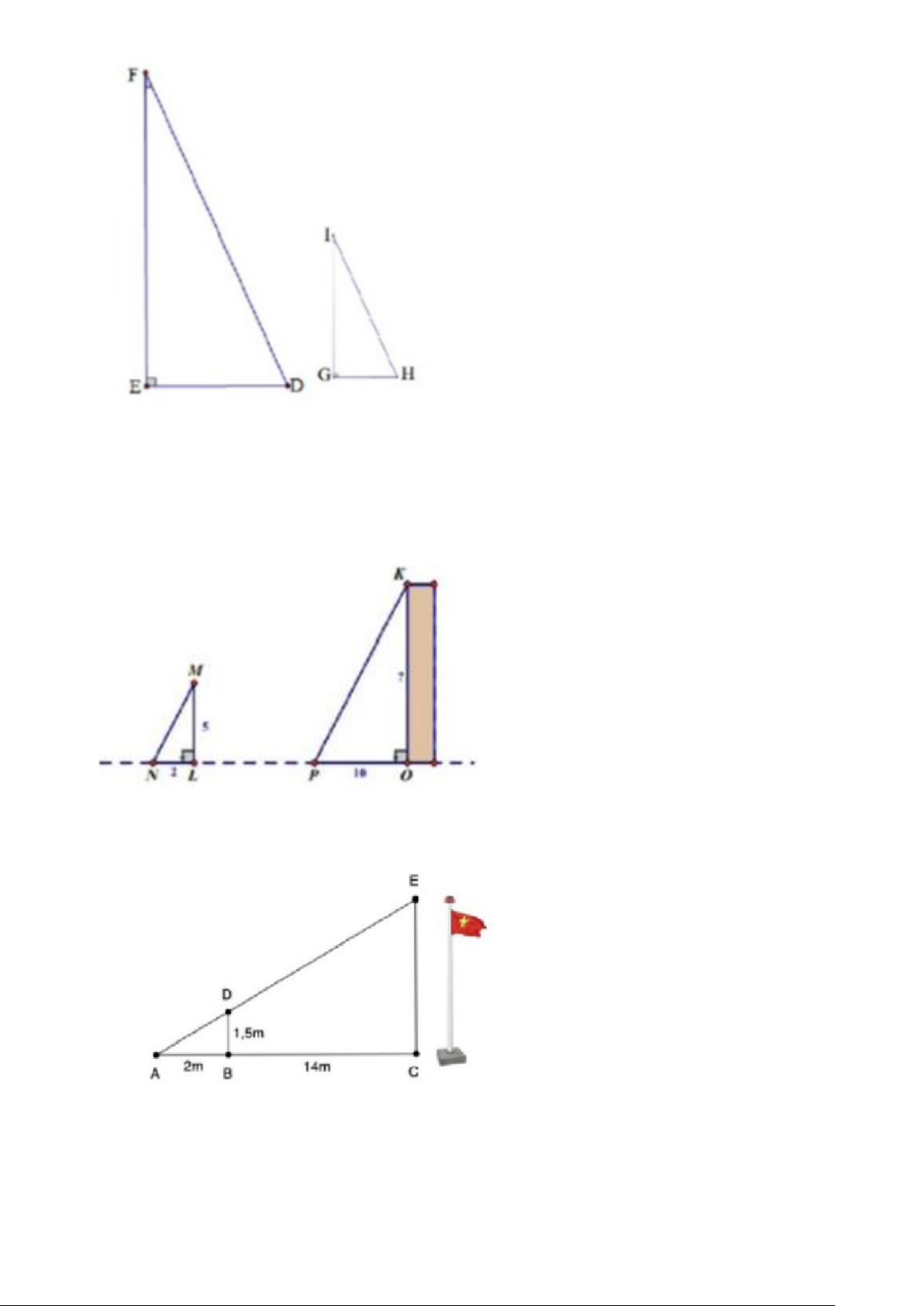
Bài 1. Để tính chiều cao cột cờ Hà Nội (không tính trụ treo cờ), một nhóm bạn lớp 8 đã
làm như sau: Vào 11 giờ trưa các bạn đo chiều dài bóng cột cờ và chiều dài bóng của một
bạn cao 1,76m đứng cạnh cột cờ. Kết quả đo được lần lượt là 3m và 0,16m . Tính chiều cao cột cờ. Trang 4
Hình vẽ chỉ mang tính chất minh họa.
Chiều cao cột cờ EF ; Bóng cột cờ ED = 3m ;
Chiều cao bạn đứng cạnh cột cờ IG =1,76m ; Bóng của bạn đó GH = 0,16m .
Bài 2. Bóng của một tòa nhà trên mặt đất dài 10m . Cùng thời điểm này, một cây cột điện
cao 5m có bóng trên mặt đất dài 2m . Hãy tính chiều cao của tòa nhà.
Bài 3. Để xác định chiều cao cột cờ người ta cắm cọc BD sao cho bóng AB của cọc trùng
lên bóng AC của cột cờ rồi đo các khoảng cách BC, AB . Biết BC =14m ;
AB = 2m; BD = 1,5m (hình vẽ). Tính chiều cao của cột cờ (đoạn CE ).
Bài 4. Một người cao 1,6m đứng cách một gốc cây 4,75m . Bóng của người đó trên mặt
đất dài 1,25m và trùng với bóng của cây (Hình vẽ). Hỏi cây cao bao nhiêu mét? (làm tròn đển hàng đon vị). Trang 5
Bài 5. Một nhà toán học muốn ước lượng chiều rộng của một cái hồ. Ông ta đánh dấu 5
điểm gần hồ và dùng kỹ thuật đo đạc để có được các số liệu như hình vẽ bên (tính theo đơn vị mét).
Biết QR / /ST , hỏi chiều rộng của hồ (đoạn PQ ) là bao nhiêu mét? Giải thích.
PHẦN 3. MỞ RộNG VÀ NÂNG CAO Bài 1. Cho biểu thức 2 2
P = x + y với x , y là hai số thực thay đổi nhưng luôn thỏa mãn
x + y + xy = 15. Tìm giá trị nhỏ nhất của biểu thức P .
Bài 2: Tìm giá trị nhỏ nhất của các biểu thức: a) A= 2 4x + 4x +11
(x − )1(x + 2)(x +3)(x + 6) b) B= 2 2
c) C= x − 2x + y − 4y + 8
Bài 3: Cho x+y = 1. Tìm GTNN của biểu thức M = 3 3 x + y
Bài 4: Tìm GTLN và GTNN của: 4x + 3 y = 2 x +1 Hết
Chúc các em làm bài tốt! Trang 6