Đề cương ôn thi môn Toán HK1 khối 12 năm học 2017 – 2018 trường THPT Thạnh Đông – Kiên Giang

Đề cương ôn thi môn Toán HK1 khối 12 năm học 2017 – 2018 trường THPT Thạnh Đông – Kiên Giang được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

105 53 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

38 trang 5 tháng trước

Tác giả:

Profile Mai Nguyệt
 Trang 1/38
ĐỀ CƯƠNG ÔN THI MÔN TOÁN HK I – KHỐI 12
NĂM HỌC 2017 -2018
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT THẠNH ĐÔNG
Câu 1 : Đồ thị được cho trong hình
vẽ bên là đồ thị của hàm số nào trong
các hàm số sau ?
A. .
B. .
C.
D. .
ĐỀ THI THỬ HỌC KÌ I NĂM HỌC 2017 - 2018
Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Biên soạn: Thầy Đỗ Thanh Trường)
Câu 2: Hàm số nào sau đây đồng biến trên R
A. B.
C. D.
Câu 3: Hàm số có bao nhiêu điểm cực trị?
A. Có 1 điểm cực trị B. Có 2 điểm cực trị
C. Không có cực trị D. Có 3 điểm cực trị
Câu 4 : Cho hàm số liên tục trên khoảng , có bảng biến thiên như hình vẽ bên. Khẳng
định nào sau đây là sai ?
A.Không có B.
C. D.
Câu 5: Tìm tiệm cận ngang của đồ thị hàm số (C):
A. B. C. D. Không có tiệm cận ngang.
Câu 6: Cho đồ thị hàm số (C) (với m là tham số thực).Khẳng định nào sau đây là đúng ?
A. Đồ thị (C) có tiệm cận ngang
B. Đồ thị (C) không có tiệm cận
C. Đồ thị (C) có tiệm cận đứng
D. Đồ thị (C) có tiệm cận đứng và tiệm cận ngang .
Câu 7: Cho hàm số . Khẳng định nào sau đây là sai?
A. đồng biến trên khoảng B. đồng biến trên khoảng
C. nghịch biến trên khoảng
D. nghịch biến trên khoảng
Câu 8: Tìm điểm cực tiểu của hàm số
A. B. C. D.
Câu 9: Cho đồ thị hàm số : . Khẳng định nào sau đây đúng?
A. Đường thẳng là tiệm cận ngang của đồ thị
32
3
y
xx
3
31yx x
32
31yx x
3
3yx x
tanyx x
42
23yx x
cos 2yx x
3
5yx x
2
33
2
xx
y
x

yf
x
3; 2

3;2
min y
C§
y
0

3;2
max 0y
2
CT
y 
2
23yx x x
1y  1y
yx
2
1
23
x
x
y
x

32
() 2 3 12 5yfx x x x
()
x
1;1
()
f
x
0; 2
()
x
;3
()
x
1; 
32
33yx x
3x 2x 1x  0x
C
31
21
x
y
x
3y 
C
ĐỀ THI THỬ 01
(Đề thi có 5 trang)
 Trang 2/38
B. Đường thẳng là tiệm cận đứng của đồ thị
C. Đường thẳng là tiệm cận đứng của đồ thị
D. Đường thẳng là tiệm cận ngang của đồ thị
Câu 10: Cho đồ thị hàm số : . Tiếp tuyến của đồ thị song song với đường thẳng
là đường thẳng nào trong các đường thẳng sau?
A. B. C. D.
Câu 11: Đồ thị hàm số cắt trục hoành tại bao nhiêu điểm?
A. Đồ thị không cắt trục hoành B.Chỉ 1 điểm
C. 2 điểm phân biệt D.3 điểm phân biệt
Câu 12: Tìm giá trị nhỏ nhất của hàm số trên đoạn
A. B. C. D.
Câu 13 : Tìm giá trị thực của tham số m để đồ thị hàm số
42
:1
m
Cyxmxm
cắt trục hoành tại 4
điểm phân biệt.
A. B.Không có m C. D.
Câu 14: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có hai đường
tiệm cận đứng.
A. Mọi B. C. D.
Câu 15: Cho hàm số
32
21 7.ymx m x mx
Có bao nhiêu giá trị nguyên của tham số để hàm
số nghịch biến trên .
A.Không có giá trị nào B.2 C.1 D.Vô số giá trị
Câu 16: Đặt Khi đó bằng
A. B. C. D.
Câu 17: Tập xác định của hàm số là
A. B. C. D.
Câu 18: Số nghiệm của phương trình
A.2 nghiệm B. 3 nghiệm C. 1 nghiệm D. Vô nghiệm
Câu 19: Đạo hàm của hàm số trên tập xác định là
A. B. C. D.
Câu 20: Tìm khoảng đồng biến của hàm số trên tập số thực?
A. B. C. D.
Câu 21:Nghiệm của phương trình
A. B. C. D.
3
2
x
C
1
2
x
C
1
2
y 
C
C
3
21
x
y
x

C
5410xy
10 8 17 0xy 10 8 19 0xy 10 8 21 0xy 10 8 23 0xy
3
8yx x
24yx x

2; 4

2;4
3
min
2
y

2;4
3
min
2
y

2;4
min 2y

2;4
min 2y
1
2
m
m
1m 2m

2
1
:
m
x
Cy
x
xm

m
1
4
2
m
m

1
4
2
m
m

2m
m
2
log 20
20
log 5
3
1
2
4
1
3
(1 )yx

(;1] \{1}R

;1
1; 
2
275
21
xx
2
sin x
y
e
2
cos
x
e
2
sin
sin .cos
x
exx
2
sin
sin 2
x
ex
2
sin
2sin
x
ex
2
1x
y
e
(0; ) (1;1)
; 
(;1]
1
57
2
(1, 5)
3
x
x



3x 1
x
4x 2x
 Trang 3/38
Câu 22: Rút gọn biểu thức Với a ,b là số dương
A. B. C. D.
Câu 23:Tập nghiệm của phương trình
A. B. C. D.
Câu 24:
Tìm tất cả các giá trị thực của tham số để hàm số có tập xác định
A. B. C. D. hoặc
Câu 25: Tọa độ giao điểm của đồ thị hàm số và đường thẳng là:
A. B. C. D
Câu 26: Cho . Hãy biểu diễn theo a
A. B.
C. D.
Câu 27:
Cho số thực dương a, rút gọn biểu thức
A. B. C. D.
Câu 28:
Nghiệm của bất phương trình
A. B. C. D.
Câu 29:
Nghiệm của bất phương trình là:
A. B. C. D.
Câu 30: Tập nghiệm của bất phương trình là:
A. B. C. D.
Câu 31:
Tìm nguyên hàm
A. B. C. D. .
Câu 32: Hàm số là nguyên hàm của hàm số nào?
A. B. C. D.
Câu 33: Tìm nguyên hàm ?
A. B.
C. D.
Câu 34: Tìm nguyên hàm
A. B. C. D.

1
2
4Pab ab





2Pa b
 2Pa b

P
ab

Pa b

22
32.67.40
xxx

1;S 
1; 0S 
0;S 
;1S 
m

2
ln 2 4yxmx
D
22m 2m 22m 2m 2m 
3
x
y
1
3
y
1
1;
3



1
1;
3




1
1;
3



1
1;
3



2
log 5 a
4
log 1250

4
1
log 1250 1 4
2
a

4
1
log 1250 1 4
2
a
4
log 1250 2 1 4a
4
log 1250 2 1 4a
1
3
.
P
aa
7
5
Pa
5
7
Pa
5
6
Pa
6
5
Pa
2
log 3 2 0
x

3
log 2 1
x

2x 01
x
 1
x

2
3
1
8, 4 1
x
x
4x 3x 2x 1
x
1
1
1
2
16
x
x



; 

2; 
;0
0; 
2
x
edx
4
x
IeC 2
x
IeC 3
x
IeC
4
x
IeC

sin8
216
x
x
y 
sin8
8
x
y
2
sin 4yx
cos8
8
x
y
2
cos 4yx
2
dx
I
x
xx x

2
IC
xx

2
1
IC
x

2
1
IC
xx


2
1
IC
x

5x
Idx
x
5lnIx xC
2
5
Ix C
x

5lnIx xC
2
5
Ix C
x

 Trang 4/38
Câu 25: Tìm nguyên hàm
A. B. C. D.
Câu 36: Tính thể tích V của khối lập phương cạnh bằng 2
A. B. C. D.
Câu 37: Cho khối chóp có đáy là hình vuông cạnh a ,mặt bên SAB là tam giác cân tại S và
nằm trong mặt phẳng vuông góc với đáy .Biết rằng góc giữa và mặt đáy bằng .Tính thể tích
V của khối chóp
A. B. C. D.
Câu 38: Gọi n là số mặt phẳng đối xứng của hình lập phương. Tìm n.
A. B. C. D.
Câu 39: Cho hình chóp có đáy là tam giác vuông tại , , ,cạnh bên
vuông góc với đáy, đường thẳng tạo với đáy một góc . Tính thể tích của khối chóp
.
A. B. C. D.
Câu 40 : Cho hình chóp có , , . Tính thể tích V
của khối chóp .
A. B. C. D.
Câu 41 : Cho hình chóp có đáy là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy.
Biết rằng, mặt phẳng tạo với mặt phẳng đáy một góc . Tính thể tích V của khối chóp .
A. B. C. D.
Câu 42: Cho tứ diện có các tam giác là các tam
giác vuông tại A Tính khoảng cách d từ A đến mp
A. B. C. D.
Câu 43: Người ta cắt miếng bìa hình tam giác đều
cạnh bằng 1 như hình vẽ bên và gấp theo các đường
kẻ sau đó dán các mép lại để được hình tứ diện đều .
Tính thể tích V của hình tứ diện tạo thành
A. B.
C. D.
Câu 44: Cho lăng trụ đứng có đáy là tam giác đều cạnh a, .Một khối trụ có
hai đáy là hai hình tròn lần lượt nội tiếp tam giác và tam giác .Tính thể tích của khối trụ
đó.
A. B.
C.
D.
Câu 45 : Cho hình chóp tứ giác đều có , mặt bên tạo với đáy một góc . Một khối
nón có đỉnh S, đáy là hình tròn ngoại tiếp hình vuông . Tính thể tích V của khối nón đã cho
2
tanIxdx
cotIx xC cotIxxC tanIx xC tanIxxC
4
V 8V
8
3
V
4
3
V
.SABCD
SCD
0
60
.SABCD
3
15
6
a
V
3
3
6
a
V
3
3
3
a
V
3
15
3
a
V
9n 7n 8n 6n
.
SABC
A
BC
B
A
Ba
5
A
Ca
SA SB
0
60 V
.SABC
3
15
6
a
V
3
3
3
a
V
3
15
3
a
V
3
3Va
.S ABC SA SB SC a
0
60ASB CSB
0
90ASC
.SABC
3
2
12
a
V
3
2
4
a
V
3
6
3
a
V
3
3
12
a
V
.SABC
A
BC
SBC
0
60 .SABC
3
3
4
a
V
3
4
a
V
3
3
8
a
V
3
3
24
a
V
A
BCD
,2,3AB a AC a AD a
,,
A
BC ACD ABD
()
B
CD
6
3
a
d
30
5
a
d
3
2
a
d
66
11
a
V
2
96
V
3
16
V
3
32
V
2
12
V
.''C'
A
BC A B
A
BC AA ' 2a
A
BC '''
A
BC V
3
2
3
a
V
3
18
a
V
3
2
9
a
V
3
6
a
V
.S ABCD
A
Ba
0
45
A
BCD
 Trang 5/38
A. B. C. D.
Câu 46: Cho khối chóp có đáy là tam giác vuông tại B,cạnh bên SA vuông góc với đáy
Khi quay các cạnh của hình chóp quanh trục AB .Hỏi có bao nhiêu hình nón được tạo thành
A. Hai hình nón B. Một hình nón
C. Ba hình nón D. Không có hình nón nào?
Caâu 47. Cho tứ diện SABC có
2SA a
và
SA ABC
. Tam giác ABC có
,2, 5
A
BaBC aCAa
.
Diện tích mặt cầu ngoại tiếp tứ diện SABC là
A.
2
16 a
B.
2
27 a
C.
2
36 a
D.
2
9 a
Caâu 48. Một khối cầu có chu vi đường tròn lớn là
2
thì diện tích của mặt cầu đó là
A. 16
B. 8
C. 4
D.
8
3
Caâu 49. Hình khai triển mặt xung quanh của hình trụ là một hình chữ nhật có diện tích bằng 48 R
, biết
đường cao của hình trụ bằng 4. Bán kính đáy của hình trụ bằng
A.
6R
B.
4
R
C.
12
R
D.
3R
Caâu 50. Một khối trụ có bán kính đáy
5
R
cm
, khoảng cách giữa hai đáy bằng 4. Cắt khối trụ bởi mặt
phẳng song song với trục và cách trục 4 cm. Diện tích thiết diện được tạo thành là
A.
2
20 cm
B.
2
24 cm
C.
2
12 cm
D.
2
10 cm
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C D B C A C D B C B D D A B A C C A C A B D C A C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A C A B D A D B C D B C A B A C D A D D A D C B B
3
2
12
a
V
3
3
a
V
3
2
3
a
V
3
12
a
V
.SABC
A
BC
.SABC
 Trang 6/38
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT THẠNH ĐÔNG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 -2018
Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Biên soạn: Thầy Bùi sang Thọ)
Câu 1. Đường cong trong hình bên dưới là đồ thị của một hàm
số
trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D
dư
ới
đây. Hỏi hàm số đó là hàm số nào
?
A.
3
31yx x
.
B.
3
3yx x. C.
3
3yx x . D.
42
1yx x
.
Câu 2. Giá trị nhỏ nhất của hàm số
3
35yx x trên đoạn
2; 4
là:
A.

2; 4
min 3y . B.

2; 4
min 7y . C.

2; 4
min 5.y D.

2; 4
min 0.y
Câu 3. Gọi
M
,
n
lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số
2
33
2
xx
y
x

. Khi đó giá trị
của biểu thức
2
2
M
n
bằng
A. 7. B. 9. C. 8. D. 6.
Câu 4. Tiếp tuyến của đồ thị hàm số
32
32yx x có hệ số góc
3k 
có phương trình là
A.
37yx
. B.
37yx
. C.
31yx
. D.
31yx
.
Câu 5. Biết đồ thị hàm số
3
31yx x
có hai điểm cực trị
A
,
B
. Khi đó phương trình đường thẳng
A
B là
A.
21.yx
B.
2.yx
C.
2yx
. D.
21yx
.
Câu 6. Cho hàm số
32
yax bx cxd. Hỏi hàm số luôn đồng biến trên khi nào?
A.
2
0, 0
0; 3 0
ab c
abac


. B.
2
0
0; 3 0
abc
abac


.
C.
2
0, 0
0; 3 0
ab c
abac


. D.
2
0, 0
0; 3 0
ab c
abac


.
Câu 7. Cho hàm số
21
1
x
y
x
có đồ thị
C
và đường thẳng
:23dy x
. Đường thằng
d
cắt
()C
tại hai điểm
A
và
B
. Khoảng cách giữa
A
và
B
là
A.
25
5
AB
. B.
5
2
AB
. C.
55
.
2
AB
D.
2
.
5
AB
Câu 8. Giả sử hàm số
42
yax bx c có đồ thị là hình bên dưới.
O
x
y
1
1
2
2
ĐỀ THI THỬ 02
(Đề thi có 5 trang)
 Trang 7/38
Khẳng định nào sau đây là khẳng định đúng?
A.
0, 0, 1abc
. B.
0, 0, 1abc
.
C.
0, 0, 1abc
. D.
0, 0, 0abc
.
Câu 9. Xác định
a
,
b
,
c
để hàm số
1ax
y
bx c
có đồ thị như hình vẽ bên. Chọn đáp án đúng?
A.
2, 1, 1.abc
B.
2, 1, 1.abc
C.
2, 2, 1.abc
D.
2, 1, 1.ab c
Câu 10. Cho hàm số
yfx
có bảng biến thiên dưới đây
Hàm số
yfx
có bảng biến thiên trên là hàm số nào dưới đây
A.

1
1
y
xx
. B.

1.yxx
C.
1
x
y
x
. D.
1
x
y
x
.
Câu 11. Đồ thị hàm số
23
1
x
y
x
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là
A.
2x
và
1y
. B.
1
x
và
3y 
. C.
1x 
và
2y
. D.
1
x
và
2y
.
Câu 12. Đồ thị hàm số
32
31yx x
cắt đường thẳng
ym
tại ba điểm phân biệt thì tất cả các giá trị
tham số
m
thỏa mãn là
A. 1 .m B. 31 .m C. 31 .m D. 3.m 
Câu 13. Cho hàm số
32
25yx x x có đồ thị

C
. Trong các tiếp tuyến của

C
, tiếp tuyến có hệ
số góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là
A.
4
3
. B.
5
3
. C.
2
3
. D.
1
3
.
Câu 14. Hàm số

2sin sin2
f
xxx
trên đoạn
3
0;
2



có giá trị lớn nhất là
,
M
giá trị nhỏ nhất là
.m
Khi đó
.
M
m
bằng
x

1
0

y
y
1


0
1
O
x
y
2
1
O
x
y
1 1
1
 Trang 8/38
A. 33 . B. 33. C.
33
4
. D.
33
4
.
Câu 15. Cho hàm số
32
2312yx mx m x
có đồ thị
C
. Đường thẳng
:2dy x
cắt đồ thị
C
tại ba điểm phân biệt
0; 2A
,
B
và C . Với

3;1M
, giá trị của tham số
m
để tam giác
M
BC
có diện tích bằng 26 là
A. 1.m  B. 1m  hoặc 4.m C. 4.m D. Không tồn tại
.m
Câu 16. Hàm số

1
3
21fx x có tập xác định là
A.
1
;
2




. B.
1
;.
2



C.
1
;2 .
2



D.
1
\
2



.
Câu 17. Mệnh đề nào dưới đây sai?
A.
2017 2018
21 21
. B.
2019 2018
22
11
22





.
C.

2018 2017
31 31
. D.
21 3
22
.
Câu 18. Với các số thực
,, 0abc
và
,1ab
bất kì. Mệnh đề nào dưới đây sai?
A.
log . log log
aaa
bc b c
. B.
log log
c
a
a
bc b
.
C. log .log log
ab a
bc c . D.
1
log
log
a
b
b
a
.
Câu 19. Tính
2
log 2016S theo
a
và
b
biết
2
log 7 a ,
3
log 7 b .
A.
25abab
S
b

. B.
25baab
S
a

.
C.
52abab
S
b

. D.
25abab
S
a

.
Câu 20. Tìm tất cả các giá trị thực của
m
để hàm số
2
2
log 4
y
xxm
xác định trên .
A.
4m
. B.
4m
. C.
4m
. D.
4m
.
Câu 21. Cho
a
,
b
là các số thực dương thỏa
2
5
b
a
. Tính
6
2a 4
b
K 
A.
226K
. B.
246K
. C. 242K . D.
202K
.
Câu 22. Đạo hàm của hàm số 2 .3
x
x
y là:
A.
2ln2 3ln3
xx
. B.
ln 6x
.
C.
2ln2.3ln3
xx
.
D.
6ln6
x
.
Câu 23. Đạo hàm hàm số
2
8
log 3 4yxx
là
A.

2
23
34
x
xx

B.

2
1
34ln8xx
C.

2
23
34ln8
x
xx

D.

2
23
34ln2
x
xx

Câu 24. Nếu
1
log log 9 log 5 log 2
2
a aaa
x 
(
0a
;
1a
) thì
x
bằng:
A.
2
5
. B.
3
5
. C.
6
5
. D.
3
.
 Trang 9/38
Câu 25. Giải bất phương trình
2
1
2
log 2 8 4xx
A.
6
4
x
x

B.
6
4
x
x

C.
64
24
x
x


D.
64
24
x
x


Câu 26. Giải phương trình:
2(1 )
16 8
x
x
:
A. 3x  B. 2x C. 3x D. 2x 
Câu 27. Bất phương trình.
(
)
(
)
11
22
log 3 2 log 6 5
x
x-< -
có tập nghiệm là
A.
(1, )+¥
B.
6
1,
5
æö
÷
ç
÷
ç
÷
ç
èø
C.
26
,
35
æö
÷
ç
÷
ç
÷
ç
èø
D. Æ
Câu 28. Hàm số
2
() ln
f
xx x
đạt cực trị tại điểm
A.
x
e
. B.
x
e
. C.
1
x
e
. D.
1
x
e
.
Câu 29.
Một người gửi tiết kiệm với lãi suất
8, 4%
năm và lãi hàng năm được nhập vào vốn, hỏi sau
bao nhiêu tháng ngưòi đó thu được gấp đôi số tiền ban đầu (lấy giá trị quy tròn) ?
A.
96
. B.
97
. C.
98
. D.
99
.
Câu 30.
Tìm
m
để phương trình
92.32
xx
m
có nghiệm
1; 2x 
A.
165m
. B.
13
45
9
m
. C.
145m
. D.
13
65
9
m
.
Câu 31. Nguyên hàm
Fx
của hàm số
sin
f
xx x
thỏa mãn
019F
là
A.
2
cos
2
x
x
. B.
2
cos 2
2
x
x
. C.
2
cos 20
2
x
x
. D.
2
cos 20
2
x
x
Câu 32. Nguyên hàm của hàm số
2
3
() 2
f
xx x
x

là
A.
3
3
4
3ln
33
x
x
xC. B.
3
3
4
3ln
33
x
x
x .
C.
3
3
4
3ln
33
x
x
xC. D.
3
3
4
3ln
33
x
x
xC.
Câu 33.
Hàm số
F
x
nào dưới đây là nguyên hàm của hàm số
3
1yx
?
A.
 
4
3
3
1
8
Fx x C
. B.
 
4
3
4
1
3
Fx x C
.
C.
 
3
3
11
4
Fx x x C
. D.
 
3
4
3
1
4
Fx x C
.
Câu 34. Hàm số nào dưới đây là một nguyên hàm của hàm số
sin cos
2.2 cos sin
xx
yxx
?
A.
sin cos
2
xx
yC

.
B.
sin cos
2.2
ln 2
x
x
y . C.
sin cos
ln 2.2
x
x
y
.
D.
sin cos
2
ln 2
xx
yC
 .
 Trang 10/38
Câu 35. Trong các mệnh đề sau, tìm mệnh đề sai?
A.
ddkf x x k f x x

. B.
ddd
f
xgxx fxx gxx 


.
C.
 
3
2
d
3
fx
f
xf x x C

. D.
.d d. d
f
x
g
xx
f
xx
g
xx



.
Câu 36.
Cho hình chóp tứ giác
.SABCD
có đáy là vuông; mặt bên
SAB
là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm
A
đến mặt phẳng
SCD
bằng
37
7
a
. Tính thể tích V của khối chóp .S ABCD .
A.
3
1
3
Va
. B.
3
Va
. C.
3
2
3
Va
. D.
3
3
2
a
V
.
Câu 37. Thể tích của chóp tam giác đều có tất cả các cạnh đều bằng
a
là
A.
3
2
4
a
. B.
3
2
2
a
. C.
3
2
6
a
. D.
3
2
12
a
.
Câu 38. Cho hình chóp
.SABC
. Gọi
M
,
N
lần lượt là trung điểm của
SA
,
SB
. Tính tỉ số
.
.
SABC
SMNC
V
V
.
A.
4
. B.
1
2
C.
2
. D.
1
4
Câu 39. Hình bát diện đều thuộc loại khối đa diện đều nào sau đây?
A.
5;3
B.
4;3
C.
3; 3
D.
3; 4
Câu 40. Cho hình lăng trụ đứng .
A
BC A B C

, biết đáy
A
BC là tam giác đều cạnh
a
. Khoảng cách từ
tâm
O
của tam giác
A
BC
đến mặt phẳng

ABC
bằng
6
a
. Tính thể tích khối lăng trụ
.
A
BC A B C

.
A.
3
32
8
a
. B.
3
32
28
a
. C.
3
32
4
a
. D.
3
32
16
a
.
Câu 41. Cho hình chóp
.S ABCD
có đáy
A
BCD
là hình vuông cạnh
2a
, cạnh
SB
vuông góc với đáy
và mặt phẳng
SAD
tạo với đáy một góc
60
. Tính thể tích khối chóp
.SABCD
.
A.
3
33
4
a
V
. B.
3
33
8
a
V
. C.
3
83
3
a
V
. D.
3
43
3
a
V
.
Câu 42. Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
A.
3
. B.
4
. C.
6
. D.
5
.
Câu 43. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
2a
là
A.
3
4a
B.
3
3
4
a
C.
3
23a D.
3
3
12
a
Câu 44. Hình nón có góc ở đỉnh bằng
0
60
, độ dài đường sinh bằng
a
. Khi đó, diện tích xung quanh của
hình nón là
A.
2
2
ap
B.
2
2
4
a
C.
22
24
aap
+
D.
22
44
aap
+
Câu 45. Trong không gian cho tam giác
A
BC
vuông tại
A
với
3, 4
A
CaABa
.Tính độ dài đường
sinh
l
của hình nón nhận được khi quay tam giác
A
BC
quanh trục
.
A
C
 Trang 11/38
A. 7a . B.
a
. C.
7a
. D. 5a .
Câu 46.
Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có
cạnh bằng
3a
Diện tích toàn phần của khối trụ là:
A.
2
9a
. B.
2
27
2
a
. C.
2
9
2
a
. D.
2
13
6
a
.
Câu 47. Thiết diện qua trục của hình nón tròn xoay là một tam giác đều có cạnh bằng
a
. Thể tích của
khối nón bằng:
A.
3
3
8
a
. B.
3
23
9
a
. C.
3
3
24
a
. D.
3
3 a
.
Câu 48. Cho hình chữ nhật
A
BCD
biết 1AB ,
3AD
. Khi quay hình chữ nhật
A
BCD
xung quanh
trục
AB thì cạnh
CD
tạo nên hình trụ tròn xoay. Thể tích của khối trụ là
A.
3
. B.
3
. C.
. D.
3
3
.
Câu 49. Cho hình chóp
.SABC
, có
SA
vuông góc mặt phẳng
()
A
BC
; tam giác
A
BC
vuông tại
B
. Biết
2SA a ,
A
Ba ,
3
B
Ca
. Khi đó bán kính
R
của mặt cầu ngoại tiếp hình chóp là
A. 22a . B. 2a . C. 2a . D.
a
.
Câu 50.
Cho hình chóp .S ABCD có đáy
A
BCD là hình chữ nhật, =
A
Ba,
3=
A
Da
; SA vuông góc
với mặt phẳng đáy,
4=SA a
. Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
.SABCD
.
A.
2=Ra
. B.
5=
R
a
. C.
3=
R
a
. D.
=Ra
.
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C B A D A C C A A D D C B A B A C B A B B D C C A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C B D D A D D C B D D D A D D C B C A D B C A B B

Trang 12/38
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT THẠNH ĐÔNG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 -2018
Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Biên soạn: Cô Nguyễn Thị Nghĩa)
Câu 1: Cho
K
là một khoảng và hàm số

yfx
có đạo hàm trên
.K
Khẳng định nào sau đây
là sai?
A. Nếu

'0,fx xK
thì hàm số là hàm hằng trên
K
B. Nếu

'0,fx xK
thì hàm số đồng biến trên K
C. Nếu

'0,fx xK
thì hàm số đồng biến trên K
D. Nếu

'0,fx xK
thì hàm số nghịch biến trên
K
Câu 2: Cho hàm số
.yx
Khẳng định nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng

0; 
B. Hàm số đã cho đồng biến trên
C. Hàm số đã cho nghịch biến trên
D. Hàm số đã cho là hàm hằng trên khoảng

;0
Câu 3: Giá trị lớn nhất của hàm số
2
x
y
trên đoạn

1; 2
là
A.
4.
B.
1
.
2
C.
1.
D.
2.
Câu 4: Tìm tiệm cận đứng của đồ thị hàm số

52
:.
3
x
Cy
x
A.
2
3
x 
B.
5x
C.
2.x
D.
3.x
Câu 5: Cho đồ thị hàm số

3
:33Cyx x
. Khẳng định nào sau đây là sai ?
A. Đồ thị

C
nhận điểm

0;3I
làm tâm đối xứng.
B. Đồ thị

C
cắt trục
Ox
tại 2 điểm phân biệt.
C. Đồ thị

C
tiếp xúc với đường thẳng
5.y
D. Đồ thị

C
cắt trục
Oy
tại 1 điểm.
Câu 6: Cho hàm số

yfx
liên tục trên nửa khoảng
1; 2 ,
có bảng biến thiên như hình vẽ
bên.
Khẳng định nào sau đây là đúng?
A. Không tồn tại giá trị nhỏ nhất của hàm số trên
1; 2 .
B. Hàm số nghịch biến trên khoảng

1; 2 .
C.
1;2
maxy .

D. Đường thẳng
2x
là tiệm cận đứng của đồ thị hàm số

.yfx
ĐỀ THI THỬ 03
(Đề thi có 5 trang)

Trang 13/38
Câu 7: Cho hàm số
32
391yx x x
xác định trên
.
Bảng biến thiên của hàm số là bảng nào
trong các bảng biến thiên cho dưới đây?
Câu 8: Hàm số
3
2
yx
có bao nhiêu điểm cực trị?
A. Không có cực trị B. Có 1 điểm cực trị
C. Có 2 điểm cực trị D. Có vô số điểm cực trị
Câu 9: Xét
,
xy
là các số thực không âm thỏa mãn điều kiện
2.
xy
Tìm giá trị nhỏ nhất của
biểu thức
22
4Sxy xy
A.
min 3S 
B.
min 4S 
C .
min 0S
D.
min 1S
Câu 10: Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
23yx mx x
nhận điểm
1x
là điểm cực đại.
A. Không tồn tại
m
B. Có vô số
m
C. 6m D.
5
2
m
Câu 11: Biết rằng đồ thị hàm số

21
:
2
x
Cy
x
luôn cắt đường thẳng
:
dy x m
tại hai điểm
phân biệt
,.
AB
Tìm các giá trị thực của tham số
m
sao cho độ dài đoạn thẳng
AB
ngắn nhất.
A.
1m B.
23m
C. 4m D. 0m
Câu 12: Tìm tất cả các giá trị thực của tham số
m
để phương trình
32
3
xxm
có ba nghiệm
phân biệt.
A.
2m
B.
04m
C.
0m
D.
4m
Câu 13: Cho hàm số

yfx
liên tục trên
và có bảng biến thiên như hình vẽ bên. Khẳng định
nào sau đây là sai?
A.

fx
đồng biến trên khoảng

1; 3 .
C.

fx
nghịch biến trên khoảng

;1.
B. B.

fx
nghịch biến trên khoảng

3; .
D.

fx
đồng biến trên khoảng

0;6 .
Câu 14: Cho đồ thị hàm số

42
:.Cyx x
Khẳng định nào sau đây là sai?
A. Đồ thị

C
cắt trục Ox tại 3 điểm phân biệt.
B. Đồ thị

C
cắt trục
Oy
tại 2 điểm phân biệt.
 Trang 14/38
C. Đồ thị
C tiếp xúc với trục Ox .
D. Đồ thị
C
nhận trục
Oy
làm trục đối xứng.
Câu 15: Tìm giá trị lớn nhất của hàm số
23sin3 4cos3yxx
trên
.
A.
max 7y
B.
max 5y
C.
max 9y
D.
max 3y
Câu 16: Rút gọn biểu thức
21
2
1
..Pa
a



A.
5
P
a
B.
P
a
C.
7
P
a
D.
9
P
a
Câu 17: Nghiệm của phương trình
log 9
10 8 5x
là:
A.
5
8
x
B.
1
2
x
C.
7
4
x
D.
0x
Câu 18: Đạo hàm của hàm số
log 2sin 1yx trên tập xác định là:
A.
2cos
'
2sin 1
x
y
x
B .
2cos
'
2sin 1
x
y
x
C.

2cos
'
2sin 1 ln10
x
y
x
D.

2cos
'
2sin 1 ln10
x
y
x
Câu 19: Giá trị nhỏ nhất của hàm số
2
x
y trên đoạn
1; 1 .
A.
2
B.
1
C.
1
2
D.
4
Câu 20: Đặt
3
log 15 .m
Hãy biểu diễn
25
log 15
theo
.m
A.
25
log 15
1
m
m
B.

25
log 15
21
m
m
C.
25
log 15
1
m
m
D.

25
log 15
21
m
m
Câu 21: Một người gửi tiết kiệm với lãi suất
7,5%
một năm và lãi hàng năm được nhập vào vốn.
Hỏi sau bao nhiêu năm người đó thu được số tiền gấp đôi số tiền ban đầu?
A.
4 năm B.
6
năm C.
10
năm D.
8
năm
Câu 22: Cho
,
x
y
là các số thực dương thỏa mãn
22
9ln 4ln 12ln .ln .
x
yxy
Đẳng thức nào sau
đây là đúng?
A.
23
x
y
B.
32
x
y
C.
32
x
y
D.
x
y
Câu 23: Số nghiệm của phương trình

2
33
log 4log 3 7 0xx
là:
A.
1 B. 2 C. 3 D. 0
Câu 24: Tập nghiệm của bất phương trình
21
32.310
xx

trên tập số thực là:
;0
B.
0; 
C.
1; 
D.
;1
Câu 25:Cho phương trình
12
215.280
xx

, khẳng định nào sau dây đúng?
A. Có một nghiệm. B. Vô nghiệm.
C. Có hai nghiệm dương. D. Có hai nghiệm âm.
Câu 26: Phương trình
1
525 6
xx

có tích các nghiệm là :
 Trang 15/38
A.
5
121
log
2




. B.
5
121
log
2




. C. 5. D.
5
121
5log
2




.
Câu 27:Phương trình

743 2 3 6
xx

có nghiệm là:
A.
1
x
B.
2
log 3x
. C.
2
log 2 3x 
. D.

23
log 2x
.
Câu 28:Điều kiện xác định của phươg trình
2
log( 6) log( 2) 4xx x x là
A.
3x
B.
2x 
C.
\[ 2;3]
D.
2x
Câu 29: Phương trình
3
log (3 2) 3x có nghiệm là:
A.
11
3
x
B.
29
3
x
C.
25
3
x
D. 87x
Câu 30: Phương trình
2
22
log ( 1) 6log 1 2 0xx có tập nghiệm là:
A.
3;15 B.
1; 3 C.
1; 2 D.
1; 5
Câu 31:Nguyên hàm của hàm số

3
32fx x x là hàm số nào trong các hàm số sau?
A.

42
3
2
42
xx
Fx x C
 . B.

4
2
32
3
x
Fx x x C
 .
C.

42
2
42
xx
Fx x C
. D.

2
33Fx x x C
.
Câu 32:Hàm số
32
5 4 7 120Fx x x x C
là họ nguyên hàm của hàm số nào sau đây?
A.
2
547fx x x
B..
2
15 8 7fx x x
C.

232
547
432
x
xx
fx

. D.
2
547fx x x
.
Câu 33: Họ nguyên hàm của hàm số:
2
1
3yx x
x

là
A.

3
2
3
ln
32

x
Fx x x C
. B.

3
2
3
ln
32

x
Fx x x C
C.

3
2
3
ln
32

x
Fx x x C
. D.

2
1
23
F
xx C
x
.
Câu 34:Tìm nguyên hàm của hàm số
() sin2
f
xx
A.
1
sin 2 cos 2
2
x
dx x C
. B.
1
sin 2 cos 2
2
x
dx x C
.
C.
sin 2 cos 2
x
dx x C
. D.
sin 2 cos2
x
dx x C
.
Câu 35:Tìm nguyên hàm của hàm số
() cos3
6
fx x




.
A.
1
() sin3
36
f
xdx x C




. B.
(). sin3
6
f
xdx x C




.

Trang 16/38
C.
1
() sin3
36
fxdx x C




. D.
1
() sin3
66
fxdx x C




.
Câu 36: Hình nào dưới đây không phải là hình đa diện?
Câu 37: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
,
a
cạnh bên
SA
vuông góc với
đáy và
3.SA a
Tính thể tích
V
của khối chóp
..SABC
A.
3
2
a
V
B.
3
4
a
V
C.
3
3
4
a
V
D.
3
3
2
a
V
Câu 38: Cho hình lăng trụ đứng
.'' 'ABC A B C
có
0
1, 2, 120 .AB AC BAC
Giả sử
D
là trung
điểm của cạnh
'CC
và
0
'90.BDA
Tính thể tích
V
của khối lăng trụ
.'' '.ABC A B C
A.
15
.
2
V
B.
315.V
C.
15.V
D.
215.V
Câu 39: Cho đa diện

H
có tất cả các mặt đều là tam giác. Khẳng định nào sau đây là đúng?
A. Tổng số các mặt của

H
là một số chẵn
B. Tổng số các mặt của

H
luôn gấp đôi tổng số các đỉnh của

H
C. Tổng số các cạnh của

H
là một số không chia hết cho
3
D. Tổng số các cạnh của

H
luôn gấp đôi tổng số các mặt của

H
Câu 40: Cho hình chóp đều
.S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a
cạnh bên tạo với đáy
một góc
0
60 .
Tính diện tích toàn phần
tp
S
của hình chóp
..SABCD
A.
2
7
tp
Sa
B.

2
17
tp
Sa
C.

2
47
4
tp
a
S
D.
2
7
4
tp
a
S
Câu 41: Cho khối lập phương có độ dài đường chéo bằng
23.m
Tìm thể tích
V
của khối lập
phương đó.
A.
3
24 3m
B.
3
12
m
C
3
27
m
D.
3
8
m
Câu 42: Cho tứ diện
ABCD
có 2, 3,AD BC 4,BD 2 5, 5.AB AC CD Tính thể tích
V
của tứ diện
.ABCD
A.
15
2
V
B.
15
3
V
C.
15V
D.
315V
Câu 43: Tính thể tích
V
của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát
diện đều cạnh
.a
A.
3
8
27
a
V
B.
3
27
a
V
C.
3
16 2
27
a
V
D.
3
22
27
a
V
 Trang 17/38
Câu 44: Trong không gian, cho tam giác
A
BC là tam giác đều cạnh
,a
gọi
H
là trung điểm của
cạnh
.BC
Tính độ dài đường sinh
l
của hình nón nhận được khi quay tam giác
A
BC
xung quanh
trục
.
A
H
A.
3
2
a
l
B.
2
a
l
C.la D.2la
Câu 45: Cho mặt cầu

S có tâm
I
và bán kính 3.R Mặt phẳng
P
cắt mặt cầu theo giao
tuyến là đường tròn
C
có chu vi
2.
Tính khoảng cách
d
từ tâm I đến mặt phẳng

.
P
A.
2d B.22d C.
7
2
d
D.
7d
Câu 46: Cho hình chóp
.S ABC có
0
,2, 60,AB a AC a BAC cạnh bên SA vuông góc với đáy và
3.SA a
Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp
..S ABC
A.
7
2
a
R
B.
55
6
a
R
C.
10
2
a
R
D.
11
2
a
R
Câu 47: Cho hình tròn tâm
,S
bán kính
2.R
Cắt đi
1
4
hình tròn rồi dán lại để tạo ra mặt xung
quanh của một hình nón
.N
Tính diện tích toàn phần
tp
S
của hình nón
.N
A.
3
tp
S
B.
323
tp
S

C.
21
4
tp
S
D.
343
tp
S

Câu 48: Cho hình nón tròn xoay có chiều cao
4,h
bán kính đáy 3.r Tính diện tích xung
quanh
x
q
S
của hình nón đã cho.
A.
15
xq
S
B.
12
xq
S
C.
9
xq
S
D.
6
xq
S
Câu 49: Cắt một khối trụ
T bằng một mặt phẳng đi qua trục của nó, ta được một hình vuông có
diện tích bằng
9.
Khẳng định nào sau đây là sai?
A. Khối trụ
T
có thể tích
9
.
4
V
B. Khối trụ
T
có diện tích toàn phần
27
.
2
tp
S
C.Khối trụ
T
có diện tích xung quanh
9.
xq
S
D. Khối trụ
T
có độ dài đường sinh là 3.l
Câu 50: Trong không gian, cho tam giác
A
BC
là tam giác đều cạnh
.a
Gọi
S
là diện tích của mặt
tròn xoay nhận được khi quay các cạnh
A
B và
A
C
xung quanh trục
.BC
Tính
.S
A.
2
3.Sa
B.
2
3
.
2
a
S
C.
2
34 3
.
4
a
S
D.
2
32 3
.
4
a
S
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C A A D B D B B A A D B D B A B B D B D C C B B A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A D A B A A B B A A D B C A B D C D C B A C A A A
 Trang 18/38
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT THẠNH ĐÔNG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 -2018
Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Biên soạn: Thầy Đặng Phú Cường)
Câu 1: Hàm số nào sau đây nghịch biến trên R:
A.
2
x
y =
B.
42
yxx=- -
C.
1
y
x
=
D.
3
1yx=- +
Câu 2: Điểm cực đại của đồ thị hàm số
32
573yx x x=- +-
là
A.
()
0;1
B.
732
;
327
æö
-
÷
ç
÷
ç
÷
ç
÷
ç
èø
C.
()
1; 0
D.
732
;
327
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
.
Câu 3: Cho các hàm số:
()
3
31yx x I=- + -
()
2
yII
x
=
()
1
3
x
y III
-
=
(
)
42
23yx x IV=- +
Đồ thị của hàm số nào có đường tiệm cận ?
A. (II) và (III) B. Chỉ (II) C. Chỉ (I) D. (III) và (IV)
Câu 4: Với giá trị nào của m thì hàm số
32
1
22
3
yxxmx
=- + - + nghịch biến trên tập xác định của
nó?
A.
4m =
B.
4m <
C. 4m £ D.
4m >
Câu 5: Cho hàm số
(
)
32
ax x x 0ybcda=+++ ¹
. Hàm số đồng biến trên R khi:
A.
'0,yxR>"Î
B.
'0,yxR£"Î
C.
'0,yxR<"Î
D.
'0,yxR³"Î
Câu 6: Cho hàm số
32
2667yx x x=++-
. Phát biểu nào sau đây là đúng?
A. Luôn nghịch biến trên R. B. Tăng trên
(
)
;1-¥ -
và giảm trên
()
1;-+¥
.
C. Luôn đồng biến trên R. D. Tăng trên
()
1;-+¥
và giảm trên
()
;1-¥ -
.
Câu 7: Hàm số nào sau đây có đồ thị là đường cong trong hình vẽ bên:
A.
4
2
x
y
x
+
=
-
B.
21
2
x
y
x
-
=
-
C.
4
2
x
y
x
-
=
-
D.
4
2
x
y
x
-
=
+
Câu 8: Tìm tất cả các giá trị của m để hàm số
2
3
2
xm m
y
x
-+
=
+
nghịch biến trên từng khoảng xác định
của nó.
A. m > 1 B. 1 < m < 2 C. m < 2 D.
m Î
Câu 9: Cho hàm số
3
21
x
y
x
-+
=
-
.Số tiệm cận của đồ thị hàm số bằng
A. 2. B. 1. C. 3. D. 4.
Câu 10: Đồ thị hàm số
32
3yx x mx=- -
có điểm cực đại nằm trên Oy khi:
A. 0m = B. 0m ¹ C. 0m > D. 0m <
ĐỀ THI THỬ 04
(Đề thi có 5 trang)
x
y

Trang 19/38
Câu 11:
Hàm số
322
33(1)yx mx m xm=- + - +
đạt cực tiểu tại x = 2 thì m bằng
A.
Đáp án khác
B.
m = 1
C.
m = 3
D.
m= 3; m=1
Câu 12:
Gọi
,
CD CT
xx
tương ứng là điểm cực đại và điểm cực tiểu của hàm số
32
32yx x=- +
. Trong
các mệnh đề sau hãy chọn mệnh đề ĐÚNG:
A.
CD CT
xx>
B.
2
CD CT
xx-=
C.
2
CD CT
xx=
D.
0
CD CT
xx+=
Câu 13:
Hình vẽ sau đây là đồ thị của hàm số
3
3
1
22
x
yx
-
=++
Tìm m để phương trình
3
30xxm--=
có 3 nghiệm phân biệt
A.
–2 < m < 2
B.
0 < m < 2
C.
2 < m < 4
D.
–2 < m < 4
Câu 14:
Gọi
,AB
là các giao điểm của đường thẳng
1yx=-
và đường cong
1
1
x
y
x
-
=
+
. Tam giác
OAB
(
O
là gốc tọa độ) có diện tích là:
A.
3
B.
2
3
C.
3
2
D.
2
Câu 15:
Gọi T là giá trị lớn nhất của hàm số
2
1
1
mx
y
x
-
=
+
trên đoạn [2 ; 5]. Tìm m để T =
2
3
A.
1
5
2
m
m
é
=-
ê
ê
ê
=
ê
ë
B.
m = 2
C.
m = 1
D.
1
1
m
m
é
=
ê
ê
=-
ê
ë
Câu 16:
Đồ thị dưới đây là đồ thị của hàm số nào trong 4 đáp án sau:
A.
2
x
y =
B.
3
x
y =
C.
4
x
y =
D.
2
2xy =
Câu 17:
Cho biểu thức
3
2log
2
5
3 log . log 25
a
a
Ba=-
với a dương, khác 1. Khẳng định nào sau đây là
khẳng định đúng?
A.
2
4Ba=-
B. 2a 5B ³-
C.
()
2
4
log 1
a
B
-
=
D.
3B >
Câu 18:
Cho a, b, c là các số thực dương thỏa
7
311
log 11
log 7 log 25
27, 49, 11ab c== =
. Tính giá trị biểu
thức
2
22
7
311
log 11
log 7 log 25
Ta b c=++
A.
76 11T =+
B.
31141T =
C.
2017T =
D.
469T =
Câu 19:
Trong các khẳng định sau, khẳng định nào
sai
?
 Trang 20/38
A.
() ()
44
4
x
xxx
x
-=-
-
với
4x >
B.
(
)
(
)
42
33aa-=-
với
a"Î
C.
24 2
93.ab ab=-
với
0a £
D.
2
1 ab
ab
ab
+
=
-
-
với 0, 0aab³-¹
Câu 20:
Phương trình
()()
21 21 22 0
xx
-+ +- =
có tích các nghiệm là:
A. -1 B. 2 C. 0 D. 1
Câu 21: Phương trình
11
.210
93
xx
mm
æö æö
÷÷
çç
÷÷
-++=
çç
÷÷
çç
÷÷
çç
èø èø
có nghiệm khi và chỉ khi m nhận giá trị:
A.
1
425
2
m
-< <-
B.
1
2
m
<-
C.
425m ³+
D.
1
425
2
mm
<- ³ +
Câu 22: Phương trình
()
2
log 5 2 2
x
x-=- có hai nghiệm
12
,xx
. Giá trị của
1212
xxxx++
là
A. 2 B. 3 C. 9 D. 1
Câu 23: Phương trình
lg lg( 9) 1xx+-=
có nghiệm là:
A.
1 10xvàx=- =
B.
8x =
C. 9x = D.
10x =
Câu 24:
Hàm số
2
1
yln(x1)
2x
=--
-
có tập xác định là:
A.
{
}
\2R
B.
(
)
(
)
;1 1;2-¥ È
C.
(
)
(
)
;1 1;2-¥ - È
D.
()
1; 2
Câu 25: Phương trình
22
525
log 2 log 3 0xx--= có hai nghiệm
12 1 2
;( )xx x x<
. Giá trị của biểu thức
12
1
15
5
Ax x
=+ bằng:
A. 28
B.
28
25
C.100 D.
1876
625
Câu 26:
Cho phương trình
28
416
log log 4
log 2 log 8
xx
xx
=
khẳng định nào sau đây đúng:
A. Phương trình này có hai nghiệm B. Tổng các nghiệm là 17
C. Phương trình có ba nghiệm D. Phương trình có 4 nghiệm
Câu 27: Phương trình
()
2
4
2
44
log 2 log 2 0
4
x
xm-+=
có một nghiệm 2x =- thì giá trị của m là:
A.
6m =
B.
6m =
C.
8m =
D.
22m =
Câu 28: Giá trị của m để phương trình
1
4.220
xx
mm
+
-+=
có hai nghiệm
12
;xx
thỏa mãn
12
3xx+=
là
A. 3m = B. 4m = C. 0m = D.
3
2
m
=
Câu 29: Tập nghiệm của bất phương trình 47.280
xx
--³ là:
A.
(;1][8; )-¥ - È +¥
B.
[0;4]
C.
(;3]-¥
D.
[3; )+¥
Câu 30: Giải bất phương trình:
(
)
1
5
log 2 3 1x ->-
 Trang 21/38
A. 4x < B.
3
2
x
>
C.
3
4
2
x
>>
D. 4x >
Câu 31: Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x)
trên K nếu.
A.
(
)
(
)
’,Fx fx x K="Î
B.
() ()
’,Fx fx x K¹"Î
C.
() ()
’,fx Fx x K="Î
D.
() ()
’,fx Fx x K¹"Î
Câu 32: Họ nguyên hàm của hàm số
1
( ) 2 cos .fx x x
x
=- -
A.
2
sin ln Cxxx--+
B.
2
sin ln Cxxx+-+
.
C.
2
sin lnxxx-- D.
2
sin ln 1xxx+-+
Câu 33: Tính nguyên hàm
(
)
9
1 xdx-
ò
, ta được kết quả là.
A.
() ()
10
1
1
10
Fx x C
=-+
B.
() ()
10
1
1
10
Fx x C
=- - +
C.
(
)
(
)
10
10 1 CFx x-=+
D.
() ( )
10
110Fx x C=- - +
Câu 34: Tìmra kết quả sai trong các kết quả sau:
A.
2
x
x
e
dx e C
x
=+
ò
B.
sin x
12cos
12cos
dx
dx x C
x
=+ +
+
ò
C.
22
2
ee
(e ) 2
22
xx
xx
edx x C
-
-
+=+-+
ò
D.
3
1ln 2
(1 ln )
3
x
dx x C
x
+
=++
ò
Câu 35: F(x) là một nguyên hàm của hàm số
2
2
32cot
cos
y
x
x
=
-
. Nếu
10F(x) =
thì
2
2
32cot
cos
x
dx
x
-
ò
bằng:
A.
325tan x cotx-- B.
325tanx cotx-+
C.
325tanx cotx++
D.
325tanx cotx+-
Câu 36: Cho hình chóp tam giác
S.ABC
có diện tích đáy
2
3
4
a
B =
, đường cao
ha=
. Thể tích V
của khối chóp
S.ABC là
A.
3
3
4
a
V =
B.
3
3
8
a
V =
C.
3
4
a
V =
D.
3
3
12
a
V =
Câu 37: Cho hình chóp
S.ABCD
có đáy
ABCD
là hình vuông cạnh a, SA vuông góc với mặt
(
)
ABCD
, góc giữa đường thăng SC và mặt phẳng
(
)
ABCD
bằng 45
0
. Tính thể tích V của khối chóp
S.ABCD.
A.
2
42
3
a
V =
B.
3
2Va=
C.
3
3
a
V
=
D.
3
2
3
a
V =
Câu 38: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, đường cao h = 2a. Thể tích V của khối
chóp
S.ABCD .
A.
3
2
3
a
V
=
B.
3
Va= C.
3
3
a
V
=
D.
3
2Va=
Câu 39: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và
()
SA ABC^
. Cạnh bên SC hợp với
đáy một góc 45
0
. Thể tích V của khối chóp S.ABC là
A.
3
3
6
a
V =
B.
3
3
12
a
V =
C.
3
3
4
a
V =
D.
3
3
3
a
V =
 Trang 22/38
Câu 40: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a.
()
SA ABCD^
và
2SA a=
. Thể tích
V của khối chóp
S.ABCD là
A.
3
2
3
a
V =
B.
3
2
6
a
V =
C.
3
2Va=
D.
3
2
3
a
V =
Câu 41: Cho hình chóp .SABC có
()
SA ABC^
, tam giác ABC vuông tại B,AB a= ,
3AC a=
,
5SB a=
. Thể tích khối chóp .SABCbằng
A.
3
15
6
a
B.
3
36
4
a
C.
3
6
6
a
D.
3
2
3
a
Câu 42: Cho hình lập phương
ABCD.A'B'C'D'
cạnh a. Gọi O trung điểm AC’. Khi đó thể tích của
khối tứ diện
AA’B’O là:
A.
3
8
a
B.
3
12
a
C.
3
9
a
D.
3
2
3
a
Câu 43: Tính thể tích khối lập phương
ABCD.A'B'C'D'
, biết
2BD a=
.
A.
3
3
a
B.
3
22a
C.
3
a
D.
3
22
3
a
Câu 44: Cho lăng trụ ABC.A' B'C ' có đáy là tam giác đều. Hình chiếu của A’ lên
(
)
ABC
trùng với
trung điểm
BC. 2AB AA' a==. Thể tích khối chóp B'A' BC bằng mấy ?
A.
3
3
3
a
B.
3
3a
C.
3
3
4
a
D.
3
23
5
a
Câu 45: Cho hình chóp
S.ABC
có SA vuông góc với
(
)
ABC
và tam giác
ABC
vuông tại B. Tâm mặt
cầu ngoại tiếp
S.ABC
là:
A. Trung điểm SO với O là tâm đường tròn ngoại tiếp tam giác ABC .
B. Trung điểm SB
C. Trung điểm SA
D. Trung điểm SC
Câu 46: Cho khối trụ có thể tích bằng
24p
. Nếu tăng bán kính đường tròn đáy lên gấp 2 lần thì thể tích
khối trụ mới là
A. 96p B. 48p C. 32p D. 192p
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy,
3SA a= . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là
A.
5
2
a
B.
5
2
a
C.
5a
D.
3
4
a
Câu 48: Cho tam giác ABC vuông tại B, cạnh
2AB a, BC a==
, quay xung quanh cạnh AB tạo nên
một hình nón. Thể tích khối nón tạo bởi hình nón trên là:
A.
3
3 ap B.
3
1
3
a
p C.
3
4
3
a
p D.
3
3
4
a
p
Câu 49: Cho hình lăng trụ có chiều cao h, diện tích đáy bằng S. Thể tích khối lăng trụ đó được tính bằng
công thức:
A. .VhS= B.
1
.
3
VhS=
C. 2.VhSp= D.
2
2RVh=
Câu 50: Cho hình chóp S.ABCD đáy là hình vuông. Chu vi đáy bằng 8a. SA vuông góc với đáy. SC tạo
với đáy góc 60
0
. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng mấy ?
A.
3
64 2
3
ap
B.
3
64 2
3
a
C.
3
16 2
3
ap
D.
3
32
3
ap

Trang 23/38
BẢNG ĐÁP ÁN
Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
ĐA D C B D D C C B A A B B A C D A A
Câu 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
ĐA D A A D A D D A A D B D C A A B B
Câu 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
ĐA C D D A D B B D B A D A A C A A
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT THẠNH ĐÔNG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 - 2018
Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Biên soạn: Cô Kiều Thị Tho)
Câu 1:
Cho bảng biến thiên của một hàm số như hình dưới đây. Hỏi hàm số đó là hàm số nào trong các
hàm số cho dưới đây?
A.
32
24.yx x x
B.
32
33.yx x x
C.
32
2.yx xx
D.
32
33.yx x x
Câu 2:
Cho
K
là một khoảng và hàm số

yfx
có đạo hàm trên
.K
Giả sử

'0fx
chỉ tại một số
hữu hạn điểm trên
.K
Khẳng định nào sau đây là đúng?
A.
Nếu

'0,fx xK
thì hàm số là hàm hằng trên
.K
B.
Nếu

'0,fx xK
thì hàm số nghịch biến trên
.K
C.
Nếu

'0,fx xK
thì hàm số đồng biến trên
.K
D.
Nếu

'0,fx xK
thì hàm số nghịch biến trên
.K
Câu 3:
Tung độ giao điểm của hai đồ thị hàm số
3
x
y
và
11
yx
là :
A.
11
B.
3
C.
9
D.
2
Câu 4:
Cho hàm số
3
3yx x
xác định trên
.
Khẳng định nào sau đây là đúng ?
A.
3
CD CT
xx
B.
0
CD CT
yy
C.
3
CT CD
xx
D.
0
CD CT
yy
Câu 5:
Tìm phương trình các đường tiệm cậnđứng của đồ thị hàm số

3
:1.
1
Cyx
x

A.
1x 
B.
1x
C.
3x
D.

C
không có tiệm cận đứng.
ĐỀ THI THỬ 05

Trang 24/38
Câu 6:
Cho hàm số

yfx
liên tục trên nửa khoảng
1; 2 ,
có bảng biến thiên như hình vẽ bên.
Khẳng định nào sau đây là
sai?
A.
Hàm số đồng biến trên khoảng

0;1 .
B.
Đồ thị hàm số không đi qua điểm

2;5 .M
C.
1;2
miny 2.
D.
1;2
max 5.y
Câu 7:
Tìm tọa độ giao điểm
M
của đồ thị hàm số
21
2
x
y
x
và trục tung.
A.
1
0; .
2
M



B.

0; 2 .M
C.
1
;0 .
2
M



D.
1
;0 .
2
M



Câu 8
: Cho đồ thị hàm số

2
32
:.
3
x
Cy
xx
Khẳng định nào sau đây là sai?
A.
Đường thẳng
3
y 
là tiệm cận ngang của đồ thị

.C
B.
Đường thẳng
0x
là tiệm cận đứng của đồ thị

.C
C.
Đường thẳng
3
y
là tiệm cận ngang của đồ thị

.C
D.
Đường thẳng
2x
là tiệm cận đứng của đồ thị

.C
Câu 9
: Cho hàm số

2
10
31 0.
xkhix
yfx
xxkhix



biết rằng hàm số

yfx
có đồ thị

C
như hình vẽ bên. Khẳng định nào sau đây là
sai?
A.
Hàm số đã cho không có đạo hàm tại điểm
0.x
B.
Hàm số đã cho có 2 điểm cực trị.
C.
Hàm số đã cho liên tục trên
.
D.
Hàm số đã cho đồng biến trên
.
Câu 10
: Cho đồ thị hàm số

32
5
:2.
3
Cy x x x
Tiếp tuyến tại gốc tọa độ
O
của

C
cắt

C
tại
điểm thứ hai
.M
Tìm tọa độ điểm
.M
A.
10
2; .
3
M



B.
10
2; .
3
M




C.
10
2; .
3
M



D.
10
2; .
3
M



Câu 11
: Tìm các giá trị thực của tham số
m
để hàm số

32
123yx m x mx
đạt cực trị tại điểm
1.x 
A.
2.m 
B.
5
.
4
m
C.
1
.
4
m 
D.
1.m
Câu 12
: Xét
,xy
là các số thực thuộc đoạn

1; 2 .
Gọi
,
Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của biểu thức
.
xy
S
yx

Tính
.Mm
A.
5
.
2
Mm
B.
4.Mm
C.
9
.
2
Mm
D .
3.Mm
 Trang 25/38
Câu 13: Đồ thị hình bên là của hàm số:
A.
4
2
1
4
x
yx
B.
4
2
1
4
x
yx
C.
4
2
21
4
x
yx
D.
42
1
42
xx
y 
-3 -2 -1 1 2 3
-5
-4
-3
-2
-1
1
x
y
Câu 14: Đồ thị hàm số
32
32yxx
có dạng:
A B C D
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
y
Câu 15: Tìm m để hàm số
42
21 3yx m x
có ba cực trị
A.
0m
B.
1m 
C.
1m
D.
0m
Câu 16: Rút gọn biểu thức

32
2ln 3log 0, 1 .
ln log
a
a
Sa e aa
ae

A.
2.S B. 1.S C. 0.S D. 3.S
Câu 17: Rút gọn biểu thức

31
31
53 4 5
0.
.
a
Pa
aa


A.
7
P
a
B.
5
P
a
C.
P
a
D.
9
P
a
Câu 18: Tính đạo hàm của hàm số

cos2
x
fx e tại
.
6
x
A.
3
2
'
6
f
e




B. '3
6
f
e



C.
3
2
'
6
f
e




D.
'3
6
f
e




Câu 19: Tập xác định của hàm số

2
log 3 4yx
là:
A.
1;D 
B.
4
;
3
D



C.
4
;
3
D




D.
1;D 
Câu 20: Cho các số thực
k
và r thỏa mãn:
.2 3; .4 15.
rr
kk
Tìm
.r
A.
2
log 3r
B.
2
log 5r
C.
3
log 5r
D.
3
log 2r
Câu 21
: Số nghiệm của phương trình
22
2
22 3
xx xx

là:
A.
2 B.
3
C. 1 D. 4
Câu 22: Tập nghiệm của bất phương trình
24 2
log 1 2 log 5 1 log 2xxx
là:
A.
3; 5S
B.

2;3S
C.

2;5S
D.
4;3S 
 Trang 26/38
Câu 23:
2
log 3x
là nghiệm của phương trình nào trong các phương trình sau?
A.

21
22
4
log 3.3 4 log 3 log 9
x
x

B.

3
21
3
82 32
x
xx

C.

3
21
3
82 2
x
xx

D.
21
2
log 2.2 1 4
x

Câu 24: Gửi tiết kiệm ngân hàng với số tiền
,
M
theo thể thức lãi kép liên tục và lãi suất mỗi năm là
r
thì
sau
N
kỳ gửi, số tiền nhận được cả vốn lẫn lãi được tính theo công thức
..
Nr
M
e
Một người gửi tiết kiệm
số tiền 100 triệu đồng theo thể thức lãi kép liên tục, với lãi suất
8%
một năm, sau 2 năm số tiền thu về cả
vốn lẫn lãi là bao nhiêu?
A.
0,16
100.e
(Triệu đồng) B.
0,08
100.e
(Triệu đồng)
C.

0,16
100 1e (Triệu đồng) D.

0,08
100 1e (Triệu đồng)
C©u 25: NÕu
23
77 7
lo
g
x8lo
g
ab 2 lo
g
ab
(a, b > 0) th× x b»ng:
A.
46
ab B.
214
ab C.
612
ab D.
814
ab
Câu 26. Tìm tất cả các giá trị thực của tham số m để hàm số
2
ln( 2 1)yxxm có tập xác định là
A.
0m
B.
03m
C.
1m 
hoặc
0m
D.
0m
Câu 27:
Tập xác định của hàm số
1
ln
2
x
y
x



là:
A.
(;1)(2;) 
. B.
[1; 2)
. C.
(;1]
. D.
(2; )
.
Câu 28. Tìm tất cả các giá trị thực của tham số
m
để phương trình
1
42 0
xx
m

có hai nghiệm thực
phân biệt.
A.
(;1)m 
B.
(0; )m 
C.
(0;1]m
D.
(0;1)m
Câu 29. Nghiệm của bất phương trình log
2
󰇛x1󰇜

2log
4
󰇛5x󰇜1

log
2
󰇛x2󰇜là:
A,
1x2B. 4x3C. 2x5D. 2x3
C©u 30:
BÊt ph−¬ng tr×nh:
 
2
x2x 3
22
cã tËp nghiÖm lμ:
A.
2;5 B.
2; 1
C.
1; 3
D. KÕt qu¶ kh¸c
Câu 31: Tìm nguyên hàm
.
x
xe
Iedx
A.
x
e
I
eC
B.
1
x
e
I
eC

C.
x
Ie C
D.
1x
Ie C

Câu 32: Tìm nguyên hàm
.Ixdx
A.
2
3
3
2
x
IC
B.
3
2
3
2
x
IC
C.
3
2
2
3
x
IC
D.
2
3
2
3
x
IC
Câu 33: Nguyên hàm của
3
2x 1 3x
là:
A.
23
xxx C
B.
22
x13x C
C.
3
2x x x C
D.
3
2
6x
x1 C
5




Câu 34: Nguyên hàm của
2
2
11
x
x3

là:
A.
42
xx3
C
3x


B.
3
x1x
C
3x3

C.
42
xx3
C
3x

D.
3
1x
C
x3

Câu 35: Nguyên hàm của hàm số
3
fx x là:
 Trang 27/38
A.

3
2
3x
Fx C
4

B.

3
3x x
Fx C
4

C.

3
4x
Fx C
3x

D.

3
2
4x
Fx C
3x

Câu 36: Cho khối lăng trụ tam giác .' ' '
A
BC A B C có thể tích .V Khi đó, thể tích của khối tứ diện
''
A
BBClà:
A.
4
V
B.
3
V
C.
2
V
D.
2
3
V
Câu 37: Cho lăng trụ đứng
.'' '
A
BC A B C
có đáy là tam giác đều cạnh bằng1, AA' 3. Tính khoảng
cách
d
từ điểm
A
đến mặt phẳng
'.
A
BC
A.
215
5
d
B.
15
5
d
C.
3
2
d
D.
3
4
d
Câu 38: Cho hình chóp
.SABC
có đáy
A
BC
là tam giác vuông cân tại
,,
A
AB a
mặt bên
SBC
là tam
giác vuông cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích
V
của khối chóp
..S ABC
A.
3
2
12
a
V
B.
3
6
a
V
C.
3
2
6
a
V
D.
3
2
3
a
V
Câu 39: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
2a
,
SA
vuông góc với đáy, mặt phẳng
SBC
tạo với mặt đáy một góc
0
60
. Tính khoảng cách từ
A
đến mặt phẳng
SBC
.
A.
6
6
a
. B.
3
4
a
. C.
3
2
a
. D.
13
4
a
.
Câu 40: Cho hình chóp .S ABCD có đáy
A
BCD là hình vuông cạnh a , SA vuông góc với mặt đáy và
5SC a
. Tìm thể tích khối chóp
.S ABCD
.
A.
3
3a
. B.
3
3
12
a
. C.
3
3
6
a
. D.
3
3
3
a
.
Câu 41. Cho khối chóp .S ABC có đáy
A
BC là tam giác đều cạnh a . Hai mặt bên
SAB và
SAC cùng vuông
góc với đáy. Tính thể tích khối chóp biết
3SC a
A.
3
26
9
a
B.
3
6
12
a
C.
3
3
4
a
D.
3
3
2
a
Câu 42. Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC và (SBC) hợp
với đáy (ABC) một góc 60
o
. Tính thể tích hình chóp
A.
3
3
8
a
B.
3
3
12
a
C.
3
4
a
D.
3
3
4
a
Câu 43. Cho khối chóp
.S ABCD
có đay
A
BCD
là hình chữa nhật tâm
O
,
22,
A
CABa
SA
vuông góc với
đáy. Tính thể tích khối chóp biết
5SD a
A.
3
5
3
a
B.
3
15
3
a
C.
3
6a
D.
3
6
3
a
Câu 44: Hình nào sau đây có thể không nội tiếp một mặt cầu?
A.
Hình chóp lục giác đều B. Hình hộp chữ nhật
C. Hình tứ diện D. Hình chóp tứ giác
Câu 45: Cho hình chóp tam giác đều
.S ABC
có
,
A
Ba
cạnh bên
SA
tạo với đáy một góc
0
30 .
Một
hình nón có đỉnh là
,S
đáy là hình tròn ngoại tiếp tam giác
.
A
BC
Tính số đo góc ở đỉnh
của hình nón
đã cho.
A.
0
120
B.
0
60
C.
0
150
D.
0
30
Câu 46: Cắt một khối nón
N
bằng một mặt phẳng đi qua trục của nó, ta được một tam giác vuông cân có
diện tích bằng
8.
Khẳng định nào sau đây là sai?

Trang 28/38
A.
Khối nón
N
có diện tích xung quanh 16 2.
xq
S
B.
Khối nón
N
có diện tích đáy
8.S
C.
Khối nón
N
có độ dài đường sinh là
4.l
D.
Khối nón
N
có thể tích
16 2
.
3
V
Câu 47
: Một bình đựng nước dạng hình nón (không có đáy),
đựng đầy nước. Người ta thả vào đó một khối cầu có đường
kính bằng chiều cao của bình nước và đo được thể tích nước
tràn ra ngoài là

3
18 .dm
Biết rằng khối cầu tiếp xúc với
tất cả các đường sinh của hình nón và đúng một nửa của khối
cầu chìm trong nước (hình bên). Tính thể tích nước còn lại trong bình.
A.

3
6 dm
B.

3
12 dm
C.

3
54 dm
D.

3
24 dm
Câu 48:
Diện tích xung quanh của hình trụ có bán kính đáy bằng 3cm và chiều cao bằng 4cm là:
A.
2
36 cm
.
B.
2
42 cm
.
C.
2
24 cm
.
D.
2
12 cm
.
Câu 49:
Mặt cầu có bán kính bằng 10cm. Diện tích mặt cầu này bằng:
A.
2
400 cm
.
B.
2
400
cm
3
.
C.
2
100 cm
.
D.
2
100
cm
3
.
Câu 50:
Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2,
a
SA
vuông góc với mặt phẳng
()
ABCD
và
2.SA a
Tính diện tích
S
của mặt cầu ngoại tiếp hình chóp
..S ABCD
A.
2
6
Sa
.
B.
2
12
Sa
.
C.
2
3
Sa
.
D.
2
36
Sa
.
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D D C B B D A D D D C C C C B C C D A B A B B A B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D A D D C A C D A B B B A C D B A D D A A A C A A
 Trang 29/38
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT THẠNH ĐÔNG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 - 2018
Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Biên soạn: Thầy Trịnh Minh Hoạt)
Câu 1. Tìm tập xác định
D
của hàm số
()
2016
2
32 .yx x
-
=-+
A.
.D =
B.
{
}
\1;2.D =
C.
()
1; 2 .D = D.
()()
;1 2; .D =-¥ È +¥
Câu 2. Cho hàm số
32
32yx x=+ -. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đồng biến trên khoảng
()
;2-¥ -
và
()
0; +¥
.
B. Hàm số nghịch biến trên khoảng
()
;2-¥ -
và
()
0; +¥
.
C. Hàm số đồng biến trên khoảng
()
;0-¥
và
()
2; +¥
.
D. Hàm số nghịch biến trên khoảng
()
2;1-
.
Câu 3. Hỏi hàm số
2
2yxx=-
đồng biến trên khoảng nào?
A.
()
;2 .-¥ B.
()
0;1 .
C.
(
)
1; 2 . D.
()
1; .+¥
Câu 4. Cho hàm số
42
11
3
42
yxx=- + -
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đạt cực tiểu tại
0.x =
B. Hàm số đạt cực tiểu tại
1.x =
C. Hàm số đạt cực đại tại
0.x =
D. Hàm số đạt cực tiểu tại
3.x =-
Câu 5. Xét
()
fx
là một hàm số tùy ý. Khẳng định nào sau đây là khẳng định đúng?
A. Nếu
()
fx
có đạo hàm tại
0
x và đạt cực đại tại
0
x thì
()
0
'0fx =
.
B. Nếu
()
0
'0fx =
thì
()
fx
đạt cực trị tại
0
.xx=
C. Nếu
()
0
'0fx =
và
()
0
"0fx>
thì
()
fx
đạt cực đại tại
0
.xx=
D. Nếu
()
fx
đạt cực tiểu tại
0
xx= thì
()
0
"0.fx<
Câu 6. Tìm tiệm cận ngang của đồ thị hàm số
21
.
1
x
y
x
+
=
-
A.
2.y =
B.
2.y =-
C.
1.x =
D.
2.x =-
Câu 7
. Hỏi phương trình
2
251
1
2
8
xx--
=
có bao nhiêu nghiệm?
A. 0. B. 1. C. 2. D. 3.
Câu 8. Giải phương trình
3
log ( 4) 0x -=.
A.
1.x =
B.
6.x =
C.
5.x =
D.
4.x =
Câu 9.Biết F(x) là một nguyên hàm của hàm số
2
321
f
xxx
và
12F
. Trong các khẳng định
sau, đâu là khẳng định đúng?
A.
32
2Fx x x x
B.
64Fx x
C.
32
1Fx x x x
D.
32
1Fx x x x
Câu 10. Tìm giá trị nhỏ nhất của hàm số
1
23
x
y
x
-
=
-
trên
0;1
éù
êú
ëû
.
A.
0;1
min 0.y
éù
êú
ëû
= B.
0;1
1
min .
3
y
éù
êú
ëû
=- C.
0;1
min 1.y
éù
êú
ëû
=- D.
0;1
min 2.y
éù
êú
ëû
=-
Câu 11. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
32
331yx mx m=- + +
có 2 điểm cực
trị.
A.
0m > B. 0m < C. 0m ³ D.
0m ¹
ĐỀ THI THỬ 06

Trang 30/38
Câu 12.
Biết
F(x)
làmộtnguyênhàmcủahàmsố

1
1
fx
x
và

33F
. Tìm
F(8).
A.
4
B.
5
C.2
D.7
Câu 13.
Tính đạo hàm của hàm số
12
3
x
y
-
=
.
A.
12
'(2).3.
x
y
-
=-
B.
12
'(2ln3).3.
x
y
-
=-
C.
12
'3.ln3.
x
y
-
=
D.
()
2
'123.
x
yx
-
=-
Câu 14.
Tìm giá trị lớn nhất của hàm số
2x
yxe=+
trên đoạn
0;1
éù
êú
ëû
.
A.
1.
B.
2
1.e +
C.
2
.e
D.
2e.
Câu 15.
Tìm tập xác định
D
của hàm số y =
2
log 6 .x-
A.
{
}
\6.D =
B.
()
6; .D =+¥
C.
(
;6 .D
ù
=-¥
ú
û
D.
()
; 6 .D =-¥
Câu 16.
Cho
0a >
,
1a ¹
,
,xy
là 2 số dương. Khẳng định nào sau đây là khẳng định đúng?
A.
log
log .
log
a
a
a
x
x
yy
=
B.
()
log
log .
log
a
a
a
x
xy
y
-=
C.
log log log .
aaa
x
xy
y
=-
D.
()
log log log .
aaa
xy x y-= -
Câu 17.
Cho
1a >
. Khẳng định nào sau đây là khẳng định đúng?
A.
3
5
1
.a
a
-
>
B.
1
3
.aa>
C.
2016 2017
11
.
aa
<
D.
3
2
1.
a
a
>
Câu 18.
Tính đạo hàm của hàm số
3
log (2 2)yx=-
.
A.
1
'.
(2 2) ln 3
y
x
=
-
B.
1
'.
(1)ln3
y
x
=
-
C.
1
'.
1
y
x
=
-
D.
1
'.
22
y
x
=
-
Câu 19.
Họ nguyên hàm của hàm số

2
1fx xx
là:
A.


22
2
11
3
Fx x x C
B.


22
1
11
3
Fx x x C
C.

2
1
1
3
Fx x C
D.

2
2
1
3
Fx x C
Câu 20
. Đặt
55
log 4 , log 3ab==
. Hãy biểu diễn
25
log 12
theo
a
và
b
.
A.
()
2.ab+
B.
.
2
ab
C.
.
2
ab+
D.
2.ab
Câu 21.
Giải bất phương trình
() ()
22
2 log 1 log 5 1.
xx
-£ -+
A.
13.x<<
B.
13.x££
C.
33.x-£ £
D.
13.x<£
Câu 22.
Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
A.
42
y43.xx=- +
B.
4
y4²3.xx=- + -
C.
42
y45.xx=+ -
D.
4
y4²3.xx=- + +
Câu 23.
Một người gửi vào ngân hàng 100 triệu đồng với lãi suất
0, 5%
một tháng, sau mỗi tháng lãi suất
được nhập vào vốn. Hỏi sau một năm người đó rút tiền thì tổng số tiền người đó nhận được là bao nhiêu?
A.
12
100.(1, 005)
(triệu đồng). B.
12
100.(1 12 0, 005)+´
(triệu đồng).
y
x
 Trang 31/38
C.
100 1, 005´
(triệu đồng). D.
()
12
100. 1, 05 (triệu đồng).
Câu 24. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
32
39yx x xm=- -+ cắt trục
hoành tại ba điểm phân biệt.
A.
5 27.m-< < B. 27 5.m-<< C.
5 27.m-£ £
D. 27.m >
Câu 25. Tìm tất cả các giá trị thực của tham số m sao cho phương trình
42
23xx m--=
có 4 nghiệm
phân biệt.
A.
11.m-< < B.43.m-< <- C. 4.m <- D. 1.m >-
Câu 26. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
1mx
y
xm
+
=
+
đồng biến trên khoảng
()
1; +¥
A.
1m <- hoặc 1m > . B. 1.m >
C.
1m ³
. D. 11.m-< <
Câu 27. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
32
3yx xmxm=- + - +
nghịch biến
trên
.
A.
3.m > B. 3.m < C.
3m ³
. D.
3m £
.
Câu 28. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
32
31yx x mx=- + -
có hai điểm cực
trị
12
, xx thỏa mãn
22
12
3.xx+=
A.
3.-
B. 3. C.
3
.
2
-
D .
3
.
2
Câu 29.Tìm tất cả các giá trị thực của tham số m sao cho hàm số
()( )
32
32 1 12 5yx m x m x=- + + +
đồng
biến trên trên khoảng
(
)
4; +¥
.
A.
29
.
36
m >
B.
29
.
36
m ³
C.
29
.
36
m £
D.
29
.
36
m <
Câu 30. Cho
99 14
xx-
+=
. Tính giá trị của biểu thức K =
83 3
13 3
xx
xx
-
-
++
--
.
A.
5
.
2
-
B.
4
.
5
C.
4.-
D. 2.
Câu 31. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
32
(1) 3 1yx m x mx=+- - + đạt cực trị
tại điểm
0
1.
x =
A.
1.m =-
B.
1.m =
C.
2.m =
D.
2.m =-
Câu 32. Tìm tất cả các giá trị thực của tham số m sao cho hàm số
422
2+ yx mx m m=+ +
có đúng một
điểm cực trị.
A.
0.m ³
B.
0.m >
C.
0.m £
D.
0.m <
Câu 33. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
42
22yx mx m=- +
có ba điểm
cực trị tạo thành tam giác có diện tích bằng
1 .
A.
5
1
.
4
m =
B.
3.m =
C.
1.m =-
D.
1.m =
Câu 34. Tìm nguyên hàm của hàm số () 2 1.fx x
A.
1
() (2 1) 2 1 .
3
f
xdx x x C
B.
1
() 2 1 .
3
f
xdx x C
C.
1
() 2 1 .
2
f
xdx x C
D.
2
() (2 1) 2 1 .
3
f
xdx x x C
Câu 35.
Hỏi hình mười hai mặt đều có bao nhiêu đỉnh?
A. Mười hai. B. Mười sáu. C. Hai mươi. D. Ba mươi.
Câu 36. Số mặt phẳng đối xứng của khối tứ diện đều là:
A. 9. B. 2. C. 6. D. 3.
 Trang 32/38
Câu 37.Cho hình chóp
.SABCD
có đáy
ABCD
là hình vuông cạnh a ;
()
SA A BCD^
và 3SB a= . Tính
thể tích khối chóp
..SABCD
A.
3
2
.
2
a
B.
3
2.a
C.
3
2
.
3
a
D.
3
2
.
6
a
Câu 38.Cho khối lăng trụ tam giác đều, độ dài tất cả các cạnh bằng a . Tính thể tích khối lăng trụ đó.
A.
3
22
.
3
a
B.
3
.
3
a
C.
3
2
.
3
a
D.
3
3
.
4
a
Câu 39. Cho hình chóp tam giác đều
.SABC
có cạnh đáy bằng a , cạnh bên bằng 2a . Tính thể tích khối
chóp
.SABC .
A.
3
11
.
96
a
B.
3
11
.
4
a
C.
3
.
3
a
D.
3
11
.
12
a
Câu 40.Cho hình chóp .SABCDcó đáy ABCD là hình chữ nhật,biết
2; AB a AD a==
.Hình chiếu của
S
lên đáy là trung điểm
H
của cạnh AB , góc tạo bởi
SC
và đáy là
0
45 . Tính thể tích khối chóp S.ABCD.
A.
3
22
.
3
a
B.
3
.
3
a
C.
3
2
.
3
a
D.
3
3
.
2
a
Câu 41. Cho hình lập phương .’’’’ABCD A B C D có cạnh bằng a . Tính thể tích của tứ diện ’’.ACD B
A.
3
6
.
4
a
B.
3
2
.
3
a
C.
3
.
4
a
D.
3
.
3
a
Câu 42. Cho hình chóp .SABC có đáy ABC là tam giác vuông cân tại
B
, AB a= . Gọi
I
là trung điểm
AC
, tam giác
SAC
cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp
.SABC, biết góc giữa
SB
và mặt phẳng đáy bằng
0
45 .
A.
3
2
.
12
a
B.
3
3
.
12
a
C.
3
2
.
4
a
D.
3
3
.
4
a
Câu 43. Cho khối trụ có thể tích bằng
24p
. Hỏi nếu tăng bán kính đường tròn đáy của khối trụ đã cho lên
2 lần thì thể tích khối trụ mới bằng bao nhiêu?
A.
96 .p
B.
48 .p
C. 72 .p D.
12 .p
Câu 44. Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có
cạnh bằng
3a
. Tính diện tích toàn phần của hình trụ đó.
A.
2
3.ap
B.
2
27
.
2
ap
C.
2
3
.
2
ap
D.
2
13
.
6
ap
Câu 45. Cho một khối trụ có khoảng cách giữa hai đáy bằng 10, biết diện tích xung quanh của khối trụ
bằng
80p
. Tính thể tích của khối trụ đó.
A.
640
.
3
p
B.
640 .p
C.
160
.
3
p
D .
160 .p
Câu 46. Cho hình nón có bán kính đáy là
4a
, chiều cao là
3a
. Tính diện tích toàn phần của hình nón đó.
A.
2
36 .ap B.
2
20 .ap C.
2
15 .ap D.
2
24 .ap
Câu 47. Cắt một hình nón bởi một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh
bằng
a . Tính thể tích của khối nón tương ứng.
A.
3
3.ap
B.
3
23
.
9
ap
C.
3
3
.
24
ap
D.
3
3
.
8
ap
Câu 48. Một máy bơm nước có ống bơm hình trụ đường kính bằng
()
50 cm
và tốc độ dòng nước chảy
trong ống là
()
0, 5 m/s
. Hỏi trong một giờ máy bơm đó bơm được bao nhiêu nước? (giả sử nước lúc nào
cũng đầy ống).
A.
()
3
225
m.
6
p
B.
()
3
225 m .p C
()
3
450 m .p D.
()
3
225
m.
2
p
Câu 49. Cho hình chóp .SABC có
0
AS ASC CS 60BB===, 3, 6, 9SA SB SC===. Tính khoảng cách
d
từ
C
đến mặt phẳng
(
)
SAB
.
A.
96.d =
B.
26.d =
C.
27 2
.
2
d =
D.
36.d =

Trang 33/38
Câu 50.
Cho lăng trụ
'''ABCA B C
, đáy là tam giác đều cạnh bằng
a
, tứ giác
''ABB A
là hình thoi,
0
'60,AAC=
3
'
2
a
BC=
. Tính thể tích lăng trụ
'''.ABCA B C
A.
3
3
.
16
a
B.
3
33
.
16
a
C.
3
3
.
4
a
D.
3
33
.
4
a
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A B A A B C C D B D B B B D C A B B C D A A A B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B C D C C B A D A C C C D D A D A A B D A C D D B
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT THẠNH ĐÔNG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 - 2018
Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Biên soạn: Thầy Nguyễn Đức Trung)
Câu 1.
Cho hàm số có đồ thị là hình nào trong các hình sau?
Câu 2.
Cho hàm số liên tục trên và có đạo hàm . Hàm số
có bao nhiêu điểm cực trị ?
A. Có 3 điểm cực trị B. Có 1 điểm cực trị
C. Không có cực trị D. Có 2 điểm cực trị
Câu 3.
Hàm số nào trong các hàm số sau đồng biến trên ?
A. B. C. D.
Câu 4.
Tìm tiệm cận đứng của đồ thị hàm số .
A. B. C. (
C
) không có tiệm cận đứng. D.
Câu 5.
Cho hàm số liên tục trên đoạn , có đồ thị như hình bên.
3
431
y
xx
()yfx
32
() ( 1)( 2)fx xx x

()yfx
72sin3yx x
32
21yx x
tanyx
41
2
x
y
x
2
312
():
x
Cy
x
x

0, 1.xx 0x 1.x
()yfx
2;3
ĐỀ THI THỬ 07

Trang 34/38
Khẳng định nào sau đây là
sai
?
A. Hàm số không có đạo hàm tại điểm .
B. Hàm số đạt giá trị nhỏ nhất bằng .
C. Hàm số đạt giá trị lớn nhất bằng 1.
D. Hàm số nghịch biến trên khoảng .
Câu 6.
Cho hàm số có đồ thị (
C
). Khẳng định nào sau đây là
sai
?
A. Hàm số đồng biến trên .
B. Đồ thị (
C
) tiếp xúc với trục hoành.
C. Phương trình có một nghiệm với mọi
m
.
D. Hàm số đạt cực trị tại .
Câu 7.
Tìm giá trị nhỏ nhất của hàm số .
A. B. . C. . D. Không tồn tại .
Câu 8.
Hình bên là đồ thị của hàm số
Tìm tất cả các giá tị thực của tham số
m
để
phương trình có 4 nghiệm phân biệt.
A. B. .
C. . D.
Câu 9.
Tìm các giá trị thực của tham số
m
để đường thẳng cắt đồ thị hàm số
tại 3 điểm phân biệt có hoành độ lần lượt là thỏa mãn điều kiện
.
A. B. C. D.
Câu 10.
Xét là các số thực dương thỏa mãn điều kiện . Đặt . Khẳng định
nào sau đây là đúng ?
A. Biểu thức
S
không có giá trị lớn nhất. B. Biểu thức
S
không có giá trị nhỏ nhất.
C. . D. .
Câu 11.
Tìm các giá trị thực của tham số
m
để đồ thị hàm số có hai điểm
cực trị
A
,
B
sao cho đường thẳng
AB
vuông góc với đường thẳng
A. B. C. D.
Câu 12.
Tập xác định của hàm số là:
A. B. . C.

;0 2;D 
D.
Câu 13.
Rút gọn biểu thức
A. B. . C. . D.
Câu 14.
Cho Hãy biểu diễn theo
0x
3
1; 3
32
6128yx x x
32
6128
x
xxm
2x 
2
2
1x
y
x
min 2.y
min 0y
min 1y
min y
3
3.
y
xx
3
32
x
xm
20.m 2m 
1
m  10.m
:3
dy mx m
32
(): 3C
y
xx
123
,,
x
xx
222
123
15xx x
3
.
2
m
3
.
2
m 
3.m 3.m 
,
x
y
2xy
1
1
Sxy
x
y

3
min
2
S
max 1S
323
(): 3 2
m
Cyx mx m
:2.dy x
11
;.
22
m




11
;.
42
m




11
;.
24
m




11
;.
44
m




2
log(2 )
y
xx
0; 2 .D
;0 2;D 
0; 2 .D
538
14
log 3 log 6 3log 9
81 27 3 .P 
845.P 854P 458P 485.P
237
log 3, log 5, log 2.abc
140
log 63
,,.abc

Trang 35/38
A. B.
C. D.
Câu 15.
Nghiệm của phương trình là:
A. B. C. D.
Câu 16.
Đạo hàm của hàm số trên tập xác định là:
A. B. C. D.
Câu 17.
Rút gọn biểu thức
A. B. C. D.
Câu 18.
Tìm
x
, biết
333
log 4 log 7 log
xab
.
A.
36
xab
B.
47
xab
C.
37
xab
D.
46
xab
Câu 19.
là nghiệm của phương trình nào trong các phương trình sau?
A. B.
C. D. .
Câu 20.
Cho hai số thực
a
,
b
thỏa mãn đồng thời các đẳng thức và . Tính
giá trị biểu thức
A. B. C. D.
Câu 21.
Tìm tập nghiệm của bất phương trình
A.
B. C. D. .
Câu 22.
Cho hàm số liên tục trên ,
có đồ thị (
C
) như hình vẽ bên.
Khẳng định nào sau đây là
sai
?
A. Hàm số đồng biến trên khoảng .
B. Đồ thị (
C
) cắt trục hoành tại 3 điểm phân biệt.
C. Đồ thị (
C
) có hai điểm cực trị.
D. Hàm số có giá trị lớn nhất bằng 1.
Câu 23.
Các giá trị thực của
x
thỏa mãn điều kiện là:
A. B. C. D. .
Câu 24.
Đặt . Hãy biểu diễn theo
a
.
A. B. C. D.
log9000 3 2
a
.
Câu 25.
Cho phương trình: . Nghiệm của phương trình là:
A. B. C. D. .
Câu 26.
Đạo hàm của hàm số trên tập xác định là:
A. B.
C. D.
Câu 27.
Đồ thị hàm số cắt đồ thị hàm số tại điểm có tung độ là:
A. B. 0 C. 2,5 D. 1.
140
21
log 63 .
1
ac
abc c

140
21
log 63 .
21
ac
abc c

140
2
log 63 .
1
ac
abc c

140
1
log 63 .
21
ac
abc c

34 25
xx

2.x 5.x 3.x 4.x
2
2
ln
2
x
yx x
(2ln 1).yx x
 2(ln 1).
yxx
 2ln.
yxx
ln .
yxx
31
313
2
31
(a,b 0).
aa
P
b
b






3
.
P
a
2
.
P
a
2
.
P
a .
P
a
3
log 4x
223
log (9 4) log 3 log 2
x
x
24
2
log (9 4) log 3 log 9
x
x
223
log (9 4) log 3 log 2
x
x
224
log (9 4) log 3 log 9
x
x
3 .2 1152
ab
5
log ( ) 2ab
.
P
ab
3
P  9P  8P 6P 
44
log log (10 ) 2.xx
(0;10)S (2;10)S (8;10)S (2;8)S
()
yfx
()yfx (;0)
()
yfx
327
x
23x 23x 33x 33x
log 3 a log9000
log9000 2
a log9000 3 a log9000 3 2a
2
53
x
x

0x 2x 4x 1
x
1
2
4
(4)yxx

3
2
4
1
4(21)
4
yxx x


5
2
4
4
4(2 1)
5
yxx x


3
2
4
1
4
4
yxx


5
2
4
4
4
5
yxx

(2,5)
x
y
x
ye
e
 Trang 36/38
Câu 28. Đồ thị của hàm số nào trong các hàm số sau đây có tiệm cận đứng ?
A. B. C. D. .
Câu 29. Cho hàm số xác định trên đoạn . Khẳng định nào sau đây là đúng ?
A. và B. và
C. và D. và
Câu 30. Rút gọn biểu thức .
A. B. C. D. .
Câu 31. Tìm nguyên hàm
A. B. C. D.
Câu 32. Tìm nguyên hàm
A. B. C. D.
Câu 33. Tìm nguyên hàm
A. B. C. D.
Câu 34. Tìm nguyên hàm
A. B. C. D. .
Câu 35. Tìm nguyên hàm
21
2
x
Idx
A.
21
2
ln 2
x
IC

B.
4
ln 2
x
IC
C.
4
ln 4
x
IC
D.
2
2.
ln 2
x
IC
.
Câu 36. Nếu cạnh của một hình lập phương gấp lên k lần, với , thì thể tích của nó gấp lên bao
nhiêu lần ?
A. lần B. lần C. lần D. lần.
Câu 37. Trong các loại khối đa diện đều sau, tìm khối đa diện có số cạnh gấp đôi số đỉnh.
A. Khối hai mươi mặt đều B. Khối lập phương
C. Khối bát diện đều D. Khối mười hai mặt đều
Câu 38. Cho hình chóp có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác cân tại
S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SAD) và mặt phẳng đáy
bằng . Tính thể tích V của khối chóp .
A. B. C. D. .
Câu 39. Cho hình hộp chữ nhật có diện tích các mặt , ,
lần lượt bằng và . Tính thể tích V của khối chóp .
A. B. C. D. .
Câu 40. Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh
2
321
1
x
x
y
x

42
y
xx
3
32yx x
2
2
1
x
y
x
2
4yx x
2; 2

2;2
max 2 2y

2;2
min 0y

2;2
max 2y

2;2
min 0y

2;2
max 2y

2;2
min 2y


2;2
max 2 2y

2;2
min 2y

21
22
21
1
.Ma
a




(0)a
2
M
a
2
M
a
3
M
a
M
a
.
x
dx
I
e
x
Ie C
x
IeC
x
Ie C

x
Ie C

3
sin cos .
I
xxdx
4
sin
4
x
IC
4
sin
4
x
IC
4
cos
4
x
IC
4
cos
4
x
IC
.
dx
I
x
x
2ln( 1)IxC
1
2ln
1
IC
x

1
2ln( )
IxC
x

2lnIxxC
2
.
(1)
dx
I
x
2
1
IC
x

1
1
IC
x

1
1
IC
x

2
1
IC
x

*
k
3
3
k
k
2
k
3
k
.SABCD
45
.SABCD
3
3
6
a
V
3
2
3
a
V
3
6
a
V
3
5
6
a
V
.
A
BCD A B C D

()
A
BCD ()
A
BB A

()
A
DD A

22
20 ,28cm cm
2
35cm .
A
BCDABCD

3
120Vcm
3
160Vcm
3
130Vcm
3
140Vcm
22.
 Trang 37/38
A. B. C. D. .
Câu 41. Trong không gian, cho tam giác ABC vuông tại A, Tính độ dài đường sinh
của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB.
A. B. C. D.
Câu 42. Cho hình chóp tam giác đều có , cạnh bên SA tạo với đáy một góc . Một
hình nón có đỉnh là S, đáy là một hình tròn ngoại tiếp tam giác ABC. Tính diện tích xung quanh của
hình nón đã cho.
A. B. C. D. .
Câu 43. Cho hình trụ có chiều cao , bán kính đáy Một mặt phẳng (P) không vuông góc với
đáy của hình trụ, lần lượt cắt hai đáy theo các đoạn giao tuyến AB và CD sao cho tứ giác ABCD là hình
vuông. Tính diện tích S của hình vuông ABCD.
A. B. C. D. .
Câu 44. Cho hình chóp tam giác có đáy ABC là tam giác vuông cân tại B, ,
cạnh bên SA vuông góc với đáy và Tính diện tích toàn phần của hình chóp .
A. B. C. D. .
Câu 45. Cho hình chóp có đáy ABCD là hình chữ nhật, và
Biết rằng đường thẳng SA tạo với mặt phẳng đáy một góc . Tính thể tích V của
khối chóp .
A. B. C. D. .
Câu 46. Cho hình chóp có đáy ABCD là hình chữ nhật tâm O, , hình chiếu
vuông góc của đỉnh S trên mặt đáy là trung điểm H của OA. Biết rằng mặt phẳng (SBC) tạo với mặt phẳng
đáy một góc . Tính thể tích V của khối chóp .
A. B. C. D. .
Câu 47. Cho hình chóp tứ giác đều có , mặt bên tạo với đáy một góc . Một khối
nón có đỉnh là S, đáy là hình tròn ngoại tiếp hình vuông ABCD. Gọi là góc ở đỉnh hình nón. Tính
A. B. C. D. .
Câu 48. Cho hình lập phương (H) cạnh a, gọi (B) là hình bát diện đều có các đỉnh là tâm các mặt của (H).
Gọi S
1
, S
2
lần lượt là diện tích toàn phần của (H) và (B).
Tính tỉ số .
A. B. C. D. .
Câu 49. Cho hình nón có chiều cao , bán kính đáy Một hình lập phương đặt trong mặt nón
sao cho trục của hình nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nội tiếp
trong đường tròn đáy của hình nón, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Tính độ
dài cạnh của hình lập phương.
A. B. C. D. 3.
Câu 50. Cho hình chóp có đáy ABCD là hình chữ nhật, , cạnh bên SA vuông
góc với đáy và . Tính thể tích V của khối cầu ngoại tiếp hình chóp .
32
3
V
86V
256
3
V
64 2
3
V
2, .
A
BaACa l
.la
5.la 3.la 2.la
.SABC
A
Ba 60
x
q
S
2
4
3
xq
a
S
2
2
3
xq
a
S
2
6
xq
a
S
2
2
xq
a
S
2h 3.r
12S
12S 20S 20S
.SABC
A
BBCa
.SA a
tp
S
.SABC
2
2
tp
Sa
2
12
tp
Sa
2
122
2
tp
a
S
2
22
tp
Sa
.SABCD
16 3, 30 3AB AD
.SA SB SC SD 30
.S ABCD
7250V 8160V 2448V 9580V
.S ABCD
,2
A
BaBC a
60
.SABCD
3
3Va
3
15
2
a
V
3
15Va
3
3
2
a
V
.SABCD
A
Ba 45
cos .
1
cos
3

3
cos
3
6
cos
3
1
cos
3
1
2
S
S
1
2
3
8
S
S
1
2
1
23
S
S
1
2
23
S
S
1
2
83
3
S
S
6h 3.r
32
2
621

32 2
.SABCD
1, 2AB AD
11SA .SABCD
 Trang 38/38
A. B. C. D. .
BẢNG ĐÁP ÁN
1C 2D 3A 4B 5C 6D 7D 8D 9C 10B
11A 12D 13A 14B 15A 16C 17C 18B 19B 20B
21D 22D 23C 24D 25B 26A 27D 28D 29D 30C
31C 32D 33A 34B 35B 36D 37C 38C 39D 40A
41B 42B 43C 44B 45B 46D 47A 48C 49B 50C
11 11
6
32
32
3
256
3
| 1/38
| | Tải xuống

Có thể bạn quan tâm:

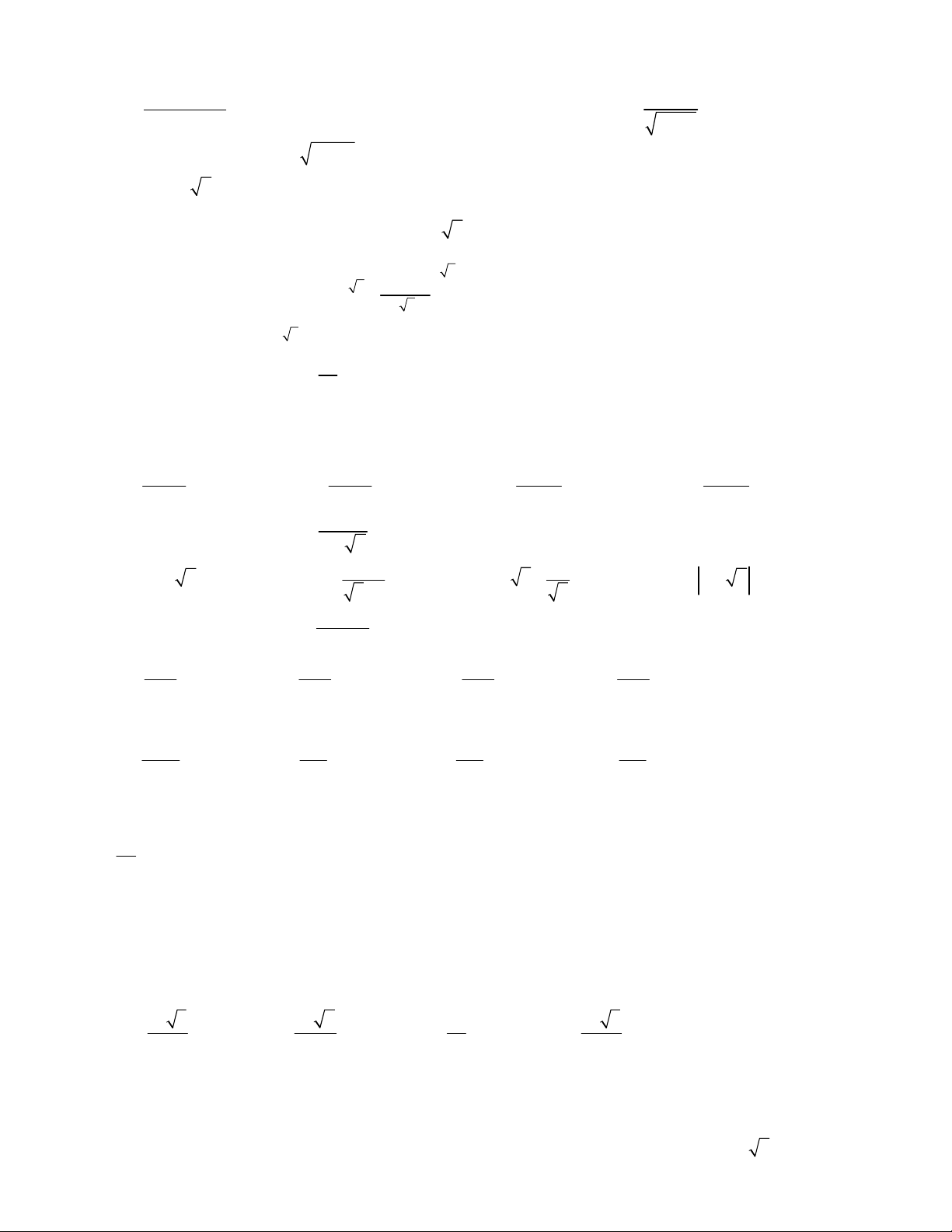
Preview text:

ĐỀ CƯƠNG ÔN THI MÔN TOÁN HK I – KHỐI 12 NĂM HỌC 2017 -2018
SỞ GD&ĐT KIÊN GIANG
ĐỀ THI THỬ HỌC KÌ I NĂM HỌC 2017 - 2018
TRƯỜNG THPT THẠNH ĐÔNG Bài thi môn Toán ĐỀ THI THỬ 01
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Biên soạn: Thầy Đỗ Thanh Trường)
(Đề thi có 5 trang)
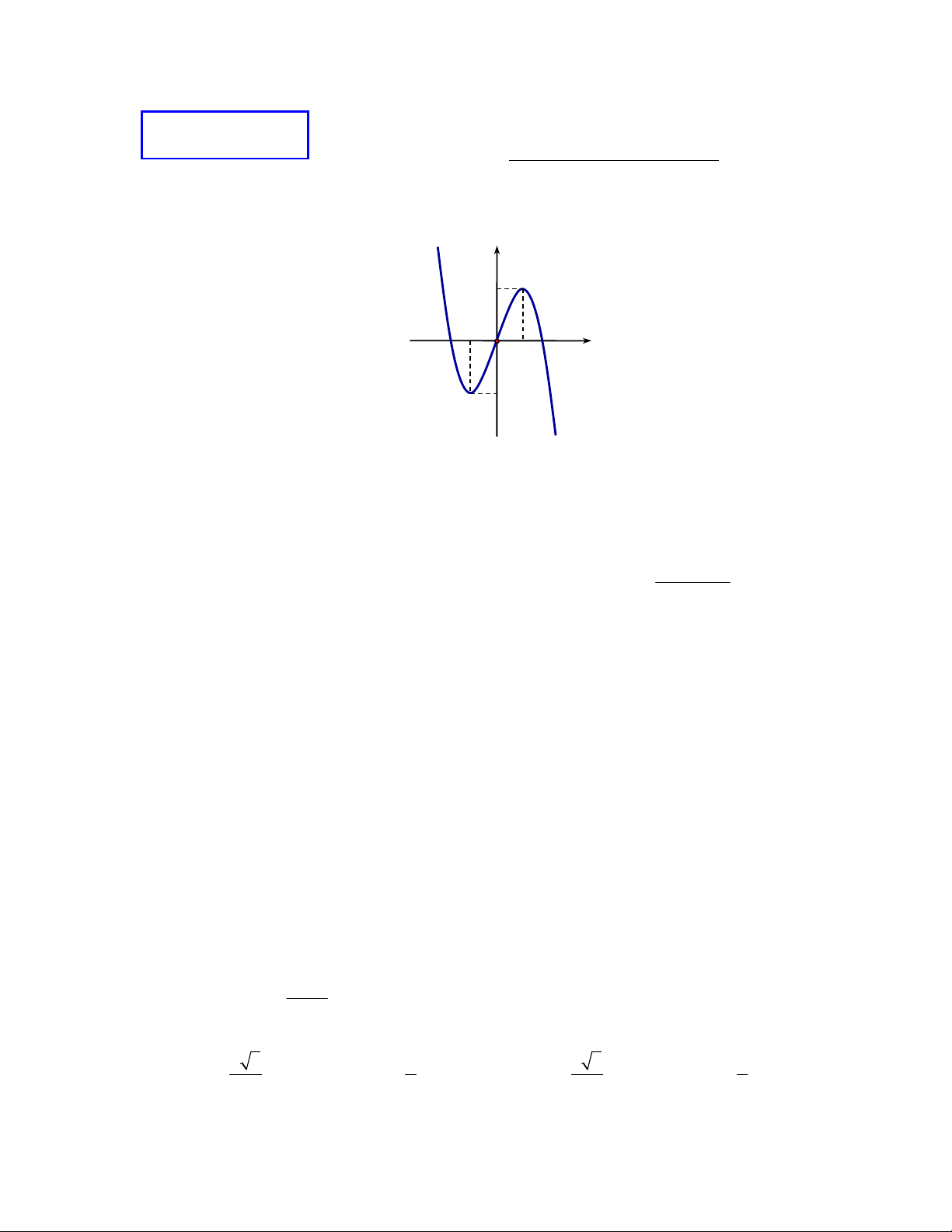
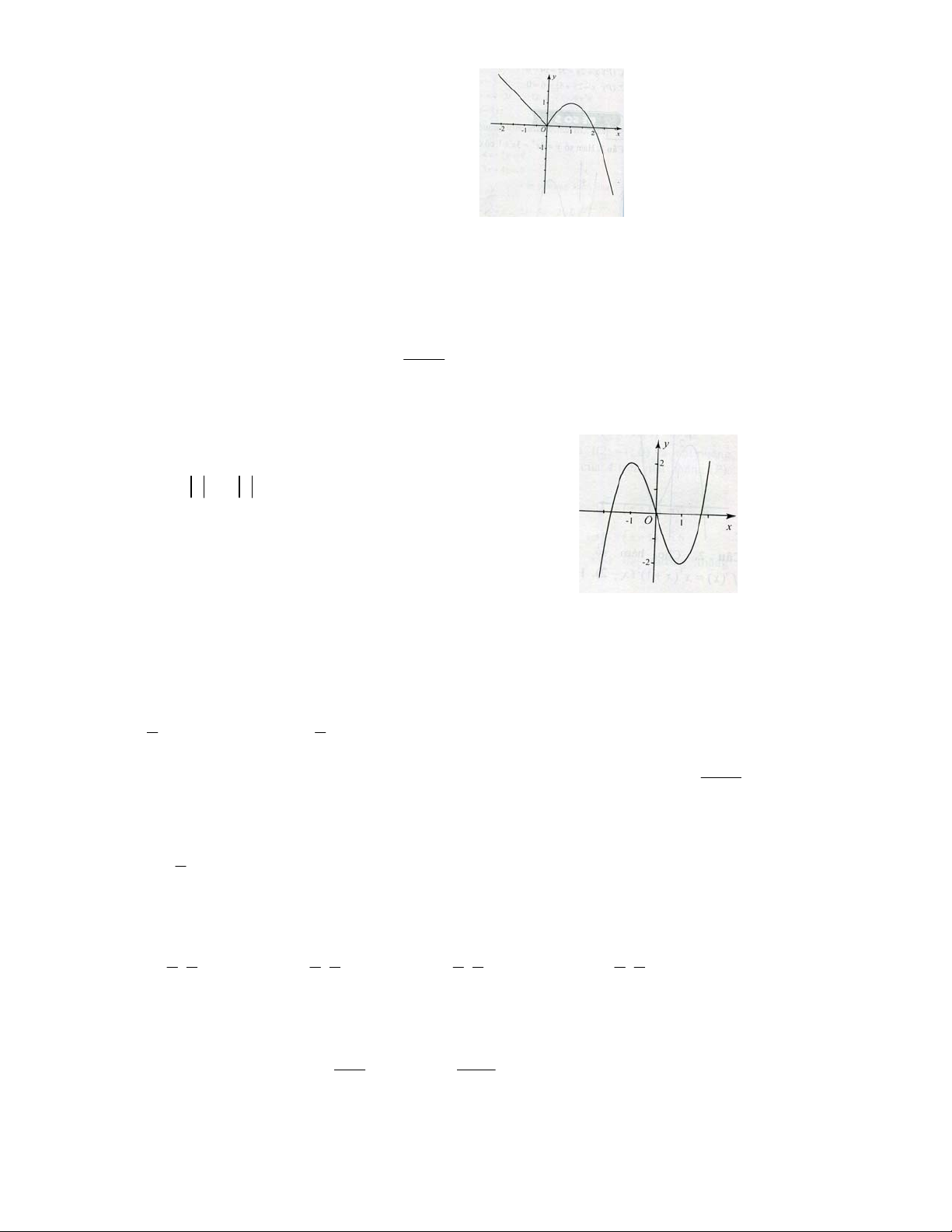
Câu 1 : Đồ thị được cho trong hình
vẽ bên là đồ thị của hàm số nào trong các hàm số sau ? A. 3 2
y x  3x . B. 3
y x  3x 1. C. 3 2
y x  3x 1 D. 3
y x  3x .
Câu 2: Hàm số nào sau đây đồng biến trên R
A. y x  tan x B. 4 2
y x  2x  3
C. y x  cos 2x D. 3
y x x  5 2 x  3x  3
Câu 3: Hàm số y
có bao nhiêu điểm cực trị? x  2
A. Có 1 điểm cực trị B. Có 2 điểm cực trị
C. Không có cực trị D. Có 3 điểm cực trị
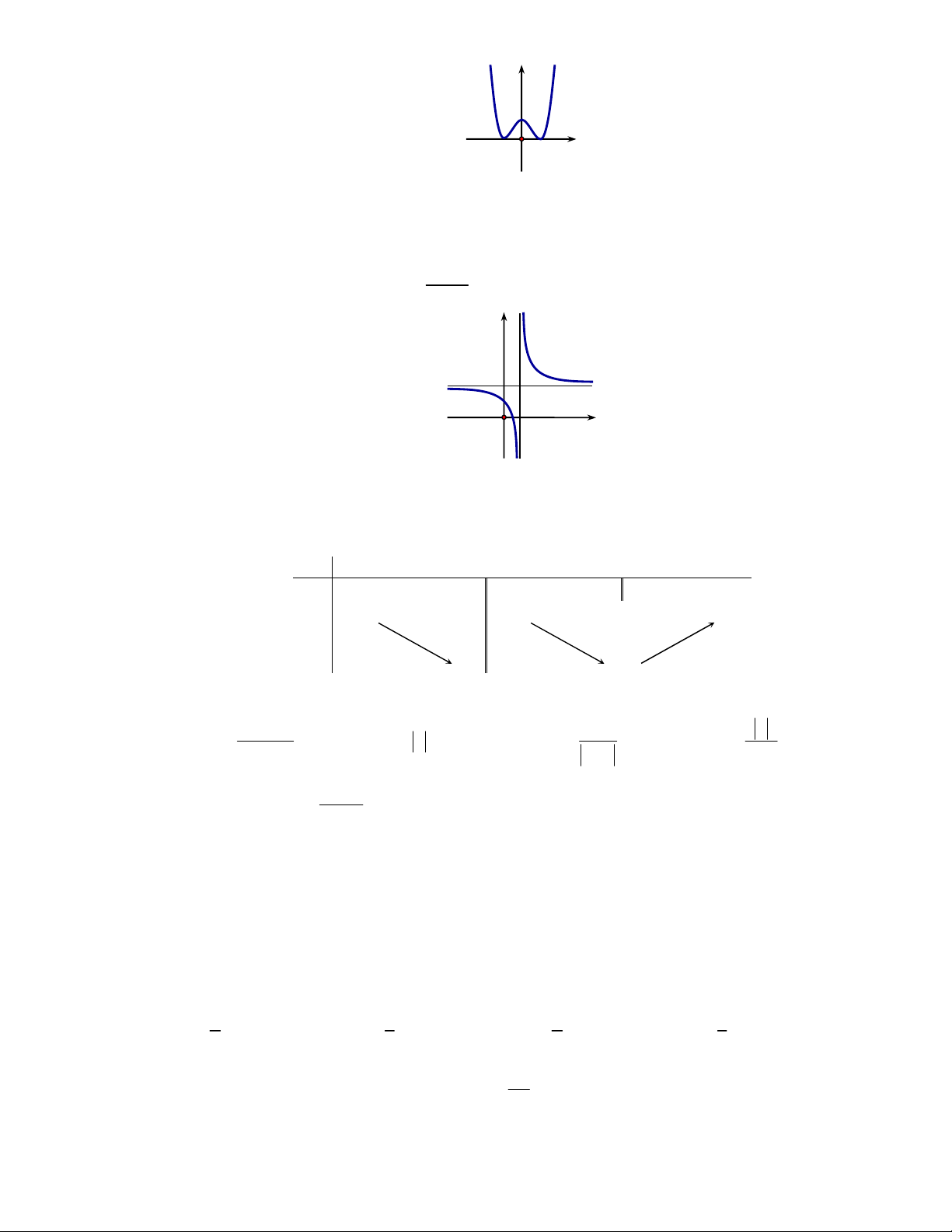
Câu 4 : Cho hàm số y f x liên tục trên khoảng  3;
 2 , có bảng biến thiên như hình vẽ bên. Khẳng
định nào sau đây là sai ?
A.Không có min y B. y  0 3;2 C§
C. max y  0 D. y  2  CT 3;2
Câu 5: Tìm tiệm cận ngang của đồ thị hàm số (C): 2
y x x  2x  3 A. y  1
B. y  1 C. y x D. Không có tiệm cận ngang. 2 x x 1
Câu 6: Cho đồ thị hàm số (C) y
(với m là tham số thực).Khẳng định nào sau đây là đúng ? 2x  3
A. Đồ thị (C) có tiệm cận ngang
B. Đồ thị (C) không có tiệm cận
C. Đồ thị (C) có tiệm cận đứng
D. Đồ thị (C) có tiệm cận đứng và tiệm cận ngang . Câu 7: Cho hàm số 3 2
y f (x)  2x  3x 12x  5 . Khẳng định nào sau đây là sai?
A. f (x) đồng biến trên khoảng  1  ;  1
B. f (x) đồng biến trên khoảng 0;2
C. f (x) nghịch biến trên khoảng  ;  3
  D. f (x) nghịch biến trên khoảng 1;
Câu 8: Tìm điểm cực tiểu của hàm số 3 2
y x  3x  3 A. x  3 B. x  2 C. x  1  D. x  0 3x 1
Câu 9: Cho đồ thị hàm số C : y
. Khẳng định nào sau đây đúng? 2x 1
A. Đường thẳng y  3
 là tiệm cận ngang của đồ thị C Trang 1/38 3
B. Đường thẳng x  là tiệm cận đứng của đồ thị C 2 1
C. Đường thẳng x  là tiệm cận đứng của đồ thị C 2 1
D. Đường thẳng y   là tiệm cận ngang của đồ thị C 2 x  3
Câu 10: Cho đồ thị hàm số C : y
. Tiếp tuyến của đồ thị C song song với đường thẳng 2x 1
5x  4 y 1  0 là đường thẳng nào trong các đường thẳng sau?
A. 10x  8y 17  0 B. 10x  8y 19  0 C. 10x  8y  21  0
D. 10x  8y  23  0
Câu 11: Đồ thị hàm số 3
y x  8x cắt trục hoành tại bao nhiêu điểm?
A. Đồ thị không cắt trục hoành B.Chỉ 1 điểm
C. 2 điểm phân biệt
D.3 điểm phân biệt
Câu 12: Tìm giá trị nhỏ nhất của hàm số y x  2  4  x trên đoạn 2;  4 3 3 A. min y B. min y C. min y  2 D. min y  2 2;4 2 2;4 2 2;4 2;4
Câu 13 : Tìm giá trị thực của tham số m để đồ thị hàm số C  4 2
: y x mx m 1 cắt trục hoành tại 4 m điểm phân biệt. m 1 A. B.Không có m C. m  1 D. m  2 m  2 x 1
Câu 14: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C y m  : có hai đường 2
x x m tiệm cận đứng.  1  1 m   m  
A. Mọi m   B.  4 C.  4 D. m  2 m  2 m  2 Câu 15: Cho hàm số 3
y mx   m   2 2
1 x mx  7. Có bao nhiêu giá trị nguyên của tham số m để hàm
số nghịch biến trên  .
A.Không có giá trị nào B.2 C.1 D.Vô số giá trị
Câu 16: Đặt   log 20 Khi đó log 5 bằng 2 20   3  1   2   4 A. B. C. D.     1 
Câu 17: Tập xác định của hàm số 3
y  (1 x) là A. ( ;
 1] B. R \{1} C.   ;1  D. 1;
Câu 18: Số nghiệm của phương trình 2 2x 7 x5 2 1
A.2 nghiệm B. 3 nghiệm C. 1 nghiệm D. Vô nghiệm
Câu 19: Đạo hàm của hàm số 2 sin x y e trên tập xác định là A. 2 cos x e B. 2 sin x e sin .
x cos x C. 2 sin x e sin 2x D. 2 sin x 2e sin x
Câu 20: Tìm khoảng đồng biến của hàm số 2 x 1 y e   trên tập số thực?
A. (0;) B. ( 1  ;1) C.  ;   D. ( ;  1  ] x 1  x  2 
Câu 21:Nghiệm của phương trình 5 7 (1,5)     3 
A. x  3 B. x  1 C. x  4 D. x  2 Trang 2/38   
Câu 22: Rút gọn biểu thức P  a  b  1
2  4 ab Với a ,b là số dương   A. P a 2b   B. P a 2b  
C. P ab 
D. P ab  
Câu 23:Tập nghiệm của phương trình 2x2 3
 2.6x  7.4x  0
A. S  1; B. S   1
 ;0 C. S  0; D. S    ;1
Câu 24: Tìm tất cả các giá trị thực của tham số m để hàm số y   2
ln x  2mx  4 có tập xác định D   A. 2   m  2 B. m  2 C. 2   m  2
D. m  2 hoặc m  2 
Câu 25: Tọa độ giao điểm của đồ thị hàm số 3x y  1
và đường thẳng y  là: 3  1   1   1   1  A. 1; B. 1;  C. 1; D 1;           3   3   3   3 
Câu 26: Cho log 5  a . Hãy biểu diễn log 1250 theo a 2 4 1 1 A. log 1250  1 4a log 1250  1 4a 4   4   B. 2 2
C. log 1250  2 1 4a log 1250  2 1 4a 4   4   D. 1
Câu 27: Cho số thực dương a, rút gọn biểu thức 3
P a . a 7 5 5 6 A. 5 P a B. 7 P a C. 6 P a D. 5 P a
Câu 28: Nghiệm của bất phương trình log 3x  2  0 2  
A. log 2  x  1
B. x  2
C. 0  x  1
D. x  1 3 x3
Câu 29: Nghiệm của bất phương trình 8,4 2x 1 1 là:
A. x  4
B. x  3
C. x  2
D. x  1 1 x  1 x
Câu 30: Tập nghiệm của bất phương trình 1 2  là:   16  A.  ;  
B. 2; C.  ;0  
D. 0;
Câu 31: Tìm nguyên hàm 2 x e dx A.  4 x I
e C B.  2 x I
e C C.  3 x I
e C D.  4 x I e C . x sin 8x
Câu 32: Hàm số y  
là nguyên hàm của hàm số nào? 2 16 sin 8x x A. y B. 2 y  cos8
sin 4x C. y D. 2 y  cos 4x 8 8 dx
Câu 33: Tìm nguyên hàm I  ?
 2xx x x 2 2 A. I    C B. I    C x x x 1 2 2 C. I    C D. I   C x x 1 x 1 x  5
Câu 34: Tìm nguyên hàm I dx x 5 5
A. I x  5ln x C B. I x   C
C. I x  5ln x C D. I x   C 2 x 2 x Trang 3/38
Câu 25: Tìm nguyên hàm 2 I  tan xdx
A. I x  cot x C B. I   cot x x C C. I x  tan x C D. I  tan x x C
Câu 36: Tính thể tích V của khối lập phương cạnh bằng 2
A. V  4 B. V  8 8 C. V  4 D. V  3 3
Câu 37: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a ,mặt bên SAB là tam giác cân tại S và
nằm trong mặt phẳng vuông góc với đáy .Biết rằng góc giữa SCD và mặt đáy bằng 0 60 .Tính thể tích
V của khối chóp S.ABCD 3 a 15 3 a 3 3 a 3 3 a 15 A. V B. V C. V D. V  6 6 3 3
Câu 38: Gọi n là số mặt phẳng đối xứng của hình lập phương. Tìm n.
A. n  9
B. n  7
C. n  8
D. n  6
Câu 39: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB a , AC a 5 ,cạnh bên
SA vuông góc với đáy, đường thẳng SB tạo với đáy một góc 0
60 . Tính thể tích V của khối chóp S.ABC . 3 a 15 3 a 3 3 a 15 A. V B. V C. V D. 3
V a 3 6 3 3
Câu 40 : Cho hình chóp S.ABC có SA SB SC a ,   0
ASB CSB  60 ,  0
ASC  90 . Tính thể tích V
của khối chóp S.ABC . 3 a 2 3 a 2 3 a 6 3 a 3 A. V B. V C. V D. V  12 4 3 12
Câu 41 : Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy.
Biết rằng, mặt phẳng SBC tạo với mặt phẳng đáy một góc 0
60 . Tính thể tích V của khối chóp S.ABC . 3 a 3 3 a 3 a 3 3 a 3 A. V B. V C. V D. V  4 4 8 24
Câu 42: Cho tứ diện ABCD có AB a, AC a 2,AD a 3 các tam giác ABC, ACD, ABD là các tam
giác vuông tại A Tính khoảng cách d từ A đến mp (BCD) a 6 a a a A. d  30 B. d  3 C. d  66 D. V  3 5 2 11
Câu 43: Người ta cắt miếng bìa hình tam giác đều
cạnh bằng 1 như hình vẽ bên và gấp theo các đường
kẻ sau đó dán các mép lại để được hình tứ diện đều .
Tính thể tích V của hình tứ diện tạo thành 2 A. V  3 B. V  96 16 3 C. V  2 D. V  32 12
Câu 44: Cho lăng trụ đứng ABC.A' B 'C' có đáy ABC là tam giác đều cạnh a, AA '  2a .Một khối trụ có
hai đáy là hai hình tròn lần lượt nội tiếp tam giác ABC và tam giác A' B 'C ' .Tính thể tích V của khối trụ đó. 3 2 a 3 a 3 2 a 3 a A. V  B. V  C. V  D. V  3 18 9 6
Câu 45 : Cho hình chóp tứ giác đều S.ABCD có AB a , mặt bên tạo với đáy một góc 0 45 . Một khối
nón có đỉnh S, đáy là hình tròn ngoại tiếp hình vuông ABCD . Tính thể tích V của khối nón đã cho Trang 4/38 3  a 2 3 a 3  a 2 3 a A. V  B. V  C. V  D. V  12 3 3 12
Câu 46: Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại B,cạnh bên SA vuông góc với đáy
Khi quay các cạnh của hình chóp S.ABC quanh trục AB .Hỏi có bao nhiêu hình nón được tạo thành A. Hai hình nón B. Một hình nón
C. Ba hình nón
D. Không có hình nón nào?
Caâu 47. Cho tứ diện SABC có SA  2a và SA   ABC . Tam giác ABC có AB a, BC  2a,CA a 5 .
Diện tích mặt cầu ngoại tiếp tứ diện SABC là A. 2 16 a B. 2 27 a C. 2 36 a D. 2 9 a
Caâu 48. Một khối cầu có chu vi đường tròn lớn là 2 thì diện tích của mặt cầu đó là 8 A. 16 B. 8 C. 4 D. 3
Caâu 49. Hình khai triển mặt xung quanh của hình trụ là một hình chữ nhật có diện tích bằng 48 R , biết
đường cao của hình trụ bằng 4. Bán kính đáy của hình trụ bằng A. 6R B. 4R C. 12R D. 3R
Caâu 50. Một khối trụ có bán kính đáy R  5 cm , khoảng cách giữa hai đáy bằng 4. Cắt khối trụ bởi mặt
phẳng song song với trục và cách trục 4 cm. Diện tích thiết diện được tạo thành là 2 2 2 2 A. 20 cm B. 24 cm C. 12 cm D. 10 cm BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C D B C A C D B C B D D A B A C C A C A B D C A C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A C A B D A D B C D B C A B A C D A D D A D C B B Trang 5/38
SỞ GD&ĐT KIÊN GIANG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 -2018
TRƯỜNG THPT THẠNH ĐÔNG Bài thi môn Toán ĐỀ THI THỬ 02
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Đề thi có 5 trang)
(Biên soạn: Thầy Bùi sang Thọ)
Câu 1. Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 2 1  O 1 x 2  A. 3
y  x  3x 1. B. 3
y x  3x . C. 3
y  x  3x . D. 4 2
y x x 1.
Câu 2. Giá trị nhỏ nhất của hàm số 3
y x  3x  5 trên đoạn 2;4 là:
A. min y  3 .
B. min y  7 . C. min y  5. D. min y  0. 2; 4 2; 4 2; 4 2; 4 2 x  3x  3
Câu 3. Gọi M , n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số y  . Khi đó giá trị x  2 của biểu thức 2
M  2n bằng A. 7. B. 9. C. 8. D. 6.
Câu 4. Tiếp tuyến của đồ thị hàm số 3 2
y x  3x  2 có hệ số góc k  3  có phương trình là
A. y  3x  7 .
B. y  3x  7 .
C. y  3x 1 .
D. y  3x 1.
Câu 5. Biết đồ thị hàm số 3
y x  3x 1 có hai điểm cực trị A , B . Khi đó phương trình đường thẳng AB là
A. y  2x 1.
B. y  x  2.
C. y x  2 .
D. y  2x 1. Câu 6. Cho hàm số 3 2
y ax bx cx d . Hỏi hàm số luôn đồng biến trên  khi nào?
a b  0,c  0
a b c  0 A.  . B.  . 2
a  0;b  3ac  0 2
a  0; b  3ac  0
a b  0,c  0
a b  0,c  0 C.  . D.  . 2
a  0;b  3ac  0 2
a  0;b  3ac  0 2x 1
Câu 7. Cho hàm số y
có đồ thị C  và đường thẳng d : y  2x  3 . Đường thằng d cắt (C) x 1
tại hai điểm A và B . Khoảng cách giữa A và B là 2 5 5 5 5 2 A. AB  . B. AB  . C. AB  . D. AB  . 5 2 2 5
Câu 8. Giả sử hàm số 4 2
y ax bx c có đồ thị là hình bên dưới. Trang 6/38 y 1 1  O 1 x
Khẳng định nào sau đây là khẳng định đúng?
A. a  0, b  0, c  1 .
B. a  0, b  0, c  1.
C. a  0, b  0, c  1.
D. a  0, b  0, c  0 . ax 1
Câu 9. Xác định a , b , c để hàm số y
có đồ thị như hình vẽ bên. Chọn đáp án đúng? bx c y 2 O x 1
A. a  2, b  1,c  1.
B. a  2, b  1,c  1.
C. a  2, b  2,c  1.
D. a  2, b  1,c  1.
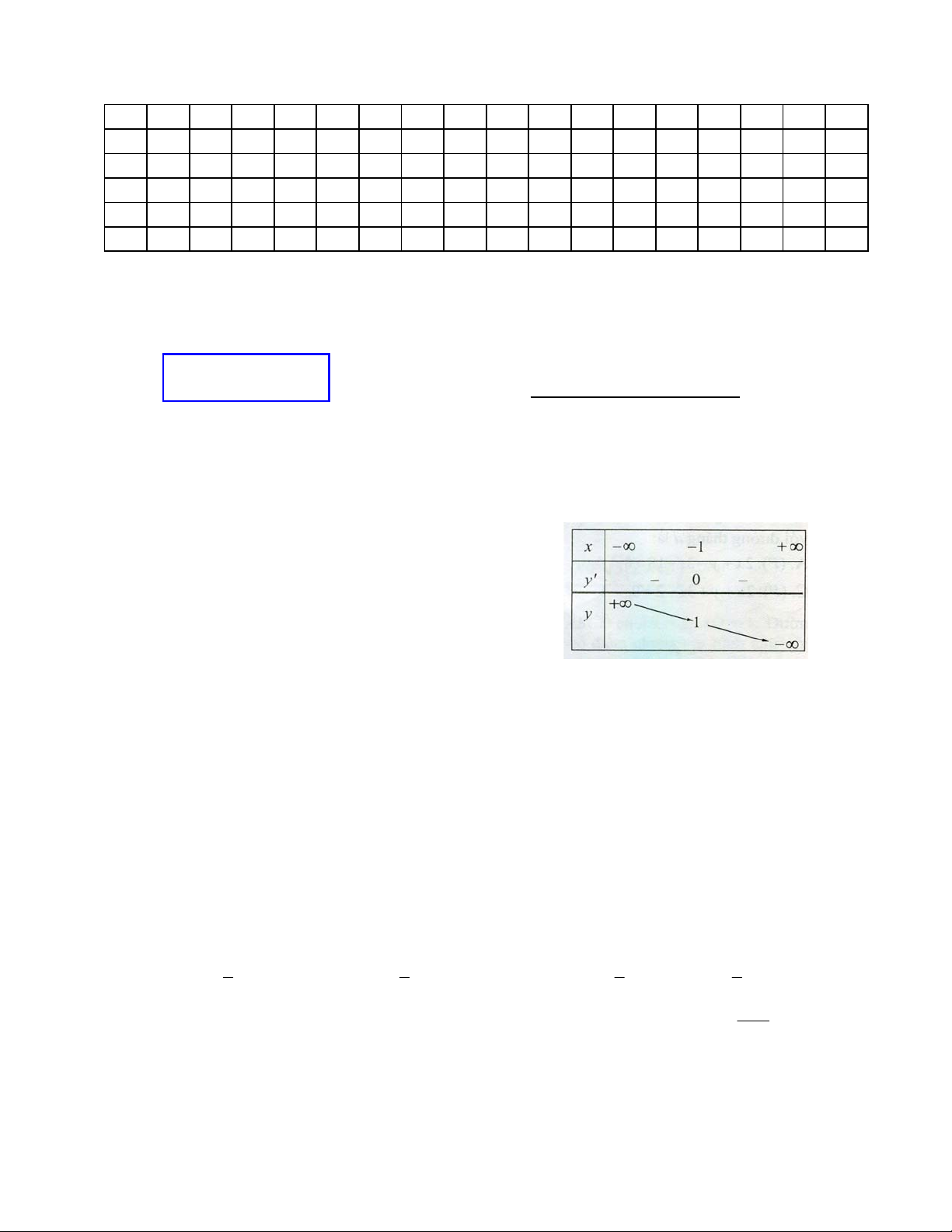
Câu 10. Cho hàm số y f x có bảng biến thiên dưới đây x  1 0  y    1  1 y  0
Hàm số y f x có bảng biến thiên trên là hàm số nào dưới đây 1 x x A. y  .
B. y x x   1 . C. y  . D. y  . xx   1 x 1 x 1 2x  3
Câu 11. Đồ thị hàm số y
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là x 1
A. x  2 và y  1.
B. x  1 và y  3 . C. x  1
 và y  2 . D. x 1 và y  2 .
Câu 12. Đồ thị hàm số 3 2
y x  3x 1 cắt đường thẳng y m tại ba điểm phân biệt thì tất cả các giá trị
tham số m thỏa mãn là A. m 1 . B. 3   m 1 . C. 3   m 1 . D. m  3.  Câu 13. Cho hàm số 3 2
y x x  2x  5 có đồ thị C  . Trong các tiếp tuyến của C  , tiếp tuyến có hệ
số góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là 4 5 2 1 A. . B. . C. . D. . 3 3 3 3  3 
Câu 14. Hàm số f x  2sin x  sin 2x trên đoạn 0; 
có giá trị lớn nhất là M , giá trị nhỏ nhất là 2   
m. Khi đó M .m bằng Trang 7/38 3 3 3 3 A. 3  3 . B. 3 3 . C.  . D. . 4 4 Câu 15. Cho hàm số 3 2
y x  2mx  3m  
1 x  2 có đồ thị C  . Đường thẳng d : y  x  2 cắt đồ thị
C tại ba điểm phân biệt A0;2 , B và C . Với M 3; 
1 , giá trị của tham số m để tam giác
MBC có diện tích bằng 2 6 là A. m  1.  B. m  1  hoặc m  4. C. m  4.
D. Không tồn tại m.
Câu 16. Hàm số f x   x  13 2 1 có tập xác định là  1  1   1  1  A. ;    . B. ;  .   C. ; 2 .   D.  \   .  2   2   2  2
Câu 17. Mệnh đề nào dưới đây sai? 2019 2018 2017 2018  2   2  A.  2   1   2  1 . B. 1   1   . 2   2      2018 2017 C.  3   1   3  1 . D. 2 1  3 2  2 .
Câu 18. Với các số thực a,b,c  0 và a,b  1 bất kì. Mệnh đề nào dưới đây sai? A. log  .
b c  log b  log c .
B. log b c b . c log a a a a a 1 C. log .
b log c  log c . D. log b  . a b a a log a b
Câu 19. Tính S  log 2016 theo a và b biết log 7  a , log 7  b . 2 2 3
2a  5b ab
2b  5a ab A. S  . B. S  . b a
5a  2b ab
2a  5b ab C. S  . D. S  . b a
Câu 20. Tìm tất cả các giá trị thực của m để hàm số y  log  2
x  4x m xác định trên  . 2  A. m  4 . B. m  4 . C. m  4 . D. m  4 .
Câu 21. Cho a , b là các số thực dương thỏa 2b a  5 . Tính 6 2a b K   4 A. K  226. B. K  246. C. K  242 . D. K  202.
Câu 22. Đạo hàm của hàm số 2 .3 x x y  là:
A. 2x ln 2 3x  ln 3. B. x ln 6 .
C. 2x ln 2.3x ln 3 . D. 6x ln 6 .
Câu 23. Đạo hàm hàm số y  log  2
x  3x  4 là 8  2x  3 1 2x  3 2x  3 A.B. C. D. 2
x  3x  4
 2x 3x4ln8
 2x 3x4ln8
 2x 3x4ln2 1
Câu 24. Nếu log x  log 9  log 5  log 2 ( a  0 ; a  1) thì x bằng: a 2 a a a 2 3 6 A. . B. . C. . D. 3 . 5 5 5 Trang 8/38
Câu 25. Giải bất phương trình log  2
x  2x  8  4  1  2 x  6 x  6  6   x  4   6   x  4  A.B.C.D.  x  4 x  4 2  x  4 2  x  4
Câu 26. Giải phương trình: x 2(1x) 16  8 : A. x  3 
B. x  2 C. x  3 D. x  2 
Câu 27. Bất phương trình. log (3x - )
2 < log (6-5x) có tập nghiệm là 1 1 2 2 æ 6ö æ2 6ö A. (1,+¥) B. 1, ç ÷ ç ÷ ç ÷ ç C. ç , D. Æ è ÷ 5÷ø çè3 5÷ø Câu 28. Hàm số 2
f (x)  x ln x đạt cực trị tại điểm 1 1
A. x e .
B. x e .
C. x . D. x . e e
Câu 29. Một người gửi tiết kiệm với lãi suất 8, 4% năm và lãi hàng năm được nhập vào vốn, hỏi sau
bao nhiêu tháng ngưòi đó thu được gấp đôi số tiền ban đầu (lấy giá trị quy tròn) ? A. 96 . B. 97 . C. 98 . D. 99 .
Câu 30. Tìm m để phương trình 9x  2.3x  2  m có nghiệm x  1  ;2 13 13
A. 1  m  65 . B. m  45 .
C. 1  m  45 . D. m  65 . 9 9
Câu 31. Nguyên hàm F x của hàm số f x  x  sin x thỏa mãn F 0 19 là 2 2 2 2 A. x x x x cos x . B.  cos x  2 . C.  cos x  20 . D.  cos x  20 2 2 2 2 3
Câu 32. Nguyên hàm của hàm số 2
f (x)  x   2 x là x 3 x 4 3 x 4 A. 3  3ln x
x C . B. 3  3ln x x . 3 3 3 3 3 x 4 3 x 4 C. 3  3ln x
x C . D. 3  3ln x
x C . 3 3 3 3
Câu 33. Hàm số F x nào dưới đây là nguyên hàm của hàm số 3
y x 1 ? 3 4
A. F x   x  43 1  C .
B. F x  x  4 3 1  C . 8 3 3 3
C. F x   x   3 1 x 1  C .
D. F x  x  3 4 1  C . 4 4
Câu 34. Hàm số nào dưới đây là một nguyên hàm của hàm số sin x cos  2 .2 x y
cos x sin x? sin x cos 2 .2 x sin xcos 2 x A. sin cos  2 x x yC . B. y  . C. sin cos ln 2.2 x x y   . D. y    C . ln 2 ln 2 Trang 9/38
Câu 35. Trong các mệnh đề sau, tìm mệnh đề sai? A. kf
 xdx k f  xdx. B.f
 x gx dx f
 xdxg  xdx. 3 f x C. f
 x 2f x   dx   C . D.f
 x.gx dx f
 xd .x g
 xdx. 3
Câu 36. Cho hình chóp tứ giác S.ABCD có đáy là vuông; mặt bên SAB là tam giác đều và nằm trong 3 7a
mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng SCD bằng 7
. Tính thể tích V của khối chóp S.ABCD . 1 2 3 3a A. 3 V a . B. 3 V a . C. 3 V a . D. V  . 3 3 2
Câu 37. Thể tích của chóp tam giác đều có tất cả các cạnh đều bằng a là 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 4 2 6 12 V
Câu 38. Cho hình chóp S.ABC . Gọi M , N lần lượt là trung điểm của SA , SB . Tính tỉ số S.ABC . VS.MNC 1 1 A. 4 . B. C. 2 . D.  2 4
Câu 39. Hình bát diện đều thuộc loại khối đa diện đều nào sau đây? A. 5;  3 B. 4;  3 C. 3;  3 D. 3;  4
Câu 40. Cho hình lăng trụ đứng A . BC A BC
 , biết đáy ABC là tam giác đều cạnh a . Khoảng cách từ a
tâm O của tam giác ABC đến mặt phẳng  ABC  bằng . Tính thể tích khối lăng trụ 6 A . BC A BC  . 3 3a 2 3 3a 2 3 3a 2 3 3a 2 A. . B. . C. . D. . 8 28 4 16
Câu 41. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , cạnh SB vuông góc với đáy
và mặt phẳng SAD tạo với đáy một góc 60 . Tính thể tích khối chóp S.ABCD . 3 3a 3 3 3a 3 3 8a 3 3 4a 3 A. V  . B. V  . C. V  . D. V  . 4 8 3 3
Câu 42. Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A. 3 . B. 4 . C. 6 . D. 5 .
Câu 43. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 2a là 3 a 3 3 a 3 A. 3 4a B. C. 3 2a 3 D. 4 12
Câu 44. Hình nón có góc ở đỉnh bằng 0
60 , độ dài đường sinh bằng a . Khi đó, diện tích xung quanh của hình nón là 2 pa 2 a 2 2 2 a pa 2 2 a pa A. B. C. + D. + 2 4 2 4 4 4
Câu 45. Trong không gian cho tam giác ABC vuông tại A với AC  3a, AB  4a .Tính độ dài đường
sinh l của hình nón nhận được khi quay tam giác ABC quanh trục AC. Trang 10/38 A. 7a . B. a . C. a 7 . D. 5a .
Câu 46. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có
cạnh bằng 3a Diện tích toàn phần của khối trụ là: 2 27 a 2 9a  2 13a A. 2 9a  . B. . C. . D. . 2 2 6
Câu 47. Thiết diện qua trục của hình nón tròn xoay là một tam giác đều có cạnh bằng a . Thể tích của khối nón bằng: 3  3 2 3 a 3 3 a A. 3 a . B. . C. . D. 3 3a . 8 9 24
Câu 48. Cho hình chữ nhật ABCD biết AB  1, AD  3 . Khi quay hình chữ nhật ABCD xung quanh
trục AB thì cạnh CD tạo nên hình trụ tròn xoay. Thể tích của khối trụ là 3 A. 3 . B.  3 . C.  . D.  . 3
Câu 49. Cho hình chóp S.ABC , có SA vuông góc mặt phẳng ( ABC ) ; tam giác ABC vuông tại B . Biết
SA  2a , AB a , BC a 3 . Khi đó bán kính R của mặt cầu ngoại tiếp hình chóp là A. 2a 2 . B. a 2 . C. 2a. D. a .
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a , AD = a 3 ; SA vuông góc
với mặt phẳng đáy, SA = 4a . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD .
A. R = 2a .
B. R = a 5 .
C. R = a 3 .
D. R = a . BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C B A D A C C A A D D C B A B A C B A B B D C C A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C B D D A D D C B D D D A D D C B C A D B C A B B Trang 11/38
SỞ GD&ĐT KIÊN GIANG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 -2018
TRƯỜNG THPT THẠNH ĐÔNG Bài thi môn Toán ĐỀ THI THỬ 03
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Đề thi có 5 trang)
(Biên soạn: Cô Nguyễn Thị Nghĩa)
Câu 1: Cho K là một khoảng và hàm số y f x có đạo hàm trên K. Khẳng định nào sau đây là sai?
A. Nếu f ' x  0, x
  K thì hàm số là hàm hằng trên K
B. Nếu f ' x  0, x
  K thì hàm số đồng biến trên K
C. Nếu f ' x  0, x
  K thì hàm số đồng biến trên K
D. Nếu f ' x  0, x
  K thì hàm số nghịch biến trên K
Câu 2: Cho hàm số y x . Khẳng định nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng0;
B. Hàm số đã cho đồng biến trên 
C. Hàm số đã cho nghịch biến trên 
D. Hàm số đã cho là hàm hằng trên khoảng ;0  
Câu 3: Giá trị lớn nhất của hàm số 2x y  trên đoạn  1  ;2 là 1 A. 4. B. . C. 1. D. 2. 2 x
Câu 4: Tìm tiệm cận đứng của đồ thị hàm số C 5 2 : y  . x  3 2 A. x   B. x  5 C. x  2. D. x  3. 3
Câu 5: Cho đồ thị hàm số C 3
: y x  3x  3. Khẳng định nào sau đây là sai ?
A. Đồ thịC nhận điểm I 0;3 làm tâm đối xứng.
B. Đồ thị C cắt trục Ox tại 2 điểm phân biệt.
C. Đồ thịC tiếp xúc với đường thẳng y  5.
D. Đồ thịC cắt trục Oy tại 1 điểm.
Câu 6: Cho hàm số y f x liên tục trên nửa khoảng  1
 ;2, có bảng biến thiên như hình vẽ bên.
Khẳng định nào sau đây là đúng?
A. Không tồn tại giá trị nhỏ nhất của hàm số trên  1  ;2.
B. Hàm số nghịch biến trên khoảng  1  ;2. C. maxy   .  1;2
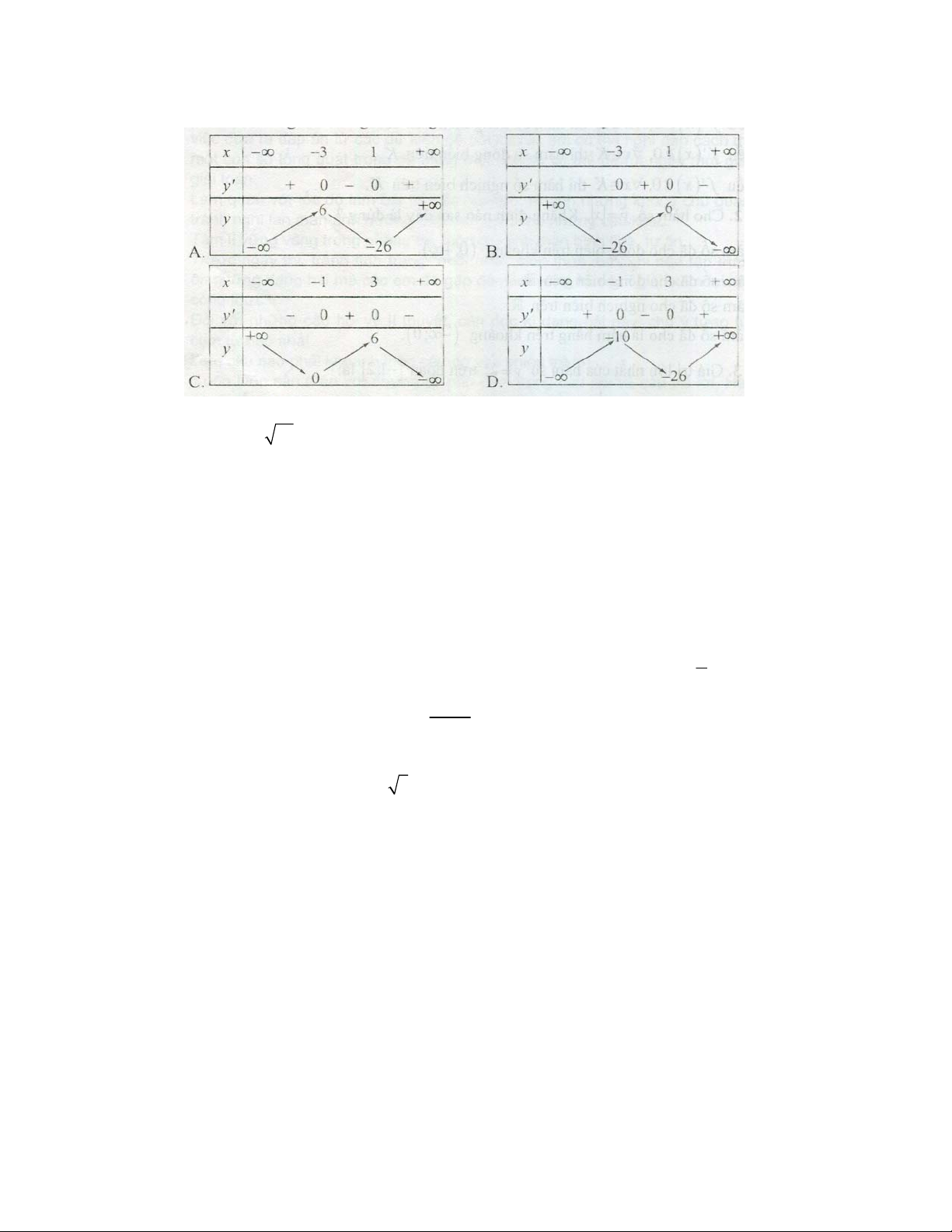
D. Đường thẳng x  2 là tiệm cận đứng của đồ thị hàm số y f x. Trang 12/38 Câu 7: Cho hàm số 3 2
y  x 3x  9x 1 xác định trên .
 Bảng biến thiên của hàm số là bảng nào
trong các bảng biến thiên cho dưới đây? Câu 8: Hàm số 3 2
y x có bao nhiêu điểm cực trị?
A. Không có cực trị B. Có 1 điểm cực trị C. Có 2 điểm cực trị
D. Có vô số điểm cực trị
Câu 9: Xét x, y là các số thực không âm thỏa mãn điều kiện x y  2. Tìm giá trị nhỏ nhất của biểu thức 2 2
S x y  4xy A. min S  3  B. min S  4  C. min S  0 D. min S 1
Câu 10: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y x mx  2x  3 nhận điểm x  1 là điểm cực đại. 5
A. Không tồn tại m B. Có vô số m C. m  6 D. m  2 x
Câu 11: Biết rằng đồ thị hàm số C 2 1 : y
luôn cắt đường thẳng d : y  x m tại hai điểm x  2 phân biệt ,
A B. Tìm các giá trị thực của tham số m sao cho độ dài đoạn thẳng AB ngắn nhất. A. m 1 B. m  2 3 C. m  4 D. m  0
Câu 12: Tìm tất cả các giá trị thực của tham số m để phương trình 3 2
x  3x m có ba nghiệm phân biệt. A. m  2 B. 0  m  4 C. m  0 D. m  4
Câu 13: Cho hàm số y f x liên tục trên  và có bảng biến thiên như hình vẽ bên. Khẳng định
nào sau đây là sai?
A. f x đồng biến trên khoảng  1  ;  3 .
C. f x nghịch biến trên khoảng  ;    1 .
B. B. f x nghịch biến trên khoảng 3;. D. f x đồng biến trên khoảng 0;6.
Câu 14: Cho đồ thị hàm số C 4 2
: y x x . Khẳng định nào sau đây là sai?
A. Đồ thị C cắt trục Ox tại 3 điểm phân biệt.
B. Đồ thị C cắt trục Oy tại 2 điểm phân biệt. Trang 13/38
C. Đồ thị C tiếp xúc với trục Ox .
D. Đồ thị C nhận trục Oy làm trục đối xứng.
Câu 15: Tìm giá trị lớn nhất của hàm số y  2  3sin 3x  4cos3x trên .  A. max y  7 B. max y  5 C. max y  9 D. max y  3     2 1  1 
Câu 16: Rút gọn biểu thức 2  P a . .    a  A. P  5a B. P a C. P  7a D. P  9a
Câu 17: Nghiệm của phương trình log9 10  8x  5 là: 5 1 7 A. x  B. x  C. x  D. x  0 8 2 4
Câu 18: Đạo hàm của hàm số y  log2sin x  
1 trên tập xác định là: 2c  os x 2cos x A. y '  B. y '  2sin x 1 2sin x 1 2c  os x 2cos x C. y '   D. y '  2sin x   1 ln10 2sin x  1ln10
Câu 19: Giá trị nhỏ nhất của hàm số 2 x y  trên đoạn  1  ;  1 . 1 A. 2 B. 1 C. D. 4 2
Câu 20: Đặt log 15  .
m Hãy biểu diễn log 15 theo . m 3 25 m m A. log 15  B. log 15  25 m 1 25 2m   1 m m C. log 15  D. log 15  25 m 1 25 2m   1
Câu 21: Một người gửi tiết kiệm với lãi suất 7,5% một năm và lãi hàng năm được nhập vào vốn.
Hỏi sau bao nhiêu năm người đó thu được số tiền gấp đôi số tiền ban đầu? A. 4 năm B. 6 năm C. 10 năm D. 8 năm
Câu 22: Cho x, y là các số thực dương thỏa mãn 2 2
9ln x  4ln y 12ln . x ln .
y Đẳng thức nào sau đây là đúng? A. 2 3 x y B. 3x  2y C. 3 2 x y D. x y
Câu 23: Số nghiệm của phương trình 2
log x  4log 3x  7  0 là: 3 3   A. 1 B. 2 C. 3 D. 0
Câu 24: Tập nghiệm của bất phương trình 2x 1
3   2.3x 1  0 trên tập số thực là:  ;0
  B. 0; C. 1; D.   ;1 
Câu 25:Cho phương trình 12
2 x 15.2x  8  0 , khẳng định nào sau dây đúng? A. Có một nghiệm. B. Vô nghiệm.
C. Có hai nghiệm dương.
D. Có hai nghiệm âm.
Câu 26: Phương trình x 1
5  25 x  6 có tích các nghiệm là : Trang 14/38          A. 1 21 1 21 1 21 log . B. log . C. 5. D. 5log . 5        2  5   5     2   2   x x
Câu 27:Phương trình 7  4 3 2 3  6 có nghiệm là: A. x 1
B. x  log 3. C. x  log 2  3 . D. x  log 2 . 2   2 2 3
Câu 28:Điều kiện xác định của phươg trình 2
log(x x  6)  x  log(x  2)  4 là A. x  3 B. x  2  C.  \ [  2;3] D. x  2
Câu 29: Phương trình log (3x  2)  3 có nghiệm là: 3 A. 11 x B. 29 x C. 25 x D. x  87 3 3 3
Câu 30: Phương trình 2 log (x 1)  6log
x 1  2  0 có tập nghiệm là: 2 2 A.3;1  5 B.1;  3 C.1;  2 D.1;  5
Câu 31:Nguyên hàm của hàm số f x 3
x  3x  2 là hàm số nào trong các hàm số sau? 4 2 4 A.   x 3x x F x    2x C .
B. F x 2 
 3x  2x C . 4 2 3 4 2 C.   x x F x    2x C .
D. F x 2
 3x  3x C . 4 2
Câu 32:Hàm số F x 3 2
 5x  4x  7x 120  C là họ nguyên hàm của hàm số nào sau đây?
A. f x 2
 5x  4x  7
B.. f x 2
15x  8x  7 2 3 2 C.   5x 4x 7x f x    .
D. f x 2
 5x  4x  7 . 4 3 2
Câu 33: Họ nguyên hàm của hàm số: 1 2
y x  3x  là x 3 3 A. x 3
F xx 3 2 
x  ln x C .
B. F x 2 
x  ln x C 3 2 3 2 3 x 3 C. 1 F x 2 
x  ln x C .
D. F x  2x  3  C . 3 2 2 x
Câu 34:Tìm nguyên hàm của hàm số f (x)  sin 2x A. 1
sin 2xdx   cos 2x C. B. 1
sin 2xdx  cos 2x C. 2 2
C. sin 2xdx  cos 2x C.
D. sin 2xdx  cos 2x C.  
Câu 35:Tìm nguyên hàm của hàm số 
f (x)  cos 3x    .  6  A. 1    
f (x)dx  sin 3x   C     .
B. f (x).dx  sin 3x   C     . 3  6   6  Trang 15/38 C. 1    
f (x)dx   sin 3x   C     . D. 1
f (x)dx  sin 3x   C     . 3  6  6  6 
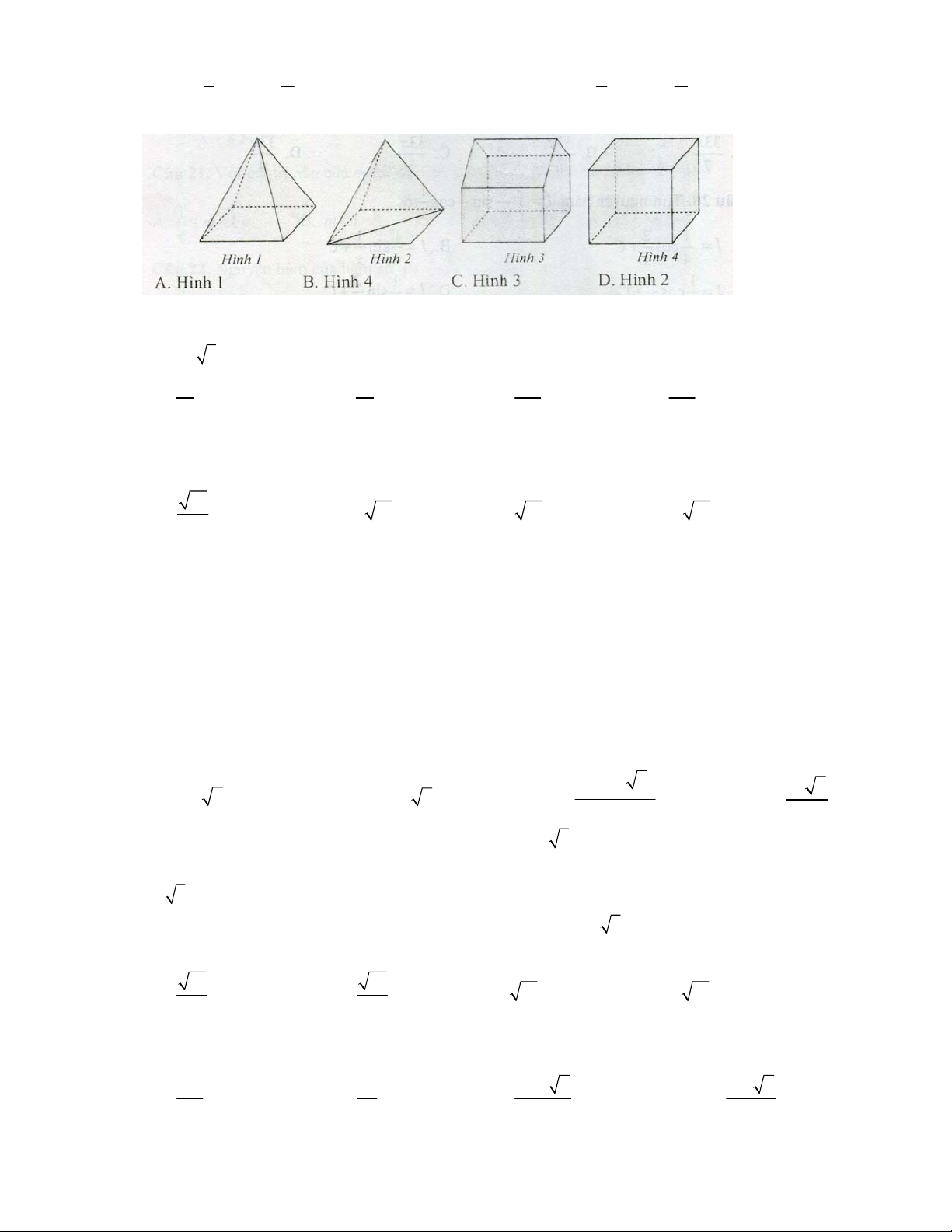
Câu 36: Hình nào dưới đây không phải là hình đa diện?
Câu 37: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với
đáy và SA a 3. Tính thể tích V của khối chóp S.ABC. 3 a 3 a 3 3a 3 3a A. V  B. V  C. V  D.V  2 4 4 2
Câu 38: Cho hình lăng trụ đứng ABC.A' B 'C ' có  0
AB  1, AC  2, BAC  120 . Giả sử D là trung
điểm của cạnh CC ' và  0
BDA'  90 . Tính thể tích V của khối lăng trụ ABC.A' B 'C '. A. 15 V  . B. V  3 15. C. V  15. D. V  2 15. 2
Câu 39: Cho đa diện H  có tất cả các mặt đều là tam giác. Khẳng định nào sau đây là đúng?
A. Tổng số các mặt của H  là một số chẵn
B. Tổng số các mặt của H  luôn gấp đôi tổng số các đỉnh của H
C. Tổng số các cạnh của H  là một số không chia hết cho 3
D. Tổng số các cạnh của H  luôn gấp đôi tổng số các mặt của H
Câu 40: Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc 0
60 . Tính diện tích toàn phần S của hình chóp S.ABC . D tp 2 a 4  7 2 A. 2 a 7 S a 7 B. 2
S a 1 7 C. S  D. S tptp tp 4 tp 4
Câu 41: Cho khối lập phương có độ dài đường chéo bằng 2 3 .
m Tìm thể tích V của khối lập phương đó. A. 3 24 3m B. 3 12m C 3 27m D. 3 8m
Câu 42: Cho tứ diện ABCD có AB  2, AC  3, AD  BC  4, BD  2 5,CD  5. Tính thể tích V của tứ diện ABC . D A. 15 V  B. 15 V  C.V  15 D. V  3 15 2 3
Câu 43: Tính thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh . a 3 3 3 3 A. 8a a 16a 2 2a 2 V  B. V  C. V  D. V  27 27 27 27 Trang 16/38
Câu 44: Trong không gian, cho tam giác ABC là tam giác đều cạnh a, gọi H là trung điểm của
cạnh BC. Tính độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC xung quanh trục AH. a A. a 3 l  B. l  C. l a D. l  2a 2 2
Câu 45: Cho mặt cầu S  có tâm I và bán kính R  3. Mặt phẳng P cắt mặt cầu theo giao
tuyến là đường tròn C có chu vi 2. Tính khoảng cách d từ tâm I đến mặt phẳng P. A. d  2 B. d  2 2 C. 7 d  D. d  7 2
Câu 46: Cho hình chóp S.ABC có  0
AB a, AC  2a, BAC  60 , cạnh bên SA vuông góc với đáy và
SA a 3. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC. A. a 7 a a a R  B. 55 R  C. 10 R  D. 11 R  2 6 2 2 1
Câu 47: Cho hình tròn tâm S, bán kính R  2.Cắt đi hình tròn rồi dán lại để tạo ra mặt xung 4
quanh của một hình nón N. Tính diện tích toàn phần S của hình nón N. tp 21 A. S  3
B. S   3 2 3 C. S
D. S   3 4 3 tptptp tp 4
Câu 48: Cho hình nón tròn xoay có chiều cao h  4, bán kính đáy r  3. Tính diện tích xung
quanh S của hình nón đã cho. xq A. S  15 B. S  12 C. S  9 D. S  6 xq xq xq xq
Câu 49: Cắt một khối trụ T bằng một mặt phẳng đi qua trục của nó, ta được một hình vuông có
diện tích bằng 9. Khẳng định nào sau đây là sai? 9
A. Khối trụ T có thể tích V
. B. Khối trụ T có diện tích toàn phần 4 27 S  . tp 2
C.Khối trụ T có diện tích xung quanh S  9.D. Khối trụ T có độ dài đường sinh là l  3. xq
Câu 50: Trong không gian, cho tam giác ABC là tam giác đều cạnh .
a Gọi S là diện tích của mặt
tròn xoay nhận được khi quay các cạnh AB và AC xung quanh trục . BC Tính S. 2  A. 2 a 3 S  a 3. B. S  . 2 2  a 3 4 3 2  a 3 2 3 C. S  . D. S  . 4 4 BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C A A D B D B B A A D B D B A B B D B D C C B B A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A D A B A A B B A A D B C A B D C D C B A C A A A Trang 17/38
SỞ GD&ĐT KIÊN GIANG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 -2018
TRƯỜNG THPT THẠNH ĐÔNG Bài thi môn Toán ĐỀ THI THỬ 04
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
(Đề thi có 5 trang)
(Biên soạn: Thầy Đặng Phú Cường)
Câu 1: Hàm số nào sau đây nghịch biến trên R: 1 A. 2x y = B. 4 2 y = x - - x C. y = D. 3 y = x - + 1 x
Câu 2: Điểm cực đại của đồ thị hàm số 3 2
y = x - 5x + 7x - 3 là æ7 32ö - æ7 32ö A. (0; ) 1 B. çç ; ÷÷ ç ÷ ç C. (1;0) D. ç ; ÷. çè3 27 ÷÷ø çè3 27÷÷ø
Câu 3: Cho các hàm số: - 3 2 x 1 y = x
- + 3x -1 (I ) y = (II) y = (III) 4 2
y = x - 2x + 3 (IV ) x 3
Đồ thị của hàm số nào có đường tiệm cận ? A. (II) và (III) B. Chỉ (II) C. Chỉ (I) D. (III) và (IV) 1
Câu 4: Với giá trị nào của m thì hàm số 3 2
y = - x + 2x - mx + 2 nghịch biến trên tập xác định của 3 nó? A. m = 4 B. m < 4 C. m £ 4 D. m > 4 Câu 5: Cho hàm số 3 2
y = ax + bx + cx + d (a ¹ 0). Hàm số đồng biến trên R khi:
A. y ' > 0, "x Î R
B. y ' £ 0, "x Î R
C. y ' < 0, "x Î R
D. y ' ³ 0, "x Î R Câu 6: Cho hàm số 3 2
y = 2x + 6x + 6x - 7 . Phát biểu nào sau đây là đúng?
A. Luôn nghịch biến trên R. B. Tăng trên ( ; -¥ - ) 1 và giảm trên (-1;+¥).
C. Luôn đồng biến trên R.
D. Tăng trên (-1;+¥) và giảm trên ( ; -¥ - ) 1 .
Câu 7: Hàm số nào sau đây có đồ thị là đường cong trong hình vẽ bên: y x x + 4 2x - 1 x - 4 x - 4 A. y = B. y = C. y = D. y = x - 2 x - 2 x - 2 x + 2 2
x - m + 3m
Câu 8: Tìm tất cả các giá trị của m để hàm số y =
nghịch biến trên từng khoảng xác định x + 2 của nó. A. m > 1 B. 1 < m < 2 C. m < 2 D. m Î  x - + 3
Câu 9: Cho hàm số y =
.Số tiệm cận của đồ thị hàm số bằng 2x - 1 A. 2. B. 1. C. 3. D. 4.
Câu 10: Đồ thị hàm số 3 2
y = x - 3x - mx có điểm cực đại nằm trên Oy khi: A. m = 0 B. m ¹ 0 C. m > 0 D. m < 0 Trang 18/38 Câu 11: Hàm số 3 2 2
y = x - 3mx + 3(m - 1)x + m đạt cực tiểu tại x = 2 thì m bằng A. Đáp án khác B. m = 1 C. m = 3 D. m= 3; m=1
Câu 12: Gọi x ,x tương ứng là điểm cực đại và điểm cực tiểu của hàm số 3 2
y = x - 3x + 2 . Trong CD CT
các mệnh đề sau hãy chọn mệnh đề ĐÚNG: A. x > x B. x - x = 2 C. x = 2x D. x + x = 0 CD CT CD CT CD CT CD CT 3 x - 3
Câu 13: Hình vẽ sau đây là đồ thị của hàm số y = + x + 1 2 2 Tìm m để phương trình 3
x - 3x - m = 0 có 3 nghiệm phân biệt A. –2 < m < 2 B. 0 < m < 2 C. 2 < m < 4 D. –2 < m < 4 x - 1 Câu 14: Gọi ,
A B là các giao điểm của đường thẳng y = 1 - x và đường cong y = . Tam giác x + 1
OAB ( O là gốc tọa độ) có diện tích là: 2 3 A. 3 B. C. D. 2 3 2 2 m x - 1 2
Câu 15: Gọi T là giá trị lớn nhất của hàm số y =
trên đoạn [2 ; 5]. Tìm m để T = x + 1 3 m é = -1 ê m é = 1 A. ê ê 5 B. m = 2 C. m = 1 D. m ê = m ê = -1 ê ê ë 2 ë
Câu 16: Đồ thị dưới đây là đồ thị của hàm số nào trong 4 đáp án sau: A. 2x y = B. 3x y = C. 4x y = D. 2 y = 2x
Câu 17: Cho biểu thức 2 log a 2 3 B = 3
- log a . log 25 với a dương, khác 1. Khẳng định nào sau đây là 5 a khẳng định đúng? A. 2 B = a - 4 B.B ³ 2a - 5 C. log B = 1 D.B > 3 2 ( ) a 4 -
Câu 18: Cho a, b, c là các số thực dương thỏa log 7 log 11 log 25 3 7 11 a = 27, 49 b = , c
= 11 . Tính giá trị biểu 2 2 2 thức log 7 log 11 log 25 3 7 11 T = a + b + c A.T = 76 + 11 B.T = 31141 C.T = 2017 D.T = 469
Câu 19: Trong các khẳng định sau, khẳng định nào sai ? Trang 19/38 x 4 2 A.(4 - x)
= x (x - 4) với x > 4
B. (a - 3) = (a - 3) với a " Î  x - 4 1 a + b C. 2 4 2 9a b = 3
- a.b với a £ 0 D. =
với a ³ 0, a -b ¹ 0 2 a -b a -b x x
Câu 20: Phương trình ( 2 - ) 1 + ( 2 + )
1 - 2 2 = 0 có tích các nghiệm là: A. -1 B. 2 C. 0 D. 1 x x æ1ö æ ç ÷ 1ö
Câu 21: Phương trình ç ÷ - m.ç ÷ ç ÷ + 2m + 1 = 0 ç
có nghiệm khi và chỉ khi m nhận giá trị: çè9÷÷ ç ø è3÷÷ø 1 1
A. - < m < 4 - 2 5
B. m < - 2 2 1
C. m ³ 4 + 2 5
D. m < - m ³ 4 + 2 5 2
Câu 22: Phương trình log 5 - 2x = 2 - x có hai nghiệm x ,x . Giá trị của x + x + x x là 2 ( ) 1 2 1 2 1 2 A. 2 B. 3 C. 9 D. 1
Câu 23: Phương trình lg x + lg(x - 9) = 1 có nghiệm là: A.x = 1 - và x = 10 B. x = 8 C.x = 9 D. 10 x = 1 Câu 24: Hàm số 2 y =
- ln(x - 1) có tập xác định là: 2 - x A. R \ { } 2 B. (-¥ ) ;1 È (1;2) C.( ; -¥ - ) 1 È (1;2) D. (1;2)
Câu 25: Phương trình 2 2
log x - 2 log x - 3 = 0 có hai nghiệm x ;x (x < x ) . Giá trị của biểu thức 5 25 1 2 1 2 1
A = 15x + x bằng: 1 2 5 28 1876 A. 28 B. C.100 D. 25 625 log x log 4x
Câu 26: Cho phương trình 2 8 =
khẳng định nào sau đây đúng: log 2x log 8x 4 16
A. Phương trình này có hai nghiệm
B. Tổng các nghiệm là 17
C. Phương trình có ba nghiệm
D. Phương trình có 4 nghiệm 2 x 4
Câu 27: Phương trình log - 2 log (2x) 2
+ m = 0 có một nghiệm x = -2 thì giá trị của m là: 4 4 4 A.m = 6 B.m =  6 C.m = 8 D.m = 2 2
Câu 28: Giá trị của m để phương trình x x 1 4 . m 2 + -
+ 2m = 0 có hai nghiệm x ;x thỏa mãn 1 2 x + x = 3 là 1 2 3 A. m = 3 B. m = 4 C. m = 0 D. m = 2
Câu 29: Tập nghiệm của bất phương trình 4x 7.2x - - 8 ³ 0 là: A. ( ; -¥ -1] È [8;+ )
¥ B. [0;4] C. ( ; -¥ 3] D. [3; ) +¥
Câu 30: Giải bất phương trình: log 2x - 3 > -1 1 ( ) 5 Trang 20/38 3 3 A.x < 4 B. x >
C. 4 > x > D.x > 4 2 2
Câu 31: Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu.
A.F’(x) = f (x), "x Î K
B. F’(x) ¹ f (x), "x Î K
C. f ’(x) = F (x), "x Î K
D. f ’(x) ¹ F (x), "x Î K 1
Câu 32: Họ nguyên hàm của hàm số f (x) = 2x - cos x - . x A. 2
x - sin x - ln x + C B. 2
x + sin x - ln x + C . C. 2
x - sin x - ln x D. 2
x + sin x - ln x + 1
Câu 33: Tính nguyên hàm ( - ò )9
1 x dx , ta được kết quả là. 1 1 A.F (x) =
(1-x)10 +C
B. F (x) = - (1 - x)10 +C 10 10
C. F (x) = ( - x)10 10 1 +C
D. F (x) = 10 - ( - x)10 1 +C
Câu 34: Tìmra kết quả sai trong các kết quả sau: x e sin xdx dx = 2 x e +C ò
dx = 1 + 2 cos x +C ò A. x B. 1 + 2 cos x 2x -2 + - e e x 1 ln x 2 x x 2
(e + e ) dx = 2x + - +C ò 3 dx = (1 + ln x) +C ò C. 2 2 D. x 3 2 3 - 2 cot x 2 3 - 2 cot x
Câu 35: F(x) là một nguyên hàm của hàm sốy = . Nếu F(x) = 10 thì dx ò 2 cos x 2 cos x bằng:
A. 3tanx - 2cotx - 5
B. 3tanx - 2cotx + 5
C. 3tanx + 2cotx + 5
D. 3tanx + 2cotx - 5 2 a 3
Câu 36: Cho hình chóp tam giác S.ABC có diện tích đáy B =
, đường cao h = a . Thể tích V 4
của khối chóp S.ABC là 3 3a 3 3a 3 a 3 3a A. V = B. V = C. V = D. V = 4 8 4 12
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt
(ABCD), góc giữa đường thăng SC và mặt phẳng (ABCD) bằng 450. Tính thể tích V của khối chóp S.ABCD. 2 4 2a 3 a 3 2a A. V = B. 3 V = 2a C. V = D. V = 3 3 3
Câu 38: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, đường cao h = 2a. Thể tích V của khối chóp S.ABCD . 3 2a 3 a A. V = B. 3 V = a C. V = D. 3 V = 2a 3 3
Câu 39: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA ^ (ABC ). Cạnh bên SC hợp với
đáy một góc 450. Thể tích V của khối chóp S.ABC là 3 3a 3 3a 3 3a 3 3a A. V = B. V = C. V = D. V = 6 12 4 3 Trang 21/38
Câu 40: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA ^ (ABCD)và SA = a 2 . Thể tích
V của khối chóp S.ABCD là 3 2a 3 2a 3 2a A. V = B. V = C. 3 V = 2a D. V = 3 6 3
Câu 41: Cho hình chóp S.ABC có SA ^ (ABC ), tam giác ABC vuông tại B,AB = a ,AC = a 3 ,
SB = a 5 . Thể tích khối chóp S.ABC bằng 3 a 15 3 3a 6 3 a 6 3 a 2 A. B. C. D. 6 4 6 3
Câu 42: Cho hình lập phương ABCD.A' B'C ' D' cạnh a. Gọi O trung điểm AC’. Khi đó thể tích của
khối tứ diện AA’B’O là: 3 a 3 a 3 a 3 a 2 A. B. C. D. 8 12 9 3
Câu 43: Tính thể tích khối lập phương ABCD.A' B'C ' D' , biết BD = 2a . 3 a 3 2 2a A. B. 3 2 2a C. 3 a D. 3 3
Câu 44: Cho lăng trụ ABC.A' B'C ' có đáy là tam giác đều. Hình chiếu của A’ lên (ABC ) trùng với
trung điểm BC. AB = AA' = 2a . Thể tích khối chóp B'A' BC bằng mấy ? 3 3 2 3 A. 3 a B. 3 3a C. 3 a D. 3 a 3 4 5
Câu 45: Cho hình chóp S.ABC có SA vuông góc với (ABC )và tam giác ABC vuông tại B. Tâm mặt
cầu ngoại tiếp S.ABC là:
A. Trung điểm SO với O là tâm đường tròn ngoại tiếp tam giác ABC . B. Trung điểm SB C. Trung điểm SA D. Trung điểm SC
Câu 46: Cho khối trụ có thể tích bằng 24p . Nếu tăng bán kính đường tròn đáy lên gấp 2 lần thì thể tích khối trụ mới là A. 96p B. 48p C. 32p D. 192p
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy,
SA = a 3 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là 5 5 3 A. a B. a C. 5a D. a 2 2 4
Câu 48: Cho tam giác ABC vuông tại B, cạnh AB = a, BC = 2a , quay xung quanh cạnh AB tạo nên
một hình nón. Thể tích khối nón tạo bởi hình nón trên là: 1 4 3 A. 3 3 a p B. 3 a p C. 3 a p D. 3 a p 3 3 4
Câu 49: Cho hình lăng trụ có chiều cao h, diện tích đáy bằng S. Thể tích khối lăng trụ đó được tính bằng công thức: 1
A. V = h.S
B. V = h.S
C. V = 2 h p .S D. 2 V = 2R h 3
Câu 50: Cho hình chóp S.ABCD đáy là hình vuông. Chu vi đáy bằng 8a. SA vuông góc với đáy. SC tạo
với đáy góc 600. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng mấy ? 3 64 2 a p 3 64 2a 3 16 2 a p 3 32 a p A. B. C. D. 3 3 3 3 Trang 22/38 BẢNG ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ĐA D C B D D C C B A A B B A C D A A Câu 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 ĐA D A A D A D D A A D B D C A A B B Câu 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 ĐA C D D A D B B D B A D A A C A A
SỞ GD&ĐT KIÊN GIANG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 - 2018
TRƯỜNG THPT THẠNH ĐÔNG Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề. ĐỀ THI THỬ 05
(Biên soạn: Cô Kiều Thị Tho)
Câu 1: Cho bảng biến thiên của một hàm số như hình dưới đây. Hỏi hàm số đó là hàm số nào trong các hàm số cho dưới đây? A. 3 2
y x  2x  4 . x B. 3 2
y x  3x  3 . x C. 3 2
y  x  2x  . x D. 3 2
y  x 3x 3 . x
Câu 2: Cho K là một khoảng và hàm số y f x có đạo hàm trên K.Giả sử f ' x  0 chỉ tại một số
hữu hạn điểm trên K.Khẳng định nào sau đây là đúng?
A. Nếu f ' x  0, x
  K thì hàm số là hàm hằng trên K.
B. Nếu f ' x  0, x
  K thì hàm số nghịch biến trên K.
C. Nếu f ' x  0, x
  K thì hàm số đồng biến trên K.
D. Nếu f ' x  0, x
  K thì hàm số nghịch biến trên K.
Câu 3: Tung độ giao điểm của hai đồ thị hàm số 3x y
và y  11 x là : A.11 B. 3 C. 9 D. 2 Câu 4: Cho hàm số 3
y x  3x xác định trên .
 Khẳng định nào sau đây là đúng ? A. x  3x B. yy  0
C. x  3x D. yy  0 CD CT CD CT CT CD CD CT
Câu 5: Tìm phương trình các đường tiệm cậnđứng của đồ thị hàm số C 3
: y x 1 . x 1 A. x  1  B. x  1
C. x  3 D. C không có tiệm cận đứng. Trang 23/38
Câu 6: Cho hàm số y f x liên tục trên nửa khoảng  1
 ;2, có bảng biến thiên như hình vẽ bên.
Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên khoảng 0;  1 .
B. Đồ thị hàm số không đi qua điểm M 2;5. C. miny  2. 1;2 D. max y  5.  1;  2 2x 1
Câu 7: Tìm tọa độ giao điểm M của đồ thị hàm số y  và trục tung. x  2  1   1   1  A. M 0;  .   B. M 0; 2  . C. M ;0 .   D. M  ;0 .    2   2   2  3x  2
Câu 8: Cho đồ thị hàm số C : y
. Khẳng định nào sau đây là sai? 2 x  3x
A. Đường thẳng y  3 là tiệm cận ngang của đồ thị C.
B. Đường thẳng x  0 là tiệm cận đứng của đồ thị C.
C. Đường thẳng y  3 là tiệm cận ngang của đồ thị C.
D. Đường thẳng x  2 là tiệm cận đứng của đồ thị C. x 1 khi x  0
Câu 9: Cho hàm số y f x   2
x  3x 1 khi x  0.
biết rằng hàm số y f x có đồ thị C
như hình vẽ bên. Khẳng định nào sau đây là sai?
A. Hàm số đã cho không có đạo hàm tại điểm x  0.
B. Hàm số đã cho có 2 điểm cực trị.
C. Hàm số đã cho liên tục trên . 
D. Hàm số đã cho đồng biến trên .  5
Câu 10: Cho đồ thị hàm số C 3 2
: y  x  2x  .
x Tiếp tuyến tại gốc tọa độ O của C cắt C tại 3
điểm thứ hai M . Tìm tọa độ điểm M .  10   10   10   10  A. M 2; .   B. M 2;   .   C. M 2;  .   D. M 2; .    3   3   3   3 
Câu 11: Tìm các giá trị thực của tham số m để hàm số 3
y x  m   2
1 x  2mx  3 đạt cực trị tại điểm x  1.  5 1 A. m  2.  B. m  . C. m   . D. m  1. 4 4
Câu 12: Xét x, y là các số thực thuộc đoạn 1;2. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất x y
của biểu thức S   . Tính M  . m y x 5 9
A. M m  .
B. M m  4.
C. M m  .
D. M m  3. 2 2 Trang 24/38
Câu 13: Đồ thị hình bên là của hàm số: y 4 x 4 x A. 2 y   x 1 B. 2 y    x 1 1 4 4 x -3 -2 -1 1 2 3 4 x 4 2 x x -1 C. 2 y
 2x 1 D. y   1 -2 4 4 2 -3 -4 -5
Câu 14: Đồ thị hàm số 3 2
y  x  3x  2 có dạng: A B C D y y y y 3 3 3 3 2 2 2 2 1 1 1 1 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -1 -1 -2 -2 -2 -2 -3 -3 -3 -3
Câu 15: Tìm m để hàm số 4
y x  m   2 2
1 x  3 có ba cực trị A. m  0 B. m  1  C. m 1 D. m  0 3 2
Câu 16: Rút gọn biểu thức S  2ln a  3log e   a a a  0,  1 . ln a log e a A. S  2. B. S 1. C. S  0. D. S  3.   a   3 1 3 1
Câu 17: Rút gọn biểu thức P  a  0. 53 4 5 a .a A. P  7a B. P  5a C. P a D. P  9a
Câu 18: Tính đạo hàm của hàm số   cos2x f x e tại x  . 6 3      A.  2 f '  e   B. f '  3e    6   6  3      C.  2 f '  e   D. f '   3e    6   6 
Câu 19: Tập xác định của hàm số y  log 3x  4 là: 2    4 
A. D  1; B. D   ;     3   4  C. D   ;    D. D   1  ;  3 
Câu 20: Cho các số thực k và r thỏa mãn: .2r  3; .4r k k 15. Tìm r. A. r  log 3 B. r  log 5 C. r  log 5 D. r  log 2 2 2 3 3
Câu 21: Số nghiệm của phương trình 2 2 x x 2 2
 2 xx  3 là: A. 2 B. 3 C. 1 D. 4
Câu 22: Tập nghiệm của bất phương trình log x 1  2log 5  x  1 log x  2 là: 2   4   2   A. S  3;5 B. S  2;3 C. S  2;5 D. S   4;  3 Trang 25/38
Câu 23: x  log 3 là nghiệm của phương trình nào trong các phương trình sau? 2 x A. log  2x 1
3.3   4  x log 3  log 9 B. x x    3 2 1 3 8 2 3 2 2  2 4 x C. x x    3 2 1 3 8 2 2 D. log  2x 1 2.2  1  4 2 
Câu 24: Gửi tiết kiệm ngân hàng với số tiền M , theo thể thức lãi kép liên tục và lãi suất mỗi năm là r thì
sau N kỳ gửi, số tiền nhận được cả vốn lẫn lãi được tính theo công thức . Nr
M e . Một người gửi tiết kiệm
số tiền 100 triệu đồng theo thể thức lãi kép liên tục, với lãi suất8% một năm, sau 2 năm số tiền thu về cả
vốn lẫn lãi là bao nhiêu? A. 0,16 100.e (Triệu đồng) B. 0,08 100.e (Triệu đồng) C.  0,16 100 e   1 (Triệu đồng) D.  0,08 100 e   1 (Triệu đồng) C©u 25: NÕu 2 3
log x  8 log ab  2 log a b (a, b > 0) th× x b»ng: 7 7 7 A. 4 6 a b B. 2 14 a b C. 6 12 a b D. 8 14 a b
Câu 26. Tìm tất cả các giá trị thực của tham số m để hàm số 2
y  ln(x  2x m 1) có tập xác định là 
A. m  0
B. 0  m  3 C. m  1  hoặc m  0
D. m  0 x 1 
Câu 27: Tập xác định của hàm số y  ln   là:  x  2  A. ( ;  1) (2; )  . B. [1;2) . C. ( ;  1]. D. (2; )  .
Câu 28. Tìm tất cả các giá trị thực của tham số m để phương trình x x 1 4 2  
m  0 có hai nghiệm thực phân biệt.
A. m  (;1)
B. m  (0; )
C. m  (0;1] D. m  (0;1)
Câu 29. Nghiệm của bất phương trình log2 x 1 2 log4 5 x 1 log2 x 2 là:
A, 1 x 2 B. 4 x 3 C. 2 x 5 D. 2 x 3 2 x 2x 3
C©u 30: BÊt ph−¬ng tr×nh:  2 
  2  cã tËp nghiÖm lμ: A. 2;5 B. 2;  1 C. 1; 3 D. KÕt qu¶ kh¸c
Câu 31: Tìm nguyên hàm x xe I e d . x  A. x e
I e C B. x e 1 I e   C C. x
I e C D. x 1 I e    C
Câu 32: Tìm nguyên hàm I xd . x  2 3 3 2 3 3x 2 3x 2 2x 3 2x A. I   C B. I   C C. I   C D. I   C 2 2 3 3
Câu 33: Nguyên hàm của  3 2x 1 3x  là: 3  6x  A. 2  3 x x  x   C B. 2  2 x 1 3x   C C.  3 2x x  x   C D. 2 x 1     C  5  1 1
Câu 34: Nguyên hàm của 2  x  là: 2 x 3 4 2 x  x  3 3 x 1 x 4 2 x  x  3 3 1 x A.   C B.     C C.  C D.    C 3x 3 x 3 3x x 3
Câu 35: Nguyên hàm của hàm số   3 f x  x là: Trang 26/38 3 2 3 x 4x 4x A. Fx   C B.   3 3x x F x   C C. Fx   C D. Fx   C 4 4 3 3 x 3 2 3 x
Câu 36: Cho khối lăng trụ tam giác ABC.A' B 'C ' có thể tích V. Khi đó, thể tích của khối tứ diện
A' B ' BC là: V V V 2V A. B. C. D. 4 3 2 3
Câu 37: Cho lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác đều cạnh bằng1, AA'  3. Tính khoảng
cách d từ điểm A đến mặt phẳng  A' BC. 2 15 15 3 3 A. d  B. d  C. d  D. d  5 5 2 4
Câu 38: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A AB a, mặt bên SBC là tam
giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V của khối chóp S.ABC. 3 a 2 3 a 3 a 2 3 a 2 A. V  B. V  C. V  D. V  12 6 6 3
Câu 39: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SA vuông góc với đáy, mặt phẳng
SBC tạo với mặt đáy một góc 0
60 . Tính khoảng cách từ A đến mặt phẳng SBC . a 6 3a 3a a 13 A. . B. . C. . D. . 6 4 2 4
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt đáy và
SC a 5 . Tìm thể tích khối chóp S.ABCD . 3 a 3 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. . 12 6 3
Câu 41. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hai mặt bên SAB và SAC cùng vuông
góc với đáy. Tính thể tích khối chóp biết SC a 3 3 2a 6 3 a 6 3 a 3 3 a 3 A. B. C. D. 9 12 4 2
Câu 42. Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC và (SBC) hợp
với đáy (ABC) một góc 60o. Tính thể tích hình chóp 3 a 3 3 a 3 3 a 3 a 3 A. B. C. D. 8 12 4 4
Câu 43. Cho khối chóp S.ABCD có đay ABCD là hình chữa nhật tâm O , AC  2AB  2a, SA vuông góc với
đáy. Tính thể tích khối chóp biết SD a 5 3 a 5 3 a 15 3 a 6 A. B. C. 3 a 6 D. 3 3 3
Câu 44: Hình nào sau đây có thể không nội tiếp một mặt cầu?
A. Hình chóp lục giác đều B. Hình hộp chữ nhật C. Hình tứ diện D. Hình chóp tứ giác
Câu 45: Cho hình chóp tam giác đều S.ABC có AB a, cạnh bên SA tạo với đáy một góc 0 30 . Một
hình nón có đỉnh là S, đáy là hình tròn ngoại tiếp tam giác ABC. Tính số đo góc ở đỉnh  của hình nón đã cho. A. 0   120 B. 0   60 C. 0   150 D. 0   30
Câu 46: Cắt một khối nón N bằng một mặt phẳng đi qua trục của nó, ta được một tam giác vuông cân có
diện tích bằng 8. Khẳng định nào sau đây là sai? Trang 27/38
A. Khối nón N có diện tích xung quanh S  16 2. xq
B. Khối nón N có diện tích đáy S  8.
C. Khối nón N có độ dài đường sinh là l  4. 16 2
D. Khối nón N có thể tích V  . 3
Câu 47: Một bình đựng nước dạng hình nón (không có đáy),
đựng đầy nước. Người ta thả vào đó một khối cầu có đường
kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là   3 18
dm . Biết rằng khối cầu tiếp xúc với
tất cả các đường sinh của hình nón và đúng một nửa của khối
cầu chìm trong nước (hình bên). Tính thể tích nước còn lại trong bình.   3 6 dm  B.   3 12 dm  C.   3 54 dm  D.   3 24 dm  A.
Câu 48: Diện tích xung quanh của hình trụ có bán kính đáy bằng 3cm và chiều cao bằng 4cm là: A. 2 36 cm . B. 2 42 cm . C. 2 24 cm . D. 2 12 cm .
Câu 49: Mặt cầu có bán kính bằng 10cm. Diện tích mặt cầu này bằng: 400 100 A. 2 400 cm . B. 2 cm . C. 2 100 cm . D. 2 cm . 3 3
Câu 50: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA vuông góc với mặt phẳng
( ABCD) và SA  2 .
a Tính diện tích S của mặt cầu ngoại tiếp hình chóp S. . ABCD A. 2 S  6 a . B. 2 S  12 a . C. 2 S  3 a . D. 2 S  36 a . BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D D C B B D A D D D C C C C B C C D A B A B B A B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
D A D D C A C D A B B B A C D B A D D A A A C A A Trang 28/38
SỞ GD&ĐT KIÊN GIANG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 - 2018
TRƯỜNG THPT THẠNH ĐÔNG Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề. ĐỀ THI THỬ 06
(Biên soạn: Thầy Trịnh Minh Hoạt)
Câu 1. Tìm tập xác định -
D của hàm số y = (x - x + ) 2016 2 3 2 . A. D = .  B. D =  \ {1; } 2 . C. D = (1; ) 2 . D. D = (-¥ ) ;1 È (2;+¥). Câu 2. Cho hàm số 3 2
y = x + 3x - 2 . Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đồng biến trên khoảng ( ; -¥ - ) 2 và (0;+¥).
B. Hàm số nghịch biến trên khoảng ( ; -¥ - ) 2 và (0; ) +¥ .
C. Hàm số đồng biến trên khoảng ( ; -¥ ) 0 và (2;+¥) .
D. Hàm số nghịch biến trên khoảng (-2; ) 1 .
Câu 3. Hỏi hàm số 2
y = 2x - x đồng biến trên khoảng nào? A. (-¥ ) ;2 . B. (0; ) 1 . C.(1; ) 2 . D. (1;+ ) ¥ . Câu 4. Cho hàm số 1 4 1 2
y = - x + x - 3 . Khẳng định nào sau đây là khẳng định đúng? 4 2
A. Hàm số đạt cực tiểu tại x = 0.
B. Hàm số đạt cực tiểu tại x = 1.
C. Hàm số đạt cực đại tại x = 0.
D. Hàm số đạt cực tiểu tại x = 3. -
Câu 5. Xét f (x) là một hàm số tùy ý. Khẳng định nào sau đây là khẳng định đúng?
A. Nếu f (x) có đạo hàm tại x và đạt cực đại tại x thì f '(x = 0 . 0 ) 0 0
B. Nếu f '(x = 0 thì f (x) đạt cực trị tại x = x . 0 ) 0
C. Nếu f '(x = 0 và f "(x > 0 thì f (x) đạt cực đại tại x = x . 0 ) 0 ) 0
D. Nếu f (x) đạt cực tiểu tại x = x thì f "(x < 0. 0 ) 0
Câu 6. Tìm tiệm cận ngang của đồ thị hàm số 2x + 1 y = . 1 - x A.y = 2. B. y = -2. C. x = 1. D. x = 2. -
Câu 7. Hỏi phương trình 2 2 x - 5 x -1 1 2 = có bao nhiêu nghiệm? 8 A. 0. B. 1. C. 2. D. 3.
Câu 8. Giải phương trình log (x - 4) = 0 . 3 A. x = 1. B. x = 6. C. x = 5. D. x = 4.
Câu 9.Biết F(x) là một nguyên hàm của hàm số f x 2
 3x  2x 1 và F  
1  2 . Trong các khẳng định
sau, đâu là khẳng định đúng? A. F x 3 2
x x x  2
B. F x  6x  4 C. F x 3 2
x x x 1
D. F x 3 2
x x x 1
Câu 10. Tìm giá trị nhỏ nhất của hàm số 1 - x y = trên é0;1ù 2x - 3 êë úû . A. 1 min y = 0. B. miny = - .
C. miny = -1. D. miny = -2. é0;1ù é ù é ù é ù êë úû 0;1 êë úû 3 0;1 êë úû 0;1 êë úû
Câu 11. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y = x - 3mx + 3m + 1 có 2 điểm cực trị. A. m > 0 B. m < 0 C. m ³ 0 D.m ¹ 0 Trang 29/38
Câu 12.BiếtF(x)làmộtnguyênhàmcủahàmsố f x 1 
và F 3  3 . TìmF(8). x 1 A.4 B.5 C.2 D.7
Câu 13. Tính đạo hàm của hàm số 1 2 3 x y - = . A. 1 2 ' ( 2).3 x y - = - . B. 1 2 ' ( 2 ln 3).3 x y - = - . C. 1 2 ' 3 x y - = .ln 3. D. ( ) 2 ' 1 2 3 x y x - = - .
Câu 14. Tìm giá trị lớn nhất của hàm số 2x
y = x +e trên đoạn é0;1ù êë úû . A. 1. B. 2 e + 1. C. 2 e . D. 2e.
Câu 15. Tìm tập xác định D của hàm số y = log 6 - x. 2 A. D =  \ { } 6 . B. D = (6;+ ) ¥ . C. D ( ;6ù = -¥ . úû D. D = (- ; ¥ ) 6 .
Câu 16. Cho a > 0 , a ¹ 1 , x,y là 2 số dương. Khẳng định nào sau đây là khẳng định đúng? x log x x A. log a = . B. x - y = a ( ) log log a . a y log y log y a a C. x log
= log x - log y. D. log x - y = x - y a ( ) log log . a a a y a a
Câu 17. Cho a > 1 . Khẳng định nào sau đây là khẳng định đúng? 1 3 2 A. - a 3 1 1 1 a > . B. 3 a > a. C. < . D. > 1. 5 a 2016 2017 a a a
Câu 18. Tính đạo hàm của hàm số y = log (2x - 2) . 3 A. 1 y ' = . B. 1 y ' = . C. 1 y ' = . D. 1 y ' = . (2x - 2)ln 3 (x - 1) ln 3 x -1 2x - 2
Câu 19. Họ nguyên hàm của hàm số f x 2  x x 1 là: 2 1
A. F x   2 x   2 1 x 1  C
B. F x   2 x   2 1 x 1  C 3 3 1 2 C. F x 2  x 1  C D. F x 2  x 1  C 3 3
Câu 20. Đặt log 4 = a, log 3 = b . Hãy biểu diễn log 12 theo a và b . 5 5 25 A. ab a +b 2(a +b). B. . C. . D. 2 . ab 2 2
Câu 21. Giải bất phương trình 2 log x -1 £ log 5 - x + 1. 2 ( ) 2 ( ) A. 1 < x < 3. B. 1 £ x £ 3. C. -3 £ x £ 3. D.1 < x £ 3. y
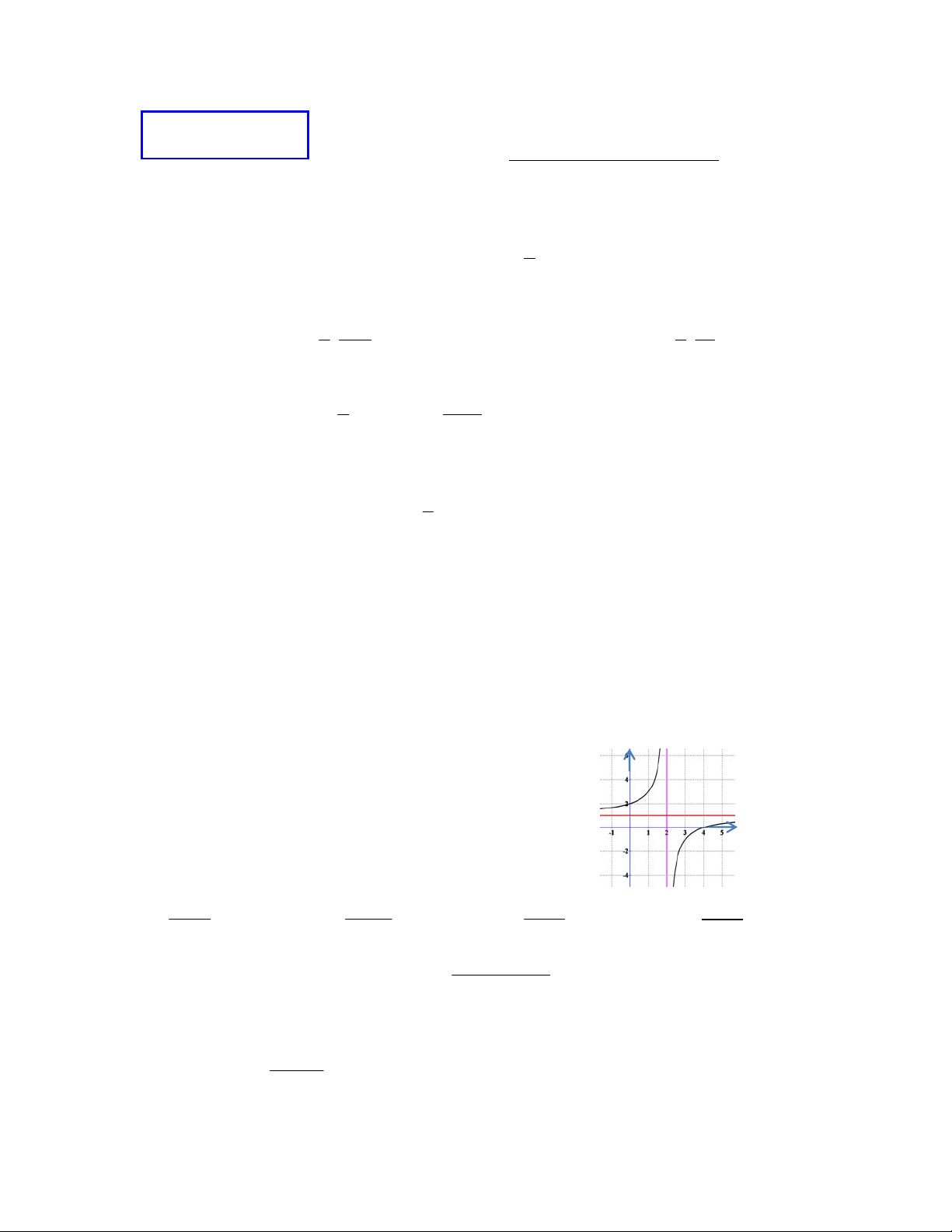
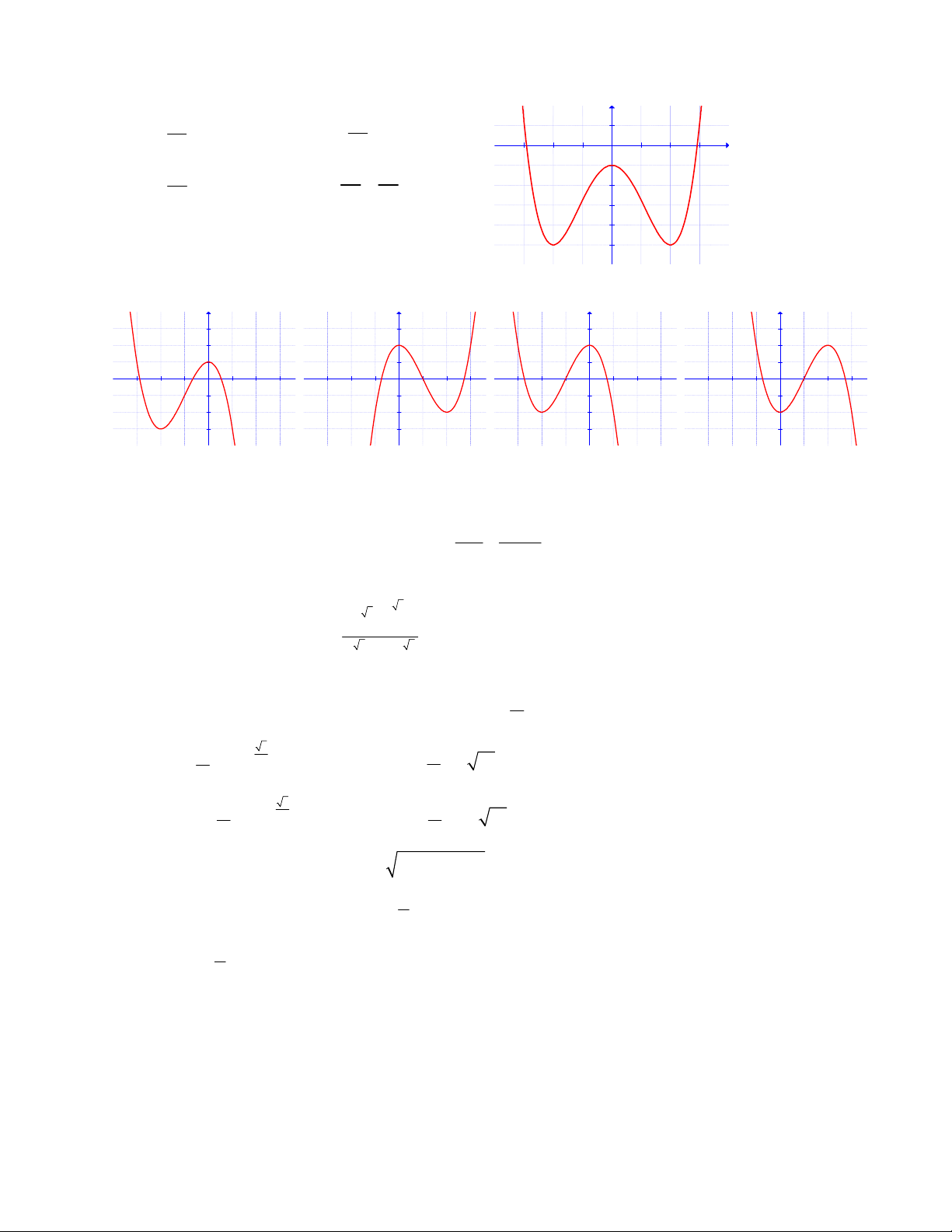
Câu 22. Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào? A. 4 2 y = x - 4x + 3. B. 4 y = x - + 4x² - 3. C. 4 2 y = x + 4x - 5. D. 4 y = x - + 4x² + 3. x
Câu 23. Một người gửi vào ngân hàng 100 triệu đồng với lãi suất 0,5% một tháng, sau mỗi tháng lãi suất
được nhập vào vốn. Hỏi sau một năm người đó rút tiền thì tổng số tiền người đó nhận được là bao nhiêu? A. 12
100.(1, 005) (triệu đồng). B. 12
100.(1 + 12´ 0, 005) (triệu đồng). Trang 30/38
C.100´1, 005 (triệu đồng). D. ( )12 100. 1, 05 (triệu đồng).
Câu 24. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 3 2
y = x - 3x - 9x + m cắt trục
hoành tại ba điểm phân biệt. A.-5 < m < 27. B. -27 < m < 5. C. -5 £ m £ 27. D. m > 27.
Câu 25. Tìm tất cả các giá trị thực của tham số m sao cho phương trình 4 2
x - 2x - 3 = m có 4 nghiệm phân biệt. A. -1 < m < 1. B.-4 < m < -3. C. m < 4. - D. m > 1. -
Câu 26. Tìm tất cả các giá trị thực của tham số mx + m sao cho hàm số 1 y =
đồng biến trên khoảng x + m (1;+¥) A. m < 1 - hoặc m > 1 . B. m > 1. C. m ³ 1 . D. -1 < m < 1.
Câu 27. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2 y = x
- + 3x - mx + m nghịch biến trên  . A. m > 3. B. m < 3. C.m ³ 3 . D.m £ 3 .
Câu 28. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y = x - 3x + mx -1 có hai điểm cực
trị x , x thỏa mãn 2 2 x + x = 3. 1 2 1 2 A. 3. - B. 3. C. 3 - . D. 3 . 2 2
Câu 29.Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3
y = x - ( m + ) 2 3 2 1 x + (12m + ) 5 x đồng biến trên trên khoảng(4; ) +¥ . A. 29 m > . B. 29 m ³ . C. 29 m £ . D. 29 m < . 36 36 36 36 x x - Câu 30. Cho + + 9x 9 x - +
= 14 . Tính giá trị của biểu thức K = 8 3 3 . 1 - 3x - 3 x - A. 5 - . B. 4 . C. 4. - D. 2. 2 5
Câu 31. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 3 2
y = x + (m - 1)x - 3mx + 1 đạt cực trị tại điểm x = 1. 0 A. m = 1. -
B.m = 1. C. m = 2. D. m = 2. -
Câu 32. Tìm tất cả các giá trị thực của tham số m sao cho hàm số 4 2 2
y = x + 2mx + m + m có đúng một điểm cực trị. A.m ³ 0.
B. m > 0. C. m £ 0. D. m < 0.
Câu 33. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 4 2
y = x - 2mx + 2m có ba điểm
cực trị tạo thành tam giác có diện tích bằng 1 . A. 1 m = . B. m = 3. C. m = 1. - D.m = 1. 5 4
Câu 34. Tìm nguyên hàm của hàm số f (x)  2x 1. 1 1
A. f (x)dx  (2x 1) 2x 1  C. 
B. f (x)dx   2x 1  C.  3 3 1 2
C. f (x)dx  2x 1  C. 
D. f (x)dx  (2x 1) 2x 1  C.  2 3
Câu 35. Hỏi hình mười hai mặt đều có bao nhiêu đỉnh?
A. Mười hai. B. Mười sáu. C. Hai mươi. D. Ba mươi.
Câu 36. Số mặt phẳng đối xứng của khối tứ diện đều là: A. 9. B. 2. C. 6. D. 3. Trang 31/38
Câu 37.Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ; SA ^ (ABCD) và SB = 3a . Tính
thể tích khối chóp S.ABC . D 3 3 3 A. 2a 2a 2a . B. 3 2a . C. . D. . 2 3 6
Câu 38.Cho khối lăng trụ tam giác đều, độ dài tất cả các cạnh bằng a . Tính thể tích khối lăng trụ đó. 3 3 3 3 A. 2 2a a 2a 3a . B. . C. . D. . 3 3 3 4
Câu 39. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên bằng 2a . Tính thể tích khối chóp S.ABC . 3 3 3 3 A. 11a 11a a 11a . B. . C. . D. . 96 4 3 12
Câu 40.Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,biết AB = 2a; AD = a .Hình chiếu của S
lên đáy là trung điểm H của cạnh AB , góc tạo bởi SC và đáy là 0
45 . Tính thể tích khối chóp S.ABCD. 3 3 3 3 A. 2 2a a 2a 3a . B. . C. . D. . 3 3 3 2
Câu 41. Cho hình lập phương ABCD. ’ A B’C’ ’
D có cạnh bằng a . Tính thể tích của tứ diện ’ ACD ’ B . 3 3 3 3 A. 6a 2a a a . B. . C. . D. . 4 3 4 3
Câu 42. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB = a . Gọi I là trung điểm
AC , tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp
S.ABC , biết góc giữa SB và mặt phẳng đáy bằng 0 45 . 3 3 3 3 A. 2a 3a 2a 3a . B. . C. . D. . 12 12 4 4
Câu 43. Cho khối trụ có thể tích bằng 24p . Hỏi nếu tăng bán kính đường tròn đáy của khối trụ đã cho lên
2 lần thì thể tích khối trụ mới bằng bao nhiêu? A. 96 . p B. 48 . p C. 72 . p D. 12 . p
Câu 44. Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có
cạnh bằng 3a . Tính diện tích toàn phần của hình trụ đó. 2 2 2 A. 2 27 a p 3 a p 13 a p p 3a . B. . C. . D. . 2 2 6
Câu 45. Cho một khối trụ có khoảng cách giữa hai đáy bằng 10, biết diện tích xung quanh của khối trụ
bằng 80p . Tính thể tích của khối trụ đó. A. 640p p . B. 640 . p C. 160 . D.160 . p 3 3
Câu 46. Cho hình nón có bán kính đáy là 4a , chiều cao là 3a . Tính diện tích toàn phần của hình nón đó. A. 2 36 a p . B. 2 20 a p . C. 2 15 a p . D. 2 24 a p .
Câu 47. Cắt một hình nón bởi một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh
bằng a . Tính thể tích của khối nón tương ứng. 3 3 3 A. 3 2 3 a p 3 a p 3 a p 3 a p . B. . C. . D. . 9 24 8
Câu 48. Một máy bơm nước có ống bơm hình trụ đường kính bằng 50(cm) và tốc độ dòng nước chảy
trong ống là 0,5(m/s). Hỏi trong một giờ máy bơm đó bơm được bao nhiêu nước? (giả sử nước lúc nào cũng đầy ống). A. 225p ( p 3 225 m ). B. p ( 3 225 m ). C p ( 3 450 m ). D. ( 3 m ). 6 2
Câu 49. Cho hình chóp S.ABC có    0
ASB = ASC = CSB = 60 , SA = 3,SB = 6,SC = 9 . Tính khoảng cách d
từ C đến mặt phẳng (SAB) . A. d = 9 6. B. d = 2 6. C. 27 2 d = . D.d = 3 6. 2 Trang 32/38
Câu 50. Cho lăng trụ ABCA'B 'C ' , đáy là tam giác đều cạnh bằng a , tứ giác ABB 'A' là hình thoi,  0 a 3
A' AC = 60 , B 'C =
. Tính thể tích lăng trụ ABCA'B 'C '. 2 3 3 3 3 A. 3a 3 3a 3a 3 3a . B. . C. . D. . 16 16 4 4 BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A B A A B C C D B D B B B D C A B B C D A A A B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B C D C C B A D A C C C D D A D A A B D A C D D B
SỞ GD&ĐT KIÊN GIANG
ĐỀ THI THỬ HK I – NĂM HỌC 2017 - 2018
TRƯỜNG THPT THẠNH ĐÔNG Bài thi môn Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề. ĐỀ THI THỬ 07
(Biên soạn: Thầy Nguyễn Đức Trung) Câu 1. Cho hàm số 3
y  4x  3x 1 có đồ thị là hình nào trong các hình sau?
Câu 2. Cho hàm số y f (x) liên tục trên  và có đạo hàm 3 2 f (
x)  x (x 1) (x  2) . Hàm số
y f (x) có bao nhiêu điểm cực trị ?
A. Có 3 điểm cực trị B. Có 1 điểm cực trị
C. Không có cực trị D. Có 2 điểm cực trị
Câu 3. Hàm số nào trong các hàm số sau đồng biến trên  ? x
A. y  7x  2sin 3x B. 3 2
y x  2x 1 C. y  4 1 tan x D. y x  2 3x 1  2
Câu 4. Tìm tiệm cận đứng của đồ thị hàm số (C) : y  . 2 x x
A. x  0, x  1. B. x  0 C. (C) không có tiệm cận đứng. D. x  1.
Câu 5. Cho hàm số y f (x) liên tục trên đoạn  2; 
3 , có đồ thị như hình bên. Trang 33/38
Khẳng định nào sau đây là sai ?
A. Hàm số không có đạo hàm tại điểm x  0 .
B. Hàm số đạt giá trị nhỏ nhất bằng 3  .
C. Hàm số đạt giá trị lớn nhất bằng 1.
D. Hàm số nghịch biến trên khoảng 1;3 . Câu 6. Cho hàm số 3 2
y x  6x 12x  8 có đồ thị (C). Khẳng định nào sau đây là sai ?
A. Hàm số đồng biến trên  .
B. Đồ thị (C) tiếp xúc với trục hoành. C. Phương trình 3 2
x  6x 12x  8  m có một nghiệm với mọi m.
D. Hàm số đạt cực trị tại x  2  . 2 x 1
Câu 7. Tìm giá trị nhỏ nhất của hàm số y  . 2 x
A. min y  2. B. min y  0 . C. min y  1. D. Không tồn tại min y .    
Câu 8. Hình bên là đồ thị của hàm số 3 y x  3 . x
Tìm tất cả các giá tị thực của tham số m để phương trình 3
x  3 x  2m có 4 nghiệm phân biệt.
A. 2  m  0. B. m  2  .
C. m  1. D. 1  m  0.
Câu 9. Tìm các giá trị thực của tham số m để đường thẳng d : y mx  3m cắt đồ thị hàm số 3 2
(C) : y x  3x tại 3 điểm phân biệt có hoành độ lần lượt là x , x , x thỏa mãn điều kiện 1 2 3 2 2 2
x x x  . 1 2 3 15 3 A. m  3 . B. m   .
C. m  3. D. m  3.  2 2
Câu 10. Xét x, y là các số thực dương thỏa mãn điều kiện x y  1
2 . Đặt S xy  . Khẳng định xy 1 nào sau đây là đúng ?
A. Biểu thức S không có giá trị lớn nhất. B. Biểu thức S không có giá trị nhỏ nhất. 3
C. min S  . D. max S  1. 2
Câu 11. Tìm các giá trị thực của tham số m để đồ thị hàm số 3 2 3 ( ) :    3  2 có hai điểm m C y x mx m
cực trị A, B sao cho đường thẳng AB vuông góc với đường thẳng d : y  2  . x  1 1   1 1   1 1   1 1 
A. m   ; . B. m   ; . C. m   ; . D. m   ; .  2 2  4 2  2 4  4 4
Câu 12. Tập xác định của hàm số 2
y  log(2x x ) là:
A. D  0;2. B. D   ;0
 2; . C. D  ;0  2; D. D  0;2. 1 4
Câu 13. Rút gọn biểu thức log 3 log 6 3log 9 5 3 8 P  81  27  3 .
A. P  845. B. P  854 . C. P  458 . D. P  485.
Câu 14. Cho a  log 3,b  log 5, c  log 2. Hãy biểu diễn log 63 theo a, , b . c 2 3 7 140 Trang 34/38 2ac 1 2ac 1 A. log 63  . B. log 63  . 140 abc c 1 140 abc  2c 1 ac  2 ac 1 C. log 63  . D. log 63  . 140 abc c 1 140 abc  2c 1
Câu 15. Nghiệm của phương trình 3x 4x   25 là:
A. x  2. B. x  5. C. x  3. D. x  4. 2 x
Câu 16. Đạo hàm của hàm số 2
y x ln x
trên tập xác định là: 2
A. y  x(2ln x 1). B. y  2x(ln x 1). C. y  2x ln .
x D. y  x ln . x 3 1   3  1   3 a a
Câu 17. Rút gọn biểu thức P    (a, b  0).  3 1  2  bb   A. 3 P a . B. 2 P a  . C. 2
P a . D. P  . a
Câu 18.Tìm x, biết log   3 x
4 log3 a 7log3 b . A. 3 6 x a b B. 4 7 x a b C. 3 7 x a b D. 4 6 x a b
Câu 19. x  log 4 là nghiệm của phương trình nào trong các phương trình sau? 3
A. log (9x  4)  x log
3  log 2 B. log (9x  4)  x log 3  log 9 2 2 3 2 2 4
C. log (9x  4)  x log 3  log 2 D. log (9x  4)  x log 3  log 9 . 2 2 3 2 2 4
Câu 20. Cho hai số thực a, b thỏa mãn đồng thời các đẳng thức 3a.2b  1152 và log (a b)  2 . Tính 5
giá trị biểu thức P a  . b
A. P  3 B. P  9 C. P  8 D. P  6
Câu 21. Tìm tập nghiệm của bất phương trình log x  log (10  x)  2. 4 4
A. S  (0;10) B. S  (2;10) C. S  (8;10) D. S  (2;8) .
Câu 22. Cho hàm số y f (x) liên tục trên  ,
có đồ thị (C) như hình vẽ bên.
Khẳng định nào sau đây là sai ?
A. Hàm số y f (x) đồng biến trên khoảng ( ;  0) .
B. Đồ thị (C) cắt trục hoành tại 3 điểm phân biệt.
C. Đồ thị (C) có hai điểm cực trị.
D. Hàm số y f (x) có giá trị lớn nhất bằng 1.
Câu 23. Các giá trị thực của x thỏa mãn điều kiện 3 x  27 là: A. 2   x  3 B. 2   x  3 C. 3   x  3 D. 3   x  3 .
Câu 24. Đặt log 3  a . Hãy biểu diễn log 9000 theo a.
A. log 9000  2a B. log 9000  3  a C. log 9000  3  2a D. log 9000  3  2a .
Câu 25. Cho phương trình: x2 5
x  3 . Nghiệm của phương trình là:
A. x  0 B. x  2 C. x  4 D. x  1. 1
Câu 26. Đạo hàm của hàm số 2 4
y  (x x  4) trên tập xác định là: 1  4
A. y  x x  4 3 2
4 (2x 1) B. y  x x  45 2 4 (2x 1) 4 5 1  4
C. y  x x  4 3 2
4 D. y  x x  45 2 4 4 5
Câu 27. Đồ thị hàm số (2,5)x y  cắt đồ thị hàm số x
y e tại điểm có tung độ là:
A. e B. 0 C. 2,5 D. 1. Trang 35/38
Câu 28. Đồ thị của hàm số nào trong các hàm số sau đây có tiệm cận đứng ? 2 3x  2x 1 x  2 A. y  B. 4 2
y x x C. 3
y x  3x  2 D. y  . x 1 2 1 x Câu 29. Cho hàm số 2
y x  4  x xác định trên đoạn  2;
 2 . Khẳng định nào sau đây là đúng ?
A. max y  2 2 và min y  0 B. max y  2 và min y  0  2;  2  2;  2 2;2  2;  2
C. max y  2 và min y  2 D. max y  2 2 và min y  2 2;2 2;2  2;  2 2;2 2 1    1 
Câu 30. Rút gọn biểu thức 2 2 M a .  (a  0) .  2 1  a   A. 2 M a B. 2 M a C. 3
M a D. M a . dx
Câu 31. Tìm nguyên hàm I  .  x e A. x
I e C B. x
I  e C C. x I  eC D. x I eC
Câu 32. Tìm nguyên hàm 3
I  sin x cos xd . x  4 sin x 4 sin x 4 cos x 4 cos x A. I
C B. I    C C. I
C D. I    C 4 4 4 4 dx
Câu 33. Tìm nguyên hàm I  .  xx 1 1
A. I  2 ln( x 1)  C B. I  2ln
C C. I  2ln( x
)  C D. I  2 ln x x C x 1 x dx
Câu 34. Tìm nguyên hàm I  .  2 (x 1) 2 1 1 2 A. I   C B. I   C C. I   C D. I   C . x 1 x 1 x 1 x 1
Câu 35. Tìm nguyên hàm 2 1 2 x I   dx  2x 1 2  4x 4x 2x A. I   C B. I   C C. I
C D. I  2.  C . ln 2 ln 2 ln 4 ln 2
Câu 36. Nếu cạnh của một hình lập phương gấp lên k lần, với *
k   , thì thể tích của nó gấp lên bao nhiêu lần ? 3 k A. lần B. k lần C. 2 k lần D. 3 k lần. 3
Câu 37. Trong các loại khối đa diện đều sau, tìm khối đa diện có số cạnh gấp đôi số đỉnh.
A. Khối hai mươi mặt đều B. Khối lập phương
C. Khối bát diện đều D. Khối mười hai mặt đều
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác cân tại
S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SAD) và mặt phẳng đáy
bằng 45 . Tính thể tích V của khối chóp S.ABCD . 3 a 3 3 a 2 3 a 3 a 5 A. V  B. V  C. V  D. V  . 6 3 6 6
Câu 39. Cho hình hộp chữ nhật A . BCD A BCD
  có diện tích các mặt (ABCD) , (ABB A  ) , (ADD A  ) lần lượt bằng 2 2
20cm , 28cm và 2
35cm . Tính thể tích V của khối chóp ABC . D AB CD   . A. 3 V  120cm B. 3 V  160cm C. 3 V  130cm D. 3 V  140cm .
Câu 40. Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh 2 2. Trang 36/38 32   A. V  B. V  256 8 6 C. V  64 2 D. V  . 3 3 3
Câu 41. Trong không gian, cho tam giác ABC vuông tại A, AB  2a, AC  .
a Tính độ dài đường sinh l
của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB. A. l  .
a B. l a 5. C. l a 3. D. l  2 . a
Câu 42. Cho hình chóp tam giác đều S.ABC có AB a , cạnh bên SA tạo với đáy một góc 60 . Một
hình nón có đỉnh là S, đáy là một hình tròn ngoại tiếp tam giác ABC. Tính diện tích xung quanh S của xq hình nón đã cho. 2 4 a 2 2 a 2  a 2  a A. S  B. S  C. S  D. S  . xq 3 xq 3 xq 6 xq 2
Câu 43. Cho hình trụ có chiều cao h  2 , bán kính đáy r  3. Một mặt phẳng (P) không vuông góc với
đáy của hình trụ, lần lượt cắt hai đáy theo các đoạn giao tuyến AB và CD sao cho tứ giác ABCD là hình
vuông. Tính diện tích S của hình vuông ABCD.
A. S  12 B. S  12 C. S  20 D. S  20 .
Câu 44. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB BC a ,
cạnh bên SA vuông góc với đáy và SA  .
a Tính diện tích toàn phần S của hình chóp S.ABC . tp 2 a 1 2 2 A. 2 S  2a B. 2
S a 1 2 2  tp  C. S  D. 2 2 . tp tp 2 tp S a
Câu 45. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  16 3, AD  30 3 và
SA SB SC  .
SD Biết rằng đường thẳng SA tạo với mặt phẳng đáy một góc 30 . Tính thể tích V của
khối chóp S.ABCD .
A. V  7250 B. V  8160 C. V  2448 D. V  9580.
Câu 46. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB a, BC  2a , hình chiếu
vuông góc của đỉnh S trên mặt đáy là trung điểm H của OA. Biết rằng mặt phẳng (SBC) tạo với mặt phẳng
đáy một góc 60 . Tính thể tích V của khối chóp S.ABCD . 3 a 15 3 a 3 A. 3 V a 3 B. V  C. 3
V a 15 D. V  . 2 2
Câu 47. Cho hình chóp tứ giác đều S.ABCD có AB a , mặt bên tạo với đáy một góc 45 . Một khối
nón có đỉnh là S, đáy là hình tròn ngoại tiếp hình vuông ABCD. Gọi  là góc ở đỉnh hình nón. Tính cos. 1 A. cos   3 B. cos  6 C. cos  1 D. cos  . 3 3 3 3
Câu 48. Cho hình lập phương (H) cạnh a, gọi (B) là hình bát diện đều có các đỉnh là tâm các mặt của (H).
Gọi S1, S2 lần lượt là diện tích toàn phần của (H) và (B). S Tính tỉ số 1 . S2 S 3 S 1 S S 8 3 A. 1  B. 1  C. 1  2 3 D. 1  . S2 8 S2 2 3 S2 S2 3
Câu 49. Cho hình nón có chiều cao h  6 , bán kính đáy r  3. Một hình lập phương đặt trong mặt nón
sao cho trục của hình nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nội tiếp
trong đường tròn đáy của hình nón, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Tính độ
dài cạnh của hình lập phương. 3 2 A. B. 6 2   1 C. 32  2 D. 3. 2
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  1, AD  2 , cạnh bên SA vuông
góc với đáy và SA  11 . Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABCD . Trang 37/38 11 11  256 A. B. 32 32 C. D. . 6 3 3 BẢNG ĐÁP ÁN 1C 2D 3A 4B 5C 6D 7D 8D 9C 10B 11A 12D 13A 14B 15A 16C 17C 18B 19B 20B 21D 22D 23C 24D 25B 26A 27D 28D 29D 30C 31C 32D 33A 34B 35B 36D 37C 38C 39D 40A 41B 42B 43C 44B 45B 46D 47A 48C 49B 50C Trang 38/38