

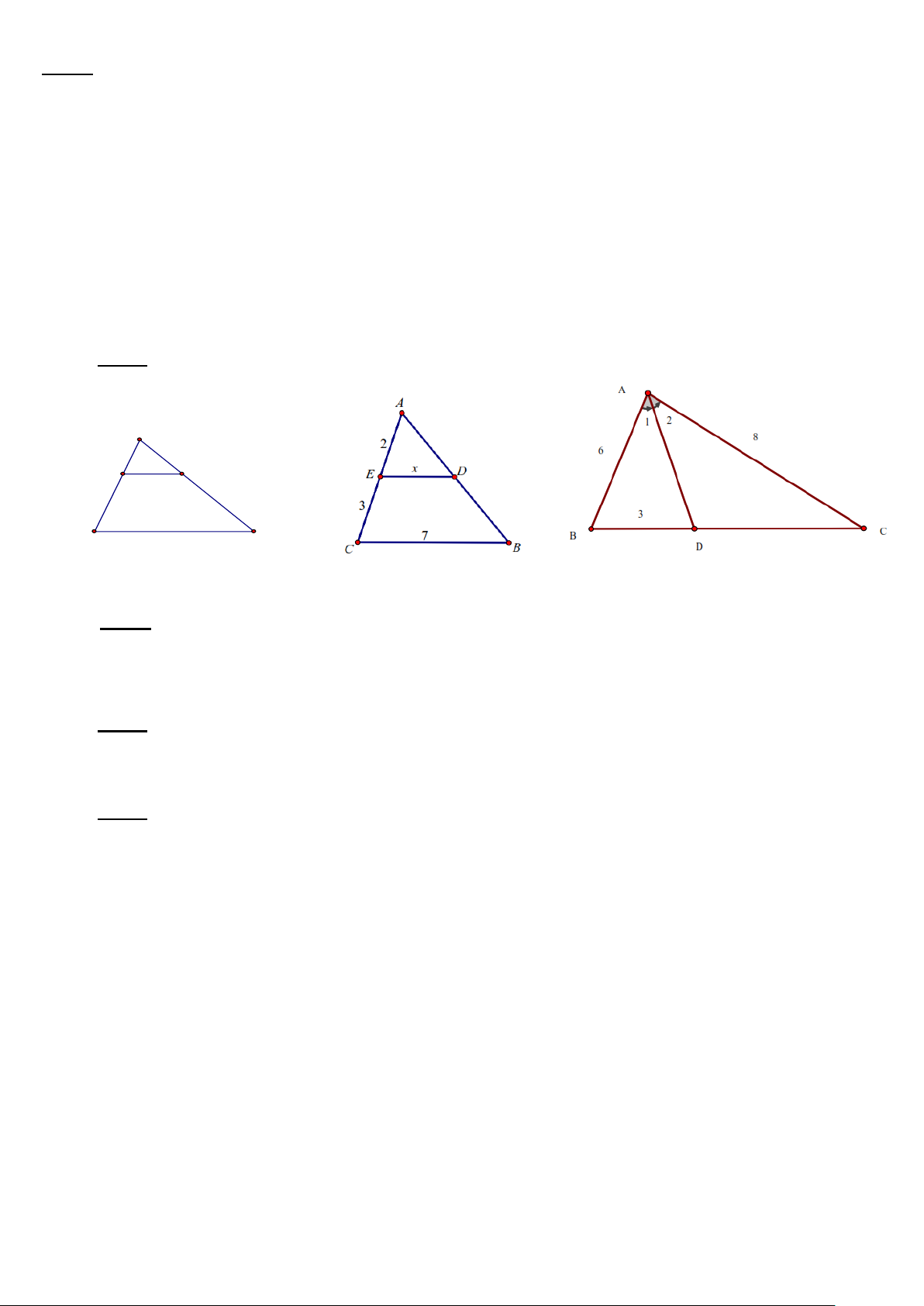
Preview text:
ĐỀ CƯƠNG ÔN TẬP MÔN TOÁN LỚP 8 – GIỮA HỌC KÌ II LÝ THUYẾT I. ĐẠI SỐ:
1) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a 0.
Ví dụ : 2x – 1 = 0 (a = 2; b = - 1)
- Phương trình bậc nhất một ẩn luôn có 1 nghiệm duy nhất là −𝑏 𝑥 = . 𝑎
- Hai quy tắc biến đổi phương trình : SGK trang 8
Ví dụ: Giải phương trình sau: 3x − 2 = 2x +1
3x − 2x =1+ 2 x = 3
Vậy tập nghiệm của phương trình là S = {3}
2) Các bước chủ yếu để giải phương trình đưa về dạng ax + b = 0
• Bước 1: Quy đồng mẫu rồi khử mẫu hai (nếu có)
• Bước 2: Thực hiện phép tính để bỏ ngoặc (Nhân đa thức hoặc dùng quy tắc dấu ngoặc).
• Bước 3: Chuyển vế: Chuyển các hạng tử chứa ẩn sang 1 vế ; các hằng số sang vế kia.
(Chú ý: Khi chuyển vế hạng tử thì phải đổi dấu số hạng đó)
• Bước 4: Thu gọn và giải phương trình. (Cộng trừ các hạng tử đồng dạng, Chia hai vế cho hệ số của ẩn). x +1 2 − x Ví dụ: = 5 2
2(x +1) = 5(2 − x)
2x + 2 = 10 − 5x 2x + 5x = 10 − 2 8 x = 7 8
Vậy tập nghiệm phương trình là: 𝑆 = { }. 7
3) Phương trình tích và cách giải:
Cách trình bày 1: A(x).B(x) = 0 ⇔ 𝐴(𝑥) = 0 ℎ𝑜ặ𝑐 𝐵(𝑥) = 0 A(x ) = 0
Cách trình bày 2: A(x).B(x) = 0 B(x ) = 0
Ví dụ: Giải phương trình: (2x + 4) 3 ( x – 7) = 0 Cách trình bày 1: Cách trình bày 2: (2x + 4) 3 ( x – 9) = 0 (2x + 4) 3 ( x – 7) = 0
2x + 4 = 0 hoặc 3x – 9 = 0 2x + 4 = 0
∗ 2𝑥 + 4 = 0 ⇔ 𝑥 = −2 3x–9=0
∗ 3𝑥 = 9 ⇔ x = 3
Vậy phương trình có tập nghiệm là S={-2; 3} 2x = 4 − 3x = 9 x = 2 − x =3
Vậy phương trình có tập nghiệm là S={-2; 3}
4) Các bước giải phương trình chứa ẩn ở mẫu.
• Bước 1: Tìm ĐKXĐ của phương trình
• Bước 2: Quy đồng mẫu hai vế rồi khử mẫu.
• Bước 3: Giải phương trình vừa nhận được.
• Bước 4: Đối chiếu ĐKXĐ để trả lời.
5) Giải bài toán bằng cách lập phương trình: Trang 1
• Bước 1. Lập phương trình:
+ Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. (Ghi đơn vị cho ẩn nếu có).
+ Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
• Bước 2. Giải phương trình.
• Bước 3. Kiểm tra xem trong các nghiệm vừa tìm được nghiệm nào thỏa mãn, nghiệm nào
không so với điều kiện ẩn số rồi kết luận. II.HÌNH HỌC:
* Học thuộc các định lý đã học.
Tóm tắt lý thuyết AB A 'B'
1. Đoạn thẳng tỉ lệ: Cặp đoạn thẳng AB và CD tỉ lệ với cặp đoạn thẳng A’B’ và C’D’ = CD C'D'
2. Một số tính chất của tỉ lệ thức: • AB A'B' =
AB.C'D' = A 'B'.CD CD C'D' AB A 'B' AB CD • = ; = = CD C'D' A 'B' C'D' AB.C'D' A 'B'.CD C'D' = A'B' C'D' ; = CD CD AB A 'B' AB
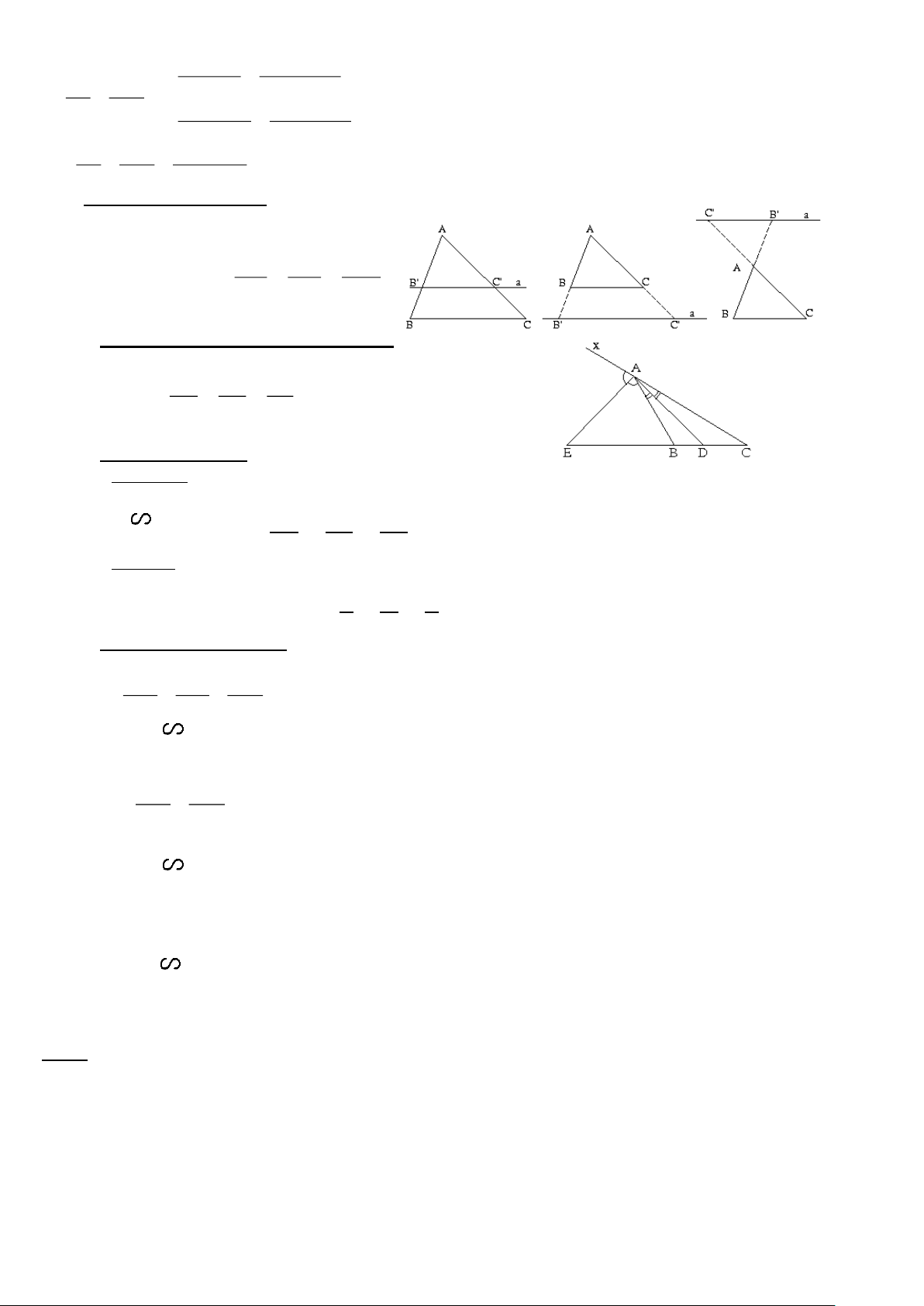
3. Định lý Ta-lét thuận và đảo: A AB' AC' = AB AC • ABC B' C ' AB' AC' a = a / /BC BB' CC' BB' CC' = AB AC B C Trang 2 AB CD A 'B' C'D' = AB A 'B' CD C'D' = CD C'D' AB A 'B' = AB C'D' A'B' C'D' • AB A'B' AB A'B' = = CD C'D' CD C'D'
4. Hệ quả của định lý Ta-lét: ABC • AB' AC' B'C' = = a / /BC AB AC BC
5. Tính chất đường phân giác trong tam giác:
AD là tia phân giác của BÂC, AE là tia phân giác của 𝐵𝐴𝑥 ̂ AB DB EB = = AC DC EC
6. Tam giác đồng dạng: a. Định nghĩa: 𝐴̂ = 𝐴′ ̂ ; 𝐵̂ = 𝐵′ ̂ ; 𝐶̂ = 𝐶′; ̂ ABC
A’B’C’ ⇔ { 𝐴𝐵 𝐴𝐶 𝐵𝐶
(k là tỉ số đồng dạng) = = = 𝑘 𝐴′𝐵′ 𝐴′𝐶′ 𝐵′𝐶′ b. Tính chất:
Gọi P, P’, m, m’, d, d’ lần lượt là chu vi, trung tuyến, phân giác của 2 tam giác đồng dạng ABC và A’B’C’ : 𝑃 𝑚 𝑑 = = = 𝑘; 𝑃′ 𝑚′ 𝑑′
7. Các trường hợp đồng dạng:
a. Xét A’B’C’ và ABC có: A 'B' B'C' C' A ' • = = AB BC CA Vậy A’B’C’ ABC (c.c.c)
b. Xét A’B’C’ và ABC có: A 'B' A 'C' • = (...) AB AC • Â ' = Â (...) Vậy A’B’C’ ABC (c.g.c) c.
Xét A’B’C’ và ABC có: • Â ' = Â (...) • ˆ = ˆ B' B (...) Vậy A’B’C’ ABC (g.g) BÀI TẬP
I. Giải phương trình và bất phương trình:
Bài 1: Giải các phương trình: Trang 3 A) 𝑥 − 2022 = 0
F) 10𝑥 + 3 − 5𝑥 = 4𝑥 + 12 B) 2𝑥 − 10 = 0
G) 11𝑥 + 42 − 2𝑥 = 100 − 9𝑥 − 22 C) 3𝑥 − 2 = 2𝑥 − 3
H) 2𝑥 − (3 − 5𝑥) = 4(𝑥 + 3) D) 2𝑥 + 3 = 5𝑥 + 9
I) 𝑥(𝑥 + 2) = 𝑥(𝑥 + 3) E) 5 − 2𝑥 = 7
J) 2(𝑥 − 3) + 5𝑥(𝑥 − 1) = 5𝑥2
Bài 2: Giải các phương trình:
a/ (2𝑥 + 1)(𝑥 − 1) = 0 2 1 b/(𝑥 + ) (𝑥 − ) = 0 3 2
c/ (3𝑥 − 1)(2𝑥 − 3)(𝑥 + 5) = 0
d/ 3𝑥 − 15 = 2𝑥(𝑥 − 5) e/ 𝑥2 − 𝑥 = 0 f/ 𝑥2 − 2𝑥 = 0 g/ 𝑥2 − 3𝑥 = 0
h/ (𝑥 + 1)(𝑥 + 2) = (2 − 𝑥)(𝑥 + 2)
Bài 3: Giải các phương trình: 3x + 2 3x +1 5 a/ − = + 2x 2 6 3 x 4 + 3 x 6 − 2 x 5 + 4 b/ − = + 3 5 7 3
Bài 4: Giải các phương trình sau: 7x − 3 2 a) = x −1 3 1 3 − x b) + 3 = x − 2 x − 2 x + 5 x − 5 20 c) − = 2 x − 5 x + 5 x − 25
II. Giải bài toán bằng cách lập phương trình:
Bài 1 : Một xe máy khởi hành từ Hà Nội đi Nam Định với vận tốc 35km/h. Sau đó 24 phút, trên cùng tuyến
đường đó, một ô tô xuất phát từ Nam Định đi Hà Nội với vận tốc 45km/h. Biết quãng đường Nam Định - Hà Nội
dài 90 km. Hỏi sau bao lâu, kể từ lúc xe máy khởi hành hai xe gặp nhau?
Bài 2 : Một người đi xe máy từ Hà Nội về Thái Bình với vận tốc 45km/h. Một người khác cũng đi xe máy từ Thái
Bình lên Hà Nội với vận tốc 30km/h. Hỏi sau bao lâu kể từ khi xuất phát họ gặp nhau ? Biết quãng đường Hà Nội -
Thái Bình là 110km.
Bài 3 : Một ôtô đi từ A đến B với vận tốc 60km/h và đi từ B về A với vận tốc 45km/h. Thời gian cả đi và về hết
7giờ. Tính quãng đường AB Trang 4
Bài 4 : Một người đi xe đạp từ A đến B với vận tốc 30km/h. Lúc về, người đó đi với vận tốc 40km/h. Do đó thời
gian về ít hơn thời gian đi là 45 phút. Tính quảng đường AB? III. HÌNH HỌC:
Bài 1: Tìm x, y trong các hình sau: A 4 6 D E x 7 B C a) DE // BC b) DE // BC c)
Bài 2: Vẽ ∆𝐴𝐵𝐶 có 𝐵𝐴𝐶
̂ = 70o, 𝐴𝐵 = 5𝑐𝑚, 𝐴𝐶 = 7,5𝑐𝑚. Lấy trên các cạnh AB, AC
lần lượt hai điểm D, E sao cho 𝐴𝐷 = 3𝑐𝑚, 𝐴𝐸 = 2𝑐𝑚. ∆𝐴𝐸𝐷 và ∆𝐴𝐵𝐶 có đồng dạng với nhau không? Vì sao?
Bài 3: Cho 𝑥𝑂𝑦
̂ , trên tia Ox lấy điểm hai A và C, trên tia Oy lấy hai điểm B và D. Chứng
minh rằng: ∆AOD∽∆BOC nếu 𝑂𝐴 = 4𝑐𝑚, 𝑂𝐶 = 15𝑐𝑚, 𝑂𝐵 = 6𝑐𝑚 𝑣à 𝑂𝐷 = 10𝑐𝑚.
Bài 4: Cho tam giác ABC vuông ở A, có 𝐴𝐵 = 6𝑐𝑚; 𝐴𝐶 = 8𝑐𝑚. Vẽ đường cao AH. a. Tính BC. b. Chứng minh AB2 = BH.BC c. Tính BH; HC. -----------HẾT------
CHÚC CÁC EM ÔN TẬP VÀ THI TỐT ^^ Trang 5




