














Preview text:
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I NĂM HỌC 2017-2018
501:DDCBADAAADA CCDDDA CABDA CDD BAAACBDDCA BBBA CBBBBCBCCCD Môn TO ÁN –Lớp 12
MA TRẬN ĐỀ THI HỌC KỲ I, NĂM HỌC 2017 – 2018
Chuyên đề kiến thức NB TH VD VDC 1
Sự đồng biến nghịch biến của hàm số 1 1 2 Cực trị của hàm số 1 1 3
GTLN - GTNN của hàm số (VDC: Bài toán thực tế) 1 1 4 Đường tiệm cận 1 1 5
Khảo sát sự biến thiên và vẽ đồ thi HS bậc 3 1 1 6
Khảo sát sự biến thiên và vẽ đồ thi hàm trùng phương 1 1 7
Khảo sát sự biến thiên và vẽ đồ thi HS bậc nhất trên bậc nhất 1 8
Chủ đề 5, 6, 7 (Đọc đồ thị) 1 9 Tiếp tuyến 1 1
10 Tương giao của hai đồ thị 1 1 11 Luỹ thừa 1 1 12 Hàm số luỹ thừa 1 1 13 Lôgarit 2 1 14 Hàm số mũ 1 1 15 Hàm số lôgarit 1 1 16 Phương trình mũ 1 1 17 Phương trình lôgarit 1 1
18 Câu hỏi tổng hợp 16, 17 1
19 Câu hỏi tổng hợp 14, 15, 16, 17 1
20 Phân chia, lắp ghép khối đa diện. Đa diện lồi, đa diện đều 1 1
21 Thể tích khối đa diện 1 1 1 22 Tính khoảng cách 1 1 23 Mặt nón 1 1 24 Mặt trụ 1 1 25 Mặt cầu 1 1 1
26 Câu hỏi tổng hợp 22, 23, 24, 25 1 Tổ ng 22 18 7 3 0123
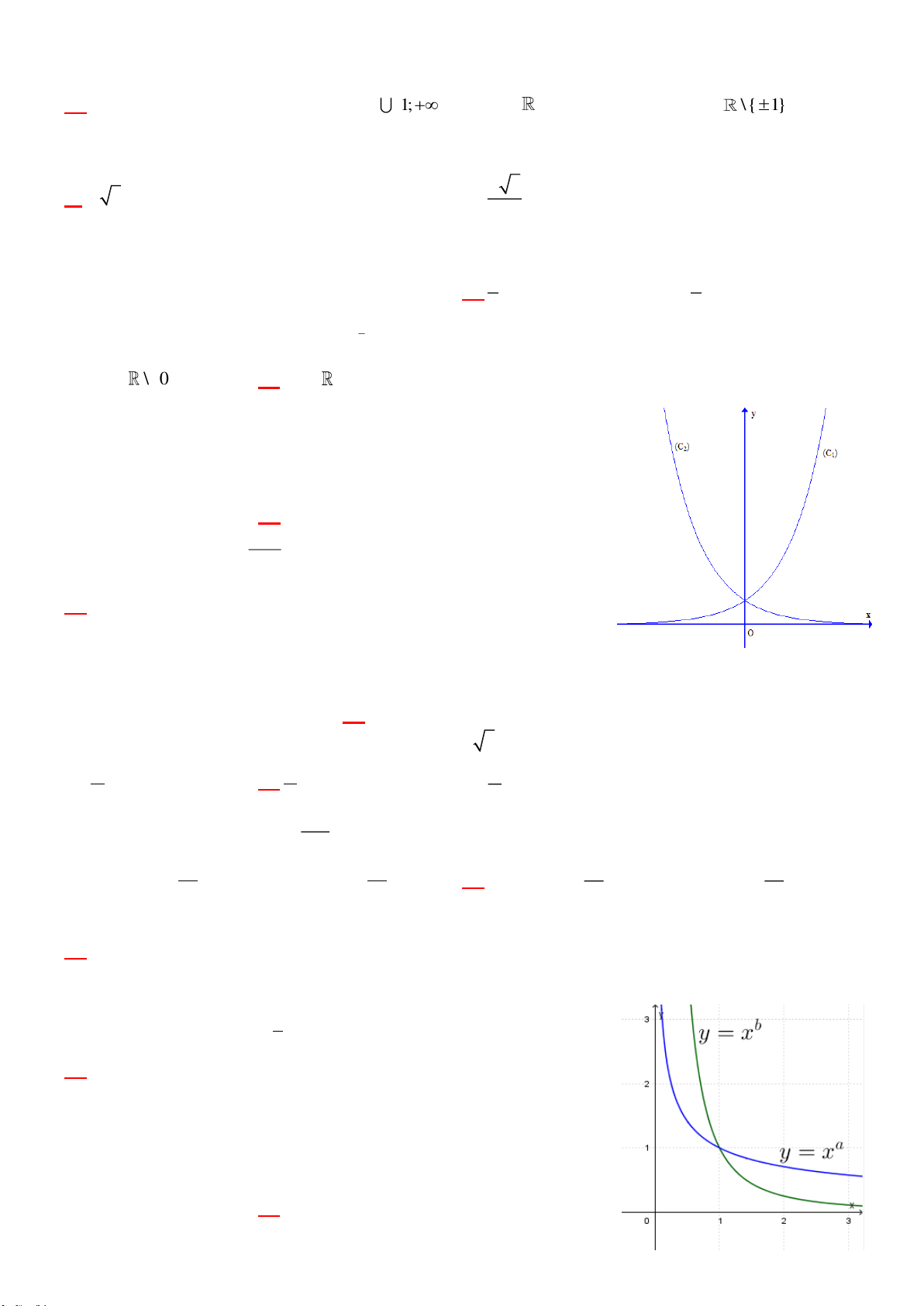
44567477747554447576475446777564457666756666565554 9 ! "# $% &'() * 9 +, +-. / 9 0 1 9. 23 4 51 ! 56 78"# $% &'() 9:; <; =# > )9?@ AAAAAAAB C DEFGHC IJC K ELM C HM NGC OEPK C QRC S TU V WXY Z[\ ]^_` abc Zd e fg fhY i[ 2 k l m n p h Z\ qY r as e tc Zu k j o 1v w r 2y m mx jz {v O w r j mymx 2z v w r j m x y 2z /v w2 r ymx jz TU V |hY i[ _h} ~\ ZX Zd_` \ _ e _ e ]a Zg _f abc _s 1v Ol p n}` kz {v l p n}` kz v l p n}` kz /v l p n}` kz j 1z 0 j TU V |hY i[ _h} ic ZX _`fg af \ _ e _ e _` f}_` ]a Zg _f abc _s 1v jk 2 Ol o n z {v k 2 l m n z v k j l m n z /v k 0 l o n z k m k 2 o jk 2 m k m 2 m TU V t\ k k p h _`f\ Y abc f_` e _f p} ` k p } ` k p } ` j0 m 0 o 1 n \ k k z \ e g abcj k k o p h 2 j 2 j 2 j 1v p}0 ` 2 o z {v p }0 ` 2 O o z v z /v 01z TU V W _f Z } fhY abc fhY i[ z k ln 1v ¡ k2 l z k m n p _z {v ¡ O k ln p _ z v ¡ 2 z k l k m n z /v ¡ n p k l _kz TU ¢V 5f} fhY i[ j l k n o k 2 m as Zd e fg £ 5¤ z ¥f_` e _f e \ e _ abc Zd e fg £ 5¤ e \ `\ c} Z\ qY abc £ 5¤ \ e ¦a e _` p h 1v ln k m 2 o z {v Oln 2 mz v l j n z /v l j n k 2 o z TU V 5f} fc\ i[ e f§a e ¨ © ª« h i[ e f§a ~_` ¬z f®_` Zg _f _h} ic ZX p h f®_` Zg _f ¯=; ª 1v z ¬ w¬xª ª« « n z {v ª « m ¬ ¬ n z v ¬ª « o O ¬ª n ¬« o z /v w x« ª z ¬ ¬ª« n z ¬« TU !V ° } fhY abc fhY i[ j 0k k l m o n p h3 j 0kmk k o m ¡ w x j 1v w x j ¡ j z 0k k l k m o n m z {v ln z p _0 v j ¡ k m k l 0 o n p _0z /v Ol wk x j ¡ k m k j 0 o n m p _0z Trang 1
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018 0123
44567477747554447576475446777564457666756666565554 2 TU >V ° } fhY abc fhY i[ j l £ njk k m 2 o¤ p h3 j m j m 1v ¡ 2 m j j ln £k 2 m¤ £jk k m 2 o¤ v {v ¡ j ln £k 2 m¤ £jk k m 2 o¤ z j m j m v ¡ 2 j j m O ln £k 2 m¤ £jk k m 2 o¤ z /v ¡ j ln £k 2 m¤ £jk k m 2 o¤ v TU V ¥f_` e _fp }`wk j m j n as _`f\ Y p h 3 j x 1v k j n z {v k n z v k n z /v Ok ± n z TU V Wfc_` Z} ²\ afe ³ p h Yue p } \ e fc_` Z} Zq ]a Zg _f i^a e h_ f abc a_ Zu_` Z´e z Wfc_` Z} ²\ afe ³ as Z_ g p h Zu ²\ afe ³ Zu ²\ afe ³ Zµa ]a Zg _f e f³} a¶_` e f^a ic3 ¸ p n}`¹ p } m `¹ \ ¹ p h \ _ Zu · e [\ Zc Zµa Z} º_` Zg c af´_ aaf e XY af´_ 211Y ¹ p h Yue \ _ Zu af»_z ¼½Y j121 ¨_` ¾cp ³ · £ 5f\ p ³¤ Z¿ afg _f fÀ_` fc\ a_ Zu_` Z´e e _ e f^ _f´e Zµa ]a Zg _f p h 1 Zu ²\ afe ³ y e _ e f^ fc\ Zµa ]a Zg _f p h Zu ²\ afe ³ z W _f e Á i[ \ _ Zu e [\ Zc abc e _ e f^ fc\ h e _ e f^ _f´e £  ÃÄÅ Æ ÇÈÉÅ ÊËÉÅ ÌÃÉÍÅ ÎÌÏÉÅ Æ ÇÐÄÑ Ò 1v ± 2z {v ±1jz v ±jz /v O±2z TU V \ e g abcp }` 1 2j0 º_`3 1 0 1v Ó {v Ó j v O /v j TU V t\ Ô p h e \ e _ abc Zd e fg fhY i[ j l k n m k 2 o e \ Z\ qY as f}h_f Zukn 2 m z | i[ `sa abc Ô p h 1v Oz {v Ó z v Ó z /v z TU V Õ[ `\ c} Z\ qY abc Zd e fg fhY i[l k n m k j o ln h ZÖ_` e f®_` j p h 1v 1z {v O z v jz /v 2z TU V 5f} fhY i[ j ln k m o k j o 12 as Zd e fg £ 5¤ z 5ft_ f_` _ Z×_` 1v ° O defg£5¤asjZ\qYa§aegz {v °d e fg £ 5¤ as Z\ qY a§a e g z v °d e fg £ 5¤ f¶_` as Z\ qY a§a e g z /v °d e fg £ 5¤ as 2 Z\ qY a§a e g z TU ¢V |hY i[ l n k 0 o Zd_` \ _ e _ f}_` _h} 1v wmØ x y1z {v Ù 2y Ú m oØ Ù Ú Û z v w O 1yo x Ø z /v 2 m y Øm z j Ü Ý Þ Û jÜ Ý Þ 2 m 2 o TU V ²×e `t_ \ q e f^a £¬ ¤ ßn 0 m 2m 0 ¬ z ¬ 1v ß ¬ n z {v ß 2 n z v Oß ¬ n z /v ß ¬m n z TU !V t\ É p h i[ _`f\ Y abc f_` à á â _fp }`wj k ± m p n}` k j m 2 o z \ e g abcÉ p h 3 x w x 1v É 1 n z {v É n z v É j n z /v OÉ 2 n z TU >V W ]a Zg _f abc fhY i[ jk 2 l o n p h k m 1v ãyo x Ø z {v Oç ä æ å z v wmØ è yz /v çz Trang 2
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018 0123
44567477747554447576475446777564457666756666565554 TU V 5f}¬ p n}` z f\ Zs `\ e g abcp }` 20 e f³}¬ p h3 20 j0 1v 2 z {v 2 ¬ m z v 2 O z /v j¬ 2 o z 2 ¬ m j j m ¬ TU V \ \ f_` e _fkj m 2 j n z ± 1v k j n z {v k 2 n z v k 1 n z /v O kn 2 m z TU V 5f} fhY i[ 2 j ln k j m k 2 o z f®_` Zg _f _h} ic ZX Z×_` 1v |hY i[ Z e a§a Z e e \ k j n z {v ° O defgfhYi[Z\écZ\qY¸w1 x y 2z v |hY i[ Z e a§a e \ q e \ k 1 n z /v |hY i[ p ¶_ Zd_` \ _ e _ ²z TU V W Y e ´e a aa `\ e g e f§a abcÄ Zq Zd e fg fhY i[ j j l k n j m Ä k 2 o as c Z\ qY a§a e g e } e fh_f Yue e cY `\ a Zêz 1v Ä 1 n z {v Ä 1 n f}ëa ± Änì z v ± OÄnì z /v Än 2 ìz TU V ¾ue e ´Y c f _f afí _fe as af\ ê u_` º_`jaY af\ ê ~h\ º_`0aYz î Yï\ `sa _ e \ £ ]³Y f _f Y\ _f ftc¤ _`Ö\ e c aðe ñ Yue f _f ¶_` a _fy k À Yï\ `sa_f\ aðe ñYue f _fafí_fe asaf\ ê u_`z kò\ fó_ caô_p \ _`Ö\ e c `´ e f³} aa ZÖ_` af £ ]³Y f _f Y\ _f ftc¤ Zq e f Zµa Yue f _f fu afí _fe £ fó_ e ¶ Z³_ e À e fh_f Yëe _ð¤ z W Yk Zq f _f fu afí _fe e f Zµa as e fq e af p _ _f´e z 1v Ok 0 n aYz {v k n aYz v k n aYz /v k 2 n aYz TU V °Ö_` e f®_`k 2 n p h e \ Y a_ Z^_` abc Zd e fg fhY i[ _h} ic ZX j j 1v jk j l m n z {v 2 k l o n z v 2 k Ol o n z /v jk 2 l o n z k j o 2 k o 2 k m j k m TU ¢V W _`f\ Y abc f_` e _fk2 m 0 0 k m o j n ± p h 3 1v ä O 2 å yz {v õz v ä å y0z /v ä2yå z TU V |hY i[ln w j p _ k m 0 o km x ± as e ]a Zg _f p h3 1v Owj x yz {v wyo x Ø z v wmØ x yjz /v wmØ x yj w ö yo x Ø z TU !V °d e fg _ p h Zd e fg abc fhY i[ _h} 1v Ol k n m kz {v j l k n j m kz v ln k m o kz /v l k n o kz TU >V W Y `\ e g _fñ _f´e abc fhY i[ k l o n e _ Z} _ ãj è yz k 2 m 1v Y\ _l 0 n z {v OY\_ln z v Y\ _ln z /v Y\ _l n z ãj è y ãj è y ãj è y ãj è y TU V 5f}p }`j z ¬ n \ e g abcp }`j0 e _f e f³}¬ p h3 1v j ¬ o z {v 2 j m ¬z v O w j2 x ¬ m z /v j j o ¬z Trang 3
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018 0123
44567477747554447576475446777564457666756666565554 TU V Õ[ ZÖ_` e \ Y a_ abc Zd e fg fhY i[ ln p h k 2 o 1v j O z {v z v 2z /v 1z TU V 5f} fhY i[ w ÷ x j k k n m k 2 o as Zd e fg £ 5¤ `t\ ø p h Z\ qY e fua Zd e fg £ 5¤ as f}h_f Zu p h _`f\ Y abc f_` e _f÷w ù x k 1 n z Wtc Zu Z\ qY ø p h 1v wj r ymx z {v w r 2y m mx z v O w2 r ymx 2z /v w1 r x y 2z TU V 5f} fhY i[ j l k n j o k j m 12±z f®_` Zg _f _h} ic ZX p h f®_` Zg _f úNM C 1v °d e fg fhY i[ Z¿ af} f¶_` as ZÖ_` e \ Y a_z {v °
O defgfhYi[Z¿af}aðee¦aûke \Z\qYfX_\ez v |hY i[ Z¿ af} as Yue a§a e \ qz /v °d e fg fhY i[ Z¿ af} as e ¦a Z[\ ]^_` p h e ¦aûlz TU V W ]a Zg _f abc fhY i[ l km n p h3 1v ý £ nm y Ø 1üz {v Oýnç ä æ1þz v ýnçz /v ý £ n1yo ¤ Ø z TU V W Y e ´e a aa `\ e g e f§a abc e fcY i[Ä Zq f_` e _f k m k Ä o 2 m 1 n as _`f\ Y fX_ \ e z 1v j m ÿÄ j ÿ z {v m Ä 0 2 0 z v j m Ä 0 j 0 z /v Å O 2 m Ä 0 0 Ò Å TU ¢V ¼`Ö\ e c ] [_ é aó _fñ as _ _f º_`jaY h Yue é aó p _ as _ _f º_`aY h} e }_` Yue a\ fu f _f fu afí _fe _f ic 3 Yï\ é aó _fñ e \ ]×a Yëe Z h fc\ Yëe _ abc fu Zd_` e fÖ\ fc\ é aó _fñ a _f _fc e \ ]×a \ _fc y é aó p _ e \ ]×a \ Yï\ é aó _fñ h e \ ]×a \ _ð e _ abc fu £ ]³Y f _f Y\ _f ftc¤ z W _f af\ ê ac}Ì abc f _f fu _hz 1v Ì n 0aYz {v Ì £ n0o j2¤aYz v Ì 2 n 1aYz /v OÌ £ n0o 2¤aYz TU V 5ðe Yue f _f _s_ º_` Yue Yëe f®_` éc e ¦a abc _s e c Zµa e f\ e ~\ _ p h e cY `\ a Zê a _fj¬z W Y e fq e af 1abc f[\ _s_ z 1v ¬ 1 n z {v ¬ 1 n z v ¬ j 1 n z /v ¬ 1 O n z j TU!V 5f}f _fp ½_`e ¦e cY`\ a¹2 z 3 ù ¹ ù 2 ù 3 asZ¹23p he cY`\ a¶_`e \ 2 ¹2n ¬23 ¬ n f _f af\ abc ù ¹ ][_` Yëe Zw¹2 x 3 p h e _` Z\ qY4 abc Z} _¹3z 6\ e e fq e af f[\ p ½_` e ¦ Z¿ af} p h¬ z W _f f}_` aaf e ¹ Z_ Yëe f®_`w ù ¹2 x 3 z ± 1v ¬ z {v ¬2z v j¬ z /v j¬2 O z 2 2 TU >V 4\ _ e af ]_` éc_f abc f _f e ¦ as _ _f Z º_` aY h af\ ê ac} º_` aY p h3 1v j j a Y z {v j ± a Y z v j 2j a Y z /v j Oj a Y z Trang 4
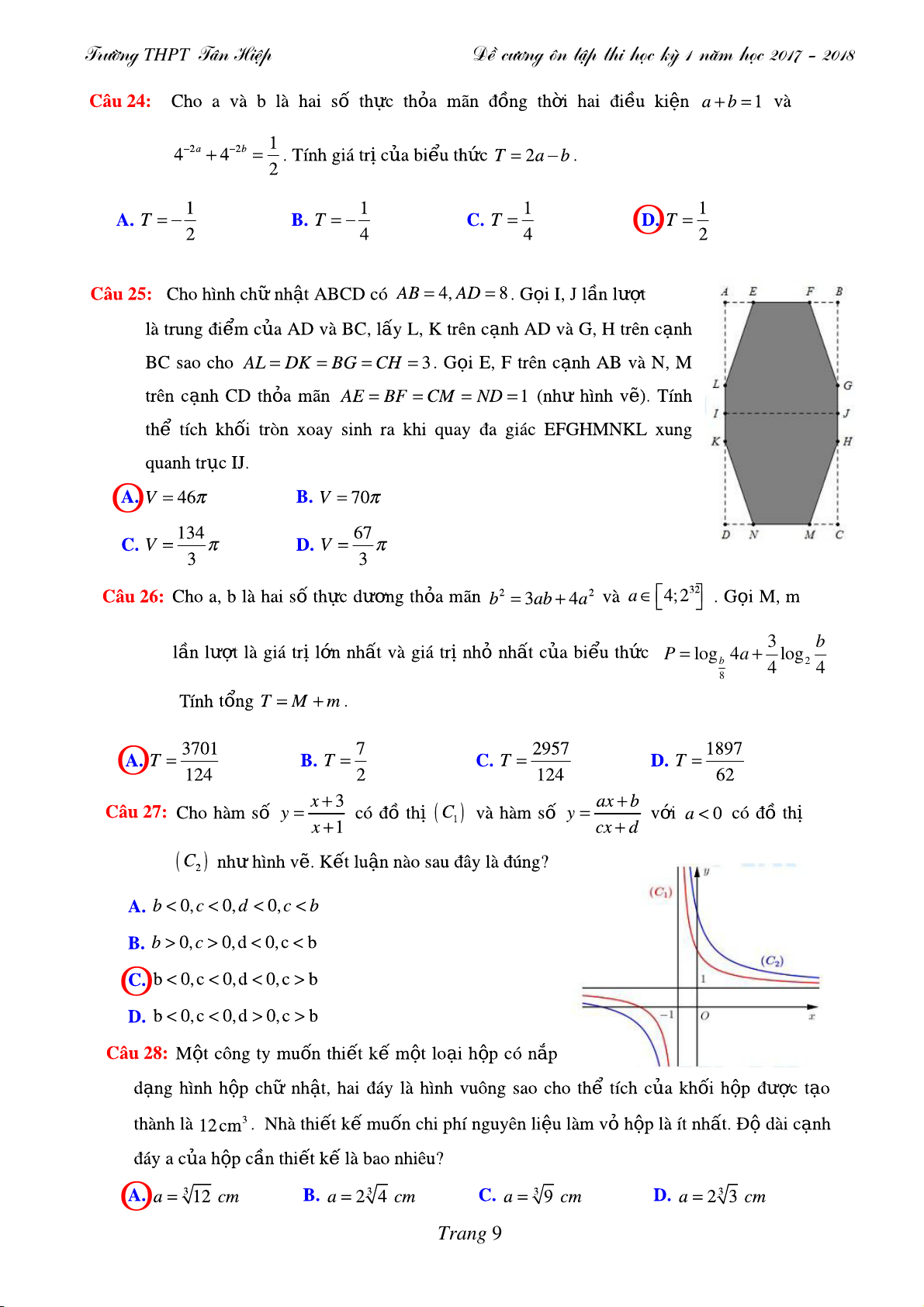
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018 0123
44567477747554447576475446777564457666756666565554 TU V 5f} f _f afsz 5¹23ý as Z p h f _f ¶_` a _fz ¬ 6\ e 5¹ ¶_` `sa \ Z£¹23 ¤ ý h 5¹ z ¬ n ¾ëe aó _`} \ e \ f _f afsz 5¹23ý as _ _f6 º_` c} _f\ 1v ¬ O6n z {v ¬ 6n z v ¬ ± 6n z /v 6 ¬ n z j ± j TU V 5f} f _f p ½_` e ¦ e cY `\ a Zê¹2 z 3 ù ¹ ù 2 ù 3 as e fq e af º_` ¬ h Zu ~h\ a _f _¹ ù ¹ ¬ n z W Y Zu ~h\ a _f Z abc p ½_` e ¦z 1v ¬ z {v j O ¬z v ¬z /v ¬ jz TUV 5f}f _fafs z 5¹23 asZ¹23p he cY`\ a¶_`e \ ¹ 52¶_``sa\ Zh ¹2 n ¬ ¹3 n ¬ 53 ± n z ¬ W Y e fq e af abc f[\ afsz 5¹23z 1v ¬ 22z {v ¬ 22z v j O ¬ 22z /v ¬ 22z TU V 5f} f _f afs e cY `\ az 5¹23 as Z¹23p h e cY `\ a Zê as a _f º_`¬ a _f _5¹ ¶_` `sa \ Z h5¹n ¬ z W Y e fq e af 1 abc f[\ afsz 5¹23z 1v ¬ 1n z {v ¬ O1n z v 1n j¬z /v ¬ 1n z TU V Wfq e af ò abc f[\ aó as _ _f 7 p h3 1v O1 n ±z {v 1 n z v 1 n jz /v 2± 1 n z TU V W _f ~\ _ e af ]_` éc_f5 abc Yue f _f _s_ as _ _f ZÖ_` e ô_ Z p h¬ h Zu ~h\ ZÖ_` k8 i\ _f p h¬z 1v j O5 n ¬ z {v j 5 n ¬ 5 n ¬ v /v j 5 n ¬ z k8 k8 j k8 2 j v v j k8 2 0 TU ¢V ¾ue f[\ e ¦ as e fq e af º_` 2 Y h ZÖ_` i\ _f `´ p ó_ _ _f Zz °u ~h\ ZÖ_` i\ _f abc f[\ e ¦ _h p h3 1v OYz {v 2jYz v ±Yz /v Yz TU V W Y e fq e af 1abc f[\ fu afí _fe as aa af e fa p ó_ p µe p h ¬ j ¬ ¬z 1v 1 ¬ n z {v 1 n ¬z v 1 O ± n ¬z /v 1 j n ¬z TU!V 5f}f _fafs z 5¹23z W _a _f5 ¹ 5 2 53p ó_p µe p ´aaZ\ qY ù ¹ ù 2 ù 3 ic}af} 5 ù ¹ 5 ù 2 j 5 ù 3 j n n n zW Y e Á i[ e fq e af abc f[\ afsz 5 ù ¹ ù 2 ù 3 h z 5¹23z 5¹ 52 53 1v 21z {v 2 z v 0z /v 2 O z j2 j2 j2 j 2 TU >V 5f} Yëe aó e XYr _ _f6 j n ±aYz ¾ue Yëe f®_` aaf e XYr Yue f}_`jaY aðe Yëe aó _h e f³} Yue ZÖ_` e ô_z W _f _ _fÇ abc ZÖ_` e ô_ Zsz 1v Ç 2 njaYz {v OÇ 2 n aYz v Ç 2 n aYz /v Ç 2 naYz TUV 5f}f _fafs z 5¹23asZ¹23p he cY`\ a¶_`e \ 2 5¹¶_``sa\ Z 53 ¬ n 0 23 ¬ n h e fq e af f[\ afs p h ¬ 1n z W Y f}_` aaf e ¹ Z_ Yëe f®_`w52 x 3 z ± 1v ¬z {v ¬ O z v ±¬z /v ¬ z j j Trang 5 0123
44567477747554447576475446777564457666756666565554 9 +, +-. / 9 0 1 9. 23 4 51 ! 56 78"# $% &'() 9:; <; =# > )9?@ AAAAAAAB C DEFGHC IJC K ELM C HM NGC OEPK C QRC S ! ( " # $ %! & ) & ' %!* R + , -! 2. -$! 3 & $ %! ! 4 /01 56 7 5 8 96 : ; 8 < 8 ; 8 96 56 = 5 >! D. ! ( ! /0 ?@ # A! D. ! ( B!.C EF G ! H. -$! 3 & ' %! A! 2. = 5I9 6 F G ! H. -$! 3 & ' %! A! 2.56 I8 JF G ! . ( -$! 3 & ' %! A! 2.5 I 65 7 +8I9 6 KLF G O ! . ( -$! 3 & ' %! A! 2. 7 5 I8K MR4 ! T. !. S ! -%! # & H ( / U ! & ' !. V 4 $ W ?@C EF X 7 5 X 9 = 5 JF X 7 5 X 5 = 5 F X 7 X 5 = 9 LF X 7 O X 9 = 5 N YS &Z \ !.$ ] [ / U Z4 ! ^. & ' S !# ! 7 _ EF[ ` 7 a b b 7b O JF ` a 7b c Fc ` ba LFc ` a7 7b O Y d ! e / U 7 EF f 7 JF f 7 # ! F O f7# !7 LF g f K 7 5 PR4 ! T. & ! D. g # 4 ! T. & $ ] ! \ ! h . / U & H ( ! V4 $ W ?@C EF g 7 5 g 9 9 JF g O g 5 9 F X 7 5 5 X 9 X 5 LF gg 7 9 g 5 g 9 g g Q X 7 5 g 57 g 5 K i ! ] ! j /0 ?@ # B!.C X 7 EF G ! . ( -$! 3 & ' %! A! 2. XI 5 9 6 JF G O ! H. -$! 3 & ' %! A! 2.=I9 6 F G ! . ( -$! 3 & ' %! A! 2.56 I= LF G ! H. -$! 3 & ' %! A! 2. X 5 I= 7 # ! 5 9 YS &Z \ ! ( k / U l5 m EF5 I 65 g n mI9 6 JF g 5 Im F O 7 IX LF56 I7 n XI9 6 Câu 7: Tính thể tích kh i ố nón, biết kh i
ố nón đó có chu vi đáy là 6 + $0 j / -! p. lK EFq X 8o JFq = lo Fq O g lo LFq g 8o Trang 6 13
66765475757565777554776464566464564755444654645767
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018
Câu 8: Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA, SB. Hãy tính © £¤¥¦ ª« © r £§¨¦ r r r ¬ ® ª« ° ® Oª« sª ± « ² ® ª« ¯ ± ³ stuv wxr ´ r r µr ¶ r r ¶ r r r ·r r º r » r r ¸ ¼¹ r ¬ r ¶ rr ·¸r r ½ µ rr r ° r ¶ r ¸ ¾ s r ¶ r ¿r r À  Á r ² r O ¶r·¸rrµ r r r r stuv yzxr ·r Ãr Ár Ä r r Å Ær ǹ r ¬ r ° r ¿ s r ² r µ stuv yyxr r r r Ê« È Ë É Ìr Ár Âr Ár r Ñ Ír ·r Î r Ï r ¶ r ÃÁr Å Ð r r r r r r r r r r r ¼ Òr Âr r r Æ r Ór r ¢r r Î r ´ Ï ¶ r r Ô r Õ µr µr r Ï ¢r r r r ¡ ¸ Ör ¶ r È Ë É Ì Ù « ³ Ú ×®Ør ·r r Æ r ¸Ûr Ã Æ ¬Ù È ß ³×®ÜÝ³×®É Þ °Ù È ß ³×®ØÝ³×®É Þ sÙ È ß Ú Ý à³×®É Ø È á ³×®ØÝâ É à ²Ù O È ß ³×®ÜÝ³×®É Ø È á ³×®ØÝ³×®É Þ ³ r Ì Ì Ú ® â stuv y{xr ´¶ r µr r Ï Ðr r Ô ¢r r r Ê« ³ Ì Ì â ® â r r r r ® ¬ÀÊ Ü « ° OÀÊ ä « sÀÊ« ²ÀÊ ® « R R R ä R ³Ì® â Ì stuv y|x r r ´¶ r ¸ Ór Æ r r ¢ r r à r Ô ¸ Ör ¶ r³ Ú rä â ³ ® Ú × å r ¬£ O æ « ® Ú ç Ý× °£ È « Ú Ý à ç ® Ú æ á ×Ýâ É à ®é ® é s£ è « Ý ® ²£ î « Ú Ý à ï ë æ á ®Ýâ É à ³ ê ë ì í ð ³ í r r r r stuv y}xr ´ r µr r r r r r r ·r r ¡ r ñr r »Ír r ¾ ¡ r ñr ¡¹ ¬ ± ³ Ê« Ì Ú Ì Ú ä â ° ± ³ Ê Ì « Ì Ú ä â s ± ³ Ê« Ì Ú Ì â ä â ² ± ³ OÊ Ì « Ì â ä â stuv y~xr ¼r ³ ò « r Í Ø ó « ³ r ¶ Üôr Ã Ò ¬ò ó â ° O È òóâ É ä sòó ² È óòâ É ä Trang 13
66765475757565777554776464566464564755444654645767
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018 ö÷øù ú| õ ü23 4õ 56 õ 789õ õ õ 9 õ 4õ õ õ õ õ õ O R ! " # ' $ & % ö ' R ( ' R $ & % õ 1 0 ! ö÷øù úûüõ 23 4 õ õ 55 õ , 9õ 9 - 89õ )* 8õ 5 +õ 5 9 .õõ 9 õ 5 4õ õ 4 õ õ / 4 õ õ õ õ )9 õõ 2* 4õ 5 + 3 1 ! 56 -)õ" 78 = 1 9 < 7 19 #1: 7 ö> ( O 1 < 9 7 1 @ ; ?
ö÷øùúýüCho hình chóp B 8 CDA8 õ E * õ K Fõ G õ 5 + H)õ *4 / õ 9 õ 6 L õ BCI õ Jõ G *4 / õ 5 + 3õ M N) õ WQRST 8 õ õ õ 5 O)õ BAõ 6õ 96õW 8 õ 2+ 6)õ 989õ 5 O)õ õ HI õ 5 3 4õ 5 O)õ õ X)8 QUTV P 8 õ Jõ 5 H9 Zõ 5 * õ ABõ Yõ 4 [ õ )6* õ 6 Lõ AB8 # õ Jõ 4 [ õ 5 + 3õ 6 Lõ BAõ M )õ 5\)õ 6* õ -5 + H)õ *4 / õ BA8 ö õ J O õ5H9 Zõ 5 * õ BAõ Yõ 4 [ õ )6* õ 6 Lõ BA8 ( õ Jõ G õ 5 + H)õ *4 / õ 9 õ 6 Lõ BA8 ö÷øù úþüõ]^õ õ *H _ õFIõ4õG ` õG M 5 aõG õ)* 8õ5 +õG b õ, õ 5õYõ õ c 5 ,õ9 õ4õ * ! * 8 õ 2^ õR 1 8 õ õ OR 1 #R 1 öR 1 7 (R 1 0 ö÷øù ÿ0üõ A6õ I õ 2õ G õ 989õ õ d M e)õ Y P G 6) g G 6)hi G 6)hi f f f 8 õ E* 8õ 5 +õ 9 õ 7õ M 9 aõ Y*5 4 dMb õ * õ d L)õj hi k l 8 õ ]* õ õ mk l ! õ 2 [)õ 26õ * 3Hõ õ n õ õ # õ 7; ö õ 7 O o ( õ 7g 0 ö÷øù ÿúüõ E * õ Kõ G õ õ )*4 _ õ 6uõ 2*5 õ _9 õ 6M e)õ 5 + 3 õ G ! 0 8 õ 23 4õ 8 O õ 0 õ # õ 7 õ ö õ õ ( õ P õ ö÷øùÿÿü õ 2*5 õ 4 d* _õ pHõ 5 +9 sõ 9 õ 3 õ 5 +õ 5 s + qõ 76rõ G õ 3 õ YH\)õ 9 Lõ 2 [)õ 8 õ 2^ õ 5 / 5 ^ 9õ tõ 9 õ 5* õ mõ 5 + qõ 76rõ 9mM N)õ 5 + qõ 8rõ G 8rõ 9 õ 3 õ 5 +õ Y s v õ G õ 5 u4õ 9 M N)õ 5 + qõ 8rõ 9qõ G* õ L9 õ 3 õ 5 +8 s õ 7 0 P W h w # P W O h w ö P W h w ( P W h w P P P ö÷øù ÿ1ü õA6õ2*5 4 õ4õ õ P x h ! i ! y ! 5 L õ99 . õ5 *H / õ5* L õ*4 / 7 I x 7 P õY õ 5 z õ 4õ õ 9 5 õ { 5 +9 sõ 5 H)õ 5* õ L *4 / õ 9mõ 5 H)õ õ G Z õ 8 õ 2^ õ )* 8õ 5 +õ 9 4õ õ 5 * õ L 8 x 7 o # O x 0 ö x ( x 0 Trang 8 13
66765475757565777554776464566464564755444654645767
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018 ~ } }}}} }} } } }} } }} } ¡ }£ ¤ ¥ ¢ ¦ } § ©£ § ©¤ ¢ ¨ ¨ ¥ ¦ ª } «¬ } } ®} ¯ °} ±} ²} ³ § ¦ £ ¤ © ª § ´µ ¢ ³¦© ¶µ ¢ ³¦© ~µ ¢ ³¦ ·µ ¢ ³ O ¦ § ¨ ¨ § ~ } } ¸ } } ½ } ¾ ¹º»} ¼Á ¨ ¦ ¿Áà À ¦ ª } Ä } Ç Å ¿ } Æ} È} É Ê } ® } ± } °} ¹»} } º¿ } Ë Ð } Ì¿ } Í} ® Î} Ñ} ¹»} } Ä¿ } Ï} ® Î} Ñ º } } } }ÁÓ Ã ¦ Ô Â ¦ Õ Ö ¦ × Ò ¦ ª } Ä } Ç Ø¿ }} Ù} ® Î} Ñ} ¹º} } Ú¿ } Û ® Î} Ñ} »} } }ÁÜ Â ¦ Ý Ö ¦ Þ ß ¦ à ¢ ¦ }à } É ¸ } á ª â } «¬ } } } ± ¬ } } ® ã} äË} } ® } } åË}} } ØÙÄÏÛÚÍÌ} ä å} ® æ} Šƪ O ´µè ¨ ¦ çé ¶µè ê ¦ ëé } } } } ~µ ¢Ò¨ è¦ é ·µ çê è¦ é Ò Ò ~ } } ¿ } } } } } } øÉ 1} } }§ § ¤ Ò ¦ £¤ ¨ ¥ £} Ò§ £5 ¨2 3 §4 6 7ª } Ä } Ç Û¿ } } } È } É } Ê } } ®} ¯ ò } } Ð } } ®} ¯ } } Ð °} ± } ² } 3 b P log a b 4 log 2 } } 4 4 8 } «¬ 9} ³ Þ ¦ ÿ ¥ ª Òêë¢ ê §0ê ¢À0ê ´µ O } ³¦ ¶µ } ³¦ ~µ } ³¦ ·µ } ³¦ ¢§¨ § ¢§¨ ç§ ~ } ì Ò ¥ } £ì ¤ ¥ } } } } í¦ } ¼ } } ¯îÖï}}}} í¦ } } ò £ ë ó } ¼ } ¯ ì ¢ ¥ ¢ ðì ñ ¥ } } } } îÖï}} É ¸ } ª } âÍ } ÷ ¾} } } ôË} õö § ´µ¤ ë ó ¿ð ë ó ¿ñ ë ó ¿ð ¤ ó } } } } ¶µ¤ ë ù ¿ð ë ù ¿ø ë ó ¿ ó O ~µ ë ó ¿ ë ó ¿ ø ë ó ¿ ù } ·µ ë ó ¿ ë ó ¿ ø ë ù ¿ ù ~ }Û } ü ú} Ë} }} } ÷ } ÷ } ü } Ñ û ü } } ¼} û ý } ø Ñ} ¸ } û ü } } ½ ¿ ¾ } } Ë} } ¸ } ú} } } } ± ¬ } ° } } û ü } É Ê} Ñ } Ò ¢§ ª }Ú} } ÷ } ÷ } } û¬ } ËÎ} ¡} } } û ü} ¬ } ª Ð } þ } ø ü } Ñ Ë} } °} û ü} È} } ÷ } ÷ } } Îö ´µ Ò £ O ¦ ¢§ðÿ ¶µ Ò £ § ¦ ¨ðÿ ~µ Ò £¦ 0ðÿ ·µ Ò £ § ¦ Òðÿ Trang 9
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018 13
66765475757565777554776464566464564755444654645767 TU >V t\ ¬¹ p ó_ p µe p h `\ e g _fñ _f´e `\ e g p _ _f´e abc fhY i[ j l k n o k m z f®_` Zg _f _h} ic ZX p h ¯=; 3 1v j ¹ {v j ¹ j o ¬ n v Oj¬ ¹ o 1 n /v j ¬ ¹ TU V |hY i[ k 2 l m n k 2 o 1v °d_` \ _ e _ ² {v °d_` \ _ e _ ²æ Ó 2þ v ¼`fg af\ _ e _² /v ° O d_`\_e_wm y Ømx 2 hw2y m o x Ø TU V 5f} i[ ~_`¬h ¬ 2 z W Y fe \ q ¯=; 1v p }`2n {v p }`¬n v Op}` ¬ É n /v p}`¬ ¬ 2 ¬ 1 É ¬ ¬ n TU V W YÄ Zq Zd e fg fhY i[ j l k n j m Äk Ä o j o aðe e ¦a ] e \ Z\ qY fX_ \ e 1v OÄ w jyo x Ø {v Ä w mØ x y 2 v Ä w m y Ø x 2 m w ö jyo x Ø /v Ä w 1yo x Ø TU V 5f}p }`n ¬ z f\ Zs `\ e g \ q e f^ap }` p h ¬ ¬ 1v 2 m {v 2 m v 2 o /v 2 m O j o j m TU V W }_` aa Y_f Zê ic Y_f Zê _h} Z×_` 1v Wd_ e \ Yue f _f Zc ~\ _ as i[ a _f º_` i[ ZÁ _f {v W
O d_e \Yuef_fZc~\_asi[ZÁ_fhi[Yëeº_`_fc v Õ[ ZÁ _f h i[ Yëe abc Yue f _f Zc ~\ _ p ¶_ º_` _fc /v Wd_ e \ Yue f _f Zc ~\ _ as i[ a _f h i[ Yëe º_` _fc TU V W YÄZq fhY i[ k ln w mÄoxj 2ko w Äo x jk Ä o Zd_` \ _ e _wyo x Ø 1v Ä 1 {v Ä 1 ÿ v Ä 1 0 /v OÄ 2 ÿ TU ¢V 5f} f _f afs e cY `\ a as ZÖ_` ac} º_` 211aY h aa a _f Z º_` j1aY j2aY jaYz Wfq e af f[\ afs Zs p h 3 1v O111Ä {v ±j2Ä v ±111Ä /v 111 jÄ TU V Wfq e af abc f[\ Zc ~\ _ e } À\ f _f ic p h3 1v jÄ {v 0±Ä v 0 O Ä /v 2jÄ Trang 10
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018 13
66765475757565777554776464566464564755444654645767 TU!V 5f}f _fafsÕz 765asZp he cY`\ aZêa _fc `sa`\ ícÕ5hZ£ 765¤ p h 1 0 z | _f af\ ¶_` `sa abc Õ p _ Yëe f®_` £ 765¤ p h Z\ qY | e fua 76 ic} af}4¹ j n 42z 6\ e ¬ 34n z f}_` aaf `\ íc j ZÖ_` e f®_` Õ7 65 p h3 1v ¬ j21 {v ¬ j21 v ¬ j21 /v ¬ j21 O 20 0 1 j1 TU >V 5f} f _f afs Õz 765 as ù ¹ ù 2 p ó_ p µe p h e _` Z\ qY abc Õ7 Õ6z f\ Zs e Á i[1z 5¹23 p h 3 1z 5 ù ¹ ù 23 1v 2 {v j v 2 /v O j TUV 5f}f _fafsZêÕz 765z ¼`Ö\ e ce ½_`a _fZp _jp ó_z °qe fqe aff[\ afsÕz 765`\ í _`_ e f e c_ `sa `\ íc a _f _ h Yëe f®_` Z e ½_` p _ c} _f\ p ó_3 1v {v j O v /v TU V \ e g p _ _f´e `\ e g _fñ _f´e abc fhY i[ l k n m k 2 m e _ Z} _ ã2 m è y p h 1v OYc]l 0 n 2Y\ _ln m {v Yc]l 2 nY\ _ln 2 m ã 2mè y ã2 m è y ã2 m è y ã2 m è y v Yc]l 0 n 2Y\ _ln 2 m /v Yc]l 0 n 2Y\ _l 2 n ã2 m è y ã2 m è y ã2 m è y ã2 m è y TU V f®_` Zg _f _h} ic ZX ¯=; 1v | O hYi[ jk 2 l m n p ¶_ Zd_` \ _ e _ e _` f}_` ]a Zg _fz k 2 m {v |hY i[l j n k a o }ijkp ¶_ Zd_` \ _ e _ ²z v |hY i[ ln k m m k 2 o p ¶_ _`fg af \ _ e _²z /v |hY i[ j l j n k k o o _`fg af \ _ e _ f}_`wmØ x y1 j TU V ° } fhY abc fhY i[ 0 jk k l m o n p h 1v w O k x jk0mk j 0j o m z p _j {v w x j j 0 0 jk k k k m o m o v wk k x j j k 0 m k 0 j o m o z p _j /v w x j 0 j 0jk k k m o m TU V °d e fg f _f _ p h Zd e fg abc fhY i[ _h} ~\ ZX 1v j l k n j m k m {v j Ol k n j m k v j ln k m j o k m /v j ln k m j o k Trang 11
Tröôøng THPT Taân Hieäp Ñeà cöông oân taäp thi hoïc kyø 1 naêm hoïc 2017 - 2018 13
66765475757565777554776464566464564755444654645767 TU V ¾ï\ ZÁ _f abc f _f Zc ~\ _ p h ZÁ _f af_` abc e _f´e 1v 6 O cYëe {v ¼½Y Yëe v 6[_ Yëe /v |c\ Yëe TU ¢V 5f} f _f afs e cY `\ a Õz 765 as5 ¹5 253 Z¶\ Yue ¶_` `sa 5¹ 5 n 2 5 n 3 ¬ n z f\ Zs e fq e af abc f[\ afs Z¿ af} p h3 1v ¬ O {v ¬ v ¬ /v j¬ ± TU V 5f} f _f afs Õz 7654 as Z 7654 p h f _f e f}\ a _f c ¹3 ¬ n | p h e _` Z\ qY abc 76 Õ| ¶_` `sa \ £ 7654¤ e cY `\ a Õ76 ¶_` e \ Õz f}_` aaf `\ íc fc\ ZÖ_` e f®_` 64 Õ5 e f³}¬ p h3 1v ¬ {v j¬ v ¬ O /v ¬ 2 2 2 j2 TU !V Wtc Zu `\ c} Z\ qY abcZd e fg £ 5¤ 3 k j l m n hZÖ_` e f®_`l j n k 2 m p h jk o 1v ¸w x 2 2 2y 2Ù y Ú m {v ¸w x 2 2yÙ y Ú m m m m Û jÜ Ý Þ Û jÜ Ý Þ v ¸w x 2 2y 2Ù y Ú m m Ú Û /v O¸wm mx 2 2 2yÙ ym jÜ Ý Þ Û jÜ Ý Þ j TU >V t\ k k m j o ĸ p ó_ p µe p h `\ e g _fñ _f´e `\ e g p _ _f´e abc fhY i[ln e _ ã è y±z f\ Zs k j m 1v Äm ¸ ± n {v ¸ j n Ä v j ¸ Ä /v j j O¸ Ä o 2 n 2 TU V ¾ue a¶ `\ } `\ j11 e \ Zd_` p } \ f _ ± e f_` h} _`X_ fh_` \ p ¿\ i´e ± Yue _½Yz Õc ± _½Y e f_` a¶ `\ } _h ×e Zµa c} _f\ e \ ê_ a [_ p _ p ¿\ h p ¿\ a¶ `\ } f¶_` ×e À e Xe a aa f _ _ ×e e a _`X_ fh_` i e p ¿\ i´e e f³} p } \ p ¿\ i´e f¶_` f _ p h 1 11j Yue _`h £ 2 e f_` e _f 1 _`h¤ z 1v 2±j {v 1j1 v O 22j1102 /v j200±jj Trang 12
501:DDCBADAAADACCDDDACABDACDDBAAACBDDCABBBACBBBBCBCCCD
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I NĂM HỌC 2017-2018 Môn TOÁN –Lớp 12
403:BBABCDACACACBCAAACCDAABDBDCBBDBDCBDACCDDDBCDBDCABA ĐỀ SỐ 3
SỞ GD-ĐT KIÊN GIANG ĐỀ MẪU KIỂM TRA HỌC KÌ I- NĂM HỌC 2017-2018 TRƯỜNG THPT T
ÂN HIỆP Môn TOÁN –Lớp 12 - Thời gian 90 phút
………………… ( Không kể thời gian phát đề )
Hãy chọn một phương án trả lời đúng nhất cho mỗi câu.
Câu 01: Trong các mệnh đề sau đây, mệnh đề nào sai ?
A. Bất kì một hình tứ diện nào cũng có mặt cầu ngoại tiếp.
B. Bất kì một hình chóp đều nào cũng có một mặt cầu ngoại tiếp .
C. Bất kì một hình hộp chữ nhật nào cũng có một mặt cầu ngoại tiếp .
D. Bất kì một hình hộp nào cũng có một mặt cầu ngoại tiếp.
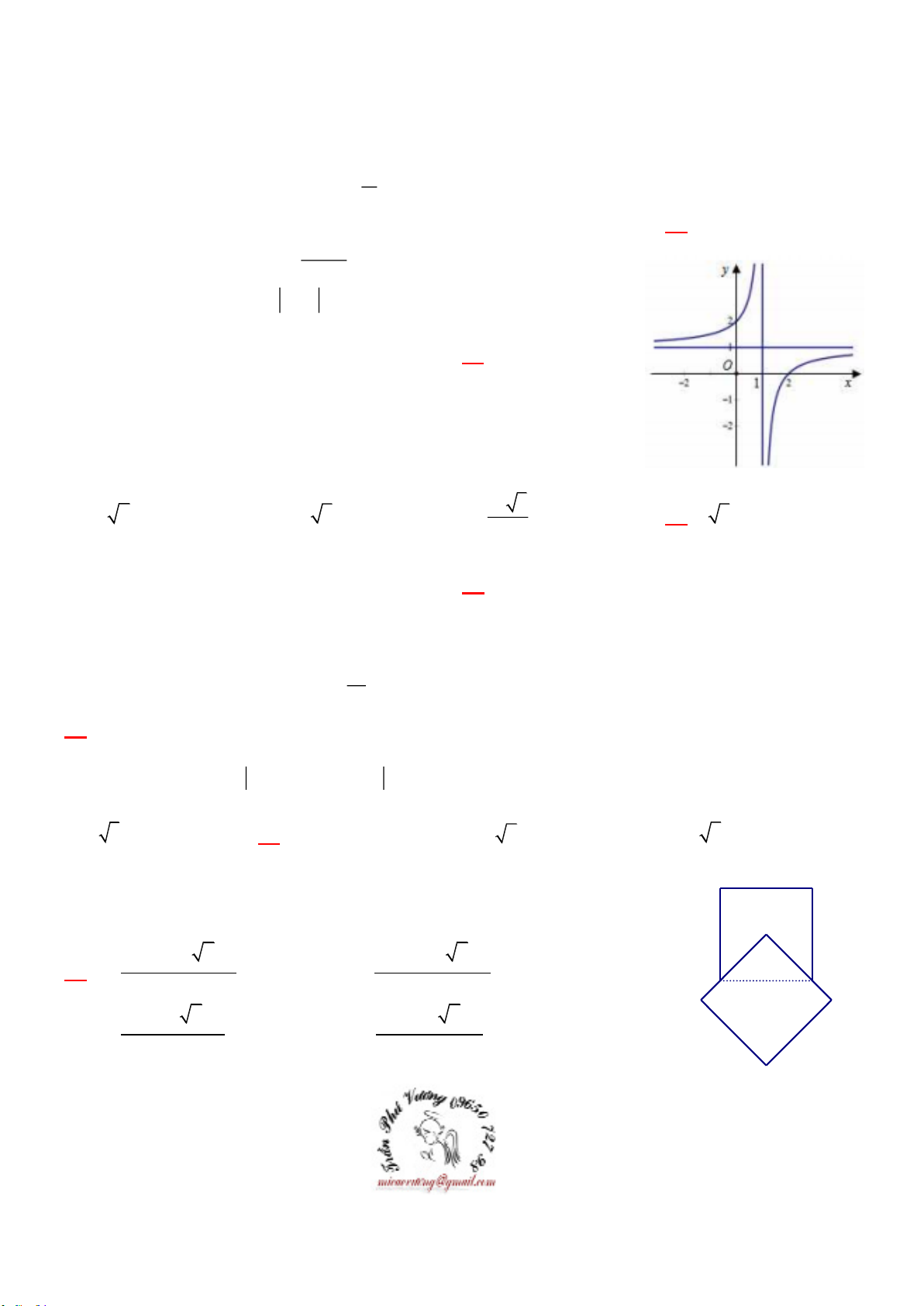
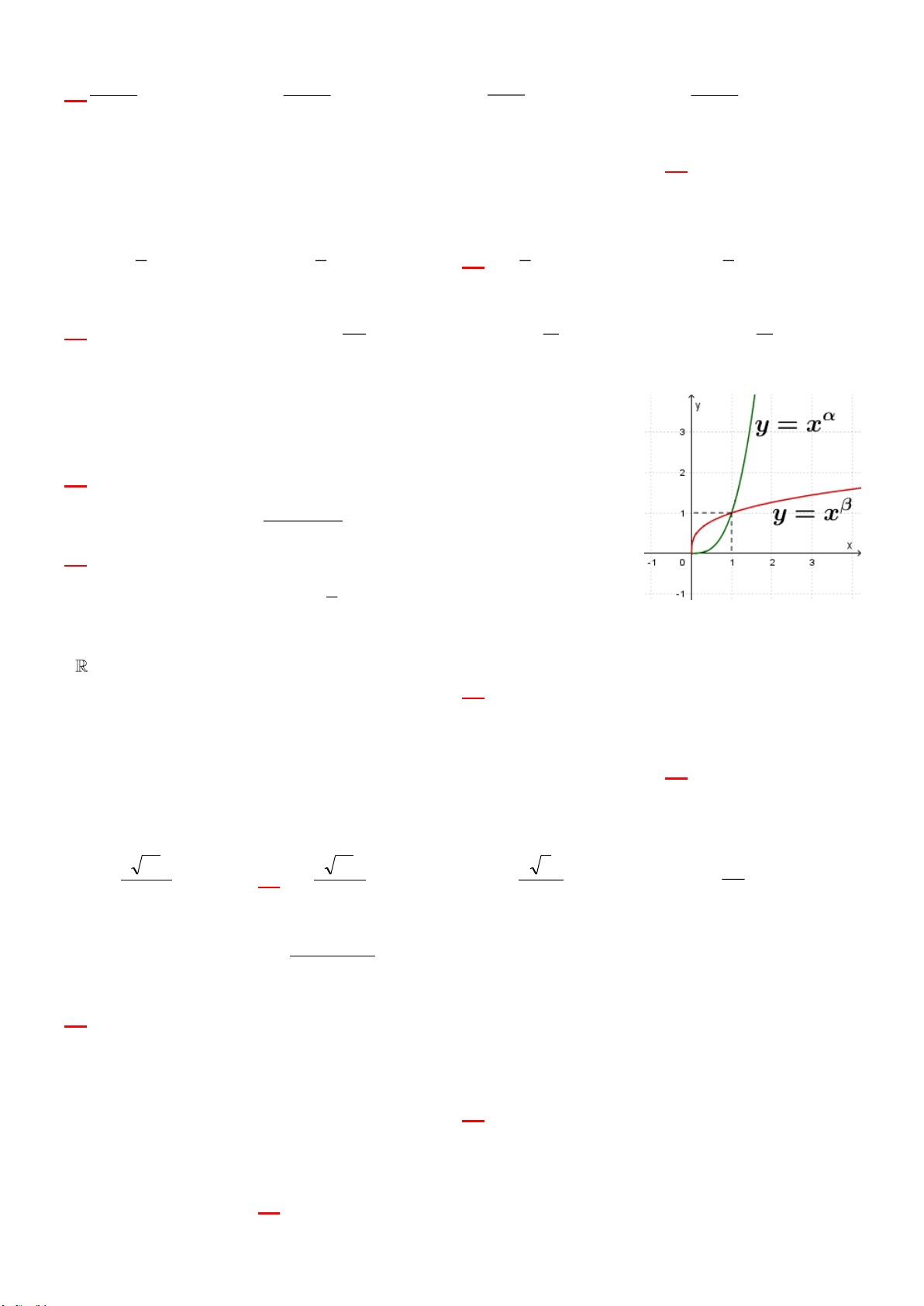
Câu 02: Đồ thị của hàm nào dưới đây là một đường đi lên : x 1
A. y log x B. y log x C.
D. y log x 1 0,8 y 3 e
Câu 03: Cho hàm số y f x liên tục, đồng biến trên đoạn a; b . Mệnh đề nào sau đây đúng?
A. Hàm số đã cho có cực trị trên đoạn a; b .
B. Phương trình f x 0 có nghiệm duy nhất thuộc đoạn a; b .
C. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn a; b .
D. Hàm số đã cho có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng a; b .
Câu 04: Tập xác định của hàm số y x 23 5 là : 2 2
A. D ;
B. D ;5
C. D 5;
D. D ; 3 3
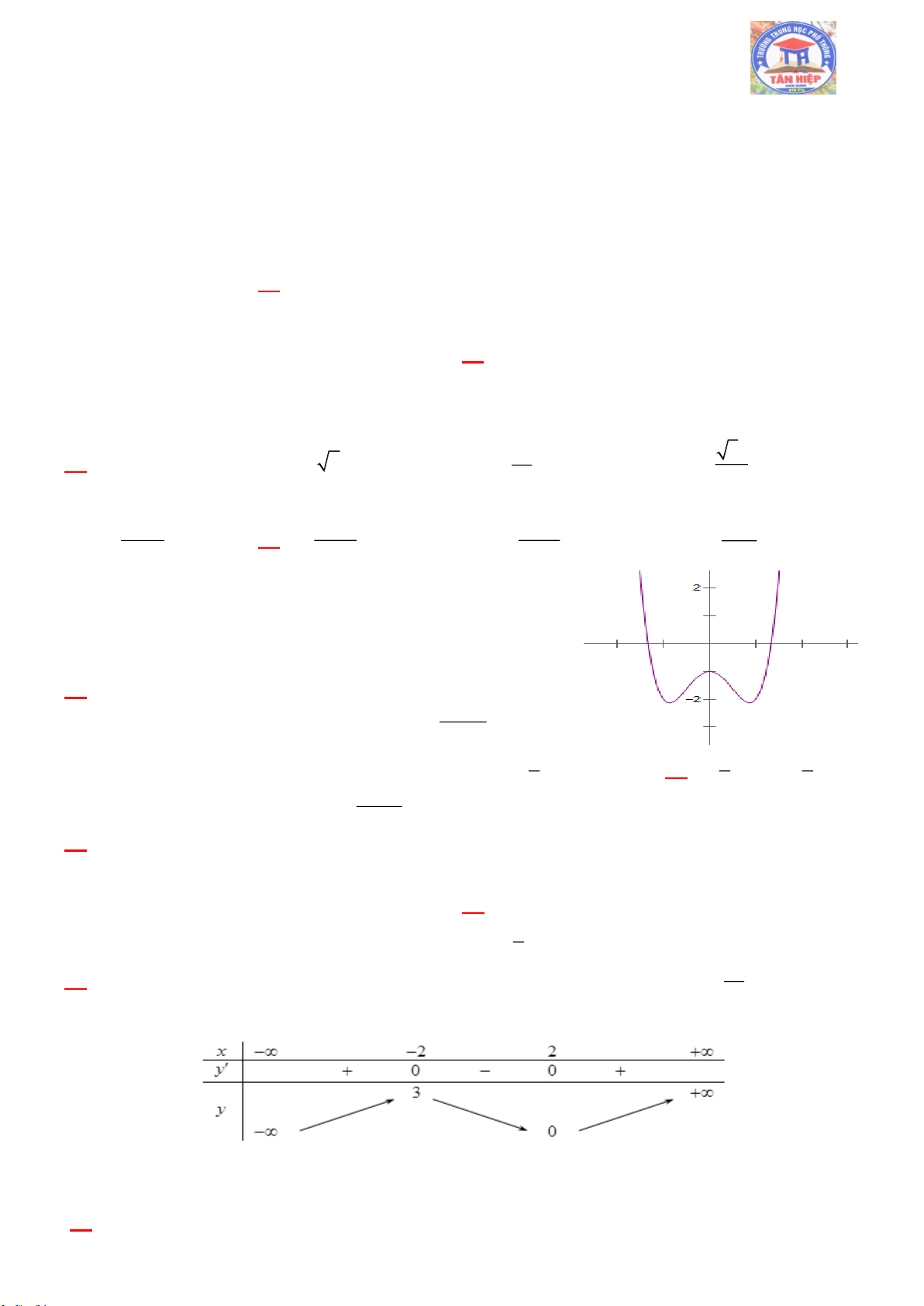
Câu 05: [CT17] Cho hàm số y f x có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng ?
A. Hàm số đạt cực tiểu tại x 2 .
B. Hàm số có bốn điểm cực trị.
C. Hàm số không có cực đại.
D. Hàm số đạt cực tiểu tại x 5 .
Câu 06: Tính diện tích toàn phần của khối nón có đường
sinh l và bán kính đường tròn đáy bằng r.
A. s 2 r(1 2r)
B. s 2 r(1 r)
C. s r(21 r)
D. s r(1 r) tp tp tp tp
Câu 07: Cho hình chóp có diện tích đáy S và chiều cao h. Tính thể tích khối chóp. 1 1 1 A. V S.h B. V S.h . C. V S.h .
D. V S.h . 6 3 2
Câu 08: [CT17] Cho a là số thực dương tùy ý khác 1. Mệnh đề nào dưới đây đúng ? 1 1 A. log a . B. log a . 2 log 2 2 log a a 2 y
C. log a log 2.
D. log a log 2. 2 a 2 a
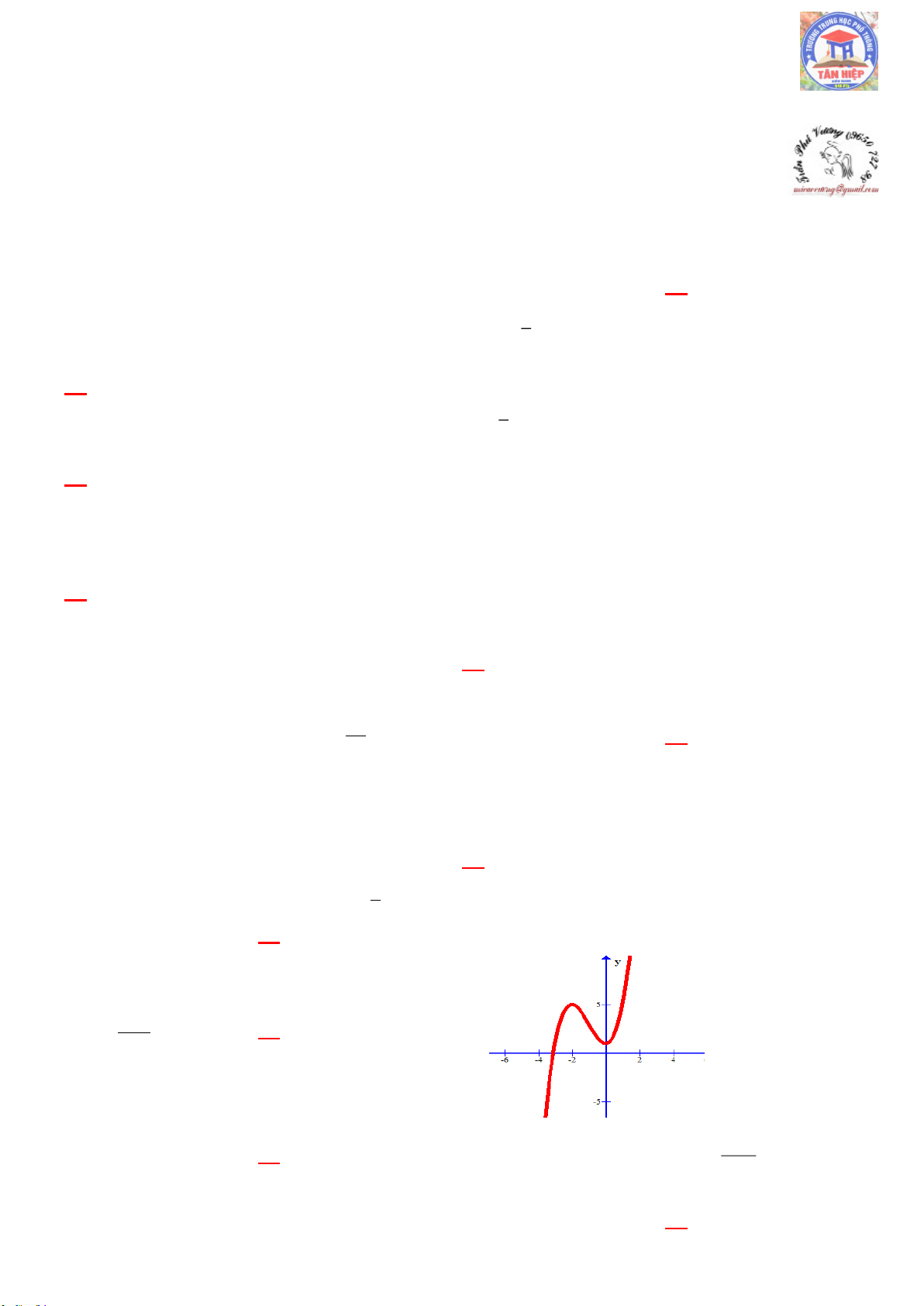
Câu 09: [CT17] Cho hàm số 4 2
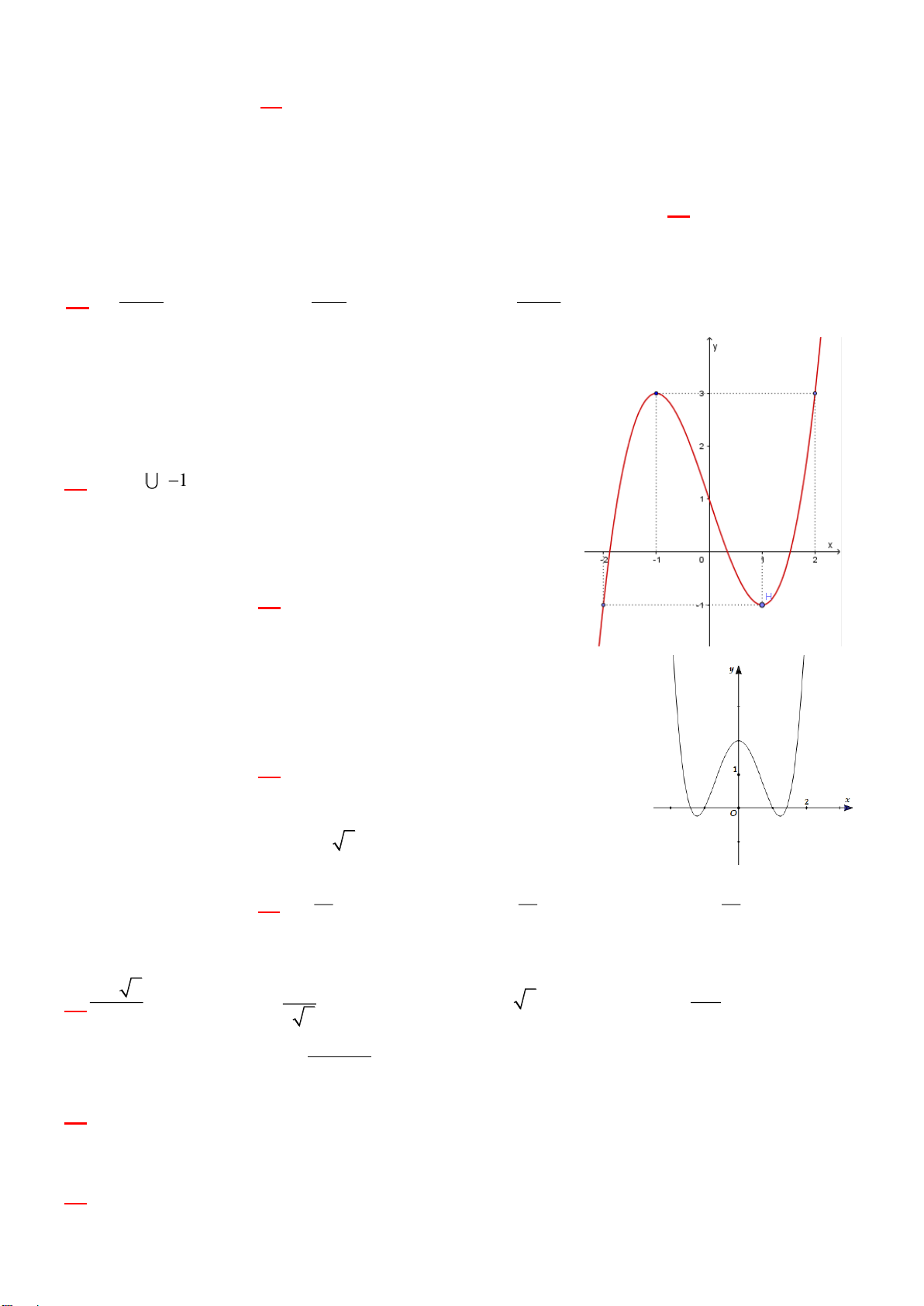
y x 2x có đồ thị như hình bên. Tìm tất 1
cả các giá trị thực của tham số m để phương trình 4 2
x 2x m có bốn nghiệm thực phân biệt. -1 1 0 x
A. 0 m 1
B. 0 m 1. C. m 0 . D. m 1.
501:DDCBADAAADA CCDDDA CABDA CDD BAAACBDDCA BBBA CBBBBCBCCCD
Câu 10: [MH3] Cho a là số thực dương, a khác 1 và 3 P log
a . Mệnh đề nào dưới đây đúng ? 3 a 1 A. P 1. B. P 3. C. P . D. P 9. 3
Câu 11: [CT17] Tính thể tích V của khối trụ có bán kính đáy r 4 và chiều cao h 4 2 .
A. V 64 2 B. V 128 C. V 32
D. V 32 2
Câu 12: Cho a và *
n 2k 1(k ) , n
a có căn bậc n là : n A. a . B. 2n 1 a . C. a . D. | a | .
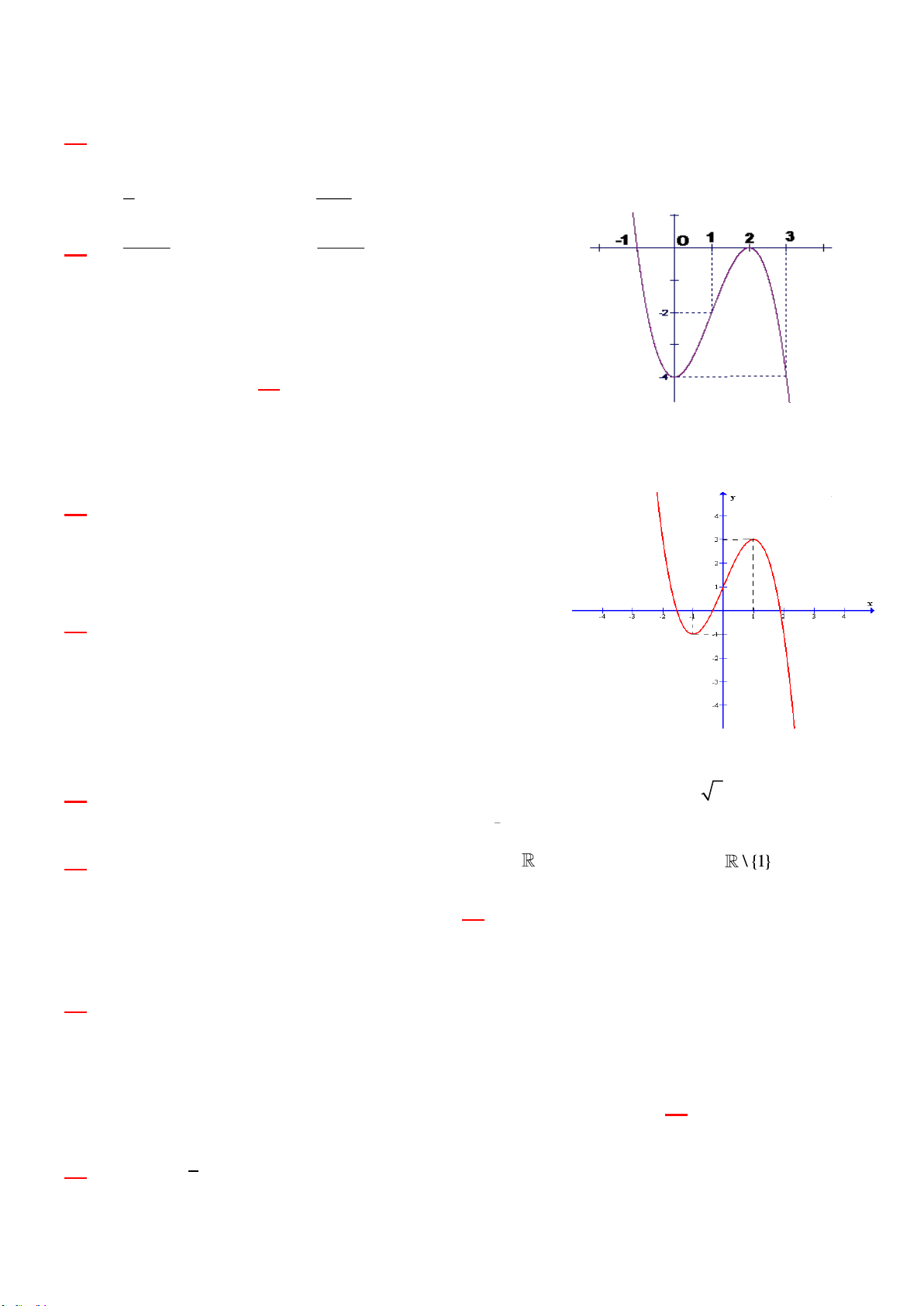
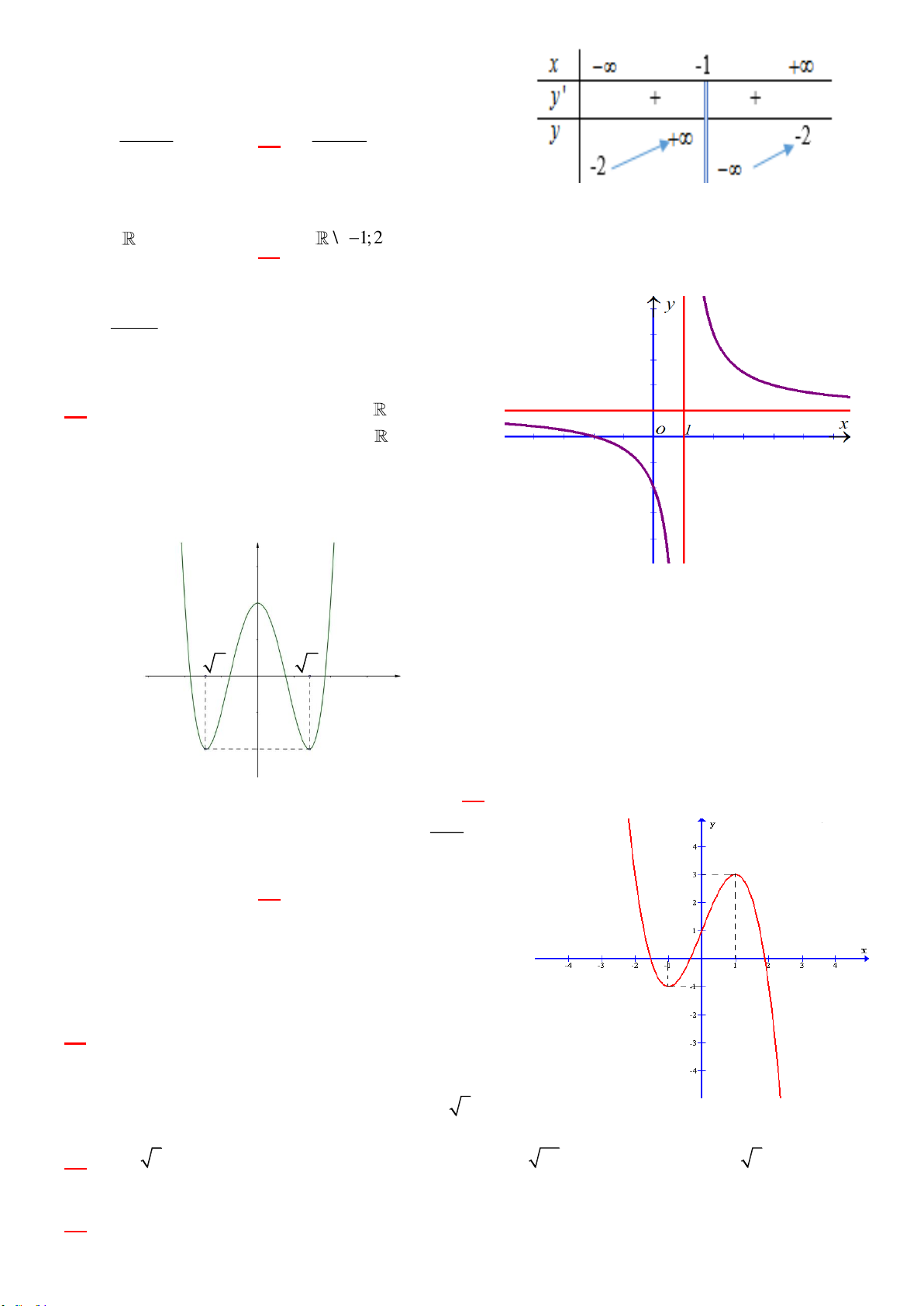
Câu 13: Cho hàm số y f (x) xác định và có đồ thị là đường cong trong hình vẽ bên
Hàm số y f (x) đạt cực tiểu tại điểm nào dưới đây? A. x = -2. B. x = 4. C. x = 0. D. x = 2. 4 x 2
Câu 14: Hàm số y
x 1 đồng biến trên khoảng nào? 2 A. ;0 .
B. ;1. C. 1 ;.
D. 0;
Câu 15: Số cạnh của hình 20 mặt đều là A. 20 B. 16 C. 12 D. 30 x 1
Câu 16: [MH2] Tìm các nghiệm của phương trình 3 27. A. x 3.
B. x 9. C. x 10. D. x 4.
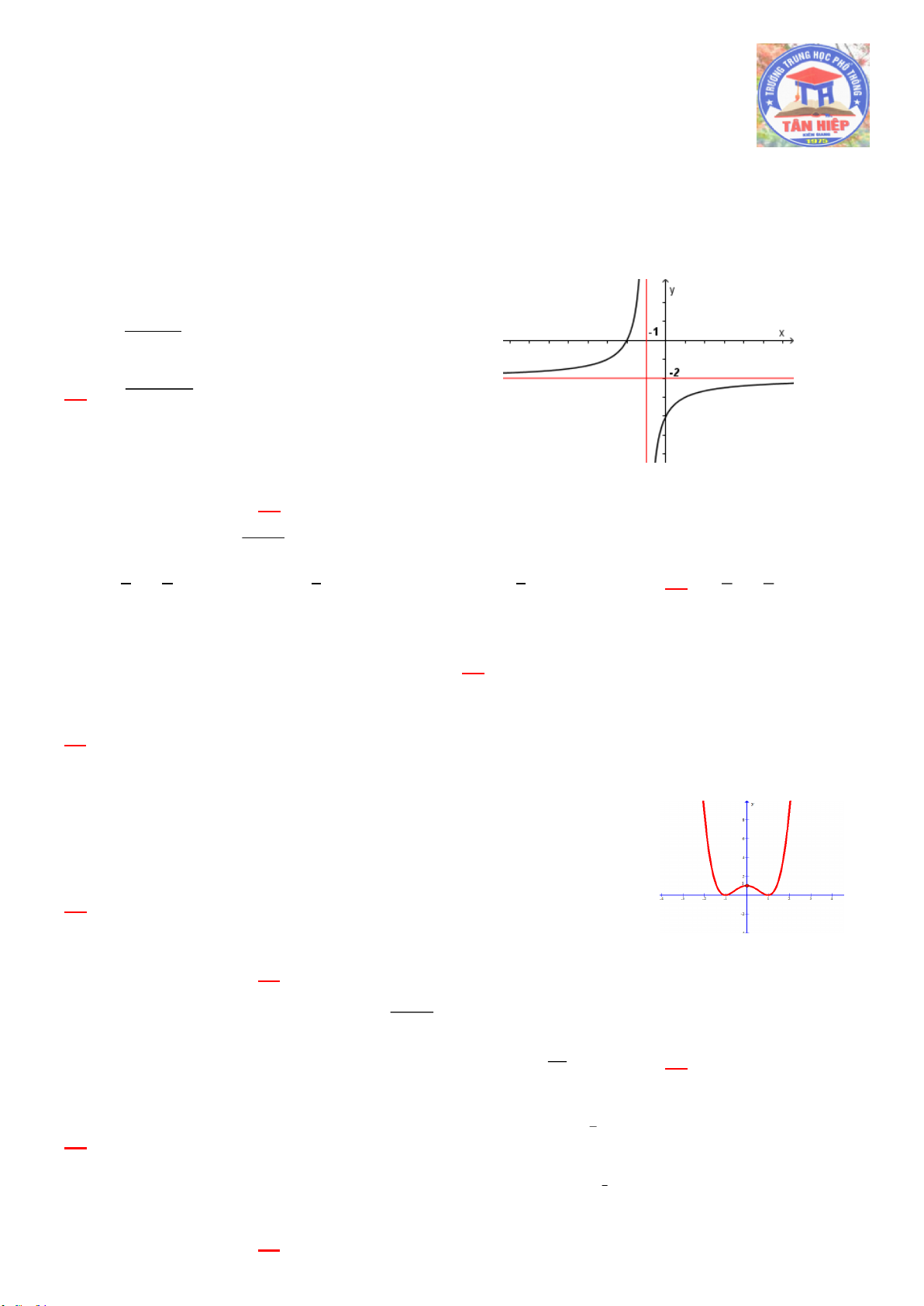
Câu 17: Hàm số nào trong các hàm số sau có đồ thị cắt trục tung tại điểm có tung độ âm ? 3x 4 3 x 4 2 x 3 3x 4 A. y B. y C. y D. y x 1 x 1 x 1 x 1 Câu 18: Cho hàm số x 1 y
. Khẳng định nào sau đây đúng? x 1
A. Đồ thị hàm số có tiệm cận ngang là x 1
B. Đồ thị hàm số có tiệm cận ngang là y 1
C. Đồ thị hàm số có tiệm cận ngang là y 1
D. Đồ thị hàm số có tiệm cận đứng là x 1
Câu 19: Cho hình chóp S.ABCD có thể tích bằng 2 3
a và đáy ABCD là hình vuông cạnh a 2 . Tính khoảng
cách từ S đến mặt phẳng (ABC). A. 3a B. a 2 C. a 3 D. a . 3 2
Câu 20: Đạo hàm của hàm số 9 x x y là. 3 2 2xx 3 2xx A. 2 3 x .9 .ln 9 B. 3 2 2 2 3 .9 x x x .ln 9 C. 3 2 2 2 3 .9 x x x D. 9 .ln 9 Câu 21: Cho hàm số 4 2
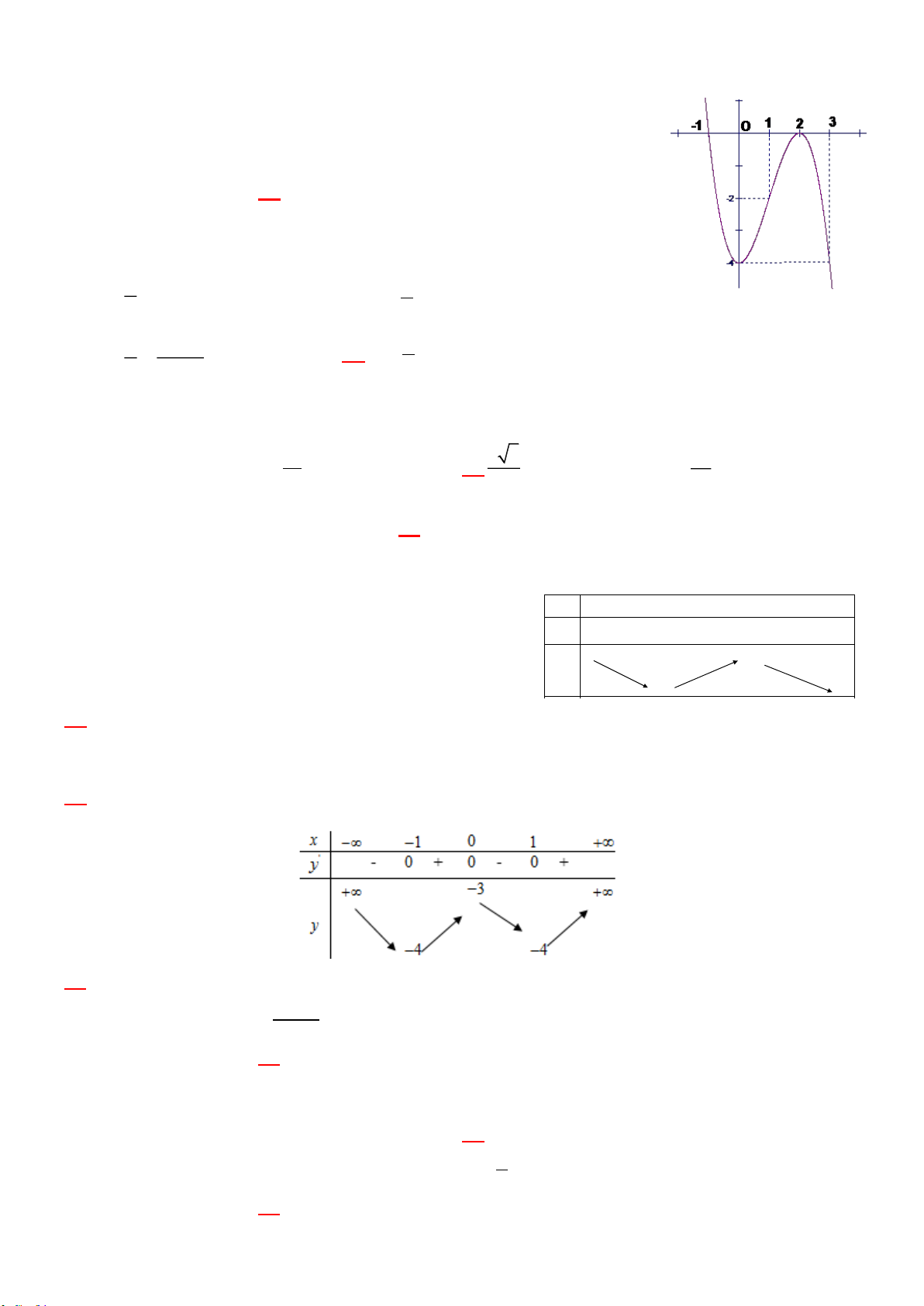
y x 4x 3 có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng 1 là :
A. y 4x 2 B. y 4 x 2 C. y 4 x 2
D. y 4x 2
Câu 22: Cho a 0 là tham số. Nghiệm của phương trình ln 2x 3 a ln 3a là . 2a 3 a 3 3a 3 A. x B. x C. x D. Kết quả khác 2 2 2
501:DDCBADAAADA CCDDDA CABDA CDD BAAACBDDCA BBBA CBBBBCBCCCD
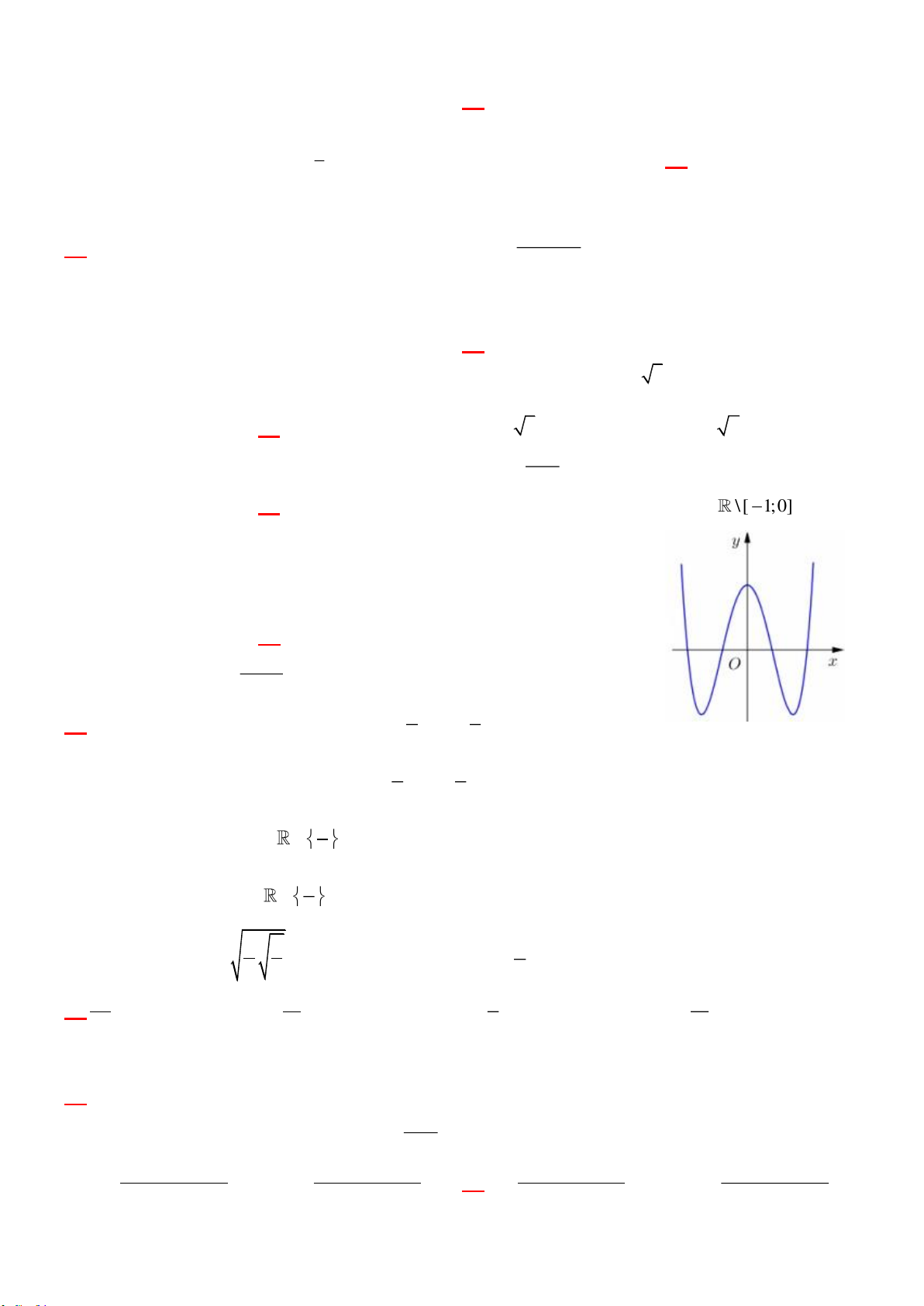
Câu 23: Cho hàm số y f (x) xác định và liên tục trên R, có đồ thị
như hình vẽ sau. Khi đó tập nghiệm của bất phương trình f x 3 là: A. ; 2
B. 2; \ 1
C. 2; 1 D. 2;
Câu 24: [CT17] Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A. 1 mặt phẳng. B. 2 mặt phẳng. C. 3 mặt phẳng. D. 4 mặt phẳng.
Câu 25: Đường cong hình sau là đồ thị hàm số của một hàm số trong bốn hàm
số được liệt kê ở bốn phương án , A ,
B C, D . Hỏi hàm số đó là hàm số nào: A. 4 2
y x x 1. B. 4 2
y x 2x 1. C. 4 2
y x 5x 4 . D. 4 2
y x 3x 2 .
Câu 26: [CT17] Cho khối lăng trụ đứng AB . C A B C
có BB a , đáy ABC là
tam giác vuông cân tại B và AC a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. 3 V a . B. V . C. V . D. V . 2 3 6
Câu 27: Thiết diện qua trục của một hình nón là một tam giác vuông cân có diện tích 50cm2. Thể tích khối nón là 250 2 A. 100 cm3 B. cm3 C. 150 2 200 cm³ D. cm3 3 3 2 3 mx m
Câu 28: [CT17] Cho hàm số 4 y
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của x m
m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S . A. 3 . B. 4 . C. Vô số. D. 5 . 2
Câu 29: Cho hàm số y x 4x 1 có đồ thị (P). Phương trình tiếp tuyến của (P) tại giao điểm của (P) với trục tung là: A. y 4 x 1 B. y 2x 1 C. y 4x 1 D. y 2x 1
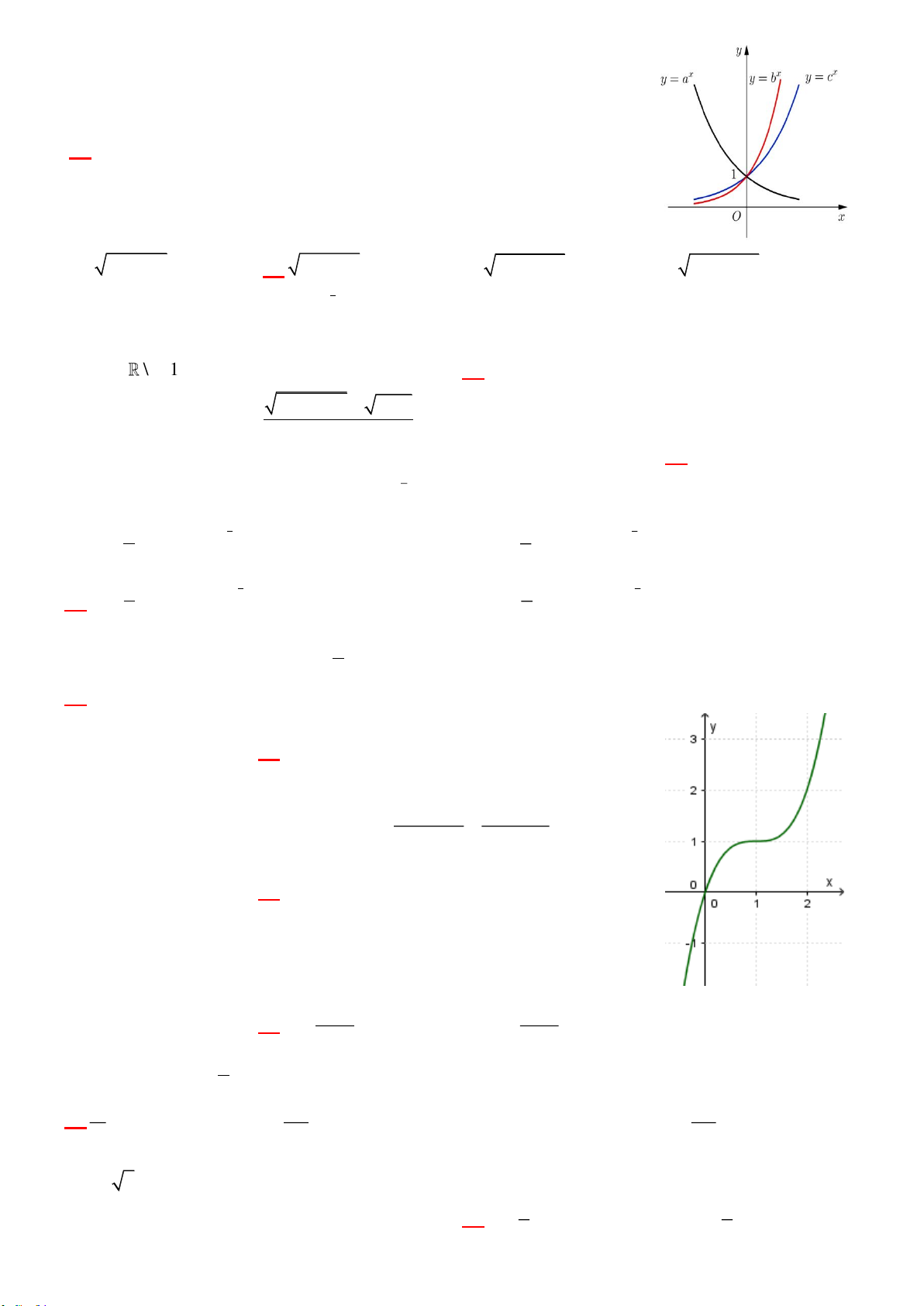
Câu 30: [MH2] Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số x , x , x y a y b y c
được cho trong hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. b c a .
B. c a b .-
C. a c b .
D. a b c .
Câu 31: Cho mặt cầu S(O; R) và điểm A cố định với OA d R . Qua A , kẻ
đường thẳng tiếp xúc với mặt cầu S(O; R) tại M . Công thức nào sau đây
được dùng để tính độ dài đoạn thẳng AM . A. 2 2 d R B. 2 2 d R C. 2 2 R 2d D. 2 2 2R d
Câu 32: Tìm x để biểu thức x 1 2 3 1 có nghĩa:
501:DDCBADAAADA CCDDDA CABDA CDD BAAACBDDCA BBBA CBBBBCBCCCD A. x ;1 1; . B. x 1 ;1 . C. x \ 1 . D. x ; 1 1; . 2
x x 2 x 8
Câu 33: Đồ thị hàm số y có mấy tiệm cận ngang 2x 1 A. 0 B. 2 C. 3 D. 1
Câu 34: Đạo hàm của hàm số y x x 2 2 3 3 1 là : 1 2 2 2 A. y '
x 3x 3 1 2x 3 B. y '
x 3x 1 2 3 1 3 3 1 2 1 2 2 2 C. y '
x 3x 3 1 2x3 D. y '
x 3x 3 1 x3 3 3 xc xb
Câu 35: Cho phương trình a5 1 , 0 a
1 . Tìm tổng b c để phương trình có nghiệm x = 1. a A. 4 B. 6 C. -4 D. -6
Câu 36: Đường cong trong hình là đồ thị của hàm số nào? 3 3 2
A. y x 3x
B. y x 3x 3x 3 2 4 2
C. y x 3x 3x
D. y x 2x 1 2
Câu 37: Nếu đặt t log x thì phương trình 1 trở thành 2 5 log x 1 log x 2 2 phương trình nào. A. 2
t 5t 6 0 B. 2
t 5t 6 0 C. 2
t 6t 5 0 D. 2
t 6t 5 0
Câu 38: [MH2] Cho hình lăng trụ tam giác đều ' ' '
ABC.A B C có độ dài cạnh đáy
bằng a và chiều cao bằng h. Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho. 2 a h 2 a h
A. V a 2 h B. V C. V D. V a 2 3 h 3 9 1
Câu 39: Nếu log x
log 9 log 5 log 4 (với 0 a 1) thì x bằng a 2 a a a 12 3 20 A. B. C. 60 D. 5 20 3
Câu 40: Một đường thẳng cắt mặt cầu tâm O tại hai điểm A,B sao cho tam giác OAB vuông cân tại O và
AB a 2 . Thể tích khối cầu là 4 2 A. 3 V a . B. 3
V 4 a . C. 3 V a . D. 3 V a . 3 3
Câu 41: Đồ thị sau là của hàm số nào sau đây? 2x 3 2x 3
A. y x y 1 . B. x . 1 2x 3 2x 3 y C. y x 1 . D. x 1 .
Câu 42: Tính thể tích của khối chóp tứ giác đều SABCD có chiều
cao h, góc ở đỉnh của mặt bên bằng 60 0 . 3 3 2 3 h 2h 3h h A. B. C. D. 6 3 2 3
501:DDCBADAAADA CCDDDA CABDA CDD BAAACBDDCA BBBA CBBBBCBCCCD
Câu 43: [CT17] Tìm giá trị thực của tham số m để phương trình x x 1 9 2.3
m 0 có hai nghiệm thực x , 1
x thỏa mãn x x 1. 2 1 2 A. m 1. B. m 3. C. m 3. D. m 6. 1
Câu 44: [CT17] Tìm giá trị thực của tham số m để hàm số 3 2 y x mx 2
m 4 x 3 đạt cực đại tại x 3 3 A. m 1. B. m 5 . C. m 7 . D. m 1 . a
Câu 45: Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông cân tại B có AB =
. Biết A’C = a và A’C hợp 2
với mặt bên (AA’B’B) một góc 30°. Tính thể tích lăng trụ 3 a 2 3 27a 3 a 2 3 a 6 A. B. C. D. 4 8 16 4
Câu 46: Tìm tất cả các giá trị thực của tham số m để phương trình x x
8 3.2 m 0 có nghiệm . A. Kết quả khác. B. m 2 C. 2 m 2 D. m 2
Câu 47: Một cốc nước có dạng hình trụ đựng nước chiều cao 12cm,
đường kính đáy 4cm, lượng nước trong cốc cao 10cm. Thả vào cốc
nước 4 viên bi có cùng đường kính 2cm. Hỏi nước dâng cao cách mép
cốc bao nhiêu xăng - ti - mét (Làm tròn sau dấu phẩy 2 chữ số thập phân)? A. 0,33cm B. 0,75cm C. 0,67cm D. 0,25cm
Câu 48: Cho hình chóp S.ABCD có đáy là hình thoi, góc BAD 0 120
và BD a , hai mặt phẳng SAB và SAD cùng vuông góc với mặt
phẳng đáy. Góc giữa mặt phẳng SBC và mặt phẳng đáy bằng 0 60 .
Tính thể tích khối chóp S.ABCD . 3 a 3 3 a 3 a 3 2a 15 A. . B. . C. . D. . 12 12 4 15
Câu 49: Tìm tất cả giá trị m để bất phương trình log (2x 1) log (4x 3) m có nghiệm. 2 3
A. m R . B. m . C. m 1. D. m 1. 2 2 2
a b c 6
Câu 50: Cho các số thực a, , b c thoả mãn:
. Gọi M, m là giá trị lớn nhất, nhỏ nhất của
ab bc ca 3. biểu thức 6 6 6
P a b c . Tìm M m . A. 18. B. 21. C. 10. D. 12.
-----------------------HẾT----------------------
403:BBABCDACACACBCAAACCDAABDBDCBBDBDCBDACCDDDBCDBDCABA ĐỀ SỐ 4
SỞ GD-ĐT KIÊN GIANG
ĐỀ MẪU KIỂM TRA HỌC KÌ I- NĂM HỌC 2017-2018
TRƯỜNG THPT TÂN HIỆP Môn TOÁN –Lớp 12 - Thời gi
………………… ( Không kể thời gian phát đề )
Hãy chọn một phương án trả lời đúng nhất cho mỗi câu.
Câu 01: Đồ thị sau là của hàm số nào sau đây? 2x 4 3 A. y y x . x . B. 1 2 x 4 4 2 C. y
y x 2x 1. x . D. 1
Câu 02: [CT17] Cho phương trình x x 1 4 2 3 0 . Khi đặt 2x t
, ta được phương trình nào dưới đây ? A. 2
t t 3 0 .
B. 4t 3 0 . C. 2 2t 3 0 . D. 2
t 2t 3 0 . x Câu 03: Cho hàm số 2 1 y
. Phương trình tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng 2 là x 1 1 1 1 1 1 1 A. y x
B. y x 1
C. y x D. y x 3 3 3 3 3 3 2 x 3x 9
Câu 04: Đạo hàm của hàm số y e là: 2 x 3x 9 2 A. e B. (2 3) x x e C. 3x 9 (2 3) x x e D. x e
Câu 05: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mọi hình hộp đứng đều có mặt cầu ngoại tiếp.
B. Một hình chóp có đáy nội tiếp trong một đường tròn thì có mặt cầu ngoại tiếp hình chóp đó.
C. Mọi hình hộp đều có mặt cầu ngoại tiếp.
D. Mọi lăng trụ tam giác đều có mặt cầu ngoại tiếp.
Câu 06: Cho hàm số y f ( x ) có đồ thị
Tìm tất cả các giá trị thực của tham số m để phương trình f ( x ) m có 3 nghiệm thực phân biệt. A. m <0 B. m >1 C. m=1 D. m = 0
Câu 07: Tính thể tích của khối nón có chiều cao bằng 8 và độ dài đường sinh bằng 10. A. 124 B. 96 C. 128 D. 140 2 x 3
Câu 08: Tìm giá trị nhỏ nhất của hàm số y trên 2; 4 . x 1 19 A. min y 2 . B. min y 3 . C. min y .
D. min y 6 . 2;4 2;4 2;4 3 2;4
Câu 09: Chọn khẳng định sai trong các khẳng định sau: x
A. Hàm số y ln x đồng biến trên R. B. Hàm số 2
y 3 đồng biến trên R.
C. Hàm số y log x đồng biến trên 0; .
D. Hàm số y log x nghịch biến trên 0; . 1 e
Câu 10: [MH1] Giải phương trình log (x ) 1 3 . 4 A. x = 80 B. x = 65 C. x = 82 D. x = 63
602:CDD CBCBDABDD CBD CA BCBAACBDADBCAA BCCBA BADCCDA BDDADAA Câu 11: C
ho hàm số y f (x) xác đị nh và có đồ thị
là đường cong trong hình vẽ bên :
Hàm số y f (x) đạt cực đại tại điểm nào dưới đây? A. x = 0. B. x = -1. C. x = -4. D. x = 2.
Câu 12: [CT17] Cho a là số thực dương khác 1. Mệnh đề nào dưới
đây đúng với mọi số dương x , y . x x A. log log x y B. log
log x log y a a y a a a y x log x x C. log a D. log
log x log y a a a a y log y y a
Câu 13: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 2 cm, cạnh bên SA vuông góc với mặt
phẳng đáy và SA 5cm . Tính t
hể tích khối chóp S.ABC . 10 5 3 40 A. 3 10cm . B. 3 cm . C. 3 cm . D. 3 cm . 3 3 3
Câu 14: Cho khối bát diện đều ABCDEF, khẳng định nào sau đây là đúng?
A. Tam giác AEC đều.
B. Các điểm A, B, C, D cùng thuộc một mặt phẳng.
C. AB và AE vuông góc với nhau.
D. Các điểm A, B, C, D không cùng thuộc một mặt phẳng.
Câu 15: Cho hàm số y=f(x) xác định , liên tục trên R và có bảng biến thiên :
Khẳng định nào sau đây là khẳng định đúng ? x 2 0
A. Hàm số nghịch biến trên R. y' 0 0
B. Hàm số nghịch biến trong khoảng 2;0 . 1 y
C. Hàm số đồng biến trong các khoảng ;2 và 0; . 3
D. Hàm số nghịch biến trong các khoảng ;2 và 0; .
Câu 16: Quay tam giác ABC vuông tại A quanh trục là cạnh AB ta đuợc A. một hình trụ.
B. hình trụ có đường sinh AC . C. một hình nón.
D. hình nón có đường sinh là BC .
Câu 17: Bảng biến thiên sau là của hàm số nào sau đây? 4 2 3 2 3 2 2
A. y x 2x 3 .
B. y x 3x 4x 2.
y x 3x 2
y x 4x 4 C. . D. . 2x 3
Câu 18: [CT17] Hàm số y
có bao nhiêu điểm cực trị ? x 1 A. 1. B. 0. C. 3. D. 2 .
Câu 19: [CT17] Với mọi a , b , x là các số thực dương thoả mãn log x 5 log a 3log b . Mệnh đề nào 2 2 2 dưới đây đúng ? A. 5 3
x a b .
B. x 3a 5b . C. 5 3 x a b .
D. x 5a 3b . 1
Câu 20: Tìm đường tiệm cận ngang của đồ thị hàm số y 2 x A. y 3 B. y 2 C. y 1 D. y 0
602:CDD CBCBDABDD CBD CA BCBAACBDADBCAA BCCBA BADCCDA BDDADAA
Câu 21: Tìm tập xác định D của hàm số 2 y (1 x ) A. D ( 1 ;1) B. D ( ; 1
) 1; C. D D. D \ { 1}
Câu 22: Cho tứ diện ABCD có thể tích bằng 3
a và BCD là tam giác đều có cạnh bằng 2a . Tính khoảng cách
từ A đến mặt phẳng (BCD). a 3 A. a 3 B. a . C. D. 3a 3
Câu 23: Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Diện tích xung
quanh của hình nón đó bằng? 1 3 A. 2 2 a . B. 2 a . C. 2 a . D. 2 a . 2 4
Câu 24: Tìm x để biểu thức x x 2 2 3 1 có nghĩa: A. x \ 0 B. x
C. Không tồn tại x D. x 1
Câu 25: [CT17] Cho hai hàm số x y a , x
y b với a , b là 2 số thực
dương khác 1 , lần lượt có đồ thị là C và C như hình bên. Mệnh đề 2 1 nào dưới đây đúng?
A. 0 a b 1.
B. 0 a 1 b .
C. 0 b a 1.
D. 0 b 1 a . x 1
Câu 26: Cho hàm số y
có đồ thị (C). Phương trình tiếp tuyến của x 1
(C) tại giao điểm của (C) với trục tung là :
A. y 2x 1 B. y 2x 1 C. y 2 x 1 D. y 2x 1
Câu 27: [CT17] Mặt phẳng AB C
chia khối lăng trụ AB . C A B C
thành các khối đa diện nào?
A. Hai khối chóp tam giác.
B. Một khối chóp tam giác và một khối chóp ngũ giác.
C. Hai khối chóp tứ giác.
D. Một khối chóp tam giác và một khối chóp tứ giác. 3
Câu 28: Giá trị rút gọn của biểu thức log . b log a .log c là a c b 1 3 2 A. B. C. D. 6 6 2 3 ln x
Câu 29: [MH3] Cho hàm số y
, mệnh đề nào dưới đây đúng ? x 1 1 1 1
A. y xy .
B. 2y xy .
C. 2y xy .
D. y xy . 2 x 2 x 2 x 2 x
Câu 30: [CT17] Cho hàm số 3 2
y x 3x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng 0; 2 .
B. Hàm số đồng biến trên khoảng 0; 2 .
C. Hàm số nghịch biến trên khoảng 2; .
D. Hàm số nghịch biến trên khoảng ; 0 . 12 x x 1
Câu 31: Phương trình 3 5
có bao nhiêu nghiệm. 5 A. 3 nghiệm B. 5 nghiệm C. 1 nghiệm D. 2 nghiệm a b
Câu 32: Cho a, b , là các số thực. Đồ thị các hàm số y x , y x trên
khoảng 0; được cho trong hình vẽ bên.
Khẳng định nào đây là đúng? A. a b 0 B. b a 0
C. 0 b 1 a D. 0 a 1 b
602:CDD CBCBDABDD CBD CA BCBAACBDADBCAA BCCBA BADCCDA BDDADAA
Câu 33: Tìm đường tiệm cận ngang của đồ thị hàm số y
2x 1 2x 3 A. y 2
B. Không có tiệm cận ngang C. y 0 D. y 4
Câu 34: Nếu đặt t log x thì phương trình 2 3
log x 20log x 1 0 trở thành phương trình nào? A. 2
9t 20 t 1 0 . B. 2
3t 10t 1 0 . C. 2
9t 10t 1 0 . D. 2
3t 20t 1 0 .
Câu 35: Một hình hộp chữ nhật có ba kích thước là a, ,
b c . Gọi (S ) là mặt cầu đi qua 8 đỉnh của hình hộp chữ
nhật đó. Tính diện tích của hình cầu (S ) theo a, , b c . A. 2 2 2
(a b c ) B. 2 2 2
(a b c ) C. 2 2 2
2 (a b c ) D. 2 2 2
4 (a b c ) 2
Câu 36: Cho hình đa diện H có c cạnh m mặt d đỉnh. Mệnh đề nào sau đây là đúng? A. c m .
B. m d .
C. d c .
D. m c .
Câu 37: [CT17] Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở
dưới đây. Hàm số đó là hàm số nào ? A. 4 2
y x x 1.- B. 4 2
y x x 1. C. 3 2
y x x 1. D. 3 2
y x x 1 .
Câu 38: Tìm tọa độ tâm đối xứng I của đồ thị hàm số 3
y x 3x 1 . A. I 0; 1
B. I 1;3
C. I 1; 1 D. I 2;3
Câu 39: [MH3] Tính thể tích V của khối trụ ngoại tiếp hình lập phương có cạnh bằng a. 3 a 3 a 3 a A. 3 V a . B. V . C. V . D. V . 4 2 6
Câu 40: Tính thể tích của khối cầu ngoại tiếp tứ diện đều ABCD cạnh a. 3 a 3 a 6 3 a 3 A. V B. Đáp án khác C. V D. V 8 8 8 2 x 3x 3
Câu 41: Hàm số y x đạt cực đại tại 2 A. x 3 . B. x 0 . C. x 1 . D. x 2 .
Câu 42: Cho hàm số y f x xác định trên
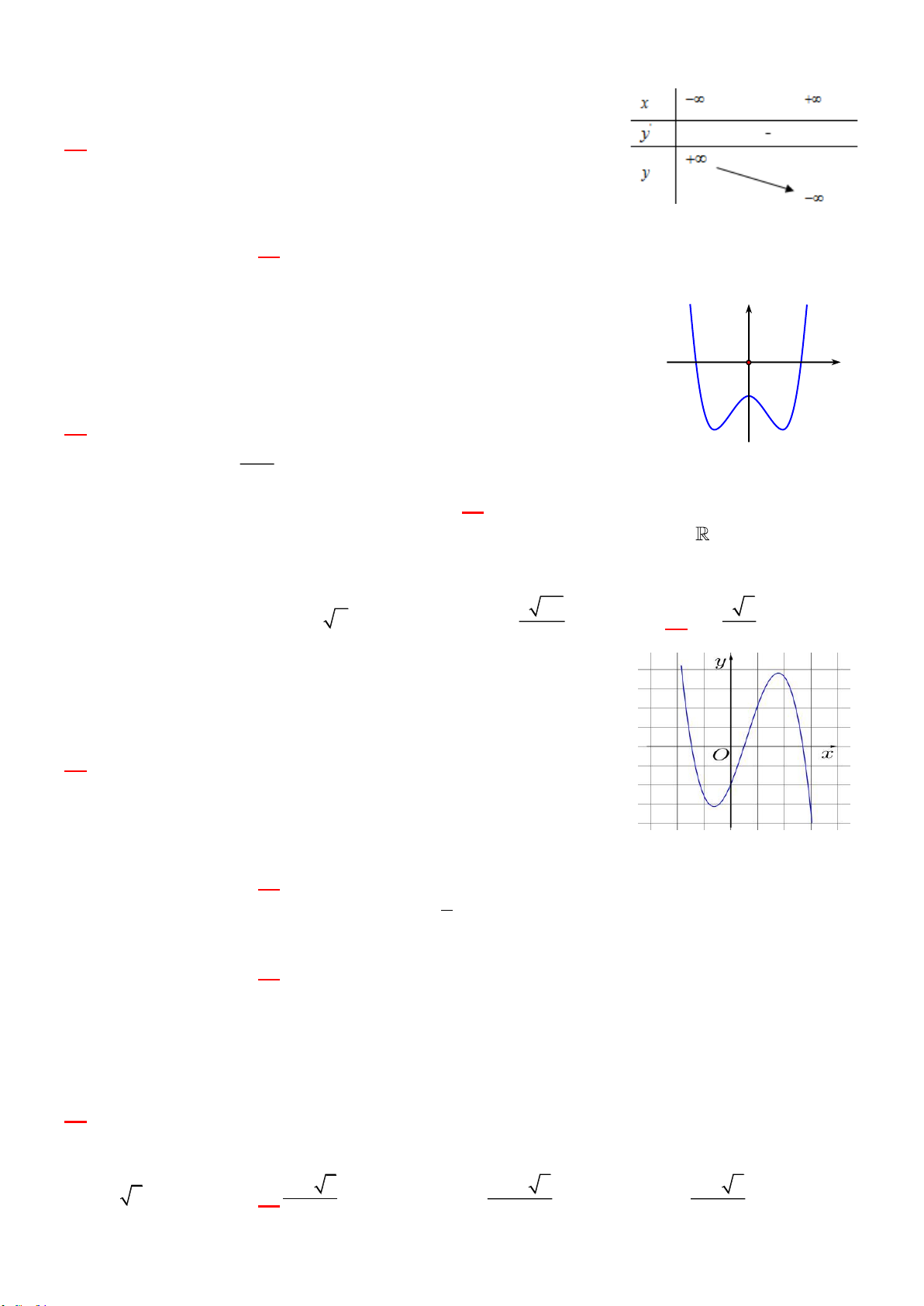
\ 0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ bên.
Tìm tất cả các giá trị của tham số thực m để phương trình 2f x 1 m có nghiệm. A. 0 m .
B. 1 m 7 . C. m 7 . D. m 1.
602:CDD CBCBDABDD CBD CA BCBAACBDADBCAA BCCBA BADCCDA BDDADAA
Câu 43: Một tấm bìa hình vuông, người ta cắt bỏ mỗi góc của tấm bìa một hình vuông cạnh bằng 12cm rồi
gấp lại thành một hình hộp chữ nhật không có nắp. Nếu thể tích của cái hộp đó bằng 3
4800cm thì cạnh của
tấm bìa có độ dài bằng A. 44 cm. B. 36 cm. C. 42 cm. D. 38 cm.
Câu 44: [CT17] Tìm tất cả các giá trị thực của tham số m để phương trình x x 1 4 2
m 0 có hai nghiệm thực phân biệt
A. m 0; .
B. m 0 ;1 .
C. m 0; 1 .
D. m ;1 . 2x 1
Câu 45: Cho hàm số y
có đồ thị (C). Tìm tất cả các giá trị của tham số m để đường thẳng x 1
d : y x m 1 cắt đồ thị (C) tại hai điểm A, B sao cho AB 2 3
A. m 2 10 m m B. Kết quả khác. C. 4 3 D. 4 10 1
Câu 46: Cho khối chóp S.ABCD có thể tích bằng V . Lấy điểm A ' trên cạnh SA sao cho SA ' SA . Mặt 3
phẳng qua A’ và song song với đáy ABCD cắt các cạnh SB, SC, SD lần lượt tại B', C ', D ' . Khi đó
thể tích khối chóp S.A ' B'C' D ' bằng V V V V A. B. C. D. 9 3 81 27
Câu 47: Một sợi dây có chiều dài 28m được cắt thành hai đoạn để làm thành một hình vuông và một hình tròn.
Giả sử đoạn xếp thành hình tròn có chiều dài là x.Tìm x để tổng diện tích của hình vuông và diện tích của hình tròn là nhỏ nhất. 28 14 7 56 A. m B. m C. m D. m 4 4 4 4
Câu 48: Tìm tất cả giá trị m để bất phương trình 2
log x 4 log x 5m 1 vô nghiệm . A. ( ;1 ). B. [1; ) . C. ( ;1 ]. D. 1; .
Câu 49: Người ta bỏ 30 viên bi có đường kính 2 cm vào một bình nước hình trụ có đường kính đáy 10 cm ,
chiều cao 20 cm. Tính thể tích của lượng nước đổ vào để đầy bình. A. 3 460(cm ) . B. 3 480(cm ) . C. 3 490(cm ) . D. 3 470(cm ) .
Câu 50: Cho hình lập phương ABCDA’B’C’D’. Mặt phẳng (BDC’) chia khối lập phương thành 2 phần có tỉ
số thể tích phần bé chia phần lớn bằng 1 1 1 1 A. B. C. D. 5 3 4 6
-----------------------HẾT----------------------
403:BBABCDACACACBCAAACCDAABDBDCBBDBDCBDACCDDDBCDBDCABA ĐỀ SỐ 5
SỞ GD-ĐT KIÊN GIANG ĐỀ MẪU KIỂM TRA HỌC KÌ I- NĂM HỌC 2017-2018
TRƯỜNG THPT TÂN HIỆP Môn TOÁN –Lớp 12 - Thời gian 90 phút
………………… ( Không kể thời gian phát đề )
Hãy chọn một phương án trả lời đúng nhất cho mỗi câu. 3 2
Câu 01: Tiếp tuyến của đồ thị hàm số y x 3x 2 tại điểm M 1
;2 có phương trình là:
A. y 9x 2
B. y 9x 7
C. y 24x 22
D. y 24x 2
Câu 02: Cho tứ diện đều ABCD . Gọi F, E, I, J, M, N lần lượt là trung điểm của các cạ nh AB, CB, AC, DB,
CD, AD . Khẳng định nào sau đây là đúng? A. MNEFI
J là một lục giác đều.
B. MNEFIJ là một bát diện đều. C. MNEFI J là một bát diện không đều.
D. MNEFIJ là một lục giác không đều.
Câu 03: [MH3] Cho hình nón có diện tích xung quanh bằng 2
3 a và bán kính đáy bằng a . Tính độ dài đường
sinh l của hình nón đã cho. 3a 5a A. l 3 . a B. l 2 2 . a C. l . D. l . 2 2
Câu 04: Thể tích của một mặt cầu có bán kính R là 2 4 R 3 4 R 3 3 R 4 R A. V . B. V . C. V . D. V . 3 3 4 3
Câu 05: Đường cong sau là đồ thị của hàm số nào? 3 2 4 2
A. y x 2x 2x 1
B. y x 5x 1 4 2
C. y 2x 3x 1 D. 4 2 y x 2x 1 x
Câu 06: Các đường tiệm cận của đồ thị hàm số 2 3 y là 2 4x 1 1 1
A. x 2 và y 1
B. x 1 và y 2 C. x và y 2 D. x và y 2 2 2 4
Câu 07: Giá trị lớn nhất của hàm số y là: 2 x 2 A. 2. B. -5. C. 3. D. 10.
Câu 08: [CT17] Tìm nghiệm của phương trình log 1 x 2 . 2 A. x 3. B. x 5 . C. x 3 . D. x 4 . 1
Câu 09: [CT17] Tìm nghiệm của phương trình log x 1 . 25 2 23 A. x 4 . B. x 6 . C. x 6 . D. x . 2
Câu 10: [CT17] Cho hàm số y f x có bảng biến thiên như sau
403:BBA BCDA CACA CBCAAA CCDAA BDBD CBBD BDCBDACCDDDBCD BDCA BA
Tìm giá trị cực đại y
và giá trị cực tiểu y của hàm số đã cho. CĐ CT A. y 2 và y 2 . B. y 2 và y 0 . CĐ CT CĐ CT C. y 3 và y 0 . D. y 3 và y 2 . CĐ CT CĐ CT
Câu 11: [CT17] Tìm tất cả các giá trị thực của m để phương trình 3x m có nghiệm thực. A. m 0 B. m 0 C. m 1. D. m 0
Câu 12: Tìm đạo hàm của hàm số y log . x 1 ln10 A. y . B. y . x x 1 1 C. y . D. y . x ln10 10ln x
Câu 13: Cho hàm số y f (x) xác định và có đồ thị là đường cong trong hình vẽ bên :
Hàm số y f (x) đạt cực tiểu tại điểm nào dưới đây? A. x = 2. B. x = 0. C. x = -4. D. x = -1.
Câu 14: Cho hình lập phương ABC .
D A' B 'C ' D ' với AB 10cm . Tính thể tích khối lập phương ABC .
D A' B 'C ' D ' . A. 3 600cm B. 3 100cm C. 3 1000cm D. 3 400cm
Câu 15: Cho hàm số y f ( x ) có đồ thị như sau Tìm tất cả các
giá trị thực của tham số m để phương trình f ( x ) m có 1 nghiệm thực.
A. m>3 hoặc m <-1 B. m = -1 hoặc m =3
C. Không có giá trị thực nào m thỏa mãn yêu cầu đề bài. D. -1 < m< 3
Câu 16: Cho lăng trụ AB . C ' A ' B '
C có thể tích bằng 3 12a và A' B ' 3 ; a B 'C 4 ;
a CA' 5a . Tính khoảng cách từ B đến mặt phẳng (A’B’C). A. 2a . B. 3a C. a D. a 3 1
Câu 17: [CT17] Tìm tập xác định D của hàm số 3 y (x 1)
A. D (1; ) B. D ( ; 1) C. D D. D \ {1}
Câu 18: Các căn bậc bốn của 81 là : A. 3 B. 9 C. 3 D. 3
Câu 19: Trong các mệnh đề sau đây, mệnh đề nào sai ?
A. Luôn có hai đường tròn có bán kính khác nhau cùng nằm trên một mặt nón
B. Mặt trụ và mặt nón luôn có vô số đường sinh.
C. Mọi hình chóp luôn nội tiếp trong mặt cầu.
D. Có vô số mặt phẳng cắt mặt cầu theo những đường tròn bằng nhau
Câu 20: [CT17] Cho log b 2 và log c 3 . Tính P 2 3 log b c . a a a A. P 108 . B. P 31. C. P 30. D. P 13 .
Câu 21: Chọn khẳng định sai trong các khẳng định sau: x 1
A. Hàm số y chỉ nghịch biến trên 0; . B. Hàm số 15x y đồng biến trên R.
403:BBA BCDA CACA CBCAAA CCDAA BDBD CBBD BDCBDACCDDDBCD BDCA BA 5 C. Hàm số 0,3x y nghịch biến trên R. D. Hàm số 8x y
đồng biến trên 0; .
Câu 22: Bảng biến thiên sau của hàm số nào? 3 2 2
A. y x 3x 4x 2. B. y x 4x 4. 4 2 3 2
C. y x 5x 4.
y x 3x 4x 2. D.
Câu 23: Tìm các giá trị m để phương trình 4xm 2xm 12 0 có các nghiệm lớn hơn 5 . A. m 5 B. m 3 C. m 5 D. m 4
Câu 24: [CT17] Đường cong ở hình bên là đồ thị của hàm số 4 2
y ax bx c với a, ,
b c là các số thực. Mệnh
đề nào dưới đây đúng ? y
A. Phương trình y 0 có đúng một nghiệm thực.
B. Phương trình y 0 có hai nghiệm thực phân biệt. O x
C. Phương trình y 0 vô nghiệm trên tập số thực.
D. Phương trình y 0 có ba nghiệm thực phân biệt. x 1
Câu 25: Cho hàm số y
.Khẳng định sau đây là đúng ? x 3
A. Hàm số đồng biến trên ;3 và 3; .
B. Hàm số nghịch biến trên ;3 và 3; .
C. Tiệm cận ngang của đồ thị hàm số là y=3.
D. Tập xác định của hàm số là .
Câu 26: [CT17] Cho hình trụ có diện tích xung quanh bằng 50 và độ dài đường sinh bằng đường kính đường
tròn đáy. Tính bán kính r của đường tròn đáy. 5 2 5 2 A. r 5 .
B. r 5 . C. r . D. r . 2 2
Câu 27: [MH2] Cho hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. a 0,b 0,c 0, d 0 .
B. a 0,b 0,c 0, d 0 .
C. a 0,b 0,c 0, d 0 .
D. a 0,b 0,c 0, d 0 .
Câu 28: Một người gửi tiết kiệm 250 triệu với lãi suất 7%/năm và lãi suất
hàng năm được nhập vào vốn. Hỏi sau 2 năm số tiền người đó thu được là bao nhiêu. A. 296,225 triệu. B. 286,225 triệu. C. 285,225 triệu. D. 295,225 triệu. 1 3 2 3
Câu 29: Tập xác định D của hàm số y 4 x là :
A. D R \ 2 ;2 B. D 2 ;2
C. D R
D. D R \{ 2 }
Câu 30: Trong các mệnh đề sau , mệnh đề nào đúng?
A. Tồn tại một hình đa diện có số cạnh bằng số đỉnh.
B. Tồn tại hình đa diện có số cạnh và số mặt bằng nhau
C. Số đỉnh và số mặt của một hình đa diện luôn luôn bằng nhau
D. Tồn tại một hình đa diện có số đỉnh và số mặt bằng nhau.
Câu 31: Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a . Tính diện
tích xung quanh của hình nón. 2 a 2 2 2 a 2 2 a 2 A. 2 a 2 B. C. D. 2 3 4
403:BBA BCDA CACA CBCAAA CCDAA BDBD CBBD BDCBDACCDDDBCD BDCA BA 3 2 4
Câu 32: Viết biểu thức
về dạng lũy thừa 2m ta được m ? . 0,75 16 13 5 5 13 A. . B. . C. . D. . 6 6 6 6
Câu 33: Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a , chiều cao AH . Quay đường
tròn (C) xung quanh trục AH , ta được một mặt cầu. Thể tích của khối cầu tương ứng là: 3 a 3 3 4 a 3 4 a 3 3 4 a A. B. C. D. 54 3 27 9
Câu 34: Tìm m để phương trình 2
log x 2log x m 1 0 có nghiệm. 3 3 A. m 2 B. m 2 C. m 2 D. m 2 x 3
Câu 35: [CT17] Tìm tập xác định của hàm số y log . 5 x 2 A. D ( ; 2 ) [3; ) B. D ( 2 ;3) . C. D \ { 2} D. D ( ; 2 ) [4; ) 2x 1
Câu 36: Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số y 2 x 3x 2 A. x 1 ; x 2 B. x 2
C. x 1 và x 2 D. x 1
Câu 37: Cho hình lăng trụ đứng tam giác AB .
C A' B 'C ' , đáy ABC là tam giác vuông tại B, có AB 5c , m BC 6c ,
m AA ' 7cm . Tính thể tích khối lăng trụ AB .
C A' B 'C ' ? A. 3 35cm B. 3 210cm C. 3 105cm D. 3 150cm 3
Câu 38: Cho hàm số y x x có đồ thị (C) . Phương trình tiếp tuyến của đồ thị (C) tại điểm A1; 0 là:
A. y 2x 2 B. y 2x 2 C. y 2x 2 D. y 2x 2 2 3
Câu 39: Giá trị rút gọn của biểu thức log b .log . a log c là a c b 3 1 2 A. B. 6 C. D. 2 6 3
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , cạnh bên SA vuông góc với mặt
phẳng đáy, M là trung điểm của SB, góc giữa SC và mặt phẳng đáy bằng 0
60 . Tính thể tích của khối chóp M.BCD . 3 2a 2 3 a 6 3 2a 3 3 2a 6 A. B. C. D. 3 3 3 3
Câu 41: Giá trị cực đại của hàm số y x 2 cos x trên khoảng 0; là 5 5 A. 3 . B. . C. . D. 3 . 6 6 6 6 1
Câu 42: Tìm tất cả các giá trị của tham số m để hàm số 3 2 y
x mx 4x 10 đồng biến trên 3 A. 2 m 2 B. 2 m 2 C. m 2 D. m 2
Câu 43: Tìm m để phương trình sau có 2 nghiệm phân biệt: x 1 x2 25 5 m 0 25 25 A. m B. 0 m C. 0 m
D. 0 m 25 4 4
403:BBA BCDA CACA CBCAAA CCDAA BDBD CBBD BDCBDACCDDDBCD BDCA BA
Câu 44: Cho hình tứ diện S.ABC có các cạnh SA, SB, SC đôi một vuông góc nhau và SA = a, SB = SC = 2a.
Gọi (S) là mặt cầu ngoại tiếp hình chóp SABC, S’ là diện tích của mặt cầu (S) và V là thể tích của khối cầu S'
tạo nên bởi mặt cầu (S) bằng. Tính tỷ số . V A. 3a B. a C. 4a D. 2a. Câu 45: Cho hàm số ax b y f x
có đồ thị như hình vẽ bên. Tất cả các cx d
giá trị của m để phương trình f x m có hai nghiệm phân biệt là:
A. m 2 và m 1 .
B. 0 m 1 và m 1 C. 0 m 1.
D. m 2 và m 1 .
Câu 46: Lăng trụ đứng AB . C ’ A ’ B ’
C có đáy ABC là tam giác vuông tại , A BC 2 ,
a AB a . Mặt bên B ’ B ’
C C là hình vuông. Khi đó thể tích lăng trụ là 3 a 3 A. 3 a 2 B. 3 2a 3 C. D. 3 a 3 3
Câu 47: Tìm m để bất phương trình log (5x 1).log (2.5x 2) m có nghiệm x 1. 2 2
A. m 3
B. m 3
C. m 3
D. m 3
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB 20cm , AD 32cm và hình chiếu
vuông góc của S lên mặt đáy (ABCD) trùng với giao điểm hai đường chéo AC và BD . Biết mặt phẳng (SCD) 8
tạo với đáy một góc sao cho cos
. Tính thể tích hình chóp S.ABCD . 17 A. 3 6400cm . B. 3 6800cm . C. 3 6600cm . D. 3 6900cm .
Câu 49: Cho hàm số y 3cos x 4 sin x 8 với x 0; 2 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số. Khi đó tổng M m bằng bao nhiêu? A. 7 3 . B. 16. C. 8 2 . D. 8 3 .
Câu 50: [MH2] Cho hai hình vuông cùng có cạnh bằng 5 được xếp chồng lên nhau
sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại( như hình vẽ bên).
Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY . X 1255 4 2 1255 2 2 A. V B. V 24 12 1251 2 1252 2 C. V D. V - 6 4
-----------------------HẾT---------------------- Y 404: ĐỀ SỐ 6
SỞ GD-ĐT KIÊN GIANG ĐỀ MẪU KIỂM TRA HỌC KÌ I- NĂM HỌC 2017-2018
TRƯỜNG THPT TÂN HIỆP Môn TOÁN –Lớp 12 - Thời gian 90 phút
………………… ( Không kể thời gian phát đ ề )
Hãy chọn một phương án trả lời đúng nhất cho mỗi câu.
Câu 01: Tập xác định của hàm số y log x 2 1 là : 3 A. 1; B. R C. 0; . D. R \{ 1 } . 1
Câu 02: Khối đa diện nào sau đây có công thức thể tích V
S.h ( trong đó S là diện tích đáy, h là chiều 3 cao)?
A. Khối chóp. B. Khối cầu C. Khối lăng trụ
D. Khối lập phương 1
Câu 03: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số 3 2 y
x 2x 3x 5 : 3
A. Có hệ số góc bằng -1
B. Có hệ số góc dương
C. Song song với trục hoành
D. Song song với đường thẳng x=1
Câu 04: Cho khối bát diện đều ABCDEF, khẳng định nào sau đây là sai?
A. Mặt phẳng (ABCD) và mặt phẳng (EDFB) vuông góc với nhau.
B. Mặt phẳng (ABCD) và mặt phẳng (ECFA) vuông góc với nhau.
C. Mặt phẳng (EDFB) và mặt phẳng (ECFA) vuông góc với nhau.
D. Hai đường thẳng ED và BF chéo nhau.
Câu 05: Cho mặt cầu có bán kính bằng 2cm. Diện tích mặt cầu là A. 2 12 cm . B. 2 8 cm . C. 2 16 cm . D. 2 4 cm .
Câu 06: Tìm giá trị lớn nhất của hàm số 3 2
y x 2x 4x 1 trên đoạn 1; 3 . 67 A. max y 4 . B. max y . C. max y 7 . D. max y 2 . 1; 3 1; 3 27 1; 3 1; 3
Câu 07: Công thức nào sau đây sai
A. log b .log b
B. log c log b.log c a a a a b
C. log b .b log b log b
D. log b log a a 1 2 a 1 a 2 a b 1
Câu 08: Số điểm cực trị của hàm số 3 y
x x 7 là 3 A. 1. B. 0. C. 3. D. 2.
Câu 09: Đường cong trong hình là đồ thị của hàm số nào? x 1 3 2 A. y B. y x 3x 1 x 1 4 2 2
C. y x 5x 1 D. y 4 x 3x 1
Câu 10: [MH1] Tính đạo hàm của hàm số x y 13 . 13x A. y' 1 13 . x x B. ' 13 . x y ln 13 . C. x y' 13 . D. y' . ln 13 Câu 11: C
ho m là tham số. Nghiệm của phương trình x 1 m 2 x 3 3 3 là .
A. x 1 m
B. x 2 m
C. x 1 m
D. x 2 m
404:DACD CDD BBBDDBA CDBAA DDACBBDAAA CADCA CA CDBCCBBCD BCCAB
Câu 12: Bảng biến thiên sau là của hàm số nào? 3 2 4 2
A. y x 3x 4x 2 . B. y x 2x 1. 3 x 1 2 x 4 C. y . D. y . x 1 x 1
Câu 13: [CT17] Tìm tập xác định D của hàm số y x x 3 2 2 . A. D . D \ 1 ; 2 .
D 0; . D ; 1 2; . B. C. D.
Câu 14: [CT17] Đường cong ở hình bên là đồ thị của hàm ax b số y
với a, b, c, d là các số thực. Mệnh đề nào cx d dưới đây đúng ?
A. y 0, x 1
B. y 0, x
C. y 0, x 1
D. y 0, x
Câu 15: Đường cong trong hình bên là đồ thị một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây. Hỏi đó là đồ thị hàm số nào? y 2 2 2 x O 2 A. 4 2
y x 4x 2 . B. 4 2
y x 4x 2 . C. 4 2
y x 4x 2 . D. 4 2
y x 4x 2 . x
Câu 16: Số đường tiệm cận của đồ thị hàm số 1 y là 1 x A. 0 B. 1 C. 3 D. 2
Câu 17: Cho hàm số y f ( x ) có đồ thị như sau
Tìm tất cả các giá trị thực của tham số m để phương trình
f ( x ) m có 2 nghiệm thực. A. -1 < m< 3 B. m = -1 hoặc m =3
C. Không có giá trị thực nào m thỏa mãn yêu cầu đề bài.
D. m>3 hoặc m <-1
Câu 18: [CT17] Cho hình nón có bán kính đáy r 3 và độ
dài đường sinh l 4. Tính diện tích xung quanh của hình nón đã cho. A. S 4 3 .
B. S 12 . C. S 39 . D. S 8 3 . xq xq xq xq
Câu 19: [CT17] Tìm nghiệm của phương trình log x 5 4 . 2 A. x 21. B. x 3 . C. x 11. D. x 13.
404:DACD CDD BBBDDBA CDBAA DDACBBDAAA CADCA CA CDBCCBBCD BCCAB
Câu 20: Khẳng định nào sau đây đúng? A. Phương trình 21 x
21 có 2 nghiệm phân biệt. B. Phương trình 2015 x 2 vô nghiệm.
C. Phương trình 2015 x 2 có vô số nghiệm. D. Phương trình 32 x
có 2 nghiệm phân biệt.
Câu 21: Thể tích của khối trụ có bán kính đáy r và có đường cao h là 1 A. 2 V rh B. 2 V r h . C. 2
V 2 r h . D. 2 V r h . 3
Câu 22: Rút gọn biểu thức A log . a b . a 1 log b
A. A .1 log b
B. A .log b C. a A
D. A log b a a a
Câu 23: Gọi V là thể tích hình hộp ABC .
D A' B 'C ' D ' và V1 là thể tích tứ diện A' ABD . Hệ thức nào sau đây là đúng?
A. V 2V V 4V V 6V V 3V 1 . B. 1 . C. . D. . 1 1
Câu 24: Trong không gian, cho tam giác ABC vuông tại A , AB a và AC
3a . Tính độ dài đường sinh l
của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB .
A. l a
B. l 2a C. l 3a
D. l 2a x
Câu 25: Điều kiện xác định của phương trình log (x 1) log là: 5 5 x 1
A. x ;1
B. x 1; C. x 1 ;0 D. x \ [ 1; 0] Câu 26: Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. a 0, b 0, c 0 .
B. a 0, b 0, c 0 .
C. a 0, b 0, c 0 .
D. a 0, b 0, c 0 . 5x 1
Câu 27: Cho hàm số y
. Khẳng định nào sau đây là khẳng định đúng ? 2x 1 1 1
A. Hàm số nghịch biến trên các khoảng ; và ; . 2 2 1 1
B. Hàm số đồng biến trên các khoảng ; và ; . 2 2 1
C. Hàm số nghịch biến trên \ . 2 1
D. Hàm số đồng biến trên \ . 2 m b a a
Câu 28: Viết biểu thức 5 3
, a, b 0 về dạng lũy thừa ta được m ?. a b b 2 4 2 2 A. . B. . C. . D. . 15 15 5 15
Câu 29: Cho hình chữ nhật ABCD có cạnh AB = 2a, AD = 4a. Gọi M, N lần lượt là trung điểm của AB và CD
. Quay hình vuông ABCD quanh trục MN ta được khối trụ tròn xoay. Tính thể tích của khối trụ đó. A. 3 4 a B. 3 2 a C. 3 a D. 3 3 a x 1
Câu 30: [MH1] Tính đạo hàm của hàm số y . x 4 1 ( 2 x ) 1 ln 2 1 ( 2 x ) 1 ln 2 1 ( 2 x ) 1 ln 2 1 ( 2 x ) 1 ln 2 A. y' . B. y' . C. y' . D. y' . 2 2 x 2 x 2 2x 2 2 2x
404:DACD CDD BBBDDBA CDBAA DDACBBDAAA CADCA CA CDBCCBBCD BCCAB
Câu 31: Cho a log 3 log 18 2 . Hãy tinh giá trị của 24 theo a . 1 2a 1 2a 2a 1 2a A. B. C. D. 3 a 3a 3 a 1 3a
Câu 32: Có thể chia một hình lập phương thành bao nhiêu tứ diện bằng nhau? B. 5 A. 6 C. 4 D. Vô số
Câu 33: [CT17] Tìm giá trị thực của tham số m để đường thẳng d : y 2m
1 x 3 m vuông góc với đường
thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x 3x 1. 1 1 3 3 A. m . B. m . C. m . D. m . 2 4 4 2
Câu 34: Giải phương trình x x 1 x 1 2 2 2
m với m>0 kết quả nghiệm là. 5m m m A. Kết quả khác. B. x log C. x log D. x log 2 2 5 2 3
Câu 35: Cho , , là các số thực. Đồ thị các hàm số y x , y x trên khoảng 0; được cho trong hình vẽ bên.
Khẳng định nào đây là đúng?
A. 0 1
B. 0 1
C. 0 1 D. 2 2x x 3
Câu 36: Đồ thị hàm số y
có đường tiệm cận ngang là 2 x 2 A. y 2 B. y 2 3 C. y 1 D. y 2
Câu 37: [CT17] Tìm tất cả các giá trị thực của tham số m để hàm số y 2
log x 2x m 1 có tập xác định là . A. m 2 . B. m 2 . C. m 0 . D. m 0 . 3 2
Câu 38: Cho hàm số y x x 5x 1 có đồ thị (C). Phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung là : A. y 1 B. y 1 C. y 5x 1 D. y 5x 1
Câu 39: [MH1] Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. 5 15 5 15 4 3 5 A. V . B. V . C. V . D. V . 18 54 27 3 x2 mx
Câu 40: Tìm m để hàm số y
1 đạt cực đại tại x = 2 x m
A. Không tồn tại giá trị m thỏa mãn yêu cầu đề bài. B. m 1 C. m 3 D. m 1.
Câu 41: Thiết diện của mặt phẳng (P) tạo với hình cầu (S) là hình tròn có diện tích bằng 9 . Tính khoảng
cách từ tâm hình cầu đến mặt phẳng (P), biết chu vi hình tròn lớn của hình cầu bằng 10 . A. 6. B. 3. C. 4. D. 5.
Câu 42: Cho tứ diện ABCD có thể tích bằng 3
a , AB CD a và AC CB BD DA . Tính khoảng cách
giữ hai đường thẳng AB và CD . A. 4a . B. 6a C. 3a D. 12a
404:DACD CDD BBBDDBA CDBAA DDACBBDAAA CADCA CA CDBCCBBCD BCCAB
Câu 43: [CT17] Cho hàm số y f x có bảng biến thiên như sau x 1 3 y 0 0 5 y 1
Đồ thị của hàm số y f x có bao nhiêu điểm cực trị ? A. 2 . B. 3 . C. 5 . D. 4 . 2x 3
Câu 44: Cho hàm số y
có đồ thị (C). Tìm tất cả các giá trị của tham số m để đường thẳng d : y x m x 2
cắt đồ thị (C) tại hai điểm phân biệt A. m 6 B. m 2
C. m 2 hoặc m 6
D. 2 m 6
Câu 45: Lăng trụ tam giác AB . C A B C
có đáy tam giác đều cạnh a , góc giữa cạnh bên và mặt đáy bằng 300.
Hình chiếu A lên ABC là trung điểm I của BC . Thể tích khối lăng trụ là 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 2 6 8
Câu 46: Tính thể tích khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, biết rằng AB = BC =
a, AD = 2a, SA vuông với mặt đáy và cạnh bên SC hợp với đáy một góc bằng 60 3 a 15 3 a 6 3 a 6 3 a 6 A. B. C. D. 6 2 3 6
Câu 47: Cho hình lập phương ABCD.A’B’C’D’. Gọi I là trung điểm BB’. Mặt phẳng (DIC’) chia khối lập
phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng 4 1 7 1 A. B. C. D. 14 2 17 3
Câu 48: Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 log 2 x 1 log 2
mx 4x m 5 5 có nghiệm đúng . x
A. m 2;3 B. m 2 ;3
C. m 2; 3 D. m 2 ; 3 4 2
Câu 49: Giả sử trên khoảng ;
0 thì hàm số. y a 1 x 1 2a b 1 x
1 8a 4b đạt giá trị 1
lớn nhất tại x 3
. Hỏi rằng trên đoạn
;3 thì hàm số đạt giá trị lớn nhất là bao nhiêu? 2 A. 12. B. 11. C. 10. D. 13.
Câu 50: Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dung tích 3 2000 cm . Biết
rằng bán kính của nắp đậy sao cho nhà sản xuất tiết kiệm nguyên liệu nhất có giá trị là a . Hỏi giá trị a gần
với giá trị nào nhất trong các giá trị sau. A. 6, 9 cm . B. 6,8cm . C. 6,1cm . D. 6, 5 cm .
-----------------------HẾT----------------------
Document Outline
- 4-DE-ON-THI-12(50 CAU TRAC NGHIEM).pdf
- 2-de-dau-CODA.pdf
- 4-DE-ON-THI-12(50 CAU TRAC NGHIEM) - Copy.pdf