

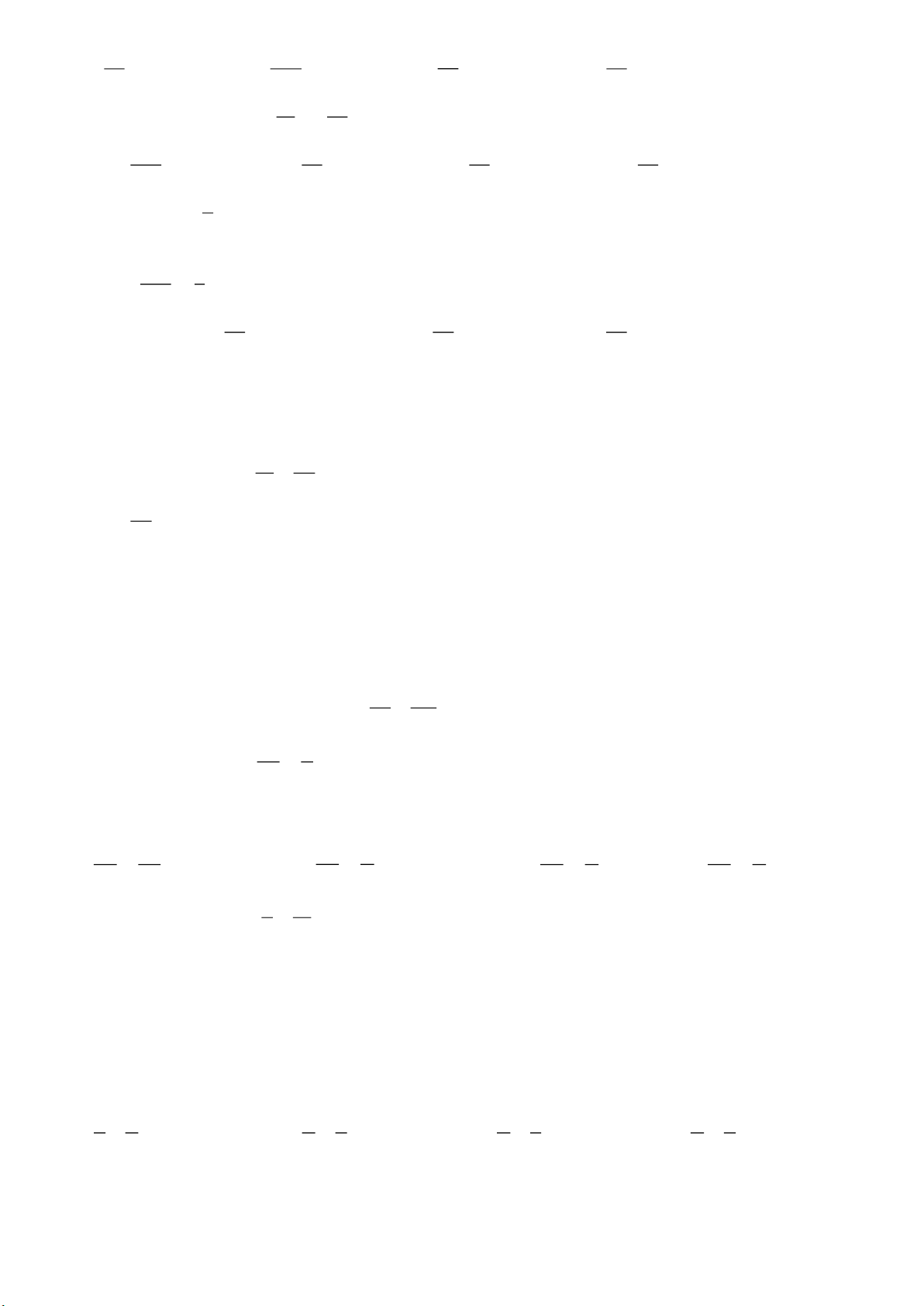

Preview text:
ÔN TẬP GIỮA HỌC KÌ I _ TOÁN 7_NH 2024 - 2025 A. ĐẠI SỐ I. TÓM TẮT LÝ THUYẾT
1) Tính chất của phép cộng các số hữu tỉ: + Giao hoán: a + b = b + a
+ Kết hợp: a + (b + c) = (a + b) + c
+ Cộng với số 0 : a + 0 = 0 + a = a
+ Cộng với số đối: a + (-a) = 0
2) Tính chất của phép nhân các số hữu tỉ: + Giao hoán: a . b = b . a
+ Kết hợp: a . (b . c) = (a . b) . c
+ Nhân với số 1 : a . 1 = a
+ Tính chất phân phối của phép nhân đối với phép cộng: a . ( b + c) = a.b + a.c
3) Phép tính luỹ thừa với số mũ tự nhiên:
Với n là một số tự nhiên lớn hơn 1 , luỹ thừa bậc n của một số hữu tỉ x , ký hiệu là n x là tích của
n thừa số x . n x . x . x . x . .
. ..x x , n , n 1 4 2 43 ¤ ¥ 1 n thöø a soáx
Số x gọi là cơ số, n gọi là số mũ. Quy ước: 1 x 0 ,
x x 1 (x 0)
4) Tích và thương của hai luỹ thừa cùng cơ số
- Khi nhân hai luỹ thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: m. n m n x x x
- Khi chia hai luỹ thừa cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của luỹ thừa bị chia trừ đi
số mũ của luỹ thừa chia m : n mn x x x
x 0, m n
5) Luỹ thừa của luỹ thừa:
Khi tính luỹ thừa của một luỹ thừa, ta giữ nguyên cơ số và nhân các số mũ: n m . m n x x
6) Thứ tự thực hiện các phép tính:
- Đối với biểu thức không có ngoặc : luỹ thừa nhân (chia) cộng (trừ)
-Đối với biểu thức có ngoặc: ( ) [ ]
7) Quy tắc dấu ngoặc:
- Khi bỏ dấu ngoặc có trước có dấu “+” đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc
-Khi bỏ dấu ngoặc có trước có dấu “ ” đằng trước, ta giữ phải đổi dấu các số hạng trong ngoặc:
dấu “+” thành dấu “ ” và dấu “ ” thành dấu “+”
*Chú ý: Nếu đưa các số hạng vào trong dấu ngoặc có dấu “ - ” đằng trước, ta phải đổi dấu các số hạng đó II. BÀI TẬP 5 5 11
Bài 1. Tìm số đối của các số sau: ; 15,8; 0; 2 ; 1; -0,5; 7 7 7
Bài 2. Viết kết quả phép tính sau dưới dạng lũy thừa 9 5 7 1 1 6 5 6 4 16 a) : b) 0 .7 . 0 .7 c) .1.25 d) : e) a5.a7 3 3 5 9 81
Bài 3. Thực hiện phép tính 1 1 5 1 8 4 1 1 3 1 a) 0, 4 b). 0,3 : 1 c) 6 8 2 3 3 5 7 14 2 2 2 1 3 2 4 2 3 2 1 d) . e) 12. f) 2. 4. 5 5 4 3 3 3 3
Bài 4. Thực hiện phép tính 2 2 4 4 2 1 1 5 5 2 1 5 .20 a) 3 ( 0 ,5) b) 3 : (0,5) ( 6) c) 2 4 : ( 2 ,25) d) 3 6 2 8 3 3 6 5 5 25 .4 3 2 0 5 4 1 1 3 1 1 1 1 1 e) 2 1 : 10 9 f) 2 ( 2) . 0,25 : 2 1 g) 4. 3. 2. 6 9 12 2 4 4 6 2 2 2
Bài 5. Thực hiện phép tính 2 3 2 5 9 3 1 1 2 1 4 3 a) : . b) 6 5 c) 1 . 4 3 9 4 5 3 3 3 4 5 4 2 3 1 2 2. 1 7 5 5 3 5 d)
: 2 3 e) 0,8 : 0, 2 8 f )-12 : 2 2 2 48 24 16 4 6
Bài 6. Thực hiện phép tính 3 1 4 2 2 5 4 1 1 a) . 64 1 b) c) 16. : 25 2 25 9 9 2 2 1 4 8 4 1 1 3 1 d) . 64 1 e). 0 ,3 : 1 f) 2 25 3 3 5 7 14 2
Bài 7. Tính một cách hợp lí 3 1 3 1 2 4 5 4 16 3 1 3 1 3 a) .26 .19 b) 1 0,5 c) 16 . 13 . 7 3 7 3 5 23 21 23 21 5 3 5 3 4 15 6 2 7 4 11 11 5 4 3 6 9 d) e) ( 3 4,5) 65,5 f) 19 13 5 13 19 25 25 11 13 17 11 13 2 3 2 3 5 3 15 6 4 5 1 4 3 g) 16 : 28 : h) i) . . 7 5 7 5 11 17 13 11 6 2 9 3 9 9
Bài 8. Tính một cách hợp 31 7 8 1 12 13 79 28 31 a) b) c) ( 3 0,75) 69,25 ( 6 ,9) 23 32 23 3 67 41 67 41 10 d) 7, 2 ( 3 ,7 2,8) 0,3
Bài 9. Tìm x, biết 4 7 4 3 x 15 3 5 1 1 2 a) x b) x : : 0,25 c) d) . x e) x 3 : 9 6 3 2 3 2 7 21 2 2 7 3 1 4 3x 7 2 3 4 5 2 3 1 3 f) 1 x 1 g) h) x i) : x 1 k) : x 4 2 5 5 2 3 2 3 7 7 7 7 14
Bài 10. Tìm x, biết: 3 8 7 3 1 1 5 1 4 2 2 1 1 1 2 a) x
b) . 1, 2 x c) x :
d) x x 1 0 5 4 2 4 3 3 5 3 7 7 3 5
Bài 11. Tìm x, biết: 3 2 1 8 x a) x 2 3 16 b) 3 x 343 c) x d) 27 3 27 243 2 3 1 1 1 2 7 1 5 1 e) x3 7 27 f) x g) x x h) 3x x 2 27 3 3 5 15 3 4
Bài 12. Tìm các số nguyên n biết: n 1 1 8 2n a) 2n 8 b) c) 2 d) 2 e) 1 n n 1 3 .3 5.3 162 3 81 2n 16
Bài 13. Tìm x, biết: 4 3 3 1 a) x = 8 b) x - = c) x 5 0 d) x 0 5 4 4 2 B. HÌNH HỌC I. TÓM TẮT LÝ THUYẾT
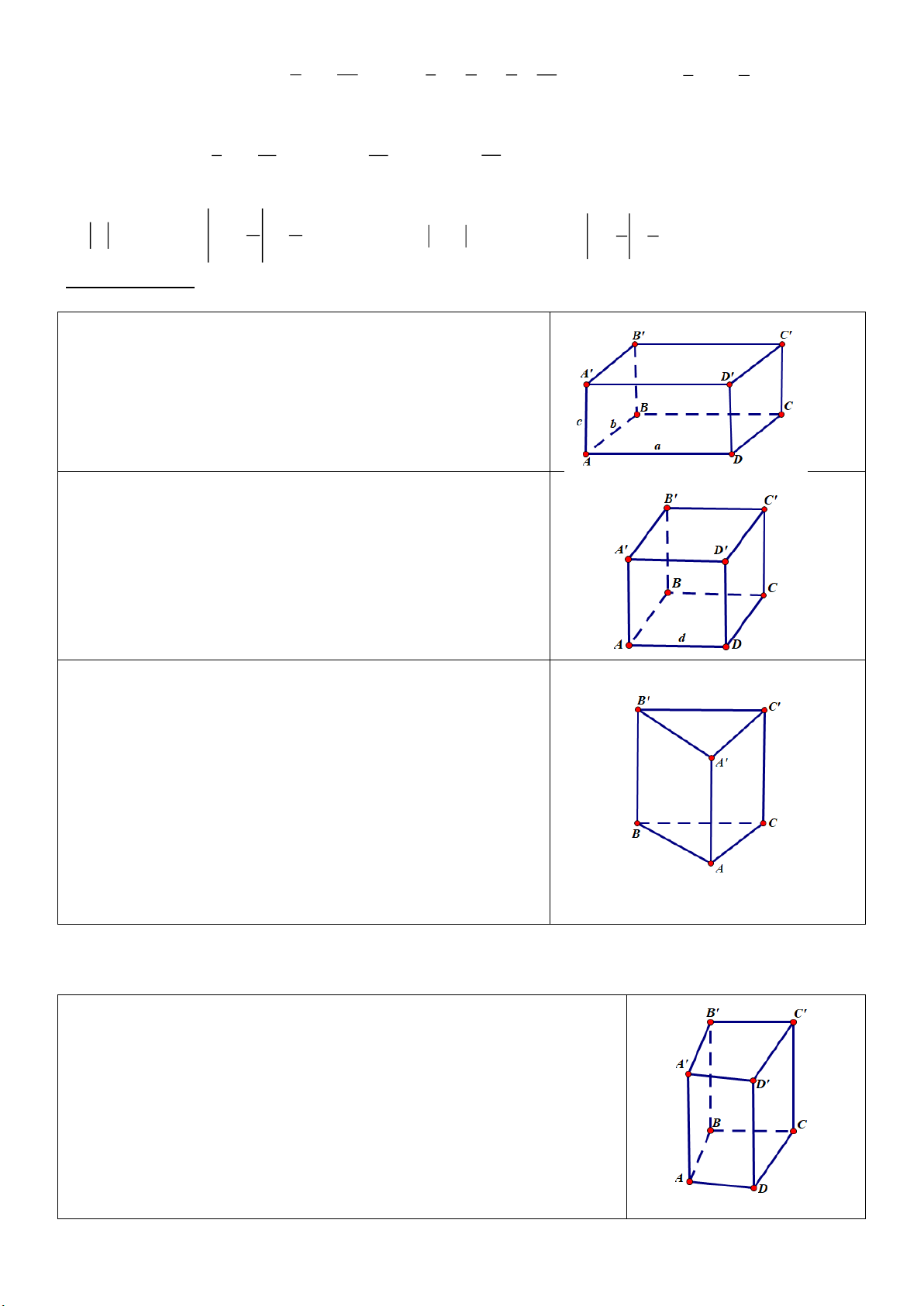
1. Hình hộp chữ nhật
- Có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình chữ nhật.
- Diện tích xung quanh: S 2 a b c xq
- Thể tích: V abc
(a: Chiều dài, b: chiều rộng, c: chiều cao)
2. Hình lập phương
- Có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình vuông
- Các cạnh đều bằng nhau - Diện tích xung quanh: 2 S 4d xq - Thể tích: 3 V d (d: Độ dài cạnh)
3. Hình lăng trụ đứng tam giác - Có 5 mặt, 9 cạnh
- Có 2 mặt đáy cùng là tam giác và song song với nhau, 3
mặt bên mặt bên là các hình chữ nhật.
- Các cạnh bên bằng nhau
- Chiều cao là độ dài một cạnh bên.
- Diện tích xung quanh: S C.h xq
(C: Chu vi đáy, h: chiều cao)
- Thể tích: V S.h
(S: Diện tích đáy, h: chiều cao)
4. Hình lăng trụ đứng tứ giác - Có 8 đỉnh
- Có 2 mặt đáy cùng là tứ giác và song song với nhau, 4 mặt bên là các hình chữ nhật.
- Các cạnh bên bằng nhau.
- Chiều cao là độ dài một cạnh bên.
- Diện tích xung quanh: S C.h xq
(C: Chu vi đáy, h: chiều cao)
- Thể tích: V S.h 3
(S: Diện tích đáy, h: chiều cao)
*Chú ý: Diện tích toàn phần của hình lăng trụ đứng được tính bởi công thức: S S 2S tp xq d
(Spt : Diện tích toàn phần, Sxq : Diện tích xung quanh , Sđ: Diện tích đáy)
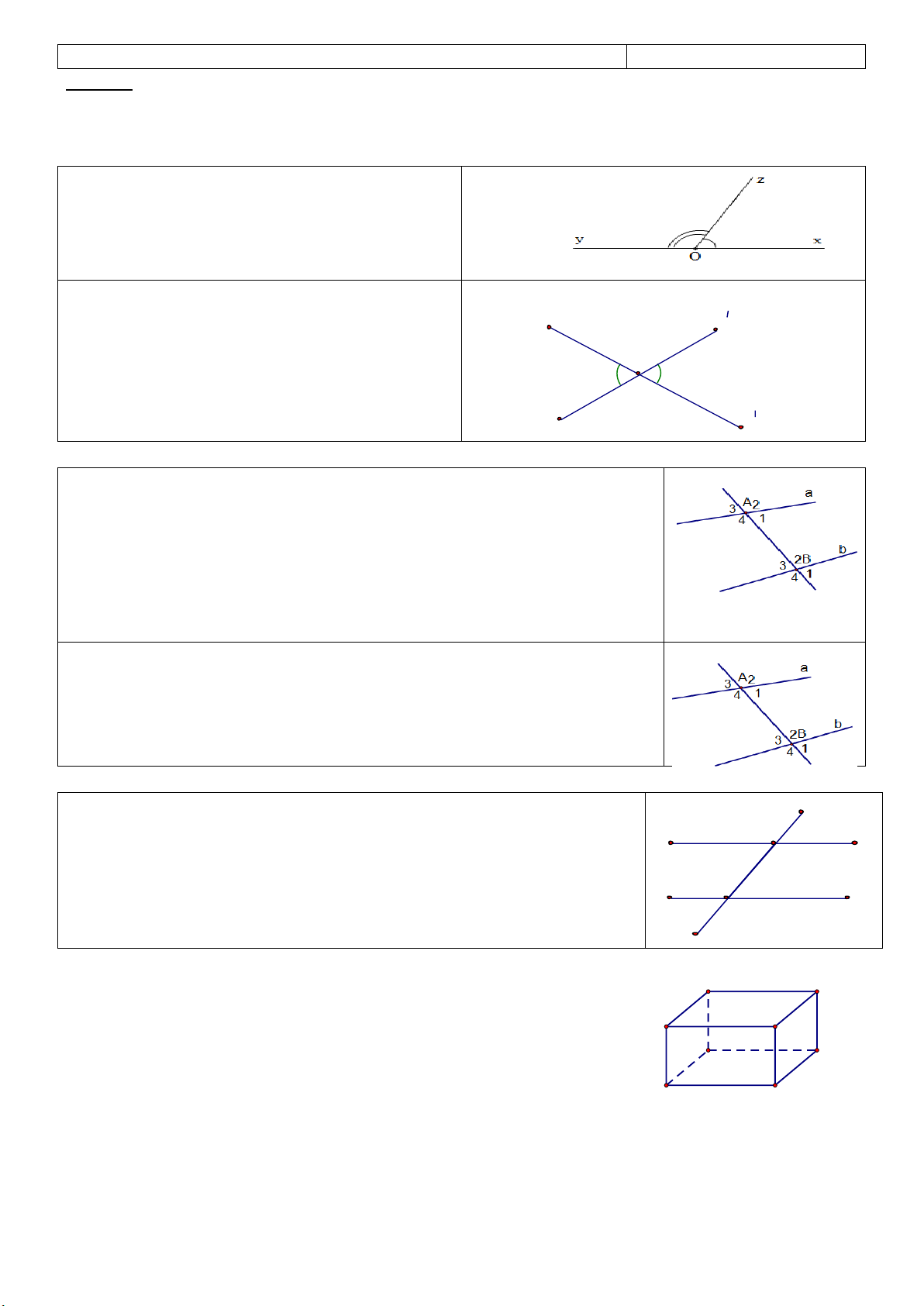
5. Hai góc kề bù Nếu · xOz , ·
yOz là hai góc kề bù thì · xOz + · yOz = 1800
6. Hai góc đối đỉnh: x y
Nếu Ô1 và Ô3 đối đỉnh thì Ô1 = Ô3 O2 1 3 4 y x
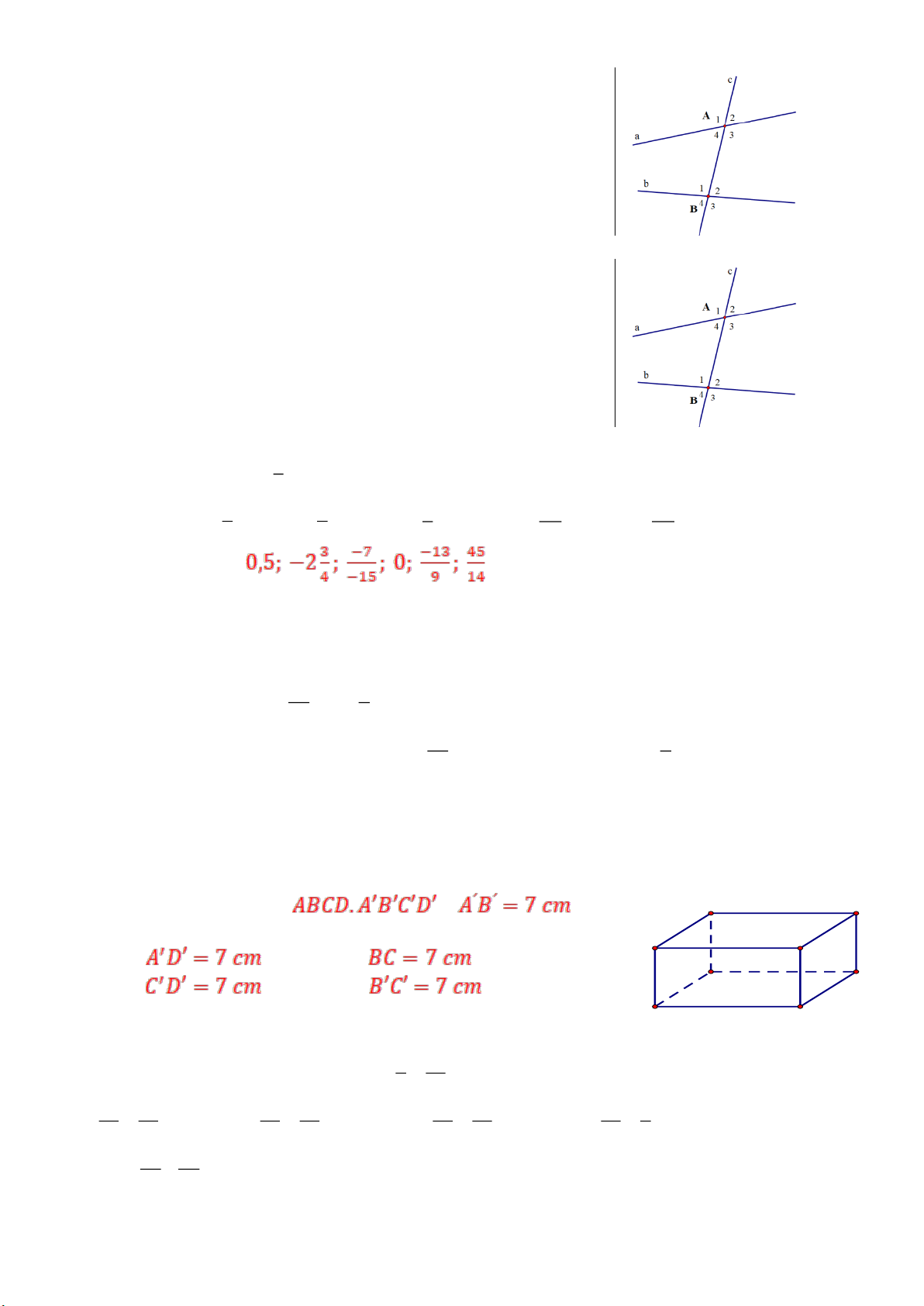
5. Hai góc đồng vị, hai góc so le trong, hai góc trong cùng phía
a) Các cặp góc so le trong: µ µ A µ µ 1 vµ B3 ; A 4 vµ B 2 .
b) Các cặp góc đồng vị: µ µ A µ µ µ µ
1 vµ B1 ; A 2 vµ B2 ; A 3 vµ B3 ; µ µ A 4 vµ B4
c) Các cặp góc trong cùng phía: µ µ A µ µ 1 vµ B2 ; A 4 vµ B3
6. Dấu hiệu nhận biết hai đường thẳng song song a ) Nếu µ A1 và µ B1 đồng vị , µ µ A1 = B1 thì a //b b) Nếu µ µ µ A1 và µ
B3 so le trong, A1 = B3 thì a //b
7. Tính chất một đường thẳng cắt hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song thì: 2 1 a
a) Hai góc so le trong bằng nhau 4 3 A
b) Hai góc đồng vị bằng nhau 2 b
c) Hai góc trong cùng phía có tổng bằng 180 1 0 4 3 B II. BÀI TẬP
Bài 1. Cho hình hộp chữ nhật A BCD.A ' B 'C ' D' như hình vẽ, có B C
A B = 5 cm , BC = 6 cm , AA ' = 8 cm. Tính diện tích xung D
quanh và thể tích của hình hộp chữ nhật. A B' C' A' D' 4
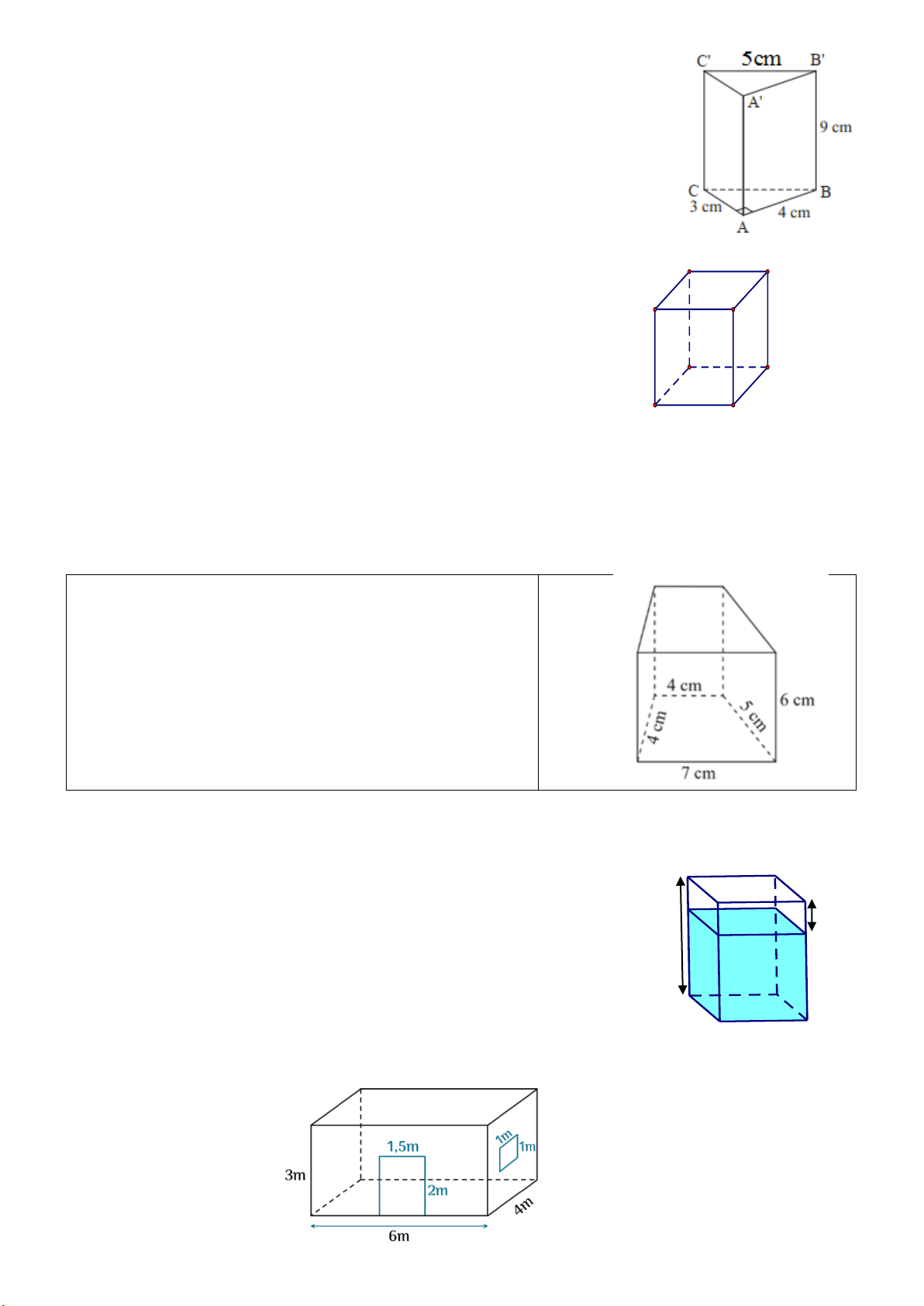
Bài 2. Cho hình lăng trụ đứng tam giác vuông A BC .A ' B 'C ' như hình
vẽ. Biết A B = 4cm , A C = 3cm , B’C’ = 5cm BB ' = 9cm. Tính diện
tích xung quanh và thể tích của hình lăng trụ đứng này.
Bài 3. Cho hình hộp chữ nhật A BCD.EFGH như hình vẽ, có B C
A B = 5 cm , EH = 6 cm , CG = 8 cm . 5 cm A D
a) Kể tên các đường chéo của hình hộp chữ nhật. 8 cm
b)Tính diện tích xung quanh, thể tích của hình hộp chữ nhật này. F G E 6 cm H
Bài 4. Cho hình lăng trụ đứng tam giác có độ dài ba cạnh đáy là 4 c , m 4 c ,
m 6 cm . Cạnh bên là 9.
Tính diện tích xung quanh của hình lăng trụ đứng?
Bài 5. Một hộp sữa có dạng hình hộp chữ nhật với các kích thước của đáy dưới là 4cm, 5cm và
chiều cao là 12cm. Tính diện tích xung quanh và thể tích hộp sữa đó?
Bài 6. Cho hình lập phương có có độ dài cạnh là 30cm. Tính điện tích xung quanh và thể tích của hình lập phương?
Bài 7. Tính diện tích xung quanh của hình lăng trụ đứng
có đáy là hình thang cho trong hình bên
Bài 8. Cho hình lăng trụ đứng có độ dài cạnh bên là 10cm và đáy là tam giác. Biết tam giác đó
có độ dài các cạnh là 4cm, 5cm, 6cm. Tính diện tích xung quanh của hình lăng trụ đứng đã cho.
Bài 9. Một hình lăng trụ có kích thước đáy và chiều cao như hình.
Hùng đổ vào đó một lượng nước, rồi đo khoảng cách từ mực nước
sau khi đổ vào tới miệng bình được 6cm. Hỏi số lít nước Hùng đổ 6cm vào là bao nhiêu? 30cm 8cm 10cm
Bài 10: Căn phòng của anh Nam có một cửa lớn hình chữ nhật và một cửa sổ hình vuông với
kích thước như hình vẽ: 5
Anh Nam cần tốn bao nhiêu tiền để sơn bốn bức tường xung quanh của căn phòng này (không
sơn cửa)? Biết rằng để sơn mỗi mét vuông phải tốn 50 nghìn đồng.
Bài 11. Cho hình hộp chữ nhật AB .
CD A' B 'C ' D ' có diện tích đáy 2 S
24 cm và có thể tích ABCD 3
V 84 cm . Chiều cao của hình hộp chữ nhật có độ dài là?
Bài 12. Cho hình lập phương có diện tích một mặt bên là 2
81 cm . Tính thể tích của hình lập phương?
Bài 13. Cho hình lăng trụ đứng tam giác có độ dài ba cạnh đáy là 4 c , m 4 c ,
m 6 cm . Biết diện tích xung quanh bằng 2
98 cm . Tính chiều cao của hình lăng trụ?
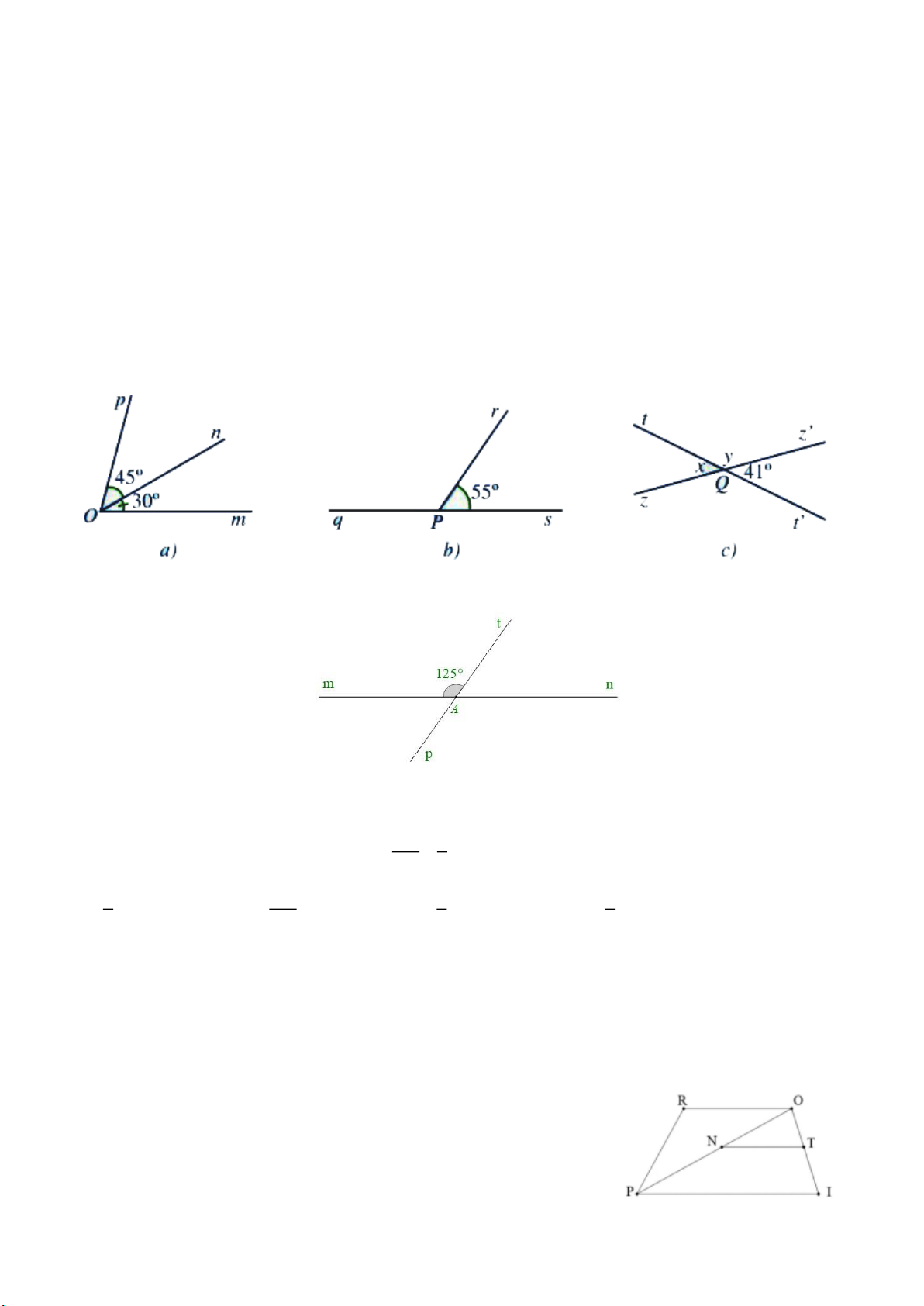
Bài 14. Tìm số đo: a) Góc mOp trong Hình a; b) Góc qPr trong Hình b; c) x, y trong Hình c.
Bài 15. Cho hình vẽ dưới đây, biết góc mAt=125°. Tính số đo các góc còn lại trong hình vẽ.
C. BÀI TẬP TRẮC NGHIỆM 3 27 3
Câu 1: Biểu diễn kết quả của phép tính
. được dạng lũy thừa của một số hữu tỉ là: 125 5 6 5 5 4 3 27 3 3 A. B. C. D. 5 125 5 5
Câu 2: Số cạnh của hình hộp chữ nhật là: A.12 B.6 C.8 D. 10
Câu 3: Hình hộp chữ nhật ABC .
D A' B 'C ' D ' có BB ' 6cm . Khẳng định nào sau đây đúng?
A. A' D ' 6cm
B. CC ' 6cm
C. D 'C ' 6cm
D. AC ' 6cm Câu 4: Cho ·
xOy kề bù với góc · yOz ; biết · 0
xOy 135 thì số đo · yOz bằng A. 0 135 B. 0 55 C. 0 35 D. 0 45
Câu 5: Cho hình vẽ bên, góc · OPI và góc ·
TNO là một cặp góc gì?
A. So le trong B. Đồng vị
C.Trong cùng phía D. Kề bù 6
Câu 6: Cho hình vẽ bên, µ A và góc µ
B là một cặp góc gì? 3 1
A. So le trong B. Đồng vị
C.Trong cùng phía D. Kề bù
Câu 7: Cho hình vẽ bên, µ A và góc µ
B là một cặp góc gì? 3 3
A. So le trong B. Đồng vị
C.Trong cùng phía D. Kề bù
Câu 8: Khẳng định nào sau đây đúng? 1 A. 9 ¢ B. ¤ C. 5 ¥ D. 2,5¢ 3 5 5 9 5 5
Câu 9: Số đối của là: A. B. C. D. 9 9 5 9 9
Câu 10. Trong các số
có bao nhiêu số hữu tỉ dương? A. 1 B. 2 C. 3 D. 4
Câu 11. Thứ tự thực hiện phép tính trên tập số hữu tỉ nào sau đây là đúng đối với biểu thức có dấu ngoặc?
A. { } → [ ] → ( ). B. ( ) → [ ] → { }. C. [ ] → ( ) → { }. D. [ ] → { } → ( ). 5 2
Câu 12. Trong các số 0,3;
; 0; 1 . Số nhỏ nhất là: 2 3 5 2 A. 0 B. -0,3 C. D. 1 2 3
Câu 13. Hình hộp chữ nhật và hình lập phương đều có: A. 8 mặt B. 10 đỉnh C. 6 mặt bằng nhau D. 6 mặt
Câu 14. Cho hình lập phương có cạnh bằng 4cm. Diện tích xung quanh của hình lập phương bằng: A. 4.4cm2 B. 16.4 cm2 C. 42 .4 cm D. 4.4.4cm
Câu 15. Hình hộp chữ nhật có . B C
Khẳng định nào sau đây đúng? D A A. B. C' C. D. B' A' D' 5 35
Câu 16. Chỉ ra đáp án sai . Từ tỉ lệ thức
ta có tỉ lệ thức sau : 9 63 5 9 63 35 35 63 63 9 A. B. C. D. 35 63 9 5 9 5 35 5 3 2 Câu 17. 20 15 7 1 17 5 1 A. B. C. D. 60 60 35 60 3 5
Câu 18. Cho biết : x + thì : 16 24 19 1 1 19 A x = B. x = C. x = D. x = 48 48 48 48 2 Câu 19. - 0,35 . 7 A. - 0,1 B. -1 C. -10 D. -100 2 6 3 Câu 20. : 2 15 5 3 2 3 A. -6 B. C. D. 2 3 4
Câu 21. Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là : A. - 1,8 B. 1,8 C. 0 D. - 2,2
Câu 22. Số x12 không bằng số nào trong các số sau đây ? A. x18 : x6 ( x 0 ) B. x4 . x8 C. x2 . x6 D. (x3 )4 x 4
Câu 23. Cho tỉ lệ thức thì : 15 5 4 A. x = B. x = 4 C. x = -12 D . x = -10 3
Câu 24. Kết quả làm tròn số 0, 7125 đến chữ số thập phân thứ ba là A. 0, 712 B. 0, 713 C. 0, 710 D. 0, 700
Câu 25. Làm tròn số 674 đến hàng chục là : A. 680 B. 670 C. 770 D. 780
Câu 26. Thực hiện phép tính 13 : 27 rồi làm tròn đến chữ số thập phân thứ hai được kết quả là: A. 0,50 B. 0,48 C. 0,49 D. 0, 47 x 2
Câu 27. Giá trị của x trong tỉ lệ thức
là: A. 1,5 B.1,8 C.12,5 D.-15 27 3, 6 x 2
Câu 28: Cho tỉ lệ thức
. Giá trị của x bằng bao nhiêu ? 3 6 A. -1 B. 1 C. 6 D. -3
Câu 29: Cho đẳng thức sau: . x y 2
.3. Tỉ lệ thức nào đúng khi được suy ra từ đẳng thức đó. 2 y 2 3 2 y x y A. B. C. D. x 3 x y x 3 2 3 2 x
Câu 30: Cho tỉ lệ thức:
thì giá trị của x bằng: 3 12 A. 6; B. 8; C. 4; D. 9.
Câu 31. Khi nhân hai lũy thừa cùng cơ số, ta thực hiện: A. xm.xn = xm+n; B. xm:xn = xm−n ; C. xm.xn = xm:n ; D. xm.xn = xm.n .
Câu 32. Công thức tính luỹ thừa của luỹ thừa là: x n m . m n A. x B. xm.xn = xm+n;
C. xm:xn = xm−n (x ≠ 0, m ≥≥ n ); D. (x.y)n = xn.yn.
Câu 33: Cho đẳng thức . a d . b .
c Khẳng định nào dưới đây là sai? a c d c a b d b A. B. . C. . D. . b d b a d c c a
Câu 34: Cho Ot là phân giác của góc xOy . Biết góc xOy bằng o
100 . Số đo của xOt là: A. o 40 . B. o 60 . C. o 200 . D. o 50 . 8
Câu 35: Chọn khẳng định đúng trong các khẳng định sau: 3 - 9 4 A. Î ¤ . B. Î ¢. C. Î ¥ . D. - 16 Î ¥ . 4 8 5
Câu 36. Kết quả phép tính 25 5 3 : 3 là? A. 20 3 . B. 30 6 . C. 30 3 . D. 20 1 . 1 4
Câu 37. Trong các số hữu tỉ: 0, 75; 1 ; 5 ; số nào lớn nhất: 2 5 1 4 A. 1 B. . C. – 5. D. 0.75. 2 5
Câu 38. Chọn khẳng định Đúng trong các khẳng định sau:
A. Hai góc đối đỉnh thì bằng nhau.
B. Hai đường thẳng song song thì cắt nhau.
C. Hai góc bằng nhau thì đối đỉnh.
D. Hai đường thẳng cắt nhau thì vuông góc. 2 3 6 3 5 5 1 1 1 1 1 1
Câu 39: Kết quả của phép tính . bằng: A. B. C. D. 2 2 2 2 2 4 3 5 3
Câu 40: Số đối của là: A. - 5 B. - 3 C. - D. - . 5 3 - 5 3 5
Câu 41: Kết quả của phép tính 36 : 32 là: A. 3 B. 32 C. 33 D. 34 3 5 3
Câu 42: Kết quả của phép tính là: A. 35 B. 38 C. 315 D. 33 6 2 1 1
Câu 43: Kết quả của phép tính . 5 5 là: 3 8 4 12 1 1 1 1 A. B. C. D. 5 5 5 5
Câu 44: Kết quả lũy thừa của phép tính (33)4 bằng: A.37 B. 94 C. 31 D. 312
Câu 45: So sánh 2,125 và 2,13 được kết quả là: A.2,125 > 2,13 B. 2,125 < 0,13
C. 2,125 2,13 D. 2,125 = 2,13 3
Câu 46: Sắp xếp các số sau theo thứ tự từ bé đến lớn: 1 ; 1,2(03); ; 4 ; 0 2 2 1 3 1 3 A. ; 1, 2(03); ; 4; 0 B. 4; ; 1, 2(03); ; 0 2 2 2 2 1 3 1 3 C. 4; ; 1, 2(03); 0; D. 4; ; 0; 1, 2(03); 2 2 2 2
Câu 47: Số đối của - 3 là: A. - 3 . B. 3 . C. 2 - (- 3) . D. ± 3 . Câu 48: Tính 2 ,5 bằng: A.3. B. 2 ,5. C. 2,5 . D. 3 .
Câu 49: Hai góc nào dưới đây là hai góc đối đỉnh?
Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4 9 7 3
Câu 50. Kết quả của phép tính: bằng: A. 10 21 4 3 B. 3 C. 1 D. 3 3 3
Câu 51. Trong các số sau, số nào là số hữu tỉ. 2 5 A. 3 . B. - . C. . D. 2 . 3 0
Câu 52. Biểu thức ( - 0,2)3 . ( - 0,2)2 biến đổi được thành: A. (- 0,2)5; B. (- 0,2)6; C. (0,2)6; D. (0,2)5.
Câu 53. Chỉ ra đáp án sai. Từ tỉ lệ thức 5.63 = 9.35 ta có tỉ lệ thức sau : 5 9 63 35 35 63 63 9 A. B. C. D. 35 63 9 5 9 5 35 5
Câu 54. Kết quả của phép tính 7,118 + 9,52 – 8,7 + 2,21 sau khi làm tròn đến hàng phần trăm A. 10,148 B. 10,14 C. 10,1 D. 10,15
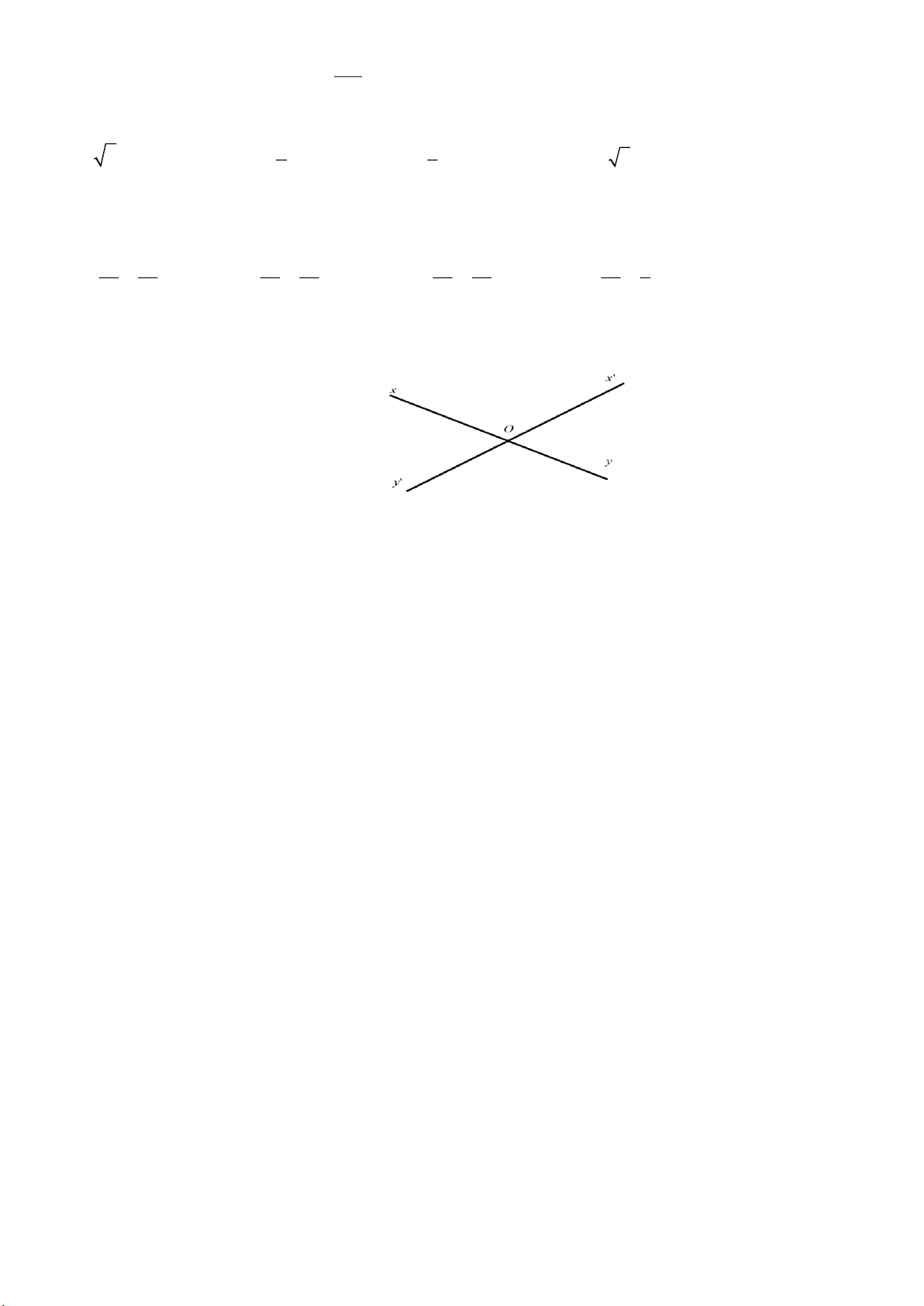
Câu 55. Cho hình vẽ, góc đối đỉnh của góc xOx ' là · · · · A. xOy . B. xOy ' . C. yOy ' . D. x ' Oy .
Câu 56. Tính chất kết hợp của phép cộng là: A. a + b = b + a B. (a + b) + c = b + (a + c) C. a(b + c) = ab + ac D. a + (-a) = 0
Câu 57. Tính chất phân phối của phép nhân đối với phép cộng là: A. a + b = b + a B. (a + b) + c = b + (a + c) C. a(b + c) = ab + ac D. a + (-a) = 0
Câu 58. Công thức tính diện tích xung quanh của hình lăng tụ đứng là: A. S C.h
B. V S.h C. S
2 a b c D. V abc xq xq
Câu 59. Công thức tính thể tích của hình lăng tụ đứng là: A. S C.h
B. V S.h C. S
2 a b c D. V abc xq xq 10




