Đề cương Toán rời rạc DHTI16A4HN
Phần I (Nguyễn Anh Tuấn) : Bài toán giải hệ thức truy hồi (2đ)
an = 6an-1 – 8an-2 (1) – hệ thức truy hồi tuyến tính thuần nhất bậc hai ( k=2) với c0 = 1, c1 = 6, c2 = -8
Phương trình đặc trưng có dạng: c0 λk – c1 λk-1 – c2
- Từ phương trình (1) ta xác định phương trình đặc trưng là: (0,25đ) 2 – 6  + 8 = 0 (*)
- Giải phương trình đặc trưng (*) ta thu được hai nghiệm phân biệt là: (0,5đ) 1 = 2, 2 = 4
- Phương trình đặc trưng có hai nghiệm phân biệt nên
nghiệm tổng quát có dạng: a n n
n = A. λ1 + B . λ 2
Vậy ta xác định được nghiệm tổng quát của phương trình (1) là: a n n n= A.2 + B.4 (**) (0,5đ) =4 - Ta lại có: a0
lần lượt thay điều kiện này vào nghiệm tổng a =10 1
quát (**) ta thu được hệ phương trình sau: 0 =
{ A.20+B.4 4 (***) (0,25đ) A .21+ B . 41=10
- Giải hệ (***)ra ta được: A = 3, B=1 , thay thế các giá trị
này vào nghiệm tổng quát (**) ta có nghiệm hệ thức truy hồi là: a n n n = 3.2 + 4 (0.25đ)
- Vậy nghiệm của hệ thức truy hồi là dãy {a n n} với an = 3.2 + 4n (0,25đ)
an = 5an-1 + 6an-2 (1) – hệ thức truy hồi tuyến tính thuần nhất bậc hai ( k=2) với c0 = 1, c1 = 5, c2 = 6
Phương trình đặc trưng có dạng: c0 λk – c1 λk-1 – c2
- Từ phương trình (1) ta xác định được phương trình đặc trưng là: (0,25đ)
λ2 - 5λ - 6 = 0 (*)
- Giải phương trình đặc trưng (*) ta thu được hai nghiệm phân biệt là: (0,5đ)
λ1 = -1; λ 2 =6
- Phương trình đặc trưng có hai nghiệm phân biệt nên
nghiệm tổng quát có dạng: a n n
n = A. λ1 + B . λ 2
Vậy ta xác định được nghiệm tổng quát của phương trình (1) là: (0,5đ) a n n n= A. (-1) + B. 6 (**) =4 - Từ lại có: a0
a =1 lần lượt thay vài nghiệm tổng quát (**) ta 1
thu được hệ phương trình sau:
{A .(−1)0+B.60=4 ⇔ { A+B=4 (***) (0,25đ)
A . (−1)1+ B .61=1 − A +6 B=1
- Giải hệ phương trình (***) ra ta được: A = 23 , B = 5 thay 7 7
thế các giá trị này vào nghiệm tổng quát (**) ta có nghiệm
phương trình truy hồi là: a 23 n 5 n n = . (-1) + . 6 7 7 (0,25đ) 23
- Vậy nghiệm của phương trình truy hồi là: a n 5 n = . (-1) + 7 7 . 6n (0,25đ)
an = 10an-1 +11an-2 (1) – hệ thức truy hồi tuyến tính thuần nhất bậc hai ( k=2) với c0 = 1, c1 = 10, c2 = 11
Phương trình đặc trưng có dạng: c0 λk – c1 λ k-1 – c2
- Từ phương trình (1) ta xác định phương trình đặc trưng là: (0,25đ)
λ2−10 λ − 11=0 (*)
- Giải phương trình đặc trưng (*) ta thu được hai nghiệm là:
λ =− 1 ; λ =11 (0.5đ) 1 2
- Phương trình đặc trưng có hai nghiệm phân biệt nên
nghiệm tổng quát có dạng: a n n
n = A. λ1 + B . λ 2
Vậy ta xác định được nghiệm tổng quát của phương trình (1) là: (0,5đ)
a = A . (−1)n+B . 11n (**) n a =1 - Ta lại có: 0
lần lượt thay vào nghiệm tổng quát (**) ta a =4 1
thu được hệ phương trình sau:
{A. (−1)0+B.110=1 ⇔ { A+B=1 (***) (0,25đ)
A . (− 1)1+ B 1 .11 =4 − A + B .11=4
- Giải hệ phương trình (***) ra ta thu được: A = 7 , B = 5 , 12 12
thay thế các giá trị này vào nghiệm tổng quát (**) ta có
phương trình nghiệm truy hồi (1) là: a n 5 n n = 7 . (-1) + . 11 12 12 (0,25đ)
- Vậy nghiệm của phương trình truy hồi (1) là: a 7 n = . (- 12 1)n + 5 . 11n (0,25đ) 12 Từ MISSISSIPI
- Từ này có 10 chữ cái gồm 4 chữ S, 4 chữ I, 1 chữ P, 1 chữ M
 Có C4 cách chọn chỗ cho 4 chữ S 10
Có C4 cách chọn chỗ cho 4 chữ I 6 1
Có C cách chọn chỗ cho 1 chữ P 2
Có C1 cách chọn chỗ cho 1 chữ M 1
- Vậy số xâu khác nhau có thể được tạo theo nguyên kỳ nhân là: 4 4 1 1
C . C . C . C = 10 ! = 6300 10 6 2 1
4 ! . 4 ! .1! .1 !
 Tương tự từ COMPUTER có:
- C1 cách chọn chỗ cho chữ C 8
- C1 cách chọn chỗ cho chữ 0 7 - 1
C cách chọn chỗ cho chữ M 6
- C1 cách chọn chỗ cho chữ P 5
- C1 cách chọn chỗ cho chữ U 4
- C1 cách chọn chỗ cho chữ T 3
- C1 cách chọn chỗ cho chữ E 2
- C1 cách chọn chỗ cho chữ R 1
Vậy số xâu khác nhau có thể lập được là: 1 1 1 1 1 1
C . C . C . C . C . C . 8 7 6 5 4 3 1 1 C . C = 40320 2 1 PHẦN 2: (Cao Bá Giáp) Câu 1: ∞ 1 1 4 4 0 0 0 ∞ 1 2 8 8 4 3 1 ∞ 2 0 2 4 1 4 3 ∞ 0 0 4 Giải:
Cố định thành phố xuất phát là 1
Từ ma trận chi phí ta có Cmin=08 là chi phí đi lại nhỏ nhất giữa
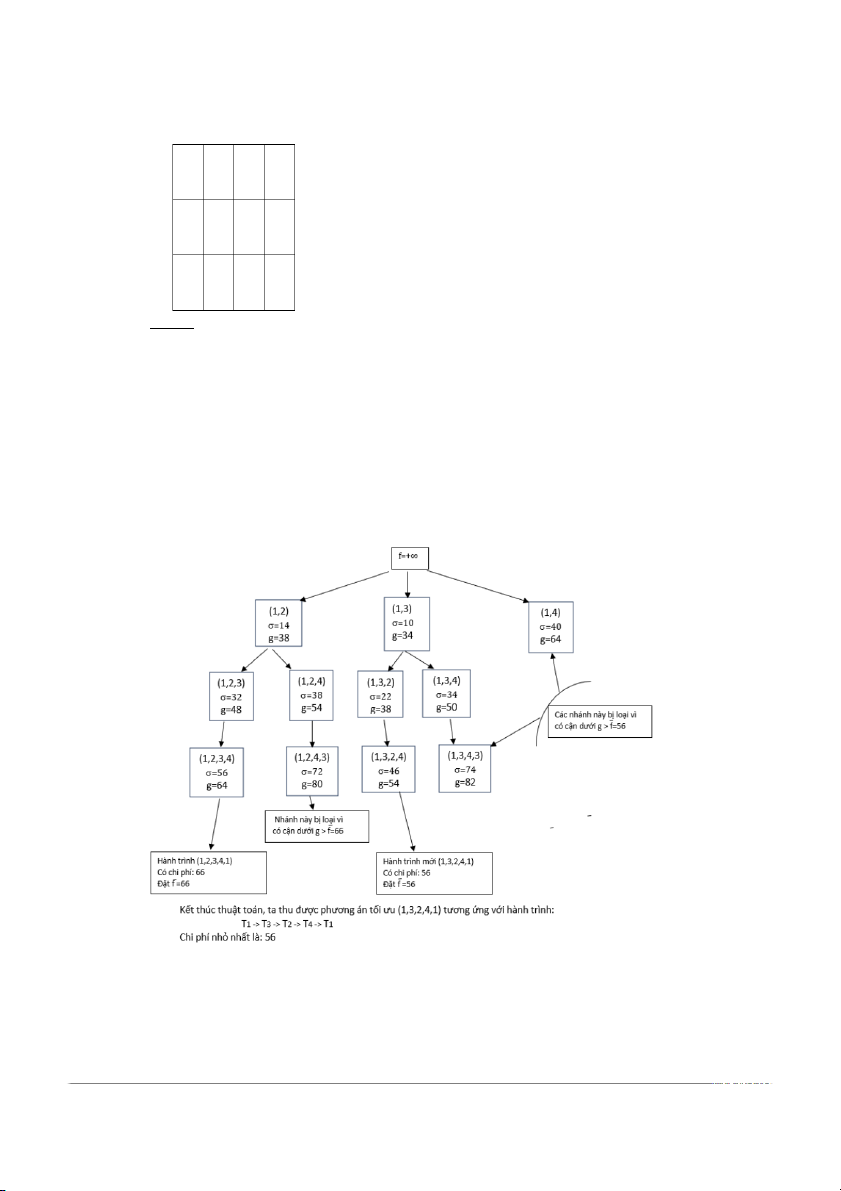
các thành phố.Qúa trình thực hiện thuật toán được mô tả bơi cây tìm kiếm lời giải.
Thông tin được ghi trong các ô trên hình vẽ theo thứ tự sau:
- Đầu tiên là các thành phần của phương án.
- Tiếp đến  là chi phí theo hành trình bộ phận
- g là cận dưới: g(u1, u , ..., uk 2 ) =  + ( 
n-k+1) cmin Câu 2:
5x1 + x2 + 9x3 -> max, 4x1 + 2x2 + 6x3 ≤ 10,
Với xj >=0 nguyên, j = 1,2,3 Giải: Ta có :b=10,n=3 c1=5 ; c2=1 ; c3=9 a1=4 ; a2=2 ; a3=6
Ta có: c3 = 9 > c1 = 5 > c2= 1 a 6 a 4 a 2 3 1 2
Từ đó ta nhận thấy đề bài chưa thỏa mãn bất đẳng thức:
c1 ≥ c2≥ . . . ≥ cn a a a 1 2 n
(Có nghĩa là các đồ vật được sắp xếp theo thứ tự không tăng
của giá trị một đơn vị trọng lượng)
Sắp xếp lại theo chiều giảm dần:
- : giá trị các đồ vật đang chất
c3 =9 > c1= 5 > c2 =1 trong túi a 6 a 4 a 2 3 1 2
- w: trọng lượng còn lại của túi Sau khi sắp xếp:
- g: cận trên. gk = k + ck+1 /
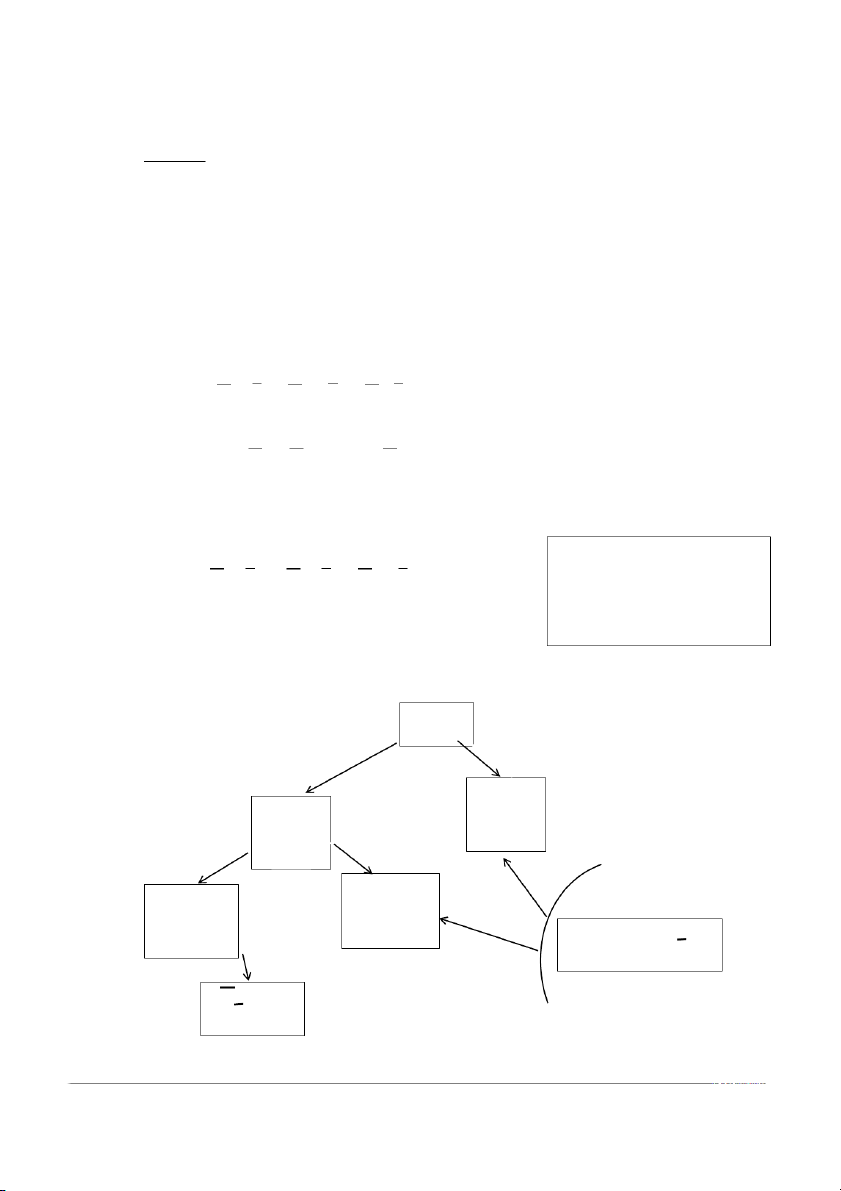
f(x)= 9x3 + 5x1 + x2 -> max, ak+1 * wk 6x3 + 4x1 + 2x2 ≤ 10,
Với xj >=0 nguyên, j = 1,2,3 f=-∞ X3=1 X3=0 (0); =0 (1); =9 w=10 X1=1 w=4 X1=0 g=12,5 g=14 (1,0); =9 (1,1); =14 w=4 w=0 g=11
Các nhánh này bị loại vì g=14 X2=0
cận trên g < kỷ lục f=14 X=(1,1,0) f=14
Thu được phương án của bài toán Cập nhật lại kỷ lục
Kết thúc thuật toán, ta thu được:
+)Phương án tối ưu: x*=(1,1,0) +)Gía trị tối ưu: f*=14 Câu 3: Máy D1 D2 D3 D4 D5 Chi tiết A 5 7 7 8 4 B 8 5 2 7 6 Giải:
Áp dụng thuật toán Johnson,ta chia các chi tiết trên 2 máy A và B thành 2 nhóm: N1= {D1, D5} N2= {D2, D3, D4} Sắp xếp các chi tiết: N1{D5,D1} N2= {D4, D2, D3}
Nối N2 vào đuôi N1, ta được lịch gia công tối ưu: Π=(D5, D1, D4, D2, D3)
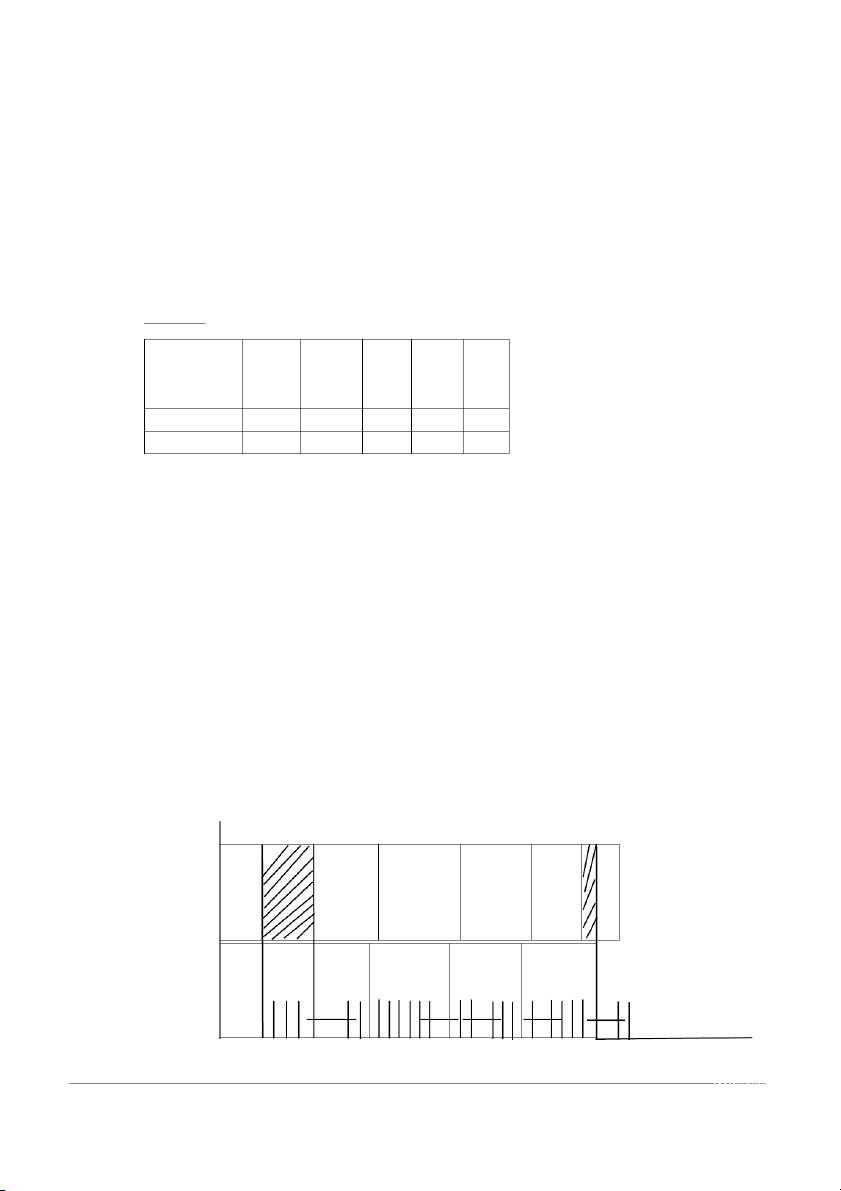
Sơ đồ Gantt cho lịch gia công chi tiết : B D5 D1 D4 D2 D 3 A D5 D1 D4 D2 D3
Vậy thời gian gia công tối ưu T(Π)=33
Phần 3 (Đỗ Thị Huyền)
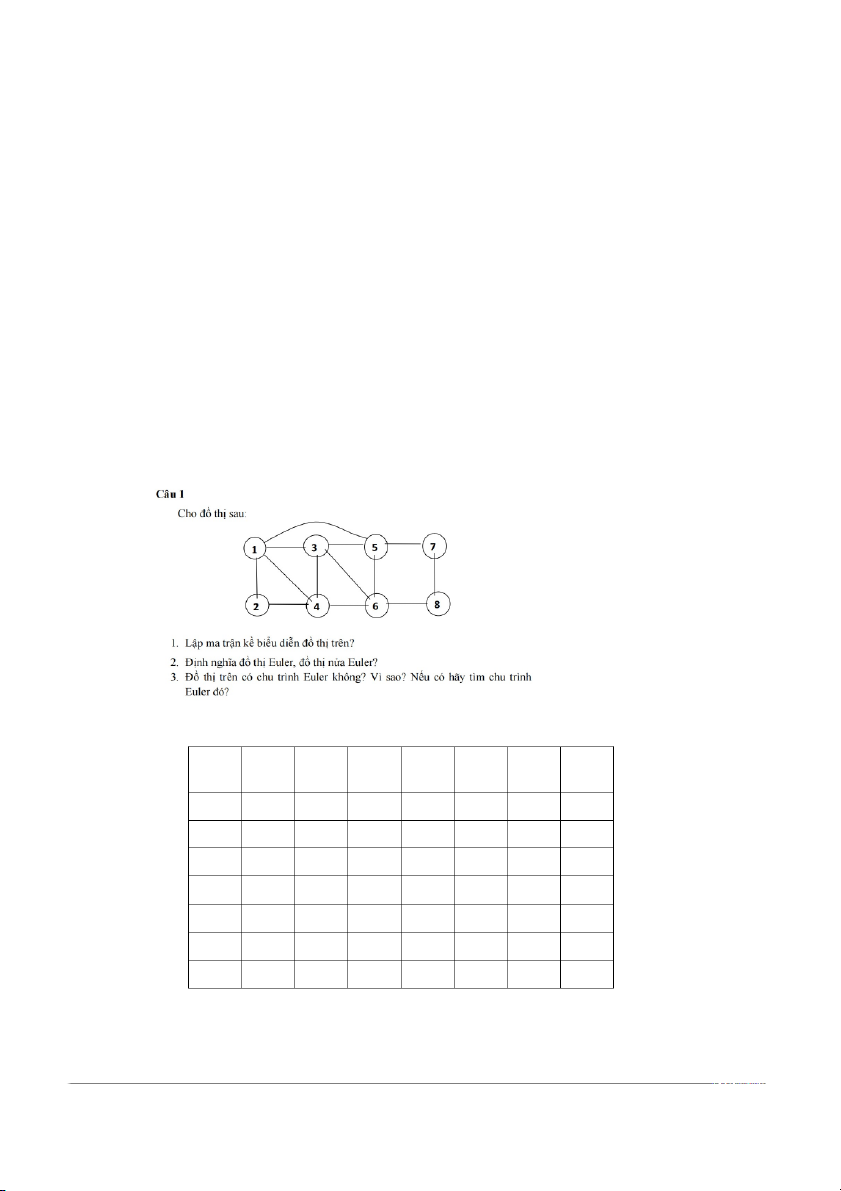
1.Lập ma trận kề của đồ thị 0 1 1 1 1 0 0 0 1 0 0 1 0 0 0 0 1 0 0 1 1 1 0 0 1 1 1 0 0 1 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 1 1 0
2.Định nghĩa đồ thị Euler, Đồ thị nửa Euler
- Đường đi Euler là đường đi đơn qua tất cả các cạnh của đồ thị
mỗi cạnh đúng một lần.
-Chu trình Euler là chu trình đơn đi qua tất cả các cạnh của đồ
thị mỗi cạnh đúng một lần.
- Đồ thị được gọi là đồ thị Euler nếu nó có chu trình Euler.
-Đồ thị là nửa Euler nếu nó có đường đi Euler
3.Đồ thị trên có chu trình Euler vì tất cả các đỉnh của đồ thị đều là bậc chẵn
( đỉnh 1,3,4,5 bậc 4 ; đỉnh 2,7,8 bậc 2) Đỉnh Danh sách kề 1 2,3,4,5 2 1,4 3 1,4,5,6 4 1,2,3,6 5 1,3,6,7 6 3,4,5,8 7 5,7 8 6,7 Bước Stack CE 1 1 # 2 1,2 # 3 1,2,4 # 4 1,2,4,1 # 5 1,2,4,1,3 # 6 1,2,4,1,3,5 # 7 1,2,4,1,3,5,1 # 8 1,2,4,1,3,5 1 9 1,2,4,1,3,5,6 1 10 1,2,4,1,3,5,6,3 1 11 1,2,4,1,3,5,6,3,4 1 12 1,2,4,1,3,5,6,3,4,6 1 13 1,2,4,1,3,5,6,3,4,6 1 ,8 14 1,2,4,1,3,5,6,3,4,6 1 ,8,7 15 1,2,4,1,3,5,6,3,4,6 1 ,8,7,5 16 1,2,4,1,3,5,6,3,4,6 1,5 ,8,7 17 1,2,4,1,3,5,6,3,4,6 1,5,7 ,8 18 1,2,4,1,3,5,6,3,4,6 1,5,7,8 19 1,2,4,1,3,5,6,3,4, 1,5,7,8,6 20 1,2,4,1,3,5,6,3, 1,5,7,8,6,4 21 1,2,4,1,3,5,6 1,5,7,8,6,4,3 22 1,2,4,1,3,5 1,5,7,8,6,4,3,6 23 1,2,4,1,3 1,5,7,8,6,4,3,6,5 24 1,2,4,1 1,5,7,8,6,4,3,6,5,3 25 1,2,4 1,5,7,8,6,4,3,6,5,3,1 26 1,2 1,5,7,8,6,4,3,6,5,3,1 ,4 27 1 1,5,7,8,6,4,3,6,5,3,1 ,4,2 28 # 1,5,7,8,6,4,3,6,5,3,1 ,4,2,1
Kết quả chu trình Euler : 1,2,4,1,3,5,6,3,4,6,8,7,5,1
GIẢI THÍCH THUẬT TOÁN