2.4. Tóm tắt ý chủ đạo của phương pháp tinh chỉnh từng bước
- Phương pháp tinh chỉnh từng bước là phương pháp thiết kế giải
thuật, phản ánh quá trình module hóa bài toán và thiết kế kiểu top-down.
- Quá trình tinh chỉnh từng bước bắt đầu từ quá trình trình bày
bằng ngôn ngữ tự nhiên, sau đó sẽ được thay thế dần dần bởi
các câu lệnh vào các bước sau để hướng về ngôn ngữ lập trình
đã chọn, hay nói cách khác đi từ “làm cái gì” đến “làm như thế nào”
- Ngôn ngữ thường dùng là pseudo language hay pseudo code
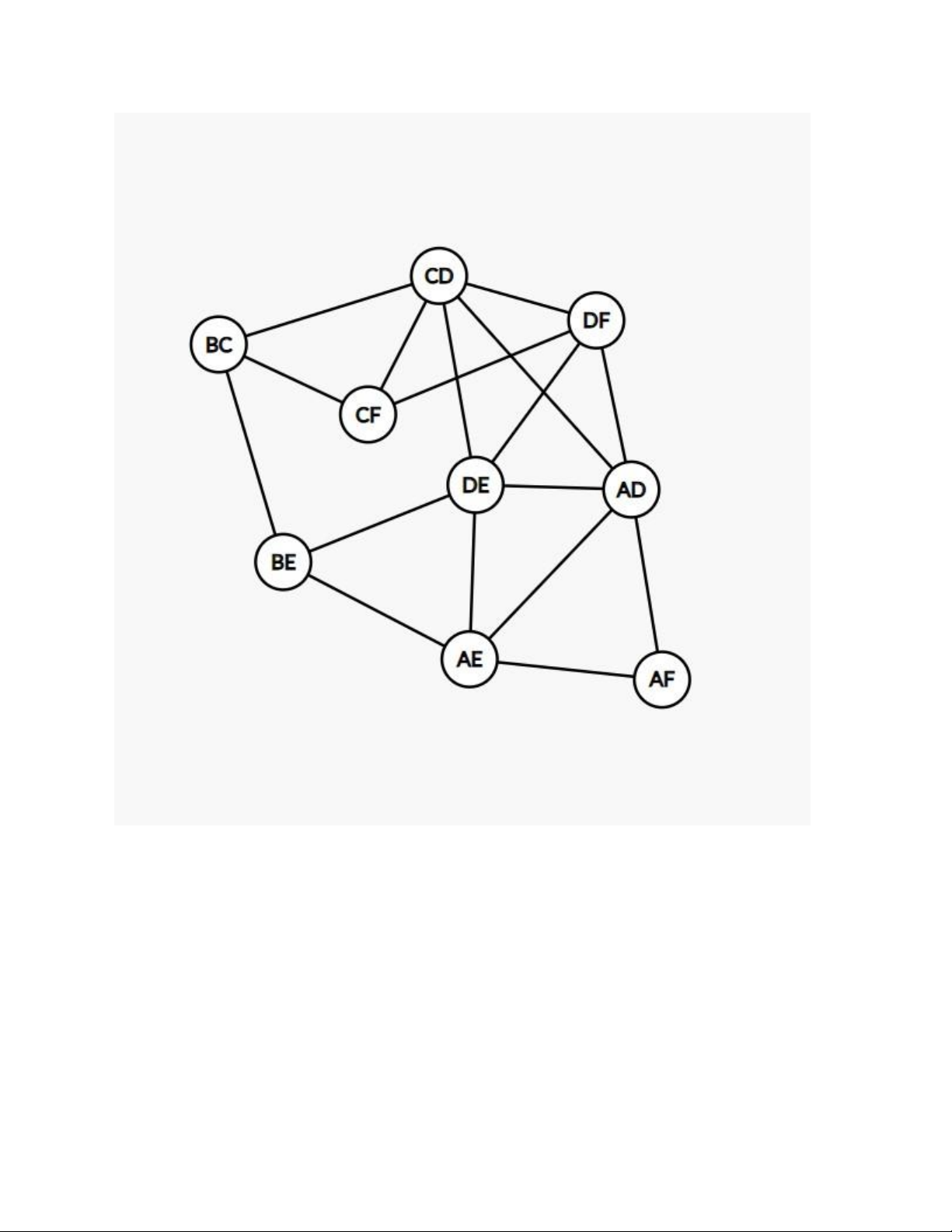
2.5. Các trận còn lại là AD, AE, AF, BC, BE,CD, CF, DE, DF. Ta có thể tìm bằng cách lập bảng A B C D E F A x x x B x x x x C x x x D x x E x x x F x x x
Ta có đồ thị như sau: Các đỉnh nối đại diện cho lịch thi đấu bị trùng
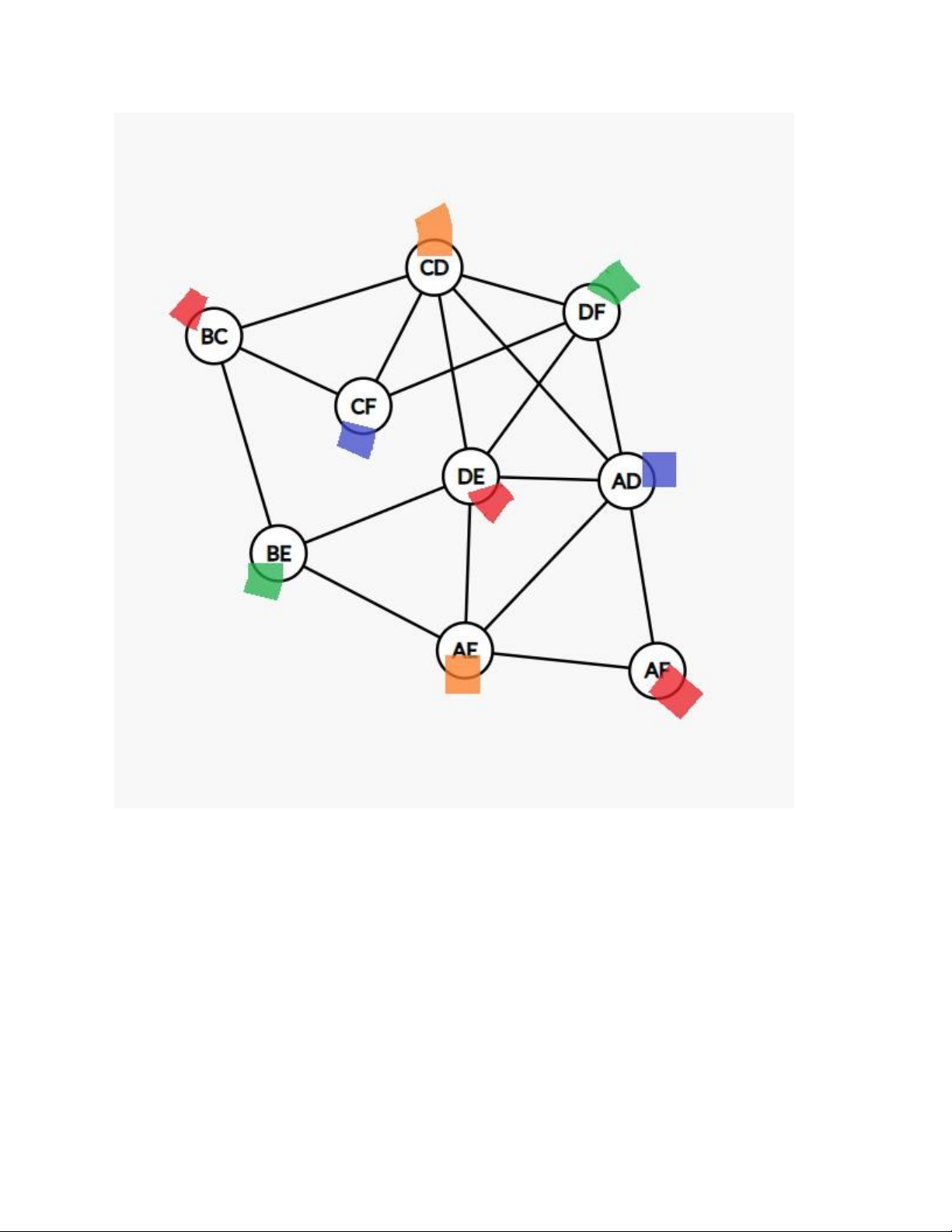
Ta tô màu các đỉnh dựa vào thuật toán tham lam:
Vậy ta có thể xếp lịch như sau:
Ngày 1: B đấu với C, D đấu với E, A đấu với F
Ngày 2: B đấu với E, D đấu với F
Ngày 3: A đấu với D, C đấu với F
Ngày 4: A đấu với E, C đấu với D
2.6. Một giải thuật mà độ tính toán của nó là O(1) là giải thuật tính
tổng của hai số.Khi đó thời gian thực hiện x = a + b sẽ có thời gian
thực hiện bằng hằng số c nên độ tính toán là O(1)
2.7a) Độ phứctạptínhtoán của giải thuậtlà O(n) vì phép gánSum =0
có thời gian thực hiện là O(1), vòng lặp có thời gian thực hiện là O(n)
b) Có ba vòng lặp lồng nhau nên độ phức tạp sẽ là O(n^3)
c) Trường hợp xấu nhất là mọi phần từ phải được đổi chỗ, khi đó i
chạy từ 1 đến n - 1 và j chạy từ i đến n - 1 nên số phép toán sẽ
là n(n-1)/2 nên độ phức tạp của thuật toán là O(n^2) 4.1
void giaiHPT(float* a, int n, float* b, float* x) {
for (int i = 1; i <= n; i++) { double sum = b[i];
for (int j = 1; j < i; j++) {
sum -= a[(i * (i - 1)) / 2 + j - 1] * x[j - 1]; }
x[i - 1] = sum / a[(i * (i + 1)) / 2 - 1]; } }
4.2.a) Cách lưu trữ theo dạng (�, � , � , .., � , � ) có những ưu, � � − 1 1 0 nhược sau:
- Ưu:+ Đơngiảnvàtrựcquan
+ Dễ dàng truy xuất các phần tử
+ Tính giá trị đa thức bằng lược đồ Horner O(n)
+ Hiệu quả với đa thức “dày”
+ Dễ dàng cộng trừ đa thức theo từng hệ số - Nhược:
+ Không hiệu quả đối với đa thức thưa
+ Nếu bậc của đa thức thay đổi thì khó khăn trong việc chỉnh sửa
+ Nhân đa thức có độ phức tạp O(n^2)
+ Chưa tối ưu được hiệu suất
+ chẳng hạn như tìm đạo hàm, tích phân, tìm nghiệm, …
b) Ưu và nhược điểm của cách lưu trữ mũ và hệ số của các số hạng
- Ưu:+ Hiệu quảchođathứcthưa + Dễ dàng mở rộng
+ Phù hợp với các phép tính toán đa thức - Nhược:
+ Không hiệu quả với đa thức dày do sẽ tốn kém bộ nhớ
+ Phức tạp trong việc truy cập trực tiếp các hệ số
+ Cần xử lý thêm khi thực hiện các phép toán c) Cộng hai đa thức
- Bước 1: Khởi tạo mảng rỗng để lưu kết quả cuối cùng
- Bước 2: Duyệt qua các số hạng của hai đa thức:
+ So sánh số mũ của hai đa thức
+ Nếu mũ bằng nhau, cộng các hệ số tương ứng và lưu vào mảng kết quả
+ Nếu mũ khác nhau thì thêm trực tiếp số hạng có mũ
lớn hơn vào mảng kết quả
- Bước 3: Thêm các số hạng còn lại nếu một trong hai đa
thức đã được duyệt hết
- Bước 4: Trả về kết quả Giải thuật :
int* congDaThuc(int a[], int size1, int b[], int size2, int* resultSize) { // Tao mang ket qua
int* result = (int*)mal oc((size1 + size2) * sizeof(int)); int i = 1, j = 1, k = 1;
// Tong so phan tu cua mang khoi tao bang 0 result[0] = 0;
while (i < size1 && j < size2) {
// Neu so mu bang nhau thi cong he so if (a[i] == b[j]) {
int coefficient = a[i + 1] + b[j + 1]; if (coefficient != 0) { result[k++] = a[i]; result[k++] = coefficient; result[0] += 2; } // Sang phan tu tiep theo i += 2; j += 2; }
// Neu so mu lon hon thi cho phan tu lon hon vao mang ket
qua roi dich chuyen den so mu nho hon else if (a[i] > b[j]) { result[k++] = a[i]; result[k++] = a[i + 1]; result[0] += 2; i += 2; } else {result[k++]=b[j]; result[k++] = b[j + 1]; result[0] += 2; j += 2; } } while (i < size1) { result[k++] = a[i]; result[k++] = a[i + 1]; result[0] += 2; i += 2; } while (j < size2) { result[k++] = b[j]; result[k++] = b[j + 1]; result[0] += 2; j += 2; } *resultSize = result[0] + 1; return result; } 4.3.
Dãy các phép toán vào ra để đổi thứ tự đầu tàu thành 3 2 5 6 4 1: VVVRRVVRVRRR
Dãy các phép toán vào ra để đổi thứ tự đầu tàu thành: 1 5 4 6 2 3:
VRVVVVRRVRRR ( lúc này là 1 5 4 6 3 2). Ta thực hiện thêm phép
toán VRVRVRVRVVRR thì lúc này toa tàu sẽ đổi thứ tự thành 1 5 4 6 2 3
4.4- Phép bổ sung và loại bỏ đối với ngăn xếp có đáy là S[0]
void boSung(int* s, int n, int value) {
s = (int*)real oc(s, sizeof(int) * (n + 1)); // Dich cac phan tu
for (int i = n; i > 0; i--) s[i] = s[i - 1];
// Cho phan tu moi vao dau danh sach s[0] = value; return; }
void loaiBo(int* s, int &n) { // Dich cac phan tu
for (int i = 0; i < n; i++) s[i] = s[i + 1]; // Resize lai ngan xep
s = (int*)real oc(s, sizeof(int) * (n - 1)); n = n - 1; return;
} - Phép bổ sung và loại bỏ đối với ngăn xếp có đáy là S[n - 1]
void boSung(int* s, int n, int value) { // Cap nhat kich thuoc mang n = n + 1;
s = (int*)real oc(s, sizeof(int) * n);
// Cho phan tu moi vao cuoi danh sach s[n - 1] = value; return; }
void loaiBo(int* s, int &n) { // Resize lai ngan xep n = n - 1;
s = (int*)real oc(s, sizeof(int) * n); return; } 4.5. 4.6.
Biểu thức (A*B)/(C+D) dưới dạng hậu tố: A B * C D - /
Minh họa tính giá trị biểu thức với A = 20, B = 4, C = 9, D = 7 4.7.
Giải thuật: Ta sẽ dùng giải thuật BFS để tìm đường đi ngắn nhất
- Khởi tạo hàng đợi: Bắt đầu với vị trí A, đánh dấu là đã được thăm
- Duyệt BFS: Từ vị trí hiện tại, tính tất cả các bước nhảy hợp lệ
của con mã. Nếu có chứa vị trí B thì kết thúc. Không thì thêm tất
cả các vị trí hợp lệ chưa được thăm vào hàng đợi và tiếp tục
- Kết thúc khi hàng đợi rỗng hoặc có đường đi Code:
int duongDiNganNhat(int A_x, int A_y, int B_x, int B_y) { // Khoi tao hang doi
Queue* queue = create_queue(M * N);
bool visited[M][N] = { false }; // Them vi tri bat dau vao Node start = { A_x, A_y, 0 }; enqueue(queue, start); visited[A_x][A_y] = true; // Giai thuat BFS while (!is_empty(queue)) { // Kiem tra xem hang doi co trong khong
Node current = dequeue(queue) // Lay phan tu ra khoi hang doi
if (current.x == B_x && current.y = B_y) return current.steps;
// Duyet tat ca cac buoc nhay cua con ma
for (int i = 0; i < 8; i++) { int nx = current.x + dx[i]; int ny = current.y + dy[i];
if (kiemtra(nx, ny) && !visited[nx][ny]) { visited[nx][ny] = true;
Node next = { nx, ny, current.steps + 1 }; //
Them cac vi tri co the vao hang doi enqueue(queue, next); } } }
return -1; // Neu khong co duong di ngan nhat nao }
4.8.a) Giải thuật tìm số lượng các nút trong danh sách int countNode() { Node* temp = L;
if (temp == nul ptr) // Neu head tro den nul ptr thi khong co phan tu nao return 0; int count = 0;
// Cho bien temp duoc tro den phan tu cuoi cung while (temp != nul ptr) { temp = temp->next; count += 1; } return count; }
b) Tìm tới nút thứ k trong danh sách, nếu có nút thứ k thì in ra dữ liệu của nút đó void findNode_k(int k) { int soNode = countNode();
// Kiem tra xem danh sach co du k nut khong
if (soNode < k) std :: cout << "Trong danh sach khong co nut thu k" << std :: endl;
else {//Taocontrochaydetimnutkvaindexdeluuvitri Node* temp = L; int index = 1; while (index < k) { temp = temp->next; index += 1; }
std :: cout << "Gia tri cua nut thu k la " << temp->info << std :: endl; return; }
} c) Bổ sung 1 nút vào sau nút k
- Bước 1: Kiểm tra xem có tồn tại nút k không, nếu không tồn tại thì kết thúc
- Bước 2: Nếu tồn tại nút k, tạo một con trỏ và chạy đến nút k và
gán nút mới sau nó, nối nút mới vào nút k + 1 và return Code:
void insertAfter(int k, int value){
Node* newnode = new Node(value);
// Kiem tra xem co nut thu k trong danh sach khong int soNode = countNode();
if (soNode < k) std::cout << "Khong ton tai nut thu k trong danh sach" << std::endl; else {//Chay den nut k Node* temp = L; int index = 1; while (index < k) { temp = temp->next; index += 1; } // Gan nut moi sau nut k
newnode->next = temp->next; temp->next = newnode; } return;
} d) Loại bỏ nút đứng trước nút k
Bước 1: Kiểm tra xem có nút k trong danh sách không
Bước 2: Nếu tồn tại nút k trong danh sách, có các trường hợp là
nút k đứng thứ 2 trong danh sách và ở các vị trí còn lại
- Nếu đứng thứ 2, chỉ cần xóa nút đầu tiên và cho L trỏ đến
- Nếu đứng ở các vị trí khác, lập 1 biến temp và chạy đến khi
nào (temp->next)->next = k. Khi đó chỉ cần xóa temp->next
và cho temp->next trỏ đến k Code: void deleteBefore(int k) {
// Kiem tra xem nut thu k co trong danh sach khong int soNode = countNode();
if (soNode < k) std::cout << "Khong ton tai nut thu k trong danh sach" << std::endl;
else {//Truonghopnutcanxoalanutdautien if (k == 2) { Node* deletenode = L; L = L->next; delete(deletenode); } else {int index = 3; Node* temp = L; //Chay den khi tim thay nut k while (index < k) { temp = temp->next; index += 1; } //Xoa nut dung truoc nut thu k
Node* deletenode = temp->next;
temp->next = (temp->next)->next; delete(deletenode); } } return;
} e) ChothêncontrỏQ trỏ tớimột nút có trongdanhsáchvàmột
danh sách móc nối đơn khác có nút đầu tiên trỏ bởi P. Chèn
danh sách P vào sau nút trỏ bởi Q
- Bước 1: tạo một biến tạm để lưu địa chỉ của nút sau Q và nút cuối của danh sách P
- Bước 2: Cho Q->next trỏ đến địa chỉ của P.
- Bước 3: Cho nút tiếp theo của nút cuối của P trỏ đến nút trước đó sau Q Code:
void insertLinkedList(Node* Q, Node* P) {
// Can chen danh sach P sau con tro Q tro den mot nut nao do trong danh sach
// Kiem tra xem Q co tro den nut cuoi hay khong, neu co thi gan P vao sau
if (Q->next == nul ptr) Q->next = P;
else {//LuunutsaucontroQ vanutcuoicuaP Node* temp1 = Q->next; Node* temp2 = P;
while (temp2->next != nul ptr) temp2 = temp2->next; // Chen P sau con tro Q Q->next = P; temp2->next = temp1; } return; }
f) Tách thành 2 danh sách mà danh sách sau được trỏ bởi Q
Bước 1: - Kiểm tra xem nút Q có phải L không, nếu có thì print ra
“Khong tach duoc” va return nul ptr. Nếu không phải thì chuyển sang bước 2
Bước 2: Tạo một con trỏ tạm, chạy từ đầu đến khi nút tiếp theo của
con trỏ có địa chỉ được trỏ bởi Q.
Bước 3: Cho con trỏ tạm ấy có next là nul ptr và return. Ta sẽ được 2
danh sách, 1 được trỏ bởi L và 2 được trỏ bởi Q Code:
void splitLinkedList(Node* Q) {
// Xem Q co tro den nut dau tien khong
if (Q == L) std::cout << "Q tro den phan tu dau tien, khong tach duoc" << std::endl; else {
//Tao bien tam va chay den nut truoc con tro Q Node* temp = L;
while (temp->next != Q) temp = temp->next; // Tach danh sach temp->next = nul ptr; } return;
} g) Tạo ra danh sách mới là đảo ngược của danh sách đã cho
Bước 1: Kiểm tra xem list có rỗng không, nếu có thì return nul ptr
Bước 2: Tạo một biến temp cho chạy đến hết danh sách L. Mỗi
lần chạy, tạo một nút mới có giá trị bằng giá trị của nút temp
nhưng khác địa chỉ, sau đó chèn nó vào trước danh sách newL
mới và chuyển đến bước 3 Bước 3: Return newL Code: Node* reverseLinkedList() {
// Kiem tra xem danh sach co rong hay khong
if (head == nul ptr) return head; // Tao con tro newL va temp Node* newL = nul ptr; Node* temp = head; // vong lap while (temp != nul ptr) {
Node* newnode = new Node(temp->info);
// Chen nut moi vao danh sach moi newnode->next = newL; newL = newnode; temp = temp->next; } return newL; }
4.9.a) Bổ sung 1 nút mới nhưng vẫn đảm bảo thứ tự
Bước 1: Kiểm tra xem danh sách có nul không, nếu có thì cho P trỏ
đến node cần thêm và chuyển đến bước 3, không thì tạo 2 con trỏ prev và current. Bước 2:
Cho current chạy đến nút cần thêm, ở vị trí mà X < (current->DATA).
- Trong quá trình chạy, nếu (current->DATA) = X thì in ra (“Đã tồn
tại nút có giá trị X”) và chuyển đến bước 3
- Nếu chưa tồn tại: Khi đó (prev->DATA) < X và (current ->DATA)
> X. Tạo ra node mới có DATA = X và chèn giữa 2 nút prev và
current. Chuyển đến bước 3
Bước 3: Kết thúc thuật toán Code:
void insertIntoAscendingOrdered(int X) { Node* newnode = new Node(X);
// Kiem tra xem danh sach co rong khong if (P == nul ptr) P = newnode; else {
// Khoi tao hai con tro prev va current Node* prev = nul ptr; Node* current = P; //Tim nut can chen do {
// Kiem tra xem da ton tai chua if (current->DATA == X) {
std::cout << "Da ton tai" << std::endl; break; } prev = current; current = current->next;
} while (current->DATA < X);
// Chen nut moi vao giua prev va current prev->next = newnode; newnode->next = current; } return;
} b) Loại bỏ nút cógiá trị DATA bằng k
Bước 1: Kiểm tra xem danh sách có rỗng không, nếu có thì chuyển
đến bước 4, không thì chuyển sang bước 2
Bước 2: Kiểm tra xem P->DATA == k không, nếu có thì xóa nút đầu và
chuyển sang bước 4. Ngược lại chuyển sang bước 3
Bước 3: Tạo 2 biến prev và current. Biến current sẽ tìm nút có giá trị DATA bằng k
- Nếu chạy đến khi current = nul ptr hoặc current->DATA thì in ra
không tồn tại nút DATA bằng k và chuyển sang bước 3
- Nếu có thì ta xóa nút đó và nối lại danh sách Bước 4: Kết thúc Code: void removeNodeK(int k) {
//Kiem tra xem danh sach co rong khong if (checkEmpty()) {
std::cout << ("Danh sach rong") << std::endl; } else {//Taocontrotamthoi
Node* prev = nul ptr, *current = head;
// Neu nut dau co DATA bang k thi dich chuyen P
if (current != nul ptr && current->info == k) { head = head->next; delete(current); return; } // Tim vi tri nut DATA k
while (current != nul ptr && current->info < k) { prev = current; current = current->next; }
// Kiem tra xem co ton tai nut co DATA = k hoac da di het cac phan tu chua
if (current != nul ptr || current->info != k) {
std::cout << "Khong tim duoc nut co DATA = k" << std::endl; return; } // Xoa nut
prev->next = current->next; delete(current); } } 4.10. a) Giải thuật
Bước 1: Xác định hai danh sách liên kết vòng P và Q. Cả hai
đều là danh sách liên kết vòng, tức là phần tử cuối của mỗi danh
sách trỏ về phần tử đầu của danh sách đó.
Bước 2: Kiểm tra nếu một trong hai danh sách P hoặc Q trống (không có phần tử).
- Nếu P rỗng, trả về Q.
- Nếu Q rỗng, trả về P.
Bước 3: Tìm phần tử cuối của danh sách P. Đây là phần tử mà con
trỏ next của nó trỏ về phần tử đầu của P (phần tử mà P trỏ tới).
Bước 4: Tìm phần tử cuối của danh sách Q. Đây là phần tử mà con
trỏ next của nó trỏ về phần tử đầu của Q (phần tử mà Q trỏ tới).
Bước 5: Hợp nhất hai danh sách:
● Cập nhật con trỏ next của phần tử cuối cùng của danh sách P
để trỏ đến phần tử đầu tiên của danh sách Q.
● Cập nhật con trỏ next của phần tử cuối cùng của danh sách Q
để trỏ đến phần tử đầu tiên của danh sách P.
Bước 6: Trả về danh sách hợp nhất, bắt đầu từ phần tử đầu tiên của danh sách P.
b) Bước 1: Kiểm tra nếu danh sách L trống.
- Nếu L == NULL, trả về NULL vì không có danh sách nào để sao chép.
Bước 2: Tạo nút đầu tiên của danh sách mới newL với giá trị bằng
giá trị của nút đầu tiên của danh sách L. Đặt newL trỏ đến nút
đầu tiên của danh sách mới.
Bước 3: Sử dụng một con trỏ tạm (temp) để duyệt qua danh sách gốc L:
- Duyệt từ nút đầu tiên của L cho đến khi gặp lại nút đầu (vì
đây là danh sách liên kết vòng).
- Với mỗi nút, tạo một bản sao (tạo nút mới) và thêm nút đó vào danh sách mới (newL).
Bước 4: Sau khi duyệt qua toàn bộ danh sách L, kết nối nút cuối
của danh sách mới với nút đầu của nó, tạo thành một danh sách liên kết vòng.
Bước 5: Trả về con trỏ newL trỏ đến danh sách sao chép hoàn chỉnh. 4.11 - Bổ sung:
+ Bước 1: Tạo một nút mới với giá trị cần thêm.