Đề đánh giá năng lực - HSA số 2 môn Toán

Tài Liệu Ôn Thi Group
ĐÁNH GIÁ NĂNG LỰC – HSA 2K8
GIÁO VIÊN PHỤ TRÁCH: ĐOÀN THU TRANG ĐỀ HSA SỐ 02 HSA 01:
Cho tập hợp số A = ( 3; - ] 4 ; B = [ ;
m m + 2). Có bao nhiêu số nguyên m để AÇ B ¹ Æ ? A. 9. B. 10. C. 8. D. 7.
HSA 02: Một ý nghĩa của khoảng tứ phân vị là
A. Khoảng tứ phân vị của mẫu số liệu ghép nhóm giúp xác định các giá trị không bất
thường của mẫu số liệu đó.
B. Khoảng tứ phân vị thường không được sử dụng thay cho khoảng biến thiên.
C. Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số
liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.
D. Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số
liệu gốc và là một đại lượng cho biết mức độ không phân tán của nửa giữa mẫu số liệu.
HSA 03: Trong không gian Oxyz, cho phương trình 2 2 2
x + y + z + 2mx + 4y +13 = 0. Tìm m để
phương trình đã cho là phương trình mặt cầu. ém ³ 3 ém > 3 A. ê . B. ê . C. 3 - < m < 3. D. 3 - £ m £ 3. m £ 3 - ë m < 3 - ë HSA 04:
Tìm hệ số của số hạng chứa 3
xy trong khai triển ( x - y)4 3 2 . A. 96 - . B. 81. C. 16 . D. 216 - . HSA 05:
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng
được ghi lại ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group A. [9; 1 ) 1 . B. [7; 9). C. [11; 13). D. [13; 15).
HSA 06: Trong dịp nghỉ hè bạn Lan rất thích đi bơi. Thời gian đi bơi mỗi ngày trong thời gian gần
đây của bạn Lan được thống kê lại ở bảng sau: Thời gian (phút) 30 é 35 ë ; ) 35 é 40 ë ; ) é45 50 ë ; ) 50 é 55 ë ; ) 55 é 60 ë ; ) Số ngày 3 6 4 8 4
Nhóm chứa tứ phân vị thứ nhất Q là 1 A. 30 é 35 ë ; ). B. 35 é 40 ë ; ). C. é45 50 ë ; ). D. 50 é 55 ë ; ). HSA 07:
Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x
(1 £ x £ 4) thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và . x Thể tích vật thể là bao nhiêu? ! ! ! !
HSA 08: Trong không gian với hệ tọa độ Oxyz , cho hai véctơ a và b thỏa mãn a = 2 3 , b = 3 và ( ! ! ! !
a,b ) = 30°. Độ dài của véctơ 3a - 2b bằng A. 54 - . B. 6 . C. 9. D. 54 . 3n + a HSA 09: Cho dãy số (u u = a (un)
n ) có số hạng tổng quát n
. Tìm tất cả các giá trị của để 4n +1 là dãy số tăng. A. 3 3 3 3 a = .
B. a < .
C. a ¹ . D. a > . 4 4 4 4 1 æ 2x ö
HSA 10: Cho hàm số f (x) = log , m n (0 ) ;1 m + n = 1 2 ç ÷ và hai số thực thuộc khoảng sao cho . 2 è1- x ø
Tính f (m)+ f (n). A. 1 2 . B. 0 . C. 1. D. . 2 HSA 11:
Cho tứ giác ABCD , trên cạnh AB , CD lấy lần lượt các điểm M , N sao cho !!!!" !!!" !!!" !!!" !!!!" !!!" !!!"
3 AM = 2 AB và 3 DN = 2 DC . Tính vectơ MN theo hai vectơ AD , BC. !!!!" !!!" !!!" !!!!" !!!" !!!" A. 1 1 2 1
MN = AD + BC .
B. MN = AD + BC . 3 3 3 3 !!!!" !!!" !!!" !!!!" !!!" !!!" C. 1 2 1 2
MN = AD - BC.
D. MN = AD + BC . 3 3 3 3 TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group HSA 12:
Khảo sát thời gian sử dụng điện thoại một ngày của học sinh lớp 12A thì được mẫu số liệu ghép nhóm sau:
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên thuộc khoảng nào dưới đây? A. (22;24). B. (20;22). C. (18;20). D. (24;26). HSA 13:
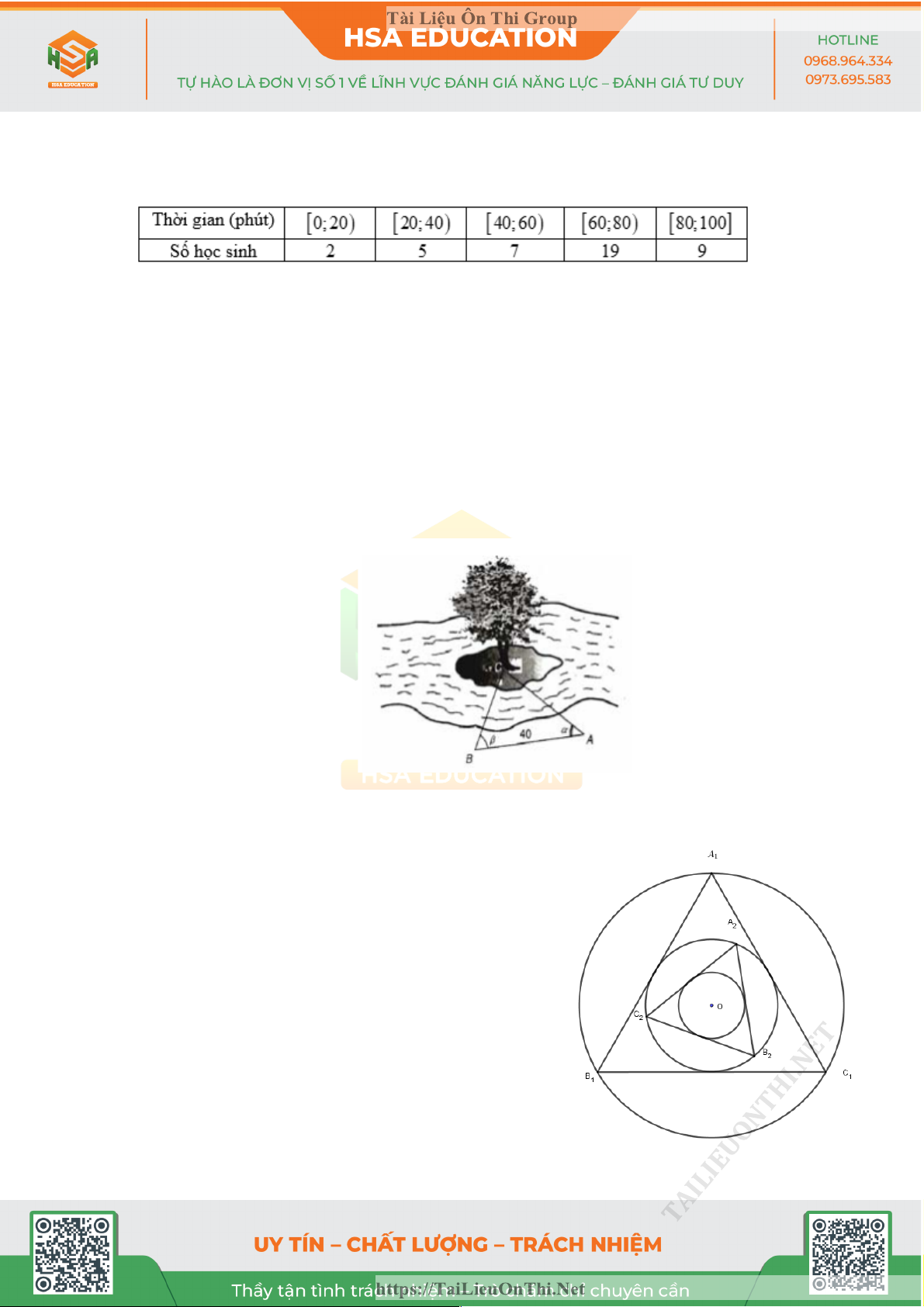
Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông,
người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C .
Ta đo được khoảng cách AB = 40m , ∑ CAB = 45° và ∑
CBA = 70°. Vậy sau khi đo đạc và tính toán ta
được khoảng cách AC bằng bao nhiêu?
A. AC = 41,47.
B. AC = 31,21.
C. AC = 53,16. D. AC = 30,10.
HSA 14: Cho một hình tròn tâm O bán kính là R = 60m .
Dựng tam giác đều A B C
1 1 1 nội tiếp đường tròn, sau đó
lấy đường tròn nội tiếp tam giác A B C
1 1 1 . Cứ tiếp tục làm
quá trình như trên. Diện tích của tam giác A B C 9 9 9 là A. 2 0,285m . B. 2 1,14m . C. 2 0,071m . D. 2 145,92m . TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group
HSA 15: Thống kê cân nặng của học sinh lớp 11A cho trong bảng dưới đây: Cân nặng é40 5 45 5 ë , ; , ) é45 5 50 5 ë , ; , ) 50 é 5 55 5 ë , ; , ) 55 é 5 60 5 ë , ; , ) é60 5 65 5 ë , ; , ) é65 5 70 5 ë , ; , ) Số học sinh 10 7 16 4 2 3
Tính cân nặng trung bình của học sinh lớp 11A? A. 50 1 , . B. 52,83. C. 50,81. D. 51,81.
HSA 16: Cho hình chóp .
S ABC có SA vuông góc với đáy (ABC). H là hình chiếu vuông góc của
A lên BC . Góc phẳng nhị diện éS,BC,Aù là: ë û A. ∑ SAH. B. ∑ SB . A C. ∑ SHA. D. ∑ ASH. !!!" !!!" !!!" !!!!" HSA 17:
Tìm tập các hợp điểm M thỏa mãn MB(MA+ MB + MC) = 0 với ,
A B, C là ba đỉnh của tam giác.
A. một điểm.
B. đoạn thẳng.
C. đường thẳng.
D. đường tròn. HSA 18:
Bác An gửi tiết kiệm 200 triệu đồng ở một ngân hàng với lãi suất không đổi 6,5%
một năm theo thể thức lãi kép kì hạn 12 tháng. Thời gian tối thiểu để bác An thu được ít nhất
350 triệu đồng là A. 10. B. 8 . C. 9. D. 7 .
HSA 19: Giả sử A , B là hai điểm cực trị của đồ thị hàm số ( ) 3 2
f x = x + ax + bx + c và đường thẳng
AB đi qua gốc tọa độ. Tìm giá trị nhỏ nhất của P = abc + ab + c. A. 16 - . B. 25 9 - . C. - . D. 1. 25 9 HSA 20:
Cho hình chóp S.ABC có đáy là tam giác đều, mặt bên SAB là tam giác vuông cân tại
S và nằm trong mặt phẳng vuông góc với đáy. Biết SA = 2a 2 , tính góc giữa SC và mặt phẳng (SAB). A. 60° . B. 90° . C. 30° . D. 45°.
HSA 21: Trong không gian với hệ trục toạ độ cho trước (đơn vị đo lấy theo kilomet), ra đa phát
hiện một máy bay di chuyển với vận tốc và hướng không đổi từ điểm (7
A 50;450;7) đến điểm
B(950;550;9) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ
của máy bay sau 10 phút tiếp theo là gì?
HSA 22: Cho hàm số y = f (x) có đạo hàm trên ! và không có cực trị, đồ thị của hàm số y = f (x)
là đường cong của như hình vẽ dưới đây. TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group
Xét hàm số h(x) 1 = é f ë ( x) 2 ù - 2 . x f û (x) 2
+ 2x . Mệnh đề nào sau đây đúng? 2
A. Đồ thị của hàm số y = h(x) có điểm cực tiểu là M (1;0).
B. Hàm số y = h(x) không có cực trị.
C. Đồ thị hàm số y = h(x) có điểm cực đại là N (1;2).
D. Đồ thị hàm số y = h(x) có điểm cực đại là M (1;0).
HSA 23: Một hình hộp chữ nhật ABCD A¢B¢C¢D¢ × có ba kích thước là 2 ,
cm 3 cm và 6 cm . Tính thể tích của khối tứ diện ACB¢D¢. HSA 24:
Cho hàm số f (x) 3 2 = x - x + ( 2 3
3 m - 2m + 2) x + m ( với
m là tham số) có giá trị lớn nhất trên [ 1 - ; ]
1 bằng 2 , khi đó tổng các giá trị của tham số m là A. 5 . B. 2 . C. 0. D. 7 . 3 3 3 HSA 25:
Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong
một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn
đồng. Chi phí cho n máy chạy trong một giờ là 10(6n +10) nghìn đồng.
Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy in để được lãi nhiều nhất? HSA 26:
Cho mặt cầu (S) (x - )2 +( y - )2 +(z - )2 : 2 1
3 = 9 và hai điểm A(1;1;3), B(21;9;-13).
Điểm M (a;b;c) thuộc mặt cầu (S) sao cho 2 2
3MA + MB đạt giá trị nhỏ nhất. Khi đó giá trị của biểu thức T = . a . b c bằng TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group A. 3. B. 8. C. 18 - . D. 6 .
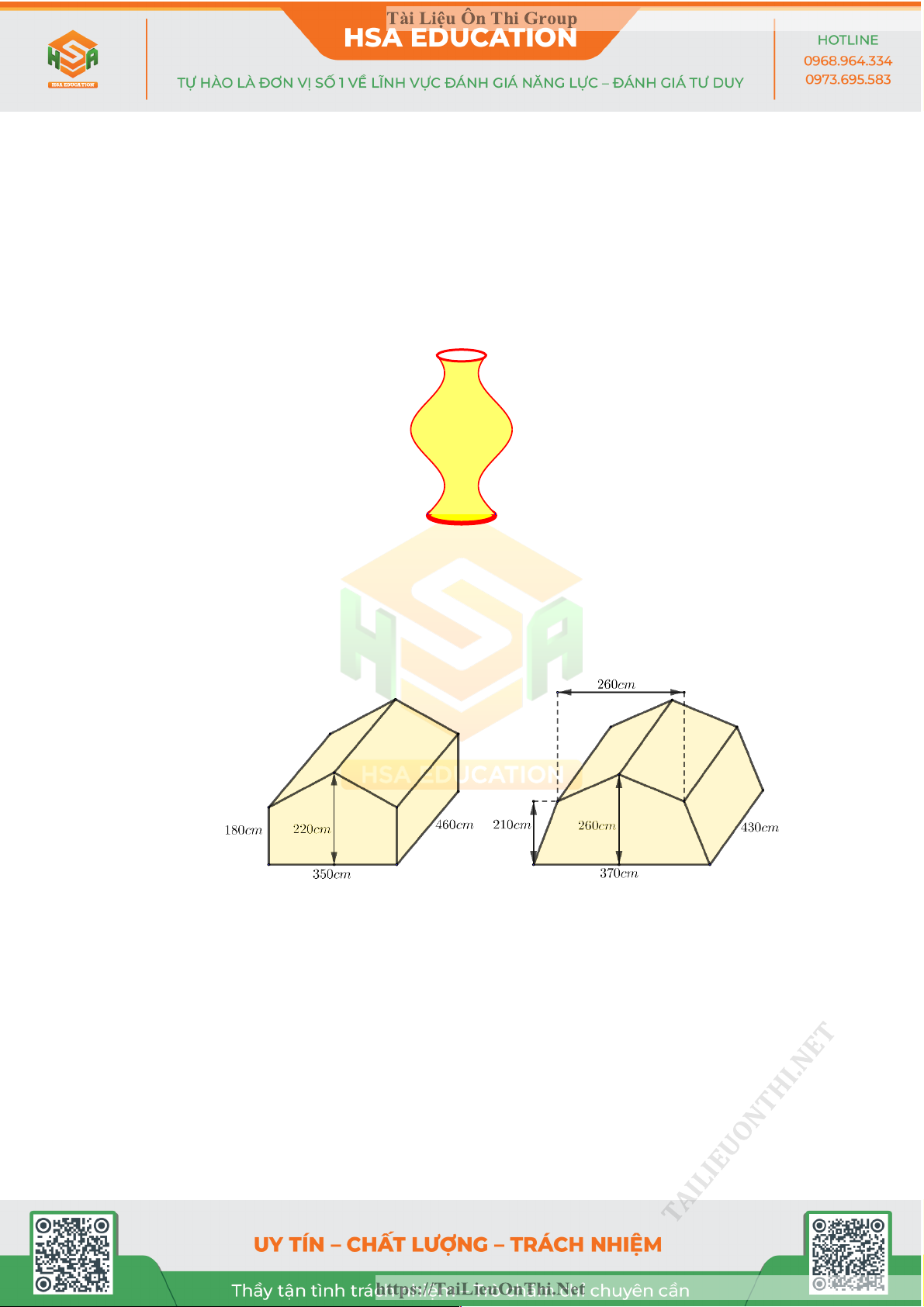
HSA 27: Một bình hoa dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ
thị hàm số y = -sin x + 2 và trục Ox (tham khảo hình vẽ bên dưới). Biết đáy bình hoa là hình tròn
có bán kính bằng 2 dm, miệng bình hoa là đường tròn bán kính bằng 1.5 dm. Bỏ qua độ dày của
bình hoa, Thể tích của bình hoa gần với giá trị nào trong các giá trị sau đây? A. 100 3 dm . B. 104 3 dm . C. 102 3 dm . D. 103 3 dm . HSA 28:
Số 253125000 có bao nhiêu ước số tự nhiên? A. 240 . B. 120. C. 160. D. 180. HSA 29:
Để chuẩn bị cho hoạt động cắm trại, bạn An tìm hiểu các mẫu lều cắm trại có kích thước như hình vẽ.
Bạn An muốn biết thể tích chênh lệch của hai lều nên thực hiện tính V - V V V 1 2 , trong đó 1 , 2 lần
lượt là thể tích của mẫu lều cắm trại ở hình trái & phải. Giá trị của V - V bằng bao nhiêu decimét 1 2
khối (làm tròn kết quả đến hàng đơn vị)? A.961 B.960. C.962. D.691. HSA 30:
Một xưởng sản xuất có hai máy, sản xuất ra hai loại sản phẩm I và II . Một tấn sản phẩm loại I lãi 2
triệu đồng, một tấn sản phẩm loại II lãi 1, 6 triệu đồng. Để sản xuất một tấn sản phẩm loại I cần máy thứ nhất
làm việc trong 3 giờ, máy thứ hai làm việc trong 1giờ. Để sản xuất một tấn sản phẩm loại II cần máy thứ nhất làm
việc trong 1giờ, máy thứ hai làm việc trong 1giờ. Một ngày máy thứ nhất làm việc không quá 6 giờ, máy thứ hai
làm việc không quá 4 giờ. Hỏi một ngày Nền lãi lớn nhất là bao nhiêu? TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group A. 9,6triệu.
B. 6, 4 triệu. C. 10triệu. D. 6,8triệu.
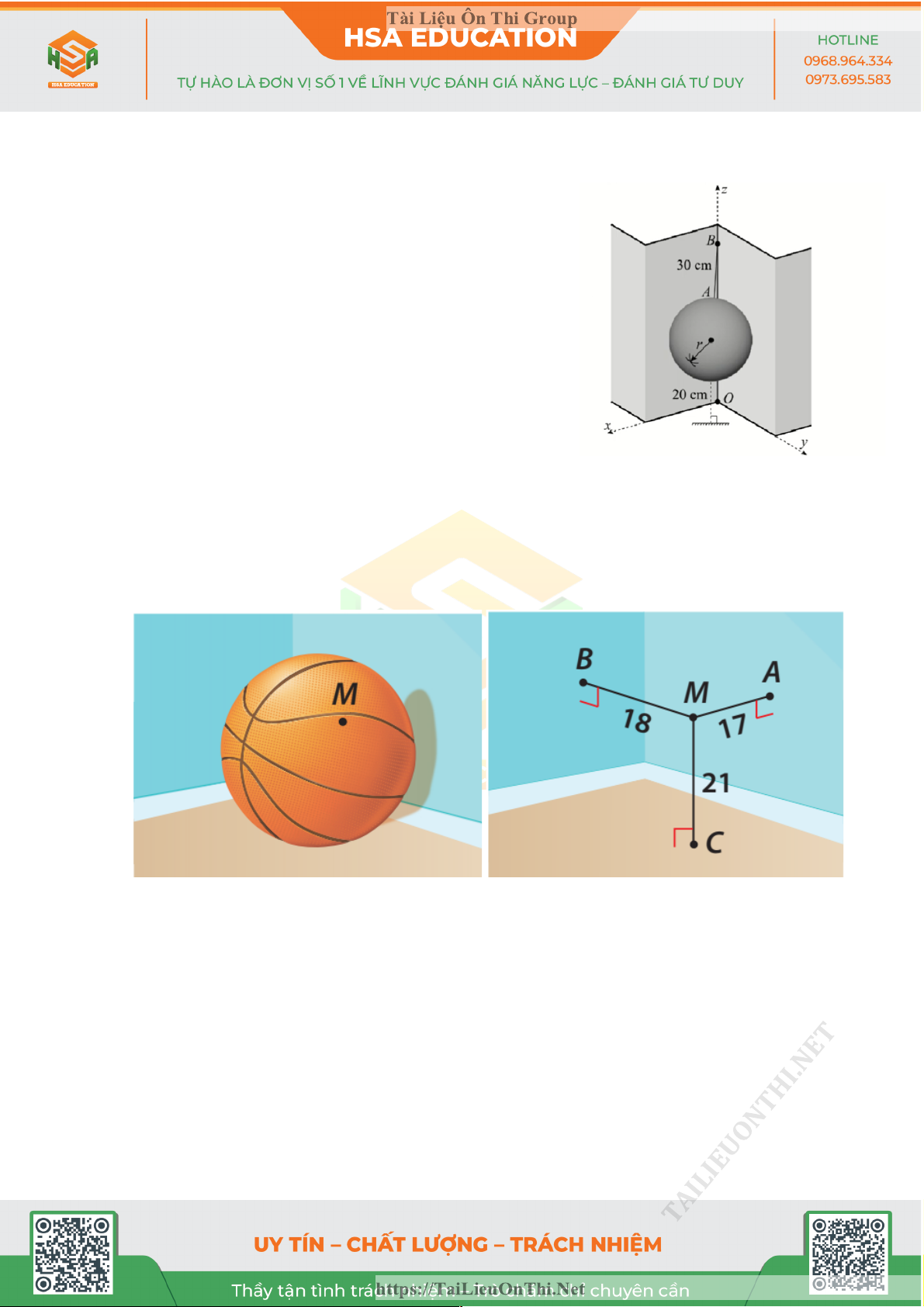
HSA 31: Một quả bóng hình cầu có bán kính r đang được treo
trong một góc của tường nhà (hai bờ tường vuông góc),
một điểm B cố định nằm trên mép của hai bờ tường và
cách mặt đất 80 cm, sợi dây treo bóng có độ dài AB = 30 cm
và đây cũng là độ dài ngắn nhất nối điểm B với mặt xung
quanh của quả bóng. Biết rằng quả bóng tiếp xúc với hai
bên bờ tường và điềm thấp nhất của quả bóng cách mặt đất
20 cm. Hỏi đường kính của quả bóng là bao nhiêu centimet
(làm tròn kết quả đến hàng đơn vị).
TỰ LUYỆN THÊM Bạn Bình đố bạn Nam tìm được đường
kính của quả bóng rổ, biết rằng nếu đặt quả bóng ở một góc căn phòng hình hộp chữ nhật, sao
cho quả bóng chạm với hai bức tường và nền nhà của căn phòng đó thì có một điểm M trên quả
bóng với khoảng cách đến hai bức tường và nền nhà lần lượt là 17 cm, 18 cm, 21cm. Bán kính
quả bóng bằng bao nhiêu biết loại bóng tiêu chuẩn có đường kính nằm trong khoảng từ 23cm đến 24,5 cm HSA 32:
Tìm số nguyên dương n sao cho 1 2 2 3 C - 2.2.C +3.2 C -. .+ n + C + = n+ n+ n+ (2 ) 2n 2n 1 1 2 2019 2 1 2 1 2 1 2n 1 +
A. n =1008.
B. n =1009 .
C. n =1119 .
D. n =107 .
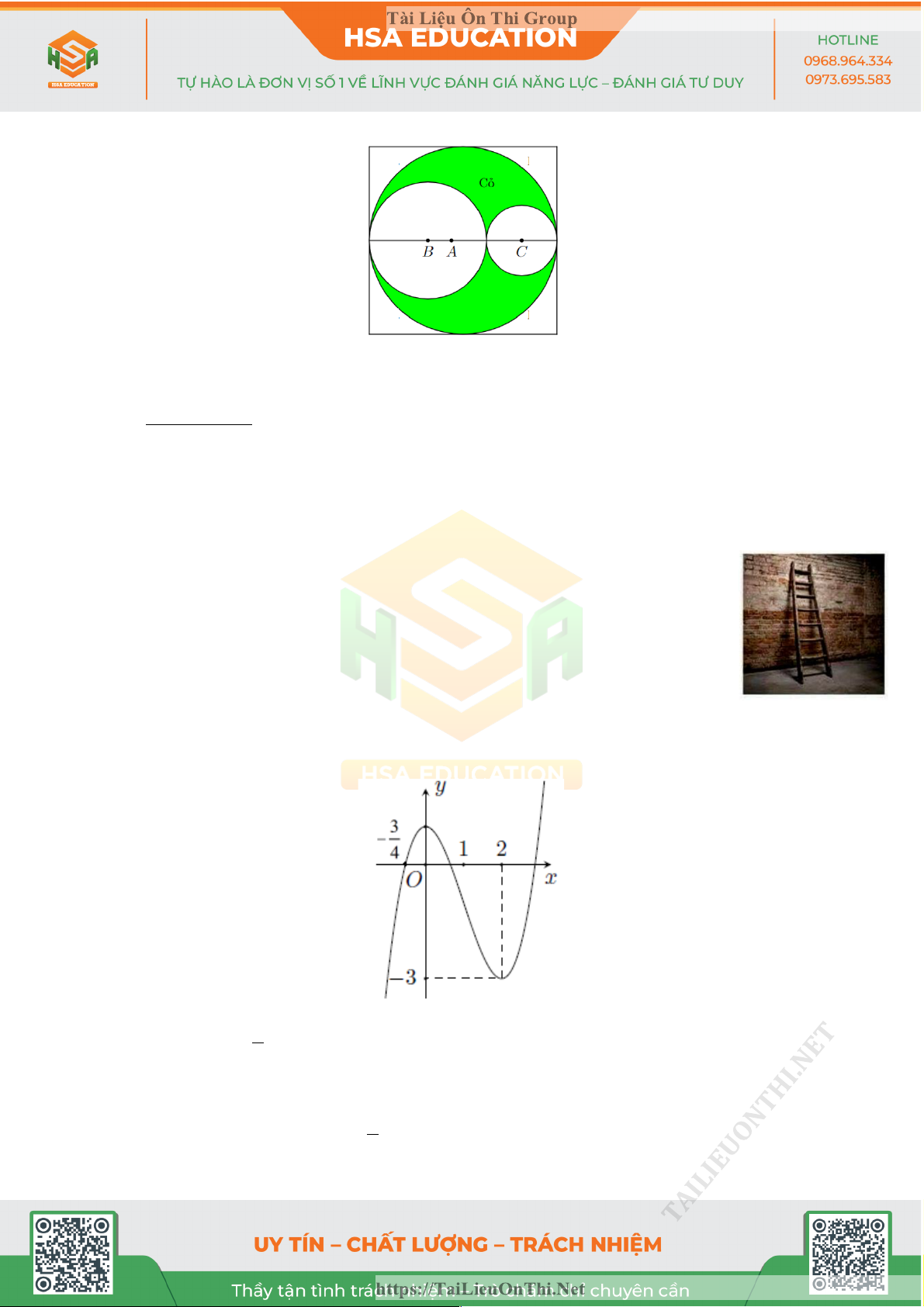
HSA 33: Ông Bình có một khu vườn hình vuông diện tích 2
100m . Ông muốn chia làm 3 phần,
phần hai đường tròn tâm B và C dùng trồng hoa, phần tô đậm dùng để trồng cỏ, phần còn
lại lát gạch . Biết mỗi mét vuông trồng cỏ chi phí 100 nghìn đồng, mỗi mét vuông trồng hoa
chi phí 1 triệu đồng, mỗi mét vuông lát gạch chi phí 300 nghìn đồng. Khi diện tích phần trồng
hoa là nhỏ nhất thì tổng chi phí thi công vườn bằng........., TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group
HSA 34: Cho hàm số F ( x) , biết F ( )
1 = 4 và F ( x) là một nguyên hàm của hàm + +
f ( x) ( x ) 1 ln x 2 =
. Tính giá trị F (e) . 1 + x ln x
A. ln(1+ e) + 2 + e .
B. ln(1+ e) + 3+ e.
C. 2ln(1+ e) +1.
D. ln(2 + e) + 3+ e. HSA 35:
Một chiếc thang dài 9 mét tựa vào một bức tường thẳng đứng trên
một mặt đất bằng phẳng. Khi đầu dưới của thang di chuyển (trên mặt đất) ra
xa bức tường với vận tốc không đổi là 2 (m/s) thì đầu trên cùng của thang sẽ
trượt xuống dọc theo bức tường. Khi điểm đầu thang cách mặt đất 3 mét thì
tốc độ di chuyển của nó bằng bao nhiêu? (đơn vị: (m/s) và kết quả làm tròn đến hàng phần trăm) HSA 36:
Cho hàm số f (x) 3 2
= ax + 3bx - 2cx + d ( a, , b ,
c d là các hằng số, a ¹ 0 ) có đồ thị như hình vẽ.
Hàm số g (x) a 4
= x + (a +b) 3
x + ( b - c) 2 3
x + (d - 2c) x + d - 2019 nghịch biến trên khoảng 4 nào sau đây? A. ( æ 3 ö ;0 -¥ ). B. - ;0 . ç ÷ C. (1;2). D. (2;+¥). è 4 ø TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group x y - 3 z - 2
HSA 37: Trong không gian Oxyz , cho đường thẳng d : = =
và mặt phẳng (P) : 2 1 3 -
x - y + 2z - 6 = 0 . Đường thẳng nằm trong mặt phẳng (P) , cắt và vuông góc với d có phương trình là
A. x + 2 y - 2 z - 5 - - + = = .
B. x 2 y 4 z 1 = = . 1 7 3 1 7 3
C. x - 2 y + 2 z + 5 + + - = = .
D. x 2 y 4 z 1 = = . 1 7 3 1 7 3
HSA 38: Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(11;4;0) và !
chuyển động đều theo đường cáp có véc tơ chỉ phương u = ( 3 - ; 4
- ;0) với tốc độ là 5m / s (Đơn
vị trên mỗi trục tọa độ là mét); giả sử sau t(s) kể từ lúc xuất phát (t ³ 0), cabin đến điểm M ;
Một người đứng tại điểm O quan sát cabin chạy trên cáp treo, sau thời gian bao nhiêu thì
khoảng cách giữa người quan sát và cabin gần nhau nhất? HSA 39:
Một nhóm các kỹ sư muốn xây dựng một cây cầu vòm dàn thép với giá
đỡ dưới bằng thép cao cấp có hình dáng là một đường cong Parabol nối từ 2 cột trụ A và B nằm
bên dưới cây cầu, biết hai cột trụ cách nhau 400 m, khoảng cách từ trụ A đến cây cầu là 50 m và
AB song song với mặt đường.
Gắn hệ trục tọa độ Oxy vào cây cầu với đơn vị trục tọa độ là 10 m. Giá đỡ dưới bằng thép
là đường cong Parabol tạo với 2 trục tọa độ các hình phẳng có diện tích S ,S như hình vẽ 1 2 bên, biết rằng 2200 S - 2S =
. Điểm cao nhất của giá đỡ dưới bằng thép cao cấp cách mặt 2 1 21
đường cây cầu bao nhiêu mét (làm tròn đến hàng phần mười) TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group A. 63,4. B. 64,3. C. 64,2 D. 46,3
HSA 40: Một khu vườn hình vuông được chia làm hai mảnh đất để trồng hoa
màu khác nhau. Mảnh đất hình tròn được người ta sử dụng để trồng rau
còn mảnh đất hình parabol để trồng ngô. Minh họa trong hệ trục tọa độ
Oxy với các ô lưới hình vuông như nhau và kích thước của ô lưới hình
vuông là 1(m) x 1(m) tương ứng với một đơn vị trên hệ trục tọa độ. Người
ta muốn tạo một lối đi để di chuyển qua lại giữa hai mảnh đất này (minh
họa hình vẽ dưới đây). Tính độ dài ngắn nhất của lối đi này (Kết quả làm
tròn đến chữ số thập phân thứ hai sau dấu phẩy) HSA 41:
Một hộp bút bi Thiên Long có 15 chiếc bút trong đó có 9 chiếc bút mới. Người ta lấy
ngẫu nhiên 1 chiếc bút để sử dụng sau đó trả lại vào hộp. Lần thứ hai lấy ngẫu nhiên 2 chiếc
bút, tính xác suất cả hai chiếc bút lấy ra đều là chiếc mới. A. 52 . B. 52 . C. 53 . D. 25 . 175 177 175 175 x - 2 y +1 z
HSA 42: Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d : = = 1 và 1 2 1 x y - 3 z d : =
= . (P) là mặt phẳng chứa d d 1 và tạo với
2 một góc lớn nhất. Phương trình mặt 2 2 2 - 1 phẳng (P) là
A. 13x -10y + 7z + 36 = 0 .
B. 13x -10y + 7z -36 = 0.
C. 13x +10y + 7z - 36 = 0 .
D. -13x -10y + 7z + 36 = 0.
HSA 43: Giả sử tăng cân nặng ( tính bằng kg ) của một giống vật nuôi ( trong vòng một số tháng
nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số f (t) 150 = , t ³ 0 1+ 3 t e-
Trong đó thời gian t được tính bằng tháng kể từ khi vật nuôi đó bắt đầu sinh ra. Khi đó đạo hàm
f ¢(t) sẽ biểu thị tốc độ tăng cân nặng của loài cây đó. Hỏi sau khi vật nuôi sinh ra thì sau bao
nhiêu tháng tốc độ tăng cân nặng của vật nuôi là nhanh nhất? HSA 44:
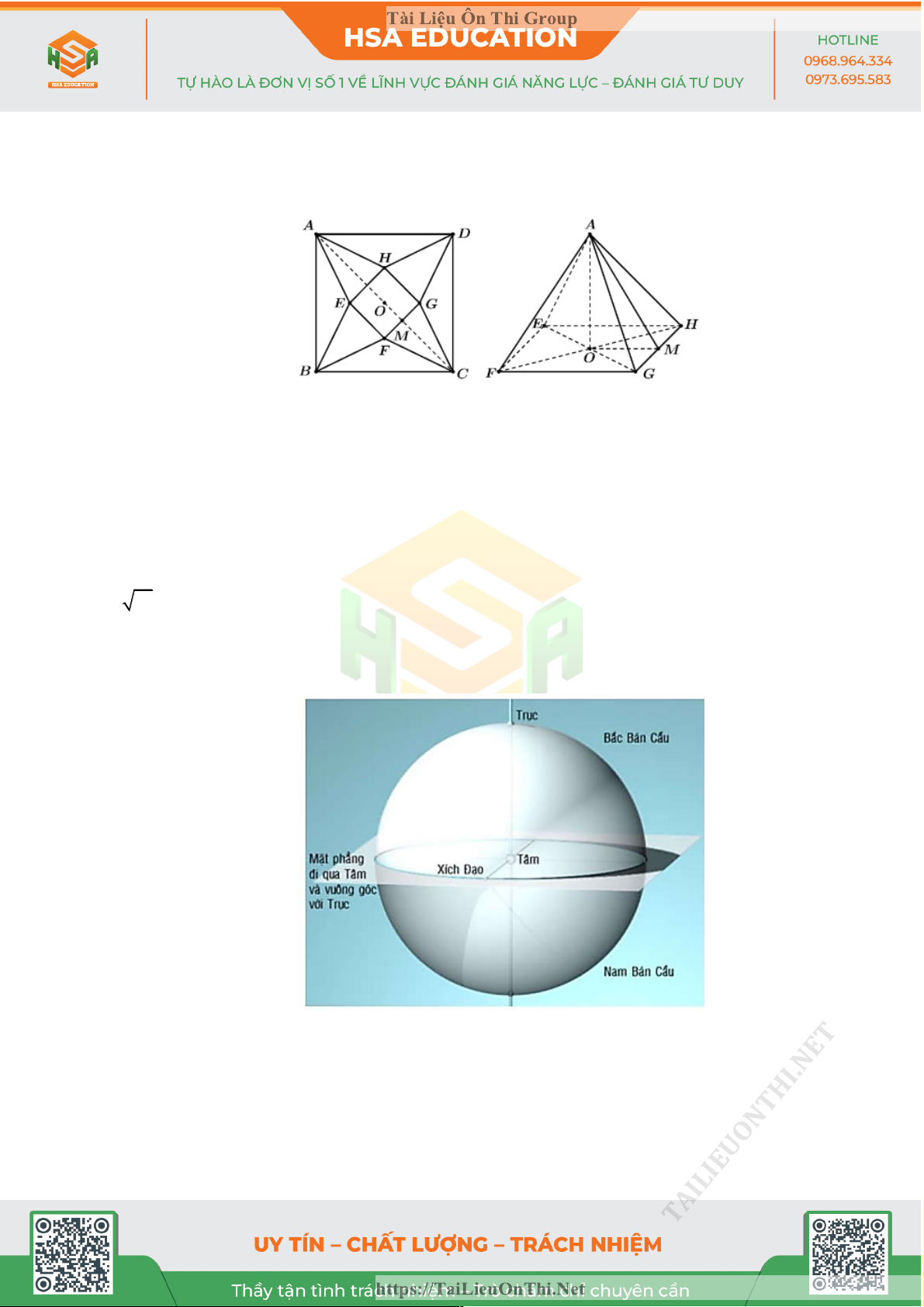
Trong tiết học Toán, giáo viên phát cho 4 tổ, mỗi tổ một tấm bìa hình vuông ABCD
cạnh bằng 10 cm . Giáo viên yêu cầu mỗi tổ cắt tấm bìa theo tam giác cân , AEB BFC,CG , D DHA
. Sau đó gấp các tam giác AEH, BEF,CFG, DGH sao cho bốn đỉnh ABCD trùng nhau tạo thành a b
khối chóp tứ giác đều. Khi đó thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng c
với a,b,c là các số nguyên dương. Tính P = a + b + c . TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group A.45 B.54. C.60. D.15.
HSA 45: Một người săn thỏ trong rừng, khả năng anh ta bắn trúng thỏ trong mỗi lần bắn tỷ lệ
nghịch với khoảng cách bắn. Anh ta bắn lần đầu ở khoảng cách 20m với xác suất trúng thỏ là
0,5; nếu bị trượt anh ta bắn viên thứ hai ở khoảng cách 30m ; nếu lại trượt anh ta bắn viên thứ
ba ở khoảng cách 40m. Tính xác suất để người thợ săn bắn được thỏ. HSA 46:
Bán kính Trái Đất lấy bằng 6400 km, khi gắn hệ trục toạ độ Oxyz thì bề mặt Trái Đất
là mặt cầu có phương trình 2 2 2
x + y + z = 64, đường xích đạo nằm trên mặt phẳng (Oxy). Một tàu
vũ trụ X rời khỏi bề mặt Trái Đất theo phương tiếp tuyến với đường tròn vĩ tuyến tại điểm (
A 6; 19;3) , với giả thiết rằng sau khi rời khỏi bề mặt Trái Đất tàu vũ trụ X bay theo quỹ đạo
thẳng với tốc độ không đổi bằng 7,9 km / s. Hỏi sau đúng 15 phút kể từ khi rời khỏi bề mặt Trái
Đất thì khoảng cách từ tàu vũ trụ đến một điểm trên đường tròn xích đạo ngắn nhất bằng bao
nhiêu kilomet (làm tròn kết quả đến hàng đơn vị) ?
HSA 47: Bé Minh có hộp màu gồm 6 màu khác nhau. Bé Minh mang hộp màu có 6 màu khác nhau
đó đi tô màu các cạnh của hình vuông ABCD sao cho mỗi cạnh được tô bởi một màu và hai
cạnh kề nhau thì tô bởi hai màu khác nhau. Hỏi bé Minh có bao nhiêu cách tô hình vuông ABCD A. 360. B. 480 . C. 600 . D. 630 . TAILIEUONTHI.NET https://TaiLieuOnThi.Net Tài Liệu Ôn Thi Group HSA 48:
Trong không gian Oxyz , cho điểm M (1;2;3). Mặt phẳng (P): x + Ay + Bz + C = 0 chứa
trục Oz và cách điểm M một khoảng lớn nhất, khi đó tính tổng A + B + C . 3 2 x x 16
HSA 49: Cho hàm số y = f (x) = (m + ) 1 + (m -5m- 4) - (x+ )3 2 1 - ( 2
3m - 6m -19) x + 2019. 3 2 3
Tổng tất cả các giá trị của tham số thực m để hàm số đồng biến trên nửa khoảng [ 1 - ;+¥) là A. 3 - . B. 3. C. 1 - . D. 1. HSA 50:
Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ có cạnh bằng a . Gọi K là trung điểm của DD¢
. Tính khoảng cách giữa hai đường thẳng CK , A¢D . A. 3a . B. 2a a a . C. . D. . 8 5 3 . TAILIEUONTHI.NET https://TaiLieuOnThi.Net