

Preview text:
PHÒNG GD&ĐT TAM DƯƠNG
GIAO LƯU HỌC SINH GIỎI CẤP HUYỆN NĂM HỌC 2017-2018 ĐỀ THI MÔN: TOÁN 7 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Đề thi này gồm 01 trang
Thí sinh không được sử dụng máy tính cầm tay! 4 2 10 .8116.15
Câu 1. (2,0 điểm) Rút gọn biểu thức sau: A 4 4 .675 x y z
Câu 2. (2,0 điểm) Tìm ba số x, y, z thỏa mãn: và 2 2 x 2 2 y 3 2 z 100 . 3 4 5
Câu 3. (2,0 điểm) Cho các số x, y thỏa mãn (x - 2)4 + (2y - 1)2018 0 .
Tính giá trị của biểu thức M = 11x2y + 4xy2.
Câu 4. (2,0 điểm) Cho các số thực a, b, c, d thỏa mãn dãy tỉ số bằng nhau: 2a b c d a b 2 c d a b 2c d a b c 2d a b c d a b b c c d d a
Tính giá trị của biểu thức: M c d d a a b b c
Câu 5. (2,0 điểm) Cho đa thức bậc hai: 2
f x ax bx c (x là ẩn; a, b, c là hệ số).
Biết rằng: f 0 2018 , f 1 2019 , f
1 2017 . Tính f 2019. 27 2x
Câu 6. (2,0 điểm) Tìm giá trị lớn nhất của biểu thức Q = (với x là số nguyên). 12 x
Câu 7. (2,0 điểm) Tìm các số nguyên dương a, b, c thoả mãn a3+ 3a2 +5 = 5b và a + 3 = 5c
Câu 8. (2,0 điểm) Cho góc xOy bằng 600. Tia Oz là phân giác của góc xOy. Từ điểm B bất kì trên
tia Ox kẻ BH, BK lần lượt vuông góc với Oy, Oz tại H và K. Qua B kẻ đường song song với Oy cắt
Oz tại M. Chứng minh rằng BH=MK.
Câu 9. (2,0 điểm) Cho tam giác ABC vuông cân tại A. Điểm M nằm bên trong tam giác sao cho MA=2cm, MB=3cm và 0 AMC 135 . Tính MC.
Câu 10. (2,0 điểm) Từ 200 số tự nhiên 1; 2; 3;...; 200, ta lấy ra k số bất kì sao cho trong các số vừa
lấy luôn tìm được 2 số mà số này là bội của số kia. Tìm giá trị nhỏ nhất của k.
-------------HẾT------------
Cán bộ coi thi không giải thích gì thêm!
Họ và tên thí sinh: .................................... Số báo danh: ...............Phòng thi: ....... PHÒNG GD&ĐT TAM DƯƠNG
HƯỚNG DẪN CHẤM GIAO LƯU CHỌN HSG Năm học: 2017 – 2018 Môn Toán – Lớp 7 Hướng dẫn chung:
-Học sinh giải theo cách khác mà đúng, đảm bảo tính lôgic, khoa học thì giám khảo vẫn cho điểm tối đa.
-Câu hình học, học sinh không vẽ hình hoặc vẽ hình sai phần nào không chấm điểm phần đó. Câu Nội dung Điểm 4 2 10 .8116.15 4 4 4 4 2 2 A 2 5 . 3 . 2 .3 5 . = 4 4 .675 8 3 2 2 .3 5 . 0,5 4 2 2 2 2 2 3 . .5 5 ( .3 ) 1 225 1 1 = = 0,5 8 3 2 2 3 . 5 . 4 2 .3 224 25.7 = = = 14 0,5 4 2 .3 24.3 3 0,5 x y z 2 2 2 x y z 2 2 x 2 2 y 3 2 z 2 2 x 2 2 y 3 2 z 100 0,5 Từ ta suy ra: 4 3 4 5 9 16 25 18 32 75 25 25 0,5 x 6 y 2 8 x 36 2 x 2 10 Suy ra: y 64 ( Vì x, y, z cùng dấu) x 6 0,5 2 z 100 y 8 z 10
KL: Có hai bộ (x; y; z) thỏa mãn là : (6; 8 ;10) và (-6; -8;-10) 0,5
Vì (x - 2)4 0; (2y – 1) 2018 0 với mọi x, y nên 0,25
(x - 2)4 + (2y – 1) 2014 0 với mọi x, y. 0,25
Mà theo đề bài : (x - 2)4 + (2y – 1) 2014 0
Suy ra (x - 2)4 + (2y – 1) 2014 = 0 0,25 3
Hay: (x - 2)4 = 0 và (2y – 1) 2018 = 0 0,25 suy ra x = 2, y = 1 0,25 2 0,25
Khi đó tính được: M = 24. 0,5 2a b c d a b 2 c d a b 2c d a b c 2d Từ: a b c d 2a b c d a 2b c d a b 2c d a b c 2d Suy ra : 1 1 1 1 0,25 a b c d a b c d a b c d a b c d a b c d (*) 0,5 4 a b c d
Nếu a + b + c + d = 0 a + b = -(c+d) ; (b + c) = -(a + d) a b b c c d d a 0,25 M = -4 c d d a a b b c 0,25
Nếu a + b + c + d 0 thì từ (*) a = b = c = d 0,25 a b b c c d d a M = 4 c d d a a b b c 0,25 KL: ...... 0,25
Xét x =0: f (0) 2018 c 2018 0,25
Xét x =1: f (1) 2019 a b c 2018 a b 1 (1) 0,25
Xét x =-1: f (1) 2017 a b c 2017 a b 1 (2) 0,25 5
Cộng vế (1) và (2) suy ra a=0
Thay a=0 vào (1) tìm được: b=1 0,25 0,25
Từ đó tìm được f x x 2018 0,25
Suy ra: f 2019 1 0,5 27 2x 3 Ta có: Q = = 2+ . 0,25 12 x 12 x 3 0,25 Suy ra Q lớn nhất khi lớn nhất 12 x 3 0,25
* Nếu x > 12 thì 12 x 0 0 . 12 x 3 0,25
* Nếu x < 12 thì 12 x 0 0 . 6 12 x 3
Từ 2 trường hợp trên suy ra lớn nhất khi 12-x>0 12 x 0,25 3 Vì phân số
có tử và mẫu là các số nguyên dương, tử không đổi nên phân số có 12 x
giá trị lớn nhất khi mẫu là số nguyên dương nhỏ nhất. 0,25 Hay 12 x 1 x 11
Suy ra A có giá trị lớn nhất là 5 khi x =11 0,25 0,25
Do a Z+ 5b = a3 + 3a2 + 5 > a + 3 = 5c 0,25
Vậy 5b > 5c b>c 5b 5c 0,25 Hay (a3 + 3a2 + 5) (a+3) a2 (a+3) + 5 a + 3 0,25
Mà a2 (a+3) a + 3 5 a + 3 a + 3 Ư (5) 7 0,25
Hay: a+ 3 { 1 ; 5 } (1)
Do a Z+ a + 3 4 (2) 0,25
Từ (1) và (2) suy ra a + 3 = 5 a =2 0,25
Từ đó tính được: 5b =23 + 3.22 + 5 = 25 = 52 b = 2
Và 5c =a + 3 = 2+3= 5 c = 1 0,25 0,25 Vậy: a = 2; b = 2; c = 1
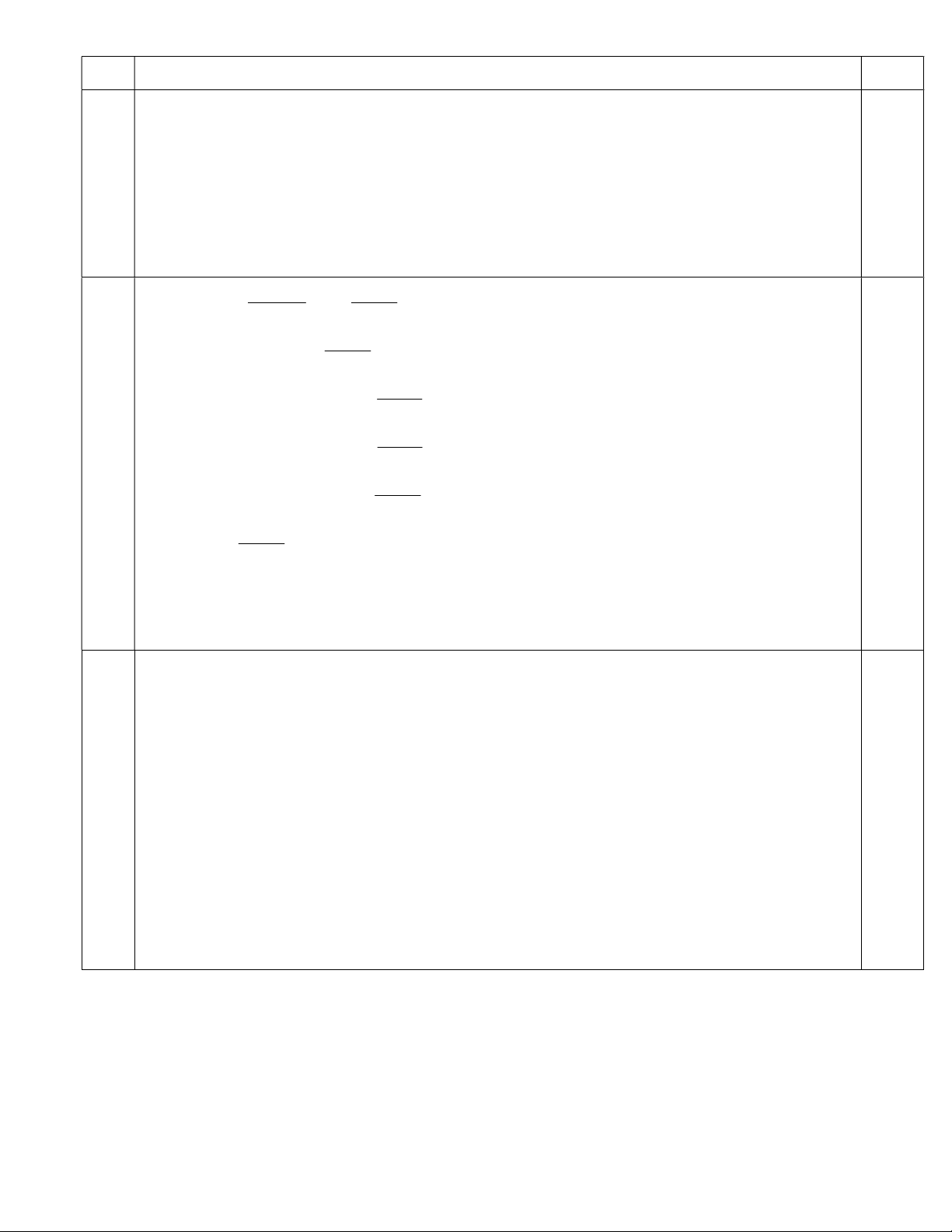
- Chứng minh tam giác BOM cân tại B vì x BOM 0 BMO 30
- BK là đường cao của tam giác cân BMO 0,5
nên K là trung điểm của OM =>KM=KO (1) 0,5 B - Chứng minh BKO O HB (c.h g.n) z 8 0,5 M - Suy ra BH=OK (2) K 0,25
- Từ (1) và (2) suy ra BH=MK. đpcm O H 0,25 y
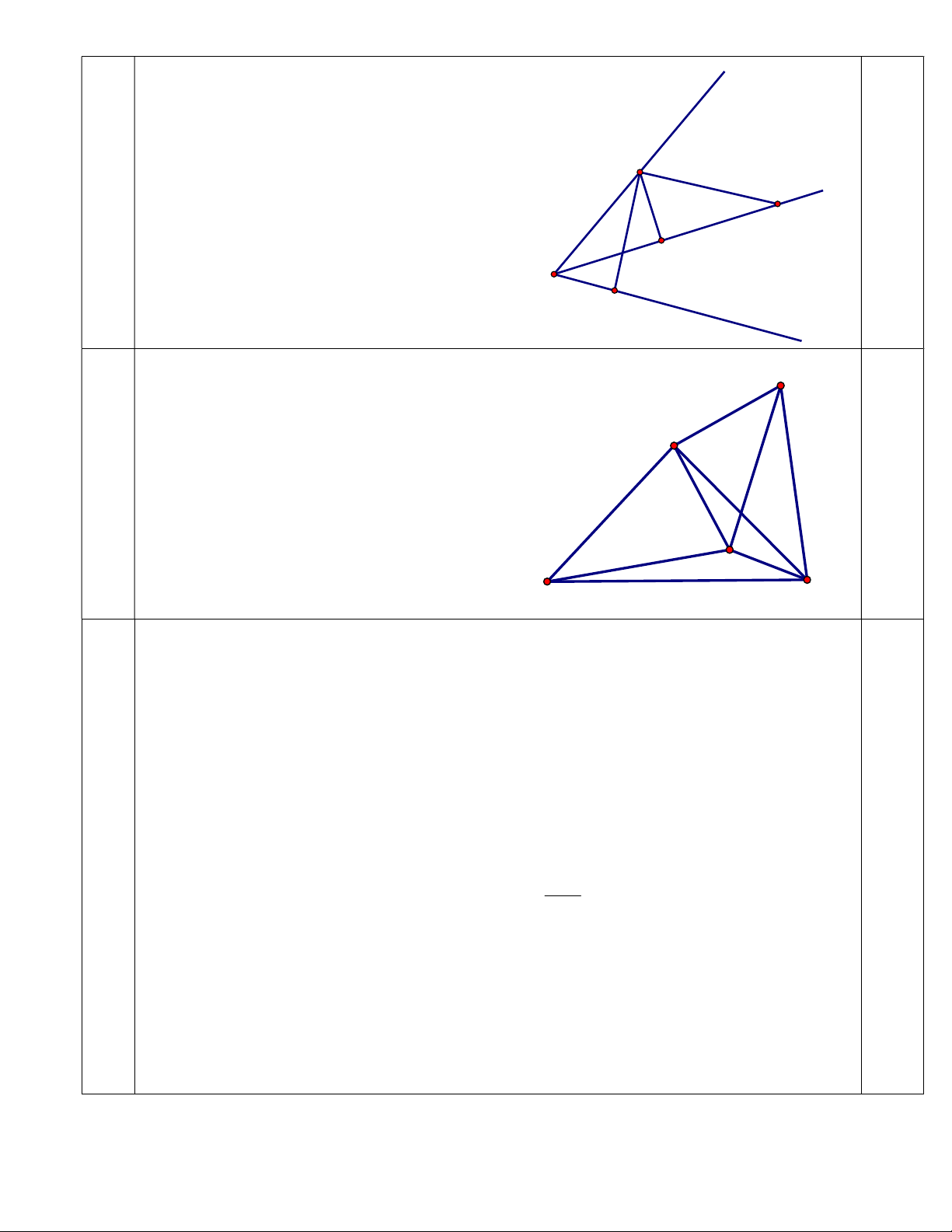
- Dựng tam giác ADM vuông cân tại A D 0,25
(D, B khác phía đối với AM) - Chứng minh ABM A CD (c.g.c) vì:
AD=AM ( AMD vuông cân tại A) A BAM CAD (cùng phụ với CAM 0,5 9 AB=AC (giả thiết) - Suy ra: CD=BM=3cm 0,25
- Tính được MD2=AD2+AM2 = 8 0,25
- Chỉ ra tam giác DMC vuông tại M 0,25 M
- Suy ra: MC2 = CD2-MD2 =9-8=1 B 0,25 C =>CD=1cm 0,25
- Xét 100 số 101; 102; 103; ....; 200. Trong 100 số này rõ ràng không có số nào là bội 0,25
của số kia (vì 101.2>200). Do đó k 101 (1) 0,25
- Xét 101 số bất kì lấy ra từ 200 số đã cho: 1 a a a ... a 200 . 1 2 3 101 0,25
Ta viết 101 số vừa lấy ra dưới dạng: 1 a 2n .b 1 1 2 a 2n .b 2 2 3 a 2n .b 3 3 ........... 10 1 n 01 a 2 .b 101 101 Với n 0,25
i là số tự nhiên, còn bi là các các số lẻ. ( i 1;101 )
Suy ra các bi là các phần tử của tập gồm 100 số tự nhiên lẻ đầu tiên: {1; 3; 5; ...;199}.
Vì có 101 các số bi mà chỉ có 100 giá trị nên sẽ tồn tại ít nhất 2 số bi và bj nào đó bằng 0,25 nhau. Suy ra trong hai số a 2 n i
n .b và a 2 j.b sẽ có một số là bội của số còn lại. i i j j 0,25
Như vậy nếu lấy ra 101 số trong 200 số đã cho thì luôn có 2 số mà số này là bội của số kia (2) 0,25
Từ (1) và (2) suy ra giá trị nhỏ nhất của k là 101. 0,25 ----------Hết---------




