Đề giao lưu Toán vào 10 lần 2 năm 2023 trường THPT Quảng Xương 1 – Thanh Hoá

`
GIAO LƯU KIẾN THỨC TUYỂN SINH VÀO 10 NĂM HỌC 2022 - 2023 MÔN: TOÁN
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
(Đề có 5 câu , gồm 01 trang)
Họ tên thí sinh…………………….…………………………… SBD……………………Phòng ……………    
Câu I( 2đ): Cho biểu thức 4 a 1 1 2 K =  +  : −  với 1
a > 0;a ≠ .  2 a −1 a − 2a  
  2 a +1 1− 4a  4
1. Rút gọn biểu thức K
2. Tìm các giá trị của a sao cho K < 0 Câu II(2đ):
1. Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d) có phương trình y = ax + b ( a,b là tham số)
tìm a,b để (d) có hệ số góc bằng 3 và cắt đường thẳng (∆) : y = 2x + 3 tại điểm có tung độ bằng 5 2x + y = 3
2. Giải hệ phương trình:  x − 3y = 5 Câu III(2đ):
1. Giải phương trình : 2 x + 5x + 6 = 0
2. Tìm tất các giá trị của tham số m để phương trình 2 2
x − 2x − m − 2m −1 = 0
có hai nghiệm phân biệt x , x thỏa mãn điều kiện 2 2
2x − x − x x −8 = 0 1 2 1 2 1 2
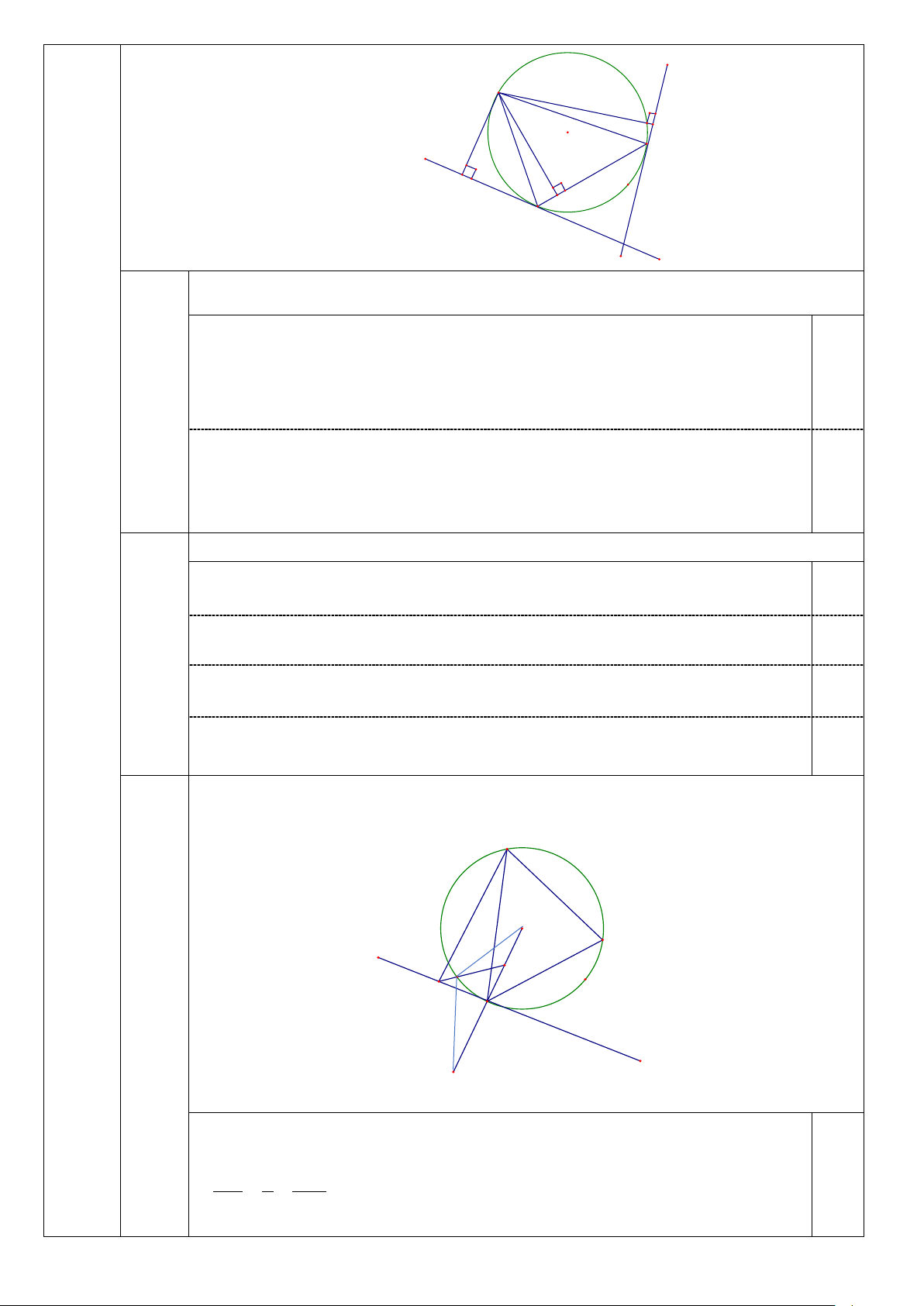
Câu IV(3đ): Cho tam giác ABC có góc 
BAC nhọn,đường cao AH (H ∈ BC) nội tiếp trong đường tròn
(O) bán kính R ,gọi I và K lần lượt là hình chiếu của A lên các tiếp tuyến của (O) tại B vàC
1. Chứng minh tứ giác AIBH và tứ giác AHCK nội tiếp 2. Cho  0
BAC = 35 .Tính góc  IAK
3. Lấy điểm M trên tia OB sao cho OM = 2R . Tìm vị trí điểm N trên (O) sao cho
2NI + NM đạt giá trị nhỏ nhất
Câu V(1đ): Cho a , b , c là các số dương thỏa mãn a +b + c + 2 = abc
Tìm giá trị lớn nhất của biểu thức 1 1 1 P = + + ab bc ca
------------------------------------ Hết -------------------------------------
Lưu ý - Quét mã QR trên phiếu dự thi để xem kết quả (ngày 09/05/2023)
HƯỚNG DẪN CHẤM ĐỀ THI VÀO LỚP 10 Môn thi: TOÁN
(Hướng dẫn chấm gồm 04 trang) Hướng dẫn chung:
1) Nếu học sinh giải cách khác với cách nêu trong HDC này, mà đúng, thì vẫn được điểm tối đa của
phần (câu) tương ứng.
2) Trong câu hình, nếu học sinh không vẽ hình hoặc vẽ sai cơ bản thì không cho điểm câu đó. Câu Ý NỘI DUNG Điểm     Cho biểu thức 4 a 1 1 2 K =  +  : −  với 1
a > 0;a ≠ .  2 a −1 a − 2a  
  2 a +1 1− 4a  4
1. Rút gọn biểu thức K .
2. Tìm các giá trị của a sao cho K < 0 . Rút gọn biểu thức K: 1
a > 0;a ≠ . 4     4 a 1 1 2 K =  −  : + 
 2 a −1 2a − a  
  2 a +1 4a −1 0,25 1     (1,0đ) 4 a 1 1 2 K     = − +  a − a (2 a − ) : 2 1
1   2 a +1 (2 a + )1(2 a −    )1 I  (2,0đ)  4a −1   2 a +1  K     =  0,25 a ( a ) : 2
1   (2 a )1(2 a )1  − + −      4a 1  − 4a −1   = − =  0,25 a  ( a ) .(2 a )1 2 1  − a  Vậy : 4a −1 K = ,với điều kiện 1
a > 0;a ≠ . a 4 0,25
Tìm các giá trị của a sao cho K < 0. 4a −1 1 2 K < 0 ⇔
< 0 ⇒ 4a −1< 0 ⇔ a < 0,50 (1,0đ) a 4
Kết hợp với điều kiện 1
a > 0;a ≠ . ta được 1 0 < a < . 0,50 4 4
Cho hàm số y = ax + b ( a,b là tham số), có đồ thị là đường thẳng (d) Tìm a,b để
(d) có hệ số góc bằng 3 và cắt đường thẳng (∆) : y = 2x + 3 tại điểm có tung độ bằng 5
Do đường thẳng (d) có hệ số góc bằng 3 nên a = 3 khi đó (d) : y = 3x + b 0,25 II 1
Xét đường thẳng (∆) y = 2x + 3 : với y = 5 ⇒ 2x + 3 = 5 ⇔ x =1.
(2,0đ) (1,0đ) Vậy (∆) cắt (d)tại điểm ( A 1;5) . 0,50 Do (
A 1;5)∈(d) nên 5 = 3.1+ b ⇒ b = 2
Kết luận a = 3;b = 2. 2x + y = 3
Giải hệ phương trình  . x − 3y = 5 2x + y = 3 6x + 3y = 9 7x = 14 2  ⇔  ⇔ (1,0đ) Ta có: x - 3y = 5 x - 3y = 5  0,50   x - 3y = 5 x = 2 x = 2 ⇔ 
. Vậy nghiệm của hệ phương trình là:  0,50 y = 1 − y = 1 −
1.Giải phương trình: 2
x + 5x + 6 = 0.
Ta có: ∆ = 25 − 24 =1 > 0 nên phương trình có hai nghiệm 1 − + − − ( 5 1 5 1 1,0đ) x = = 2; − x = = 3 − . 0,50 1 2 2 2
Vậy phương trình có hai nghiệm. x = 2; − x = 3 − . 1 2 0,50
2. Tìm tất các giá trị của tham số m để phương trình 2 2
x − 2x − m − 2m −1 = 0 (1)
có hai nghiệm phân biệt x , x thỏa mãn điều kiện 2 2
2x − x − x x −8 = 0. 1 2 1 2 1 2 2 2
∆ ' =1+ m + 2m +1 = (m +1) +1 > 0. m ∀ x + x = 2 (2)
Áp dụng định lí vi-et cho pt (1) ta được 1 2  0,25 2
x x = −m − 2m −  1 (3) 1 2 III (2,0đ) 2 2 2 2 2 2
2x − x − x x 8
− = 0⇔ 2x −8 = x + x x = x − m − 2m −1 1 2 1 2 1 2 1 2 2 2
Do x là nghiệm của phương (1) nên 2 (1,0đ) 2 2 2 2
x − 2x − m − 2m −1 = 0 ⇒ x − m − 2m −1 = 2x , 2 2 2 2 0,25 thay vào ( ) ∗ ta được 2 2
2x −8 = 2x ⇔ x − x − 4 = 0 .Kết hợp với (2) ta có 1 2 1 2 2
x + x − 6 = 0 ⇔ x = 2; x = 3 − . 1 1 1 1
Với x = 2 thay vào (2) ta được x = 0 , từ (3) suy ra 1 2 0,25 2
m + 2m +1 = 0 ⇔ m = 1 − . Với x = 3
− thay vào (2) ta được x = 5 . Thay x = 3
− , x = 5 vào (3) ta 1 2 1 2 được 2 2 15
− = −m − 2m −1 ⇔ m + 2m −14 = 0 ⇔ m = 1 − ± 15. 0,25 Vậy m∈{ 1 − , 1 − − 15, 1 − + 15}.
Câu IV(3đ): Cho tam giác ABC có góc 
BAC nhọn, đường cao AH (H ∈ BC) nội tiếp trong
đường tròn (O) bán kính R ,gọi I và K lần lượt là hình chiếu của A trên các tiếp tuyến
của (O) tại B vàC . IV
1. Chứng minh tứ giác AIBH và tứ giác AHCK nội tiếp . (3,0đ) 2. Cho  0
BAC = 35 .Tính góc  IAK
3. Lấy điểm M trên tia OB sao cho OM = 2R tìm vị trí điểm N trên (O) sao cho
2NI + NM đạt giá trị nhỏ nhất. A O K C I H B L
1. Chứng minh các tứ giác AHBI và tứ giác AHCK nội tiếp .
Do I là hình chiếu của A lên tiếp tuyến(O) tại B nên  AIB = 90° . Mặt khác : ⊥ ⇒  AH BC (gt) AHB = 90° 0,50 1 Nên :  +  0 0 0 AIB AHB = 90 + 90 =180
(1,0đ) Vậy : tứ giác AIBH nội tiếp đường tròn .
Do K là hình chiếu của A lên tiếp tuyến(O) tại C Nên ta có  0 AKC = 90 0,50 Suy ra :  +  0 0 0 AKC AHC = 90 + 90 =180
Vậy : tứ giác AKCH nội tiếp đường tròn. 2. Cho  0
BAC = 35 .Tính góc  IAK .
Gọi L là giao điểm của IB và KC do tứ giác AIBH nội tiếp nên  =  LBC IAH 0,25 (cùng bù với góc  IBH ) 2
do tứ giác AKCH nội tiếp nên  = 
BCL HAK (cùng bù với góc  HCK ) 0,25
(1,0đ) Suy ra   +
=  +  ⇔  =  +  IAH HAK LBC BCL IAK LBC BCL 0,25 Lại có  =  = 
LBC BCL BAC ( Góc nội tiếp chắn cung 
BC , góc tạo bởi tiếp 0,25
tuyến và dây cung BC trong đường tròn (O) )⇒  =  0 IAK 2BAC = 70
3. Lấy điểm M trên tia OB sao cho OM = 2R .Tìm vị trí điểm N trên (O) sao cho
2NI + NM đạt giá trị nhỏ nhất. A O C N E 3 I (1,0đ) B M -Xét N
∀ ∈(O), N ∉OB .
Gọi E là trung điểm của OB ,tam giác OMN và tam giác ONE có OE 1 ON 0,50 = = và góc 
MON chung nên ON ∆ E  OM ∆ N ON 2 OM Do đó NE 1
= ⇒ MN = 2NE ta có NM+ 2NI = 2NE + 2NI ≥ 2IE . Dấu bằng MN 2
xảy ra khi N là giao điểm của đoạn IE với đường tròn (O) .
-Xét N ≡ B 0,5
dễ thấy 2BI + BM = 2BI + 2BE ≥ 2IE dấu ' = ' xảy ra khi B thuộc đoạn IE
,điều này xảy ra khi A
∆ BC vuông tại C và N ≡ B ≡ I .Khi đó điểm N cũnglà
giao điểm của đoạn IE với đường tròn.
Vậy N là giao điểm của đoạn IE với đường tròn là điểm cần tìm.
Cho a , b , c là các số dương thỏa mãn a +b + c + 2 = abc .
Tìm giá trị lớn nhất của biểu thức 1 1 1 P = + + . ab bc ca Ta có: Từ giả thiết 1 1 1 2
a + b + c + 2 = abc ⇒ + + + =1 ( ) 1 . ab bc ca abc Đặt 1 = x 1 = y 1 = z < x y z < ab
, bc , ca .Từ gt ta có 0 , , 1 0,25 ( ) 2 2 2 2 2 2 2 2 2 2
1 ⇔ x + y + z + 2xyz −1 = 0⇔ x + 2xyz + y z = y z − y − z +1
⇔ (x + yz)2 = ( 2 1− y )( 2
1− z ) ⇔ x = −yz + ( 2 1− y )( 2 1− z ) V (1,0đ) ( )( ) 2 2 2 2 2 1 1 y z x yz y z − − ⇔ + = − − ≤ 2 0,25 (1,0đ) y + z ( y + z)2 2 2 Suyra x + yz + ≤ 1 ⇔ x + ≤ 1 0,25 2 2
lại có ( y + z)2 +1≥ 2( y + z) nên ta có 2( y + z) −1 3 x +
≤ 1 ⇔ x + y + z ≤ = xảy ra khi 1
x = y = z = . 2 2 .Dấu ' ' 2 0,25 Vậy 1 1 1 P = + +
đạt giá trị nhỏ nhất bằng 3 khi a = b = c = 2. ab bc ca 2