Đề giữa kỳ 1 Toán 12 năm 2024 – 2025 trường Nguyễn Bỉnh Khiêm – Hà Nội

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra giữa học kỳ 1 môn Toán 12 năm học 2024 – 2025 trường THCS & THPT Nguyễn Bỉnh Khiêm, quận Cầu Giấy, thành phố Hà Nội. Đề thi gồm mã đề lẻ và mã đề chẵn, cấu trúc trắc nghiệm 03 phần (trắc nghiệm 04 phương án lựa chọn, trắc nghiệm đúng hoặc sai, trắc nghiệm trả lời ngắn), thời gian làm bài 90 phút. Kỳ thi được diễn ra vào ngày 04 tháng 10 năm 2024. Mời bạn đọc đón xem!

80 40 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 12

Môn: Toán 12

Thông tin:

18 trang 4 tuần trước

Tác giả:

Profile Lê Phương
TRƯỜNG THCS&THPT
NGUYỄN BỈNH KHIÊM - CẦU GIẤY
ĐỀ THI CHÍNH THỨC
(Đề thi có 4 trang)
ĐỀ KIỂM TRA GIỮA KỲ I LỚP 12
NĂM HỌC 2024 - 2025
Môn: TOÁN
Thời gian làm bài: 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 101
PHẦN I. TRẮC NGHIỆM 4 PHƯƠNG ÁN. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào
trong các hàm số được cho dưới đây?
A. y =
2x − 1
x − 1
. B. y =
2x + 1
x + 1
.
C. y =
2x
x + 1
. D. y =
2x − 1
x + 1
.
x
y
O
−1 1
−1
2
Câu 2. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
f
′
(x)
f(x)
−∞
−2
1
+∞
+
0
− +
11
33
−∞ −3
11
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. 2. B. 1. C. 3. D. 4.
Câu 3. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y =
3x − 2
x − 1
lần lượt là
A. x = 1, y = 3. B. x = 3, y = 1. C. x = 1, y = −3. D. x = −1, y = 3.
Câu 4. Cho hàm số y = f(x) liên tục trên R và có đạo hàm f
′
(x) = x
2
(3 − x)(x + 1) với mọi
x ∈ R. Khẳng định nào sau đây đúng?
A. f(−2) < f(−1). B. f(3) > f(4). C. f (2) > f(3). D. f(−1) > f(2).
Câu 5. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ sau:
x
y
′
y
−∞
0 2
+∞
−
0
+
0
−
+∞+∞
−3−3
11
−∞−∞
Hàm số y = f (x) nghịch biến trên khoảng nào sau đây?
A. (0; 2). B. (2; 5). C. (0; +∞). D. (−2; 2).
Trang 1/4 − Mã đề 101
Câu 6. Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm f
′
(x) như sau:
x
f
′
(x)
−∞
−2
0 3
+∞
+
0
− +
0
−
Hàm số đã cho có bao nhiêu điểm cực trị?
A. 2. B. 3. C. 0. D. 1.
Câu 7. Giá trị nhỏ nhất của hàm số y = 4x
3
− 3x
4
trên đoạn [−1; 2] bằng
A. −24. B. 0. C. −7. D. −16.
Câu 8. Cho hàm số y = f (x) có đồ thị trên đoạn [−2; 3]
như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của hàm số y = f (x) trên đoạn [−2; 3]. Tính
2M − m.
A. 5. B. 7. C. 6. D. 8.
x
y
O
1
2 3
−2 −1
−3
−1
1
2
Câu 9. Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau
đây?
A. y = −x
3
− 3x
2
+ 1. B. y = −x
3
+ 3x − 1.
C. y = x
3
− 3x − 1. D. y = −x
3
+ 3x
2
− 1.
x
y
O
2
3
−1
Câu 10. Hàm số nào dưới đây có bảng biến thiên như sau?
x
f
′
(x)
f(x)
−∞
−1
1 3
+∞
+
0
− −
0
+
−∞−∞
−5−5
−∞
+∞
33
+∞+∞
A. y =
x
2
+ 3x − 6
1 − x
. B. y =
x
2
− 3x + 6
x + 1
. C. y =
x
2
+ 3x + 6
x − 1
. D. y =
x
2
− 3x + 6
x − 1
.
Câu 11. Cho hàm số y = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có đồ thị
như hình vẽ. Giá trị cực đại của hàm số bằng
A. 1. B. 0. C. −1. D. −4.
O
x
y
1
−4
−1
2
−2
Trang 2/4 − Mã đề 101
Câu 12. Cho hàm số y =
2x − 1
x + 2
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (−∞; −2) và (−2; +∞).
B. Hàm số nghịch biến trên khoảng (−∞; −2) và (−2; +∞).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (−∞; −2) ∪ (−2; +∞).
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI. Thí sinh trả lời từ câu 1 đến câu 4. Mỗi ý a), b),
c), d) ở mỗi câu hỏi, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số y =
2x + m
x + 1
.
a) Khi m = −1 thì hàm số nghịch biến trên khoảng (−1; +∞).
b) Tập xác định của hàm số là D = R \ {−1}.
c) Đồ thị hàm số có tâm đối xứng là điểm I(−1; 2).
d) Có hai giá trị nguyên dương của m để hàm số đồng biến trên các khoảng xác định.
Câu 2. Một vật chuyển động theo phương trình s(t) = −
1
3
t
3
+ 6t
2
với t tính bằng giây (s) và s(t)
được tính bằng mét (m) là quãng đường vật di chuyển được.
a) Sau 3 giây vật đi được quãng đường dài 45 m.
b) Gia tốc tức thời của vật tại thời điểm t = 7 giây bằng 2 m/s
2
.
c) Vận tốc của vật được tính bởi công thức v(t) = −t
2
+ 12t.
d) Vận tốc lớn nhất của vật trong 8 giây đầu tiên là 36 m/s.
Câu 3. Cho hàm số f(x) =
4x
2
+ 60
x + 1
.
a) Hàm số đã cho đạt cực đại tại điểm x = −5.
b) Hàm số f(x) đồng biến trên khoảng (−1; +∞).
c) Đạo hàm của hàm số đã cho f
′
(x) = 4 −
64
(x + 1)
2
.
d) Tiệm cận xiên của đồ thị hàm số có phương trình y = 4x − 4.
Câu 4. Cho hàm số f(x) = x
3
− 3x
2
+ 2.
a) Bảng biến thiên của hàm số đã cho là
x
f
′
(x)
f(x)
−∞
0 2
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
b) Đạo hàm của hàm số đã cho là f
′
(x) = 3x
2
− 6x.
c) Giá trị lớn nhất của hàm số đã cho trên R bằng 2.
d) Với mỗi giá trị của m ∈ (−2; 2) phương trình f(x) = m có ba nghiệm phân biệt.
PHẦN III. TRẮC NGHIỆM TRẢ LỜI NGẮN. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Đồ thị hàm số y = 2x − 1 +
3
x − 2
có tâm đối xứng là điểm I(a; b). Giá trị của biểu thức
a
2
+ b
2
bằng KQ:
Câu 2. Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y = m không cắt đồ thị
hàm số y =
−x
2
+ 2x − 4
x − 2
? KQ:
Trang 3/4 − Mã đề 101
Câu 3. Gọi S là tập hợp tất cả các số nguyên m sao cho hàm số y =
4
3
x
3
− mx
2
+ 4x − 1 đồng
biến trên R. Số phần tử của tập hợp S bằng KQ:
Câu 4. Dân số Việt Nam sau t năm tính từ năm 2023 được dự đoán theo công thức
N(t) = 100 · e
0,012t
(triệu người), với 0 < t ≤ 50. Biết rằng đạo hàm của hàm số N(t) biểu thị tốc
độ gia tăng dân số của Việt Nam (đơn vị là triệu người/năm). Sau ít nhất bao nhiêu năm thì tốc
độ gia tăng dân số của Việt Nam sẽ lớn hơn 2 triệu người/năm? KQ:
Câu 5. Cho hàm số y = f (x) có đạo hàm trên R và có đồ thị như hình
vẽ bên. Tìm m để giá trị lớn nhất của hàm số g(x) = f (2x
3
+x−1)+m
trên đoạn [0; 1] bằng −10.
O
x
y
−1 2
−2
1
1
−1
3
KQ:
Câu 6. Bác Nam dự định làm một máng thoát nước mưa từ một miếng tôn hình chữ nhật có
chiều dài 8 m và chiều rộng 45 cm. Bác Nam chia chiều rộng của miếng tôn thành ba phần bằng
nhau, mỗi phần dài 15 cm, rồi gập hai bên lên một góc θ (đơn vị radian) như hình vẽ dưới đây
45 cm
15 cm 15 cm 15 cm
θ θ
Gọi S (cm
2
) là diện tích của mặt cắt ngang của máng nước. Tìm góc θ (làm tròn kết quả đến
chữ số thứ hai sau dấu phẩy) để diện tích S là lớn nhất (sẽ cho phép nước thoát qua máng nhiều
nhất). KQ:
HẾT
Trang 4/4 − Mã đề 101
TRƯỜNG THCS&THPT
NGUYỄN BỈNH KHIÊM - CẦU GIẤY
ĐỀ THI CHÍNH THỨC
(Đề thi có 4 trang)
ĐỀ KIỂM TRA GIỮA KỲ I LỚP 12
NĂM HỌC 2024 - 2025
Môn: TOÁN
Thời gian làm bài: 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 102
PHẦN I. TRẮC NGHIỆM 4 PHƯƠNG ÁN. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
f
′
(x)
f(x)
−∞
−1
2
+∞
−
0
+ −
00
−2−2
+∞ +∞
00
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. 2. B. 4. C. 1. D. 3.
Câu 2. Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm f
′
(x) như sau:
x
f
′
(x)
−∞
−1
1 3
+∞
−
0
+ −
0
+
Hàm số đã cho có bao nhiêu điểm cực trị?
A. 2. B. 1. C. 0. D. 3.
Câu 3. Giá trị lớn nhất của hàm số y = 3x
4
− 4x
3
+ 1 trên đoạn [−1; 2] bằng
A. 8. B. 18. C. 16. D. 17.
Câu 4. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y =
4x − 1
x − 2
lần lượt là
A. x = 2, y = −4. B. x = 4, y = 2. C. x = 2, y = 4. D. x = −2, y = 4.
Câu 5. Cho hàm số y = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có đồ thị
như hình vẽ. Giá trị cực đại của hàm số bằng
A. −1. B. 1. C. −4. D. 0.
x
y
O
−1
1
−4
−2
Câu 6. Cho hàm số y =
2x + 3
x + 1
. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên (−∞; −1) ∪ (−1; +∞).
B. Hàm số nghịch biến trên khoảng (−∞; −1) và (−1; +∞).
C. Hàm số nghịch biến trên R.
D. Hàm số đồng biến trên khoảng (−∞; −1) và (−1; +∞).
Trang 1/4 − Mã đề 102
Câu 7. Cho hàm số y = f(x) có đồ thị trên đoạn [−4; 2] như
hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số y = f (x) trên đoạn [−4; 2]. Tính M − 2m.
A. 7. B. 8. C. 10. D. 5.
x
y
O
−4 −2
2
−1
−3
1
2
Câu 8. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ sau:
x
y
′
y
−∞
−1
1
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
Hàm số y = f (x) đồng biến trên khoảng nào sau đây?
A. (−1; 1). B. (1; 5). C. (−2; +∞). D. (−∞; 2).
Câu 9. Cho hàm số y = f(x) liên tục trên R và có đạo hàm f
′
(x) = x(3 − x)(x + 1)
2
với mọi
x ∈ R. Khẳng định nào sau đây đúng?
A. f(0) > f(−1). B. f(1) > f(2). C. f (3) > f(1). D. f(4) > f(3).
Câu 10. Đường cong trong hình vẽ bên là đồ thị của hàm
số nào trong các hàm số được cho dưới đây?
A. y =
2x
x − 1
. B. y =
2x + 1
x − 1
.
C. y =
2x − 1
x − 1
. D. y =
2x − 1
x + 1
.
x
y
O
1
1
2
Câu 11. Hàm số nào dưới đây có bảng biến thiên như sau?
x
f
′
(x)
f(x)
−∞
−3 −1
1
+∞
−
0
+ +
0
−
+∞+∞
77
+∞
−∞
−1−1
−∞−∞
A. y =
−x
2
+ x − 2
x + 1
. B. y =
−x
2
− x − 2
x + 1
. C. y =
x
2
− x − 2
x + 1
. D. y =
x
2
− x + 2
x − 1
.
Trang 2/4 − Mã đề 102
Câu 12. Đường cong trong hình vẽ bên là đồ thị của hàm số nào
sau đây?
A. y = x
3
− 3x. B. y = −x
3
+ 3x + 1.
C. y = −x
3
+ 3x. D. y = −x
3
+ 3x
2
.
x
y
O
1
−1
2
−2
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI. Thí sinh trả lời từ câu 1 đến câu 4. Mỗi ý a), b),
c), d) ở mỗi câu hỏi, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số f(x) =
3x
2
+ 45
x − 1
.
a) Hàm số đã cho đạt cực tiểu tại điểm x = 5.
b) Hàm số f(x) nghịch biến trên khoảng (−∞; 1).
c) Đạo hàm của hàm số đã cho f
′
(x) = 3 −
48
(x − 1)
2
.
d) Tiệm cận xiên của đồ thị hàm số có phương trình y = 3x + 3.
Câu 2. Một vật chuyển động theo phương trình s(t) = −
1
3
t
3
+ 5t
2
với t tính bằng giây (s) và s(t)
được tính bằng mét (m) là quãng đường vật di chuyển được.
a) Sau 3 giây vật đi được quãng đường dài 36 m.
b) Vận tốc của vật được tính bởi công thức v(t) = −t
2
+ 10t.
c) Gia tốc tức thời của vật tại thời điểm t = 6 giây bằng 2 m/s
2
.
d) Vận tốc lớn nhất của vật trong 8 giây đầu tiên là 25 m/s.
Câu 3. Cho hàm số y =
3x − m
x − 2
.
a) Đồ thị hàm số có tâm đối xứng là điểm I(2; 3).
b) Tập xác định của hàm số là D = R \ {2}.
c) Khi m = 1 thì hàm số đồng biến trên khoảng (2; +∞).
d) Có năm giá trị nguyên dương của m để hàm số nghịch biến trên các khoảng xác định.
Câu 4. Cho hàm số f(x) = −x
3
− 3x
2
+ 4.
a) Bảng biến thiên của hàm số đã cho là
x
f
′
(x)
f(x)
−∞
−2
0
+∞
−
0
+
0
−
+∞+∞
00
44
−∞−∞
b) Đạo hàm của hàm số đã cho là f
′
(x) = −3x
2
− 6x.
c) Giá trị nhỏ nhất của hàm số đã cho trên R bằng 0.
d) Với mỗi giá trị của m ∈ (0; 4) phương trình f(x) = m có ba nghiệm phân biệt.
PHẦN III. TRẮC NGHIỆM TRẢ LỜI NGẮN. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cắt bỏ hình quạt tròn AOB (hình phẳng có nét gạch trong hình vẽ dưới đây) từ một
mảnh giấy hình tròn bán kính bằng 30 cm rồi dán hai bán kính OA và OB của hình quạt tròn
còn lại với nhau để được một cái phễu có dạng một hình nón.
Trang 3/4 − Mã đề 102
O
A
B
θ
h
r
B
O
H
Gọi θ (đơn vị radian) là góc ở tâm của quạt tròn dùng làm phễu (0 < θ < 2π). Tìm θ để khối nón có
thể tích lớn nhất (làm tròn kết quả đến chữ số thứ hai sau dấu phẩy). KQ:
Câu 2. Dân số Việt Nam sau t năm tính từ năm 2023 được dự đoán theo công thức
N(t) = 100 · e
0,012t
(triệu người), với 0 < t ≤ 50. Biết rằng đạo hàm của hàm số N(t) biểu thị tốc
độ gia tăng dân số của Việt Nam (đơn vị là triệu người/năm). Sau ít nhất bao nhiêu năm thì tốc
độ gia tăng dân số của Việt Nam sẽ lớn hơn 1,5 triệu người/năm? KQ:
Câu 3. Cho hàm số y = f (x) có đạo hàm trên R và có đồ thị như hình
vẽ bên. Tìm m để giá trị nhỏ nhất của hàm số g(x) = f (2x
3
+x−1)+m
trên đoạn [0; 1] bằng −16.
O
x
y
−1 2
−2
1
1
−1
3
KQ:
Câu 4. Tiệm cận xiên của đồ thị hàm số y = 2x − 5 +
3
x + 2
tạo với hai trục tọa độ một tam
giác có diện tích bằng KQ:
Câu 5. Có bao nhiêu số nguyên m để hàm số y =
1
3
x
3
− x
2
+ (m
2
− 7)x + 2 có cực đại và cực
tiểu? KQ:
Câu 6. Có bao nhiêu số nguyên m ∈ [−2024; 2024] để đường thẳng y = m cắt đồ thị hàm số
y =
−x
2
+ 2x − 4
x − 2
tại hai điểm phân biệt? KQ:
HẾT
Trang 4/4 − Mã đề 102
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12
B A C B B B D B D D B A
HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Đường cong của hình vẽ bên là đồ thị của hàm số nào trong các hàm số được cho dưới đây?
A.
2 1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
1
x
y
x
. D.
2 1
1
x
y
x
.
Lời giải
Chọn B
Dựa vào đồ thị suy ra tiệm cận đứng
1x
, tiệm cận ngang là
2y
.
Đồ thị hàm số giao với trục hoành có hoành độ dương suy ra chọn B.
Câu 2. Cho hàm số
y f x
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn A
Từ bảng biến thiên đã cho ta có:
lim 1
x
f x

nên đường thẳng
1y
là một tiệm cận ngang của đồ thị hàm số.
1
lim
x
f x

nên đường thẳng
1x
là một tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Câu 3. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
3 2
1
x
y
x
lần lượt là
A.
1, 3x y
. B.
1, 3x y
. C.
1, 3x y
. D.
1, 3x y
.
Lời giải
Chọn C
Ta có
1
3 2
lim
1
x
x
x

và
1
3 2
lim
1
x
x
x

nên
1x
là tiệm cận đứng của đồ thị hàm số.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
3 2
lim lim 3
x x
x
y
x
 
và
3 2
lim lim 3
x x
x
y
x
 
nên
3y
là tiệm cận ngang của đồ
thị hàm số.
Câu 4. Cho hàm số
y f x
liên tục trên
và có đạo hàm
2
(3 )( 1)f x x x x
với mọi
x
.
Khẳng định nào sau đây đúng?
A.
2 1f f
. B.
3 4f f
. C.
2 3f f
. D.
1 2f f
.
Lời giải
Chọn B
Ta có
2
0
' (3 )( 1) 0 3
1
x
f x x x x x
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên cho thấy hàm số nghịch biến trên
3;

do đó
3 4 .
f f
Câu 5. Cho hàm số
y f x
có bảng biến thiên như hình vẽ sau:
Hàm số
y f x
nghịch biến trên khoảng nào sau đây?
A.
0;2
. B.
(2;5)
. C.
(0; )
. D.
( 2;2)
.
Lời giải
Chọn B
Hàm số
y f x
nghịch biến trên khoảng
(2;5)
.
Câu 6. Cho hàm số
y f x
liên tục trên
và có bảng xét dấu của đạo hàm
f x
như sau:
Hàm số đã cho có bao nhiêu điểm cực trị?
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn B
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hàm số đã cho có điểm
3
cực trị.
Câu 7. Giá trị nhỏ nhất của hàm số
3 4
4 3y x x
trên đoạn
1;2
bằng:
A.
24
. B.
0
. C.
7
. D.
16
.
Lời giải
Chọn D
+) Ta có
2 3
0( )
' 12 12 0
1( )
x tm
y x x
x tm
.
+) Ta tính được
1 7; 0 0; 1 1; 2 16y y y y
.
Vậy
1;2
min (2) 16y y
.
Câu 8. Cho hàm số
y f x
có đồ thị trên đoạn
2;3
như hình vẽ bên. Gọi
,M m
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của hàm số
y f x
trên đoạn
2;3
. Tính
2M m
.
A. 6. B. 7. C. 5. D. 8.
Lời giải
Chọn B
Dựa vào đồ thị trên đoạn
2;3
ta có
2M
và
3m
suy ra
2 2.2 3 7M m
.
Câu 9. Đường cong hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
3 2
3 1
y x x
. B.
3
3 1
y x x
. C.
3
3 1
y x x
. D.
3 2
3 1
y x x
.
Lời giải
Chọn D
-Dựa vào đồ thị ta thấy
lim
x
f x


nên loại đáp án C.
-Ta có:
0 1f
nên loại đáp án A
2 3f
nên loại đáp án B.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy đáp án đúng là D.
Câu 10. Hàm số nào dưới đây có bảng biến thiên như sau?
A.
2
3 6
1
x x
y
x
. B.
2
3 6
1
x x
y
x
. C.
2
3 6
1
x x
y
x
. D.
2
3 6
1
x x
y
x
.
Lời giải
Chọn D
Dựa vào BBT ta thấy hàm số
y f x
có tiệm cận đứng
1x
, vậy loại B
Ta thấy
1 5f
vậy chỉ có đáp án D thỏa mãn.
Vậy đáp án đúng là D.
Câu 11. Cho hàm số
3 2
, , ,y ax bx cx d a b c d
có đồ thị như hình vẽ. Giá trị cực đại của hàm
số bằng
A.
1
. B.
0
. C.
1
. D.
4
.
Lời giải
Chọn B
Dựa vào đồ thị ta thấy giá trị cực đại của hàm số bằng 0.
Vậy đáp án đúng là B.
Câu 12. Cho hàm số
2 1
2
x
y
x
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
; 2

và
2;

.
B. Hàm số nghịch biến trên khoảng
; 2
và
2; 
.
C. Hàm số đồng biến trên
.
D. Hàm số đồng biến trên khoảng
; 2 2; 
.
Lời giải
Chọn A
TXĐ:
\ 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có:
2
\ 2
3
0
2
y x
x
Vậy hàm số đồng biến trên các khoảng xác định của nó là
; 2

và
2;

.
Chọn đáp án A.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số
2
1
x m
y
x
.
a) Khi
1
m
thì hàm số nghịch biến trên khoảng
1;

.
b) Tập xác định của hàm số là
\ 1 .
D
c) Đồ thị hàm số có tâm đối xứng là điểm
1;2 .
I
d) Có hai giá trị nguyên dương của
m
để hàm số đồng biến trên các khoảng xác định.
Lời giải
Chọn a) Sai | b) Đúng | c) Đúng | d) Sai.
a) Khi
1
m
thì
2 1
.
1
x
y
x
Khi đó
2
3
0, 1.
1
y x
x
Hàm số luôn đồng biến trên khoảng
; 1

và
1; .

b) Tập xác định của hàm số là
\ 1 .
D
c) Đồ thị hàm số có tiệm cận đứng là
1,
x
tiệm cận ngang là
2.
y
Do đó tâm đối xứng là
1;2 .
I
d) Ta có
2
2
.
1
m
y
x
Hàm số đồng biến trên khoảng trên các khoảng xác định
0, 2 0 2.
y x D m m
Vì
*
m
nên
1
m
.
Câu 2. Một vật chuyển động theo phương trình
3 2
1
( ) 6
3
s t t t
với
t
tính bằng giây
( )
s
và
( )
s t
được
tính bằng mét
( )
m
là quãng đường vật di chuyển được.
a) Sau
3
giây vật đi được quãng đường dài
45m
.
b) Gia tốc tức thời của vật tại thời điểm
7
t
giây bằng
2
2m/s
.
c) Vận tốc của vật được tính bởi công thức
2
( ) 12
v t t t
.
d) Vận tốc lớn nhất của vật trong
8
giây đầu tiên là
36m/s
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn a) Đúng | b) Sai | c) Đúng | d) Đúng
a) Sau
3
giây vật đi được quãng đường dài:
3 2
1
(3) .3 6.3 45.
3
s
b) Gia tốc tức thời của vật được xác định bởi công thức
( ) ( ) 2 12.a t s t t
Do đó
2
(7) 2.7 12 2 \ .a m s
c) Vận tốc của vật được tính bởi công thức
2
( ) ( ) 12 .v t s t t t
d) Ta có
2
( ) 12 .v t t t
( ) 2 12 0 6.v t t t
Bảng biến thiên:
Dựa vào bảng biến thiên, trong
8
giây đâu tiên vận tốc lớn nhất của vật đạt
36 / .m s
.
Câu 3. Cho hàm số
2
4 60
1
x
f x
x
.
a) Hàm số đã cho đạt cực đại tại
5x
.
b) Hàm số
f x
đồng biến trên khoảng
1;

.
c) Đạo hàm của hàm số đã cho
2
64
4
1
f x
x
.
d) Tiệm cận xiên của đồ thị hàm số có phương trình là
4 4y x
.
Lời giải
a)Đ
b) S
c) Đ
d) Đ
Tập xác định:
\ 1
D
.
2
4 60 64
4 4
1 1
x
f x x
x x
Ta có:
2
64
4 , 1
1
f x x
x
2
5
64
0 4 0
3
1
x
f x
x
x
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hàm số đạt cực đại tại
5x
và
40
CÐ
y
.
Hàm số đạt cực tiểu tại
3x
và
24
CT
y
.
Hàm số đồng biến trên các khoảng
; 5

và
3;

.
Hàm số nghịch biến trên các khoảng
5; 1
và
1;3
.
Ta có:
64
lim 4 4 lim 0 4 4
1
x x
f x x y x
x
 
là đường tiệm cận xiên của đồ thị
hàm số.
Câu 4. Cho hàm số bậc ba
3 2
3 2f x x x
a) Bảng biến thiên của hàm số đã cho là
b) Đạo hàm của hàm số đã cho là
2
3 6f x x x
.
c) Giá trị lớn nhất của hàm số đã cho trên
bằng 2.
d) Với mỗi giá trị
2;2
m
phương trình
f x m
có ba nghiệm phân biệt.
Lời giải
a)Đ
b) Đ
c) S
d) Đ
Ta có:
2
3 6
f x x x
2
0
0 3 6 0
2
x
f x x x
x
Bảng biến thiên:
e
Giá trị lớn nhất của hàm số đã cho trên
không tồn tại.
Với mỗi giá trị
2;2m
phương trình
f x m
có ba nghiệm phân biệt.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Câu 1. Đồ thị hàm số
3
2 1
2
y x
x
có tâm đối xứng là điểm
,I a b
. Giá trị của biểu thức
2 2
a b
bằng
Lời giải
Đáp số: 13
Ta có
2
lim
x
f x

suy ra
2x
là tiệm cận ngang của đồ thị hàm số.
lim 2 1 0
x
f x x

và
lim 2 1 0
x
f x x

nên
2 1y x
là tiệm cận xiên của đồ
thị hàm số.
Giao điểm của hai đường tiệm cận là nghiệm của hệ phương trình:
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
2 2
2;3
2 1 3
x x
I
y x y
.
Vậy
2 2 2 2
2 3 13
a b
.
Câu 2. Có bao nhiêu giá trị nguyên của tham số
m
để đường thẳng
y m
không cắt đồ thị hàm số
2
2 4
2
x x
y
x
?
Lời giải
Đáp số
7
.
Để đường thẳng
y m
không cắt đồ thị hàm số
2
2 4
2
x x
y
x
thì phương trình
2
2 4
x x
m
x
vô nghiệm.
Ta có
2
2 4
2
x x
m
x
2
2 4 2 0
x m x m
với
2
x
.
Để phương trình vô nghiệm cần
2
2 4 4 2 0
m m
2
4 4 16 8 0
m m m
2
4 12 0
m m
6 2
m
.
Vậy có
7
giá trị nguyên của
m
.
Câu 3. Gọi
S
là tập hợp tất cả các số nguyên
m
sao cho hàm số
3 2
4
4 1
3
y x mx x
đồng biến trên
. Số phần tử của tập hợp
S
bằng
Lời giải
Trả lời: 9
Tập xác định
D
Ta có
2
4 2 4
y x mx
.
Để hàm số
3 2
4
4 1
3
y x mx x
đồng biến trên
.
2
0
0, 16 0 4 4
0
a
y x m m
.
Vì
m
có
9
giá trị thỏa mãn.
Câu 4. Dân số Việt Nam sau
t
năm tính từ năm
2023
được dự đoán theo công thức
0,012
100.
t
N t e
(triệu người), với
0 50
t
. Biết rằng đạo hàm của hàm số
N t
biểu thị tốc độ gia tăng dân số
của Việt Nam (đơn vị là triệu người/ năm). Sau ít nhất bao nhiêu năm thì tốc độ gia tăng dân số
của Việt Nam sẽ lớn hơn
2
triệu người/ năm?
Lời giải
Trả lời: 43
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
0,012 0,012
100. 1,2.
t t
N t e N t e
.
Tốc độ gia tăng dân số của Việt Nam sẽ lớn hơn
2
triệu người/ năm
0,012
2 1, 2. 2 42,56
t
N t e t
.
Suy ra, sau ít nhất
43
năm thì tốc độ gia tăng dân số của Việt Nam sẽ lớn hơn
2
triệu người/
năm.
Câu 5. Cho hàm số
y f x
có đạo hàm trên
và có đồ thị như hình bên. Tìm
m
để giá trị lớn nhất
của hàm số
3
2 1g x f x x m
trên đoạn
0;1
bằng
10
.
Lời giải
Có
2 3
6 1 . 2 1g x x f x x
3 3
3
3 3
0
0
2 1 1 2 0
0 2 1 0 .
0,84
2 1 1 2 2 0
x
x x x x
g x f x x
x x
x x x x
Tính được
0
0 1 3 , 1 2 3 , 1 1 .g f m m g f m m g x f m m
Nên
0;1
3 10 13max g x m m
.
Câu 6. Bác Nam dự định làm một máng thoát nước mưa từ một miếng tôn hình chữ nhật có chiều dài
8
m và chiều rộng
45
cm. Bác Nam chia chiều rộng của miếng tôn thành ba phần bằng nhau,
mỗi phần dài 15 cm, rồi gập hai bên lên một góc
( đơn vị radian) như hình vẽ dưới đây.
Gọi
S
(cm
2
) là diện tích của mặt cắt ngang của máng nước. Tìm góc
(làm tròn kết quả đến
chữ số thứ hai sau dấu phẩy) để diện tích
S
là lớn nhất (sẽ cho phép nước thoát qua máng là
nhiều nhất).
Lời giải
Mặt cắt ngang của máng nước là hình thang cân
ABCD
như hình vẽ. Gọi
,AH BK
là các đường
cao, ta có
15DA AB BC
cm.
15sin , 15cos .AH BK DH KC
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khi đó diện tích mặt cắt ngang của máng nước là
.
225 1 cos sin
3
AB DC AH
S
với
0;
2
.
Xét hàm số
2 2
2 2 2 2 2
225 1 cos sin 225 1 cos 1 cosS
2
2 2 2 2 4 3
225 1 cos sin 225 cos 2cos 2cos 1S
Đặt
cos , 0;1t t
, xét hàm số
4 3
2 2 1f t t t t
trên
0;1 ,
có
3 2
4 6 2f t t t
,
1
0 .
2
1
t
f t
t
Lập bảng biến thiên của hàm số
f t
Ta thấy
f t
đạt giá trị lớn nhất khi
1
2
t
hay
1,05.
3
Khi đó diện tích lớn nhất của mặt
cắt ngang của máng nước là
225 1 cos60 sin 60 292,28S
(cm
2
).
HẾT
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THCS&THPT
ĐỀ KIỂM TRA GIỮA KỲ I LỚP 12
NGUYỄN BỈNH KHIÊM - CẦU GIẤY NĂM HỌC 2024 - 2025 ĐỀ THI CHÍNH THỨC Môn: TOÁN (Đề thi có 4 trang)
Thời gian làm bài: 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 101
PHẦN I. TRẮC NGHIỆM 4 PHƯƠNG ÁN. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án. Câu 1.
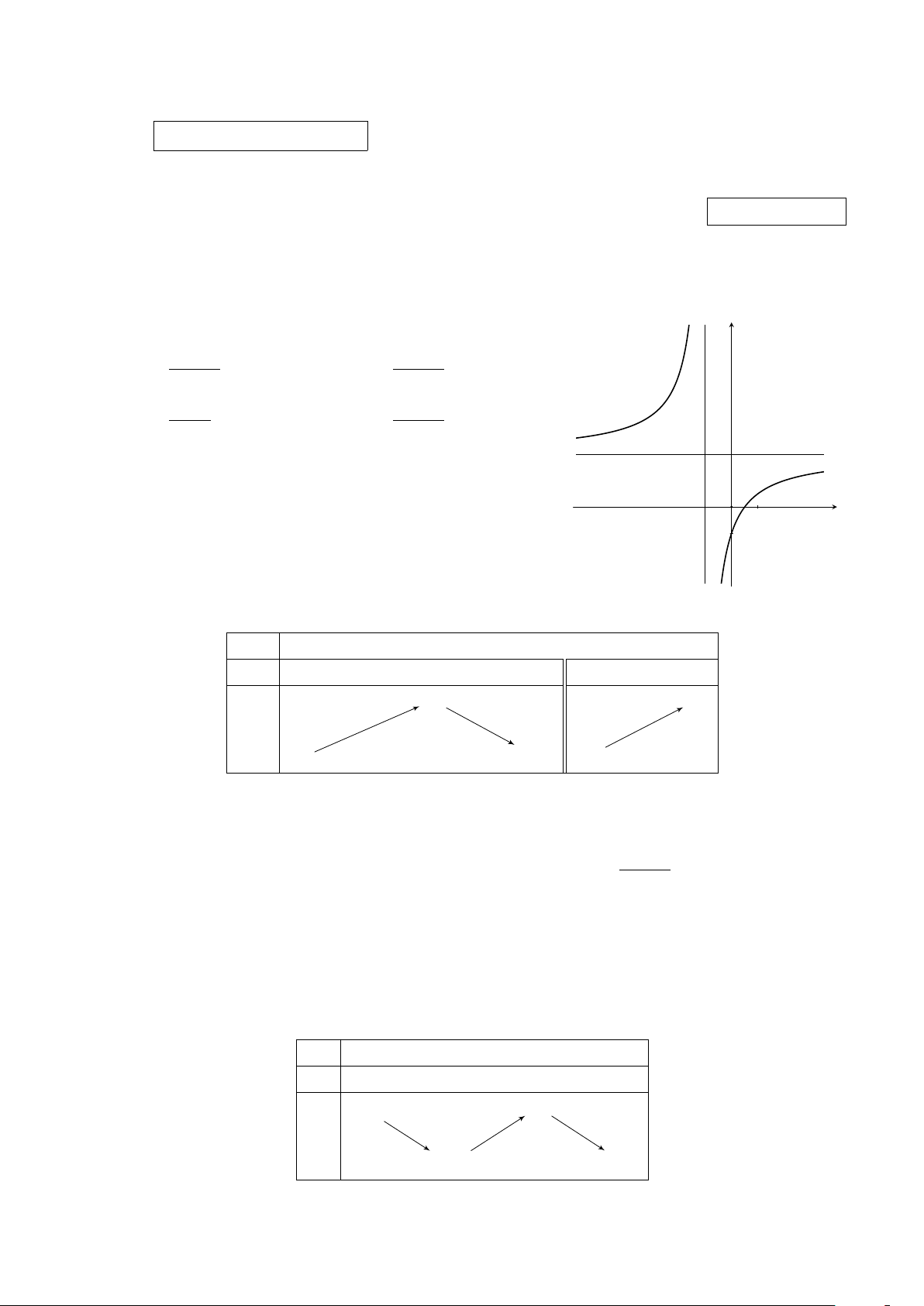
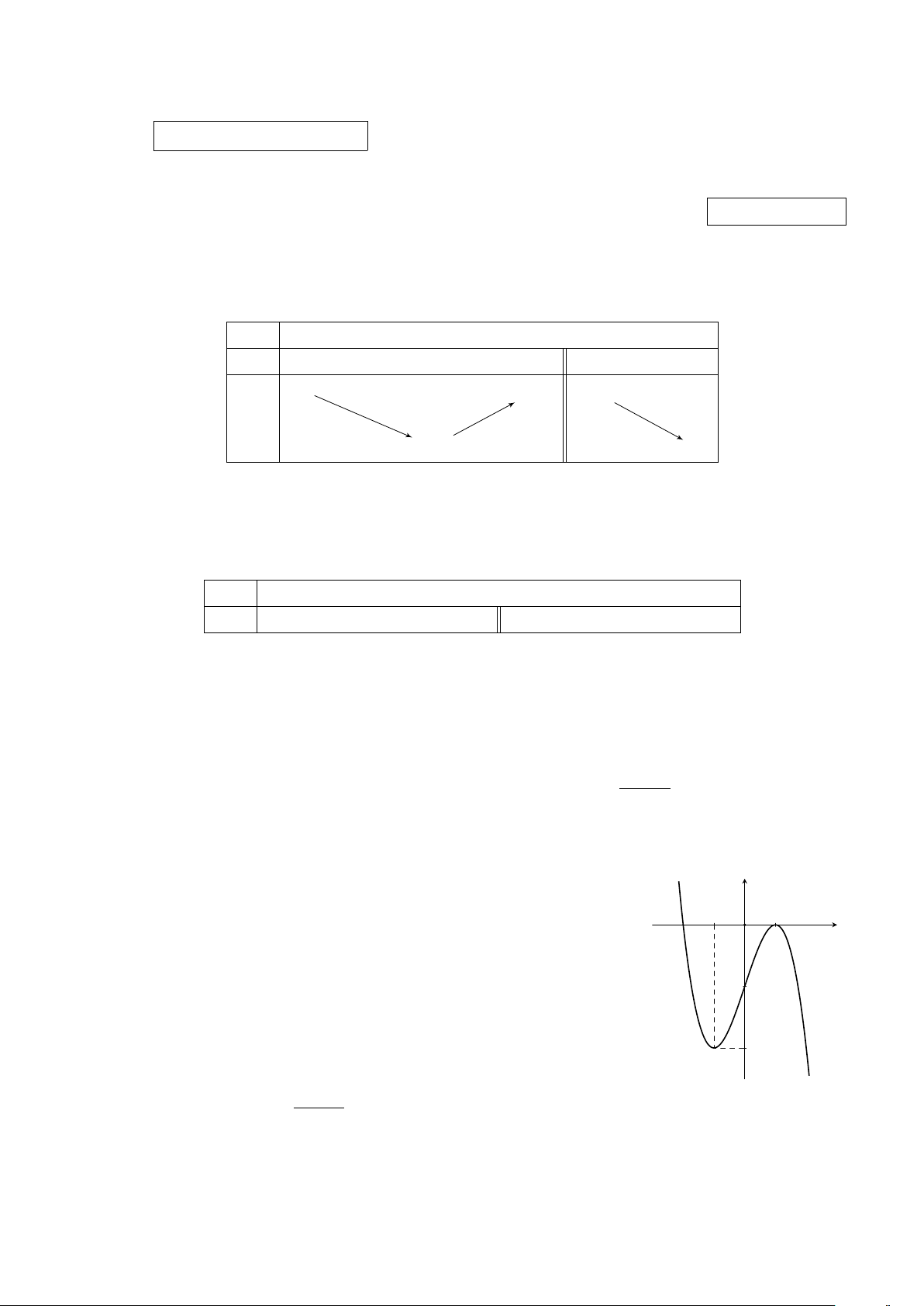
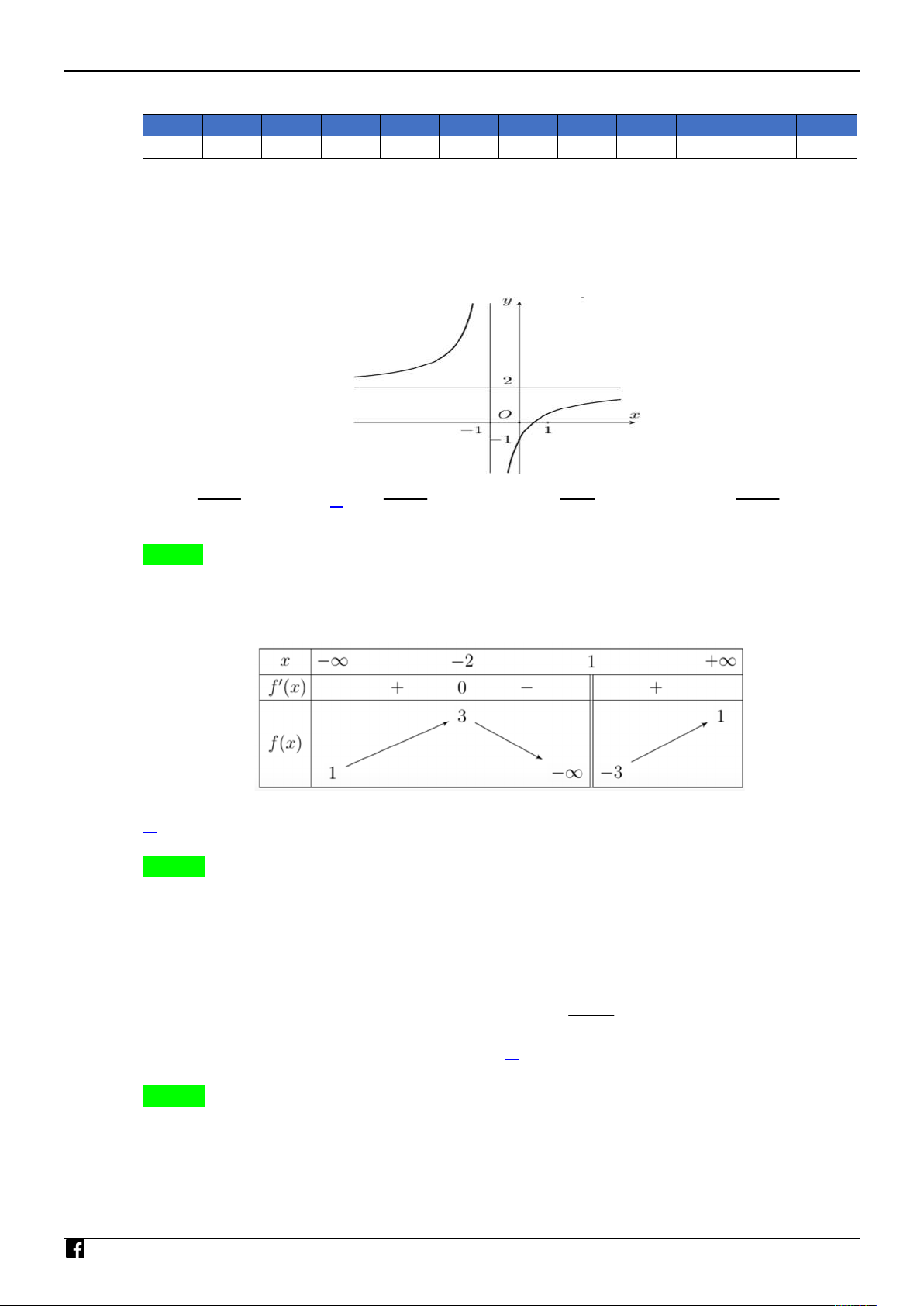
Đường cong trong hình vẽ bên là đồ thị của hàm số nào y
trong các hàm số được cho dưới đây? 2x − 1 2x + 1 A. y = . B. y = . x − 1 x + 1 2x 2x − 1 C. y = . D. y = . x + 1 x + 1 2 O x −1 1 −1
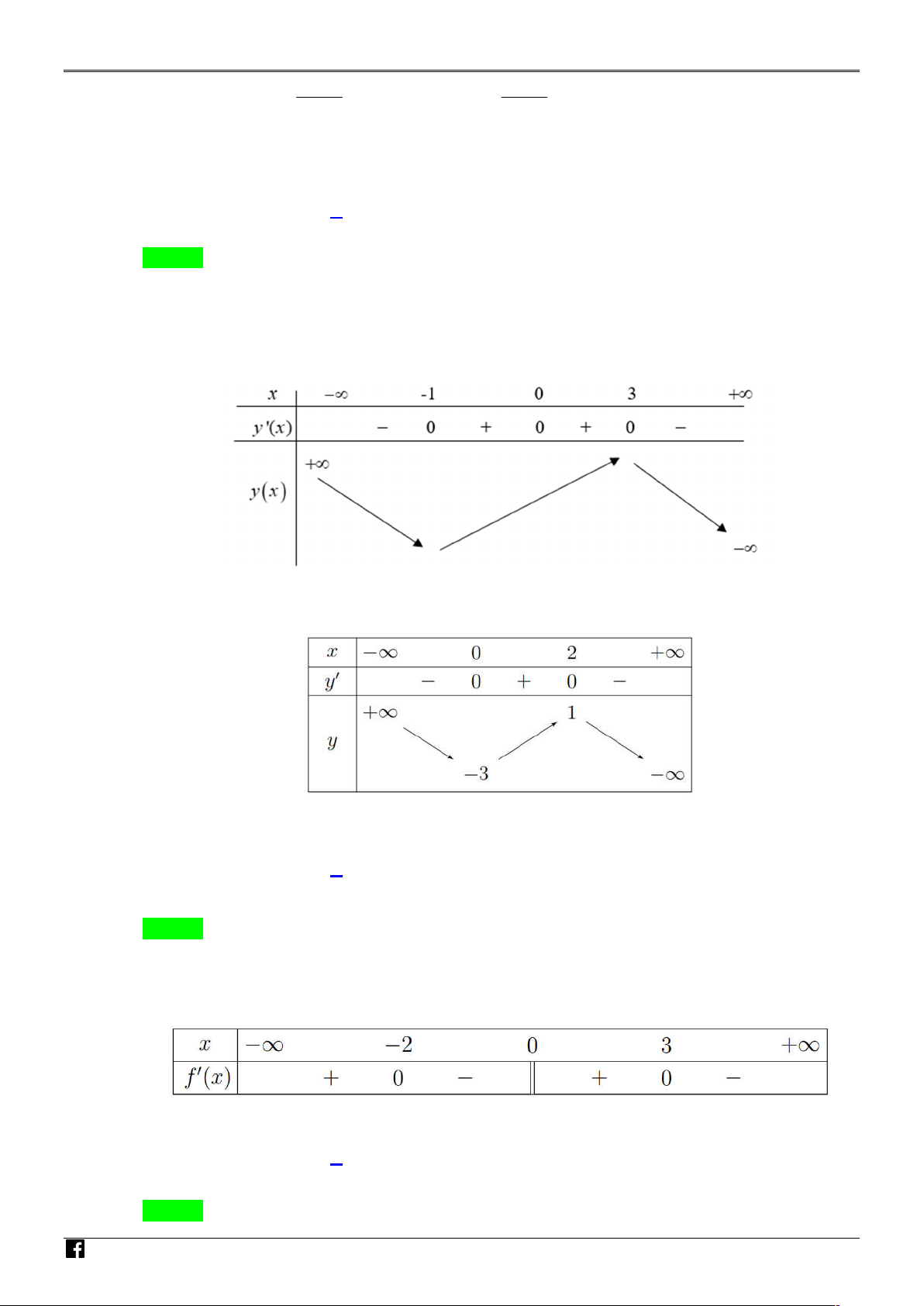
Câu 2. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −2 1 +∞ f ′(x) + 0 − + 3 1 f (x) 1 −∞ −3
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 2. B. 1. C. 3. D. 4. 3x − 2
Câu 3. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = lần lượt là x − 1 A. x = 1, y = 3. B. x = 3, y = 1. C. x = 1, y = −3. D. x = −1, y = 3.
Câu 4. Cho hàm số y = f (x) liên tục trên R và có đạo hàm f ′(x) = x2(3 − x)(x + 1) với mọi
x ∈ R. Khẳng định nào sau đây đúng? A. f (−2) < f (−1). B. f (3) > f (4). C. f (2) > f (3). D. f (−1) > f (2).
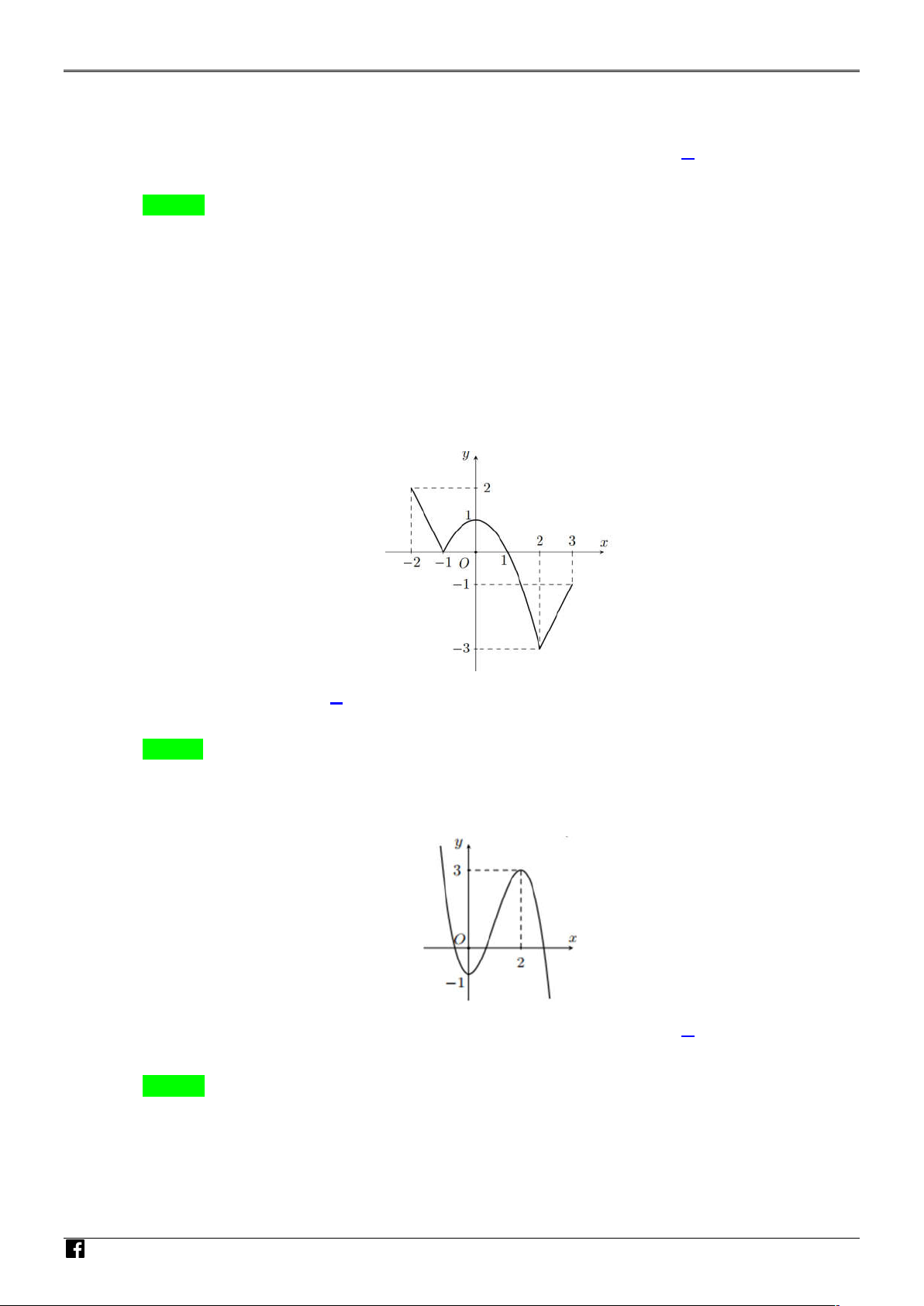
Câu 5. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ sau: x −∞ 0 2 +∞ y′ − 0 + 0 − +∞ + 1 y −3 −∞
Hàm số y = f (x) nghịch biến trên khoảng nào sau đây? A. (0; 2). B. (2; 5). C. (0; +∞). D. (−2; 2). Trang 1/4 − Mã đề 101
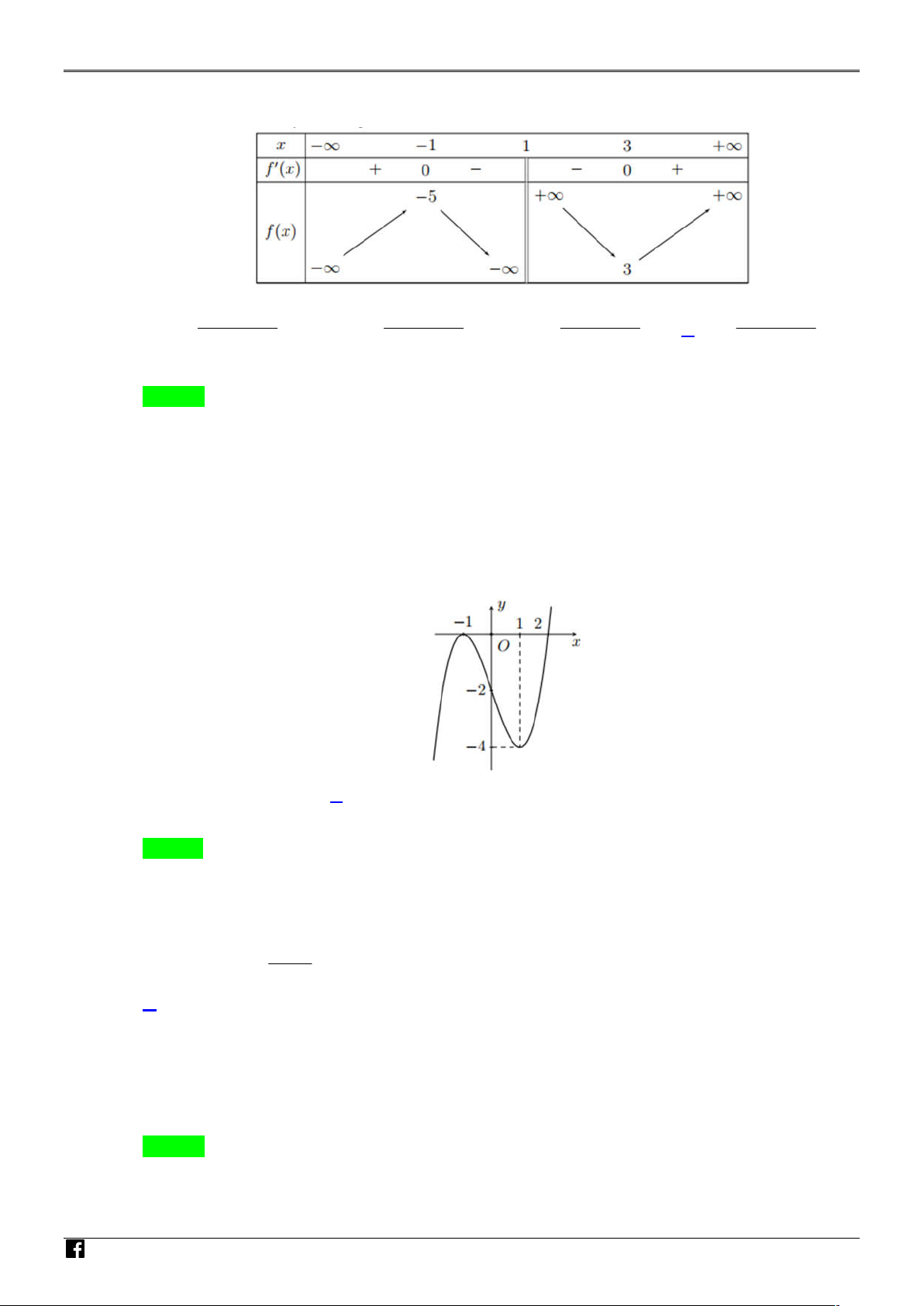
Câu 6. Cho hàm số y = f (x) liên tục trên R và có bảng xét dấu của đạo hàm f ′(x) như sau: x −∞ −2 0 3 +∞ f ′(x) + 0 − + 0 −
Hàm số đã cho có bao nhiêu điểm cực trị? A. 2. B. 3. C. 0. D. 1.
Câu 7. Giá trị nhỏ nhất của hàm số y = 4x3 − 3x4 trên đoạn [−1; 2] bằng A. −24. B. 0. C. −7. D. −16.
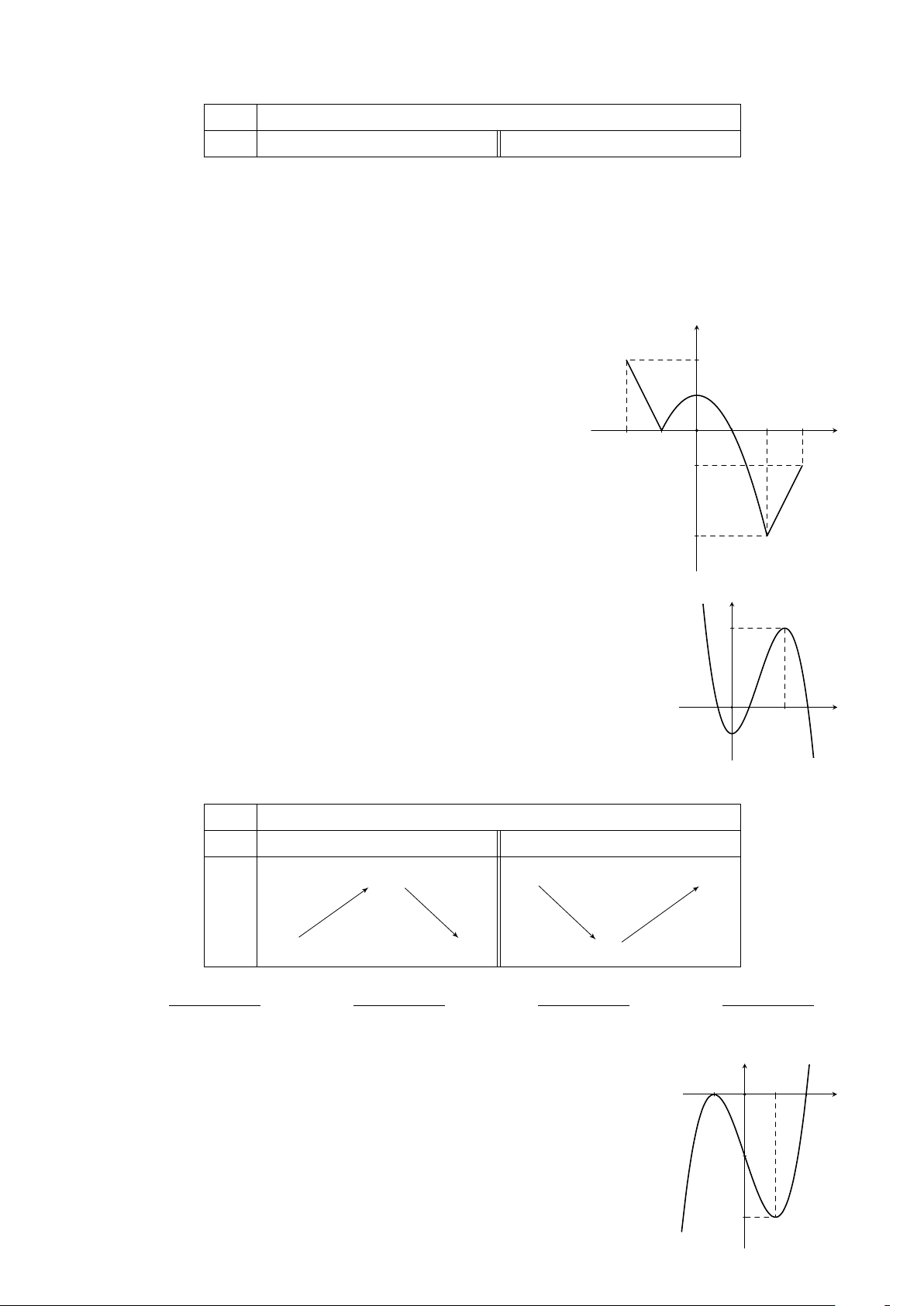
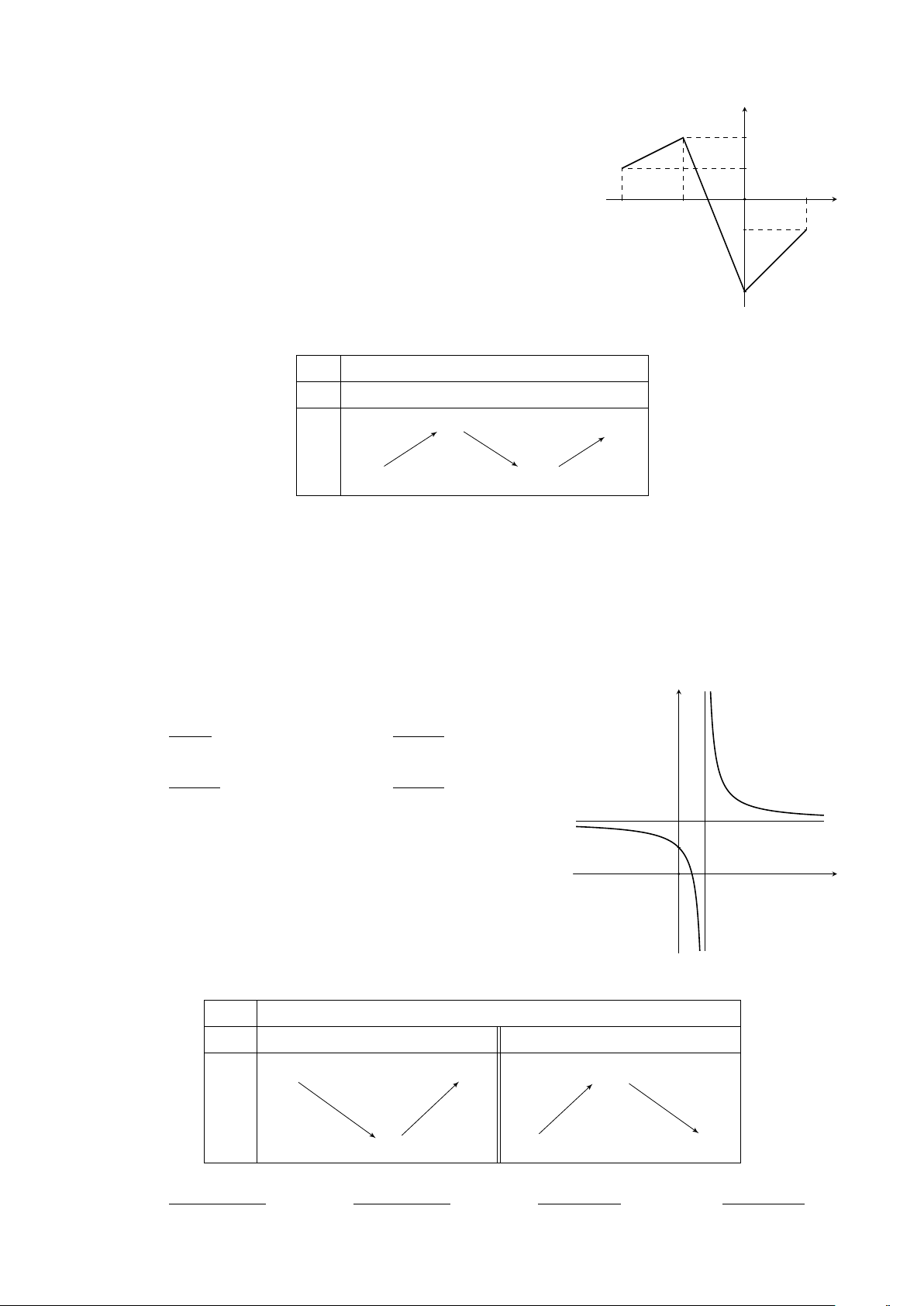
Câu 8. Cho hàm số y = f (x) có đồ thị trên đoạn [−2; 3] y
như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của hàm số y = f (x) trên đoạn [−2; 3]. Tính 2 2M − m. 1 A. 5. B. 7. C. 6. D. 8. 2 3 x −2 −1 O 1 −1 −3
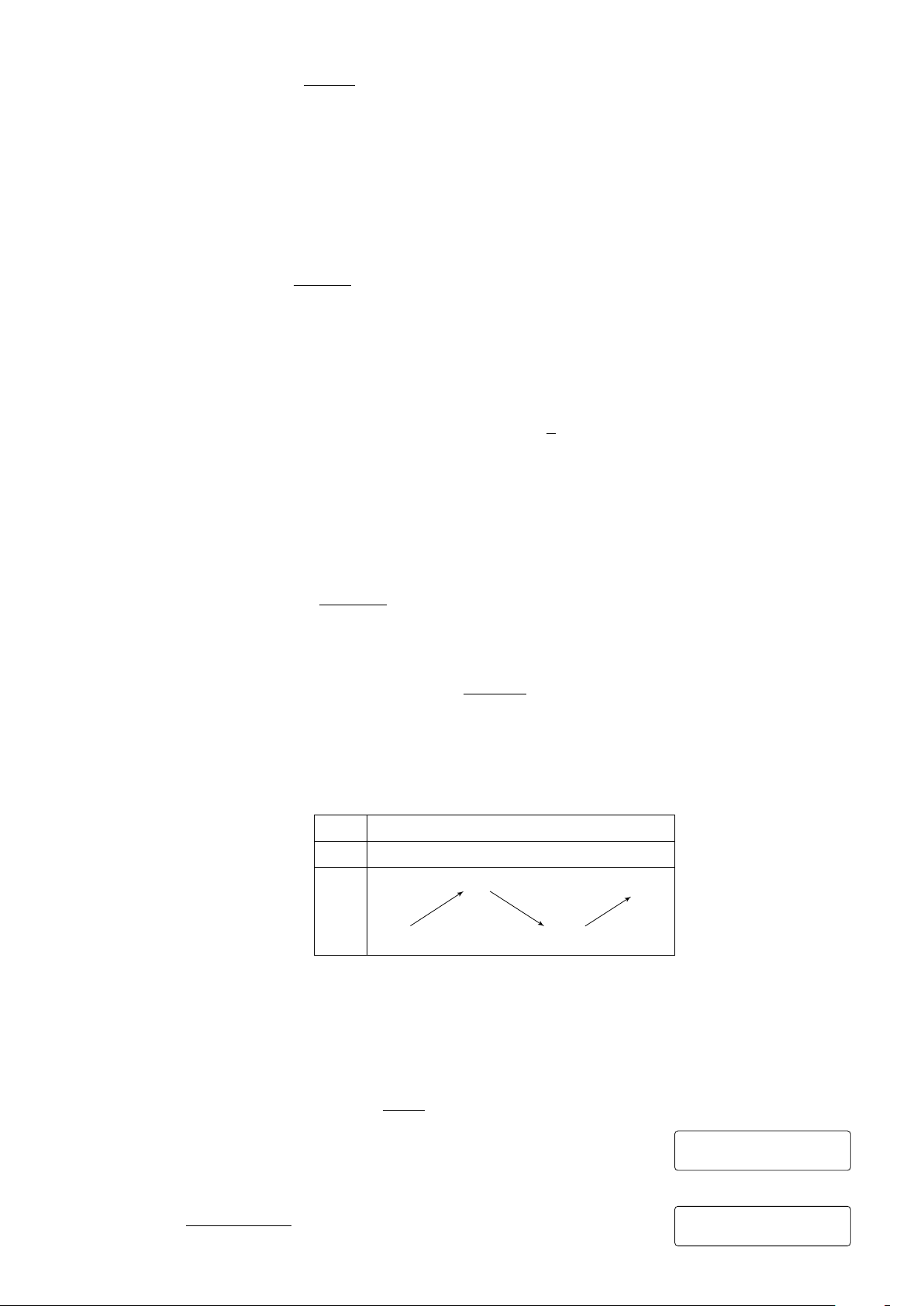
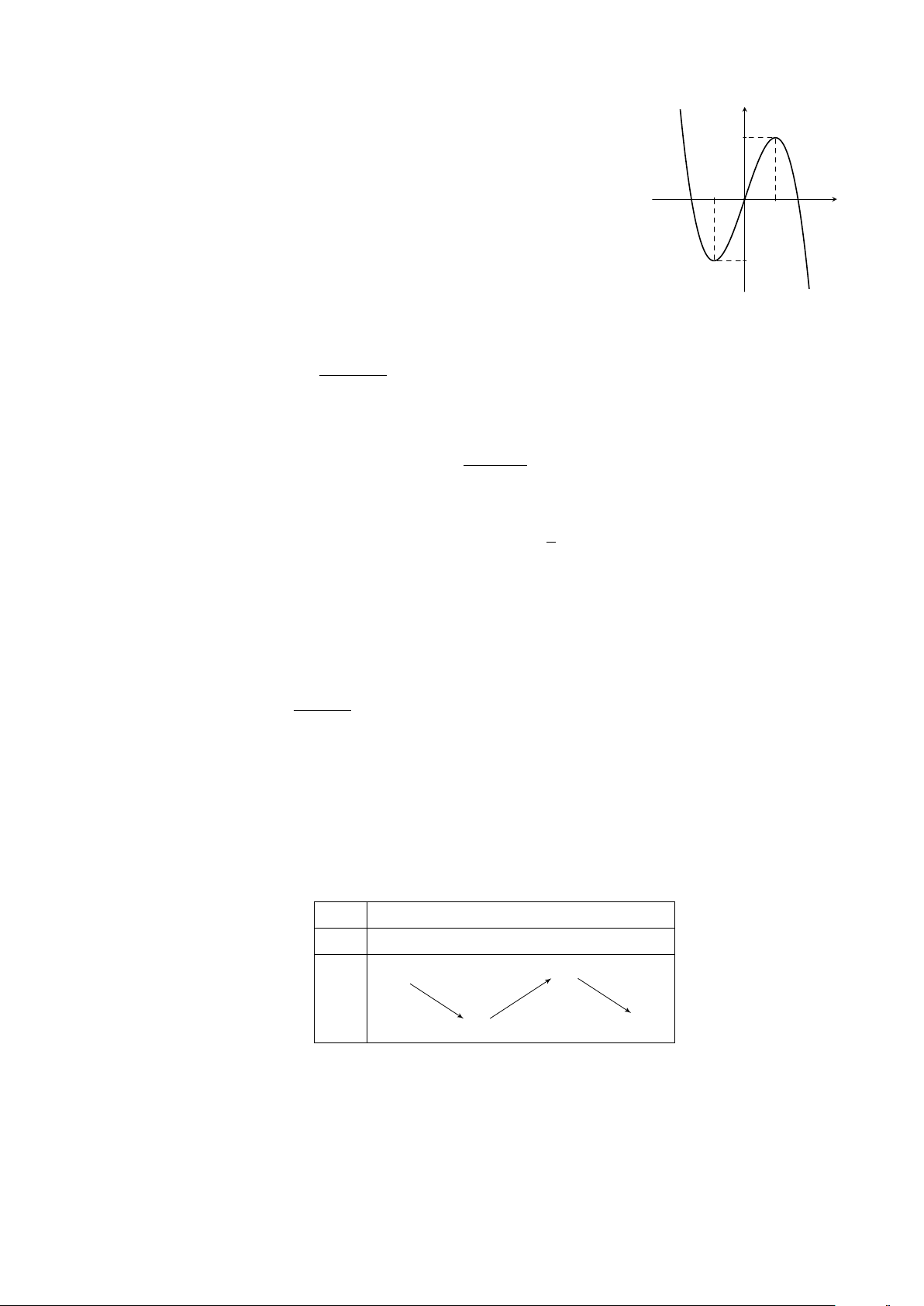
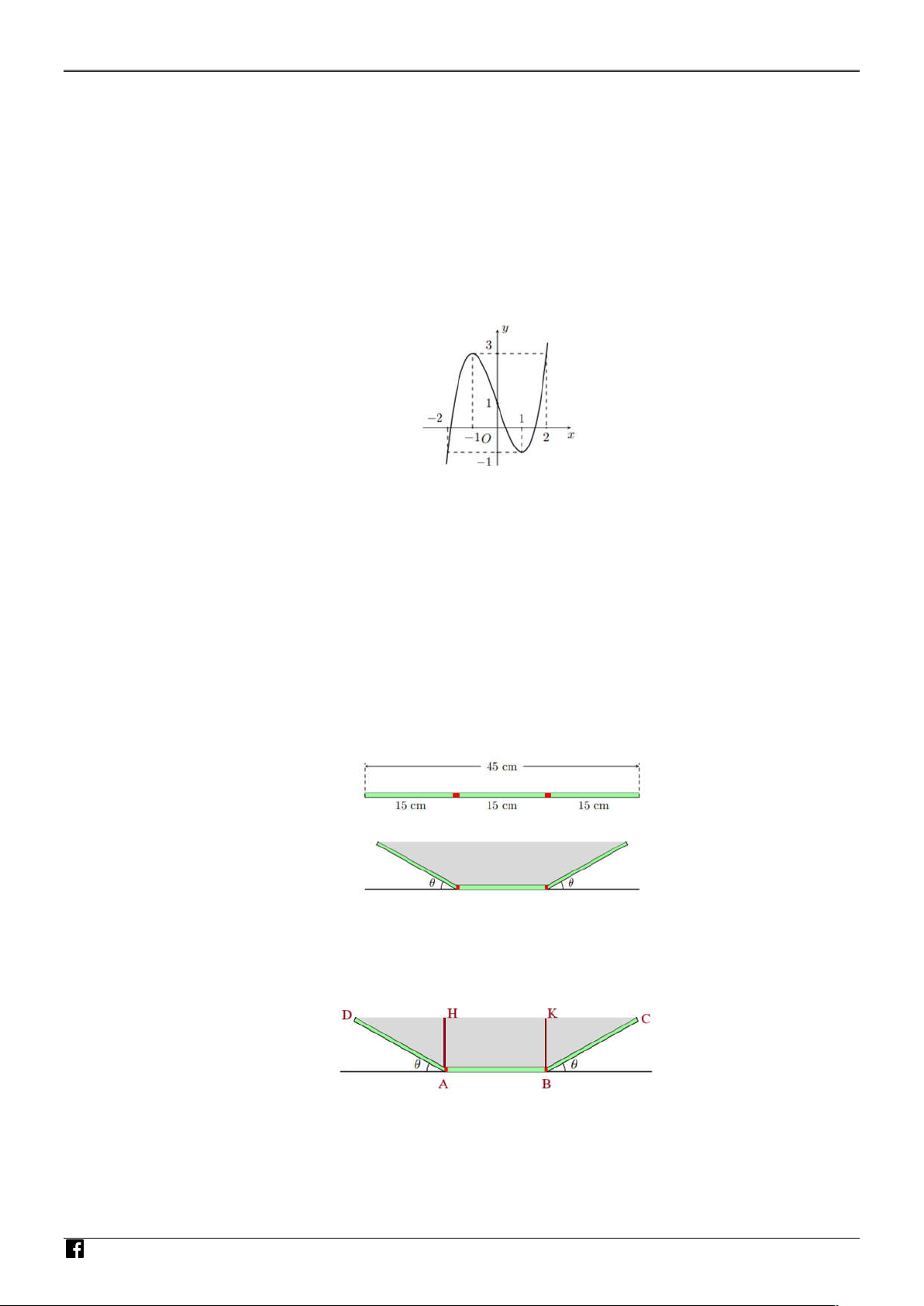
Câu 9. Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau y đây? 3 A. y = −x3 − 3x2 + 1. B. y = −x3 + 3x − 1. C. y = x3 − 3x − 1. D. y = −x3 + 3x2 − 1. O x 2 −1
Câu 10. Hàm số nào dưới đây có bảng biến thiên như sau? x −∞ −1 1 3 +∞ f ′(x) + 0 − − 0 + −5 +∞ +∞ + f (x) −∞ −∞ 3 x2 + 3x − 6 x2 − 3x + 6 x2 + 3x + 6 x2 − 3x + 6 A. y = . B. y = . C. y = . D. y = . 1 − x x + 1 x − 1 x − 1
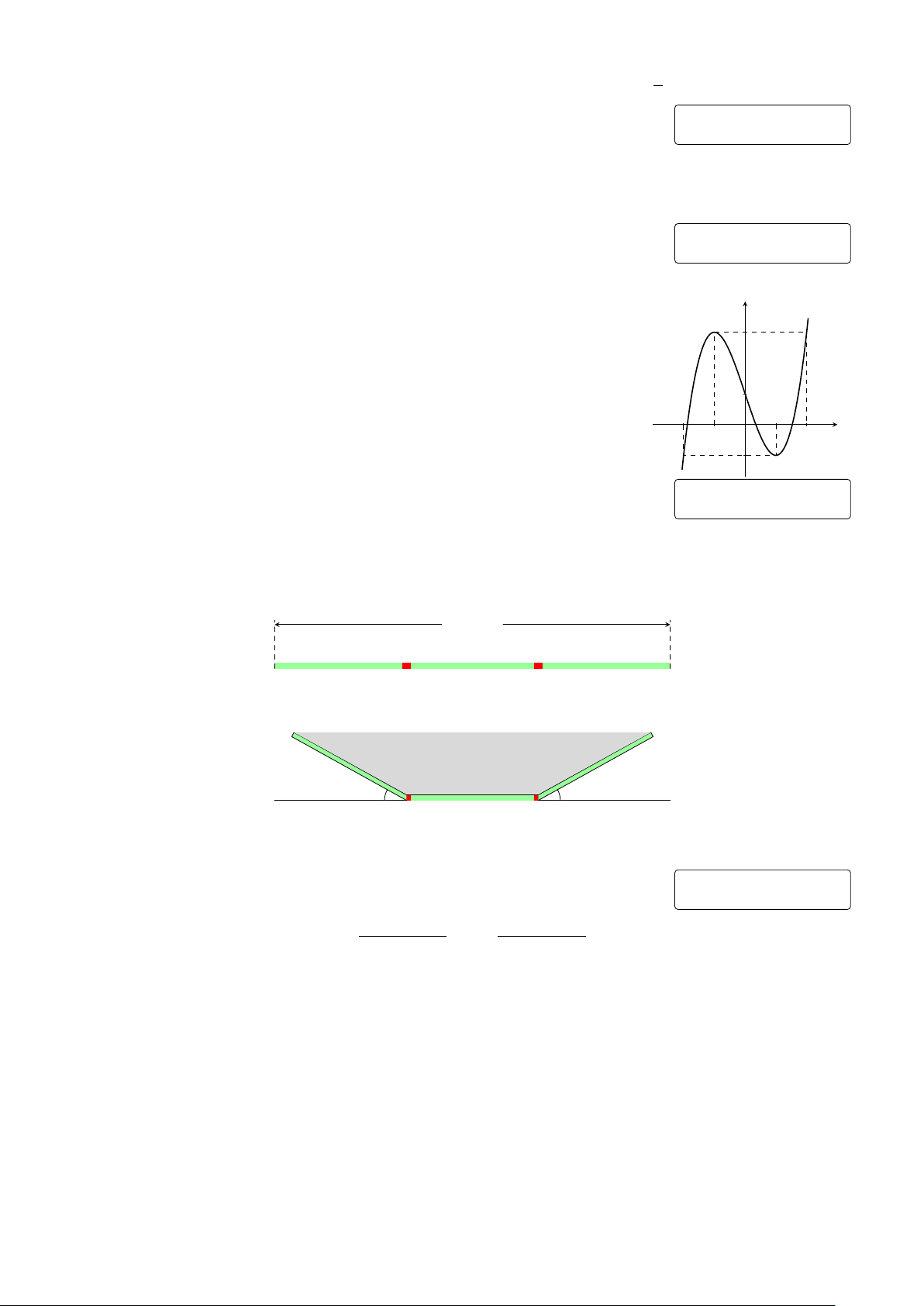
Câu 11. Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ R) có đồ thị y
như hình vẽ. Giá trị cực đại của hàm số bằng −1 1 2 A. 1. B. 0. C. −1. D. −4. O x −2 −4 Trang 2/4 − Mã đề 101 2x − 1 Câu 12. Cho hàm số y =
. Khẳng định nào sau đây đúng? x + 2
A. Hàm số đồng biến trên khoảng (−∞; −2) và (−2; +∞).
B. Hàm số nghịch biến trên khoảng (−∞; −2) và (−2; +∞).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (−∞; −2) ∪ (−2; +∞).
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI. Thí sinh trả lời từ câu 1 đến câu 4. Mỗi ý a), b),
c), d) ở mỗi câu hỏi, thí sinh chọn đúng hoặc sai. 2x + m Câu 1. Cho hàm số y = . x + 1
a) Khi m = −1 thì hàm số nghịch biến trên khoảng (−1; +∞).
b) Tập xác định của hàm số là D = R \ {−1}.
c) Đồ thị hàm số có tâm đối xứng là điểm I(−1; 2).
d) Có hai giá trị nguyên dương của m để hàm số đồng biến trên các khoảng xác định. 1
Câu 2. Một vật chuyển động theo phương trình s(t) = − t3 + 6t2 với t tính bằng giây (s) và s(t) 3
được tính bằng mét (m) là quãng đường vật di chuyển được.
a) Sau 3 giây vật đi được quãng đường dài 45 m.
b) Gia tốc tức thời của vật tại thời điểm t = 7 giây bằng 2 m/s2.
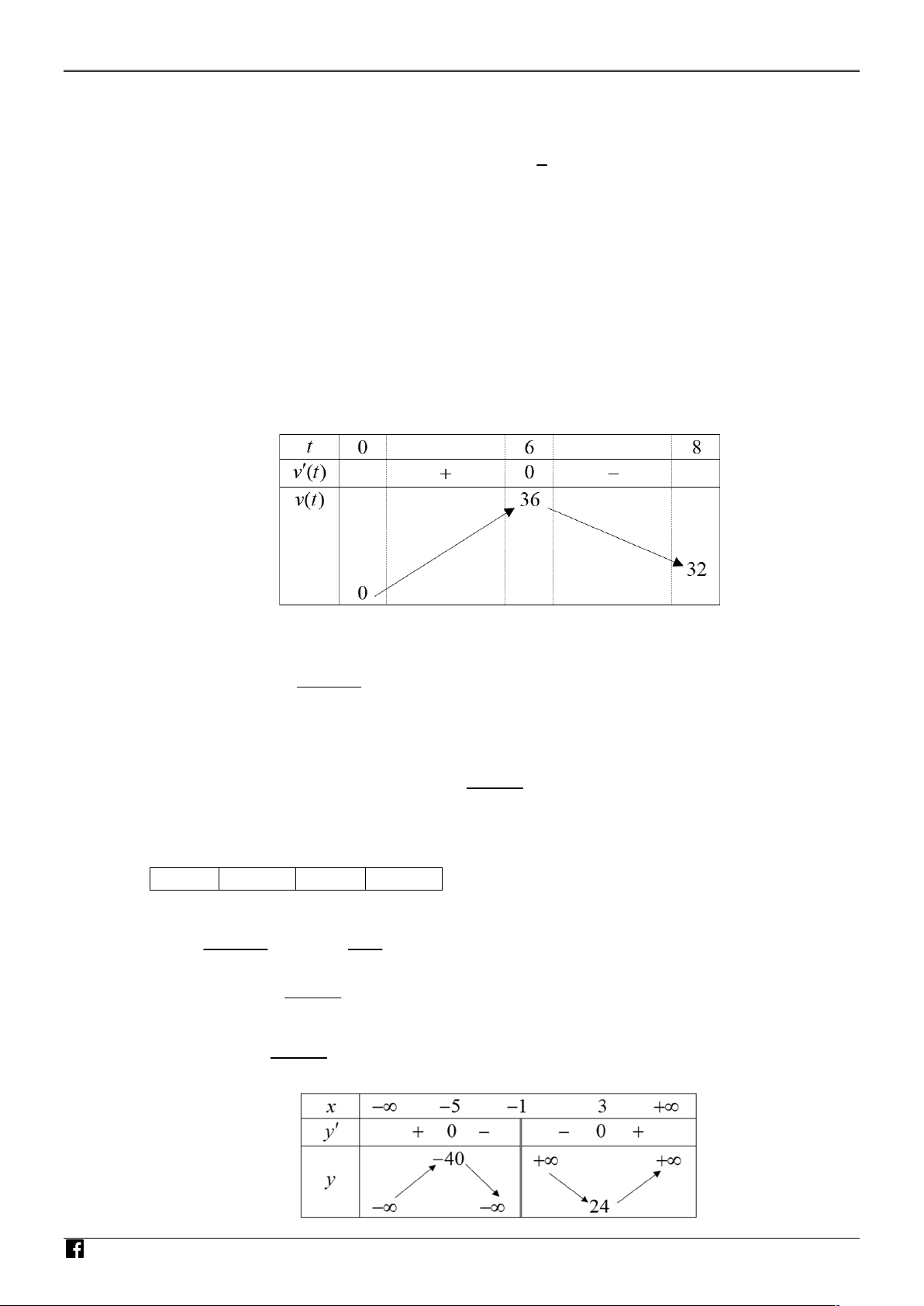
c) Vận tốc của vật được tính bởi công thức v(t) = −t2 + 12t.
d) Vận tốc lớn nhất của vật trong 8 giây đầu tiên là 36 m/s. 4x2 + 60 Câu 3. Cho hàm số f (x) = . x + 1
a) Hàm số đã cho đạt cực đại tại điểm x = −5.
b) Hàm số f (x) đồng biến trên khoảng (−1; +∞). 64
c) Đạo hàm của hàm số đã cho f ′(x) = 4 − . (x + 1)2
d) Tiệm cận xiên của đồ thị hàm số có phương trình y = 4x − 4.
Câu 4. Cho hàm số f (x) = x3 − 3x2 + 2.
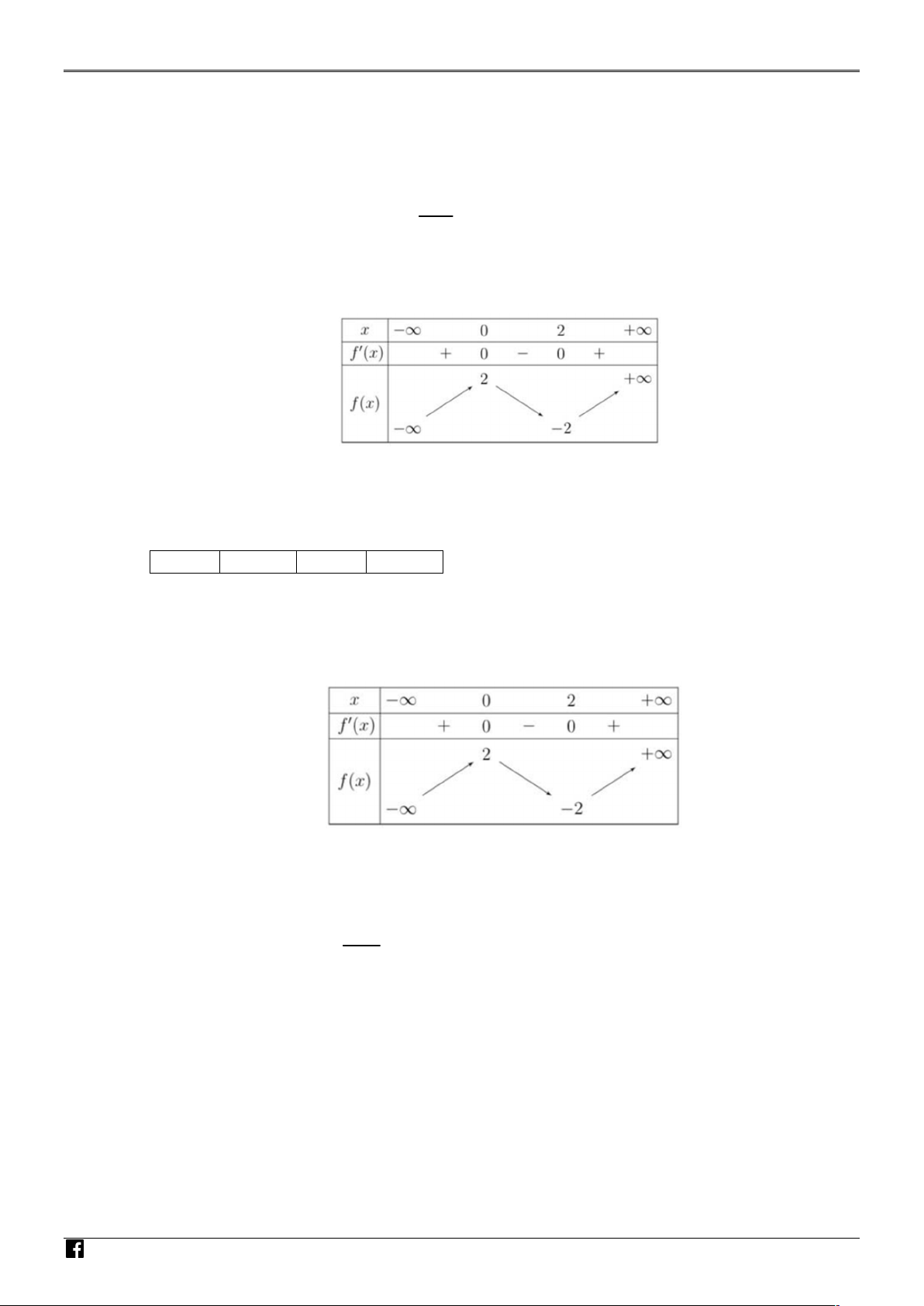
a) Bảng biến thiên của hàm số đã cho là x −∞ 0 2 +∞ f ′(x) + 0 − 0 + 2 +∞ + f (x) −∞ −2 −
b) Đạo hàm của hàm số đã cho là f ′(x) = 3x2 − 6x.
c) Giá trị lớn nhất của hàm số đã cho trên R bằng 2.
d) Với mỗi giá trị của m ∈ (−2; 2) phương trình f (x) = m có ba nghiệm phân biệt.
PHẦN III. TRẮC NGHIỆM TRẢ LỜI NGẮN. Thí sinh trả lời từ câu 1 đến câu 6. 3
Câu 1. Đồ thị hàm số y = 2x − 1 +
có tâm đối xứng là điểm I(a; b). Giá trị của biểu thức x − 2 a2 + b2 bằng KQ:
Câu 2. Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y = m không cắt đồ thị −x2 + 2x − 4 hàm số y = ? KQ: x − 2 Trang 3/4 − Mã đề 101 4
Câu 3. Gọi S là tập hợp tất cả các số nguyên m sao cho hàm số y = x3 − mx2 + 4x − 1 đồng 3
biến trên R. Số phần tử của tập hợp S bằng KQ:
Câu 4. Dân số Việt Nam sau t năm tính từ năm 2023 được dự đoán theo công thức
N (t) = 100 · e0,012t (triệu người), với 0 < t ≤ 50. Biết rằng đạo hàm của hàm số N (t) biểu thị tốc
độ gia tăng dân số của Việt Nam (đơn vị là triệu người/năm). Sau ít nhất bao nhiêu năm thì tốc
độ gia tăng dân số của Việt Nam sẽ lớn hơn 2 triệu người/năm? KQ:
Câu 5. Cho hàm số y = f (x) có đạo hàm trên R và có đồ thị như hình y
vẽ bên. Tìm m để giá trị lớn nhất của hàm số g(x) = f (2x3+x−1)+m 3
trên đoạn [0; 1] bằng −10. 1 −2 1 −1 O x 2 −1 KQ:
Câu 6. Bác Nam dự định làm một máng thoát nước mưa từ một miếng tôn hình chữ nhật có
chiều dài 8 m và chiều rộng 45 cm. Bác Nam chia chiều rộng của miếng tôn thành ba phần bằng
nhau, mỗi phần dài 15 cm, rồi gập hai bên lên một góc θ (đơn vị radian) như hình vẽ dưới đây 45 cm 15 cm 15 cm 15 cm θ θ
Gọi S (cm2) là diện tích của mặt cắt ngang của máng nước. Tìm góc θ (làm tròn kết quả đến
chữ số thứ hai sau dấu phẩy) để diện tích S là lớn nhất (sẽ cho phép nước thoát qua máng nhiều nhất). KQ: HẾT Trang 4/4 − Mã đề 101 TRƯỜNG THCS&THPT
ĐỀ KIỂM TRA GIỮA KỲ I LỚP 12
NGUYỄN BỈNH KHIÊM - CẦU GIẤY NĂM HỌC 2024 - 2025 ĐỀ THI CHÍNH THỨC Môn: TOÁN (Đề thi có 4 trang)
Thời gian làm bài: 90 phút
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 102
PHẦN I. TRẮC NGHIỆM 4 PHƯƠNG ÁN. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −1 2 +∞ f ′(x) − 0 + − 0 +∞ +∞ f (x) −2 − 0
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 2. B. 4. C. 1. D. 3.
Câu 2. Cho hàm số y = f (x) liên tục trên R và có bảng xét dấu của đạo hàm f ′(x) như sau: x −∞ −1 1 3 +∞ f ′(x) − 0 + − 0 +
Hàm số đã cho có bao nhiêu điểm cực trị? A. 2. B. 1. C. 0. D. 3.
Câu 3. Giá trị lớn nhất của hàm số y = 3x4 − 4x3 + 1 trên đoạn [−1; 2] bằng A. 8. B. 18. C. 16. D. 17. 4x − 1
Câu 4. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = lần lượt là x − 2 A. x = 2, y = −4. B. x = 4, y = 2. C. x = 2, y = 4. D. x = −2, y = 4.
Câu 5. Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ R) có đồ thị y
như hình vẽ. Giá trị cực đại của hàm số bằng A. −1. B. 1. C. −4. D. 0. −1 1 x O −2 −4 2x + 3 Câu 6. Cho hàm số y =
. Khẳng định nào sau đây đúng? x + 1
A. Hàm số nghịch biến trên (−∞; −1) ∪ (−1; +∞).
B. Hàm số nghịch biến trên khoảng (−∞; −1) và (−1; +∞).
C. Hàm số nghịch biến trên R.
D. Hàm số đồng biến trên khoảng (−∞; −1) và (−1; +∞). Trang 1/4 − Mã đề 102
Câu 7. Cho hàm số y = f (x) có đồ thị trên đoạn [−4; 2] như y
hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số y = f (x) trên đoạn [−4; 2]. Tính M − 2m. 2 A. 7. B. 8. C. 10. D. 5. 1 O 2 x −4 −2 −1 −3
Câu 8. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ sau: x −∞ −1 1 +∞ y′ + 0 − 0 + 2 +∞ + y −∞ −2
Hàm số y = f (x) đồng biến trên khoảng nào sau đây? A. (−1; 1). B. (1; 5). C. (−2; +∞). D. (−∞; 2).
Câu 9. Cho hàm số y = f (x) liên tục trên R và có đạo hàm f ′(x) = x(3 − x)(x + 1)2 với mọi
x ∈ R. Khẳng định nào sau đây đúng? A. f (0) > f (−1). B. f (1) > f (2). C. f (3) > f (1). D. f (4) > f (3).
Câu 10. Đường cong trong hình vẽ bên là đồ thị của hàm y
số nào trong các hàm số được cho dưới đây? 2x 2x + 1 A. y = . B. y = . x − 1 x − 1 2x − 1 2x − 1 C. y = . D. y = . x − 1 x + 1 2 1 x O 1
Câu 11. Hàm số nào dưới đây có bảng biến thiên như sau? x −∞ −3 −1 1 +∞ f ′(x) − 0 + + 0 − +∞ + +∞ −1 − f (x) 7 −∞ −∞ −x2 + x − 2 −x2 − x − 2 x2 − x − 2 x2 − x + 2 A. y = . B. y = . C. y = . D. y = . x + 1 x + 1 x + 1 x − 1 Trang 2/4 − Mã đề 102
Câu 12. Đường cong trong hình vẽ bên là đồ thị của hàm số nào y sau đây? A. y = x3 − 3x. B. y = −x3 + 3x + 1. 2 C. y = −x3 + 3x. D. y = −x3 + 3x2. −1 x O 1 −2
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI. Thí sinh trả lời từ câu 1 đến câu 4. Mỗi ý a), b),
c), d) ở mỗi câu hỏi, thí sinh chọn đúng hoặc sai. 3x2 + 45 Câu 1. Cho hàm số f (x) = . x − 1
a) Hàm số đã cho đạt cực tiểu tại điểm x = 5.
b) Hàm số f (x) nghịch biến trên khoảng (−∞; 1). 48
c) Đạo hàm của hàm số đã cho f ′(x) = 3 − . (x − 1)2
d) Tiệm cận xiên của đồ thị hàm số có phương trình y = 3x + 3. 1
Câu 2. Một vật chuyển động theo phương trình s(t) = − t3 + 5t2 với t tính bằng giây (s) và s(t) 3
được tính bằng mét (m) là quãng đường vật di chuyển được.
a) Sau 3 giây vật đi được quãng đường dài 36 m.
b) Vận tốc của vật được tính bởi công thức v(t) = −t2 + 10t.
c) Gia tốc tức thời của vật tại thời điểm t = 6 giây bằng 2 m/s2.
d) Vận tốc lớn nhất của vật trong 8 giây đầu tiên là 25 m/s. 3x − m Câu 3. Cho hàm số y = . x − 2
a) Đồ thị hàm số có tâm đối xứng là điểm I(2; 3).
b) Tập xác định của hàm số là D = R \ {2}.
c) Khi m = 1 thì hàm số đồng biến trên khoảng (2; +∞).
d) Có năm giá trị nguyên dương của m để hàm số nghịch biến trên các khoảng xác định.
Câu 4. Cho hàm số f (x) = −x3 − 3x2 + 4.
a) Bảng biến thiên của hàm số đã cho là x −∞ −2 0 +∞ f ′(x) − 0 + 0 − +∞ + 4 f (x) 0 −∞
b) Đạo hàm của hàm số đã cho là f ′(x) = −3x2 − 6x.
c) Giá trị nhỏ nhất của hàm số đã cho trên R bằng 0.
d) Với mỗi giá trị của m ∈ (0; 4) phương trình f (x) = m có ba nghiệm phân biệt.
PHẦN III. TRẮC NGHIỆM TRẢ LỜI NGẮN. Thí sinh trả lời từ câu 1 đến câu 6.
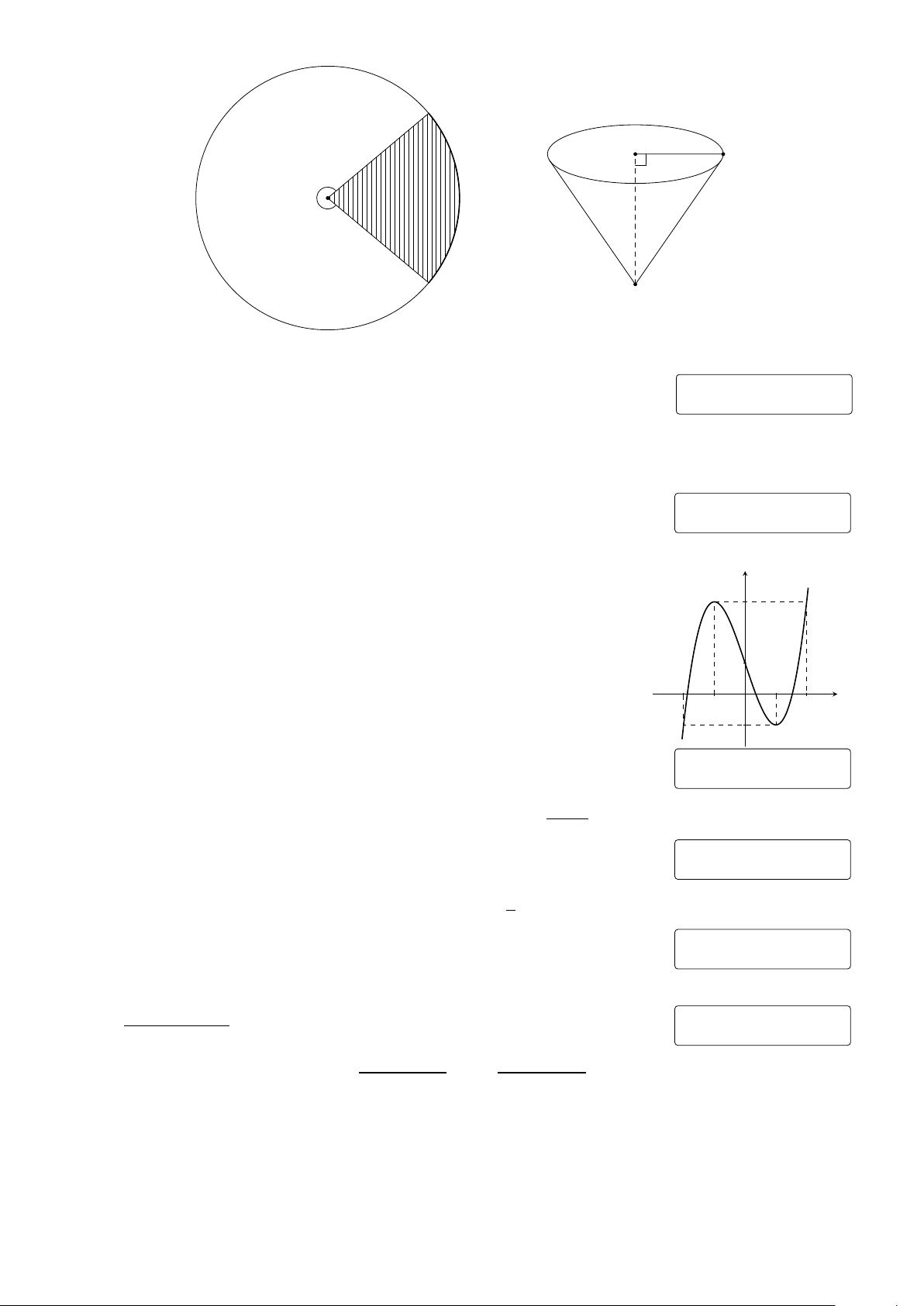
Câu 1. Cắt bỏ hình quạt tròn AOB (hình phẳng có nét gạch trong hình vẽ dưới đây) từ một
mảnh giấy hình tròn bán kính bằng 30 cm rồi dán hai bán kính OA và OB của hình quạt tròn
còn lại với nhau để được một cái phễu có dạng một hình nón. Trang 3/4 − Mã đề 102 A H B r θ O h B O
Gọi θ (đơn vị radian) là góc ở tâm của quạt tròn dùng làm phễu (0 < θ < 2π). Tìm θ để khối nón có
thể tích lớn nhất (làm tròn kết quả đến chữ số thứ hai sau dấu phẩy). KQ:
Câu 2. Dân số Việt Nam sau t năm tính từ năm 2023 được dự đoán theo công thức
N (t) = 100 · e0,012t (triệu người), với 0 < t ≤ 50. Biết rằng đạo hàm của hàm số N (t) biểu thị tốc
độ gia tăng dân số của Việt Nam (đơn vị là triệu người/năm). Sau ít nhất bao nhiêu năm thì tốc
độ gia tăng dân số của Việt Nam sẽ lớn hơn 1,5 triệu người/năm? KQ:
Câu 3. Cho hàm số y = f (x) có đạo hàm trên R và có đồ thị như hình y
vẽ bên. Tìm m để giá trị nhỏ nhất của hàm số g(x) = f (2x3+x−1)+m 3
trên đoạn [0; 1] bằng −16. 1 −2 1 −1 O x 2 −1 KQ: 3
Câu 4. Tiệm cận xiên của đồ thị hàm số y = 2x − 5 +
tạo với hai trục tọa độ một tam x + 2 giác có diện tích bằng KQ: 1
Câu 5. Có bao nhiêu số nguyên m để hàm số y =
x3 − x2 + (m2 − 7)x + 2 có cực đại và cực 3 tiểu? KQ:
Câu 6. Có bao nhiêu số nguyên m ∈ [−2024; 2024] để đường thẳng y = m cắt đồ thị hàm số −x2 + 2x − 4 y =
tại hai điểm phân biệt? KQ: x − 2 HẾT Trang 4/4 − Mã đề 102
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25 BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 B A C B B B D B D D B A HƯỚNG DẪN GIẢI
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1.
Đường cong của hình vẽ bên là đồ thị của hàm số nào trong các hàm số được cho dưới đây? NHÓM GIÁO VIÊ 2x 1 2x 1 2x 2x 1 N A. y  . B. y  . C. y  . D. y  . T x 1 x 1 x 1 x 1 OÁN Lời giải Chọn B VI
Dựa vào đồ thị suy ra tiệm cận đứng x  1
 , tiệm cận ngang là y  2 . Ệ T
Đồ thị hàm số giao với trục hoành có hoành độ dương suy ra chọn B. N Câu 2.
Cho hàm số y f x có bảng biến thiên như sau: AM
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 2 . B. 1. C. 3 . D. 4 . NHÓM Lời giải Chọn A
Từ bảng biến thiên đã cho ta có: GIÁO VIÊ
lim f x  1 nên đường thẳng y  1 là một tiệm cận ngang của đồ thị hàm số. x
lim f x   nên đường thẳng x  1 là một tiệm cận đứng của đồ thị hàm số. x 1 
Vậy đồ thị hàm số đã cho có hai đường tiệm cận. N 3x  2 T Câu 3.
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  lần lượt là OÁN x 1
A. x  1, y  3 .
B. x  1, y  3 .
C. x  1, y  3 .
D. x  1, y  3 . VI Lời giải Ệ Chọn C T N 3x  2 3x  2 Ta có lim   và lim
  nên x  1 là tiệm cận đứng của đồ thị hàm số. AM x 1  x 1 x 1  x 1
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25 3x  2 3x  2 Ta có: lim y  lim  3 và lim y  lim
 3 nên y  3 là tiệm cận ngang của đồ x x x 1 x x x 1 thị hàm số. Câu 4.
Cho hàm số y f x liên tục trên  và có đạo hàm f  x 2
x (3  x)(x 1) với mọi x   .
Khẳng định nào sau đây đúng? A. f  2
   f   1 .
B. f 3  f 4 .
C. f 2  f 3 . D. f   1  f 2 . Lời giải Chọn Bx  0 
Ta có f ' x 2
x (3  x)(x 1)  0  x  3 .  NHÓM x  1  Bảng biến thiên: GIÁO VIÊ N T OÁN VI
Dựa vào bảng biến thiên cho thấy hàm số nghịch biến trên 3;  do đó f 3  f 4 . Ệ       T Câu 5.
Cho hàm số y f x có bảng biến thiên như hình vẽ sau: N   AM
Hàm số y f x nghịch biến trên khoảng nào sau đây? NHÓM A. 0; 2 . B. (2;5) . C. (0; ) . D. ( 2  ; 2) . Lời giải GIÁO VIÊ Chọn B
Hàm số y f x nghịch biến trên khoảng (2;5) . N T Câu 6.
Cho hàm số y f x liên tục trên  và có bảng xét dấu của đạo hàm f  x như sau: OÁN VI Ệ T N
Hàm số đã cho có bao nhiêu điểm cực trị? AM A. 2 . B. 3 . C. 0 . D. 1. Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
Hàm số đã cho có điểm 3 cực trị. Câu 7.
Giá trị nhỏ nhất của hàm số 3 4
y  4x  3x trên đoạn  1  ; 2 bằng: A. 24  . B. 0 . C. 7 . D. 1  6 . Lời giải Chọn Dx  0 (tm) +) Ta có 2 3
y '  12x 12x  0   . x  1(tm) 
+) Ta tính được y   1  7
 ; y 0  0; y  
1  1; y 2  16  . NHÓM
Vậy min y y(2)  16 . 1;2 GIÁO VIÊ Câu 8.
Cho hàm số y f x có đồ thị trên đoạn  2  ; 
3 như hình vẽ bên. Gọi M , m lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của hàm số y f x trên đoạn 2; 
3 . Tính 2M m . N T OÁN VI Ệ T N AM A. 6. B. 7. C. 5. D. 8. Lời giải Chọn B
Dựa vào đồ thị trên đoạn  2  ; 
3 ta có M  2 và m  3
 suy ra 2M m  2.2  3  7 . Câu 9.
Đường cong hình vẽ bên là đồ thị của hàm số nào sau đây? NHÓM GIÁO VIÊ N T OÁN A. 3 2
y  x  3x 1. B. 3
y  x  3x 1. C. 3
y x  3x 1. D. 3 2
y  x  3x 1. Lời giải VI Chọn D Ệ T N
-Dựa vào đồ thị ta thấy lim f x   nên loại đáp án C. AM x
-Ta có: f 0  1  nên loại đáp án A
f 2  3 nên loại đáp án B.
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
Vậy đáp án đúng là D.
Câu 10. Hàm số nào dưới đây có bảng biến thiên như sau? 2 x  3x  6 2 x  3x  6 2 x  3x  6 2 x  3x  6 A. y  . B. y  . C. y  . D. y  . NHÓM 1 x x 1 x 1 x 1 Lời giải GIÁO VIÊ Chọn D
Dựa vào BBT ta thấy hàm số y f x có tiệm cận đứng x  1, vậy loại B Ta thấy f   1  5
 vậy chỉ có đáp án D thỏa mãn. N T
Vậy đáp án đúng là D. OÁN Câu 11. Cho hàm số 3 2
y ax bx cx d a, ,
b c, d   có đồ thị như hình vẽ. Giá trị cực đại của hàm VI số bằng Ệ T N AM A. 1. B. 0 . C. 1. D. 4 . Lời giải NHÓM Chọn B
Dựa vào đồ thị ta thấy giá trị cực đại của hàm số bằng 0. GIÁO VIÊ
Vậy đáp án đúng là B. 2x 1
Câu 12. Cho hàm số y
. Khẳng định nào sau đây đúng? x  2 N
A. Hàm số đồng biến trên khoảng  ;  2   và  2  ;  . T OÁN
B. Hàm số nghịch biến trên khoảng  ;
 2 và 2;  .
C. Hàm số đồng biến trên  . VI
D. Hàm số đồng biến trên khoảng  ;  2     2  ;  . Ệ T N Lời giải AM Chọn A TXĐ:  \   2
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25 3 Ta có: y   0 x    \ 2  2    x  2
Vậy hàm số đồng biến trên các khoảng xác định của nó là  ;  2
  và 2;  . Chọn đáp án A.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. 2x m Câu 1. Cho hàm số y  . x 1 NHÓM a) Khi m  1
 thì hàm số nghịch biến trên khoảng  1  ;  .
b) Tập xác định của hàm số là D   \   1 . GIÁO VIÊ
c) Đồ thị hàm số có tâm đối xứng là điểm I  1  ; 2.
d) Có hai giá trị nguyên dương của m để hàm số đồng biến trên các khoảng xác định. N Lời giải T OÁN
Chọn a) Sai | b) Đúng | c) Đúng | d) Sai. VI 2x 1 3 a) Khi m  1  thì y  . Khi đó y   0, x   1.  Ệ x 1 T  x  2 1 N AM
Hàm số luôn đồng biến trên khoảng  ;    1 và 1; .
b) Tập xác định của hàm số là D   \   1 .
c) Đồ thị hàm số có tiệm cận đứng là x  1
 , tiệm cận ngang là y  2.
Do đó tâm đối xứng là I  1  ; 2. 2  m d) Ta có y  . NHÓM  x  2 1
Hàm số đồng biến trên khoảng trên các khoảng xác định GIÁO VIÊ
y  0, x
  D  2  m  0  m  2. Vì *
m   nên m   1 . N 1 Câu 2.
Một vật chuyển động theo phương trình 3 2
s(t)   t  6t với t tính bằng giây (s) và s(t) được T 3 OÁN
tính bằng mét (m) là quãng đường vật di chuyển được.
a) Sau 3 giây vật đi được quãng đường dài 45 m . VI Ệ T N
b) Gia tốc tức thời của vật tại thời điểm t  7 giây bằng 2 2 m/s . AM
c) Vận tốc của vật được tính bởi công thức 2
v(t)  t  12t .
d) Vận tốc lớn nhất của vật trong 8 giây đầu tiên là 36 m/s .
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25 Lời giải
Chọn a) Đúng | b) Sai | c) Đúng | d) Đúng 1
a) Sau 3 giây vật đi được quãng đường dài: 3 2
s(3)   .3  6.3  45. 3
b) Gia tốc tức thời của vật được xác định bởi công thức a(t)  s (  t)  2  t 12. Do đó 2 a(7)  2  .7 12  2  m \ s .
c) Vận tốc của vật được tính bởi công thức 2
v(t)  s (  t)  t  12t. d) Ta có 2
v(t)  t  12t. NHÓM v (  t)  2
t 12  0  t  6. GIÁO VIÊ Bảng biến thiên: N T OÁN VI Ệ T N AM
Dựa vào bảng biến thiên, trong 8 giây đâu tiên vận tốc lớn nhất của vật đạt 36 m / . s . 2 4x  60 Câu 3.
Cho hàm số f x  . x 1
a) Hàm số đã cho đạt cực đại tại x  5  .
b) Hàm số f x đồng biến trên khoảng  1  ;  . 64
c) Đạo hàm của hàm số đã cho f  x  4  .  x  2 1
d) Tiệm cận xiên của đồ thị hàm số có phương trình là y  4x  4 . NHÓM Lời giải a)Đ b) S c) Đ d) Đ GIÁO VIÊ
Tập xác định: D   \   1 . 2 4x  60 64 f x   4x  4  x 1 x 1 64 N
Ta có: f  x  4  , x   1  T  x  2 1 OÁN 64 x  5
f  x  0  4   0   VI  x  2 1 x  3  Ệ T N AM
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
Hàm số đạt cực đại tại x  5  và y  4  0 . CÐ
Hàm số đạt cực tiểu tại x  3 và y  24 . CT
Hàm số đồng biến trên các khoảng  ;  5   và 3; .
Hàm số nghịch biến trên các khoảng 5;   1 và  1  ; 3 . 64
Ta có: lim  f x  4x  4  lim
 0  y  4x  4  
là đường tiệm cận xiên của đồ thị x
x x 1 hàm số. Câu 4.
Cho hàm số bậc ba f x 3 2
x  3x  2
a) Bảng biến thiên của hàm số đã cho là NHÓM GIÁO VIÊ
b) Đạo hàm của hàm số đã cho là f  x 2  3x  6x . N
c) Giá trị lớn nhất của hàm số đã cho trên  bằng 2. T
d) Với mỗi giá trị m  2;2 phương trình f x  m có ba nghiệm phân biệt. OÁN Lời giải a)Đ b) Đ c) S d) Đ VI  Ệ
Ta có: f x 2  3x  6x T N x  0
f x  0  3x  6x  0  AM   2 x  2  Bảng biến thiên: e NHÓM
Giá trị lớn nhất của hàm số đã cho trên  không tồn tại.
Với mỗi giá trị m   2
 ; 2 phương trình f x  m có ba nghiệm phân biệt.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 GIÁO VIÊ 3 Câu 1.
Đồ thị hàm số y  2x 1
có tâm đối xứng là điểm I a,b . Giá trị của biểu thức 2 2 a b x  2 bằng N Lời giải T OÁN Đáp số: 13 VI
Ta có lim f x   suy ra x  2 là tiệm cận ngang của đồ thị hàm số. x 2  Ệ T N
lim  f x  2x   1   0  
và lim  f x  2x   1   0  
nên y  2x 1 là tiệm cận xiên của đồ x x AM thị hàm số.
Giao điểm của hai đường tiệm cận là nghiệm của hệ phương trình:
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25 x  2 x  2     I 2;3 . y  2x 1 y  3   Vậy 2 2 2 2
a b  2  3  13 . Câu 2.
Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y m không cắt đồ thị hàm số 2
x  2x  4 y  ? x  2 Lời giải Đáp số 7 . 2 NHÓM
x  2x  4
Để đường thẳng y m không cắt đồ thị hàm số y  thì phương trình x  2 2
x  2x  4 GIÁO VIÊ  m vô nghiệm. x  2 2
x  2x  4 Ta có  m  2
x  2  mx  4  2m  0 với x  2 . x  2 N T
Để phương trình vô nghiệm cần OÁN     m2 2
 4 4  2m  0 VI Ệ 2
 4  4m m 16  8m  0 2
m  4m 12  0  6   m  2 . T N AM
Vậy có 7 giá trị nguyên của m . 4 Câu 3.
Gọi S là tập hợp tất cả các số nguyên m sao cho hàm số 3 2 y
x mx  4x 1 đồng biến trên 3
 . Số phần tử của tập hợp S bằng Lời giải Trả lời: 9
Tập xác định D   NHÓM Ta có 2
y  4x  2mx  4 . GIÁO VIÊ 4 Để hàm số 3 2 y
x mx  4x 1 đồng biến trên  . 3 a  0 2 y  0, x       m 16  0  4   m  4 . N   0  T OÁN
Vì m    có 9 giá trị thỏa mãn. VI Câu 4.
Dân số Việt Nam sau t năm tính từ năm 2023 được dự đoán theo công thức   0,012  100. t N t e Ệ T N
(triệu người), với 0  t  50 . Biết rằng đạo hàm của hàm số N t  biểu thị tốc độ gia tăng dân số AM
của Việt Nam (đơn vị là triệu người/ năm). Sau ít nhất bao nhiêu năm thì tốc độ gia tăng dân số
của Việt Nam sẽ lớn hơn 2 triệu người/ năm? Lời giải Trả lời: 43
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25 Ta có   0,012t     0,012 100.  1, 2. t N t e N t e .
Tốc độ gia tăng dân số của Việt Nam sẽ lớn hơn 2 triệu người/ năm   0,012  2  1, 2. t N t e
 2  t  42,56 .
Suy ra, sau ít nhất 43 năm thì tốc độ gia tăng dân số của Việt Nam sẽ lớn hơn 2 triệu người/ năm. Câu 5.
Cho hàm số y f x có đạo hàm trên  và có đồ thị như hình bên. Tìm m để giá trị lớn nhất
của hàm số g x  f  3 2x x  
1  m trên đoạn 0  ;1 bằng 1  0 . NHÓM GIÁO VIÊ N Lời giải T Có 2 3
gx  6x  1 . f  2x x 1 OÁN       3 3
2x x 1  1
 2x x  0  x  0 3 VI
g x  0  f 2x x   1  0    .  3  3 
2x x 1  1
2x x  2  0 x x  0,84 Ệ    0 T N
Tính được g 0  f   1  m  3  , m g  
1  f 2  m  3  ,
m g x f 1  m  1 . m 0    AM
Nên max g x  3  m  10   m  13 . 0;  1 Câu 6.
Bác Nam dự định làm một máng thoát nước mưa từ một miếng tôn hình chữ nhật có chiều dài
8 m và chiều rộng 45 cm. Bác Nam chia chiều rộng của miếng tôn thành ba phần bằng nhau,
mỗi phần dài 15 cm, rồi gập hai bên lên một góc  ( đơn vị radian) như hình vẽ dưới đây. NHÓM GIÁO VIÊ
Gọi S (cm2) là diện tích của mặt cắt ngang của máng nước. Tìm góc  (làm tròn kết quả đến
chữ số thứ hai sau dấu phẩy) để diện tích S là lớn nhất (sẽ cho phép nước thoát qua máng là nhiều nhất). N Lời giải T OÁN VI Ệ T N
Mặt cắt ngang của máng nước là hình thang cân ABCD như hình vẽ. Gọi AH , BK là các đường AM
cao, ta có DA AB BC  15 cm. AH BK  15sin , DH KC  15 cos.
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NGUYỄN BỈNH KHIÊM- 24-25
AB DC.AH
Khi đó diện tích mặt cắt ngang của máng nước là S
 2251 cos sin với 3      0;   .  2  2 2 Xét hàm số 2 2 S      2 2        2 225 1 cos sin 225 1 cos 1 cos   S     2 2 2 2 2    4 3 225 1 cos sin 225
 cos   2 cos   2 cos   1
Đặt t  cos , t  0 
;1 , xét hàm số f t  4 3  t
 2t  2t 1 trên 0; 
1 , có f t  3 2  4
t  6t  2  1 NHÓM t  , f t  0     2 . t  1  GIÁO VIÊ
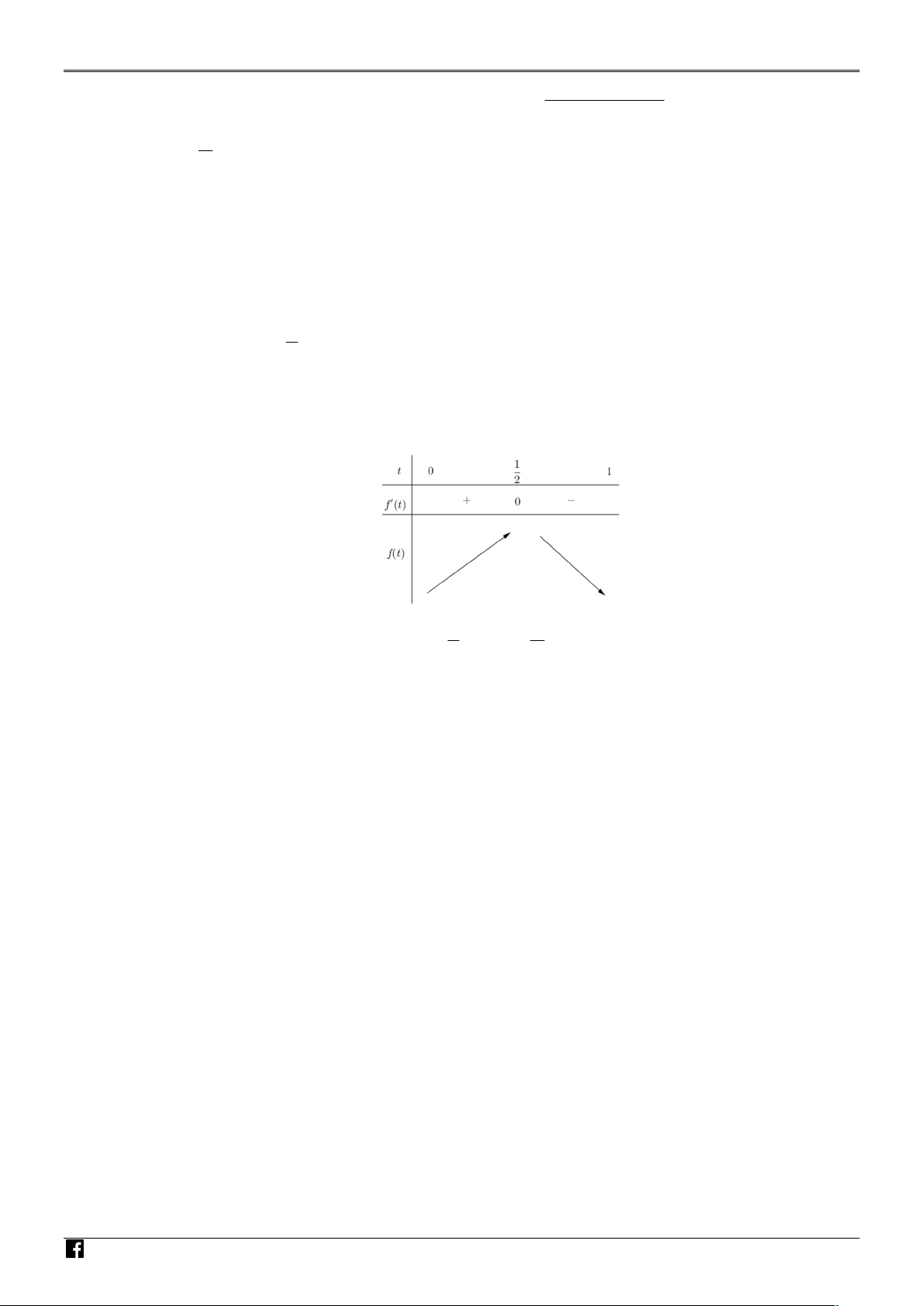
Lập bảng biến thiên của hàm số f t  N T OÁN VI Ệ T N 1  AM
Ta thấy f t  đạt giá trị lớn nhất khi t  hay  
 1,05. Khi đó diện tích lớn nhất của mặt 2 3
cắt ngang của máng nước là S  2251 cos 60sin 60  292, 28 (cm2).  HẾT  NHÓM GIÁO VIÊ N T OÁN VI Ệ T N AM
https://www.facebook.com/groups/toanvd.vdc Trang 14
Document Outline

  • de-giua-ky-1-toan-12-nam-2024-2025-truong-nguyen-binh-khiem-ha-noi
    • Mã đề thi 101
    • Mã đề thi 102
  • 25-LỚP-12-GKI-THPT-NGUYỄN-BỈNH-KHIÊM-CẦU-GIẤY-HN-NH-24-25-NHÓM-GVTVN