Đề học kỳ 1 Toán 10 năm 2022 – 2023 trường THPT Nguyễn Văn Cừ – Quảng Nam

SỞ GD & ĐT QUẢNG NAM
KIỂM TRA HỌC KỲ I
TRƯỜNG THPT NGUYỄN VĂN CỪ NĂM HỌC 2022 - 2023 -------------------- MÔN: Toán
(Đề thi có 03 trang)
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
Họ và tên: ............................................................................ Số báo danh: ......... Mã đề 100
A. TRẮC NGHIỆM (5 điểm):
Câu 1. Hệ nào dưới đây là hệ bất phương trình bậc nhất hai Nn? 3
x  2y  0
x  2y  0
x  2y  0 x  y  0 A.  . B.  . C.  . D.  . x  0 x  0 2 x  y  0 2
x  4y  0
Câu 2. Cho tập hợp A  n N | n  
5 . Tập hợp A viết dưới dạng liệt kê các phần tử là A. A  1;2;3;4;5; 
6 . B. A  0;1;2;3;4;  5 .
C. A  1;2;3;4;  5 .
D. A  0;1;2;3;4;5;  6 .
Câu 3. Số quy tròn của số gần đúng 673582 với độ chính xác d = 500 là A. 674000. B. 673000. C. 673600. D. 673500.
Câu 4. Cho góc lượng giác  thoả mãn 0 0
90    180 . Mệnh đề nào dưới đây đúng? A. cos  0 . B. cot  0 . C. tan  0. D. sin  0 .
Câu 5. Phát biểu nào dưới đây là một mệnh đề? A. x  3. B. Bạn có đi chơi không? C.
Hà Nội là thủ đô của Việt Nam. D.
Mùa thu Hà Nội thật đẹp!
Câu 6. Gọi M , N lần lượt là trung điểm của các cạnh AB, AC của tam giác đều ABC . Hỏi cặp
vectơ nào sau đây cùng hướng? A.
𝑀𝑁⃗ và 𝐶𝐵⃗. B.
𝑀𝐴⃗ và 𝑀𝐵⃗. C.
𝐴𝑁⃗ và 𝐶𝐴⃗. D. 𝐴𝐵⃗ và 𝑀𝐵⃗.
Câu 7. Cho ba điểm , ,
A B C phân biệt. Khẳng định nào sau đây đúng? A. 𝐴𝐵⃗ 𝐵𝐶⃗ 𝐶𝐴⃗. B. 𝐴𝐶⃗ 𝐶𝐵⃗ 𝐴𝐵⃗. C. 𝐵𝐴⃗ 𝐵𝐶⃗ 𝐴𝐶⃗. D. 𝐶𝐴⃗ 𝐶𝐵⃗ 𝐴𝐵⃗. 
Câu 8. Trong hệ tọa độ Oxy, cho A5;2, B
10;8. Tìm tọa độ của vectơ AB ?    
A. AB = (2;4) . B. AB = (15;10) . C.
AB = (50;16) . D. AB = (5;6) .       
Câu 9. Cho hai vectơ a và b khác 0 ,  là góc giữa hai vectơ a và b. Tích vô hướng . ab là                 A. . ab=- . a b . B. .
ab= a . b sina. C. .
ab= a . b cosa. D. . ab= . a b .
Câu 10. Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là       A.
IA = 2.IB B. IA= IB C. IA I =- B D. AI = BI
Câu 11. Cho góc a thỏa mãn 0 𝛼
180 . Khẳng định nào sau đây đúng? A.
cos(180-a)= cosa . B. tan(180-a)= tan a .
C. sin(180-a)= sina . D. cot(180-a)= cot a .
Câu 12. Cho hình bình hành ABCD (như hình vẽ sau). Đẳng thức nào sau đây đúng? Mã đề 100 Trang 1/10 A B D C        
A. AD = BC . B.
AB = CD . C.
BC = DA . D. AC = BD .
Câu 13. Cho tam giác ABC có độ dài ba cạnh là BC  a, AC  ,
b AB  c . Gọi R là bán kính
đường tròn ngoại tiếp và S là diện tích của tam giác ABC . Mệnh đề nào dưới đây đúng? ac abc abc R A. S  . B. S  . C. S  . D. S  . 4R 4R R 4abc
Câu 14. Cặp số 1; 
1 thuộc miền nghiệm của bất phương trình nào sau đây? A.
x  y  0 . B.
x  3y 1  0 . C.
x  y  3  0. D. x  3y 1  0 .
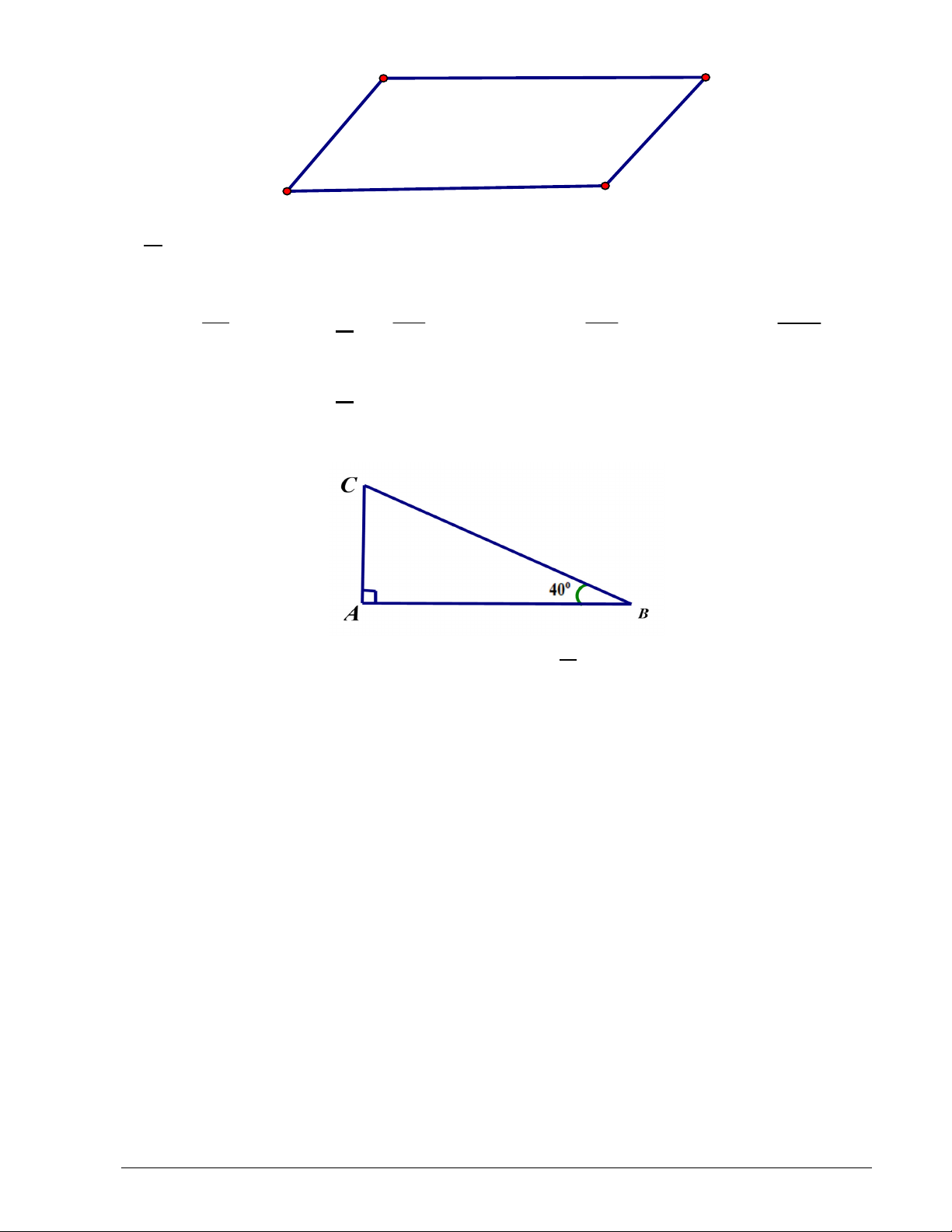
Câu 15. Cho tam giác ABC vuông tại A và có ABC
40 . Tính CA⃗, CB⃗ (góc giữa hai vectơ CA⃗ và CB⃗ . A. CA⃗, CB⃗ 40 . B. CA⃗, CB⃗ 50 . C. CA⃗, CB⃗ 130 . D. CA⃗, CB⃗ 140 .
B. TỰ LUẬN (5 điểm). ĐỀ 1:
Bài 1(1,0 điểm): Cho tập hợp A  2; 3; 5; 
7 và B  1; 2; 3;  4 .
Hãy tìm các tập 𝐴 ∩ 𝐵, 𝐴 ∪ 𝐵, 𝐴\𝐵, 𝐵\𝐴.
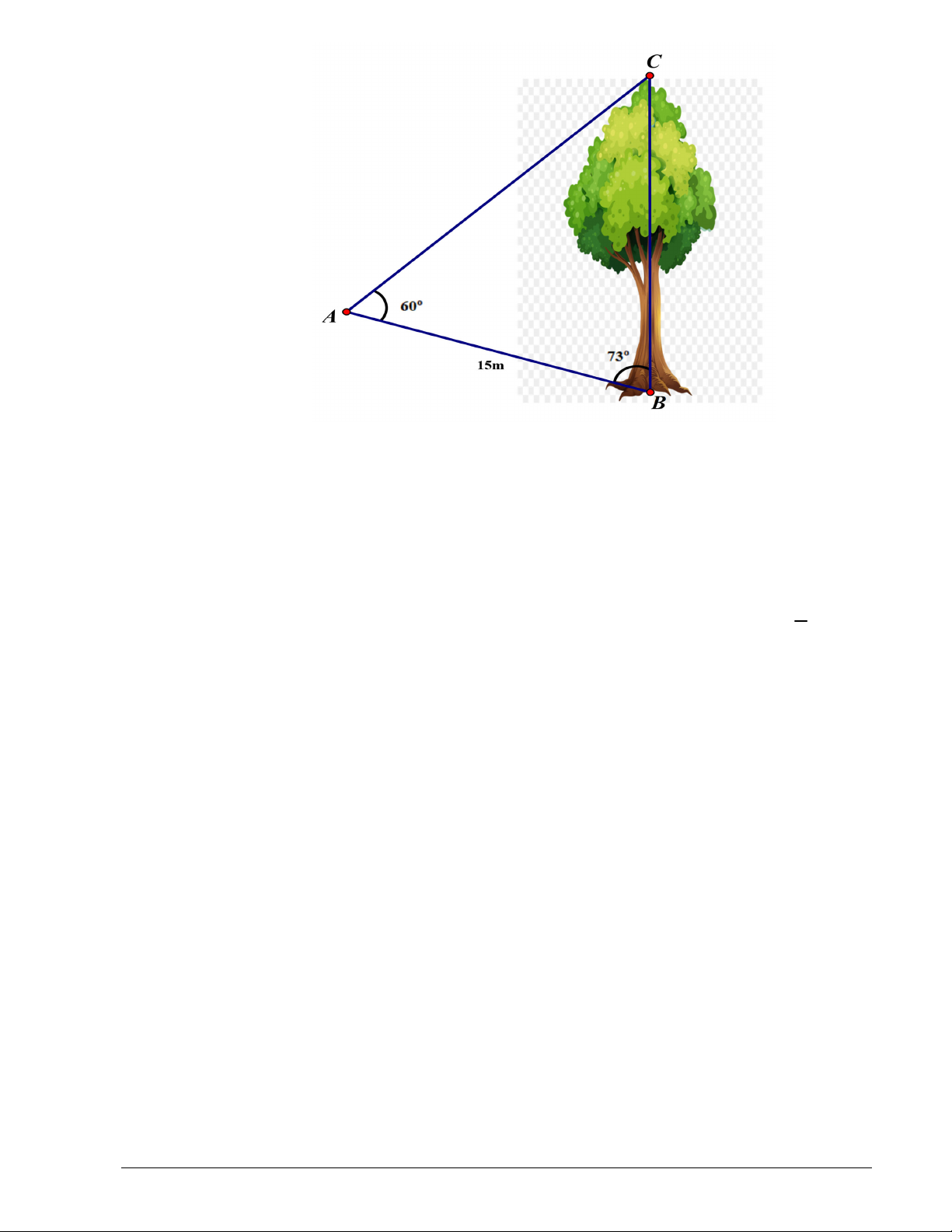
Bài 2 (1,0 điểm): Từ vị trí 𝐴 người ta quan sát một cây cao, giả sử 𝐵𝐶 là chiều cao của cây
(như hình vẽ). Người ta đo được khoảng cách 𝐴𝐵 15𝑚, góc 𝐶𝐴𝐵 60° và 𝐴𝐵𝐶
73°. Tính chiều cao 𝐵𝐶 của cây (kết quả làm tròn đến 2 chữ thập phân). Mã đề 100 Trang 2/10 Bài 3 (2,0 điểm):
a. Trong mặt phẳng toạ độ 𝑂𝑥𝑦 cho ba điểm 𝐴 1; 5 , 𝐵 2; 3 và 𝐶 2; 4 .
Tìm toạ độ điểm 𝑀 sao cho 𝐴𝑀⃗ 𝐴𝐵⃗ 3. 𝐵𝐶⃗.
b. Cho bốn điểm bất kỳ A, 𝐵, 𝐶, 𝐷. Chứng minh rằng: 𝐴𝐶⃗ 𝐵𝐷⃗ 𝐶𝐵⃗ 𝐷𝐴⃗ 0⃗. 1
Bài 4 (1,0 điểm): Cho hình vuông 𝐴𝐵𝐶𝐷, điểm 𝑀 nằm trên đoạn BD sao cho BM  BD , 4
𝑁 là trung điểm của đoạn thẳng AD. Tính tích vô hướng 𝑀𝐶⃗. 𝑀𝑁⃗. ĐỀ 2:
B. TỰ LUẬN (5 điểm).
Bài 1 (1,0 điểm): Cho tập hợp A  0; 2; 4;  6 và B   2;  4; 8 .
Hãy tìm các tập 𝐴 ∩ 𝐵, 𝐴 ∪ 𝐵, 𝐴\𝐵, 𝐵\𝐴.
Bài 2 (1,0 điểm): Từ vị trí 𝐴 người ta quan sát một cây cao, giả sử 𝐵𝐶 là chiều cao của cây (như
hình vẽ). Người ta đo được khoảng cách 𝐴𝐵 12𝑚, góc 𝐶𝐴𝐵 67° và 𝐴𝐵𝐶 74°. Tính chiều
cao 𝐵𝐶 của cây (kết quả làm tròn đến 2 chữ số thập phân). Mã đề 100 Trang 3/10 Bài 3 (2,0 điểm):
a.Trong mặt phẳng toạ độ 𝑂𝑥𝑦 cho ba điểm 𝐴
2; 3 , 𝐵 5; 5 và 𝐶 1; 2 .
Tìm toạ độ điểm 𝑁 sao cho 𝐴𝑁⃗ 3. 𝐴𝐵⃗ 𝐵𝐶⃗ .
b. Cho bốn điểm bất kỳ 𝑀, 𝑁, 𝑃, 𝑄. Chứng minh rằng: 𝑀𝑁⃗ 𝑃𝑄⃗ 𝑁𝑃⃗ 𝑄𝑀⃗ 0⃗. 1
Bài 4 (1,0 điểm): Cho hình vuông 𝐴𝐵𝐶𝐷, điểm 𝐸 nằm trên đoạn AC sao cho AE  AC , 4
𝐹 là trung điểm của đoạn thẳng CD. Tính tích vô hướng 𝐸𝐵⃗. 𝐸𝐹⃗.
------ HẾT ------ Mã đề 100 Trang 4/10
HƯỚNG DẪN CHẤM TỰ LUẬN
B/ TỰ LUẬN: (5,0 điểm)
ĐỀ 1: MÃ ĐỀ LẺ.
Bài 1 ( 1,0 điểm ).
Cho tập hợp A  2; 3; 5; 
7 và B  1; 2; 3;  4 .
Hãy tìm các tập 𝐴 ∩ 𝐵, 𝐴 ∪ 𝐵, 𝐴\𝐵, 𝐵\𝐴. 𝐴 ∩ 𝐵 2; 3 0,25 𝐴 ∪ 𝐵 1; 2; 3; 4; 5; 7 0,25 𝐴\𝐵 5; 7 0,25 𝐵\𝐴 1; 4 0,25
Bài 2 ( 1,0 điểm ).
Từ vị trí 𝐴 người ta quan sát một cây cao, giả sử 𝐵𝐶 là chiều cao của cây (như hình vẽ). Người
ta đo được khoảng cách 𝐴𝐵 15𝑚, góc 𝐶𝐴𝐵 60° và 𝐴𝐵𝐶
73°. Tính chiều cao 𝐵𝐶 của
cây (kết quả làm tròn đến 2 chữ số thập phân).
Trong tam giác 𝐴𝐵𝐶 , tính được: 𝐴𝐶𝐵 180° 60° 73° 47°. 0,25
Áp dụng định lý Sin vào tam giác 𝐴𝐵𝐶 ta có: 𝐵𝐶 𝐴𝐵 0,25 𝑠𝑖𝑛𝐴 𝑠𝑖𝑛𝐶 𝐴𝐵. 𝑠𝑖𝑛𝐴 𝐵𝐶 0,25 𝑠𝑖𝑛𝐶 Suy ra: 0,25 𝐵𝐶 17,76. Mã đề 100 Trang 5/10
Bài 3 ( 2,0 điểm ).
a. Trong mặt phẳng toạ độ 𝑂𝑥𝑦 cho ba điểm 𝐴 1; 5 , 𝐵 2; 3 và 𝐶 2; 4 .
Tìm toạ độ điểm 𝑀 sao cho 𝐴𝑀⃗ 𝐴𝐵⃗ 3. 𝐵𝐶⃗ .
b. Cho bốn điểm bất kỳ A, 𝐵, 𝐶, 𝐷. Chứng minh rằng: 𝐴𝐶⃗ 𝐵𝐷⃗ 𝐶𝐵⃗ 𝐷𝐴⃗ 0⃗. Tính đúng: 𝐴𝐵⃗ 1; 8 , 𝐵𝐶⃗ 4; 1 . 0,5 đ 3a Gọi 𝑀 𝑥; 𝑦 . x 1 1 3. 4 0,25 đ Suy ra: 𝐴𝑀⃗ 𝐴𝐵⃗ 3. 𝐵𝐶⃗ ⇔ 𝑦 5 8 3. 1 . x 10
Kết quả: 𝑦 6 . Vậy 𝑀 10; 6 . 0,25 đ VT = 𝐴𝐶⃗ 𝐶𝐵⃗ 𝐵𝐷⃗ 𝐷𝐴⃗ 0,5 đ 3b 𝐴𝐵⃗ 𝐵𝐴⃗. 0,25 đ 𝐴𝐴⃗ 0⃗ 𝑉𝑃. 0,25 đ
Bài 4 ( 1,0 điểm ).
Cho hình vuông 𝐴𝐵𝐶𝐷, điểm 𝑀 nằm trên đoạn BD sao cho 1
BM  BD , 𝑁 là trung điểm của 4 đoạn thẳng AD.
a. Tính tích vô hướng 𝑀𝐶⃗. 𝑀𝑁⃗.
b. Tam giác CMN là tam giác gì? Giải thích. A B M N O D C 0,25 đ 𝑀𝐶⃗ 𝐵𝐶⃗ 𝐵𝑀⃗ 𝐵𝐶⃗
1 𝐵𝐷⃗ 𝐵𝐶⃗ 1 𝐵𝐴⃗ 𝐵𝐶⃗ 3𝐵𝐶⃗ 1𝐵𝐴⃗. 4 4 4 4 4 0,25 đ 𝑀𝑁⃗ 𝐵𝑁⃗ 𝐵𝑀⃗
1 𝐵𝐴⃗ 𝐵𝐷⃗ 1𝐵𝐷⃗ 1𝐵𝐴⃗ 1𝐵𝐷⃗ 2 4 2 4 Mã đề 100 Trang 6/10 1 𝐵𝐴⃗
1 𝐵𝐴⃗ 𝐵𝐶⃗ 3𝐵𝐴⃗ 1𝐵𝐶⃗. 2 4 4 4 𝑀𝐶⃗. 𝑀𝑁⃗ 𝐵𝐶⃗ 𝐵𝐴⃗ . 𝐵𝐴⃗ 𝐵𝐶⃗ =… 0,25 đ 𝑀𝐶⃗. 𝑀𝑁⃗= 0 0,25 đ
ĐỀ 2: MÃ ĐỀ CHẴN.
Bài 1 ( 1,0 điểm ).
Cho tập hợp A  0; 2; ; 4  6 và B   2;  4; 8 .
Hãy tìm các tập 𝐴 ∩ 𝐵, 𝐴 ∪ 𝐵, 𝐴\𝐵, 𝐵\𝐴. 𝐴 ∩ 𝐵 2; 4 0,25 𝐴 ∪ 𝐵 0; 2; 4; 6; 8 0,25 𝐴\𝐵 0; 6 0,25 𝐵\𝐴 8 0,25
Bài 2 ( 1,0 điểm ).
Từ vị trí 𝐴 người ta quan sát một cây cao, giả sử 𝐵𝐶 là chiều cao của cây (như hình vẽ). Người
ta đo được khoảng cách 𝐴𝐵 12𝑚, góc 𝐶𝐴𝐵 67° và 𝐴𝐵𝐶
74°. Tính chiều cao 𝐵𝐶 của
cây (kết quả làm tròn đến 2 chữ số thập phân).
Trong tam giác 𝐴𝐵𝐶 , tính được: 𝐴𝐶𝐵 180° 67° 74° 39°. 0,25
Áp dụng định lý Sin vào tam giác 𝐴𝐵𝐶 ta có: 𝐵𝐶 𝐴𝐵 0,25 𝑠𝑖𝑛𝐴 𝑠𝑖𝑛𝐶 𝐴𝐵. 𝑠𝑖𝑛𝐴 𝐵𝐶 𝑠𝑖𝑛𝐶 0,25 Mã đề 100 Trang 7/10 Suy ra: 0,25 𝐵𝐶 17,55.
Bài 3 ( 2,0 điểm ).
a.Trong mặt phẳng toạ độ 𝑂𝑥𝑦 cho ba điểm 𝐴
2; 3 , 𝐵 5; 5 và 𝐶 1; 2 .
Tìm toạ độ điểm 𝑁 sao cho 𝐴𝑁⃗ 3. 𝐴𝐵⃗ 𝐵𝐶⃗ .
b. Cho bốn điểm bất kỳ 𝑀, 𝑁, 𝑃, 𝑄. Chứng minh rằng: 𝑀𝑁⃗ 𝑃𝑄⃗ 𝑁𝑃⃗ 𝑄𝑀⃗ 0⃗. Tính đúng: 𝐴𝐵⃗ 7; 2 , 𝐵𝐶⃗ 4; 7 . 0,5 đ 3a Gọi N 𝑥; 𝑦 . x 2 3. 7 4 0,25 đ Suy ra: 𝐴𝑁⃗ 3. 𝐴𝐵⃗ 𝐵𝐶⃗ ⇔ 𝑦 3 3.2 7 . x 15
Kết quả: 𝑦 2 . Vậy N 15; 2 . 0,25 đ VT = 𝑀𝑁⃗ 𝑁𝑃⃗ 𝑃𝑄⃗ 𝑄𝑀⃗ 0,5 đ 3b 𝑀𝑃⃗ 𝑃𝑀⃗. 0,25 đ 𝑀𝑀⃗ 0⃗ 𝑉𝑃. 0,25 đ
Bài 4 ( 1,0 điểm ).
Cho hình vuông 𝐴𝐵𝐶𝐷, điểm 𝐸 nằm trên đoạn AC sao cho 1
AE  AC , 𝐹 là trung điểm của 4 đoạn thẳng CD.
a. Tính tích vô hướng 𝐸𝐵⃗. 𝐸𝐹⃗.
b. Tam giác BEF là tam giác gì? Giải thích. A B E O D C F Mã đề 100 Trang 8/10 0,25 đ 𝐸𝐵⃗ 𝐴𝐵⃗ 𝐴𝐸⃗ 𝐴𝐵⃗
1 𝐴𝐶⃗ 𝐴𝐵⃗ 1 𝐴𝐵⃗ 𝐴𝐷⃗ 3𝐴𝐵⃗ 1𝐴𝐷⃗. 4 4 4 4 4 𝐸𝐹⃗ 𝐴𝐹⃗ 𝐴𝐸⃗ 𝐴𝐷⃗ 𝐴𝐶⃗ 𝐴𝐶⃗ 𝐴𝐷⃗ 𝐴𝐶⃗ 0,25 đ 1 𝐴𝐷⃗
1 𝐴𝐵⃗ 𝐴𝐷⃗ 3𝐴𝐷⃗ 1𝐴𝐵⃗. 2 4 4 4 𝐸𝐵⃗. 𝐸𝐹⃗ 𝐴𝐵⃗ 𝐴𝐷⃗ . 𝐴𝐷⃗ 𝐴𝐵⃗ =… 0,25 đ 𝐸𝐵⃗. 𝐸𝐹⃗=0 0,25 đ
Ghi chú: - Học sinh giải cách khác giáo viên chia biểu điểm tương tự câu đó.
TRƯỜNG THPT NGUYỄN VĂN CỪ CẤU TRÚC MA TRẬN ĐỀ KIỂM TRA HỌC KÌ 1 TỔ TOÁN
NĂM HỌC 2022-2023 MÔN: TOÁN, LỚP 10
THỜI GIAN LÀM BÀI: 60 phút
Câu hỏi trắc nghiệm: 15câu (50%) Câu hỏi tự luận: 5câu (50%) VẬN DỤNG TỔNG NHẬN BIẾT THÔNG HIỂU VẬN DỤNG CAO CÂU Trắc Tự NỘI Đơn vị Trắc Tự Trắc Tự Trắc Tự TT nghiệ luậ DUNG kiến thức nghiệm luận nghiệm luận nghiệm luận m n 1.1. Mệnh (Câu 1) 1 đề 1. 1.2. Tập 1
đề và tập hợp và các hợp> phép toán (Câu 2) (Câu 2 trên tập 1) hợp 2.1. Bất 2. phương phương 1 trình bậc (Câu 3) trình và nhất hai Nn 2 hệ bất 2.2. Hệ bất phương phương bậc nhất 1 trình bậc (Câu 4) hai ẩn> nhất hai Nn 3.1. Giá trị lượng giác (Câu 3. của một 2 (Câu 5) 13) thức góc từ 00 3 lượng đến 1800 trong tam 3.2. Hệ giác> thức lượng (Câu 6) (Câu 2 trong tam 3) giác 4.1. Các khái niệm (Câu 7) 1 4. mở đầu 4 (Câ 4.2. Tổng u 5)
và hiệu của (Câu 8) (Câu 2 hai vectơ 2) 1 Mã đề 100 Trang 9/10 4.3. Tích của một (Câu (Câu 9) 2 vectơ với 14) một số 4.4. Vectơ trong mặt (Câu (Câu 2 phẳng tọa 10) 4) độ 4.5. Tích vô hướng (Câu (Câu 2 của hai 11) 15) vectơ 5. đặc trưng của mẫu 5.1. Số gần (Câu 5 số liệu đúng và sai 1 12) không số ghép nhóm> Tổng 12 3 2 2 1 20 Tỉ lệ (%) Mã đề 100 Trang 10/10