



Preview text:
PHÒNG GD & ĐT HUYỆN THANH
ĐỀ THI HỌC KỲ 1 TOÁN 7 TRÌ Thời gian: 90 phút
TRƯỜNG THCS TẢ THANH OAI
Tả Thanh Oai, Ngày 20 tháng 12 năm 2023 ---------***--------- ĐỀ BÀI
(Đề thi gồm 2 trang)
I. TRẮC NGHIỆM (2,0 điểm)
Câu 1. Kết quả phép tính 25 5 3 :3 là? A. 20 3 . B. 30 6 . C. 30 3 . D. 20 1 .
Câu 2. Hai số nào sau đây cùng biểu diễn một số hữu tỉ? A. 1
5 và 6 . B. 1 5 − − −
và 9 . C. 1
5 và 5,2 . D. 1 5 − và 11. 2 2 2 2 2 2 2
Câu 3. Trong các số hữu tỉ: 1 4 0,75; 1 ; 5; − − −
số nào lớn nhất: 2 5 − A. 1 1 − − B. 4 . C. – 5. D. 0.75. 2 5 −
Câu 4. Số hữu tỉ x thỏa mãn 4 − 5 3 x − + = là: 5 2 10 A. 1 x − = . B. 1 x = . C. 2 x = . x − = . 5 5 5 D. 2 5
Câu 5. Cho Hình 1, biết m∥ n . Trong các khẳng
định sau, khẳng định nào đúng? A. + P Q =180° . B. = P Q . 1 1 1 1 C. + P Q =180° . D. + P Q = 90° . 2 1 2 1 Hình 1
Câu 6. Cho ∆ ABC vuông tại A, 0
B = 75 . Số đo của góc C bằng: A. 0 75 B. 0 25 C. 0 15 D. 0 115 Câu 7. Cho M ∆ NP và H ∆ IK có
M = H ; MN = HI . Bổ sung thêm điều kiện nào sau đây để M ∆ NP bằng H
∆ IK theo trường hợp cạnh – góc – cạnh: A. NP = IK.
B. MP = HK. C. PM = IK. D. MN = IK.
Câu 8. Chọn khẳng định Đúng trong các khẳng định sau:
A. Hai góc đối đỉnh thì bằng nhau.
B. Hai đường thẳng song song thì cắt nhau.
C. Hai góc bằng nhau thì đối đỉnh.
D. Hai đường thẳng cắt nhau thì vuông góc.
II. PHẦN TỰ LUẬN (6,0 điểm)
Bài 1. (1,5 điểm). Thực hiện phép tính: 2 a) 4 4 9 1 2 5 .
. b) : 25 . 5 3 20 9 3 3
Bài 2. (1,5 điểm). Tìm x biết: 2 a) 4 2 1 5
x . b) x 3 4. 9 3 3 6
Bài 3. (1,0 điểm).
Biểu đồ hình quạt tròn ở Hình 6 thể hiện
kết quả học tập học kỳ I của học sinh lớp Tốt 7 5%
E (tính theo tỉ số phần trăm) được đánh
giá ở bốn mức: Tốt, Khá, Đạt, Chưa đạt.
a) Em hãy lập bảng thống kê kết quả học Đạt 35%
tập học kỳ I của học sinh lớp 7E (đơn vị Khá 57%
% ) theo bốn mức: Tốt, Khá, Đạt, Chưa đạt. Chưa
b) Biết lớp 7E có 40 học sinh. Tính số học đạt 3%
sinh xếp loại học tập Tốt của lớp 7E trong học kỳ I . Hình 6
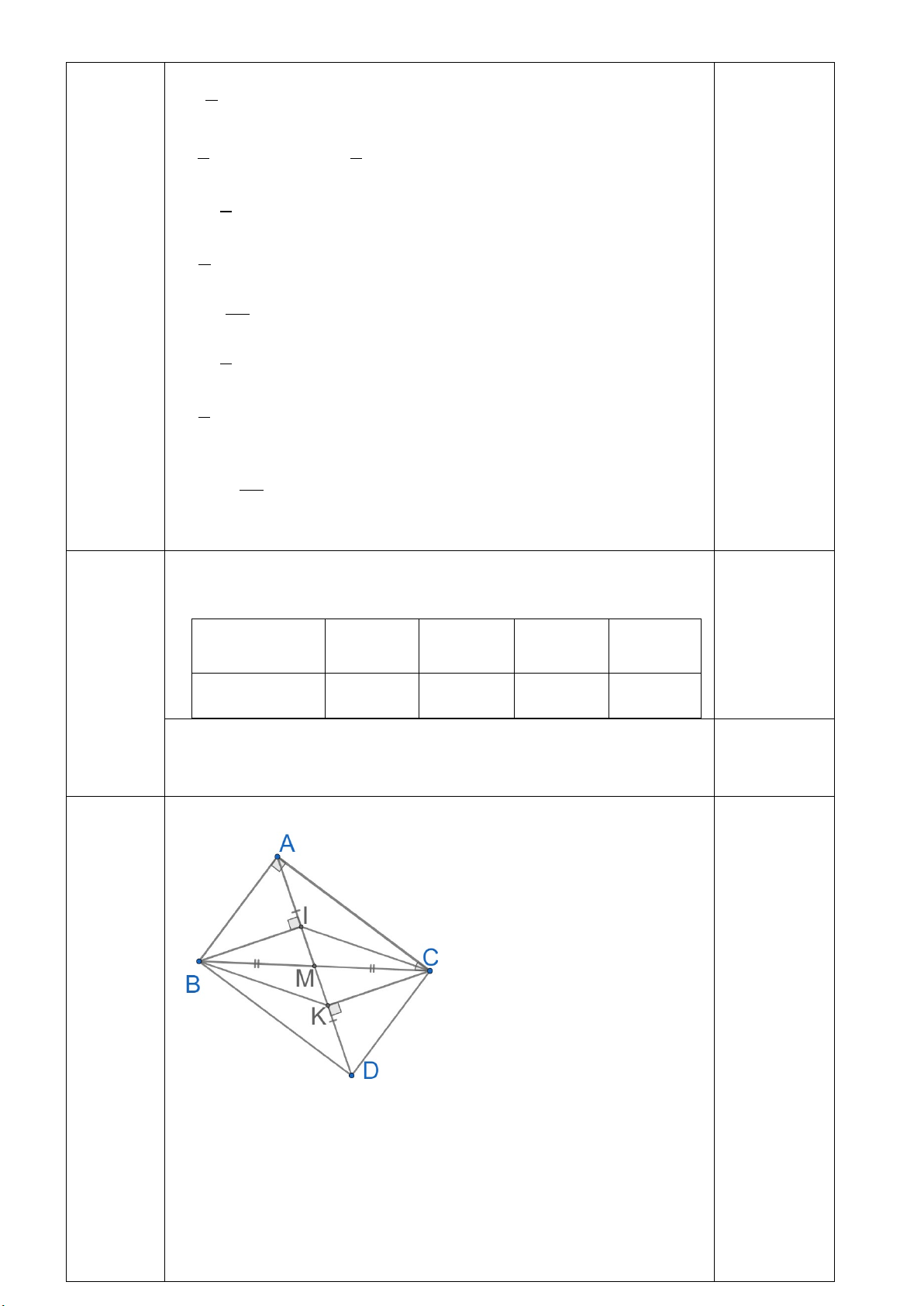
Bài 4. (3,5 điểm). Cho AB ∆
C vuông tại A, M là trung điểm
của BC. Trên tia đối của tia MA lấy điểm D sao cho AM = MD.
a) Chứng minh ∆AMB = ∆DMC (1 điểm)
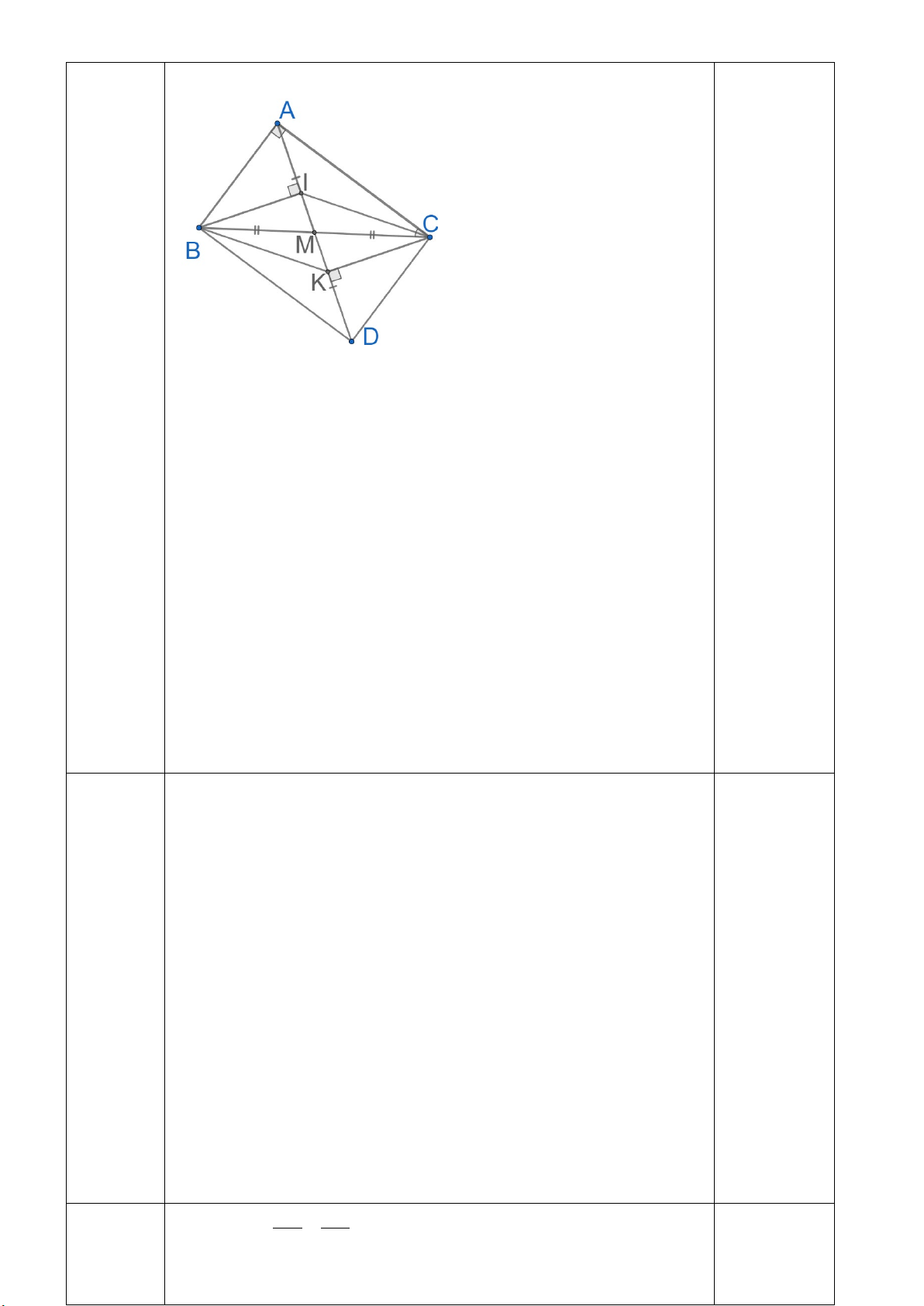
b) Kẻ BI ⊥ AD(I ∈ AD)và CK ⊥ AD(K ∈ AD)
Chứng minh BI // CK và AI = DK (1 điểm) c) Chứng minh 0
ACD = 90 và AD = BC (1 điểm)
d) Dành riêng cho lớp 7A11:
Tam giác ABC thỏa mãn thêm điều kiện gì để AI = IM = MK = KD.
(Vẽ hình hết câu b + viết gt, kl được 0,5 điểm và ký hiệu trên hình có thể thay đổi sau câu C ) Bài 5. (0,5 điểm) 4
a) Tìm GTLN của biểu thức B = ( 2 x ≤ ) 3 + 2 − x
b) Dành riêng cho lớp 7A11:
Tìm tất cả các cặp số nguyên dương (x;y) thỏa mãn 2x + 2y = 2x+y
---------------- Hết--------------- HƯỚNG DẪN CHẤM
Bài 1. ( 2 điểm) Mỗi đáp án đúng được 0,25 điểm. Câu 1 2 3 4 5 6 7 8 Đáp án A D B B B C B A Bài Nội dung Điểm 1 TS: 1,5 đ a) 4 4 9 . 5 3 20 4 3 − = + 0,25 5 5 1 = 5 0,5 2 b) 1 2 5 : 25 9 3 3 2 7 5 1 0,25 = − . 9 3 5 49 1 = − 0,25 81 3 49 27 = − 81 81 0,25 22 = 81 2 TS: 1,5 đ 4 2 1 a) x 9 3 3 2 4 1 x = − 3 9 3 0,25 2 1 x = 3 91 2 1 3 0,25 x = : = . 9 3 9 2 1 x = 6 1 Vaäy x = 0,25 6 2 b) 5
x 3 4 . 6 5 ⇒ x + 3 = 2 5 ⇒ x + 3 = 2 − 6 hoặc 6 0,25 5 x+3= 2 TH1: 6 5 0,25
⇒ x = 2 − 3 = 1 − 6 6 x − ⇒ = 5 5 x+3= 2 − TH2: 6 5 ⇒ x = 2 − − 3 = 5 − 6 0,25 ⇒ x = 6 − Vậy 6 x − = ; x = 6 − 5 TS: 1 đ 3
a) Bảng thống kê kết quả học tập học kì I của học sinh lớp 7E Mức độ Tốt Khá Đạt Chưa đạt 0,5 Kết quả (%) 5 57 35 3
b) Số học sinh xếp loại học tập Tốt của lớp 7E trong học kì I là: 40.5% = 2 ( học sinh) 0,5 4a TS: 3 đ Hình vẽ 0,25
Xét tam giác AMB và tam giác DMC có: 1đ
AM = MD(gt) AMB DMC = ⇒ A ∆ MB = D ∆ MC( . c . g c) BM MC(gt) = 4b
BI ⊥ AD ⇒ 0 Có 90 BIA = ;⇒ BIK = 0 CKI = 90
CK ⊥ AD ⇒ 0 CKD = 90
Mà 2 góc này so le trong, từ đây suy ra BI// CK 0,25 AB = CD
AMB = DMC(cmt) ∆ ∆ ⇒ (t / c) BAI = CDM Xét A ∆ BI và D ∆ CK có: AB = CD(cmt) 0 BIA = CKD = 90 ⇒ A ∆ BI = D ∆ CK(ch-gn) 0,5 BAI = CDK
⇒ AI = DK(t / c) 0,25 4c
∆AMB =∆DMC(cmt) ⇒ ABM = DCM (2 góc tương ứng)
Xét tam giác ABC vuông tại A (gt) có: 0,25 ABM + ACB = 90 ( ° t / c)
màABM = DCM (cmt)
⇒ DCM + ACB = 90°
màDCM + ACB = ACD ⇒ ACD = 90° 0,25
Xét ∆BAC và D ∆ CA có: 0,25 AB = CD(cmt) 0
BAC = ACD = 90 ⇒ ∆BAC = ∆DC ( A c-g-c) ACchung
⇒ AD = BC (2 cạnh tương ứng) 0,25 4d 0,5 = ⇒ AD = BC AD BC
⇒ AM = MD = BM = MC 2 2
Nếu AI = IM thì A ∆ BI = M ∆ BI( . c . g c)
⇒ AB = BM⇒ A ∆ BM đều AM = BM 0 ⇒ ABC = 60
Ta sẽ chứng minh khi AI = IM
thì AI = IM = MK = KD Thật vậy: AI = IM Ta có
⇒ AI = IM = DK (1) AI DK(cmt) =
AI + IM = AM Lại có
MK + DK = MD ⇒ AI + IM = MK + DK (2) AM MD(gt) =
Từ (1)(2)⇒ AI = IM = MK = DK
Vậy tam giác vuông ABC cần thêm điều kiện 0 ABC = 60 thì AI = IM = MK = KD 5a
Ta có x ≤ 2 ⇔ 2 − x ≥ 0 ⇔ 2 − x ≥ 0 ⇔ 2 − x + 3 ≥ 3 TS: 0,5 đ 4 4 4 ⇔ ≤ ⇔ B ≤ 2 − x + 3 3 3 0,25
Dấu “=” xảy ra khi x = 2 (tmđk) 4
Vaäy B = ⇔ x = 2 max 3 0,25 5b 2x 2y 2x+ + = y TS: 0,5 đ
Không mất tính tổng quát giả sử x ≥ y +) Xét x > y. Khi đó: 0,25 2x
2x ⇒ 2x +2y2x ⇒VT2x 2y 2x Mà 2 + = x y 2x VP
⇒ không thỏa mãn ⇒ loại ⇒ x = y x y 2 ⇒ 2 + 2 = 2 x 0,25 x 2 ⇒ 2 .2 = 2 x x 1 + 2 ⇒ 2 = 2 x ⇒ x +1 = 2x
⇒ x =1 = y(t / m) Vậy x = y =1
Document Outline
- ĐỀ THI HỌC KỲ 1 TOÁN 7




