Đề học sinh giỏi cấp tỉnh Toán 9 năm 2022 – 2023 sở GD&ĐT Hà Nam

UBND TỈNH HÀ NAM
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2022 - 2023 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
(Đề thi gồm 01 trang)
Câu I. (3,0 điểm) Cho biểu thức 2
a +1 a a −1 a − a a + a −1 P = + +
với a > 0,a ≠ 1. a a − a a − a a
a) Rút gọn biểu thức . P
b) Tìm điều kiện của 8
a để biểu thức Q = nhận giá trị nguyên. P
Câu II. (4,0 điểm)
1. Giải phương trình 2 3 2
x − 3 x − 3x + 4x − 2 = 0 . 2 2
 x − y + 4x − 6y − 5 =  0
2. Giải hệ phương trình  2
 2x + 3 + 2y + 2x + x = 26.
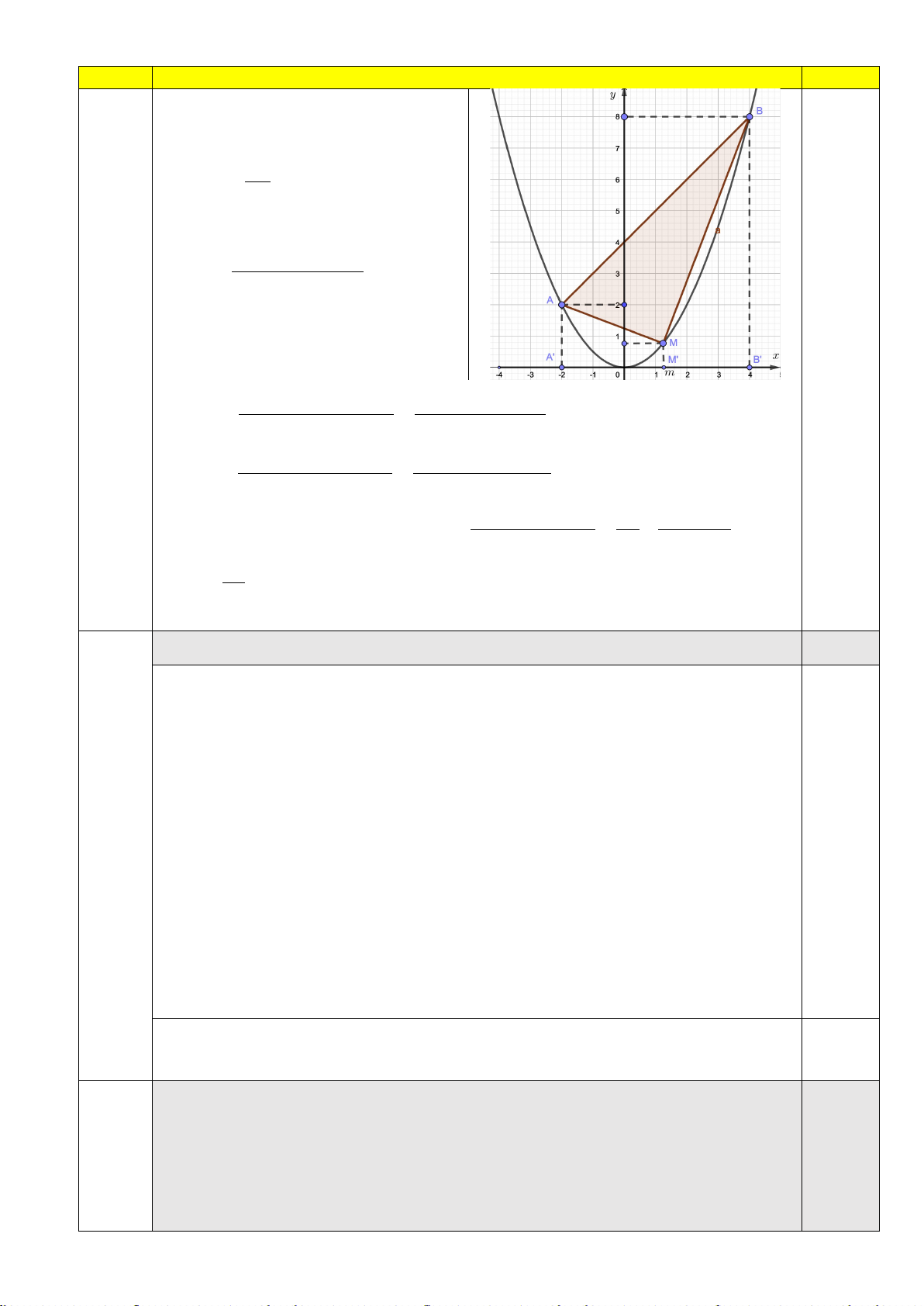
Câu III. (2,0 điểm) Cho parabol (P) 1 2
: y = x và hai điểm A( 2; − 2), B( 4;8) nằm trên (P). 2
Gọi M là điểm thay đổi trên (P) và có hoành độ là m( 2
− < m < 4). Tìm m để tam giác
ABM có diện tích lớn nhất.
Câu IV. ( 2,0 điểm) Tìm nghiệm nguyên của phương trình (x − y)(x + y) 3 2
2 + 4y = x + x .
Câu V. (7,0 điểm)
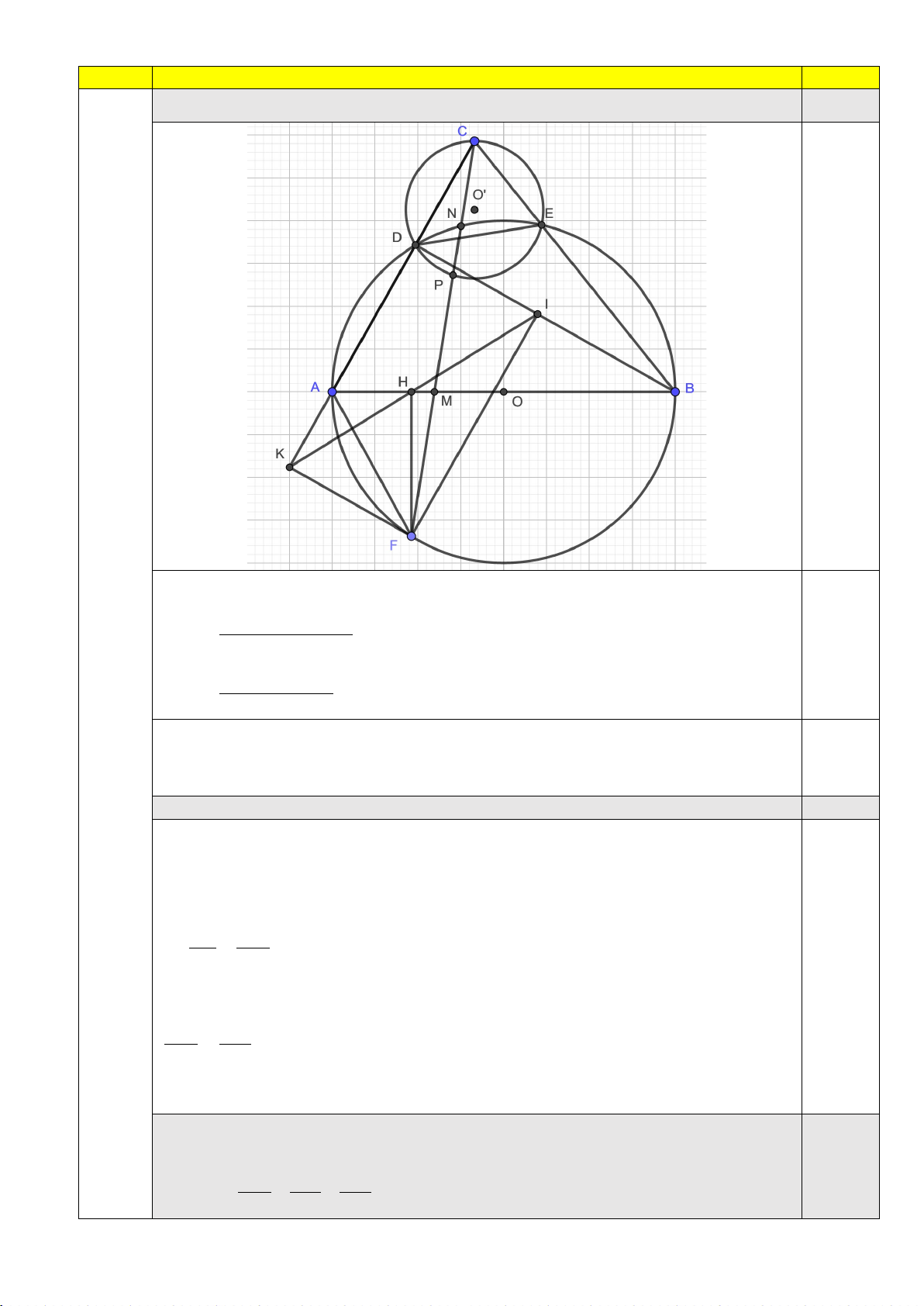
1. Cho đường tròn ( ; O R) đường kính .
AB Gọi C là điểm thỏa mãn tam giác ABC
nhọn. Các đường thẳng ,
CA CB cắt đường tròn (O) tại điểm thứ hai tương ứng là D, E.
Trên cung AB của (O) không chứa D lấy điểm F (0 < FA ≤ FB ). Đường thẳng CF cắt
AB tại M , cắt đường tròn (O) tại N ( N không trùng với F) và cắt đường tròn (O')
ngoại tiếp tam giác CDE tại P ( P không trùng với C ). a) Giả sử  0
ACB = 60 , tính DE theo . R
b) Chứng minh CN.CF = . CP CM.
c) Gọi I,H theo thứ tự là hình chiếu vuông góc của F trên các đường thẳng BD, .
AB Các đường thẳng IH và CD cắt nhau tại K. Tìm vị trí của điểm F để biểu thức AB BD AD + +
đạt giá trị nhỏ nhất. FH FI FK
2. Cho góc nhọn xOy cố định và A là điểm cố định trên .
Ox Đường tròn (I ) thay
đổi nhưng luôn tiếp xúc với Ox, Oy lần lượt tại E, .
D Gọi AF là tiếp tuyến thứ hai kẻ
từ A đến (I ) ( F là tiếp điểm). Chứng minh DF luôn đi qua một điểm cố định.
Câu VI. (2,0 điểm) (a + b − )2 1 (a −b + )2 1 (b − a + )2 Cho 1 2 số dương a, . b Chứng minh: 3 + + ≥ .
(a + b)2 +1 (a + )2 1 + b (b + )2 2 2 1 + a 5 --- HẾT---
Họ và tên thí sinh:………………………….Số báo danh:..............................................
Người coi thi số 1………………………………Người coi thi số 2…………….......................... UBND TỈNH HÀ NAM
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
SỞ GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2022 – 2023 ĐỀ CHÍNH THỨC Môn: TOÁN HƯỚNG DẪN CHẤM
(Hướng dẫn chấm gồm 06 trang)
I. HƯỚNG DẪN CHUNG
o Hướng dẫn chấm chỉ trình bày sơ lược các bước giải, lời giải của học sinh cần lập luận chặt
chẽ, hợp logic. Nếu học sinh trình bày cách làm khác mà đúng thì vẫn được điểm theo thang điểm tương ứng.
o Đối với bài toán hình học nếu học sinh chứng minh có sử dụng đến hình vẽ thì yêu cầu phải vẽ
hình, nếu học sinh vẽ hình sai hoặc không vẽ hình thì không cho điểm phần tương ứng.
o Điểm toàn bài không làm tròn.
II. ĐÁP ÁN VÀ THANG ĐIỂM Câu
Sơ lược lời giải Điểm Cho biểu thức 2
a +1 a a −1 a − a a + a −1 P = + +
với a > 0,a ≠ 1. a a − a a − a a
a) Rút gọn biểu thức . P 2,0
( a)3 −1 (1−a)( 1 1 − − a + + a a ) P = + + 0,75 a a ( a − ) 1 a (1− a)
a +1 a + a +1 1 − − a + a = + + 0,75 a a a a + 2 a +1 = 0,5 a I. 8
b) Tìm điểu kiện của a để biểu thức Q = nhận giá trị nguyên. 1,0 (3,0 P điểm) 1 1 Có P = a + + 2 ≥ 2 a. + 2 = 4 (Theo BĐT Côsi) a a 1 P = 4 ⇔ a =
⇔ a =1(loại do a ≠ 1) a 0,5 Vậy P > 4 a ∀ > 0,a ≠ 1. 8
⇒ 0 < < 2 ⇒ 0 < Q < 2 P
Do đó để Q ∈ ⇔ Q = ⇔ P = ⇔ ( a )2 1 8 − 6 a +1 = 0 0,25  a = 3− 2 2 a =17 −12 2 ⇔  ⇔  (thỏa mãn điều kiện)  a = 3+ 2 2 a =17 +12 2 0,25
Vậy a = 17 ±12 2 là các giá trị cần tìm
1. Giải phương trình 2 3 2
x − 3 x − 3x + 4x − 2 = 0 . 2,0 II. Điều kiện 3 2
x − 3x + 4x − 2 ≥ 0 0,25 (4,0 3 2 2
điểm) Có x − 3x + 4x − 2 = ( x − )
1 (x − 2x + 2) 0,25 nên 3 2
x − 3x + 4x − 2 ≥ 0 ⇔ x ≥1 vì x − x + = (x − )2 2 2 2 1 +1 > 0 x ∀ Page 1 of 6 Câu
Sơ lược lời giải Điểm
( ) ⇔ (x − ) + ( 2x − x + ) − (x − )( 2 1 2 1 2 2 3
1 x − 2x + 2) = 0 x −1 x −1 0,25 ⇔ 2. − 3. +1 = 0 2 2 x − 2x + 2 x − 2x + 2 x  = −1 t 1 Đặt t =
,t ≥ 0 ta được phương trình 2 2t 3t 1 0  − + = ⇔ 0,5 2 x − 2x + 2 1 t =  2 x −1 x −1 t =1 ⇔ = 1 ⇔ = 1 2
⇔ x − 3x + 3 = 0 (vô nghiệm) 0,25 2 2 x − 2x + 2 x − 2x + 2 1 x −1 1 x −1 1 t = ⇔ = ⇔ = 2 2 2 x − 2x + 2 2 x − 2x + 2 4 0,5 2
⇔ x − 6x + 6 = 0 ⇔ x = 3 ± 3 (thỏa mãn điều kiện)
Vậy pt có 2 nghiệm x = 3 ± 3 2 2
x − y + 4x − 6y − 5 =  0 (1)
2. Giải hệ phương trình  2,0 2
 2x + 3 + 2y + 2x + x = 26(2)  3 x ≥ − Điều kiện  2 0,25 y ≥ 0 ( ) ⇔ (  + = +
x + )2 = ( y + )2 x 2 y 3 1 2 3 ⇔  0,5
x + 2 = −y − 3
+)x + 2 = −y − 3 ⇔ (x + 5) + y = 0 vô nghiệm 0,5 vì (x + ) 3 5 + y > 0 x ∀ ≥ − , y ≥ 0. 2
+)x + 2 = y + 3 ⇔ y = x −1 thay vào (2) ta được x + + (x − ) 2 2 3 2 1 + 2x + x = 26
⇔ ( x + − ) + ( x − − ) 2 2 3 3 2
2 2 + 2x + x − 21 = 0 2x + 3 − 9 2x − 2 − 2 ⇔ +
+ (x − 3)(2x + 7) = 0 2x + 3 + 3 2x − 2 + 2 0,5 (x ) 2 2 3 2x 7 ⇔ − + + + =   0  2x + 3 + 3 2x − 2 + 2  2 2 ⇔ x = 3,do +
+ 2x + 7 > 0 x ∀ ≥ 1 2x + 3 + 3 2x − 2 + 2
+)x = 3 ⇒ y = 2
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = (3;2) 0,25 1 III. Cho parabol (P) 2
: y = x và hai điểm A( 2; − 2), B(
4;8) nằm trên (P). Gọi M (2,0 2
điểm) là điểm thay đổi trên (P) và có hoành độ là m( 2
− < m < 4). Tìm m để tam giác
ABM có diện tích lớn nhất. Page 2 of 6 Câu
Sơ lược lời giải Điểm 2  m  Có M  ; m 2    Gọi A'( 2 − ;0),M '( ;0 m ), B'(4;0) 0,5
( AA'+ BB') A'B S = = ABB A 30 ' ' 2
( AA'+ MM ') A'M ' ( 2 4 + m )(2 + m) S = = AMM ' A' 2 4 ( 0,5
MM '+ BB')M 'B' ( 2
16 + m )(4 − m) S = = MBB'M ' 2 4 2 2
6m 12m 72 27 3(m 1) S S S S − + − = − − = − = − ABM ABA B AMM A MBB M 30 ' ' ' ' ' ' 4 2 2 0,75 27 S ≤ m ∀ ABM 2
Vậy m = 1 là giá trị cần tìm 0,25
Tìm nghiệm nguyên của phương trình (x − y)(x + y) 3 2
2 + 4y = x + x . 2,0
(x − 2y)(x + 2y) 3
+ 4y = x + x ⇔ (x + ) x + = ( y − )2 2 1 ( 1) 2 1 (1) 0,25
y ∈ ⇒ ( y − )2
2 1 là số nguyên dương lẻ ⇒ (x + )( 2 1 x + )
1 là số nguyên dươnglẻ 0,5 2
⇒ x +1, x +1 cùng lẻ và 1+ x ≥ 0 IV. Giả sử ( 2
1+ x,1+ x ) = d ⇒ d là số lẻ. (2,0
điểm) Do ( + x)d ⇒ ( 2 1 1− x )d . 0,5 Lại có ( 2
1+ x )d ⇒ ( 2 + x ) + ( 2 1
1− x ) d ⇒ 2 d ⇒ d =1   (do d lẻ) Mặt khác, ⇒ (x + )( 2 (1) 1 x + ) 1 là số chính phương. 2
1+ x,1+ x là 2 số nguyên tố cùng nhau nên 2
1+ x,1+ x đều là số chính phương 0,5 Do 2 2
x , x +1 là hai số nguyên liên tiếp và cùng là số chính phương nên x = 0  y = 0 2 x = 0 ⇒ 4
− y + 4y = 0 ⇔  . Vậy ( ; x y) = (0;0) hoặc ( ; x y) = (0; ) 1 0,25  y = 1 Cho đường tròn ( ; O R) đường kính .
AB Gọi C là điểm thỏa mãn tam giác ABC
V. (7,0 nhọn. Các đường thẳng ,
CA CB cắt đường tròn (O) tại điểm thứ hai tương ứng là điểm)
D, E. Trên cung AB của (O) không chứa D lấy điểm F (0 < FA ≤ FB ). Đường
thẳng CF cắt AB tại M , cắt đường tròn (O) tại N ( N không trùng với F) và
cắt đường tròn (O') ngoại tiếp tam giác CDE tại P ( P không trùng với C ). Page 3 of 6 Câu
Sơ lược lời giải Điểm a)Giả sử  0
ACB = 60 , tính DE theo . R 2,0
Xét đường tròn (O)   − 
sdBFA sdDNE BCA =
(Góc có đỉnh ở bên ngoài đường tròn) 2 0,75 0  −  180 sdDNE = ⇒  0 BCA
sdDNE = 60 ⇒  0 EOD = 60 2 OED ∆
có OD = OE ⇒ OED ∆ cân tại O 0,75 Mà  0 EOD = 60 ⇒ ODE ∆ là tam giác đều
⇒ OD = DE ⇒ ED = R 0,5
b)Chứng minh CN.CF = . CP CM. 1,5  = 
CPE CDE (2 góc nội tiếp chắn cung CE của đường tròn (O′) ) Mà  = 
CBM CDE (Vì tứ giác ABED nội tiếp đường tròn (O) ) ⇒  = 
CBM CPE nên tam giác CPE đồng dạng với tam giác CBM 0,75 ⇒ CE CM =
⇒ CE.CB = CM.CP (1) CP CB
Tương tự chứng minh tam giác CNE đồng dạng với tam giác CBF CE CF =
⇒ CE.CB = CN.CF (2) CN CB 0,5
Từ (1) và (2) suy ra: CN.CF = . CP CM 0,25
c) Gọi I, H theo thứ tự là hình chiếu vuông góc của F trên các đường thẳng BD, .
AB Các đường thẳng IH và CD cắt nhau tại K. Tìm vị trí của điểm F để AB BD AD 1,5 biểu thức + +
đạt giá trị nhỏ nhất. FH FI FK Page 4 of 6 Câu
Sơ lược lời giải Điểm
Tứ giác BIHF, BDAF nội tiếp nên  =  FHK FAK (= 
FBD ), suy ra tứ giác AKFH 0,5 nội tiếp nên  0 FKA = 90 . Xét DFK ∆ và BFH ∆ có  =  0 FKD FHB = 90 và  = 
FBH FDA(Hai góc nội tiếp cùng chắn 
AF của đường tròn (O) ) 0,25 ⇒ DFK ∆  BFH ∆ ⇒ DK BH = (1) FK FH ID HA
Tương tự tam giác IDF đồng dạng với tam giác HAF⇒ = 0,25 IF HF
Tương tự tam giác AFK đồng dạng tam giác BFI nên: AK BI = (2) FK FI DK AK BH BI (1) , (2)⇒ − = − hay: DA BH BI = − FK FK FH FI FK FH FI DA BD BH BD BI BH ID 0,25 ⇒ + = + − = + FK FI FH FI FI FH FI Mà ID HA = suy ra: DA BD BH HA AB + = + = FI FH FK FI FH FH FH
Vậy AB BD AD 2AB + + = FH FI FK FH 0,25 nên AB BD AD + +
nhỏ nhất khi FH lớn nhất khi 𝐹𝐹 là trung điểm cung 𝐴𝐴𝐴𝐴 FH FI FK 2. Cho góc 
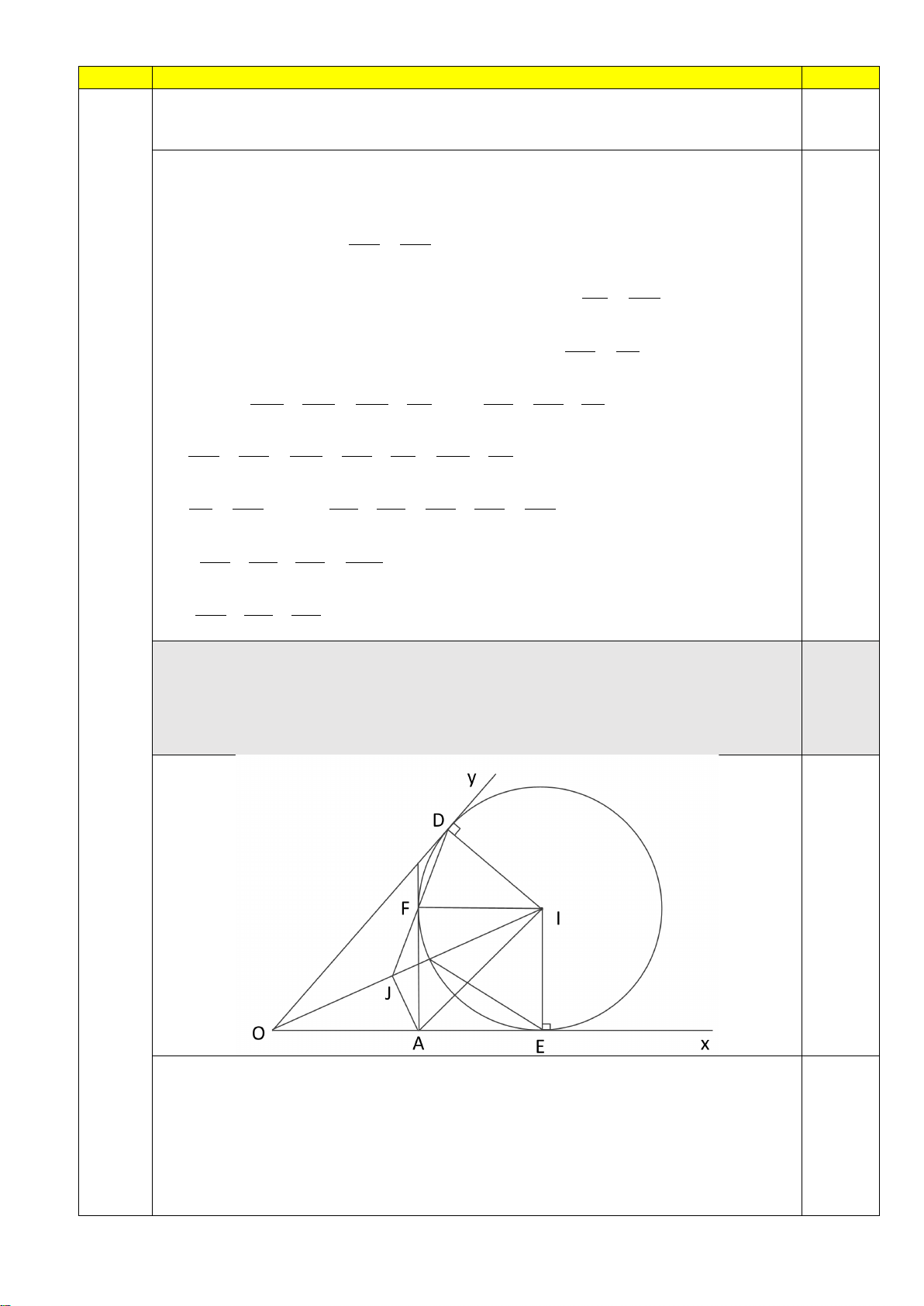
xOy cố định và A là điểm cố định trên .
Ox Đường tròn (I ) thay đổi
nhưng luôn tiếp xúc với Ox, Oy lần lượt tại E, .
D Gọi AF là tiếp tuyến thứ hai 2,0
kẻ A từ đến (I ) ( F là tiếp điểm). Chứng minh DF luôn đi qua một điểm cố định.
Kéo dài DF cắt OI tại J
Chứng minh được 4 điểm , A E, ,
I F cùng thuộc một đường tròn 0,75
Chứng minh được  = 
JFE JIE => 4 điểm J, F, ,
I E cùng thuộc một đường tròn. 0,75 Do đó 5 điểm , A E, ,
I F, J cùng thuộc một đường tròn Góc  0
AJI = 90 => J là điểm cố định 0,5 Page 5 of 6 Câu
Sơ lược lời giải Điểm Cho 2 số dương a, . b Chứng minh: (a + b − )2 1 (a −b + )2 1 (b − a + )2 1 3 + + ≥ (1) (
a + b)2 +1 (a + )2 1 + b (b + )2 2 2 1 + a 5 2 2  a +1   b +1  (a b )2 −1 −    1 1 b a  + −     3 (1) ⇔ + + ≥ (*) ( a + b)2 2 2 +1  a +1  b +1 5 +1 +     1  b   a  a b 1 Đặt x = ; y = ; z = a + b +1 a + b +1 a + b +1 b +1 1 a +1 1 1 0,5 ta được = −1;
= −1;a + b = −1; a x b y z Vì ; a b > 0 ⇒ ; ; x y z > 0
Ta lại có x + y + z = 1 ⇒ 0 < ; ; x y z <1 (1− 2z)2 (1− 2y)2 (1− 2x)2 3 Thay vào (*) ta được + + ≥
z + (1− z)2 y + (1− y)2 x + (1− x)2 2 2 2 5 2 2 2
4z − 4z +1 4y − 4y +1 4x − 4x +1 3 ⇔ + + ≥ 2 2 2
2z − 2z +1 2y − 2y +1 2x − 2x +1 5 0,5 1 1 1 27 ⇔ + + ≤ VI. 2 2 2
2z − 2z +1 2y − 2y +1 2x − 2x +1 5 (2,0 1 9 54  1  điểm) Ta có ≤ + t − 
 (*) với mọi t thuộc khoảng (0; 1) 2
2t − 2t +1 5 25  3  1 9 18(3t − ) 1 Thật vậy (*) ⇔ ≤ + 2 2t − 2t +1 5 25 18(3t − ) 1 9 1 ⇔ + − ≥ 0 2 25 5 2t − 2t +1 18(3t − ) 2 1 18t −18t + 4 ⇔ + ≥ 25 5( 0 2 2t − 2t + ) 1 9(3t − )
1 (3t − 2)(3t − ) 1 0,5 ⇔ + ≥ 0 2 5 2t − 2t +1 ( t )9 3t − 2 3 1  ⇔ − + ≥ 0  2 5 2t 2t 1 − +  ⇔ ( t − )( 2
3 1 18t − 3t − ) 1 ≥ 0 vì 2
2t − 2t +1 > 0 t ∀ ⇔ ( t − )2 3 1 (6t + )
1 ≥ 0 luôn đúng với mọi t thỏa mãn 0 < t <1 1
Dấu bằng xảy ra khi t = 3 Sử dụng (*) 3 lần cho ;
x y; z rồi cộng từng vế 3 bất đẳng thức cùng chiều ta có điều phải chứng minh. 1 0,5
Dấu bằng xảy ra khi x = y = z = hay a = b = 1 3 -----HẾT----- Page 6 of 6
Document Outline

• HSG TOAN 9_ĐỀ CHÍNH THỨC 2023
• HSG_TOAN 9_ĐÁP ÁN CHÍNH THỨC 2023