Đề học sinh giỏi cấp tỉnh Toán 9 năm 2022 – 2023 sở GD&ĐT Hải Dương

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH HẢI DƯƠNG
NĂM HỌC 2022 – 2023
MÔN THI: TOÁN – LỚP 9 ĐỀ CHÍ NH THỨC Ngày thi 11/01/2023 (Đề thi có 01 trang)
Thời gian làm bài: 150 phút, không kể thời gian phát đề
Câu I. (2 điểm) 4 3 2
x + 5x − 20x − 27x + 30 1) Cho 23 x =
. Tính giá trị của biểu thức P = 31 2 +12 3 x + 4x − 21
2) Cho a,b,c > 0 thỏa mãn a +b + c + 2 abc =1 . Chứng minh rằng
a(1− b)(1− c) + b(1− c)(1− a) + c(1− a)(1− b) − abc =1
Câu II. (2 điểm)
1) Giải phương trình 3 2
x + x − x +1 = 3x +1
xy + 2x − y = 3
2) Giải hệ phương trình  1 2 + =1  2 2
 x − 2x + 2 y + 4y + 7
Câu III. (2 điểm)
1) Giải phương trình nghiệm nguyên 3 3 2
x − y − 2y − 3y −1 = 0
2) Tìm số nguyên tố p để 2
2041− p không chia hết cho 24
Câu IV. (3 điểm)
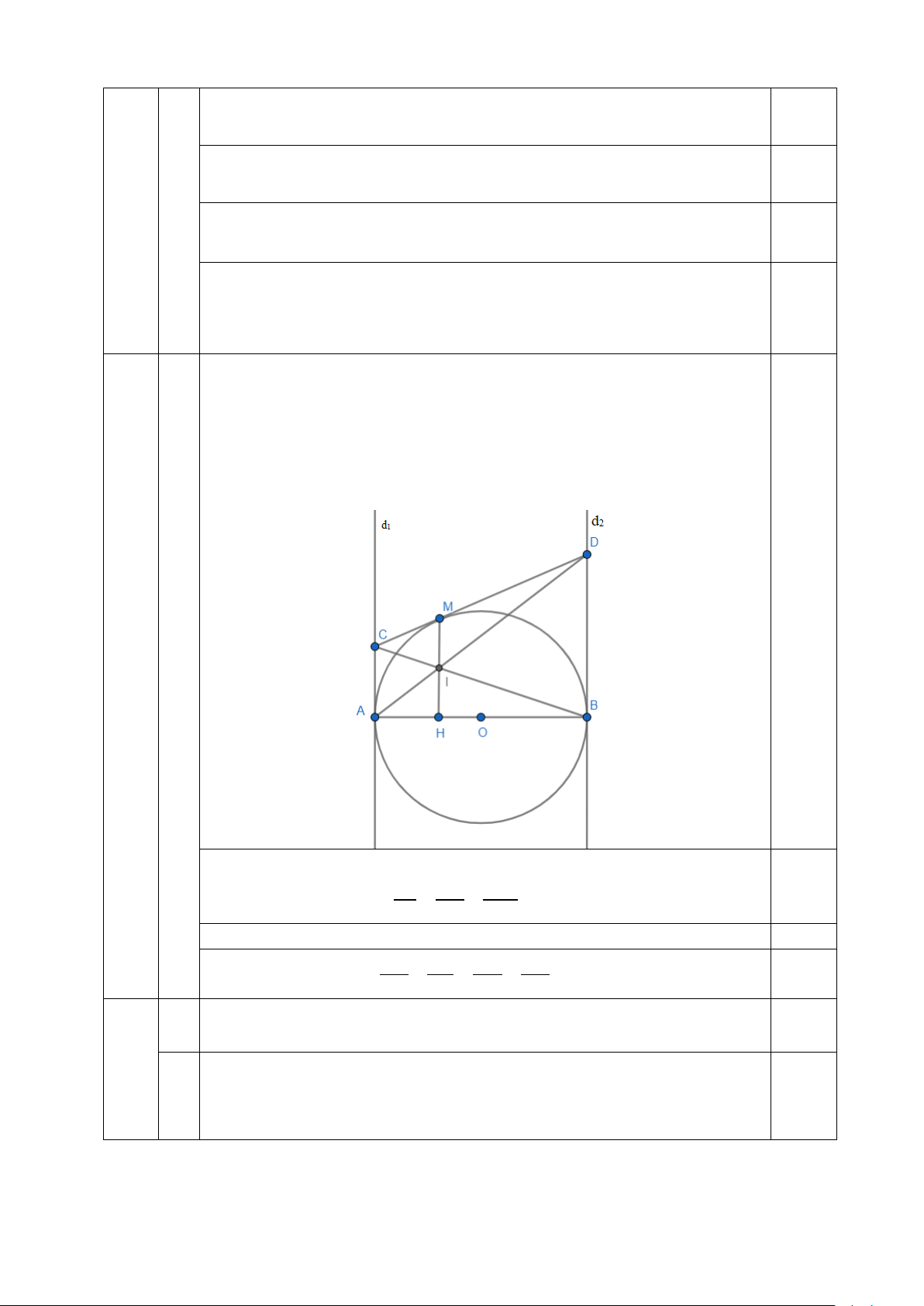
1) Cho đường tròn (O) đường kính AB, qua A và B lần lượt vẽ các tiếp tuyến d1 và d d
2 với (O) . Từ điểm M bất kỳ trên (O) vẽ tiếp tuyến với đường tròn, cắt 1 tại
C và cắt d2 tại D. Kẻ MH vuông góc với AB tại H.
a) Chứng minh rằng: AD, BC, MH đồng quy tại trung điểm của MH.
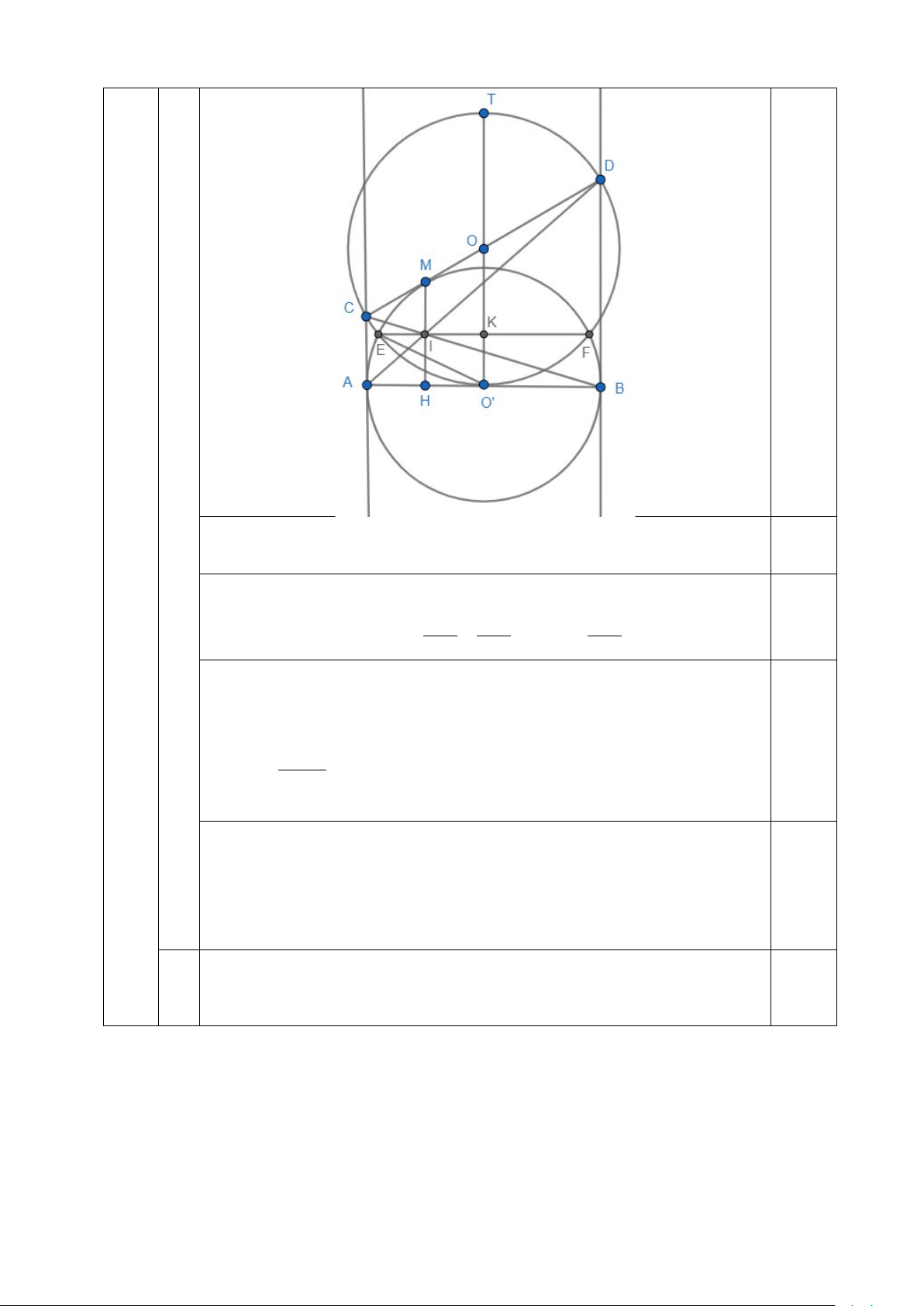
b) Đường tròn (O') đường kính CD cắt đường tròn (O) tại E và F (E thuộc cung 
AM ). Chứng minh EF đi qua trung điểm của MH
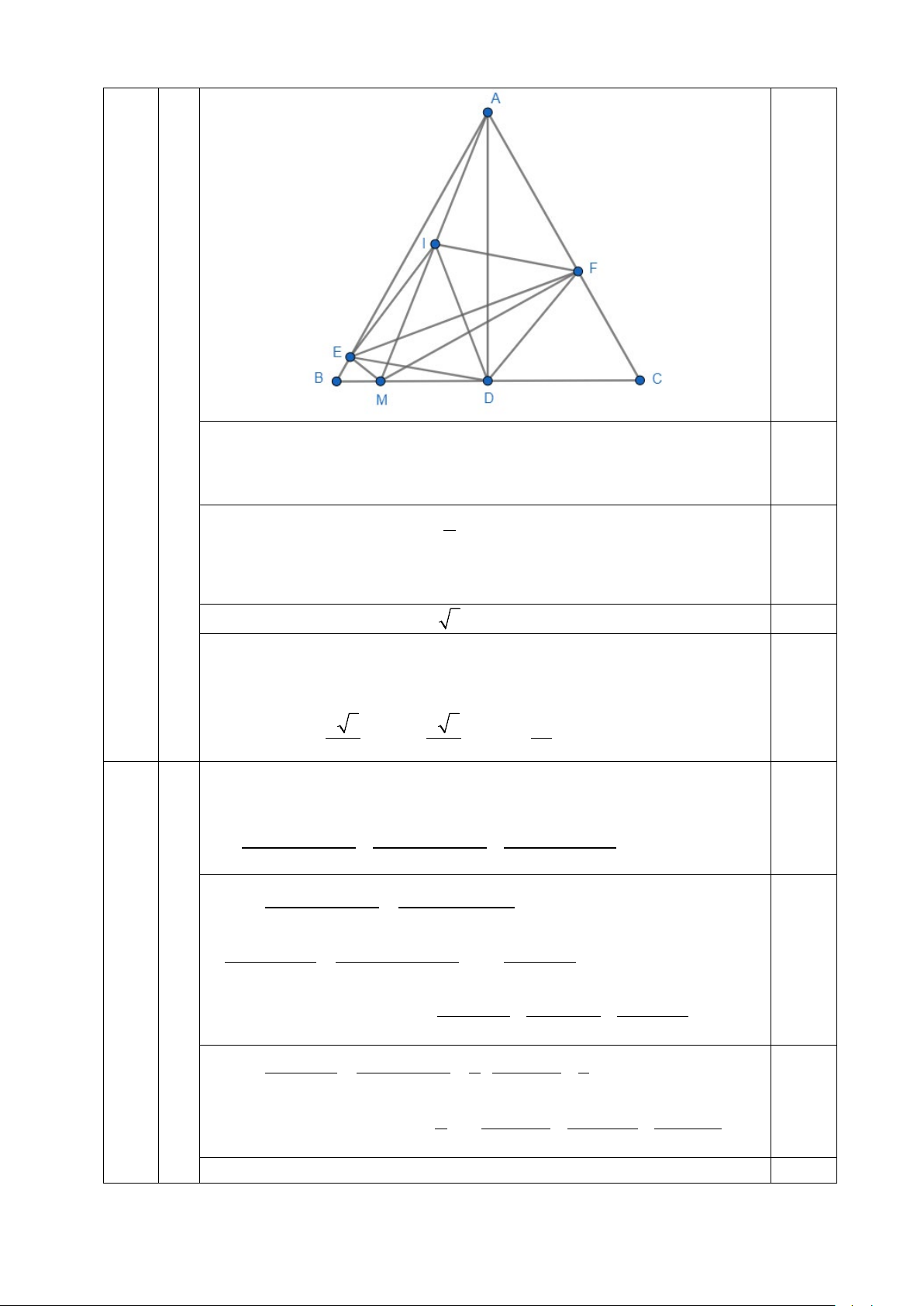
2) Cho tam giác ABC đều cạnh a. Điểm M di động trên đoạn BC. Vẽ ME vuông
góc với AB tại E, MF vuông góc với AC tại F. Tính giá trị nhỏ nhất của đoạn EF theo a. Câu V. (1 điểm)
Cho các số dương x, y, z thõa mãn xyz =1. Tìm giá trị nhỏ nhất của biểu thức: (x + )2 2 + y + ( y + )2 2 + z + (z + )2 2 1 1 1 1 1 + x +1 P = + + xy + x + 4 yz + y + 4 zx + z + 4
------------------Hết------------------
Thí sinh không được sử dụng tài liệu và máy tính cầm tay
DỰ THẢO HƯỚNG DẪN CHẤM
ĐỀ THI HỌC SINH GIỎI TỈNH TOÁN 9 SỞ GD&ĐT HẢI DƯƠNG 2022 - 2023 Câu Ý Nội dung Điểm Cho 23 x =
. Tính giá trị của biểu thức 31+12 3 1.0 4 3 2
x + 5x − 20x − 27x + 30 P = 2 x + 4x − 21 23(3 3 − 2 23 23 23 ) x = = = = = 3 3 − 2 0.25 31+12 3 (3 3+2)2 3 3+2 23 2 2
⇒ x + 2 = 3 3 ⇒ x + 4x + 4 = 27 ⇒ x + 4x − 23 = 0 0.25 1 4 3 2
x + 5x − 20x − 27x + 30 P = 2 x + 4x − 21 2 x ( 2
x + 4x − 23) + x( 2
x + 4x − 23) −( 2
x + 4x − 23) + 7 P = ( 2x +4x−23)+2 0.25
( 2x +4x−23)( 2x + x− )1+7 P = ( 2
x + 4x − 23) + 2 I ⋅( 2 0 x + x − ) 1 + 7 7 P = = 0.25 0 + 2 2
Cho a,b,c > 0 thỏa mãn a +b + c + 2 abc =1. Chứng minh rằng
a(1− b)(1− c) + b(1− c)(1− a) + c(1− a)(1− b) − abc =1 1.0
Do a,b,c > 0 và a +b + c + 2 abc =1
⇒ a + 2 abc + bc =1− b − c + bc = (1− b)(1− c) 0.25
⇒ a( − b)( − c) = a + a abc + abc = (a + abc)2 2 1 1 2 = a + abc 0.25 2 Tương tự:
⇒ b(1− c)(1− a) = b + abc ; 0.25
c(1− a)(1−b) = c + abc Do đó:
a(1− b)(1− c) + b(1− c)(1− a) + c(1− a)(1− b) − abc 0.25
= a + b + c + 2 abc =1
II 1 Giải phương trình 3 2
x + x − x +1 = 3x +1 1.0 Điều kiện: 1 x ≥ − 3 0.25 3 2 3 2
x + x − x +1 = 3x +1 ⇔ x + x − 2x + (x +1) − 3x +1 = 0 (x + )2 1 − 3x +1 3 2 ( )
⇔ x + x − 2x + = 0 0.25 x +1+ 3x +1 ⇔ ( − ) 2 2 ( + 2) x − x x x x + = 0 0.25 x +1+ 3x +1 ( 2x x) 1 x 2  ⇔ − + + =   0 (*)  x +1+ 3x +1  Với 1 x ≥ − thì 1 x + 2 + > 0 3 (x +1) + 3x +1 nên (*) x = 0 3
⇔ x − x = 0 ⇔ 0.25  (t/m) x = 1
Vậy phương trình có tập nghiệm S ={0; } 1
xy + 2x − y = 3
Giải hệ phương trình  1 2 + =1 1.0  2 2
 x − 2x + 2 y + 4y + 7 (  x − ) 1 ( y + 2) =1 Hệ phương trình  ⇔  1 2 + = 1 0.25  ( x − )2 1 +1 ( y + 2)2 + 3 uv  =1
Đặt u = x −1,v = y + 2 . Hệ đã cho trở thành  1 2 2 + =  1 2 2 u +1 v + 3 0.25 uv  = 1 uv  = 1 ⇔  ⇔ 2 2 2 2 2 2  2 2 2 u
 v + 3u + v + 3 = 2u + v + 5 u  v + u = 2 uv  = 1 u = v = 1 ⇔  ⇔ 0.25 u  1  = ± u = v = 1 −
Từ đó suy ra nghiệm của hệ phương trình là x = 2 x = 0  ; y 1  = − y = 3 − 0.25
Vậy nghiệm của hệ phương trình là x = 2 x = 0  ; y 1  = − y = 3 −
Giải phương trình nghiệm nguyên 3 3 2
x − y − 2y − 3y −1 = 0 1.0
Phương trình đã cho tương đương với 3 3 2
x = y + 2y + 3y +1 Nhận xét rằng: 2 3 3 2 2
y ≥ 0 ⇒ x ≤ y + 2y + 3y +1+ y = ( y + )3 1 (1) 0.25 2 3 3 2
y + > ⇒ x > y + y + y + − ( 2 5 2 0 2
3 1 5y + 2) = ( y − )3 1 (2)
Từ (1) và (2) suy ra: ( y − )3 3
1 < x ≤ ( y + )3 1 3 3 3 2 3  =  1 x y
y + 2y + 3y +1 = y
Vì x, y∈Ζ ⇒  ⇔  0.25 3 3 3 2 3 III x =  ( y + )1
 y + 2y + 3y +1 =  ( y + )1 2
2y + 3y +1 = 0  y = 1 ( − do y ∈ Ζ)  y = 1 − ⇔  ⇔ ⇔ 0.25 2  y = 0   y 0  =  y = 0 Với y = 1 − ⇒ x = 1 −
Với y = 0 ⇒ x =1 0.25
Vậy phương trình có 2 cặp nghiệm nguyên là ( 1; − − ) 1 và (1;0)
Tìm số nguyên tố p để 2
2041− p không chia hết cho 24 1.0 2 Đặt 2 a = − p = − ( 2 2041 2040 p − ) 1 = 2040 − ( p − ) 1 ( p + ) 1 0.25
Nếu p = 2 ⇒ a = 2037 không chia hết cho 24 ⇒ p = 2 (nhận)
Nếu p = 3⇒ a = 2032 không chia hết cho 24 ⇒ p = 3 (nhận)
Nếu p > 3 mà p là số nguyên tố. Do đó 2 p chia cho 3 dư 1 2 ⇒ p −13 0.25
p > 3 mà p là số nguyên tố. Do đó p lẻ nên p −1 và p +1 là hai
số chẵn liên tiếp ⇒ ( p − ) 1 ( p + )
1 8. Mà (3;8) =1⇒ ( p − ) 1 ( p + ) 1 24 0.25
⇒ a = 2040 − ( p − ) 1 ( p + ) 1 24
Do đó p > 3 không thỏa mãn điều kiện đề bài. Vậy 0.25 p = 2; p = 3
Cho đường tròn (O) đường kính AB, qua A và B lần lượt
vẽ các tiếp tuyến d d
1 và 2 với (O) . Từ điểm M bất kỳ trên
(O) vẽ tiếp tuyến với đường tròn, cắt d d
1 tại C và cắt 2 tại
D. Kẻ MH vuông góc với AB tại H. Chứng minh rằng: AD,
BC, MH đồng quy tại trung điểm của MH. 1.0 IV 1a
Gọi giao điểm của AD và BC là I. Ta có IC CA CM IC ∆ A  IB ∆ D ⇒ = =
⇒ MI / /BD ⇒ MI ⊥ AB 0.25 IB BD DM
Mà MH ⊥ AB ⇒ I ∈MH 0.25
Chứng minh được: MI CI AI IH = = = 0.25 BD CB AD BD
⇒ MI = IH hay I trung điểm MH Vậy AD, BC,
MH đồng quy tại trung điểm của MH 0.25
Đường tròn (O') đường kính CD cắt đường tròn (O) tại E
1b và F (E thuộc cung 
AM ). Chứng minh EF đi qua trung 1.0
điểm của MH
Ta chứng minh tam giác COD vuông tại O nên O’O là bán kính
của (O') và O'O ⊥ EF 0.25
Gọi R bán kính đường tròn (O) 2 0.25 Ta có ∆  ∆ ' MH OM R MHO OMO ⇒ = ⇒ MH = (1) OM OO ' OO '
Vẽ đường kính OT của đường tròn (O')
Tam giác OET vuông tại E có EK là đường cao nên 2
OE = OK.OT 0.25 2 R ⇒ OK =
(2). Từ (1) và (2) suy ra MH = 2.OK 2.OO'
Do I là trung điểm của MH nên IH = OK, suy ra IK / /AB
Ta có O’O là đường trung bình của hình thang vuông ABDC
nên O'O ⊥ AB, từ đó suy ra EF / /AB
Hai đường thẳng IK và EF cùng song song với AB và cùng đi 0.25
qua K nên bốn điểm E, I, K, F thẳng hàng. Vậy EF đi qua trung điểm của MH
Cho tam giác ABC đều cạnh a. Điểm M di động trên đoạn
2 BC. Vẽ ME vuông góc với AB tại E, MF vuông góc với AC 1.0
tại F. Tính giá trị nhỏ nhất của đoạn EF theo a.
Kẻ đường cao AD của tam giác ABC. Lấy I là trung điểm AM
AD là đường cao đồng thời là phân giác ⇒  0 BAD = 30 0.25 Chứng minh được  0 =  0 = ⇒  0 EID 60 , EIF 120 DIF = 60 Chứng minh 1
EI = DI = FI = AM , mà  =  0 EID DIF = 60 2
Suy ra tam giác EID và FID là tam giác đều và EIFD là hình 0.25 thoi
Chứng minh được EF = ID 3 0.25
Vậy EF ngắn nhất khi và chỉ khi ID ngắn nhất
ID ngắn nhất khi và chỉ khi AM ngắn nhất ⇒ AM là đường cao 0.25 Khi đó a 3 a 3 3a AM = ⇒ ID = ⇒ EF = 2 4 4
Cho các số dương x, y, z thõa mãn xyz =1 . Tìm giá trị nhỏ
nhất của biểu thức: ( 1.0 x + )2 2 + y + ( y + )2 2 + z + (z + )2 2 1 1 1 1 1 + x +1 P = + + xy + x + 4 yz + y + 4 zx + z + 4 Ta có (x + )2 2 2 2
1 + y +1 x + y + 2x + 2 = xy + x + 4 xy + x + 4
2xy + 2x + 2 2(xy + x + 4) − 6 6 V ≥ = = 2 − 0.25 xy + x + 4 xy + x + 4 xy + x + 4 Tương tự, suy ra  1 1 1  P ≥ 6 − 6 + + 
 xy x 4 yz y 4 zx z 4  + + + + + +  Ta có 1 1 1  1 1  = ≤ +
xy x 4 xy x 1 3 4  xy x 1 3 + + + + + + +  0.25 Tương tự, suy ra 1  1 1 1  P ≥ 6 − 6⋅ 1+ + +
4  xy x 1 yz y 1 zx z 1 + + + + + +  Mặt khác 0.25 1 1 1 1 xyz xyz + + = + +
xy + x +1 yz + y +1 zx + z +1 xy + x +1 yz + y + xyz zx + z + xyz 1 xz xy 1 xz xy = + + = + +
xy + x +1 z +1+ xz x +1+ xy xy + x +1 z + xyz + xz x +1+ xy 1 x xy = + + =1
xy + x +1 1+ xy + x x +1+ xy 1
⇒ P ≥ 6 − 6⋅ (1+ ) 1 = 6 − 3 = 3 0.25 4
(Lưu ý: Học sinh có cách giải đúng khác cũng cho điểm tối đa) UBND TỈNH HẢI DƯƠNG
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO
LỚP 9 THCS NĂM HỌC 2022- 2023 MÔN THI: TOÁN
Thời gian làm bài: 150 phút, không kể thời gian giao đề ĐỀ CHÍNH THỨC
(Đề thi có 05 câu, 01 trang)
Câu I. (2,0 điểm)
1) Cho a, b, c là các số thực dương thỏa mãna + b + c = 6 và a + b + c = 4. Chứng minh rằng: a b c 10 + + = . a + 5 b + 5 c + 5 (a + 5)( b + 5)(c + 5) 3 2) Cho ( ) x f x =
. Hãy tính giá trị của biểu thức sau: 2 1- 3x + 3x  1   2   2020   2021 A = f  + f   + .. + f   + f   2022 2022 2022  2022        
Câu II. (2,0 điểm) 1) Giải phương trình: 2 x+7 3x + 6x - 3 = . 3
2) Giải hệ phương trình: xy + x +1= 7y  2 2 2
x y + xy +1 = 13y
Câu III. (2,0 điểm)
1) Tìm các số nguyên x, y thỏa mãn đẳng thức: 2 2 2 2
8x y + x + y =10xy .
2) Cho p; x; y là các số tự nhiên thoả mãn 2 ( ) 2 px + x = p + 1 y + y .
Chứng minh rằng px + py + 1 là số chính phương.
Câu IV. (3,0 điểm)
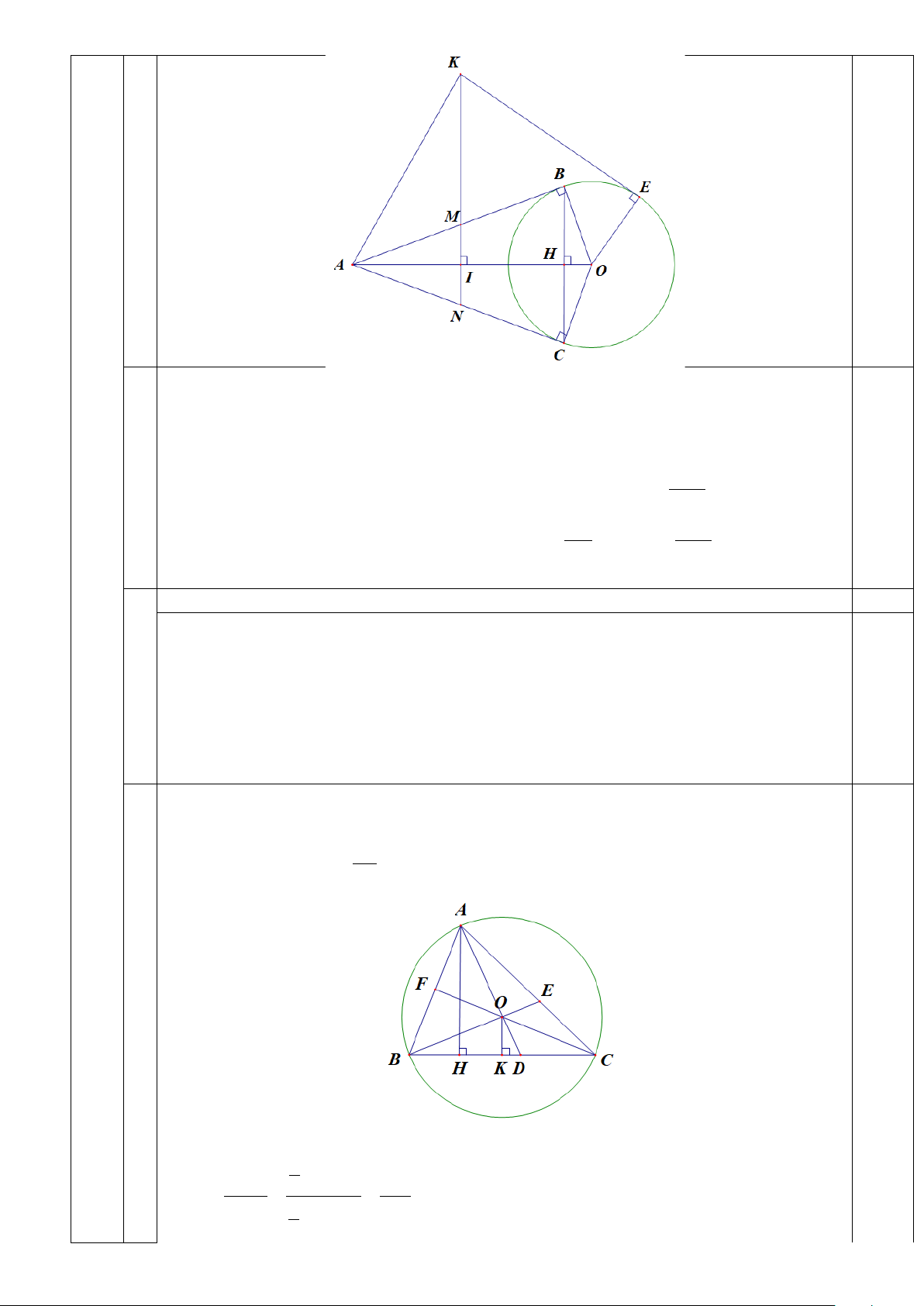
1) Cho đường tròn tâm O, bán kính R. Điểm A nằm bên ngoài đường tròn tâm O. Qua A
vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Gọi M, N lần lượt là trung
điểm của AB, AC; H là giao điểm của AO với BC. Lấy điểm E bất kì trên đường tròn (E
khác B và C). Qua E vẽ tiếp tuyến với đường tròn tâm O, tiếp tuyến này cắt đường thẳng MN tại K. a) Chứng minh rằng: 2 MN = AH.HO ;
b) Chứng minh rằng: KA = KE .
2) Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn (O; R) . Gọi D, E, F lần lượt là
giao điểm của các đường thẳng AO với BC, BO với AC, CO với AB. Chứng minh rằng: 9R AD + BE + CF ≥ . 2
Câu V. (1,0 điểm)
Cho a,b,c là các số thực dương thỏa mãn:a + b + c =1. 2 2 2 2 2 2
Tìm giá trị nhỏ nhất của biểu thức:
a + b + 2 a + c + 2 c + b + 2 S = + + .
a + b − ab
a + c − ac
c + b − cb
-------------------HẾT-------------------
Họ và tên thí sinh:.................................................... Số báo danh:..................................................
Cán bộ coi thi số 1:.......................................Cán bộ coi thi số 2:.................................................... UBND TỈNH HẢI DƯƠNG
DỰ THẢO HƯỚNG DẪN CHẤM
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI TỈNH LỚP 9 Năm học 2022 - 2023 MÔN THI : TOÁN
Lưu ý: Thí sinh làm theo cách khác đúng vẫn cho điểm tối đa. Điểm bài thi làm tròn đến 0,25đ. Câu Ý Nội dung Điểm
1 Cho a,b,c là các số thực dương thỏa mãna +b + c = 6 và a + b + c = 4. Chứng minh rằng: a b c 10 1,0 + + =
a + 5 b + 5 c + 5
(a + 5)(b + 5)(c + 5) Ta có
a + b + c = 4 ⇔ a + b + c + 2( ab + bc + ca) =16 ⇒ ab + bc + ca = 5 0,25
Do đó: a + 5 = a + ab + bc + ca = ( a + b)( a + c) Tương tự ta có:
b + 5 = b + ab + bc + ca = ( b + c)( b + a) 0,25
c + 5 = c + ab + bc + ca = ( c + a)( c + b) Suy ra: a b c a b c + + = + +
a + 5 b + 5 c + 5 ( a + b)( a + c) ( b + c)( b + a) ( c + a)( c + b) 0,25
a ( b + c)+ b ( c + a )+ c ( a + b) =
( a + b)( b + c)( c + a)
2( ab + bc + ca) 10 I = = (a 0,25
+ 5)(b + 5)(c + 5)
(a + 5)(b + 5)(c + 5) Vậy a b c 10 + + =
a + 5 b + 5 c + 5
(a + 5)(b + 5)(c + 5) 2 3 Cho ( ) x f x =
. Hãy tính giá trị của biểu thức sau: 2 1− 3x + 3x 1,0  1   2   2020   2021 A f  f   ... f   f  = + + + +  2022 2022 2022  2022        
Nhận xét: với x + y =1thì f (x) + f ( y) =1. 3 3 Thật vậy, ta có − f (x) x 1 x =
⇒ f y = f 1− x = 3 3 ( ) ( ) ( ) x + (1− x) 3 x + (1− x)3 x (1− x)3 3
Suy ra f (x) + f ( y) = f (x) + f (1− x) = + = 1. 0,25 3 x + (1− x)3 3 x + (1− x)3 Ta có 1 1 f   =  . 0,25 2    2
Theo nhận xét trên ta có:   1   2021    2   2020 A =  f +  f +    f +   f  +   ...+    2022 
 2022    2022   2022    1010   1012   1011  f  f   f  + +    2022   2022    2022  0,25 1 A 1010 f   = + =   1010,5 0,25  2 
1 Giải phương trình: 2 x + 7 3x + 6x − 3 = 1,0 3 Điều kiện: x ≥ 7 − . 2 x + 7 x + x − = ⇔ (x + )2 x + 7 3 6 3 3 1 = + 6 (2) 3 3 0,25 Đặt x + 7 y +1 = ≥ 0 ⇒ 3( y + )2
1 = x + 7 . Từ (2) ta có: (x + )2 3 1 = y + 7 3 3  (x + )2 2 1 = y + 7 3
 x + 6x − y − 4 = 0 Ta ó c :  ⇔  3  ( y + )2 2 1 = x + 7 3
 y + 6y − x − 4 = 0  y = x 0,25 ( 2 2 3 x
y ) 7(x y) 0 (x y)(3x 3y 7) 0  ⇒ − + − = ⇔ − + + = ⇔ 7 −  y = − x  3 x + 7 x ≥ 1 − 73 − 5 TH1: y = x ⇒ = x +1 ⇔  ⇔ x = 2 3 3 0,25
 x + 5x − 4 = 0 6  4 − 7 x + 7 4 x ≤ − 69 − 7
TH2: y = − − x ⇒ = − − x ⇔  3 ⇔ x = 3 3 3  2 6 9
 x + 21x − 5 = 0 0,25 II  73 −5 − 69 − 7
VËy tËp nghiÖm cña pt lµ : S ;  =  6 6    2
xy + x +1 = 7 y
Giải hệ phương trình:  1,0 2 2 2
x y + xy +1 = 13y
y = 0 không thoả mãn hệ . y ≠ 0  1 x  1 x x + + = 7 x + + = 7 xy x 1 7 y  + + = 0,25  y y  y y   ⇔  ⇔  2 2 2 2
x y + xy +1 = 13y  2 1 x   1 + + = 13  x x 2 x + − =   13  y y     y  y  1 a = x +  Đặt  y  x b  =  y a = 4 0,25 a + b = 7 b  = 7 − a  b   = 3 Ta có:  ⇔  ⇔ 2 2 a b 13 a a 20 0  − = + − = a = 5 −   b   = 12 x =1  1  x + = 4   1 a = 4  y x = 3y y = Với  ⇒  ⇔  ⇔  3 0,25 2 b  = 3 x  3
 y − 4y +1 = 0 = 3 x = 3  y  y =1  1 x + = 5 − a = 5  −  y x =12y  ∈∅ Với x  ⇒  ⇔  ⇔ 2 b  12 x  =  12
 y + 5y +1 = 0 =12 y ∈∅  0,25  y
Kết luận: Hệ phương trình có nghiệm là  1 ( ; x y) (1; ),(3;1) ∈  3   
1 Tìm các số nguyên x, y thỏa mãn đẳng thức: 2 2 2 2
8x y + x + y =10xy . 1,0 2 2 2 2 2 2 2 2
8x y + x + y =10xy ⇔ x + y − 2xy = 8xy −8x y 0,25
⇔ (x − y)2 = 8xy(1− xy)
Ta có (x − y)2 ≥ 0 với mọi x, y suy ra 8xy(1− xy) ≥ 0 ⇔ 0 ≤ xy ≤1 0,25 Vì xy = 0 ;
x y ∈ Z ⇒  xy = 1
x = 0 ⇒ y = 0(tm) Nếu xy = 0 ⇔  0,25
 y = 0 ⇒ x = 0(tm) Nếu
x = y =1(tm) xy =1 ⇔  x = y = 1( − tm) 0,25 III
Vậy các cặp số nguyên (x;y) cần tìm là (0;0), ( 1; − 1 − ),(1;1) .
2 Cho ;p ;x y là các số tự nhiên thoả mãn 2
px + x = ( p + ) 2 1 y + y . 1,0
Chứng minh rằng px + py +1 là số chính phương. 2
px + x = ( p + ) 2
y + y ⇔ p( 2 2 x − y ) 2
+ x − y = y ⇔ (x − y)( px + py + ) 2 1 1 = y 0,25  − Đặt  = ( x y d d
x − y, px + py + ) 1 ,(d ∈ N*) ⇒  0,25
 px + py +1d
Vì (x − y)( px + py + ) 2 2 2
1 = y ⇒ y d ⇒ yd
Mà x − yd ⇒ xd ⇒ px + pyd 0,25
Vì px + py +1d ⇒1d ⇒ d =1
Vậy x − y và px + py +1 là các số nguyên tố cùng nhau, mà (x − y)( px + py + ) 1
là số chính phương nên px + py +1 là số chính phương. 0,25
1 Cho đường tròn tâm O, bán kính R. Điểm A nằm bên ngoài đường tròn tâm O. Qua
A vẽ hai tiếp tuyến AB, AC với đường tròn ( B, C là các tiếp điểm). Gọi M, N lần
lượt là trung điểm của AB, AC; H là giao điểm của AO với BC. Lấy điểm E bất kì IV
trên đường tròn ( E khác B và C). Qua E vẽ tiếp tuyến với đường tròn tâm O, tiếp 2,0
tuyến này cắt đường thẳng MN tại K. a) Chứng minh rằng : 2
MN = AH.HO ;
b) Chứng minh rằng : KA = KE . 0,25 a) Ta có A
∆ BC cân tại A suy ra AB = AC OB ∆
C cân tại O suy ra OB = OC Suy ra 0,25
AO là đường trung trực của BC suy ra AO ⊥ BC tại H và H là trung điểm của BC. 2 Xét A
∆ BO vuông tại B có đường cao BH nên 2 . BC AH HO = BH = . 0,25 4 2
Vì MN là đường trung bình của A ∆ BC nên BC 2 BC MN = ⇒ MN = . 2 4 0,25 Do đó 2
MN = AH.HO .
b) Chứng minh rằng : KA = KE
Xét tam giác vuông KEO có 2 2 2 2 2
KE = KO − OE = KO − R (1)
Vì MN / /BC, BC ⊥ AO ⇒ MN ⊥ AO . 0,25
Gọi I là giao điểm của MN và AO thì I là trung điểm AH, ta có: 2 2 2 2 2 2 2 = + = − + = + ( + )( − ) 2 KA KI IA KO OI IA KO
AI OI AI OI = KO − AO(OI − AI ) 0,25 2 2
⇒ KA = KO − AO (OI − IH ) 2 2 2 2 2 . = KO − A .
O OH = KO − OB = KO − R (2) 0,25 Từ (1) và (2) suy ra 2 2
KE = KA ⇒ KE = KA 0,25
2 Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn ( ;
O R) . Gọi D, E, F lần lượt
là giao điểm của các đường thẳng AO với BC, BO với AC, CO với AB. Chứng minh 1,0 rằng : 9R
AD + BE + CF ≥ . 2
Kẻ OK và AH lần lượt vuông góc với BC ( K, H thuộc BC). 1 OK.BC Ta có: S ∆ OK BOC 2 = = S 1 ∆ AH ABC AH.BC 2 Mà AH // OK nên OK OD OD S − ∆ AD AO S∆ AO S BOC BOC ⇒ = ⇒ = ⇒ = ⇒ = 1 B ∆ OC − AH AD AD S ∆ AD S∆ AD S ABC ABC ABC ∆ 0,25
Tương tự ta có: BO =1 S∆ CO S AOC − ; =1 B ∆ OA − BE S 0,25 ∆ CF S ABC ABC ∆ Suy ra: OA OB OC S + + ∆ S∆ S AOC BOC A ∆ OB 1 1 1 2 + + = 3− = 3−1 = 2 ⇒ + + = AD BE CF S 0,25 ∆ AD BE CF R ABC Ta có: ( + + ) 1 1 1  9 + + ≥  9 R AD BE CF
⇒ AD + BE + CF ≥   AD BE CF  2 0,25
Cho a,b,c là các số thực dương thỏa mãn: a + b + c =1. Tìm giá trị nhỏ nhất của biểu 1,0 2 2 2 2 2 2 thức:
a + b + 2 a + c + 2 c + b + 2 S = + + .
a + b − ab
a + c − ac
c + b − cb Ta có: 2 2 2 2 2 2 a + b + 2 a +1+ b +1 a +1 b +1 = = +
a + b − ab (a + b)(a + b + c) 2 2 2 2
− ab a + b + ab + ac + bc a + b + ab + ac + bc 2 2 2 2 0,25
Tương tự: a + c + 2 a +1 c +1 = + 2 2 2 2
a + c − ac
a + c + ab + ac + bc a + c + ab + ac + bc 2 2 2 2 b + c + 2 b +1 c +1 = + 2 2 2 2
b + c − bc
b + c + ab + ac + bc b + c + ab + ac + bc Suy ra 2 2 2 a +1 b +1 a +1 S = + + 2 2 2 2 2 2
a + b + ab + ac + bc a + b + ab + ac + bc a + c + ab + ac + bc 0,25 2 2 2 c +1 b +1 c +1 + + + 2 2 2 2 2 2
a + c + ab + ac + bc b + c + ab + ac + bc b + c + ab + ac + bc V Áp dụng: 1 1 4 + ≥ ∀ ; x y > 0. x y x + y Ta có: a +1 a +1 4( 2 2 2 a + ) 1 + ≥ 2 2 2 2 2 2 2
a + b + ab + ac + bc a + c + ab + ac + bc 2a + b + c + 2ab + 2ac + 2bc 4( 2 a + ) 1 4( 2 a + ) 1 = = = 4. 0,25 2
a + (a + b + c)2 2 a +1 2 2 Tương tự ta có: b +1 b +1 + ≥ 4 2 2 2 2
a + b + ab + ac + bc b + c + ab + ac + bc 2 2 c +1 c +1 + ≥ 4 2 2 2 2
a + c + ab + ac + bc b + c + ab + ac + bc Suy ra S ≥12. Dấu bằng xảy ra khi 1
a = b = c = . 3 0,25
Vậy giá trị nhỏ nhất của S bằng 12 khi 1
a = b = c = . 3
Document Outline