Đề học sinh giỏi cấp tỉnh Toán THCS năm 2022 – 2023 sở GD&ĐT Khánh Hòa

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS KHÁNH HÒA
CẤP TỈNH NĂM HỌC 2022 - 2023 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC Ngày thi: 07/12/2022
Thời gian: 150 phút (không kể thời gian phát đề) Câu 1 (4,00 điểm): ( − ) 3 3 1 . 10 + 6 3
1) Rút gọn biểu thức A = . 6 + 2 5 − 5 2 2) Cho  + 
x, y là các số nguyên thỏa mãn đẳng thức 2 2 xy 1 x + y + =   2.  x + y 
Chứng minh rằng xy +1 là một số chính phương. Câu 2 (4,00 điểm):
1) Cho đa thức f (x) với các hệ số nguyên thỏa mãn f (3). f (4) = 7 . Chứng minh rằng
đa thức f (x) −12 không có nghiệm nguyên.
2) Tìm 3 số nguyên tố sao cho tích của chúng gấp 5 lần tổng của chúng. Câu 3 (4,00 điểm): 1) Giải phương trình 6x − 4
2x + 4 − 2 2 − x = . 2 x + 4
2) Cho a, b là hai số thực lớn hơn 1 và thỏa mãn điều kiện a + b ≤ 4. Tìm giá trị nhỏ 4 4 nhất của biểu thức a b A = + .
(b − )3 (a − )3 1 1 Câu 4 (6,00 điểm):
1) Cho tam giác ABC , I là một điểm bất kỳ nằm trong tam giác. Qua I vẽ đường
thẳng DE song song với AB ( D ∈ AC , E ∈ BC ) và đường thẳng IM song song với BC
( M ∈ AC ). Tính giá trị của biểu thức ID BE CM + + . AB BC CA
2) Cho hình vuông ABCD có tâm O . Điểm E thay đổi trên cạnh BC ( E khác B và
C ).Gọi F là giao điểm của tia AE và đường thẳng CD , gọi H là giao điểm của OE và BF . a) Chứng minh rằng 1 1 + không đổi. 2 2 AE AF
b) Tìm vị trí của điểm E để diện tích tam giác HAD đạt giá trị lớn nhất. Câu 5 (2,00 điểm):
Một tứ giác lồi có độ dài bốn cạnh đều là số tự nhiên sao cho tổng ba số bất kì trong
chúng chia hết cho số còn lại. Chứng minh rằng tứ giác đó có ít nhất hai cạnh bằng nhau.  HẾT 
- Giám thị không giải thích gì thêm.
- Họ và tên thí sinh:…………………………...…… SBD:……………/Phòng: …………………….
- Giám thị 1: ……………………………….....…… Giám thị 2: …………………………………… Trang 1/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS KHÁNH HÒA
CẤP TỈNH NĂM HỌC 2022 - 2023 HƯỚNG DẪN CHẤM Môn thi: TOÁN ĐỀ THI C HÍNH THỨC Ngày thi: 07/12/2022
(Hướng dẫn chấm có 06 trang) Câu 1 (4,00 điểm): ( − ) 3 3 1 . 10 + 6 3
1) Rút gọn biểu thức A = . 6 + 2 5 − 5 Hướng dẫn chấm Điểm Ta có : 1,00 3 10 + 6 3 ( 3 − ) 3 3 1 = ( 3 +1) ( 3 − )1 2 6 + 2 5 − 5 = ( 5 +1) − 5 0,50 3 3 10 6 3( 3 1) 3
( 3 +1) ( 3 −1) ( 3 +1)( 3 −1) Suy ra A + − = = = 1,00 6 + 2 5 − 5 2 ( 5 +1) − 5 5 +1− 5 3 −1 = = 2 1 0,50 Vậy A = 2 . 2 2) Cho  + 
x, y là các số nguyên thỏa mãn đẳng thức 2 2 xy 1 x + y + =   2.  x + y 
Chứng minh rằng xy +1 là một số chính phương. Hướng dẫn chấm Điểm
Với điều kiện x + y ≠ 0 , ta có: 2 2 2  xy +1 x + y + =   2  x + y  2 ⇔ (  +  x + y)2 xy 1 − 2(xy +1) + =   0  x + y  0,50 2  xy +1 ⇔ x + y − =   0  x + y  xy +1 ⇔ x + y − = 0 x + y
⇔ xy + = (x + y)2 1
Do x, y là các số nguyên nên x + y là số nguyên. 0,50
Vậy xy +1 là một số chính phương. Trang 2/6 Câu 2 (4,00 điểm):
1) Cho đa thức f (x) khác hằng với các hệ số nguyên thỏa mãn f (3). f (4) = 7 .
Chứng minh rằng đa thức f (x) −12 không có nghiệm nguyên. Hướng dẫn chấm Điểm
+) Giả sử đa thức f (x) −12 có nghiệm nguyên a . 0,50
Khi đó f (x) −12 = (x − a).Q(x) với Q(x) là đa thức có hệ số nguyên.
Suy ra f (3) = (3− a).Q(3) +12 và f (4) = (4 − a).Q(4) +12 (1) 0,50
+) Ta có: f (3). f (4) = 7
⇔ (3− a).Q(3) +12.
 (4 − a).Q(4) +12 = 7  0,50
⇔ (3 − a).(4 − a).Q(3).Q(4) +12(3 − a).Q(3) +12(4 − a).Q(4) +144 = 7 (2)
+) Do 3 − a và 4 − a là hai số nguyên liên tiếp nên (3− a)(4 − a) là số chẵn. Do đó
VT của (2) là số chẵn, nhưng VP của (2) là số lẻ, điều này mâu thuẫn. 0,50
Vậy giả sử trên sai. Suy ra đa thức f (x) −12 không có nghiệm nguyên.
2) Tìm 3 số nguyên tố sao cho tích của chúng gấp 5 lần tổng của chúng. Hướng dẫn chấm Điểm
+) Gọi 3 số nguyên tố cần tìm là a,b,c . Khi đó, ta có: . a .
b c = 5(a + b + c) ⇒ . a . b c5 0,50
+) Vì a,b,c có vai trò bình đẳng nên không mất tính tổng quát, giả sử a5 ⇒ a = 5 (vì a ∈ P ) +) Khi đó: 5. .
b c = 5(5 + b + c) ⇔ 5 + b + c = . b c ⇔ .
b c − b − c +1 = 6 ⇔ b(c − ) 1 − (c − ) 1 = 6 ⇔ (c − ) 1 (b − ) 1 = 6 0,50  − =  − =  =  = Suy ra b 1 1 b b 2 b  hoặc 1 2  ⇔  hoặc 3  c −1 = 6
c −1 = 3 c = 7 c = 4 0,50 b  = 2 b  = b  = ⇔  hoặc 3  (loại vì c ∉ P) 2 ⇔  c = 7 c = 4 c = 7
+) Do vai trò của a,b,c là bình đẳng nên ba số cần tìm là 2; 5; 7 0,50
Vậy ba số cần tìm là 2; 5; 7 Câu 3 (4,00 điểm):
1) Giải phương trình 6x − 4 2x + 4 − 2 2 − x = 2 x + 4 Hướng dẫn chấm Điểm
+) ĐK: 2 − ≤ x ≤ 2 +) Ta có: 6x − 4 2x + 4 − 2 2 − x = 2 x + 4 1,00 2(3x − 2) 2 3x ( − 2) ⇔ = 2 2x + 4 + 2 2 − x x + 4 Trang 3/6  2 x = ⇔ 3  1,00 2
 2x + 4 + 2 2− x = x + 4 (*)
+) Ta có: (*) ⇔ 4 2(2 + x)(2 − x) + (2 − x)(x + 4) = 0 0,50
⇔ 2 − x (4 2(2+ x) + (2− x).(x + 4)) = 0  2 − x = 0 ⇔ 
4 2(2 + x) + (2 − x).(x + 4) =  0 (**)
+) Với 2 − x = 0 ⇔ x = 2 (thỏa ĐK) 0,50 +) Với 2
− ≤ x ≤ 2 thì VT của (**) luôn dương nên (**) vô nghiệm.
Vậy tập nghiệm của phương trình là S = {2; 2 } 3
2) Cho a,b là hai số thực lớn hơn 1 và thỏa mãn điều kiện a + b ≤ 4. Tìm giá trị 4 4
nhỏ nhất của biểu thức a b B = + .
(b − )3 (a − )3 1 1 Hướng dẫn chấm Điểm
+ Do a >1, b >1 nên a −1 > 0, b −1 > 0
+ Áp dụng BĐT Cauchy cho hai số dương, ta có: 2 2 2a b B ≥ (1) (a − ) 1 (b − ) 1 (a − ) 1 (b − ) 1 2
+ Ta lại có: 0 <1.( − ) 1 b b ≤ (2) 0,50 42 0 <1.( − ) 1 a a ≤ (3) 4
4 ≥ a + b ≥ 2 ab ⇒ab ≤ 4 (4)
Từ (1), (2), (3) và (4) suy ra 2 2 3 2a b .4 B ≥ = 128 ≥ 128 = 32 3 3 a .b . a b 4 4 4  a b = 0,50
Dấu “=” xảy ra khi và chỉ khi (b − )3 (a − )3 1 1 ⇔ a = b = 2 
a −1 = b −1 = 1;a + b = 4
Vậy giá trị nhỏ nhất của B là 32 và đạt được khi a = b = 2
Câu 4 (6,00 điểm): ( Học sinh không vẽ hình hoặc vẽ hình sai không chấm)
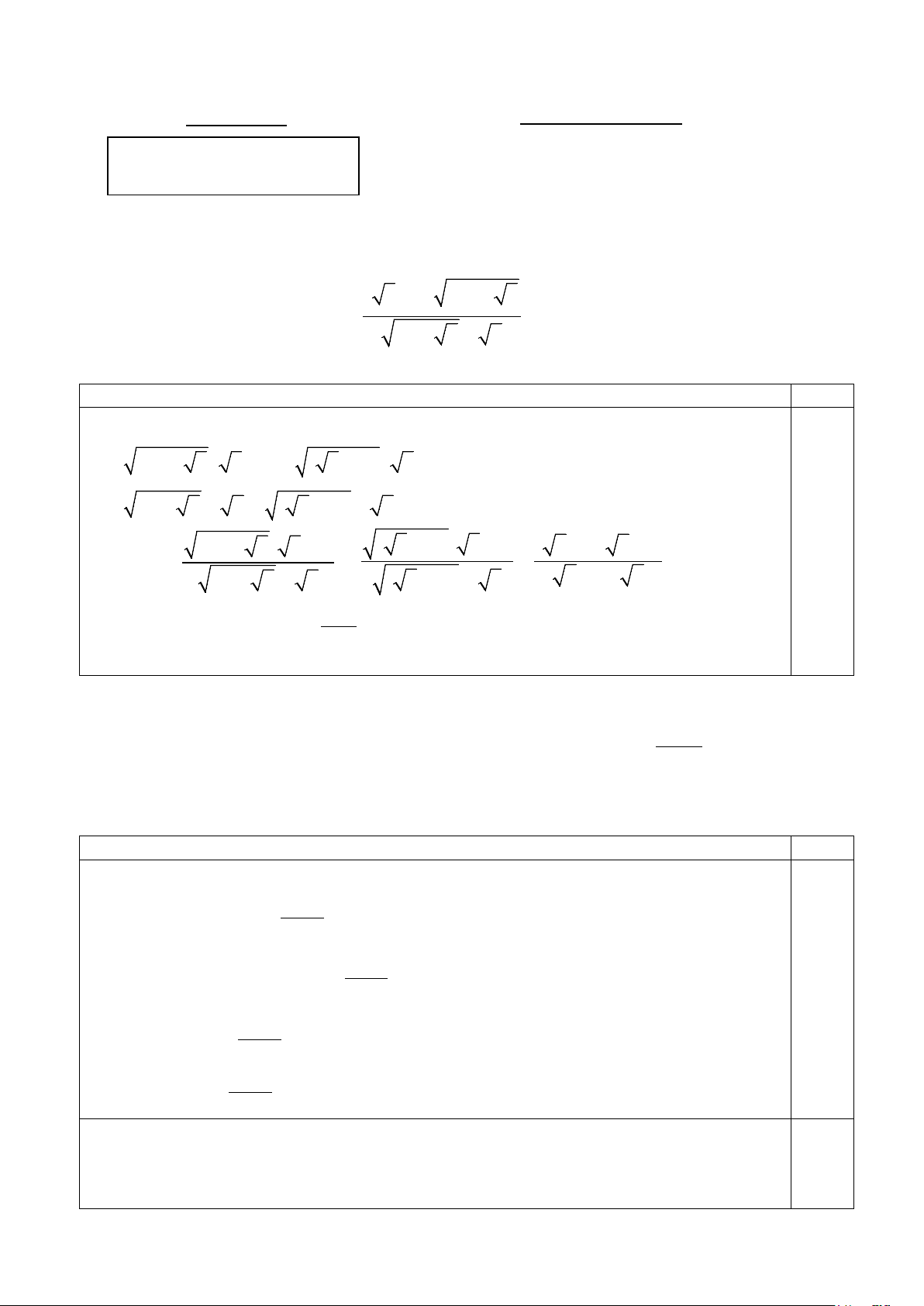
1) Cho tam giác ABC , I là một điểm bất kỳ nằm trong tam giác. Qua I vẽ đường
thẳng DE song song với AB ( D ∈ AC , E ∈ BC ) và đường thẳng IM song song với BC
( M ∈ AC ). Tính giá trị của biểu thức ID BE CM + + . AB BC CA Trang 4/6 Hướng dẫn chấm Điểm B N E I A D M C
+) Gọi N là giao điểm của IM và AB .
+) Xét ΔABC , ta có: MN // BC CM BN IE ⇒ = =
(vì tứ giác BNIE là hình bình hành) 0,50 CA BA AB Suy ra ID CM IE ID DE + = + = . 0,50 AB CA AB AB AB
+) Ta lại có: DE // AB DE CE ⇒ = .Suy ra ID CM CE + = . 0,50 AB CB AB CA BC ID CM BE CE BE BC ⇒ + + = + = = 1. AB CA CB BC BC BC 0,50 Vậy ID BE CM + + = 1 AB BC CA
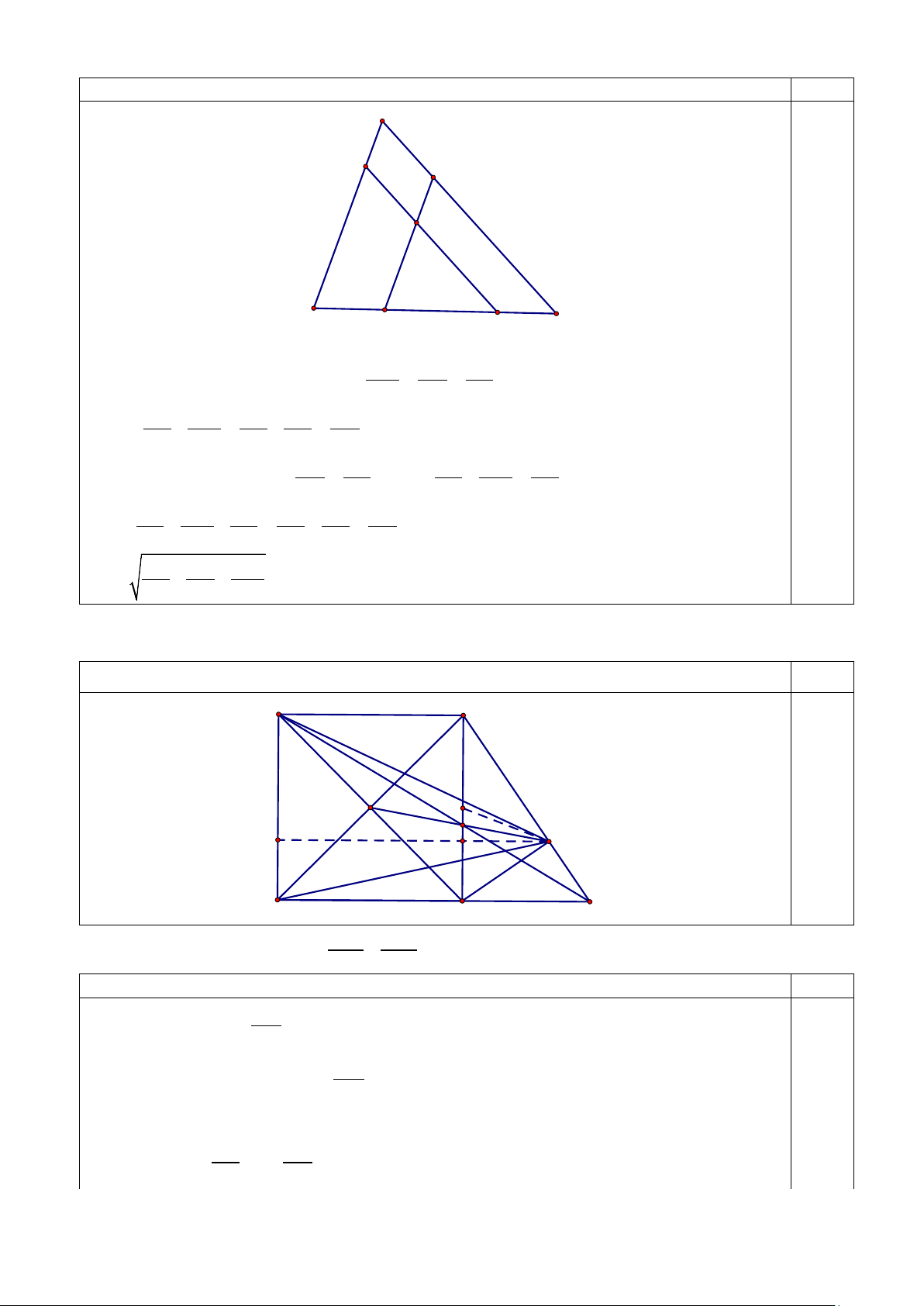
2) Cho hình vuông ABCD có tâm O . Điểm E thay đổi trên cạnh BC ( E khác B và C ).
Gọi F là giao điểm của tia AE và đường thẳng CD ,gọi H là giao điểm của OE và BF . Hướng dẫn chấm Điểm A B O M E H P Q H' F D C
a) Chứng minh rằng 1 1 + không đổi. 2 2 AE AF Hướng dẫn chấm Điểm + Ta có: cos AB BAE = 0,50 AE sin = sin AD BAE DFA = 1,00 AF + Ta lại có: 2 2
sin BAE + cos BAE =1 2 2 Suy ra  AB   AD  + =     1 0,50  AE   AF  Trang 5/6 ⇔ 2  1 1 AB .  + =   1 2 2  AE AF  ⇔ 1 1 1 + =
(không đổi vì AB không đổi) 0,50 2 2 2 AE AF AB Vậy 1 1 + không đổi. 2 2 AE AF
b) Tìm vị trí của điểm E để diện tích tam giác HAD đạt giá trị lớn nhất. Hướng dẫn chấm Điểm
+) Gọi H ' là chân đường vuông góc hạ từ C xuống BF
+) Xét ΔBCF vuông tại C , ta có: 2
CH ' ⊥ BF ⇒ BC = BH '.BF
Xét ΔBCD vuông tại C , ta có: 2
CO ⊥ BD ⇒ BC = . BO BD
Suy ra BH '.BF = .
BO BD hay BH ' BO = BD BF 0,50
+) Xét ΔBH 'O và ΔBDF , ta có: B chung và BH ' BO = (cmt) BD BF
Suy ra ΔBH 'O ∽ Δ BDF ⇒   0 BH 'O = 45 BDF =
Suy ra H 'O là tia phân giác của  BH 'C (1)
+) Ta có: ΔBH 'C ∽ Δ
BCF (vì B chung và   0 H ' = C = 90 ). BH ' CH ' ⇒ = BH ' BC AB ⇒ = = , mà BE AB =
(vì AB // CF ) BC CF CH ' CF CF CE CF 0,50 Suy ra BE BH ' =
⇒ H 'E là tia phân giác của  BH 'C (2) CE CH '
Từ (1) và (2) suy ra H ', ,
O E thẳng hàng . Do đó H ' ≡ H . Suy ra CH ⊥ BF
+) Gọi M là trung điểm của BC . Khi đó 1
HM = AD (vì ΔBHC vuông tại H ) 2 +) Ta có: 2S
= AD HP = AD HQ + PQ = AD + AD HQ ≤ AD + AD HM = AD HAD . .( ) 2 2 2 . . 3 2 3 0,50 2 ⇒ S ≤ AD . HAD 4
Dấu “=” xảy ra khi HQ = HM ⇔ Q ≡ M ⇔ O, ,
Q H thẳng hàng ⇔ E ≡ M (vì H, ,
O E thẳng hàng). Vậy để diện tích tam giác HAD đạt giá trị lớn nhất thì E là
trung điểm của BC .
Câu 5 (2,00 điểm): Một tứ giác lồi có độ dài bốn cạnh đều là số tự nhiên sao cho tổng ba
số bất kì trong chúng chia hết cho số còn lại. Chứng minh rằng tứ giác đó có ít nhất hai cạnh bằng nhau. Hướng dẫn chấm Điểm
+) Gọi độ dài các cạnh của tứ giác là * a, b, ,
c d (a, b, , c d ∈  .)
+) Giả sử không có 2 cạnh nào của tứ giác bằng nhau. 0,50
+) Không mất tính tổng quát, giả sử a > b > c > d. (*)
+) Do tứ giác lồi nên a < b + c + d ⇒ a < b + c + d < 3a
⇒ 2a < a + b + c + d < 4a (**) 0,50 Trang 6/6
+) Từ giả thiết bài toán suy ra a + b + c + d chia hết cho các số a, b, , c d .
Kết hợp với (**), ta có : a + b + c + d = 3a (1)
+) Đặt a + b + c + d = mb với * m∈  (2) 0,50
a + b + c + d = nc với * n∈  (3)
Do a > b > c ⇒ n > m > 3 ⇒ n ≥ 5, m ≥ 4.
Cộng (1), (2), (3) vế theo vế ta có: 3(a + b + c + d ) = 3a + mb + nc ≥ 3a + 4b + 5c
mà 3a + mb + nc ≥ 3a + 4b + 5c (vì n ≥ 5, m ≥ 4)
Suy ra 3(a + b + c + d ≥
) 3a + 4b + 5c 0,50
⇔ (b – d ) + 2(c – d ) ≤ 0 mâu thuẫn (*)
Vậy tứ giác có ít nhất 2 cạnh bằng nhau.
Mọi cách giải khác đúng đều cho điểm tương ứng theo biểu điểm.
 HẾT  Trang 7/6
Document Outline

• ĐỀ THI CHÍNH THỨC
• HƯỚNG DẪN CHẤM ĐỀ THI CHÍNH THỨC