Đề học sinh giỏi tỉnh Toán THCS năm 2022 – 2023 sở GD&ĐT Thanh Hóa

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THANH HÓA
NĂM HỌC 2022 - 2023 MÔN THI: TOÁN - THCS ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian giao đề
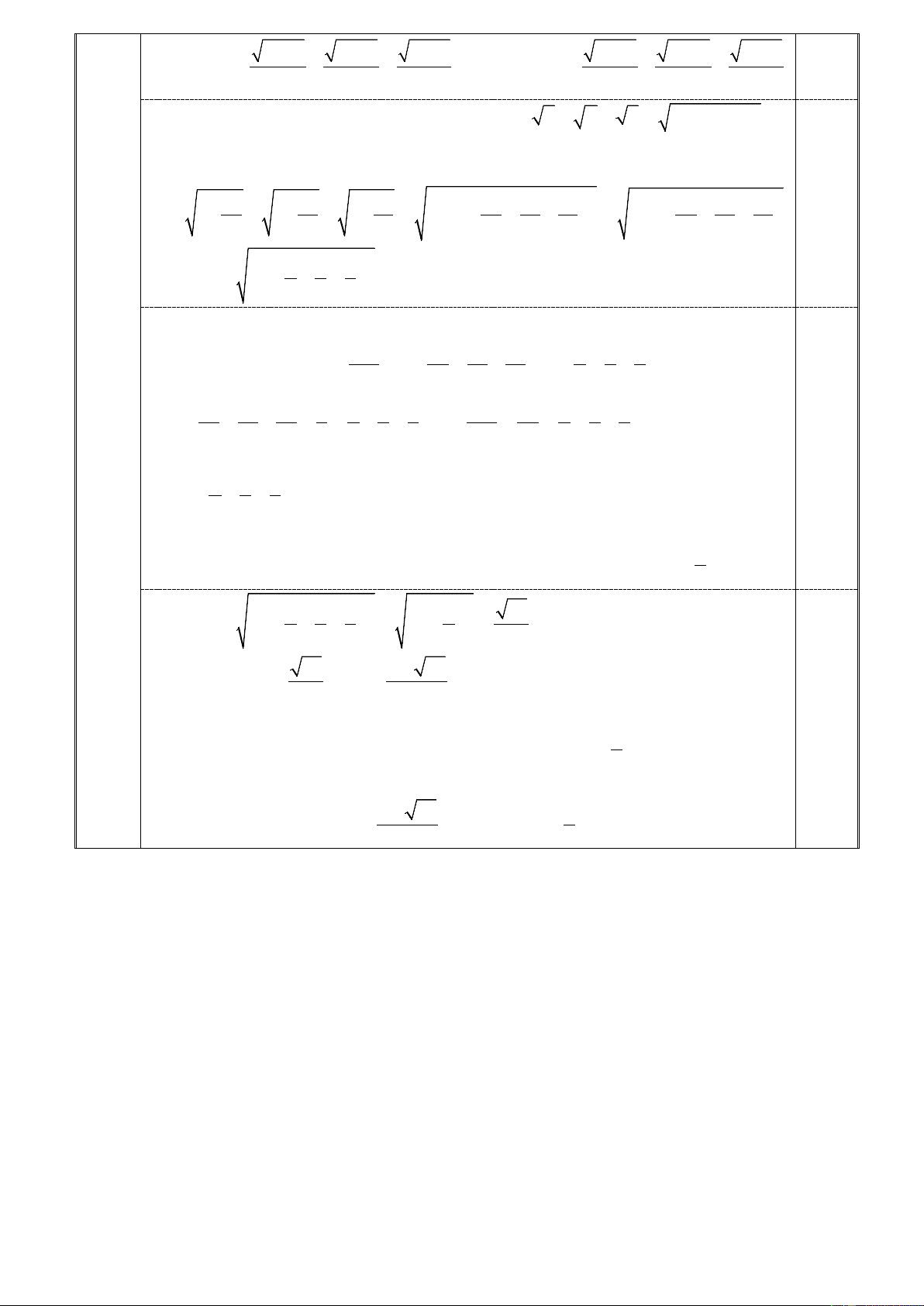
(Đề thi có 01 trang) Câu I (4, 0 điểm). x   x + 1 Cho biểu thức 2 1 9 14 P = ⋅ 1+ +   với x ≥ 0 . x + 3  x + 2  x + 3 x + 2
Rút gọn biều thức P và tìm các giá trị của x để biểu thức P có giá trị là số tự nhiên.
2 Cho các số thực a,b, c thỏa mãn đồng thời 2 4 2 4 2 4
a + 2 = b ;b + 2 = c ; c + 2 = a .
Tính giá trị biểu thức 2 2 2 2 2 2
B = a + b + c + a b c − ( 2 2 2 2 2 2
a b + b c + c a ) + 2022 . Câu II (4,0 điểm).
2. Giải phương trình 3 2
4x + 13x − 14x = 3 − 15x + 9 . 3 2
x + 3xy + 49 = 0
3. Giải hệ phương trình  . 2 2
x − 8xy + y = 8y −17x
Câu III (4, 0 điểm).
1. Tìm tất cả các bộ số nguyên ( ,
m p, q) thỏa mãn: m 2 5
2 ⋅ p + 1 = q trong đó m > 0; p, q là hai số nguyên tố.
2. Cho a, b là hai số nguyên thỏa mãn a khác b và ab (a + b) chia hết cho 2 2
a + ab + b . Chứng minh rằng 2 a − b > ab . Câu IV (6,0 điểm).
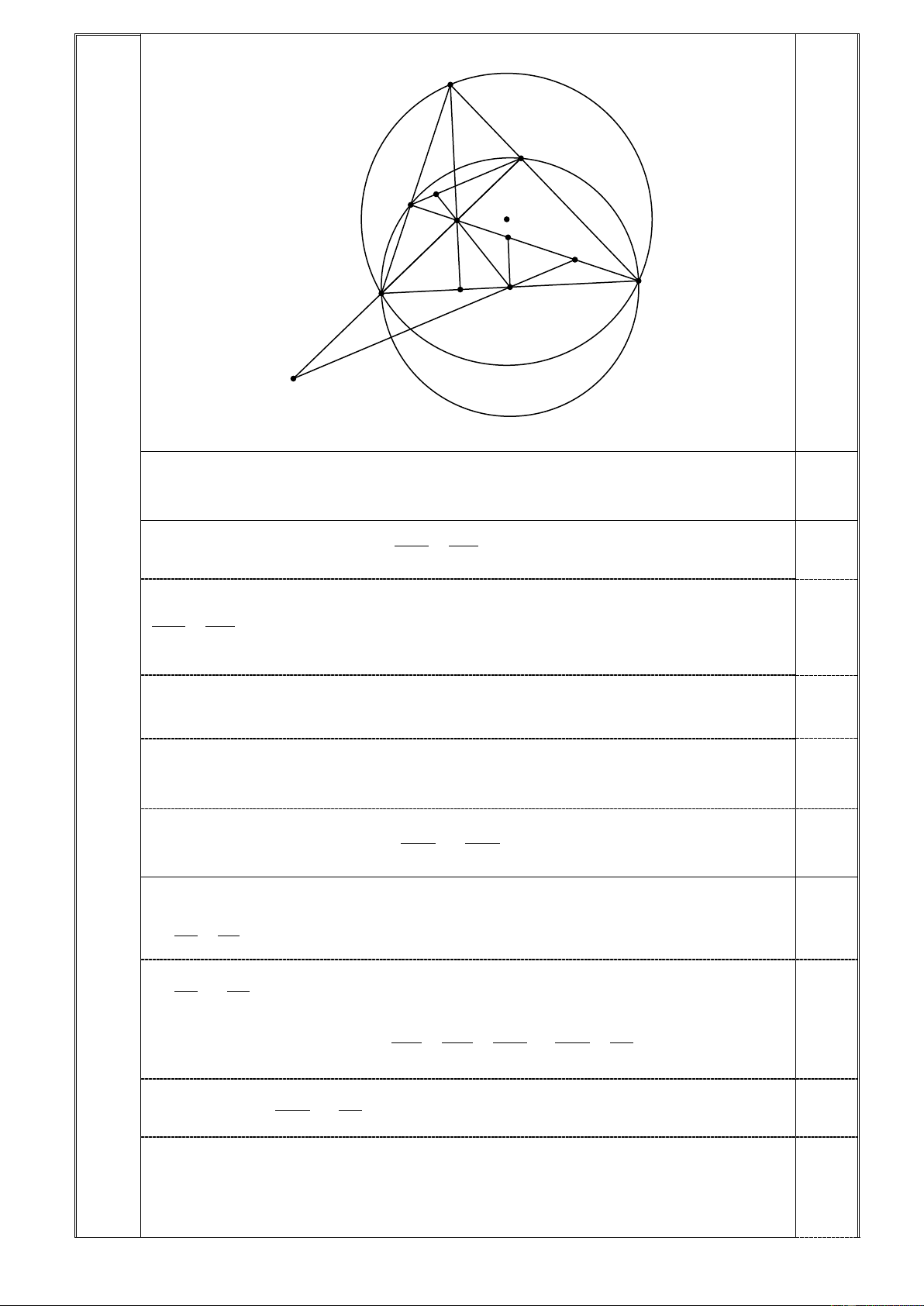
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O bán kính R . Đường tròn tâm I đường kính
BC cắt các cạnh AB và AC lần lượt ở M và N . Các tia BN và CM cắt nhau tại H . Gọi K là giao
điềm của IH với MN . Qua I kẻ đường thẳng song song với MN cắt các đường thẳng CM và BN lần
lượt ở E và Q .
1 Chứng minh ∆ANM đồng dạng với ∆ABC và  BQI =  ECI . 2 KN  HN  2 Chứng minh 2 IQIE = IC và =   . KM  HM 
3 Gọi D la giao điểm của AH với BC . Chứng minh rằng 1 1 1 4 + + ≤ . 2 AD ⋅ BN BN ⋅ CM CM ⋅ AD 3(R − OH )
Câu V (2,0 điểm) Cho ba số a,b,c ≥ 1 thỏa mãn 16abc + 4(ab + bc + ca) = 81+ 24(a + b + c) . Tim giá trị
nhỏ nhất của biểu thức 1 1 1 Q = a ( + + 2
a − 1 + a) b( 2
b − 1 + b) c( 2 c − 1 + c)
------------- HẾT --------------
Họ và tên thí sinh:…………………………………………SBD……………
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THANH HÓA NĂM HỌC: 2022-2023 HƯỚNG DẪN CHẤM
Môn thi: TOÁN – THCS
(Hướng dẫn chấm có 06 trang) Câu NỘI DUNG Điểm I x   x + 4,0
1. Cho biếu thức 2 1 9 14 P = ⋅ 1+ +  
với x ≥ 0 . điểm x + 3  x + 2  x + 3 x + 2 2,0
Rút gọn biều thức P và tìm các giá trị của x để biếu thửc P có giá trị là số tự nhiên.
Điều kiện x ≥ 0 . Ta có: 2 x x x ( x +   + )1 2 1 9 14 9 x + 14 0,5 P = ⋅ 1+ + = +   x + 3  x + 2  x + 3 x + 2
( x + )1( x +2) ( x +2)( x + )1 x + x + ( x +2)(2 x +7 2 11 14 ) 2 x + 7 = ( = = x + 2)( x + ) 1 ( x +2)( x + )1 x + 1 0,5 Vậy 2 x + 7 P = với x ≥ 0 x + 1 2 ( x + ) 1 + 5 5 5 Ta có P = = 2 +
, vì x ≥ 0 nên 0 <
≤ 5 suy ra 2 < P ≤ 7 x + 1 x + 1 x + 1 0,25 5  5 5 5 
Do P ∈  nên P ∈{3; 4;5;6; } 7 ⇔ ∈{1;2;3;4; } 5 ⇔ x + 1∈ 5  ; ; ; ;1 . x + 1  2 3 4  0,25  3 2 1   9 4 1 
⇔ x ∈ 4; ; ; ;0 ⇔ x ∈ 1  6; ; ; ; 0 .  2 3 4   4 9 16    0,25
Kết hợp với điều kiện ta thấy 9 4 1 x ∈ 1  6; ; ;
; 0 là giá trị cần tìm.  4 9 16  Vậy để  
P có giá trị là số tự nhiên thì 9 4 1 x ∈ 1  6; ; ; ; 0 0,25  4 9 16 
2. Cho các số thực a,b, c thỏa mãn đồng thời: 2 4 2 4 2 4
a + 2 = b , b + 2 = c , c + 2 = a .
Tính giá trị biểu thức 2,0 2 2 2 2 2 2
B = a + b + c + a b c − ( 2 2 2 2 2 2
a b + b c + c a ) + 2022 . 2 4
a +1 = b −1 = ( 2 b − ) 1 ( 2 b + ) 1 
Từ giả thiết ta suy ra:  2 4
b +1 = c −1 = ( 2 c − ) 1 ( 2 c + ) 1 0,5  2 4
c +1 = a −1 = 
( 2a − )1( 2a + )1
Nhân vế với vế 3 đằng thức trên với nhau ta được:
( 2a + )( 2b + )( 2c + ) = ( 2b − )( 2c − )( 2a − )( 2b + )( 2c + )( 2 1 1 1 1 1 1 1 1 a + ) 1 0,5 Do ( 2 a + )( 2 b + )( 2 1 1 c + ) 1 > 0 nên ( 2 b − )( 2 c − )( 2 1 1 a − ) 1 = 1 . 0,5 Khai triền ta được 2 2 2 2 2 2 2 2 2 2 2 2
b c a − a b − b c − c a + a + b + c − 1 = 1 2 2 2 2 2 2
⇔ a b c + a + b + c − ( 2 2 2 2 2 2
a b + b c + c a ) = 2. 0,5
Vậy B = 2 + 2022 = 2024 . II
1.Giải phương trình: 3 2
4x + 13x − 14x = 3 − 15x + 9 . 2,0 4,0 điểm x ≥ − ĐKXĐ: 3 . 0,25 5 Pt đã cho 3 2
4x + 13x − 14x − 3 + 15x + 9 = 0 3 2
⇔ x + x − x − ( x + ) + x + = ⇔ ( 2 4 13 12 2 3 15 9 0
4x − 3x)( x + 4) − (2x + 3) − 15x +  0,5 ( x + − x + ⇔ 4x − 3x) 2 (2 3) 15 9 2 (x + 4) ( ) − = ( x + ) 0 2 3 + 15x + 9 ( x + x + − x −
⇔ 4x − 3x)(x + 4) 2 4 12 9 15 9 2 − = ( x + ) 0 2 3 + 15x + 9 2
4x − 3x = 0 (1) 0,25 ⇔ (  1   2
4x − 3x) x + 4 − = 0 ⇔   1  
2x + 3 + 15x + 9  x + 4 − = 0 (2)  2x + 3 + 15x + 9 x = 0  −Pt ( ) 1 ⇔ 3  (đều thoả mãn ĐKXĐ) x =  0,25 4 1 Xét Pt (2): x + 4 − = 0 2x + 3 + 15x + 9 3 17 9 1 5 Vì x ≥ − ⇒ x + 4 ≥
và 2x + 3 + 15x + 9 ≥ ⇒ ≤ 0,5 5 5 5 2x + 3 + 15x + 9 9 1 128 Suy ra x + 4 − ≥
> 0 nên pt (2) vô nghiệm. 2x + 3 + 15x + 9 45
Vậy phương trình đã cho có tập nghiệm là  3 S = 0;  .  4 0,25 3 2
x + 3xy + 49 = 0
2. Giải hệ phương trình  . 2 2 2,0
x − 8xy + y = 8y −17x
Nhân hai vế của phương trình (2) với 3, rồi cộng với phương trình (1) vế theo vế ta được pt: 3 2 2 2
x + 3x + 3xy − 24xy + 3y + 49 = 24 y − 51x 0,5 3 2 2
⇔ x + 3x + 3x +1+ 3y (x + )
1 − 24 y ( x + ) 1 + 48( x + ) 1 = 0 ⇔ (x + ) 2 2  x + + y − y +  = ⇔ (x + ) 2 2 1 ( 1) 3 24 48 0
1 (x + 1) + 3( y − 4)  = 0     0,75  x + 1 = 0 ⇔  2 2
(x +1) + 3(y − 4) = 0  x = 1 −  x = 1 − TH1:  ⇔  3 2 x + 3xy = 4 − 9  y = 4; y = 4 − 0,25 2 2
(x +1) + 3(y − 4) = 0 x = 1 − TH2:  ⇔  3 2 x + 3xy = 49 −   y = 4 0,25
Vậy hệ đã cho có hai nghiệm (x, y)∈ ( { 1 − ;4),( 1 − ; 4 − )} 0,25 III
1. Tìm tất cả các bộ số nguyên ( ,
m p, q) thỏa mãn m 2 5
2 p + 1 = q trong đó 4,0 2,0
m > 0; p, q là hai số nguyên tố.
điểm Vì m > 0 và p nguyên tố nên m 2
2 p + 1 lẻ ⇒ q lẻ m+2 5 4 3 2 m+2 Nếu p = 2 thì 2
+1 = q ⇔ (q − )
1 (q + q + q + q + ) 1 = 2 0,5 Vì q lẻ 4 3 2
⇒ q + q + q + q +1 lẻ lớn hơn 2 1 2 +
⇒ m có ước lẻ lớn hơn 1 , vô lý. Do đó p lẻ.
Ta viết phương trình đã cho dưới dạng (q − ) 1 ( 4 3 2
q + q + q + q + ) 2 = m 1 2 p Do 4 3 2
q + q + q + q + 1 lẻ và lớn hơn 1 nên 4 3 2
q + q + q + q + 1 = p 0,5 hoặc 4 3 2 2
q + q + q + q + 1 = p + Xét trường hợp 4 3 2 + + + +1 = ⇒ −1 = 2m q q q q p q
p . Do 2m p > p nên 0,25 4 3 2
q − > q + q + q + q + 1 1 (vô lý) + Xét trường hợp 4 3 2 2 4 3 2 2 4 3 2
q + q + q + q + 1 = p ⇒ 4q + 4q + q < 4 p = 4q + 4q + 4q + 4q + 4
< q + q + q + q + ⇒ ( q + q)2 < p < ( q + q + )2 4 3 2 2 2 2 4 4 9 4 4 2 4 2 2 . Từ đó suy ra 0,5
p = ( q + q + )2 2 2 4 2
1 . Ta được phương trình (q + q + q + q + ) = ( q + q + )2 4 3 2 2 4 1 2 1 2
⇔ q − 2q − 3 = 0, mà q nguyên tố, suy ra q = 3, từ đó tìm được p = 11;m = 1
Vậy ta có bộ ba số nguyên thoả mãn yêu cầu bài toán là: ( ,
m p, q) = (1;11;3) 0,25
2.Cho a, b là hai số nguyên thỏa mãn a khác b và ab (a + b) chia hết cho 2,0 2 2
a + ab + b . Chứng minh rằng 3 a − b > ab
Đặt d = ƯCLN(a, b) Suy ra a = xd,b = yd với ƯCLN(x, y) = 1 Khi đó:
ab (a + b)
dxy ( x + y) = ∈ 0,5  2 2 2 2
a + ab + b
x + xy + y 2 2 2
UCLN x + xy + y x = y x = Ta có ( ; ) UCLN ( ; ) 1. 0,5 Tương tự ( 2 2
UCLN x + xy + y ; y ) = 1 Đặt d = 2 2
x + y x + xy + UCCLN ( , y )    ( 2 2  x + xy + 
y ) − x ( x + + y ) 2 d x y d x d ⇒  ⇒  ⇒  ⇒ d = 1 (Vì ƯCLN 0,25 2 2 2 x + xy +  y d ( 2 2
 x + xy + y y x y d y    )− ( + )  d (x, y) = )1 Do đó 2 2 2 2
d : x + xy + y ⇒ d ≥ x + xy + y Mặt khác 3 3 3 2 3 2
a − b = d x − y = d x − y
⋅d ≥ d ⋅ ⋅ ( 2 2
x + xy + y ) 2 | | | 1 d xy = ab . 0,5 Vậy 3 a − b > ab . 0,25
IV Cho tam giác ABC nhọn nội tiếp đường tròn tâm O bán kính R . Đường
6,0 tròn tâm I đường kính BC cắt các cạnh AB và AC lần lượt ở M và N . Các điểm 6,0
tia BN và CM cắt nhau tại H . Gọi K là giao điềm của IH với MN . Qua I
kẻ đường thẳng song song với
MN cắt các đường thẳng CM và BN lần lượt
ở E và Q . A N K M O H E P B D C I Q
1.Chứng minh ∆ANM đồng dạng với ∆ABC và  BQI =  ECI . 2,0 AN AB
Ta có: ∆ANB ∼ ∆AMC ( g ⋅ g ) ⇒ = 0,5 AM AC
Xét ∆ANM và ∆ABC có: AN = AB  ; A là góc chung 0,5 AM AC
⇒ ∆ANM ∼ ∆ABC( c.g.c ) (Đpcm)
Vì ∆ANM ∼ ∆ABC ⇒  ANM =  ABC 0,5
Mà  +  =  +  = 90 ANM MNB ABC MCB
(Do BN ⊥ AC CM ⊥ AB) ⇒  MNB =  ; MCB mà  MNB = 
BQI (2 góc so le trong) ⇒  0,5 BQI =  MCB hay  BQI =  ECI ( đpcm ) 2 KN  HN  2. Chứng minh 2
IQIE = IC và =   . 2,0 KM  HM  Theo câu a,  BQI =  ECI lại có  BIQ = 
EIC (2 góc đối đỉnh) ⇒ ∆BIQ ∼ ∆EIC ( g.g )
⇒ IQ = IB ⇒ IQ ⋅ IE = IC.IB mà IB = IC (gt) 2 ⇒ . IQ IE = IC 0,5 IC IE 2 IQ  IC  ⇒ =   ( ) 1 IE  IE  0,25 Áp dụng hệ quả KN HK KM KN IQ Ta - Lét ta có: = = ⇒ = (2) IQ HI IE KM IE 2 Từ (1) và (2) KN  IC  ⇒ =   0,25 KM  IE 
Trên cạnh EM lấy P sao cho IP = IE (P ≠ E) ⇒ ∆IPE cân tại I ⇒  IPC =  IEP Mà  IEP = 
HMN (2 góc so le trong, MN  EQ ) ⇒  HMN =  IPE hay  HMN =  IPC 0,5 Lại có:  ICP = 
HNM ⇒ ∆HMN ∼ ∆IPC ( g.g ) ⇒ IC = HN IC HN
mà IP = IE (cách lấy điểm P ) ⇒ = (4) IP HM IE HM 2 Từ (3) và (4) KN  HN  ⇒ = 0,5   (đpcm) KM  HM 
3. Gọi D la giao điểm của AH với BC . Chứng minh rằng 1 1 1 4 + + ≤ . 2 2,0 AD ⋅ BN BN ⋅ CM CM ⋅ AD 3(R − OH )
Vì BN ⊥ AC;CM ⊥ A ;
B {H} = BN ∩ CM ⇒ H là trực tâm ∆ABC
⇒ AH ⊥ BC hay AD ⊥ BC
Do đó ta có: HD + HN + HM = S S S
HBC + HAC + HAB = 1 0,5 AD BN CM S S S ABC ABC ABC AD − AH BN − BH CM − ⇒ + + CH = AH BH CH 1 ⇔ + + = 2 AD BN CM AD BN CM
Do H là trực tâm ∆ABC nhọn nên H nằm trong ∆ABC
AH ≥ AO − OH = R − OH > 0 
⇒ BH ≥ BO − OH = R − OH > 0 (BĐT ba điểm)  0,5
CH ≥ CO − OH = R − OH > 0 
⇒ = AH + BH + CH ≥ (R − OH ) 1 1 1  1 1 1 2 2 + + ⇒ + + ≤   (5) AD BN CM  AD BN CM  AD BN CM R − OH
Với mọi x, y ta có : 2 2 2
(x − y) ≥ 0 ⇔ x + y ≥ 2xy Chứng minh tương tự : 2 2 2 2
y + z ≥ 2 yz;
z + x ≥ 2zy
Cộng theo từng vế ba BĐT trên ta được: 0,5 2 ( 2 2 2
x + y + z ) ≥ 2( xy + z + zx) 2 2 2
⇔ x + y + z ≥ xy + yz + zx 2
⇔ (x + y + z) ≥ 3( xy + yz + zx) Áp dụng BĐT trên với 1 1 1 x = ; y = ; z = ta suy ra được: AD BN CM  1 1 1 2  1 1 1  + + ≥ 3 + +      AD BN CM   AD ⋅ BN
BN ⋅CM CM ⋅ AD  1 1 1 4 Töø (5) vaø (6 ⇒ ) + + ≤ (ñpcm) 0,5
AD ⋅ BN BN ⋅CM CM ⋅ AD 3(R − 2 OH)
Dấu " =" xảy ra ⇔ dấu " =" của các bất đẳng thức trên đồng thời xảy ra ⇔ ∆ABC đều. V
Cho ba số a,b,c ≥ 1 thỏa mãn 16abc + 4(ab + bc + ca) = 81+ 24(a + b + c) . 2,0
Tim giá trị nhỏ nhất của biểu thức điểm 1 1 1 2,0 Q = a ( + + 2
a − 1 + a) b( 2
b − 1 + b) c( 2 c − 1 + c) 2 a −1 − 2 a b −1 − 2 b c −1 − Ta coù: c Q = a( 2 2 a 1 a ) + b( 2 2 b 1 b ) + − − − −
c( 2c −1− 2c ) 2 2 2  2 2 2  a −1 − a b −1 − b c −1 − c a −1 b −1 c −1 = + + = 3 −  + +  −a −b −c  a b c  0,5    2 2 2  a − b − c − 2 a − 2 b − 2 1 1 1 1 1 c −1 ⇒ Q − 3 = − + +
 = −P. Vôùi P = + +  a b c    a b c
Sử dụng bất đẳng thức : Với x, y, z ≥ 0 , ta luôn có x + y + z ≤ 3(x + y + z)
Dấu "=" xảy ra khi và chỉ khi x = y = z .
Từ bất đẳng thức đã cho ta có:      1 1 1 1 1 1 1 1 1 0,5 P = 1 − + 1− + 1− ≤ 3 3 − + + = 9 − 3 + +      2 2 2 2 2 2 2 2 2 a b c   a b c   a b c  2  1 1 1  Suy ra P ≤ 9 − + +    a b c 
Từ giả thiết 16abc + 4(ab + bc + ca) = 81+ 24(a + b + c)     81 1 1 1 1 1 1 ⇔ 16 = + 24 + + − 4 + +    ( * ) abc  ab bc ca   a b c  2 3 1 1 1 1  1 1 1  1 1  1 1 1  Ta có + + ≤ ⋅ + +   và ≤ ⋅ + +   ab bc ca 3  a b c  abc 27  a b c 
Dấu "=" xảy ra khi và chỉ khi 0,5
a = b = c . Đặt 1 1 1 t =
+ + ;0 < t ≤ 3 (Vì a,b,c ≥ ) 1 . Từ ( * ) ta có a b c 4 3 2 3 2
16 ≤ 3t + 8t − 4t ⇔ 3t + 8t − 4t − 16 ≥ 0 ⇔ (3t − 4) 2
(t + 2) ≥ 0 ⇔ t ≥ ( Vi 0 < t ≤ 3 3 2 2  1 1 1   4  65 Suy ra P ≤ 9 − + + ≤ 9 − =      a b c   3  3 65 9 − 65
⇒ Q − 3 = −P ≥ − ⇔ Q ≥
. Dấu "=" xảy ra khi và chỉ khi 3 3 16
 abc + 4(ab + bc + ca) = 81+ 24(a + b + c). 0,5  9
a = b = c
⇔ a = b = c = 4
a,b,c ≥1 
Vậy giá trị nhỏ nhất của 9 − 65 9 Q là
khi a = b = c = . 3 4
----------- Hết ----------- Chú ý:
- Các cách làm khác nếu đúng vẫn cho điểm tối đa, điểm thành phần giám khảo tự phân chia
trên cơ sở tham khảo điểm thành phần của đáp án.
- Các trường hợp khác tổ chấm thống nhất phương án chấm.