Đề học sinh giỏi Toán 9 năm 2023 – 2024 phòng GD&ĐT Bình Xuyên – Vĩnh Phúc

PHÒNG GD&ĐT BÌNH XUYÊN
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP HUYỆN NĂM HỌC 2023 - 2024 MÔN TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian giao đề
Câu 1. (4,0 điểm).  x   x  x  a) Cho biểu thức 1 2 1 P     :      
. Rút gọn biểu thức P. x 1 x x  x  x 1 x x  x  x 1 x 1     5 1 b) Cho biểu thức 4 3 2
Q  x  2x  x  2023 . Tính giá trị của biểu thức Q với x  . 5 1
Câu 2. (2,0 điểm). Cho ba số thực dương , a , b c thỏa mãn 2 2 2
a  b  c  abc  4 . Chứng minh a  2 b  2
c  b  2 c  2
 a  c  2  a  2 . 4 4 . 4 4 . 4
4  b   8 abc .
Câu 3. (2,0 điểm). Tìm tất cả các số tự nhiên n thỏa mãn 4 3 2
n  2n  2n  2n 1 là số chính phương. 2 2        Câu x 2 x 6 3x 6
4. (2,0 điểm). Giải phương trình: 2       .  x  6   x  9  x  9
Câu 5. (2,0 điểm). Chia đa thức px 2024 2023 2022  x  x  x
... x 1 cho đa thức qx 2  x 1 ta
được thương là đa thức hx và phần dư là đa thức r  x. Tính h  1 .
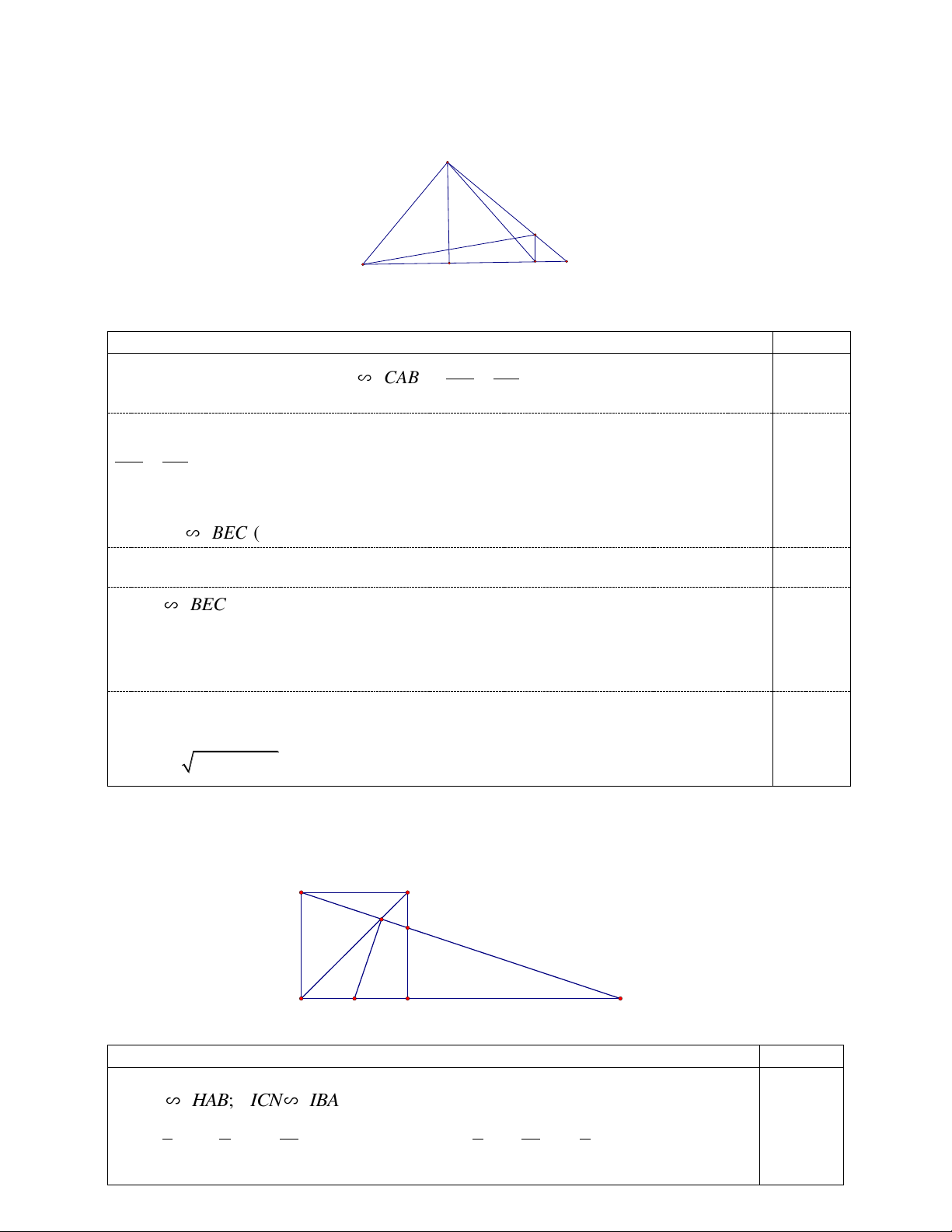
Câu 6. (2,0 điểm). Cho tam giác ABC vuông tại A AB  ACcó đường cao AH H BC . Trên tia
HC lấy điểm D thỏa mãn HD  HA . Đường thẳng qua D song song với AH cắt AC tại E. Chứng
minh tam giác ADC đồng dạng với tam giác BEC và tính độ dài BC khi AE  6cm, EC  2cm .
Câu 7. (2,0 điểm). Cho hình vuông ABCD, điểm N thuộc cạnh CD thỏa mãn NC  2ND . Gọi H là
giao điểm của AN với BD và M là trung điểm BC. Chứng minh tam giác AHM vuông cân.
Câu 8. (2,0 điểm). Cầu thang đi từ tầng một lên tầng hai của
một ngôi nhà được thiết kế liên tục một nhịp với 21 bậc, mỗi
bậc có chiều cao và chiều rộng mặt bậc bằng nhau (Ảnh
bên). Biết chiều cao từ mặt sàn tầng một đến mặt sàn tầng
hai là 3,57m và chiều rộng của mỗi mặt bậc là 25cm. Hỏi vị
trí bắt đầu xây cầu thang ở mặt sàn tầng một cách ví trí chân
tường xây chắn tại cuối cầu thang bao nhiêu mét và cầu thang dài bao nhiêu mét?
Câu 9. (2,0 điểm). Cho , a ,
b c là các số thực dương và thỏa mãn a b  c  1. Tìm giá trị nhỏ a b c
nhất của biểu thức: T    . 2 2 2 a  8bc b  8ca c  8ab ----- HẾT------
Thí sinh không được sử dụng máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm!
Họ và tên thí sinh:............................................................ Số báo danh:...........................................
PHÒNG GD&ĐT BÌNH XUYÊN
ĐÁP ÁN KSCL ĐỘI TUYỂN HSG LỚP 9 NĂM HỌC 2023-2024 MÔN: TOÁN
Câu 1.a (2,0 điểm)      Cho biểu thức 1 2 x x x 1 P     :      
. Rút gọn biểu thức P. x 1 x x  x  x 1 x x  x  x 1 x 1     Nội dung Điểm
Điều kiện x  0, x 1 0,5      0,5 1 2 x  x x 1 Ta có 1 P         x 1 x   1  x   : 1    x   1  x     1 x1 0,5     x  x x x 2 1 1 2 1 x 1    x   1  x   : 1 x  x   1  x   : 1 1 x 1 x 1 x 1 x 1 0,5  .  x 1 x 1 x 1
Câu 1.b (2,0 điểm). Cho biểu thức 4 3 2
Q  x  2x  x  2023 . Tính giá trị của biểu thức Q với 5 1 x  . 5 1 Nội dung Điểm 0,5  5 1  2 5 1  Ta có 5 1 x    5 1  5 1 5 1 2 5  1 0,5 x 
 2x  1  5  2x  2 2 1
 5  x  x 1  0  1 2   0,5
Q  x  x  x 
 x  x2 4 3 2 2     2
x  x   2 2 2023 1 2024
1 x  x   1  20242  
Từ (1) và (2) ta được Q  2024 0,5
Câu 2 (2,0 điểm). Cho ba số thực dương , a , b c thỏa mãn 2 2 2
a  b  c  abc  4 . Chứng minh a  2 b  2
 c  b  2  c  2
 a  c  2  a  2 4 4 4 4 4
4  b   8 abc . Nội dung Điểm Ta có 0,5 a  2 4  b  2
4  c   a 16  4 2 2 b  c  2 2
 b c  a 16  4 2
4  a  abc 2 2  b c
 a 4a  4abc  b c  a 2a  bc2 2 2 2
 a 2a  bc 2  2a  abc Tương tự 0,5 b  2 c  2  a  2
 b  abc c  2  a  2 b  2 4 4 2 ; 4 4  2c  abc 0,5 a  2 b  2
c  b  2 c  2
 a  c  2  a  2 b    2 2 2 4 4 4 4 4 4
2 a  b  c   3abc   2 2 2
2 a  b  c  abc  abc  8 abc 0,5
Câu 3. (2,0 điểm). Tìm tất cả các số tự nhiên n thỏa mãn 4 3 2
n  2n  2n  2n 1là số chính phương. Nội dung Điểm Ta có 0,5
n  2n  2n  2n 1  n  2n  n   n  2n  
1  n  n2  n  2 4 3 2 4 3 2 2 2 1
 n n  2 1  n  2 1  n  2 2 2 1 n 1  
* Nếu n 1  0  n  1 thì 4 3 2
n  2n  2n  2n 1  0 là số chính phương. 0,5
* Nếu n 1  0  n  1thì 4 3 2
n  2n  2n  2n 1 là số chính phương khi 2 2
n 1  m m ,m  n m  n  1 0,5 2 2
m  n  1  m  nm  n  1.1     ; m n  1;0 m  n 1 KL n 0;  1 0,5 2 2        Câu x 2 x 6 3x 6
4. (2,0 điểm). Giải phương trình: 2       .  x  6   x  9  x  9 Nội dung Điểm ĐK x  6  , x  9  0,5 2 2 2 2  x  2   x  6  3x  6  x  2   x  6  x  2 2    2   3          x  6   x  9  x  9  x  6   x  9  x  9    0,5 Đặ x 2 x 6 x 2 t a  , b    ab x  6 x  9 x  9 a  b Phương trình có dạng 2 2
2a  b  3ab  a  b2a  b  0   2a  b x  2 x  6 0,5 * a  b  
 x 18  0  x  18 x  6 x  thỏa mãn. 9 2x  4 x  6 x  0 0, 5 * 2 2a  b  
 x 10x  0   thỏa mãn. x  6 x  9 x  10  Kết luận......
Câu 5. (2,0 điểm). Chia đa thức px 2024 2023 2022  x  x  x
... x 1 cho đa thức qx 2  x 1 ta
được thương là đa thức hx và phần dư là đa thức r  x. Tính h  1 . Nội dung Điểm
Dễ thấy r  x  ax  b và 0,5
p  x  q x h x  r  x 2024 2023 2022  x  x  x   x    2 . ... 1 x  
1 .h  x  ax  b  1
Thay lần lượt các giá trị x 1, x  1
 vào hai vế của (1) ta được 0,5
a  b  2025    ;
a b  1012;1013
a  b  1 2024 2023 2022  x  x  x   x    2 ... 1 x  
1 .h x 1012x 1013  1   2024 2023 x  x  2022 2021 x  x
... 2x  x11012x1013   2x  1.hx 0,5 2023  x x   2021 1  x x  
1  ....  x  x   1 1012  x   1   x   1  x   1 h  x 2023 2021 2019  x  x  x
 ... x 1012  x  
1 h  x2  x   1
Cho x  1 vào hai vế của (2) ta được 2  024  2  .h  1  h   1  1012 0,5
Câu 6. (2,0 điểm) Cho tam giác ABC vuông tại A AB  ACcó đường cao AH H BC . Trên tia
HC lấy điểm D thỏa mãn HD  HA . Đường thẳng qua D song song với AH cắt AC tại E. Chứng
minh tam giác ADC đồng dạng với tam giác BEC và tính độ dài BC khi AE  6cm, EC  2cm . A E C B H D Nội dung Điểm 0,5 Ta có hai tam giác vuông CD CA C  DE C  AB   CE CB
Xét ADC và BEC 0,5 CD CE  , CA CB C - chung
 ADC BEC (c-g-c)
Do tam giác AHD cân đỉnh H 0 0 0 0
 ADC 180  HDA 180  45 135 0,5 0 0 A  DC B
 EC  BEC  ADC 135  BEA  45 nên tam giác ABE vuông cân đỉnh
A  AB  AE  6cm
AC  AE  EC  6  2  8cm 0,25
Do ABC vuông tại A ta có: 2 2 2
 BC  AB  AC 2 2
 BC  AB  BC 10cm 0,25
Câu 7. (2,0 điểm) Cho hình vuông ABCD, điểm N thuộc cạnh CD thỏa mãn NC  2ND . Gọi H là
giao điểm của AN với BD và M là trung điểm BC. Chứng minh tam giác AHM vuông cân. A D H N M I B C Nội dung Điểm
Gọi I là giao điểm của AN với BC từ sự đồng dạng của các cặp tam giác H  ND H  A ; B I  CN I
 BAta có so sanh sau: 1 1 1 2 1 3 HN  HA  AN 
IA  IH  IN  HN  IA  IA  IA   1 0,25 3 4 12 3 12 4 1 1 2 1 5 MC  BC 
IB  IM  IC  CM  IB  IB  IB 2 2 6 3 6 6 0,25 Ta có 0,5 3 3      IH.IA  IA  AB  IB  2 3 1 5 2 2 2 2 2   IB  IB     IB  4 4 4   3   6   
  IH.IA  IM.IB3 5  2 IM .IB  IB  6    IM IA 0,5 0 3  
 IHM IBA  IHM  IBA  90 4 IH IB IH IM 0,5 Mặt khác   0 3  
 IHB IMA  IAM  IBH  45 5 IB IA
Từ (4),(5) ta được điều phải chứng minh
Câu 8 (2,0 điểm). Cầu thang đi từ tầng một lên tầng hai của một ngôi nhà được thiết kế liên tục một
nhịp với 21 bậc, mỗi bậc có chiều cao và chiều rộng mặt bậc bằng nhau. Biết chiều cao từ mặt sàn
tầng một đến mặt sàn tầng hai là 3,57m và chiều rộng của mỗi mặt bậc là 25cm. Hỏi vị trí bắt đầu
xây cầu thang ở mặt sàn tầng một cách ví trí chân tường xây chắn tại cuối cầu thang bao nhiêu mét
và cầu thang dài bao nhiêu mét F B E H A
(Hình vẽ mặt cắt minh họa cho cầu thang có 8 bậc) Nội dung Điểm
Cầu thang có 21 bậc từ tầng một lên tầng hai thì số mặt bậc không phải mặt sàn nhà 0,5
là 20 mặt. Nên ví trí xây cách vị trí chân tường chắn cuối cầu thang là 20.0, 25  5m
Do chiều cao từ mặt sàn tầng một đến mặt sàn tầng hai bằng tổng chiều cao 21 bậc 0,5
nên chiều cao một bậc là 3,57 : 21 0,17m 914 0,5
Áp dụng định lí Pitago ta có chiều dài một bậc là 2 2 0,17  0, 25  m 100 914 914 0,5
Vậy chiều dài cầu thang là 20  6, 05m 100 5
Câu 9 (2,0 điểm). Cho , a ,
b c là các số thực dương và thỏa mãn a b  c  1. Tìm giá trị nhỏ a b c
nhất của biểu thức: T    . 2 2 2 a  8bc b  8ca c  8ab Nội dung Điểm Với các số , a , b c dương. Ta có a b c T    2 2 2 a  8bc b  8ca c  8ab 0,5 2 2 2 2 a b c
(a  b  c)  T     3 3 3 3 3 3 a  8abc b  8abc c  8abc
a  b  c  24abc Ta lại có 3 3 3 3
(a  b  c)  a  b  c  3(a  b  c)(ab  bc  ca)  3abc 0,5 3 3 3 3 2 3 3 3 3
 a  b  c  27 abc. (abc)  3abc  a  b  c  24abc Suy ra 3 3 3 3
a  b  c  24abc  (a  b  c) 2 2
(a  b  c)
(a  b  c) 1    1 3 3 3 3
a  b  c  24abc
(a  b  c)
a  b  c 0,5 Do đó T  1 1
Dấu “=” xảy ra khi a  b  c  3 1 0,5
Vậy MinT 1, khi a  b  c  3 ----- HẾT------