Đề học sinh giỏi Toán 9 năm 2023 – 2024 phòng GD&ĐT Việt Trì – Phú Thọ

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 VIỆT TRÌ
CẤP THÀNH PHỐ, NĂM HỌC 2023 - 2024 Môn: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút (Không kể thời gian giao đề)
(Đề thi có: 03 trang)
Thí sinh làm bài (cả phần trắc nghiệm khách quan và phần tự luận) trên tờ giấy thi.
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (16 câu; 8,0 điểm) 2 2 x 1 x 1 x 2 Câu 1. Cho a ; b với x
1. Giá trị của biểu thức 2 1 x x x 2 a b P bằng 1 ab x A. −1 . B. 1 . C. x . D. . 2 Câu 2. Cho 3 x 1
2 . Giá trị của biểu thức 5 4 3 2 B x 2x x 3x 1979 bằng A. 1979 . B. 1982 . C. 2023 . D. 2024 .
Câu 3. Biết đồ thị hàm số y m 1 x 2m
1 luôn đi qua điểm cố định A . Đường thẳng
d đi qua A và song song với đường thẳng d : y x 2023 có phương trình 1
A. y = −x + 10 .
B. y = −x − 10 .
C. y = −x + 1 .
D. y = x + 2023 .
Câu 4. Diện tích tam giác tạo bởi đường thẳng (d ) : y = 4x − 16 và hai trục tọa độ bằng A. 32 đvdt . B. 64 đvdt . C.16 đvdt . D.128 đvdt .
Câu 5. Tập hợp các giá trị của tham số m để phương trình 2 x 4m 1 x 2 m 4 0
có hai nghiệm x , x thỏa mãn x x 17 là 1 2 1 2 A.   8 . B.   4 . C. −4;  4 . D. −8; 8. 2m 1 2
Câu 6. Có bao nhiêu giá trị nguyên của m để hàm số y
1 x đồng biến khi m 2 x 0 ? A. 1 . B. 2 . C. 3 . D. 4 .
Câu 7. Cho hình bình hành ABCD có AC là J
đường chéo lớn. Gọi I, J theo thứ tự là các
hình chiếu của C trên các đường thẳng AD và
AB . Khẳng định nào sau đây đúng? B C A. IJ AC.sinBAD . B. IJ AC.cos BAD C. IJ AC.tanBAD . D. IJ
AC.cotBAD . A D I
Câu 8. Cho tam giác ABC nhọn nội tiếp đường tròn ;2
O cm . Khẳng định đúng là A. 2 S 8 tan .
A tan B. tanC cm . B. 2 S 8 sin .
A sin B.sinC cm . ABC ABC C. 2 S 8 cot .
A cotB.cotC cm . ABC D. 2 S 8 cos .
A cos B.cosC cm . ABC x my m 1
Câu 9. Cho hệ phương trình
(m là tham số). Giá trị của m để hệ có nghiệm mx y 3m 1
duy nhất (x;y ) sao cho x.y đạt giá trị nhỏ nhất là
A. m = 2 .
B. m = 0 .
C. m = 1. D. m = −1 .
Câu 10. Cho hình vuông ABCD có cạnh bằng 2 . Gọi E là trung điểm của AB , F là trung
điểm của BC ; I là giao điểm của AF và DE ; H là giao điểm của BD và AF . Diện tích tứ giác BEIH bằng 4 7 11 13 A. . B. . C. . D. . 15 15 15 15
Câu 11. Cho tam giác ABC . Lấy điểm M trên cạnh BC ( M khác B,C ). Qua B,C dựng các
đường thẳng song song với AM cắtAC,AB thứ tự tại P,Q . Khẳng định đúng là 1 2 1 1 1 2 A. . B. . AM PB QC AM PB QC 1 2 1 1 1 1 C. . D. . AM PB QC AM PB QC
Câu 12. Cho đường tròn ;
O R có đường kính AB và dây CD thỏa mãn COD 90 . Giả sử
đường thẳng CD cắt đường thẳng AB tại M (D nằm giữaC và M ) và OM 2R . Khẳng định đúng là R ( 14 − 2) C A. MD = . B. 2 D R ( 14 + 2) M O B A MD = . 2 R ( 7 + 2) R ( 7 − ) 1 C. MD = . D. MD = . 2 2 2 x
Câu 13. Trên Parabol P : y
lấy các điểm P;Q có hoành độ lần lượt là 2 và 4 . Biết 4
M là điểm nằm trên trục Ox sao cho MP
MQ nhỏ nhất. Tọa độ điểm M là 4 1 A. ;0 . B. ;0 . C. 4;0 . 5 4 4 D. ; 0 . 3
Câu 14. Cho hình hộp chữ nhật ABC . D AB C D có AB 1;AD 2 và đường chéo 1 1 1 1 AC
6 . Thể tích của hình hộp đã cho bằng 1 A. 4 . B. 3 . C. 2 . D. 5 .
Câu 15. Một công ty cổ phần cấp nước áp dụng định mức tiêu thụ nước mỗi người là 3
4m /người/tháng và đơn giá được cho bởi bảng sau:
Lượng nước tiêu thụ ( 3 m ) Giá cước (đồng/ 3 m ) Đến 3 4m /người/tháng 5300 Trên 3
4m /người/tháng đến 3 6m /người/tháng 10200 Trên 3 6m /người/tháng 11400
Gia đình bạn An có 9 người. Trong tháng 7 năm 2017, gia đình bạn An phải trả tiền nước theo
hóa đơn là 653430đồng (hóa đơn này bao gồm thuế giá trị gia tăng (VAT) 5% và 10% phí bảo
vệ môi trường). Lượng nước máy mà nhà bạn An đã sử dụng trong tháng 7 năm 2017 là A. 3 66m . B. 3 68m . C. 3 70m . D. 3 71m .
Câu 16. Từ điểm M ngoài đường tròn ;6
O cm vẽ cát tuyến MAB , A B O . Biết MO 12cm . Tích M . A MB bằng A. 2 144cm . B. 2 108cm . C. 2 180cm . D. 2 72cm .
II. PHẦN TỰ LUẬN (4 câu; 12,0 điểm)
Câu 1 (3,0 điểm).
a) Tìm tất cả các số nguyên x,y thỏa mãn 3 y xy 3x 5 y .
b) Tìm tất cả các số nguyên tố p và các số tự nhiên n để n p 144 là một số chính phương.
Câu 2 (4,0 điểm). ab 1 bc 1 ca 1
a) Cho các số thực a, ,
b c khác 0 và thỏa mãn . Chứng minh b c a rằng abc 1 hoặc a b c . b) Giải phương trình: 2 2 3 4x 3(x x) x 1 2(x 1) . 2xy x 2y 3
c) Giải hệ phương trình: . 3 3 2 x 4y 3x 6y 4
Câu 3 (4,0 điểm). Cho nửa đường tròn ;
O R đường kính BC . Điểm A di động trên nửa
đường tròn đã cho ( A khác B,C ), vẽ AH vuông góc với BC tại H . Đường tròn đường kính
AH cắt AB,AC và nửa đường tròn ;
O R lần lượt tại D,E,M . Đường thẳng AM cắt đường
thẳng BC tại N .
a) Chứng minh rằng AME ACN 3 2 3 2 3 và 2 BC BD CE .
b) Chứng minh rằng ba điểm ,
D E,N thẳng hàng.
c) Xác định vị trí của điểm A trên nửa đường tròn đã cho để tam giác ABH có diện tích lớn nhất.
Câu 4 (1,0 điểm). Xét các tam giác có chu vì bằng 1 và độ dài ba cạnh là x, ,
y z . Tìm giá trị lớn 4 4 4 1 x y z nhất của T . x y y z z x 2xyz 2yz 2zx 2xy
…………HẾT………
Họ và tên thí sinh:…………………………………Số báo danh:…………………..
Cán bộ coi thi không giải thích gì thêm
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH LỚP 9 VIỆT TRÌ
CẤP THÀNH PHỐ, NĂM HỌC 2023 - 2024
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC MÔN TOÁN (HDC gồm 7 trang)
PHẦN I. ĐÁP ÁN TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm) . Câu 1 2 3 4 5 6 7 8 Đáp án B B C A C B A B Câu 9 10 11 12 13 14 15 16 Đáp án B B D A A C D B
PHẦN II. ĐÁP ÁN PHẦN TỰ LUẬN (12,0 điểm) Nội dung Điểm
Câu 1 (3,0 điểm).
a) Tìm tất cả các số nguyên x,y thỏa mãn 3 y xy 3x 5 y 3,0
b) Tìm tất cả các số nguyên tố p và các số nguyên dương n để tổng n p 144 là một số chính phương.
a) Tìm tất cả các số nguyên x,y thỏa mãn 3 y xy 3x 5 y 1,5 Ta có 3 y xy 5 y 3x 0,25 3 2 2 y 3y 3y 9y xy 3x 8y 24 29 2 y 3 y 3y x 8 29 0,25 Vì x,y nên 2 y 3 , y 3y x 8 là các ước của 29 0,25 2 y 3 , y 3y x 8 1; 29 0,25 Xét bảng y 3 29 1 1 29 2 y 3y x 8 1 29 29 1 0,25 y 26 2 4 32 x 605 11 65 1129 Vậy x;y 605; 26 ; 11;2 ; 65; 4 ; 1129; 32 0,25
b) Tìm tất cả các số nguyên tố p và các số nguyên dương n để tổng n p 144 là một số chính 1,5 phương. Trang 1/7 Giả sử n 2 144 n p k k p k 12 k 12 0,25 k 12 x p Do đó x y n;x,y ;x y k 12 y p 0,25 x y 24 y x y 1 24 y p p p p
p là ước dương của y 1 2 3 1 24 p 1;2 ;2 ;2 ; 3 0,25 Từ đó có các TH sau: - Khi y p 1 y 0 k 13; p 5;n 2 ; n p 2;5 0,25 - Khi y 1 x 1 p 2 y 1 2 13 loại - Khi y 2 x 2 p 2 y 2 2 7 loại 0,25 - Khi y 3 x 3 p 2 y 3; p 2 2 4 x 5 ; n p 8;2 - Khi y 1 x 1 p 3 y 1; p 3 3 9 x 2 ; n p 4;3 0,25
Vậy ta có n; p 4; 3 ; 8;2 ; 2;5
Câu 2 (4,0 điểm). ab 1 bc 1 ca 1
a) Cho các số thực a, ,
b c khác 0 và thỏa mãn . Chứng minh rằng b c a abc 1 hoặc a b c . 4,0 b) Giải phương trình: 2 2 3 4x 3(x x) x 1 2(x 1) 2xy x 2y 3
c) Giải hệ phương trình: 3 3 2 x 4y 3x 6y 4 ab 1 bc 1 ca 1
a) Cho các số thực a, ,
b c khác 0 và thỏa mãn . Chứng minh rằng b c a 1,0 abc 1 hoặc a b c . ab 1 bc 1 ca 1 1 1 1 Ta có a b c b c a b c a 0,25 b c c a a b Do đó a b ;b c ;c a bc ac ab 0,25 (a b)(b c)(c a) (a b)(b c)(c a) 2 2 2 a b c 0,25 2 2 2 (a b)(b c)(c a)(a b c 1) 0 a b b c c a 0 đpcm. 0,25 abc 1 Trang 2/7 b) Giải phương trình sau 2 2 3 4x 3(x x) x 1 2(x 1) 1,5 b) ĐKXĐ: x 1. Khi đó 2 2 3 4x 3(x x) x 1 2(x 1) 0,25 2 (x 1) 2x 2x 2 3x x 1 0 x 1 2 2x 2x 2 3x x 1 0 Xét phương trình: 2 2 2x 2x 2 3x x 1 0 2x 3x x 1 2(x 1) 0 0,25 x 2 x 1 2x x 1 0 x 2 x 1 1 2x x 1 2 0,25 x 0 Ta có 1 x 2 2 2 2 x 4x 4 0 0,25 x 0 1 17 Ta có 2 x 2 4x x 1 0 8 0,25 1 17
Kết hợp điều kiện ta suy ra các nghiệm của phương trình là x 1;2 2 2; . 8 0,25 2xy x 2y 3
c) Giải hệ phương trình sau 3 3 2 x 4y 3x 6y 4 1,5 (x 1)(2y 1) 2
Hệ đã cho viết lại như sau: 1 3 3 3 2 (x 1) (2y 1) 3(x 1) (2y 1) 5 2 2 0,25 Đặt u x 1;v 2y 1
Khi đó ta có hệ phương trình: uv 2 uv 2 0,25 1 3 3 3 2 3 3 2 u v 3u v 5 2u v 6u 3v 10 2 2 Trang 3/7
Từ hệ phương trình ban đầu ta nhẩm được nghiệm là x y 1 u 2,v 1 (u 2)v 2(1 v) 0,25
Do đó ta sẽ phân tích hệ về dạng: 2 2 2(u 2) (u 1) (v 1) (v 2) 2(1 v) Vì ta luôn cóv
0 nên từ phương trình trên ta rút ra u 2 v
Thế xuống phương trình dưới ta được: 2 8(v 1) 0,25 2 2 2 (u 1) (v 1) (v 2) (v 1) 8(u 1) v (v 2) 0 2 v v 1 2 8(u 1) v (v 2) 0 Với v 1 u 2 x y 1 v 2 0,25 Với 2 8(u 1) v (v 2) 0 . Ta lại có uv 2 v(u 1) v 2 u 1 v
Thế lên phương trình trên ta có: 8(v 2) 2 3 v (v 2) 0 v 2 v 8 0 v 2 v 1 u 1;x 2;y 2 0,25 1
Vậy hệ đã cho có 2 nghiệm là x;y 1;1 ; 2; 2
Câu 3 (4,0 điểm). Cho nửa đường tròn ;
O R đường kính BC . Điểm A di động trên nửa đường
tròn đã cho ( A khác B,C ), vẽ AH vuông góc với BC tại H . Đường tròn đường kính AH cắt
AB,AC và nửa đường tròn ;
O R lần lượt tại D,E,M . Đường thẳng AM cắt đường thẳng BC tại N . 4,0
a) Chứng minh rằng AME ACN 3 2 3 2 3 và 2 BC BD CE ;
b) Chứng minh rằng ba điểm ,
D E,N thẳng hàng;
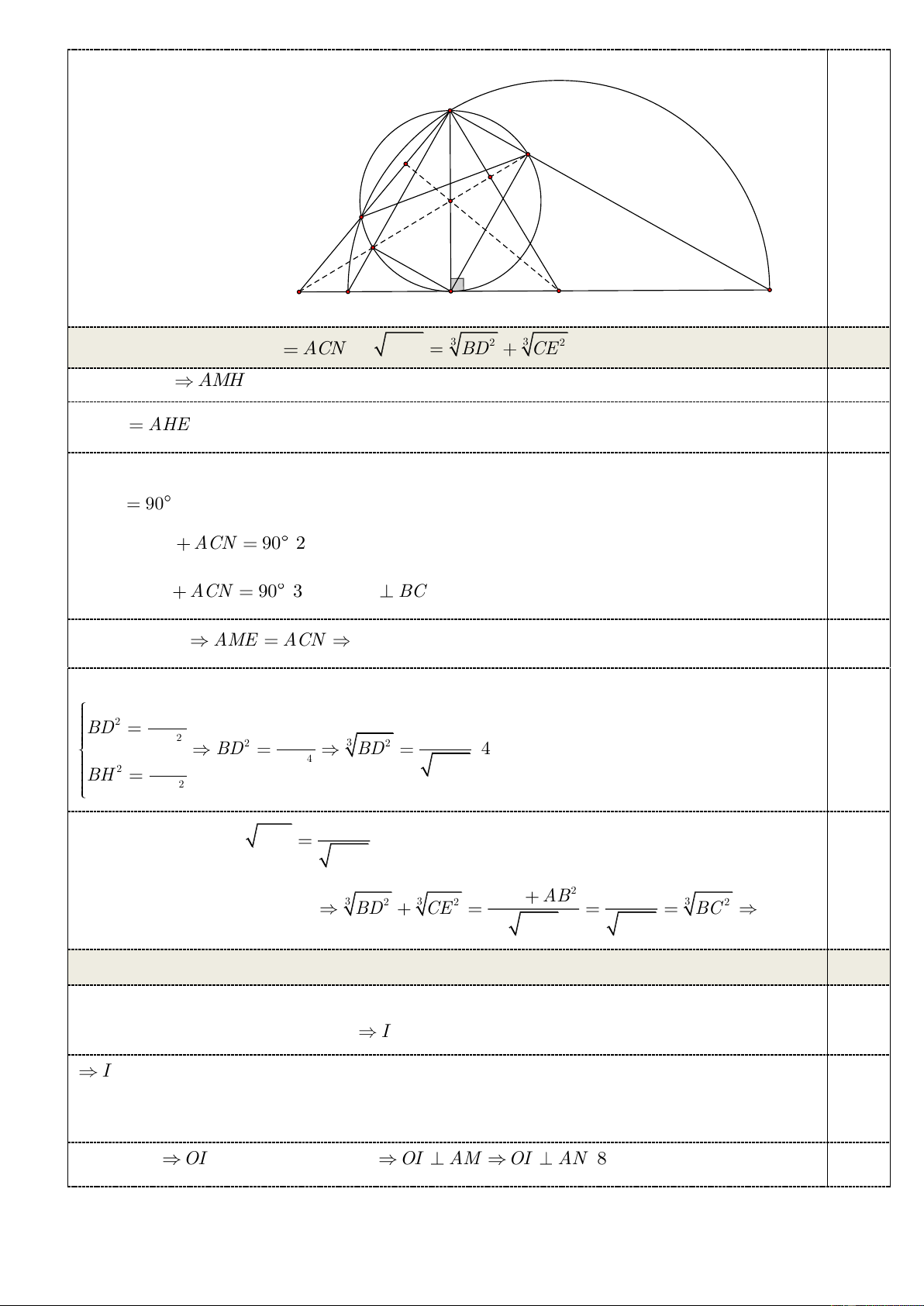
c) Xác định vị trí của điểm A di động trên nửa đường tròn đã cho để tam giác ABH có diện tích lớn nhất. Trang 4/7 A E J K M I D N B H O C
a) Chứng minh rằng AME ACN và 3 2 3 2 3 2 BC BD CE ; 1,5 Từ giả thiết
AMHE là tứ giác nội tiếp 0,25 AME
AHE 1 (cùng chắn AE ) 0,25 Mặt khác AHE
90 (góc nội tiếp chắn nửa ĐT) Do đó EHC ACN 90 2 0,25 Ta có AHE ACN 90 3 (do AH BC ) Từ 1 , 2 , 3 AME ACN đpcm. 0,25
Theo hệ thức giữa cạnh và đường cao trong tam giác vuông suy ra 4 BH 2 BD 6 2 2 BA BA 2 3 2 BA BD BD 4 0,25 4 4 3 4 BA 2 BC BC BH 2 BC 2 CA Chứng minh tương tự 3 2 CE 5 3 4 BC 0,25 2 2 2 CA AB BC Theo ĐL Py 3 2 3 2 3 -ta-go và từ 2 4 , 5 BD CE BC đpcm. 3 4 3 4 BC BC
b) Chứng minh rằng ba điểm ,
D E,N thẳng hàng; 1,5
Gọi I ;K thứ tự là giao điểm của DE với AH;AO
Chỉ ra được ADHE là hình chữ nhật
I là trung điểm của AH,DE 0,25
I là tâm của đường tròn đường kính AH 6 0,25
Mặt khác O là tâm của nửa đường tròn đường kính BC 7 Từ 6 , 7
OI là trung trực của AM OI AM OI AN 8 0,25 Trang 5/7 Ta lại có AH BC 9 0,25 Từ 8 , 9
I là trực tâm tam giác AON NI AO 10 Chỉ ra được IAE IE ; A OAC OCA OCA IAE IEA OAC 90 DE AO 11 0,25 Từ 10 , 11
DE,NI trùng nhau ,
D E,N thẳng hàng đpcm. 0,25
c) Xác định vị trí của điểm A di động trên nửa đường tròn đã cho để tam giác ABH có diện tích lớn nhất. 1,0 1 1 3 BH Ta có S AH.BH H . B H . B HC H . B .HC ABH 2 2 2 3 0,25 Theo BĐT AM-GM ta có 3 BH 3 2 S HB. HC S HB 2R BH 0,25 do HB HC 2R ABH 4 3 ABH 4 3 Theo BĐT AM-GM ta có 2 2 1 2 2 2 3 2 H . B 2R BH HB 2R BH R H . B 2R BH R 0,25 3 3 2 3 3 3 2 3 3 3 3 Do đó 2 2 S . R S R ABH 4 2 ABH 8 3
Dấu đẳng thức xảy ra khi BH R
H là trung điểm OC 0,25 2
Vậy khi A là giao điểm trung trực của OC với nủa ĐT đã cho.
Câu 4 (1,0 điểm). Xét các tam giác có chu vì bằng 1 và độ dài ba cạnh là x, ,
y z . Tìm giá trị lớn 4 4 4 1 x y z nhất của T 1,0 . x y y z z x 2xyz 2yz 2zx 2xy Ta có 2 2 2 1 4 4 4 x y z T x y y z z x 2xyz 2 2 2 2 4 4 4 x y z x y z x y y z z x 2xyz 4 4 4 xy yz zx 0,25 x y y z z x xyz 4 1 4 1 4 1 1 z z 1 x x 1 y y 5x 1 5y 1 5z 1 2 2 2 x x y y z z Trang 6/7 5 1 1 Ta chứng minh BĐT phụ 18 3 với 0 2 2 2 2 5 1 18 3 3 1 2 1 0,25 5 1 Thật vậy 18 3 0 0 2 2 1 1 BĐT này luôn đúng với 0
nên BĐT phụ được chứng minh 2 0,25 Áp dụng ta có T 18 x y z 9 T 9 . 1
Dấu đẳng thức xảy ra khi x y z 3 0,25 1 Vậy maxT 9 x y z . 3
---------------------------------Hết--------------------------------- Lưu ý:
- Chỉ cho điểm tối đa với những bài làm chính xác, bố cục hợp lý, trình bày rõ ràng, đủ nội dụng;
- Điểm toàn bài là điểm trắc nghiệm và tự luận, không làm tròn (điểm lẻ tự luận
0,25;điểm trắc nghiệm theo cấu trúc).
- Khuyến khích những bài làm sáng tạo, thể hiện quan điểm của học sinh (mở), cách
diễn đạt khác mà vẫn đảm bảo nội dung theo yêu cầu./. Trang 7/7
Document Outline

• DE HSG TOAN 9-VT 2023-2024
• HD CHAM HSG TOAN 9-VT 2023-2024