Đề học sinh giỏi Toán 9 vòng 2 năm 2022 – 2023 phòng GD&ĐT Tứ Kỳ – Hải Dương

PHÒNG GIÁO DỤC & ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9, VÒNG II HUYỆN TỨ KỲ Năm học 2022 - 2023 MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
(Đề thi này gồm 05 câu, 01 trang)
Câu 1. (2,0 điểm) 2 1) Rút gọn biểu thức: a a 2 P   1 a  với 1   a  0. a  1 a  2 1 2) Cho ; x ;
y z là các số dương thỏa mãn: 2 3 3
z  x  y  3xy  z .
Tính giá trị biểu thức: 
x  y2022 2022 M 2025  z
Câu 2. (2,0 điểm) 2 x 1) Giải phương trình: 2 x    x   15 2 1 3 x 2) Giải phương trình: 2  8x  40 2 5  x
Câu 3. (2,0 điểm) 1) Cho hai số nguyên , x y thỏa mãn 2 2
x  y 1  2 xy  x  y . Chứng minh rằng
x và y là hai số chính phương liên tiếp.
2) Tìm các cặp số tự nhiên  ;
x y thỏa mãn  x  y6  30y  x .
Câu 4. (3,0 điểm)
1) Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE, CF cắt nhau tại H.
Trên đoạn thẳng AD lấy điểm M sao cho 0
BMC  90 . Gọi S, S , S lần lượt là diện tích các 1 2 tam giác BAC, BMC, BHC.
a) Chứng minh rằng: S  S.S 1 2
b) Gọi K, P lần lượt là hình chiếu của D trên BE, CF . Chứng minh rằng KP//EF
2) Trên các cạnh BC, CA, AB của tam giác ABC lần lượt lấy các điểm M, N, P .
Đặt S , S ,S , S lần lượt là diện tích các tam giác 1 2 3
ANP, BMP, CMN, ABC . Chứng minh 1 rằng: 3 S .S .S  S . 1 2 3 64
Câu 5. (1,0 điểm)
Cho các số a, b, c dương, thỏa mãn a  b  c  3. Tìm giá trị nhỏ nhất của biểu thức: a b c P    3 3 3 b  ab c  bc a  ca
-------- Hết --------
* Lưu ý: Thí sinh không được sử dụng máy tính cầm tay khi làm bài.
Họ và tên thí sinh: ................................................................................................. SBD: .............................
HƯỚNG DẪN CHẤM
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 - VÒNG II Năm học 2022 - 2023 MÔN: TOÁN 9
(Hướng dẫn chấm gồm 05 trang) Câu Đáp án Điểm 1) Rút gọn: 2 a a    2 P   1 a  với 1 a 0 . a  1 a  2 1 2 2 2  a  2 a a Ta có 1  a   1 a 2  2a    a     a 1 a   1 2 1 a  2 1 0,25 2 a a Do đó 2 1  a      a   1 a 2 1 a 1 0,25 a a với 1
  a  0  a 1 0;  0  a 1  0 a 1 a  1 0,25 a a Suy ra P   a 1  a 1 a 1 a  1 0,25 1 (2 điểm)
z  x  y  xy  2) Cho ; x ;
y z là các số dương thỏa mãn: 2 3 3 3 z .
Tính giá trị biểu thức: 
 x  y2022 2022 M 2025  z 2 3 3 2 3 3
z  x  y
z  x  y Có 3 3 3   
 z  3xyz  x  y 2 3 2
z  3xy  z
z  3xyz  z 0,25 3 3 3
 x  y  z  3xyz  0 1   0,25
x  y  z  
 x  z2  y  z2 x  y2  0 2   Vì ; x ;
y z là các số dương nên
x  y  z   x  y  z   x  y2022 2022 0  z 0,25 Suy ra M 
 x  y2022 2022 2025  z  2025  45 0,25 2
1) Giải phương trình: x 2 x  15 2 x   1 ĐK: x  1  2 2 x x x x 2 2 x    x  x     x x   15 2 . 15 2 . 2 1 x 1 x  2 1 x 1 0,25 2 2 2 2  x  x  x     x x 2 . x 15  0       2 15  0  x 1  x 1  x 1 x 1 2 2 x (2 điểm) Đặt
 a, PT trở thành a  a    a  2 2 2 15 0 1 16 0,25 x 1   Giải được a 3  a  5  2 x * Với 2 a  3 
 3  x  3x  3  0  x 1 0,25  Giải được 3 21 x  2 2 x * Với 2 a  5    5   x  5x  5  0 x 1   0,25 Giải được 5 5 x  2
Đối chiếu với điều kiện và kết luận nghiệm 3
2) Giải phương trình: x 2  8x  40 2 5  x ĐK: 2
5  x  0   5  x  5 3 x 2 3 2 2 2
 8x  40  x  8x . 5  x  40. 5  x 0,25 2 5  x 3 2  x   x  2 8 5 . x  5  0  x    x 3 3 2 2 2 5
 x  2 5  x (*) 0,25 x  0 x  0 (*)     0,25 2 2 2
x  4(5  x ) x  4 x  2 Giải được  x  2  0,25
Đối chiếu và kết luận x = 2 là nghiệm duy nhất của phương trình.
1) Cho hai số nguyên ,
x y thỏa mãn 2 2
x  y 1  2 xy  x  y . Chứng
minh rằng x và y là hai số chính phương liên tiếp. Ta có 2 2
x  y    xy  x  y 2 2 1 2
 x  y 1 2xy  2x  2y  0 0,25 2 2
 x  y 1 2xy  2x  2y  4x
 x  y  2  x  x  y  2 2 1 4 1  2 .x 0,25
Do x,y là các số nguyên nên x là một số chính phương 2 2 2 Đặt 2
x  a với a là một số tự nhiên, ta có:  a  y   1  2a 0,25 2
 a  y 1 2a  y  a  2 1 Vì 2
x  a và y  a  2
1 nên x và y là hai số chính phương liên 0,25 3 tiếp.
(2 điểm) 2) Tìm các cặp số tự nhiên  ;x y thỏa mãn: x y6 30y  x
Ta có:  x  y6  30y  x 0,25
 x  y6  30y  x  30y  30x  30x  y (*) x  0
+ Nếu x  y  0   y  0 x  0 Thử lại thấy  thỏa mãn đề bài 0,25 y  0
+ Nếu x  y  0, từ (*)   x  y5 5  30  32  2
 x  y  2  x  y 1 x  0 x   1  0,25 hoặc  y 1 y  0
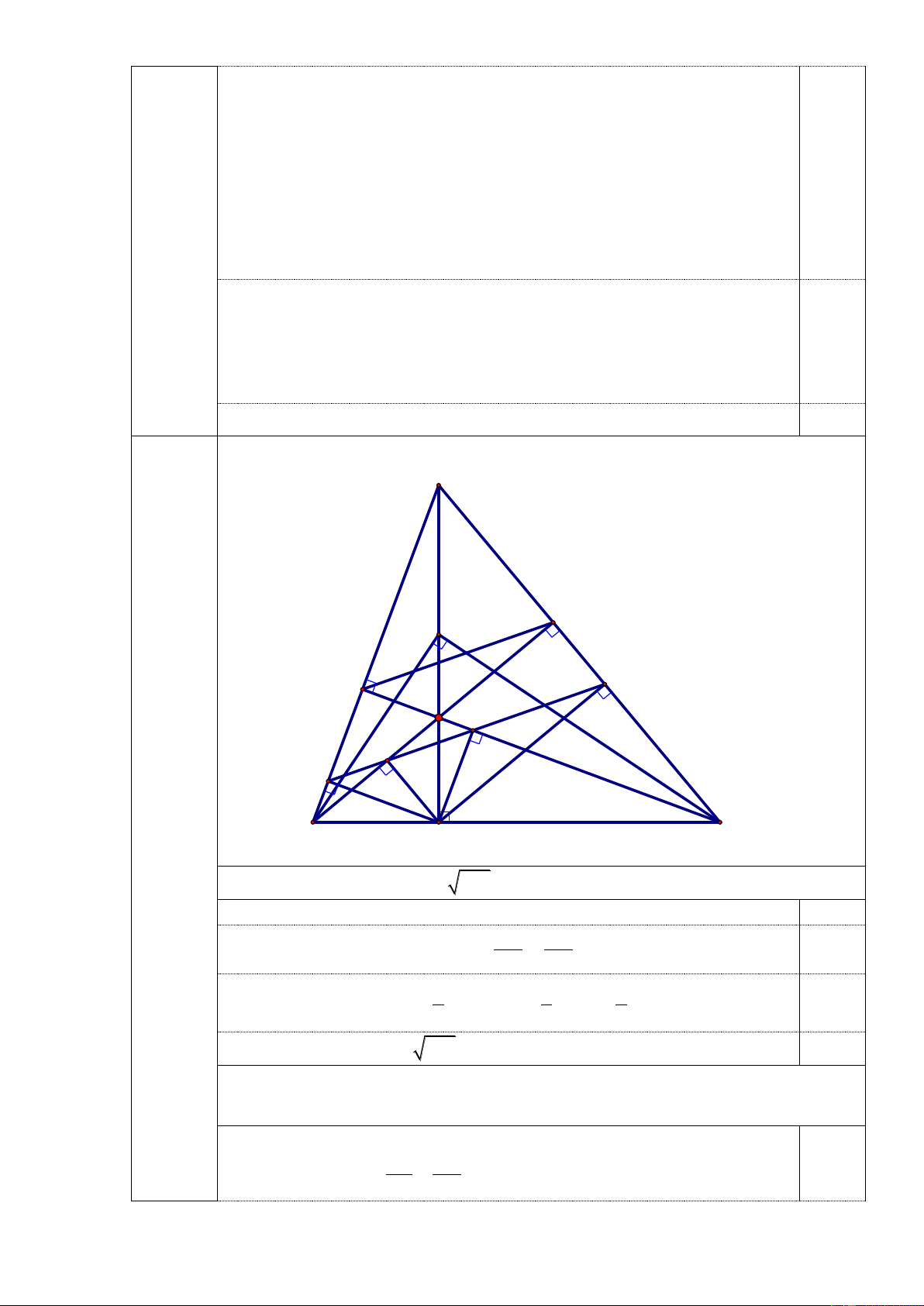
Thử lại và kết luận có hai cặp số thỏa mãn là 0;0,1;0 0,25 1) Vẽ hình: A E M Q F H P K I B D C  4
a) Chứng minh rằng: S S.S 1 2
(3 điểm) Ta có tam giác BMC vuông tại M, đường cao MD nên 2 MD  BD.CD 0,25 AD BD Mặt khác A  DB C  DH(g.g)    AD.DH  BD.CD 0,25 CD DH 2  1  1 1 Do đó 2 MD  AD.DH  MD.BC  AD.BC. DH.BC   0,25  2  2 2 2 Suy ra S  S.S  S  S.S 1 2 1 2 0,25
b) Gọi K, P lần lượt là hình chiếu của D trên BE, CF . Chứng minh KP // EF
Gọi I, Q lần lượt là hình chiếu của D trên AB và AC. AE AH Ta có HE//DQ nên  0,25 EQ HD AF AH HF//DI nên  FI HD AE AF Do đó   IQ//EF (1) EQ FI BI BD Lại có: DI//EC nên  IF DC BD BK DK//EC nên  DC KE 0,5 BI BK Do đó   IK//EF (2) IF KE
Tương tự ta có PQ//EF (3)
Từ (1), (2) và (3) suy ra bốn điểm I, K, P, Q thẳng hàng 0,25 Do đó KP//EF
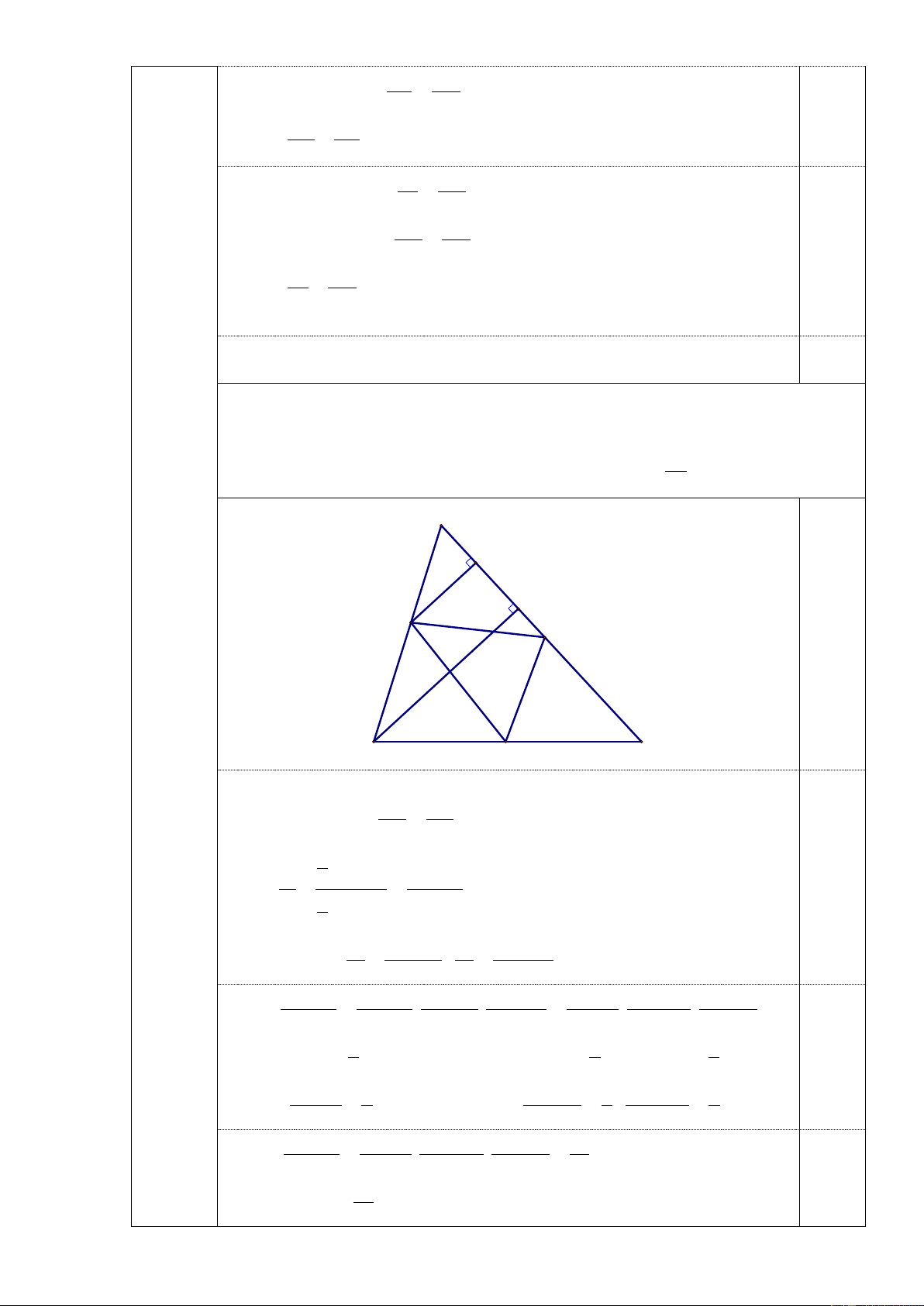
2) (1 điểm) Trên các cạnh BC, CA, AB của tam giác ABC lần lượt lấy các
điểm M, N, P . Đặt S , S ,S , S lần lượt là diện tích các tam giác 1 2 3 1
ANP, BMP, CMN, ABC . Chứng minh rằng: 3 S .S .S  S . 1 2 3 64 A K H P N B C M
Kẻ BH  AC, PK  AC ( H, K  AC ) PK AP Ta có PK//BH nên  BH AB 1 PK.AN S AP.AN 2 0,25 Lại có 1   S 1 AB.AC BH.AC 2 S BP.BM S CM.CN Tương tự ta có: 2 3  ,  S AB.BC S CA.BC S .S .S AP.AN BP.BM CM.CN AP.BP BM.CM CN.AN Suy ra 1 2 3  . .  . . 3 2 2 2 S AB.AC AB.BC CA.BC AB BC AC 1 2 2 1 2 1 2       Lại có AP.BP . AP BP
AP BP  AP  BP  AB 0,5 4   4 4 AP.BP 1 AN.CN 1 BM.CM 1 Suy ra  , tương tự ta có:  ;  2 AB 4 2 2 AC 4 BC 4 S .S .S AP.BP BM.CM CN.AN 1 Do đó 1 2 3  . .  3 2 2 2 S AB BC AC 64 0,25 1 3 Suy ra S .S .S  S 1 2 3 64
Cho các số a, b, c dương, thỏa mãn a  b  c  3. Tìm giá trị nhỏ nhất của a b c biểu thức: P    3 3 3 b  ab c  bc a  ca Ta có : 2 a a 1 a 1  b  1  b  1 1   .  1   1   .   3 b  ab b  2 b  a  2 2 b a  b b  a  b  b  2 a  b 2 a 0,5 5 Tương tự : b 1 1 c 1 1     (1 điểm) ; . 3 3 c  bc c 2 b a  ca a 2 c 1 1 1 1 1 1 3 1  1 1 1  Ta có :          .   4a 4 2 a 2 a 2 b 2 c 4 4  a b c  0,5 Vậy : a b c
 1 1 1  1  1 1 1  3              3 3 3 b  ab c  bc a  ca
 a b c  4  a b c  4 a b c 3  9  3     1  .   3 3 3 b  ab c  bc a  ca 4  a  b  c  2
Ghi chú: HS làm cách khác so với đáp án ở mỗi câu nếu đúng vẫn cho điểm tối đa
----------Hết----------