
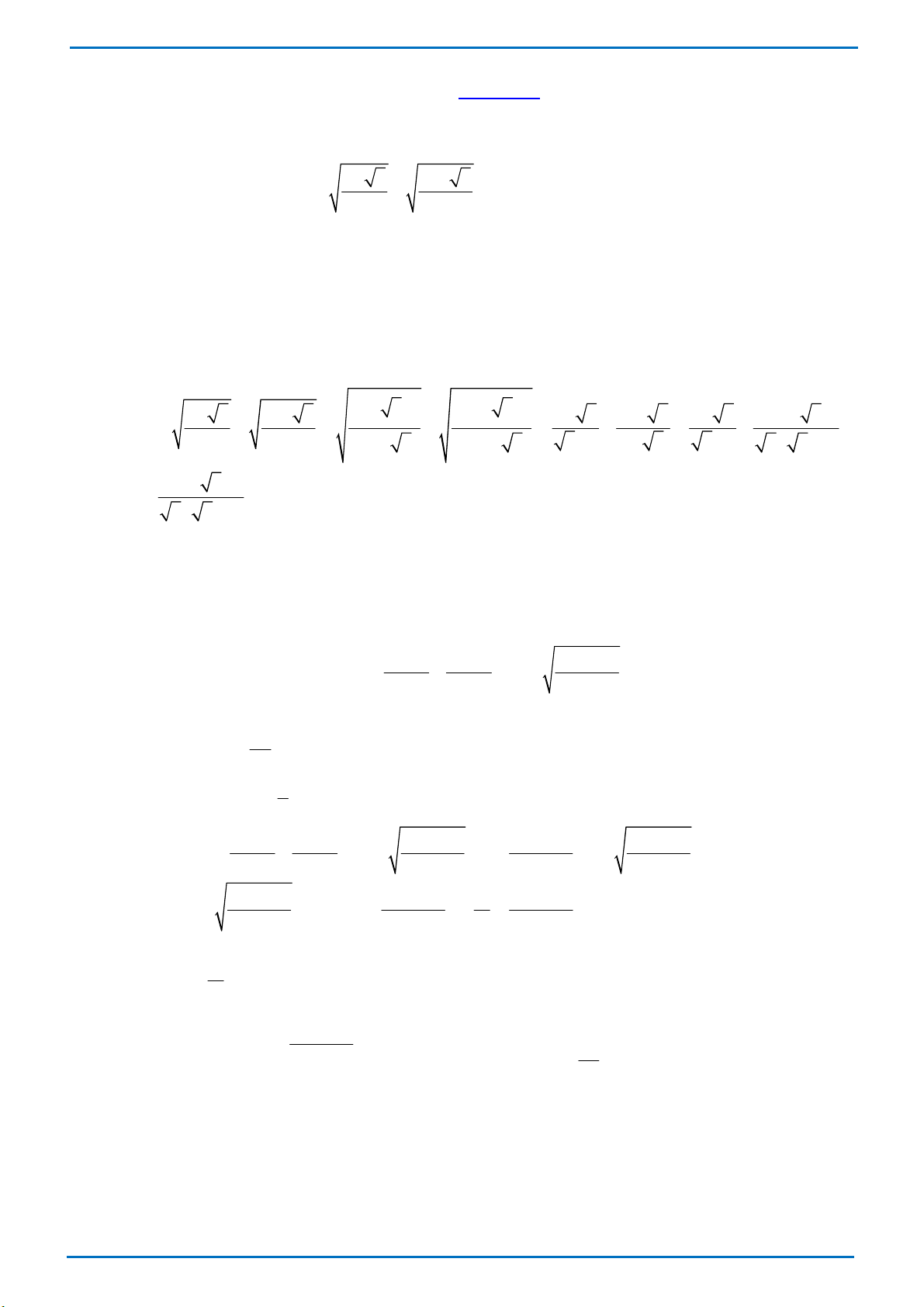


Preview text:
https://thcs.toanmath.com/de-thi-hsg-toan-9
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS TỈNH YÊN BÁI NĂM HỌC 2022 - 2023 ĐỀ THI CHÍNH THỨC MÔN TOÁN
Thời gian làm bài: 150 phút (không kể thời gian phát đề)
Câu 1. (4,0 điểm) 1. 2 - 3 6 - 3 3 Rút gọn biểu thức S = + . 2 2 2. Cho ( x) 3 2 P
= x + ax + bx + c với a, ,
b c là các số thực. Biết rằng P(2) = P( ) 3 = 2023.
Tính giá trị biểu thức Q = P(5) − P(0). 2 Câu 2. 1 1 9x − 25
(3,0 điểm) Giải phương trình 8 + +1 = . 3x − 5 3x + 5 x
Câu 3. (6,0 điểm) Cho đường tròn tâm O đường kính AB . Một điểm H cố định thuộc bán kính OB (
H khác O và B ). Qua điểm H kẻ dây cung MN vuông góc với đường kính AB . Một điểm C
đi động trên cung nhỏ AN ( C khác A và N ). Gọi L là giao điểm của BC và MN .
a) Chứng minh rằng ACLH là một tứ giác nội tiếp và BH.BA = B . L BC .
b) Chứng minh rằng BN là tiếp tuyến của đường tròn ngoại tiếp tam giác CLN .
c) Đường thẳng qua N và vuông góc với AC cắt MC tại D . Tìm vị trí của điểm C trên cung
nhỏ AN của đường tròn tâm O sao cho diện tích tam giác ADM đạt giá trị lớn nhất.
Câu 4. (4,0 điểm)
1. Tìm tất cả các bộ ba số nguyên tố ( , p , q r ) thỏa mãn ( 2 p + )( 2 q + ) 2 1 1 = r +1.
2. Cho m và n là các số nguyên dương thỏa mãn mn 1
+ chia hết cho 24 . Chứng minh rằng m + n cũng chia hết cho 24 .
Câu 5. (3,0 điểm) 1. Cho ,
x y, z là các số thực dương thỏa mãn x + y + z = 3 . Chứng minh rằng y + z z + x x + y + + ≥ 3 . x +1 y +1 z +1
2. Để chuẩn bị cho Kỳ thi chọn học sinh giỏi cấp tỉnh, bạn Tùng quyết định luyện tập giải một số
bài toán trong vòng 6 tuần. Theo dự định, bạn Tùng sẽ giải ít nhất một bài toán mỗi ngày và
không quá 10 bài toán mỗi tuần. Chứng minh rằng luôn tồn tại một chuỗi ngày liên tiếp mà trong
khoảng thời gian đó tổng số bài toán Tùng giải bằng 23.
___________________ Hết ___________________ THCS.TOANMATH.com LỜI GIẢI
Câu 1. (4,0 điểm) 1. 2 - 3 6 - 3 3 Rút gọn biểu thức S = + . 2 2 2. Cho ( x) 3 2 P
= x + ax + bx + c với a, ,
b c là các số thực. Biết rằng P(2) = P( ) 3 = 2023.
Tính giá trị biểu thức Q = P(5) − P(0). Lời giải 1. Ta có: ( )2 ( )2 2 - 3 6 - 3 3 2 - 3 6 - 3 3 2 - 3 6 - 3 3 2 - 3 6 - 3 3 S = + = + = + = + 2 2 2(2 - 3) 2(6 -3 3) 3 −1 3 - 3 3 −1 3 ( 3 − ) 1 3 - 3 = = 1 3 ( 3 − ) 1 2. Ta có: P(2) = P( )
3 = 2023 ⇔ 8+ 4a + 2b + c = 27 + 9a + 3b + c = 2023 5a + b = 1 − 9 Do đó:
Q = P(5) − P(0) = (125 + 25a +5b + c) − c =125+5(5a +b) =125+ 5( 1 − 9) = 30. 2 Câu 2. 1 1 9x − 25
(3,0 điểm) Giải phương trình 8 + +1 = . 3x − 5 3x + 5 x Lời giải −5 < x < 0 + Điều kiện: 3 5 x > 3 2 2 1 1 9x − 25 6x 9x − 25 + Ta có: 8 + +1 = ⇔ 8. + 1 = (*) 2 3x − 5 3x + 5 x 9x − 25 x 2 2 9x − 25 9x − 25 1 + Đặt 2 = > 0 x t ⇔ t = ⇔ = 2 2 x x t 9x − 25 + Khi đó, phương trình 6 (*) 3 2 3 2 2 ⇔ 8.
+1 = t ⇔ t − t − 48 = 0 ⇔ t − 4t + 3t − 48 = 0 ⇔ (t − 4) ( 2
t − 3t +12 = 0 ⇔ t = 4 2 ) t
x = −1, t . 2 ( h m) + Với 2 9x − 25 2 t = 4 ⇔ 4 =
⇔ 9x −16x − 25 = 0 ⇔ 25 x x = , (loai) 19
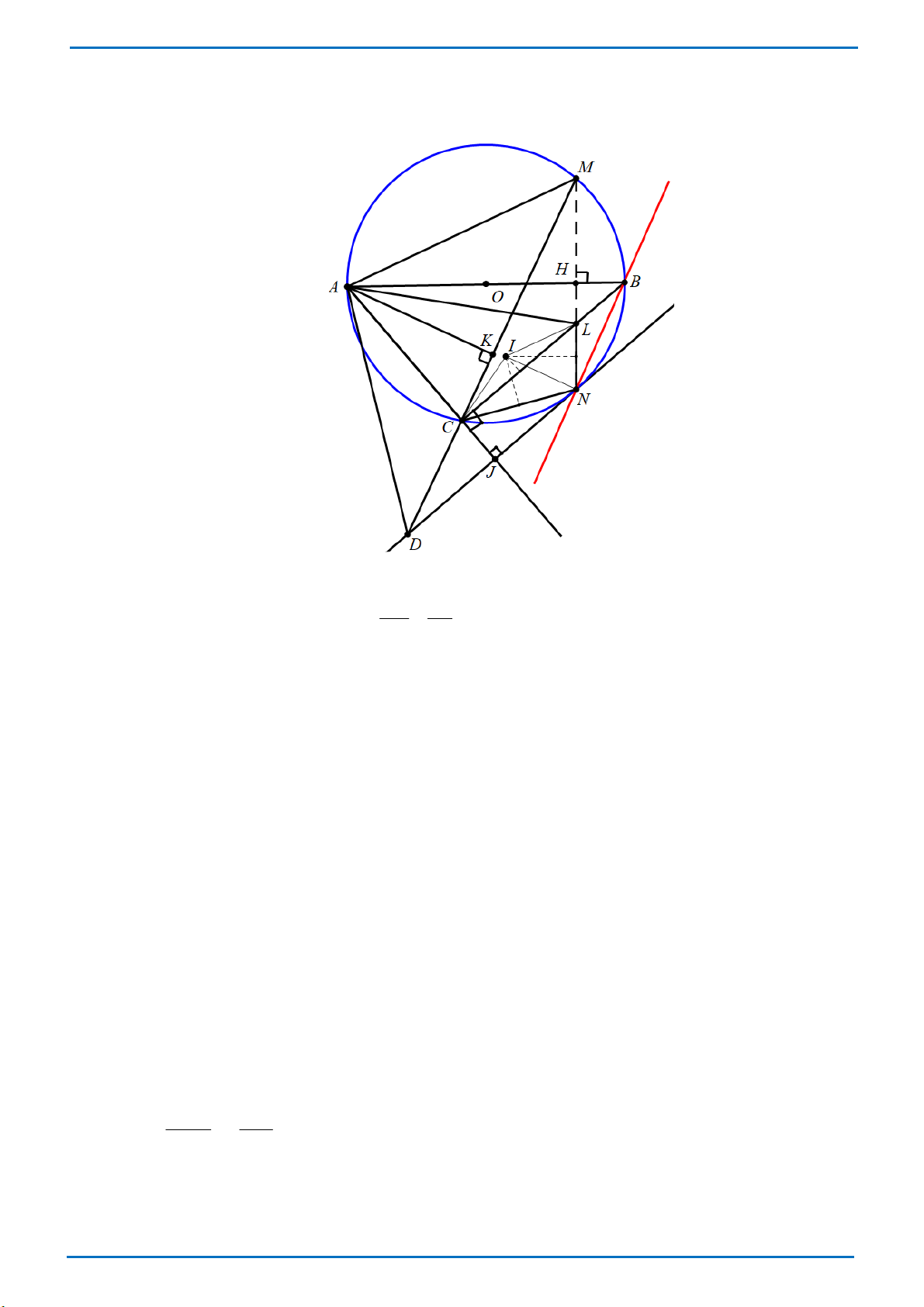
+ Vậy: Phương trình đã cho có tập nghiệm là S = {− } 1 . Câu 3. (6,0 điểm)
Cho đường tròn tâm O đường kính AB . Một điểm H cố định thuộc bán kính OB ( H khác O
và B ). Qua điểm H kẻ dây cung MN vuông góc với đường kính AB . Một điểm C đi động trên
cung nhỏ AN ( C khác A và N ). Gọi L là giao điểm của BC và MN .
a) Chứng minh rằng ACLH là một tứ giác nội tiếp và BH.BA = B . L BC . THCS.TOANMATH.com
b) Chứng minh rằng BN là tiếp tuyến của đường tròn ngoại tiếp tam giác CLN .
c) Đường thẳng qua N và vuông góc với AC cắt MC tại D . Tìm vị trí của điểm C trên cung
nhỏ AN của đường tròn tâm O sao cho diện tích tam giác ADM đạt giá trị lớn nhất. Lời giải
a) Tứ giác ACLH có: AHL = 90° và ACL = ACB = 90° . Suy ra ACLH nội tiếp. BH BL Ta có: H ∆ LB C ∆ A , B ( . g g) = BH.BA = ∽ B . L BC BC BA b) Ta có: BNL = BNM . NCL = NCB .
Do AB ⊥ MN B là điểm chính giữa cung MN . Do đó BNM = BCN .
Suy ra BNL = NCL . Suy ra BL là tiếp tuyến của đường tròn ngoại tiếp tam giác CNL.
c) Do ND ⊥ AC và BC ⊥ AC nên ND // BC .
Gọi J là giao điểm của AC và DN .
Ta có: JCN + NCB = 90° , DCJ + JCN + NCB + BCM = 180° mà
BCM = BCN DCJ = NCJ .
Suy ra CJ là đường trung trực của ND hay AC là trung trực của ND .
Ta có: AD = AN = AM .
Kẻ AK ⊥ DM A ∆ KM A ∆ ∽ C , B ( . g g) 2 S AM A ∆ KM =
= const S = . a S , a = const A ∆ KM A ∆ CB ( ) S AB A ∆ CB Ta có : S lớn nhất ⇔ S lớn nhất ⇔ S lớn nhất A ∆ DM A ∆ KM A ∆ CB THCS.TOANMATH.com 1 Mà: S =
d C AB AB lớn nhất ⇔ C là điểm chính giữa cung AB , ( vì d (C, AB) ≤ R ) AC ∆ B ( , ). 2
Câu 4. (4,0 điểm)
1. Tìm tất cả các bộ ba số nguyên tố ( , p , q r ) thỏa mãn ( 2 p + )( 2 q + ) 2 1 1 = r + ( 1 ) * . Lời giải 1. Vì ( , p ,
q r ) là một bộ ba số nguyên tố thỏa mãn ( 2 p + )( 2 q + ) 2 1
1 = r +1 r > 3 r lẻ 2 r +1 chẵn 2 2
p +1;q +1 không cùng lẻ Giả sử rằng 2
p = 2 p +1 = 5 lẻ 2
q +1 chẵn. Từ ( ) 2 2 * 5q + 4 = r
+ Nếu q là số nguyên tố không chia hết cho 3 thì 2 2 2 2
q ≡ 1 (mod 3) 5q ≡ 2 (mod 3) 5q + ≡ 0 (mod 3) ⇔ r ≡ 0 (mod 3) ⇔ r ≡ 0 (mod 3) , mà r
là số nguyên tố lớn hơn 3 , (không thỏa mãn) q = 3 . + Khi đó: 2 r = 49 r = 7
Vậy: các bộ ba số nguyên tố ( , p , q r ) thỏa mãn ( 2 p + )( 2 q + ) 2 1 1 = r + ( 1 )
* là : (2;3;7);(3;2;7)
2. Cho m và n là các số nguyên dương thỏa mãn mn 1
+ chia hết cho 24 . Chứng minh rằng m + n cũng chia hết cho 24 . Lời giải
+ Đặt : A = mn +1+ m+ n = (m+ ) 1 (n+ )
1 ;B = mn+1−m−n = (m− ) 1 (n− ) 1 + Xét A B = ( 2 m − )( 2 . 1 n − ) 1 + Vì mn 1
+ ⋮24 m ⋮ 24 và n ⋮ 24 m ⋮ 3 và n ⋮ 3 2 m − 1⋮3 và 2 n − 1⋮3 2 . A B⋮3 , (1) + Mặt khác, vì mn 1 + ⋮24 .
mn lẻ m và n cùng lẻ 2 m − 1⋮8 và 2 n − 1⋮8 2 . A B 8 ⋮ , (2) A⋮24 ( mn + )
1 + m+ n⋮24 m+ n⋮24 + Từ (1) và (2) suy ra: 2 . A B⋮24 ,(vì(mn+ ) 1 ⋮24) B⋮24 ( mn + )
1 −(m+n)⋮24 m+n⋮24 Câu 5. (3,0 điểm) 1. Cho ,
x y, z là các số thực dương thỏa mãn x + y + z = 3 . Chứng minh rằng y + z z + x x + y + + ≥ 3 . x +1 y +1 z +1 Lời giải + + + 1. y z z x x y Đặt A = + + x +1 y +1 z +1
+ Vì: x + y + z = 3 x + y = 3 − z; y + z = 3 − ;
x x + z = 3 − y + Khi đó:
3 − x 3− y 3 − z 3 − x 3 − y 3 = + + + 3 = +1 + +1 − z A A + +1 x +1 y +1 z +1 x +1 y +1 z +1 4 4 4 A + 3 = + + x +1 y +1 z +1
+ Vì x + y + z = 3 x + y + z +1+1+1 = 6 . 4 4 4 + Ta có: A + 3+ 6 = + x +1+ + y +1+ + z +1 x +1 y +1 z +1 4 4
+ Áp dụng, bất đẳng thức Cô- Si, ta có: + x +1 ≥ .( x + ) 1 = 4 x +1 x +1 THCS.TOANMATH.com 4 4 Tương tự: + y +1 ≥ .( y + ) 1 = 4 y +1 y +1 4 4 và + z +1 ≥ .( z + ) 1 = 4 z +1 z +1
+ Cộng vế với vế ba bất đẳng thức trên, suy ra: A + 9 ≥ 4 + 4 + 4 ⇔ A ≥ 3 + Dấu “ = ” xảy ra 4 = x+ 1 x +1 4
A + 9 ≥ 4 + 4 + 4 ⇔
= y +1 ⇔ x = y = z = 1 y +1 4 = z +1 z +1
2. Để chuẩn bị cho Kỳ thi chọn học sinh giỏi cấp tỉnh, bạn Tùng quyết định luyện tập giải một
số bài toán trong vòng 6 tuần. Theo dự định, bạn Tùng sẽ giải ít nhất một bài toán mỗi ngày và
không quá 10 bài toán mỗi tuần. Chứng minh rằng luôn tồn tại một chuỗi ngày liên tiếp mà
trong khoảng thời gian đó tổng số bài toán Tùng giải bằng 23. Lời giải
+ Gọi x lần lượt là số bài toán mà Tùng giải trong ngày thứ i , (1 ≤ i ≤ 42,i ∈ℤ ). i
Do Tùng sẽ giải ít nhất một bài toán mỗi ngày và không quá 10 bài toán trong mỗi tuần nên: 1 ≤ x ≤ 4 i
+ Đặt : S = x + x + ...+ x , i = 1, 42 , ta có: S ≠ S ,( i
∀ ≠ j; j = 1, 42 i j ) i 1 2 i ( )
+ Xét tập hợp A = {S ; S ;...;
với 1 ≤ S ≤ 60 và B = {S + 23; S + 23;...; S + 23 với 1 2 42 } 1 2 S42} i 24 ≤ S + 23 ≤ 83. j
Hai tập hợp A và B có tất cả 84 phần tử, nhận các giá trị trong tập hợp {1; 2;3;...;8 } 3 , (vì S
= x + x + ... + x ≤ 6.10 = 60 nên S + 23 ≤ 60 + 23 = 83 ) nên theo nguyên lý 42 1 2 42 42 Đi- rích -lê,
tồn tại hai phần tử bằng nhau.
Mặt khác, hai phần tử bằng nhau này không cùng thuộc A, không cùng thuộc B vì S ≠ S nên i j
một phần tử thuộc A và một phần tử thuộc B, chẳng hạn S ∈ A và S + 23∈ B . i j
Khi đó: S = S + 23, i > j nên S − S = 23 i j ( ) i j
Vậy, từ ngày thứ j đến ngày thứ i là chuỗi ngày liên tiếp mà trong khoảng thời gian đó tổng số
bài toán Tùng giải bằng 23. ---Hết--- THCS.TOANMATH.com
Document Outline
- de-hoc-sinh-gioi-toan-thcs-nam-2022-2023-so-gddt-yen-bai
- tuyển tập các đề thi hsg cấp tỉnh lớp 9 năm 2022-2023 các tỉnh





