


Preview text:
PHÒNG GD-ĐT SÔNG LÔ
KÌ THI CHỌN HSG LỚP 9 CẤP HUYỆN NĂM HỌC 2019-2020 ĐỀ CHÍNH THỨC MÔN TOÁN LỚP 9
Thời gian làm bài:150 phút (không kể thời gian giao đề)
Đề thi này gồm 01 trang Ngày thi : 06/11/2019 2 x 9 x 3 2 x 1
Câu 1 (2 điểm) Cho biểu thức: P x 5 x 6 x 2 3 x
a) Rút gọn biểu thức P .
b) Tìm các giá trị của x để P 0 .
Câu 2 (2 điểm) Cho biết 2 x x 2 2019
y 2019 y 2019 .
Tính giá trị biểu thức 2019 2019 A x y . 1 1
Câu 3 (2 điểm) Giải phương trình: x x x 2 . 2 4
Câu 4 (2 điểm) Tìm tất cả các số nguyên ; x y thỏa mãn: 2
x 2019 y y
1 y 2 y 3 .
Câu 5 (2 điểm) Tìm tất cả các số nguyên tố p sao cho 2 3 4
1 p p p p là số tự nhiên.
Câu 6 (2 điểm) Các cạnh a, ,
b c của tam giác ABC thỏa mãn đẳng thức: 1 1 1 1
a b c với p
. Hỏi tam giác ABC là tam giác gì? Vì sao? p p a p b p c 2
Câu 7 (2 điểm) Cho các số thực dương a, ,
b c thỏa mãn a b c 3 . 1 1 1 1
Tìm giá trị nhỏ nhất của P . 2 2 2 2 2 2 a b c
a b c
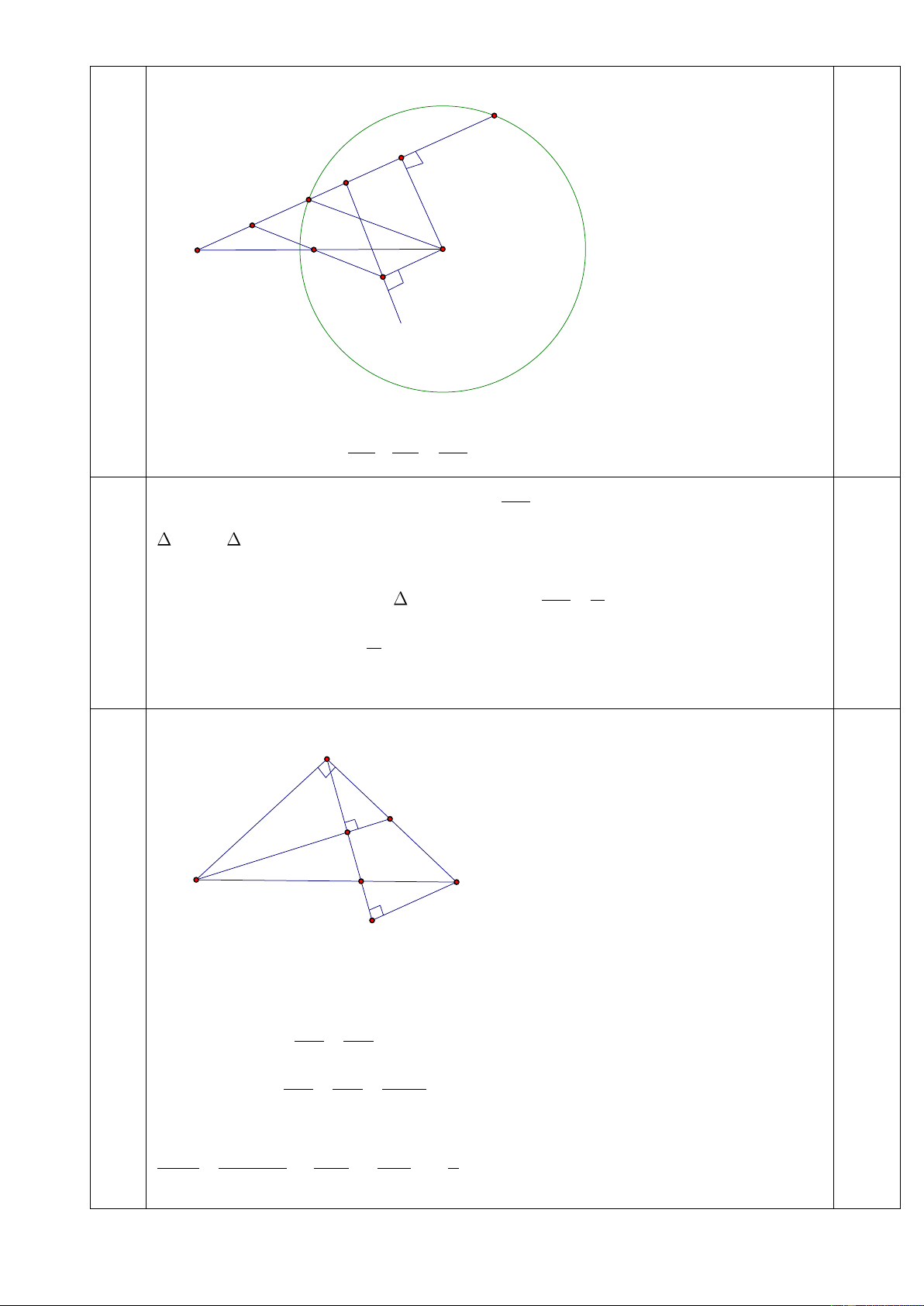
Câu 8 (4 điểm) Qua điểm K nằm ngoài đường tròn (O;R), kẻ đường thẳng cắt đường tròn (O)
tại A và B (A nằm giữa K và B, AB < 2R). Gọi d là đường trung trực của KB, H là hình chiếu
của O trên d. Gọi I là trung điểm của OK, N là trung điểm của AB, M là giao điểm của d và KB.
a) Chứng minh tứ giác OHMN là hình chữ nhật và AK = 2OH.
b) Tính IH theo R.
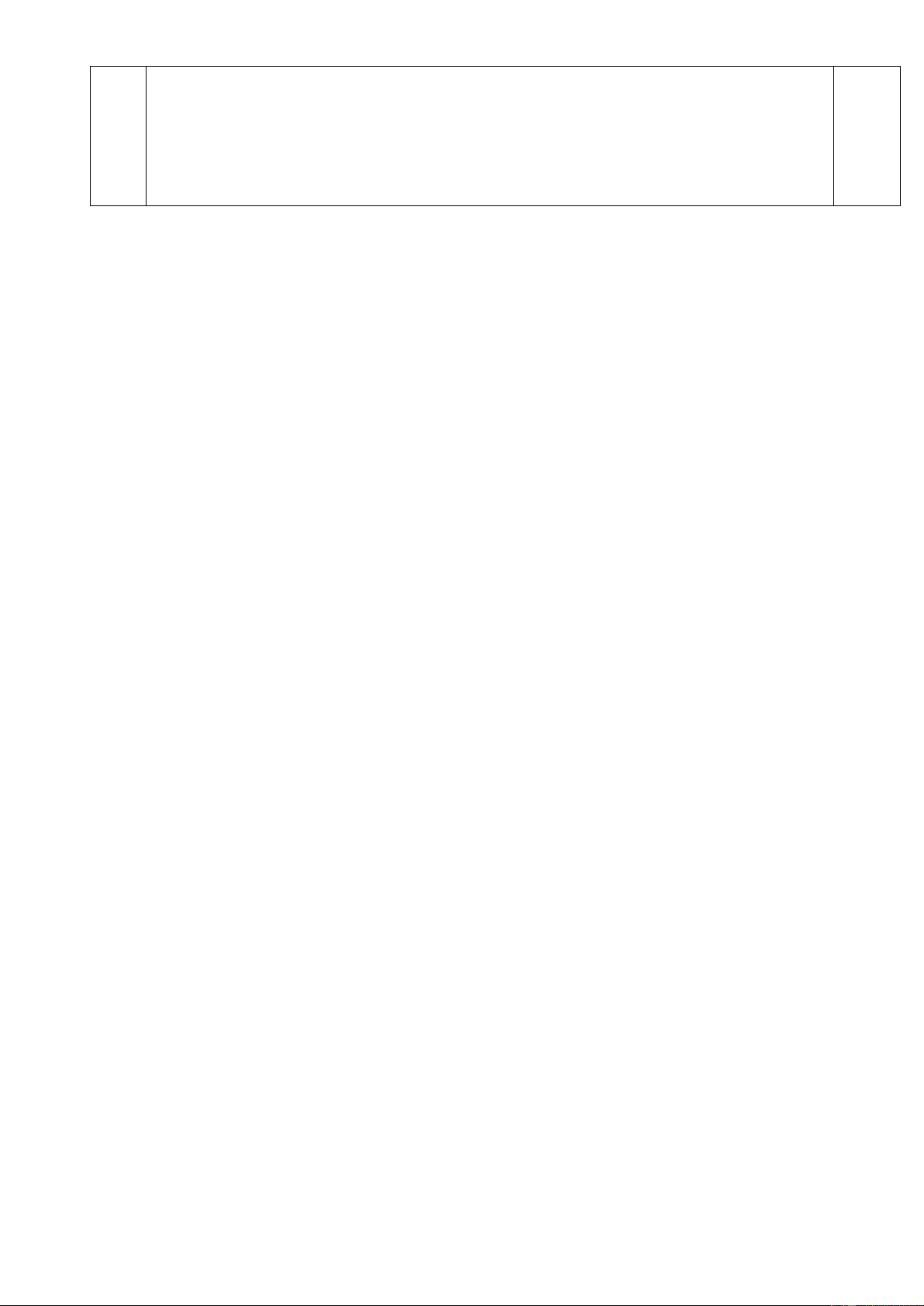
Câu 9 (1 điểm) Cho tam giác ABC vuông cân tại A . Gọi M là trung điểm của AC . Đường
thẳng qua A vuông góc với BM cắt BC tại D . Chứng minh DB 2DC .
Câu 10 (1 điểm) Trên đường tròn cho 6 điểm phân biệt. Hai điểm bất kì trong 6 điểm này
đều được nối với nhau bằng một đoạn thẳng màu xanh hoặc màu đỏ. Chứng minh rằng tồn tại
một tam giác có ba cạnh cùng màu. ==== HẾT ====
Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh.........................................................SBD:..................Phòng thi................
PHÒNG GD&ĐT SÔNG LÔ
HDC ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN
Năm học: 2019 – 2020 Môn Toán – Lớp 9
Thời gian làm bài: 150 phút, không kể thời gian giao đề. Câu Hướng dẫn chấm Điểm
Điều kiện để P xác định là : x 0;x 4;x 9 .
2 x 9 x 3 x 3 2 x 1 x 2 0,25 P
x 3 x 2 x x
x 1 x 2 2 x 1 1 0,25
x 3 x 2 x 3 x 2 x 3 0,5 Với x 1
x 0; x 4; x 9 , ta có P 0
0 x 3 0 x 9 x 3 0,5
Kết luận: 0 x 9 và x 4 thì P 0 0,5 Ta có: 2 x x 2
x x 2 y y 2 2019 2019 2019 2019
2019 x x 0,5 2 2
y 2019 y 2019 x x (1) 0,5 2 Tương tự ta có: 2 2
x 2019 x 2019 y y (2) 0,5
Từ (1) và (2) suy ra x y 0 x y A 0 0,5 ĐKXĐ 1 x 4 0,5 2 x x x
x 2 1 1 1 1 2 2 3 2 4 4 2 0,5 1 1 1 1 x
2 0 (vì x 2 0 ) 4 2 4 2 0,5
x 2 2 (tmđk) 0,5
Phương trình đã cho tương đương x
2 2y y 2 2019 3
y 3y 2 Đặt 2 2 2
t y 3y Khi đó pt trở thành: x
tt x 2 2019 2 2019 t 2t
+ Nếu t 0 ta có t t t t t t t t t 2 2 2 2 2 2 2 2 1 2 1 0,5 t x 2 t 2 2 2019 1 ( vô lí) 4
+ Nếu t 0 ta có 2
y 3y 0 y y 3 0 3 y 0 0,5
Vì y Z nên y 3 ; 2 ; 1 ; 0 0,5 Suy ra ; x y
2019;0,2019; 1,2019; 2 2019; 3 0,5 Theo bài ra ta có 2 3 4 2 * 1 p p p p n n N 5 2 3 4 2
4 4 p 4 p 4 p 4 p 4n (1) 0,5 2 2
Suy ra: p p n2 2 2 2 2
2 p p 2 0,5 2 2 2
2p p 2n 2p p 2 2n 2p p 1
Theo (1) ta có p p p p p p 2 2 3 4 4 4 4 4 4 2 1 0,5 2
p 2 p 3 0 p 3 ( do p là số nguyên tố p 0 ) Thử lại với p 3 ta có 2 3 4 2 3 4
1 p p p p 1 3 3 3 3 11 (tm) Vậy 0,5 p 3 0,5 1 1 1 1 p p c p a p b
p c p
p b p a
p p c
p a p b 2 p c a b 0,5
p p c
p a p b 6 a b a b
a b ca b c
b c aa c b 0,5 a b a b 2a 1
a b2 c
c a b2 2 2 4ab 2b
ba b 2 2 2 2 2 2 2
a b 2ab c c b a 0,5
Suy ra tam giác ABC vuông tại A 1 1 1 1 1 1 9 27 Ta có: 2 2 2 a b c ab bc ca
abc a b c
abbc ca2 27 1 P (1)
ab bc ca2 2 2 2
a b c 0,5 Áp dụng AM-GM ta 3 2 2 2
a b c 2ab 2bc 2ca
có a b c ab bc ca2 2 2 2 27 3 0,5 7 27 2 2 2 (2)
ab bc ca a b c 2 0,5 Từ (1) và (2) suy ra 1 1 2 2 2
P a b c t với 2 2 2
t a b c 3 2 2 2
a b c t Khi đó t 1 8t 2 8 10 P 9 t 9 3 3 3 0,5
Dấu “=” khi t 3 a b c 1. Vậy giá trị nhỏ nhất của P bằng 10 khi và 3
chỉ khi a b c 1 8a B N M A C K O I H d 0,5
Chứng minh OHMN là hình chữ nhật, 0,5 KB AB A K OH = MN=MB-NB= A K 2OH 2 2 2 A K
Gọi C là trung điểm của KA ta có 0,5 KC . Do đó OH =KC 2 HOI= CKI( c-g-c) Suy ra IH = IC (1) 8b
Do IC là đường trung bình OA R OKA nên IC 2 2 0,5 R
Từ (1) và (2) Suy ra IH 2 A M H B C D K 9 Kẻ CK vuông góc AD, K D A .
Gọi H là giao điểm AD với BM DC CK 0,5 Vì BH//CK nên (1) DB BH Mặt khác DC CK 2HM (2) DB BH BH
Áp dụng hệ thức về cạnh và đường cao ta có: 2 2 0,5 AM HM .BM HM AM 1
,thay vào (2) ta được DB 2DC 2 AB BH.BM BH AB 4
Giả sử 6 điểm A, B, C, D, M, N trên cùng 1 đường tròn.
Từ 1 điểm vẽ đến 5 điểm còn lại được 5 đoạn thẳng thì có ít nhất 3 đoạn thẳng
cùng màu. Giả sử 3 đoạn thẳng AB, AC, AD cùng màu đỏ( nếu cùng màu xanh thì 10 0,5 lập luận tương tự).
Xét tam giác BCD nếu có 1 cạnh, chẳng hạn BC màu đỏ thì tam giác ABC có 3 0,5
cạnh màu đỏ. Trái lại thì tam giác ABC có ba cạnh màu xanh.




