Đề khảo sát chất lượng – Tháng 1 năm học 2025 - 2026 môn Toán lớp 9

UBND PHƯỜNG KIM LIÊN
ĐỀ KHẢO SÁT CHẤT LƯỢNG – THÁNG 1
TRƯỜNG THCS ĐỐNG ĐA NĂM HỌC 2025 - 2026 ĐỀ CHÍNH THỨC
Môn: TOÁN – Lớp 9
(Đề gồm 02 trang)
Thời gian: 120 phút (không kể thời gian giao đề)
(Học sinh được sử dụng máy tính bỏ túi) Bài 1.(1,5 điểm):
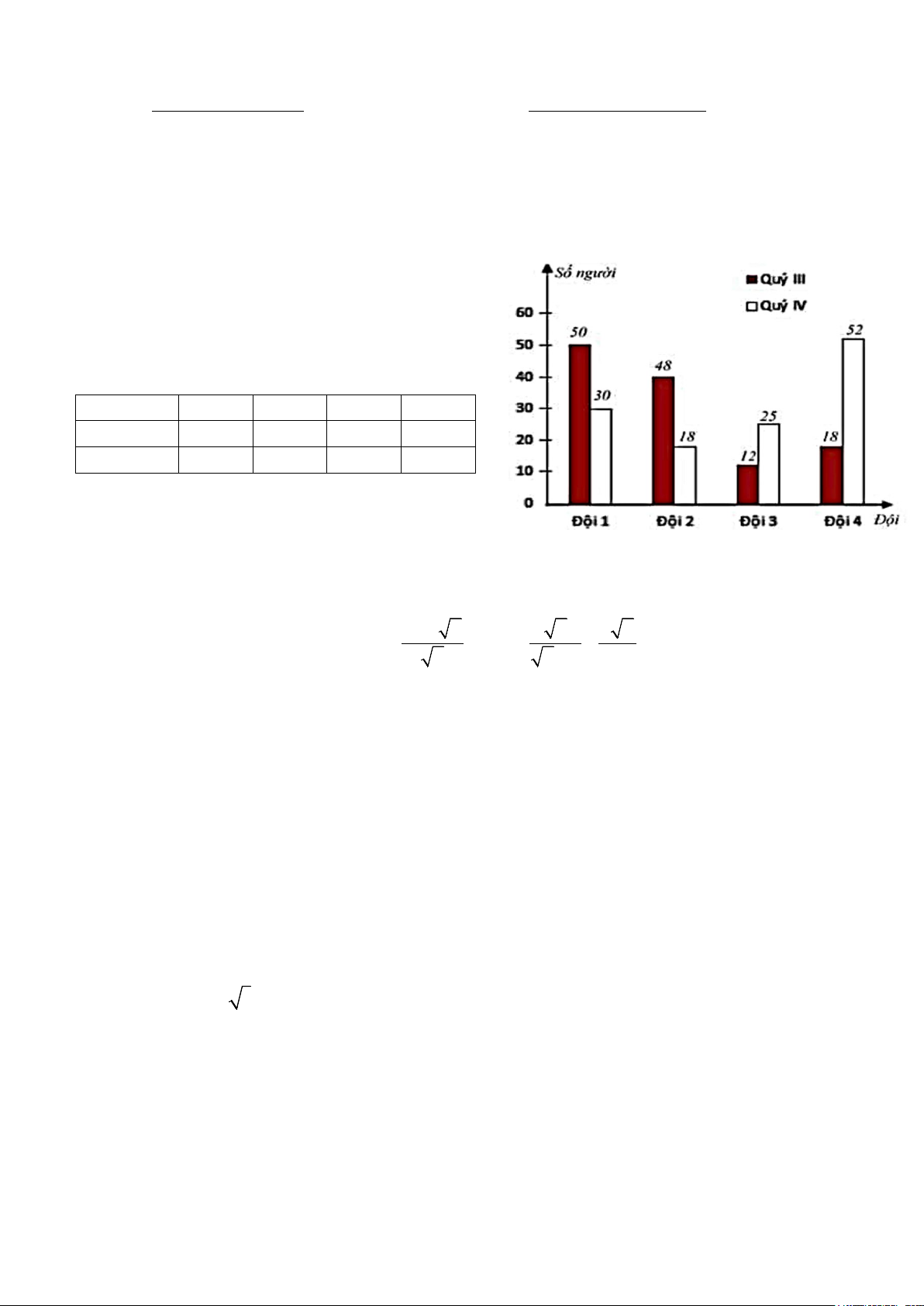
1. Biểu đồ kép (hình bên) biểu diễn số công nhân
xếp loại Tốt trong quý III và quý IV của 4 đội công nhân.
a) Lập bảng thống kê số công nhân xếp loại Tốt
trong quý III và quý IV và vẽ bảng vào giấy kiểm tra Đội 1 2 3 4 Quý III ? ? ? ? Quý IV ? ? ? ?
b) Tổng số công nhân xếp loại Tốt quý IV tăng hay
giảm bao nhiêu phần trăm so với quý III? (làm tròn
đến hàng phần trăm)
2. Viết ngẫu nhiên một số tự nhiên có 1 chữ số. Tính xác suất của biến cố “ Số tự nhiên được viết
ra là số chia hết cho 3 ”.
Bài 2. (2,0 điểm): Cho hai biểu thức x + 3 x A = và x 4 = − x B
với x > 0; x ≠ 4 x x + 2 4 − x
1. Tính giá trị của biểu thức A biết x =16 .
2. Rút gọn biểu thức B .
3. Cho P = A.B . Tìm các số tự nhiên x để P ≤ 3. Bài 3. (2,5 điểm):
1. Bạn Bình dự định dùng hết số tiền 600 nghìn đồng để mua một số chiếc áo đồng giá tặng các
bạn có hoàn cảnh khó khăn. Khi đến cửa hàng, loại áo mà bạn Bình dự định mua được giảm giá 30
nghìn đồng/chiếc. Do vậy bạn Bình đã mua được số lượng áo gấp 1,25 lần so với số lượng dự định.
Tính giá tiền của mỗi chiếc áo mà bạn Bình đã mua.
2. Chiều cao ngang vai của một con voi đực ở Châu Phi là h (cm) có thể được tính xấp xỉ bằng
công thức h = 62,5. 3 t +75,8 với t là tuổi của con voi tính theo năm.
( nguồn Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby,năm 2017)
a) Một con voi đực 8 tuổi ở châu Phi sẽ có chiều cao ngang vai là bao nhiêu centimet?
b) Nếu một con voi đực ở châu Phi có chiều cao ngang vai là 230 cm thì con voi đó bao nhiêu tuổi
( làm tròn kết quả đến hàng đơn vị)
3. Xác định a và b để đồ thị hàm số y = ax + b đi qua hai điểm A( 2; 8) và B(-4; 5) . Bài 4.(3,5 điểm):
1. Hình bên mô tả mảnh vải có dạng một phần tư hình vành khuyên
giới hạn bởi 2 đường tròn cùng tâm và có bán kính lần lượt là 3,5 dm
và 5,2 dm. Diện tích mảnh vải đó bằng bao nhiêu dm2 (lấy π ≈ 3,14,
làm tròn kết quả đến hàng phần mười).
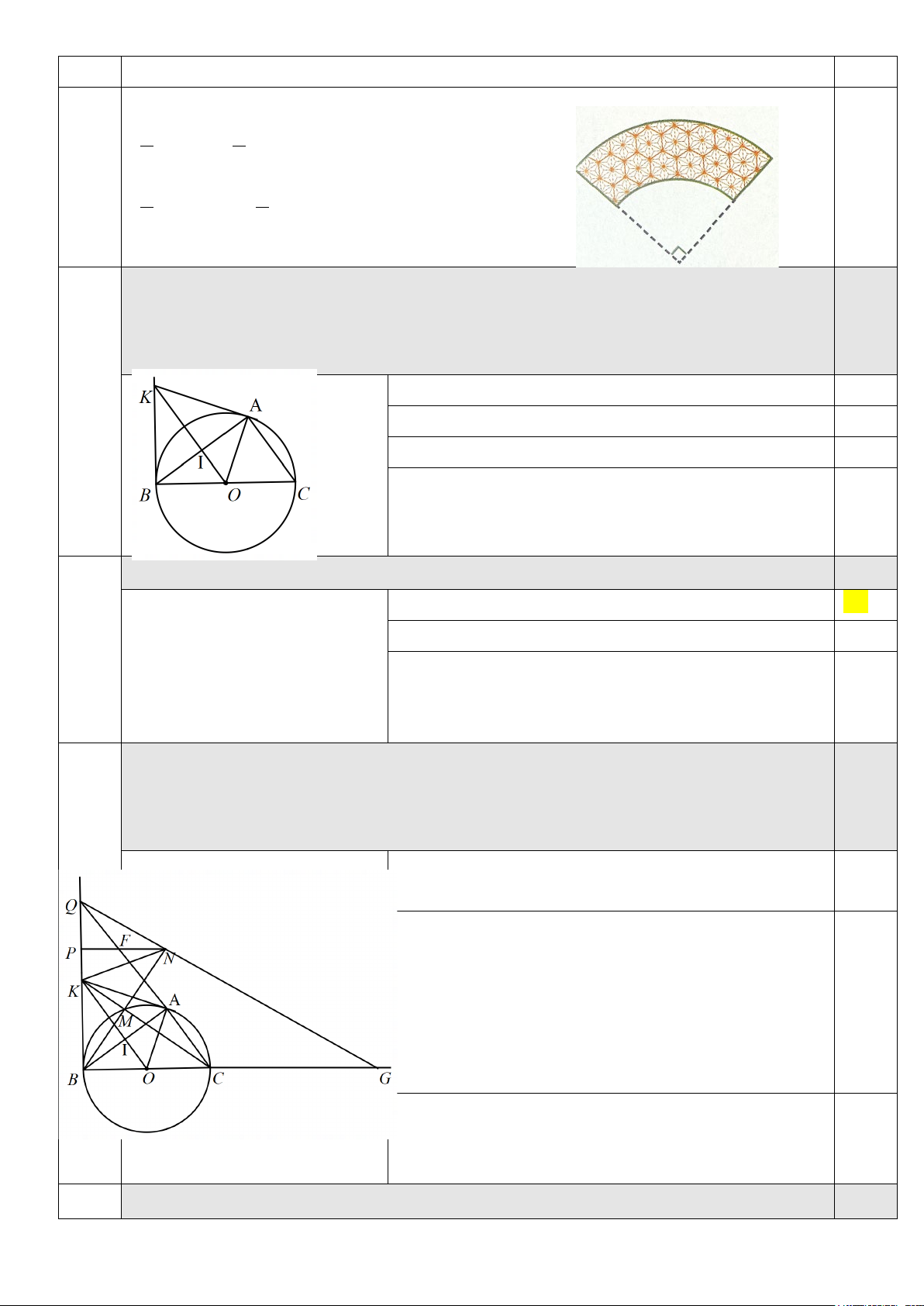
2. Cho đường tròn (O) đường kính BC và một điểm A thuộc đường tròn (O) (A khác C, B) sao cho
AB > AC. Vẽ tiếp tuyến Bx của đường tròn (O), qua O vẽ đường thẳng vuông góc với dây cung
AB tại I cắt tia Bx tại K.
a) Chứng minh IA = IB và OK // AC.
b) Chứng minh: KA là tiếp tuyến của đường tròn (O).
c) Đoạn thẳng KC cắt đường tròn (O) tại M, trên tia đối của tia MB lấy điểm N sao cho M là trung
điểm của cạnh BN. Từ N vẽ đường thẳng vuông góc với Bx tại P. Chứng minh: NK = KB và AC
đi qua trung điểm của NP.
Bài 5(0,5 điểm): Cho các số dương x, y thỏa mãn x +3y = 6. 2 2 x y + 2025
Tìm giá trị nhỏ nhất của biểu thức A = xy
HƯỚNG DẪN CHẤM BÀI
Ghi chú: Học sinh giải cách khác đúng cho đủ điểm theo từng phần. Bài/ý Nội dung Điểm
Bài 1 1. Biểu đồ kép (hình bên) biểu diễn số công nhân xếp loại Tốt trong quý III và quý IV của 4 đội công nhân. (1,5đ) 0,5 a)
a) Lập bảng thống kê số công nhân xếp loại Tốt trong quý III và quý IV và vẽ bảng vào giấy kiểm tra
Bảng thống kê số công nhân xếp loại Tốt trong quý III và quý IV của công ty. Đội 1 2 3 Quý III 50 48 12 1 0,25 Quý IV 30 18 25 5 0,25 b)
b) Tổng số công nhân xếp loại Tốt quý IV tăng hay giảm bao nhiêu phần trăm so với quý III? 0,5
Số công nhân xếp loại Tốt của công ty quý III là: 50+48+12+18 = 128 (công nhân)
Số công nhân xếp loại Tốt của công ty quý IV là: 30+18+25+52 = 125 (công nhân) 0,25
Số công nhân xếp loại Tốt của quý IV ít hơn của quý III là : 128 – 125 = 3 (công nhân)
Số công nhân của quý IV giảm số % so với quí III là 0,25 3 .100% ≈ 2,34% 128 2)
Viết ngẫu nhiên một số tự nhiên có 1 chữ số. Tính xác suất của biến cố “ Số tự nhiên
được viết ra là số chia hết cho 3”. 0,5
Tập hợp các kết quả có thể xảy ra đối với số tự nhiên được viết ra là:
{0;1;2;3;4;5;6;7;8;9 }, có 10 kết quả 0,25
Các kết quả thuận lợi cho biến cố “ Số tự nhiên được viết ra là số chia hết cho 3” là: 0; 3; 6; 9 4 2
Xác suất của bến cố đó là = 0,25 10 5
Bài Cho hai biểu thức x+3 x = và x 4 B = −
x với x > 0; x ≠ 4 2 A x x + 2 4 − x 0,5 1)
Tính giá trị của biểu thức A biết x =16 . 1) Có x + 3 x A =
(x > 0, x ≠ 4) x 0,5 Bài/ý Nội dung Điểm
Thay x =16 (TMĐK) vào biểu thức A ta có: 16 3 16 A + = = 7 16 2)
Rút gọn biểu thức B . 1,0 x 4 = − x B
(x > 0, x ≠ 4) x + 2 4 − x x 4 − = + x B x( x 2) 4 x = +
x + 2 ( x − 2)( x + 2) ( x − 2)( x + 2) ( x − 2)( x + 2) 0,25 x − 2 x + 4 + 0,5 = x B x 2 x =
( x − 2)( x + 2) ( x − 2)( x + 2) x( x + 2) 0,25 B x = =
( x − 2)( x + 2) x − 2 Vậy = x B
với x > 0, x ≠ 4 x − 2 3)
Cho P = A.B . Tìm các số tự nhiên x để P ≤ 3. 0,5 3) Có x + 3 x A = và = x B
(x > 0, x ≠ 4) x x − 2 + + P x 3 = . A B x 3 x x = ⋅ x = x x − 2 x − 2 Để + + P x 6
≤ 3 thì x 3 x ≤ 3 hay ≤ 0 x − 2 x − 2 Giải ra được x < 4 0,25
mà x > 0, x ≠ 4 và x là số tự nhiên nên x∈{1;2;3} 0,25
Vậy để P ≤ 3 thì x∈{1;2;3}
Bài 3 1) Bạn Bình dự định dùng hết số tiền 600 nghìn đồng để mua một số chiếc áo đồng giá 1)
tặng các bạn có hoàn cảnh khó khăn. Khi đến cửa hàng, loại áo mà bạn Bình dự định
mua được giảm giá 30 nghìn đồng/chiếc. Do vậy bạn Bình đã mua được số lượng áo 1,0
gấp 1,25 lần so với số lượng dự định. Tính giá tiền của mỗi chiếc áo mà bạn Bình đã mua.
Gọi giá tiền của mỗi chiếc áo mà bạn Bình đã mua là x ( nghìn đồng), ( x > 30) 0,25
Giá tiền của mỗi chiếc áo ban đầu là x + 30 ( nghìn đồng) 600
Số lượng áo bạn Bình mua được theo dự định là ( chiếc) x + 30 Bài/ý Nội dung Điểm 600
Số lượng áo bạn Bình mua được thực tế là ( chiếc) x 0,25
Do bạn Bình đã mua được số lượng áo gấp 1,25 lần so với số lượng dự định 600 600
Nên ta có phương trình 1,25. = x + 30 x
Giải phương trình ta được x = 120 0,25 x = 120 ( TMĐK) 0,25
Vậy giá tiền của mỗi chiếc áo mà bạn Bình đã mua là 120 nghìn đồng 2)
Chiều cao ngang vai của một con voi đực ở Châu Phi là h (cm) có thể được tính xấp xỉ bằng công thức
h = 62,5. 3 t + 75,8 với t là tuổi của con voi tính theo năm ( nguồn Math for Real Life:
Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby,năm 1,0 2017)
a) Một con voi đực 8 tuổi ở châu Phi sẽ có chiều cao ngang vai là bao nhiêu centimet?
b) Nếu một con voi đực ở châu Phi có chiều cao ngang vai là 230 cm thì con voi đó bao
nhiêu tuổi ( làm tròn kết quả đến hàng đơn vị)
Với t = 8 (tuổi), một con voi ở châu Phi sẽ có chiều cao ngang vai là : 0,5
h = 62,5. 3 8 + 75,8 = 200,8 (cm) 62,5. 3 t + 75,8 = 230 0,25 Tìm được t ≈ 15
Nếu một con voi đực ở châu Phi có chiều cao ngang vai là h = 230 cm thì con voi đó 0,25
có số tuổi xấp xỉ 15 tuổi 3)
Xác định a và b để đồ thị hàm số y = ax + b đi qua hai điểm A( 2; 8) và B(-4; 5) 0,5
Đồ thị hàm số y = ax + b đi qua hai điểm A( 2; 8) và B(-4; 5) nên ta có hệ phương trình 2a + b = 8 0,25   4 − a + b = 5 1
Giải hệ phương trình ta được a = và b = 7 0,25 2
Bài 4 Hình 1 mô tả mảnh vải có dạng một phần tư hình vành khuyên giới hạn bởi 2 đường 1)
tròn cùng tâm và có bán kính lần lượt là 3,5 dm và 5,2 dm. Diện tích mảnh vải đó 0,5
bằng bao nhiêu dm2 (Lấy π ≈ 3,14, làm tròn kết quả đến hàng phần mười) Bài/ý Nội dung Điểm
Diện tích mảnh vải đó bằng 1 0,25 2 1 2 π.5,2 − π.3,5 ≈ 4 4 1 2 1 2 2
3,14.5,2 − 3,14.3,5 ≈11,6(dm ) 4 4 0,25 2a)
2) Cho đường tròn (O) đường kính BC và một điểm A thuộc đường tròn (O) (A khác
C, B) sao cho AB > AC. Vẽ tiếp tuyến Bx của đường tròn (O). Qua O vẽ đường thẳng
vuông góc với dây cung AB tại I cắt tia Bx tại K. 1,25
Chứng minh IA = IB và OK // AC Hình vẽ cho câu a. 0,25 Chứng minh IA = IB 0,5 Chứng minh OK // AC 0,5 2b)
Chứng minh: KA là tiếp tuyến của đường tròn (O) 1,0 Chứng minh: O  BK = OA  K . 0,5 Suy ra góc OBK = góc OAK 0,25
Từ đó suy ra OA ⊥ AK tại A Mà A thuộc (O) 0,25
Suy ra KA là tiếp tuyến của đường tròn (O) 2c)
c) Đoạn thẳng KC cắt đường tròn (O) tại M, trên tia đối của tia MB lấy điểm N sao cho
M là trung điểm của cạnh BN. Từ N vẽ đường thẳng vuông góc với Bx tại P. Chứng
minh: NK = KB và AC đi qua trung điểm của NP. 0,75
Chứng minh KC là đường trung trực của BN 0,25 Suy ra NK = KB (1)
Gọi giao của AC với BK và NP là Q và F, QN cắt BC tại G 0,25 Chứng minh KB = KQ (2)
Từ (1) và (2) suy ra Tam giác BNQ vuông tại N Suy ra KC // QG Chứng minh BC = CG
từ đó chứng minh FP = FN 0,25
Bài 5 Cho các số dương x, y thỏa mãn x +3y = 6. 0,5 Bài/ý Nội dung Điểm 2 2 x y + 2025
Tìm giá trị nhỏ nhất của biểu thức A = xy
Chứng minh bất đẳng thức a + b ≥ 2 ab với a ≥ 0; b ≥ 0
Từ x +3y = 6 chứng minh xy ≤ 3, dấu đẳng thức xẩy ra khi x = 3 và y = 1 0,25 2025 9 2016 A = xy + = xy + + xy xy xy 9 9 9 Ta có xy + ≥ 2 x . y ⇒ xy +
≥ 6 dấu đẳng thức xẩy ra khi xy=3 xy xy xy 0,25 1 1 2016 Ta có xy ≤ 3 nên ≥ ⇒
≥ 672, dấu đẳng thức xảy ra khi xy=3 xy 3 xy Do đó A ≥678
A nhỏ nhất là 678 khi x = 3 và y = 1