Đề khảo sát chất lượng Toán 9 năm 2021 – 2022 trường THCS Dịch Vọng – Hà Nội

PHÒNG GD –ĐT QUẬN CẦU GIẤY
ĐỀ KHẢO SÁT CHẤT LƯỢNG MÔN TOÁN 9
TRƯỜNG THCS DỊCH VỌNG Năm học 2021 -2022 Ngày: 19/5/2022
Thời gian làm bài: 90 phút
Bài I (2 điểm): Cho hai biểu thức: x − 3 x − x − 7 x + 2 x − 3 A = ; B = + +
với x  0; x  4 x + 1 x + x − 6 x + 3 2 − x
a) Tính giá trị của biểu thức A khi x = 9 x + 1 b) Chứng minh B = x + 3
c) Cho biểu thức M = A.B. Tìm số nguyên x lớn nhất để M nhận giá trị nguyên
Bài II (2,5 điểm):
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Nhân dịp kỷ niệm sinh nhật Bác Hồ tỉnh Lâm Đồng phát động phong trào trồng cây gây
rừng, một lớp 9 của trường THCS được giao trồng 240 cây. Nhưng khi thực hiện có 8 bạn
nghỉ nên mỗi học sinh còn lại của lớp phải trồng thêm 1 cây so với dự định. Hỏi lớp 9 đó có
bao nhiêu học sinh? (biết số cây trồng của mỗi học sinh như nhau)
2) Quả bóng đá thi đấu chính thức SEA Games 31 chọn sắc đỏ và vàng trên quốc kỳ nước
chủ nhà Việt Nam làm chủ đạo. Họa tiết trên bóng lấy cảm hứng từ tinh thần thi đấu rực lửa
của các chiến binh sao vàng và tình yêu mãnh liệt của hàng triệu người dân Việt Nam dành
cho môn thể thao vua. Quả bóng đá có đường kính 22cm. Để bơm căng quả bóng cần bao
nhiêu ml khí? (Cho   3,14, làm tròn kết quả đến chữ số thập phân thứ nhất).
Bài III (2 điểm):  5 + 2y − 3 = 6  x − 2
1) Giải hệ phương trình:  1  − 3 2y − 3 = 2 −  x − 2
2) Cho hàm số y = mx – m + 4 ( với m là tham số, m ≠ 0) có đồ thị là đường thẳng (d).
a) Vẽ đồ thị hàm số khi m = 2
b) Tìm m để (d) tạo với hai trục tọa độ Ox, Oy một tam giác có diện tích bằng 1 (đvdt).
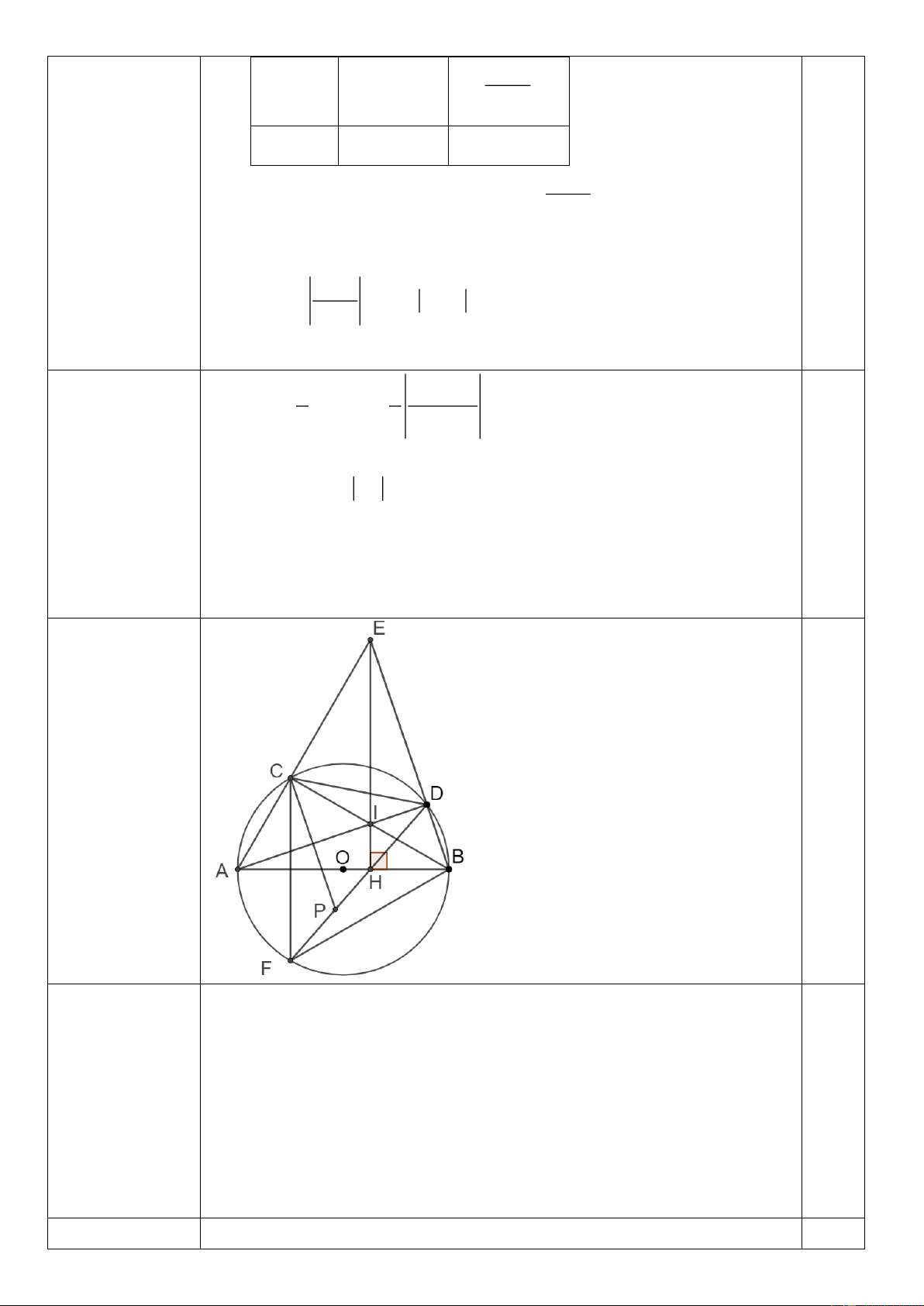
Bài IV (3 điểm): Cho đường tròn (O; R) đường kính AB. Lấy điểm C thuộc đường tròn sao
cho AC = R. Trên cung nhỏ BC lấy điểm D (D khác B, C) ; AC cắt BD cắt tại E; hạ EH
vuông góc với AB tại H, EH cắt AD tại I. Tia DH cắt (O; R) tại điểm thứ hai là F
1) Chứng minh tứ giác AHDE là tứ giác nội tiếp 2) Chứng minh 𝐷𝐻𝐸 ̂ = 𝐷𝐹𝐶 ̂ từ đó suy ra CF ⊥ AB
3) Chứng minh  BCF là tam giác đều. Xác định vị trí của D để chu vi tứ giác ABDC đạt giá trị lớn nhất.
Bài V(0,5 điểm): Giải phương trình 2
x − 6x +11 = x − 2 + 4 − x . ---HẾT--- ĐÁP ÁN Bài I. + x = 9 (TMĐK) (2điểm)
+ Thay x = 9 vào biểu thức A ta có: x − 3 9 − 3 6 3 A = = = = 0.25 x + 1 3 + 1 4 2 0.25 + KL: Vậy A = 3/2 khi x = 9 x − x − 7 x + 2 x − 3 B = + +
với x  0; x  4 x + x − 6 x + 3 2 − x
* x + x - 6 = ( x + 3)( x - 2) x − x − 7 x + 2 x − 3 B = + − 0.25
( x + 3)( x − 2) x + 3 x − 2
x − x − 7 + ( x + 2)( x − 2) − ( x − 3)( x + 3) B =
( x + 3)( x − 2) x − 2 x − 2 B = 0.25
( x + 3)( x − 2)
( x − 2)( x +1) B =
( x + 3)( x − 2) x + 1 0.25 B = x + 3 + KL 0.25 x − 3 x + 1 x − 3 M = A.B = . = (x  0; x  4 ) x + 1 x + 3 x + 3
* TH1: x – 3 = 0 => x = 3 (tmđk) => M = 0  Z
Vậy x = 3 thì M nguyên (1)
* TH2: x – 3 ≠ 0 => x ≠ 3 x − 3 6 M = = x − 3 + x + 3 x + 3 6
M  Z => x − 3 +  Z x + 3
=> x là số chính phương và x + 3U (6) = { 1; 6  ; 2  ; 3  }
Mà: x ≥ 0 => x ≥ 0 => x + 3 ≥ 3
=> x + 3 thuộc {3; 6}
=> x thuộc {0; 9} (tmđk) (2) 0.25
+ Từ (1) và (2): x thuộc {0; 3; 9} thì M nguyên 0.25
Vì x là số nguyên lớn nhất => x = 9 Bài II.
1) Gọi số học sinh lớp 9 đó là x (học sinh) (x  N*, x > 8) 0,25 (2,5điểm) 240
Theo kế hoạch mỗi học sinh phải trồng là: (cây) x 0,25
Số học sinh còn lại là: x – 8 (học sinh) 0,25 240
Khi thực hiện mỗi học sinh còn lại phải trồng là: (cây) x − 8 0,25 Ta có phương trình: 240 240 − = 1 x − 8 x 0,25
Giải PT ta được: x = 48 (TMĐK) 0,5
Vậy số học sinh lớp 9 đó là 48 học sinh. 0,25
+ Bán kính của quả bóng là: 22: 2 = 11 (cm)
+ Thể tích của quả bóng là: V = 4  4 . R3 = . 113 ≈ 5572,5 (cm3) 3 3 ≈ 5572,5 ml 0,25
+ KL: Cần 5572,5ml khí để bơm căng quả bóng. 0.25 Bài III.  5 + 2 y − 3 = 6 (2điểm)  x − 2  (I) 1  − 3 2 y − 3 = 2 −  x − 2
+ ĐK: x – 2 > 0 => x > 2 0.25  15  16 + 3 2 y − 3 = 18 =16    x − 2  x − 2    1 1  3 2 y 3 2  − − = − − 3 2y − 3 = 2 −  x − 2  x − 2  0.25 x − 2 = 1 x = 3     1  − 3 2y − 3 = 2 − 2 y − 3 = 1   x = 3 x = 3(TM )  
 2y − 3 =1  y = 2   2y − 3 = 1 −  y =1 0.25
+ KL: HPT có nghiệm là : (x;y) =∈ {(3 ; 2) ; (3 ; 1)} 0.25 2a) +) Lập bảng x 0 -1 0.25 y = 2x+2 2 0 0.25
+) Vẽ đồ thị chính xác
2b) (d ) tạo với hai trục tọa độ một tam giác  (d ) cắt hai trục tọa 0.25 điểm m  m 
độ tại hai điểm phân biệt  0 0    4 − m  0 m  4 Ta có bảng: x 0 m − 4 m y 4 − m 0   m − 4 
Đường thẳng (d ) cắt Ox tại A ;0 , cắt Oy tại    m  B(0;4 − m) . m − 4  OA = ;OB = 4 − m . m 0.25 1 1 (m − )2 4 S = O . A OB = = 1 OAB 2 2 m  m − 4 = 2m 2 ( )2
 (m − 4) = 2m   (m−4)2 = 2 − m m = 2 2
 m −10m +16 = 0  (m − 2)(m −8) = 0  (TMĐK).  m = 8 Bài IV. (3 điểm) 0.25 1
Xét đường tròn (O) có:
(0,75đ) EH ⊥ AB =H EHA = EHB = 90 . 0,25
Mặt khác: AB là đường kính của (O) . D (O). 
ADB = 90 (góc nội tiếp chắn nửa đường tròn) Mà 0,25
ADB + ADE =180( kề bù)  ADE = 90 . Xét tứ giác
AHDE có: ADE = AHE = 90 .
tứ giác AHDE nội tiếp (tứ giác có 2 đỉnh kề nhau cùng nhìn 0,25 cạnh AE góc 90 ) . 2 Tứ giác AHDE nội tiếp (1 điểm)
 EAD = EHD (hai góc nội tiếp cùng chắn cung ED) ( ) 1 0,25
Xét đường tròn (O) có: 0,25
EAD = CFD (hai góc nội tiếp cùng chắn cung CD) (2) 0,25
Từ (1) và (2) CFD = EHD . Mà hai góc ở vị trí đồng vị  CF / / EH . 0,25 3
Xét đường tròn (O) có: (1 điểm)
CF ⊥ AB , CF là dây cung ; AB là đường kính
 AB là trung trực của CF (quan hệ đường kính vuông góc với dây cung) 0,25
 BC = BF  B
 CF cân tại B . (3) ACB 90 =
(góc nội tiếp chắn nửa đường tròn)  A
 CB vuông tại C . 0,25 AC R 1 Xét A
 CB vuông tại C có : 0 cos CAB = = =  CAB = 60 . AB 2R 2 Lại có : 0
CAB = CFB = 60 (hai góc nội tiếp cùng chắn cung CB ) (4) Từ (3), (4)  B
 CF là tam giác đều.
Trên cạnh DF lấy điểm P sao cho DC = DP  D
 CP cân tại P . 0,25 (5) Lại có : 0
CDF = CBF = 60 ( hai góc nội tiếp cùng chắn cung CF ) 0 CDP = 60 (6)  D
 CP là tam giác đều  DC = CP . Do B
 CF là tam giác đều  CB = CF . Xét C  PF và C  DB có: CD = CP   PCF = DCB ( 0 = 0 6
− PCB)  C  PF = C
 DB( .cgc)  PF = D B  CF = CB 
Chu vi tứ giác ABDC bằng : 0,25
AB + BD + DC + CA = 3R + BD + DC = 3R + PF + DP = 3R + DF
Chu vi tứ giác ABDC lớn nhất khi DF lớn nhất  DF là đường
kính của đường tròn (O; R)  D là điểm chính giữa của cung nhỏ BC . Bài V. ĐK: 2  x  4. (0,5 điểm)
Ta có: x − x + = (x − )2 2 6 11 3 + 2  2 ( x − + − x )2 2 4
 2(x −3+ 5 − x) = 4
 x − 2 + 4− x  2 0.25 Dấu “=” xảy ra
 x − 2 + 4 − x = 2    x = 3(TM) 2
x − 6x +11 = 2 KL…. 0.25