SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9 THANH HÓA NĂM HỌC 2022 - 2023
HƯỚNG DẪN CHẤM ĐỀ THI CHÍNH THỨC Môn thi: TOÁN
(Hướng dẫn chấm gồm 06 trang) Câu Ý NỘI DUNG Điểm Cho biểu thức x − 2 x + 3 x −1 1 P = + − , với x ≥ 0 . x x +1 x − x +1 x +1
Rút gọn biểu thức P .
Với điều kiện x ≥ 0 , ta có x − 2 x + 3 x −1 1 P = ( + − 0,25
x + )1(x − x + )1 x − x +1 x +1 1
x − 2 x + 3+ ( x + )
1 ( x − )1−(x − x + )1 = (1,0đ)
( x + )1(x− x + )1 0,25 I
x − 2 x + 3+ x −1− x + x −1 = (
x + )1(x − x + )1 0,25 (2,0đ) x − x +1 1 = ( = .
x + )1(x − x + )1 x +1 0,25 Vậy 1 P = . x +1
Tìm x để 1 P = 2 2
Với x ≥ 0 , ta có: 1 P = 1 1 ⇔ = ⇔ x +1 = 2 0,50 (1,0đ) 2 x +1 2
⇔ x =1 ⇔ x =1(thỏa mãn). 0,50
Vậy x =1 là giá trị cần tìm. = − + − II d : y a 1 x b 2 1
Trong mặt phẳng tọa độ Oxy , cho đường thẳng ( )
( a,b là
tham số). Biết đường thẳng d song song với đường thẳng d ': y = 3x + 8 và đi
(2,0đ) (1,0đ) qua điểm A(2;3). Tính 2 2
T = a + 2b . 1
Đường thẳng d song song với đường thẳng d ': y = 3x + 8, nên ta có a −1 = 3 (1) 0,50
Đường thẳng d đi qua điểm A(2;3) , nên ta có 3 = (a − )
1 2 + b − 2 ⇔ 2a + b = 7 (2) a −1 = 3 a = 4
Từ (1) và (2) ta có hệ  ⇔ 2a b 7 b  + =  = 1 − 0,50 Khi dó ta có 2 2
T = a + 2b =16 + 2 =18. 2x − y = 4
Giải hệ phương trình  . 5  x + y = 3 2 2x − y = 4 7x = 7 Ta có  ⇔ 0,50 (1,0đ) 5  x y 3  + = 2x − y = 4 x = 1 x = 1 ⇔  ⇔
. Vậy hệ có nghiệm ( ; x y) = (1; 2 − ). 0,50 2 y 4  − = y = 2 −
Giải phương trình 2
x + 6x + 5 = 0. 1
Ta có : a =1;b = 6;c = 5 0,50
(1,0đ) Ta thấy a − b + c =1− 6 + 5 = 0
Suy ra phương trình có hai nghiệm phân biệt x = 1; − x = 5 − . 0,50 1 2 Cho phương trình 2
x − 2(m −1)x + 2m − 5 = 0 .Tìm các giá trị của m để phương trình có hai nghiệm x , x 1 2 thỏa mãn điều kiện:
( 2x −2mx +2m− )1( 2x −2mx +2m−1 < 0. 1 1 2 2 ) Xét phương trình 2
x − 2(m −1)x + 2m − 5 = 0 (1) III
Ta có = (m − m + )− m + = m − m + = (m − )2 2 2 Δ ' 2 1 2 5 4 6 2 + 2 > 0, m ∀ nên (2,0đ) 2
phương trình (1) luôn có hai nghiệm phân biệt x , x với mọi m . 0,25 1 2 (1,0đ)
x + x = 2(m −1) (2)
Áp dụng định lí Viét cho phương trình (1) ta có 1 2  x x = 2m −  5 (3) 1 2
Vì x là nghiệm phương trình (1) nên: 2
x − 2(m −1)x + 2m − 5 = 0 1 1 1 2
⇔ x − 2mx + 2m −1 = 2 − x + 4 0,25 1 1 1 Tương tự ta có 2
x − 2mx + 2m −1 = 2 − x + 4 2 2 2 Khi đó ( 2
x − 2mx + 2m − ) 1 ( 2
x − 2mx + 2m −1 < 0 1 1 2 2 ) 0,25 2 ⇔ ( 2 − x + 4)( 2
− x + 4) < 0 ⇔ 4 x x − 2(x + x ) + 4 < 0 1 2 [ 1 2 1 2 ]
⇔ x x − 2(x + x ) + 4 < 0 (4) 1 2 1 2
Thế (2) và (3) vào (4) ta được 3
2m − 5 − 2.2(m −1) + 4 < 0 ⇔ 2
− m + 3 < 0 ⇔ m > 2 0,25 Vậy 3 m > . 2
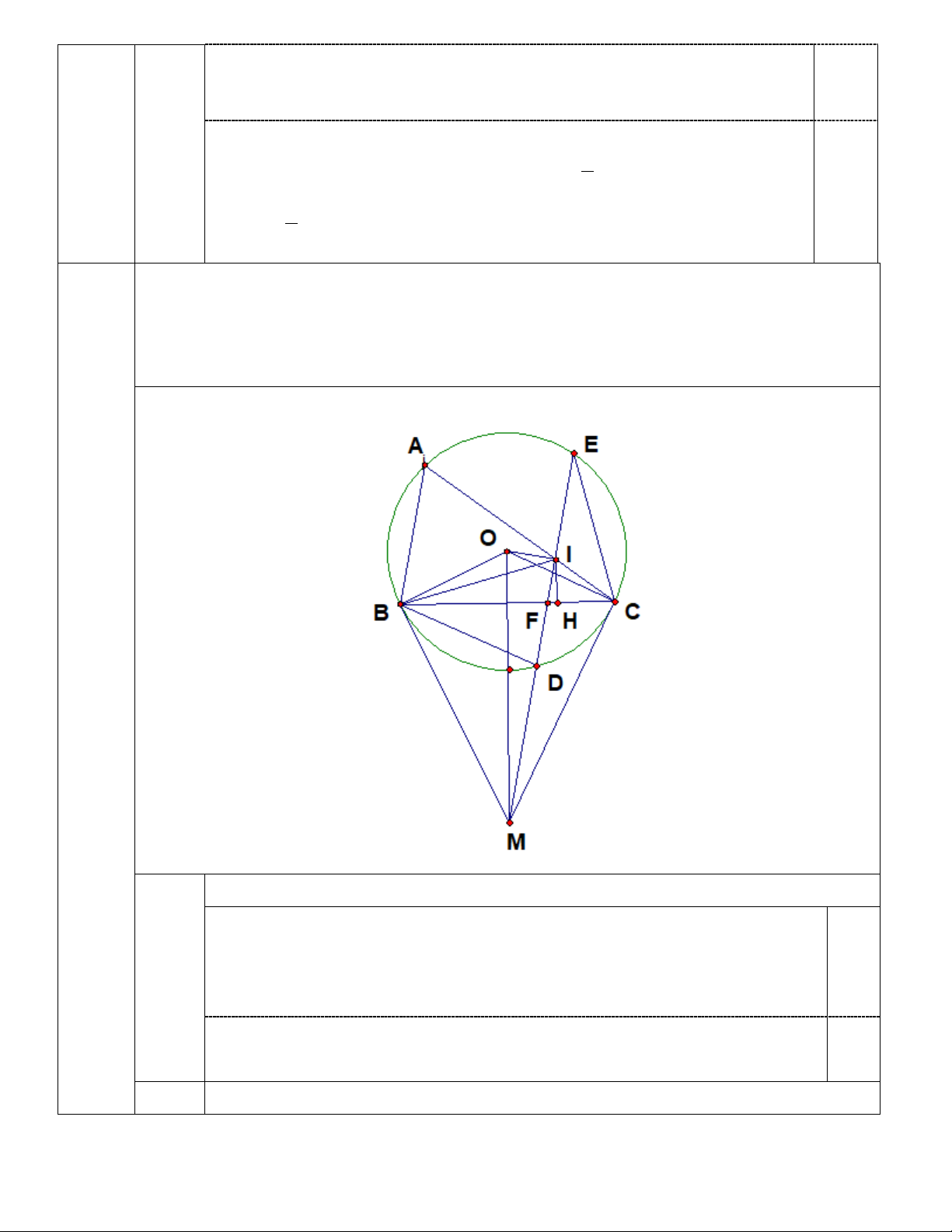
Cho tam giác ABC không có góc tù ( AB < AC ) và nội tiếp đường tròn (O) (
B,C cố định và A di động trên cung lớn BC ). Các tiếp tuyến tại B và C cắt nhau
tại M . Từ M kẻ đường thẳng song song với AB , đường thẳng này cắt (O) tại D và
E ( D thuộc cung nhỏ BC ), cắt BC tại F , cắt AC tại I . IV (3,0đ)
Chứng minh MBOC là tứ giác nội tiếp.
Xét tứ giác MBOC ,ta có: 1  0
MBO = 90 (vì MB là tiếp tuyến của đường tròn (O) tại B ) 0,50 (1,0đ)  0
MCO = 90 (vì MC là tiếp tuyến của đường tròn (O) tại C ) Suy ra  +  0 0 0
MBO MCO = 90 + 90 = 180 0,50
Vậy tứ giác MBOC là tứ giác nội tiếp. 2
Chứng minh FI.FM = F . D FE 3
(1,0đ) * Xét 2 tam giác: FBD và FEC , ta thấy:  = 
BFD CFE (đối đỉnh)  = 
DBF CEF (hai góc nội tiếp cùng chắn cung CD ) 0,25 Suy ra F
∆ BD đồng dạng với F ∆ EC (g-g) Suy ra FD FB = ⇔ F . D FE = F . B FC (1) FC FE
* Xét tứ giác MBIC , ta có :  = 
MBC BAC (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BC )  = 
BAC MIC (đồng vị) 0,25 Suy ra  =  MBC BIC
Ta thấy tứ giác MBIC có hai đỉnh B và I cùng nhìn cạnh MC dưới một
góc bằng nhau. Vậy tứ giác MBIC là tứ giác nội tiếp.
* Xét 2 tam giác: FBM và FIC , ta thấy  = 
BFM CFI (đối đỉnh)  = 
MBF FIC (hai góc nội tiếp cùng chắn cung MC ) 0,25 Suy ra F
∆ BM đồng dạng với F ∆ IC (g-g) Suy ra FB FM =
⇔ FI.FM = F . B FC (2) FI FC
Từ (1) và (2), ta suy ra FI.FM = F . D FE (đpcm) 0,25
Tìm vị trí của đỉnh A trên cung lớn BC sao cho tam giác IBC có diện tích lớn nhất.
Do tứ giác MBOC và tứ giác MBIC là hai tứ giác nội tiếp, suy ra 5 điểm
M , B,O, I,C cùng nằm trên một đường tròn 0,25 3
Gọi H là hình chiếu của I lên BC , ta có diện tích tam giác IBC là: (1,0đ) 1
S = BC.IH 2 0,25
Do BC không đổi nên diện tích tam giác IBC lớn nhất khi IH lớn nhất.
Ta thấy, khi A chạy trên cung lớn BC thì I luôn thuộc đường tròn đường 0,25
kính OM . Do đó IH lớn nhất khi I trùng với O hay AC là đường kính 4
của đường tròn tâm (O) .
Vậy khi A là điểm đối xứng với C qua O thì tam giác IBC có diện tích lớn nhất. 0,25
Cho a,b,c là các số thực dương. Chứng minh rằng 2 2 2
3a + bc 3b + ca 3c + ab + +
− 2 a + b + c ≥ 2 − . b + c c + a a + b 2 2 2 Đặt
3a + bc 3b + ca 3c + ab P = + +
− 2 a + b + c b + c c + a a + b 2 2 2 2 2 2 2a 2b 2c
a + bc b + ca c + ab = + + + + +
− 2 a + b + c
b + c c + a a + b b + c c + a a + b
Dễ chứng minh được với mọi số thực dương x, y, z ta có (  
x + y + z) 1 1 1 + + ≥ 
 9 . Dấu bằng xảy ra khi x = y = z  x y z  Ta có a b c  a 1  b 1  c 1 + + = + + + + + −       3
b + c c + a a + b  b + c   c + a   a + b  (a b c) 1 1 1  = + + + + −   3
 b + c c + a a + b  1  1 1 1  1 3 0,25 V
= ((b + c) + (a + c) + (a + b)) + + −   3 ≥ .9 − 3 = . 2
 b + c c + a a + b  2 2 (1,0đ) 2 2 2 Khi đó 2a 2b 2c + + (1,0đ)
b + c c + a a + b 2 2 2  2a   2b   2  =  + 2  +  + 2 c a b + 
+ 2c − 2(a + b + c)  b c   c a   a b  + + +       2  a 1 2  b 1 2  c a b c 1 = + + + + + − 2(a + b +       c)  b + c   c + a   a + b  2( ) a b c a b c  = + + + + − 2(a + b +   c)
 b + c c + a a + b 
≥ (a + b + c) 3 2
. − 2(a + b + c) = (a + b + c) 2 2 2 a + bc
a + bc + ab + ac (a + b)(a + c) Tacó + a = = b + c b + c b + c 2
a + bc (a + b)(a + c) ⇒ = − a b + c b + c 0,25 2
b + ca (b + c)(b + a) 2
c + ab (a + c)(c + b) Tương tự ta có: = − b ; = − c c + a c + a a + b a + b 5 2 2 2
Khi đó a + bc b + ca c + ab + + b + c c + a a + b
(a +b)(a + c) (b + c)(b + a) (c + a)(c +b) = + +
− (a + b + c) . b + c c + a a + b
ÁP dụng bất đẳng thức AM-GM
(a +b)(a + c) (b + c)(b + a) + ≥ 2(a + b) b + c c + a
(b + c)(b + a) (c + a)(c +b) + ≥ 2(b + c) c + a a + b
(c + a)(c +b) (a +b)(a + c) 0,25 + ≥ 2(c + a) a + b b + c
 (a + b)(a + c) (b + c)(b + a) (c + a)(c + b)  ⇒ 2 + +
 ≥ 4(a + b + c) b + c c + a a +  b 
(a +b)(a + c) (b + c)(b + a) (c + a)(c +b) ⇔ + +
≥ 2(a + b + c) b + c c + a a + b 2
⇒ P ≥ (a + b + c)  1  1 1 2
− 2 a + b + c = 2 a + b + c − − ≥ − >  2 −  .  2  2 2
Vậy, với a,b,c là các số thực dương thì 0,25 2 2 2
3a + bc 3b + ca 3c + ab + +
− 2 a + b + c ≥ 2 − (đpcm) b + c c + a a + b
------------------------ HẾT ------------------------
Đáp án đã điều chỉnh (câu V thay 4 a + b + c bằng 2 a + b + c ) 6
Document Outline

• de-khao-sat-chat-luong-toan-9-nam-2022-2023-so-gddt-thanh-hoa
• Đ.a. KSCL LỚP 9-bản đã đính chính câu V ( 26-4)