Đề khảo sát đội tuyển HSG Toán 9 năm 2019 – 2020 phòng GD&ĐT Sầm Sơn – Thanh Hoá

UBND THÀNH PHỐ SẦM SƠN
ĐỀ KHẢO SÁT CHỌN ĐỘI TUYỂN HSG
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
CẤP TỈNH NĂM HỌC 2019-2020 MÔN: TOÁN ĐỀ CHÍNH THỨC Ngày khảo sát: 06/01/2020
Thời gian làm bài: 150 phút Câu 1: (4điểm)  ( 2 a + b) a   3 3  a + 2 b 2
a) Cho biểu thức P =  −   . − a  a3 − 2 b 2 3
a + 2ab + b 2   b 2 + 2ab 
Tìm điều kiện của a và b để biểu thức P xác định và rút gọn P. 3 1 3 b) Biết: a= 1+ và b= −
. Tính giá trị của biểu thức P. 2 2 4 Câu 2: (4điểm)
(𝑥 − 1)√14 − 𝑦 + √(𝑦 − 2)(11 + 2𝑥 − 𝑥2) = 12
a) Giải hệ phương trình: {
𝑥3 − 3𝑥2 − 5𝑥 + 6 = 2√𝑦 − 4 b) x
là 2 nghiệm của phương trình: 2x2 1,x2
- (3a -1)x -2 = 0 ,Tìm giả trị nhỏ nhất của 2 3  −  2 x x 1 1
biểu thức: P= ( x − x ) 1 2 + 2 + −  1 2 2 2 x x  1 2  Câu 3: (4điểm)
a)Tìm các số nguyên dương x, y ,z với z 6 thỏa mãn phương trình sau:
x2 + y2 - 4x - 2y - 7z - 2 = 0
b) Cho số nguyên dương n thỏa mãn 2 + 2 12 2
n + 1 là số nguyên. Chứng minh 2 + 2 12 2
n + 1 là số chính phương. Câu 4: (6điểm)
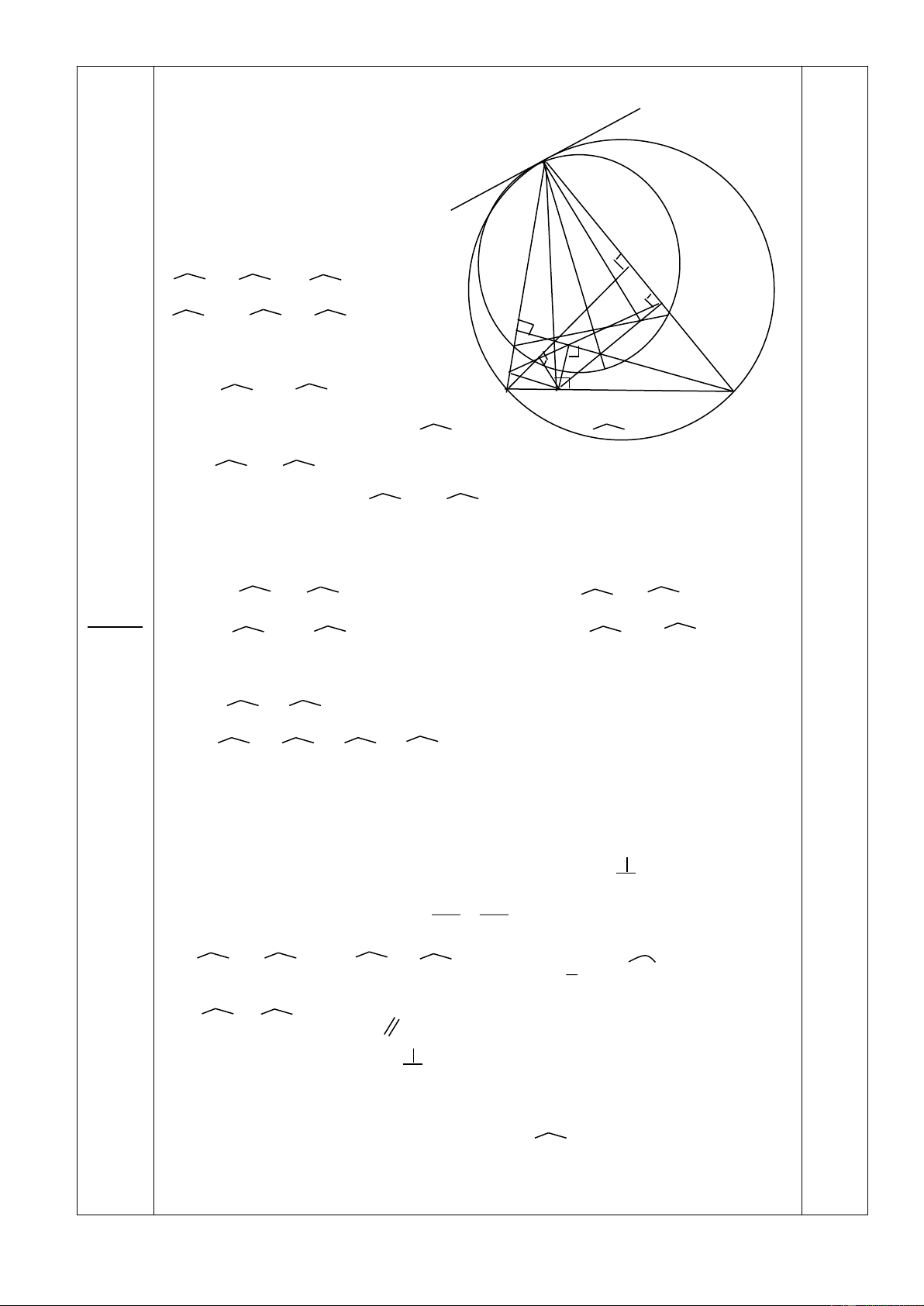
Cho đường tròn (O, R), và dây cung BC cố định (BC < 2R). Điểm A di động trên
(O;R) sao cho tam giác ABC là tam giác nhọn, AD là đường cao và H là trực tâm của tam giác ABC.
a) Đường thẳng chứa tia phân giác ngoài của góc BHC cắt AB, AC lần lượt tại các
điểm M,N. Chứng minh ∆AMN là tam giác cân
b) Gọi E, F lần lượt là hình chiếu của D trên các đường thẳng BH, CH. Chứng minh: OA EF.
c) Đường tròn ngoại tiếp ∆ AMN cắt đường phân giác trong của góc BAC tại K.
Chứng minh đường thẳng HK luôn đi qua điểm cố định. Câu5( 2 điểm)
Cho 3 số thực dương a, b, c thỏa mãn: abc = 1. Chứng minh bất đẳng thức : 1 1 1 + +  1. 5 2 5 2 5 2
a + b + ab + 6
b + c + bc + 6
c + a + ca + 6
Họ và tên: …………………………………...…………………… SBD: ………….. HƯỚNG DẪN CHẤM MÔN: TOÁN CÂU NỘI DUNG TRÌNH BÀY ĐIỂM
a- (2 điểm):  ( 2 a + b) a   3 3  a + 2 2 P = b  −   . − a  a3 − 2 b 2 3
a + 2ab + b 2   b 2 + 2ab  a3  0   b 2 3  0 a  0
Điều kiện để biểu thức P xác định là:  3 3   a − 2 b 2  0 = b  0   0,5
a + 2ab + b 2  0 a   b 2   b 2 + 2ab  0 Câu1:  (
2 a + b) − a ( a − b 2 )  (a + b 2 )(a − ab 2 + b 2 )  4điểm P =  . − a 0,5 ( a − b 2 )(a + ab 2 + b 2 )    b 2 ( b 2 + a )   + 2 + 2 − 2 + 2 − 2 P = ( a ab b . a − b
2 )(a + 2ab + b 2 ) a ab b ab b 2 0,5 2 1 ( a − b2) a − b 2 P = . = 0,5 a − b 2 b 2 b 2
b- (2 điểm): 1  3   3  1 1 Ta có: ab = 1+ 1− = = b 2 =     1,0 2 2 2 8 a 4     Do đó: P = a − b 2 a 1,0 = −1= 4 2
a − 1 = 2a − 1 = 1 + 3 b 2 2b 2
(x −1) 14− y + (y −2)(11+ 2x − x ) =12
2b) (2,0 điểm) Giải hệ:  0,5 3 2
x − 3x − 5x + 6 = 2 y − 4  2
(x −1) +14 − y
(x −1) 14 − y  (1) Theo Cô si ta có 2 0,5 2
y − 2 +11+ 2x − x 2
( y − 2)(11+ 2x − x )  (2) 2
Câu 2 Từ (1) và (2) ta có :( 2
(x −1) 14 − y + ( y − 2)(11+ 2x − x  12 0,5 4điểm  x −1  0 Dấu bằng xảy ra khi  2 
y − 2 = 11+ 2x − x
Thay vào phương trình thứ 2 của hệ ta được: 3 2 2
x − 3x − 5x + 4 + 2(1− 9 + 2x − x ) = 0 2(x + 2) 0,5 2
 (x − 4)(x + x −1+ ) = 0 2 1+ 9 + 2x − x Do 2(x + 2) 2
x  1  (x + x −1+ )  o 2 1+ 9 + 2x − x
Buộc x=4 từ đó tìm được y=5 (T/M) Vậy (x;y)=(4;5) 0,5 b- (2 điểm): 2x2 - (3a-1)x - 2 = 0 (1) 0,5
phương trình (1) có: ∆ = − (3a − )
1 2 +16  0 . phương trình (1) luôn có 2 nghiệm phân biệt x 0,5
1, x2 . Theo định lí Viets ta có: 2 3 P = (
 x x x − x − x − x  x − x + = x − x 1 2 )2 1 2 ( 1 2 ) ( 2 1 2 ) 2  ( 6 1 2 )2 2 2  x x 1 2  2  a −  = 6 (x + x − x x =  +   1 2 )2 4 1 2  (3 )1 6 4 24 4  
Đẳng thức xảy ra khi và chỉ khi: 3a 1 - 1 = 0 => a = 3 Vậy Mi 1 n P = 24 <=> a = 3
a- (2 điểm):
Biến đổi phương trình thành: (x-2)2 + (y-1)2 = 7(z+1) (*)
Nhận thấy một số chính phương chia cho 7 có số dư là 0; 1; 2; 4 nên 0,5
tổng 2 số chính phương chia hết cho 7 thì cả 2 số chính phương đó chia hết cho 7 0,5
Từ (*) suy ra: (x-2)  7 và (y-1)  7 Do đó (z + 1)  7 mà 1 z  6 nên
z = 6. Ta có: : (x-2)2 + (y-1)2 = 49; 49 = 02 + 72
Từ đó tìm được : (x; y) = (2; 8) , (9;1) 0,5
Vậy phương trình có nghiệm nguyên dương là: (x;y;z)  (  6; 8 ; 2 ),( 6; 1 ; 9 ) 0,5
b- (2 điểm):
Câu 3 Hiển nhiên 2 + 2 là số nguyên mà
là số lẻ nên tồn tại 4điểm 12 2 n + 1 12 2 n +1
số tự nhiên k mà 12 2 n +1 = (2k +1)2  12 2
n +1 = 4k2 + 4k + 1  k(k+1) = 3n2 . Vì (k; k+1)= 1 nên xảy ra hai trường hợp 0,5 Trường hợp 1: 0,5 2 k  = a  ( , a b  N) 2 = a − 3 2 b = 1 −  ( 2 mod ) 3 2 = a  ( 2 mod )( 3 vôl ) í k  +1= 3 2 b 0,5 Trường hợp 2: 2 k = 3a 2 2 2 2 4 2   b (b − )
1 = 3n  2 + 2 12n + 1 = 2 + 2 4b − 4b + 1 2 k +1 = b 2 2 = 0,5 2 + ( 2 2b − ) 1 = 4b Nên 2 + 2 12 2
n + 1 là số chính phương y A y a- 2 điểm: x
Gọi B/ là hình chiếu của B trên AC
C/ là hình chiếu của C trên AB B/ 0,5 P Q AMN= ABH + MHB; O N (1) C// H ANM = ACH + NHC 0,5 M F E Tứ giác BCB
/C/ là tứ giác nội tiếp P K 0,5 B C nên : ABH = ACH (2) D
MN là phân giác ngoài góc BHC 0,5 nên MHB = NHC (3)
Từ (1); (2); (3) suy ra AMN = ANM Hay tam giác AMN cân b- 2 điểm:
Gọi P; Q lần lượt là hình chiếu của D trên AB, AC.
Ta có BEP = BDP ( Tứ giác BPED nội tiếp), BDP = BAD ( cùng phụ 0,5 Câu 4 6điểm
ABD), BAD = HDF ( do ∆AC/H ~ ∆DFH), HDF = HEF ( Tứ giác HEDF nội tiếp) Suy ra BEP = HEF
Ta có BEP + BEF = BEF + FEH = 1800 => P, E, F thẳng hàng 0,5
Tương tự Q, F, E thẳng hàng
vậy đường thẳng EF trùng với đường thẳng PQ (4) 0,5
Kẻ tiếp tuyến xAy của đường tròn (O), ta có OA xAy (5) AP AQ AP. AB = AD2 = AQ . AC => = = A  PQ ~ ∆ACB AC AB
=> APQ = ACB mà ACB = xAB ( cùng bằng 1 sđ AB ) 0,5 2
=> APQ = xAB => xAy PQ (6)
Từ (4) , (5), (6) suy ra OA EF c- 2 điểm: 0,5
Gọi T là giao điểm của KM và BH , S là giao điểm của KN và CH.
Do AM = AN và AK là phân giác của MAN nên AK là đường kính
đường tròn ngoại tiếp tam giác AMN
Suy ra HTKS là hình bình hành => HK đi qua trung điểm của TS (7) 0,5 TH MC/ MC/ HC / Ta có = ( vì KM CC/ ) , = (Vì HM là phân giác TB MB MB HB 0,5 TH HC / góc BHC/ ) suy ra = TB HB / 0,5 Tương tự SH HB =
. Tứ giác BC/B/C nội tiếp) SC HC TH SH => C/BH = B/CH => = => TS BC (8) TB SC
Từ (7), (8) suy ra HK đi qua trung điểm của BC.
Câu 5: (2,0 điểm) Cho 3 số thực dương a, b, c thỏa mãn: abc = 1.
Chứng minh bất đẳng thức : 0,5 1 1 1 + +  1. 5 2 5 2 5 2
a + b + ab + 6
b + c + bc + 6
c + a + ca + 6
Ta có: a5 = a(a4 + 1 + 1 + 1) - 3a  a.4a - 3a = 4a2 - 3a dấu bằng  a = 1
(Vì (a4+1+1+1)  4a bất đẳng thức cô si dấu bằng  a=1) 0,5  5 2 2 2
a  4a − 3a = 3a − 3a + a  3(2a-1) - 3a + a2 = a2 + 3a - 3 0,5
(do: a2  2a - 1 dấu bằng  a=1)
 a5 + b2 + ab + 6  a2 + 3a - 3 + b2 + ab + 6 = a2 + b2 + 3a + 3 + ab 
3(ab + a + 1)  ( ab + a + 1)2.
(do a2 + b2  2ab và do BĐT BunhiaCopSky; dấu bằng  a = b = 1). 0,5  5 2 1 1
a + b + ab +  ab + a +1   5 2 + + + + + Câu 5 a b ab 6 ab a 1
2điểm Chứng minh tương tự ta có: 1 1  a = 5 2
b + c + bc + 6
bc + b +1 1+ ab + a
(do abc =1; dấu bằng khi b = c = 1). 1 1 ab Và ta có:  = 5 2
c + a + ca + 6 ca + c +1 a +1+ do abc = 1; ab dấu bằng khi c = a = 1.
 P 1, dấu đẳng thức xẩy ra  a = b = c = 1.