Đề khảo sát HSG Toán 9 lần 5 năm 2023 – 2024 trường Hồng Phương – Vĩnh Phúc

PHÒNG GD&ĐT YÊN LẠC
ĐỀ THI KS HSG LỚP 9 NĂM HỌC 2023 – 2024
TRƯỜNG TH&THCS HỒNG PHƯƠNG
LẦN 5 – MÔN TOÁN 9
Thời gian: 150 phút, không kể thời gian giao đề.
Câu 1. (2,5 điểm) Cho x = 4 + 10 + 2 5 + 4 − 10 + 2 5 . 4 3 2
x − 4x + x + 6x +12
Tính giá trị của biểu thức: P = 2 x − 2x +12
Câu 2. (2,5 điểm) Tìm số tự nhiên x , biết  1 1 1 1 1 1   1+ + + 1+ + ++ 1+ + . 1+ 2 ++ x =1612  . 2 2 2 2 2 2 ( ) 2 3 3 4 14 15   
Câu 3. (2,0 điểm) Giải phương trình x + 3 + 3x +1 = x + 3.
Câu 4. (2,0 điểm) Tìm tất cả các nghiệm nguyên của phương trình: 2 2 2
x + 5y + 6z + 2xy − 4xz =10
Câu 5. (2,0 điểm) Với các số thực a,b,c thỏa mãn 0 ≤ a,b,c ≤1 và a + b + c = 2 , tìm giá trị lớn nhất và
giá trị nhỏ nhất của biểu thức ab bc ca P = + + .
1+ ab 1+ bc 1+ ca
Câu 6. (2,0 điểm) Cho tam giác nhọn ABC đường cao CK; H là trực tâm của tam giác. Gọi M là một điểm trên CK sao cho  0
AMB = 90 . Gọi S;S ;S theo thứ tự là diện tích các tam giác AM ; B ABC; ABH . 1 2
a) Chứng minh : HK.CK = AK.BK
b) Chứng minh: S = S .S 1 2
Câu 7. (5,0 điểm) Cho tam giác ABC vuông tại A , AH vuông góc với BC , AD là đường phân giác.
Gọi HM , HN là đường phân giác của tam giác HAB , HAC .
a. Chứng minh DM //AC và AD = MB .
b. Gọi AP, AQ là đường phân giác của tam giác AHB , AHC . Chứng minh rằng: 2 PQ = 2P . B CQ .
Câu 8. (1,0 điểm) Cho tam giác đều ABC , đường cao AH . Lấy điểm M nằm giữa B và C , vẽ MD
vuông góc với AB tại D , ME vuông góc với AC tại E . Tìm vị trí của điểm M trên BC để diện tích
MDE lớn nhất.
Câu 9. (1,0 điểm) Bảy người câu được 100 con cá. Biết rằng không có hai người nào câu được số cá như
nhau. Chứng minh rằng có ba người câu được tổng cộng không ít hơn 50 con cá. ==== HẾT ====
Cán bộ coi thi không giải thích gì thêm!
Họ tên thí sinh.........................................................SBD:.......................Phòng thi................
PHÒNG GD&ĐT YÊN LẠC
ĐỀ THI KS HSG LỚP 9 NĂM HỌC 2023 – 2024
TRƯỜNG TH&THCS HỒNG PHƯƠNG
LẦN 5 – MÔN TOÁN 9
Thời gian: 150 phút, không kể thời gian giao đề. Hướng dẫn chung:
- Học sinh giải theo cách khác mà đúng, đảm bảo tính lôgic, khoa học thì giám khảo vẫn cho điểm tối đa.
- Các câu hình học, học sinh không vẽ hình hoặc vẽ hình sai phần nào không chấm điểm phần đó. Câu Nội dung Điểm
Câu 1. (2,5 điểm) Cho x = 4 + 10 + 2 5 + 4 − 10 + 2 5 . 4 3 2
x − 4x + x + 6x +12
Tính giá trị của biểu thức: P = 2 x − 2x +12 Ta có:
x = 4 + 10 + 2 5 + 4 − 10 + 2 5 với x > 0 1,0 2 2
⇒ x = 8 + 2 16 − (10 + 2 5 = 8 + 2 6 − 2 5 = 8 + 2 ( 5 −1) = 8 + 2( 5 −1) = 6 + 2 5
2,5 đ Vì x > 0 nên x = 5 +1 Ta có: 2 2
x = 5 +1⇒ x −1 = 5 ⇒ (x −1) = 5 ⇒ x − 2x = 4 0,5 Mặt khác ta lại có: 4 3 2 2 2 2 2
x − 4x + x + 6x +12 (x − 2x) − 3(x − 2x) +12 4 − 3.4 +12 1,0 P = = = =1 2 2 x − 2x +12 x − 2x +12 4 +12
Câu 2. (2,5 điểm) Tìm số tự nhiên x, biết  1 1 1 1 1 1   1+ + + 1+ + ++ 1+ + . 1+ 2 ++ x =1612  . 2 2 2 2 2 2 ( ) 2 3 3 4 14 15    2 1 1 n (n + )2 1 + (n + )2 2 4 2 3 2 1 + n Ta thấy
n + n +1+ 2n + 2n + 2 1 n + + = = 2 n (n + )2 2 1 n (n + )2 2 1 n (n + )2 1 1,0 (n +n+ )2 2 2 1 1 1 n + n +1 1 1 = ⇒ 1+ + = = 1+ − 2 n (n + )2 2 1 n (n + )2 1 n(n + ) 1 n n +1
2,5 đ Áp dụng với n = 2,3,4...,14ta có: 1 1 1 1 1 1 1 1 0,75 1+ + + 1+ + + 1+ + + ...+ 1+ + 2 2 2 2 2 2 2 2 2 3 3 4 4 5 14 15 1 1 1 1 1 1 1 1 1 1 13
= 1+ − +1+ − +1+ − +...+1+ − = 13+ − = 13 2 3 3 4 4 5 14 15 2 15 30 13 x(x + ) 1 403x(x + ) 1
Khi đó phương trình đã cho ⇔ 13 . = 1612 ⇔ = 1612 30 2 60 0,75 ⇔ x(x + ) 2
1 = 240 ⇔ x + 2 − 240 = 0 ⇔ (x −15)(x +16) = 0
⇔ x −15 = 0 (do x +16 ≥16 > 0) ⇔ x =15 Vậy x =15.
Câu 3. (2,0 điểm) Giải phương trình x + 3 + 3x +1 = x + 3. Điều kiện xác định 1 x ≥ − . 0,25 3 Ta có:
x + 3 + 3x +1 = x + 3
⇔ 4 x + 3 + 4 3x +1 = 4x +12 0,75
⇔ (x + 3) − 4 x + 3 + 4 + 3x +1− 4 3x +1 + 4 = 0 2,0 đ 2 2
⇔ ( x + 3 − 2) + ( 3x +1 − 2) = 0 Vì 2 2
( x + 3 − 2) ≥ 0;( 3x +1 − 2) ≥ 0 0,75   x + 3 = 2 x + 3 = 4 Nên ta có:  ⇔  ⇔ x =1.  3x +1 = 2 3  x +1 = 4
Kết hợp với điều kiện xác định: phương trình có nghiệm là x =1 0,25
Câu 4. (2,0 điểm) Tìm nghiệm nguyên của phương trình: 2 2 2
x + 5y + 6z + 2xy − 4xz =10
Biến đổi phương trình ta có: 2 2 2
x + 5y + 6z + 2xy − 4xz =10 2 2 2 2 2
⇔ x + 2x(y − 2z) + (y − 2z)  − (y − 2z) + 5y + 6z =10   0,5 2 2 2
⇔ (x + y − 2z) + 4y + 4yz + 2z =10 2 2 2
⇔ (x + y − 2z) + (2y + z) + z =10
Do x, y, z là các số nguyên và 2y + z + z = 2(y + z) là số chẵn nên
(2y + z)2 và z2 là hai số chính phương cùng tính chẵn lẻ.
Nên viết: 10 = 02 + 32 + 12 0,5
Ta xét các trường hợp sau: 2,0 đ 2
(x + y − 2z) = 0  2 2
1) (2y + z) = 3 0,5  2 z =1 
Ta tìm được các nghiệm (x, y, z) là:
(1; 1; 1); (4; -2; 1); (-4; 2; -1); (-1; -1; -1) 2 (x + y − 2z) = 0  2 2) 0,5 (2y + z) = 1  2 z = 9 
Từ đó tìm được các nghiệm (x, y, z) là:
(7; -1; 3); (8; -2; 3); (-8; 2; -3); (-7; 1; -3)
Vậy phương trình có tất cả 8 nghiệm nguyên.
Câu 5. (2,0 điểm) Với các số thực a,b,c thỏa mãn 0 ≤ a,b,c ≤1 và a + b + c = 2 , tìm giá trị lớn nhất và giá
trị nhỏ nhất của biểu thức ab bc ca P = + + .
1+ ab 1+ bc 1+ ca
*Tìm giá trị lớn nhất. Ta có: 0,25 3− = 1 ab − + 1 bc − + 1 ac P ( ) ( ) ( − ) 1+ ab 1+ bc 1+ ac 1 1 1 9 9 27 = + + ≥ ≥ = 0,5 2
ab +1 bc +1 ca +1 ab + bc + ca + 3 ( a + b + c ) 13 + 3 3 Suy ra: 12 P ≤ . 13 0,25
Vậy giá trị lớn nhất của P là 12 khi 2
a = b = c = . 13 3
2,0 đ *Tìm giá trị nhỏ nhất. Không mất tính tổng quát, giả sử 1≥ a ≥ b ≥ c ≥ 0 .
Vì 0 ≤ a,b,c ≤1 nên (a − ) 1 (b − )
1 ≥ 0 suy ra ab +1≥ a + b , dẫn đến a + b ≤1. 0,25 ab +1
Chứng minh tương tự: a + b b + c c + a + + ≤ 3.
ab +1 bc +1 ca +1 0,25 Từ đó, 2 (3− )
a + b + c a + b + c a + b + c . P = + + ab +1 bc +1 ca +1 0,25 1 1 1  c a b  ≤ + + + + +
≤ 3 a + b + c +
≤ 3+ a + b + c =   5.
 ab +1 bc +1 ca +1 bc +1 Nên ta có 5 1
3− P ≤ ⇒ P ≥ . 2 2 0,25
Vậy giá trị nhỏ nhất của P là 1 khi a = b =1,c = 0 . 2
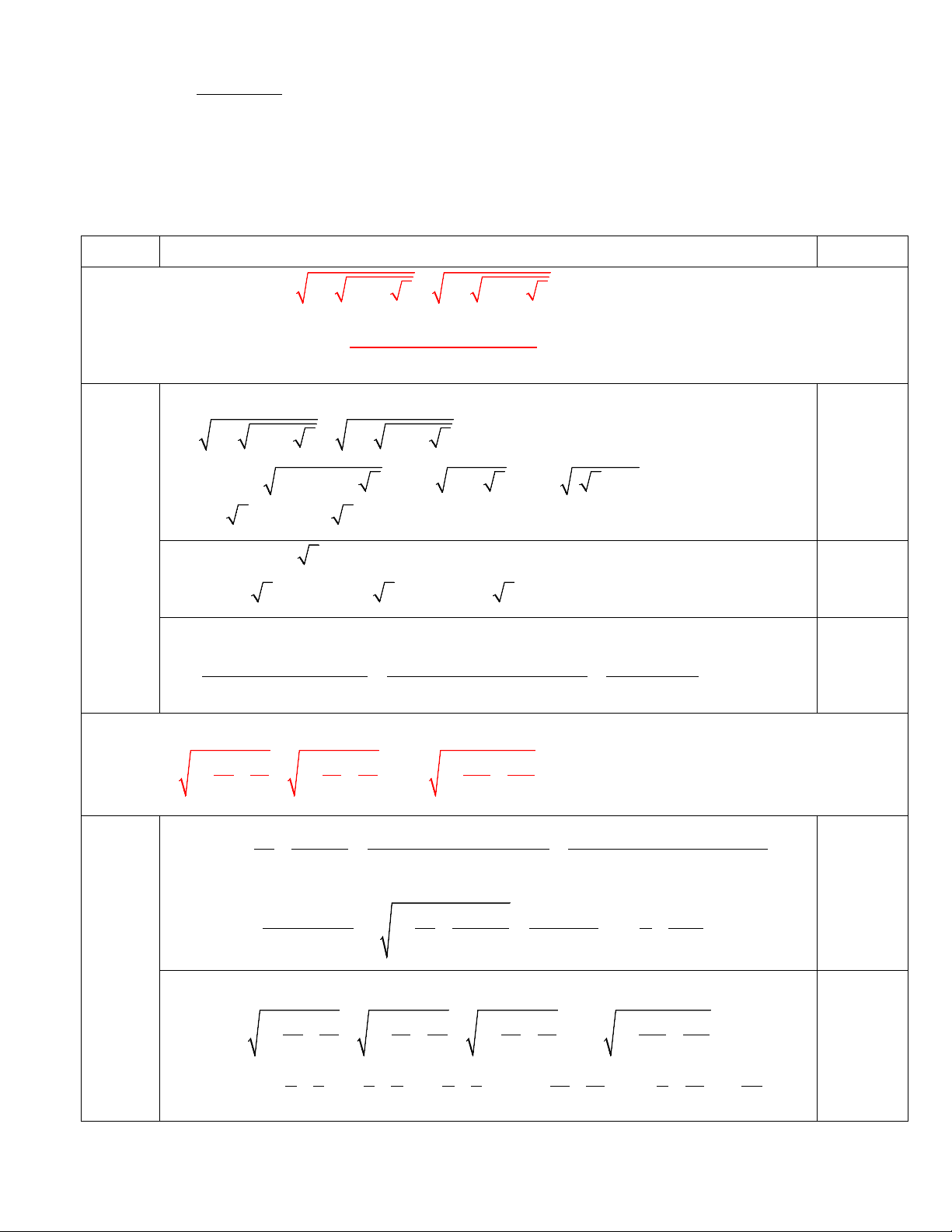
Câu 6. (2,0 điểm) Cho tam giác nhọn ABC đường cao CK; H là trực tâm của tam giác. Gọi M là một điểm trên CK sao cho  0
AMB = 90 . Gọi S;S ;S theo thứ tự là diện tích các tam giác AM ; B ABC; ABH . 1 2
a) Chứng minh : HK.CK = AK.BK
b) Chứng minh: S = S .S 1 2
a) Xét HKB và AKC co:  = 
KBH KCA (cùng phụ với  BAC) 0,5   BKH CKA( 90° = = ) 0,25
⇒HKB AKC(g ⋅ g) HK BK ⇒ =
⇒ HK ⋅CK = AK ⋅ BK (1) 0,25 AK CK b) 2,0 đ 2
AB ⋅(KH ⋅CK) ⇒ S ⋅ S = 0,25 1 2 4
AB ⋅ KH.CK ⇒ S S = ⋅ 0,25 1 2 2 Lại có: A
 MB vuông ở M có đường cao MK 0,25 2
 AK  BK  MK (Hệ thức lượng trong tam giác vuông) (2) Từ (1) và 2
(2)  CH.CK  MK . 0,25
Suy ra KH.CK  MK (3) Thay (3) vào (*) ta dưọc: AB  MK S S   S  S. 1 2 2 ANM 
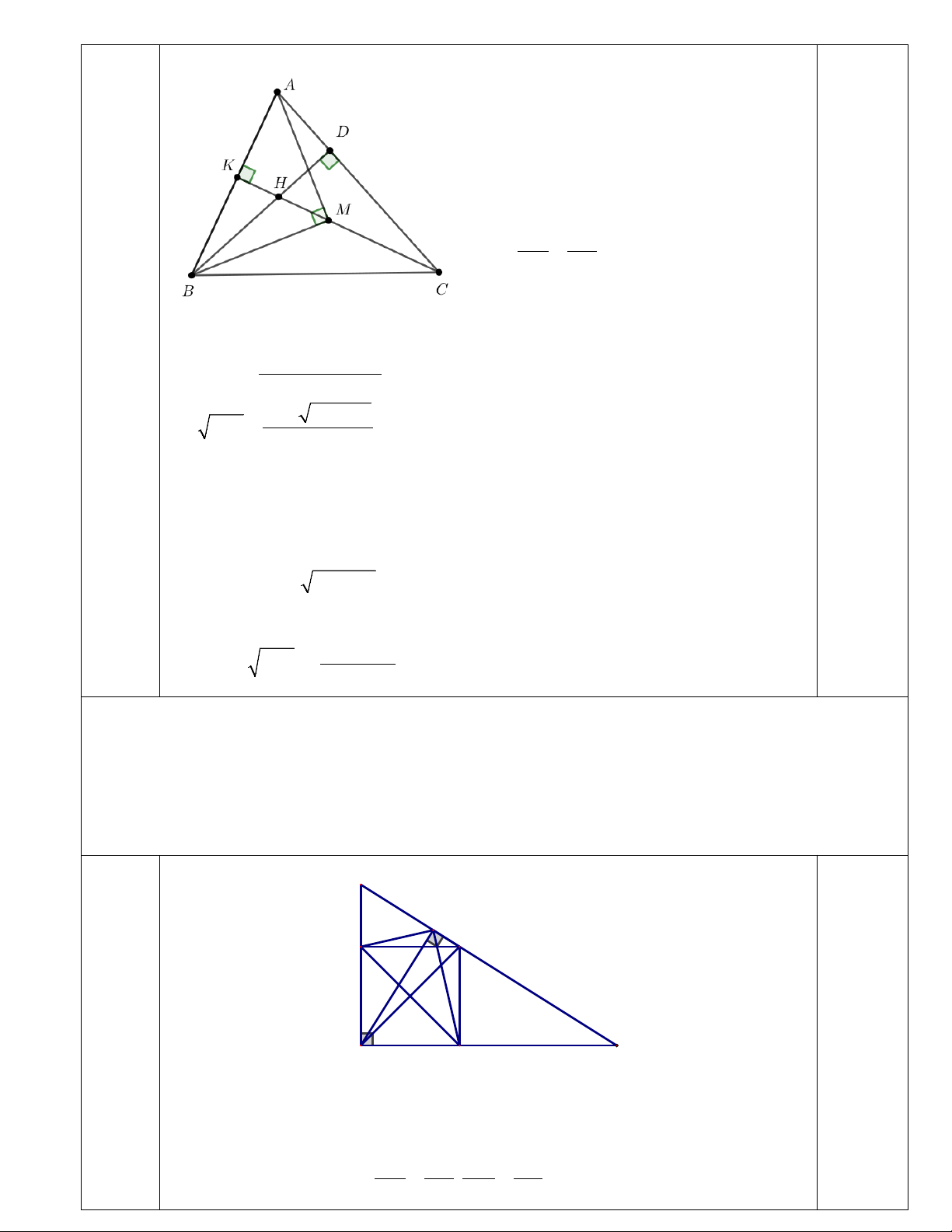
Câu 7. (5,0 điểm) Cho tam giác ABC vuông tại A , AH vuông góc với BC , AD là đường phân giác. Gọi
HM , HN là đường phân giác của tam giác HAB , HAC .
a. Chứng minh DM //AC và AD = MB .
b. Gọi AP, AQ là đường phân giác của tam giác AHB , AHC . Chứng minh rằng: 2 PQ = 2P . B CQ . B H M D 5,0 đ A N C
a) Chứng minh MD  AC
Áp dụng tính chất tia phân giác AD, HM tương ứng của tam giác A ∆ BC, A ∆ HB ta có DB AB = , MB HB = (1) DC AC MC HA Xét A ∆ BC và H ∆ BAcó 1,5  =  BAC BHA( 0 =  90 )    =  ABH ABC Suy ra ∆ ∽∆ ( . ) DB MB ABC HBA g g ⇒ = (2) DC MC
Từ (1) và (2) suy ra DB MB =
. Theo định lí Ta-lét đảo ta có MD  AC . DC MC
*Chứng minh AD = MN
Chứng minh hoàn toàn tương tự ta có DN  AB MD  AC Tứ giác AMDN có 
nên AMDN là hình bình hành. 1,5 DN  AB
Lại có AD là phân giác 
MAN nên AMDN là hình thoi. Hơn nữa,  0 MAN = 90 khi đó
AMDN là hình vuông. Vậy AD = MN b) Chứng minh 2 PQ = 2P . B CQ B P H M D 2,0 Q A N C Ta có  =  + 
CAP PAH HAC và  =  + 
CPA PAB PBA(góc ngoài) Mà  =   = 
PAH PAB, HAC PBA do đó  =  CAP CPA ⇒ C
∆ AP cân ở C ⇒ CA = CP .
Tương tự BA = BQ .
Khi đó PQ = AB + AC − BC; BP = BC − AC;CQ = BC − AB Suy ra 2B .
P CQ = 2(BC − AC)(BC − AB) 2
= 2BC − 2BC ( AB + AC) + 2A . B AC 2 2 2
= BC + AB + AC − 2BC ( AB + AC) + 2A . B AC 2
= BC − 2BC ( AB + AC) + ( AB + AC)2
= ( AB + AC − BC)2 2 = PQ . Vậy 2 PQ = 2P . B CQ .
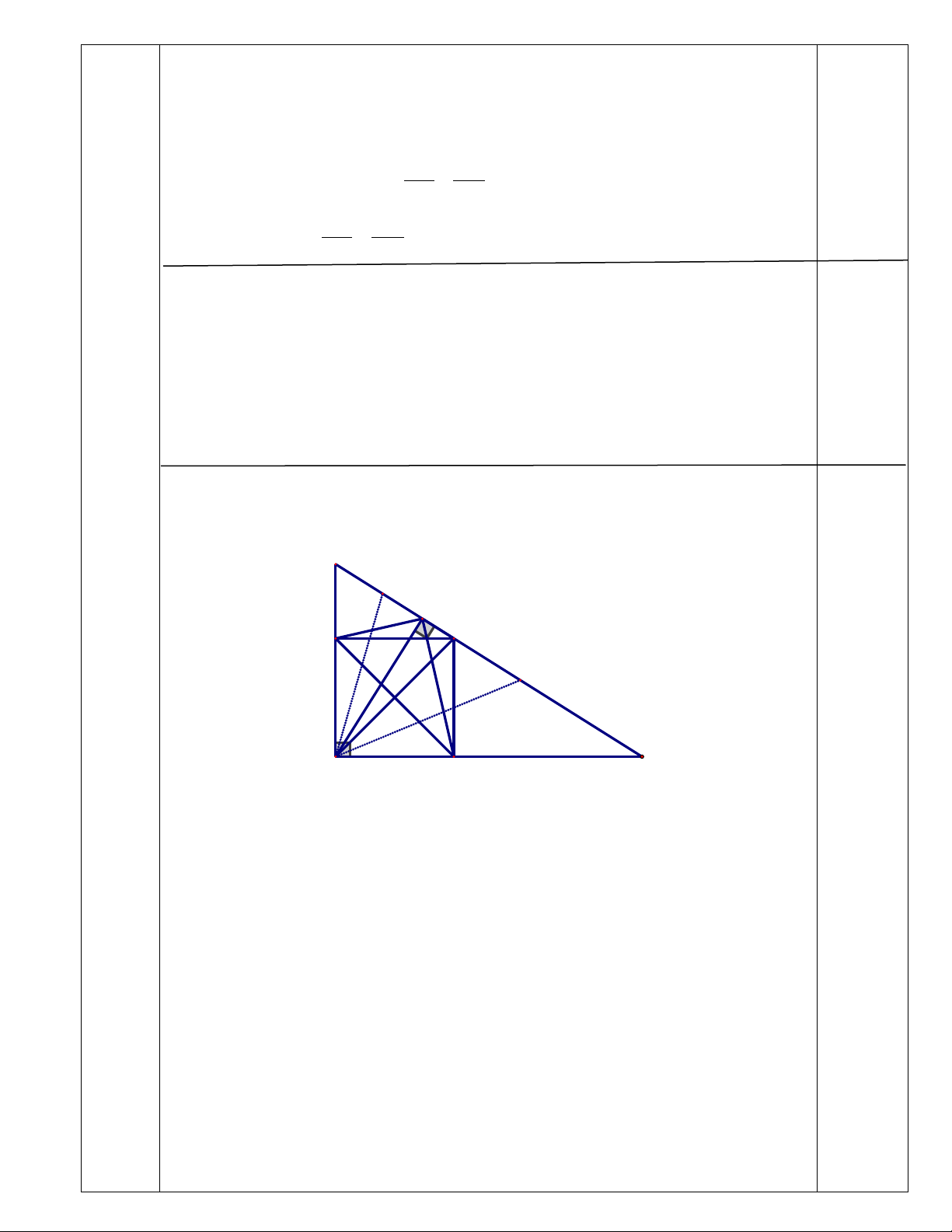
Câu 8. (1,0 điểm) Cho tam giác đều ABC , đường cao AH . Lấy điểm M nằm giữa B và C, vẽ MD vuông
góc với AB tại D, ME vuông góc với AC tại E.
Tìm vị trí của điểm M trên BC để diện tích MDE lớn nhất. A E D B H C M K 0,25
Đặt AB = AC = BC = a, AH = h . Nhận xét a,h là các đại lượng không đổi. Ta có . MD AB ME.AC a S = S + S = + = (MD + ME) 2SABC ⇒ MD + ME = (1) ABC ABM ACM 2 2 2 a 0,25 Hơn nữa AH.BC ah 2SABC S = = ⇒ h = (2) ABC 2 2 a
1,0 đ Từ (1) và (2) suy ra MD+ME = h
Hạ EK ⊥ DM , ta có 1 S = DM EK MDE . 2 0,25 Mà = 
EK ME.sin EMK và  =  +  =  +  0 = −  0 + −  0
EMK CMK CME DMB CME (90 B) (90 C) = 60 Do đó 1 0 3 S = DM ME = DM ME MDE . .sin 60 . . 2 4 ( a + b)2 (DM + ME)2 2
Áp dụng bất đẳng thức ≤ ⇒ . h ab DM ME ≤ = 4 4 4 0,25 Khi đó 3 3 2 S = DM ME ≤ h (không đổi) MDE . . . 4 8
Dấu ‘’=’’ xảy ra ⇔ MD = ME ⇔ M là trung điểm của BC . 2
Vậy giá trị lớn nhất của S là h 3 (đvdt) khi MDE
M là trung điểm của BC. 8
Câu 9. (1,0 điểm) Bảy người câu được 100 con cá. Biết rằng không có hai người nào câu được số cá như
nhau. Chứng minh rằng có ba người câu được tổng cộng không ít hơn 50 con cá. Cách 1: 1,0 đ Gọi *
a ∈ i = … là số con cá mỗi người câu được. i , 1, ,7,
Giả sử a < a < a < < a . 0,25 1 2 3 7
• Trường hợp 1: a ≤14 . 4 0,25
Khi đó, a + a + a + a ≤14 +13+12 +11 = 50 . Suy ra a + a + a ≥ 50 . 1 2 3 4 5 6 7
• Trường hợp 2: a >14 . 4 0,25
Khi đó, a + a + a ≥16 +17 +18 = 51. 5 6 7 0,25
Vậy, a + a + a ≥ 50 . 5 6 7 Cách 2:
Ta sắp xếp các người câu cá theo thứ tự để số cá câu được của họ giảm
dần. Như thế người thứ nhất câu được nhiều cá nhất và người thứ bảy câu được ít cá nhất.
Nếu người thứ tư câu được không ít hơn 15 con cá, thì ba người đầu câu
được không ít hơn 16 +17 +18 = 51 con cá.
Nếu người thứ tư câu được 14 con cá hoặc ít hơn thì cả bốn người sau câu
được không quá 14 +13 +12 +11 = 50 con. Như vậy ba người đầu câu
được không ít hơn 50 con.
Vậy ba người đầu luôn câu được tổng cộng không dưới 50 con cá.
----------Hết---------
Document Outline

• Câu 2. (2,5 điểm) Tìm số tự nhiên , biết
• .