Đề khảo sát HSG vòng 5 Toán 9 năm 2024 – 2025 phòng GD&ĐT Đông Hưng – Thái Bình

UBND HUYỆN ĐÔNG HƯNG
ĐỀ KHẢO SÁT CHỌN NGUỒN HỌC SINH GIỎI VÒNG 5
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO MÔN TOÁN 9 NĂM HỌC 2024 – 2025
(Thời gian làm bài: 120 phút) Bài 1: (5,0 điểm).  x   y x  y   x   y  2xy 1. Cho biểu thức: P   : 1         1   xy 1 xy     1 xy  2
a. Rút gọn P b. Tính giá trị của P khi x 
c. Tìm giá trị lớn nhất của P. 2  3 3 10  6 3( 3 1) 2. Cho x 
. Tính giá trị của  2025 2 P 12x + 4x – 55 . 6  2 5  5
Bài 2: (4,0 điểm): Cho phương trình 2 2
(m  5)x  2mx 6m  0(1) với m là tham số.
a. Tìm m sao cho phương trình (1) có hai nghiệm phân biệt. Chứng minh rằng khi đó tổng của
hai nghiệm không thể là số nguyên.
b. Tìm m sao cho phương trình (1) có hai nghiệm x1;x2 thỏa mãn điều kiện.
x x  x  x 4 16 1 2 1 2 Bài 3: (4,0 điểm)
1. Bạn Phong đi siêu thị nếu mua 1 chiếc áo polo Lacoste và 1 đôi giày hãng Li-Ning theo
giá niêm yết hết 800 000 đồng. Nhưng gặp đợt khuyến mãi nên 1 chiếc áo polo Lacoste giảm
5% và 1 đôi giày hãng Li-Ning giảm 10%, vì vậy bạn Phong chỉ phải trả 735 000 đồng.
a. Hãy tính giá niêm yết ban đầu của 1 chiếc áo polo Lacoste và 1 đôi giày hãng Li-Ning ?
b. Ngoài ra, siêu thị có thêm ưu đãi nếu khách hàng có hóa đơn từ 2 000 000 đồng trở lên sẽ
được giảm tiếp 10% trên tổng số tiền đã mua. Trong dịp này, bạn Phong đã mua 4 chiếc áo
polo Lacoste và 2 đôi giày hãng Li-Ning. Hỏi bạn Phong trả hết tất cả bao nhiêu tiền ? 3 3 2
x  y 3x 6x3y  4 0
2. Giải hệ phương trình  2 2 x   y 3x 1 
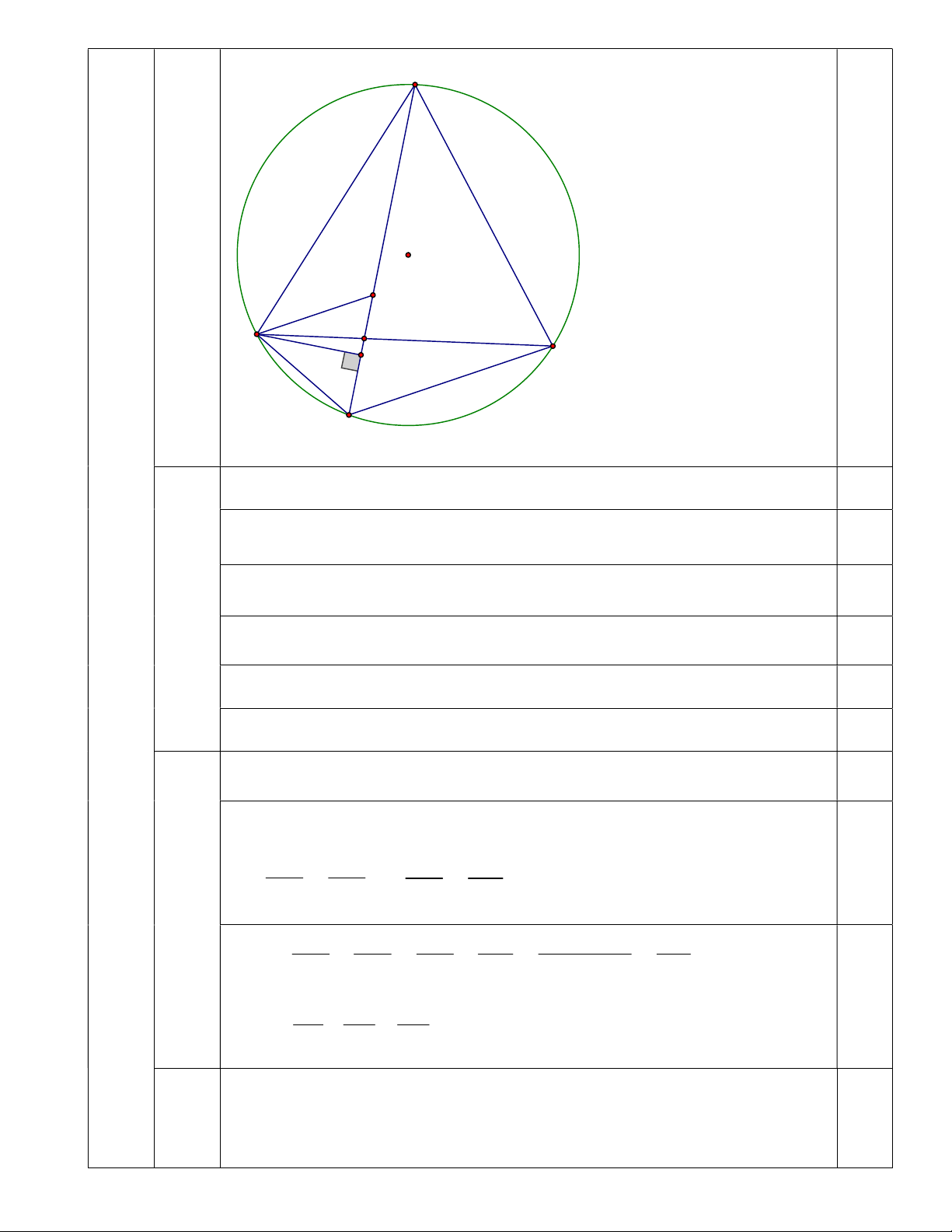
Bài 4 (6 điểm). Cho tam giác đều ABC nội tiếp đường tròn (O). Gọi M là một điểm bất kì thuộc
cung nhỏ BC của đường tròn (O). Trên MA lấy điểm I sao cho MI = MB.
a. Chứng minh rằng ABI  C  BM suy ra MA = MB + MC. 1 1 1
b. Gọi D là giao điểm của MA và BC. Chứng minh rằng   MB MC MD c. Chứng minh rằng 2 2 2 2 MA  MB  MC  2AB
Bài 5: (1,0 điểm) Cho x, y, z là ba số thực dương thỏa mãn x + y + z = 1. Tìm giá trị nhỏ nhất của 2 2 2 x y z biểu thức: T =   y  z z  x x  y ---Hết--- HƯỚNG DẪN CHẤM Bài ý
Đáp án và hướng dẫn chấm Điểm  x   y x  y   x   y  2xy P   : 1         1   xy 1 xy     1 xy  ĐKXĐ x, y 0; xy  1 0.25  x y  
1 xy  x y1 xy      1  xyx y2xy P  0.25    
1 xy1 xy 1 xy1 xy : 1  xy 
x  x y  y  y x  x  x y  y  y x x  y  xy 1 P   0.25 1 xy1 xy : 1xy 1a) 1.5đ 2 x  2y x (x 1)(y 1) P   0.25  xy  xy: 1 1 1 xy1 xy 2 x 1 y 1 xy1 xy P  
1 xy1 xy. x  1y  1 0.25 1 2 x P  x 1 2 x
Với x 0 ; y 0; xy  1 thì P  x 1 0.25 ĐKXĐ x, y 0; xy  1 22 3 2  x    3  2 1 (tm) 0.25 2  3 1 suy ra x  3 1 0.25 1b) 1.0đ 2 3  1 6 3  2 nên P   4  2 3 1 13 0.25 2 6 3  2 Với x  thì P = 2  3 13 0.25
ĐK: x 0 ; y  0; xy  1
Áp dụng bất đẳng thức côsi cho hai số không âm ta được: 0.25 x 1 2 x 1c) 2 x x 1 P   1 0.25 1.0đ x 1 x 1 P
max = 1 khi và chỉ khi x = 1 0.25
Kết hợp với đk suy ra x =1; y  0; y  1
Vậy x =1; y  0; y  1 thì Pmax = 1 0.25
Ta có : 3 10  6 3  3   3 3 1  ( 3 1)  3 1 0,25 2
6  2 5  5  ( 5 1)  5 0,25 3 3
( 3 1)  3 1  3  1 3 1 31 x     2(TMĐK) 2) 0,5 2 5 1 5 1 1.5đ  5 1  5
Thay giá trị của x vào P ta được:  2 P
12.2  4. 2 5 2025 2025 5 1 1 0,5 3 10  6 3( 3 1)
Vậy giá trị của P 1 tại x  6  2 5  5 2 2
(m  5)x  2mx 6m  0 (1) * Phương trình (1) có 2 a  m  5 0 2 2 ' m  (m 5).6m 0,25 2 3 ' m  6m 30m
Để phương trình (1) có hai nghiệm phân biệt x ; x thì ' 0 1 2 a) 2 suy ra 2 3 m  6m  30m  0 2.0đ 0.25 2   1 119 suy ra 2
m(6m  m 30)  0 suy ra 2 m 5m m       0  2 4    0.25 2   suy ra m  0 vì 2 1 119 5m m      0   2 4
Vậy với m > 0 thì phương trình có hai nghiệm phân biệt. 0,25 2m
* Khi đó theo định lý Viète ta có: x  x  1 2 2 m  5 0,25 Xét 2 2
m  5 2m  (m1)  4 0 . Mà m > 0 => 2 m  5 2m  0 2m 0,25  0 1 0 x  x 1 2 1 2 m  5
Vậy tổng hai nghiệm của phương trình (1) không thể là số nguyên. 0,25 0,25
Phương trình (1) có hai nghiệm x ; x 1 2 suy ra ' 0 2   1 119 suy ra 2 m 5m m       0  2 4    suy ra m  0 0,25
Với m  0 thì phương trình có hai nghiệm x ; x 1 2  2m x  x  1 2  2  m  5
Khi đó, theo định lý Viète:  0,25 b) 6m  x x   1 2 2.0đ 2  m  5 Ta có: 4 (x x  x  x ) 16 1 2 1 2 0,25
suy ra x x  x  x  2 hoặc x x  x  x  2 1 2 1 2 1 2 1 2 TH1: x x  x  x  2 1 2 1 2  6m 2m suy ra   2(2) 2 2 m  5 m  5 0,25 2m Đặt t 
 0 phương trình (2) trở thành 2 3t t 2  0 2 m  5 0,25 Xét 2  1 4( 3  )( 2
 ) 230 suy ra phương trình (2) vô nghiệm. TH 2 : x x  x  x  2  1 2 1 2 6m 2m suy ra   2  (3) 2 2 m  5 m  5 0,25 2m Đặt t 
 0 phương trình (3) trở thành 2 3t t  2  0 2 m  5 2
suy ra : t = -1( ktm) hoặc t = (tm) 0,25 3 2 t  3 2m 4  2 m  5 9 2 4m 18m  20  0  0.25 m  24m10 0 5
Suy ra : m = 2 (tm) hoặc m = (tm) 2  5   Vậy m 2;   
thỏa mãn điều kiện đề bài. 2     3
Gọi giá niêm yết của 1 chiếc áo polo Lacoste và 1 đôi giày hãng Li-Ning
lần lượt là x, y (nghìn đồng) ( x, y > 0) 0.25
Theo bài ta có hệ phương trình: 1a) x  y 800   0.25 0  ,95x 0,9y  735  1.25đ x  300(tm) Giải được  0.5 y  500(tm) 
Vậy giá niêm yết của chiếc áo polo Lacoste và 1 đôi giày hãng Li-Ning 0.25
lần lượt là 300.000 đồng và 500.000 đồng.
Số tiền bạn Phong trả khi mua 4 chiếc áo polo Lacoste và 2 đôi giày hãng Li-Ning là: 0.25
4.300.0,95  2.500.0,9  2040 (nghìn đồng) 1b)
0.75đ Do hóa đơn từ 2 000 000 đồng trở lên sẽ được giảm tiếp 10% nên số tiền
bạn Phong phải trả là: 2040.0,9 1836 (nghìn đồng) 0.25 0.25
Vậy số tiền bạn Phong đã trả là 1 836 000 đồng 3 3 2
x  y 3x 6x3y  4 0(1)  2 2 x   y 3x 1(2)  Từ PT(1) ta được: 3 2 3
x  3x  3x 1 y  3x 3y  3  0 3 3
(x 1)  y  3x 3y  3  0 0.25 2 2
(x 1 y) (x 1)  (x 1)y  y   3(x 1 y)  0   2 2
(x 1 y) (x 1)  (x 1)y  y  3  0   0.25 suy ra x + 1 – y = 0 do 2 2
(x 1)  (x 1)y  y  3>0 mọi x, y. suy ra y = x + 1 0.25 2)
2.0đ Thay y = x + 1 vào phương trình (2) ta được: 0.25 2 2x  x  0 x(2x 1)  0 1 x = 0 hoặc x = 0.25 2 + Với x = 0 suy ra r = 1 0.25 1 3 + Với x = suy ra y = 0.25 2 2 1 3
Vậy hệ phương trình có hai nghiệm là (0;1);  ;    2 2 0.25 A O I D B H C M a
C/m được tam giác MBI đều 0,5 (2đ) Suy ra  0 IBM 60 0,25 4 Do đó  ABI   CBM 0,25 C/m ABI  C  BM ( .cg.c) 0,5 Suy ra AI = MC 0,25 Từ đó suy ra MA = MB + MC 0,25 b C/m MCD∽ M  AB(g.g) 1,0 (2đ) Do MCD∽ M  AB(g.g) 0,5 MD MC MD MB nên   MB MA và MC MA MD MD MC MB MC  MB MA 0,25 Do đó:      1 MB MC MA MA MA MA Suy ra 1 1 1   0,25 MB MC MD c
Đặt MA = x, MB = y. Ta có: 0,25 (2đ)       2 2 2 2 2 2 MA MB MC x y x y   2 2 2 x  y  xy (1) 0,25 Kẻ BH  AM 0,5 2 2 y  y y Do  0 BMH  60 nên 2 2 3 MH  , BH  y      2 2 4 2 2  y 3y 0,5 Do đó 2 2 2 2 2 AB  AH  BH x      x  y  xy  2 (2) 4 Từ (1) và (2) suy ra 2 2 2 2 MA  MB  MC  2AB 0,5
Do x, y, z dương. Theo bất đẳng thức Côsi, ta có : 2 2 x y  z x y  z +)   2. .  x (1) y  z 4 y  z 4 0.25 Dấu “=” xảy ra khi : 2 x y  z  suy ra x y  z2 2 4 hay 2x  y  z y  z 4 2 2 y z  x y z  x 0.25 Chứng minh tương tự :+)   2. .  y (2) z  x 4 z  x 4 Dấu “=” xảy ra khi : 2 y z  x 2 5 2 
suy ra 4y z  x hay 2y  z  x z  x 4 2 2 z x  y z x  y +)   2. .  z (3) x  y 4 x  y 4 Dấu “=” xảy ra khi : 2 z x  y  suy ra z x  y2 2 4 hay 2z  x  y x  y 4
Cộng theo vế 3 bất đẳng thức cùng chiều (1), (2) và (3) ta có : 0.25 2 2 2 x y z y  z z  x x  y       x  y  z y  z z  x x  y 4 4 4 2 2 2 x y z x  y  z    1 y  z z  x x  y 2 2  x  y  z  2  y  z x  0.25 Dấu “=” xảy ra khi 2  z   x  y  x y z  2  ;xy;z   0  2 ta được x  y  z  3 2
Vậy giá trị nhỏ nhất của T là 1 khi x  y  z  3