Đề khảo sát lần 1 Toán 12 năm 2024 – 2025 trường THPT Lý Thường Kiệt – Hà Nội
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi khảo sát chất lượng lần 1 môn Toán 12 bộ sách Cánh Diều năm học 2024 – 2025 trường THPT Lý Thường Kiệt, thành phố Hà Nội. Đề thi gồm 03 trang, định dạng trắc nghiệm 03 phần (nhiều phương án lựa chọn, đúng hoặc sai, trả lời ngắn), thời gian làm bài 90 phút có đáp án chi tiết và hướng dẫn chấm điểm. Mời bạn đọc đón xem!
Chủ đề: Đề khảo sát Toán 12 48 tài liệu
Môn: Toán 12 4.3 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KHẢO SÁT CHẤT LƯỢNG LẦN I
TRƯỜNG THPT LÝ THƯỜNG KIỆT NĂM HỌC 2024 - 2025
Môn: TOÁN - Lớp 12 – Cánh diều (Đề này có 3 trang)
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên thí sinh:........................................ SBD:..................... 101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng 2a, góc 0 ADC 60 . Gọi O là
giao điểm của AC và BD, SO ABCD và SO 3a . Góc giữa đường thẳng SD và mặt phẳng
ABCD có số đo bằng A. 0 30 . B. 0 45 . C. 0 60 . D. 0 75 .
Câu 2. Trong các hàm số sau hàm số nào đồng biến trên ? A. 3x 1 y . B. 3 2 y x 2x 6x 1. x 2 C. y tan x 2 . D. 3 y x 2x .
Câu 3. Giá trị lớn nhất 1 4 M của hàm số 3 2
y x x x trên 1; 1. 3 3 A. 4 M . B. M 1 . C. 11 M . D. M 1. 3 3
Câu 4. Tập giá trị của m để hàm số 4 2
y x 2(m 1)x 3 m có đúng một điểm cực trị. A. m 1. B. m 1. C. m 1. D. m 1.
Câu 5. Tập xác định của hàm số 2 x y log là. x 3 A. D ;
32; . B. D ;
3 2; . C. D 3;2 . D. D 3;2.
Câu 6. Cho hình hộp ABCD.EFGH có AB , a AD , b AE .
c Gọi I là điểm thuộc đoạn
thẳng BG sao cho 4BI BG . Biểu thị AI qua a, , b c ta được A. 1 1 AI a b c . B. 1 1 AI a b c . 2 2 4 4 C. 7 7 AI a b c . D. 1 1 AI a b c . 4 4 3 3 Câu 7. Tập xác định
D của hàm số y x x 2 3 2 3 4 . A. D \ 1; 4 . B. D . C. D ; 1 4;.
D. D ; 14;.
Câu 8. Biết bất phương trình x x2 3sin 4cos
6sin x 8cos x 2m1 nghiệm đúng với mọi
x . Mệnh đề nào sau đây đúng ? A. m 18. B. m 0 . C. m 8 . D. m 0.
Câu 9. Cho tứ diện ABCD có AB CD 2a . Gọi M , N lần lượt là trung điểm của AD và
BC . Biết MN 3a , góc giữa hai đường thẳng AB và CD có số đo bằng A. 60. B. 30. C. 45. D. 90. Trang 1/3 - Mã đề 101
Câu 10. Một người gửi 50 triệu đồng vào một ngân hàng theo thể thức lãi kép, với lãi suất
1,85% trên một quý. Hỏi sau tối thiểu bao nhiêu quý, người đó nhận được số tiền ít nhất 72
triệu đồng. Biết trong khoảng thời gian này người đó không rút tiền và lãi suất ngân hàng không thay đổi? A. 15 quý. B. 20 quý. C. 19 quý. D. 14 quý.
Câu 11. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A , mặt bên SBC là tam
giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa
hai đường thẳng SAvà BC bằng A. a 3 . B. a 2 . C. a 5 . D. a 3 . 4 4 4 3
Câu 12. Giá trị của biểu thức P logtan1 logtan 2 logtan3 ... logtan89 bằng ? A. P 1. B. P 2 . C. 1 P . D. P 0 . 2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý (I),
(II), (III), (IV) ở mỗi câu, thí sinh chọn đúng hoặc sai.
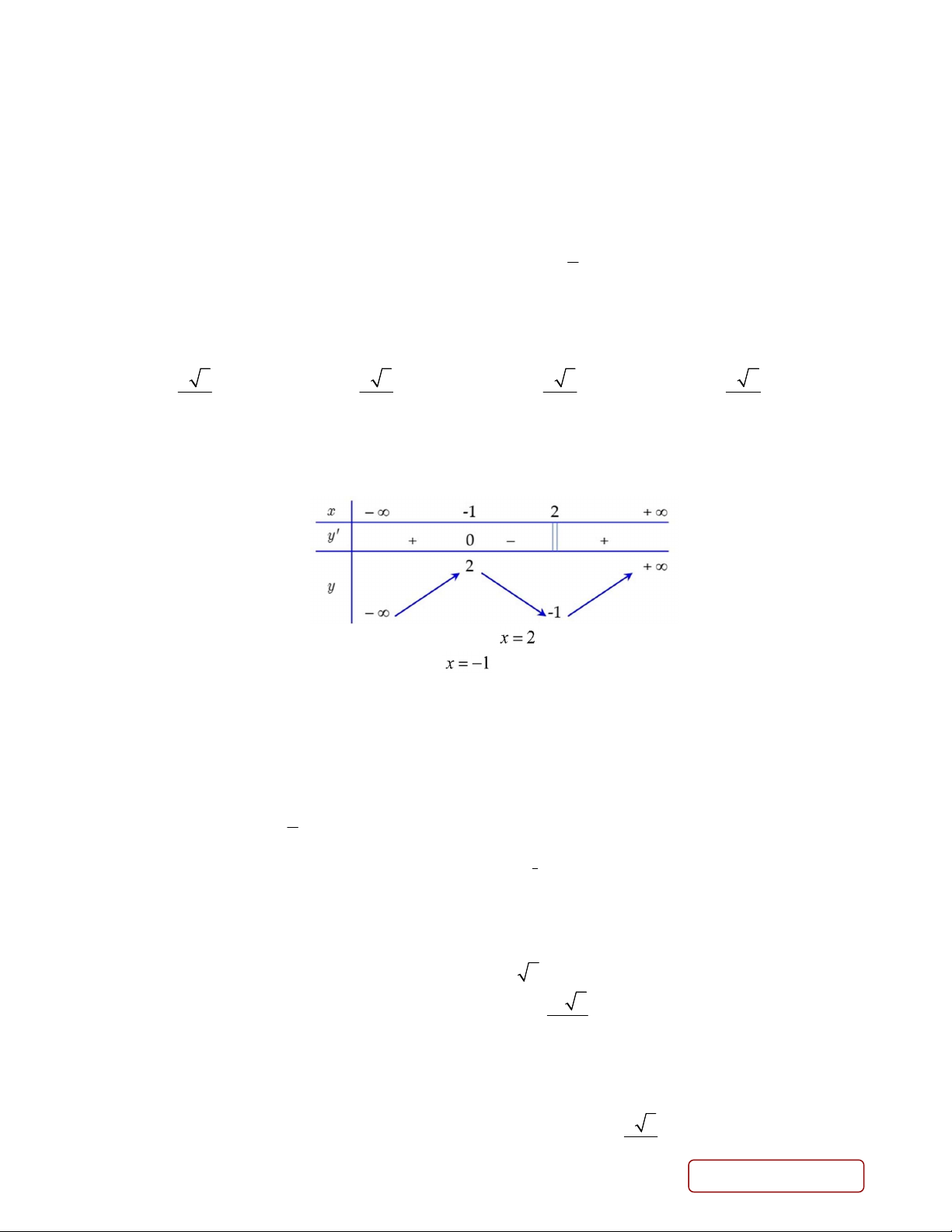
Câu 1: Cho hàm số y = f(x) có bảng biến thiên như sau.
(I) Hàm số đạt cực tiểu tại x = −5 (II)
Hàm số có 4 điểm cực trị (III)
Hàm số đạt cực tiểu tại x = 2 (IV)
Hàm số không có cực đại Câu 2. Cho hàm số 3 2
y x mx 2m 3 x 1. (I) Với m 1 thì 2 y 3x 2x 1.
(II) Với m 1 phương trình y 0 có hai nghiệm là 1 x 1; x . 3
(III) Không có giá trị nào của m để mọi tiếp tuyến của đồ thị hàm số 3 2
y x mx 2m 3 x 1 có hệ số góc dương.
(IV) Có 5 giá trị nguyên của m để phương trình y y 0 vô nghiệm
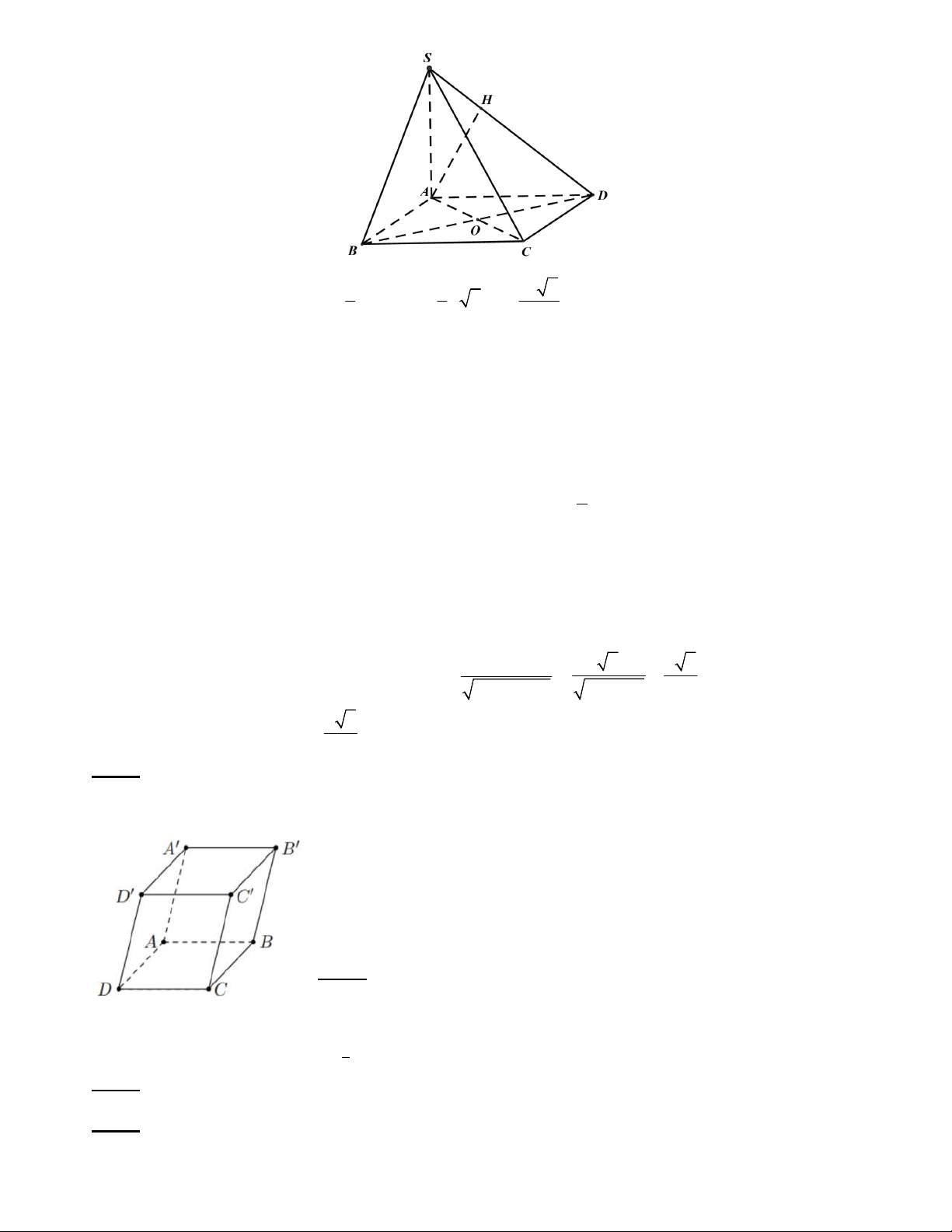
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông tâm O và AB a . Biết SA vuông góc
với mặt phẳng đáy và SB tạo với đáy góc 60 . Vẽ các đường cao AH của tam giác
SAB , AK của tam giác SAD và AE của tam giác SAO .
(I) Đường thẳng AB song song với mặt phẳngSCD .
(II) Đường thẳng AE vuông góc với mặt phẳng SBD 3
(III) Thể tích khối chóp a 3 S.ABO bằng . 6 (V) Khoảng cách từ a
C đến mặt phẳng AHK bằng: 2 5 5 Trang 2/3 - Mã đề 101
Câu 4. Cho hình hộp chữ nhật ABCD.A’B’C’D’ , cạnh AB = a; AD = a√3; AA’ = 2a
(I) 𝐴𝐵′⃗ + 𝐶𝐷′⃗ = 0⃗ (II) 𝐴′𝐷⃗ + 𝐶𝐵′⃗ = 0⃗
(III) 𝐴𝐵⃗ + 𝐴𝐷⃗ = 𝑎√5 (IV) 𝐴𝐵⃗ + 𝐴′𝐷′⃗ + 𝐶𝐶′⃗ = 2√2𝑎
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. 3
Câu 1. Cho hàm số f x x 2
mx m 2 x 7 . Có bao nhiêu giá trị nguyên của tham số 3
m để f x 0 mọi x
Câu 2. Tìm tập hợp tất cả các giá trị của tham số m dể hàm số 3 2 y x mx 2 2 m
3 x 3 đạt cực đại tại x 1. Câu 3. Cho b
a,b là hai số thực dương thỏa mãn 3 log a log 1. 3 3 a Giá trị 2 T a .b ? Câu 4. Cho hàm số. 3 y x 3x 2 .
Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x 2 bằng ? 0
Câu 5. Cho khối chóp tam giác đều có cạnh bên bằng a 42 và mặt bên tạo với mặt phẳng 6
đáy một góc 60. Khi a 6 thì thể tích của khối chóp đã cho bằng bao nhiêu?
Câu 6. Cho hình chóp S.ABC có 𝑆𝐴⃗ = 𝑎⃗, 𝑆𝐵⃗ = 𝑏⃗, 𝑆𝐶⃗ = 𝑐⃗ và các điểm M, N lần lượt là
trung điểm của các cạnh AB, SC. Các điểm P, Q trên các đường thẳng SA, BN sao cho PQ
song song với CM. Biểu diễn vecto 𝑃𝑄⃗ theo ba vecto 𝑎⃗, 𝑏⃗, 𝑐⃗, ta được:
𝑃𝑄⃗ = − 𝑎⃗ − 𝑏⃗ + 𝑐⃗ ( với , , là các phân số tối giản và m, n, q, q, r, z ∈ Z). Giá trị biểu thức M = − + bằng bao nhiêu ?
------------- HẾT ------------- Trang 3/3 - Mã đề 101
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KHẢO SÁT CHẤT LƯỢNG LẦN I
TRƯỜNG THPT LÝ THƯỜNG KIỆT NĂM HỌC 2024 - 2025
Môn: TOÁN - Lớp 12 – Cánh diều (Đề này có 3 trang)
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên thí sinh:................................................................ SBD:..................... 102
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hình chóp S.ABCD có đáy là hình thoi cạnh 2a, góc 0 ADC 60 . Gọi O là giao
điểm của AC và BD, SO ABCD và SO 3a . Góc giữa đường thẳng SD và mặt phẳng
ABCD có số đo bằng ? A. 0 45 . B. 0 60 . C. 0 75 . D. 0 30 .
Câu 2. Cho hình hộp ABCD.EFGH có AB a, AD , b AE .
c Gọi I là điểm thuộc đoạn
thẳng BG sao cho 4BI BG . Biểu thị AI qua a, , b c ta được A. 1 1 AI a b c . B. 1 1 AI a b c . 4 4 3 3 C. 1 1 AI a b c . D. 7 7 AI a b c . 2 2 4 4
Câu 3. Trong các hàm số sau hàm số nào đồng biến trên ? A. 3x 1 y . B. 3 2 y x 2x 6x 1. x 2 C. y tan x 2 . D. 3 y x 2x . Câu 4. Tập xác định
D của hàm số y x x 2 3 2 3 4 .
A. D ; 14;. B. D \ 1; 4 . C. D . D. D ; 1 4;.
Câu 5. Tập xác định của hàm số 2 x y log . x 3 A. D 3;2 . B. D 3;2.
C. D ;32; .
D. D ;3 2; .
Câu 6. Tập giá trị của m để hàm số 4 2
y x 2(m 1)x 3 m có đúng một điểm cực trị. A. m 1. B. m 1. C. m 1. D. m 1. 1 4
Câu 7. Giá trị lớn nhất M của hàm số 3 2
y x x x trên 1; 1. 3 3 11 4 A. M 1 . B. M . C. M 1. D. M . 3 3
Câu 8. Cho tứ diện ABCD có AB CD 2a . Gọi M , N lần lượt là trung điểm của AD và
BC . Biết MN 3a , góc giữa hai đường thẳng AB và CD có số đo bằng A. 90. B. 60. C. 30 . D. 45.
Câu 9. Một người gửi 50 triệu đồng vào một ngân hàng theo thể thức lãi kép, với lãi suất
1,85% trên một quý. Hỏi sau tối thiểu bao nhiêu quý, người đó nhận được số tiền ít nhất Trang 1/3 - Mã đề 102
72 triệu đồng. Biết trong khoảng thời gian này người đó không rút tiền và lãi suất ngân hàng không thay đổi? A. 15 quý. B. 20 quý. C. 19 quý. D. 14 quý.
Câu 10. Biết bất phương trình x x2 3sin 4cos
6sin x 8cos x 2m 1 nghiệm đúng với mọi
x . Mệnh đề nào sau đây đúng. A. m 8 . B. m 0 . C. m 18 . D. m 0 .
Câu 11. Giá trị của biểu thức P logtan1 logtan 2 logtan3 ... logtan89bằng? A. P 1. B. P 2 . C. 1 P . D. P 0 . 2
Câu 12. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A , mặt bên SBC là tam
giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa
hai đường thẳng SA và BC bằng A. a 5 . B. a 3 . C. a 3 . D. a 2 . 4 3 4 4
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý
(I), (II), (III), (IV) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số y = f(x) có bảng biến thiên như sau:
(I) Hàm số không đạt cực tiểu tại diểm .
(II) Hàm số đạt cực đại tại điềm .
(III) Điểm cực đại của đồ thị hàm số là (-1;2).
(IV) Giá trị cực đại của hàm số là y = 2. Câu 2. Cho phương trình x x 1 9 3 2m 1 0 . (I) Hàm số 1 3x y nghịch biến trên . (II) Khi 1 m , đặt 3x t
(điều kiện t 0 ), phương trình 1 trở thành 2 t 3t 0. 2
(III) Tập xác định của hàm số x x y 1 1 3 9 3 là D 0;.
(IV) Có hai giá trị m nguyên để phương trình
1 có hai nghiệm phân biệt.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên SA
vuông góc với mặt phẳng đáy và SA a 2 . 3 (I) Thể tích khối chóp a 2 S.ABCD bằng . 3
(II) Góc giữa SC và mp ABCD là SCA .
(III) Góc giữa mặt phẳng SAC và SBD bằng 0 60 . (IV) Khoảng cách từ a
O đến mặt phẳng SCD 6 . 3 Trang 2/3 - Mã đề 102
Câu 4. Cho hình hộp ABCD.A’B’C’D’:
(I) 𝐴𝐵⃗ + 𝐶𝐶′⃗ = 𝐴′𝐵′⃗ + 𝐵𝐵′⃗ (II) 𝐴𝐵⃗ = 𝐶𝐷⃗
(III) 𝐴𝐵⃗ − 𝐵𝐶′⃗ = 𝐵𝐷′⃗ (IV) 𝐴𝐵⃗ + 𝐴𝐷⃗ + 𝐴𝐴′⃗ = 𝐴𝐶′⃗
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Có bao nhiêu giá trị nguyên của m để hàm số
y= 𝑥 − 2𝑚𝑥 + (𝑚 + 3)𝑥 − 5 + 𝑚 đồng biến trên R
Câu 2. Tìm giá trị thực của m để hàm số 1 3 2 y x mx 2
m 4 x 3 đạt cực đại tại x 3. 3 Câu 3. Cho hàm số 3 2 y 2x 6x 5 .
Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x 3 bằng bao nhiêu? 0
Câu 4. Xét tất cả các số thực dương a , b thỏa mãn log a log 2 ab 0. 9 1 3 Tính giá trị 2 T ab
Câu 5. Cho Hình chóp S.ABC có đáy ABC là tam giác vuông cân tại , A biết AB a , a
SA vuông góc với mặt phẳng đáy và khoảng cách từ A đến mặt phẳng SBC bằng 21 . 7
Khi a 3 thì thể tích của khối chóp đã cho bằng bao nhiêu?
Câu 6. Cho hình chóp S.ABC có 𝑆𝐴⃗ = 𝑎⃗, 𝑆𝐵⃗ = 𝑏⃗, 𝑆𝐶⃗ = 𝑐⃗ và các điểm M, N lần lượt là
trung điểm của các cạnh AB, SC. Các điểm P, Q trên các đường thẳng SA, BN sao cho PQ
song song với CM. Biểu diễn vecto 𝑃𝑄⃗ theo ba vecto 𝑎⃗, 𝑏⃗, 𝑐⃗, ta được:
𝑃𝑄⃗ = − 𝑎⃗ − 𝑏⃗ + 𝑐⃗ ( với , , là các phân số tối giản và m, n, q, q, r, z ∈ Z). Giá trị biểu thức M = + − bằng bao nhiêu?
------------- HẾT ------------- Trang 3/3 - Mã đề 102
ĐÁP ÁN CÁC MÃ ĐỀ [DS12259]
------------------------ ------------------------ Mã đề [101] 1 2 3 4 5 6 C B B D C B 7 8 9 10 11 12 C A A B A D Mã đề [102] 1 2 3 4 5 6 B A B D A C 7 8 9 10 11 12 A B B C D C Mã đề [103] 1 2 3 4 5 6 D C B C A D 7 8 9 10 11 12 B A D B A C Mã đề [104] 1 2 3 4 5 6 A B C D B C 7 8 9 10 11 12 A B D C D B
ĐÁP ÁN ĐỀ THI THỬ LẦN I 101 , 103 PHẦN II.
Điểm tối đa của 01 câu hỏi là 1 điểm.
- Thí sinh chỉ lựa chọn đúng chính xác 01 ý trong 1 câu hỏi được 0,1 điểm
- Thí sinh chỉ lựa chọn đúng chính xác 02 ý trong 1 câu hỏi được 0,25 điểm
- Thí sinh chỉ lựa chọn đúng chính xác 03 ý trong 1 câu hỏi được 0,5 điểm
- Thí sinh chỉ lựa chọn đúng chính xác 04 ý trong 1 câu hỏi được 1 điểm Câu 1 Câu 2 Câu 3 Câu 4 I) S I) S I) Đ I) S I) S II) Đ II) Đ II) Đ III) Đ III) Đ III) S III) S IV) S IV) S IV) Đ IV) Đ PHẦN III.
(Mỗi câu trả lời đúng thí sinh được 0,5 điểm) Câu 1 2 3 4 5 6 Chọn 4 4 3 9 3 4/3
PHẦN II. Câu trắc nghiệm đúng sai.
Câu 1. (I) S (II) S (III) Đ (IV) S
Câu 2.(I) Sai: Với m 1 thì 3 2 y x x x 1 2 y ' 3x 2x 1. x 1
(II) Đúng Với m 1 thì phương trình 2
y 0 3x 2x 1 0 1 x 3
(III) Đúng: Hệ số góc tiếp tuyến của đồ thị hàm số 3 2
y x mx 2m 3 x 1 là 2
y 3x 2mx 2m 3
Vì hệ số góc dương với mọi x nên ta có: a 3 0
y 3x 2mx 2m 3 0
m 6m 9 0 m 32 2 2 0 m 0
(IV) Sai: Ta có y 6x 2m . Khi đó: y y 0 2
3x 2mx 2m 3 6x 2m 0 2
3x 2m 3 x 3 0 Biệt thức 2 ' m 6m 18
Phương trình y y 0 vô nghiệm 2
' 0 m 6m 18 0 do bất phương trình vô nghiệm. Câu 3. AB / /CD
(I) Đúng: Ta có CD SCD AB / /SCD AB SCD SA BD (II) Đúng: Ta có nên BD SAC . AO BD
Kẻ đường cao AE của SAO thì AE BD . Vậy AE SBD (III) Sai: Ta có S ; B ABCD SBA 60 Ta có: SA tan SBA
SA AB tan 60 a 3 AB 3 Ta có 2 1 a 3 S a suy ra V Bh . ABCD S.ABCD 3 3 3 3 Mặt khác 1 1 1 a 3 a 3 S S nên V V . . ABO 4 ABCD S.ABO S. 4 ABCD 4 3 12
BC SA do SA ABCD (IV) Đúng: Ta có:
BC SAB BC AH , BC AB
Mà SB AH nên AH SBC
DC SAdo SA ABCD Ta có:
DC (SAD) DC AK , DC AD
Mà SD AK nên AK SDC SC AH Khi đó: SC (AHK) . SC AK
Gọi F SC (AHK) thì SC AF .
Khi đó: d C, AHK CF . Ta có: 2 2 2 2
SC SA AC 3a 2a a 5 .
Tam giác SAC vuông tại A có đường cao AF 2 2 nên: AC 2a 2a 5 2 CF.CS AC CF . CS a 5 5 Vậy d C AHK 2a 5 , CF 5
Câu 4. (I) S (II) Đ (III) S (IV) Đ
(I) 𝐴𝐵′⃗ và 𝐶𝐷′⃗ không đối nhau nên 𝐴𝐵′⃗ + 𝐶𝐷′⃗ ≠ 0⃗ nên (I) SAI
(II) 𝐴′𝐷⃗ và 𝐶𝐵′⃗ đối nhau nên 𝐴𝐵′⃗ + 𝐶𝐷′⃗ = 0⃗ nên (II) ĐÚNG
(III) 𝐴𝐵⃗ + 𝐴𝐷⃗ = 𝐴𝐶⃗ = 𝐴𝐶 = √𝐴𝐵 + 𝐴𝐷 =2a nên (III) SAI
(IV) 𝐴𝐵⃗ + 𝐴′𝐷′⃗ + 𝐶𝐶′⃗ = 𝐴𝐵⃗ + 𝐴′𝐷′⃗ + 𝐴𝐴′⃗ = 𝐴𝐶 = √𝐴𝐵 + 𝐴𝐷 + 𝐴𝐴 = 2√2 a nên (IV) Đ
PHẦN III. Câu trắc nghiệm trả lời ngắn. Câu 1. Ta có f x 2 x 2mx m 2 . Khi đó, f x 2
0, x x 2mx m 2 0, x a 1 0 2 m m 2 0 1 m 2 2 m m 2 0 Vậy 1
m 2 nên có 4 giá trị nguyên của tham số m thoả mãn. ĐÁP ÁN 4 Câu 2. ĐÁP ÁN 4 Câu 3. b b Ta có 3 3 2 log a log 1 log a 1 a b 3 . 3 3 3 a a
Câu 4. Hệ số góc của tiếp tuyến là k 9 . ĐÁP ÁN 9 Câu 5.
Góc giữa mặt bên và đáy bằng 0 0 60 SMO 60 x 3 AO Đặt 3 AB x x 3 OM 6 x 3 x
Xét SOM : SO OM .tan 60 . 3 6 2 2 2 2 x x 3 a 42 Xét SOA : 2 2 2 AO SO SA x a 2 2 3 6 a 2 SO 2 3 2 1 a 2 a 3 a 6 ĐÁP ÁN 3 a V V a 2 6 2 . . 3 . 3 2 3 2 2 12 a 3 S A BC 4 2 Câu 6.
Đặt 𝑃𝐴⃗ = 𝑥𝑆𝐴⃗, 𝐵𝑄⃗ = 𝑦𝐵𝑁⃗ Suy ra:
𝑃𝑄⃗ = 𝑃𝐴⃗ + 𝐴𝐵⃗ + 𝐵𝑄⃗ = 𝑥𝑆𝐴⃗ + 𝑆𝐵⃗ − 𝑆𝐴⃗ + 𝑦𝐵𝑁⃗ = (𝑥 − 1)𝑆𝐴⃗ + 𝑆𝐵⃗ + 𝑦 𝑆𝑁⃗ − 𝑆𝐵⃗ 𝑦
= (𝑥 − 1)𝑎⃗ + (1 − 𝑦)𝑏⃗ + 𝑐⃗ 2
Lại có: 𝐶𝑀⃗ = 𝑆𝑀⃗ − 𝑆𝐶⃗ =
𝑆𝐴⃗ + 𝑆𝐵⃗ − 𝑆𝐶⃗ = 𝑎⃗ + 𝑏⃗ − 𝑐⃗ 𝑥 =
PQ//CM 𝑃𝑄⃗ = 𝑘𝐶𝑀⃗ = =
Vậy 𝑃𝑄⃗ = − 𝑎⃗ − 𝑏⃗ + 𝑐⃗ ĐÁP ÁN 𝟑 . . 𝑦 =
ĐÁP ÁN ĐỀ THI THỬ LẦN I 102, 104 PHẦN II.
Điểm tối đa của 01 câu hỏi là 1 điểm.
- Thí sinh chỉ lựa chọn đúng chính xác 01 ý trong 1 câu hỏi được 0,1 điểm
- Thí sinh chỉ lựa chọn đúng chính xác 02 ý trong 1 câu hỏi được 0,25 điểm
- Thí sinh chỉ lựa chọn đúng chính xác 03 ý trong 1 câu hỏi được 0,5 điểm
- Thí sinh chỉ lựa chọn đúng chính xác 04 ý trong 1 câu hỏi được 1 điểm Câu 1 Câu 2 Câu 3 Câu 4 I) S I) S I) Đ I) Đ II) Đ II) Đ III) Đ II) S II) Đ III) S III) S III) S IV) Đ IV) S IV) S IV) Đ PHẦN III.
(Mỗi câu trả lời đúng thí sinh được 0,5 điểm) Câu 1 2 3 4 5 6 Chọn 2 5 -18 1 1,5 4/3
PHẦN II. Câu trắc nghiệm đúng sai.
Câu 1.(I) S (II) Đ (III) Đ (IV) Đ
(I) Dựa vào BBT ta thấy hàm số đạt cực tiểu tại . Câu 2.
(I) Sai: Vì 3 1 nên hàm số x 1 3 3.3x y đồng biến trên . 1 (II) Đúng: Đặt 3x t
(điều kiện t 0 ), m , phương trình 1 trở thành 2 t 3t 0. 2 (III) Sai: Điều kiện x x 1 9 3 0 3x 3x
3 0 3x 3 0 x 1.
Vậy tập xác định của hàm số đã cho là D 1; . (IV) Sai: Đặt 3x
t (điều kiện t 0 ), phương trình 1 trở thành 2
t 3t 2m 1 0. 2
1 có hai nghiệm phân biệt khi và chỉ khi 2 có hai nghiệm phân biệt dương. 0 1 3 8m 0 1 13 m m 1. 2m 1 0 2m 1 0 2 8
Vậy có một giá trị m nguyên thỏa mãn yêu cầu. Câu 3. 3 1 1 a 2 (I) Đúng: Ta có 2 V S . A S a 2.a . S. ABCD 3 ABCD 3 3
(II) Đúng: Vì SA ABCD nên hình chiếu của SC trên mặt phẳng ABCD là AC .
Suy ra góc giữa SC và mặt phẳng ABCD là SCA . AC BD (III) Sai: Ta có
BD SAC SBD SAC . SA BD
Suy ra góc giữa mặt phẳng SAC và SBD bằng 90 . 1
(IV) Sai: Vì O là trung điểm của AC nên d O,SCD d , A SCD 2
Trong mặt phẳng SAD , dựng AH SD H SD (1). C D AD Ta có
CD (SAD) CD AH (2). C D SA
Từ (1) và (2) ta có AH SCD AH d , A SCD . S . A AD a 2.a a 6
Xét tam giác vuông SAD tại D có AH . 2 2 SA AD 2 2 2a a 3 a Suy ra O SCD 6 d , .(II) SAI Vì AB=DC 6 Câu 4. (I) Đ (II) S (III) S (IV) Đ
(I) ĐÚNG Vì 𝐴𝐵⃗ = 𝐴′𝐵′⃗ và 𝐶𝐶′⃗ = 𝐵𝐵′⃗
(II) SAI Vì 𝐴𝐵⃗ = 𝐷𝐶⃗
(III) SAI Vì 𝐵𝐶′⃗ = 𝐴𝐷′⃗→𝐴𝐵⃗ − 𝐵𝐶′⃗ = 𝐴𝐵⃗ − 𝐴𝐷′⃗ = 𝐷′𝐵⃗
(IV) ĐÚNG Vì 𝐴𝐵⃗ + 𝐴𝐷⃗ + 𝐴𝐴′⃗ = 𝐴𝐶⃗ + 𝐴𝐴′⃗ = 𝐴𝐶′⃗ (Quy tắc hình hộp)
PHẦN III. Câu trắc nghiệm trả lời ngắn
Câu 1.Ta có tập xác định D=R
y’=0 𝑥 − 4𝑚𝑥 + 𝑚 + 3 = 0
Hàm số đồng biến trên R khi và chỉ khi y’≥0, ∀x∈R, đẳng thức chỉ xảy ra tại hữu hạn điểm
∆’≤0 (−2m)2−(m+3)≤0 − ≤ 𝑚 ≤1 ĐÁP ÁN 2 Câu 2. ĐÁP ÁN 5 Câu 3. y f x 2 6
x 12x , f 3 1 8 . ĐÁP ÁN -18 1
Câu 4.Ta có log a log 2 a.b log a log 2 a.b 0 log 2 ab 2
0 ab 1 ĐÁP ÁN 1 9 1 3 3 3 2 3 Câu 5.
Gọi M là trung điểm của BC , A
BC vuông cân tại A nên AM BC . BC AM Ta có BC SAM . BC SA BC SAM
Trong mặt phẳng SAM , kẻ AH SM tại H mà . AH BC AH SAM AH SM Ta có
AH SBC d A,(SBC) AH . AH BC
Xét ABC vuông cân tại A , AB a do đó BC a 2 . 1 a 2 2 1 a AM BC và 2 S AB đvdt . A BC 2 2 2 2 Xét S
AM vuông tại A , AH là đường cao nên ta có: 1 1 1 1 1 1 SA a 3 . 2 2 2 2 2 2 AH SA AM 21 SA a a 2 7 2 2 3 1 1 a a 3
Thể tích của khối chóp đã cho a 3 V SA.S a 3. V 1,5 . S.ABC A BC S. 3 3 2 6 ABC ĐÁP ÁN 1,5 Câu 6.
Đặt 𝑃𝐴⃗ = 𝑥𝑆𝐴⃗, 𝐵𝑄⃗ = 𝑦𝐵𝑁⃗ Suy ra:
𝑃𝑄⃗ = 𝑃𝐴⃗ + 𝐴𝐵⃗ + 𝐵𝑄⃗ = 𝑥𝑆𝐴⃗ + 𝑆𝐵⃗ − 𝑆𝐴⃗ + 𝑦𝐵𝑁⃗ = (𝑥 − 1)𝑆𝐴⃗ + 𝑆𝐵⃗ + 𝑦 𝑆𝑁⃗ − 𝑆𝐵⃗ 𝑦
= (𝑥 − 1)𝑎⃗ + (1 − 𝑦)𝑏⃗ + 𝑐⃗ 2
Lại có: 𝐶𝑀⃗ = 𝑆𝑀⃗ − 𝑆𝐶⃗ =
𝑆𝐴⃗ + 𝑆𝐵⃗ − 𝑆𝐶⃗ = 𝑎⃗ + 𝑏⃗ − 𝑐⃗ 𝑥 =
PQ//CM 𝑃𝑄⃗ = 𝑘𝐶𝑀⃗ = = . . 𝑦 =
Vậy 𝑃𝑄⃗ = − 𝑎⃗ − 𝑏⃗ + 𝑐⃗ ĐÁP ÁN M = 1
Document Outline
- made 101
- made 102
- Đáp án