Đề khảo sát Toán 9 lần 1 năm 2023 – 2024 phòng GD&ĐT Việt Yên – Bắc Giang
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2023 – 2024 phòng GD&ĐT Việt Yên – Bắc Giang giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
trường
Preview text:
UBND HUYỆN VIỆT YÊN
ĐỀ KHẢO SÁT HS LỚP 9 LẦN I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023-2024 Môn: Toán 9 Mã đề: 358
Thời gian làm bài: 120 phút, không kể thời gian phát đề (Đề gồm 03 trang)
Họ, tên thí sinh:.......................................................................; Số báo danh:.........................
(Thí sinh không được sử dụng tài liệu)
PHẦN I. TRẮC NGHIỆM (3,0 điểm)
Câu 1: Từ một điểm M ở ngoài đường tròn (O;R) vẽ tiếp tuyến MT và cát tuyến MCD qua tâm O.
Cho MT = 20cm, MD = 40cm. Khi đó độ dài R là A. 30cm B. 15cm C. 20cm D. 25cm Câu 2: Công thức 3
h 0,4 x biểu diễn mối tương quan giữa cân nặng x (tính bằng kg) và chiều
cao h (tính bằng m) của một con hươu cao cổ. Một con hươu cao cổ có chiều cao 2,56m thì có cân
nặng (kết quả làm tròn đến chữ số thập phân thứ nhất) là A. 1,9kg. B. 6,4kg. C. 262,2kg. D. 262,1kg.
Câu 3: Số các giá trị nguyên dương của tham số m để phương trình 2 x − 2(m + )
1 x + m − 5 = 0 có
hai nghiệm trái dấu là A. 5 B. 3 C. 6 D. 4
Câu 4: Đường thẳng đi qua điểm M (1; )
1 và song song với đường thẳng d : y = 2x − 3 có phương trình là
A. y = 2x −1. B. y = 2 − x −1.
C. y = 2x +1. D. y = 2 − x + 3.
Câu 5: Cho đường tròn (O; 5cm). Hai dây AB = 6cm, CD = 8cm song song nằm khác phía so với
tâm O của đường tròn. Khoảng cách giữa hai dây AB và CD là A. 5cm. B. 6cm. C. 8cm. D. 7 cm. Câu 6: Biểu thức 3 − P =
xác định với các giá trị của x thoả mãn x −1 A. x ∀ ∈ R B. x ≠ 1 − C. x ≥ 0
D. x ≥ 0; x ≠1
Câu 7: Giá trị của biểu thức 35 −12 6 − 31−12 3 bằng A. 4 − B. 2 − C. 4 D. 2 3 +1 2 +1 3 +1 1+ 2
Câu 8: Một chiếc đu quay có bán kính 75m , tâm của vòng quay ở độ cao 90m , thời gian thực
hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng
quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét? A. 165 m . B. 165,5 m . C. 127,5 m . D. 127 m.
Trang 1/3 - Mã đề thi 358
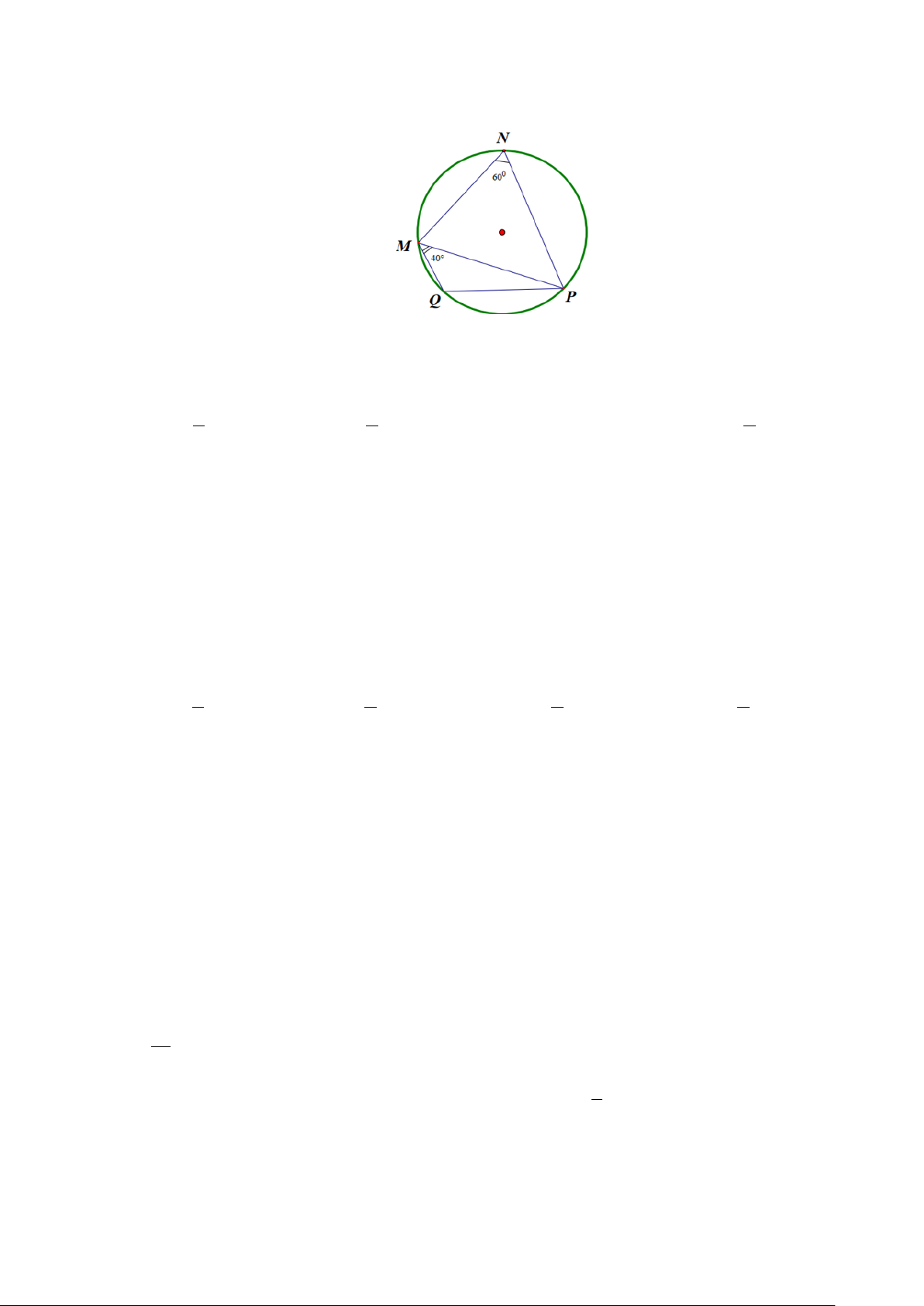
Câu 9: Cho tứ giác MNPQ nội tiếp một đường tròn có 60o MNP = và 40o PMQ = (hình vẽ bên). Số đo MPQ bằng A. 20 .o B. 40 .o C. 10 .o D. 50 .o
Câu 10: Cho hai hàm số bậc nhất y = (k − 2)x + k ( k ≠ 2 ) và y = x − 2 . Giá trị của k để đồ thị
của hai hàm số đã cho cắt nhau tại một điểm trên trục hoành là A. 4 k = − . B. 4 k = . C. k = 0 D. 4 k ≠ . 3 3 3
Câu 11: Đồ thị hàm số y = ax + b là một đường thẳng đi qua hai điểm A(1;− )1; B( 2 − ;5) . Khi đó tích ab bằng A. 1 − . B. 5. C. 2 − . D. 6 − .
Câu 12: Căn bậc hai số học của 4 bằng A. 16 − B. 16 C. 2 D. 2 −
Câu 13: Hàm số y = (2 + m)x −1 đồng biến trên R khi và chỉ khi A. m > 0 B. m > 2 − C. m = 2 − D. m < 2 −
Câu 14: Đồ thị hàm số y = ( − a) 2 3
x (tham số a) đi qua điểm M( 2;
− 2) thì giá trị của tham số a là A. 3 a = − B. 2 a = C. 3 a = D. 5 a = 2 5 2 2
Câu 15: Phương trình 2
− x − y = 0 có nghiệm tổng quát là ∈ ∈ ∈ ∈ A. x R y R x R x R B. C. D. y = −x x = 2 − y y = 2 − x y = 2x
Câu 16: Biết phương trình 2
x + 2x −15 = 0 có hai nghiệm x x x .x
1 , 2 . Giá trị của biểu thức 1 2 bằng A. 15. B. 15 − . C. 2 . D. 2 − .
mx − y = m
Câu 17: Hệ phương trình
(m là tham số) có nghiệm duy nhất với
4x + my = m A. m ≠ 2 ± và m ≠ 0 B. m ≠ 4 − C. m ≠ 4 − và m ≠ 0
D. Mọi số thực m.
Câu 18: Cho tam giác ABC vuông tại A, biết AB = 3 cm, AC = 4 cm. Độ dài đường cao AH là A. 5 cm B. 2,4cm C. 2 cm D. 5 cm 12
Câu 19: Cho tam giác ABC vuông tại A có AB=6cm, 3
cos B = . Diện tích hình tròn nội tiếp tam 5 giác vuông ABC là A. 2 2π cm B. 4π cm C. 2 4π cm D. 2 π cm
Câu 20: Biết phương trình 2 x − ( m + ) 2 2 2
1 x + m +1 = 0 có nghiệm là x = 2 . Tích các giá trị m bằng A. 3 − B. 3 C. 1 D. 8 −
Trang 2/3 - Mã đề thi 358
PHẦN II. TỰ LUẬN (7,0 điểm)
Câu 21: (2,5 điểm). 3 x − y = 7
1. Giải hệ phương trình: x + 5y = 3 − 1 1 4 x x +1
2. Rút gọn biểu thức: A = − − :
(với x ≥ 0; x ≠ 4 ). x − 2
x + 2 4 − x x − 4
3. Cho hàm số y = (m − ) 1 x + 2m + 3 ( )
1 . Tìm m để đồ thị hàm số (1) cắt đường thẳng
y = 3x + 2 tại điểm có hoành độ bằng 1.
Câu 22: (1,0 điểm). Cho phương trình: 2
x (m4)xm2 0 (x là ẩn, m là tham số) (1).
1. Giải phương trình (1) với m = 2 − ;
2. Tìm tất cả các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt x ; x 1 2 thỏa mãn: 2
x + 2024 + x (m −8 − x ) 2
= x + 2024 + x m − x 1 1 1 2 2 ( 2 )
Câu 23: (1,0 điểm). Nhân dịp kỉ niệm 10 năm thành lập, cửa hàng GNH có thực hiện chương trình
giảm giá cho mặt hàng X là 20% và mặt hàng Y là 15% so với giá niêm yết. Bà Hiền mua 2 món
hàng X và 1 món hàng Y thì phải trả số tiền là 395000 đồng. Ngày cuối cùng của chương trình, cửa
hàng thay đổi bằng cách giảm giá mặt hàng X là 30% và mặt hàng Y là 25% so với giá niêm yết.
Vào ngày hôm đó, cô Định mua 3 món hàng X và 2 món hàng Y thì trả số tiền là 603000 đồng.
Tính giá niêm yết của mỗi món hàng X và Y (Giá niêm yết là giá ghi trên món hàng nhưng chưa thực hiện giảm giá).
Câu 24: (2,0 điểm). Cho tam giác ABC nhọn, nội tiếp đường tròn (O; R) và AB < AC . Ba đường
cao AD, BE, CF của tam giác ABC (D, E, F là chân các đường cao) đồng quy tại điểm H. Kẻ đường
kính AK của đường tròn (O; R). Gọi M là hình chiếu vuông góc của C trên đường thẳng AK.
a) Chứng minh rằng tứ giác ACMD nội tiếp đường tròn.
b) Chứng minh rằng MD song song với BK.
c) Giả sử hai đỉnh B, C cố định trên đường tròn (O; R) và đỉnh A di động trên cung lớn BC
của đường tròn (O; R). Chứng minh rằng đường thẳng MF luôn đi qua một điểm cố định .
Câu 25: (0,5 điểm). Cho a,b > 0;2b ≥ ab + 4 . Tìm giá trị lớn nhất của biểu thức: ab P = 2 2 a + 2b ----------- HẾT ----------
Trang 3/3 - Mã đề thi 358