Đề khảo sát Toán 9 lần 2 năm 2023 – 2024 phòng GD&ĐT Hà Trung – Thanh Hóa

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề khảo sát chất lượng môn Toán 9 lần 2 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Hà Trung, tỉnh Thanh Hóa; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!

220 110 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

6 trang 6 tháng trước

Tác giả:

Profile M. Hậu
Câu 1 (2,0 điểm).
a) Giải hệ phương trình:
3x + 2y = 8
2x - y = 3
b) Cho hai hàm số
( )
=
2
:Pyx
và
( )
=−−+:2 3d y xm
với
m
là tham số. Tìm
m
để đường thẳng
( )
d
đi qua điểm
A
thuộc
( )
P
có hoành độ bằng
2.
Câu 2 (2,0 điểm). Cho biểu thức: ) P =
11 x
:
x - x x 1 x - 2 x 1

+

−+

(với x > 0, x
1)
a) Rút gọn biểu thức P.
b) Tìm các giá trị của x để P >
1
2
.
Câu 3 (2,0 điểm). Cho phương trình
2
( 2) 1 0x m xm+ + + −=
với
m
là tham số
a) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m
b) Gọi
12
;xx
là hai nghiệm phân biệt của phương trình. Tìm m để
22
11 2 2
6x xx x
−+ − =
Câu 4: (3,0 điểm) Cho tam giác
ABC
( )
AB AC<
nội tiếp đường tròn tâm
O
.
M
là điểm nằm trên
cung
BC
không chứa điểm
A
. Gọi
D
,
E
,
F
lần lượt là hình chiếu của
M
trên
BC
,
CA
,
AB
.
a) Chứng minh bốn điểm
M
,
B
,
D
,
F
cùng thuộc một đường tròn
b) Chứng minh
D
,
E
,
F
thẳng hàng.
c) Chứng minh
BC AC AB
MD ME MF
= +
.
Câu 5( 1,0 điểm) : Cho
,,abc
là các số thực dương. Chứng minh rằng
( ) ( ) ( )
222
222
22 2
1
.
3
555
abc
a bc b ca c ab
++≤
++ ++ ++
-------------------------------------Hết-----------------------------------
PHÒNG GD&ĐT HÀ TRUNG
ĐỀ KHẢO SÁT HỌC SINH LỚP 9 LẦN 2
NĂM HỌC 2023- 2024
Môn thi: Toán
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
(Đề thi có 01 trang, gồm 05 câu
HƯỚNG DẪN CHẤM KHẢO SÁT LỚP 9
Câu
Ý
Nội dung
Điểm
Câu 1 a
a) Giải hệ phương trình:
3x + 2y = 8 3 2 8
2x - y = 3 4 2 6
7 14 2
23 1
xy
xy
xx
xy y
+=

⇔

−=

= =

⇔⇔

−= =

0,5
0,5
b
Vì điểm
A
nằm trên
( )
P
có hoành độ bằng
2.
Thay
2x =
vào
( )
2
: Pyx=
ta được
4
y
=
( )
2; 4 .A⇒
Vì
( )
Ad∈
. Thay
2; 4xy= =
vào đường thẳng
( )
d
ta được
4 2.2 3 44 30 50 5m mmm
=− − +⇒++ −=⇒ +=⇒ =−
Vậy để đường thẳng
( )
d
đi qua điểm
A
nằm trên
(
)
P
có hoành độ bằng
2
thì
5.m = −
0,5
0,5
Câu 2
a) ĐKXĐ: x > 0 ; x ≠ 1
11 x
P = :
x - x x 1 x - 2 x 1

+

−+

(
) ( )
(
)
2
x1
1x
.
x
x x1 x x1

−

= +

−−

( )
( ) ( )
( )
2
x1 x1 x1
1 x x - 1
.
x
x x. x
x x1
− +−
+
= = =
−
Vậy: Với x > 0 ; x ≠ 1 thì
x - 1
x
P =
0,5
0,5
b) P >
1
2
<=>
x - 1 1
x2
>
Với x > 0, x
≠
1 thì
( )
x - 1 1
x2
2 x - 1 x
>
⇔>
x > 2⇔
(TM).
Vậy : Với x > 2 thì P >
1
2
.
0,5
0,5
Câu 3
(2,0đ)
a
(1,0đ
)
a)
2
( 2) 1 0x m xm+ + + −=
Ta có
22 2 2
4 ( 2) 4.1.( 1) 4 4 4 4 8b ac m m m m m m∆= − = + − − = + + − + = +
Ta có
22
0; 8 8 0;m mR m mR≥ ∀∈ ⇔ +≥> ∀∈
Vì
0∆>
nên phương trình luôn có hai nghiệm phân biệt với mọi m.
0,5
0,5
b) Với
0∆>
, theo hệ thức Vi-et, ta được
( )
12
12
2
1
b
xx m
a
xx m
−
+= =−+
= −
Theo bài ra
( )
22
1 12 2 12 1 2
22 6x xx x xx x x+ +− −+ =
( ) ( )
2
12 12 12
26xx xx xx⇔+ − −+ =
( ) ( ) ( )
2
2 2 1 26m mm⇔ + − −+ + =
2
4422 26mm m m⇔ + +− ++ +=
2
3 20mm⇔ + +=
12
1; 2mm⇒=− =−
Vậy,
{ }
1; 2m ∈− −
thì phương trình có hai nghiệm thoả mãn
22
11 2 2
6x xx x−+ − =
0,25
0,25
0,25
0,25
4
(3,0đ)
a).Bốn điểm
M
,
B
,
D
,
F
cùng thuộc một đường tròn và bốn điểm
M
,
D
,
E
,
C
cùng thuộc một đường tròn.
Ta có:
MF AB⊥
nên
90MFB = °
.
0,25
l
1
2
2
1
O
F
B
C
A
M
D
E
MD BC⊥
nên
90MDB = °
.
Tứ giác
MDBF
có
90 90 180
MFB MDB+ = °+ °= °
Do đó tứ giác
MDBF
nột tiếp.
Suy ra 4 điểm
M
,
B
,
D
,
F
cùng thuộc một đường tròn.
0,25
0,25
0,25
b).Chứng minh
D
,
E
,
F
thẳng hàng.
Vì tứ giác
MDBF
nội tiếp. Nên:
11
MD=
(cùng chắn
BF
).
Vì tứ giác
MDEC
nội tiếp nên
22
MD=
.
Mặt khác tứ giác
MBAC
nội tiếp.
Nên
1
BC=
(góc ngoài của tứ giác nội tiếp).
Do đó
12
MM=
(cùng phụ với
1
;
BC
).
Suy ra:
12
DD=
.
Mà
2
180D BDE+=°
Nên
1
180D BDE+=°
.
Vậy,
D
,
E
,
F
thẳng hàng
0,25
0,25
0,25
0,25
c)
BC AC AB
MD ME MF
= +
Ta có :
AC AB AE EC AF FC AE EC AF FC
ME MF ME MF ME ME MF MF
+−
+= + =++−
21
tan tan tan tanAME M AMF M= ++ −
. Mà
12
MM=
Nên
tan tan
AC AB
AME AMF
ME MF
+= +
.
0,25
0,25
Mặt khác: tứ giác
AFME
nội tiếp nên:
AME AFE BMD= =
AMF AEF DMC
= =
Do đó:
tan tan
AC AB
AME AMF
ME MF
+= +
tan tanBMD MDC= +
BD DC BD DC BC
MD MD MD MD
+
=+= =
.
0,25
0,25
Câu 5
(1điểm)
Ta có :
(
) ( ) ( )
222
222
22 2
555
abc
VT
a bc b ca c ab
=++
++ ++ ++
( )
( )
( )
2 2 22
2 222 2
222 2
2
9 ( 2) 2
2
22
5
a aa a a
abc abc
abc abc
a bc
+
= ≤+
++ +
++ + +
++
Tương tự rồi cộng vế với vế của các BĐT ta được :
222
22 2
222
91
222
abc
VT
a bc b ca c ab
≤+++
+++
D
ấu “=” xảy ra khi
.abc
= =
Ta chứng minh:
222
22 2
1
222
abc
A
a bc b ca c ab
=++≤
+++
.
Ta có:
222
22 2
3111
-
2222
222
abc
A
a bc b ca c ab
=− +− +−
+++
22 2
1
2
222
bc ca ab
a bc b ca c ab

= ++

+++

( )
( )
( )
( )
( )
( )
222
2 22
31 1
-
22 2
2. 2. 2.
1
bc ca ab
A
bc ab ac ca bc ab ab ca bc
A


= ++ ≥


+++

≤
Do đó:
9 12VT ≤+
hay
1
.
3
VT
≤
Vậy:
( ) ( ) ( )
222
222
22 2
1
.
3
555
abc
a bc b ca c ab
++≤
++ ++ ++
0,25
0,25
0,25
0,25
Lưu ý:
- Bài hình HS không vẽ hình hoặc vẽ hình sai không chấm điểm
- -HS làm cách khác đúng vẫn cho điểm tối đa
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GD&ĐT HÀ TRUNG
ĐỀ KHẢO SÁT HỌC SINH LỚP 9 LẦN 2 NĂM HỌC 2023- 2024 Môn thi: Toán
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
(Đề thi có 01 trang, gồm 05 câu
Câu 1 (2,0 điểm). 3x +  2y = 8
a) Giải hệ phương trình:  2x - y = 3
b) Cho hai hàm số (P) y = 2 :
x và (d ) : y = −2x − m + 3 với m là tham số. Tìm m để đường thẳng
(d) đi qua điểm A thuộc (P) có hoành độ bằng 2.
Câu 2 (2,0 điểm). Cho biểu thức: ) P =  1 1  x +   : (với x > 0, x ≠ 1)  x - x x −1 x - 2 x +1
a) Rút gọn biểu thức P.
b) Tìm các giá trị của x để P > 1 . 2
Câu 3 (2,0 điểm). Cho phương trình 2
x + (m + 2)x + m −1 = 0 với m là tham số
a) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m
b) Gọi x ; x là hai nghiệm phân biệt của phương trình. Tìm m để 2 2
x − x + x − x = 6 1 2 1 1 2 2
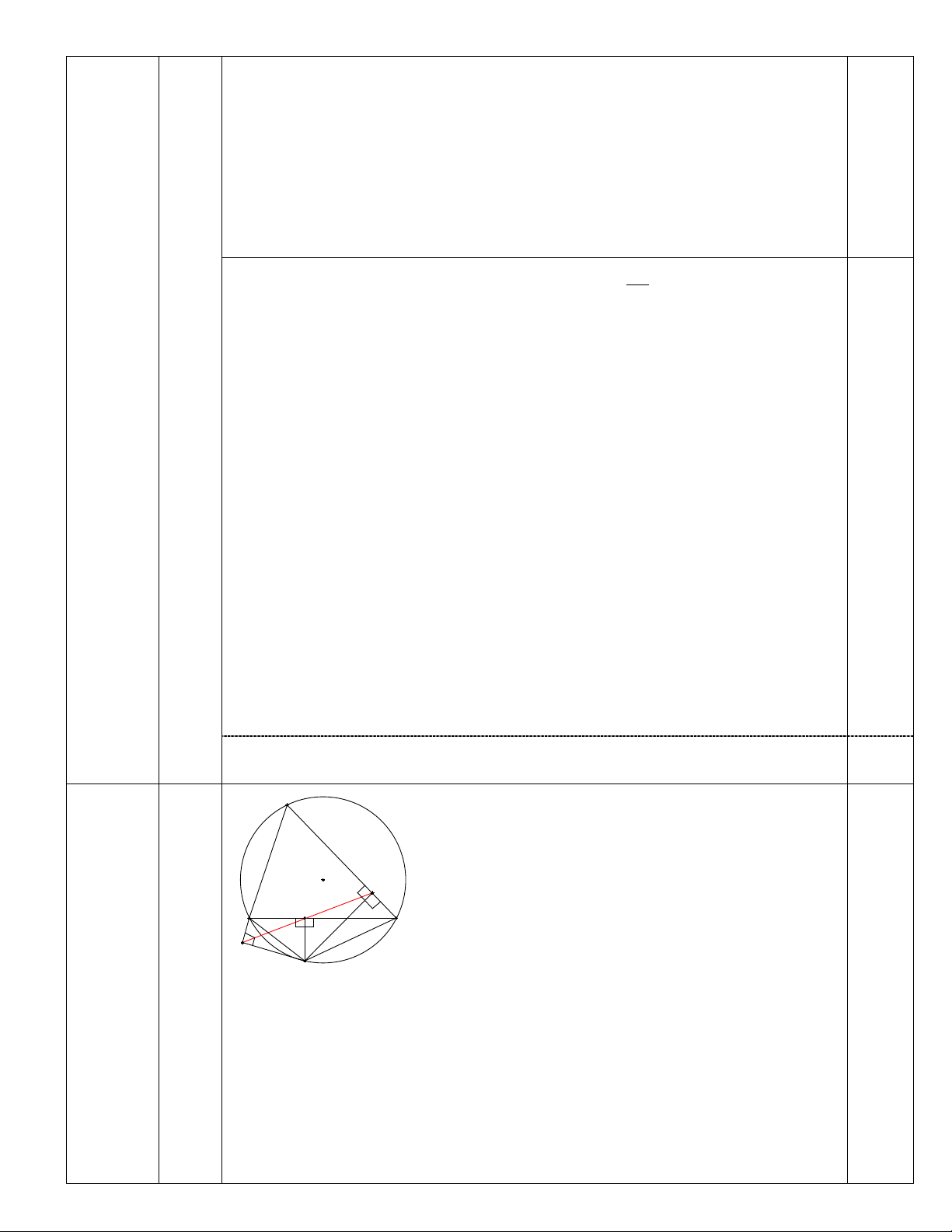
Câu 4: (3,0 điểm) Cho tam giác ABC ( AB < AC) nội tiếp đường tròn tâm O . M là điểm nằm trên
cung BC không chứa điểm A . Gọi D , E , F lần lượt là hình chiếu của M trên BC , CA , AB .
a) Chứng minh bốn điểm M , B , D , F cùng thuộc một đường tròn
b) Chứng minh D , E , F thẳng hàng.
c) Chứng minh BC AC AB = + . MD ME MF
Câu 5( 1,0 điểm) : Cho a, ,bc là các số thực dương. Chứng minh rằng 2 2 2 a b c 1 + + ≤
a + (b + c) . 2
b + (c + a)2
c + (a + b)2 2 2 2 3 5 5 5
-------------------------------------Hết-----------------------------------
HƯỚNG DẪN CHẤM KHẢO SÁT LỚP 9 Câu Ý Nội dung Điểm
a) Giải hệ phương trình: 3x +  2y = 8 3  x + 2y = 8 0,5  ⇔  Câu 1 a 2x - y = 3
4x − 2y = 6 7x =14 x = 2 ⇔  ⇔ 0,5 2x y 3  − = y = 1
Vì điểm A nằm trên (P) có hoành độ bằng 2. Thay x = 2 vào (P) 2 : y = x ta được 0,5
y = 4 ⇒ A(2;4). b
Vì A ∈ (d) . Thay x = 2;y = 4 vào đường thẳng (d) ta được 4 = 2
− .2 − m + 3 ⇒ 4 + 4 + m − 3 = 0 ⇒ m + 5 = 0 ⇒ m = 5 −
Vậy để đường thẳng (d) đi qua điểm A nằm trên (P) có hoành độ bằng2 0,5 thì m = 5. − Câu 2 a) ĐKXĐ: x > 0 ; x ≠ 1  1 1  x P = +   :  x - x x −1 x - 2 x +1 0,5  1 x  ( − )2 x 1   = + .  x  ( x )1 x ( x )1 − − x  1 x ( − )2 x 1 ( x + )1( x − + )1 x - 1 = = = x ( x − ). 1 x x. x x
Vậy: Với x > 0 ; x ≠ 1 thì x - 1 P = 0,5 x b) P > 1 <=> x - 1 1 > 2 x 2 x - 1 1 Với x > 0, x > ≠ 1 thì x 2 0,5 ⇔ 2(x - ) 1 > x ⇔ x > 2 (TM).
Vậy : Với x > 2 thì P > 1 . 2 0,5 Câu 3 (2,0đ) a) 2
x + (m + 2)x + m −1 = 0 0,5 Ta có 2 2 2 2
∆ = b − 4ac = (m + 2) − 4.1.(m −1) = m + 4m + 4 − 4m + 4 = m + 8 Ta có 2 2 m ≥ 0; m
∀ ∈ R ⇔ m + 8 ≥ 8 > 0; m ∀ ∈ R
Vì ∆ > 0 nên phương trình luôn có hai nghiệm phân biệt với mọi m. 0,5  b − x + x = = − m + 2 1 2 ( )
b) Với ∆ > 0 , theo hệ thức Vi-et, ta được  a 0,25 x x = m −  1 1 2 Theo bài ra a 2 2 (1,0đ
x + 2x x + x − 2x x − x + x = 6 1 1 2 2 1 2 ( 1 2) )
⇔ (x + x )2 − 2x x − x + x = 6 0,25 1 2 1 2 ( 1 2) ⇔ (m + )2 2 − 2(m − ) 1 + (m + 2) = 6 0,25 2
⇔ m + 4m + 4 − 2m + 2 + m + 2 = 6 2
⇔ m + 3m + 2 = 0 ⇒ m = 1; − m = 2 − 1 2 Vậy, m ∈{ 1; − − }
2 thì phương trình có hai nghiệm thoả mãn 0,25 2 2
x − x + x − x = 6 1 1 2 2 A O E D 2 B 1 C 1 2 4 F l M (3,0đ)
a).Bốn điểm M , B , D , F cùng thuộc một đường tròn và bốn điểm M ,
D , E , C cùng thuộc một đường tròn.
Ta có: MF ⊥ AB nên  MFB = 90° . 0,25
MD ⊥ BC nên  MDB = 90°. 0,25 Tứ giác MDBF có  + 
MFB MDB = 90° + 90° =180° 0,25
Do đó tứ giác MDBF nột tiếp.
Suy ra 4 điểm M , B , D , F cùng thuộc một đường tròn. 0,25
b).Chứng minh D , E , F thẳng hàng.
Vì tứ giác MDBF nội tiếp. Nên:  =  M D (cùng chắn  BF ). 1 1 0,25
Vì tứ giác MDEC nội tiếp nên  =  M D . 2 2 Mặt khác tứ giác MBAC nội tiếp. Nên  = 
B C (góc ngoài của tứ giác nội tiếp). 1 Do đó  =  M
M (cùng phụ với   B ; C ). 1 2 1 0,25 Suy ra:  =  D D . 1 2 Mà  0,25 +  D BDE =180° 2 Nên  +  D BDE =180°. 1 0,25
Vậy, D , E , F thẳng hàng c) BC AC AB = + MD ME MF Ta có : AC AB
AE + EC AF − FC AE EC AF FC + = + = + + − ME MF ME MF ME ME MF MF 0,25 =  +  +  −  tan AME tan M
tan AMF tan M . Mà  =  M M 2 1 1 2 Nên AC AB + =  + 
tan AME tan AMF . 0,25 ME MF
Mặt khác: tứ giác AFME nội tiếp nên:  =  =  AME AFE BMD 0,25  =  =  AMF AEF DMC Do đó: AC AB + =  + 
tan AME tan AMF =  +  tan BMD tan MDC ME MF 0,25 BD DC BD + DC BC = + = = . MD MD MD MD Câu 5 Ta có : 2 2 2 a b c VT = + + (1điểm)
a + (b + c)2
b + (c + a)2
c + (a + b)2 2 2 2 5 5 5 0,25 2 2 2 2 9a (a + 2a) a 2a = ≤ + + ( + )2 ( 2 2 2
a + b + c ) + 2( 2 2 2 5 a + bc a b c ) 2 2 2 2 a + b + c 2a + bc
Tương tự rồi cộng vế với vế của các BĐT ta được : 2 2 2 2a 2b 2c 9VT ≤ 1 + + + 2 2 2 2a + bc 2b + ca 2c + ab Dấu “=” xảy ra khi a = b = . c 2 2 2 Ta chứng minh: a b c A = + + ≤ 1. 2 2 2 2a + bc 2b + ca 2c + ab 0,25 2 2 2 Ta có: 3 1 a 1 b 1 c - A = − + − + − 2 2 2 2
2 2a + bc 2 2b + ca 2 2c + ab 1  bc ca ab  =  + +  2 2 2
2  2a + bc 2b + ca 2c + ab    0,25 3 1  (bc)2 (ca)2 (ab)2  1 - A = + + ≥ 2 2   ( 
bc)2 + abac (ca)2 + bcab (ab)2 +  2 2 . 2 . 2ca.bc A ≤ 1 Do đó: 9VT ≤ 1 + 2 hay 1 VT ≤ . 3 0,25 Vậy: 2 2 2 a b c 1 + + ≤
a + (b + c) . 2
b + (c + a)2
c + (a + b)2 2 2 2 3 5 5 5 Lưu ý:
- Bài hình HS không vẽ hình hoặc vẽ hình sai không chấm điểm
- -HS làm cách khác đúng vẫn cho điểm tối đa