Đề khảo sát Toán 9 tháng 3 năm 2024 phòng GD&ĐT Gia Lâm – Hà Nội

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG THÁNG 3 HUYỆN GIA LÂM NĂM HỌC 2023-2024 MÔN: TOÁN 9
Thời gian làm bài: 120 phút
Bài 1 (2 điểm): Cho hai biểu thức x + 5 + − + A = ; 2x 4 x 15 x 5 B = −
(với x > 0; x ≠ 9 ). x − 3 x − 3 x x
1) Tính giá trị của biểu thức A khi x = 25 . 2) Rút gọn B. 3) Cho A
M = . Tìm giá trị nhỏ nhất của M B
Bài 2 (1,5 điểm): Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Theo kế hoạch, hai tổ sản xuất 800 sản phẩm trong một thời gian nhất định. Khi thực hiện,
tổ I do sự cố về máy nên đã bị giảm 15% kế hoạch, còn tổ II nhờ áp dụng kĩ thuật mới nên đã
vượt mức 25% kế hoạch. Vì vậy, trong thời gian quy định cả hai tổ làm được 880 sản phẩm. Tính
số sản phẩm của mỗi tổ phải làm theo kế hoạch.
Bài 3 (2,5 điểm):  x 8 + = 1   x − 4 y + 5
1) Giải hệ phương trình:  5x 6  − = 18 −  x − 4 y +  5
2) Trong mặt phẳng toạ độ Oxy, cho prarabol (P): y = x2
và đường thẳng (d): y = - 2mx + m2 + 2
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt với mọi giá trị của m.
b) Với m = - 1, tìm toạ độ giao điểm A, B của (d) và (P). Xác định vị trí của C trên
cung AB của parabol sao cho diện tích tam giác ABC lớn nhất.
Bài 4 (3,5 điểm): Cho tam giác ABC vuông tại A. Vẽ đường tròn (O) đường kính AB cắt BC
tại D. Từ A kẻ AH vuông góc với OC tại H.
1) Chứng minh tứ giác AHDC nội tiếp.
2) Gọi I là trung điểm của BD, tia IO cắt tia CA tại E. Chứng minh IB.IC = IO. IE
3) Gọi K, M lần lượt là giao điểm của AH với BD và đường tròn (O). Chứng minh HM là phân giác của  BHD và KI.KC = KB.KD
4) BE cắt đường tròn (O) tại N. Chứng minh N, H, D thẳng hàng.
Bài 5 (0,5 điểm):
Cho a,b,c là ba số dương. Chứng minh rằng:
a + b + c > 2 b + c c + a a + b __________Hết__________
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh:…………………………………………..Số báo danh:…………………….
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HUYỆN GIA LÂM
ĐỀ KHẢO SÁT CHẤT LƯỢNG THÁNG 3 NĂM HỌC 2023-2024 MÔN: TOÁN 9 Bài - Nội dung Biểu câu điểm 1.1
Thay x = 25 (TMĐK) vào biểu thức A , ta được: 25 5 A + = 25 − 3 0,25 30 30 = = =15 5 − 3 2 0,25
Vậy tại x = 25 thì A = 15. 1.2 2x + 4 x −15 x + 5 B = −
ĐKXĐ: x > 0; x ≠ 9 x − 3 x x 2x + 4 x −15 x + 5 = − 0,25 x ( x −3) x x x ( x +5)( x − + − 3 2 4 15 ) = − x ( x −3) x ( x −3)
2x + 4 x −15 x − 3 x + 5 x −15 = − 0,25 x ( x −3) x ( x −3)
2x + 4 x −15 − x + 3 x − 5 x +15 = x ( x −3) x + 2 x = x ( x −3) 0,25 x ( x + 2) = x ( x −3) x + 2 0,25 = x − 3 1.3 A M = x + 5 x + 2 x + 5 = : = B x − 3 x − 3 x + 2 x − 4 + 9 9 9 = = x − 2 + = x + 2 + − 4 x + 2 x + 2 x + 2
Với x > 0, ta có x + 2 và 9 là 2 số dương. Áp dụng bất đẳng thức Cô-si cho x + 2 0,25 2 số trên ta có : 9 x + + ≥ ( x + ) 9 2 2 2 . = 2 9 = 6 x + 2 x + 2 ⇒ 9 x + 2 + − 4 ≥ 6 − 4 x + 2 Do đó M ≥ 2
Dấu “=” xảy ra khi x + = ⇔ ( x + )2 9 2 2 = 9 x + 2 0,25
⇔ x + 2 = 3 (vì x + 2 > 0) ⇔ x =1 ⇔ x =1 (TMĐK) Vậy Mmin = 2 khi x = 1 2
+ Gọi số sản phẩm tổ I phải làm theo kế hoạch là x (sp) (x∈N*, x < 800)
+ Gọi số sản phẩm tổ II phải làm theo kế hoạch là y (sp) (y∈N*, x < 800) 0,25
+ Vì theo kế hoạch hai tổ sản xuất 800 sản phẩm nên ta có phương trình: x + y = 800 (1) 0,25
+ Số sản phẩm tổ I làm trong thực tế là 0,85x (sp)
+ Số sản phẩm tổ II làm trong thực tế là 1,25y (sp)
+ Vì trong thực tế hai tổ sản xuất 880 sản phẩm nên ta có phương trình: 0,25 0,85x + 1,25y = 880 (2) Từ ( )
1 ,(2) ta có hệ phương trình: x + y = 800  x + y = 0, 4x = 120  1,25 1,25 1000 ⇔  ⇔  0,85x +1, 25y = 880
0,85x +1, 25y = 880 x + y = 800 x = 300( d tm k ) ⇔  y = 500  ( d tm k ) 0,5
Vậy số sản phẩm tổ I phải làm theo kế hoạch là 300 sản phẩm.
số sản phẩm tổ II phải làm theo kế hoạch là 500 sản phẩm. 0,25 3.1  x 8 + = 1   x − 4 y + 5 
ĐKXĐ: x ≠ 4; y > 5 − 5x 6 0,25  − = 18 −  x − 4 y +  5  5x 40 + = 5  x 8  + = 1   x − 4 y + 5  x − 4 y + 5 ⇔  ⇔ 5x 6   − = 18 − 46  = 23  x − 4 y +  5  y +  5 0,5  x 8 + = 1   x  x − 4 y + 5 =  3 − ⇔  ⇔ x − 4 1 1  =  y +5 =  2  y +  5 2  3 − x +12 = x x = 3 (tm) ⇔  ⇔  y + 5 = 4 y = 1( − tm)
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (3; -1). 0,25
Xét phương trình hoành độ giao điểm của (P) và (d):
3.2a x2 = - 2mx + m2 + 2 ⇔ x2 + 2mx – m2 – 2 = 0 (1) Có a = 1 ≠ 0 0,25
∆ = b2 – 4ac = (2m)2 – 4.1.(– m2 – 2) = 8m2 + 8 > 0 với mọi giá trị của m
⇒ phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị của m
⇒ đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt với mọi giá trị của m. 0,25 3.2b Với m = 1
− ta có (d): y = 2x + 3; y = x2 (P).
Xét phương trình hoành độ giao điểm của (P) và (d): x2 – 2x – 3 = 0
Giải đúng x1 = - 1, x2 = 3 0,25
Tìm đúng toạ độ giao điểm A(- 1; 1), B(3; 9) 0,25
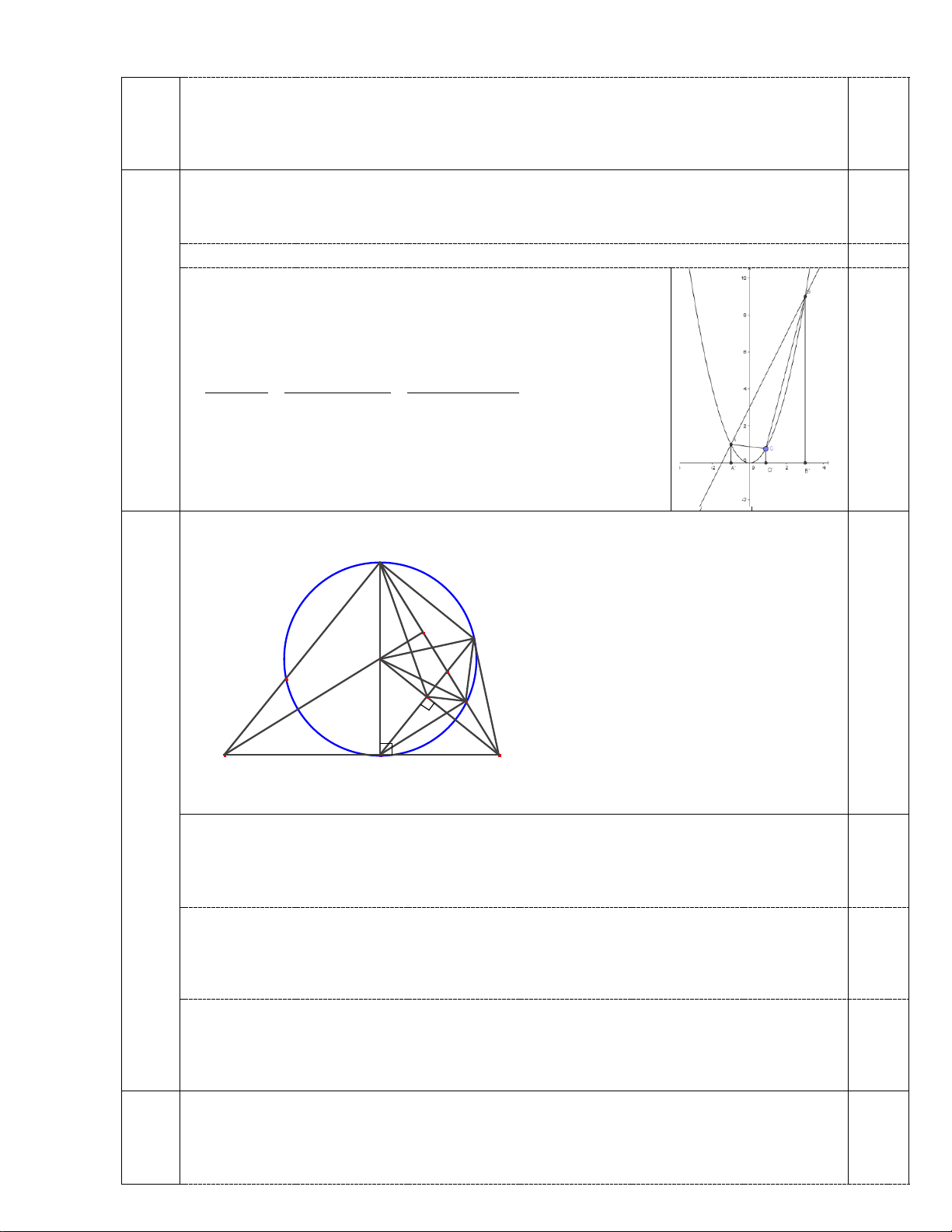
+ Giả sử C(c;c2) thuộc (P) với – 1< c <3
+ Gọi A’, B’, C’lần lượt là hình chiếu của A, B, C trên Ox.
SABC = SAA’B’B – SAA’C’C – SBB’C’C (1+9).4 ( 2 1+ c ).(c + ) 1 ( 2 9 + c ).(3− c) 0,25 = − − 2 2 2 = 8 − 2(c − )2 1 ≤ 8
⇒ diện tích ABC lớn nhất bằng 8 khi C(1;1) 0,25 4.1 Vẽ đúng hình B x I M 0,25 O x N K D H E A C
1) Xét (O) đường kính AB có: 
ADB = 90° (góc nội tiếp chắn nửa đường tròn) ⇒ 
ADC = 90° (kề bù với  ADB ) 0,25 Xét tứ giác AHDC có:  ADC = 90° (cmt)  0,25 AHC = 90° (AH ⊥ OC) ⇒  =  ADC AHC
mà hai góc này ở vị trí 2 đỉnh kề cùng nhìn AC 0,25
⇒ tứ giác AHDC nội tiếp (dhnb) 4.2 + Xét (O) có: IB = ID BD là dây không qua tâm O ⇒OI ⊥ BD ⇒  =  OIB OIC = 90° 0,25
+ Chứng minh được  = 
OBI IEC (cùng phụ  ACB ) 0,25 + Xét IO ∆ B và IC ∆ E có:  = 
OIB EIC = 90° và  =  OBI IEC (cmt) => IO ∆ B∽ IC
∆ E (g.g) 0,25 => IO IB =
(cạnh tương ứng tỉ lệ) ⇒ . IB IC = . IO IE (đpcm). IC IE 0,25 4.3
+ AC ⊥ OC ⇒ AC là tiếp tuyến của (O) đường kính AB +  = 
ABD DAC (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn  AD )
+ Tứ giác AHDC nội tiếp (cmt) ⇒  = 
DHC DAC (2 góc nội tiếp cùng chắn  DC ) ⇒  =  OBD DHC (1)
⇒ tứ giác OBHD nội tiếp (tứ giác có góc trong tại một đỉnh bằng góc ngoài đỉnh 0,25
đối diện với đỉnh đó) ⇒  =  OHB ODB (2) mà  = 
ODB OBD (∆OBD cân) (3) (1), (2), (3) ⇒  =  OHB DHC mà  +  =  +  0 OHB BHM DHC DHM = 90 0,25 ⇒  = 
BHM DHM ⇒ HM là phân giác của  BHD
+ Chứng minh được  =  OMC OAC ⇒  0
OMC = 90 và 5 điểm A, O, I, M, C cùng thuộc 1 đường tròn 0,25 ⇒ KI ∆ M ∽ KA ∆
C (g.g) ⇒ KI.KC = . KA KM (4)
+ Chứng minh được KB ∆ M ∽ KA ∆
D(g.g) ⇒ . KB KD = . KA KM (5) (4), (5) ⇒ KI.KC = KB.KD 0,25 4.4 + Chứng minh  =  HMD DHC (cùng =  ABD ) mà  +  0 DHC DHM = 90 0,25 ⇒  +  0 HMD DHM = 90 ⇒ 
HDM = 90° ⇒ HD ⊥ MD (6)
+ Chứng minh được EB // AM, mà  AMB = 90° ⇒  MBN = 90°
⇒ MN là đường kính của (O) ⇒ 
MDN = 90° ⇒ ND ⊥ MD (7)
(6), (7) ⇒ ND trùng HD ⇒ N, H, D thẳng hàng 0,25 5 Áp dụng BĐT Cô-si ta có
a + b + c b + c b + = +1 ≥ c 2 ⇔ a 2a ≥
dấu "=" xẩy ra khi b + c = a a a a
b + c a + b + c Tương tự b b ≥ 2 ; c 2c ≥
dấu "=" khi c + a = b; a + b = c
c + a a + b + c
a + b a + b + c 0,25
Cộng từng vế ta được:
a + b + c ≥ 2 b + c c + a a + b
Dấu "=" khi a = b = c = 0 (vô lý vì a, b, c dương) Vậy
a + b + c > 2 b + c c + a a + b 0,25
Học sinh làm cách khác, nếu đúng cho điểm tối đa
Document Outline

• Đề khảo sát Toán 9_Tháng 3
• Đáp án_Toán 9_Tháng 3