


Preview text:
UBND QUẬN CẦU GIẤY
ĐỀ THI KHẢO SÁT THÁNG 3
TRƯỜNG THCS NGHĨA TÂN
NĂM HỌC 2023 – 2024 MÔN: TOÁN 9
Thời gian làm bài: 90 phút
Câu I (2,0 điểm). Cho hai biểu thức x + 7 √x 2 x + 3 A = và B = + − với x ≥ 0 ; x ≠ 9. √x − 3
√x + 1 3 − √x �√x + 1��√x − 3�
1) Tính giá trị của biểu thức A khi x = 4. −5 2) Chứng minh B = . √x − 3
3) Đặt P = A + B. Tìm số nguyên x lớn nhất thỏa mãn |P| > P.
Câu II (2,0 điểm). Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
1) Một ca nô xuôi dòng trên một khúc sông từ bến A đến bến B dài 90 km, sau đó lại đi
ngược dòng đến địa điểm C cách bến B 60 km. Thời gian ca nô ngược dòng ít hơn thời
gian ca nô xuôi dòng là 15 phút. Tính vận tốc của ca nô khi dòng nước yên lặng (biết vận
tốc của dòng nước là 5 km/h, vận tốc của ca nô khi dòng nước yên lặng nhỏ hơn 50 km/h)
2) Một hộp sữa dạng hình trụ có đường kính đáy là 8 cm và chiều cao là 12 cm. Tính thể
tích của hộp sữa đó (lấy π ≈ 3,14).
Câu III (2,5 điểm)
1) Giải hệ phương trình 2 3 ⎧ = 7 ⎪x + 2 + �y − 3 ⎨ 3 4 ⎪ = 2 ⎩2 + x − �y − 3
2) Cho phương trình x2 − (2m + 1)x + m − 2 = 0 (1).
a) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt.
b) Gọi x1, x2 là hai nghiệm của phương trình (1). Tìm tất cả giá trị của m để x1 x2 5 x + = 2 x1 m − 2
Câu IV (3,0 điểm)
Cho tam giác ABC có ba góc nhọn (ABBE, CF cắt nhau ở H.
1) Chứng minh tứ giác BFEC là tứ giác nội tiếp.
2) Tia EF cắt tia CB tại M. Chứng minh MF. ME = MB. MC.
3) Tia AH cắt BC tại D. Đường thẳng qua B và song song với AC, cắt tia AD tại P, cắt đoạn
thẳng AM tại Q. Chứng minh FC là tia phân giác của góc EFD và BP=BQ.
Câu V (0,5 điểm). Cho a, b là các số thực thỏa mãn (a + b − 1)2 = ab. Tìm giá trị nhỏ nhất của biểu thức: 9 P = a + b + a + b
---------------- HẾT ----------------
Cán bộ coi thi không giải thích gì thêm. UBND QUẬN CẦU GIẤY
ĐÁP ÁN ĐỀ THI KHẢO SÁT THÁNG 3
TRƯỜNG THCS NGHĨA TÂN
NĂM HỌC 2023 – 2024 MÔN: TOÁN 9 Câu Ý Đáp án Điểm
Thay x = 4 vào biểu thức A, ta được 4+7 1) A = 0,25 √4 − 3 Tính được A = −11. 0,25 √x 2 x + 3 B = − − 0,25
√x + 1 √x − 3 �√x + 1��√x − 3�
√x�√x − 3� − 2�√x + 1� − (x + 3) B = 0,25 2) �√x + 1��√x − 3� Câu I −5√x − 5 0,25 (2,0 điểm)
B = �√x+1��√x −3� −5 B = 0,25 √x − 3 x+7 −5 x+2 P = A + B = + =
√x − 3 √x − 3 √x − 3 0,25 3) |P| > P ⟺ P < 0 x + 2 P < 0 ⟺ < 0 ⟺ x < 9 √x − 3 Mà x nguyên lớn nhất, 0,25 x ≥ 0; x ≠ 9 Suy ra x = 8
Gọi vận tốc của ca nô khi dòng nước yên lặng là x (km/h) (5 < x < 50) 0,25
Vận tốc của ca nô khi xuôi dòng là: x + 5 (km/h) 0,25
Vận tốc của ca nô khi ngược dòng là: x − 5 (km/h) 90
Thời gian ca nô đi xuôi dòng là: x + 5 (h) 60 0,25
Thời gian ca nô đi ngược dòng là: x − 5 (h) Câu II
Vì thời gian ca nô ngược dòng ít hơn thời gian ca nô xuôi dòng là 15 phút = 1 h (2,0 điểm) 4 nên ta có phương trình 1) 0,25 60 1 90 x − 5 + 4 = x + 5 240 + x − 5 90 ⟺ 4x − 20 = x + 5
⟺ (x + 5)(x + 235) = 90(4x − 20)
⟺ x2 + 240x + 1175 = 360x − 1800 0,25 ⟺ x2 − 120x + 2975 = 0
⟺ x = 85 (KTM) hoặc x = 35(TM)
Vậy vận tốc của ca nô khi dòng nước yên lặng là: 35 (km/h) 0,25
Bán kính đáy của hộp sữa dạng hình trụ là 8: 2 = 4 (cm) 0,25 2
Thể tích của hộp sữa dạng hình trụ là:
V = πR2h = π. 42. 12 ≈ 602,88 �cm3� 0,25 x ≠ −2 ĐK: � y ≥ 0 0,25 y ≠ 9 ⎧ 1 ⎪ a = x + 2 Đặt
. Hệ phương trình trở thành ⎨ 1 ⎪b = 0,25 ⎩ �y − 3 1) �2a + 3b = 7 3a − 4b = 2 ⟺ �a = 2 b = 1 −3 ⟹ �x = 2 (TM) 0,25 y = 16 (TM) −3
Vậy hệ phương trình có nghiệm �x = 2 0,25 Câu III y = 16 (2,5 điểm)
Ta có a = 1 ≠ 0 ⟹ (1) là phương trình bậc hai. 0,25 2a) Δ = 4m2 + 9 Δ = 4m2 + 9 ≥ 9 > 0 0,25
Suy ra phương trình (1) luôn có hai nghiệm phân biệt 0,25 Theo hệ thức Vi-ét �x1 + x2 = 2m + 1 x1x2 = m − 2 0,25 x x 1 x 5 1 ≠ 0 + 2 = x2 ≠ 0 ⟺ m ≠ 2 2b) x2
x1 m − 2 ĐKBS: �m − 2 ≠ 0 x2 + x2 5 (2m + 1)2 − 2(m − 2) 5 ⟺ 1 2 x = 1x2 m − 2 ⟹ m − 2
= m − 2 ⟺ 4m2 + 2m = 0 0,25 1
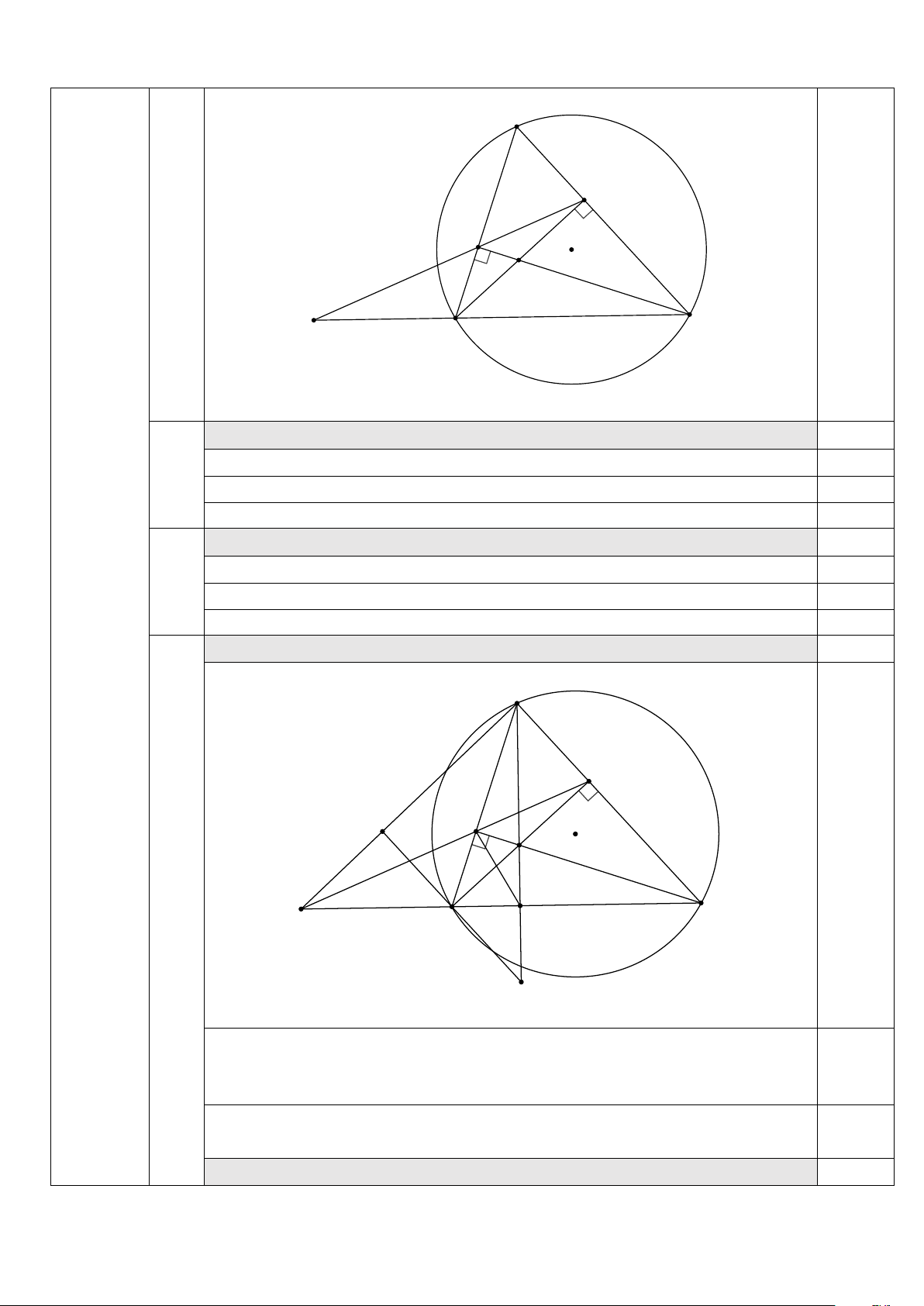
Tìm được m ∈ �0; − 2� 0,25 A E F O 0,25 H M B C
Vẽ hình đúng đến ý 1) được 0,25 điểm
Chứng minh tứ giác BFEC là tứ giác nội tiếp. 1) Chứng minh được BEC � = 900 0,25 Chứng minh được BFC � = 900 0,25
Chứng minh được tứ giác BFEC là tứ giác nội tiếp 0,25
Chứng minh 𝐌𝐌𝐌𝐌. 𝐌𝐌𝐌𝐌 = 𝐌𝐌𝐌𝐌. 𝐌𝐌𝐌𝐌.
2) Từ tứ giác BFEC là tứ giác nội tiếp, suy ra FEB � = FCB � 0,25
Từ đó suy ra ΔMBE đồng dạng ΔMFC 0,5 Câu IV
Từ đó suy ra MF. ME = MB. MC 0,25 (3,0 điểm)
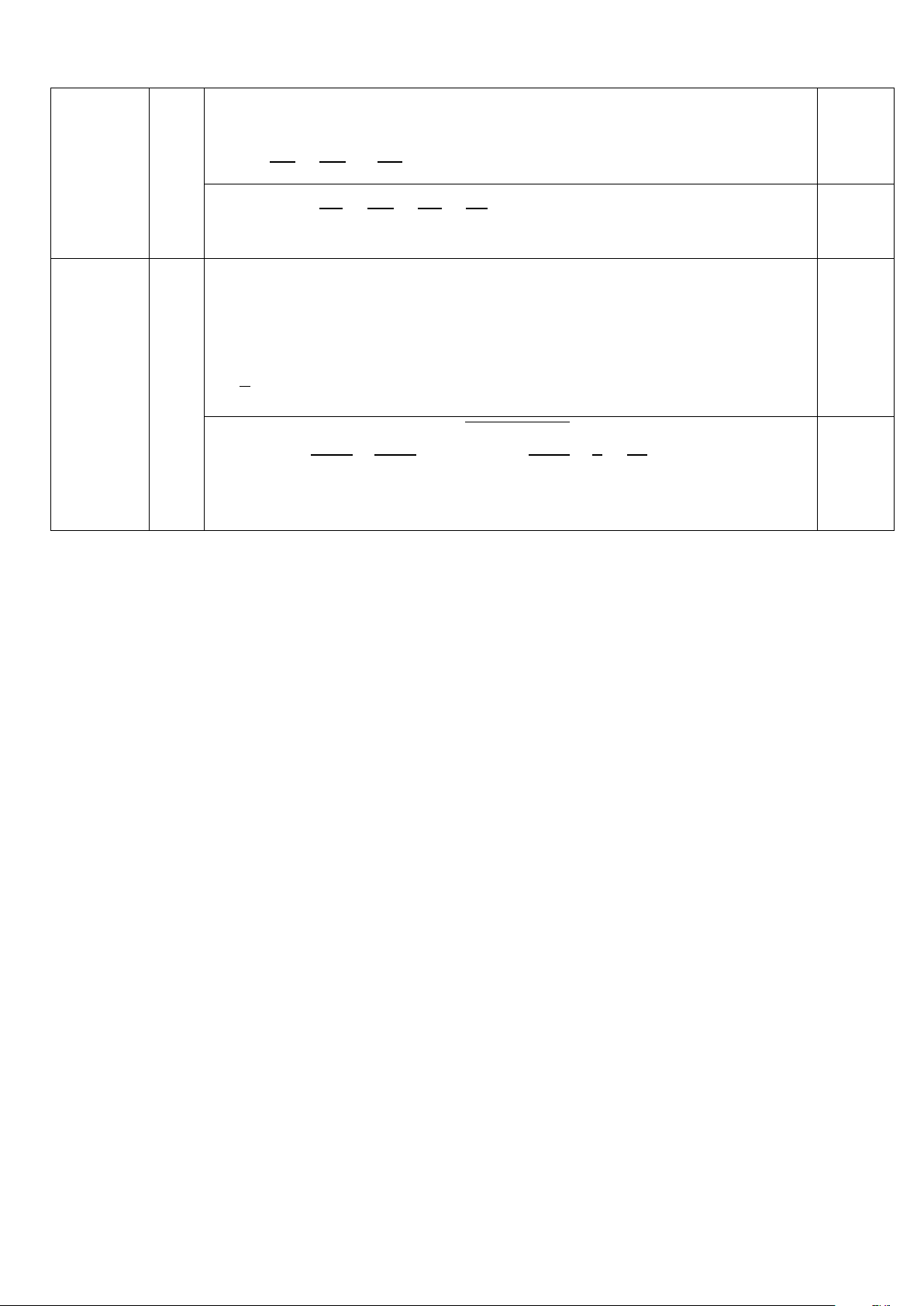
Chứng minh FC là tia phân giác của góc EFD. A E Q F O H 3) B D M C P
Chứng minh được H là trực tâm ΔABC
Từ đó suy ra BFHD là tứ giác nội tiếp 0,25 Suy ra HFD � = HBD �
Từ tứ giác nội tiếp BFEC, suy ra EFC � = EBC � 0,25 Suy ra EFC � = CFD
� ⟹ đpcm Chứng minh BP=BQ.
Chứng minh được FB là phân giác của góc trong tam giác FMD
Mà FC là phân giác của góc ngoài tam giác FMD 0,25 CD BD FD Suy ra CM = BM�= FM� AC CM CD AC Từ đó suy ra QB = BM = BD = BP 0,25 Suy ra BP = BQ
Ta có 4(a + b − 1)2 = 4ab ≤ (a + b)2
⟺ (2a + 2b − 2 − a − b)(2a + 2b − 2 + a + b) ≤ 0
⟺ (a + b − 2)(3a + 3b − 2) ≤ 0 0,25 Câu V 2 ⟺ (0,5 điểm) 3 ≤ a + b ≤ 2 4 5 4 5 13 P = a + b +
a + b + a + b ≥ 2�(a + b). a + b + 2 = 2 0,25
Dấu bằng xảy ra khi a = b = 1.




